Dual-Order Inventory Planning: A Novel Approach to Managing Seasonal Fluctuations in Fashion Retail

Abstract

We develop and employ a novel dual-order inventory planning model tailored to the inventory planning policy of a fashion retailer in the city of Thessaloniki, Greece. In our approach, the first order is placed at the beginning of the season, while the second order is placed if the stock level of a stock-keeping unit (SKU) falls below a threshold inventory level during the optimal review period. With this dual-order model, the retailer can capture random changes in consumer preferences during the season. The insights derived from implementing the developed methodology in a real-world case of a fashion retailer reveal that the dual-order model significantly mitigates the risks of overstock and stockouts by allowing dynamic adjustments to stock levels in response to actual sales trends and market changes. Moreover, a late ordering policy in week 19 of the season will result, on average, in a 7.9% reduction in total inventory planning costs compared to the costs associated with the different review periods examined.

1. Introduction

Product demand in the fashion retail industry is characterized by pronounced seasonality, weekly cyclicality, and rapidly evolving consumer preferences, which render demand forecasting particularly challenging [1]. The fast fashion phenomenon further exacerbates these challenges by increasing demand volatility and uncertainty [2]. Rapid product turnover in fast fashion also creates significant uncertainty in demand estimation [3,4]. Forecasting demand profiles for new products remains a considerable challenge due to inherent uncertainties in consumer behavior [5]. Sustainable supply chain considerations add another layer of complexity, as corporate reports highlight the difficulties of balancing rapid replenishment with ethical and environmental concerns [6]. Moreover, the interplay between consumer ethics, sustainability, and purchasing behavior further complicates demand and prediction in retail clothing [7]. Advanced customer analytics reveal that modern consumers expect access to an extensive range of products coupled with exceptionally fast delivery times [8]. This expectation compels fashion retailers to make timely and efficient inventory replenishment decisions based on accurate demand forecasts [9].

Despite these expectations, though, traditional inventory planning models mainly optimize single-period replenishment orders at the beginning of the season [10]. These models could, however, be inadequate in capturing dynamically changing demand behaviors while highlighting the need for the development of more adaptive inventory planning models [11].

In this context, this paper suggests an adaptive dual-order inventory planning model tailored to the inventory planning policy of a fashion retailer in Thessaloniki, which optimizes the total seasonal order quantity for an SKU category to be scheduled between two different replenishment orders. The first order arrives at the start of the season. This initial order quantity is estimated as a predefined percentage of the optimized order quantity. The remaining percentage of the optimal order quantity is the optimized threshold inventory level, which is used to determine the need for secondary replenishment. More precisely, if the net stock of the SKU at an optimally defined review period is lower than this threshold inventory level, an emergency order is placed to increase the inventory position up to the threshold quantity. This second order arrives after a predefined lead time. We assume that the review period plus the lead time must be less than the season length. The applicability of the developed methodology is evaluated in the case of a fashion retailer located in Central Macedonia focusing on long-sleeved sports shirts, which are known to have high sales and profit margins.

The rest of the paper is organized as follows. Section 2 provides a critical synthesis of the recent academic articles employing adaptive inventory planning policies. Section 3 provides the theoretical description of the developed inventory planning policy, while Section 4 contains the mathematical model development. Section 5 examines the applicability of the developed methodology in the real case of a fashion retailer established in Thessaloniki, while Section 6 contains the numerical results of the implemented inventory planning model. Finally, the last Section sums up the findings of the research and derives insights.

2. Literature Review

The analysis of the literature on inventory management strategies reveals a rich base of research that focuses on developing solutions for handling dynamic and adaptive order replenishments.

Regarding single-period inventory planning models, Serel [12] deals with a single-period pricing and inventory planning problem in which demand that exceeds net stocks can be met through an emergency supply. The decision variables optimized involve the optimal price and production quantity under a stochastic emergency supply capacity. Patra and Jha [13] developed a two-order news vendor model for disaster preparedness where they considered two decisions: pre-disaster stocking and post-disaster replenishment. Arıkan and Jammernegg [14] incorporate dual-sourcing options and carbon footprint constraints in the optimization of order quantities within environmental limits. The decision variables optimized involve the initial order quantity from the first supply option, along with the emergency order quantity from the second supply option triggered by the actual demand and the available carbon budget.

Bylka [15] develops a capacitated lot sizing model that allows for emergency orders to cope with increases in demand and aims to determine the optimal regular and emergency order quantities where the decision variables are a function of demand distribution and costs such as shortage and holding costs. Zhao et al. [16] propose a model to determine the optimal initial order quantity and the additional emergency order quantity under a dynamic pricing strategy. Similarly, Ni. [17] analyse pricing decisions in a news vendor problem with identifiable information and markdowns for initial and in-season pricing and order quantities. The model optimizes in-season prices and order quantities based on updated demand information within the season. Zhang et al. [18] analyze the impact of emergency orders on a price-dependent news vendor problem and the decision to accommodate more than the optimal order quantity through emergency ordering or to pay for lost sales. Huang et al. [19] combine the news vendor model with prospect theory for optimizing the order quantities before the season begins and the emergency order quantity in the case of a stockout due to unpredictable events such as the pandemic. Zheng et al. [20] developed a single-period dynamic programming model for optimizing an initial order quantity based on initial demand forecasts and an emergency order considering updated forecasts and higher inventory costs. Finally, Pando et al. [21] provide an extension of the newsboy model by allowing an emergency order to satisfy a fraction of the shortages. The decision variables optimized involve the initial order quantity before the season starts and the fraction of stockouts compensated by the emergency order.

Regarding multi-period inventory planning models, Barron [22] develops a continuous-review inventory planning model where normal and emergency supplies are considered to manage disruptions. The decision variables are the regular order levels, reorder points, and the emergency order quantity. Similarly, Vlachos and Tagaras [23] developed and employed a periodic review inventory planning model (R, S) that optimizes the up to S order quantity and the reorder point in two ordering policies. The first policy is the late-ordering policy, where an emergency order is set at an emergency lead time $L_e$ with time units before a predefined review period R arrives at the review period R; the early-ordering policy is where the emergency order is placed at $L_e-1$ time units before the review period R and arrives at R − 1 time units. Finally, Chiang [24] dynamically optimizes a periodic review inventory planning model with two supply chains, basic and enhanced, with the objective of determining the replenishment strategy that would meet the inventory targets set by the organization depending on the lead times and order costs. The decision variables optimized involve the regular and emergency order quantities along with the reorder level below which an emergency order is set.

Table 1. Critical synthesis of the examined literature.

Authors	Ref.	Models Employed	Decision Variables Optimized
Serel (2017)	[12]	Single period	Optimal price and production quantity under stochastic emergency supply
Patra and Jha (2021)	[13]	Single period	Pre-disaster and post-disaster orders
Barron (2022)	[22]	Multi -period continuous review inventory planning model	Regular order levels, reorder points, emergency order levels
Arıkan and Jammernegg (2014)	[14]	Single period with environmental constraints	Initial order quantity, emergency order quantity under carbon footprint constraints
Chiang (2003)	[24]	Multi-period periodic review inventory planning model with dual supply channels	Regular and emergency order quantities and reorder levels
Bylka (2005)	[15]	Single-period capacitated lot sizing	Optimal regular and emergency order quantities
Zhao et al. (2021)	[16]	Single-period model with dynamic pricing	Optimal initial and additional emergency order quantities
Ni et al. (2023)	[17]	Single period with discount promotions	Optimized initial and in-season pricing and order quantities
Zhang et al. (2017)	[18]	Single period price-dependent	Optimal order and emergency order quantity
Pando et. al. (2013)	[21]	Single period	Initial Order Quantity and Fraction of demand covered by the emergency orders
Vlachos and Tagaras (2001)	[23]	Multi-period periodic review inventory planning model with two supply channels	Optimal up to S base stock level and emergency reorder point
Huang et al. (2022)	[19]	Single period	Order quantities before and during the season
Zheng et al. (2014)	[20]	Multi-period periodic review inventory planning	Initial order quantity, emergency order under supply constraints

provides a critical synthesis of the examined literature review.

To our knowledge, the critical analysis of the above Table reveals a gap in existing research efforts:

• Optimizing the review periods for assessing the inventory levels of an SKU.
• Optimizing a threshold for reordering and evaluating stochastic order quantities in a single-period inventory planning model.
• Developing inventory planning models tailored to real-world companies in the fashion industry that face rapid changes in trends and consumer preferences.
• This paper addresses the identified research gaps by:
• Optimizing the review period for evaluating the net stock levels for emergency orders. This allows for a dynamic adjustment of inventory replenishment based on updated inventory needs.
• Optimizing the threshold order quantity as a function of our model’s optimal single-period seasonal order quantity.
• Structuring the proposed model based on a real-world fashion retailer’s inventory planning problem developed under a research project.

3. System Description

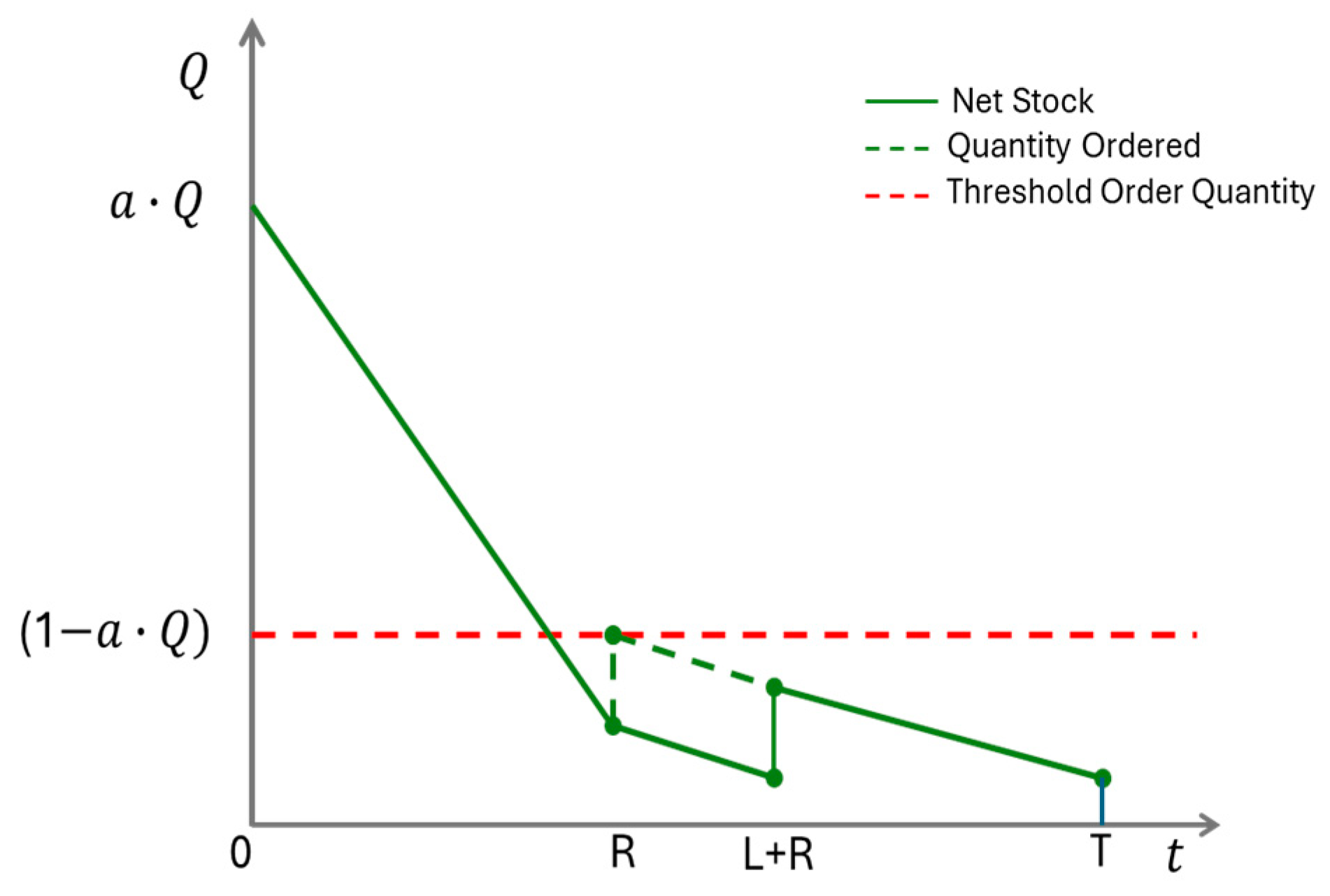
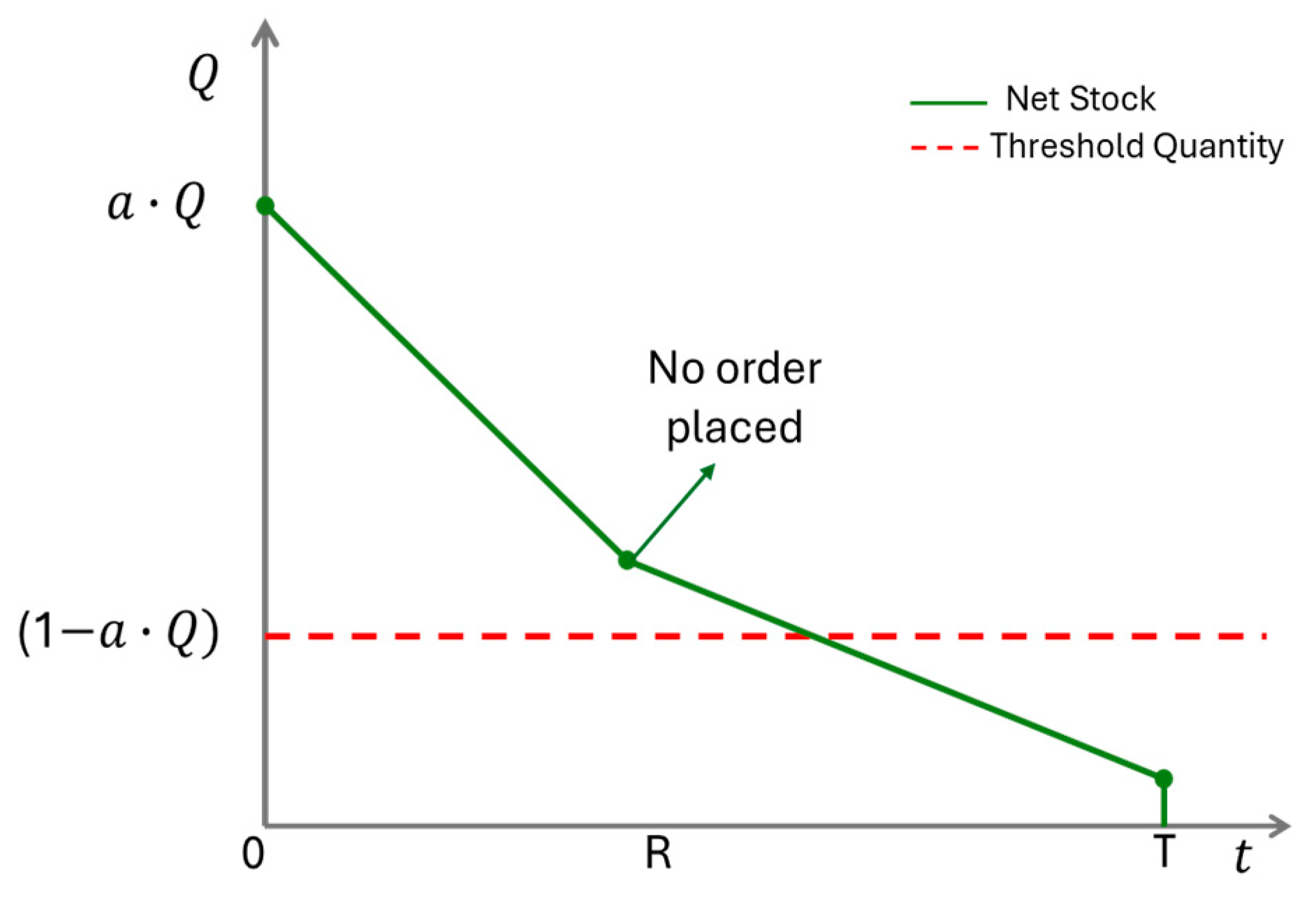
We examine a fashion retailer’s dual ordering inventory planning policy. The optimal season’s order quantity is split into two distinct orders. The first order is set before the beginning of the season and arrives at the season’s starting period. This initial order corresponds to a specific percentage of the optimally determined order quantity of the season. During the season, the retailer reviews the central warehouse’s stock, and if the stock is less than the remaining optimal order quantity, then the second order is set, which increases the inventory position of the examined SKU up to this quantity. The second order set then arrives after a specific lead time.

We assume the following: (i) The review period plus the lead time is less than the examined season’s duration length. This assumption provides an additional realistic attribute to our model as it does not allow orders to arrive after the end of the season, and in the case of the latest optimized emergency ordering scenario, the model provides the company with a time buffer to sell its emergency order; (ii) An initial order placed from the retailer to the manufacturer is received at the beginning of the season. This assumption aligns with standard practices in inventory planning models, facilitating a clear starting point for inventory management within the season; (iii) The demand that the retailer faces per SKU for a specific product category is a stochastic, normally distributed random variable. This assumption is based on the central limit theorem, which justifies the normal approximation of demand, given the large sample size of the examined product category’s independent weekly demands as provided by the fashion retailer’s database

In the case of a product stockout at the end of the season, sales are lost, and thus, the retailer loses the profit per unit of lost sales. In the case of remaining net stock at the end of the season, the retailer sells the remaining product at the next season and at a lower price. Thus, the cost that the retailer incurs in the case of positive net stock at the end of the season is estimated as the difference between the unit selling prices in and out of the season.

The model parameters considered for optimizing the order quantity per SKU involve the (i) sales price per SKU to the consumers, (ii) purchase price per SKU from the manufacturer, (iii) mean and standard deviation of the retailer’s demand per SKU of a product category, (iv) the selling price of the SKU in the next season, and (v) the transportation cost per truckload from the manufacturer to the retailer. Figure 1 and Figure 2 depict the inventory behavior under the two distinct scenarios.

4. Model Development

Let $Q$ denote the optimal order quantity per SKU category in the single-period inventory planning model over a season of length T. The initial order quantity received at the beginning of the season is given by $\alpha ·Q$, where α represents a predefined percentage set by the retailer. At the review period $R$, the retailer evaluates the net inventory level. If the inventory of a given SKU falls below $\left(1-\alpha \right)·Q$, a replenishment order is placed to restore stock up to $\left(1-\alpha \right)·Q$. Otherwise, no order will be placed. The replenishment order arrives after a lead time by $L$, ensuring that the constraint $R+L<T$ is met.

Let $x,y$ represent the demand during the review period plus the lead time ($R+L)$ and the remaining period $\left(T-R-L\right)$. To compute the expected-on hand ${E(OH}_T)$ and backorder ${E(BO}_T)$ at the end of cycle T, along with the order quantity ${(OQ}_R)$ at the time epoch $R$, we notice the following:

• If $x>\alpha ·Q$, then the quantity ordered during the review period $R$ is equal to ${OQ}_R=\left(1-\alpha \right)·Q$ as no back orders are allowed, and thus, any unmet demand is lost;
• If $y>\left(1-\alpha \right)·Q,$ then, the stockouts at the end of season T are ${BO}_T=y-\left(1-\alpha \right)·Q+x-\alpha ·Q$ and ${OH}_T=0$;

  ○

  else, ${BO}_T=0$ and ${OH}_T=\left(1-\alpha \right)·Q-y$

else:

• If $\alpha ·Q-x>\left(1-\alpha \right)·Q\iff x<Q·\left(2·\alpha -1\right),$ no order is set: ${OQ}_R=0$;
• If $y>\alpha ·Q-x,{BO}_T=y+x-\alpha ·Q$, and ${OH}_T=0$;

  ○

  else, ${BO}_T=0$ and ${OH}_T=\alpha ·Q-(x+y)$;

• If $\alpha ·Q-x<\left(1-\alpha \right)·Q\iff x>Q·\left(2·\alpha -1\right)$, then ${OQ}_R=\mathrm{x}-Q·\left(2·\alpha -1\right)$;
• If $y>Q·\left(1-\alpha \right),{BO}_T=y-Q·\left(1-\alpha \right)$, and ${OH}_T=0$;

  ○

  else, ${BO}_T=0$ and ${OH}_T=Q·\left(1-\alpha \right)-y$.

Consequently, the expected-on hand (${OH}_T$) and backorder (${BO}_T$) at the end of cycle T and order quantity at the review period R (${OQ}_R$) can be determined by the following Equations (1)–(3) as follows:

$$\begin{array}{c}{E(OH}_T)={\int }_{\alpha Q}^{\mathrm{\infty }}{\int }_0^{\left(1-\alpha \right)·Q}\left[\left(1-\alpha \right)·Q-y\right]·{\phi }_{{\rm Y}}\left(y\right)\partial y{\phi }_X\left(x\right)\partial x+{\int }_0^{\alpha ·Q}{\int }_0^{\alpha ·Q-x}\left[\alpha ·Q-\left(x+y\right)\right]·\\ {\phi }_{{\rm Y}}\left(y\right)\partial y{\phi }_X\left(x\right)\partial x+{\int }_{Q·\left(2·\alpha -1\right)}^{\alpha ·Q}{\int }_0^{Q·\left(1-\alpha \right)}\left[\left(1-\alpha \right)·Q-y\right]·{\phi }_{{\rm Y}}\left(y\right)\partial y{\phi }_X\left(x\right)\partial x,\end{array}$$

(1)

$$\begin{array}{cc}\hfill {E(BO}_T)={\int }_{\alpha ·Q}^{\mathrm{\infty }}{\int }_{\left(1-\alpha \right)·Q}^{\mathrm{\infty }}& \left[y-\left(1-\alpha \right)·Q+x-\alpha ·Q\right]·{\phi }_{{\rm Y}}\left(y\right)\partial y{\phi }_X\left(x\right)\partial x+{\int }_0^{\alpha ·Q}{\int }_{\alpha ·Q-x}^{\mathrm{\infty }}\left[y+x-\alpha ·Q\right]·\hfill \\ & {\phi }_{{\rm Y}}\left(y\right)\partial y{\phi }_X\left(x\right)\partial x+{\int }_{Q·\left(2·\alpha -1\right)}^{\alpha ·Q}{\int }_{Q·\left(1-\alpha \right)}^{\mathrm{\infty }}\left[y-\left(1-\alpha \right)·Q\right]·\hfill \\ & {\phi }_{{\rm Y}}\left(y\right)\partial y{\phi }_X\left(x\right)\partial x\hfill \end{array}$$

(2)

$${E(OQ}_R)={\int }_{\alpha ·Q}^{\mathrm{\infty }}\left(1-\alpha \right)·Q{·\phi }_X\left(x\right)\partial x+{\int }_{Q\left(2·\alpha -1\right)}^{\alpha ·Q}(\mathrm{x}-Q·\left(2·\alpha -1\right))·{\phi }_X\left(x\right)\partial x,$$

(3)

where ${\phi }_X\left(x\right)$ and ${\phi }_{{\rm Y}}\left(y\right)$, represent the probability density functions of the stochastic random variables x and y, respectively.

The cost of demand overestimation leads to an overage cost $c_o=p-p^{\prime }$, where $p^{\prime }$ corresponds to the lower unit selling price in the next season. On the other hand, the cost of demand underestimation leads to an underage cost $c_o=p-c$, which is the lost sales cost

Table 2. Nomenclature of decision variables.

Decision Variables	Description
$Q$	Optimal order quantity per season and product category
$R$	Optimal review period length

and

Table 3. Nomenclature of model parameters.

Parameters	Description
$T$	Season’s time length
$\mu$	Mean weekly demand of the examined product type (SKUs per time unit)
$\sigma$	Standard deviation of weekly demand of the examined SKU (SKUs per time unit)
α	% of the Q quantity ordered at the beginning of the cycle
$L$	Order lead time from the manufacturer (weeks)
$p$	Selling price of the examined SKU type during the season (€/unit)
$p^{\prime }$	Selling price of the examined SKU in the next season (€/unit)
$c$	Purchase price of the examined SKU type from the manufacturer (€/unit)
$c_o$	Demand overestimation cost = $p-p^{\prime }$
$c_u$	Demand underestimation cost = $p-c$
$x$	Random demand of the product category examined during R + L time units
$y$	Random demand of the SKU type examined during $T-R-L$ time units
$t_c$	Transportation costs per truckload from the manufacturer to the retailer
FTL	Capacity of the full truckload in transport units
${\phi }_X\left(x\right)$, ${\phi }_{{\rm Y}}\left(y\right)$	Probability density functions of the stochastic random variables x and y, respectively.

summarize the nomenclature of the developed model’s decision variables and parameters.

Consequently, and given Equations (1)–(3) of the retailer’s expected cost per season T, the optimal value of $Q$ for $\forall$ $R$, ranging from 1 to $T-L-1$ (to meet the constraint of $L+R<T$), is given through the minimization of Equation (4):

$$ETC\left(Q\right)=c_o·{E(OH}_T)+c_u·{E(BO}_T)+t_c·\left({\displaystyle \frac{\mathsf{\alpha }·Q}{FTL}}+{\displaystyle \frac{{E(OQ}_R)}{FTL}}\right),$$

(4)

To further prove the convexity of Equation (4), we need to evaluate the second-order derivatives of $ETC\left(Q\right)$. Considering, however, the complexity of Equations (1)–(3), this derivation is significantly cumbersome. Thus, to prove the convexity of Equation (4), we will initially focus on its unimodality. This unimodality is based on the behavior of the overestimation and transportation costs that constantly increase for higher $Q$ values, and on the behavior of the underestimation costs that constantly decrease for higher values of $Q$. These opposing cost behaviors reveal the existence of one single $Q$ value where the constantly decreasing underestimation costs meet the constantly increasing overestimations and transportation costs. To determine the optimal value of $Q$ for each $R$ from 1 to $T-L-1$ discrete time units, we will employ the ternary search method provided by Arora [25] and adjusted for continuous cost function minimization. An analysis of the employed ternary search algorithm is provided through the following pseudocode (Algorithm 1).

Algorithm 1 Ternary Search for Minimizing Cost

1: procedure TERNARYSEARCH (min_Q, max_Q, epsilon)

2:              while (max_Q − min_Q) > epsilon do

3:                          m1 ← min_Q + (max_Q − min_Q)/3

4:                          m2 ← max_Q − (max_Q − min_Q)/3

5:                        cost m1 ← ETC (m1)

6:                        cost m2 ← ETC (m2)

7:                          if cost m1 < cost m2 then

8:                                      max_Q ← m2

9:                        else

10:                          min_Q ← m1

11:                     end if

12:            end while

13:            return (min_Q + max_Q)/2

14: end procedure

5. Real-Life Inventory Planning Case Study

The developed inventory planning methodology models the real inventory system of a fashion retailer operating in the wider area of Central Macedonia, focusing on one of its highest-selling SKUs, namely the long-sleeved sports shirts. The retailer currently orders 80% of the product’s seasonal order quantity from its Bulgarian manufacturer, which arrives before the season at the retailer’s central warehouse. The length of the season is 24 weeks. A new order is placed during the season based on the net stock levels of the product at the central warehouse. Finally, weekly demand is assumed to be a normally distributed stochastic random variable with a mean of 1109 units and a standard deviation of 877 units per week. We have estimated the mean and standard deviation of weekly demand based on actual weekly demand data of the examined product category for 2024 as provided by the company’s database

Table 4. Model parameter values.

Parameters	Values
$T$ (weeks)	24
$\mu$ (units per week)	1109
$\sigma$ (units per week)	877
α (%)	80
$L$ (weeks)	3
$p$ (€/unit)	49
$p^{\prime }$ (€/unit)	25
$c$ (€/unit)	13
$c_o=p-p^{\prime }$ (€/unit)	24
$c_u=p-c$ (€/unit)	36
$t_c$ (€/truck delivery)	250
FTL (units)	3500

summarizes the required model parameter values for optimizing the examined $R$ and $Q$ inventory planning decisions.

6. Results

Considering lead time L = 3 weeks, a season of T = 24 weeks, and the constraint that R + L − 1 < T, we enumerate values of R from 1 to 20 weeks with a step of 1 week and estimate the optimal $Q$ using the employed Ternary Search Algorithm. We consider a starting min_Q = 0 units and a starting max_Q = 100,000 units. Moreover, the epsilon = 0.1%, which is considered a reasonable accepted error. The optimal (Q,R) combination will correspond to the minimum total costs.

Table 5. Optimal Q values and expected total costs for each R.

R	Initial Order Quantity (α*Q)	Overage Costs	Underage Costs	Transportation Costs	Emergency Order Quantity	Total Cost
1	27,712.8	54,779.9	43,940.9	1979.5	0.0	100,700.2
2	27,700.9	55,051.0	44,129.8	1978.6	0.0	101,159.5
3	27,695.4	55,185.8	44,211.4	1978.2	0.0	101,375.4
4	27,693.1	55,253.8	44,246.4	1978.1	0.0	101,478.3
5	27,692.1	55,289.1	44,260.4	1978.0	0.0	101,527.6
6	27,693.3	55,328.8	44,250.7	1978.1	0.0	101,557.7
7	27,705.6	55,517.8	44,138.8	1979.0	0.2	101,635.6
8	27,757.6	56,274.4	43,731.0	1982.8	1.3	101,988.2
9	27,884.5	58,135.1	43,931.2	1992.2	6.0	104,058.4
10	28,086.3	61,169.4	44,021.1	2007.6	20.3	107,198.1
11	28,315.5	64,747.1	44,055.0	2026.4	54.3	110,828.5
12	28,500.4	67,832.8	44,455.4	2044.7	125.6	114,333.0
13	28,564.3	69,397.8	44,591.4	2059.2	265.1	116,048.4
14	28,432.2	68,915.1	44,732.3	2068.5	526.8	115,715.8
15	28,018.3	66,893.0	45,373.9	2072.5	997.3	114,339.4
16	27,139.6	65,026.3	45,579.6	2068.4	1818.4	112,674.4
17	23,652.0	58,726.4	46,081.0	1957.7	3755.8	106,765.1
18	19,990.0	73,669.8	34,074.2	1753.6	4560.6	109,497.6
19	16,291.2	78,456.4	20,044.0	1502.3	4741.2	100,002.7
20	11,172.4	85,885.1	14,482.6	1162.0	5096.1	101,529.8

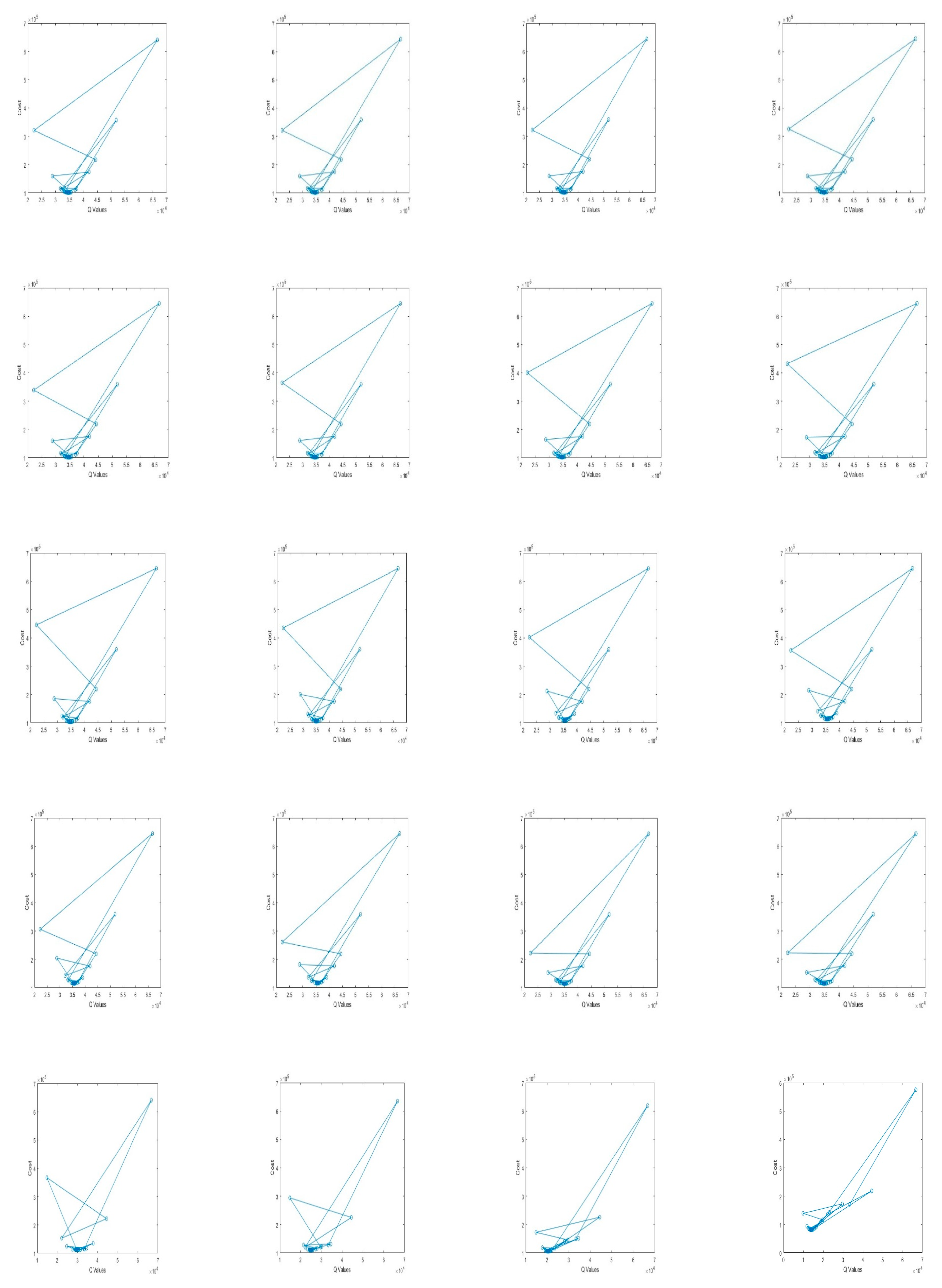
summarizes the optimal $Q$ values and expected seasonal costs for each enumerated R, while Figure A1 in the Appendix A shows the $Q$ progression of the Ternary Search Algorithm.

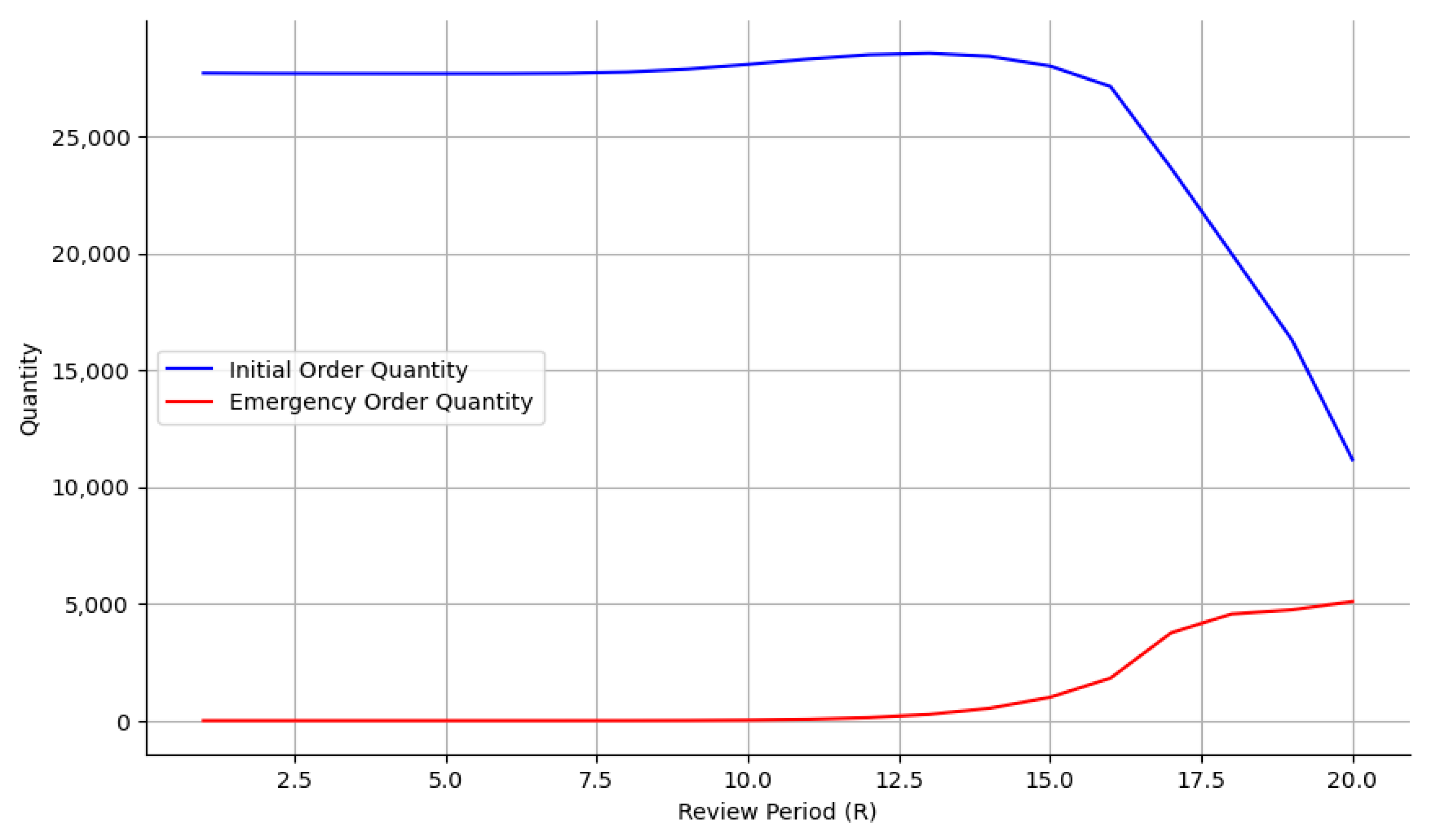
The results of Table 5 reveal that the initial order quantities exhibit static behavior for early review periods, peaking at R = 13 weeks. This could be attributed to the system’s proactiveness in increasing the net stocks to handle lost sales events. If the company placed an emergency order in week 18, however, the initial order quantity would significantly drop. By ordering late within the season, the company has the flexibility to set a lower initial order, then check the net stocks and adjust them more efficiently through an emergency order (see Figure 3).

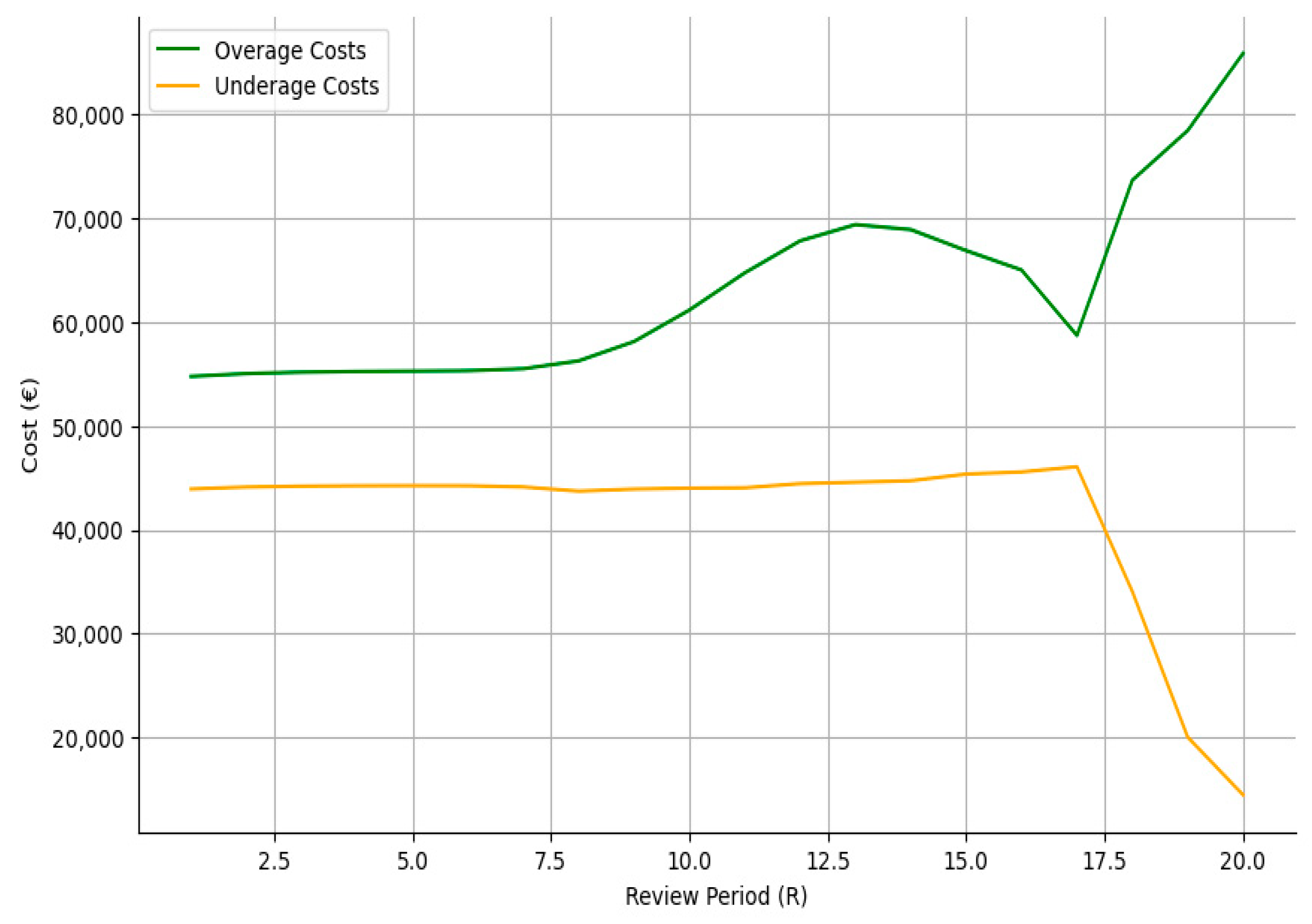
Regarding overage costs, we observe that these costs increase due to the high initial order quantities. However, as the review period increases, and even though the initial order size decreases, the higher emergency order quantities later in the season result in higher net stocks at the end of the season as these stocks could not be sold timely. This is also evident by the sharp reduction of the underage cost at the end of the cycle, which clearly indicates that the emergency order quantities are more than adequate to handle the demand realized until the end of the season (see Figure 4).

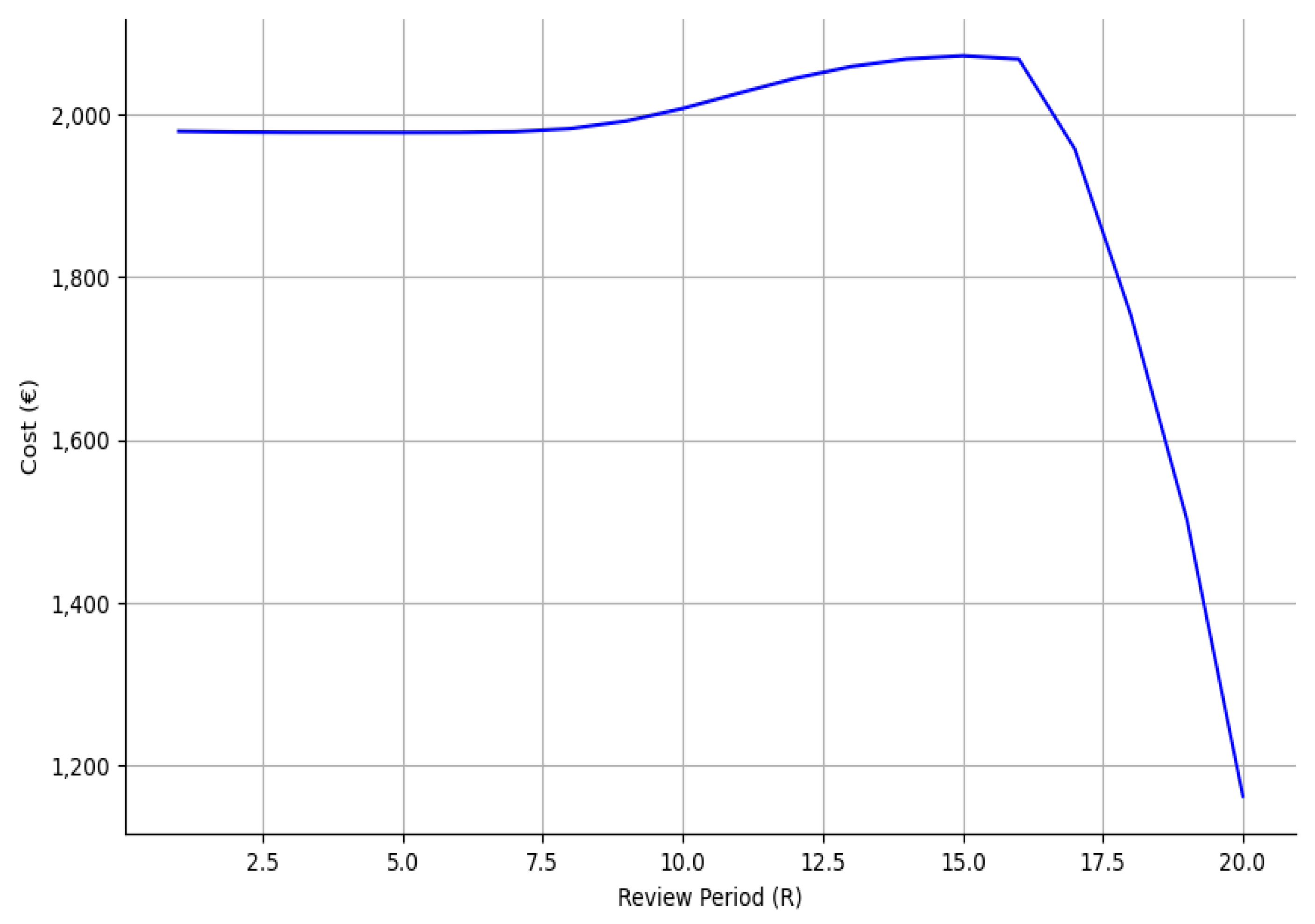
Transportation costs exhibit a stable high-cost behavior due to the high initial order quantities. However, as the company progresses through the late ordering policy, it manages to achieve more effective management of its inventory, which leads to lower initial order quantities and, thus, lowers transportation costs (see Figure 5).

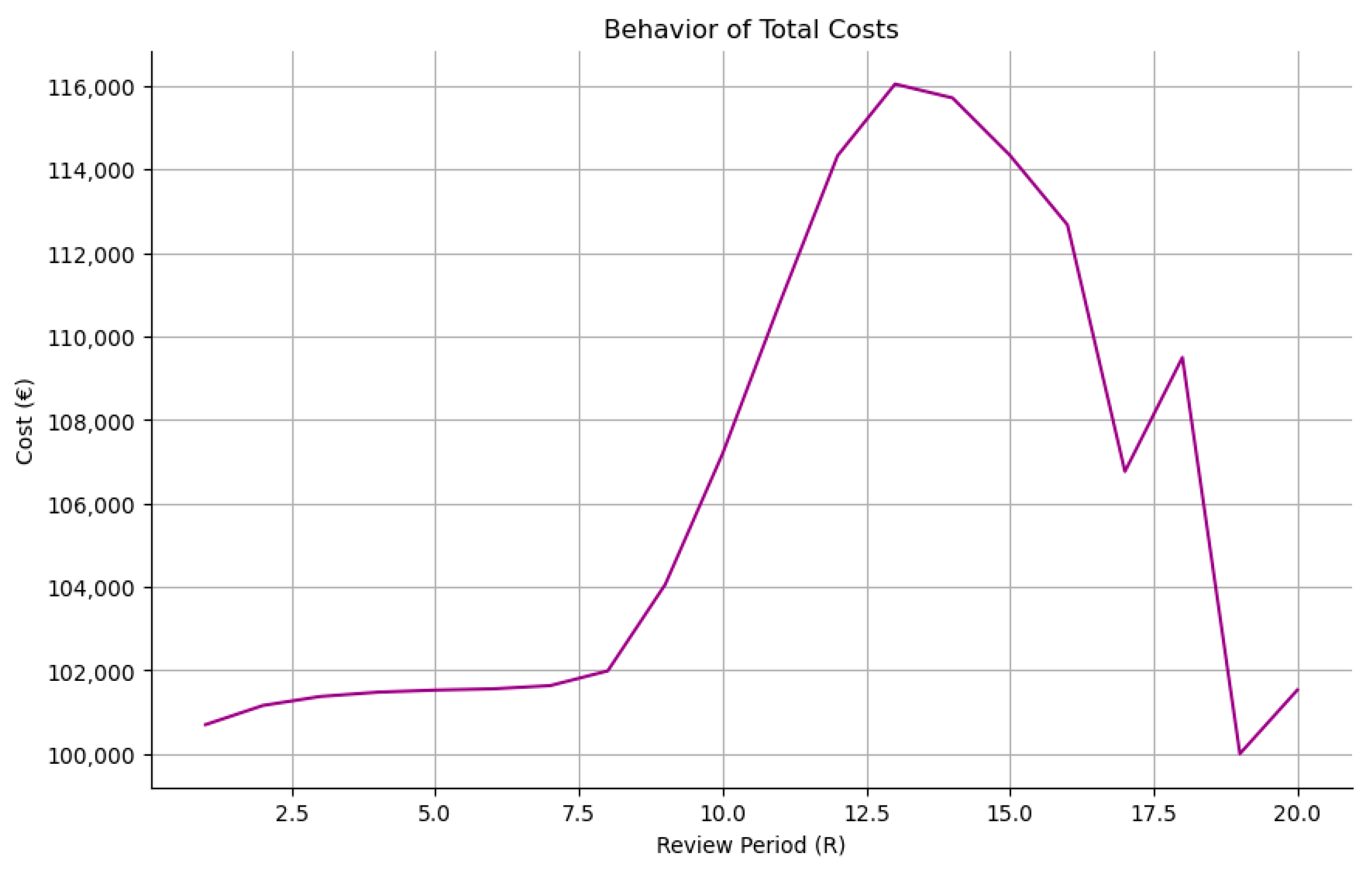
Finally, regarding total inventory planning costs, we observe that its behavior is mainly affected by the behavior of overage costs until week 18. However, the sharp decrease in underage costs after week 18 dominates, leading to a reduction in the total inventory planning costs (see Figure 6).

To conclude, we observe that the late ordering policy, which allows for adjustment of net stocks during the season, seems to effectively reduce inventory planning costs as these are found at a review period of 19 weeks, a lower initial order quantity of 19,990 and a higher emergency order quantity of 4741.2. This optimal strategy results, on average, in a 7.9% reduction in total inventory planning costs compared to the costs associated with the different review periods examined.

7. Summary and Conclusions

This paper develops and employs a novel dual-order inventory planning model tailored to the specific inventory management operations of a fashion retailer in the city of Thessaloniki. The main insights derived from its real-world implementation are summarized as follows:

• The emergency order capability of the model highlights the flexibility of late-season inventory adjustments, which allows the company to respond to actual demands and thus reduce over-ordering. For example, between weeks 17 and 18, the initial order quantity sharply decreases by 15.5% and continues to decrease as the review period progresses to week 20.
• The significant reductions of underage costs towards the end of the season, i.e., a 26.1% reduction between weeks 17 and 18 that continues to decrease as the review periods progress to week 20, highlights the efficiency of the emergency order to effectively meet actual demands.
• A lower initial order quantity and a higher emergency order quantity in week 19 led to an average total inventory planning cost reduction of 7.9% compared to the other review periods.

However, the developed methodology exerts several limitations that could have an impact on the model’s efficiency and generalizability. These involve the following:

• Data dependency as the model depends heavily on the timely provision of updated demand data to accurately adjust the inventory position through the emergency order quantity. Thus, delays or inaccuracies in the provision of stochastic demand parameters could lead to suboptimal adjustments of inventory levels.
• Adaptability to other retail markets which employ different demand patterns and economic characteristics. These changes could necessitate model modifications.
• The scalability of the model to serve multiple retailers in a broader geographical area could result in complexities that cannot be addressed by the current model structure.

To this end, future research perspectives should aim to address these limitations using recurrent neural networks that dynamically forecast weekly demand, thus offering more accurate adjustments to order quantities. Additionally, expanding the application of this model to other retail sectors that deal with seasonal demand behaviors could provide broader insights into its adaptability and effectiveness across diverse market conditions.