Abstract
The implementation of universal designated verifier signatures proofs (UDVSPs) enhances data privacy and security in various digital communication systems. However, practical applications of UDVSP face challenges such as high computational overhead, onerous certificate management, and complex public key initialization. These issues hinder UDVSP adoption in daily life. To address these limitations, existing solutions attempt to eliminate bilinear pairing operations, but their proposal still involves cumbersome certificate management and inherent interactive operations that can sometimes significantly degrade system efficiency. In this paper, we first utilize the identity-based (ID-based) SM2 digital signature scheme to construct an ID-based UDVSP system which sidesteps the cumbersome certificate management issue. To further remove the interactive requirement, we also employ the OR proof and Fiat–Shamir technologies to design the other ID-based UDVSP system. Our designs not only possess the same bilinear pairing-free advantage as Lin et al.’s proposal, but also achieve the certificate-free or non-interactive goals. Security proofs and performance analysis confirm the viability and efficiency of our systems.
MSC:
94A60
1. Introduction
In modern society, with the widespread application of digital signatures, protecting the privacy of signers has become a major concern for researchers. To address this issue, universal designated verifier signatures (UDVSs) were proposed by Steinfeld et al. in Asiacrypt 2003 [1]. UDVSs ensure that the designated verifier has the ability to verify digital signatures, while preventing the verifier from conveying the reliability of the signature to anyone else. This characteristic makes it suitable for scenarios where only a few specifically designated verifiers are required for signature verification. As an illustration, in the realm of e-government, government departments can utilize UDVSs to provide a proof of confidential information to relevant staff members as required for their work. However, these personnel are unable to convince third parties of the authenticity of this confidential information. This mechanism is critical to prevent malicious dissemination of confidential information. There are numerous such application scenarios, including electronic voting systems, electronic medical records, and electronic income certificates.
Universal designated verifier signature proof (UDVSP), as an enhanced variant of UDVS, eliminates the requirement for designated verifiers to generate their public/private key pairs using parameters that are predefined by signers. However, UDVSP systems still encounter several inherent limitations, including the need for complex public key certificate management, computationally intensive bilinear pairing operations, and the inherent constraints of interactive protocols. While Lin et al. [2] proposed a UDVSP scheme that eliminates the need for bilinear pairings, their solution still grapples with the persistent challenges of cumbersome certificate management and the limitations imposed by interactive protocols.
Driven by the problem of the UDVSP schemes mentioned above, we would like to obtain ID-based UDVSP systems to resolve these issues. In this paper, we construct ID-based UDVSP systems that are engineered to simultaneously resolve the four aforementioned issues. Firstly, using the ID-based SM2 digital signature scheme, we build the ID-based UDVSP system, which avoids the complex issue of certificate management. To further dispense with the need for interactivity, we make use of the OR proof and Fiat–Shamir methodologies to design an alternative ID-based UDVSP system. These schemes possess not only the same bilinear pairing-free advantage as the proposal by Lin et al. [2], but also attain the certificate-free or non-interactive objective. Moreover, we carry out an analysis of the security and performance aspects of the two schemes.
The subsequent content presents the layout of the remaining part of this paper: Some related work is introduced in Section 2. Some methodologies are introduced in Section 3. Section 4 provides our interactive ID-based UDVSP system along with its security analysis. In Section 5, our non-interactive ID-based UDVSP system and its corresponding security analysis are detailed. Section 6 is dedicated to conducting a performance analysis of the two schemes. Finally, Section 7 contains the conclusions.
2. Related Work
To protect the signer’s privacy and prevent signatures from being verified by unauthorized third parties, the undeniable signature scheme was proposed by Chaum and Antwerpen in 1990 [3]. In this scheme, the verifier must collaborate with the signer to verify the signature, which is equivalent to the signer having the power to decide who can verify the signature. However, the undeniable signature scheme is limited by the requirement of reciprocal communication, which poses a significant drawback.
In order to avoid interactive communication between signer and verifier, in 1996, Jakobsson et al. [4] introduced the designated verifier signature (DVS) schemes. In the DVS scheme, the signer generates the DVS by incorporating the public key of the designated verifier. This eliminates the need for the signer to assist in the verification process. The designated verifier is not only able to validate the DVS but can also generate an indistinguishable DVS using the same private key. This latter property, known as transcript simulation, ensures that the verifier cannot convince a third party by transferring the proof, thereby achieving the same objective as the undeniable signature scheme.
Subsequently, Steinfeld et al. [1] proposed UDVS in 2003, which is regarded as an extended variant of DVS. Unlike DVS, in the UDVS scheme, the signer and the signature holder can be different individuals. This means that anyone in possession of an ordinary signature (not limited to the original signer) can convert the signature into a designated one for a specific verifier.
Nevertheless, in Asiacrypt 2005, Baek et al. [5] indicated that in this UDVS scheme, the designated verifier is required to create a public/private key pair by using the parameters set by the signer. This is impractical in certain scenarios. In certificate-based (CA-based) public key systems, regenerating public/private key pairs entails cumbersome public key certificate management and results in significant computational overhead. Even incertificateless systems where the overhead of regenerating key pairs is relatively smaller, it still places an additional burden on the verifier. If the verifier has already generated public/private key pairs with public key parameters different from those set by the signer, it is unlikely that they will generate another key pair just for verifying a signature. Baek et al. [5] proposed the universal designated verifier signature proof (UDVSP) to circumvent the issue of key initialization by the verifier. In contrast to UDVS, UDVSP employs an interactive protocol with the designated verifier to demonstrate the validity of a signature. Therefore, the verifier’s key pairs play no role in this particular proof, which eliminates the need for the verifier to reinitialize a key.
Interestingly, with the introduction of the UDVSP, a new issue has emerged. The application of the interactive protocol in UDVSP can sometimes lead to a substantial decrease in the efficiency of the system. Specifically, interactive proofs necessitate that both parties be online concurrently. If either party is offline or in a network environment with high latency, it will incur additional time spent waiting and more communication overhead due to the need to resend messages.
Beyond the problem of interactive proofs, the onerous management of public key certificates is also an issue of widespread concern. The UDVS/UDVSP schemes of Steinfeld et al. [1,5,6] are all constructed under CA-based system. To be more specific, these schemes involve cumbersome certificate processes, including application, issuance, query, and revocation. As a direct consequence, this gives rise to a significant amount of overhead. In contrast, ID-based systems [7] streamline the key management process while ensuring a moderate level of security. This makes them a favorable substitute to CA-based systems. In light of this, Zhang et al. [8] constructed an ID-based UDVS in 2005. Subsequently, Chen et al. [9] introduced an ID-based UDVSP in 2008. These schemes allow UDVS and UDVSP to avoid the complex certificate management process.
In addition to the above-mentioned issues, the substantial computation cost associated with UDVS/UDVSP is also not something that can be overlooked. As Lin et al. [2] point out, existing UDVSP schemes [5,9] involve time-consuming bilinear pairing operations (one bilinear pairing operation on a mobile terminal takes about 32 ms, which is approximately 9 times the time demanded by an elliptic curve multiplication operation [10]). In order to reduce the computational overhead of UDVSP, Lin et al. [2] designed a UDVSP scheme based on the Chinese cryptographic SM2 algorithm. This scheme eschews bilinear pairing operations and instead makes use of operations on elliptic curves. This approach enhances the computational efficiency of the scheme. However, it is still constructed under CA-based public key systems. Moreover, it is encumbered with the intricacies and challenges inherent to the interactive protocol.
3. Methodology
3.1. Symbols and Definitions
Table 1 lists the symbols and definitions involved.

Table 1.
Symbols and definitions.
3.2. The ID-Based Digital Signature Based on SM2
The SM2 digital signature algorithm is a component of elliptic curve-based key cryptography algorithms. This algorithm was released by the Chinese National Cryptography Administration (see “SM2 Public Key Cryptographic Algorithms Based on Elliptic Curves”, China’s State Cryptography Administration, December 2010 [11]).
The ID-based digital signature based on SM2 [12] is an improved algorithm derived from the SM2 digital signature. Compared with the SM2 digital signature, the ID-based digital signature based on SM2 utilizes identity information to create the user’s private key. Its application and management do not revolve around digital certificates. Consequently, this obviates the necessity of managing and maintaining public key certificates and circumvents time-consuming procedures. The ID-based digital signature based on SM2 consists of four steps: setup, extract, sign, and verify. The process of the scheme is as shown in Figure 1.

Figure 1.
The process of ID-based digital signature based on SM2.
- (1)
- Setup: With the security parameter provided, the key generation center (KGC) randomly selects a large prime number q and determines a non-singular elliptic curve (where ). From all the points on E (including the point at infinity), select a cyclic group G of prime order n and a generator . Choose three secure hash functions , , and . Randomly select and generate the partial system public key . The algorithm outputs the system public key and the master private key .
- (2)
- Extract: Given , , and user information , the KGC randomly selects and computes the partial user private key , and the intermediate variable . The partial user private key d is calculated as . The algorithm gives out the user’s private key .
- (3)
- Sign: Given , , and the message m, the signer computes the user’s distinguishable identifier and its hash value , where is the bit length of , and and are the coordinates of and L, respectively. Select a random number , and then compute the elliptic curve point and the partial signature . If or , select a new k and repeat the calculations. Otherwise, compute the partial signature . If , the algorithm outputs the message–signature pair m and .
- (4)
- Verify: Given , , m, and the signature to be verified . If , the verifier outputs 0. Otherwise, the verifier computes . If , the verifier outputs 0. If , the following series of computations are carried out. First, compute . Then, calculate . Next, determine . After that, obtain . Finally, calculate . If , the algorithm outputs 1 to denote the validity of the signature; otherwise, it outputs 0 to denote the invalidity of the signature.
The ID-based digital signature algorithm based on SM2 satisfies correctness and existential unforgeability under adaptively chosen message attacks (EUF-CMA) [13].
3.3. Zero-Knowledge Proof, -Protocol with Its or Construction
Suppose the interactive protocol consists of two entities, a prover and a verifier . can convince about the binary relation (where x and w refer to the instance and the witness, respectively). If the protocol meets the requirements of completeness and soundness, it is called a proof of knowledge system. Additionally, if further satisfies honest verifier zero-knowledge (HVZK), then it is known as an interactive honest verifier zero-knowledge proof system [14,15].
The -protocol is an interactive three-move zero-knowledge proof system. Assume and execute the OR proof [16] and obtain the result , P chooses a challenge , where or 1. Another challenge is determined by ’s random challenge c. The commitment and response are generated by using the private witness w based on . The completeness of the -protocol means that if there exists a valid function , then accepts . Special soundness means that given two valid tuples and with , one can recover ’s witness w. Special HVZK means that given ’s random challenge c, there is a probabilistic polynomial-time (PPT) simulator that can interact with to output a valid tuple . Assume the real interaction between and outputs , then and are indistinguishable.
The OR proof [16] is a fundamental construction of the -protocol. It allows to prove that for two computational problems and , knows the witness w for one of the problems, such that either or , without disclosing which one.
The last property of the OR proof is known as witness indistinguishable (WI). This property sets it apart from other -protocols. To elaborate, might be aware of which one in several distinct values of w would enable them to successfully complete the protocol. However, for arbitrary , it is impossible to determine which of these possible values the actually knows merely from the conversations.
The -protocol is capable of being changed into a non-interactive instance through the utilization of the Fiat–Shamir heuristic [17]. However, using the normal -protocol to construct a non-interactive scheme will undermine the non-transferable privacy property of the UDVS. Therefore, we utilize the OR proof to construct our scheme, leveraging the WI property of the OR proof. In the non-interactive form of the OR proof, computes and , and then directly calls to obtain the challenge value c and determine . Using the private witness w, then computes ( and finally sends to . The non-interactive protocol obtained through the Fiat–Shamir transformation still satisfies the properties of interactive form [17].
4. Interactive ID-Based UDVSP Based on SM2 Digital Signature
4.1. The Proposed System
The interactive ID-based UDVSP scheme was constructed by ID-based SM2 signatures and the -protocol. Specifically, it is formed by five algorithms and one protocol. The process of the scheme is as shown in Figure 2.
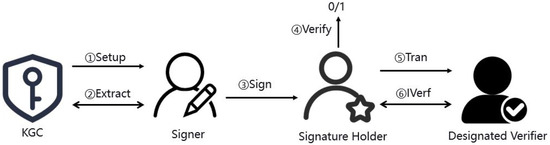
Figure 2.
The process of interactive ID-based UDVSP based on SM2 digital signature.
- Setup: Provided the security parameter , the KGC randomly picks a large prime number q and determines a non-singular elliptic curve (where ). Among all the points on E (including the point at infinity), a cyclic group G of prime order n and a generator are selected. Secure hash functions are chosen as follows: , , and . Here, and are secure cryptographic hash functions. A random is selected, and the partial system public key is computed as . The algorithm outputs the system public key and the master private key . This invention is based on the SM2 digital identity signature design, so it uses the same system parameters as the identity-based SM2 digital signature. For specific parameter symbols and definitions, refer to the detailed implementation in Section 3.1 (Symbols and Definitions).
- Extract: Given the system’s master public key , master private key , and user information , the KGC randomly selects , computes the partial user private key , and the intermediate variable . The partial user private key d is calculated as . The user’s private key is output.
- Sign: Given the system’s master public key , the user’s private key , and the message m, the signer computes the user’s distinguishable identifier and the hash value , where is the bit length of , and and are the coordinates of and L, respectively. A random is selected, then the elliptic curve point and the partial signature are computed. If or , a new k is selected and the calculations are repeated. Otherwise, the partial signature is computed. If , the algorithm outputs the message m and the signature .
- Verify: Given the system’s master public key , user information , message m, and the signature to be verified , if , the verifier (which may be the signature holder or others) outputs 0. Otherwise, it computes . If , the verifier outputs 0. Otherwise, it computes , , , , and . If , the algorithm outputs 1 to denote the validity of the signature; in contrast, it outputs 0 to denote the invalidity of the signature.
- Tran: Given the system public key mpk, user information , message m, and the signature to be verified , the signature holder randomly selects and computes , , , . The algorithm outputs the transformed signature and the transformation key .
- IVerf: Provided the system public key mpk, user information , and the transformed signature , the signature owner additionally takes the transformation key and the signature as input. The signature owner and the designated verifier perform the following interaction:
- first computes , , . Then, randomly selects and , and computes the commitment value . Finally, sends D to .
- randomly selects a challenge value and returns c to .
- calculates the response to the challenge , , , and sends to .
- calculates , , , and . If , outputs 1, indicating acceptance; otherwise, outputs 0.
4.2. Security Analysis
This section will show that the constructed interactive ID-based UDVSP system constructed from SM2 can achieve the anticipated security properties. Based on the security framework introduced by Baek et al. [5], a (UDVSP) scheme must satisfy two critical security requirements: existential unforgeability under adaptive chosen message and identity attacks (EUF-CM-ID-A), and resistance to impersonation attacks (R-IM).
Since the EUF-CM-ID-A of UDVSP is consistent with the EUF-CM-ID-A of the SM2 ID-based digital signature scheme (the SM2 ID-based digital signature has been proven to be EUF-CM-GID-A by Lin et al. [13]), this paper only analyzes the security of the UDVSP system against impersonation attacks. Specifically, we examine two distinct attack scenarios: resistance against Type 1 impersonation attacks (R-IM-TYPE-1) and resistance against Type 2 impersonation attacks (R-IM-TYPE-2).
Theorem 1.
If the IVerf protocol of UDVSP satisfies honest verifier zero-knowledge (HVZK), then UDVSP satisfies R-IM-TYPE-1.
Proof.
First, we construct a simulator SI (Algorithm 1) to prove that the IVerf protocol of UDVSP satisfies HVZK. SI first generates a valid message–signature pair and replicates all interactions with the honest verifier . Due to the random numbers in steps (1) and (2), the first two steps of SI are completely blind. The point L is a random point derived from the user’s private key, and the verifier cannot recover the original signature from the transformed signature . Additionally, steps (3) to (5) form a -protocol, which satisfies special HVZK, effectively preventing the disclosure of the transformation key . Therefore, the IVerf protocol of UDVSP satisfies HVZK.
| Algorithm 1 Simulator SI for the IVerf protocol. |
|
If there exists a PPT adversary that successfully breaks the R-IM-TYPE-1 security of UDVSP, it implies that A can obtain information about to successfully interact with other designated verifiers. This would violate the HVZK property of the IVerf protocol in UDVSP. Therefore, UDVSP satisfies R-IM-TYPE-1. □
Theorem 2.
If the SM2 identity-based digital signature has the property of EUF-CM-GID-A, then UDVSP has the property of R-IM-TYPE-2.
Proof.
Suppose there exists an algorithm A that successfully breaks the R-IM-TYPE-2 property of UDVSP. Then, there exists an algorithm B that can use the capability of A to successfully break the EUF-CM-GID-A property of the SM2 identity-based digital signature. Algorithm B is given the system public key . The goal is to output a valid message–signature pair.
First, B sends to A and calls A to obtain the transformed signature for m. Then, B and A execute step 1 of the IVerf protocol to obtain , and D is returned to B. B computes , , , and verifies . If this does not hold, B terminates the current interaction; otherwise, B calls A again with a new challenge value to obtain new proof values . If , then B can compute , , , where can be solved using the extended Euclidean algorithm. B uses to recover , and finally outputs the forged message–signature pair . This contradicts the EUF-CM-GID-A property of the SM2 identity-based digital signature; thus, UDVSP satisfies R-IM-TYPE-2. □
5. Non-Interactive ID-Based UDVSP Based on SM2 Digital Signature
5.1. The Proposed System
The non-interactive ID-based UDVSP scheme is also relies on ID-based SM2 signatures. However, unlike the previous scheme, it uses the OR form of the -protocol for protocol design. Although the designated verifier still needs to have a pair of public and private keys, these required key pairs do not have to be generated based on the signer’s public key parameters. Instead, the designated verifier can make use of an existing public/private key pair. The scheme specifically comprises five algorithms and one protocol. The process of the scheme is as shown in Figure 3.
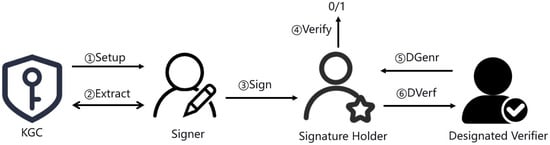
Figure 3.
The process of non-interactive ID-based UDVSP based on SM2 digital signature.
- Setup: Given the security parameter , the KGC randomly picks a large prime number q and determines a non-singular elliptic curve (where ). Among all the points on E (including the point at infinity), a cyclic group G of prime order n and a generator are selected. Secure hash functions are chosen as follows: , , and . Here, is a cryptographic hash function with a message digest length of v bits, and is a secure cryptographic hash function. A random is selected, and the partial system public key is computed as . The algorithm outputs the system public key and the master private key . This invention is based on the SM2 digital identity signature design, so it uses the same system parameters as the identity-based SM2 digital signature. For specific parameter symbols and definitions, refer to the detailed implementation in Section 3.1 (Symbols and Definitions).
- Extract: Given the system’s master public key , master private key , and user information , the KGC randomly selects , computes the partial user private key , and the intermediate variable . The partial user private key d is calculated as . The algorithm outputs the user’s private key .
- Sign: Given the system’s master public key , the user’s private key , and the message m, the signer computes the user’s distinguishable identifier and the hash value , where is the bit length of , and and are the coordinates of and L, respectively. A random is selected, and the elliptic curve point and the partial signature are computed. If or , a new k is selected and the calculations are repeated. Otherwise, the partial signature is computed. If , the algorithm outputs the message m and the signature .
- Verify: Given the system’s master public key , user information , message m, and the signature to be verified , if , the verifier (which may be the signature holder or others) outputs 0. Otherwise, it computes . If , it outputs 0. Otherwise, the verifier computes , , , , and . If , the algorithm outputs 1 to denote the validity of the signature; in contrast, it outputs 0 to denote the invalidity of the signature.
- DGenr: Given the system public key mpk, it randomly selects and computes . The algorithm outputs the designated verifier ’s private key and public key . The public key parameters of the designated verifier and are published, while is kept by .
- DVerf: In this protocol, the signature owner proves to the designated verifier that they possess a signature that can be verified or that they possess ’s private key . If has not leaked , they will believe that has a valid , but cannot disclose this fact to a third party (because , who possesses , can forge the related proof). First, selects a hash function based on ’s public key parameters. and then execute the following protocol:
- 1.
- First, computes , and . Then, randomly selects , , and , and computes and
- 2.
- obtains .
- 3.
- designates and , then computes , , and . The proof is then formed. Subsequently, sends and the hash function to .
- 4.
- V computes: , then , , . If , , and , then it outputs 1 to indicate acceptance; otherwise, it outputs 0.
5.2. Security Analysis
This section will show that the constructed interactive ID-based UDVSP system constructed from SM2 can achieve the anticipated security properties. Based on the security framework introduced by Baek et al. [5], a UDVSP scheme must satisfy two critical security requirements: existential unforgeability under adaptive chosen message and identity attacks (EUF-CM-ID-A), and resistance to impersonation attacks (R-IM).
As in the previous section, this section focuses exclusively on analyzing the security of the UDVSP system against impersonation attacks.
Theorem 3.
If the identity-based digital signature based on SM2 has the property of EUF-CM-GID-A, and the elliptic curve discrete logarithm problem (ECDLP) is intractable, then the UDVSP has the property of R-IM-TYPE-2.
Proof.
This section will illustrate that the constructed non-interactive identity-based UDVSP system based on SM2 can hold the anticipated security properties. The ID-based digital signature EUF-CM-GID-A based on SM2 has been verified by Lin et al. [13], and Chen et al. [9] have demonstrated that without signature conversion (Tran), due to the zero-knowledge property of the protocol, Type 1 impersonation attacks are equivalent to Type 2 impersonation attacks. Hence, this paper only needs to prove that the UDVSP system satisfies R-IM-TYPE- 2.
First, B sends and to A, and calls A to obtain the hash functions and . Then, B and A execute the DVerf protocol to obtain the commitment value, challenge value, and proof values . B computes and verifies , , . If this does not hold, B terminates the current interaction. Otherwise, B calls A again, and B obtains the challenge value and proof values . If , , holds, then B can compute , or . Here, , which can be solved using the extended Euclidean algorithm. B can recover , and finally output the forged message–signature pair or obtain the discrete logarithm of the ECDLP instance . This contradicts the EUF-CM-GID-A property of the identity-based digital signature based on SM2 and the computational hardness of ECDLP; thus, UDVSP has the property of R-IM-TYPE-2. □
6. Performance Evaluation
Firstly, an analytical study of the calculation and communication consumptions of our scheme is presented in this section, along with a comparison to prevalent existing solutions such as UDVSP [2,5] and UDVS [18,19]. The study is based on a theoretical analysis, where we calculate the total cost by summing up every operation involved in the schemes. The cost of each operation was measured through 10,000 practical tests on our hardware, with average execution times calculated to estimate the ideal performance of the schemes. Unlike practical analysis, operations that need to be executed only once (e.g., system initialization) and extremely low consumption computation (e.g., if statements) are not accounted for in this theoretical model, which may lead to some discrepancies compared to the actual execution results.
In this context, the two key-producing procedures within UDVS systems are both considered in KGen, and the focus regarding communication overheads lies primarily on the IVerf interactive protocol. As illustrated in Table 2, compared to existing UDVSP/UDVS schemes, our schemes exhibit optimized computational consumptions and communication overheads. This advantage stems from the elimination of the laborious bilinear map operation and hash function for mapping to a point in our scheme.

Table 2.
Theoretical performance comparison results.
Lin et al. [2] developed a prototype for each operation within these comparable schemes to acquire the empirical effectiveness. The execution was carried out on a laptop computer equipped with an i7-9750H 2.59 GHz processor, 16 GB of memory, and the Windows 10 operating system. The cryptographic library used was the MIRACL library (a widely used cryptographic library, version 7.0). In particular, they utilized the BLS (Boneh–Lynn–Shacham) curve with an ate pairing embedding degree of 24, which is highly suitable for the security level AES-256. As a result, the sizes of the elements in Zq, G1, G2, and GT are 64 bytes, 160 bytes, 640 bytes, and 1920 bytes, respectively. The corresponding notations and execution times are presented in Table 3. According to the test results of various cryptographic operations (Table 3), the actual computational overhead and communication costs can be analyzed and compared (Figure 4).

Table 3.
Symbol definition and time cost.
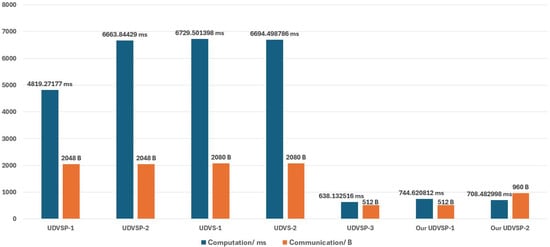
Figure 4.
Real performance comparison results.
Through theoretical analysis, the proposed Our UDVSP-1 and Our UDVSP-2 schemes reduce computational overhead by at least 85.55% compared to other schemes (except UDVSP-3). Although their computational cost is 1.1625 times higher than UDVSP-3, this is acceptable, as they avoid the complex public key certificate management required by UDVSP-3.
In terms of communication overhead, Our UDVSP-1 (512 bytes) and Our UDVSP-2 (960 bytes) significantly outperform UDVSP-1/UDVSP-2 (2048 bytes) and UDVS-1/UDVS-2 (2080 bytes). Overall, the proposed schemes offer a balanced improvement in efficiency and practicality.
7. Conclusions
Although Lin et al.’s scheme addresses the issue that existing UDVSP schemes all involve, such as highly time-consuming bilinear pairing operations, their scheme still suffers from the cumbersome certificate management problem and the drawbacks brought about by the interactive protocol. To address these issues, we first propose the ID-based UDVSP system based on the ID-based SM2 digital signature scheme to eschew the intricate certificate management procedures. Moreover, we construct non-interactive ID-based UDVSP by using the OR proof and Fiat–Shamir technologies. Our work not only exhibits the same bilinear pairing-free merit as the proposition of Lin et al. [2], but also fulfills the goal of certificate-free or non-interactive verification.
Although our ID-based UDVSP systems show improvements over existing schemes, they are limited to achieving certificate-free operation or non-interactive verification separately, rather than both simultaneously. Future work will focus on developing an efficient scheme that combines both features.
Furthermore, the ID-based digital signature based on SM2 employed in this scheme is based on the elliptic curve discrete logarithm problem (ECDLP), whose long-term security is potentially vulnerable to attacks by quantum computers. To address the threat posed by quantum computing, future work will consider adopting post-quantum cryptographic techniques to enhance the security of the scheme.
Author Contributions
Conceptualization, Y.Y. and X.Z.; formal analysis, Y.Y., X.Z. and B.S.; funding acquisition, W.W.; investigation, B.S.; methodology, Y.Y. and X.Z.; resources, W.W.; software, Y.Y.; supervision, B.S. and W.W.; visualization, X.Z. and W.W.; writing—original draft, Y.Y.; writing—review and editing, X.Z. and B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant U21A20466 and Grant 62372108.
Data Availability Statement
We used the data from Lin et al.’s paper. The DOI is https://doi.org/10.1109/tsc.2023.3289319.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Steinfeld, R.; Bull, L.; Wang, H.; Pieprzyk, J. Universal Designated-Verifier Signatures. IACR Cryptol. ePrint Arch. 2003, 192. [Google Scholar] [CrossRef]
- Lin, C.; He, D.; Huang, X. Blockchain-based electronic medical record secure sharing. J. Comput. Appl. 2022, 42, 3465. [Google Scholar]
- Chaum, D.; van Antwerpen, H. Undeniable Signatures. In Proceedings of the Advances in Cryptology—CRYPTO’ 89 Proceedings, Santa Barbara, CA, USA, 20–24 August 1989; Brassard, G., Ed.; Springer: New York, NY, USA, 1990; pp. 212–216. [Google Scholar]
- Jakobsson, M.; Sako, K.; Impagliazzo, R. Designated Verifier Proofs and Their Applications. In Proceedings of the Advances in Cryptology—EUROCRYPT ’96, Saragossa, Spain, 12–16 May 1996; Maurer, U., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 143–154. [Google Scholar]
- Baek, J.; Safavi-Naini, R.; Susilo, W. Universal designated verifier signature proof (or how to efficiently prove knowledge of a signature). In Proceedings of the Advances in Cryptology-ASIACRYPT 2005: 11th International Conference on the Theory and Application of Cryptology and Information Security, Chennai, India, 4–8 December 2005; Proceedings 11. Springer: Berlin/Heidelberg, Germany, 2005; pp. 644–661. [Google Scholar]
- Steinfeld, R.; Wang, H.; Pieprzyk, J. Efficient extension of standard Schnorr/RSA signatures into universal designated-verifier signatures. In Proceedings of the Public Key Cryptography–PKC 2004: 7th International Workshop on Theory and Practice in Public Key Cryptography, Singapore, 1–4 March 2004; Proceedings 7. Springer: Berlin/Heidelberg, Germany, 2004; pp. 86–100. [Google Scholar]
- Shamir, A. Identity-based cryptosystems and signature schemes. In Proceedings of the Advances in Cryptology: CRYPTO 84 4; Springer: Berlin/Heidelberg, Germany, 1985; pp. 47–53. [Google Scholar]
- Zhang, F.; Susilo, W.; Mu, Y.; Chen, X. Identity-based universal designated verifier signatures. In Proceedings of the International Conference on Embedded and Ubiquitous Computing, Nagasaki, Japan, 6–9 December 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 825–834. [Google Scholar]
- Chen, X.; Chen, G.; Zhang, F.; Wei, B.; Mu, Y. Identity-Based Universal Designated Verifier Signature Proof System. Int. J. Netw. Secur. 2009, 1, 52–58. [Google Scholar]
- Abbasinezhad-Mood, D.; Nikooghadam, M. An anonymous ECC-based self-certified key distribution scheme for the smart grid. IEEE Trans. Ind. Electron. 2018, 65, 7996–8004. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, K.; Zhang, J.; Chen, C. Security of the SM2 signature scheme against generalized key substitution attacks. In Proceedings of the International Conference on Research in Security Standardisation, Tokyo, Japan, 15–16 December 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 140–153. [Google Scholar]
- He, D.; Zhang, J.; Chen, B.; Zhang, Y. An Identity-Based Digital Signature Method and System Based on SM2; China National Intellectual Property Administration: Beijing, China, 2021. (In Chinese) [Google Scholar]
- Lin, C.; Huang, X.; He, D. Efficient Range Proof Protocols Based on Chinese Cryptographic SM2. Chin. J. Comput. 2022, 45, 148–159. [Google Scholar]
- Bellare, M.; Goldreich, O. On Defining Proofs of Knowledge. In Proceedings of the Advances in Cryptology-CRYPTO’92, 12th Annual International Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 1992; Proceedings. Brickell, E.F., Ed.; Springer: Berlin/Heidelberg, Germany, 1992. Lecture Notes in Computer Science. Volume 740, pp. 390–420. [Google Scholar] [CrossRef]
- Cramer, R.; Damgård, I.; MacKenzie, P.D. Efficient Zero-Knowledge Proofs of Knowledge Without Intractability Assumptions. In Proceedings of the Public Key Cryptography, Third International Workshop on Practice and Theory in Public Key Cryptography, PKC 2000, Melbourne, Victoria, Australia, 18–20 January 2000; Proceedings. Imai, H., Zheng, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2000. Lecture Notes in Computer Science. Volume 1751, pp. 354–373. [Google Scholar] [CrossRef]
- Ivan, D. On Σ-Protocols; LectureNote; University of Aarhus, Department for Computer Science: Aarhus, Denmark, 2002. [Google Scholar]
- Faust, S.; Kohlweiss, M.; Marson, G.A.; Venturi, D. On the non-malleability of the Fiat-Shamir transform. In Proceedings of the Progress in Cryptology-INDOCRYPT 2012: 13th International Conference on Cryptology in India, Kolkata, India, 9–12 December 2012; Proceedings 13. Springer: Berlin/Heidelberg, Germany, 2012; pp. 60–79. [Google Scholar]
- Huang, X.; Susilo, W.; Mu, Y.; Wu, W. Secure universal designated verifier signature without random oracles. Int. J. Inf. Sec. 2008, 7, 171–183. [Google Scholar] [CrossRef]
- Rastegari, P.; Berenjkoub, M.; Dakhilalian, M.; Susilo, W. Universal designated verifier signature scheme with non-delegatability in the standard model. Inf. Sci. 2019, 479, 321–334. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).