A Novel Fixed-Point Iterative Process for Multivalued Mappings Applied in Solving a HIV Model of Fractional Order

Abstract

We introduce a new and a faster iterative method for the approximation of the fixed point of multivalued nonexpansive mappings in the setting of uniformly convex Banach spaces. We prove some stability and data-dependence results for this novel iterative scheme. A series of numerical illustrations and examples was constructed to validate our results. As an application, we propose a novel method for solving a certain fractional differential equation using our newly developed iterative scheme. Our results extend, unify, and improve several of the known results in the literature.

1. Introduction

Well-known mathematicians have extensively studied multivalued nonlinear mappings and proved some interesting fixed-point theorems in the framework of Banach spaces. Consequently, many problems in some areas of mathematics such as game theory and market economy, among others, can be transformed into fixed-point problems of multivalued nonlinear mathematical models. It is well known that if the fixed point of a given multivalued nonlinear map T exists, then finding the value of the fixed point p of the multivalued nonlinear map T is demanding. As a remedy to this task, mathematicians developed a fruitful way of solving this problem by using the fixed-point iteration method. An important way in determining the choice of a fixed-point iteration scheme to be used for the approximation of the fixed point of a given multivalued nonlinear mapping is the rate of convergence of the iteration process under consideration. For instance, for a comparison of two iterative processes in a one-dimensional case, we refer the reader to Rhoades [1]. Several mathematicians have developed certain iterative processes for the approximation of the fixed point of some nonlinear mappings in the literature (see, e.g., Agarwal [2,3,4], Mann [5], Ishikawa [6], Noor [7], Okeke [8], and Khan [9,10,11], among others). Next, we present some well-known fixed-point iterative schemes in the literature. The Picard [12] or successive iterative process is defined by the sequence ${\left\{u_n\right\}}_{n=0}^{\infty }$ as follows:

$$\left\{\begin{array}{ccc}{u}_1=u\in C,\hfill & \hfill & \\ u_{n+1}=T{u}_n,\forall n\in \mathbb{N}.\hfill & \hfill \end{array}\right.$$

(1)

The Mann [5] iterative process is defined by the sequence ${\left\{v_n\right\}}_{n=0}^{\infty }$ as follows:

$$\left\{\begin{array}{ccc}{v}_1=v\in C,\hfill & \hfill & \\ v_{n+1}=(1-{\alpha }_n)v_n+{\alpha }_{n}T{v}_n,\forall n\in \mathbb{N},\hfill & \hfill \end{array}\right.$$

(2)

where ${\left\{{\alpha }_n\right\}}_{n=0}^{\infty }\in (0,1).$

The Ishikawa [6] iterative process is given by the sequence ${\left\{z_n\right\}}_{n=0}^{\infty }$ defined as follows:

$$\left\{\begin{array}{ccc}{z}_1=z\in C,\hfill & \hfill & \\ y_n=(1-{\beta }_n)z_n+{\beta }_{n}T{z}_n\hfill & \hfill & \\ z_{n+1}=(1-{\alpha }_n)z_n+{\alpha }_{n}T{y}_n,\forall n\in \mathbb{N},\hfill & \hfill \end{array}\right.$$

(3)

where ${\left\{{\alpha }_n\right\}}_{n=0}^{\infty }$ and ${\left\{{\beta }_n\right\}}_{n=0}^{\infty }$ are real sequences in $(0,1).$

The Krasnosel’skii [13] iterative process is defined by the sequence $\left\{s_n\right\}$ as follows:

$$\left\{\begin{array}{ccc}\hfill & s_1=s\in C\hfill & \\ \hfill & s_{n+1}=(1-\lambda )s_n+\lambda T{s}_n,\forall n\in \mathbb{N}.\hfill & \end{array}\right.$$

(4)

where $\left\{\lambda \right\}$ is a real sequences in (0, 1).

Ullah and Arshad [14] introduced the iterative sequence $\left\{x_n\right\}$ defined by

$$\left\{\begin{array}{ccc}\hfill & x_1=x\in C\hfill & \\ \hfill & z_n=(1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n\hfill & \\ \hfill & y_n=T{z}_n\hfill & \\ \hfill & x_{n+1}=T{y}_n,\forall n\in \mathbb{N}\hfill & \end{array}\right.$$

(5)

where $\left\{{\alpha }_n\right\}$ are real sequences in (0, 1). They established that this iterative scheme converges faster than several existing iterative processes.

Noor [7] introduced the iterative process $\left\{u_n\right\}$ defined by

$$\left\{\begin{array}{ccc}\hfill & u_1=u\in C\hfill & \\ \hfill & y_n=(1-{\gamma }_n)u_n+{\gamma }_{n}T{u}_n\hfill & \\ \hfill & w_n=(1-{\beta }_n)u_n+{\beta }_{n}T{y}_n\hfill & \\ \hfill & u_{n+1}=(1-{\alpha }_n)u_n+{\alpha }_{n}T{w}_n,\forall n\in \mathbb{N}.\hfill & \end{array}\right.$$

(6)

where $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in (0, 1).

Okeke [8] developed a novel iterative process called the Picard–Ishikawa hybrid scheme, defined by the sequence ${\left\{x_n\right\}}_{n=0}^{\infty }$ as follows:

$$\left\{\begin{array}{ccc}\hfill & x_1=x\in C\hfill & \\ \\ \hfill & z_n=(1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n\hfill & \\ \\ \hfill & y_n=(1-{\beta }_n)x_n+{\beta }_{n}T{z}_n\hfill & \\ \\ \hfill & x_{n+1}=T{y}_n,\forall n\in \mathbb{N}.\hfill & \\ \end{array}\right.$$

(7)

where $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ are real sequences in $(0,1)$. The author established that this iterative process converges faster than several existing iterative schemes. Next, we pose the following crucial question.

Problem 1.

Is it possible to develop an iteration process whose rate of convergence is even faster than those defined above?

The essence of this paper is to propose a faster and more efficient iterative process for approximating the fixed point of some classes of generalized nonlinear mappings. This novel iterative scheme converges faster than some of the iterative schemes listed above in the sense of Berinde [15]. To answer this natural question, as posed in Problem 1 above, we introduce the following iterative method, called the IA-iterative scheme and defined by the sequence ${\left\{x_n\right\}}_{n=0}^{\infty }$ as follows:

$$\left\{\begin{array}{ccc}\hfill & x_1=x\in C\hfill & \\ \\ \hfill & z_n={\alpha }_n{x}_n+{\beta }_n{x}_n+{\gamma }_{n}T\left(x_n\right)\hfill & \\ \\ \hfill & y_n=T[(1-{\lambda }_n)T\left(z_n\right)+{\lambda }_{n}T\left(x_n\right)]\hfill & \\ \\ \hfill & x_{n+1}=T\left(y_n\right)\forall n\in \mathbb{N},\hfill & \\ \end{array}\right.$$

(8)

where $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{{\gamma }_n\right\}$ and $\left\{{\lambda }_n\right\}$ are real sequences in $(0,1)$ and ${\alpha }_n+{\beta }_n+{\gamma }_n=1.$

Several mathematical models for addressing the issue of infection disease especially HIV transmission disease have been developed (see [16,17]). As a result of this, several fractional derivatives in the sense of Caputo were developed as one of the novel formulations that have found widespread usage in the simulation of many kinds of infection models. It was suggested as part of the method of preventing and treating infection disease. One of the differential equations was developed by Caputo–Fabrizio and was named the Caputo–Fabrizio fractional differential equation. Consequently, the Krasnoselskii’s and Banach’s fixed-point approach, in combination with the kernels, were part of the methods adopted in solving the Caputo–Fabrizio fractional differential equation (CFFD) [16]. Readers interested in studies involving Riemann–Liouville fractional differential equations, Delta fractional differential equations, and conformable fractional differential equations may consult [18,19,20] and the references therein. Several works of literature involve several other methods for solving fractional differential equations, such as the Laplace differential transform method, hyperbolic non-polynomial spline method, homotopy perturbation method, fractional non-polynomial spline method, and Pade differential transform method, among others.

In the present paper, we prove that our newly developed fixed-point iterative process, called the IA-iterative scheme, is highly efficient in solving the Caputo–Fabrizio fractional differential equation (CFFD). We present several numerical experiments to validate our results. Our results generalize and extend several known results.

2. Preliminaries

Throughout this paper, we denote $F\left(T\right)$ as the set of all fixed points of the mapping $T.$ A point p is called a fixed point of T if $p\in Tp.$

The following definitions will be useful in this study.

Definition 1

([21]). Suppose E is a Banach space. A subset K is said to be proximinal if for every $x\in E$ there exists a $k\in K$ such that

$$d(x,k)=inf\{\parallel x-y\parallel :y\in K\}=d(x,K)$$

(9)

It has been proven in the literature that every closed convex subset of a uniformly convex Banach space is proximinal. We denote $P\left(K\right)$ as the family of a nonempty bounded proximinal subset of K.

Definition 2

([21]). The Hausdorff distance $H(.,.)$ on $P\left(K\right)$ is defined by

$$H(A,B)=max\{\underset{a\in A}{sup}d(a,B),\underset{b\in B}{sup}d(b,B)\},$$

(10)

where $A,B\in P\left(K\right)$ and $d(a,B)=inf\{\parallel a-b\parallel :b\in B\}.$

Definition 3

([21]). Suppose K is a nonvoid convex subset of normed space E. A mapping $T:K\to K$ is said to be a contraction if for every $x,y\in K$ there exists a $\delta \in (0,1)$ such that

$$\parallel Tx-Ty\parallel \le \delta \parallel x-y\parallel .$$

(11)

Definition 4

([21]). A multivalued mapping $T:K\to P\left(K\right)$ is said to be nonexpansive if for each $x,y\in K$ we have

$$H(Tx,Ty) \le \parallel x-y\parallel .$$

(12)

Definition 5

([15]). Suppose that E is a Banach space and $T,\tilde{T}:E\to E$ is self mapping on E. Then, $\tilde{T}$ is said to be approximate mapping of T if for each $x\in E$ and for fixed $ϵ>0$, we have

$$\parallel Tx-\tilde{T}x\parallel \le ϵ.$$

(13)

Definition 6

([15]). Let $\left\{a_n\right\}$ and $\left\{b_n\right\}$ be two sequences of real numbers converging to x and y, respectively. The sequence $\left\{a_n\right\}$ is said to converge faster than the sequence $\left\{b_n\right\}$ if

$$\underset{n\to \infty }{lim}{\displaystyle \frac{|a_n-x|}{|b_n-y|}}=0.$$

Definition 7

([15]). Let $\left\{u_n\right\}$ and $\left\{v_n\right\}$ be two fixed-point iteration schemes that converge to a certain fixed point p of a given operator T. Suppose that the error estimates

$$\parallel u_n-p\parallel \le a_n,\forall n\in \mathbb{N}$$

$$\parallel v_n-p\parallel \le b_n,\forall n\in \mathbb{N}$$

exist, where $\left\{a_n\right\}$ and $\left\{b_n\right\}$ are two sequences of nonnegative numbers converging to 0. If $\left\{a_n\right\}$ converges faster than $\left\{b_n\right\}$, then $\left\{u_n\right\}$ converges faster than $\left\{v_n\right\}$ to $p.$

Lemma 1

([22]). Let ${\lambda }_n$ be a positive sequence, such that there exist $n_0\in \mathbb{N},$, such that for all $n\ge n_0$ satisfying the inequality

$${\lambda }_{n+1}=(1-{\mu }_n){\nu }_n+{\mu }_n{\sigma }_n,$$

where $\left\{{\mu }_n\right\}\in (0,1)$ for all $n\in \mathbb{N},{\mathrm{\Sigma }}_{n=1}^{\infty }{\mu }_n$ and ${\sigma }_n\ge 0$ for all $n\in \mathbb{N}.$ Then, the inequality below holds

$$\underset{n\to \infty }{lim\; sup}{\nu }_n\le \underset{n\to \infty }{lim\; sup}{\sigma }_n.$$

Lemma 2

([23]). Let ${\left\{x_n\right\}}_{n=0}^{\infty }$ be a sequence of nonnegative real numbers, including zero, satisfying

$$s_{n+1}\le (1-{\lambda }_n)s_n.$$

If $\left\{{\lambda }_n\right\}\subset (0,1)$ and ${\mathrm{\Sigma }}_{n=0}^{\infty }{\lambda }_n=\infty$ then ${lim}_{n\to \infty }{s}_n=0.$

Lemma 3

([24]). Let ${\left\{{\alpha }_n\right\}}_{n=0}^{\infty }$, ${\left\{{\beta }_n\right\}}_{n=0}^{\infty }$, and ${\left\{{\gamma }_n\right\}}_{n=0}^{\infty }$ be real sequences, such that

(i) 

$0\le {\alpha }_n$, ${\beta }_n<1$ and ${\gamma }_n<1$

(ii) 

${\beta }_n\to 0$, ${\gamma }_n\to 0$ as $n\to 0.$

Let $\left\{{\theta }_n\right\}$ be a positive real sequence, such that $\mathrm{\Sigma }{\beta }_n{\gamma }_n(1-{\gamma }_n){\theta }_n$ is bounded. Then, $\left\{{\theta }_n\right\}$ has a subsequence which converges to zero.

Lemma 4.

Suppose that E is a Banach space. Then, E is uniformly convex if for any given number $\rho >0$, there exists a continuous strictly increasing function $\phi :[0,\infty )\to [0,\infty )$ with $\phi \left(0\right)=0$, such that for each $x,y\in B_{\rho },$ we have the following:

$$\parallel {\alpha }_n{x}_n+(1-{\alpha }_n)y_n{\parallel }^2\le {\alpha }_n\parallel x_n{\parallel }^2+(1-{\alpha }_n)\parallel y_n{\parallel }^2-{\alpha }_n(1-{\alpha }_n)\phi (\parallel x_n-y_n\parallel ).$$

Lemma 5

([16]). For $n-1<k\le n,\zeta >-1,\rho \ge 0,$ and $\omega \in R,$ we have:

(1) 

$D_{\sigma }^k{\sigma }^{\omega }={\displaystyle \frac{\mathrm{\Gamma }(k+1)}{\mathrm{\Gamma }(\omega -k+1)}}{\sigma }^{\omega -k}$

(2) 

$D_{\sigma }^k\rho =0$

(3) 

$D_{\sigma }^k{R}_{\sigma }^k\psi (\nu ,\sigma )=\psi (\nu ,\sigma )$

(4) 

$R_{\sigma }^k{D}_{\sigma }^k\psi (\nu ,\sigma )=\psi (\nu ,\sigma )-{\mathrm{\Sigma }}_{i=0}^{n-1}{\partial }^i\psi (\nu ,0){\displaystyle \frac{{\sigma }^i}{i!}}.$

3. Convergence Analysis

We begin this section by proving the following results.

Theorem 1.

Suppose that K is a nonvoid compact convex subset of a uniformly convex Banach space E and the map $T:K\to P\left(K\right)$ is a nonexpansive mapping with $F\left(T\right)\ne \varnothing$. Let $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{{\gamma }_n\right\}$ and $\left\{{\lambda }_n\right\}$ be four sequences in (0, 1). Suppose $\left\{x_n\right\}$ is the sequence defined by (8), satisfying

(i) 

$0\le {\alpha }_n,{\lambda }_n<1,{\gamma }_n<1$

(ii) 

${\beta }_n\to 0,{\gamma }_n\to 0,{\lambda }_n\to 0$ and

(iii) 

${\sum }_{n=1}^{\infty }{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)(1-{\lambda }_n)=\infty .$

Then, the sequence $\left\{x_n\right\}$ converges strongly to fixed point $p\in F\left(T\right).$

Proof. 

Let $p\in F\left(T\right)\ne 0$ and $n\ge 0$. Using the fact that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and $w_n\in T{x}_n$ is such that $\parallel w_n-p\parallel =d(p,T{x}_n)$, we obtain

$$\begin{array}{ccc}\parallel z_n{-p\parallel }^2\hfill & =\hfill & \parallel {\alpha }_n{x}_n+{\beta }_n{x}_n+{\gamma }_n{w}_n{-p\parallel }^2\hfill \\ & =\hfill & \parallel (1-{\gamma }_n)(x_n-p)+{\gamma }_n(w_n-p){\parallel }^2\hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n{-p\parallel }^2+{\gamma }_n\parallel w_n{-p\parallel }^2-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)\phi (\parallel x_n-w_n\parallel )\hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n{-p\parallel }^2+{\gamma }_n{H}^2(T{x}_n,Tp)-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)\phi (\parallel x_n-w_n\parallel )\hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n{-p\parallel }^2+{\gamma }_n\parallel x_n{-p\parallel }^2-{\gamma }_n(1-{\gamma }_n)\phi (\parallel x_n-w_n\parallel )\hfill \\ & =\hfill & \parallel x_n{-p\parallel }^2-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)\phi (\parallel x_n-w_n\parallel ).\hfill \end{array}$$

(14)

Secondly, let $d_n=(1-{\lambda }_n)v_n+{\lambda }_n{w}_n$, where $v_n\in T{z}_n$ and $w_n\in T{x}_n$ are such that $\parallel v_n-p\parallel =d(p,T{z}_n)$ and $\parallel w_n-p\parallel =d(p,T{x}_n).$ Therefore, considering (14), we obtain

$$\begin{array}{ccc}\parallel d_n{-p\parallel }^2\hfill & =\hfill & \parallel (1-{\lambda }_n)(v_n-p)+{\lambda }_n(z_n-p){\parallel }^2\hfill \\ & \le \hfill & (1-{\lambda }_n)\parallel v_n{-p\parallel }^2+{\lambda }_n\parallel w_n{-p\parallel }^2-{\lambda }_n(1-{\lambda }_n)\phi (\parallel v_n-w_n\parallel )\hfill \\ & \le \hfill & (1-{\lambda }_n)H^2(T{z}_n,Tp)+{\lambda }_n{H}^2(T{x}_n,Tp)-{\lambda }_n(1-{\lambda }_n)\phi (\parallel v_n-w_n\parallel )\hfill \\ & \le \hfill & (1-{\lambda }_n)\parallel z_n{-p\parallel }^2+{\lambda }_n\parallel x_n{-p\parallel }^2-{\lambda }_n(1-{\lambda }_n)\phi (\parallel v_n-w_n\parallel )\hfill \\ & \le \hfill & (1-{\lambda }_n)[\parallel x_n{-p\parallel }^2-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)\phi (\parallel x_n-w_n\parallel \left)\right]\hfill \\ & +\hfill & {\lambda }_n\parallel x_n{-p\parallel }^2-{\lambda }_n(1-{\lambda }_n)\phi (\parallel v_n-w_n\parallel )\hfill \\ & \le \hfill & \parallel x_n{-p\parallel }^2-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)(1-{\lambda }_n)\phi (\parallel x_n-w_n\parallel ).\hfill \end{array}$$

(15)

Considering that $y_n=T\left(d_n\right)$ where $f_n\in T\left(d_n\right)$, such that $\parallel f_n-p\parallel =d(p,T{d}_n)$ and, using (15), we have the following:

$$\begin{array}{ccc}\parallel y_n{-p\parallel }^2\hfill & =\hfill & \parallel f_n{-p\parallel }^2\hfill \\ & \le \hfill & H^2(T{d}_n,Tp)\hfill \\ & \le \hfill & \parallel d_n{-p\parallel }^2\hfill \\ & \le \hfill & \parallel x_n{-p\parallel }^2-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)(1-{\lambda }_n)\phi (\parallel x_n-w_n\parallel ).\hfill \end{array}$$

(16)

Thus, $x_{n+1}=T\left(y_n\right)$ where $g_n\in T\left(y_n\right)$, such that $\parallel g_n-p\parallel =d(p,T{y}_n)$ and, using (16), we have the following:

$$\begin{array}{ccc}\parallel x_{n+1}{-p\parallel }^2\hfill & =\hfill & \parallel g_n{-p\parallel }^2\hfill \\ & \le \hfill & H^2(T{y}_n,Tp)\hfill \\ & \le \hfill & \parallel y_n{-p\parallel }^2\hfill \\ & \le \hfill & \parallel x_n{-p\parallel }^2-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)(1-{\lambda }_n)\phi (\parallel x_n-w_n\parallel ).\hfill \end{array}$$

(17)

From (17), we have

$$\begin{array}{ccc}\parallel x_{n+1}{-p\parallel }^2\hfill & \le \hfill & \parallel x_n{-p\parallel }^2-{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)(1-{\lambda }_n)\phi (\parallel x_n-w_n\parallel ).\hfill \end{array}$$

(18)

Hence, we obtain the following

$$\begin{array}{ccc}{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)(1-{\lambda }_n)\phi (\parallel x_n-w_n\parallel )\hfill & \le \hfill & \parallel x_n{-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2.\hfill \end{array}$$

(19)

Consequently, it implies that

$$\begin{array}{ccc}{\mathrm{\Sigma }}_{n=1}^{\infty }{\alpha }_n{\beta }_n{\gamma }_n(1-{\gamma }_n)(1-{\lambda }_n)\phi (\parallel x_n-w_n\parallel )\hfill & \le \hfill & \parallel x_1{-p\parallel }^2<\infty .\hfill \end{array}$$

(20)

Using Lemma 4, there exists a subsequence $\{x_{n_k}-w_{n_k}\}$ of $\{x_n-w_n\}$ such that ${lim}_{k\to \infty }\phi (\parallel x_n-w_n\parallel )=0,$ by considering the continuity and strictly increasing property of $\phi$. By the compactness of K, we assume that $x_{n_k}\to q$ for some $q\in K$, Therefore,

$$d(q,Tq)\le \parallel q-x_{n_k}\parallel +d(x_{n_k},T{x}_{n_k})+H(T{x}_{n_k},q).$$

Furthermore,

$$d(q,Tq)\le \parallel q-x_{n_k}\parallel +\parallel x_{n_k}-w_{n_k}\parallel +\parallel x_{n_k}-q\parallel \to 0\mathrm{as}n\to \infty .$$

Consequently, q is a fixed point of mapping T. Now, replacing q with p, we obtain $\{\parallel x_n-q\parallel \}$, which is a decreasing sequence by (19). Since $\{\parallel x_n-q\parallel \}\to 0$ as $n\to \infty$, it then follows that $\{\parallel x_n-q\parallel \}$ decreases to 0. □

4. Rate of Convergence

In this section, we show that the IA-iterative scheme converges better than some other iterative processes mentioned above.

Proposition 1.

Suppose K is a nonvoid closed convex subset of a normed space E and $T:K\to K$ is a contraction map satisfying (11) with $\delta \in (0,1)$. Suppose that each of the iterative schemes (1)–(7) converge to the same fixed point p of T, where $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{{\gamma }_n\right\}$, and $\left\{{\lambda }_n\right\}$ are four sequences in (0, 1). Then, the IA-iterative process (8) converges faster than iterative schemes (1)–(7).

Proof. 

Suppose p is a fixed point of T and also that $\delta \in (0,1)$. Using (11) and the Picard iterative scheme (1), we have the following

$$\begin{array}{ccc}\parallel u_{n+1}-p\parallel \hfill & =\hfill & \parallel T{u}_n-p\parallel \hfill \\ & \le \hfill & \delta \parallel u_n-p\parallel \hfill \\ & .\hfill & \\ & .\hfill & \\ & .\hfill & \\ & \le \hfill & {\delta }^n\parallel u_1-p\parallel .\hfill \end{array}$$

(21)

Now, let

$$\begin{array}{c}{\theta }_n={\delta }^n\parallel u_1-p\parallel .\hfill \end{array}$$

(22)

Considering Mann iterative scheme (2) and (3), we obtain the following

$$\begin{array}{ccc}\parallel v_{n+1}-p\parallel \hfill & =\hfill & \parallel (1-{\alpha }_n)v_n+{\alpha }_{n}T{v}_n-p\parallel \hfill \\ & \le \hfill & (1-{\alpha }_n)\parallel v_n-p\parallel +\parallel T{v}_n-p\parallel \hfill \\ & \le \hfill & (1-{\alpha }_n)\parallel v_n-p\parallel +\delta \parallel v_n-p\parallel \hfill \\ & \le \hfill & (1-{\alpha }_n(1-\delta ))\parallel v_n-p\parallel \hfill \\ & .\hfill & \\ & .\hfill & \\ & .\hfill & \\ & \le \hfill & {(1-\alpha (1-\delta ))}^n\parallel v_1-p\parallel .\hfill \end{array}$$

(23)

Therefore, consider

$$\begin{array}{c}{\vartheta }_n={(1-\alpha (1-\delta ))}^n\parallel v_1-p\parallel .\hfill \end{array}$$

(24)

Considering Picard–Mann (5) and (11), we obtain

$$\begin{array}{ccc}\parallel s_{n+1}-p\parallel \hfill & =\hfill & \parallel T{t}_n-p\parallel \hfill \\ & \le \hfill & \delta \parallel t_n-p\parallel .\hfill \end{array}$$

(25)

Secondly, we obtain

$$\begin{array}{ccc}\parallel t_n-p\parallel \hfill & =\hfill & \parallel (1-{\alpha }_n)s_n+{\alpha }_{n}T{s}_n-p\parallel \hfill \\ & \le \hfill & (1-{\alpha }_n)\parallel s_n-p\parallel +{\alpha }_n\parallel T{s}_n-p\parallel \hfill \\ & \le \hfill & (1-{\alpha }_n)\parallel s_n-p\parallel +\delta {\alpha }_n\parallel s_n-p\parallel \hfill \\ & \le \hfill & (1-{\alpha }_n(1-\delta ))\parallel s_n-p\parallel .\hfill \end{array}$$

(26)

Combining (25) and (26), we have the following

$$\begin{array}{ccc}\parallel s_{n+1}-p\parallel \hfill & =\hfill & \parallel T{t}_n-p\parallel \hfill \\ & \le \hfill & \delta \parallel t_n-p\parallel \hfill \\ & \le \hfill & \delta (1-{\alpha }_n(1-\delta ))\parallel s_n-p\parallel \hfill \\ & \le \hfill & \delta (1-{\alpha }_n(1-\delta ))\parallel s_n-p\parallel \hfill \\ & .\hfill & \\ & .\hfill & \\ & .\hfill & \\ & \le \hfill & {\left(\delta (1-\alpha (1-\delta ))\right)}^n\parallel s_1-p\parallel .\hfill \end{array}$$

(27)

Moreover, take

$$\begin{array}{c}{\iota }_n={\left(\delta (1-\alpha (1-\delta ))\right)}^n\parallel s_1-p\parallel .\hfill \end{array}$$

(28)

Now, we consider the new explicit iterative process named the IA-iterative scheme. Also, using (11) and (8)

$$\begin{array}{ccc}\parallel z_n-p\parallel \hfill & =\hfill & \parallel {\alpha }_n{x}_n+{\beta }_n{x}_n+{\gamma }_{n}T{x}_n-p\parallel \hfill \\ & \le \hfill & {\alpha }_n\parallel x_n-p\parallel +{\beta }_n\parallel x_n-p\parallel +{\gamma }_n\parallel T{x}_n-p\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-p\parallel +\delta {\gamma }_n\parallel x_n-p\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n(1-\delta ))\parallel x_n-p\parallel .\hfill \end{array}$$

(29)

Using (11), (8), and (29), we have

$$\begin{array}{ccc}\parallel y_n-p\parallel \hfill & =\hfill & \parallel T[(1-{\lambda }_n)T{z}_n+{\lambda }_{n}T{x}_n]-p\parallel \hfill \\ & \le \hfill & \delta [\parallel (1-{\lambda }_n)T{z}_n+{\lambda }_{n}T{x}_n-p\parallel ]\hfill \\ & \le \hfill & \delta [(1-{\lambda }_n)\parallel T{z}_n-p\parallel +{\lambda }_n\parallel T{x}_n-p\parallel ]\hfill \\ & \le \hfill & [1-{\gamma }_n{\lambda }_n(1-{\delta }_n)]\parallel x_n-p\parallel .\hfill \end{array}$$

(30)

Moreover, considering (11), (8), and (30), we obtain

$$\begin{array}{ccc}\parallel x_{n+1}-p\parallel \hfill & =\hfill & \parallel T\left(y_n\right)-p\parallel \hfill \\ & \le \hfill & \delta \parallel y_n-p\parallel \hfill \\ & \le \hfill & {\delta }^3(1-{\gamma }_n{\lambda }_n(1-\delta ))\parallel x_n-p\parallel \hfill \\ & .\hfill & \\ & .\hfill & \\ & .\hfill & \\ & \le \hfill & {\left({\delta }^3(1-{\gamma }_n{\lambda }_n(1-\delta ))\right)}^n\parallel x_1-p\parallel .\hfill \end{array}$$

(31)

Now, we have

$$\begin{array}{c}{\varpi }_n=({\delta }^3{(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n\parallel x_1-p\parallel .\hfill \end{array}$$

(32)

We now justify the rate of convergence of our iterative process (8) as follows:

(i)

$${\displaystyle \frac{{\varpi }_n}{{\theta }_n}}={\displaystyle \frac{({\delta }^3{(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n\parallel x_1-p\parallel }{{\delta }^n\parallel u_1-p\parallel }}={\delta }^{2n}({(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n{\displaystyle \frac{\parallel x_1-p\parallel }{\parallel u_1-p\parallel }}\to 0$$

as $n\to \infty$. This implies that IA-iterative process (8) converges faster to p than the Picard iterative process (1).

(ii)

$${\displaystyle \frac{{\varpi }_n}{{\vartheta }_n}}={\displaystyle \frac{({\delta }^3{(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n}{{(1-\alpha (1-\delta ))}^n}}{\displaystyle \frac{\parallel x_1-p\parallel }{\parallel v_1-p\parallel }}={\displaystyle \frac{{\delta }^{3n}({(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n}{{(1-\alpha (1-\delta ))}^n}}{\displaystyle \frac{\parallel x_1-p\parallel }{\parallel v_1-p\parallel }}\to 0$$

as $n\to \infty$. This implies that IA-iterative process (8) converges faster to p than the Mann iterative process (2).

(iii)

$${\displaystyle \frac{{\varpi }_n}{{\iota }_n}}={\displaystyle \frac{({\delta }^3{(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n}{{\left(\delta (1-\alpha (1-\delta ))\right)}^n}}{\displaystyle \frac{\parallel x_1-p\parallel }{\parallel s_1-p\parallel }}={\displaystyle \frac{{\delta }^{2n}({(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n}{{(1-\alpha (1-\delta ))}^n}}{\displaystyle \frac{\parallel x_1-p\parallel }{\parallel v_1-p\parallel }}\to 0$$

as $n\to \infty$. This implies that IA-iterative process (8) converges faster to p than the Picard–Mann iterative process (5). Similarly, from (3)–(7), following the same method as above, the IA-iterative process (8) then converges faster to p than from (3)–(7).

$${\displaystyle \frac{{\varpi }_n}{{\kappa }_n}}={\displaystyle \frac{({\delta }^3{(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n\parallel x_1-p\parallel }{{(1-\alpha (1-\delta ))}^n\parallel u_1-p\parallel }}={\displaystyle \frac{{\delta }^{3n}({(1-{\gamma }_n{\lambda }_n(1-\delta ))}^n}{{(1-\alpha (1-\delta ))}^n}}{\displaystyle \frac{\parallel x_1-p\parallel }{\parallel u_1-p\parallel }}\to 0$$

as $n\to \infty$. This implies that IA-iterative process (8) converges faster to p than from (3)–(7). □

5. Data-Dependence Results

In this section, we establish some data dependence results for the newly introduced IA-iterative scheme (8).

Theorem 2.

Let $\tilde{T}$ be an approximate operator of T satisfying (11). Let ${\left\{x_n\right\}}_{n=1}^{\infty }$ be an iterative sequence generated by the new explicit iterative process named the IA-iterative scheme (8) for mapping T and define an iterative sequence ${\left\{{\tilde{x}}_n\right\}}_{n=1}^{\infty }$ as follows

$$\left\{\begin{array}{ccc}{\tilde{x}}_1=\tilde{x}\in C,\hfill & \hfill & \\ {\tilde{z}}_n={\alpha }_n{\tilde{x}}_n+{\beta }_n{\tilde{x}}_n+{\gamma }_n\tilde{T}\left({\tilde{x}}_n\right)\hfill & \hfill & \\ {\tilde{y}}_n=\tilde{T}[(1-{\lambda }_n)\tilde{T}\left({\tilde{z}}_n\right)+{\lambda }_n\tilde{T}\left({\tilde{x}}_n\right)]\hfill & \hfill & \\ {\tilde{x}}_{n+1}=\tilde{T}\left(\widetilde{y_n}\right),n\in \mathbb{N},\hfill & \hfill \end{array}\right.$$

(33)

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are real sequences in (0,1) satisfying the following conditions:

(i) 

${\mathrm{\Sigma }}_{n=1}^{\infty }{\gamma }_n=\infty ,$

(ii) 

${\displaystyle \frac{1}{2}}\le \left[{\gamma }_n(1-\delta )\right]$ for all $n\in \mathbb{N},$ and

(iii) 

${\sum }_{n=1}^{\infty }\left[{\gamma }_n(1-\delta )\right]=\infty$.

If $T{x}^{*}=x^{*}$ and $\tilde{T}{\tilde{x}}^{*}={\tilde{x}}^{*}$ such that ${\tilde{x}}_n\to {\tilde{x}}^{*}$ as $n\to \infty$, then we have $\parallel x^{*}-{\tilde{x}}^{*}\parallel \le {\displaystyle \frac{7ϵ}{1-\delta }}.$ where $ϵ>0$ is fixed number.

Proof. 

Using (8), (11), (13), and (33), we obtain

$$\begin{array}{ccc}\parallel z_n-{\tilde{z}}_n\parallel \hfill & =\hfill & \parallel {\alpha }_n{x}_n+{\beta }_n{x}_n+{\gamma }_{n}T{x}_n-[{\alpha }_n\widetilde{x_n}+{\beta }_n\widetilde{x_n}+{\gamma }_n\tilde{T}\widetilde{x_n}]\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-\widetilde{x_n}\parallel +{\gamma }_n\parallel T{x}_n-\tilde{T}\widetilde{x_n}\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-\widetilde{x_n}\parallel +{\gamma }_n\parallel T{x}_n-T\widetilde{x_n}\parallel +{\gamma }_n\parallel T\widetilde{x_n}-\tilde{T}\widetilde{x_n}\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-\widetilde{x_n}\parallel +{\gamma }_n\delta \parallel x_n-\widetilde{x_n}\parallel +{\gamma }_nϵ\hfill \\ & =\hfill & (1-{\gamma }_n(1-\delta ))\parallel x_n-\widetilde{x_n}\parallel +{\gamma }_nϵ.\hfill \end{array}$$

(34)

However, considering (8), (11), (13), (33) and (34) we have the following:

$$\begin{array}{ccc}\parallel y_n-\widetilde{y_n}\parallel \hfill & =\hfill & \parallel T[(1-{\lambda }_n)T\left(z_n\right)+{\lambda }_{n}T\left(x_n\right)]-\tilde{T}[(1-{\lambda }_n)\tilde{T}\left({\tilde{z}}_n\right)+{\lambda }_n\tilde{T}\left({\tilde{x}}_n\right)]\parallel \hfill \\ & \le \hfill & \delta \parallel (1-{\lambda }_n)T\left(z_n\right)+{\lambda }_{n}T\left(x_n\right)-[(1-{\lambda }_n)\tilde{T}\left({\tilde{z}}_n\right)+{\lambda }_n\tilde{T}\left({\tilde{x}}_n\right)]\parallel \hfill \\ & \le \hfill & \delta [(1-{\lambda }_n)\parallel T\left(z_n\right)-\tilde{T}\left({\tilde{z}}_n\right)\parallel +{\lambda }_n\parallel T\left(x_n\right)-\tilde{T}\left({\tilde{x}}_n\right)\parallel ]\hfill \\ & \le \hfill & (1-{\lambda }_n)\parallel T\left(z_n\right)-T\left({\tilde{z}}_n\right)\parallel +(1-{\lambda }_n)\parallel T\left({\tilde{z}}_n\right)-\tilde{T}\left({\tilde{z}}_n\right)\parallel \hfill \\ & +\hfill & {\lambda }_n\parallel T\left(x_n\right)-T\left({\tilde{x}}_n\right)\parallel +{\lambda }_n\parallel T\left({\tilde{x}}_n\right)-\tilde{T}\left({\tilde{x}}_n\right)\parallel \hfill \\ & \le \hfill & (1-{\lambda }_n)\delta \parallel z_n-{\tilde{z}}_n\parallel +{\lambda }_n\delta \parallel x_n-{\tilde{x}}_n\parallel +ϵ\hfill \\ & \le \hfill & (1-{\lambda }_n)\delta [(1-{\gamma }_n(1-\delta ))\parallel x_n-\widetilde{x_n}\parallel +{\gamma }_nϵ]+{\lambda }_n\delta \parallel x_n-{\tilde{x}}_n\parallel +ϵ\hfill \\ & \le \hfill & (1-{\gamma }_n(1-\delta ))\parallel x_n-\widetilde{x_n}\parallel +(1+{\gamma }_n)ϵ.\hfill \end{array}$$

(35)

Using (8), (11), (13), (33) and (35), we obtain

$$\begin{array}{ccc}\parallel x_{n+1}-\widetilde{x_{n+1}}\parallel \hfill & =\hfill & \parallel T\left(y_n\right)-\tilde{T}\left(\widetilde{y_n}\right)\parallel \hfill \\ & \le \hfill & \parallel T\left(y_n\right)-T\left(\widetilde{y_n}\right)\parallel +\parallel T\left(\widetilde{y_n}\right)-\tilde{T}\left(\widetilde{y_n}\right)\parallel \hfill \\ & \le \hfill & \delta \parallel y_n-\widetilde{y_n}\parallel +ϵ\hfill \\ & \le \hfill & (1-{\gamma }_n(1-\delta ))\parallel x_n-\widetilde{x_n}\parallel +(2+{\gamma }_n)ϵ.\hfill \end{array}$$

(36)

From the conditions (i) and (ii), we observe that $\left(36\right)$ gives

$$\begin{array}{ccc}\parallel x_{n+1}-\widetilde{x_{n+1}}\parallel \hfill & \le \hfill & (1-{\gamma }_n(1-\delta ))\parallel x_n-\widetilde{x_n}\parallel +(2+{\gamma }_n)ϵ\times {\displaystyle \frac{7ϵ}{1-\delta }}.\hfill \end{array}$$

(37)

Let ${\nu }_n:=\parallel x_n-{\tilde{x}}_n\parallel$, ${\Omega }_n:=\left[(1-{\gamma }_n(1-\delta ))\right]\in (0,1)$, ${\sigma }_n:={\displaystyle \frac{7ϵ}{(1-\delta )}}.$

Moreover, using Lemma (1), it shows that

$$0\le \underset{n\to \infty }{lim\; sup}\parallel x_n-{\tilde{x}}_n\parallel \le \underset{n\to \infty }{lim\; sup}{\displaystyle \frac{7ϵ}{(1-\delta )}}.$$

Therefore,

$$\underset{n\to \infty }{lim\; sup}\parallel x_n-{\tilde{x}}_n\parallel \le \underset{n\to \infty }{lim\; sup}{\displaystyle \frac{7ϵ}{(1-\delta )}}.$$

Considering the results of Theorem 1, we know that ${lim}_{n\to \infty }{x}_n=x^{*}$. Using the above, together with the conditions that ${lim}_{n\to \infty }{\tilde{x}}_n={\tilde{x}}^{*}$, we obtain

$$\parallel x^{*}-{\tilde{x}}^{*}\parallel \le {\displaystyle \frac{7ϵ}{1-\delta }}.$$

The proof of Theorem 2 is completed. □

6. Stability Results

In this section, we prove some stability results of our novel iterative process.

Theorem 3.

Let $(E,\parallel .\parallel )$ be an arbitrary Banach space and $T:C\to C$ be a contraction mapping defined by (11). Suppose there exists $x^{*}\in F\left(T\right)$ such that the IA-iterative process (8) satisfies ${\mathrm{\Sigma }}_{n=0}^{\infty }{\gamma }_n=\infty$ and ${\gamma }_n\le \gamma \in (0,1)$ for each $n\in \mathbb{N}$, ${\left\{x_n\right\}}_{n=1}^{\infty }$ converges to $x^{*}$. Then, the IA-iterative process (8) is T-stable.

Proof. 

Suppose that ${\left\{a_n\right\}}_{n=1}^{\infty }\subset E$ is an arbitrary sequence; put

$${\epsilon }_n=\parallel a_n-T{x}_{n+1}\parallel ,$$

(38)

where

$$x_{n+1}=T\left(y_n\right).$$

(39)

Therefore, with the IA-iterative scheme (8), and using contractive condition (11) with $\delta \in (0,1)$, we have

$$\begin{array}{ccc}\parallel a_n-x^{*}\parallel \hfill & \le \hfill & \parallel a_n-T{x}_{n+1}\parallel +\parallel T{x}_{n+1}-x^{*}\parallel \hfill \\ & \le \hfill & {\epsilon }_n+\delta [\parallel x_{n+1}-x^{*}\parallel ]\hfill \\ & =\hfill & {\epsilon }_n+\delta [\parallel T\left(y_n\right)-x^{*}\parallel ]\hfill \\ & \le \hfill & {\epsilon }_n+{\delta }^2[\parallel y_n-x^{*}\parallel ].\hfill \end{array}$$

(40)

Using (8), (11) and (40)

$$\begin{array}{ccc}\parallel y_n-x^{*}\parallel \hfill & =\hfill & \parallel T[(1-{\lambda }_n)T\left(z_n\right)+{\lambda }_{n}T\left(x_n\right)]-x^{*}\parallel \hfill \\ & \le \hfill & \delta [(1-{\lambda }_n)\delta \parallel z_n-x^{*}\parallel +{\lambda }_n\parallel T{x}_n-x^{*}\parallel ]\hfill \\ & \le \hfill & (1-{\lambda }_n)\delta \parallel z_n-x^{*}\parallel +{\lambda }_n\delta \parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(41)

Using (8), (11) and (41), we have

$$\begin{array}{ccc}\parallel z_n-x^{*}\parallel \hfill & =\hfill & \parallel {\alpha }_n{x}_n+{\beta }_n{x}_n+{\gamma }_{n}T\left(x_n\right)-x^{*}\parallel \hfill \\ & \le \hfill & ({\alpha }_n+{\beta }_n)\parallel x_n-x^{*}\parallel +{\gamma }_n\parallel T\left(x_n\right)-x^{*}\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +{\gamma }_n\delta \parallel x_n-x^{*}\parallel \hfill \\ & \le \hfill & [1-{\gamma }_n(1-\delta )]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(42)

Inserting (42) into (41), we obtain

$$\begin{array}{ccc}\parallel y_n-x^{*}\parallel \hfill & \le \hfill & (1-{\lambda }_n)\delta \parallel z_n-x^{*}\parallel +\delta {\lambda }_n\parallel x_n-x^{*}\parallel \hfill \\ & \le \hfill & (1-{\lambda }_n)\delta [1-{\gamma }_n(1-\delta )]\parallel x_n-x^{*}\parallel +{\lambda }_n\delta \parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(43)

Putting (43) into (40), we obtain

$$\begin{array}{ccc}\parallel a_n-x^{*}\parallel \hfill & \le \hfill & {\epsilon }_n+{\delta }^2[\parallel y_n-x^{*}\parallel ]\hfill \\ & \le \hfill & {\epsilon }_n+{\delta }^2[(1-{\lambda }_n)\delta [1-{\gamma }_n(1-\delta )]\parallel x_n-x^{*}\parallel +{\lambda }_n\delta \parallel x_n-x^{*}\parallel ]\hfill \\ & \le \hfill & {\epsilon }_n+{\delta }^3[1-{\gamma }_n(1-\delta )]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(44)

Considering that ${\gamma }_n\le \gamma \in (0,1)$ for all $n\in \mathbb{N},$. It follows by Lemma 2 and (44) that

$$\underset{n\to \infty }{lim}{a}_n=x^{*}.$$

(45)

Conversely, let ${lim}_{n\to \infty }{a}_n=x^{*}$. Using (11), (39) and (40), we obtain

$$\begin{array}{ccc}{\epsilon }_n\hfill & =\hfill & \parallel a_n-T{g}_{n+1}\parallel \hfill \\ & \le \hfill & \parallel a_n-x^{*}\parallel +\parallel x^{*}-T{x}_{n+1}\parallel \hfill \\ & \le \hfill & \parallel a_n-x^{*}\parallel +\delta [\parallel x^{*}-x_{n+1}\parallel ]\hfill \\ & \le \hfill & \parallel a_n-x^{*}\parallel +\delta [\parallel T{y}_n-x^{*}\parallel ]\hfill \\ & \le \hfill & \parallel a_n-x^{*}\parallel +{\delta }^2[\parallel y_n-x^{*}\parallel ]\hfill \\ & \le \hfill & \parallel a_n-x^{*}\parallel +{\delta }^5[1-{\gamma }_n(1-\delta )]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(46)

Therefore, we have

$$\begin{array}{ccc}{\epsilon }_n\hfill & \le \hfill & \parallel a_n-x^{*}\parallel +{\delta }^5[1-{\gamma }_n(1-\delta )]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(47)

So,

$$\underset{n\to \infty }{lim}{\epsilon }_n=0.$$

It implies that IA-iterative process (8) is T-stable. □

7. Application to Disease Model

Many interested models have been developed to obtain the solutions of infectious diseases. These models have actually become various differential equations and the case remains how to solve the various differential equations. In this application, we study a special case of infection disease model, i.e, the mathematical modeling of acquired immune deficiency syndrome (AIDS). Consequently, comprehending the dynamics of acquired immune deficiency syndrome (AIDS) and evaluating prospective methods of preventing and treatment have both outstandingly benefited from the use of mathematical modeling. Based on this, a fractional differential equation emanated from the mathematical modeling of the prevention and treatment of AIDS, which was developed by Caputo–Fabrizio and was named the Caputo–Fabrizio fractional differential equation [16]. Moreover, solving the Caputo–Fabrizio differential equation is taxing, and many authors have suggested ways of solving the Caputo–Fabrizio differential equation. Krasnoselskii’s and Banach’s fixed-point approach in combination with the kernels were part of the methods adopted in solving the Caputo–Fabrizio fractional differential equation (CFFD). In this study, we suggest that the best approach is to use our newer and faster fixed-point iterative process called the IA-iterative scheme (8) in solving the Caputo–Fabrizio fractional differential equation (CFFD). Furthermore, this novel iterative scheme can be applied in solving wider classes of diseases models, such as diseases with direct transmission among individuals, as in the case of HIV with long latency phases. The scheme can also be applied in solving models of diseases with indirect transmission via vectors (see, e.g., [25]).

Consider the following Caputo–Fabrizio fractional differential equation.

$$\left\{\begin{array}{ccc}{}_{0 }{}^{LC}D_t^{\vartheta }{h}_t=F(t,h\left(t\right)),0<\varrho \le 1\hfill & \hfill & \\ h\left(0\right)=h_0.\hfill & \hfill \end{array}\right.$$

(48)

The solution to Equation (48) is provided by Lemma 5 if and only if the right side vanishes at 0, i.e.,

$$h\left(t\right)+h_0+GF(t,h\left(t\right))+G^{\prime }{\int }_0^{t}F(\xi ,h\left(\mathrm{\Theta }\right))d\mathrm{\Theta },$$

(49)

where $G={\displaystyle \frac{1-\varrho }{K\left(\varrho \right)}}$ and $G^{\prime }={\displaystyle \frac{\varrho }{K\left(\varrho \right)}}.$

Moreover, define the Banach space $D=L[0,T]$ and the norm of $D=L[0,T]$ on $0<t\le T<\infty$ by

$$\parallel h\parallel =\underset{t\in [0,T]}{sup}\left\{\right|h\left(t\right)|:h\in D\}.$$

Assume that the following assumptions are met.

• $\left(C_1\right)$ Let $k_F>0$ be a constant, then
• $|F(t,h\left(t\right))-F(t,h^{\prime }\left(t\right))|\le K_F|h-h^{\prime }|.$
• $\left(C_2\right)$ Assume that ${\gamma }_n(1-({\lambda }_n+G^{\prime }{K}_F(1+T)))<1$.

We now prove the next theorem as follows

Theorem 4.

Assume that the conditions $\left(C_1\right)-\left(C_2\right)$ are met. Then, problems (48) and (49) have a unique solution; say $x^{*},$ in $(D[0,T],\mathbb{R})\cap D^1([0,T],\mathbb{R})$, then the new and faster iterative process named IA-iterative scheme (8) with ${\alpha }_n$, ${\beta }_n$, ${\gamma }_n$ and ${\lambda }_n$ are real sequences in $(0,1)$, such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ and ${\mathrm{\Sigma }}_{n=1}^{\infty }{\gamma }_n(1-({\lambda }_n+G^{\prime }{K}_F(1+T)))=\infty ,$ converges to $x^{*}.$

Proof. 

We consider the Banach space $D=\left(L\right[0,T],\parallel .\parallel )$, where $\parallel .\parallel$ is the norm of $D=L[0,T]$. Let ${\left\{x_n\right\}}_{n=1}^{\infty }$ be an iterative sequence generated by a newer and a faster iterative process named the IA-iterative scheme for an operator $T:D\to D$ defined by

$$T\left(x\right)\left(t\right)=x_0+GF(t,x_n\left(t\right))+G^{\prime }{\int }_0^{t}F(t,x_n\left(s\right))ds.$$

(50)

Consequently, we will show that $x_n$ converges to the solution $x^{*}$ as n tends to $\infty .$ Now, using (8), (50), and $\left(C_1\right)$, we have the following

$$\begin{array}{ccc}\parallel z_n-x^{*}\parallel \hfill & =\hfill & \parallel {\alpha }_n{x}_n+{\beta }_n{x}_n+{\gamma }_{n}T{x}_n-x^{*}\parallel \hfill \\ & =\hfill & \parallel (1-{\gamma }_n)x_n+{\gamma }_{n}T{x}_n-x^{*}\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +{\gamma }_n\parallel T{x}_n-T{x}^{*}\parallel \hfill \\ & =\hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +{\gamma }_n|x_0+GF(t,x_n\left(t\right))+{\int }_0^{t}GF(t,x_n\left(s\right))ds\hfill \\ & -\hfill & [x_0+GF(t,x^{*}\left(t\right))+G^{\prime }{\int }_0^{t}F(s,x^{*}\left(s\right))ds]|\hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +{\gamma }_n|GF(t,x_n\left(t\right))-GF(t,x^{*}\left(t\right))|\hfill \\ & +\hfill & {\gamma }_n|G^{\prime }{\int }_0^{t}F(t,x_n\left(s\right))ds-G^{\prime }{\int }_0^{t}F(t,x^{*}\left(s\right))ds|\hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +{\gamma }_n|GF(t,x_n\left(t\right))-GF(t,x^{*}\left(t\right))|\hfill \\ & +\hfill & {\gamma }_n{G}^{\prime }{\int }_0^t\left[\right|F(t,x_n\left(s\right))ds-F(t,x^{*}\left(s\right))\left|\right]ds\hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +\underset{t\in [0,T]}{sup}|GF(t,x_n\left(t\right))-GF(t,x^{*}\left(t\right))|\hfill \\ & +\hfill & {\gamma }_n{G}^{\prime }\underset{t\in [0,T]}{sup}[{\int }_0^t|F(t,x_n\left(s\right))-F(t,x^{*}\left(s\right))\left|ds\right]\hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +{\gamma }_{n}G{K}_F\parallel x_n-x^{*}\parallel +{\gamma }_n{G}^{\prime }{K}_{F}T\parallel x_n-x^{*}\parallel \hfill \\ & \le \hfill & (1-{\gamma }_n)\parallel x_n-x^{*}\parallel +{\gamma }_n{G}^{\prime }{K}_F\parallel x_n-x^{*}\parallel +{\gamma }_n{G}^{\prime }{K}_{F}T\parallel x_n-x^{*}\parallel \hfill \\ & \le \hfill & [1-{\gamma }_n(1-G^{\prime }{K}_F(1+T))]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(51)

Let $f_n=(1-{\lambda }_n)T{z}_n+{\lambda }_{n}T{x}_n$; then, using (8), (50), (51), and $\left(C_1\right)$, we obtain

$$\begin{array}{ccc}\parallel y_n-x^{*}\parallel \hfill & =\hfill & \parallel T{f}_n-x^{*}\parallel \hfill \\ & =\hfill & \parallel T{f}_n-T{x}^{*}\parallel \hfill \\ & \le \hfill & |x_0+GF(t,f_n\left(t\right))+G^{\prime }{\int }_0^{t}F(t,f_n\left(s\right))ds\hfill \\ & -\hfill & [x_0+GF(t,x^{*}\left(t\right))+G^{\prime }{\int }_0^{t}F(s,x^{*}\left(s\right))ds]|\hfill \\ & \le \hfill & |GF(t,f_n\left(t\right))-GF(t,x^{*}\left(t\right))|+G^{\prime }{\int }_0^t\left[\right|F(t,f_n\left(s\right))ds-F(t,x^{*}\left(s\right))\left|\right]ds\hfill \\ & \le \hfill & \underset{t\in [0,T]}{sup}|GF(t,f_n\left(t\right))-GF(t,x^{*}\left(t\right))|\hfill \\ & +\hfill & G^{\prime }\underset{t\in [0,T]}{sup}[{\int }_0^t|F(t,f_n\left(s\right))-F(t,x^{*}\left(s\right))\left|ds\right]\hfill \\ & \le \hfill & G{K}_F\parallel f_n-x^{*}\parallel +G^{\prime }{K}_{F}T\parallel f_n-x^{*}\parallel \hfill \\ & \le \hfill & G^{\prime }{K}_F(1+T)\parallel f_n-x^{*}\parallel \hfill \\ & \le \hfill & \parallel f_n-x^{*}\parallel .\hfill \end{array}$$

(52)

Since $f_n=(1-{\lambda }_n)T{z}_n+{\lambda }_{n}T{x}_n$ and considering (8), (50), (52), and $\left(C_1\right)$, we have

$$\begin{array}{ccc}\parallel y_n-x^{*}\parallel \hfill & \le \hfill & \parallel f_n-x^{*}\parallel \hfill \\ & =\hfill & (1-{\lambda }_n)\parallel T{z}_n-x^{*}\parallel +{\lambda }_n\parallel T{x}_n-x^{*}\parallel \hfill \\ & \le \hfill & (1-{\lambda }_n)\left[\right|x_0+GF(t,z_n\left(t\right))+G^{\prime }{\int }_0^{t}F(t,z_n\left(s\right))ds\hfill \\ & -\hfill & [x_0+GF(t,x^{*}\left(t\right))+G^{\prime }{\int }_0^{t}F(s,x^{*}\left(s\right))ds]\left|\right]\hfill \\ & +\hfill & {\lambda }_n\left[\right|x_0+GF(t,x_n\left(t\right))+G^{\prime }{\int }_0^{t}F(t,z_n\left(s\right))ds\hfill \\ & -\hfill & [x_0+GF(t,x^{*}\left(t\right))+G^{\prime }{\int }_0^{t}F(s,x^{*}\left(s\right))ds]\left|\right]\hfill \\ & \le \hfill & (1-{\lambda }_n)|GF(t,z_n\left(t\right))-GF(t,x^{*}\left(t\right))|+(1-{\lambda }_n)G^{\prime }{\int }_0^t\left[\right|F(t,z_n\left(s\right))ds-F(t,x^{*}\left(s\right))\left|\right]ds\hfill \\ & +\hfill & {\lambda }_n|GF(t,x_n\left(t\right))-GF(t,x^{*}\left(t\right))|+{\lambda }_n{G}^{\prime }{\int }_0^t\left[\right|F(t,x_n\left(s\right))ds-F(t,x^{*}\left(s\right))\left|\right]ds\hfill \\ & \le \hfill & (1-{\lambda }_n)\underset{t\in [0,T]}{sup}|GF(t,z_n\left(t\right))-GF(t,x^{*}\left(t\right))|\hfill \\ & +\hfill & (1-{\lambda }_n)G^{\prime }\underset{t\in [0,T]}{sup}[{\int }_0^t|F(t,z_n\left(s\right))-F(t,x^{*}\left(s\right))\left|ds\right]\hfill \\ & +\hfill & {\lambda }_n\underset{t\in [0,T]}{sup}|GF(t,x_n\left(t\right))-GF(t,x^{*}\left(t\right))|+{\lambda }_n{G}^{\prime }\underset{t\in [0,T]}{sup}[{\int }_0^t|F(t,x_n\left(s\right))-F(t,x^{*}\left(s\right))\left|ds\right]\hfill \\ & \le \hfill & (1-{\lambda }_n)G{K}_F\parallel z_n-x^{*}\parallel +(1-{\lambda }_n)G^{\prime }{K}_{F}T\parallel z_n-x^{*}\parallel \hfill \\ & +\hfill & {\lambda }_{n}G{K}_F\parallel x_n-x^{*}\parallel +{\lambda }_n{G}^{\prime }{K}_{F}T\parallel x_n-x^{*}\parallel \hfill \\ & \le \hfill & (1-{\lambda }_n)G^{\prime }{K}_F(1+T)\parallel z_n-x^{*}\parallel +{\lambda }_n{G}^{\prime }{K}_F(1+T)\parallel x_n-x^{*}\parallel \hfill \\ & \le \hfill & (1-{\lambda }_n)G^{\prime }{K}_F(1+T)[1-{\gamma }_n(1-G^{\prime }{K}_F(1+T))]\parallel x_n-x^{*}\parallel +{\lambda }_n{G}^{\prime }{K}_F(1+T)\parallel x_n-x^{*}\parallel \hfill \\ & \le \hfill & [1-{\gamma }_n(1-({\lambda }_n+G^{\prime }{K}_F(1+T)))]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(53)

Considering (8), (50), (53), and $\left(C_1\right)$, we have

$$\begin{array}{ccc}\parallel x_{n+1}-x^{*}\parallel \hfill & =\hfill & \parallel T{y}_n-T{x}^{*}\parallel \hfill \\ & \le \hfill & |x_0+GF(t,y_n\left(t\right))+{\int }_0^{t}GF(t,y_n\left(s\right))ds\hfill \\ & -\hfill & [x_0+GF(t,x^{*}\left(t\right))+G^{\prime }{\int }_0^{t}F(s,x^{*}\left(s\right))ds]|\hfill \\ & \le \hfill & |GF(t,y_n\left(t\right))-GF(t,x^{*}\left(t\right))|+G^{\prime }{\int }_0^t\left[\right|F(t,y_n\left(s\right))ds-F(t,x^{*}\left(s\right))\left|\right]ds\hfill \\ & \le \hfill & \underset{t\in [0,T]}{sup}|GF(t,y_n\left(t\right))-GF(t,x^{*}\left(t\right))|\hfill \\ & +\hfill & G^{\prime }\underset{t\in [0,T]}{sup}[{\int }_0^t|F(t,y_n\left(s\right))-F(t,x^{*}\left(s\right))\left|ds\right]\hfill \\ & \le \hfill & G^{\prime }{K}_F\parallel y_n-x^{*}\parallel +G^{\prime }{K}_{F}T\parallel y_n-x^{*}\parallel \hfill \\ & =\hfill & G^{\prime }{K}_F(1+T)\parallel y_n-x^{*}\parallel \hfill \\ & \le \hfill & \parallel y_n-x^{*}\parallel \hfill \\ & \le \hfill & [1-{\gamma }_n(1-({\lambda }_n+G^{\prime }{K}_F(1+T)))]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(54)

Therefore, we have the following from (54)

$$\begin{array}{ccc}\parallel x_{n+1}-x^{*}\parallel \hfill & \le \hfill & [1-{\gamma }_n(1-({\lambda }_n+G^{\prime }{K}_F(1+T)))]\parallel x_n-x^{*}\parallel .\hfill \end{array}$$

(55)

From (55) and considering Lemma 2, we take ${\mu }_n={\gamma }_n(1-({\lambda }_n+G^{\prime }{K}_F(1+T)))<1$

and $\parallel x_n-x^{*}\parallel =s_n,$; then, the conditions of Lemma 2 are satisfied.

Hence, ${lim}_{n\to \infty }\parallel x_n-x^{*}\parallel =0.$

It follows that the proof of Theorem 4 is completed. □

8. Numerical Examples

Numerically, we compare our iteration process with seven existing iteration schemes. In Table 1 and Table 2 below, we compare the speed of convergence of various iterative schemes, viz: Picard, Mann, Ishikawa, Kransel’kii, Ullah and Arshad, Noor, Picard–Ishikawa, and the IA-iterative scheme. Choose ${\alpha }_n={\beta }_n=\lambda ={\gamma }_n={\lambda }_n={\displaystyle \frac{1}{2}}$ with the initial value $x_0=0.1$ and the operator $T\left(x\right)={\displaystyle \frac{1}{5}}x+3$, where $F\left(T\right)=\left\{3.75\right\}.$. Using Python 3.7, we obtain the following numerical results:

Table 1. A comparison of the speed of convergence among various iterative processes.

Step	Picard	Mann	Ishikawa	Krasnosel’kii	Ullah and Arshad
0	0.100000	0.1000000	0.1000000	0.1000000	0.1000000
1	3.02000000	1.56000000	1.706000000	1.56000000	3.6624000000
2	3.604000000	2.436000000	2.60536000000	2.436000000	3.7478976000000
3	3.7208000000	2.9616000000	3.1090016000000	2.9616000000	3.7499495424000000
4	3.74416000000	3.2696000000	3.391040896000000	3.27696000000	3.7499987890176000
5	3.74883200000	3.46617600000	3.3.5489829017599996	3.4661760000	3.7499999709364227
6	3.74976640000	3.5797056000	3.637430424985599800	3.5797056000	3.7499999993024744
7	3.74995328000	3.64782336000	3.68696103799193600	3.64782336000	3.74999999983200
8	3.49990656000	3.688694016000	3.7146981812755000	3.68869401600	3.749999999999598
9	3.7499981312	3.713216409600	3.7302309815142713	3.71316409600	3.74999999999902
10	3.74999962624	3.72792984576	3.738929349647992	3.72792984576	3.7500000000000
⋮	⋮	⋮	⋮	⋮	⋮

Table 2. A comparison of the speed of convergence among various iterative processes.

Step	Noor	Picard–Ishikawa	IA-Iteration
0	0.1000000	0.1000000	0.1000000
1	1.720600000	3.314120000	3.7268400000
2	2.621653600000	3.7042144000000	3.75730545600000
3	3.1226394016000	3.74487201280000	3.7575613658304
4	3.4011875072896	3.7494256654336000	3.7575635154730000
5	3.5560602540530173	3.7499356745285635	3.7575635335299733
6	3.642169501253478	3.749992795547199	3.757563533681652
7	3.69004624269693	3.7499991931012864	3.757563533682926
8	3.7166657109394947	3.749999909627344	3.7575635336829367
9	3.731466135282359	3.7499999898782628	3.7575635336829367
10	3.7396951712169915	3.7499999988663655	3.7575635336829367
⋮	⋮	⋮

Moreover, the Table 1 and Table 2 show the numerical data obtained from the operator T defined above with the initial value $x_0=0.1$. Clearly, we use the numerical data to compare the rate of convergence of the IA-iterative process among other existing iterative schemes viz: Picard, Ishikawa, Kransel’skii, Ullah & Arshad, Noor, and Picard–Ishikawa.

Remark 1.

Clearly, from Table 1 and Table 2, we compare the IA-iteration process numerically among other existing iterative processes, i.e., Picard, Mann, Ishikawa, Kransel’skii, Ullah & Arshad, Noor, and Picard–Ishikawa, to the fixed point of T.

Furthermore, we provide a graphical representation of the numerical data in Table 1 and Table 2 above as follows.

Remark 2.

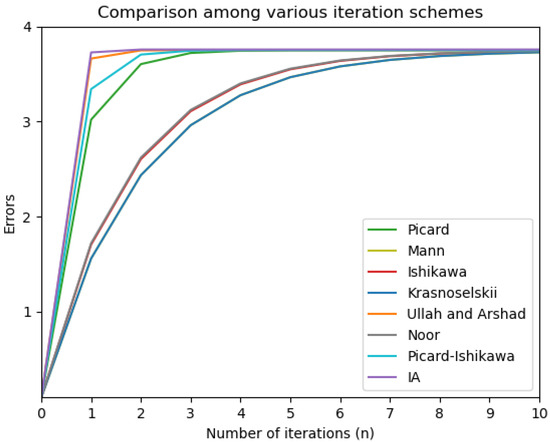
Clearly, from Table 1 and Table 2 and Figure 1, we see that the IA-iteration process converges faster than Picard, Mann, Ishikawa, Kransel’skii, Ullah & Arshad, Noor, and Picard–Ishikawa to the fixed point of $T,$ which is 3.75.

Figure 1. Comparison of rate of convergence among various iteration schemes.

9. Conclusions

In this paper, we introduced a new and a faster iterative scheme. Moreover, we then proved that the constructed IA-type iterative process converges strongly to the fixed point of multivalued nonexpansive mapping T in uniformly convex Banach spaces. Consequently, we showed that the IA-iterative process is stable and data dependent. We showed that the newly iterative method converges faster and is more efficient than some of the iterative processes in the literature, i.e., Picard, Mann, Ishikawa, Kranselskii, Picard–Mann, Kranselskii, and Picard–Ishikawa, among others. In terms of application, we suggested a newer and faster method for solving one of the Caputo’s derivatives that emanated from the infection disease models, named the Caputo–Fabrizio fractional differential equation. Our results extend, unify, and improve several of the known results in the literature.