Uncertain Particle Filtering: A New Real-Time State Estimation Method for Failure Prognostics
Abstract
1. Introduction
- (1)
- A novel Uncertain Particle Filtering (UPF) method based on Uncertainty Theory is proposed, which significantly improves sensitivity to dynamic parameter changes compared to traditional PF methods.
- (2)
- Advanced resampling techniques tailored for the UPF method are introduced to address particle phagocytosis, thereby enhancing computational accuracy.
- (3)
- The effectiveness of the proposed UPF method is validated through two case studies: the degradation of a capacitor in an electromagnetic railgun and the degradation of a battery. These case studies demonstrate its superior performance in real-time state estimation and RUL prediction.
- (4)
- A comprehensive discussion is provided on the application of the UPF method in real-world scenarios, such as aerospace systems and industrial control systems, highlighting its potential to address challenges such as real-time prediction failures.
2. Preliminaries
2.1. Uncertainty Theory
2.2. Likelihood Function and Posterior Uncertainty Function
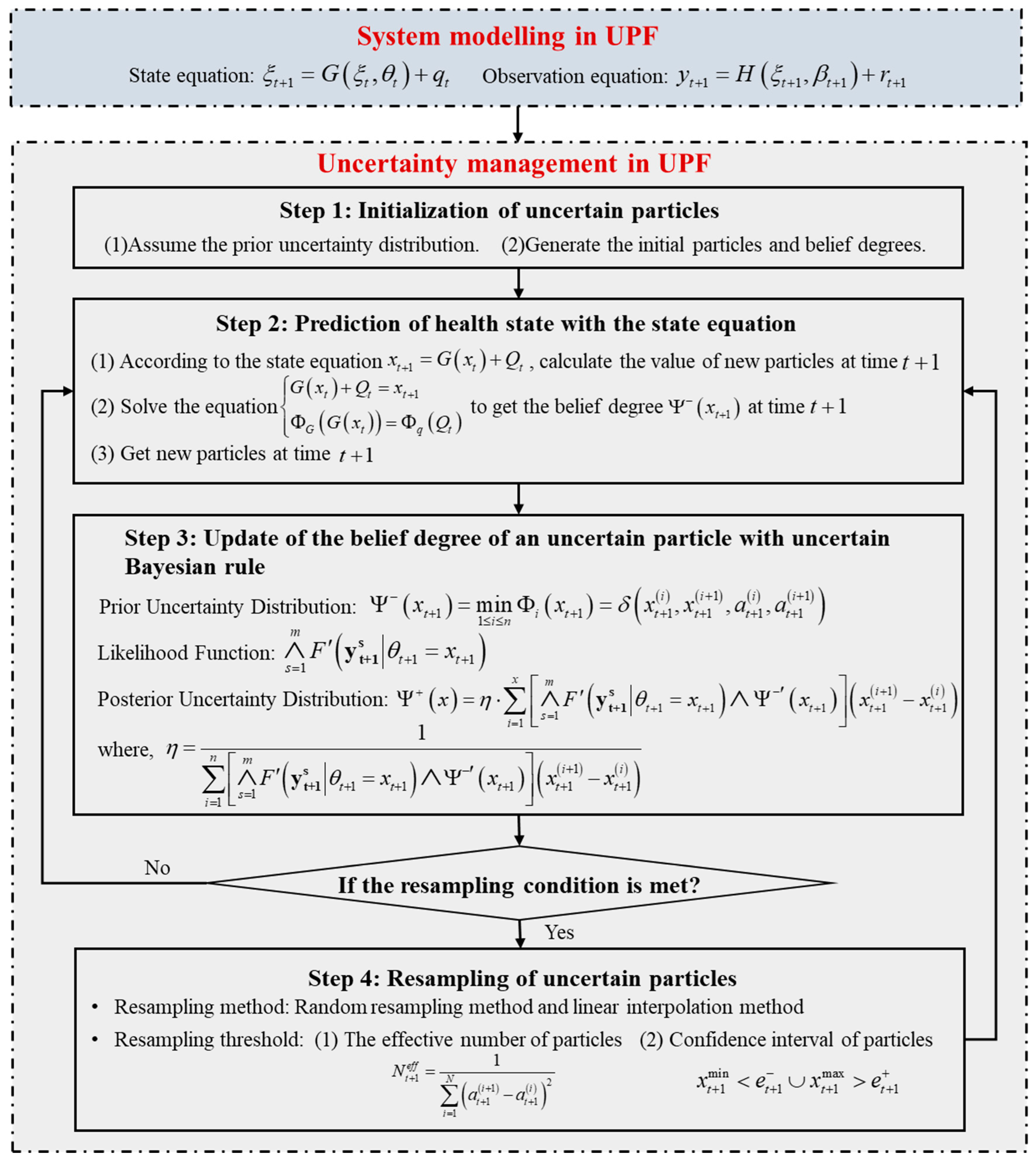
3. The Proposed Uncertain Particle Filtering Method
3.1. System Modeling in Uncertain Particle Filtering
3.2. Uncertainty Management in UPF
3.2.1. Initialization of Uncertain Particles
3.2.2. Prediction of Health State with the State Equation
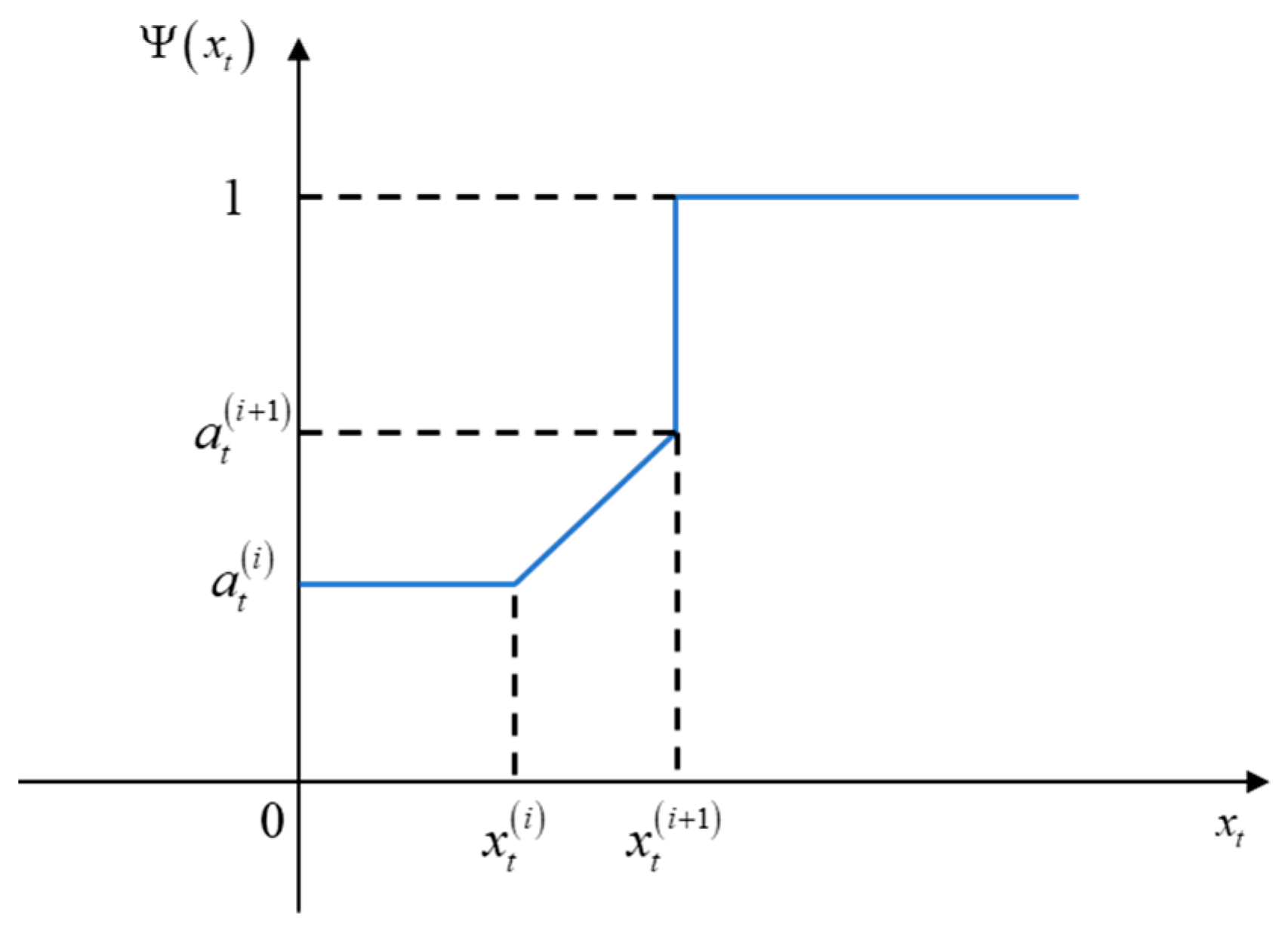
3.2.3. Update of the Belief Degree of an Uncertain Particle with Uncertain Bayesian Rule
- (1)
- Prior distribution
- (2)
- Uncertain maximum likelihood
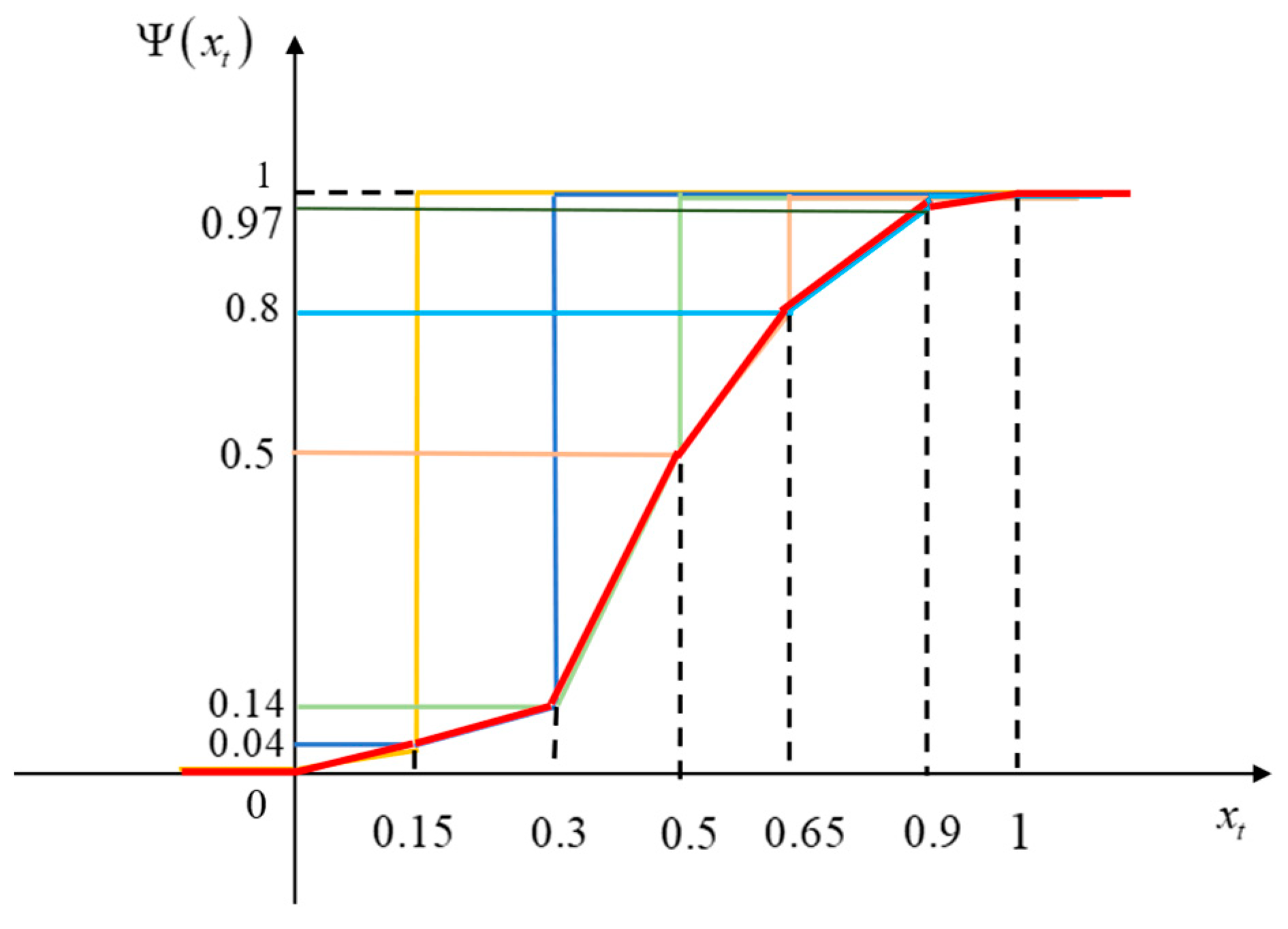
3.2.4. Resampling of Uncertain Particles
Resampling Procedure
- (1)
- Derive the posterior uncertainty distribution of and the uncertain particles through initialization, prediction, and update steps mentioned in previous subsections.
- (2)
- Determine the number of resampling particles. Generally, the number of particles should be the same as the number of original particles.
- (3)
- Determine the value range of the system state for resampling. In this work, the 95% confidence interval is taken as the value range for resampling.
- (4)
- Randomly generate the values of new uncertain particles. In the predefined value range, random numbers are generated in the order ranging from smallest to largest. These random numbers represent the values of particles after resampling, that is, .
- (5)
- Calculate the belief degree of new uncertain particles. With the linear interpolation method in Equation (24), the corresponding belief degree of new particles can be obtained.
Resampling Threshold
- (1)
- The effective number of uncertain particles
- (2)
- Confidence interval of particles
4. Case Studies
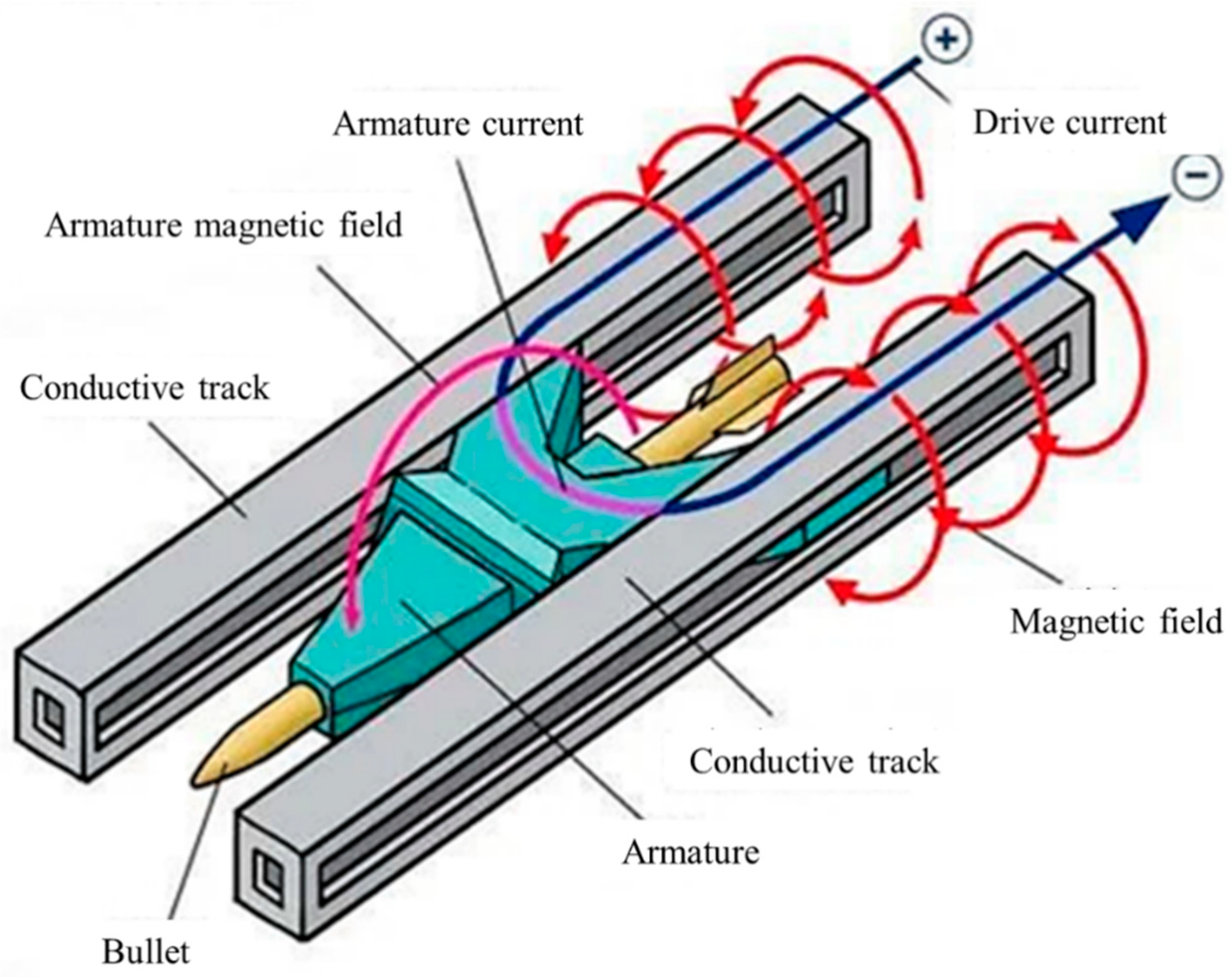
4.1. Degradation State Estimation of the Capacitor in the Enhanced Electromagnetic Railgun
4.1.1. System Modeling of the Energy Storage Capacitor
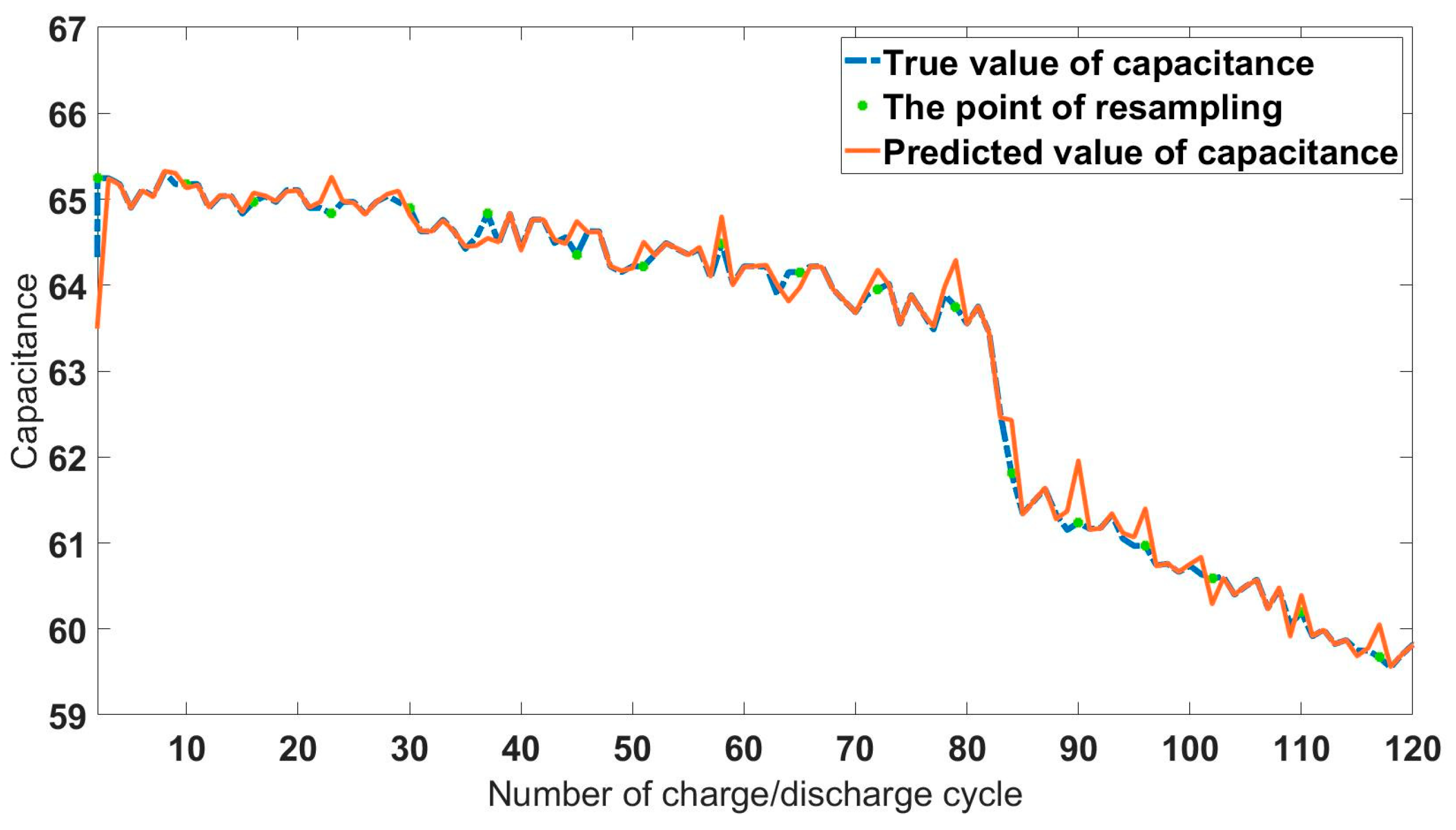
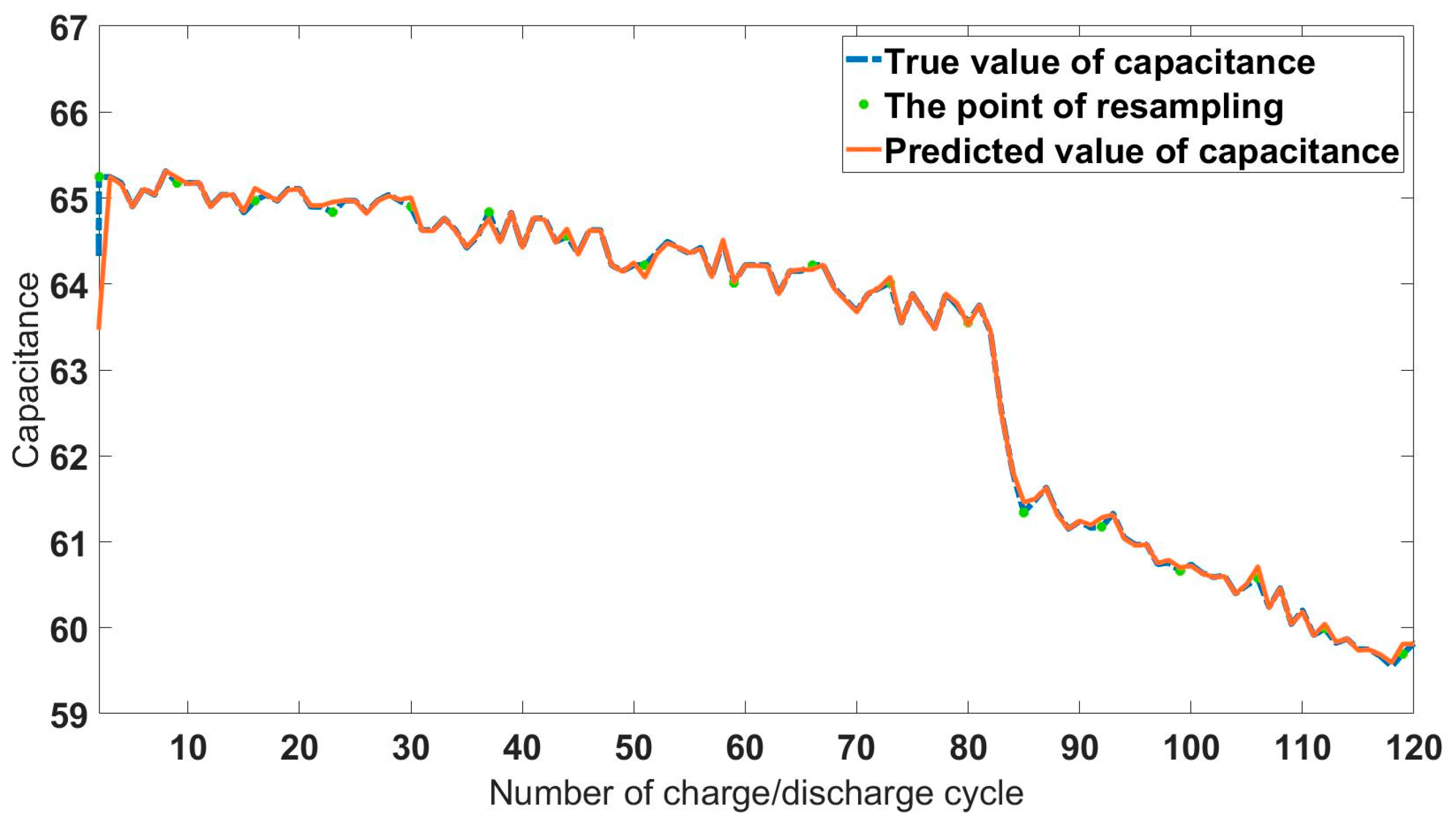
4.1.2. Degradation State Estimation Using UPF Method
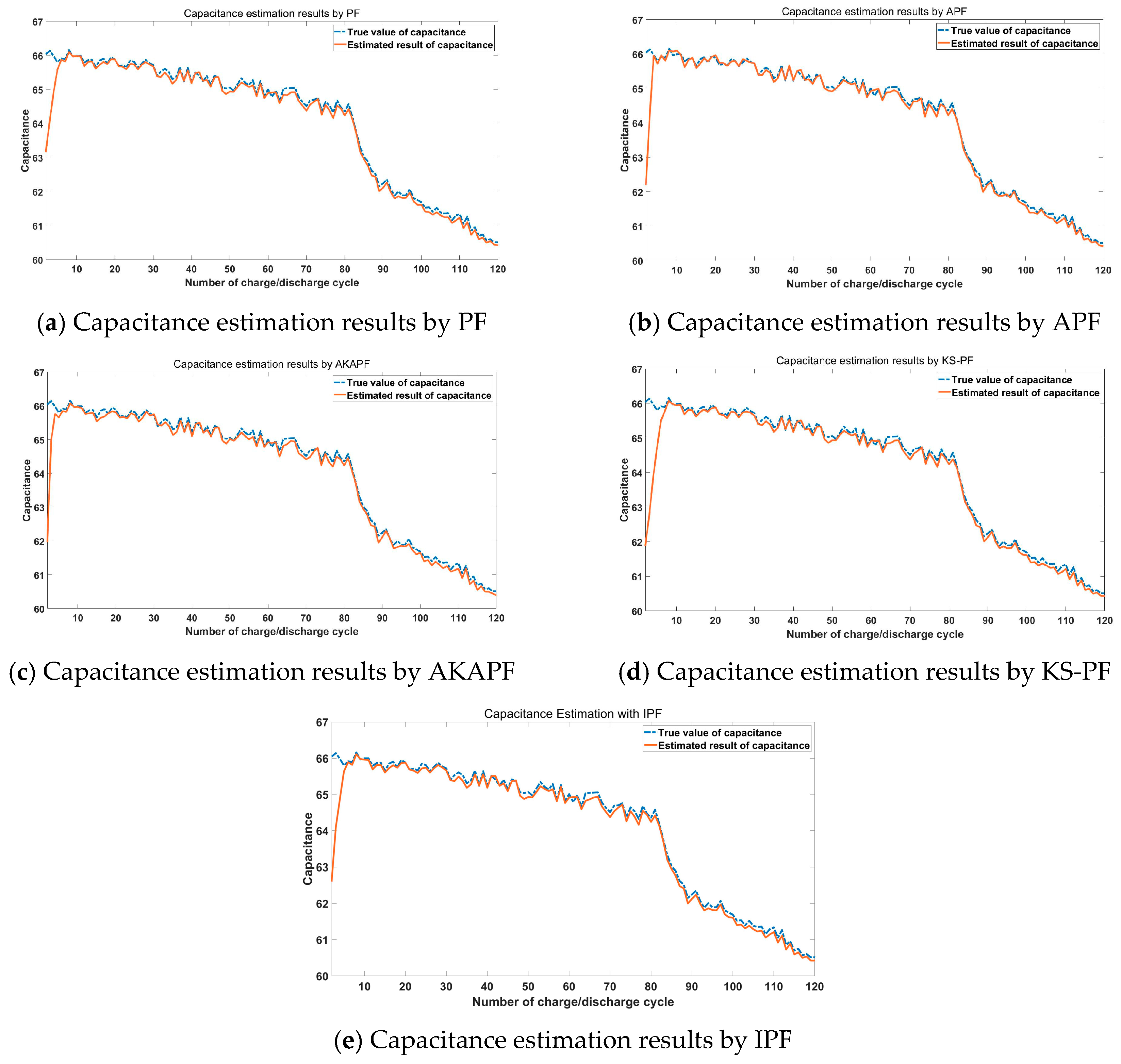
4.1.3. Comparative Studies
4.2. Unknown Parameter Estimation of Battery Degradation Model
4.2.1. System Modeling of the Battery Degradation Model
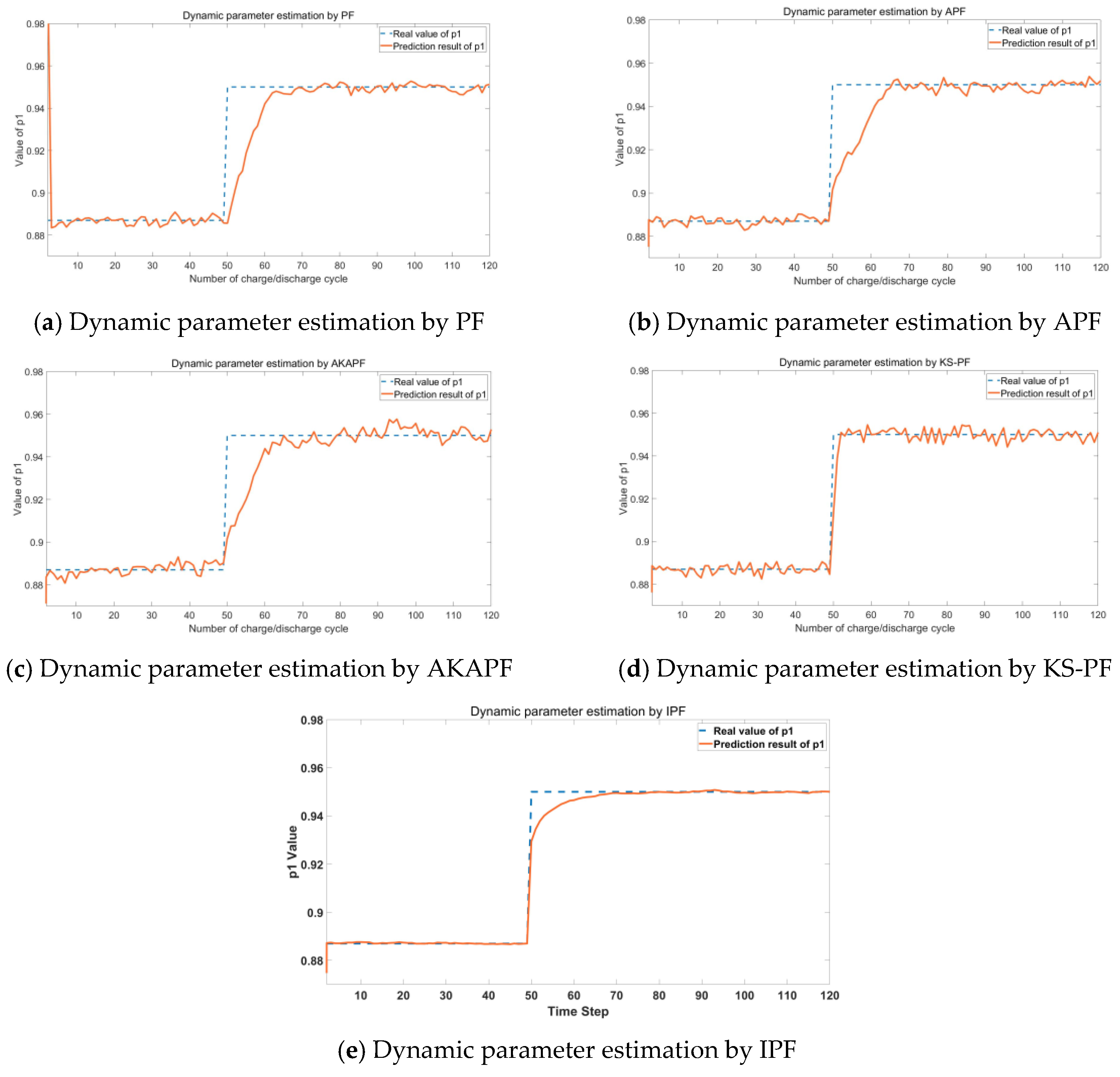
4.2.2. Parameter Estimation and Comparison Results
4.2.3. Computational Complexity Analysis
- (1)
- Prediction: Propagating each of the particles through the state transition model, costing .
- (2)
- Weight Update: Calculating the likelihood for each particle, which is .
- (3)
- Resampling: It is typically performed in using efficient algorithms.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, S.; Pan, K.; Liu, J.; Chen, Y. Empirical study on fine-tuning pre-trained large language models for fault diagnosis of complex systems. Reliab. Eng. Syst. Saf. 2024, 252, 110382. [Google Scholar] [CrossRef]
- Wang, C.; Liu, J. Anomaly Detection Method for Complex Systems Based on a Domain-Adaptive Causal Decoupling Model. IEEE Trans. Ind. Inform. 2024. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, C.; Zio, E.; Liu, J. Fault detection in complex mechatronic systems by a hierarchical graph convolution attention network based on causal paths. Reliab. Eng. Syst. Saf. 2024, 243, 109872. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, S.; Wang, C. Causal Graph Attention Network with Disentangled Representations for Complex Systems Fault Detection. Reliab. Eng. Syst. Saf. 2023, 235, 109232. [Google Scholar] [CrossRef]
- Tang, H.; Du, Y.; Dai, H.-L. Rolling element bearing diagnosis based on probability box theory. Appl. Math. Model. 2020, 80, 944–960. [Google Scholar] [CrossRef]
- Abdi, H. The method of least squares. Encycl. Meas. Stat. 2007, 1, 530–532. [Google Scholar]
- Wooldridge, J.M. Applications of generalized method of moments estimation. J. Econ. Perspect. 2001, 15, 87–100. [Google Scholar] [CrossRef]
- Pan, J.; Fang, K. Maximum likelihood estimation. In Growth Curve Models and Statistical Diagnostics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 77–158. [Google Scholar]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Zhang, Q.B.; Wang, P.; Chen, Z.H. An improved particle filter for mobile robot localization based on particle swarm optimization. Expert Syst. Appl. 2019, 135, 181–193. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.-C.; Zerhouni, N. Particle filter-based prognostics: Review, discussion and perspectives. Mech. Syst. Signal Process. 2016, 72–73, 2–31. [Google Scholar] [CrossRef]
- Li, T.; Sun, S.; Sattar, T.P.; Corchado, J.M. Fight sample degeneracy and impoverishment in particle filters: A review of intelligent approaches. Expert Syst. Appl. 2014, 41, 3944–3954. [Google Scholar] [CrossRef]
- Kanthalakshmi, S.; Raghappriya, M. Active fault diagnosis of 2 DoF helicopter using particle filter-based log-likelihood ratio. Int. J. Control 2022, 95, 3148–3165. [Google Scholar] [CrossRef]
- Zhang, Y.; Vacca, A.; Gong, G.; Yang, H. Quantitative Fault Diagnostics of Hydraulic Cylinder Using Particle Filter. Machines 2023, 11, 1019. [Google Scholar] [CrossRef]
- Li, T.; Bolic, M.; Djuric, P.M. Resampling methods for particle filtering: Classification, implementation, and strategies. IEEE Signal Process. Mag. 2015, 32, 70–86. [Google Scholar] [CrossRef]
- Zhao, F.F.; Cai, R.J. Adaptive particle filter for state estimation with application to non-linear system. IET Signal Process. 2022, 16, 1023–1033. [Google Scholar] [CrossRef]
- Hao, P.C.; Karaku, O.; Achim, A. A hybrid particle-stochastic map filter. Signal Process. 2023, 207, 108969. [Google Scholar] [CrossRef]
- Pan, C.; Huang, A.; He, Z.; Lin, C.; Sun, Y.; Zhao, S.; Wang, L. Prediction of remaining useful life for lithium-ion battery based on particle filter with residual resampling. Energy Sci. Eng. 2021, 9, 1115–1133. [Google Scholar] [CrossRef]
- Zafar, T.; Mairaj, T.; Alam, A.; Rasheed, H. Hybrid resampling scheme for particle filter-based inversion. IET Sci. Meas. Technol. 2020, 14, 396–406. [Google Scholar] [CrossRef]
- Hu, Y.; Baraldi, P.; Di Maio, F.; Zio, E. A particle filtering and kernel smoothing-based approach for new design component prognostics. Reliab. Eng. Syst. Saf. 2015, 134, 19–31. [Google Scholar] [CrossRef]
- Haque, M.S.; Choi, S.; Baek, J. Auxiliary particle filtering-based estimation of remaining useful life of IGBT. IEEE Trans. Ind. Electron. 2017, 65, 2693–2703. [Google Scholar] [CrossRef]
- Bahadorinejad, A.; Imani, M.; Braga-Neto, U.M. Adaptive Particle Filtering for Fault Detection in Partially-Observed Boolean Dynamical Systems. IEEE-Acm Trans. Comput. Biol. Bioinform. 2020, 17, 1105–1114. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Jiao, X.L. Adaptive Kernel Auxiliary Particle Filter Method for Degradation State Estimation. Reliab. Eng. Syst. Saf. 2021, 211. [Google Scholar] [CrossRef]
- Xiahou, T.; Liu, Y.; Zeng, Z.; Wu, M. Remaining useful life prediction with imprecise observations: An interval particle filtering approach. IISE Trans. 2023, 55, 1075–1090. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Song, Q.F.; Liang, F.M. A langevinized ensemble kalman filter for large-scale dynamic learning. Stat. Sin. 2024, 34, 1071–1091. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Liu, B. Some research problems in uncertainy theory. J. Uncertain Syst. 2009, 3, 3–10. [Google Scholar]
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty; Springer: Berlin, Germany, 2010. [Google Scholar]
- Lio, W.; Liu, B. Uncertain maximum likelihood estimation with application to uncertain regression analysis. Soft Comput. 2020, 24, 9351–9360. [Google Scholar] [CrossRef]
- Lio, W.; Kang, R. Bayesian rule in the framework of uncertainty theory. Fuzzy Optim. Decis. Mak. 2023, 22, 337–358. [Google Scholar] [CrossRef]
- Peng, Z.; Iwamura, K. A sufficient and necessary condition of uncertainty distribution. J. Interdiscip. Math. 2010, 13, 277–285. [Google Scholar] [CrossRef]
- Liu, Y.; Lio, W. A revision of sufficient and necessary condition of uncertainty distribution. J. Intell. Fuzzy Syst. 2020, 38, 4845–4854. [Google Scholar] [CrossRef]
- Xie, H.-B.; Yang, H.-Y.; Yu, J.; Gao, M.-Y.; Shou, J.-D.; Fang, Y.-T.; Liu, J.-B.; Wang, H.-T. Research progress on advanced rail materials for electromagnetic railgun technology. Def. Technol. 2021, 17, 429–439. [Google Scholar] [CrossRef]
- Celaya, J.R.; Kulkarni, C.S.; Biswas, G.; Goebel, K. Towards a model-based prognostics methodology for electrolytic capacitors: A case study based on electrical overstress accelerated aging. Int. J. Progn. Health Magag. 2012, 3, 33. [Google Scholar] [CrossRef]
- Taher, S.A.; Jafari, M.; Pakdel, M. A new approach for modeling electromagnetic railguns. IEEE Trans. Plasma Sci. 2015, 43, 1733–1741. [Google Scholar] [CrossRef]
- Yu, X.; Fan, Z. Simulation and two-objective optimization of the electromagnetic-railgun model considering VSEC resistance and contact resistance. IEEE Trans. Plasma Sci. 2010, 39, 405–410. [Google Scholar] [CrossRef]
- Renwick, J.; Kulkarni, C.S.; Celaya, J.R. Analysis of electrolytic capacitor degradation under electrical overstress for prognostic studies. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Austin, TX, USA, 22–25 June 2015. [Google Scholar]
- Kulkarni, C.; Biswas, G.; Saha, S.; Goebel, K. A model-based prognostics methodology for electrolytic capacitors based on electrical overstress accelerated aging. In Proceedings of the Annual Conference of the PHM Society, Montreal, QC, Canada, 25–29 September 2011. [Google Scholar]
- Djuric, P.M.; Kotecha, J.H.; Zhang, J.; Huang, Y.; Ghirmai, T.; Bugallo, M.F.; Miguez, J. Particle filtering. IEEE Signal Process. Mag. 2003, 20, 19–38. [Google Scholar] [CrossRef]


| State equation | |
| Observation equation | |
| Process noise | |
| Observation noise | |
| Initial value of capacitance | |
| Initial distribution of state | Normal uncertainty distribution, |
| Number of particles | |
| Number of charge/discharge cycles | 196 times |
| No. | Threshold | Number of Resampling |
|---|---|---|
| 1 | 18 | |
| 2 | 95% confidence interval | 17 |
| Methods | MSE | Var MSE | RMSE |
|---|---|---|---|
| UPF | 0.0347 | 0.1547 | 0.1864 |
| PF | 0.0886 | 0.5332 | 0.2977 |
| APF | 0.0668 | 0.6353 | 0.2585 |
| AKAPF | 0.0914 | 0.8985 | 0.3024 |
| KS-PF | 0.2002 | 2.2778 | 0.4474 |
| IPF | 0.0952 | 0.7172 | 0.3085 |
| Parameter | ||||
| True Value | 0.887 | −0.000886 | −0.000232 | 0.0458 |
| State equation | |
| Observation equation | |
| Process noise | |
| Observation noise | |
| initial distribution | Normal uncertainty distribution, |
| Number of particles | |
| Number of charge/discharge cycles | 120 times |
| True value of the dynamic parameter | |
| Methods | Mean MSE | Var MSE | RMSE |
|---|---|---|---|
| UPF | 2.9842 × 10−6 | 6.2237 × 10−11 | 0.0017 |
| PF | 2.5451 × 10−4 | 1.9875 × 10−6 | 0.0160 |
| APF | 1.1124 × 10−4 | 1.8219 × 10−7 | 0.0105 |
| AKAPF | 9.6442 × 10−5 | 1.2096 × 10−7 | 0.0098 |
| KS-PF | 1.7814 × 10−5 | 1.5345 × 10−8 | 0.0042 |
| IPF | 1.0223 × 10−5 | 2.345 × 10−10 | 0.0032 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Shao, Y.; Lio, W.; Liu, J.; Kang, R. Uncertain Particle Filtering: A New Real-Time State Estimation Method for Failure Prognostics. Mathematics 2025, 13, 702. https://doi.org/10.3390/math13050702
Liang J, Shao Y, Lio W, Liu J, Kang R. Uncertain Particle Filtering: A New Real-Time State Estimation Method for Failure Prognostics. Mathematics. 2025; 13(5):702. https://doi.org/10.3390/math13050702
Chicago/Turabian StyleLiang, Jingyu, Yinghua Shao, Waichon Lio, Jie Liu, and Rui Kang. 2025. "Uncertain Particle Filtering: A New Real-Time State Estimation Method for Failure Prognostics" Mathematics 13, no. 5: 702. https://doi.org/10.3390/math13050702
APA StyleLiang, J., Shao, Y., Lio, W., Liu, J., & Kang, R. (2025). Uncertain Particle Filtering: A New Real-Time State Estimation Method for Failure Prognostics. Mathematics, 13(5), 702. https://doi.org/10.3390/math13050702







