Spectral Analysis of Lattice Schrödinger-Type Operators Associated with the Nonstationary Anderson Model and Intermittency

Abstract

We investigate the nonstationary parabolic Anderson problem ${\displaystyle \frac{\partial u}{\partial t}}=\varkappa \mathcal{L}u(t,x)+{\xi }_t(x)u(t,x),u(0,x)\equiv 1,(t,x)\in [0,\infty )\times Z^d$ where $\varkappa \mathcal{L}$ denotes a nonlocal Laplacian and ${\xi }_t(x)$ is a correlated white-noise potential. The irregularity of the solution is linked to the upper spectrum of certain multiparticle Schrödinger operators that govern the moment functions $m_p(t,x_1,x_2,\cdots ,x_p)=⟨u(t,x_1)u(t,x_2)\cdots u(t,x_p)⟩$. First, we establish a weak form of intermittency under broad assumptions on $\mathcal{L}$ and on a positive-definite noise correlator $B=B(x)$. We then examine strong intermittency, which emerges from the existence of a positive eigenvalue in a related lattice Schrödinger-type operator with potential B. Here, B does not have to be positive definite but must satisfy $\sum B(x)\ge 0$. The presence of such an eigenvalue intensifies the growth properties of the second moment $m_2$, revealing a more pronounced intermittent regime.

1. Introduction

The study of random Schrödinger operators on a lattice, typically taking the form of the parabolic Anderson Schrödinger equation

$$\begin{array}{cc}\hfill H(\omega )& =\Delta +V(\omega ,x),x\in Z^d\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \Delta f(x)& =\sum _{x^{\prime }\in Z^d:|x^{\prime }-x|=1}(f(x^{\prime })-f(x))\mathrm{for}z\in Z^d,f:Z^d\to R\hfill \end{array}$$

(2)

has long been a cornerstone of mathematical physics and probability theory. A principal motivation for investigating such operators is the phenomenon of Anderson localization, originally introduced by Anderson [1] to explain the absence of electronic diffusion in disordered solids. Subsequent rigorous treatments in the 1970s and 1980s established the fundamental tools of multiscale analysis and fractional moment methods, showing how disorder can cause eigenfunctions to become exponentially localized with high probability (see, e.g., [2,3,4]).

While most classical results assume stationary (time-independent) random potentials [5,6,7], growing interest in time-dependent or nonstationary disordered media has expanded the scope of the field. Such nonstationary Anderson models arise naturally when modeling phenomena in which the environment or disorder itself evolves—examples include driven disordered systems in condensed matter physics [8,9] and random turbulent flows of the conducting fluid in the solar photosphere, which is relevant to the generation and dynamics of magnetic fields [10], evolving resource landscapes in population dynamics [11,12], mutation-selection evolution of DNA or RNA sequences [13], and random polymer models under time-varying constraints [14,15]; see [16] for further applications.

Parallel investigations in the continuous setting have illuminated the impact of nonstationary time-dependent noise on parabolic Anderson-type problems. Huang et al. [17] studied a parabolic Anderson model on $R^d$ with a local (continuous) Laplacian $\Delta ={\displaystyle \sum _{i=1}^d}{\displaystyle \frac{\partial }{\partial x_i^2}}$ driven by a space–time-homogeneous Gaussian noise, whose covariance kernels are nonnegative definite functions on $R^d$. They established the existence of a unique mild solution and derived a Feynman–Kac formula for the moments of the solutions using a family of independent Brownian bridges. Balan et al. [18] subsequently investigated the magnitude of the p-th moments for solutions of a related model in $R^d$, where the noise is correlated in both space and time. These works highlight how noise correlations—particularly in the spatial domain—can substantially influence the intermittency and overall growth properties of the solution.

Despite the extensive literature on stationary random operators involving the local lattice Laplacian $\Delta$ [5,19,20,21,22,23,24], a comprehensive spectral theory that accommodates nonstationary settings and, more broadly, nonlocal operators remains comparatively undeveloped [18,25]. This gap highlights both the complexity of nonstationary models and the importance of novel analytical techniques for understanding their long-term behavior, intermittency, and localization properties.

In the present paper, we build on two recent works [26,27] and the memoir [19] to offer new insights into nonstationary lattice Anderson parabolic problems with a nonlocal operator. The central object of [26] is the nonstationary lattice Anderson parabolic problem

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial u}{\partial t}}& =\varkappa \mathcal{L}u(t,x)+{\xi }_t(x)u(t,x)\hfill \\ \hfill u(0,x)& \equiv 1,(t,x)\in [0,\infty )\times Z^d.\hfill \end{array}$$

(3)

with the nonlocal Laplacian

$$\mathcal{L}f(t,x)=\sum _{\begin{array}{c}z\ne 0\\ z\in Z^d\end{array}}a(z)(f(t,x+z)-f(t,x)).$$

(4)

The operator $\mathcal{L}$ is the generator of the random walk $x(t)$. The random walk $x(t)$ has the following structure. It spends in each site $x\in Z^d$ the time ${\tau }_x$, which is exponentially distributed with coefficient $\varkappa$, i.e., $P({\tau }_x>t)=e^{-\varkappa t}$, and it jumps at the moment ${\tau }_x+0$ from site x to site $x+z$ with probability $a(z)$. We assume that $a(z)=a(-z)\ge 0$ (symmetry), ${\displaystyle \sum _{z\in Z^d}}a(z)=1$ (normalization), $a(0)=0$, and $a(z)>0$ if $\left|z\right|=1$ (to guarantee the non-degeneracy of the random walk). The constant $\varkappa$ in (3) is the diffusion coefficient (diffusivity).

The potential ${\xi }_t(x)$, $x\in Z^d$ is a Gaussian field that is ${\delta }_0$-correlated in time and correlated in space:

$$\begin{array}{c}\hfill <{\xi }_{t_1}(x_1){\xi }_{t_2}(x_2)>={\delta }_0(t_1-t_2)B(x_1-x_2)\end{array}$$

(5)

where ${\delta }_0(t)$ is the standard Dirac delta function. It means that ${\xi }_t(x)$ is the white noise in time with space correlator $B(x_1-x_2),x_1,x_2\in Z^d$. Consequently, ${\xi }_t(x)$ behaves like a white noise in time but may exhibit nontrivial spatial correlations. This setup generalizes several classical models in both the discrete and continuous settings, providing a pathway to explore how noise correlation structures influence the large-time behavior and localization properties of the parabolic Anderson model in the nonstationary regime.

Our goal is to qualitatively analyze the field $u(t,x)$ for $t\to \infty ,x\in Z^d$, and prove that u is intermittent in space. At the physical level, intermittency means that the main contribution to the moment functions of $u(t,x),t\to \infty ,$ is given by very sparse and very high peaks [28,29]. The mathematical description and study of intermittency use Lyapunov exponents, properties of the correlation function B, and the multiparticle equation for higher-order moments of u.

Properties of the potential ${\xi }_t(x)$ and the correlation function B: We can understand ${\xi }_t(x)$ as the generalized derivative of the Wiener process $W(t,x),t\ge 0,x\in Z^d$. That is, ${\xi }_t(x)=\dot{W}(t,x)$, and Equation (3) is understood as infinite-dimensional stochastic differential equations in the Itô sense in an appropriately weighted Hilbert space $L^2(Z^d,\mu )$ with measure $\mu$. The measure $\mu$ on $Z^d$ is selected based on the jump distribution $a(z)$$z\in Z^d$; see the details in [26]. We will use the notation $<·>$ to represent the integration over the distribution of ${\xi }_t(x)=\dot{W}(t,x)$, and $E[·]$ will be the expectation of the functional of the random walk $x(t)$ with the generator $\varkappa \mathcal{L}$. Formula (5) implies that $<W(t,x)>=0$ and $<W(t_1,x_1)W(t_2,x_2)>=min(t_1,t_2)B(x_1-x_2)$. We construct the correlated Wiener process $W(t,x)$ as a linear transform of independent and identically distributed (i.i.d) standard Brownian motions $w(t,x)$, $x\in Z^d$, $t\ge 0$ with weight kernel $b(·)$:

$$\begin{array}{c}\hfill W(t,x)=\sum _{z\in Z^d}b(x-z)w(t,z).\end{array}$$

(6)

We assume that the kernel $b(·)$ satisfies $b(·)\in l^1(Z^d)$, which implies ${\displaystyle \sum _{z\in Z^d}}\left|b^2(z)\right|<\infty$ and

$$\begin{array}{cc}\hfill B(x-y)& =<W^2(1,x-y)>=\sum _{z\in Z^d}b(x-z)b(y-z)=\sum _{z\in Z^d}b(x-y-z)b(-z)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill B(0)& =<W^2(1,0)>=\sum _{z\in Z^d}{b}^2(z)<\infty .\hfill \end{array}$$

(8)

The function $B(x-y)$ is the space correlation of the stationary Gaussian field $W(t,x)$. Due to the Bochner–Khinchin theorem, B is a positively definite function, i.e., it has the representation

$$\begin{array}{c}\hfill B(x)={\displaystyle \frac{1}{{(2\pi )}^d}}{\int }_{T^d}{e}^{ikx}\widehat{B}(k)dk,T={[-\pi ,\pi ]}^d,\end{array}$$

(9)

where the spectral density is $\widehat{B}(k)={\displaystyle \sum _{x\in Z^d}}B(x)e^{ikx}\in C(T^d)$ and $\widehat{B}(k)\ge 0$.

Indeed, since $b(x)\in l^1(Z^d)\bigcap l^2(Z^d)$, Formulas (7) and (8) imply that $\widehat{B}(k)={\left|\widehat{b}(k)\right|}^2\ge 0$ where $\widehat{b}(k)={\displaystyle \sum _{x\in Z^d}}{e}^{ikx}b(x)$, $k\in T^d$. Note also that

$$\begin{array}{c}\hfill \sum _{x\in Z^d}B(x)={\displaystyle \frac{1}{{(2\pi )}^d}}{\int }_{T^d}\sum _{x\in Z^d}{e}^{ikx}\widehat{B}(k)dk={\int }_{T^d}{\delta }_0(x)\widehat{B}(k)dk=\widehat{B}(0)\ge 0.\end{array}$$

Higher-order moments and the multiparticle equation: Equation (3) can be rewritten in the integral form (in the Itô sense) as follows:

$$\begin{array}{c}\hfill u(t,x)=1+{\int }_0^t\varkappa \mathcal{L}u(s,x)ds+{\int }_0^{t}u(s,x)dW(s,x).\end{array}$$

(10)

The existence and uniqueness theorems for the stochastic differential equation in (10) are given in [26]. One also can find the derivations of the equations for the p-th moment functions $m_p(t,x_1,x_2,\cdots ,x_p)=<u(t,x_1)\cdots u(t,x_p)>,p=1,2,\cdots$ there:

$${\displaystyle \frac{d{m}_p(t,x_1,\cdots ,x_p)}{dt}}=\varkappa \left(\sum _{i=1}^p{\mathcal{L}}_{x_i}{m}_p(t,x_1,\cdots ,x_p)\right)+V_p(x_1,\cdots ,x_p)m_p(t,x_1,\cdots ,x_p)=H_p{m}_p$$

(11)

with the initial condition $m_p(0,x_1,\cdots ,x_p)=1$. Here, $V_p(x_1,\cdots ,x_p)={\displaystyle \sum _{i<j}}B(x_i-x_j)$.

The first two moments of the field $u(t,x)$, respectively, satisfy the following equations:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial m_1}{\partial t}}=(\varkappa \mathcal{L})m_1(t,x),m_1(0,x)=1,\end{array}$$

(12)

i.e., $m_1(t,x)=1$. If $m_2(t,x)=m_2(t,x+z,z)$, then

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial m_2(t,x)}{\partial t}}=2\varkappa \mathcal{L}{m}_2(t,x)+B(x)m_2(t,x)=H_2{m}_2,m_2(0,x)=1.\end{array}$$

(13)

For the special case when $\varkappa \mathcal{L}$ is the local Laplacian operator $\varkappa \Delta$ and $B(x_1-x_2)=\delta (x_1-x_2)$, the derivations and analysis of the equations for the pth moment functions $m_p(t,x_1,x_2,\cdots ,x_p)=<u(t,x_1)\cdots u(t,x_p)>,p=1,2,\cdots$ can be found in [19]. In the latter case, there exists an exact formula for $m_2(t,x)$.

All equations for higher-order moments have the form of multiparticle Schrödinger equations containing the Hamiltonian $H_p$, as in Equation (11). The “nonlocal Laplacian” $\varkappa \mathcal{L}$ is a symmetric bounded and self-adjoint operator in $l^2(Z^d)$ with the dot product $(f,g)={\displaystyle \sum _{z\in Z^d}}f(x)\overline{g}(x)$. It is isomorphic to the operator of multiplication by continuous nonpositive functions, the Fourier symbol, $\varkappa \widehat{\mathcal{L}}(k)=\varkappa {\displaystyle \sum _{z\in Z^d}}(cos(kz)-1)a(z)=\varkappa (\widehat{a}(k)-1),k\in T^d={[-\pi ,\pi ]}^d$, in the dual Fourier space $L^2(T^d,dk)$. As a result, the spectrum $Sp(\varkappa \mathcal{L})$ of $\varkappa \mathcal{L}$ coincides with $Range(\varkappa \widehat{\mathcal{L}}(k))=[\varkappa \alpha ,0],\alpha =\underset{k\in T^d}{min}\widehat{\mathcal{L}}(k)=\underset{k\in T^d}{min}(\widehat{a}(k)-1)<0$.

Spectral analysis of $H_p$ and intermittency: The notion of intermittency presented in the physical literature refers to a high irregularity of fields; see [28,29,30,31]. In the case of a solar magnetic field, intermittency pertains to the presence of high and narrow peaks that encapsulate nearly all magnetic energy. In the mathematical literature [26,29,32,33,34,35,36], this notion is described in terms of the Lyapunov exponents ${\gamma }_p$ for the moments $m_p(t,\dot{)}$ defined in (11). Estimates on ${\gamma }_p$ depend on the structure of the spectral measure for the Hamiltonian $H_p$, $p\ge 2$, near the top of the spectrum.

Due to the stationarity of the field $u(t,x),x\in Z^d,$ the moments do not depend on x: $m_p(t)=<u^p(t,x)>=<u^p(t,0)>$. We will prove (see Section 2) that the following Lyapunov exponents exist:

$$\begin{array}{c}\hfill {\gamma }_1=\underset{t\to \infty }{lim}{\displaystyle \frac{ln<u(t,0)>}{t}}=\underset{t\to \infty }{lim}{\displaystyle \frac{ln{m}_1(t)}{t}}=0\\ \hfill {\gamma }_p=\underset{t\to \infty }{lim}{\displaystyle \frac{ln<u^p(t,0)>}{t}}=\underset{t\to \infty }{lim}{\displaystyle \frac{ln{m}_p(t)}{t}},p\ge 2,\end{array}$$

and that $0={\gamma }_1\le {\displaystyle \frac{{\gamma }_2}{2}}\le {\displaystyle \frac{{\gamma }_3}{3}}\le \cdots$ (Lyapunov type inequality). If for some index $p_0$, we have

$$\begin{array}{c}\hfill 0={\gamma }_1={\displaystyle \frac{{\gamma }_2}{2}}=\cdots ={\displaystyle \frac{{\gamma }_{p_0}}{p_0}}<{\displaystyle \frac{{\gamma }_{p_0+1}}{p_0+1}}.\end{array}$$

Then, for $k\ge p_0+1$, we have ${\displaystyle \frac{{\gamma }_k}{k}}<{\displaystyle \frac{{\gamma }_{k+1}}{k+1}}$, and this fact is the manifestation of intermittency [29,37]. If ${\displaystyle \frac{{\gamma }_2}{2}}>0$, i.e., $p_0=1$, then the intermittency is strong; if $p_0>1$, the intermittency is weak. The qualitative meaning of intermittency will be discussed in a remark in Section 2. For further details, see also [19].

The main part of this paper contains two sections. In Section 2, we establish the weak intermittency of a solution $u(t,x)$. This is deduced from simple upper and lower estimations of the moments $m_p(t)$ for $p=2,3,\cdots$, which imply the following estimates on the Lyapunov exponents ${\gamma }_p$:

$$\begin{array}{c}\hfill {\displaystyle \frac{p-1}{2}}B(0)-\varkappa d\le {\displaystyle \frac{{\gamma }_p}{p}}\le {\displaystyle \frac{(p-1)B(0)}{2}}.\end{array}$$

(14)

The second part of Section 2 contains improved upper and lower estimates for ${\displaystyle \frac{{\gamma }_p}{p}},p\ge 2$ in terms of ${\gamma }_2$. These results reveal that the critical value $p_0=p_0(\varkappa )$, defined as the minimal $p_0$ such that $0<{\displaystyle \frac{{\gamma }_{p_0}}{p_0}}$, has order $O(\varkappa )$ for large $\varkappa$.

The final section, Section 3, focuses on the examination of the second moment and the second Lyapunov exponent ${\gamma }_2$. In the transient case, under minimal conditions on the generator $\varkappa \mathcal{L}$ and the correlator $B(x)$, we establish the existence of a phase transition: ${\gamma }_2(\varkappa )=0$ if $\varkappa <{\varkappa }_0$; ${\gamma }_2(\varkappa )>0$ if $\varkappa >{\varkappa }_0$ for appropriate ${\varkappa }_0$ if ${\displaystyle \sum _{x\in Z^d}}B(x)>0$. In the recurrent case, we consider a very broad class of operators and show that ${\gamma }_2(\varkappa )>0$ for any $\varkappa >0$. The positivity of ${\gamma }_2(\varkappa )$ is established for an arbitrary but not necessarily Markovian pseudodifferential operator $\varkappa \mathcal{L}$. We do not require the potential B to be positive definite. The main assumption on the potential is that ${\displaystyle \sum _{x\in Z^d}}B(x)>0$. In a specific case, we demonstrate that ${\gamma }_2(\varkappa )>0$ for $\varkappa >0$, even in the borderline scenario where ${\displaystyle \sum _{x\in Z^d}}B(x)=0$.

2. Intermittency of the Anderson Parabolic Problem

The intermittency phenomenon is associated with the progressive growth of moment functions $m_p(t,x_1,x_2,\cdots ,x_d)=<u(t,x_1)\cdots u(t,x_p)>$ as t tends to infinity. Equation (11) for $m_p(t,x_1,\cdots ,x_d)$ was derived in [26], but the analysis of the equation was limited to cases where $p=1,2$. Here, we extend the study by providing several estimations for $m_p(·,·)$, specifically for $p\ge 3$, shedding light on the phenomenon of intermittency.

The existence–uniqueness theorem for stochastic differential equations governing $u(t,x)$ in a weighted Hilbert space, along with the Itô formula, supports the derivation of Equation (11). The solution $u(t,x)$ of the stochastic differential equation in (3) is homogeneous and ergodic in space, and all of its moment functions $m_p(t,x_1,x_2,\cdots ,x_p)=<u(t,x_1)u(t,x_2)\cdots u(t,x_p)>$ are finite. Furthermore, these moment functions satisfy the p-particle-type Schrödinger Equation (11). Since $\parallel \varkappa \mathcal{L}\parallel \le \varkappa$ and $\underset{x\in Z^d}{max}\left|B(x)\right|=\underset{x\in Z^d}{max}B(x)=B(0)$, i.e., $|V_p|\le {\displaystyle \frac{p(p-1)}{2}}B(0)$, the Hamiltonian $H_p$ in (11) is bounded for any $p\ge 1$.

Note also that since $u(t,x)>0$,

$$\begin{array}{cc}\hfill m_p(t,x_1,x_2,\cdots ,x_p)& =<u(t,x_1)u(t,x_2)\cdots u(t,x_p)>\hfill \\ \hfill & \le {\displaystyle \frac{1}{p}}<u^p(t,x_1)+\cdots +u^p(t,x_p)>\hfill \\ \hfill & ={\displaystyle \frac{1}{p}}\sum _{j=1}^p<u^p(t,x_j)>=m_p(t,0,0,\cdots ,0)\hfill \end{array}$$

(15)

Due to the Kac–Feynman formula,

$$\begin{array}{c}\hfill m_p(t,0,\cdots ,0)=E_{(0,0,\cdots ,0)}{e}^{{\int }_0^t{V}_p(x_1(s),x_2(s),\cdots ,x_p(s))ds}\end{array}$$

(16)

where $x_j(s),j=1,2,\cdots ,p,$ are p independent random walks on $Z^d$ with generator $\varkappa \mathcal{L}$. Formula (16) does not contain the pre-exponent $u(0,x_1(t),\cdots ,x_p(t))$ due to the condition $u(0,x_1,x_2,\cdots ,x_p)=1$. Future estimates are based on the formula in (16).

We denote $M_p(t)=m_p(t,0,0,\cdots ,0)=\underset{x_1,x_2,\cdots ,x_p}{max}{m}_p(t,x_1,x_2,\cdots ,x_p)$; see the inequality in (15). The max principle for the parabolic equation in (11) and the independence of increments in time for the processes $x_j(t)$ lead to the inequality $M_p(t+s)\le M_p(t)M_p(s)$, where $M_p\ge 1$. The subadditivity of $ln{M}_p(t)$ implies the existence of a Lyapunov exponent, which is given by

$$\begin{array}{c}\hfill {\gamma }_p=\underset{t\to \infty }{lim}{\displaystyle \frac{ln{M}_p(t)}{t}},p=1,2,\dots .\end{array}$$

It is known that ${\gamma }_p$ is the upper bound of the spectrum of the multiparticle Hamiltonian $H_p$, $p\ge 2$; see [19]. Due to the Lyapunov inequality,

$$\begin{array}{c}\hfill 0={\gamma }_1\le {\displaystyle \frac{{\gamma }_2}{2}}\le {\displaystyle \frac{{\gamma }_3}{3}}\le \cdots \le {\displaystyle \frac{{\gamma }_p}{p}}\le \cdots \end{array}$$

(17)

Our goal now is to prove that the field $u(t,x)$ is intermittent in the sense of formal definitions from [19,29,35,37].

Let us revisit the concept of intermittency, which was briefly touched upon in the introduction. In the following remark, we will try to explain why the formal mathematical definition of intermittency implies the high irregularity of the field $u(t,x)$. We will also stress the similarity between our scaler model and models for the solar magnetic field [37,38,39,40].

Remark 1.

The field $u(t,x)$, representing solutions to the Anderson parabolic problem, is both homogeneous and ergodic. The correlation functions of any order are finite. Specifically, it leads to the following ergodic theorem:

$$\begin{array}{c}\hfill <u^{p_0}(t,x)>=<u^{p_0}(t,0)>=\underset{L\to \infty }{lim}{\displaystyle \frac{1}{{(2L)}^d}}\sum _{\left|y\right|\le L}{u}^{p_0}(t,y)\stackrel{log}{\sim }{e}^{{\gamma }_{p_0}t},t\to \infty .\end{array}$$

(18)

Let $0<\delta <{\gamma }_{p_0}/p_0$. Chebyshev’s inequality and the relation $<u(t,y)>\equiv 1,y\in Z^d,$ imply

$$\begin{array}{c}\hfill P({\displaystyle \frac{lnu(t,y)}{t}}\ge {\displaystyle \frac{{\gamma }_{p_0}}{p_0}}-\delta )=P(u(t,y)\ge e^{t({\displaystyle \frac{{\gamma }_{p_0}}{p_0}}-\delta )})\le <u(t,y)>e^{-t({\displaystyle \frac{{\gamma }_{p_0}}{p_0}}-\delta )}=e^{-{\delta }_{1}t},{\delta }_1>0.\end{array}$$

For a fixed δ and a large L, consider the cube $Q_L=\{y:|y|<L\}$, which we can partition into the set $Q_L^{\delta }=\{y\in Q_L:u(t,y)\le e^{-t({\displaystyle \frac{{\gamma }_{p_0}}{p_0}}-\delta )}\}$ and the complement set containing large values of u. In a logarithmic sense, we have ${\displaystyle \frac{1}{{(2L)}^d}}{\displaystyle \sum _{Q_L^{\delta }}}<u^{p_0}(t,x)>\le e^{t({\gamma }_{p_0}-p_0\delta )}$, which is significantly smaller than the logarithmic asymptotic $e^{{\gamma }_{p_0}t}$ of $<u^{p_0}(t,0)>$. This indicates that the primary contribution to $<u^{p_0}(t,0)>$ arises from the sparse high peaks where $u(t,x)>e^{-t({\displaystyle \frac{{\gamma }_{p_0}}{p_0}}-\delta )}$. The density $\pi (t,\delta )=|Q_L\setminus Q_L^{\delta }|/|Q_L|$ of such points in $Q_L$, $L\to \infty$, is exponentially small in t:

$$\begin{array}{c}\hfill \pi (t,\delta )\le e^{-t{\delta }_1}.\end{array}$$

A classic example of an intermittent field is the magnetic field of the Sun and a diverse array of white and yellow stars. The energy of magnetic field $\overrightarrow{H}(t,x)$ is proportional to the second moment $<\overrightarrow{H}(t,x_1)\overrightarrow{H}(t,x_2)>$. The Lyapunov exponents of $\overrightarrow{H}(x)$ satisfy the same relation $0={\gamma }_1<{\displaystyle \frac{{\gamma }_2}{2}}$ for hot stars, including the Sun. Nearly all magnetic energy of $\overrightarrow{H}(x)$ is concentrated within the black spots, covering extremely small regions of the Sun’s surface, as discussed in [29]. The lattice parabolic Anderson model, which was introduced in [19], serves as a simplified representation of the Maxwell equations governing the magnetic field in the turbulent flow of solar plasma.

Theorem 1.

The field $u(t,x)$, representing the solution to Equation (3) as an infinite-dimensional stochastic differential equation (SDE) in the appropriately weighted

Hilbert space, is weakly intermittent as $t\to \infty$. This holds without any additional restrictions on the jump distribution $a(x),x\in Z^d$ and the correlator $B(·)$, except as outlined in the introduction.

Proof. 

Due to (15) and the maximum principle,

$$\begin{array}{c}\hfill M_p(t)=\underset{x_1,x_2,\cdots ,x_p}{max}{m}_p(t,x_1,x_2,\cdots ,x_p)=M_p(t,0,·0)\le exp\{{\displaystyle \frac{p(p-1)}{2}}B(0)t\},\end{array}$$

i.e.,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p}}\le {\displaystyle \frac{p-1}{2}}B(0),p=2,3,\cdots .\end{array}$$

(19)

At the same time,

$$\begin{array}{c}\hfill M_p(t,0,\cdots ,0)\ge E_{0,0,\cdots ,0}[I_{\{y_1(s)=y_2(s)=\cdots =y_p(s)=0,s\in [0,t]\}}]e^{{\displaystyle \frac{p(p-1)}{2}}B(0)t}\end{array}$$

$$\begin{array}{c}\hfill =exp\{-p\varkappa dt+{\displaystyle \frac{p(p-1)}{2}}B(0)t\},\end{array}$$

i.e.,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p}}\ge {\displaystyle \frac{p-1}{2}}B(0)-\varkappa d.\end{array}$$

(20)

Thus,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p}}>0\mathrm{if}p>2+{\displaystyle \frac{2\varkappa }{B(0)}}.\end{array}$$

(21)

This implies the weak intermittency of the field $u(t,x)$ and provides an estimate from below on the borderline value of $p=p_0$. □

Estimates (19) and (20) are very rough. In the following, we will present significantly refined estimates for ${\gamma }_p$ with $p\ge 2$. The pivotal element in this refinement lies in the accurate estimation of the second moment $M_2(t)$ and the corresponding Lyapunov exponent ${\gamma }_2$.

2.1. Upper Estimate of Lyapunov Exponents ${\gamma }_p$ Through ${\gamma }_2$

We will start with two technical lemmas. Let us introduce a slightly more general stochastic differential Equation (10) where the white noise has an extra factor $\alpha$. We denote by $\tilde{u}(t,x),{\tilde{m}}_p(t,\overrightarrow{x}),{\tilde{\gamma }}_p$ the corresponding solution of (10) with factor $\alpha$, its moment functions, and its Lyapunov exponents. Here, $\overrightarrow{x}=(x_1,\cdots ,x_p)$. In particular, the function ${\tilde{m}}_p(t,\overrightarrow{x})$ satisfies

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\tilde{m}}_p(t,\overrightarrow{x})}{dt}}& =\varkappa \left(\sum _{i=1}^p{\mathcal{L}}_{x_i}{\tilde{m}}_p(t,\overrightarrow{x})\right)+\alpha V_p(\overrightarrow{x}){\tilde{m}}_p(t,\overrightarrow{x})={\tilde{H}}_p{\tilde{m}}_p\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\tilde{m}}_p(0,\overrightarrow{x})& =1.\hfill \end{array}$$

(23)

The solution to Equation (22) is given by

$$\begin{array}{c}\hfill {\tilde{m}}_p(t,\overrightarrow{x})=E_{\overrightarrow{x}}exp\left(\alpha {\int }_0^t{V}_p(t,{\overrightarrow{x}}_s)ds\right)\end{array}$$

(24)

where ${\overrightarrow{x}}_s=(x_1(s),x_2(s),\cdots ,x_p(s))$ is a family of independent random walks with the generator $\varkappa \mathcal{L}$. We will explicitly show the dependence of the Lyapunov exponent on two parameters: ${\tilde{\gamma }}_p={\tilde{\gamma }}_p(\varkappa ,\alpha )$.

Lemma 1.

Under the aforementioned conditions, ${\tilde{\gamma }}_p(\varkappa ,\alpha )=\alpha {\gamma }_p\left({\displaystyle \frac{\varkappa }{\alpha }}\right)$.

Proof. 

This result is derived through direct calculations. We rescale time by setting $\alpha s=\tau$ in (24) and obtain

$$\begin{array}{c}\hfill {\tilde{m}}_p(t,\overrightarrow{x})=E_{\overrightarrow{x}}exp\left({\int }_0^{\alpha t}{V}_p(t,{\overrightarrow{x}}_{\tau /\alpha })d\tau \right)\end{array}$$

(25)

The new process $\overrightarrow{y}(t)={\overrightarrow{x}}_{{\displaystyle \frac{\tau }{\alpha }}}$ has the generator ${\displaystyle \frac{\varkappa }{\alpha }}\mathcal{L}$, and

$$\begin{array}{c}\hfill \tilde{\gamma }(\varkappa ,\alpha )=\underset{t\to \infty }{lim}{\displaystyle \frac{ln{\tilde{m}}_p(t,\mathbf{0})}{t}}=\underset{t\to \infty }{lim}{\displaystyle \frac{\alpha ln{m}_p(\tau ,\mathbf{0})}{\tau }}=\alpha {\gamma }_p({\displaystyle \frac{\varkappa }{\alpha }})\end{array}$$

(26)

□

The following lemma gives a special representation of the multiparticle potential:

$$\begin{array}{c}\hfill V_p(x_1,x_2,\dots ,x_p)=\sum _{1\le i<j\le p}B(x_i-x_j).\end{array}$$

(27)

Lemma 2.

If $p=2l+1$ is odd and the number of terms in $V_p$ is $\left({\displaystyle \genfrac{}{}{0pt}{}{p}{2}}\right)=l(2l+1)$, then there exists a partition of the sum (27) in p groups, $V_p=G_1+\cdots +G_p$, such that each group contains l terms $B(x_i-x_j)$ with the following property: the group $G_k,1\le k\le p,$ does not depend on $x_k$, and each other argument $x_s$ in the terms $B(x_i-x_j)$ inside of the group $G_k$ occurs only once.

If $p=2l$ is even and the number of terms in $V_p$ is $\left({\displaystyle \genfrac{}{}{0pt}{}{p}{2}}\right)=l(2l-1)$, then there exists a partition of the sum (27) in $p-1$ groups, $V_p=G_1+\cdots +G_{p-1}$, such that each group contains l terms $B(x_i-x_j)$ with the following property: each argument $x_s$ in the terms $B(x_i-x_j)$ inside of a group occurs only once.

Figure 1 depicts the algorithmic process for constructing a configuration, with specific values assigned for l and p (namely, $l=2$ and $p=5$). It is crucial to note that this construction is not unique. Along the unit circle, we identify $p=2l+1$ points, numbered clockwise as $x_1,x_2,\dots ,x_{2l+1}$. To elaborate, we fix $1\le i\le p$, exclude $x_i$, and subsequently generate successive pairs using the remaining variables. This is achieved by moving clockwise and counterclockwise along the equal distribution of points: $(x_{i+1},x_{i-1}),(x_{i+1},x_{i-1}),\cdots$. Then,

$$\begin{array}{cc}\hfill V(x_1,x_2,x_3,x_4,x_5)=& \underset{G_1}{\underbrace{B(x_5-x_2)+B(x_4-x_3)}}+\underset{G_2}{\underbrace{B(x_1-x_3)+B(x_5-x_4)}}\hfill \\ \hfill & +\underset{G_3}{\underbrace{B(x_2-x_4)+B(x_1-x_5)}}+\underset{G_4}{\underbrace{B(x_3-x_5)+B(x_2-x_1)}}\hfill \\ \hfill & +\underset{G_5}{\underbrace{B(x_4-x_1)+B(x_3-x_2)}}.\hfill \end{array}$$

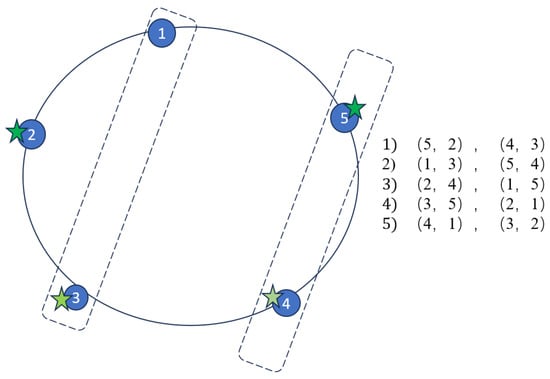
Figure 1. An example of $G_2$ outlined with dashed rectangles when $p=5,l=2$. The green starred $\{5,2,4,3\}$ forms $G_1$.

Proof. 

When $p=2l+1$, the first part directly follows from our specific partition, as depicted in Figure 1. For $p=2l$, where $l>1$, we proceed by isolating $x_p$ and applying the partition to the remaining $2l-1$ points. We divide them into $p-1=2l-1$ groups $G_i$, where $i=1,2,\cdots ,p-1$, with each $G_i$ containing $l-1$ possible pairs among $\{x_1,x_2,\cdots ,x_{p-1}\}$-$\left\{x_i\right\}$. Next, we add $B(x_p-x_i)$ to each group $G_i$. For example, when $p=6$ and $l=3$,

$$\begin{array}{cc}\hfill V& =\underset{G_1}{\underbrace{B(x_5-x_2)+B(x_4-x_3)+B(x_6-x_1)}}+\underset{G_2}{\underbrace{B(x_1-x_3)+B(x_5-x_4)+B(x_6-x_2)}}\hfill \\ \hfill & +\underset{G_3}{\underbrace{B(x_4-x_2)+B(x_5-x_1)+B(x_6-x_3)}}+\underset{G_4}{\underbrace{B(x_3-x_5)+B(x_2-x_1)+B(x_6-x_4)}}\hfill \\ \hfill & +\underset{G_5}{\underbrace{B(x_4-x_1)+B(x_3-x_2)+B(x_6-x_5)}}.\hfill \end{array}$$

This method of construction ensures a systematic and comprehensive generation of pairs, as exemplified for the given parameters. □

Theorem 2 highlights the efficiency of direct probabilistic methods within the pure spectral context. Providing a functional analytical proof for the same result is nontrivial.

Estimations of the higher moments

$$M_p(t)=<u^p(t,0,0,\cdots ,0)>=<Eexp(\sum _{1\le i<j\le p}{\int }_0^{t}B(x_i(s)-x_j(s))ds)>$$

include an additional improvement based on the fact that $(x_1(s)-x_2(s)),(x_3(s)-x_4(s)),\cdots$ are independent processes.

Theorem 2.

Upper estimate of Lyapunov exponents: For $p\ge 3$,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p}}={\displaystyle \frac{1}{p}}\underset{t\to \infty }{lim}{\displaystyle \frac{ln{M}_p(t)}{t}}\le [{\displaystyle \frac{p}{2}}]{\gamma }_2({\displaystyle \frac{\varkappa }{p}})\end{array}$$

(28)

Proof. 

Consider $M_p(t)=E_{(0,0,\cdots ,0)}[exp({\displaystyle \sum _{i<j}}{\int }_0^{t}B(x_i(s)-x_j(s)ds)]$; using the inequality

$$a_1{a}_2\cdots a_p\le {\displaystyle \frac{1}{p}}(a_1^p+\cdots a_p^p),$$

we can estimate the moment function $M_p(t)$ from the above.

$$\begin{array}{cc}\hfill M_p(t)& =E_{(0,\cdots ,0)}[exp(\sum _{1\le i<j\le p}({\int }_0^{t}B(x_i(s)-x_j(s))ds))]\hfill \\ \hfill & =E_{(0,\cdots ,0)}[exp(\sum _{l=1}^p\sum _{(i,j)\in G_l}({\int }_0^{t}B(x_i(s)-x_j(s))ds))]\hfill \\ \hfill & \le {\displaystyle \frac{1}{p}}\sum _{l=1}^p{E}_{(0,\cdots ,0)}[exp(p\sum _{(i,j)\in G_l}({\int }_0^{t}B(x_i(s)-x_j(s))ds))]\hfill \\ \hfill & =E_{(0,\cdots ,0)}[exp(p\sum _{(i,j)\in G_l}({\int }_0^{t}B(x_i(s)-x_j(s))ds))]\hfill \\ \hfill & ={\left\{E_{(0,\cdots ,0)}[exp(p({\int }_0^{t}B(x_1(s)-x_2(s))ds))]\right\}}^l,l=[{\displaystyle \frac{p}{2}}]\hfill \end{array}$$

In the last step, we use the symmetry of the potential and independence of the integrals in each group $G_l$. This independence by itself follows from the independence of the random walks $x_i(s)$, $i=1,2,\cdots ,p$. However, $E_{(0,0)}[exp(p{\int }_0^{t}B(x_1(s)-x_2(s))ds]=y(t,x_1,x_2)$ satisfies the two-particle Schrödinger equation

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial y}{\partial t}}& =\varkappa ({\mathcal{L}}_{x_1}+{\mathcal{L}}_{x_2})y+pB(x_1-x_2)y\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill y(0,x_1,x_2)& =1.\hfill \end{array}$$

(30)

Since we have a homogeneous space, $y(t,x_1,x_2)$ is a function depending on $x_1-x_2$, that is, $y(t,x_1,x_2)=\tilde{y}(t,x_1-x_2)$. After a change of variable $v=x_1-x_2$ and considering the initial conditions $y(t,x_1,x_2)=\tilde{y}(0,x_1-x_2)=1$, we eventually reduce the analysis to the following problem:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \tilde{y}}{\partial t}}={\tilde{H}}_2\tilde{y}=2\varkappa {\mathcal{L}}_v\tilde{y}(v)+pB(v)\tilde{y},\tilde{M}(0,·)=1,v\in Z^d\end{array}$$

where the potential $B(·)\in l^1(Z^d)$ is positive definite, as discussed in the introduction. Let ${\tilde{\gamma }}_2(\varkappa ,p)$ be the Lyapunov exponent for $\tilde{y}$. Due to Lemma (1),

$$\begin{array}{c}\hfill {\tilde{\gamma }}_2(\varkappa ,p)=p{\tilde{\gamma }}_2({\displaystyle \frac{\varkappa }{p}},1)=p{\gamma }_2({\displaystyle \frac{\varkappa }{p}}).\end{array}$$

(31)

Combining all of the results, for arbitrary $p\ge 3$ and $l=\left[{\displaystyle \frac{p}{2}}\right]$, we get

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{\displaystyle \frac{ln{M}_p(t)}{t}}={\gamma }_p\le lp{\gamma }_2({\displaystyle \frac{\varkappa }{p}})\end{array}$$

That is,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p}}\le l{\gamma }_2({\displaystyle \frac{\varkappa }{p}})=\left[{\displaystyle \frac{p}{2}}\right]{\gamma }_2({\displaystyle \frac{\varkappa }{p}}).\end{array}$$

(32)

□

The positivity ${\gamma }_2(\varkappa )>0$ will be discussed in Section 3.

2.2. Lower Estimate for the Lyapunov Exponent ${\gamma }_p$

Theorem 3.

For $p\ge 2$,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p-1}}>{\gamma }_2({\displaystyle \frac{\varkappa }{p-1}})+{\displaystyle \frac{B(0)(p-2)}{2}}-2\varkappa d\end{array}$$

(33)

Proof. 

Due to the Kac–Feynman formula,

$$\begin{array}{cc}\hfill M_p(t)& =E_{(0,\cdots ,0)}[exp(\sum _{1\le i<j\le p}({\int }_0^{t}B(x_i(s)-x_j(s))ds))]\hfill \\ \hfill & \ge E_{(0,\cdots ,0)}[exp(\sum _{1\le i<j\le p}({\int }_0^{t}B(x_i(s)-x_j(s))ds))I_{x_l(s)=0,l=2,3,\cdots ,p}],\hfill \\ \hfill & =E_{(0,\cdots ,0)}[exp((p-1)({\int }_0^{t}B(x_1(s)ds))]e^{{\displaystyle \frac{(p-1)(p-2)}{2}}B(0)}\prod _{l=2}^{p}P(x_l(s)=0|x_l(0)=0).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill ln{M}_p(t)& \ge ln{E}_{(0,\cdots ,0)}[exp((p-1)({\int }_0^{t}B(x_1(s)ds))]\hfill \\ \hfill +& {\displaystyle \frac{(p-1)(p-2)}{2}}B(0)t+\sum _{l=2}^{p}lnP(x_l(s)=0|x_l(0)=0).\hfill \end{array}$$

Since the number of the jumps of the random walk $x_l(s),s\in [0,t]$ is a Poisson process with the rate $2d\varkappa$, the event $\{x_l(s)=0\}$ is equivalent to the absence of jumps during $[0,t]$. Thus, $P(x_l(s)=0|x_l(0)=0)=e^{-2d\varkappa t}$. For $l=2,3,\cdots ,p$, $x_l(s)$ are independent random walks following the same law. Thus,

$$\begin{array}{cc}\hfill {\displaystyle \frac{ln{M}_p(t)}{t(p-1)}}& \ge {\displaystyle \frac{ln{E}_{(0,\cdots ,0)}[exp((p-1)({\int }_0^{t}B(x_1(s)ds))]}{t(p-1)}}+{\displaystyle \frac{(p-2)}{2}}B(0)-2d\varkappa .\hfill \end{array}$$

(34)

As $t\to \infty$,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p-1}}\ge {\displaystyle \frac{1}{p-1}}{\tilde{\gamma }}_2(\varkappa ,p-1)+{\displaystyle \frac{(p-2)}{2}}B(0)-2d\varkappa .\end{array}$$

(35)

Due to Lemma 1,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\gamma }_p}{p-1}}\ge {\displaystyle \frac{1}{p-1}}{\tilde{\gamma }}_2(\varkappa ,p-1)+{\displaystyle \frac{(p-2)}{2}}B(0)-2d\varkappa ={\gamma }_2({\displaystyle \frac{\varkappa }{p-1}})+{\displaystyle \frac{p-2}{2}}B(0)-2d\varkappa \end{array}$$

(36)

□

3. Spectral Analysis of ${\mathit{H}}_{\mathbf{2}}$ and Strong Intermittency

The analysis of the second Lyapunov exponent ${\gamma }_2$ (or the top of the spectrum of the operator $H_2$) depends significantly on the properties of the random walk $x(t)$ associated with the “Laplacian” $\varkappa \mathcal{L}$. If $p(t,x,y)=P\{x(t)=y|x(0)=x\}$, $t>0,x,y\in Z^d$, then $p(t,x,y)$ is the fundamental solution of the following parabolic problem:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dp}{dt}}& =2\varkappa \mathcal{L}p,t>0,p(0,x,y)={\delta }_y(x).\hfill \end{array}$$

(37)

The process $x(t)$ is called recurrent if ${\int }_0^{\infty }p(t,x,x)dt=\infty$; otherwise, it is transient.

Using the Fourier transform, we obtain

$$p(t,x,y)={\displaystyle \frac{1}{{(2\pi )}^d}}{\int }_{T^d}{e}^{2\varkappa \widehat{\mathcal{L}}(k)t}{e}^{ik(x-y)}dk,k\in T^d={[-\pi ,\pi ]}^d.$$

(38)

Here, $\widehat{\mathcal{L}}(k)={\displaystyle \sum _{z\ne 0}}(cos(k,z)-1)a(z)=\widehat{a}(k)-1$ represents the Fourier symbol of the operator $\mathcal{L}$. When $x=y$,

$$\begin{array}{c}\hfill {\int }_0^{\infty }p(t,x,x)dt={\displaystyle \frac{1}{{(2\pi )}^d}}{\int }_{T^d}{\displaystyle \frac{dk}{2\varkappa (1-\widehat{a}(k))}}.\end{array}$$

If $E\left[x^2(t)\right]<\infty$, i.e., ${\displaystyle \sum _{z\in Z^d}}{\left|z\right|}^{2}a(z)<\infty$, then $\widehat{a}(k)=1-{\displaystyle \frac{1}{2}}(Dk,k)+{O(|k|}^2)$, where D is the matrix of the second moments of $x(t)$. In this case, $p(t,x,x)\sim {\displaystyle \frac{c}{t^{d/2}}},t\to \infty$, and the process $x(t)$ is transient for dimensions $d\ge 3$ and recurrent for $d=1,2$.

We consider a more general situation when the second moment of $x(t)$ is infinite. We impose a certain regularity condition on the symbol $-\widehat{\mathcal{L}}(k)=1-\widehat{a}(k)$ of the operator $\mathcal{L}$. We assume that

$$\widehat{a}(k)=e^{-\beta (\dot{k}){\left|k\right|}^{\alpha }(1+o(\left|k\right|))},\left|k\right|\to 0,$$

(39)

where $\dot{k}={\displaystyle \frac{k}{\left|k\right|}}$, $0<\alpha \le 2$, and $\beta (\dot{k})=\beta (-\dot{k})>0$ is a symmetric and positive function on $T^d$. Both functions $\beta$ on the sphere and the remainder term in the exponent are assumed to be sufficiently smooth. Corresponding conditions on the jump distribution $a(x)$ can be found in [41].

Under these conditions, $p(t,x,x)\sim t^{-d/\alpha }$ as $t\to \infty$. Since $p(t,x,y)\le 1$, we have $p(t,x,x)\le C{t}^{-d/\alpha },t\ge 0,$ and the process $x(t)$ is recurrent for $d=2,\alpha =2$, and for $d=1,1\le \alpha \le 2$. It is transient in the case of $d=2,\alpha <2$ and $d=1,\alpha <1$.

3.1. Transient Case

This section is devoted to the question of the existence (or nonexistence) of a positive eigenvalue of the Schrödinger operators

$$H\psi =\mathcal{L}\psi (x)+\sigma V(x)\psi (x),x\in {\mathbb{Z}}^d,\sigma >0,$$

(40)

which includes the spectral problem for the operator $H_2$ defined in (13) as a particular case if we set $\sigma ={\displaystyle \frac{1}{2\varkappa }}$. The corresponding change in the parameter appears after rescaling $t\to t/(2\varkappa )$ in (13). We do not assume that the potential is positive definite and use the notation V instead of B.

We assume that the potential $V(x)$ satisfies the Cwickel–Lieb–Rozenblum (CLR)-type condition [42]

$$\begin{array}{c}\hfill \sum _{x\in Z^d}{\left|V(x)\right|}^{{\displaystyle \frac{d}{\alpha }}}<\infty ,d=2,\alpha <2\mathrm{or}d=1,\alpha <1,\end{array}$$

(41)

or

$$\begin{array}{c}\hfill \sum _{x\in Z^d}{\left|V(x)\right|}^{{\displaystyle \frac{d}{2}}}<\infty ,d\ge 3.\end{array}$$

(42)

Let us note that these conditions hold the potential B from Section 2, since it was assumed that $B\in L^1({\mathbb{Z}}^{\mathbb{d}})$.

We denote the number of positive eigenvalues of the operator (40) by $N_0(\sigma V)=♯\{{\lambda }_i:{\lambda }_i(H)>0\}$.

Theorem 4.

Let conditions (39), (41), and (42) hold, and let the potential $V(·)$ be positive at least at one point. Then, there exists a critical value ${\sigma }_{cr}$ such that there are no positive eigenvalues when $\sigma <{\sigma }_{cr}$, and the positive eigenvalues ${\lambda }_0(H)$ exist when $\sigma >{\sigma }_{cr}$.

Proof. 

For arbitrary $\sigma$, the following Bargmann-type estimate can be found in [43,44]:

$$\begin{array}{c}\hfill N_0(\sigma V)\le C\sum _{x\in Z^d}\sigma V(x){\int }_{{\displaystyle \frac{1}{\sigma |V(x)|}}}^{\infty }p(t,x,x)dt.\end{array}$$

Since $p(t,x,x)\le C{t}^{-d/\alpha },t\ge 0$, and $d>\alpha$, we obtain that

$$\begin{array}{c}\hfill N_0(\sigma V)\le {\displaystyle \frac{C\alpha }{d-\alpha }}{\sigma }^{{\displaystyle \frac{d}{\alpha }}}\sum _{x\in Z^d}V{(x)}^{d/\alpha }.\end{array}$$

Thus, $N_0(\sigma V)<1$ when $\sigma$ is small, i.e., there are no positive eigenvalues for small $\sigma$. In order to prove the existence of positive eigenvalues for large $\sigma$, consider a test function ${\psi }_0(x)={\delta }_{x_0}(x),$ where $x_0$ is a point such that $V(x_0)>0$. Then,

$$(H{\psi }_0,{\psi }_0)=l+\sigma V(x_0),l=(\mathcal{L}{\psi }_0,{\psi }_0)<\infty .$$

The quadratic form is positive for large $\sigma ,$ and therefore, the positive eigenvalues exist. □

If, in any dimension, $d\ge 1$, the potential is positive and decays slowly: $V(x)\ge {\displaystyle \frac{C}{1+{\left|x\right|}^{\frac{d}{\alpha }-\epsilon }}}$. Then, H with arbitrary $\sigma >0$ has infinitely many positive eigenvalues. The proof is similar to the one in [27].

3.2. Recurrent Case

We continue to study the question of the existence of a positive eigenvalue for the Schrödinger operator

$$H\psi =\mathcal{L}\psi (x)+\sigma V(x)\psi (x),x\in {\mathbb{Z}}^d,\sigma >0;\sum _{x\in Z^d}\left|V(x)\right|<\infty ,\sum _{x\in Z^d}V(x)\ge 0,$$

(43)

but now we assume that the operator $\mathcal{L}$ is recurrent, and the conditions on V are different from those in the transient case.

Since an analysis of the ground states is important for many applications and has been widely studied, we omit many of the restrictions imposed on H earlier. The operator $\mathcal{L}$ now can be unrelated to a Markov process and is defined simply as an operator that, in the Fourier images, acts as multiplication by a continuous function $\widehat{\mathcal{L}}(k),k\in T^d$:

$$\sum _{x\in Z^d}\mathcal{L}\psi (x)e^{-i<k,x>}=\widehat{\mathcal{L}}(k)\sum _{x\in Z^d}\psi (x)e^{-i<k,x>}.$$

We assume that $\widehat{\mathcal{L}}(0)=0,\widehat{\mathcal{L}}(k)<0$ for $k\ne 0$. If the opposite is not stated, we assume that

$${\int }_{T^d}{\left[\widehat{\mathcal{L}}(k)\right]}^{-1}dk=\infty .$$

(44)

This condition in the Markovian case is equivalent to the recurrence of the process. While the last condition in (43) often appears as a consequence of the potential being positive definite, we do not assume the latter property.

The spectrum of the operator $\mathcal{L}$ coincides with the range of the function $[{min}_k\widehat{\mathcal{L}}(k),0]$. The presence of the potential may lead to the appearance of positive eigenvalues. Our goal is to find conditions that guarantee the existence of a positive eigenvalue for the operator (43) with arbitrary small $\sigma >0$. Note that the same conditions will lead to the existence of a positive eigenvalue for all $\sigma >0$. Indeed, if a positive eigenvalue exists for some $\sigma >0$, then it exists for the operator ${\sigma }^{-1}\mathcal{L}+V(x)$, and then it exists for the same operator with larger values of $\sigma$ due to the monotonicity of the latter operator in $\sigma$. Hence, the operator in (43) with larger values of $\sigma$ also has positive eigenvalues.

First, we will prove a couple of statements concerning the case when

$$\sum _{x\in Z^d}V(x)>0.$$

(45)

Theorem 5.

Let (44), (45) hold. Then, the positive spectrum of the operator (43) is discrete and non-empty, i.e., the operator with arbitrary $\sigma >0$ has a positive eigenvalue.

Remark 2.

This statement in the continuous case with a slightly more restrictive assumption was proven in [27].

Proof. 

Let us show that the positive spectrum of the operator (43) is non-empty. The conditions on V imply that $\widehat{V}(0)>0$ and that $\widehat{V}(k)$ is continuous. Thus, there exists ${\epsilon }_1>0$ such that $\widehat{V}(k-\xi )>v_0>0$ when $\left|k\right|,\left|\xi \right|<{\epsilon }_1$. We construct test functions $\psi (x)={\psi }_{\epsilon }(x)$ using their Fourier images:

$${\widehat{\psi }}_{\epsilon }(k)=\left\{\begin{array}{c}{\left[\widehat{\mathcal{L}}(k)\right]}^{-1},0<\epsilon \le \left|k\right|\le {\epsilon }_1,\\ 0,\left|k\right|\notin (\epsilon ,{\epsilon }_1).\end{array}\right.$$

Then,

$$<H\psi ,\psi >={\int }_{\epsilon <\left|k\right|<{\epsilon }_1}\widehat{\mathcal{L}}(k){\left|\widehat{\psi }(k)\right|}^{2}dk+\sigma {\int }_{\epsilon <\left|k\right|<{\epsilon }_1}{\int }_{\epsilon <\left|k\right|<{\epsilon }_1}\widehat{V}(k-\xi )\widehat{\psi }(k)\overline{\widehat{\psi }(\xi )}dkd\xi$$

$$\le {\int }_{\epsilon <\left|k\right|<{\epsilon }_1}{\left[\widehat{\mathcal{L}}(k)\right]}^{-1}dk+\sigma v_0{\left({\int }_{\epsilon <\left|k\right|<{\epsilon }_1}{\left[\widehat{\mathcal{L}}(k)\right]}^{-1}dk\right)}^2\to \infty \mathrm{as}\epsilon \to 0,$$

(46)

due to (44). Hence, there are test functions for which the quadratic form (46) is positive, and therefore, the positive spectrum of H is non-empty.

It remains to be shown that the positive spectrum of H is discrete. The operators ${(\mathcal{L}-\lambda )}^{-1}$ in $L^2(Z^d)$ are analytic in $\lambda$ when $\lambda \notin [0,\infty )$, and the same is true for $T_{\lambda }:=V{(\mathcal{L}-\lambda )}^{-1}$ since $\left|V(x)\right|<C<\infty ,x\in Z^d$. Hence, the resolvent identity and the analytic Fredholm theorem will imply the discreteness of the positive spectrum of H if we show that operators $T_{\lambda },\lambda \notin [0,\infty ),$ are compact. We represent $T_{\lambda }$ as the sum $T_{\lambda }=\alpha (x/n)T_{\lambda }+(1-\alpha (x/n))T_{\lambda }$ where $\alpha (x)=1$ when $\left|x\right|\le 1$, and $\alpha (x)=0$ when $\left|x\right|>1$. The operator $\alpha (x/n)T_{\lambda }$ is finite-dimensional; therefore, it is compact, and

$$\parallel (1-\alpha (x/n))T_{\lambda }{\parallel }_{L^2(Z^d)}\to 0\mathrm{as}n\to \infty$$

since V vanishes at infinity. Thus, operators $T_{\lambda },\lambda \notin [0,\infty ),$ are compact as limits of compact operators $\alpha (x/n)T_{\lambda }$ as $n\to \infty$.

The proof is complete. □

Theorem 6.

Let condition (45) hold. Let operator $\mathcal{L}$ be a generator of a random walk, and

$${\int }_{T^d}\left|k\right|{\left[\widehat{\mathcal{L}}(k)\right]}^{-1}dk<\infty \mathrm{and}\sum _{Z^d}\left|xV(x)\right|<\infty .$$

(47)

Then, operator H defined in (43) with

$$0<\sigma <{\sigma }_0=(2{\int }_{T^d}\left|k\right|{\left[\widehat{\mathcal{L}}(k)\right]}^{-1}dk\sum _{Z^d}{\left|xV(x)\right|)}^{-1}$$

has exactly one positive eigenvalue.

Proof. 

The following estimate for the number $N_0(V)$ of positive eigenvalues of operator H follows from Theorem 1.2 in [43]:

$$N_0(V)\le 1+2\sum _{x\in Z^d}\left|V(x)\right|\underset{\lambda \to +0}{lim}[R_{\lambda }(x)-R_{\lambda }(0)]|,$$

where $R_{\lambda }(x-y)$ is the kernel of the resolvent of operator $\mathcal{L}$. The limit above does not exceed

$${\int }_{T^d}|e^{ikx}-1|{\left[\widehat{\mathcal{L}}(k)\right]}^{-1}dk\le {\int }_{T^d}\left|kx\right|{\left[\widehat{\mathcal{L}}(k)\right]}^{-1}dk.$$

The last two relations imply that $N_0(V)<2$ when $\sigma <{\sigma }_0$. Thus, H has at most one eigenvalue in this case, and it exists due to Theorem 5. □

3.3. Zero Average Potentials, One-Dimensional Case

The goal of this subsection is to expand the important part of Theorem 5 on the existence of positive eigenvalues to a particular case of operators H with ${\sum }_{x\in Z^d}V(x)\ge 0$ where the sum can be equal to zero. The operator H will be a perturbation of the second derivative on a one-dimensional lattice. We would also like to obtain this result in the continuous case; therefore, we will simultaneously consider operators H in $L^2(\mathbb{R})$ and in $L^2(\mathbb{Z})$ defined by the relations

$$H\psi ={\psi }^{″}(x)+\sigma V(x)\psi (x),x\in \mathbb{R}\mathrm{or}\mathbb{Z},\mathrm{where}{\int }_{-\infty }^{\infty }(1+|x|)\left|V(x)\right|dx<\infty ,V\not\equiv 0,$$

(48)

Here and below, ${\psi }^{″}(x)$ and the integrals must be replaced by $\psi (x-1)+\psi (x+1)-2\psi (x)$ and the corresponding infinite sums, respectively, when $x\in \mathbb{Z}$. Let us stress that the assumption on the behavior of the potential at infinity in (48) is stronger than in (43).

Theorem 7.

If ${\int }_{-\infty }^{\infty }V(x)dx\ge 0,V\not\equiv 0,$ then the operator H defined in (48) has a positive eigenvalue $\lambda =\lambda (\sigma )$ for each $\sigma >0$.

Remark 3.

The proof below will be given in the continuous case $x\in \mathbb{R}$, but one needs only to replace the integrals with sums for the proof to be valid in the lattice case.

Remark 4.

This statement for the operator on the half-axis $x>0$ with the boundary condition ${\psi }^{\prime }(0)=0$ was proved in [27]

We will need the following lemma (a similar statement can be found in [27]).

Lemma 3.

When $\left|\sigma \right|\ll 1$, there are solutions ${\psi }_1,{\psi }_2$ of the equation $H\psi =0$ on the half-axis $x\ge 0$, where H is defined in (48), such that

$${\psi }_1(x)=1+O(\sigma ),{\psi }_1^{\prime }(x)=O(\sigma ),x\ge 0;{\psi }_1(0)=1,{\psi }_1^{\prime }(0)=\alpha (\sigma ),$$

(49)

$${\psi }_2(x)=x(1+O(\sigma )),{\psi }_2^{\prime }(x)=1+O(\sigma ),x\ge 0;{\psi }_2(0)=0,{\psi }_2^{\prime }(0)=1.$$

(50)

Here, the remainder terms are uniform in x, and

$$\alpha (\sigma )=\sigma b+{\sigma }^2{c}^2+O({\sigma }^3),b={\int }_0^{\infty }V(\xi )d\xi ,c^2={\int }_0^{\infty }{\left({\int }_{\eta }^{\infty }V(\xi )d\xi \right)}^{2}d\eta .$$

(51)

Proof. 

We look for a complementary bounded solution $\psi$ in the form $\psi =1+z(x)$. Then, $z^{″}+\sigma V(x)z=-\sigma V(x)$, and this equation can be reduced to the integral equation

$$z(x)+\sigma Pz=-\sigma {\int }_x^{\infty }(\xi -x)V(\xi )d\xi ,x\ge 0,\mathrm{where}Pz={\int }_x^{\infty }(\xi -x)V(\xi )z(\xi )d\xi .$$

(52)

The operator P in the space C of continuous bounded functions on the semi-axis $x\ge 0$ is bounded, and the right-hand side in (52) has the form $-\sigma f$, where $f\in C$. Thus, Equation (52) is uniquely solvable in C when $\left|\sigma \right|\ll 1$, and the solution is analytic in $\sigma$. Hence,

$$\psi =1-\sigma f+{\sigma }^{2}Pf+O({\sigma }^3),$$

(53)

where $-\sigma f$ is the right-hand side in (52). Since (52) also admits differentiation in x, the latter expansion can be differentiated in x. This implies that $\psi$ satisfies the first two relations in (49) and has the following initial data:

$$\psi (0)=1-\sigma a+O({\sigma }^2),{\psi }^{\prime }(0)=\sigma b+{\sigma }^2(-ab+c^2)+O({\sigma }^3),$$

where $a={\int }_0^{\infty }\xi V(\xi )d\xi ,$ and $b,c^2$ are defined in (51). The evaluation of the coefficient for ${\sigma }^2$ in the expansion of ${\psi }^{\prime }(0)$ is based on (53), but it also involves an integration by parts, and more details can be found in [27] (see Lemma 3.3) if needed.

Function ${\psi }_1$ can be defined as ${\psi }_1(x)=\psi (x)/\psi (0)$. Function ${\psi }_2$ can be constructed as

$${\psi }_2(x)={\psi }_1(x){\int }_0^x{\psi }_1^{-2}(\xi )d\xi ,x\ge 0,\left|\sigma \right|\ll 1.$$

Then, (50) follows from (49). □

Proof of Theorem 7.

Theorem 3.1 from [43] implies that the positive spectrum of H is discrete. Thus, it is enough to show that the positive spectrum is not empty. It is enough to show the existence of a positive spectrum of H for arbitrarily small $\sigma >0$, since it will imply its existence for all $\sigma >0$; see the paragraph before the statement of the theorem. Hence, the theorem will be proven if, for some sequence $\sigma ={\sigma }_n\to 0,n\to \infty ,$ we construct functions $\varphi ={\varphi }_n(x)\in C^1(\mathbb{R})$ with compact supports such that

$${\int }_{-\infty }^{\infty }[-{\varphi }^{\prime 2}(x)+{\sigma }_{n}V(x){\varphi }^2(x)]dx>0.$$

We define the solutions ${\psi }_3(x),{\psi }_4(x)$ of Equation (48) on the negative half-axis $x\le 0$ similarly to ${\psi }_1(x),{\psi }_2(x)$ constructed in Lemma 3 on the semi-axis $x\ge 0$. In particular,

$${\psi }_3(0)=1,{\psi }_3^{\prime }(0)=\beta (\sigma ),{\psi }_4(0)=0,{\psi }_4^{\prime }(0)=1,$$

(54)

where

$$\beta =-\sigma b_{-}-{\sigma }^2{(c_{-})}^2+O({\sigma }^3),b_{-}={\int }_{-\infty }^{0}V(\xi )d\xi ,{(c_{-})}^2={\int }_{-\infty }^0{\left({\int }_{-\infty }^{\eta }V(\xi )d\xi \right)}^{2}d\eta .$$

For example, one can find ${\psi }_1(x),{\psi }_2(x)$ on $x\ge 0$ for the potential $V(-x)$ and can put

$${\psi }_3(x)={\psi }_1(-x),{\psi }_4(x)={\psi }_2(-x),x\le 0.$$

Let $m=\left[{\sigma }^{-3}\right]$ be the integer part of ${\sigma }^{-3}$, where $0\le \sigma \ll 1$. We put

$$\varphi =\left\{\begin{array}{cc}{\psi }_1(x)-{\epsilon }_1{\psi }_2(x),& 0\le x\le m,\\ {\psi }_3(x)+{\epsilon }_2{\psi }_4(x),& -m\le x\le 0,\\ 0,& \left|x\right|>m,\end{array}\right.$$

(55)

where ${\epsilon }_{1,2}$ are positive solutions of the equations ${\psi }_1(m)-{\epsilon }_1{\psi }_2(m)=0$ and ${\psi }_3(-m)+{\epsilon }_2{\psi }_4(-m)=0$, respectively. From the asymptotics of ${\psi }_i(x),1\le i\le 4,$ at infinity, it follows that solutions ${\epsilon }_{1,2}$ exist, and ${\epsilon }_{1,2}=m^{-1}(1+O(\sigma ))=O({\sigma }^{-3})$. Note that $\varphi (\pm m)=0$.

Since $H\varphi (x)=0,0<\left|x\right|<m,$ and $\varphi (x)$ is continuous with $\varphi (0)=1$, we have

$$H\varphi =\epsilon \delta (x),\left|x\right|<m,\epsilon ={\varphi }^{\prime }(+0)-{\varphi }^{\prime }(-0),$$

where $\delta (x)$ is the delta function; therefore,

$${\int }_{\left|x\right|<m}(H\varphi (x))\varphi (x)dx=\epsilon .$$

On the other hand, integration by parts implies

$${\int }_{\left|x\right|<m}(H\varphi (x))\varphi (x)dx={\int }_{\left|x\right|<m}[-{\varphi }^{\prime 2}(x)+\sigma V(x){\varphi }^2(x)]dx-\epsilon .$$

Thus,

$${\int }_{\mathbb{R}}([{\varphi }^{\prime 2}(x)-\sigma V(x){\varphi }^2(x)]dx=2\epsilon .$$

(56)

The asymptotics of ${\psi }_i(x),1\le i\le 4$ as $x\to \pm 0$ (see (49), (50), and (54)) lead to

$$\epsilon =\sigma {\int }_{\mathbb{R}}V(x)dx+{\sigma }^2(c^2+{(c_{-})}^2)+O({\sigma }^3)-{\epsilon }_1-{\epsilon }_2$$

$$=\sigma {\int }_{\mathbb{R}}V(x)dx+{\sigma }^2(c^2+{(c_{-})}^2)+O({\sigma }^3).$$

The coefficient for $\sigma$ here is not negative, and the coefficient for ${\sigma }^2$ is positive if $V\not\equiv 0$. Hence, $\epsilon >0$ when $\sigma >0$ is small enough. Thus, for that $\sigma$, the quadratic form on the left-hand side of (56) is positive; therefore, the positive spectrum of H is not empty. □

The analysis of the balanced case—when the potential satisfies ${\displaystyle \sum _{x\in Z^d}}V(x)=0$ for a nonlocal operator $\mathcal{L}$—is considerably more challenging and will be treated in a separate publication. Nevertheless, the general theory developed above provides important insights. In particular, Theorem 6 for the nonlocal operator $\mathcal{L}$ (which assumes ${\displaystyle \sum _{x\in Z^d}}V(x)>0$) and Theorem 7 for the local Laplacian (extended to the case ${\displaystyle \sum _{x\in Z^d}}V(x)\ge 0$) suggest strategies for approaching the nonlocal case with a zero-sum potential.

Below is an example that illustrates the spectral problem:

$$\mathcal{L}\psi (x)+\sigma V(x)\psi (x)=\lambda \psi (x),x\in Z$$

which shows that it has a positive eigenvalue for a small-enough coupling constant $\sigma >0$, provided that the potential V is balanced (i.e., ${\displaystyle \sum _{x\in Z}}V(x)=0$) yet nontrivial (i.e., $0<{\displaystyle \sum _{x\in Z}}(1+|x|)\left|V(x)\right|)<\infty$). In what follows, we present a concrete example along with a brief outline of a variational argument demonstrating the existence of a positive eigenvalue for all $\sigma >0$ in the recurrent case in (43).

Example 1. (Nonlocal Laplacian with Zero-Sum Potential on a Lattice). Consider the discrete operator on Z

$$H\psi (x)=\mathcal{L}\psi (x)+\sigma V(x)\psi (x),x\in Z$$

and the nonlocal Laplacian is defined by

$$\mathcal{L}\psi (x)={\displaystyle \frac{1}{3}}[\psi (x+1)-\psi (x)]+{\displaystyle \frac{1}{3}}[\psi (x-1)-\psi (x)]+{\displaystyle \frac{1}{6}}[\psi (x+2)-\psi (x)]+{\displaystyle \frac{1}{6}}[\psi (x-2)-\psi (x)].$$

so that the corresponding jump probabilities are $a(1)=a(-1)={\displaystyle \frac{1}{3}},a(2)=a(-2)={\displaystyle \frac{1}{6}}.$ Let the potential $V:Z\to R$ be given by

$$V(x)=\left\{\begin{array}{cc}1,\hfill & x=0\hfill \\ -{\displaystyle \frac{1}{3}},\hfill & x=\pm 1\hfill \\ -{\displaystyle \frac{1}{6}},\hfill & x=\pm 2\hfill \\ 0,\hfill & \left|x\right|>2\hfill \end{array}\right.$$

A quick calculation shows that ${\sum }_{x\in Z}V(x)=0.$ To show that H possesses a positive eigenvalue for small σ, we employ a variational argument. We define a test function ${\psi }_0:Z\to (0,\infty )$ using

$${\psi }_0(x)=\left\{\begin{array}{cc}{e}^{-\mu (x-1)},\hfill & x\ge 1\hfill \\ e^{\mu (x+1)},\hfill & x\le -1\hfill \\ h,\hfill & x=0\hfill \end{array}\right.$$

with the normalization ${\psi }_0(\pm 1)=1$. Its squared norm is

$${∥{\psi }_0∥}^2=h^2+2\sum _{x\ge 1}{e}^{-2\mu (x-1)}=h^2+{\displaystyle \frac{2}{1-e^{-2\mu }}}.$$

Thus, for small μ, we have ${∥{\psi }_0∥}^2\sim {\displaystyle \frac{1}{\mu }}$. The Rayleigh quotient is given by ${\tilde{\lambda }}_0(H)={\displaystyle \frac{\left(H{\psi }_0,{\psi }_0\right)}{{∥{\psi }_0∥}^2}},$ and by the variational principle; if ${\tilde{\lambda }}_0(H)>0$ for some choice of the parameters $h>0$ and $\mu >0$, then the top eigenvalue ${\lambda }_0(H)$ is positive.

We will write the asymptotic expansion of the Dirichlet form,

$$\left(H{\psi }_0,{\psi }_0\right)=\left(\mathcal{L}{\psi }_0,{\psi }_0\right)+\sigma \left(V{\psi }_0,{\psi }_0\right).$$

Since $\mathcal{L}$ is self-adjoint and its kernel is symmetric, we have

$$\begin{array}{cc}\hfill & ⟨\mathcal{L}{\psi }_0,{\psi }_0⟩=-{\displaystyle \frac{1}{2}}\sum _{x\in Z}\sum _{z\in \{\pm 1,\pm 2\}}a(z){\left[{\psi }_0(x+z)-{\psi }_0(x)\right]}^2\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\left\{{\displaystyle \frac{2}{3}}\left[{\displaystyle \frac{{\left(1-e^{-\mu }\right)}^2+{\left(e^{\mu }-1\right)}^2}{1-e^{-2\mu }}}+{(1-h)}^2\right]+{\displaystyle \frac{1}{3}}\left[1-e^{-2\mu }+2{\left(h-e^{-\mu }\right)}^2+{\displaystyle \frac{{\left(e^{2\mu }-1\right)}^2{e}^{-4\mu }}{1-e^{-2\mu }}}\right]\right\}\hfill \end{array}$$

A careful asymptotic analysis shows that, for our exponentially decaying trial function and for small μ, $e^{-\mu }\sim 1-\mu$, $e^{-2\mu }-1\sim -2\mu$, ${\left(e^{-\mu }-h\right)}^2\sim {(h-1+\mu )}^2$, and by choosing $h=1+{\displaystyle \frac{\sigma }{2}}+{\displaystyle \frac{{\sigma }^2}{4}}$ and $\mu ={\displaystyle \frac{{\sigma }^2}{4}},$ we get

$$⟨\mathcal{L}{\psi }_0,{\psi }_0⟩\sim -{\displaystyle \frac{1}{2}}\left\{{(h-1)}^2+2\mu +{\displaystyle \frac{2\mu (h-1)}{3}}+{\displaystyle \frac{{\mu }^2}{3}}\right\}\sim -{\displaystyle \frac{3{\sigma }^2}{8}}+O\left({\sigma }^3\right)$$

Moreover, the potential term is

$$\begin{array}{cc}\hfill & \sigma ⟨V{\psi }_0,{\psi }_0⟩=\sigma (V(0){\psi }_0{(0)}^2+V(1){\psi }_0{(1)}^2+V(-1){\psi }_0{(-1)}^2+V(2){\psi }_0{(2)}^2+V(-2){\psi }_0{(-2)}^2)\hfill \\ \hfill & =\sigma (h^2-{\displaystyle \frac{1}{3}}·1-{\displaystyle \frac{1}{3}}·1-{\displaystyle \frac{1}{6}}{e}^{-2\mu }-{\displaystyle \frac{1}{6}}{e}^{-2\mu })\hfill \\ \hfill & \sim {\sigma }^2+O\left({\sigma }^3\right)\hfill \end{array}$$

Thus,

$$⟨H{\psi }_0,{\psi }_0⟩\sim -{\displaystyle \frac{3{\sigma }^2}{8}}+{\sigma }^2+O\left({\sigma }^3\right)={\displaystyle \frac{5{\sigma }^2}{8}}+O\left({\sigma }^3\right)$$

Since the norm satisfies ${∥{\psi }_0∥}^2\sim {\displaystyle \frac{1}{\mu }}\sim {\displaystyle \frac{4}{{\sigma }^2}}$, the Rayleigh quotient is

$${\tilde{\lambda }}_0(H)={\displaystyle \frac{⟨H{\psi }_0,{\psi }_0⟩}{{∥{\psi }_0∥}^2}}\sim {\displaystyle \frac{\frac{5{\sigma }^2}{8}+O\left({\sigma }^3\right)}{\frac{4}{{\sigma }^2}}}={\displaystyle \frac{5{\sigma }^4}{32}}+O\left({\sigma }^5\right)>0.$$

For sufficiently small σ, this is positive, implying that H has a positive eigenvalue. Please note that the potential in this example is positive definite in the sense of Fourier positivity.

$$\begin{array}{cc}\hfill \widehat{V}(k)& =\sum _{x\in Z}V(x)e^{ikx}=1-{\displaystyle \frac{2}{3}}cosk-{\displaystyle \frac{1}{3}}cos2k={\displaystyle \frac{2}{3}}\left(2-cosk-{cos}^{2}k\right)\ge 0\mathrm{for}\mathrm{all}k\in [-\pi ,\pi ].\hfill \end{array}$$

Thus, even in the nonlocal setting with a zero-sum positive-definite potential V, the operator $H=\varkappa \mathcal{L}+\sigma V$ exhibits a positive eigenvalue for a small coupling σ, indicating the presence of a bound state. This example illustrates how the interplay between nonlocal diffusion and a balanced potential can lead to a positive eigenvalue, extending the classical results for local Laplacians to the nonlocal framework.

By contrast, when one considers a sparse potential that is balanced (i.e., ${\displaystyle \sum _{x\in Z}}V(x)=0$) but fails to be positive definite, the situation is more subtle. Nonetheless, one can readily construct examples of zero-sum, non-positive-definite potentials that still admit a positive eigenvalue under a local Laplacian. To illustrate this in the context of Theorem 7, we now provide such an example.

Example 2.

We take a discrete Laplacian given by $(\Delta \psi )(x)=\psi (x+1)-2\psi (x)+\psi (x-1).$ Hence, our operator on ${\ell }^2(Z)$ is $H\psi (x)=\Delta \psi (x)+\sigma V(x)\psi (x).$

We define $V:Z\to \mathbb{R}$ as $\begin{array}{cc}& V(x)=\left\{\begin{array}{cc}1,\hfill & x=0\hfill \\ 1,\hfill & x=1\hfill \\ -1,\hfill & x=2\hfill \\ -1,\hfill & x=3\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\right.\hfill \end{array}$ Please note that ${\displaystyle \sum _{x\in Z}}V(x)=0$, $\widehat{V}(k)=\sum _{x=0}^{3}V(x)e^{ikx}=1+e^{ik}-e^{2ik}-e^{3ik}$ could be strictly negative for some values of k, such as $k={\displaystyle \frac{\pi }{2}}$. V is nonzero only at $\{0,1,2,3\}$. Therefore, ${\displaystyle \sum _{x\in Z}}(1+|x|)\left|V(x)\right|<\infty$. We define the test function

$${\psi }_0(x)=\left\{\begin{array}{cc}h,\hfill & x=0\mathrm{or}x=1,\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\mathit{with}h>1\right.$$

Then,

$$\begin{array}{cc}\hfill ⟨H{\psi }_0,{\psi }_0⟩& =⟨\Delta {\psi }_0,{\psi }_0⟩+\sigma ⟨V{\psi }_0,{\psi }_0⟩\hfill \\ \hfill & =-\sum _{x\in Z}{\left[{\psi }_0(x+1)-{\psi }_0(x)\right]}^2+\sum _{x\in \{0,1,2,3\}}V(x){\psi }_0^2(x)\hfill \\ \hfill & =-2h^2+\sigma \left(2h^2\right)\hfill \end{array}$$

Since we can choose h to be arbitrarily large for any $\sigma >0$, this means that $⟨H{\psi }_0,{\psi }_0⟩>0$ whenever h is sufficiently large, implying by the variational principle that H admits a positive eigenvalue for every $\sigma >0$.