Lightweight Authentication Protocol for Smart Grids: An Energy-Efficient Authentication Scheme for Resource-Limited Smart Meters

Abstract

The limited resources available for Smart Meter (SM) devices on large-scale Smart Grid (SG) networks impose several constraints on SMs authentication. Currently, available authentication schemes are not suitable for this type of network. In particular, factors such as power and memory consumption impact the protocol efficiency and the device lifetime. Furthermore, high computational complexity leads to scalability issues in real-world scenarios, wherein large SGs need to handle a huge number of requests coming at a high rate. In this paper, we propose a lightweight authentication protocol for Smart Grids (LAP-SG), a novel scheme accounting for real resource-constrained SM providing reduced computation power, memory requirements, communication overhead, and electricity consumption. We prove the security of LAP-SG using both informal security analysis and a formal security model. We further prove the security of LAP-SG by testing it using AVISPA and ProVerif tools, showing its security against all known attacks. To assess LAP-SG performance in a real-world scenario, we measure its performance using the configuration of the Atmel family of SM devices. When compared to the state of the art, LAP-SG attains three times Smaller computation cost, reduced communication costs (up to 400 bits), and nearly four times lower storage cost.

1. Introduction

Among the promising emerging technologies, Smart Grid (SG) presents high potentiality thanks to its connection with the upcoming Industry 5.0. A SG is composed of Smart Meters (SMs), i.e., nodes that regularly send consumption information to a controller node using a secure two-way communication [1]. Such consumption may be related to different metering services, such as gas or electricity. Since SMs are installed without security measures at consumer premises [2,3], the metering information can be exploited or intercepted by an attacker for malicious purposes. For instance, the attacker may change a Smart Meter’s configuration to create a discrepancy between demand and supply or cause service unavailability. Furthermore, the attacker may use the metering data to profile users [4]. To protect against potential attackers, authentication plays a principal role. However, authentication shall account for the architectural constraints imposed by SMs. In particular, SMs are characterized by limited computing power, low battery capacity, and network confining microcontrollers [1]. Furthermore, they have limited storage capabilities.

Although other papers in the state of the art consider the problem of authentication in SG, none of them deal with their feasibility in resource-limited SM devices, especially considering the Atmel family [1] of SMs, which represent an IEEE sponsored advanced solution for metering [5]. In particular, the following issues still represent open problems and challenges for SMs authentication.

High Processing Time or Scalability Issues: Limited-capacity SMs consume substantial computational power, leading to increased execution and response times for authentication requests. This significantly hampers their ability to scale effectively in large networks that handle high volumes of requests.

High Memory and Computational Power Consumption: SMs, which are generally equipped with Small memory and limited processing power, are severely impacted by operations that require high computational resources. In addition, in a large SG network, processing a huge (i.e., million or trillion) number of authentication requests consumes enormous amounts of computational power in SMs. As a result, he performance of SMs is compromised, leading to overheating, reduced lifespan, and inefficient operation in large-scale SG networks.

Overload on the Communication Channel (CC): The existing works have high communication costs [6], which indicates the transfer of large parameters in the CC. Transferring many bits for a massive number of authentications in a real scenario can considerably increase the burden on the CC, causing losses and inefficiencies.

Authentication in SG represents a significant challenge, and different recent proposals have tried to address it. Moghadam et al. [7] illustrates the security weakness in IEC 62351 standard [8] data transfer latency proposing a secure lightweight key distribution scheme based on Elliptic Curve Cryptography (ECC). However, this scheme has high computational and communication costs which makes it ineffective to work on low-capacity devices in SG networks. Wang et al. [9] designed an ultra-lightweight RFID-based authentication mechanism by employing bit-crossing XOR rearrangement operations. However, Hosseinzadeh et al. [10] showed that the protocol in [9] is vulnerable to impersonation attacks, where a malicious node might mislead an honest node into engaging in malicious communication. To solve this problem, they proposed a modified authentication protocol. Kumar et al. [3] propose an energy-efficient secure lightweight key agreement and authentication scheme for low-capacity devices. However, Kumar et al.’s scheme requires extensive calculations to verify the node authenticity, increasing its operational costs and making it ineffective in handling large real-time authentication scenarios in SG networks. Furthermore, Yaha et al. [11] showed that the scheme in [3] suffers from a clock synchronization problem and is vulnerable to the stolen verifier and traceability attacks. Abbasinezhad-Mood et al. [12] proposed an ECC-based lightweight scheme, illustrating its suitability for real-world SG scenarios.

Cho et al. [13] provide a lossless data aggregation authentication scheme, claiming efficiency in terms of computation and communication costs. However, we later show that this scheme is vulnerable to multiple attacks. To secure communication among node devices, Tsai et al. [14] propose an anonymous secure key distribution authentication scheme. However, Odelu et al. [15] show that this technique is unable to ensure efficient credentials privacy for the SMs as well as session key security. To solve these issues, they introduced a secure authentication scheme with a reduced computational burden among node devices. However, their approach is vulnerable to impersonation attacks, message forging, and Man-in-The-Middle (MiTM). Both schemes proposed in [14,15] do not consider real SM devices, incurring in high running costs. Bhanse et al. [16] proposed a verifiable random function-based authentication scheme. It supports mutual authentication and can resist various attacks, such as Denial of Service (DoS), replay, impersonation, and MiTM. However, this scheme is not applicable to real-time scenarios due to the high computational and storage costs.

Generalization to IoT Devices: Based on the above-mentioned, existing schemes focus on general Internet of Things (IoT) devices rather than specifically addressing the unique constraints of Smart Meter (SM) devices in Smart Grid networks. These constraints include limited memory, computational capacity, and energy efficiency.

High Computational Complexity: Some schemes rely on computationally expensive cryptographic methods, such as RSA or bilinear pairing, which are impractical for resource-limited devices in large-scale SG networks.

Scalability Issues: Many schemes struggle to handle the high volume of authentication requests typical in real-world SG deployments due to high communication overhead and storage requirements.

Specific Challenges in Large Networks: Existing schemes struggle with scalability, as high-cost operations fail to efficiently handle millions or trillions of authentication requests in real-world SG networks. The computational burden they impose grows significantly with the size of the network, leading to inefficiencies and operational bottleneck.

Insufficient Security Analysis: While some schemes aim to counter specific attacks, they often lack a comprehensive security analysis, which is essential for assessing their feasibility and robustness in real-world scenarios involving resource-constrained SM devices.

We see that there still exist open problems and challenges for SMs authentication. First, SMs are usually equipped with Small memories. Therefore, high-cost operation in low memory causes SMs to slow down in performance. In addition, in a large SG network, processing a huge number of authentication requests consumes enormous amounts of computational power in SMs. As a result, the additional required power causes overheating and reduces the efficiency and lifespan of SMs. The existing works have high communication costs [6], which indicates the transfer of large parameters in the CC. Transferring many bits for a massive number of authentications in a real scenario can considerably increase the burden on the CC, causing losses and inefficiencies. Although some existing schemes partially address these issues, they do not consider them all. Nor do they consider the practical requirements of real SM devices, especially considering the Atmel family [1] of SMs, which represent an IEEE-sponsored advanced solution for metering [5].

These considerations motivate us to propose a new verification and authentication scheme for SGs considering the resources of SMs from the Atmel family of devices. In this paper, we propose Lightweight Authentication Protocol for Smart Grids (LAP-SG), a novel ecc-based authentication scheme for resource-constrained SM. LAP-SG solves the shortcomings previously discussed that render other authentication schemes unable to deal with large-scale real-world SGs. We evaluate the security and feasibility of LAP-SG over known attacks and assess its performance in terms of computation, communication, and storage costs. We prove the security of LAP-SG using a formal security model based on BPR2000 (which is mainly adopted from Bellare et al. [17,18]). We also verify the security and correctness of the mutual authentication by experimentally testing LAP-SG using AVISPA [19]. Finally, we evaluate LAP-SG’s performance by using the configuration of a real Atmel’s SM and compare results with those of other existing schemes. Our work focuses on the features of the Atmel SM devices architecture, which include a 798 MHz CPU, and 256 MB Ram [1]. LAP-SG differs from existing recent authentication schemes [3,7,9,12,13,14,15,16,20,21,22,23,24] in several key aspects related to the authenticating process:

• Resource Efficiency: LAP-SG is designed specifically for resource-constrained Smart Meter (SM) devices commonly found in Smart Grid (SG) networks. Unlike other existing methods which may impose high computational, memory, or communication overhead on these devices, LAP-SG aims to minimize resource consumption. It achieves this by utilizing lightweight cryptographic operations and optimizing the authentication process for efficiency.
• Algorithm Selection: Unlike some existing methods, LAP-SG optimizes cryptographic algorithms specifically such as lightweight parameters for the resource-constrained Smart Meter (SM) devices, balancing efficiency and security effectively.
• Security Features: Unlike some existing schemes that rely heavily on computationally costly public-key cryptography, LAP-SG leverages lightweight cryptographic operations, significantly reducing computation overhead. Additionally, LAP-SG addresses the physical security of Smart Meters, which is not adequately considered in many existing methods.
• Authentication Process Optimization: LAP-SG minimizes the number of message exchanges during authentication, which contributes to lower communication costs compared to other schemes. Additionally, LAP-SG introduces a friendly password selection and update policy, enhancing the system’s security without imposing excessive operational burdens.
• Comparison to State of the Art: When compared to existing schemes, LAP-SG achieves significantly better scalability. It reduces computation costs by a factor of three, with an average execution time of 5.742 ms compared to 14.512 ms in other state-of-the-art schemes.
  This makes LAP-SG particularly well-suited for handling the large number of authentication requests typical in real-world SG networks. Through empirical testing on real-world SM architecture, LAP-SG demonstrates superior performance in terms of resource utilization and security guarantees.

In summary, LAP-SG distinguishes itself from other existing methods by prioritizing resource efficiency, employing suitable cryptographic algorithms, enhancing security features, optimizing the authentication process, and providing comprehensive evaluation results tailored to real-world SM devices. These differences contribute to LAP-SG’s suitability for large-scale Smart Grid networks with resource-constrained SMs.

The rest of this paper is organized as follows. In Section 2, we present the system model. In Section 3, we discuss the steps of LAP-SG. Then, we provide the security analysis of LAP-SG in Section 4. In Section 5, we assess the performance of LAP-SG and compare it with other relevant state-of-the-art protocols. In Section 6, we assess the scalability and adaptability of LAP-SG and highlight its suitability for large-scale Smart Grid (SG) networks. In section, Section 7, we outline the key limitations of the protocol and propose future directions for improvement and extension. Lastly, in Section 8, we derive the conclusions.

2. System and Threat Model and Security Principal Design Guidline

In this section, we present the system model in Section 2.1 and discuss the adversary model and security principal design guideline in Section 2.2 and in Section 2.3, respectively.

2.1. System Model

We consider the SG scenario depicted in Figure 1, where houses are supplied with energy thanks to a distribution control center controlled by an enterprise.

Each house is equipped with a SM that communicates with multiple sensor nodes through ZigBee. The sensors monitor the electrical energy consumption of a home and passes this information to the SM. Each SM communicates with the Trusted Server (TS), a node with higher computational capacity responsible for receiving the data from the houses in a certain residential area. The TS is located at the very beginning of the low-voltage network together with the transformer which serves as a concentrator node. The TS is located at the very beginning of the low-voltage network together with the transformer of that network, which, besides serving as a concentrator node, can also be responsible for sensing the data of the transformer, such as current and voltage. The TS belongs to the enterprise, and stores all the information for each SM in the collector and directly informs the respective service enterprise. The distribution control center is used to distribute electrical energy in particular types of networks through enterprise. This enterprise monitors it. The energy is also sent to another zone through the transmission control center. Each SM communicates with the other SMs in the network, and with a central TS, which handles both the communication with the SMs in one zone (or residence) and with the SM deployed in other zones. The TS is deployed to manage the communications, the identity, and passwords, and to perform password (note that in this work we refer to passwords as secrets that SMs need to use for secure communication. Although conceptually similar, it is different from the concept of password manually inserted by a user for access control) change for particular nodes’ requests. We denote as $U_i$ the $i\mathrm{th}$ home Smart Meter. We assume that all devices are tamper-proof, i.e., they automatically erase all secret information from the memory in case of tampering [25]. To launch an attack on tamper-proof devices, an attacker needs special equipment, whose cost is however higher than that of purchasing tamper-proof devices. Therefore, an attacker has no economic incentives to launch an attack on them [26].

In summary, the workflow involves Smart Meters (SMs) in each home collecting and transmitting energy consumption data through sensor nodes to a centralized transformer station (TS). The TS acts as a concentrator node and further communicates with the distribution control center for enterprise monitoring. This ensures efficient data handling, identity management, secure communication, and energy distribution across zones.

2.2. Threat Model

We consider a Dolev–Yao attacker model [27], which has been widely used to validate public key systems. The model considers an active outsider attacker able to eavesdrop, intercept, and synthesize messages. The attacker has hence full control over the communication channel, and is able to analyze and deliver compromised messages, however being a non-legitimate user in the network. The attacker is also able to impersonate other nodes in the network, as well as replay old messages. An insider attacker is instead a malicious user who has been granted system access. Therefore, the attacker can send malicious information deemed as true by the other network members. The attacker can also withhold packets causing delays and network inconsistencies. In a SG scenario, an attacker may have multiple purposes. Since data reported by SMs may be used for billing purposes, an attacker may force users to pay for more than the service they actually got, or cheat to pay a Smaller fee. Furthermore, the attacker may jeopardize the service availability, hence making costumers switch to another competitor company. Furthermore, the attacker may use the data retrieved from Smart Meters for users’ profiling purposes [4]. We summarize the adversary’s ($Adv$) capabilities in

Table 1. Adversary capabilities.

Capability Notation	Description
PC-1	$Adv$ can compute cartesian product ${|ID|}_{SP}\times {|PSW|}_{SP}$, where ${|·|}_{SP}$ represent their respective sample space
PC-2	$Adv$ can infer the victim device’s identity when computing victim device security strength
PC-3	$Adv$ can have full control over the public CC between devices and server
PC-4	$Adv$ may either (i) know the device password from an attack using special instruments, (ii) capture the secret stored in the device using side-channel attacks. However, $Adv$ cannot execute both together
PC-5	$Adv$ can access and learn the previous session key
PC-6	$Adv$ can disclose the server’s private key and other security parameters stored in the database only when the server and devices fail to maintain the forward secrecy of session key and known key attacks.

.

2.3. Design Guidelines

To set clear design goals, we define the Security Goals (SGGs) and Security Characteristics (SCs), as reported in

Table 2. Security goals.

Goal Notation	Description
SG-RA, SG-IA	Replay attacks, Insider attacks
SG-ISA	Impersonation/spoofing attacks
SG-DoSA, SG-SVA	DoS attacks, Verifier attacks
SG-SDSA	Database leakage attacks
SG-MIMA	Man-in-the-middle attacks
SG-CTA	Cookie theft attacks

and

Table 3. Security characteristics.

Characteristic Notation	Description
SC-UA, SC-MA	User anonymity, Mutual authentication
SC-SKA, SC-FS	Session key agreement, Forward secrecy
SC-FPS	Friendly password selection policy
SC-WPE	Productivity for wrong password entry
SC-FPEE	Free password or ephemeral secret exposure
SC-NPS	No direct password information
SC-PD	Password-dependent

, respectively. SGGs describe attacks that our scheme must withstand, whereas SCs describe the security features of LAP-SG.

3. LAP-SG: ECC-Based Privacy-Preserving Authentication Scheme

To design a secure and lightweight authentication scheme, we optimize the use of Elliptic Curve Discrete Logarithm Problem (ECDLP) [28], Computational Diffie-Hellman Problem (CDHP) [29], hash, and exclusive-or operations. Nodes are initially registered to the enterprise TS using a secure CC [30]. In our proposed scheme, we optimize the use of ECC operations to meet the power and memory requirements of resource-limited SMs using Atmel’s configuration. Compared to existing works [16,31,32], our optimized use of ECC operations not only solves existing security issues but also improves the scalability of the authentication protocol.

After successful registration, nodes are connected in the SG network and communicate with their adjacent nodes using a public channel. Data pass through nearby nodes to reach the Smart controller meter. LAP-SG consists of four phases: the initial phase, the registration phase, and the authentication verification phase (which includes the session key distribution). We here describe the steps of LAP-SG.

3.1. Initial Phase

Initially, the TS chooses an Elliptic Curve (EC) $y^2=X^3+b_{1}X+b_2\left(\mathrm{mod}p\right)$ over $Z_p\in \{0,1,\cdots ,p-1\}$ for registering the node devices, where $p>2^{160}$ is the finite range of the group, and $b_1$ and $b_2$ are two fields chosen by the TS, such that $4b_1^3+27b_2^2\left(\mathrm{mod}p\right)\ne 0$. The TS selects G as a base point over the EC $y^2$ having prime order n, such that $n>2^{160}$, and O as the point of infinity such that $nG=O$. The TS chooses a value s from a Zipf distribution as its secret key and computes the public key $P_{ks}=sG$ using ECDLP.

3.2. Registration Phase

A company expert must register a tamper-proof node $U_i$ to the TS through a trusted secure channel. The registration phase is shown in Figure 2. In detail,

• Step 1. The company expert assigns to node $U_i$ a unique identity $I{D}_i$ and password $Ps{w}_i$. To prevent anonymity attacks, the device computes a hashed identity by combining identity and password $I_i=h_1(I{D}_i||Ps{w}_i)$. Node $U_i$ computes its public key $P_{k{e}_i}=Ps{w}_{i}G$. The security of $I{D}_i$ and $Ps{w}_i$ is protected inside the tamper-proof node via ECDLP and a hash function $h_1$.
• Step 2. Node $U_i$ sends a registration request $<I_i,P_{k{e}_i}>$ to the TS through a trusted secure tamper-proof channel.
• Step 3. After receiving a registration request, the TS checks whether identity $I_i$ has already been registered in the database.

If not, the TS randomly chooses a number $R_i$ and computes two secret challenges $<P_{xi},P_{yi}>$ such that $P_{xi}=R_{i}G$, and $P_{yi}=R_i+s{h}_2(I_i,P_{k{e}_i})$. Each s and R is generated according to a Zipf distribution D, whose size $|D|$ is a Small, fixed constant [17].

The security of $<P_{xi},P_{yi}>$ is protected by the ECDLP and a hash function $h_2$. Then, the TS hides the challenges $<P_{xi},P_{yi}>$ inside $<P_{xi}^{\prime },P_{yi}^{\prime }>$ using the exclusive-or operations $P_{x_i}^{\prime }=P_{xi}\oplus h_2(I_{TS},s)$ and $P_{yi}^{\prime }=P_{yi}\oplus I_i\oplus s$, where $I_{TS}$ is the TS identity. The TS then stores $<P_{xi}^{\prime },P_{yi}^{\prime }>$ into its database, sets working bit $W_{bit-i}$ to zero, and sends a response $<P_{xi},P_{yi}>$ to $U_i$ through a secure trusted channel. $W_{bit-i}$ set to zero indicates the availability to communicate with other nodes. After that, whenever $U_i$ communicates with the TS or with another node $U_j$, $W_{bit-i}$ is set to one and indicates that the communication is currently going from $U_i$ to TS or $U_j$.

To enhance the security of tamper-proof devices, both nodes and TS encrypt their table of data with their secret keys. The TS hides its ID as $E_{ks}=s{I}_{TS}G$, whose security is protected via ECDLP and CDHP. Any node encrypts its table with its public key $P_{k{e}_i}$.

Figure 2. LAP-SG registration scheme.

Figure 2. LAP-SG registration scheme.

3.3. Authentication Phase

The registered node is now connected to the SG and is ready for service. Before starting the communication with other nodes in the SG network, each node $U_i$ must authenticate to other nodes $U_j,j\ne i$. The steps of the authentication phase are reported in Figure 3.

We assume that each node in the SG network knows its adjacent nodes’ information (i.e., their identity and public key). Therefore, the authentication proceeds as follows.

• Step 1: $U_i\to U_j:<I_i,X_i,Y_i,P_{xi}>$. Node $U_i$ chooses a random ephemeral secret $x_{i1}\in Z_p$ and computes a challenge $X_i=x_{i1}G$ using ECC multiplication, hides $x_{i1}$ inside $Y_i=x_{i1}+P_{yi}{h}_1(I_j,x_{i1}{P}_{k{e}_j})$, and finally sends an authentication request containing challenges $<I_i,X_i,Y_i,P_{xi}>$ to node $U_j$ through a public channel. The security of $x_{i1}$ is protected inside $X_i$ using ECDLP and inside $Y_i$ using an exclusive-or operation and a hash function $h_1$.
• Step 2: $U_j\to U_i:<X_j,Y_j,P_{xj}>$. After receiving an authentication request, to check the authenticity of node $U_i$ and verify its request, node $U_j$ recomputes the challenge

  $$\begin{array}{c}\hfill Y_{i}G=?X_i+(P_{xi}+P_{ks}{h}_2(I_i,P_{k{e}_i}))h_1(I_j,X_{i}Ps{w}_j),\end{array}$$

  (1)

  where $=?$ denotes the comparison operator. The challenge is recomputed using the available information, i.e., $<P_{ks},P_{k{e}_i}>$ and the received information from $U_i$, i.e., $<I_i,X_i,Y_i,P_{xi}>$. In case of mismatch, the process is terminated. In case of success, node $U_j$ chooses a random ephemeral secret $x_{j1}\in Z_p$ and computes a challenge $X_j=x_{j1}G$ using ECC point multiplication, hides $x_{j1}$ inside $Y_j=x_{j1}+P_{yj}{h}_1(I_i,x_{j1}{P}_{k{e}_i})$, with $P_{yj}$ obtained as the j’s counterpart of $P_{yi}$, and finally sends response challenges $<X_j,Y_j,P_{xj}>$ to $U_i$ through a public channel. The security of $x_{j1}$ is hence protected inside $X_j$ using ECDLP and inside $Y_j$ using an exclusive-or operation and a hash function $h_2$.

3.4. Session Key Computation Phase

$S_{K,i}=x_{i1}{X}_{j}Ps{w}_i{P}_{k{e}_j}$. After receiving a challenge, to check the authenticity of node $U_j$, node $U_i$ recomputes and verifies the challenge

$$\begin{array}{c}\hfill Y_{j}G=?X_j+(P_x^{\prime }+P_{ks}{h}_2(I_j,P_{k{e}_j}))h_1(I_i,X_{j}Ps{w}_i)\end{array}$$

(2)

using the available information $<P_{ks},P_{k{e}_j},I_j>$ and the received information $<X_j,Y_j,P_{xj}>$. In case of failure, the session is terminated. In case of success, node $U_i$ computes the session key $S_{K,i}=x_{i1}{X}_{j}Ps{w}_i{P}_{k{e}_j}$. At the same time, node $U_j$ computes its session key $S_{K,j}=x_{j1}{X}_{i}Ps{w}_j{P}_{k{e}_i}$. Both nodes set their respective working bit $W_{bit-·}$ to 1 to indicate their working status. We report the code of LAP-SG on our GitHub page [33].

4. Security Analysis

In this section, we first discuss how the proposed scheme fulfilled security design guidelines (Section 2.3) using perform security analysis (Section 4.1). Then, we show LAP-SG security via simulation tools in (Section 4.4 and Section 4.5).

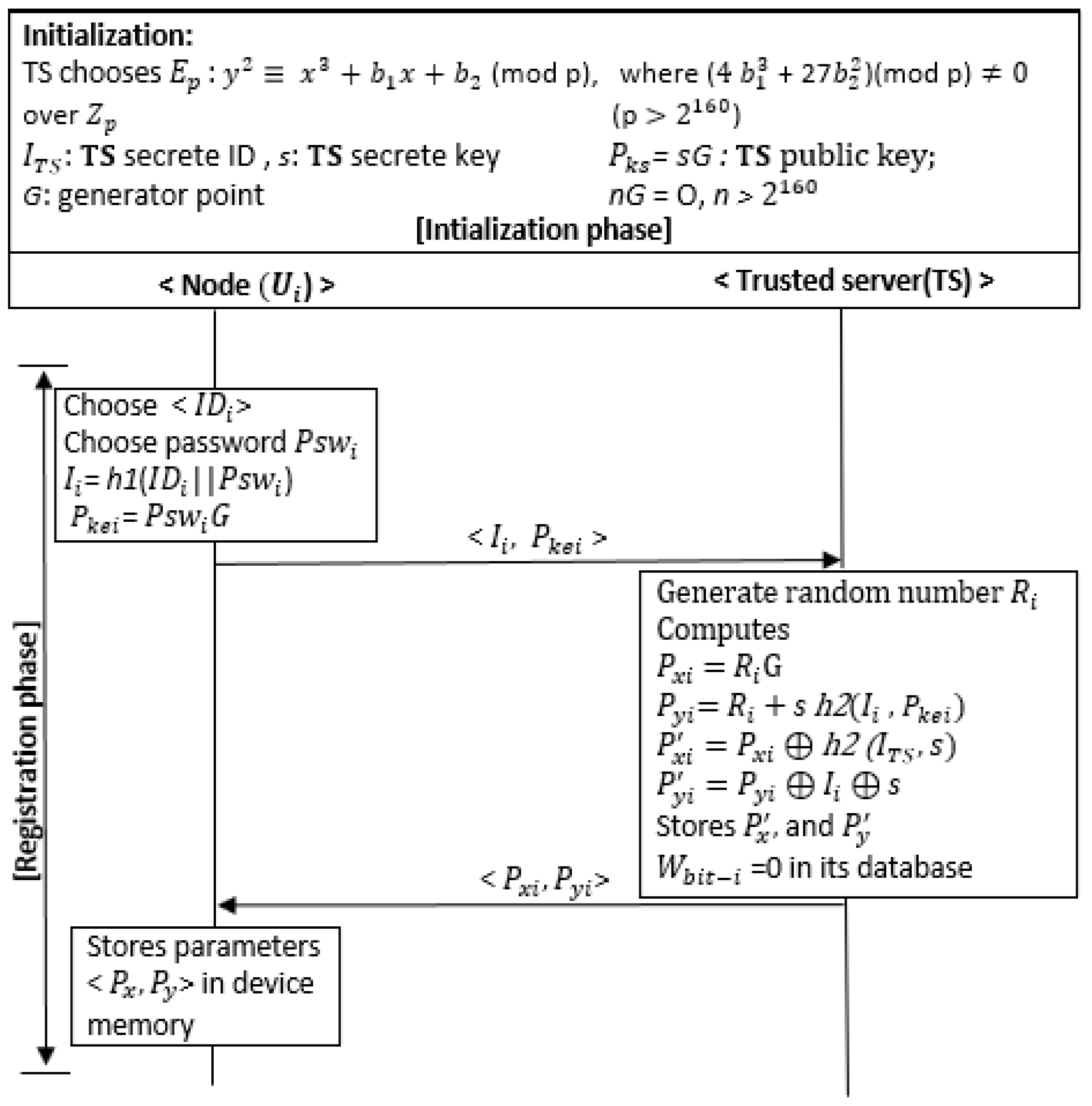
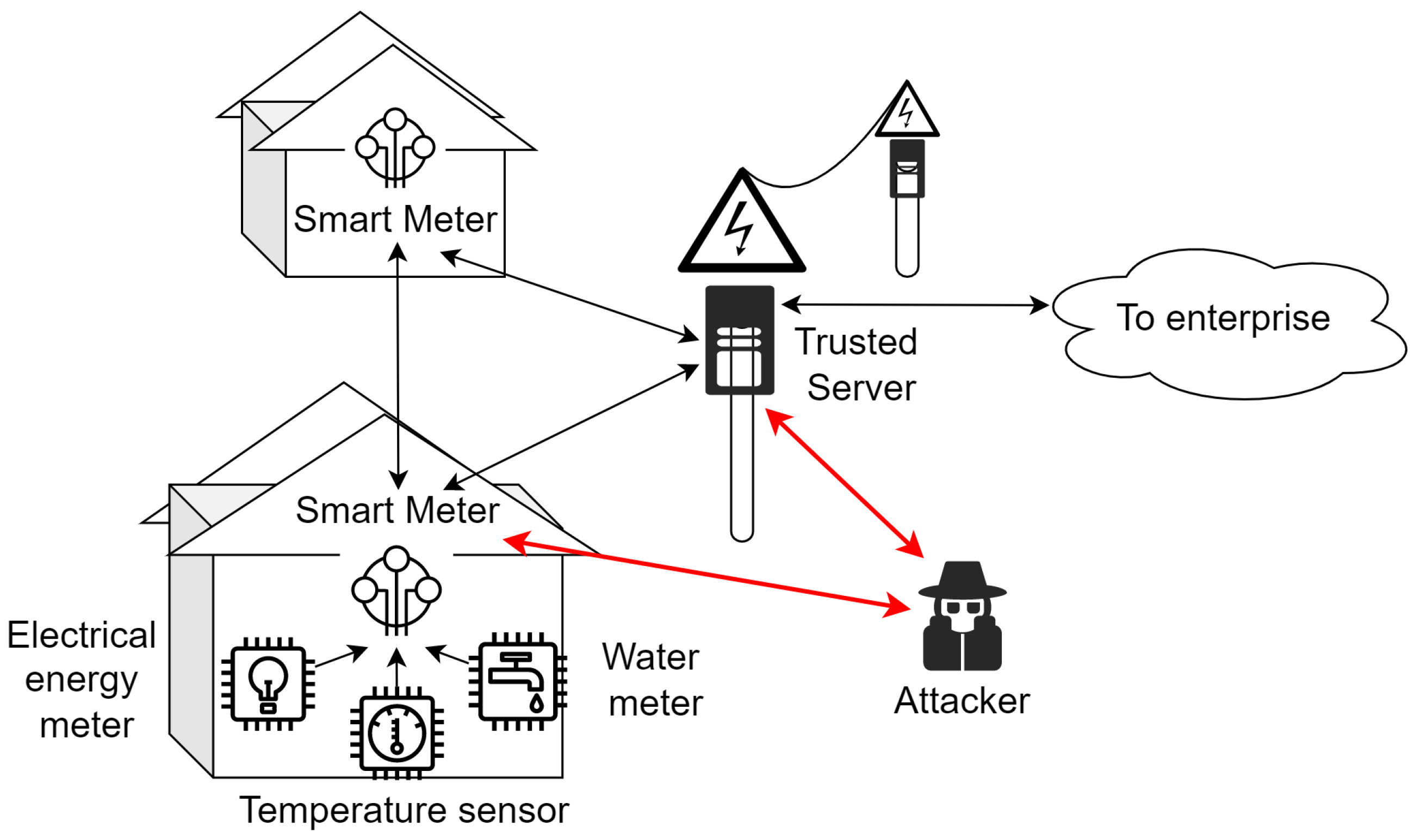
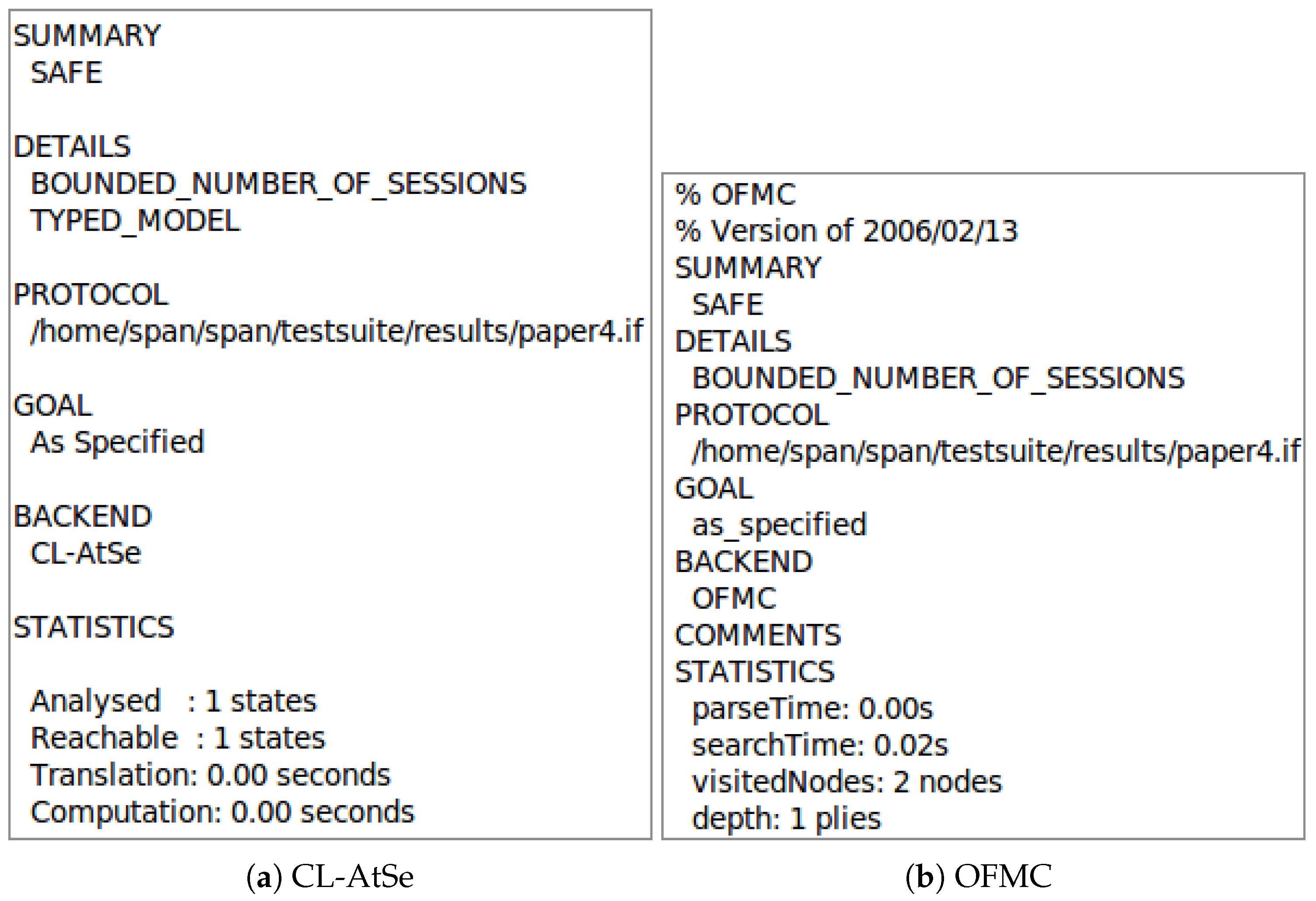
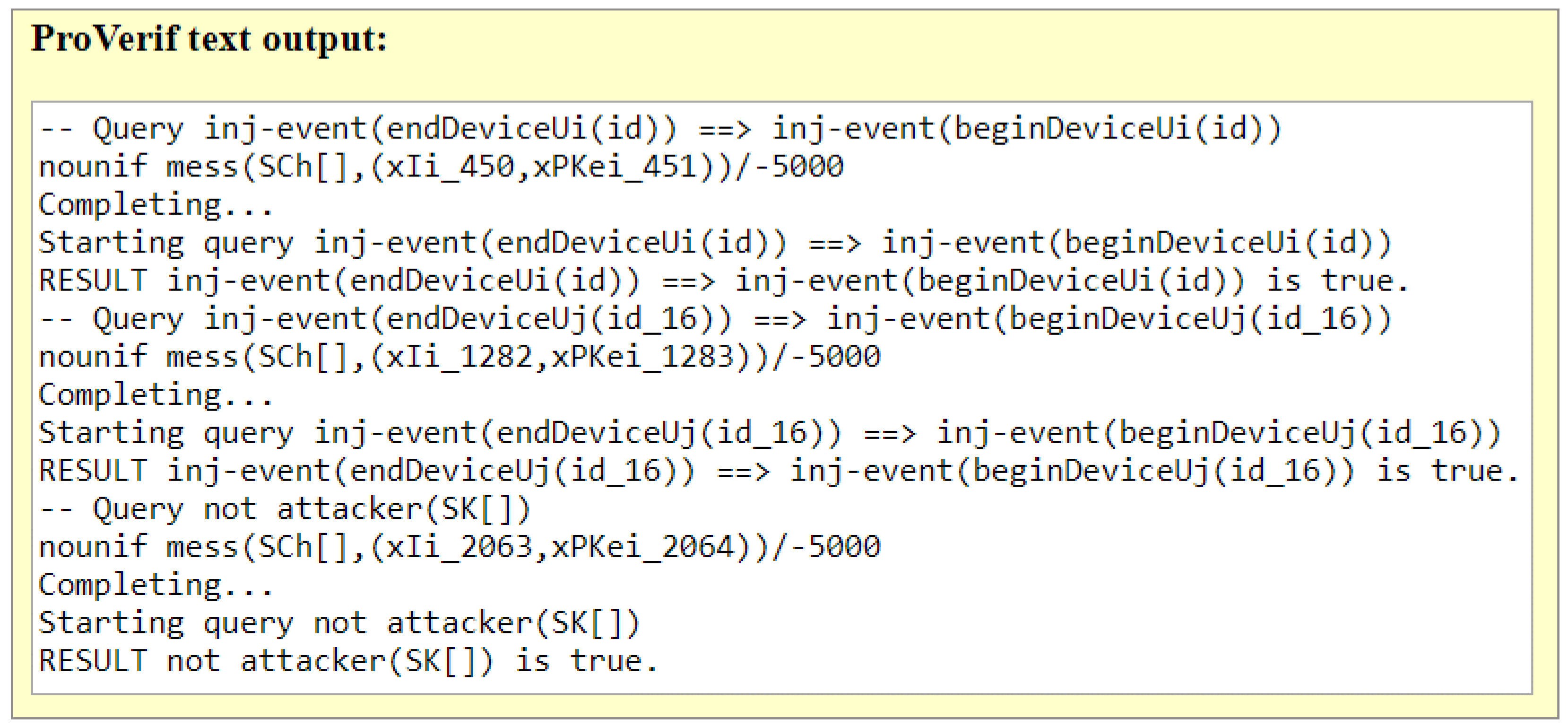
4.1. Formal Security Analysis

To assess $Adv$’s effectiveness in attacking LAP-SG and capture its interaction with a node and the ts, we leverage the BPR2000 model [17,18].

In BPR2000, queries model the actual adversary capabilities in a real attack. We consider the Send(), Reveal(), Corrupt(), Execute(), and Test() queries defined in [17]. Furthermore, we consider the following additional queries. Freshness() ensures that the session key is not revealed to $Adv$. Thus, to maintain the freshness at instant t, we must ensure that, at time t, the Authentication Protocol (AP) computes a session key $SK$. The Reveal() query must not be issued; from the start of the game, at most one Corrupt() query (where the oracle can reveal secret password $Ps{w}_i$ and all current instant $I{D}_i$ of $U_i$) has been issued; the common session key $S_K$ is established if both partners involved at t are mutually authenticated to each other. Furthermore, impersonation attacks fail only when the TS (or $U_i$) agree on a common session key that has not yet been shared with $U_i$ (or TS).

To prove the security of LAP-SG, we introduce the following.

Theorem 1.

Consider a PPT $Adv$ making at most q queries, divided in $q_{\mathrm{se}}\mathit{\left(}n\mathit{\right)}$ send(), $q_{\mathrm{exe}}\mathit{\left(}n\mathit{\right)}$ execution(), and $q_{\mathrm{h}}\mathit{\left(}n\mathit{\right)}$ hash() queries with length ${\mathsf{\ell }}^{\prime }$. Furthermore, consider $Adv$ with advantage $Ad{V}_{AP}\mathit{\left(}n\mathit{\right)}$. Then, for our, it holds

$$\begin{array}{cc}\hfill Ad{V}_{AP}\left(n\right)\le & {\displaystyle \frac{{(q_{\mathrm{se}}\left(n\right)+q_{\mathrm{exe}}\left(n\right))}^2}{2q}}+{\displaystyle \frac{q_h{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}}+{\displaystyle \frac{q_{\mathrm{se}}{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}}\hfill \\ \hfill & +Ad{V}_{\mathrm{G}}^{cdh}\left(2T_{ecc}{T}_{cdh}{q}_{exe}\left(n\right)\right),\hfill \end{array}$$

(3)

where $T_{ecm}$ is the time required to solve the ECDH problems. Therefore, LAP-SG is semantically secure.

Proof. 

To provide a proof, we exploit game theory. We define five games, denoted as $G{a}_i$, $i\in [0-4]$. $Suc{c}_i$ denotes the success of the adversary in the ith game, i.e., the adversary successfully guesses bit c after executing the $Test\left(\right)$ query in game $G{a}_i$. We define the games as follows.

Game $G{a}_0$.

This game models semantic security attacks on the proposed protocol. $Adv$ correctly guesses bit c with probability $P\left[Suc{c}_0\right]$. Therefore, the advantage of $Adv$ in $G{a}_0$ is

$$Ad{V}_{\mathrm{AP}}=2P\left[Suc{c}_0\right]-1.$$

(4)

Game $G{a}_1$.

This game models an eavesdropping attack. Via $Execute\left(\right)$ query, $Adv$ can intercept the messages $<I{D}_i,X_i,Y_i>$ and $<X_j,Y_j>$. $Adv$ also queries the $Test\left(\right)$ oracle to check whether the received data are the actual session key $S_{K,i}$. To compute the session key, $Adv$ must know the short-term secrets $(x_{i1},x_{j1})$, as well as the long-term secrets $Ps{w}_i$ and s. Therefore, $Adv$ has no additional advantage in $G{a}_1$ compared to $G{a}_0$. Therefore, $P\left[Suc{c}_1\right]=P\left[Suc{c}_0\right]$.

Game $G{a}_2$.

This game models an active attack through the use of all oracles queries. However, the selection of random ephemeral secrets $(x_{i1},x_{j1})$ among different sessions is avoided. Also, a collision in the output hash function is avoided. Therefore, game $G{a}_1$ and $G{a}_2$ are identical except for the $Send\left(\right)$ and $Hash\left(\right)$ queries in $G{a}_2$. Using the birthday paradox, we obtain

$$P\left[Suc{c}_2\right]-P\left[Suc{c}_1\right]\le {\displaystyle \frac{{(q_{\mathrm{se}}\left(n\right)+q_{\mathrm{exe}}\left(n\right))}^2}{2q}}+{\displaystyle \frac{q_h{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}},$$

(5)

where q is the overall number of queries and ${\mathsf{\ell }}^{\prime }$ is the length of the query.

Game $G{a}_3$.

This game models an active attack where, without the input of the oracle $Send\left(\right)$ query, $Adv$ is able to identify the hash values $<Y_i,Y_j>$. However, this results in the termination of the protocol authentication. Game $G{a}_3$ and $G{a}_2$ are hence indistinguishable if and only if either $U_i$ or the TS terminate the protocol. Therefore, it follows that

$$P\left[Suc{c}_3\right]-P\left[Suc{c}_2\right]\le {\displaystyle \frac{q_s{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}}.$$

(6)

Game $G{a}_4$.

This game considers the Canetti–Krawczyk (CK) adversary model and assumes that either the short-term secrets $(x_{i1},x_{j1})$ or the long-term secrets are revealed during the communication between the involved participant and the TS. In this case, the adversary’s goal is to find the session key by successfully executing the $Execute\left(\right)$ query. However, to obtain the session key it is required to solve ECDHP and CDHP problems. Therefore, the difference between $G{a}_3$ and $G{a}_4$ is negligible as long as the likelihood of solving ECDHP and CDHP is Small. Hence, we have

$$\begin{array}{cc}\hfill P\left[Suc{c}_4\right]-& P\left[Suc{c}_3\right]=Ad{V}_G^{\mathrm{cdh}}(2T_{ecc},T_{cdh},q_{exe}\left(n\right)),\hfill \end{array}$$

(7)

where $T_{ecc}$ is the time required to solve ECDHP problems, and $T_{cdh}$ is the time required to solve CDHP problems. We introduce the following Lemma 1 to prove the Theorem 1. □

Lemma 1.

Difference lemma: Let $Suc{c}_1$, $Suc{c}_2$ be the events of winning games $G{a}_1$ and $G{a}_2$. Denote an error event by E, such that event $Suc{c}_1$ occurs if and only if event $Suc{c}_2$ exists with error E. Then, $Pr\left[Suc{c}_1\right]-Pr\left[Suc{c}_2\right]\le Pr\left[E\right]$.

Now, applying difference Lemma 1 on the above games, we have

$$\begin{array}{cc}\hfill & P\left[Suc{c}_0\right]-P\left[Suc{c}_4\right]\le {\displaystyle \frac{1+Ad{V}_{\mathrm{AP}}}{2}}-{\displaystyle \frac{q_h{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}}-{\displaystyle \frac{q_s{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}}\hfill \\ \hfill & -{\displaystyle \frac{{(q_{\mathrm{se}}\left(n\right)-q_{\mathrm{exe}}\left(n\right))}^2}{2q}}-Ad{V}_G^{\mathrm{cdh}}(2T_{ecc},T_{cdh},q_{exe}\left(n\right)),\hfill \end{array}$$

(8)

that can be rewritten as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1+Ad{V}_{\mathrm{AP}}}{2}}\le {\displaystyle \frac{{(q_{\mathrm{se}}\left(n\right)+q_{\mathrm{exe}}\left(n\right))}^2}{2q}}+{\displaystyle \frac{q_h{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}}+{\displaystyle \frac{q_{\mathrm{se}}{\left(n\right)}^2}{2^{{\mathsf{\ell }}^{\prime }}}}\hfill \\ & +Ad{V}_{\mathrm{G}}^{cdh}\left(2T_{ecc}{T}_{cdh}{q}_{exe}\left(n\right)\right),\hfill \end{array}$$

(9)

Theorem 2.

Consider a PPT $Adv$ making at most q queries, divided in $q_{se}\left(n\right)$$Send\left(\right)$, $q_{exe}\left(n\right)$$Execute\left(\right)$, and $q_h\left(n\right)$$Hash\left(\right)$ queries with length ${\mathsf{\ell }}^{\prime }$, such that the resultant advantage of $Adv$ is $Ad{V}_{(}AP)\left(n\right)$. For our, it holds

$$\begin{array}{cc}\hfill Ad{V}_{A,PP}\left(n\right)\le & {\displaystyle \frac{{(q_{se}\left(n\right)+q_{exe}\left(n\right))}^2}{2q}}+{\displaystyle \frac{q_h{\left(n\right)}^2}{2^{l^{\prime }}}}+{\displaystyle \frac{q_{se}{\left(n\right)}^2}{2^{l^{\prime }}}}\hfill \\ \hfill & +Ad{V}_G^{\mathrm{CDH}}(2T_{ecc}+4T_{ecc}{T}_{cdh}{q}_{exe}\left(n\right)),\hfill \end{array}$$

(10)

where $T_{ecm}$ and $T_{cdh}$ are the times required to solve ECDH and CDHP problems. Therefore, LAP-SG provides secure mutual authentication.

Proof. 

The proof is based on the games described in the proof of Theorem 1, where proofs from $G{a}_0$ to $G{a}_3$ are given. For $G{a}_4$, we have

$$\begin{array}{cc}\hfill P\left[Suc{c}_4\right]-& P\left[Suc{c}_3\right]=Ad{V}_G^{cdh}\left(2T_{ecc}+4T_{ecc}{T}_{\mathrm{cdh}}{q}_{exe}\left(n\right)\right).\hfill \end{array}$$

(11)

Using Lemma 1 and what is derived for Theorem 1, we can derive the proof of Theorem 2. □

4.2. Secure Protocol Design Analysis

In this subsection, we discuss the trade-off between security and usability of LAP-SG when $Adv$ needs to perform a brute force attack to guess $<I{D}_i,Ps{w}_i>$, which may be unfeasible in polynomial time under the capabilities PC-2 and PC-1. For $I_i$, the number of trials is given by $|D_{ID}|\times |D|\simeq {10}^{12}$, where $|D_{ID}|=|D|={10}^6$ represents the size of the device identity space and password space.

We also consider a situation where the adversary tries to exploit security usability parameters. In this case, $Adv$ tries to change the device password, or $Adv$ may run the device. In this case, it is hard for $Adv$ to detect $Ps{w}_i$ in polynomial time using offline password guessing attacks (SC-FPEE), as the size of the space of $Ps{w}_i$ is $\simeq 1/2^{12}$. If $Adv$ attempts to perform the DoS attack (SG-DoSA) to change the password, the maximum time for the password change facility is set to five attempts per day. In this a case, $Adv$ succeeds with probability $5/2^{12}$, which is still higher than a polynomial time. In case of a successful DoS attack (SG-DoSA), the device owner can restore his device by re-registering it. The existing device credentials are then deleted. Due to the tamper-proof nature of the device, our device may have two essential threats, which include DoS attacks and online guessing attacks. However, to launch these attacks successfully on very low-cost IoT devices, $Adv$ needs high-costs instruments with little benefits. Thus, LAP-SG archives security beyond the optimal security limit $Q_{send}^{s^{\prime }}\left(n\right)/|D|+ϵ\left(n\right)$.

In the next section, we discuss the security of LAP-SG against the most significant known attacks. Due to space constraints, we neglect the attacks that we instead consider in the AVISPA and ProVerif simulations, i.e., MiTM, replay, spoofing, and eavesdropping.

We assess LAP-SG security in comparison with other existing schemes [3,7,13] and show the security capabilities of each solution in

Table 4. Comparison of vulnerabilities solved by our and other authentication protocols.

Attack \Reference	Cho et al. [13]	Odelu et al. [15]	Tasi et al. [14]	Bhanse et al. [16]	Abbas et al. [12]	Mogha et al. [7]	Kumar et al. [3]	Hamm et al. [20]	Chaud et al. [21]	Wang et al. [9]	Our (Our Proposal)
Replay attack	✓	✓	✓	✓	✓	✓	✓	✓	✓	—	✓
Password Guessing Attack	—	✓	✓	—	—	✓	✓	—	—	—	✓
Embedded Device Impersonation Attack	—	—	—	✓	—	—	✓	—	—	—	✓
Denial of Service Attack	—	—	—	✓	✓	✓	✓	—	✓	✓	✓
Many logged-in Users Attack	—	—	—	—	—	—	—	—	—	—	✓
Server Impersonation Attack	—	—	—	—	✓	—	—	✓	✓	—	✓
Forward Secrecy	—	✓	✓	✓	✓	✓	✓	✓	✓	—	✓
Known Session Attack	✓	✓	✓	—	✓	—	✓	✓	✓	✓	✓
Ephemeral Secrete Leakage	—	—	—	✓	✓	✓	—	✓	—	✓	✓
User Anonymity Attack	—	✓	✓	✓	—	✓	✓	✓	✓	—	✓
Stolen Database (or Verifier) Attack	✓	✓	✓	—	✓	✓	—	✓	✓	✓	✓
Man-in-the-Middle Attack	✓	—	—	✓	✓	✓	✓	✓	—	—	✓
Eavesdropping Attack	✓	✓	—	—	—	—	—	—	—	—	✓

Attack\References: ✓ = resistant, — = not considered/vulnerable.

. The comparison shows that LAP-SG is robust against a larger attack set compared to other existing schemes. Note that results for the state-of-the-art protocols are based on the respective authors’ claims. In addition, existing works, with an exception for Wang et al. [9], do not explicitly mention security against insider attacks.

4.3. Analysis of Known Attacks

In this section, we discuss the security of LAP-SG against the most significant active and passive attacks.

Replay attack (Active): The attacker impersonates node $U_i$ by reusing the previously sent challenges. The receiving node $U_j$ recomputes and checks $Y_{i}G$ via (1). If true, then $U_j$ computes another challenge $<X_j,Y_j,P_{x}j>$ and forwards it to $U_i$. However, the attacker is unable to verify the challenge via (2) and to compute a valid session key $S_{K,i}$, as she does not know $Ps{w}_i$. The security parameters $<Ps{w}_i,Ps{w}_j,x_{j1}$ and $x_{i1}>$ are not sent through any messages over public channel nor can be acquired from $U_i$ and $U_j$ due to their tamper-proof design. In addition, the security of $Ps{w}_i$ (or $Ps{w}_j$) and $x_{i1}$ (or $x_{j1}$) is protected inside $S_{K,i},P_{k{e}_i}$ (or $P_{k{e}_j}$) and $X_i$ (or $X_j$ ) by ECDHP and CDHP. Hence, LAP-SG is secure against replay attacks.

DoS attack (Active): LAP-SG terminates the communication if the number of incorrect attempts of entering $I_i$ exceeds a limit value. However, the authentication proceeds as long as correct $I_i$ is provided. If the adversary replaces the true challenge by randomly choosing ephemeral secrets $x_{i1}^{\prime }$ and $P{yi}^{\prime }$, the receiving node $U_j$ is unable to match the deduction and terminates the protocol with a failure message. The adversary being completely unaware of $I_i$ due to the tamper-proof nature of the device, LAP-SG is robust against DoS attacks.

Password-guessing attack (Passive): In LAP-SG, the original password $Ps{w}_i$ is stored in $I_i$ using a one-way collision resistant function, and in $P_{k{e}_i}$ using of ECDHP. An attacker is unable to guess $Ps{w}_i$ without knowing $I_i$ and $P_{k{e}_i}$, which are stored in a tamper-proof device and hence not accessible. Hence, LAP-SG is robust against password-guessing attacks.

Node Impersonation attack (Active): Consider the scenario where the adversary impersonates an authenticated node $U_i$ via parameters $<I_i,X_i,Y_i,P_{x_i}>$. The adversary randomly chooses parameters $<X_j^{\prime },Y_j^{\prime },P_{xj}^{\prime }>$ to reply to node $U_i$. Then, node $U_i$ computes (2), based on the received information. However, since the attacker ignores $x_{j1}$, $P_{kej}$, $P_{xj}$, and $P_{yj}$, the computed parameters result wrong, and the session is terminated. Since node $U_j$ is a tamper-proof device, $P_{yj}$ and $P_{xj}$ are secure. Even if the attacker succeeds somehow in tampering the device, it is impossible to compute a valid session key, since the adversary is unaware of the secret parameters $<Ps{w}_j,x_{j1}>$. In addition, $<Ps{w}_j,x_{j1}>$ is protected inside $P_{k{e}_j},X_j$ and in session key $S_{K,j}$ by ECDHP and CDHP. Therefore, LAP-SG is resistant towards node impersonation attacks.

Server Impersonation attack (Active): The adversary server randomly chooses parameters $<X_j^{\prime },Y_j^{\prime }>$ responded to node $U_i$. Then, node $U_i$ computes (1). However, since the attacker does not know $<x_{j1},P_{k{e}_i},P_{yi}>$, the result is wrong and the session is terminated. Since $U_i$ is a tamper-proof device, the security of $P_{yi}$ is protected. If an attacker somehow succeeds at tampering the device, then it is impossible for an adversary server to compute a session key as it would need the secret parameters $<s,x_{j1}>$. In addition, the security of $<s,x_{j1}>$ is protected inside $P_{ks},X_j$ and in the session key $S_{K,s}=x_{j1}{X}_{i}s{P}_{k{e}_i}$ by ECDHP and CDHP. In addition, s is protected inside the TS via ECDLP and CDHP $E_{ks}$. Hence, LAP-SG is robust against server impersonation attacks.

Sever database theft attack (Passive): The attacker tries to steal information from the server’s database. However, the database is protected by $E_{ks}$; therefore, the attacker is unable to compute $E_{ks}$ without knowing s and $I_{TS}$. It is impossible for an attacker to extract s and $I_{TS}$ from $E_{ks}$ in polynomial time, as it exploits ECDLP and CDHP. If either s or $I_{TS}$ are revealed to an attacker, it is impossible to compute the other parameter from $E_{ks}$. In addition, even if the encryption key is compromised, then attacker is unable to determine $<P_{xi},P_{yi}>$ from $<P_{xi}^{\prime },P_{yi}^{\prime }>$, as $<P_{xi},P_{yi}>$ is protected by s and $I_{TS}$. Therefore, LAP-SG is robust against server database theft attacks.

Node spoofing attack (Active): The attacker masquerades as a legitimate node $U_j$ to retrieve its secret credentials. As mentioned in the password guessing attack and replay attack, it is impossible for an attacker to extract and guess password $<Ps{w}_i,Ps{w}_j>$ from $P_{k{e}_i}$ and $P_{k{e}_j}$ thanks to ECDLP and CDHP. Furthermore, the security parameters $x_{j1}$ and $x_{i1}$ are ephemeral and expire after every session. In addition, security parameters $<P_{xi},P_{yi}>$ are stored in tamper-proof nodes. Hence, LAP-SG is secure against node spoofing attacks.

Many logged-in users attack (Active): LAP-SG maintains a working bit $W_{bit-i}$ for every communication. After a successful verification step, the involved nodes set their communication bit towards the communicating node to one. If node $U_j$ receives an authentication request from another node which uses the credentials of $U_i$, then $U_j$ checks whether the status bit $W_{bit-i}$ is equal to one. If the status is one, then node $U_j$ rejects these requests. Therefore, LAP-SG is robust against many logged-in users attacks.

Forward secrecy (Active): In LAP-SG the session key $S_{K,i}$ security depends not only on the private key $Ps{w}_i$, but also on the ephemeral secret $x_{i1}$ which expires after every session termination. For an attacker, it is computationally impossible to extract the security parameters $<Ps{w}_i$ or $x_{i1}$ from $S_{K,i}$ due to the complexity of the ECDLP and CDHP. Hence, LAP-SG is secure towards forward secrecy attacks.

Insider attack (Active): In LAP-SG, the password $Ps{w}_i$ is sent to the TS or to other nodes via $I_i$. In addition, it is impossible to extract the password $Ps{w}_i$ from $P_{k{e}_i}$ and from $S_{K,i}$ due to ECDLP and CDHP. Therefore, privileged insider attacks fail to impersonate the secret information of a legitimate node $U_i$. Hence, LAP-SG is robust against insider attacks.

Known session-specific temporary information attack (Active): The session key $S_{K,i}$ computation is performed after successful mutual authentication between node $U_i$ and $U_j$. If an adversary somehow succeeds in discovering the ephemeral secrets $x_{i1},x_{j1}$, still it would not be able to compute a session key as the password is protected via a one-way collision-resistant hash function $h\left(\right)$, ECDLP and CDHP. In addition, if either one of the parameters is revealed to the attacker, it is computationally infeasible to determine either $x_{i1}$ or $Ps{w}_i$ from $S_{K,i}$. This is due to the difficulties in solving the CDHP and ECDLP for pairs in $S_{K,i}$ using a polynomial-time algorithm. Consequently, LAP-SG withstands a known session-specific temporary information attack.

Attacks on node anonymity (Passive): Device anonymity ensures that the attacker cannot find the actual device identity $I{D}_i$ of node $U_i$. This identity is well-protected with their password by concealing it inside a one-way collision-resistant hash function, whose output is given by $I_i$. Both $I{D}_i$ and $Ps{w}_i$ are never sent through any message. In addition, for every new communication, the device is able to change its $Ps{w}_i$ periodically. In our scheme, we took the combination $I_i$ equation to present its identity to other nodes in network. However, even after knowing the combination equation value, the attacker cannot correctly guess the identity and password, which results in them failing to compute the next authentication equations and challenges. In addition, the security of the device is well protected because of the tamper-proof nature. Therefore, LAP-SG ensures the safety of the device’s identity and password over the CC.

Stolen-verifier attack (Active): During the registration phase, the TS stores $P_{x_i}^{\prime }$ and $P_{y_i}^{\prime }$ in its database. Even though the attacker may access this information, it would be unable to access the actual security parameters $P_x$ and $P_y$, which are protected using the secret server key s and $I_{TS}$. $P_x$ and $P_y$ are stored in the tamper-proof device $U_i$, encrypted with secret key $P_{k{e}_i}$. In addition, even if the attacker makes a large number of login request with another node $U_j$, it fails to verify the challenge (1) and to compute $S_{K,i}$. This is due to the attacker being unaware of $Ps{w}_i$, which is hard to extract from parameters $I_i$ and $P_{k{e}_i}$ due to the one-way collision-resistant function, ECDHP, and the device’s tamper-proof nature. Consequently, LAP-SG can resist stolen-verifier attacks.

Man-in-the-middle attack (Active): The successful mutual authentication ensures the safety of an authentication scheme from man-in-the-middle attacks. LAP-SG prevents MiTM attacks and supports successful mutual authentication, which will be shown from the result of the ProVerif tool in Section 4.5.

Eavesdropping attack (Passive): To perform a successful eavesdropping attack, the attacker needs to extract the security parameters $I_i,X_i,Y_i$, and $P_x$ from an open transmission channel. Even if the attacker succeeds in obtaining these security parameters, they cannot determine password $Ps{w}_i$. In addition, it is very hard to determine the ephemeral secret $x_{i1}$ due to the complexity of ECDHP and ECDLP, as detailed in node impersonation attacks. Therefore, LAP-SG is resistant towards eavesdropping attacks.

We assess LAP-SG security in comparison with other existing schemes [3,7,13] and show the security capabilities of each solution in Table 4. The comparison shows that LAP-SG is robust against a larger attack set compared to other existing schemes. Note that the results for the state-of-the-art protocols are based on the respective authors’ claims. In addition, existing works, with the exception of that of Wang et al. [9], do not explicitly mention security against insider attacks.

4.4. Formal Security Validation Using AVISPA Tool

In this section, we verify the security strength of LAP-SG using the widely accepted Automated Validation of Internet Security Protocols and Applications (AVISPA) tool [19,34]. The purpose of using AVISPA is to validate the security strength of LAP-SG against a wide range of active and passive attacks. The tool supports the Dolev–Yao attacker model, which assumes an adversary with complete control over the communication channel, making it ideal for testing real-world attack scenarios such as replay and man-in-the-middle (MiTM) attacks [27]. AVISPA evaluates whether nodes will engage in communication over compromised or replayed information, confirming the protocol’s safety through backend tests (e.g., CL-AtSe, OFMC) [33]. AVISPA is widely accepted in the research community as a robust framework for analyzing protocol correctness and safety against network-based threats [35].

We exploit AVISPA to test the security of LAP-SG against all active and passive attacks, including man-in-the-middle and replay attacks. We conducted the AVISPA simulation for our protocol on a SPAN Ubuntu 10.10 Virtual machine consuming CPU, RAM = 2048 MB installed on an Intel Core i5-8500, 6-core 3.10 GHz machine as operating environments.

In our implementation, we used OFMC and CL-AtSe backends in AVISPA to state whether our protocol is secure. The CC is controlled by a Dolev–Yao attacker [27], i.e., the attacker has a legitimate role in running the protocol with a non-negligible probability (code available in [33]).

For the execution tests, we selected the widely accepted CL-AtSe and OFMC backends. By looking at both passive and active attackers, the CL-AtSe and OFMC backend analyze whether the legal agents execute the specific scheme. Backend results provide the intruders with information about certain typical sessions among the legal agents or nodes (see Figure 4).

Based on the outcome of the simulation (see Figure 4), we conclude that our proposed protocol is secure as follows.

• Replay Attack. The CL-AtSe and OFMC backend test LAP-SG against a replay attack, verifying whether nodes will engage in a communication with a tentative establishment over replayed information. The test result is SAFE, concluding that LAP-SG is secure against replay attacks.
• Dolev–Yao model check. The CL-AtSe and OFMC backend check whether man-in-the-middle attacks are possible though the Dolev–Yao model test. The test result is SAFE, concluding that LAP-SG is secure against man-in-the-middle attacks.
• Active and passive attacks. The outline results for CL-AtSe and OFMC backend reveals that LAP-SG is SAFE, indicating its security against all active and passive attacks mentioned in [27].

4.5. Formal Security Validation Using ProVerif Tool

ProVerif is another widely accepted automatic cryptographic protocol simulation tool. Purpose: ProVerif was used to validate LAP-SG’s mutual authentication correctness and session key security. It also employs the Dolev–Yao attacker model, enabling a comprehensive evaluation of the protocol’s resilience to advanced cryptographic threats. Rationale: ProVerif simulates the full lifecycle of LAP-SG, including registration, mutual authentication, and session key agreement, to verify its confidentiality, integrity, and robustness against all active and passive attacks [36]. The tool is especially useful for verifying session key security under adversarial conditions and ensures that attackers cannot compromise sensitive data even in the presence of partial information [36].

We conduct the ProVerif simulation for the proposed protocol on the same machine. This simulation used a binary package of ProVerif version 2.00 to trigger the phase of registration, mutual authentication, and session key agreement among nodes. The detailed explanation of the tool can be found on the official site [36].

This model consists of three important fragments, which include parameter declaration, query execution, and principal processes, the definition of which we present in Figure 5.

Figure 5 shows the ProVerif output for LAP-SG. The code used to test LAP-SG can be found in [33]. The first two queries successfully execute, showing the successful interaction and mutual authentication between SMs. Afterwards, the successful execution of the last query for LAP-SG shows that it is secure against all kinds of active and passive attacks towards the session key. This shows the confidentiality of LAP-SG.

Combined Rationale: Using both tools provides a comprehensive security analysis of LAP-SG, ensuring its robustness against a variety of real-world attack scenarios. The complementary strengths of AVISPA (protocol safety) and ProVerif (cryptographic correctness) ensure that LAP-SG’s security is thoroughly validated across multiple dimensions [19,27,34,35,36]. These explanations highlight the importance of AVISPA and ProVerif in assessing LAP-SG’s security rigorously and comprehensively.

5. Performance Evaluation

In this section, we compare the computational complexity of LAP-SG with that of other available schemes to show its advantages. We compare the schemes based on the communication cost (ms), computation cost (bit), and storage cost (bit). To this aim, we measure the running costs by implementing the PBC library [37] on Atmel’s SM. We used the pbc$-0.5.14$ library to build a cryptosystem and measure the time needed to execute the cryptographic primitives. We also used the GMP library [38] to support cryptography operations for a large prime number, floating-point numbers, and signed integer numbers, and to perform arbitrary precision arithmetic in PBC. In the PBC library implementation, we selected the ECC curve $y^2=X^3-2X$ for pairing operations over the field $F_p$ for some prime $p=3mod4$. We also set $G_1$ as a group of points that belong to $E\left(F_p\right)$ and $G_2$ as a subgroup of $E\left(F_p^{*}\right)$. Furthermore, we choose a bilinear curve $\widehat{e}:G_1\times G_2\to G_2$ such that $\widehat{e}(mA,nB)=\widehat{e}{(A,B)}^{mn}$, where $A,B$ belongs to $G_1$ and all $m,n$ belong to Z [36]. We also selected SHA256 to compute $h\left(\right)$.

To simulate a real SM, we set the execution trap of the Ubuntu Odroid 12.0.0 machine to 26%, reflecting the computational capabilities of Atmel Smart Meter devices with a 798 MHz CPU. This configuration mirrors the real-world performance constraints of Atmel’s SMs, as mentioned in their official documentation [1]. The device is equipped with a 798 MHz CPU, showcasing the limited processing power characteristic of these devices. Additionally, the base memory of 256 MB RAM represents the limited storage and processing capacity typically found in resource-constrained Smart Meters. To replicate these real-world constraints, the testing was conducted using a virtual machine configured to utilize 26% of the CPU execution capacity, effectively mimicking the operational environment of Atmel SMs. The diagrams (Figure 6) illustrate the experimental setup used for the study, visually representing the interconnected components, such as the Odroid Ubuntu 12.0 machine, the SM, and additional hardware. This setup provides an overview of the environment’s complexity and configuration. The testing also involved elliptic curve cryptography (ECC) and lightweight cryptographic operations, optimized for devices with constrained memory and processing power.

Table 5. Primitive execution time.

Operation	Symbol	Exec. Time (ms)
Hash	$T_h$	0.227
ECC Multiplication	$T_{ecm}$	0.730
Message Authentication Code	$T_{mac}$	0.454
Modular Exponentiation	$T_{expo}$	1.452
Bilinear Pairing	$T_{pair}$	1.704
Symmetric Encryption + Decryption	$T_s$	2.904
Addition	$T_{add}$	0.212

shows the execution time of the primitive functions used in authentication schemes. To make performance comparable, we re-implemented the existing authentication schemes and computed the computation, communication, and storage costs on Atmel’s family of devices.

5.1. Communication Costs

We choose parameters $q,r$ for EC having sizes of 256 and 224 bits, respectively. We select the size of the parameters to obtain an ECC key length of 256 bits, as suggested by ECRYPR II 2031–2040 [39] and NIST 2016-2030 [40]. For LAP-SG, ECC points $(X_i,P_{xi})$ belong to the $E_P(m,n)$. Therefore, each ECC point consumes $128+128=256$ bits of memory. The costs for the other parameters are listed in

Table 6. Parameters’ size.

Components	Size (bits)
$(I{D}_i,I_j)$	$(128,128)$
$(x_{i1},x_{j1})$	$(128,128)$
$(P_{xi},P_{yi})$	$(256,128)$
$(I_i,X_i,Y_i,P_{xi})$	$(128+256+128+256)=768$
$(X_j,Y_j,P_{xj})$	$(256+128+256)=640$
$(I_i,X_i,Y_i,P_{xi})+(X_j,Y_j,P_{xj})$	$(768+640)=1408$

. To calculate the communication cost, we first identify the number of communication parameters $((I_i,X_i,Y_i,P_{xi}),(X_j,Y_j,P_{xj}))$ involved in LAP-SG, resulting in $(I_i,X_i,Y_i,P_{xi})+(X_j,Y_j,P_{xj})=(640+640+128)=1408$ bits. Likewise, we computed the communication for other recent schemes [3,7,9,12,13,14,15,16,20,21,23,24].

Table 7. Computation, communication, and storage cost comparison.

Scheme	Computation Cost (ms)	No. of Messages	Communication Cost (bit)	Storage Cost (bit)
Cho et al. [13]	$3T_s+2T_{ecm}=10.172$	4	2560	1920
Odelu et al. [15]	$2T_{pair}+2T_{expo}+5T_{ecm}+12T_h=12.686$	3	1536	384
Tsai et al. [14]	$2T_{pair}+2T_{expo}+7T_{ecm}+10T_h=13.692$	3	1664	2176
Bhanse et al. [16]	$6T_{expo}+6T_{pair}+10T_h=21.206$	5	1536	768
Abbas et al. [12]	$8T_{ecm}+8T_h+4T_{add}=8.504$	3	1664	384
Mogha et al. [7]	$4T_s+17T_h=15.475$	4	1536	640
Kumar et al. [3]	$4T_s+6T_{ecm}+4T_{mac}+9T_h=19.855$	2	2048	1536
Hamm et al. [20]	$2T_{expo}+3T_{expo}+1T_s+2T_{add}+9T_{ecm}+2T_{pair}+8T_h=19.878$	2	1024	1024
Chaud et al. [21]	$8T_{ecm}+8T_h+2T_{add}=8.08$	2	1536	512
Wang et al. [9]	$1T_{ecm}+14T_h+3T_{expo}+7T_{add}=9.948$	3	1664	512
Abbasinezhad et al. [22]	$8T_{ecm}+10T_h+2T_{add}=8.534$	3	1440	1024
Dariush et al. [23]	$3267T_{add}=741.609$	4	2616	512
Mood et al. [24]	$200T_{add}=45.4$	3	7875	10,500
LAP-SG(Ours)	$\mathbf{6}{\mathbf{T}}_{\mathbf{ecm}}+\mathbf{6}{\mathbf{T}}_{\mathbf{h}}=\mathbf{5}.\mathbf{742}$	2	1408	384

shows the results for all the analyzed schemes. From Table 7, we conclude that LAP-SG has lower communication cost compared to other existing schemes, providing a lightweight solution to handle scalability issues. Note that, during communication cost calculation, we consider communication during the authentication stage only. We eliminated the session key computation state from communication cost. This is because the calculation of the session key represents a completion of successful authentication verification stage. Thus, our proposed scheme requires only two times the exchange of messages during the authentication stage.

5.2. Computation Cost

To compute the computation cost, we first count the number of operations $(T_h,T_{ecm},$$T_{mac},$$T_{expo},$$T_{pair},$$T_s)$ needed in LAP-SG and other recent schemes. Then, we exploit the cost of the cryptography operations obtained from our PBC experiment, as reported in Table 5. Note that, due to the low computation cost of lightweight cryptography operations (i.e., concatenation, XOR, and comparison operations), we neglect them from the overall calculation. The number of $T_{ecm}$ operations involved in the device side is three and in the server side the number is three. Table 7 shows the computation cost of LAP-SG compared to other recent schemes [3,7,13,22,23,24]. We see that LAP-SG exhibits lower computation cost compared to other existing schemes, proving its lightweight computation.

5.3. Storage Cost

To compute the storage cost, we use the values reported in Table 6, obtained after successfully executing PBC library on Atmel’s SMs following the guidelines of ECRYPR II [39] and NIST [40]. In LAP-SG, node $U_i$ stores $P_{xi}$ and $P_{yi}$ in its memory. Table 7 shows the results obtained comparing LAP-SG with other relevant schemes. Based on these results, we infer that LAP-SG consumes a Smaller amount of memory (384 bits) compared to other existing schemes [3,7,13,24].

The analysis of LAP-SG’s performance in high-traffic real-world scenarios is addressed as follows:

Acknowledge the Reductions in LAP-SG: LAP-SG has achieved notable reductions in both communication and storage costs compared to existing state-of-the-art schemes. Specifically: Communication Cost: LAP-SG reduced the communication payload by 400 bits, requiring only 1408 bits compared to 1792 bits for average existing schemes. Storage Cost: The storage requirements of LAP-SG were reduced to just 384 bits, compared to up to 1115 bits in competing schemes.

Competitive Context: When compared to other protocols, LAP-SG outperforms several prominent schemes. For example, the communication cost for LAP-SG is significantly lower than Kumar et al.’s scheme, which requires 1536 bits for communication. Similarly, Chaudhry et al.’s approach, which demands 512 bits of storage, results in higher communication costs (1664 bits), further emphasizing LAP-SG’s efficiency in communication and storage. While some protocols, such as those by Kumar et al., may match LAP-SG in storage cost, their communication costs are significantly higher due to inefficient cryptographic exchanges.

Practical Implications: These reductions have meaningful implications for real-world Smart Grid deployments: Reduced Communication Cost: The lower communication cost directly translates into lower bandwidth usage and faster message exchanges, which is crucial for large-scale Smart Grid networks with high traffic. This improvement helps avoid congestion and ensures the network operates more efficiently, especially in resource-constrained environments. Lower Storage Requirements: The reduced storage requirements extend the lifespan of devices by alleviating the strain on memory and storage resources, particularly in resource-constrained Smart Meters. These devices, which have limited memory and processing power, will benefit from enhanced longevity and better management of limited resources.

Simulation on Atmel SM Configuration: LAP-SG’s performance was tested on a simulated Atmel Smart Meter configuration with 798 MHz CPU and 256 MB RAM to replicate real-world resource-constrained devices.

Scalability Assessment: The protocol’s scalability is demonstrated by its ability to handle high traffic with significantly reduced computational costs (5.742 ms compared to 14.512 ms for other schemes), reduced communication payload (1408 bits vs. higher values for other protocols), and lower storage requirements (384 bits vs. up to 1115 bits in other schemes).

Realistic Cryptographic Implementation: Lightweight cryptographic operations such as Elliptic Curve Cryptography (ECC) were employed, which are well-suited for large-scale, high-traffic Smart Grid (SG) networks, ensuring reduced processing and communication overhead.

Comparison with Existing Protocols: A detailed comparison (Table 4, Table 5 and Table 7) illustrates how LAP-SG outperforms other schemes in terms of computational, communication, and storage costs, showcasing its practicality for real-world high-traffic SG deployments.

Protocol Efficiency: LAP-SG’s two-step message exchange during authentication ensures minimal interaction, making it suitable for managing a large number of simultaneous requests in high-traffic scenarios.

These points collectively provide a robust analysis of LAP-SG’s performance in high-traffic, real-world SG environments, emphasizing its efficiency and scalability.

6. Scalability and Adaptability

In this section, we discuss the scalability and adaptability of LAP-SG, highlighting its suitability for large-scale Smart Grid (SG) networks and diverse SG architectures.

6.1. Scalability in Large-Scale SG Networks

LAP-SG is designed to efficiently handle the high demands of large-scale SG networks, where millions or even trillions of authentication requests are processed. The protocol minimizes computational, communication, and storage overhead, ensuring that it can scale effectively without compromising performance.

High Traffic Handling: LAP-SG’s optimized design allows it to process a large number of authentication requests while maintaining low overhead, making it ideal for high-traffic environments common in SG networks. Reduced Computational Complexity: One of LAP-SG’s key advantages is its computational efficiency. It achieves three times Smaller computation costs compared to state-of-the-art protocols, with only 5.742 ms per operation, in contrast to the 14.512 ms on average required by competitors. This rn computational cost ensures faster processing times, which is crucial for maintaining network efficiency in large deployments.

Optimized Communication and Storage: LAP-SG’s communication and storage requirements are also optimized. With a 1408-bit communication payload and a 384-bit storage requirement, the protocol remains lightweight, minimizing the strain on network bandwidth and device memory. This makes it ideal for large-scale implementations, where resource constraints can be significant.

6.2. Adaptability to Diverse SG Architectures

LAP-SG is not only scalable but also highly adaptable to a variety of SG architectures, including those with resource-limited devices.

Support for Resource-Limited Devices: The protocol is specifically tailored for devices like the Atmel family Smart Meters, which feature a 798 MHz CPU and 256 MB of RAM—representative of the constraints found in many SG devices. LAP-SG has been optimized to work within these limitations, ensuring that it can be deployed across a wide range of devices in heterogeneous SG networks.

Cryptographic LAP-SG leverages Elliptic Curve Cryptography (ECC), which is known for its high security at Smaller key sizes. This cryptographic efficiency reduces the resource consumption required for security operations, making LAP-SG suitable for devices with limited computational power and memory. The use of ECC allows for secure authentication without placing excessive demands on system resources, making the protocol adaptable to a broad spectrum of SG devices and architectures.

Tamper-Proof Design: To enhance security, LAP-SG assumes the presence of tamper-proof devices. This assumption mitigates risks associated with device heterogeneity and ensures a robust security model, even in environments where devices may vary significantly in terms of capabilities and security features.

6.3. Practical Implementation

LAP-SG’s scalability and adaptability have been validated through practical implementation. Performance tests were conducted using realistic hardware configurations, including devices equipped with the PBC library for cryptographic operations. These tests demonstrate LAP-SG’s effectiveness in real-world SG scenarios, confirming that it can meet the demands of both large-scale deployments and devices with varied capabilities.

The protocol’s flexibility is also highlighted by its ability to securely handle both node-to-node and node-to-server interactions. This versatility ensures that LAP-SG can adapt to a wide range of authentication requirements and communication channels typical in SG environments.

6.4. Comparative Analysis

A comparative analysis is provided in Table 7, where LAP-SG’s communication, computation, and storage costs are compared with other schemes. The results clearly show LAP-SG’s efficiency and adaptability in different SG environments, reinforcing its suitability for large-scale and resource-constrained SG networks.

These points collectively demonstrate that LAP-SG is scalable for large-scale deployments but also adaptable to the diverse hardware and software constraints found in modern Smart Grid architectures. Its efficiency in handling high-traffic loads, low computational complexity, and flexibility in supporting a wide range of devices make it a robust solution for future SG network implementations.

7. Limitations and Future Work

While LAP-SG offers substantial benefits for scalable and adaptable Smart Grid (SG) networks, certain challenges and limitations remain. This section outlines the key limitations of the protocol and proposes future directions for improvement and extension.

7.1. Limitations

Scalability Challenges in Extreme Loads: Although LAP-SG demonstrates excellent scalability, scenarios involving trillions of authentication requests in ultra-dense SG networks may still pose challenges. Further optimization is needed to ensure robust performance under such extreme traffic conditions.

Support for Legacy Devices: LAP-SG is optimized for resource-limited devices; however, older devices with even more constrained computational and memory capacities may struggle to meet its requirements. These devices may require tailored protocol variants to achieve compatibility.

Reliance on Tamper-Proof Devices: The protocol assumes the presence of tamper-proof devices to ensure security. However, this assumption may not hold in all deployment scenarios, especially in cost-sensitive or less controlled environments, where tamper-proofing is infeasible.

Emerging Technology Compatibility: With the rapid evolution of SG technologies, including 5G, IoT, and edge computing, LAP-SG requires further validation and potential adaptation to ensure seamless integration with these advanced infrastructures.

7.2. Future Directions

Lightweight Protocol Variants: Developing lightweight versions of LAP-SG tailored to legacy and ultra-resource-constrained devices will help extend the protocol’s applicability across diverse SG networks.

Adaptive Load-Balancing mechanisms: To address scalability challenges under extreme traffic loads, advanced load-balancing techniques can be designed and incorporated into the protocol. These mechanisms can dynamically allocate resources based on network conditions, ensuring consistent performance.

Alternative Security Approaches: Reducing reliance on tamper-proof devices is critical for broader deployment. Incorporating hardware-based security modules, secure enclaves, or advanced anomaly detection systems can enhance the protocol’s robustness in heterogeneous environments.

Validation for Emerging Technologies: Extensive testing and optimization of LAP-SG for integration with emerging SG technologies, such as edge computing, IoT ecosystems, and 5G-enabled networks, will ensure the protocol remains future-proof and adaptable.

8. Conclusions

The limited resources of SM devices imposes significant challenges when designing secure solutions against active and passive attackers in SGs. The issue is further complicated by the huge number of authentication requests in SGs, where the number of connected SMs is constantly increasing. To solve these problems, in this paper, we proposed LAP-SG, a novel lightweight authentication scheme. To assess its validity for real-world devices, we implemented it considering the capability of SMs from Atmel’s family. We compared LAP-SG with other available state-of-the-art schemes, and proved its improved security guarantees and higher efficiency. We conclude that LAP-SG represents a benchmark protocol for implementation in real-world large SG networks.