Novel Method for Approximating Fixed Point of Generalized α-Nonexpansive Mappings with Applications to Dynamics of a HIV Model

Abstract

In this paper, we use an existing fixed point iterative scheme to approximate a class of generalized $\alpha$-nonexpansive mapping in Banach spaces. We also prove weak and strong convergence results for the mapping using the AG iterative scheme. An example of a generalized $\alpha$-nonexpansive mapping is given to show the validity of the claims. We apply the main results to the approximation of solution of a mixed type Voltera–Fredholm functional nonlinear integral equation and to the spread of HIV modeled in terms of a fractional differential equation of the Caputo type.

1. Introduction

Suppose $\mathcal{H}$ is a Banach space and $\mathcal{B}$ is a uniformly convex subset of $\mathcal{H}$. A mapping $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ is said to be a contraction if for some $\alpha \in [0,1)$,

$$\parallel \mathcal{G}x-\mathcal{G}y\parallel \le \alpha \parallel x-y\parallel ,\forall x,y\in \mathcal{B}.$$

(1)

If $\alpha =1$, such that (1) becomes

$$\parallel \mathcal{G}x-\mathcal{G}y\parallel \le \parallel x-y\parallel ,$$

then the mapping is known as nonexpansive.

As a generalization of the nonexpansive mapping, Suzuki [1], in 2008, introduced a new class of mapping which is said to be a mapping satisfying condition (C) and defined as follows:

if

$${\displaystyle \frac{1}{2}}\parallel x-\mathcal{G}x\parallel \le \parallel x-y\parallel \mathrm{implies}\parallel \mathcal{G}x-\mathcal{G}y\parallel \le \parallel x-y\parallel ,$$

for all $x,y\in \mathcal{B}$. This mapping is also known as Suzuki’s generalized nonexpansive mapping.

In 2011, García-Falset et al. [2], further extended the class of mapping satisfying condition (C) to a new class of mapping known to satisfy condition ($E_{\mu }$), defined thus:

if for all $x,y\in \mathcal{B}$,

$$\parallel x-\mathcal{G}y\parallel \le \mu \parallel x-\mathcal{G}x\parallel +\parallel x-y\parallel ,$$

for $\mu \ge 1$.

Again, in 2011, Aoyama and Kohsaka [3] introduced the class of $\alpha$-nonexpansive mapping in Banach spaces. They defined it thus:

the mapping $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ is said to be $\alpha$-nonexpansive if for a real number $\alpha <1$,

$${\parallel \mathcal{G}x-\mathcal{G}y\parallel }^2\le {\alpha \parallel \mathcal{G}x-y\parallel }^2{+\alpha \parallel x-\mathcal{G}y\parallel }^2+(1-2\alpha ){\parallel x-y\parallel }^2,$$

for all, $x,y\in \mathcal{B}$.

The concept of $\alpha$-nonexpansive mapping is trivial for $\alpha <0$ [4].

As a way to generalize the class of $\alpha$-nonexpansive mapping, Pant and Shukla [5], in 2017, introduced the class of generalized $\alpha$-nonexpansive mapping as presented in the definition below.

 Definition 1.

Let $\mathcal{B}$ be a uniformly convex nonempty subset of a Banach space $\mathcal{H}$. A mapping $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ is called a generalized α-nonexpansive mapping if for any real number $\alpha \in [0,1)$,

$${\displaystyle \frac{1}{2}}\parallel x-\mathcal{G}x\parallel \le \parallel x-y\parallel \mathrm{implies}\parallel \mathcal{G}x-\mathcal{G}y\parallel \le \alpha \parallel \mathcal{G}x-y\parallel +\alpha \parallel \mathcal{G}y-x\parallel +(1-2\alpha )\parallel x-y\parallel$$

(2)

for all $x,y\in \mathcal{B}$.

 Remark 1.

Every class of generalized α-nonexpansive mapping fully contains the mapping satisfying condition (C) and partially contains the class of α-nonexpansive mapping.

Fixed point theory is a fundamental area of mathematics with profound implications in various branches of mathematics and sciences. It has not only provided deep theoretical insights but has also been instrumental in addressing real-world problems across disciplines. Over the years, fixed point theory has evolved into a vibrant area of research, drawing significant attention due to its versatility and applicability. Fixed point theory has established itself as a cornerstone in mathematical analysis, with broad applications that extend far beyond its foundational theorems. Its ability to address problems in fractional differential equation, ordinary differential equations, boundary value problems, integral equations, delay differential equations, and other advanced mathematical constructs underscores its significance in contemporary research and applied mathematics (see, for example, Refs. [6,7,8,9,10] and other references therein).

Modeling the spread of HIV and other biological phenomena using fractional differential equations (FDEs) has become significant in offering a more nuanced understanding of the disease’s dynamics by incorporating memory effects and hereditary properties inherent in biological systems. The application of fixed point theory, particularly through iterative schemes, plays a crucial role in approximating solutions to these complex models. FDEs extend classical differential equations by allowing derivatives of non-integer orders, effectively capturing the memory and hereditary characteristics of HIV transmission and progression. This approach provides a more accurate representation of the disease’s dynamics compared to integer-order models. Recent studies have employed various fractional derivatives, such as the Caputo and Caputo–Fabrizio operators, to model HIV/AIDS transmission dynamics (see [11] and references therein).

The aim of this paper is to use an existing fixed point iterative scheme by Okeke et al. [12] to approximate the fixed point of a class of generalized $\alpha$-nonexpansive mapping in a Banach space with a numerical example and apply the result in approximating the solution of a mixed type Voltera–Fredholm functional nonlinear integral equation and in solving the problem of the spread of HIV, modeled as a fractional differential equation of the Caputo type.

The rest of this paper is arranged as follows: Section 2 is for the preliminaries which contain the basic definitions, lemmas, and propositions. Section 3 is dedicated to the main results. Meanwhile, the numerical example and rate of convergence with a table and graphs are in Section 4. Application of the main results to the mixed type integral equation is presented in Section 5. Section 6 is for application of the main result to the spread of HIV, modeled as a fractional differential equation of the Caputo type. The concluding remark of the paper is presented in Section 7.

2. Preliminaries

Fixed point theory has been very remarkable in mathematics and its application, especially in the aspect of the approximation of the fixed point of operators and by extension to the approximation of solutions of certain mathematical problems in applications modeled as ordinary differential equations, partial differential equations, integral equations, boundary value problems, fractional differential equation, etc.

Several fixed point iterative schemes have been developed and used accordingly for approximation of the fixed point of certain classes of mappings.

In 2014, Abbas and Nazir [13] introduced a three-step iterative process called the AK iterative scheme and defined it as follows:

$$\left\{\begin{array}{c}{x}_0=x\in \mathcal{B}\hfill \\ z_n=(1-{\gamma }_n)x_n+{\gamma }_n\mathcal{G}{x}_n\hfill \\ y_n=(1-{\beta }_n)\mathcal{G}{x}_n+{\beta }_n\mathcal{G}{z}_n\hfill \\ x_{n+1}=(1-{\alpha }_n)\mathcal{G}{y}_n+{\alpha }_n\mathcal{G}{z}_n\hfill \end{array}\right.$$

(3)

for $\{{\alpha }_n\}$, $\{{\beta }_n\}$, $\{{\gamma }_n\}\in (0,1)$

In 2014, Gürsoy et al. [14] introduced an iterative scheme called the Picard-S defined thus:

$$\left\{\begin{array}{c}{x}_0=x\in \mathcal{B}\hfill \\ z_n=(1-{\beta }_n)x_n+{\beta }_n\mathcal{G}{x}_n\hfill \\ y_n=(1-{\alpha }_n)\mathcal{G}{x}_n+{\alpha }_n\mathcal{G}{z}_n\hfill \\ x_{n+1}=\mathcal{G}{y}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(4)

In 2016, Thakur et al. [15] introduced an iterative scheme defined thus:

$$\left\{\begin{array}{c}{x}_0=x\in \mathcal{B}\hfill \\ z_n=(1-{\gamma }_n)x_n+{\gamma }_n\mathcal{G}{x}_n\hfill \\ y_n=\mathcal{G}[(1-{\beta }_n)x_n+{\beta }_n{z}_n]\hfill \\ x_{n+1}=\mathcal{G}{y}_n,n\in \mathbb{N}\hfill \end{array}\right.$$

(5)

for $\{{\beta }_n\},\{{\gamma }_n\}\in \mathcal{B}$.

In 2018, Hussain et al. [16] introduced a K iterative scheme which is defined as follows:

$$\left\{\begin{array}{c}{x}_0=x\in \mathcal{B}\hfill \\ z_n=(1-{\gamma }_n)x_n+{\gamma }_n\mathcal{G}{x}_n\hfill \\ y_n=\mathcal{G}[(1-{\beta }_n)\mathcal{G}{x}_n+{\beta }_n\mathcal{G}{z}_n]\hfill \\ x_{n+1}=\mathcal{G}{y}_n,n\in \mathbb{N}\hfill \end{array}\right.$$

(6)

In 2018, Piri et al. [17] introduced the following iterative scheme,

$$\left\{\begin{array}{c}{x}_0=x\in \mathcal{B},\hfill \\ z_n=\mathcal{G}[(1-{\beta }_n)x_n+{\beta }_n\mathcal{G}{x}_n],\hfill \\ y_n=\mathcal{G}{z}_n,\hfill \\ x_{n+1}=(1-{\alpha }_n)\mathcal{G}{y}_n,n\in \mathbb{N},\hfill \end{array}\right.$$

(7)

which they used to approximate the fixed point of the class of generalized $\alpha$-nonexpansive mapping in Banach spaces for $\{{\alpha }_n\},\{{\beta }_n\}\in (0,1)$.

Recently, Ullah et al. [18] used the K iterative scheme (6) to approximate the fixed point of a class of generalized $\alpha$-nonexpansive mapping (2).

Motivated by the foregoing, we use the existing AG iterative scheme introduced by Okeke et al. [6] and defined as follows

$$\left\{\begin{array}{c}{u}_0=u\in \mathcal{B}\hfill \\ u_{n+1}=\mathcal{G}{v}_n\hfill \\ v_n=\mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\hfill \\ w_n=(1-{\beta }_n)\mathcal{G}{u}_n+{\beta }_n\mathcal{G}{x}_n\hfill \\ x_n=(1-{\gamma }_n)u_n+{\gamma }_n\mathcal{G}{u}_n,n\in \mathbb{N},\hfill \end{array}\right.$$

(8)

where $\{{\alpha }_n\}$, $\{{\beta }_n\}$ and $\{{\gamma }_n\}$ are sequences of real numbers in $[0,1]$ to answer the following question:

Question: Can the AG (8) iterative scheme be used to approximate the fixed point of the class of generalized $\alpha$-nonexpansive mapping?

The answer is in the affirmative.

Next, we outline some important basic definitions and lemmas.

 Definition 2

([19]). A mapping $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ with $\mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$ is said to satisfy condition (I) if there exists a nondecreasing function $h:[0,\infty )\to [0,\infty )$ with $h\left(0\right)=0$, $h\left(s\right)>0$ for $s\in (0,\infty )$, such that $\parallel u-\mathcal{G}u\parallel \ge h\left(\rho \right(u,\mathcal{F}\left(\mathcal{G}\right)\left)\right)$ for all $u\in \mathcal{D}$, where $\rho (u,\mathcal{F}(\mathcal{G}\left)\right)=inf\{\parallel u-\tau \parallel :\tau \in \mathcal{F}(\mathcal{G})\}$.

 Definition 3

([20]). A Banach space $\mathcal{H}$ is said to satisfy the Opial condition [21] if for each sequence $\{u_n\}$ in $\mathcal{H}$, converging weakly to $p\in \mathcal{H}$, we have

$$\underset{n\to \infty }{lim\; sup}\parallel u_n-p\parallel <\underset{n\to \infty }{lim\; sup}\parallel u_n-q\parallel ,$$

(9)

for all $q\in \mathcal{H}$ such that $p\ne q$.

 Definition 4

([20,22]). Let $\mathcal{B}$ be a nonempty closed convex subset of a Banach space $\mathcal{H}$ and $\{u_n\}$ be a bounded sequence in $\mathcal{H}$. For each $u\in \mathcal{H}$, we define

(a)

asymptotic radius of $\{u_n\}$ at u as a functional, $\mathcal{R}(·,\{u_n\}):X\to {\mathbb{R}}_{+}$ defined by $\mathcal{R}(u,\{u_n\})=\underset{n\to \infty }{lim\; sup}\parallel u-u_n\parallel$,

(b)

asymptotic radius of $\{u_n\}$ relative to the set $\mathcal{B}$ by

$$\mathcal{R}(\mathcal{B},\{u_n\})=inf\{\mathcal{R}(u,\{u_n\}):u\in \mathcal{B}\},\mathit{and}$$

(c)

asymptotic center of $\{u_n\}$ relative to the set $\mathcal{H}$ by

$$\mathcal{A}(\mathcal{B},\{u_n\})=\{u\in \mathcal{H}:\mathcal{R}(u,\{u_n\})=\mathcal{R}(\mathcal{B},\{u_n\})\}.$$

 Lemma 1

([23]). Let $\mathcal{H}$ be a uniformly convex Banach space and ${\{{\alpha }_n\}}_{n=0}^{\infty }$, ${\{{\beta }_n\}}_{n=0}^{\infty }$ and ${\{{\gamma }_n\}}_{n=0}^{\infty }$ be sequences of numbers such that $0<a\le {\alpha }_n\le b<1$, $n\ge 1$, for $a,b\in \mathbb{R}$. Let ${\{s_n\}}_{n=0}^{\infty }$ and ${\{t_n\}}_{n=0}^{\infty }$ be sequences in $\mathcal{H}$ such that $\underset{n\to \infty }{lim\; sup}\parallel s_n\parallel \le \lambda$, $\underset{n\to \infty }{lim\; sup}\parallel t_n\parallel \le \lambda$ and

$$\underset{n\to \infty }{lim\; sup}\parallel {\alpha }_n{s}_n+(1-{\alpha }_n)t_n\parallel =\lambda$$

for some $\lambda \ge 0$. Then, $\underset{n\to \infty }{lim}\parallel s_n-t_n\parallel =0$.

 Proposition 1

([5]). Let $\mathcal{B}$ be a nonempty subset of a Banach space $\mathcal{H}$ and $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ be a self mapping, and the following will hold.

• $\mathcal{G}$ is generalized α-nonexpansive whenever it satisfies condition $\left(C\right)$.
• $\mathcal{G}$ is quasi-nonexpansive whenever it is generalized α-nonexpansive.
• $\mathcal{F}\left(\mathcal{G}\right)$ is closed in $\mathcal{B}$ whenever $\mathcal{G}$ is generalized α-nonexpansive.
• For each point $x,y\in \mathcal{B}$, $\parallel x-\mathcal{G}y\parallel \le \left({\displaystyle \frac{3+\alpha }{1-\alpha }}\right)\parallel x-\mathcal{G}x\parallel +\parallel x-y\parallel$ holds, whenever $\mathcal{G}$ is generalized α-nonexpansive.
• If $\mathcal{G}$ is generalized α-nonexpansive, $\{u_n\}$ a sequence in $\mathcal{H}$ such that $\mathcal{H}$ has Opial’s condition and $\{u_n\}$ is weakly convergent with weak limit ϖ, then $\varpi \in \mathcal{F}\left(\mathcal{G}\right)$ whenever $\underset{n\to \infty }{lim}\parallel u_n-\mathcal{G}{u}_n\parallel =0$.

3. Main Results

In the sequel, the following lemmas will be useful.

 Lemma 2.

Let $\mathcal{B}$ be a nonempty closed convex subset of a Banach space $\mathcal{H}$. Let $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ be a generalized α-nonexpansive mapping with $\mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$ and $\{u_n\}$ represents a sequence generated by the AG iterative scheme (8). Then for each ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$, $\underset{n\to \infty }{lim}\parallel u_n-{\ell }^{*}\parallel$ exists.

 Proof. 

Let ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$ be a fixed point. By axiom (2) of Proposition 1 together with (8), we have,

$$\begin{array}{cc}\hfill \parallel x_n-{\ell }^{*}\parallel & =\parallel (1-{\gamma }_n)u_n+{\gamma }_n\mathcal{G}{u}_n-{\ell }^{*}\parallel \hfill \\ & \le (1-{\gamma }_n)\parallel u_n-{\ell }^{*}\parallel +{\gamma }_n\parallel \mathcal{G}{u}_n-\mathcal{G}{\ell }^{*}\parallel \hfill \\ & \le (1-{\gamma }_n)\parallel u_n-{\ell }^{*}\parallel +{\gamma }_n\parallel u_n-{\ell }^{*}\parallel \hfill \\ & =\parallel u_n-{\ell }^{*}\parallel .\hfill \end{array}$$

(10)

Again,

$$\begin{array}{cc}\hfill \parallel w_n-{\ell }^{*}\parallel & =\parallel (1-{\beta }_n)\mathcal{G}{u}_n+{\beta }_n\mathcal{G}{x}_n-{\ell }^{*}\parallel \hfill \\ & \le (1-{\beta }_n)\parallel \mathcal{G}{u}_n-{\ell }^{*}\parallel +{\beta }_n\parallel \mathcal{G}{x}_n-\mathcal{G}{\ell }^{*}\parallel \hfill \\ & \le (1-{\beta }_n)\parallel \mathcal{G}{u}_n-\mathcal{G}{\ell }^{*}\parallel +{\beta }_n\parallel \mathcal{G}{x}_n-\mathcal{G}{\ell }^{*}\parallel \hfill \\ & \le (1-{\beta }_n)\parallel u_n-{\ell }^{*}\parallel +{\beta }_n\parallel x_n-{\ell }^{*}\parallel \hfill \\ & =\parallel u_n-{\ell }^{*}\parallel .\hfill \end{array}$$

(11)

Using (8) and (11),

$$\begin{array}{cc}\hfill \parallel v_n-{\ell }^{*}\parallel & =\parallel \mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-{\ell }^{*}\parallel \hfill \\ & \le \parallel \mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-\mathcal{G}{\ell }^{*}\parallel \hfill \\ & \le \parallel [(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-{\ell }^{*}\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel w_n-{\ell }^{*}\parallel +{\alpha }_n\parallel \mathcal{G}{w}_n-\mathcal{G}{\ell }^{*}\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel w_n-{\ell }^{*}\parallel +{\alpha }_n\parallel w_n-{\ell }^{*}\parallel \hfill \\ & =\parallel w_n-{\ell }^{*}\parallel \hfill \\ & =\parallel u_n-{\ell }^{*}\parallel .\hfill \end{array}$$

(12)

Using (8) and (12), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-{\ell }^{*}\parallel & =\parallel \mathcal{G}{v}_n-{\ell }^{*}\parallel \hfill \\ & \le \parallel \mathcal{G}{v}_n-\mathcal{G}{\ell }^{*}\parallel \hfill \\ & \le \parallel v_n-{\ell }^{*}\parallel \hfill \\ & =\parallel u_n-{\ell }^{*}\parallel .\hfill \end{array}$$

(13)

Here, we can say that $\{\parallel u_n-{\ell }^{*}\parallel \}$ is bounded and nonincreasing. Therefore, for all ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$, $\underset{n\to \infty }{lim}\parallel u_n-{\ell }^{*}\parallel$ exists. □

 Lemma 3.

Suppose $\mathcal{B}$ is a nonempty closed convex subset of a uniformly convex Banach space and consider a mapping $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ which is a generalized α-nonexpansive mapping. Let $\{u_n\}$ be a sequence generated by the AG iterative scheme (8). Then, $\mathcal{F}(\mathcal{G}\ne \varnothing )$ if and only if $\{u_n\}$ is bounded and $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$ holds.

 Proof. 

Assume that $\mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$ and ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$ is a fixed point. Then by using Lemma 2, we have that $\underset{n\to \infty }{lim}\parallel u_n-{\ell }^{*}\parallel$ exists and $\{u_n\}$ is bounded. Let d be any real value.

Set

$$\underset{n\to \infty }{lim}\parallel u_n-{\ell }^{*}\parallel =d.$$

(14)

From Lemma 2 and (14), we have the following

$$\underset{n\to \infty }{lim\; sup}\parallel x_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\ell }^{*}\parallel =d$$

(15)

$$\underset{n\to \infty }{lim\; sup}\parallel w_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\ell }^{*}\parallel =d$$

(16)

and

$$\underset{n\to \infty }{lim\; sup}\parallel v_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\ell }^{*}\parallel =d.$$

(17)

By condition (2) of Proposition 1, and (14), we have

$$\underset{n\to \infty }{lim\; sup}\parallel \mathcal{G}{u}_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel u_n-{\ell }^{*}\parallel =d.$$

(18)

Now, from Lemma 2, we recall that

$$\begin{array}{cc}\hfill \parallel u_{n+1}-{\ell }^{*}\parallel & =\parallel \mathcal{G}{v}_n-{\ell }^{*}\parallel \hfill \\ & \le \parallel v_n-{\ell }^{*}\parallel .\hfill \end{array}$$

(19)

Again from condition (2) of Proposition 1, together with (14), we have

$$d=\underset{n\to \infty }{lim\; inf}\parallel u_{n+1}-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; inf}\parallel v_n-{\ell }^{*}\parallel .$$

(20)

From (17) and (20), it follows that

$$\underset{n\to \infty }{lim\; inf}\parallel v_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel v_n-{\ell }^{*}\parallel =d,$$

so that we have

$$\underset{n\to \infty }{lim}\parallel v_n-{\ell }^{*}\parallel =d.$$

(21)

From (21), we have

$$d=\underset{n\to \infty }{lim\; inf}\parallel v_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; inf}\parallel w_n-{\ell }^{*}\parallel ,$$

which follows that

$$d=\underset{n\to \infty }{lim\; inf}\parallel w_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel w_n-{\ell }^{*}\parallel =d,$$

so that

$$\underset{n\to \infty }{lim}\parallel w_n-{\ell }^{*}\parallel =d$$

(22)

and

$$\begin{array}{cc}\hfill \parallel w_n-{\ell }^{*}\parallel & =\parallel (1-{\beta }_n)\mathcal{G}{u}_n+{\beta }_n\mathcal{G}{x}_n-{\ell }^{*}\parallel \hfill \\ & \le (1-{\beta }_n)\parallel \mathcal{G}{u}_n-{\ell }^{*}\parallel +{\beta }_n\parallel \mathcal{G}{x}_n-{\ell }^{*}\parallel \hfill \\ & \le (1-{\beta }_n)\parallel u_n-{\ell }^{*}\parallel +{\beta }_n\parallel x_n-{\ell }^{*}\parallel .\hfill \end{array}$$

(23)

We have that

$$\parallel w_n-{\ell }^{*}\parallel -\parallel u_n-{\ell }^{*}\parallel \le {\displaystyle \frac{\parallel w_n-{\ell }^{*}\parallel -\parallel u_n-{\ell }^{*}\parallel }{{\beta }_n}}\le \parallel x_n-{\ell }^{*}\parallel -\parallel u_n-{\ell }^{*}\parallel$$

and therefore,

$$\parallel w_n-{\ell }^{*}\parallel \le \parallel x_n-{\ell }^{*}\parallel .$$

Here,

$$d=\underset{n\to \infty }{lim\; inf}\parallel w_n-{\ell }^{*}\parallel \le \underset{n\to \infty }{lim\; inf}\parallel x_n-{\ell }^{*}\parallel ,$$

$$d\le \underset{n\to \infty }{lim\; inf}\parallel x_n-{\ell }^{*}\parallel ,$$

(24)

so that by combining (15) and (24), we have

$$d=\underset{n\to \infty }{lim}\parallel x_n-{\ell }^{*}\parallel .$$

(25)

Using (25), we have

$$\begin{array}{cc}\hfill d=\underset{n\to \infty }{lim}\parallel x_n-{\ell }^{*}\parallel & =\underset{n\to \infty }{lim}\parallel (1-{\gamma }_n)u_n+{\gamma }_n\mathcal{G}{u}_n-{\ell }^{*}\parallel \hfill \\ & \le \underset{n\to \infty }{lim}\parallel (1-{\gamma }_n)(u_n-{\ell }^{*})+{\gamma }_n(\mathcal{G}{u}_n-{\ell }^{*})\parallel ,\hfill \end{array}$$

that is,

$$d=\underset{n\to \infty }{lim}\parallel (1-{\gamma }_n)(u_n-{\ell }^{*})+{\gamma }_n(\mathcal{G}{u}_n-{\ell }^{*})\parallel .$$

(26)

Applying Lemma 1 to (26), we have that

$$\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0.$$

Conversely, we need to show that $\mathcal{F}\left(\mathcal{G}\right)$ is nonempty whenever $\{u_n\}$ is bounded with $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$.

To achieve that, let ${\ell }^{*}\in \mathcal{A}(\mathcal{B},\{u_n\})$.

Applying condition (4) of Proposition 1, we have

$$\begin{array}{cc}\hfill \mathcal{R}(\mathcal{G}{\ell }^{*},\{u_n\})& =\underset{n\to \infty }{lim\; sup}\parallel u_n-\mathcal{G}{\ell }^{*}\parallel \hfill \\ & \le \left({\displaystyle \frac{3+\alpha }{1-\alpha }}\right)\underset{n\to \infty }{lim\; sup}\parallel u_n-\mathcal{G}{u}_n\parallel +\underset{n\to \infty }{lim\; sup}\parallel u_n-{\ell }^{*}\parallel \hfill \\ & =\underset{n\to \infty }{lim\; sup}\parallel u_n-{\ell }^{*}\parallel \hfill \\ & =\mathcal{R}({\ell }^{*},\{u_n\}).\hfill \end{array}$$

Hence, we have shown that $\mathcal{G}{\ell }^{*}\in \mathcal{A}(\mathcal{B},\{u_n\})$. However, $\mathcal{A}(\mathcal{B},\{u_n\})$ is a singleton, thus it follows that $\mathcal{G}{\ell }^{*}={\ell }^{*}$ and $\mathcal{F}\left(\mathcal{G}\right)$ is nonempty. Therefore, the proof is complete. □

Weak and Strong Convergence

 Theorem 1.

Assume $\mathcal{B}$ is a nonempty closed subset of a uniformly convex banach space $\mathcal{H}$. Let $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ be a generalized α-nonexpansive mapping with $\mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$ and ${\{u_n\}}_{n=0}^{\infty }$ be a sequence generated by the iterative scheme (8). Then ${\{u_n\}}_{n=0}^{\infty }$ converges weakly to a fixed point ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$ if $\mathcal{H}$ satisfies the Opial condition (9).

 Proof. 

In Lemma 3, it was shown that the sequence $\{u_n\}$ is bounded and $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$ holds.

Since the Banach space, $\mathcal{H}$ is convex, then we claim that it is reflexive.

Consequently, we find a convergent subsequence $\{u_{n_i}\}$ of $\{u_n\}$ such that $\{u_{n_i}\}$ converges weakly to a point $r_1\in \mathcal{B}$ (i.e., $u_{n_i}\rightharpoonup r_1$).

By condition (5) of Proposition 1, we can say that $r_1\in \mathcal{F}\left(\mathcal{G}\right)$ and we may conclude that the proof is complete.

However, suppose in the contrary that our claim fails, then there exists another subsequence $\{u_{n_j}\}$ of $\{u_n\}$ that converges weakly to a point $r_2\in \mathcal{B}$, such that $r_1\ne r_2$.

Again, using condition (5) of Proposition 1, we have that $r_2\in \mathcal{F}\left(\mathcal{G}\right)$.

By Lemma 2 and using the Opial condition (9) for the Banach space, $\mathcal{H}$, we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\parallel u_n-r_1\parallel & =\underset{i\to \infty }{lim}\parallel u_{n_i}-r_1\parallel \hfill \\ & <\underset{i\to \infty }{lim}\parallel u_{n_i}-r_2\parallel \hfill \\ & =\underset{n\to \infty }{lim}\parallel u_n-r_2\parallel \hfill \\ & =\underset{j\to \infty }{lim}\parallel u_{n_j}-r_2\parallel \hfill \\ & <\underset{j\to \infty }{lim}\parallel u_{n_j}-r_1\parallel \hfill \\ & =\underset{n\to \infty }{lim}\parallel u_n-r_1\parallel .\hfill \end{array}$$

Clearly, we obtain $\underset{n\to \infty }{lim}\parallel u_n-r_1\parallel <\underset{n\to \infty }{lim}\parallel u_n-r_1\parallel$ which is a contradiction. Hence, $r_1=r_2$, implying that there is only one limit point. It can be concluded that the sequence $\{u_n\}$ converges to a fixed point in $\mathcal{F}\left(\mathcal{G}\right)$. Thereby completing the proof. □

 Theorem 2.

Let $\mathcal{B}$ be a nonempty closed convex subset of a Banach space $\mathcal{H}$. Assume $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ is a generalized α-nonexpansive mapping with $\mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$. If ${\{u_n\}}_{n=0}^{\infty }$ is a sequence generated by the AG iterative scheme (8). Then ${\{u_n\}}_{n=0}^{\infty }$ converges strongly to a fixed point ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$.

 Proof. 

As proved in Lemma 3, $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$. Suppose $\mathcal{B}$ is compact and convex. Then, there exist a convergent subsequence ${\{u_{n_i}\}}_{i=0}^{\infty }$ of ${\{u_n\}}_{n=0}^{\infty }$ having a strong limit k for some $k\in \mathcal{B}$.

By condition (4) of Proposition 1, we have

$$\parallel u_{n_i}-\mathcal{G}k\parallel \le \left({\displaystyle \frac{3+\alpha }{1-\alpha }}\right)\parallel u_{n_i}-\mathcal{G}{u}_{n_i}\parallel +\parallel u_{n_i}-k\parallel .$$

If we consider setting $i\to \infty$, then $\mathcal{G}k=k$.

By Lemma 2, $\underset{n\to \infty }{lim}\parallel u_n-k\parallel$ exist which follows that $\{u_n\}$ converges strongly to the limit k. Hence, the proof is complete. □

 Theorem 3.

Let $\mathcal{B}$ be a nonempty closed and convex subset of a Banach space $\mathcal{H}$. Assume $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ be a generalized α-nonexpansive mapping with $\mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$ and the sequence $\{u_n\}$ generated by the AG iterative scheme (8). Then the sequence $\{u_n\}$ converges strongly to some fixed point of $\mathcal{G}$ if and only if $\underset{n\to \infty }{lim\; inf}\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))=0$, where $\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))=\underset{u\in \mathcal{F}\left(\mathcal{G}\right)}{inf}\rho (u_n,u)$ and $\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))$ denotes a distance function.

 Proof. 

Let ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$ be a fixed point. As proved earlier in Lemma 2, we have that $\underset{n\to \infty }{lim}\parallel u_n-{\ell }^{*}\parallel$ exists.

It follows that $\underset{n\to \infty }{lim}\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))$ exists.

Next, suppose that

$$\underset{n\to \infty }{lim}\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))=0.$$

(27)

With regards to (27), we want to construct a Cauchy sequence in $\mathcal{F}\left(\mathcal{G}\right)$. We begin by constructing a subsequence $\{j_k\}$ in $\mathcal{F}\left(\mathcal{G}\right)$ and $\{u_{n_k}\}$ of $\{u_n\}$ with the property that

$$\parallel u_{n_k}-j_k\parallel \le {\displaystyle \frac{1}{2^k}},\forall k\in \mathbb{N}.$$

On the other hand, if $\{j_k\}$ is nonincreasing, then we have

$$\parallel u_{n_{k+1}}-j_k\parallel \le \parallel u_{n_k}-j_k\parallel \le {\displaystyle \frac{1}{2^k}}.$$

Consequently, we have

$$\begin{array}{cc}\hfill \parallel j_{k+1}-j_k\parallel & \le \parallel j_{k+1}-u_{n_{k+1}}\parallel +\parallel u_{n_{k+1}}-j_k\parallel \hfill \\ & \le {\displaystyle \frac{1}{2^{k+1}}}+{\displaystyle \frac{1}{2^k}}\hfill \\ & \le {\displaystyle \frac{1}{2^{k-1}}}\to 0\mathrm{as}k\to \infty .\hfill \end{array}$$

The above shows that $\{j_k\}$ is a Cauchy sequence in $\mathcal{F}\left(\mathcal{G}\right)$.

Again, by condition (3) of Proposition 1, we have that $\mathcal{F}\left(\mathcal{G}\right)$ is closed in $\mathcal{B}$. Therefore, $\{j_k\}$ is a convergent sequence in $\mathcal{F}\left(\mathcal{G}\right)$ and it converges to ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$.

Hence, since

$$\parallel u_{n_k}-{\ell }^{*}\parallel \le \parallel u_{n_k}-j_k\parallel +\parallel j_k-{\ell }^{*}\parallel \to 0\mathrm{as}n\to \infty ,$$

we have $\underset{n\to \infty }{lim}\parallel u_{n_k}-{\ell }^{*}\parallel =0$ and so $\{u_{n_k}\}$ converges strongly to ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)$.

Again, by Lemma 2, $\underset{n\to \infty }{lim}\parallel u_n-{\ell }^{*}\parallel$ exists; it follows that $\{u_n\}$ converges strongly to the fixed point ${\ell }^{*}\in \mathcal{F}\left(\mathcal{G}\right)\ne \varnothing$. Thereby completing the proof. □

 Theorem 4.

Let $\mathcal{B}$ be a nonempty closed convex subset of a Banach space $\mathcal{H}$. $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ be a mapping satisfying the condition for a α-nonexpansive mapping and $\{u_n\}$ is a sequence generated by the AG iterative scheme (8). Then $\{u_n\}$ converges strongly to a limit in $\mathcal{F}\left(\mathcal{G}\right)$ if $\mathcal{G}$ satisfies condition $\left(I\right)$.

 Proof. 

From 3, we saw that $\underset{n\to \infty }{lim}\parallel \mathcal{G}{u}_n-u_n\parallel =0$. It follows that

$$\underset{n\to \infty }{lim\; inf}\parallel \mathcal{G}{u}_n-u_n\parallel =0.$$

(28)

Since $\mathcal{G}$ satisfies condition (I), we have that

$$\parallel \mathcal{G}{u}_n-u_n\parallel \ge h\left(\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))\right).$$

From (28), we have

$$\underset{n\to \infty }{lim\; inf}h\left(\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))\right)=0.$$

Again, from condition (28), we infer that $h:[0,\infty )\to [0,\infty )$ is a nondecreasing function with $h\left(0\right)=0$ and $h\left(s\right)>0$ for all $s\in (0,\infty )$, hence we infer that

$$\underset{n\to \infty }{lim\; inf}\rho (u_n,\mathcal{F}\left(\mathcal{G}\right))=0.$$

Since all claims of Theorem 3 are satisfied, then $\{u_n\}$ converges strongly to a fixed point of $\mathcal{G}$. □

4. Numerical Example and Rate of Convergence

In this section, we consider a numerical example of a generalized $\alpha$-nonexpansive mapping $\mathcal{G}$.

 Example 1.

Consider the set $\mathcal{B}=[-1,1]$ endowed with the usual norm, $\parallel ·\parallel$ and let $\mathcal{G}:\mathcal{B}\to \mathcal{B}$ be defined as

$$\mathcal{G}x=\left\{\begin{array}{c}{\displaystyle \frac{x}{2}},\mathrm{if}x\in [-1,0)\hfill \\ -x,\mathrm{if}x\in [0,1]\setminus \{{\displaystyle \frac{1}{2}}\}\hfill \\ 0,\mathrm{if}x={\displaystyle \frac{1}{2}}.\hfill \end{array}\right.$$

Then $\mathcal{G}$ is a generalized α-nonexpansive mapping. Here, we choose $\alpha ={\displaystyle \frac{1}{2}}$ and the proof continues in different cases.

Case 1:If $u,v\in [-1,0)$, we have

$$\begin{array}{cc}\hfill \alpha \parallel \mathcal{G}u-v\parallel & +\alpha \parallel \mathcal{G}v-u\parallel +(1-2\alpha )\parallel u-v\parallel \hfill \\ & ={\displaystyle \frac{1}{2}}|{\displaystyle \frac{u}{2}}-v|+{\displaystyle \frac{1}{2}}|{\displaystyle \frac{v}{2}}-u|\hfill \\ & ={\displaystyle \frac{1}{2}}|{\displaystyle \frac{u}{2}}-v|+{\displaystyle \frac{1}{2}}|u-{\displaystyle \frac{v}{2}}|\hfill \\ & \ge {\displaystyle \frac{1}{2}}|{\displaystyle \frac{u}{2}}-v+u-{\displaystyle \frac{v}{2}}|\hfill \\ & ={\displaystyle \frac{3}{4}}|u-v|\hfill \\ & \ge {\displaystyle \frac{1}{2}}|u-v|=\parallel \mathcal{G}u-\mathcal{G}v\parallel \hfill \end{array}$$

Case 2:If $u\in [-1,0)$, $v\in [0,1]\setminus \{{\displaystyle \frac{1}{2}}\}$.

Since $u<0$ and $v\ge 0$, we have

$$\parallel \mathcal{G}u-\mathcal{G}v\parallel =|{\displaystyle \frac{x}{2}}+y|=\left\{\begin{array}{c}{\displaystyle \frac{x}{2}}+y,\mathrm{if}{\displaystyle \frac{|x|}{2}}<y\hfill \\ -{\displaystyle \frac{x}{2}}-y,\mathrm{if}{\displaystyle \frac{|x|}{2}}\ge y.\hfill \end{array}\right.$$

At first, we have that

$$\begin{array}{cc}\hfill \alpha \parallel \mathcal{G}u-v\parallel & +\alpha \parallel \mathcal{G}v-u\parallel +(1-2\alpha )\parallel u-v\parallel \hfill \\ & ={\displaystyle \frac{1}{2}}|{\displaystyle \frac{u}{2}}-v|+{\displaystyle \frac{1}{2}}|-v-u|\hfill \\ & \ge {\displaystyle \frac{1}{2}}(v-{\displaystyle \frac{u}{2}})+{\displaystyle \frac{1}{2}}(v+u)\hfill \\ & ={\displaystyle \frac{u}{4}}+v\hfill \\ & \ge {\displaystyle \frac{u}{2}}+v=\parallel \mathcal{G}u-\mathcal{G}v\parallel \hfill \end{array}$$

Second, we have

$$\begin{array}{cc}\hfill \alpha \parallel \mathcal{G}u-v\parallel & +\alpha \parallel \mathcal{G}v-u\parallel +(1-2\alpha )\parallel u-v\parallel \hfill \\ & ={\displaystyle \frac{1}{2}}|{\displaystyle \frac{u}{2}}-v|+{\displaystyle \frac{1}{2}}|-v-u|\hfill \\ & \ge {\displaystyle \frac{1}{2}}(v-{\displaystyle \frac{u}{2}})+{\displaystyle \frac{1}{2}}(-v-u)\hfill \\ & =-{\displaystyle \frac{3}{4}}u\hfill \\ & \ge -{\displaystyle \frac{u}{2}}-v=\parallel \mathcal{G}u-\mathcal{G}v\parallel \hfill \end{array}$$

Case 3:If $u\in [-1,0)$ and $v={\displaystyle \frac{1}{2}}$, then

$$\begin{array}{cc}\hfill \alpha \parallel \mathcal{G}u-v\parallel & +\alpha \parallel \mathcal{G}v-u\parallel +(1-2\alpha )\parallel u-v\parallel \hfill \\ & ={\displaystyle \frac{1}{2}}|{\displaystyle \frac{u}{2}}-{\displaystyle \frac{1}{2}}|+{\displaystyle \frac{1}{2}}|0-u|\hfill \\ & ={\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{2}}-{\displaystyle \frac{u}{2}})-{\displaystyle \frac{1}{2}}u\hfill \\ & =-{\displaystyle \frac{3}{4}}u+{\displaystyle \frac{1}{4}}\hfill \\ & \ge -{\displaystyle \frac{u}{2}}=\parallel \mathcal{G}u-\mathcal{G}v\parallel \hfill \end{array}$$

Case 4:If $u,v\in [0,1]\setminus \{{\displaystyle \frac{1}{2}}\}$ and $u\le v$, then

$$\begin{array}{cc}\hfill \alpha \parallel \mathcal{G}u-v\parallel & +\alpha \parallel \mathcal{G}v-u\parallel +(1-2\alpha )\parallel u-v\parallel \hfill \\ & ={\displaystyle \frac{1}{2}}|-u-v|+{\displaystyle \frac{1}{2}}|-v-u|\hfill \\ & ={\displaystyle \frac{1}{2}}(u+v)+{\displaystyle \frac{1}{2}}(v+u)\hfill \\ & =(v+u)\ge v-u\hfill \\ & =\parallel \mathcal{G}u-\mathcal{G}v\parallel .\hfill \end{array}$$

Case 5:If $u\in [0,1]\setminus \{{\displaystyle \frac{1}{2}}\}$, $v={\displaystyle \frac{1}{2}}$, then

$$\begin{array}{cc}\hfill \alpha \parallel \mathcal{G}u-v\parallel & +\parallel \mathcal{G}v-u\parallel +(1-2\alpha )\parallel u-v\parallel \hfill \\ & ={\displaystyle \frac{1}{2}}|-u-{\displaystyle \frac{11}{2}}|+|0-u|\hfill \\ & ={\displaystyle \frac{1}{2}}(u+{\displaystyle \frac{1}{2}})+{\displaystyle \frac{1}{2}}u\hfill \\ & =u+{\displaystyle \frac{1}{4}}\ge u=\parallel \mathcal{G}u-\mathcal{G}v\parallel .\hfill \end{array}$$

The expected fixed point of $\mathcal{G}$ is 0.

Next, we use the example above to compare the rate of convergence of the AG iterative scheme with some other existing iterative schemes in the literature for ${\alpha }_n={\displaystyle \frac{18n+3}{20n+4}}$, ${\beta }_n={\displaystyle \frac{3n+2}{4n+3}}$, and ${\gamma }_n={\displaystyle \frac{18n+3}{20n+4}}$ with a maximum value achieved when $n\to \infty$. This can be shown in the table and graph below.

5. Application to Mixed Type Integral Equation

In this section, we consider the application of the AG iterative scheme (8) to the approximation of the solution of a mixed type integral equation.

Our aim is to show the convergence of the sequence $\{u_n\}$ generated by the iterative scheme to a fixed point for a mixed type Volterra–Fredholm functional nonlinear integral equation:

$$u\left(x\right)=F\left(t,u\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u\left(s\right))ds\right),$$

(29)

where $[k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]$ is an interval in ${\mathbb{R}}^n$, $K,H:[k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]\times [k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]\times \mathbb{R}\to \mathbb{R}$ continuous functions and $F:[k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]\times {\mathbb{R}}^3\to \mathbb{R}$. The following lemma will be very useful in proving the main result.

 Lemma 4.

Suppose that the following conditions are satisfied.

(C₁)

$K,H\in C([k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]\times [k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]\times \mathbb{R})$;

(C₂)

$F\in ([k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]\times {\mathbb{R}}^3)$;

(C₃)

There exists nonnegative constants α, β, γ such that

$$|F(t,f_1,p_1,q_1)-F(t,f_2,p_2,q_2)|\le \alpha |f_1-f_2|+\beta |p_1-p_2|+\gamma |q_1-q_2|,$$

for all $t\in [k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n]$, $f_1,p_1,q_1,f_2,p_2,q_2\in \mathbb{R}$;

(C₄)

There exist nonnegative constants $L_K$ and $L_H$ such that

$$\begin{array}{cc}\hfill |K(t,s,f)-K(t,s,p)|& \le L_K|f-p|,\hfill \\ \hfill |H(t,s,f)-H(t,s,p)|& \le L_H|f-p|,\hfill \end{array}$$

for all $t,s\in [k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n],f,p\in \mathbb{R}$;

(C₅)

$\alpha +(\beta L_K+\gamma L_H)({\eta }_1-k_1)\cdots ({\eta }_n-k_n)<1$.

Then, the nonlinear integral Equation (29) has a unique solution $u\in C([k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n])$.

Next is the main result.

 Theorem 5.

Suppose that all the conditions $\left(C_1\right)-\left(C_5\right)$ in Lemma 4 are satisfied. Let $\{u_n\}$ be defined by the AG iterative scheme (8) with real sequences ${\alpha }_n,{\beta }_n,{\gamma }_n\in (0,1)$, satisfying ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$. Then (29) has a unique solution and the AG iterative scheme (8) converges strongly to the unique solution of the mixed type Voltera–Fredholm functional nonlinear integral Equation (29), say $u\in C([k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n])$.

 Proof. 

Let $X=C([k_1;{\eta }_1]\times \cdots \times [k_n;{\eta }_n],\parallel ·{\parallel }_C)$, where ${\parallel ·\parallel }_C$ is the Chebychev norm. Let $\{u_n\}$ be the iterative sequence generative by the AG iterative scheme (8) for the operator,

$$\mathcal{G}\left(u\right)\left(t\right)=F\left(t,u\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u\left(s\right))ds\right).$$

(30)

Our aim is to show that $\underset{n\to \infty }{lim}{u}_n=u^{*}$.

Using (8), (29), (30) and the assumptions $\left(C_1\right)-\left(C_5\right)$, we have that

$$\begin{array}{cc}\hfill \parallel u_{n+1}-u^{*}\parallel & =\parallel \mathcal{G}{v}_n-u^{*}\parallel \hfill \\ & =|\mathcal{G}{v}_n-\mathcal{G}{u}^{*}|\hfill \\ & =|F\left(t,v_n\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,v_n\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,v_n\left(s\right))ds\right)\hfill \\ & -F\left(t,u^{*}\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds\right)|\hfill \\ & \le \alpha |v_n\left(t\right)-u^{*}\left(t\right)|+\beta |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,v_n\left(s\right))ds-{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds|\hfill \\ & +\gamma |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}H(t,s,v_n\left(s\right))ds-{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}H(t,s,u^{*}\left(s\right))ds|\hfill \\ & \le \alpha |v_n\left(t\right)-u^{*}\left(t\right)|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}|K(t,s,v_n\left(s\right))-K(t,s{u}^{*}\left(s\right))|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}|H(t,s,v_n\left(s\right))-H(t,s{u}^{*}\left(s\right))|ds\hfill \\ & \le \alpha |v_n\left(t\right)-u^{*}\left(t\right)|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}{L}_K|v_n\left(s\right)-u^{*}\left(s\right)|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}{L}_H|v_n\left(s\right)-u^{*}\left(s\right)|ds\hfill \\ & \le \alpha \parallel v_n-u^{*}\parallel +\beta \prod _{j=1}^m({\eta }_j-k_j)L_K\parallel v_n-u^{*}\parallel +\gamma \prod _{j=1}^m({\eta }_j-k_j)L_H\parallel v_n-u^{*}\parallel \hfill \\ & =[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\parallel v_n-u^{*}\parallel \hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \parallel v_n-u^{*}\parallel & =\parallel \mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}\parallel \hfill \\ & =|\mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-\mathcal{G}{u}^{*}|\hfill \\ & =|F(t,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))ds,\hfill \\ & {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))ds)\hfill \\ & -F\left(t,u^{*}\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds\right)|\hfill \\ & \le \alpha |[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(t\right)-u^{*}\left(t\right)|\hfill \\ & +\beta |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))ds-{\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds|\hfill \\ & +\gamma |{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))ds\hfill \\ & -{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds|\hfill \\ & \le \alpha |[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(t\right)-u^{*}\left(t\right)|\hfill \\ & +\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}|K(t,s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))-K(t,s,u^{*}\left(s\right))|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}|H(t,s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))-H(t,s,u^{*}\left(s\right))|ds\hfill \\ & \le \alpha |[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}{L}_K|[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}{L}_H|[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}|ds\hfill \\ & \le \alpha \parallel [(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}\parallel +\beta \prod _{j=1}^m({\eta }_j-k_j)L_K\parallel [(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}\parallel \hfill \\ & +\gamma \prod _{j=1}^m({\eta }_j-k_j)L_H\parallel [(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}\parallel \hfill \end{array}$$

(32)

$$\begin{array}{cc}& =\left\{\alpha +(L_K\beta +L_H\gamma )\prod _{j=1}^m({\eta }_j-k_j)\right\}\parallel [(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}\parallel .\hfill \end{array}$$

(33)

However,

$$\begin{array}{cc}\hfill \parallel \left[\right(1-& {\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-u^{*}\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel w_n-u^{*}\parallel +{\alpha }_n\parallel \mathcal{G}{w}_n-u^{*}\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel w_n-u^{*}\parallel +{\alpha }_n|\mathcal{G}{w}_n-\mathcal{G}{u}^{*}|\hfill \\ & \le (1-{\alpha }_n)\parallel w_n-u^{*}\parallel \hfill \\ & +{\alpha }_n|F\left(t,w_n\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,w_n\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,w_n\left(s\right))ds\right)\hfill \\ & -F\left(t,u^{*}\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds\right)|\hfill \\ & \le (1-{\alpha }_n)\parallel w_n-u^{*}\parallel +{\alpha }_n\{\alpha |w_n\left(t\right)-u^{*}\left(t\right)|\hfill \\ & +\beta |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,w_n\left(s\right))ds-{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds|\hfill \\ & +\gamma |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}H(t,s,w_n\left(s\right))ds-{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds|\}\hfill \\ & \le (1-{\alpha }_n)\parallel w_n-u^{*}\parallel +{\alpha }_n\{\alpha |w_n\left(t\right)-u^{*}\left(t\right)|\hfill \\ & +\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}|K(t,s,w_n\left(s\right))-K(t,s,u^{*}\left(s\right))|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}|H(t,s,w_n\left(s\right))-H(t,s,u^{*}\left(s\right))|ds\}\hfill \\ & \le (1-{\alpha }_n)\parallel w_n-u^{*}\parallel +{\alpha }_n\{\alpha |w_n\left(t\right)-u^{*}\left(t\right)|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}{L}_K|w_n\left(s\right))-u^{*}\left(s\right)|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}{L}_H|w_n\left(s\right))-u^{*}\left(s\right)|ds\}\hfill \\ & \le (1-{\alpha }_n)\parallel w_n-u^{*}\parallel +{\alpha }_n\{\alpha \parallel w_n-u^{*}\parallel +\beta \prod _{j=1}^m({\eta }_j-k_j)L_K\parallel w_n-u^{*}\parallel \hfill \\ & +\gamma \prod _{j=1}^m({\eta }_j-k_j)L_H\parallel w_n-u^{*}\parallel \}\hfill \\ & =(1-{\alpha }_n)\parallel w_n-u^{*}\parallel +{\alpha }_n\left\{\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)\right\}\parallel w_n-u^{*}\parallel .\hfill \end{array}$$

(34)

Putting (34) back in (32), we have

$$\begin{array}{cc}\hfill \parallel v_n-u^{*}\parallel & =[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\{(1-{\alpha }_n)\parallel w_n-u^{*}\parallel \hfill \\ & +{\alpha }_n[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\parallel w_n-u^{*}\parallel \}\hfill \\ & =[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\times \hfill \\ & \left\{1-{\alpha }_n+{\alpha }_n[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\right\}\parallel w_n-u^{*}\parallel \hfill \\ & =[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\times \hfill \\ & \left\{1-{\alpha }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])\right\}\parallel w_n-u^{*}\parallel ,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill \parallel w_n-u^{*}\parallel & =\parallel (1-{\beta }_n)\mathcal{G}{u}_n+{\beta }_n\mathcal{G}{x}_n-u^{*}\parallel \hfill \\ & \le (1-{\beta }_n)|\mathcal{G}{u}_n-u^{*}|+{\beta }_n|\mathcal{G}{x}_n-u^{*}|\hfill \\ & =(1-{\beta }_n)|\mathcal{G}{u}_n-\mathcal{G}{u}^{*}|+{\beta }_n|\mathcal{G}{x}_n-\mathcal{G}{u}^{*}|\hfill \\ & =(1-{\beta }_n)|F\left(t,u_n\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u_n\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u_n\left(s\right))ds\right)\hfill \\ & -F\left(t,u^{*}\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds\right)|\hfill \\ & +{\beta }_n|F\left(t,x_n\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,x_n\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,x_n\left(s\right))ds\right)\hfill \\ & -F\left(t,u^{*}\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds\right)|\hfill \\ & \le (1-{\beta }_n)\{\alpha |u_n\left(t\right)-u^{*}\left(t\right)|+\beta |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u_n\left(s\right))ds\hfill \\ & -{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds|\hfill \\ & +\gamma |{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u_n\left(s\right))ds-{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds|\}\hfill \\ & +{\beta }_n\{\alpha |x_n\left(t\right)-u^{*}\left(t\right)|+\beta |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,x_n\left(s\right))ds\hfill \\ & -{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds|\hfill \\ & +\gamma |{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,x_n\left(s\right))ds-{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds|\}\hfill \\ & \le (1-{\beta }_n)\{\alpha |u_n\left(t\right)-u^{*}\left(t\right)|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}|K(t,s,u_n\left(s\right))-K(t,s,u^{*}\left(s\right))|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}|H(t,s,u_n\left(s\right))ds-H(t,s,u^{*}\left(s\right))|ds\}\hfill \\ & +{\beta }_n\{\alpha |x_n\left(t\right)-u^{*}\left(t\right)|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}|K(t,s,x_n\left(s\right))ds-K(t,s,u^{*}\left(s\right))|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}|H(t,s,x_n\left(s\right))ds-H(t,s,u^{*}\left(s\right))|ds\}\hfill \\ & \le (1-{\beta }_n)\{\alpha |u_n\left(t\right)-u^{*}\left(t\right)|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}{L}_K|u_n\left(s\right)-u^{*}\left(s\right)|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}{L}_H|u_n\left(s\right)-u^{*}\left(s\right)|ds\}\hfill \\ & +{\beta }_n\{\alpha |x_n\left(t\right)-u^{*}\left(t\right)|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}{L}_K|x_n\left(s\right)-u^{*}\left(s\right)|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}{L}_H|x_n\left(s\right)-u^{*}\left(s\right)|ds\}\hfill \\ & \le (1-{\beta }_n)\{\alpha \parallel u_n-u^{*}\parallel +\beta \prod _{j=1}^m({\eta }_j-k_j)L_K\parallel u_n-u^{*}\parallel \hfill \\ & +\gamma \prod _{j=1}^m({\eta }_j-k_j)L_H\parallel u_n-u^{*}\parallel \}\hfill \\ & +{\beta }_n\left\{\alpha \parallel x_n-u^{*}\parallel +\beta \prod _{j=1}^m({\eta }_j-k_j)L_K\parallel x_n-u^{*}\parallel +\gamma \prod _{j=1}^m({\eta }_j-k_j)L_H\parallel x_n-u^{*}\parallel \right\}\hfill \\ & =(1-{\beta }_n)[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\parallel u_n-u^{*}\parallel \hfill \\ & +{\beta }_n[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\parallel x_n-u^{*}\parallel ,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \parallel x_n-u^{*}\parallel & =\parallel (1-{\gamma }_n)u_n+{\gamma }_n\mathcal{G}{u}_n-u^{*}\parallel \hfill \\ & \le (1-{\gamma }_n)|u_n-u^{*}|+{\gamma }_n|\mathcal{G}{u}_n-\mathcal{G}{u}^{*}|\hfill \\ & \le (1-{\gamma }_n)|u_n-u^{*}|\hfill \\ & +{\gamma }_n|F\left(t,u_n,{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u_n\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u_n\left(s\right))ds\right)\hfill \\ & -F\left(t,u^{*}\left(t\right),{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds,{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds\right)|\hfill \\ & \le (1-{\gamma }_n)|u_n-u^{*}|\hfill \\ & +{\gamma }_n\{\alpha |u_n-u^{*}|+\beta |{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u_n\left(s\right))ds-{\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}K(t,s,u^{*}\left(s\right))ds|\hfill \\ & +|{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u_n\left(s\right))ds-{\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}H(t,s,u^{*}\left(s\right))ds|\}\hfill \\ & \le (1-{\gamma }_n)|u_n-u^{*}|+{\gamma }_n\{\alpha |u_n-u^{*}|\hfill \\ & +\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}|K(t,s,u_n\left(s\right))-K(t,s,u^{*}\left(s\right))|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}|H(t,s,u_n\left(s\right))-H(t,s,u^{*}\left(s\right))|ds\}\hfill \\ & \le (1-{\gamma }_n)|u_n-u^{*}|+{\gamma }_n\{\alpha |u_n-u^{*}|+\beta {\int }_{k_1}^{l_1}\cdots {\int }_{k_n}^{l_n}{L}_K|u_n\left(s\right)-u^{*}\left(s\right)|ds\hfill \\ & +\gamma {\int }_{k_1}^{{\eta }_1}\cdots {\int }_{k_n}^{{\eta }_n}{L}_H|u_n\left(s\right)-u^{*}\left(s\right)|ds\}\hfill \\ & \le (1-{\gamma }_n)\parallel u_n-u^{*}\parallel +{\gamma }_n\{\alpha \parallel u_n-u^{*}\parallel +\beta \prod _{j=1}^m({\eta }_j-k_j)L_K\parallel u_n-u^{*}\parallel \hfill \\ & +\gamma \prod _{j=1}^m({\eta }_j-k_j)L_H\parallel u_n-u^{*}\parallel \}\hfill \\ & =(1-{\gamma }_n)\parallel u_n-u^{*}\parallel +{\gamma }_n[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\parallel u_n-u^{*}\parallel \hfill \\ & =[1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_n-u^{*}\parallel .\hfill \end{array}$$

(37)

Putting (37) in (36), we have,

$$\begin{array}{cc}\hfill \parallel w_n-u^{*}\parallel & =(1-{\beta }_n)[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\parallel u_n-u^{*}\parallel \hfill \\ & +{\beta }_n[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\times \hfill \\ & [1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_n-u^{*}\parallel \hfill \\ & =\{(1-{\beta }_n)[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]+{\beta }_n[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\times \hfill \\ & [1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\}\parallel u_n-u^{*}\parallel .\hfill \end{array}$$

(38)

Putting (38) in (35), we have

$$\begin{array}{cc}\hfill \parallel v_n-u^{*}\parallel & =[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\times \hfill \\ & [1-{\alpha }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\times \hfill \\ & \{(1-{\beta }_n)[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]+{\beta }_n[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)]\times \hfill \\ & [1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\}\parallel u_n-u^{*}\parallel \hfill \end{array}$$

(39)

Since $[\alpha +(\beta L_K+\gamma L_H){\prod }_{j=1}^m({\eta }_j-k_j)]<1$ from ($C_5$) of Lemma 4.

$$\begin{array}{cc}\hfill \parallel v_n-u^{*}\parallel & \le [1-{\alpha }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\times \hfill \\ & [1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_n-u^{*}\parallel .\hfill \end{array}$$

(40)

Putting (40) in (31), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-u^{*}\parallel & \le [\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)][1-{\alpha }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\times \hfill \\ & [1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_n-u^{*}\parallel .\hfill \end{array}$$

(41)

Again, since $[\alpha +(\beta L_K+\gamma L_H){\prod }_{j=1}^m({\eta }_j-k_j)]<1$, we have that (41) reduces to

$$\parallel u_{n+1}-u^{*}\parallel \le [1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_n-u^{*}\parallel .$$

(42)

From (42), we inductively generate the following inequalities,

$$\begin{array}{cc}\hfill \parallel u_{n+1}-u^{*}\parallel & \le [1-{\gamma }_n(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_n-u^{*}\parallel \hfill \\ \hfill \parallel u_n-u^{*}\parallel & \le [1-{\gamma }_{n-1}(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_{n-1}-u^{*}\parallel \hfill \\ & ⋮\hfill \\ \hfill \parallel v_1-u^{*}\parallel & \le [1-{\gamma }_0(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])]\parallel u_0-u^{*}\parallel ,\hfill \end{array}$$

(43)

from (43), we have

$$\parallel u_{n+1}-u^{*}\parallel \le \parallel u_0-u^{*}\parallel \prod _{k=0}^n[1-{\gamma }_k(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])].$$

(44)

Since ${\gamma }_k\in [0,1]$ for $k\in \mathbb{N}$ and $[\alpha +(\beta L_K+\gamma L_H){\prod }_{j=1}^m({\eta }_j-k_j)]<1$, we have that

$$1-{\gamma }_k(1-[\alpha +(\beta L_K+\gamma L_H)\prod _{j=1}^m({\eta }_j-k_j)])<1.$$

(45)

From elementary analysis, we can recall that $1-x<e^{-x}$ for all $x\in [0,1]$, then from (44), we can have that

$$\parallel u_{n+1}-u^{*}\parallel \le \parallel u_0-u^{*}\parallel e^{-(1-[\alpha +(\beta L_K+\gamma L_H){\prod }_{j=1}^m({\eta }_j-k_j)]){\sum }_{k=0}^n{\gamma }_k}.$$

(46)

Taking the limit of both sides of (46) as $n\to \infty$, we have that $\underset{n\to \infty }{lim}\parallel u_n-u^{*}\parallel =0$. Therefore, we can say that (8) converges strongly to the solution of a mixed type Voltera–Fredholm nonlinear functional integral equation. □

6. Application to the Spread of HIV Modeled as a Fractional Differential Equation of the Caputo Type

Consider a $S,I_a,I_b$ and A-model for the spread of HIV comprising susceptible, acute, asymptotic and symptomatic, or acquired immunodeficiency syndrome (AIDS) populations, respectively.

The model is represented mathematically as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{ds}{dt}}={\rm Y}-{\displaystyle \frac{{\beta }_a{I}_{a}S}{N}}-{\displaystyle \frac{{\beta }_b{I}_{b}S}{N}}-\mu S\hfill \\ {\displaystyle \frac{d{I}_a}{dt}}={\displaystyle \frac{{\beta }_a{I}_{a}S}{N}}+{\displaystyle \frac{{\beta }_b{I}_{b}S}{N}}-\nu I_b-(\alpha +\mu )I_a\hfill \\ {\displaystyle \frac{d{I}_b}{dt}}=\alpha I_a-(\nu +\gamma +\mu )I_b\hfill \\ {\displaystyle \frac{dA}{dt}}=\gamma I_b-(\mu +\sigma )A\hfill \end{array}\right.$$

(47)

subject to the initial conditions,

$$S\left(0\right)\ge 0,I_a\left(0\right)\ge 0,I_b\left(0\right)\ge 0,andA\left(0\right)\ge 0.$$

where ${\rm Y}$ is the recruitment rate, ${\beta }_a$ and ${\beta }_b$ are the effective contact rate of S with $I_a$ and $I_b$, respectively, $\nu$ is the treatment rate from asymptomatic to acute class, $\gamma$ is the rate at which $I_b$ transfers to the AIDS class, $\mu$ is the natural death rate, and $\sigma$ is the AIDS-associated death. Expressing (47) as the Caputo fractional differential equation equivalent, thus

$$\begin{array}{cc}\hfill {}_0{}^C\mathcal{D}_t^{\lambda }S\left(t\right)& ={\rm Y}-{\displaystyle \frac{{\beta }_a{I}_{a}S}{N}}-{\displaystyle \frac{{\beta }_b}{N}}-\mu S\hfill \\ \hfill {}_0{}^C\mathcal{D}_t^{\lambda }{I}_a\left(t\right)& ={\displaystyle \frac{{\beta }_a{I}_{a}S}{N}}+{\displaystyle \frac{{\beta }_b{I}_{b}S}{N}}-\nu I_b-(\alpha +\mu )I_a\hfill \\ \hfill {}_0{}^C\mathcal{D}_t^{\lambda }{I}_b\left(t\right)& =\alpha I_a-(\nu +\gamma +\mu )I_b\hfill \\ \hfill {}_0{}^C\mathcal{D}_t^{\lambda }A\left(t\right)& =\gamma I_b-(\mu +\sigma )A,\hfill \end{array}$$

(48)

subject to the initial conditions,

$$S\left(0\right)\ge 0,I_a\left(0\right)\ge 0,I_b\left(0\right)\ge 0,andA\left(0\right)\ge 0$$

Our aim here is to show the existence of a unique solution of the system (48).

To achieve that, let us express the right-hand side of (48) as follows:

$$\begin{array}{cc}\hfill g_1(t,S,I_a,I_b,A)& ={\rm Y}-{\displaystyle \frac{{\beta }_a{I}_{a}S}{N}}-{\displaystyle \frac{{\beta }_b{I}_{b}S}{N}}-\mu S\hfill \\ \hfill g_2(t,S,I_a,I_b,A)& ={\displaystyle \frac{{\beta }_a{I}_{a}S}{N}}+{\displaystyle \frac{{\beta }_b{I}_{b}S}{N}}-\nu I_b-(\alpha +\mu )I_a\hfill \\ \hfill g_3(t,S,I_a,I_b,A)& =\alpha I_a-(\nu +\gamma +\mu )I_b\hfill \\ \hfill g_4(t,S,I_a,I_b,A)& =\gamma I_b-(\mu +\sigma )A,\hfill \end{array}$$

(49)

such that

$$S\left(0\right)=K_1,I_a\left(0\right)=K_2,I_b\left(0\right)=K_3,A\left(0\right)=K_4.$$

Hence, transforming (48) to

$$\begin{array}{cc}\hfill {}_0{}^C\mathcal{D}_t^{\lambda }S\left(t\right)& =g_1(t,S,I_a,I_b,A)\hfill \\ \hfill {}_0{}^C\mathcal{D}_t^{\lambda }{I}_a\left(t\right)& =g_2(t,S,I_a,I_b,A)\hfill \\ \hfill {}_0{}^C\mathcal{D}_t^{\lambda }{I}_b\left(t\right)& =g_3(t,S,I_a,I_b,A)\hfill \\ \hfill {}_0{}^C\mathcal{D}_t^{\lambda }A\left(t\right)& =g_4(t,S,I_a,I_b,A)\hfill \end{array}$$

(50)

subject to

$$S\left(0\right)=K_1,I_a\left(0\right)=K_2,I_b\left(0\right)=K_3,A\left(0\right)=K_4.$$

Suppose, $f\left(t\right)=\left[\begin{array}{c}S\\ I_a\\ I_b\\ A\end{array}\right]$ and $f_0=\left[\begin{array}{c}{K}_1\\ K_2\\ K_3\\ K_4\end{array}\right]$ such that $G(t,f\left(t\right))=\left[\begin{array}{c}{g}_1(t,f\left(t\right))\\ g_2(t,f\left(t\right))\\ g_3(t,f\left(t\right))\\ g_4(t,f\left(t\right)).\end{array}\right]$

Hence, (50) reduces to the following equation of the Caputo type.

$$\left\{\begin{array}{c}{}_0{}^C\mathcal{D}_t^{\lambda }f\left(t\right)=G(t,f(t\left)\right),0<\lambda <1\hfill \\ f\left(0\right)=f_0.\hfill \end{array}\right.$$

(51)

Recall, our aim is to show the existence of the unique solution of (51).

To achieve that, we can express (51) in its integral equation equivalence as follows:

$$f\left(t\right)=f_0+\wp \left(\lambda \right)G(t,f\left(t\right))+\aleph \left(\lambda \right){\int }_0^{t}G(s,f\left(s\right))ds$$

(52)

where $\wp \left(\lambda \right)={\displaystyle \frac{1-\lambda }{\Gamma \left(\lambda \right)}}$ and $\aleph \left(\lambda \right)={\displaystyle \frac{\lambda }{\Gamma \left(\lambda \right)}}$.

Let $0\le t\le T$. Suppose $\mathcal{N}=[0,T]$, then we can define a Banach space as $\mathcal{H}=(\mathcal{N},{\mathbb{R}}^4)$ endowed with the maximum norm; $\parallel f\parallel =\underset{t\in \mathcal{N}}{max}\{|f\left(t\right)|:f\in \mathcal{H}\}$. The following lemma due to [24] will be useful in the sequel.

 Lemma 5.

Suppose the following conditions hold.

(D₁)

There exists a constant $L_G>0$ such that

$$|G(t,f_1\left(t\right))-G(t,f_2\left(t\right))|\le L_G|f_1-f_2|,$$

for each $f\in \mathcal{H}$ and $t\in [0,T]$,

(D₂)

$[\wp (\lambda +T\aleph \left(\lambda \right))]L_G<1$.

Then (51) has a unique solution.

 Theorem 6.

Assume that conditions $\left(D_1\right)$ and $\left(D_2\right)$ of Lemma 5 are satisfied. Let ${\alpha }_n,{\beta }_n,{\gamma }_n\in [0,1]$ be arbitrary sequences as they appear in the AG iterative scheme (8) such that ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$. Then (51) has a solution; ℓ and the sequence generated by the iterative scheme (8) converges ℓ.

 Proof. 

Let $\mathcal{H}=(\mathcal{N},{\mathbb{R}}^4)$ be a Banach space endowed with a maximum norm given as

$$\parallel f\parallel =\underset{t\in \mathcal{N}}{max}\{|f\left(t\right)|:f\in \mathcal{H}\}.$$

Assume that $\{u_n\}$ is an iterative sequence generated by the AG iterative scheme (8) for the operator $\mathcal{G}:\mathcal{H}\to \mathcal{H}$ defined by

$$\mathcal{G}f\left(t\right)=f_0+\wp \left(\lambda \right)G(t,f\left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,f\left(s\right))ds.$$

(53)

Our aim here is to show that $u_n$ converges to the point ℓ as $n\to \infty$.

Using (8) and (53) together with the conditions $\left(D_1\right)-\left(D_2\right)$ of Lemma 5, we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\ell \parallel & =\parallel \mathcal{G}{v}_n-\ell \parallel \hfill \\ & =\parallel \mathcal{G}{v}_n-\mathcal{G}\ell \parallel \hfill \\ & \le \underset{t\in [0,T]}{max}|\mathcal{G}{v}_n\left(t\right)-\mathcal{G}\ell \left(t\right)|\hfill \\ & =\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,v_n\left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,v_n\left(s\right))ds\hfill \\ & -\left(\wp \left(\lambda \right)G(t,\ell \left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))ds\right)|\hfill \\ & =\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,v_n\left(t\right))-\wp \left(\lambda \right)G(t,\ell \left(t\right))|\hfill \\ & +\underset{t\in [0,T]}{max}|\aleph \left(\lambda \right){\int }_a^{t}G(s,v_n\left(s\right))ds-\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))ds|\hfill \\ & \le \wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,v_n\left(t\right))-G(t,\ell \left(t\right))|\hfill \\ & +\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}|({\int }_a^{t}G(s,v_n\left(s\right))-{\int }_a^{t}G(s,\ell \left(s\right)))ds|\hfill \\ & \le \wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,v_n\left(t\right))-g(t,\ell \left(t\right))|\hfill \\ & +\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}{\int }_a^t|G(s,v_n\left(s\right))-G(s,\ell \left(s\right))|ds\hfill \\ & \le \wp \left(\lambda \right)L_G\underset{t\in [0,T]}{max}|v_n\left(t\right)-\ell \left(t\right)|+\aleph \left(\lambda \right)L_{G}T\underset{t\in [0,T]}{max}|v_n\left(t\right)-\ell \left(t\right)|\hfill \\ & \le \wp \left(\lambda \right)L_G\parallel v_n-\ell \parallel +\aleph \left(\lambda \right)L_{G}T\parallel v_n-\ell \parallel \hfill \\ & \le [\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]L_G\parallel v_n-\ell \parallel \hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill \parallel v_n-\ell \parallel & =\parallel \mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-\ell \parallel \hfill \\ & =\parallel \mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-\mathcal{G}\ell \parallel \hfill \\ & \le \underset{t\in [0,T]}{max}|\mathcal{G}[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]-\mathcal{G}\ell |\hfill \\ & =\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(t\right))\hfill \\ & +\aleph \left(\lambda \right){\int }_a^{t}G(s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))ds\hfill \\ & -\left(\wp \left(\lambda \right)G(t,\ell \left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))ds\right)|\hfill \\ & =\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(t\right))-G(t,\ell \left(t\right))|\hfill \\ & +\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}|{\int }_a^{t}G(s,[(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n]\left(s\right))ds-{\int }_a^{t}G(s,\ell \left(s\right))ds|\hfill \\ & \le \wp \left(\lambda \right)L_G\underset{t\in [0,T]}{max}|(1-\alpha )w_n+{\alpha }_n\mathcal{G}{w}_n-\ell |\hfill \\ & +\aleph \left(\lambda \right)L_{G}T\underset{t\in [0,T]}{max}|(1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n-\ell |\hfill \\ & \le \wp \left(\lambda \right)L_G\parallel (1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n-\ell \parallel +\aleph \left(\lambda \right)L_{G}T\parallel (1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n-\ell \parallel \hfill \\ & =L_G(\wp \left(\lambda \right)+\aleph \left(\lambda \right)T)\parallel (1-{\alpha }_n)w_n+{\alpha }_n\mathcal{G}{w}_n-\ell \parallel \hfill \\ & \le L_G(\wp \left(\lambda \right)+\aleph \left(\lambda \right)T)(1-{\alpha }_n)\parallel w_n-\ell \parallel +L_G{\alpha }_n(\wp \left(\lambda \right)+\aleph \left(\lambda \right)T)\parallel \mathcal{G}{w}_n-\ell \parallel \hfill \\ & \le L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel +L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel \mathcal{G}{w}_n-\mathcal{G}\ell \parallel \hfill \\ & \le L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel +L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\underset{t\in [0,T]}{max}|\mathcal{G}{w}_n-\mathcal{G}\ell |\hfill \\ & =L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel +L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\times \hfill \\ & \underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,w_n\left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,w_n\left(s\right))ds\hfill \\ & -(\wp \left(\lambda \right)G(t,\ell \left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))ds)|\hfill \\ & =L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel +L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\times \hfill \\ & \left\{\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|g(t,w_n\left(t\right))-G(t,\ell \left(t\right))|+\aleph \underset{t\in [0,T]}{max}|{\int }_a^{t}G(s,w_n\left(s\right))ds-{\int }_a^{t}G(s,\ell \left(s\right))ds|\right\}\hfill \\ & \le L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel +L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\times \hfill \\ & \left\{L_G\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|w_n\left(t\right)-\ell \left(t\right)|+\aleph \left(\lambda \right)L_{G}T\underset{t\in [0,T]}{max}|w_n\left(t\right)-\ell \left(t\right)|\right\}\hfill \\ & \le L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel +L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\times \hfill \\ & \{L_G\wp \left(\lambda \right)\parallel w_n-\ell \parallel +\aleph \left(\lambda \right)L_{G}T\parallel w_n-\ell \parallel \}\hfill \\ & =L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel +L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\times \hfill \\ & L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel w_n-\ell \parallel \hfill \\ & =\left\{L_G(1-{\alpha }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]+L_G{\alpha }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\right\}\parallel w_n-\ell \parallel \hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill \parallel w_n-\ell \parallel & =\parallel (1-{\beta }_n)\mathcal{G}{u}_n+{\beta }_n\mathcal{G}{x}_n-\ell \parallel \hfill \\ & \le (1-{\beta }_n)\parallel \mathcal{G}{u}_n-\ell \parallel +{\beta }_n\parallel \mathcal{G}{x}_n-\ell \parallel \hfill \\ & =(1-{\beta }_n)\parallel \mathcal{G}{u}_n-\mathcal{G}\ell \parallel +{\beta }_n\parallel \mathcal{G}{x}_n-\mathcal{G}{x}_n-\mathcal{G}\ell \parallel \hfill \\ & \le (1-{\beta }_n)\underset{t\in [0,T]}{max}|\mathcal{G}{u}_n-\mathcal{G}\ell |+{\beta }_n\underset{t\in [0,T]}{max}|\mathcal{G}{x}_n-\mathcal{G}\ell |\hfill \\ & =(1-{\beta }_n)\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,u_n\left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,u_n\left(s\right))ds\hfill \\ & -\left(\wp \left(\lambda \right)G(t,\ell \left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))ds\right)|\hfill \\ & +{\beta }_n\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,x_n\left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,x_n\left(s\right))ds\hfill \\ & -\left(\wp \left(\lambda \right)G(t,\ell \left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))\right)|\hfill \\ & =(1-{\beta }_n)\{\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,u_n\left(t\right))-\wp \left(\lambda \right)G(t,\ell \left(t\right))|\hfill \\ & +\underset{t\in [0,T]}{max}|\aleph \left(\lambda \right){\int }_a^{t}G(s,u_n\left(s\right))ds-\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))ds|\}\hfill \\ & +{\beta }_n\{\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,x_n\left(t\right))-\wp \left(\lambda \right)G(t,\ell \left(t\right))|\hfill \\ & +\underset{t\in [0,T]}{max}|\aleph \left(\lambda \right){\int }_a^{t}G(s,u_n\left(s\right))ds-\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))|\}\hfill \\ & =(1-{\beta }_n)\{\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,u_n\left(t\right))-G(t,\ell \left(t\right))|\hfill \\ & +\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}|\left({\int }_a^{t}G(s,u_n\left(s\right))ds-{\int }_a^{t}G(s,\ell \left(s\right))ds\right)|\}\hfill \\ & +{\beta }_n\{\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,x_n\left(t\right))-G(t,\ell \left(t\right))|\hfill \\ & +\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}|{\int }_a^{t}G(s,x_n\left(s\right))ds-{\int }_a^{t}G(s,\ell \left(s\right))ds|\}\hfill \\ & =(1-{\beta }_n)\{\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,u_n\left(t\right))-G(t,\ell \left(t\right))|\hfill \\ & +\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}{\int }_a^t|G(s,u_n\left(s\right))-G(s,\ell \left(s\right))|ds\}\hfill \\ & +{\beta }_n\{\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,x_n\left(t\right))-G(t,\ell \left(t\right))|\hfill \\ & +\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}{\int }_a^t|G(s,x_n\left(s\right))-G(s,x_n\left(s\right))|ds\}\hfill \\ & \le (1-{\beta }_n)\left\{\wp \left(\lambda \right)L_G\underset{t\in [0,T]}{max}|u_n\left(t\right)-\ell \left(t\right)|+\aleph \left(\lambda \right)L_{G}T\underset{t\in [0,T]}{max}|u_n\left(t\right)-\ell \left(t\right)|\right\}\hfill \\ & +{\beta }_n\left\{\wp \left(\lambda \right)L_G\underset{t\in [0,T]}{max}|x_n\left(t\right)-\ell \left(t\right)|+\aleph \left(\lambda \right)L_{G}T\underset{t\in [0,T]}{max}|x_n\left(t\right)-\ell \left(t\right)|\right\}\hfill \\ & \le (1-{\beta }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]L_G\parallel u_n-\ell \parallel +{\beta }_n[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]L_G\parallel x_n-\ell \parallel \hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill \parallel x_n-\ell \parallel & =\parallel (1-{\gamma }_n)u_n+{\gamma }_n\mathcal{G}{u}_n-\ell \parallel \hfill \\ & \le (1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\parallel \mathcal{G}{u}_n-\ell \parallel \hfill \\ & =(1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\parallel \mathcal{G}{u}_n-\mathcal{G}\ell \parallel \hfill \\ & \le (1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\underset{t\in [0,T]}{max}|\mathcal{G}{u}_n-\mathcal{G}\ell |\hfill \\ & =(1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,u_n\left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,u_n\left(s\right))ds\hfill \\ & -\left(\wp \left(\lambda \right)G(t,\ell \left(t\right))+\aleph \left(\lambda \right){\int }_a^{t}G(s,\ell \left(s\right))ds\right)|\hfill \\ & =(1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\underset{t\in [0,T]}{max}|\wp \left(\lambda \right)G(t,u_n\left(t\right))-\wp \left(\lambda \right)G(t,\ell \left(\lambda \right))|\hfill \\ & +{\gamma }_n\underset{t\in [0,T]}{max}|\aleph \left(\lambda \right){\int }_a^{t}G(s,u_n\left(s\right))ds-\aleph \left(\lambda \right){\int }_a^{t}g(s,\ell \left(s\right))ds|\hfill \\ & =(1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\wp \left(\lambda \right)\underset{t\in [0,T]}{max}|G(t,u_n\left(t\right))-G(t,\ell \left(t\right))|\hfill \\ & +{\gamma }_n\aleph \left(\lambda \right)\underset{t\in [0,T]}{max}{\int }_a^t|G(s,u_n\left(s\right))-G(s,\ell \left(s\right))|ds\hfill \\ & \le (1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\wp \left(\lambda \right)L_G\underset{t\in [0,T]}{max}|u_n\left(t\right)-\ell \left(t\right)|\hfill \\ & +{\gamma }_n\aleph \left(\lambda \right)L_{G}T\underset{t\in [0,T]}{max}|u_n\left(t\right)-\ell \left(t\right)|\hfill \\ & \le (1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n\wp \left(\lambda \right)L_G\parallel u_n-\ell \parallel +{\gamma }_n\aleph \left(\lambda \right)L_{G}T\parallel u_n-\ell \parallel \hfill \\ & =(1-{\gamma }_n)\parallel u_n-\ell \parallel +{\gamma }_n{L}_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel u_n-\ell \parallel .\hfill \end{array}$$

Since $L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]<1$

$$\parallel x_n-\ell \parallel \le \parallel u_n-\ell \parallel ,$$

(57)

putting (57) in (56), we have,

$$\begin{array}{cc}\hfill \parallel w_n-\ell \parallel & \le (1-{\beta }_n)[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]L_G\parallel u_n-\ell \parallel +{\beta }_n{L}_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel u_n-\ell \parallel \hfill \\ & =L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]\parallel u_n-\ell \parallel \hfill \end{array}$$

(58)

Putting (58) in (55),

$$\parallel v_n-\ell \parallel =\left\{1-{\alpha }_n(1-L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T])\right\}{[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]}^2{L}_G^2\parallel u_n-\ell \parallel .$$

Since $L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]<1$, we have

$$\parallel v_n-\ell \parallel \le \{1-{\alpha }_n(1-L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T])\}\parallel u_n-\ell \parallel .$$

(59)

Putting (59) in (54), we have,

$$\parallel u_{n+1}-\ell \parallel \le [\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]L_G\{1-{\alpha }_n(1-L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T])\}\parallel u_n-\ell \parallel .$$

(60)

Again, from $\left(D_2\right)$, we have that $[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]L_G<1$ such that (60) becomes

$$\parallel u_{n+1}-\ell \parallel \le \{1-{\alpha }_n(1-L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T])\}\parallel u_n-\ell \parallel .$$

(61)

By induction, we have

$$\parallel u_{n+1}-\ell \parallel =\parallel u_0-\ell \parallel \prod _{k=1}^n\{1-{\alpha }_k(1-L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T])\}.$$

(62)

Since ${\alpha }_k\in [0,1]$ for all $k\in \mathbb{N}$, and furthermore from the condition ($D_2$), we have that

$$1-{\alpha }_k(1-L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T])<1.$$

Recall from basic analysis that $1-x\le e^{-x}$ for all $x\in [0,1]$.

Therefore, (62) becomes

$$\parallel u_{n+1}-\ell \parallel \le \parallel u_0-\ell \parallel e^{-(1-L_G[\wp \left(\lambda \right)+\aleph \left(\lambda \right)T]){\sum }_{k=0}^{\infty }{\alpha }_k}.$$

Taking the limit as $n\to \infty$, we have $\underset{n\to \infty }{lim}\parallel u_n-\ell \parallel =0$, thereby completing the proof. □

7. Conclusions

Clearly, it has been shown that the AG iterative scheme (8) converges faster than all of (3), (4), (5), (6), and (7) for the class of generalized $\alpha$-nonexpansive mapping using Example 1 with pictorial evidence expressed in Table 1 and Figure 1 and Figure 2. The main result is also applied to guarantee its applicability.

Table 1. Comparison of speed of convergence of some iterative scheme for Example 1.

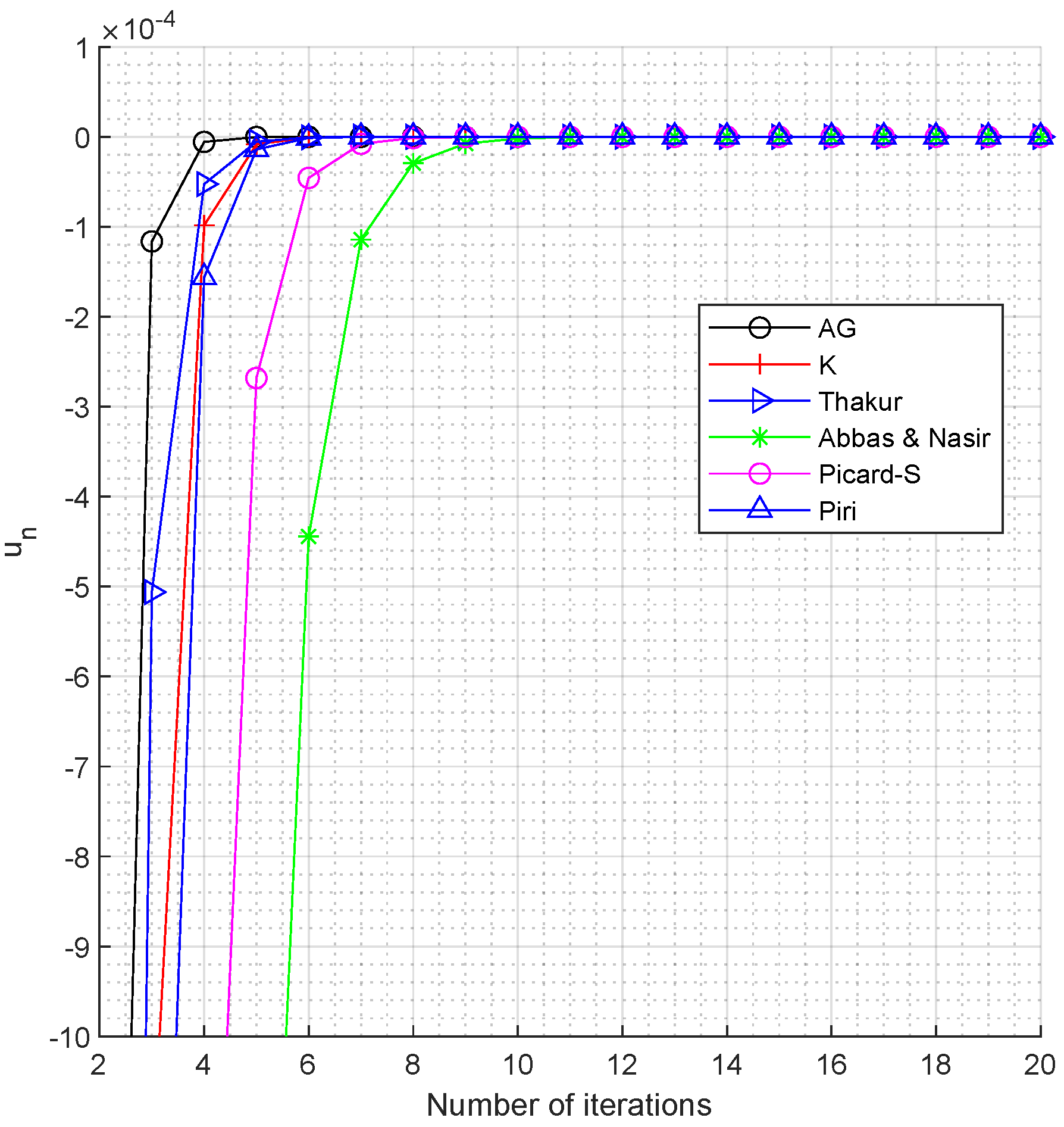
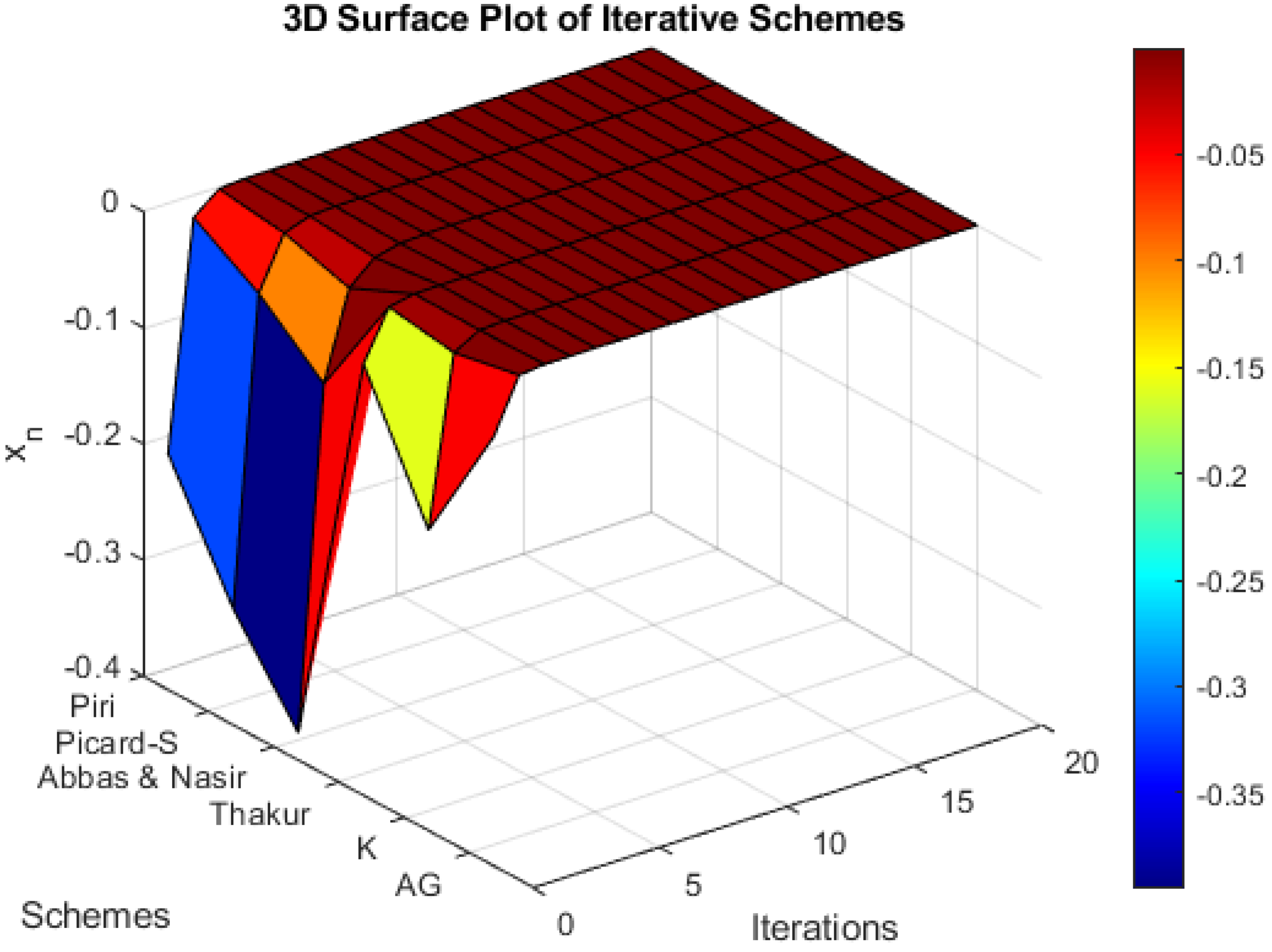
Step	AG	K	Thakur	Abass–Nasir	Picard-S	Piri
1	−0.0485	−0.1594	−0.0469	−0.3952	−0.3187	−0.2156
2	−0.0023	−0.0136	−0.0049	−0.1016	−0.0543	−0.0194
3	−0.0001	−0.0012	−0.0005	−0.0261	−0.0092	−0.0017
4	0.0000	−0.0001	−0.0001	−0.0067	−0.0016	−0.0002
5	0.0000	0.0000	0.0000	−0.0017	−0.0003	0.0000
6	0.0000	0.0000	0.0000	−0.0004	0.0000	0.0000
7	0.0000	0.0000	0.0000	−0.0001	0.0000	0.0000
8	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
9	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
10	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
11	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
12	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
13	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
14	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
15	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
16	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
17	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
18	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
19	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
20	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

Figure 1. Graph corresponding to Table 1.

Figure 2. Three-dimensional surface plot corresponding to Table 1.