Numerical Analysis of Time-Fractional Cancer Models with Different Types of Net Killing Rate
Abstract
1. Introduction
2. Preliminaries
3. Fundamentals of the Method
3.1. Highlights of RPSM
3.2. Convergence of RPSM
4. Application of RPSM to Time-Fractional Cancer Models
4.1. Application of RPSM to Case I
4.2. Application of RPSM to Case II
4.3. Application of RPSM to Case III
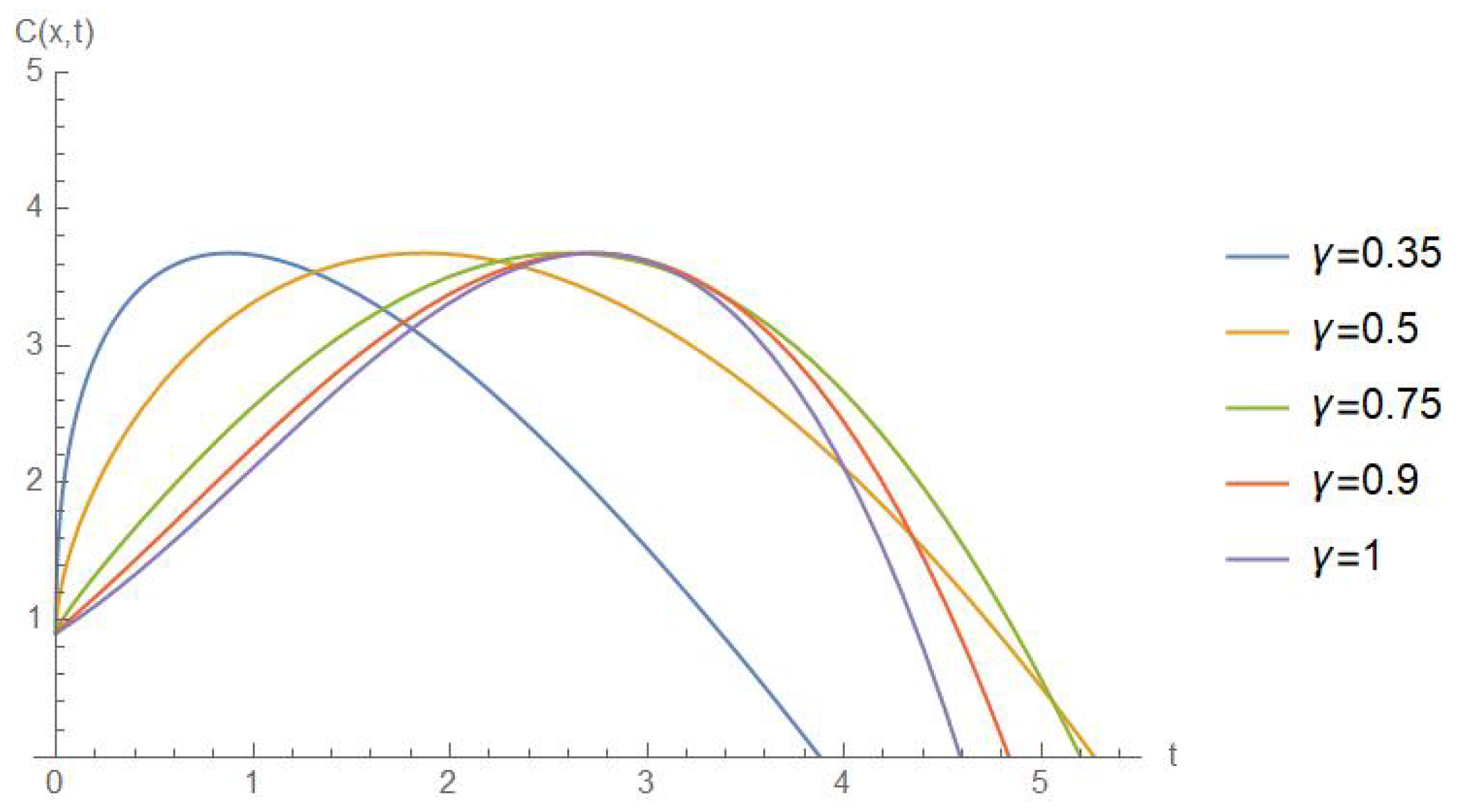
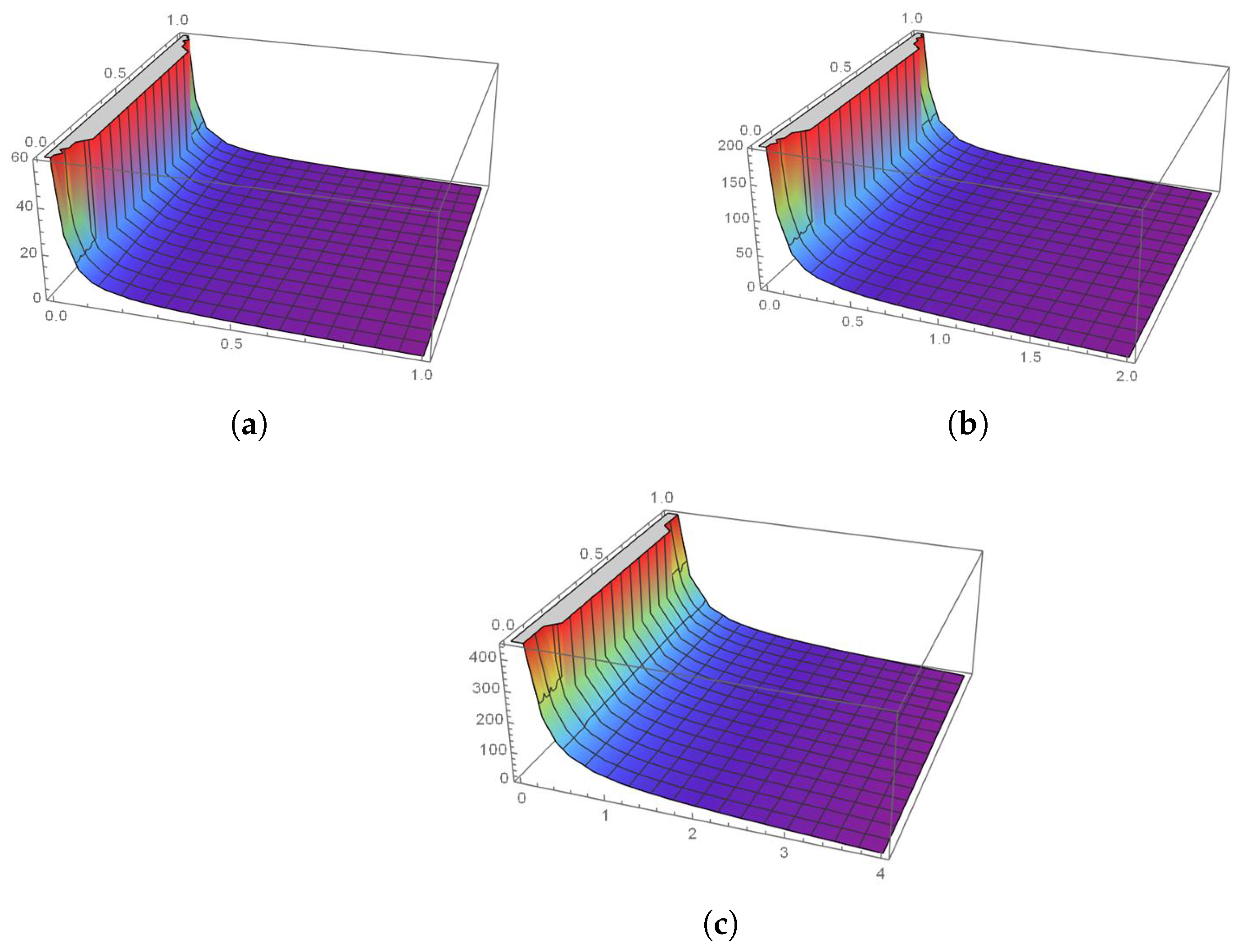
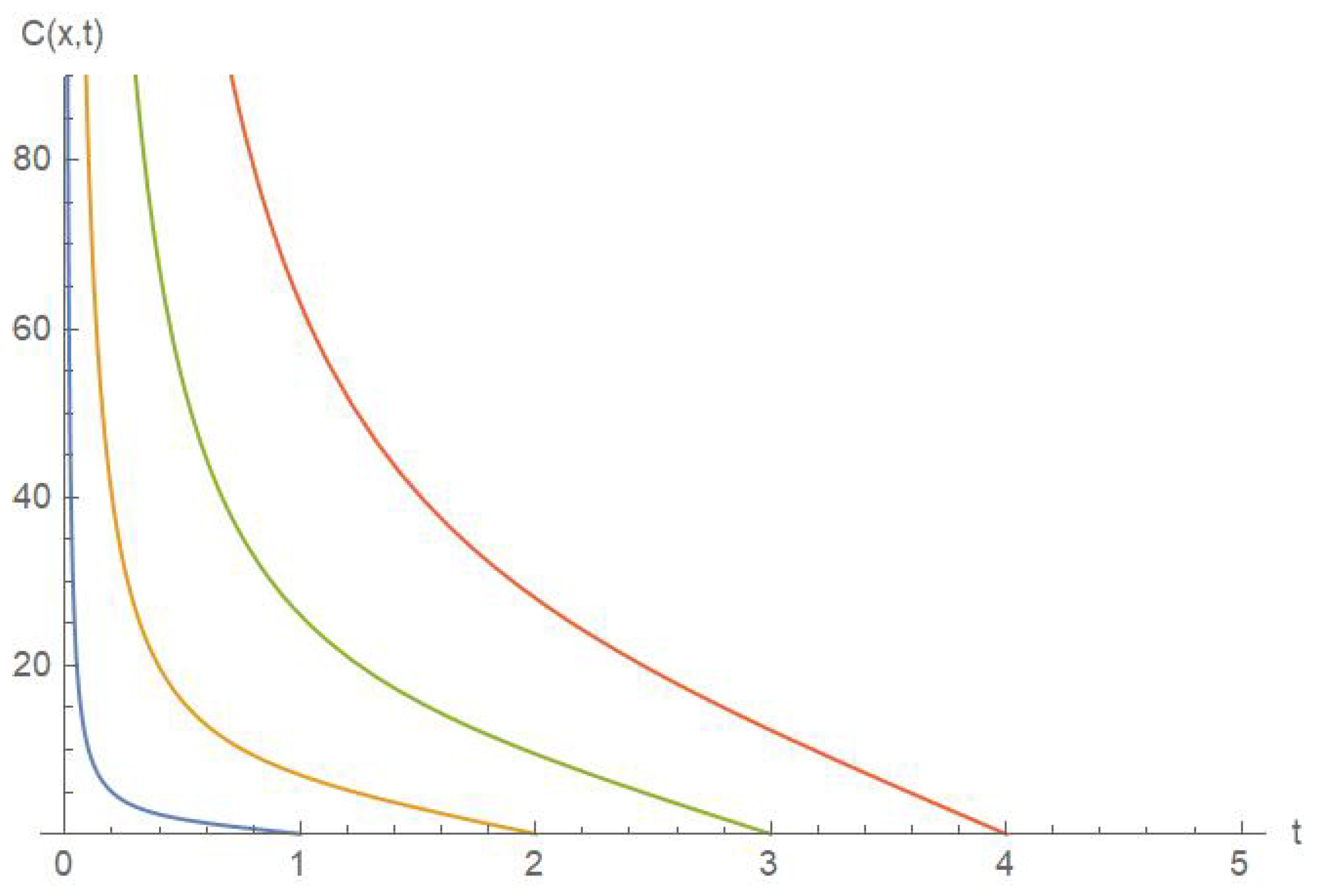
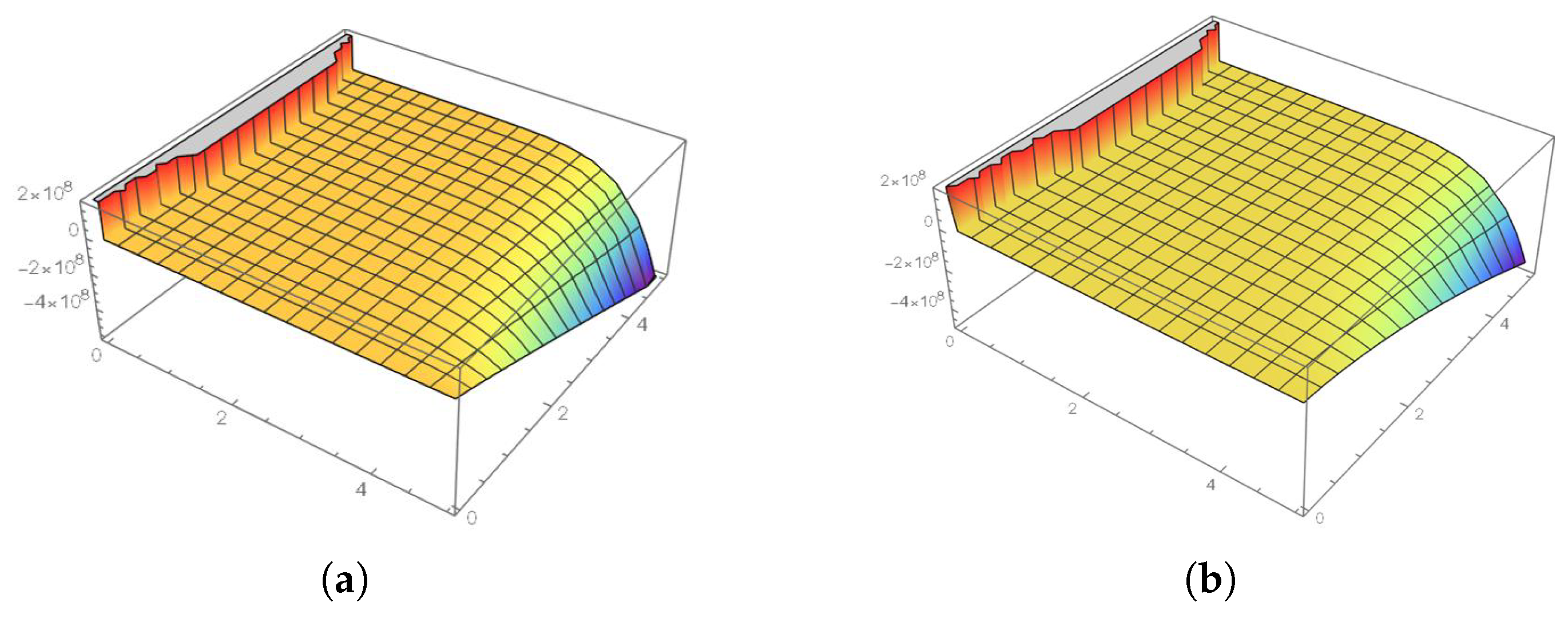
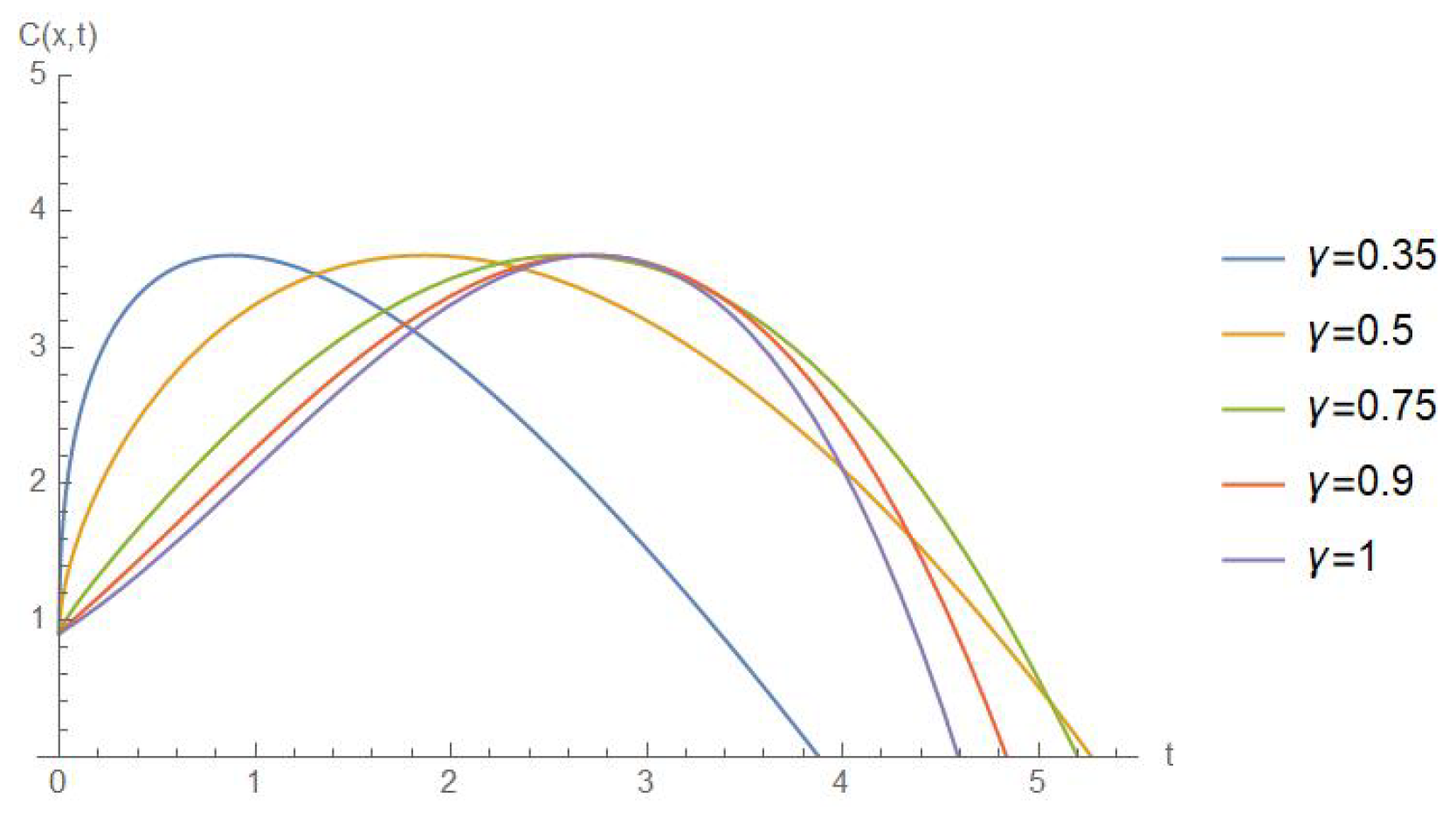
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RPSM | Residual Power Series Method |
| PDE | partial differential equation |
| FPS | fractional power series |
| PS | power series |
References
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.L.; Hlatky, L.; Hahnfeldt, P. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef] [PubMed]
- Arshad, S.; Sohail, A.; Javed, S. Dynamical study of fractional order tumor model. Int. J. Comput. Methods 2015, 12, 1550032. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Samet, B.; Gómez-Aguilar, J.F.; Osman, M.S. A chaos study of tumor and effector cells in fractional tumor-immune model for cancer treatment. Chaos Solitons Fractals 2020, 141, 110321. [Google Scholar] [CrossRef]
- Naik, P.A.; Zu, J.; Naik, M. Stability analysis of a fractional-order cancer model with chaotic dynamics. Int. J. Biomath. 2021, 14, 2150046. [Google Scholar] [CrossRef]
- Naik, P.A.; Owolabi, K.M.; Yavuz, M.; Zu, J. Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cells. Chaos Solitons Fractals 2020, 140, 110272. [Google Scholar] [CrossRef]
- Debbouche, N.; Ouannas, A.; Grassi, G.; Al-Hussein, A.B.A.; Tahir, F.R.; Saad, K.M.; Jahanshahi, H.; Aly, A.A. Chaos in cancer tumor growth model with commensurate and incommensurate fractional-order derivatives. Comput. Math. Methods Med. 2022, 2022, 5227503. [Google Scholar] [CrossRef]
- Qayyum, M.; Tahir, A. Mathematical Modeling of Cancer Tumor Dynamics with Multiple Fuzzification Approaches in Fractional Environment; Springer International Publishing: Cham, Switzerland, 2023. [Google Scholar]
- Sweilam, N.; Al-Mekhlafi, S.; Ahmed, A.; Alsheri, A.; Abo-Eldahab, E. Numerical treatments for crossover cancer model of hybrid variable-order fractional derivatives. Comput. Model Eng. Sci. 2024, 140, 1619–1645. [Google Scholar] [CrossRef]
- Nabil, H.; Hamaizia, T. A three-dimensional discrete fractional-order HIV-1 model related to cancer cells, dynamical analysis and chaos control. Math. Model. Numer. Simul. Appl. 2024, 4, 256–279. [Google Scholar] [CrossRef]
- Delgado Moya, E.M.; Rodriguez, R.A.; Pietrus, A. A mathematical model for the study of HIV/AIDS transmission with PrEP coverage increase and parameter estimation using MCMC with a Bayesian approach. Bull. Biomath. 2024, 2, 218–244. [Google Scholar] [CrossRef]
- Burgess, P.K.; Kulesa, P.M.; Murray, J.D.; Alroid, E.C. The interaction of growth rates and diffusion coefficients in a three dimensional mathematical model of gliomas. J. Neuropathol. Exp. Neurol. 1997, 56, 704–713. [Google Scholar] [CrossRef]
- Moyo, S.; Leach, P.G.L. Symmetry methods applied to a mathematical model of a tumour of the brain. Proc. Inst. Math. NAS Ukr. 2004, 50, 204–210. [Google Scholar]
- Sabir, Z.; Dirani, S.; Bou Saleh, S.; Mabsout, M.K.; Arbi, A. A Novel Radial Basis and Sigmoid Neural Network Combination to Solve the Human Immunodeficiency Virus System in Cancer Patients. Mathematics 2024, 12, 2490. [Google Scholar] [CrossRef]
- Jawad, S.; Winter, M.; Rahman, Z.-A.S.A.; Al-Yasir, Y.I.A.; Zeb, A. Dynamical Behavior of a Cancer Growth Model with Chemotherapy and Boosting of the Immune System. Mathematics 2023, 11, 406. [Google Scholar] [CrossRef]
- Joshi, H. Mechanistic insights of COVID-19 dynamics by considering the influence of neurodegeneration and memory trace. Phys. Scr. 2024, 99, 035254. [Google Scholar] [CrossRef]
- Pham, H. Mathematical Modeling the Time-Delay Interactions between Tumor Viruses and the Immune System with the Effects of Chemotherapy and Autoimmune Diseases. Mathematics 2022, 10, 756. [Google Scholar] [CrossRef]
- Rihan, F.A.; Rajivganthi, C. Dynamics of Tumor-Immune System with Random Noise. Mathematics 2021, 9, 2707. [Google Scholar] [CrossRef]
- Farman, M.; Akgül, A.; Ahmad, A.; Imtiaz, S. Analysis and dynamical behavior of fractional-order cancer model with vaccine strategy. Math. Methods Appl. Sci. 2020, 43, 4871–4882. [Google Scholar] [CrossRef]
- Uçar, E.; Özdemir, N. A fractional model of cancer-immune system with Caputo and Caputo-Fabrizio derivatives. Eur. Phys. J. Plus. 2021, 136, 43. [Google Scholar] [CrossRef]
- Uçar, S.; Koca, I.; Özdemir, N.; İnci, T. A stochastic approach to tumor modeling incorporating macrophages. Bull. Biomath. 2024, 2, 162–181. [Google Scholar] [CrossRef]
- Barbosa, M.A.G.; Xavier, C.P.R.; Pereira, R.F.; Petrikaite, V.; Vasconcelos, M.H. 3D cell culture models as recapitulators of the tumor microenvironment for the screening of anti-cancer drugs. Cancers 2021, 14, 190. [Google Scholar] [CrossRef] [PubMed]
- Özköse, F.; Yilmaz, S.; Yavuz, M.; Öztürk, I.; Senel, M.T.; Bagci, B.S.; Dogan, M.; Önal, O. A fractional modeling of tumor-immune system interaction related to lung cancer with real data. Eur. Phys. J. Plus 2021, 137, 40. [Google Scholar] [CrossRef]
- Özköse, F.; Yılmaz, S.; Şenel, M.T.; Yavuz, M.; Townley, S.; Sarıkaya, M.D. A mathematical modeling of patient-derived lung cancer stem cells with fractional-order derivative. Phys. Scr. 2024, 99, 115235. [Google Scholar] [CrossRef]
- Kalal, V.; Jha, B.K. A Kernelized Classification Approach for Cancer Recognition Using Markovian Analysis of DNA Structure Patterns as Feature Mining. Cell Biochem. Biophys. 2024, 82, 2249–2274. [Google Scholar] [CrossRef]
- Kalal, V.; Jha, B.K. Cancer detection with various classification models: A comprehensive feature analysis using HMM to extract a nucleotide pattern. Comput. Biol. Chem. 2024, 113, 108215. [Google Scholar] [CrossRef]
- Mustapha, U.T.; Ado, A.; Yusuf, A.; Qureshi, S.; Musa, S.S. Mathematical dynamics for HIV infections with public awareness and viral load detectability. Math. Model. Numer. Simul. Appl. 2023, 3, 256–280. [Google Scholar] [CrossRef]
- Raeisi, E.; Yavuz, M.; Khosravifarsani, M.; Fadaei, Y. Mathematical modeling of interactions between colon cancer and immune system with a deep learning algorithm. Eur. Phys. J. Plus 2024, 139, 345. [Google Scholar] [CrossRef]
- Keshavarz, M.; Qahremani, E.; Allahviranloo, T. Solving a fuzzy fractional diffusion model for cancer tumor by using fuzzy transforms. Fuzzy Sets Syst. 2022, 443, 198–220. [Google Scholar] [CrossRef]
- De Luca, P.; Marcellino, L. Conservation Law Analysis in Numerical Schema for a Tumor Angiogenesis PDE System. Mathematics 2025, 13, 28. [Google Scholar] [CrossRef]
- Shah, K.; Joshi, H. EOQ model for deteriorating items with fuzzy demand and finite horizon under inflation effects. Discret. Contin. Dyn. Syst.-S 2024. [Google Scholar] [CrossRef]
- Shen, J.; Tu, X.; Li, Y. Mathematical Modeling Reveals Mechanisms of Cancer-Immune Interactions Underlying Hepatocellular Carcinoma Development. Mathematics 2023, 11, 4261. [Google Scholar] [CrossRef]
- Naeem, A.; Anees, T.; Khalil, M.; Zahra, K.; Naqvi, R.A.; Lee, S.-W. SNC_Net: Skin Cancer Detection by Integrating Handcrafted and Deep Learning-Based Features Using Dermoscopy Images. Mathematics 2024, 12, 1030. [Google Scholar] [CrossRef]
- Rodrigues, J.A. Using Physics-Informed Neural Networks (PINNs) for Tumor Cell Growth Modeling. Mathematics 2024, 12, 1195. [Google Scholar] [CrossRef]
- Joshi, H.; Yavuz, M.; Taylan, O.; Alkabaa, A. Dynamic analysis of fractal-fractional cancer model under chemotherapy drug with generalized Mittag-Leffler kernel. Comput. Methods Programs Biomed. 2024, 260, 108565. [Google Scholar] [CrossRef]
- Ali, S.M.; Bokhari, A.H.; Yousuf, M.; Zaman, F.D. A spherically symmetric model for the tumor growth. J. Appl. Math. 2014, 726837. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Kara, A.H.; Zaman, F.D. On the solutions and conservation laws of the model for tumor growth in the brain. J. Math. Anal. Appl. 2009, 350, 256–261. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Zaman, F.D. A fractional diffusion equation model for cancer tumor. AIP Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Qayyum, M.; Afzal, S.; Ahmad, E.; Riaz, M.B. Fractional modeling and analysis of unsteady squeezing flow of Casson nanofluid via extended He-Laplace algorithm in Liouville-Caputo sense. Alex. Eng. J. 2023, 7, 579–591. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Tansri, K.; Kittisopaporn, A.; Chansangiam, P. Numerical solutions of the space-time fractional diffusion equation via a gradient-descent iterative procedure. J. Math. Comput. Sci 2023, 31, 353–366. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M.; Hinça, E.; Baleanu, D. Residual power series algorithm for fractional cancer tumor models. Alex. Eng. J. 2020, 59, 1405–1412. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S.; Kumar, R. A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos Solitons Fractals 2020, 133, 109619. [Google Scholar] [CrossRef]
- Arfan, M.; Shah, K.; Ullah, A.; Shutaywi, M.; Kumam, P.; Shah, Z. On fractional order model of tumor dynamics with drug interventions under nonlocal fractional derivative. Results Phys. 2021, 21, 103783. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; Baleanu, D. Theoretical and numerical analysis of fractal fractional model of tumor-immune interaction with two different kernels. Alex. Eng. J. 2022, 61, 5735–5752. [Google Scholar] [CrossRef]
- Feng, Z. The first-integral method to study the Burgers-Korteweg-de Vries equation. J. Phys. A Math. Gen. 2002, 35, 343. [Google Scholar] [CrossRef]
- Abuasad, S.; Hashim, I.; Abdul-Karim, S.A. Modified fractional reduced differential transform method for the solution of multiterm time-fractional diffusion equations. Adv. Math. Phys. 2019, 2019, 5703916. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A new efficient technique for solving fractional coupled Navier-Stokes equations using q-homotopy analysis transform method. Pramana 2019, 93, 6. [Google Scholar] [CrossRef]
- Shah, R.; El-Zahar, N.A.; Akgül, E.R.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The analysis of fractional-order nonlinear systems of third order KdV and Burgers equations via a novel transform. Complexity 2022, 2022, 4935809. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Q. Local fractional homotopy perturbation method for solving coupled sine-Gordon equations in fractal domain. Fractal Fract. 2022, 6, 404. [Google Scholar] [CrossRef]
- Gündoǧdu, H.; Gözükızıl, Ö.F. On the approximate numerical solutions of the fractional heat equation with heat source and heat loss. Therm. Sci. 2022, 26, 3773–3786. [Google Scholar] [CrossRef]
- El-Ajou, A.; Abu-Arqub, O.; Al-Zhour, Z.; Momani, S. New results on fractional power series: Theories and applications. Entropy 2013, 15, 5305–5323. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Exact analytic solutions for nonlinear diffusion equations via generalized residual power series method. Int. J. Math. Comput. Sci. 2019, 14, 69–78. [Google Scholar]
- Guo, T.; Nikan, O.; Avazzadeh, Z. Efficient alternating direction implicit numerical approaches for multi-dimensional distributed-order fractional integro differential problems. Comp. Appl. Math. 2022, 41, 236. [Google Scholar] [CrossRef]
- Gillani, R.; Dawar, A.; Khan, H. The improved residual power series method for the solutions of higher-order linear and nonlinear boundary value problems. J. Umm Al-Qura Univ. Appl. Sci. 2024. [Google Scholar] [CrossRef]
- Kittipoom, P. Extracting explicit coefficient formulas: A robust approach to the Laplace residual power series method. Alex. Eng. J. 2024, 109, 1–11. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X. Laplace-residual power series method for solving fractional generalized long wave equations. Ocean Eng. 2024, 310, 118693. [Google Scholar] [CrossRef]
- El-Ajou, A.; Arqub, O.A.; Momani, S. Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm. J. Comput. Phys. 2015, 293, 81–95. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gündoǧdu, H.; Joshi, H. Numerical Analysis of Time-Fractional Cancer Models with Different Types of Net Killing Rate. Mathematics 2025, 13, 536. https://doi.org/10.3390/math13030536
Gündoǧdu H, Joshi H. Numerical Analysis of Time-Fractional Cancer Models with Different Types of Net Killing Rate. Mathematics. 2025; 13(3):536. https://doi.org/10.3390/math13030536
Chicago/Turabian StyleGündoǧdu, Hami, and Hardik Joshi. 2025. "Numerical Analysis of Time-Fractional Cancer Models with Different Types of Net Killing Rate" Mathematics 13, no. 3: 536. https://doi.org/10.3390/math13030536
APA StyleGündoǧdu, H., & Joshi, H. (2025). Numerical Analysis of Time-Fractional Cancer Models with Different Types of Net Killing Rate. Mathematics, 13(3), 536. https://doi.org/10.3390/math13030536






