Enhanced Multilinear PCA for Efficient Image Analysis and Dimensionality Reduction: Unlocking the Potential of Complex Image Data
Abstract
1. Introduction
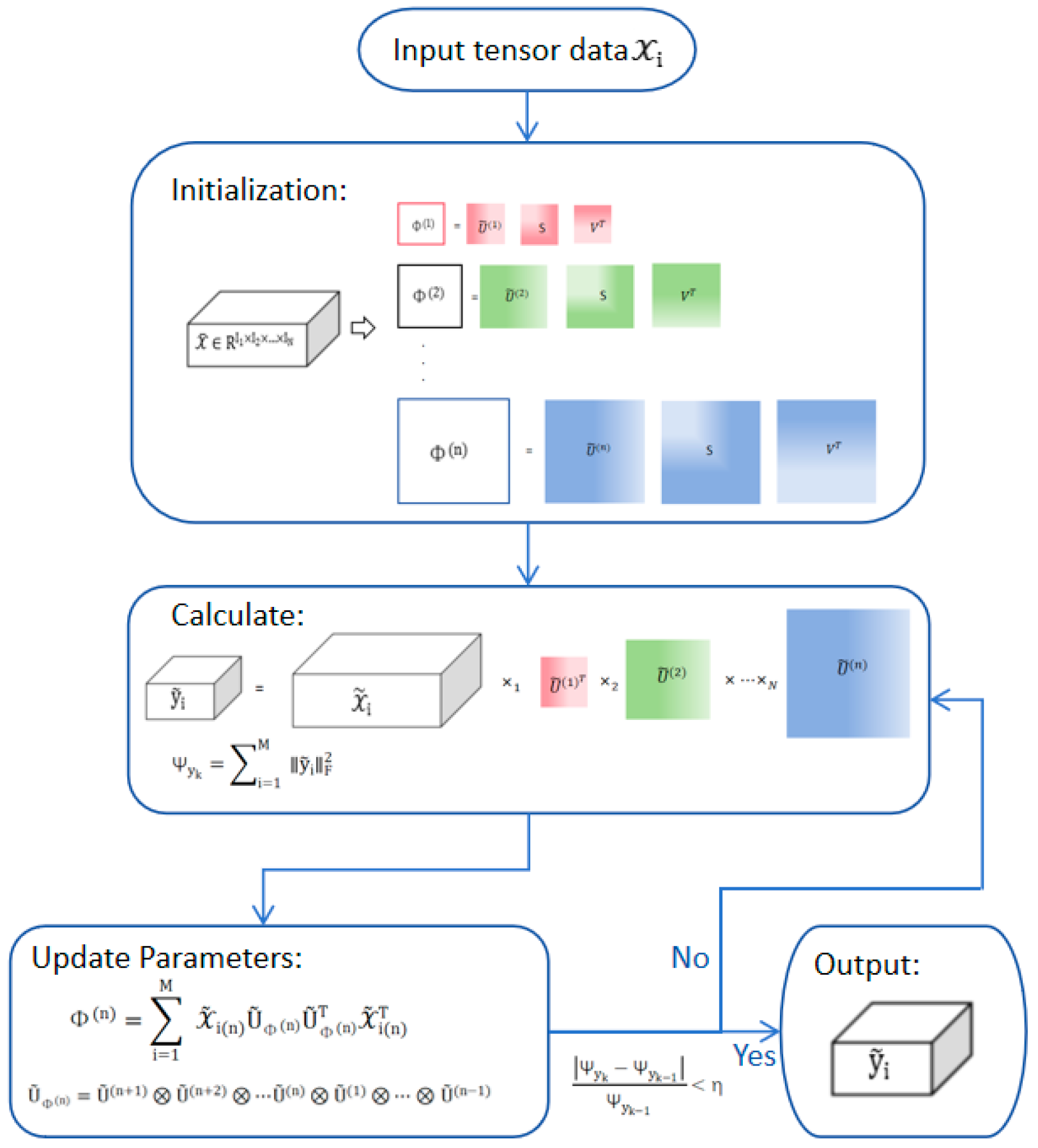
2. Enhanced Multilinear Principal Component Analysis Algorithm
2.1. Random Singular Value Decomposition Algorithm
| Algorithm 1: Random Singular Value Decomposition algorithm |
| , with rank k following a Gaussian distribution; (b) Matrix multiplication: Multiply the original matrix by the random matrix to obtain a projection matrix: (1) ; (c) Perform QR decomposition on matrix Y: . (2) n: . (3) (e) Perform singular value decomposition on matrix B: . (4) |
2.2. Multilinear Principal Component Analysis Algorithm
2.3. Enhanced Multilinear Principal Component Analysis Algorithm
| Algorithm 2: Enhanced Multilinear Principal Component Analysis Algorithm |
, where the mean is given by: (6) largest singular values from the left singular matrix. (c) Local Optimization: (1) The n-mode matrix product of a tensor and a matrix is denoted as A U, and is defined as: . (7) Compute the reduced-dimensional tensor [12]: (8) (2) Calculate the scatter: (9) (3) Iterate the following steps: (3.1) For each, perform RSVD decomposition, and obtain the matrix composed of the largest singular vectors from the left singular matrix. Additional parameters are (“” represents the Kronecker product of matrices) [12]: (10) (11) (3.2) Compute the reduced-dimensional tensor and scatter: (12) (13) (3.3) Stop when the condition becomes true: (14) (d) Projection: Obtain the final reduced-dimensional tensor: (15) |
2.4. Algorithm Performance Experiment and Specific Analysis Metrics
2.4.1. Metrics
2.4.2. Experimental Environment
2.4.3. Experimental Validation
3. Application of Enhanced Multilinear Principal Component Analysis Algorithm
3.1. Image Classification
3.2. Face Recognition
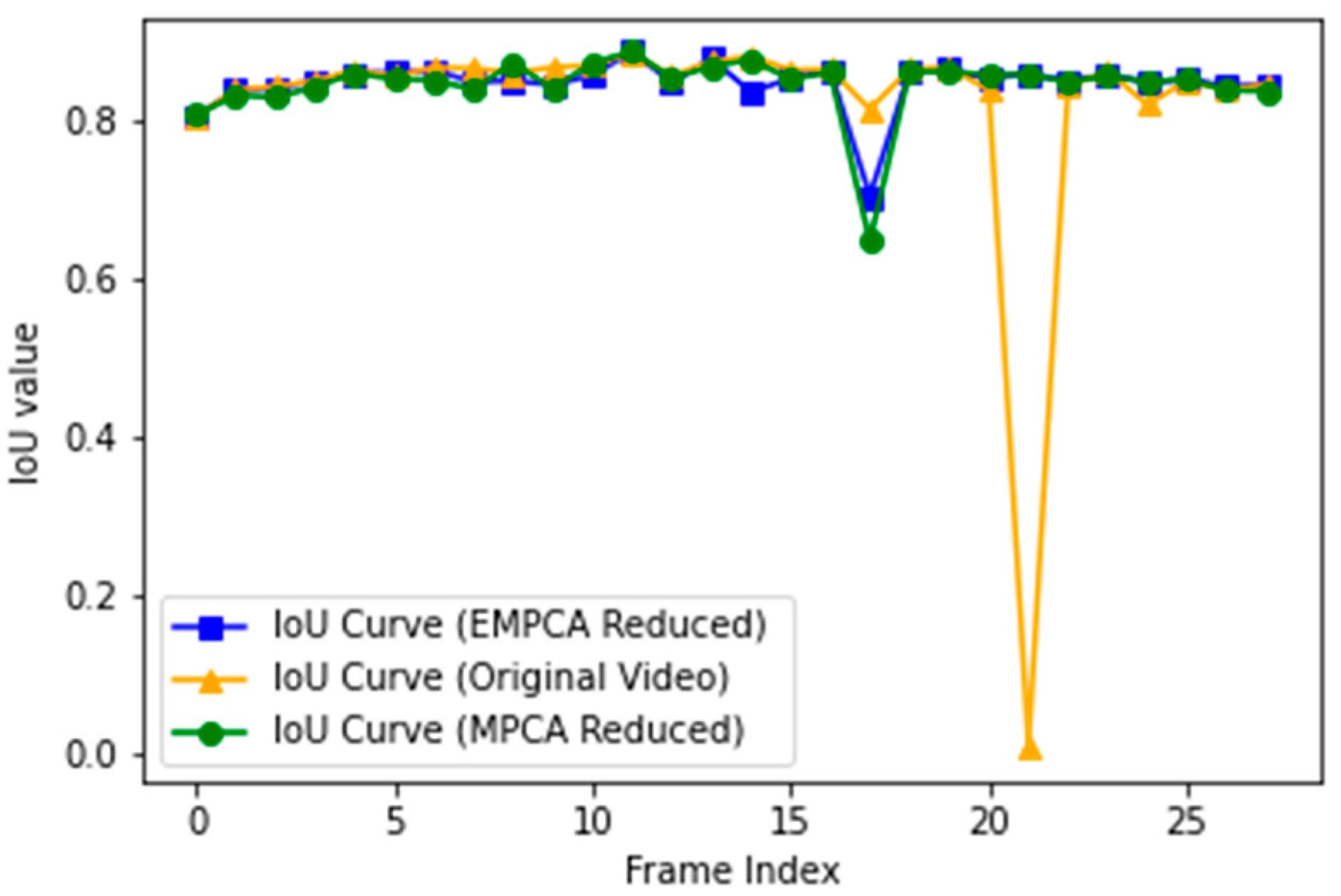
3.3. Image Segmentation
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bro, R.; Smilde, A.K. Principal component analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef]
- Bansal, A.K.; Chawla, P. Performance Evaluation of Face Recognition using PCA and N-PCA. Int. J. Comput. Appl. 2013, 76, 14–20. [Google Scholar]
- Yang, J.; Zhang, D.; Frangi, A.; Yang, J.-Y. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef]
- Chapman, K.W.; Lapidus, S.H.; Chupas, P.J. Applications of principal component analysis to pair distribution function data. J. Appl. Crystallogr. 2015, 48, 1619–1626. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Kernel principal component analysis. In International Conference on Artificial Neural Networks; Springer: Berlin, Heidelberg, 1997; pp. 583–588. [Google Scholar]
- Li, J.; Liu, M.; Ma, D.; Huang, J.; Ke, M.; Zhang, T. Learning shared subspace regularization with linear discriminant analysis for multi-label action recognition. J. Supercomput. 2020, 76, 2139–2157. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Syed, F.I.; Muther, T.; Dahaghi, A.K.; Negahban, S. Low-rank tensors applications for dimensionality reduction of complex hydrocarbon reservoirs. Energy 2022, 244, 122680. [Google Scholar] [CrossRef]
- Gao, H.; Wang, M.; Sun, X.; Cao, X.; Li, C.; Liu, Q.; Xu, P. Unsupervised dimensionality reduction of medical hyperspectral imagery in tensor space. Comput. Methods Programs Biomed. 2023, 240, 107724. [Google Scholar] [CrossRef]
- Xie, D.; Chen, S.; Duan, H.; Li, X.; Luo, C.; Ji, Y.; Duan, H. A novel grey prediction model based on tensor higher-order singular value decomposition and its application in short-term traffic flow. Eng. Appl. Artif. Intell. 2023, 126, 107068. [Google Scholar] [CrossRef]
- Yin, W.; Qu, Y.; Ma, Z.; Liu, Q. Hyperntf: A hypergraph regularized nonnegative tensor factorization for dimensionality reduction. Neurocomputing 2022, 512, 190–202. [Google Scholar] [CrossRef]
- Lu, H.; Plataniotis, K.N.; Venetsanopoulos, A.N. MPCA: Multilinear principal component analysis of tensor objects. IEEE Trans. Neural Netw. 2008, 19, 18–39. [Google Scholar]
- Xie, P.; Wu, X. Block Multilinear Principal Component Analysis and Its Application in Face Recognition Research. Comput. Sci. 2015, 42, 274–279. [Google Scholar]
- Wu, J.; Qiu, S.; Zeng, R.; Kong, Y.; Senhadji, L.; Shu, H. Multilinear principal component analysis network for tensor object classification. IEEE Access 2017, 5, 3322–3331. [Google Scholar] [CrossRef]
- Halko, N.; Martinsson, P.G.; Tropp, J.A. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 2011, 53, 217–288. [Google Scholar] [CrossRef]
- Feng, X.; Yu, W.; Li, Y. Faster matrix completion using randomized SVD. In Proceedings of the 2018 IEEE 30th International Conference on Tools with Artificial Intelligence (ICTAI), Volos, Greece, 5–7 November 2018; pp. 608–615. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Chadebec, C.; Vincent, L.; Allassonnière, S. Pythae: Unifying Generative Autoencoders in Python-A Benchmarking Use Case. Adv. Neural Inf. Process. Syst. 2022, 35, 21575–21589. [Google Scholar]
- Chadebec, C.; Thibeau-Sutre, E.; Burgos, N.; Allassonnière, S. Data augmentation in high dimensional low sample size setting sing a geometry-based variational autoencoder. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 2879–2896. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Wolf, L.; Jhuang, H.; Hazan, T. Modeling appearances with low-rank SVM. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Liu, Y.; Liu, J.; Long, Z.; Zhu, C. Tensor Computation for Data Analysis; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Die9OrigEphit. Children vs. Adults Images. Kaggle [Dataset]. Available online: https://www.kaggle.com/datasets/die9origephit/children-vs-adults-images (accessed on 13 May 2024).
- Agarwal, S. Flower Classification. Kaggle [Dataset]. Available online: https://www.kaggle.com/datasets/sauravagarwal/flower-classification (accessed on 15 May 2024).
- Nefifian, A. Georgia Tech Face Database. 2013. Available online: https://www.anefian.com/research/face_reco.htm (accessed on 21 March 2024).
- Li, X.; Ng, M.K.; Xu, X.; Ye, Y. Block principal component analysis for tensor objects with frequency or time information. Neurocomputing 2018, 302, 12–22. [Google Scholar] [CrossRef]
- Samaria, F.S.; Harter, A.C. Parameterisation of a stochastic model for human face identification. In Proceedings of the 1994 IEEE Workshop on Applications of Computer Vision, Sarasota, FL, USA, 5–7 December 1994; pp. 138–142. [Google Scholar]
- Khan, Z.; Shafait, F.; Mian, A. Joint group sparse PCA for compressed hyperspectral imaging. IEEE Trans. Image Process. 2015, 24, 4934–4942. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Nazir, A.; Cheema, M.N.; Sheng, B.; Li, H.; Li, P.; Yang, P.; Jung, Y.; Qin, J.; Kim, J.; Feng, D.D. OFF-eNET: An optimally fused fully end-to-end network for automatic dense volumetric 3D intracranial blood vessels segmentation. IEEE Trans. Image Process. 2020, 29, 7192–7202. [Google Scholar] [CrossRef]
- Olafenwa, Ayoola. PixelLib Library. GitHub. 2021. Available online: https://github.com/ayoolaolafenwa/PixelLib (accessed on 3 June 2024).
- Perazzi, F.; Pont-Tuset, J.; McWilliams, B.; Van Gool, L.; Gross, M.; Sorkine-Hornung, A. A benchmark dataset and evaluation methodology for video object segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 724–732. [Google Scholar]

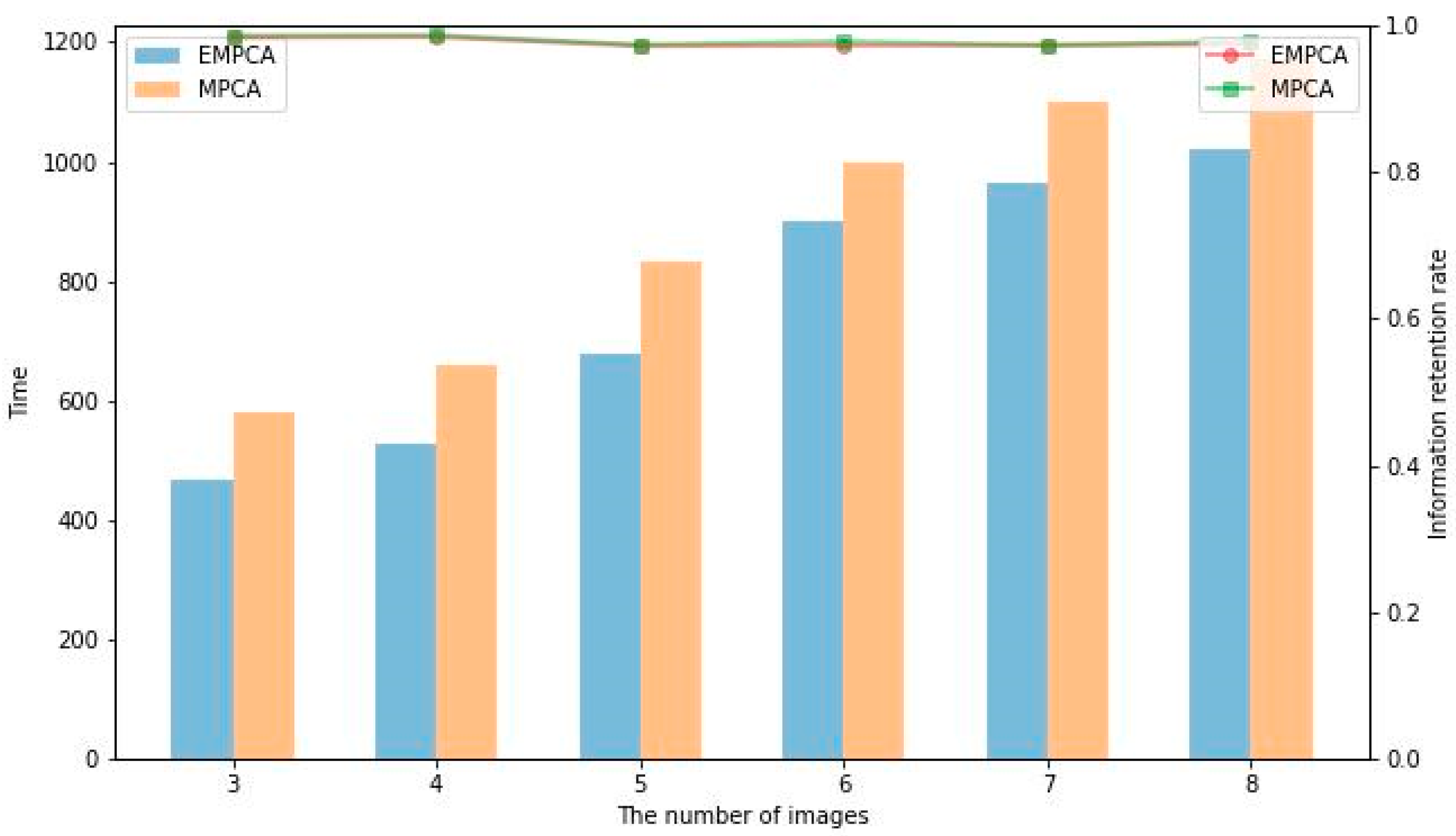
| Method | Time/s | Time Standard Deviation | Reserved Rate | Accuracy Standard Deviation |
|---|---|---|---|---|
| MPCA | 688 | 29.462 | 0.956 | 0.0160 |
| EMPCA | 566 | 20.486 | 0.954 | 0.0194 |
| Method | Time/s | Time Standard Deviation | Reserved Rate | Accuracy Standard Deviation |
|---|---|---|---|---|
| EMPCA | 79 | 3.431 | 0.921 | 0.018 |
| MPCA | 86 | 5.523 | 0.930 | 0.023 |
| VAE | 152 | 3.860 | 0.746 | 0.021 |
| RHVAE | 139 | 5.431 | 0.707 | 0.027 |
| PCA | 203 | 4.273 | 0.738 | 0.022 |
| SVD | 365 | 3.347 | 0.740 | 0.017 |
| Comparison | Time p-Value | Accuracy p-Value |
|---|---|---|
| EMPCA vs. MPCA | ||
| EMPCA vs. VAE | 0.0000 ** | 0.0000 ** |
| EMPCA vs. RHVAE | 0.0000 ** | 0.0000 ** |
| EMPCA vs. PCA | 0.0000 ** | 0.0000 ** |
| EMPCA vs. SVD | 0.0000 ** | 0.0000 ** |
| Datasets | Method | Time/s | Time Standard Deviation | Time p-Value | Accuracy/% | Accuracy Standard Deviation | Accuracy p-Value |
|---|---|---|---|---|---|---|---|
| Children | SVM | 115 | 5.100 | 0.0000 ** | 45 | 1.355 | 0.0014 |
| MPCA+SVM | 7.9 | 0.458 | 0.0165 | 48 | 2.574 | 0.2411 | |
| EMPCA+SVM | 7.4 | 0.424 | 50 | 3.594 | |||
| STM | 694 | 20.148 | 0.0000 ** | 48 | 0.874 | 0.0006 | |
| MPCA+STM | 197 | 10.132 | 0.0453 | 44 | 3.095 | 0.0000 ** | |
| EMPCA+STM | 186 | 9.981 | 54 | 4.418 | |||
| Flower | SVM | 96 | 4.762 | 0.0000 ** | 55 | 3.534 | 0.0142 |
| MPCA+SVM | 17 | 0.853 | 0.0000 ** | 57 | 2.625 | 0.1658 | |
| EMPCA+SVM | 14 | 0.650 | 59 | 3.700 | |||
| STM | 694 | 25.751 | 0.0000 ** | 34 | 2.173 | 0.0000 ** | |
| MPCA+STM | 159 | 8.345 | 0.0000 ** | 44 | 1.710 | 0.0000 ** | |
| EMPCA+STM | 145 | 7.713 | 50 | 1.337 | |||
| IMAGENET | SVM | 42 | 2.358 | 0.0000 ** | 59 | 3.840 | 0.0001 |
| MPCA+SVM | 3.5 | 0.206 | 0.0266 | 65 | 5.088 | 0.1226 | |
| EMPCA+SVM | 3.3 | 0.232 | 69 | 5.484 | |||
| STM | 391 | 22.214 | 0.0000 ** | 55 | 3.700 | 0.0213 | |
| MPCA+STM | 58 | 3.700 | 0.0389 | 55 | 3.932 | 0.0244 | |
| EMPCA+STM | 54 | 3.132 | 59 | 3.951 |
| Datasets | Method | Time/s | Time Standard Deviation | Time p-Value | Accuracy/% | Accuracy Standard Deviation | Accuracy p-Value |
|---|---|---|---|---|---|---|---|
| Georgia | SVM | 6.9 | 0.193 | 0.0000 ** | 99 | 0.539 | 0.6601 |
| MPCA+SVM | 2.1 | 0.052 | 0.0000 ** | 99 | 0.447 | 0.3306 | |
| EMPCA+SVM | 1.5 | 0.043 | 99 | 0.400 | |||
| STM | 35 | 2.358 | 0.0000 ** | 95 | 0.800 | 0.0232 | |
| MPCA+STM | 5.7 | 0.473 | 0.0107 | 96 | 0.980 | 0.0000 ** | |
| EMPCA+STM | 5.2 | 0.255 | 97 | 0.900 | |||
| ORL | SVM | 1.1 | 0.021 | 0.0000 ** | 96 | 1.136 | 0.8451 |
| MPCA+SVM | 0.2 | 0.044 | 0.0000 ** | 95 | 0.640 | 0.0939 | |
| EMPCA+SVM | 0.1 | 0.014 | 96 | 1.044 | |||
| STM | 45 | 1.367 | 0.0000 ** | 63 | 1.100 | 0.0019 | |
| MPCA+STM | 5.8 | 0.256 | 0.0000 ** | 64 | 1.077 | 0.0000 ** | |
| EMPCA+STM | 5.7 | 0.115 | 65 | 0.894 | |||
| UWA | SVM | 1.0 | 0.015 | 0.0000 ** | 100 | 0.400 | 0.5560 |
| MPCA+SVM | 0.2 | 0.014 | 0.0000 ** | 100 | 0.600 | 0.6606 | |
| EMPCA+SVM | 0.1 | 0.017 | 100 | 0.300 | |||
| STM | 51 | 3.240 | 0.0000 ** | 93 | 1.375 | 0.0000 ** | |
| MPCA+STM | 4.3 | 0.078 | 0.0000 ** | 90 | 0.872 | 0.0027 | |
| EMPCA+STM | 3.4 | 0.095 | 95 | 1.183 |
| Method | IoU | IoU Standard Deviation | IoU p-Value |
|---|---|---|---|
| Mask R-CNN | 0.83 | 0.012 | 0.0000 ** |
| MPCA+Mask R-CNN | 0.84 | 0.008 | 0.0031 |
| EMPCA+Mask R-CNN | 0.85 | 0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; He, L.; Fang, X.; Xie, L. Enhanced Multilinear PCA for Efficient Image Analysis and Dimensionality Reduction: Unlocking the Potential of Complex Image Data. Mathematics 2025, 13, 531. https://doi.org/10.3390/math13030531
Sun T, He L, Fang X, Xie L. Enhanced Multilinear PCA for Efficient Image Analysis and Dimensionality Reduction: Unlocking the Potential of Complex Image Data. Mathematics. 2025; 13(3):531. https://doi.org/10.3390/math13030531
Chicago/Turabian StyleSun, Tianyu, Lang He, Xi Fang, and Liang Xie. 2025. "Enhanced Multilinear PCA for Efficient Image Analysis and Dimensionality Reduction: Unlocking the Potential of Complex Image Data" Mathematics 13, no. 3: 531. https://doi.org/10.3390/math13030531
APA StyleSun, T., He, L., Fang, X., & Xie, L. (2025). Enhanced Multilinear PCA for Efficient Image Analysis and Dimensionality Reduction: Unlocking the Potential of Complex Image Data. Mathematics, 13(3), 531. https://doi.org/10.3390/math13030531





