N-Bipolar Soft Expert Sets and Their Applications in Robust Multi-Attribute Group Decision-Making

Abstract

This paper presents N-bipolar soft expert (N-BSE) sets, a novel framework designed to enhance multi-attribute group decision-making (MAGDM) by incorporating expert input, bipolarity, and non-binary evaluations. Existing MAGDM approaches often lack the ability to simultaneously integrate positive and negative assessments, especially in nuanced, multi-valued evaluation spaces. The proposed N-BSE model addresses this limitation by offering a comprehensive, mathematically rigorous structure for decision-making (DM). Fundamental operations of the N-BSE model are defined and analyzed, ensuring its theoretical consistency and applicability. To demonstrate its practical utility, the N-BSE model is applied to a general case study on sustainable energy solutions, illustrating its effectiveness in handling complex DM scenarios. An algorithm is proposed to streamline the DM process, enabling systematic and transparent identification of optimal alternatives. Additionally, a comparative analysis emphasizes the advantages of the N-BSE model over existing MAGDM frameworks, highlighting its capacity to integrate diverse expert opinions, evaluate both positive and negative attributes, and support multi-valued assessments. By bridging the gap between theoretical development and practical application, this paper contributes to advancing DM methodologies.

1. Introduction

In 1965, Zadeh [1] introduced fuzzy set theory, revolutionizing mathematics by allowing partial membership to better represent imprecise human knowledge, which quickly spread to various fields. This concept was later generalized in numerous successful ways, including L-fuzzy sets [2], type-2 fuzzy sets [3], intuitionistic fuzzy sets [4], rough fuzzy sets and fuzzy rough sets [5], bipolar fuzzy sets [6], complex fuzzy sets [7], hesitant fuzzy sets [8], Pythagorean fuzzy sets [9], picture fuzzy sets [10], spherical fuzzy sets [11], Fermatean fuzzy sets [12], neutrosophic fuzzy sets [13], q-rung orthopair fuzzy sets [14], and others. Pawlak [15] introduced rough set theory in 1982, utilizing an equivalence relation called the indiscernibility relation to define lower and upper approximations and the boundary region of a set. The lower approximation includes elements definitely belonging to a concept, while the upper approximation contains elements that may belong. The difference between these approximations is the boundary region, which is empty for crisp sets and non-empty for rough sets. Rough set theory offers the advantage of extracting useful information without requiring extra parameters or information about the data. In 1994, Pawlak [16] proposed a unified approach that combined classical set theory, rough sets, and fuzzy sets to represent soft sets (S-sets). This approach inspired Molodtsov [17] to create S-set theory in 1999, where he explored its basic principles, applications, and future directions. S-set theory, which is especially useful in handling imprecise data, has shown promise in resolving ambiguities in data mining problems. Furthermore, S-set theory can expand and enhance existing concepts such as probability, fuzzy sets, rough sets, and intuitionistic fuzzy sets, addressing the lack of parameterization tools in these areas. Since its introduction, numerous authors have proposed extensions, hybridizations, and generalizations of S-set theory.

The fundamental operations associated with S-sets and their properties were initially presented in [18], and subsequently refined in [19]. Notable contributors to this field, such as [20,21], demonstrated how Molodtsov’s concept could be integrated with other well-established theories, including fuzzy sets and intuitionistic fuzzy sets. These connections between models continued to be explored [22,23]. Over time, various extensions and hybrid models emerged, including generalized intuitionistic fuzzy S-sets [24], Fermatean vague soft sets [25], bipolar soft (BS) sets [26], fuzzy BS sets [27], bipolar complex fuzzy soft sets [28], probabilistic and dual probabilistic S-sets [29,30], N-soft (N-S) sets [31], N-bipolar soft (N-BS) sets [32], N-hypersoft sets [33], bipolar hypersoft sets [34,35,36,37], M-parametrized N-S sets [38], bipolar M-parametrized N-S sets [39], hesitant fuzzy S-sets [40], m-polar fuzzy S-sets [41], ranked S-sets [42], soft rough sets, and rough S-sets [43,44]. A comprehensive literature review of S-set theory was conducted in [45]. A key area of research pertains to DM, with foundational work credited to [46,47], while [48] introduced DM within the hybrid fuzzy S-set framework, later enhanced in [49,50]. DM in generalized intuitionistic fuzzy S-sets appeared in [24]. A recent perspective on these topics can be found in [51,52].

It is worth noting that, over time, S-set theory and its hybrid models have been effectively applied in group DM, particularly in fields such as medicine, physics, and social sciences, where uncertain data often arises. One challenge faced by practitioners using questionnaires is that these mathematical techniques typically process data from only a single expert’s assessment, limiting their ability to incorporate multiple perspectives. To address this, the concept of soft expert (SE) sets was introduced by Alkhazaleh and Salleh [53], allowing for the full inclusion of each selected expert’s opinion in DM problems. The concept was later extended by [54] through the integration of fuzzy sets. Further developments in SE sets have led to the incorporation of various models aimed at DM under uncertainty, including intuitionistic fuzzy SE sets [55], N-soft expert (N-SE) sets and fuzzy N-SE sets [56], generalized neutrosophic SE sets [57], and bipolar soft expert (BSE) sets [58,59]. Convexity-cum-concavity on fuzzy SE sets [60], complex neutrosophic SE sets [61], and the use of Pythagorean fuzzy N-SE knowledge in group DM [62] have broadened the scope of the theory. Other models, such as spherical fuzzy N-SE sets [63], bipolar N-SE sets [64], and possibility neutrosophic SE sets [65], showcase the flexibility of these models in multi-criteria DM. Additional applications of these methods can be found in fields like recruitment [66] and election prediction [67]. Another perspective on the SE set and its application in multi-criteria decision-making is discussed in [68].

1.1. Motivations, Objectives, and Contributions

The motivation behind this paper stems from the limitations of existing MAGDM models in handling nuanced evaluations and expert opinions. Current approaches often fall short in incorporating both positive and negative assessments simultaneously, particularly in multi-valued evaluation spaces. The need for a comprehensive framework that balances expert input, bipolarity, and non-binary evaluations is evident in various real-world scenarios, such as sustainability assessments, healthcare prioritizations, and engineering project evaluations. This gap inspired the development of the N-BSE model, which aims to address these shortcomings by offering a robust and versatile DM framework.

The primary objectives of this paper are as follows:

• Proposing a novel N-BSE model that extends traditional SE set frameworks by integrating bipolarity and multinary evaluations.
• Defining and analyzing the core operations of the N-BSE model, ensuring its mathematical consistency and applicability.
• Demonstrating the practical utility of the N-BSE model in solving complex MAGDM problems, particularly those requiring nuanced assessments and expert collaboration.
• Conducting a comparative analysis between the N-BSE model and existing frameworks, highlighting its advantages and addressing its limitations.

This paper makes the following key contributions to the field of DM:

• Introducing the N-BSE model, a hybrid set-theoretic framework that combines expert input, bipolarity, and non-binary evaluations, addressing a significant gap in MAGDM methodologies.
• Providing rigorous definitions and fundamental operations for the N-BSE model, establishing its theoretical underpinnings.
• Proposing a systematic algorithm for applying the N-BSE model to MAGDM scenarios, enabling objective and transparent DM processes.
• Demonstrating the applicability of the N-BSE model through a detailed case study on sustainable energy solutions, illustrating its potential for real-world DM.
• Offering a comprehensive comparison with existing MAGDM models, showcasing the N-BSE model’s ability to integrate expert opinions, handle bipolarity, and support multi-valued assessments effectively.

By addressing both theoretical and practical aspects, this paper establishes the groundwork for further research and application of the N-BSE model in various domains, contributing to the progress of DM frameworks.

1.2. Outline of the Paper

This paper is organized as follows: Section 2 reviews the foundational concepts related to S-sets, SE sets, BS sets, BSE sets, N-S sets, N-SE sets, and N-BS sets, which provide the theoretical background for the study. Section 3 presents the novel N-BSE model, defines its core operations, and discusses its algebraic properties, illustrated with examples. In Section 4, the application of the N-BSE model to MAGDM is explored, including a general case study on selecting sustainable energy solutions. Section 5 provides a comparative analysis of the N-BSE model, highlighting its advantages, comparing it to existing models, and discussing its limitations. Finally, Section 6 concludes the paper and outlines potential directions for future research.

2. Preliminary Concepts

This section reviews the key concepts of S-set, SE set, BS set, BSE set, N-S set, N-SE set, and N-BS set, which serve as the foundation for this study. In this context, $\mathcal{Z}$ represents the universal set of alternatives (or objects), $\mathbb{P}$ stands for a set of attributes (or parameters), and $G=\{0,1,\dots ,N-1\}$ where $N\in \{2,3,\dots \}$ refers to a set of ordered grades. The set $\mathbb{E}$ denotes a set of experts, and $\mathbb{O}=\{0=\mathrm{disagree},1=\mathrm{agree}\}$ corresponds to a set of opinions. Furthermore, ¥ $=\mathbb{P}\times \mathbb{E}\times \mathbb{O}$ and $A\subset$ ¥.

Definition 1

([17]). An S-set is defined as an ordered pair $(\Gamma ,\mathbb{P})$, where $\Gamma :\mathbb{P}\to P\left(\mathcal{Z}\right)$, and $P\left(\mathcal{Z}\right)$ denotes the power set of $\mathcal{Z}$, which comprises all subsets of $\mathcal{Z}$.

Definition 2

([53]). An SE set is described as a pair $(\Delta ,A)$, where $\Delta :A\to P\left(\mathcal{Z}\mathcal{\right)}$, mapping each element in A to a subset of $\mathcal{Z}$.

Definition 3

([53]). The NOT set of a set A, denoted by $\neg A$, is defined as $\neg A=\{\neg a\mid a\in A\}$, where $\neg a=(\neg p,e,o)$ represents the negation of an element $a=(p,e,o)$.

Definition 4

([26]). A BS set is a structure $(\zeta ,\psi ,\mathbb{P})$, where $\zeta :\mathbb{P}\to P\left(\mathcal{Z}\right)$ and $\psi :\neg \mathbb{P}\to P\left(\mathcal{Z}\right)$. For each $p\in \mathbb{P}$, it holds that $\zeta \left(p\right)\cap \psi (\neg p)=\varnothing$, where $\zeta \left(p\right)$ and $\psi (\neg p)$ are subsets of $\mathcal{Z}$.

Definition 5

([59]). A BSE set is defined as a triple $(\delta ,\lambda ,A)$, where $\delta :A\to P\left(\mathcal{Z}\right)$ and $\lambda :\neg A\to P\left(\mathcal{Z}\right)$. The functions satisfy the condition that for every $a\in A$, $\delta \left(a\right)\cap \lambda (\neg a)=\varnothing$, with $\delta \left(a\right)$ and $\lambda (\neg a)$ being subsets of $\mathcal{Z}$.

Definition 6

([31]). An N-S set is characterized as a triple $(\Psi ,\mathbb{P},N)$, where $\Psi :\mathbb{P}\to P(\mathcal{Z}\times G)$. For each $p\in \mathbb{P}$, there exists a unique pair $(z,g_p)\in \mathcal{Z}\times G$ such that $(z,g_p)\in \Psi \left(p\right)$ or, equivalently, $\Psi \left(p\right)\left(z\right)=g_p$, with $z\in \mathcal{Z}$ and $g_p\in G$. Here, $P(\mathcal{Z}\times G)$ represents the power set of $\mathcal{Z}\times G$, which includes all subsets of $\mathcal{Z}\times G$.

Definition 7

([56]). An N-SE set is expressed as a triple $(\Theta ,A,N)$, where $\Theta :A\to P(\mathcal{Z}\times G)$. For every $a\in A$, there exists a unique pair $(z,g_a)\in \mathcal{Z}\times G$ such that $(z,g_a)\in \Theta \left(a\right)$ or, equivalently, $\Theta \left(a\right)\left(z\right)=g_a$, with $z\in \mathcal{Z}$ and $g_a\in G$.

Definition 8

([32]). An N-BS set is described as a quadruple $(\mathcal{h},f,\mathbb{P},N)$, where $\mathcal{h}:\mathbb{P}\to P(\mathcal{Z}\times G)$ and $f:\neg \mathbb{P}\to P(\mathcal{Z}\times G)$. These mappings satisfy the following conditions: For each $p\in \mathbb{P}$, there exists a unique pair $(z,g_p)\in \mathcal{Z}\times G$ such that $(z,g_p)\in \mathcal{h}\left(p\right)$ or, equivalently, $\mathcal{h}\left(p\right)\left(z\right)=g_p$. Similarly, for each $\neg p\in \neg \mathbb{P}$, there exists a unique pair $(z,g_{\neg p})\in \mathcal{Z}\times G$ such that $(z,g_{\neg p})\in f(\neg p)$ or, equivalently, $f(\neg p)\left(z\right)=g_{\neg p}$. Moreover, it is required that $g_p+g_{\neg p}\le N-1$, where $z\in \mathcal{Z}$ and $g_p,g_{\neg p}\in G$.

3. N-Bipolar Soft Expert Sets

In this section, we introduce the novel N-BSE model, present its fundamental operations, and explore its algebraic properties, supported by illustrative examples.

Definition 9.

A quadruple $(\gamma ,\eta ,A,N)$ is called an N-BSE set, where $\gamma :A\to \mathcal{P}(\mathcal{Z}\times G)$ and $\eta :\neg A\to \mathcal{P}(\mathcal{Z}\times G)$, with the property that for each $a\in A$, there exists a unique pair $(z,g_a)\in \mathcal{Z}\times G$ such that $(z,g_a)\in \gamma \left(a\right)$, and for each $\neg a\in \neg A$, there exists a unique pair $(z,g_{\neg a})\in \mathcal{Z}\times G$ such that $(z,g_{\neg a})\in \eta (\neg a)$.

For each $a\in A$ and $z\in \mathcal{Z}$, there exists a unique evaluation from the assessment space G, denoted by $g_a$, such that $(z,g_a)\in \gamma \left(a\right)$ or, equivalently, $\gamma \left(a\right)\left(z\right)=g_a$. Similarly, for each $\neg a\in \neg A$ and $z\in \mathcal{Z}$, there exists a unique evaluation from the assessment space G, denoted by $g_{\neg a}$, such that $(z,g_{\neg a})\in \eta (\neg a)$ or, equivalently, $\eta (\neg a)\left(z\right)=g_{\neg a}$.

Additionally, the following condition holds:

$$\gamma \left(a\right)\left(z\right)+\eta (\neg a)\left(z\right)\le N-1.$$

The N-BSE set $(\gamma ,\eta ,A,N)$ can be represented in tabular form, where $\mathcal{Z}=\{z_1,z_2,\dots ,z_n\}$, $\mathbb{P}=\{p_1,p_2,\dots ,p_m\}$, and $\mathbb{E}=\{e_1,e_2,\dots ,e_t\}$ are finite, unless otherwise specified. This tabular representation is shown in

Table 1. Tabular representation of the N-BSE set $(\gamma ,\eta ,A,N)$.

$(\mathit{\gamma },\mathit{\eta },\mathit{A},\mathit{N})$	${\mathit{z}}_1$	${\mathit{z}}_2$	⋯	${\mathit{z}}_{\mathit{n}}$
$(p_1,e_1,1)$	$\gamma \left((p_1,e_1,1)\right)\left(z_1\right)$	$\gamma \left((p_1,e_1,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_1,1)\right)\left(z_n\right)$
$(p_1,e_2,1)$	$\gamma \left((p_1,e_2,1)\right)\left(z_1\right)$	$\gamma \left((p_1,e_2,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_2,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_1,e_t,1)$	$\gamma \left((p_1,e_t,1)\right)\left(z_1\right)$	$\gamma \left((p_1,e_t,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_t,1)\right)\left(z_n\right)$
$(p_2,e_1,1)$	$\gamma \left((p_2,e_1,1)\right)\left(z_1\right)$	$\gamma \left((p_2,e_1,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_2,e_1,1)\right)\left(z_n\right)$
$(p_2,e_2,1)$	$\gamma \left((p_2,e_2,1)\right)\left(z_1\right)$	$\gamma \left((p_2,e_2,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_2,e_2,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_2,e_t,1)$	$\gamma \left((p_2,e_t,1)\right)\left(z_1\right)$	$\gamma \left((p_2,e_t,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_2,e_t,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_m,e_1,1)$	$\gamma \left((p_m,e_1,1)\right)\left(z_1\right)$	$\gamma \left((p_m,e_1,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_m,e_1,1)\right)\left(z_n\right)$
$(p_m,e_2,1)$	$\gamma \left((p_m,e_2,1)\right)\left(z_1\right)$	$\gamma \left((p_m,e_2,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_2,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_m,e_t,1)$	$\gamma \left((p_m,e_t,1)\right)\left(z_1\right)$	$\gamma \left((p_m,e_t,1)\right)\left(z_2\right)$	⋯	$\gamma \left((p_m,e_t,1)\right)\left(z_n\right)$
$(p_1,e_1,0)$	$\gamma \left((p_1,e_1,0)\right)\left(z_1\right)$	$\gamma \left((p_1,e_1,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_1,0)\right)\left(z_n\right)$
$(p_1,e_2,0)$	$\gamma \left((p_1,e_2,0)\right)\left(z_1\right)$	$\gamma \left((p_1,e_2,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_2,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_1,e_t,0)$	$\gamma \left((p_1,e_t,0)\right)\left(z_1\right)$	$\gamma \left((p_1,e_t,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_t,0)\right)\left(z_n\right)$
$(p_2,e_1,0)$	$\gamma \left((p_2,e_1,0)\right)\left(z_1\right)$	$\gamma \left((p_2,e_1,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_2,e_1,0)\right)\left(z_n\right)$
$(p_2,e_2,0)$	$\gamma \left((p_2,e_2,0)\right)\left(z_1\right)$	$\gamma \left((p_2,e_2,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_2,e_2,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_2,e_t,0)$	$\gamma \left((p_2,e_t,0)\right)\left(z_1\right)$	$\gamma \left((p_2,e_t,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_2,e_t,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_m,e_1,0)$	$\gamma \left((p_m,e_1,0)\right)\left(z_1\right)$	$\gamma \left((p_m,e_1,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_m,e_1,0)\right)\left(z_n\right)$
$(p_m,e_2,0)$	$\gamma \left((p_m,e_2,0)\right)\left(z_1\right)$	$\gamma \left((p_m,e_2,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_1,e_2,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(p_m,e_t,0)$	$\gamma \left((p_m,e_t,0)\right)\left(z_1\right)$	$\gamma \left((p_m,e_t,0)\right)\left(z_2\right)$	⋯	$\gamma \left((p_m,e_t,0)\right)\left(z_n\right)$
$(\neg p_1,e_1,1)$	$\eta \left((\neg p_1,e_1,1)\right)\left(z_1\right)$	$\eta \left((\neg p_1,e_1,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_1,e_1,1)\right)\left(z_n\right)$
$(\neg p_1,e_2,1)$	$\eta \left((\neg p_1,e_2,1)\right)\left(z_1\right)$	$\eta \left((\neg p_1,e_2,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_1,e_2,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_1,e_t,1)$	$\eta \left((\neg p_1,e_t,1)\right)\left(z_1\right)$	$\eta \left((\neg p_1,e_t,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_1,e_t,1)\right)\left(z_n\right)$
$(\neg p_2,e_1,1)$	$\eta \left((\neg p_2,e_1,1)\right)\left(z_1\right)$	$\eta \left((\neg p_2,e_1,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_2,e_1,1)\right)\left(z_n\right)$
$(\neg p_2,e_2,1)$	$\eta \left((\neg p_2,e_2,1)\right)\left(z_1\right)$	$\eta \left((\neg p_2,e_2,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_2,e_2,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_2,e_t,1)$	$\eta \left((\neg p_2,e_t,1)\right)\left(z_1\right)$	$\eta \left((\neg p_2,e_t,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_2,e_t,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_m,e_1,1)$	$\eta \left((\neg p_m,e_1,1)\right)\left(z_1\right)$	$\eta \left((\neg p_m,e_1,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_m,e_1,1)\right)\left(z_n\right)$
$(\neg p_m,e_2,1)$	$\eta \left((\neg p_m,e_2,1)\right)\left(z_1\right)$	$\eta \left((\neg p_m,e_2,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_m,e_2,1)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_m,e_t,1)$	$\eta \left((\neg p_m,e_t,1)\right)\left(z_1\right)$	$\eta \left((\neg p_m,e_t,1)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_m,e_t,1)\right)\left(z_n\right)$
$(\neg p_1,e_1,0)$	$\eta \left((\neg p_1,e_1,0)\right)\left(z_1\right)$	$\eta \left((\neg p_1,e_1,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_1,e_1,0)\right)\left(z_n\right)$
$(\neg p_1,e_2,0)$	$\eta \left((\neg p_1,e_2,0)\right)\left(z_1\right)$	$\eta \left((\neg p_1,e_2,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_1,e_2,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_1,e_t,0)$	$\eta \left((\neg p_1,e_t,0)\right)\left(z_1\right)$	$\eta \left((\neg p_1,e_t,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_1,e_t,0)\right)\left(z_n\right)$
$(\neg p_2,e_1,0)$	$\eta \left((\neg p_2,e_1,0)\right)\left(z_1\right)$	$\eta \left((\neg p_2,e_1,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_2,e_1,0)\right)\left(z_n\right)$
$(\neg p_2,e_2,0)$	$\eta \left((\neg p_2,e_2,0)\right)\left(z_1\right)$	$\eta \left((\neg p_2,e_2,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_2,e_2,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_2,e_t,0)$	$\eta \left((\neg p_2,e_t,0)\right)\left(z_1\right)$	$\eta \left((\neg p_2,e_t,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_2,e_t,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_m,e_1,0)$	$\eta \left((\neg p_m,e_1,0)\right)\left(z_1\right)$	$\eta \left((\neg p_m,e_1,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_m,e_1,0)\right)\left(z_n\right)$
$(\neg p_m,e_2,0)$	$\eta \left((\neg p_m,e_2,0)\right)\left(z_1\right)$	$\eta \left((\neg p_m,e_2,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_m,e_2,0)\right)\left(z_n\right)$
⋮	⋮	⋮	⋱	⋮
$(\neg p_m,e_t,0)$	$\eta \left((\neg p_m,e_t,0)\right)\left(z_1\right)$	$\eta \left((\neg p_m,e_t,0)\right)\left(z_2\right)$	⋯	$\eta \left((\neg p_m,e_t,0)\right)\left(z_n\right)$

.

Remark 1.

In the framework of N-BSE sets, logical consistency must be maintained in the evaluation of attributes by experts:

1. 

It is inconsistent for an expert e to evaluate an attribute p with high degrees of agreement (disagreement) and simultaneously evaluate its opposite attribute $\neg p$ with high degrees of agreement (disagreement) for the same alternative z. Specifically, the evaluations must satisfy

$$\gamma \left(\right(p,e,o\left)\right)\left(z\right)+\eta \left(\right(\neg p,e,o\left)\right)\left(z\right)\le N-1,$$

for any $o\in \mathbb{O}$.

2. 

It is not logical for an expert e to assign high degrees of agreement and disagreement simultaneously to the same attribute p for the same alternative z. The evaluations must satisfy

$$\gamma \left((p,e,o_1)\right)\left(z\right)+\gamma \left((p,e,o_2)\right)\left(z\right)\le N-1,$$

where $o_1\ne o_2$ and $o_1,o_2\in \mathbb{O}$. This also applies to $\neg p$.

To gain a deeper understanding of the core features of our new model, we will examine the following example.

Example 1.

Suppose a medical research institute is tasked with selecting the most appropriate treatment protocol for a specific disease from five available options: $\mathcal{Z}=\{z_1,z_2,z_3,z_4,z_5\}$. The institute forms a committee of experienced employees to create a detailed report assessing the treatment options based on several parameters: $\mathbb{P}=\{p_1=\mathit{efficacy},p_2=\mathit{tolerability},p_3=\mathit{cost}\}$, along with their corresponding negative attributes: $\neg \mathbb{P}=\{\neg p_1=\mathit{inefficiency},\neg p_2=\mathit{adverse}\mathit{effects},\neg p_3=\mathit{high}\mathit{cost}\}$. To ensure a well-rounded decision, the institute shares the report with three medical experts $\mathbb{E}=\{e_1,e_2,e_3\}$, who specialize in the disease, and considers their opinions $\mathbb{O}=\{0=\mathit{disagree},1=\mathit{agree}\}$ as shown in

Table 2. Data overview.

$\mathit{A}\setminus \mathcal{Z}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	$★★★★$	$★★$	$★★★★$	★	∘
$(p_1,e_2,1)$	★	$★★$	$★★$	$★★★$	∘
$(p_1,e_3,1)$	$★★$	$★★$	$★★$	$★★★$	★
$(p_2,e_1,1)$	$★★$	$★★$	$★★★$	★	∘
$(p_2,e_2,1)$	$★★★$	$★★$	$★★$	$★★$	∘
$(p_2,e_3,1)$	∘	★	$★★★★$	$★★$	$★★$
$(p_3,e_1,1)$	$★★★$	$★★★$	$★★$	$★★$	$★★$
$(p_3,e_2,1)$	★	∘	$★★★$	∘	$★★★$
$(p_3,e_3,1)$	$★★★$	$★★★$	$★★$	★	★
$(p_1,e_1,0)$	∘	$★★$	∘	∘	★
$(p_1,e_2,0)$	★	$★★$	$★★$	∘	$★★$
$(p_1,e_3,0)$	∘	★	$★★$	★	★
$(p_2,e_1,0)$	★	∘	∘	$★★$	$★★$
$(p_2,e_2,0)$	★	$★★$	★	★	∘
$(p_2,e_3,0)$	$★★★$	$★★$	∘	$★★$	$★★$
$(p_3,e_1,0)$	★	★	★	★	★
$(p_3,e_2,0)$	$★★★$	$★★★★$	★	$★★$	∘
$(p_3,e_3,0)$	∘	∘	$★★$	$★★$	$★★$
$(\neg p_1,e_1,1)$	∘	$★★$	∘	$★★$	∘
$(\neg p_1,e_2,1)$	$★★$	$★★$	★	∘	∘
$(\neg p_1,e_3,1)$	★	★	$★★$	∘	∘
$(\neg p_2,e_1,1)$	∘	★	∘	$★★$	∘
$(\neg p_2,e_2,1)$	★	$★★$	∘	$★★$	∘
$(\neg p_2,e_3,1)$	∘	∘	∘	$★★$	★
$(\neg p_3,e_1,1)$	★	★	★	★	★
$(\neg p_3,e_2,1)$	$★★$	∘	★	∘	★
$(\neg p_3,e_3,1)$	★	★	$★★$	$★★$	$★★$
$(\neg p_1,e_1,0)$	$★★$	★	∘	∘	$★★$
$(\neg p_1,e_2,0)$	∘	★	★	$★★★$	★
$(\neg p_1,e_3,0)$	$★★★$	$★★$	★	$★★$	$★★$
$(\neg p_2,e_1,0)$	$★★$	∘	$★★★$	★	★
$(\neg p_2,e_2,0)$	$★★★$	★	$★★★$	★	$★★★★$
$(\neg p_2,e_3,0)$	★	$★★$	★	★	★
$(\neg p_3,e_1,0)$	$★★$	$★★$	∘	$★★$	∘
$(\neg p_3,e_2,0)$	★	∘	$★★$	★	∘
$(\neg p_3,e_3,0)$	∘	$★★★$	★	★	$★★$

, where

• One circle “∘” represents poor performance.
• One star “★” represents slightly poor performance.
• Two stars “$★★$” represent moderate performance.
• Three stars “$★★★$” represent good performance.
• Four stars “$★★★★$” represent excellent performance.

This graded evaluation using symbols can be easily mapped to numerical values, such as $G=\{0,1,2,3,4\}$, where

• 0 corresponds to ∘;
• 1 corresponds to ★;
• 2 corresponds to $★★$;
• 3 corresponds to $★★★$;
• 4 corresponds to $★★★★$.

Therefore, the 5-BSES set $(\gamma ,\eta ,A,5)$ can be derived from Table 2 and represented in tabular form, as shown in

Table 3. Tabular representation of the 5-BSE set $(\gamma ,\eta ,A,5)$.

$(\mathit{\gamma },\mathit{\eta },\mathit{A},5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	4	2	4	1	0
$(p_1,e_2,1)$	1	2	2	3	0
$(p_1,e_3,1)$	2	2	2	3	1
$(p_2,e_1,1)$	2	2	3	1	0
$(p_2,e_2,1)$	3	2	2	2	0
$(p_2,e_3,1)$	0	1	4	2	2
$(p_3,e_1,1)$	3	3	2	2	2
$(p_3,e_2,1)$	1	0	3	0	3
$(p_3,e_3,1)$	3	3	2	1	1
$(p_1,e_1,0)$	0	2	0	0	1
$(p_1,e_2,0)$	1	2	2	0	2
$(p_1,e_3,0)$	0	1	2	1	1
$(p_2,e_1,0)$	1	0	0	2	2
$(p_2,e_2,0)$	1	2	1	1	0
$(p_2,e_3,0)$	3	2	0	2	2
$(p_3,e_1,0)$	1	1	1	1	1
$(p_3,e_2,0)$	3	4	1	2	0
$(p_3,e_3,0)$	0	0	2	2	2
$(\neg p_1,e_1,1)$	0	2	0	2	0
$(\neg p_1,e_2,1)$	2	2	1	0	0
$(\neg p_1,e_3,1)$	1	1	2	0	0
$(\neg p_2,e_1,1)$	0	1	0	2	0
$(\neg p_2,e_2,1)$	1	2	0	2	0
$(\neg p_2,e_3,1)$	0	0	0	2	1
$(\neg p_3,e_1,1)$	1	1	1	1	1
$(\neg p_3,e_2,1)$	2	0	1	0	1
$(\neg p_3,e_3,1)$	1	1	2	2	2
$(\neg p_1,e_1,0)$	2	1	0	0	2
$(\neg p_1,e_2,0)$	0	1	1	3	1
$(\neg p_1,e_3,0)$	3	2	1	2	2
$(\neg p_2,e_1,0)$	2	0	3	1	1
$(\neg p_2,e_2,0)$	3	1	3	1	4
$(\neg p_2,e_3,0)$	1	2	1	1	1
$(\neg p_3,e_1,0)$	2	2	0	2	0
$(\neg p_3,e_2,0)$	1	0	2	1	0
$(\neg p_3,e_3,0)$	0	3	1	1	2

.

Notice that expert $e_1$ agrees that treatment $z_1$ has excellent performance with respect to attribute efficacy $p_1$, i.e., $\gamma \left((p_1,e_1,1)\right)\left(z_1\right)=4$, while expert $e_1$ disagrees that treatment $z_1$ has poor performance with respect to attribute efficacy $p_1$, i.e., $\gamma \left((p_1,e_1,0)\right)\left(z_1\right)=0$. On the other hand, expert $e_1$ agrees that treatment $z_1$ has poor performance with respect to the corresponding negative attribute inefficiency $\neg p_1$, i.e., $\eta \left((\neg p_1,e_1,1)\right)\left(z_1\right)=0$, while expert $e_1$ disagrees that treatment $z_1$ has moderate performance with respect to negative attribute inefficiency $\neg p_1$, i.e., $\eta \left((\neg p_1,e_1,0)\right)\left(z_1\right)=2$, and so on.

We now present some fundamental operations on N-BSE sets, along with illustrative examples. These operations include the null set, the whole set, subset, equality, agreement and disagreement, complement, union, intersection, OR, and AND. Following this, we will discuss the algebraic properties of these operations.

Definition 10.

An N-BSE set $({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A,N)$ is called a relative null N-BSE set if, for every $a\in A$ and $z\in \mathcal{Z}$, ${\gamma }^{\mathbb{O}}\left(a\right)\left(z\right)=0$, and for every $\neg a\in \neg A$ and $z\in \mathcal{Z}$, ${\eta }^{\mathbb{O}}(\neg a)\left(z\right)=N-1$.

Definition 11.

An N-BSE set $({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A,N)$ is referred to as a relative whole N-BSE set if, for all $a\in A$ and $z\in \mathcal{Z}$, ${\gamma }^{\mathbb{W}}\left(a\right)\left(z\right)=N-1$, and for all $\neg a\in \neg A$ and $z\in \mathcal{Z}$, ${\eta }^{\mathbb{W}}(\neg a)\left(z\right)=0$.

Definition 12.

An N-BSE set $({\gamma }^1,{\eta }^1,A^1,N)$ is considered a subset of $({\gamma }^2,{\eta }^2,A^2,N)$, denoted as $({\gamma }^1,{\eta }^1,A^1,N)$ $\widetilde{⊑}$ $({\gamma }^2,{\eta }^2,A^2,N)$, if the following conditions are satisfied:

1. 

$A^1\subseteq A^2$.

2. 

For every $a\in A^1$ and $z\in \mathcal{Z}$, ${\gamma }^1\left(a\right)\left(z\right)\le {\gamma }^2\left(a\right)\left(z\right)$ and for every $\neg a\in \neg A^1$ and $z\in \mathcal{Z}$, ${\eta }^2(\neg a)\left(z\right)\le {\eta }^1(\neg a)\left(z\right)$.

Example 2.

Consider Example 1. Let $({\gamma }^1,{\eta }^1,A^1,5)$ and $({\gamma }^2,{\eta }^2,A^2,5)$ be two 5-BSE sets represented in tabular form in

Table 4. Tabular representation of the 5-BSE set $({\gamma }^1,{\eta }^1,A^1,5)$ in Example 2.

$({\mathit{\gamma }}^1,{\mathit{\eta }}^1,{\mathit{A}}^1,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	2	1	0	3	0
$(p_1,e_2,1)$	2	2	0	1	0
$(p_2,e_2,1)$	1	0	3	0	3
$(p_2,e_3,1)$	3	3	2	1	1
$(p_1,e_3,0)$	0	1	2	1	1
$(p_3,e_1,0)$	3	3	2	2	1
$(\neg p_1,e_1,1)$	1	1	2	0	1
$(\neg p_1,e_2,1)$	2	2	4	1	3
$(\neg p_2,e_2,1)$	3	4	1	4	0
$(\neg p_2,e_3,1)$	1	1	2	2	2
$(\neg p_1,e_3,0)$	0	0	1	3	3
$(\neg p_3,e_1,0)$	0	1	2	2	3

and

Table 5. Tabular representation of the 5-BSE set $({\gamma }^2,{\eta }^2,A^2,5)$ in Example 2.

$({\mathit{\gamma }}^2,{\mathit{\eta }}^2,{\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	3	2	0	3	0
$(p_1,e_2,1)$	2	2	0	3	0
$(p_1,e_3,1)$	2	0	1	1	3
$(p_2,e_2,1)$	1	0	3	0	4
$(p_2,e_3,1)$	4	3	2	2	1
$(p_1,e_3,0)$	2	3	3	1	1
$(p_3,e_1,0)$	4	3	2	2	1
$(\neg p_1,e_1,1)$	0	0	1	0	0
$(\neg p_1,e_2,1)$	1	2	0	0	2
$(\neg p_1,e_3,1)$	2	1	1	3	0
$(\neg p_2,e_2,1)$	1	4	0	4	0
$(\neg p_2,e_3,1)$	0	1	2	2	1
$(\neg p_1,e_3,0)$	0	0	1	0	2
$(\neg p_3,e_1,0)$	0	0	2	1	3

, respectively. It is evident that $({\gamma }^1,{\eta }^1,A^1,5)$ $\widetilde{⊑}$ $({\gamma }^2,{\eta }^2,A^2,5)$.

Definition 13.

Two N-BSE sets $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$ are said to be equal if both $({\gamma }^1,{\eta }^1,A^1,N)$ $\widetilde{⊑}$ $({\gamma }^2,{\eta }^2,A^2,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$ $\widetilde{⊑}$ $({\gamma }^1,{\eta }^1,A^1,N)$ hold true.

Definition 14.

Let $(\gamma ,\eta ,A,N)$ be an N-BSE set. The positive agree N-BSE set, denoted by ${(\gamma ,\eta ,A,N)}_1^{+}$, is an N-BSE subset of $(\gamma ,\eta ,A,N)$, defined as

$${(\gamma ,\eta ,A,N)}_1^{+}=\{{\gamma }_1^{+}\left(a\right)\mid a\in \mathbb{P}\times \mathbb{E}\times \left\{1\right\}\}.$$

Definition 15.

Let $(\gamma ,\eta ,A,N)$ be an N-BSE set. The positive disagree N-BSE set, denoted by ${(\gamma ,\eta ,A,N)}_0^{+}$, is an N-BSE subset of $(\gamma ,\eta ,A,N)$ defined as

$${(\gamma ,\eta ,A,N)}_0^{+}=\{{\gamma }_0^{+}\left(a\right)\mid a\in \mathbb{P}\times \mathbb{E}\times \left\{0\right\}\}.$$

Definition 16.

Let $(\gamma ,\eta ,A,N)$ be an N-BSE set. The negative agree N-BSE set, denoted by ${(\gamma ,\eta ,A,N)}_1^{-}$, is an N-BSE subset of $(\gamma ,\eta ,A,N)$ defined as

$${(\gamma ,\eta ,A,N)}_1^{-}=\{{\eta }_1^{-}(\neg a)\mid \neg a\in \mathbb{P}\times \mathbb{E}\times \left\{1\right\}\}.$$

Definition 17.

Let $(\gamma ,\eta ,A,N)$ be an N-BSE set. The negative disagree N-BSE set, denoted by ${(\gamma ,\eta ,A,N)}_0^{-}$, is an N-BSE subset of $(\gamma ,\eta ,A,N)$ defined as

$${(\gamma ,\eta ,A,N)}_0^{-}=\{{\eta }_0^{-}(\neg a)\mid \neg a\in \mathbb{P}\times \mathbb{E}\times \left\{0\right\}\}.$$

Example 3.

Consider the N-BSE set $(\gamma ,\eta ,A,N)$ provided in Table 3 of Example 1. Its positive agree, positive disagree, negative agree, and negative disagree N-BSE subsets are shown in

Table 6. Positive agree 5-BSE set ${(\gamma ,\eta ,A,5)}_1^{+}$ derived from the 5-BSE set $(\gamma ,\eta ,A,5)$ in Example 3.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_1^{+}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	4	2	4	1	0
$(p_1,e_2,1)$	1	2	2	3	0
$(p_1,e_3,1)$	2	2	2	3	1
$(p_2,e_1,1)$	2	2	3	1	0
$(p_2,e_2,1)$	3	2	2	2	0
$(p_2,e_3,1)$	0	1	4	2	2
$(p_3,e_1,1)$	3	3	2	2	2
$(p_3,e_2,1)$	1	0	3	0	3
$(p_3,e_3,1)$	3	3	2	1	1

,

Table 7. Positive disagree 5-BSE set ${(\gamma ,\eta ,A,5)}_0^{+}$ derived from the 5-BSE set $(\gamma ,\eta ,A,5)$ in Example 3.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_0^{+}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,0)$	0	2	0	0	1
$(p_1,e_2,0)$	1	2	2	0	2
$(p_1,e_3,0)$	0	1	2	1	1
$(p_2,e_1,0)$	1	0	0	2	2
$(p_2,e_2,0)$	1	2	1	1	0
$(p_2,e_3,0)$	3	2	0	2	2
$(p_3,e_1,0)$	1	1	1	1	1
$(p_3,e_2,0)$	3	4	1	2	0
$(p_3,e_3,0)$	0	0	2	2	2

,

Table 8. Negative agree 5-BSE set ${(\gamma ,\eta ,A,5)}_1^{-}$ derived from the 5-BSE set $(\gamma ,\eta ,A,5)$ in Example 3.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_1^{-}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(\neg p_1,e_1,1)$	0	2	0	2	0
$(\neg p_1,e_2,1)$	2	2	1	0	0
$(\neg p_1,e_3,1)$	1	1	2	0	0
$(\neg p_2,e_1,1)$	0	1	0	2	0
$(\neg p_2,e_2,1)$	1	2	0	2	0
$(\neg p_2,e_3,1)$	0	0	0	2	1
$(\neg p_3,e_1,1)$	1	1	1	1	1
$(\neg p_3,e_2,1)$	2	0	1	0	1
$(\neg p_3,e_3,1)$	1	1	2	2	2

and

Table 9. Negative disagree 5-BSE set ${(\gamma ,\eta ,A,5)}_0^{-}$ derived from the 5-BSE set $(\gamma ,\eta ,A,5)$ in Example 3.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_0^{-}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(\neg p_1,e_1,0)$	2	1	0	0	2
$(\neg p_1,e_2,0)$	0	1	1	3	1
$(\neg p_1,e_3,0)$	3	2	1	2	2
$(\neg p_2,e_1,0)$	2	0	3	1	1
$(\neg p_2,e_2,0)$	3	1	3	1	4
$(\neg p_2,e_3,0)$	1	2	1	1	1
$(\neg p_3,e_1,0)$	2	2	0	2	0
$(\neg p_3,e_2,0)$	1	0	2	1	0
$(\neg p_3,e_3,0)$	0	3	1	1	2

.

Definition 18.

The N-BSE complement of $(\gamma ,\eta ,A,N)$, denoted by ${(\gamma ,\eta ,A,N)}^{\tilde{c}}$, is defined as ${(\gamma ,\eta ,A,N)}^{\tilde{c}}=({\gamma }^{\tilde{c}},{\eta }^{\tilde{c}},A,N)$, such that for all $a\in A$, $\neg a\in \neg A$, and for all $z\in \mathcal{Z}$, we have ${\gamma }^{\tilde{c}}\left(a\right)\left(z\right)=\eta (\neg a)\left(z\right)$ and ${\eta }^{\tilde{c}}(\neg a)\left(z\right)=\gamma \left(a\right)\left(z\right)$.

Example 4.

Consider the 5-BSE set $({\gamma }^1,{\eta }^1,A^1,5)$ presented in Table 4 of Example 2. Its 5-BSE complement, ${({\gamma }^1,{\eta }^1,A^1,5)}^{\tilde{c}}$, is shown in

Table 10. The 5-BSE complement ${({\gamma }^1,{\eta }^1,A^1,5)}^{\tilde{c}}$ of the 5-BSE set $({\gamma }^1,{\eta }^1,A^1,5)$ in Example 4.

${({\mathit{\gamma }}^1,{\mathit{\eta }}^1,{\mathit{A}}^1,5)}^{\tilde{\mathit{c}}}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	1	1	2	0	1
$(p_1,e_2,1)$	2	2	4	1	3
$(p_1,e_3,0)$	0	0	1	3	3
$(p_3,e_1,0)$	0	1	2	2	3
$(p_3,e_2,1)$	3	4	1	4	0
$(p_3,e_3,1)$	1	1	2	2	2
$(\neg p_1,e_1,1)$	2	1	0	3	0
$(\neg p_1,e_2,1)$	2	2	0	1	0
$(\neg p_1,e_3,0)$	0	1	2	1	1
$(\neg p_3,e_1,0)$	3	3	2	2	1
$(\neg p_3,e_2,1)$	1	0	3	0	3
$(\neg p_3,e_3,1)$	3	3	2	1	1

.

Definition 19.

The N-BSE extended union of $({\gamma }^1,{\eta }^1,A^1,N^1)$ and $({\gamma }^2,{\eta }^2,A^2,N^2)$ is denoted and defined as $({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N^2)$ = $(\gamma ,\eta ,A^1\cup A^2,max(N^1,N^2))$, where for all $a\in A^1\cup A^2$ and $z\in \mathcal{Z}$,

$$\gamma \left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^1\left(a\right)\left(z\right),\hfill & \mathit{if}a\in A^1\setminus A^2\hfill \\ {\gamma }^2\left(a\right)\left(z\right),\hfill & \mathit{if}a\in A^2\setminus A^1\hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},\hfill & \mathit{if}a\in A^1\cap A^2\hfill \end{array}\right.$$

and for all $\neg a\in \neg A^1\cup \neg A^2$ and $z\in \mathcal{Z}$,

$$\eta (\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^1(\neg a)\left(z\right),\hfill & \mathit{if}\neg a\in \neg A^1\setminus \neg A^2\hfill \\ {\eta }^2(\neg a)\left(z\right),\hfill & \mathit{if}\neg a\in \neg A^2\setminus \neg A^1\hfill \\ min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},\hfill & \mathit{if}\neg a\in \neg A^1\cap \neg A^2.\hfill \end{array}\right.$$

Definition 20.

The N-BSE extended intersection of $({\gamma }^1,{\eta }^1,A^1,N^1)$ and $({\gamma }^2,{\eta }^2,A^2,N^2)$ is denoted and defined as $({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N^2)$ = $(\gamma ,\eta ,A^1\cup A^2,max(N^1,N^2))$, where for all $a\in A^1\cup A^2$ and $z\in \mathcal{Z}$,

$$\gamma \left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^1\left(a\right)\left(z\right),\hfill & \mathit{if}a\in A^1\setminus A^2\hfill \\ {\gamma }^2\left(a\right)\left(z\right),\hfill & \mathit{if}a\in A^2\setminus A^1\hfill \\ min\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},\hfill & \mathit{if}a\in A^2\cap A^1\hfill \end{array}\right.$$

and for all $\neg a\in \neg A^1\cup \neg A^2$ and $z\in \mathcal{Z}$,

$$\eta (\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^1(\neg a)\left(z\right),\hfill & \mathit{if}\neg a\in \neg A^1\setminus \neg A^2\hfill \\ {\eta }^2(\neg a)\left(z\right),\hfill & \mathit{if}\neg a\in \neg A^2\setminus \neg A^1\hfill \\ max\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},\hfill & \mathit{if}\neg a\in \neg A^1\cap \neg A^2.\hfill \end{array}\right.$$

Definition 21.

The N-BSE restricted union of $({\gamma }^1,{\eta }^1,A^1,N^1)$ and $({\gamma }^2,{\eta }^2,A^2,N^2)$ is denoted and defined as $({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N^2)$ = $(\gamma ,\eta ,A^1\cap A^2,max(N^1,N^2))$, where for all $a\in A^1\cap A^2\ne \varnothing$ and $z\in \mathcal{Z}$,

$$\gamma \left(a\right)\left(z\right)=max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},$$

and for all $\neg a\in \neg A^1\cap \neg A^2\ne \varnothing$ and $z\in \mathcal{Z}$,

$$\eta (\neg a)\left(z\right)=min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\}.$$

Definition 22.

The N-BSE restricted intersection of $({\gamma }^1,{\eta }^1,A^1,N^1)$ and $({\gamma }^2,{\eta }^2,A^2,N^2)$ is denoted and defined as $({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N^2)$ = $(\gamma ,\eta ,A^1\cap A^2,max(N^1,N^2))$, where for all $a\in A^1\cap A^2\ne \varnothing$ and $z\in \mathcal{Z}$,

$$\gamma \left(a\right)\left(z\right)=min\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},$$

and for all $\neg a\in \neg A^1\cap \neg A^2\ne \varnothing$ and $z\in \mathcal{Z}$,

$$\eta (\neg a)\left(z\right)=max\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\}.$$

Example 5.

Reconsider Example 1. Let $({\gamma }^1,{\eta }^1,A^1,5)$ and $({\gamma }^2,{\eta }^2,A^2,5)$ be two 5-BSE sets presented in

Table 11. Tabular representation of the 5-BSE set $({\gamma }^1,{\eta }^1,A^1,5)$ in Example 5.

$({\mathit{\gamma }}^1,{\mathit{\eta }}^1,{\mathit{A}}^1,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	3	2	4	0	4
$(p_1,e_2,1)$	2	1	3	4	0
$(p_2,e_1,0)$	2	0	2	0	1
$(p_3,e_3,0)$	2	2	2	3	3
$(\neg p_1,e_1,1)$	0	2	0	1	0
$(\neg p_1,e_2,1)$	1	3	1	0	4
$(\neg p_2,e_1,0)$	2	0	1	4	3
$(\neg p_3,e_3,0)$	1	1	1	0	0

and

Table 12. Tabular representation of the 5-BSE set $({\gamma }^2,{\eta }^2,A^2,5)$ in Example 5.

$({\mathit{\gamma }}^2,{\mathit{\eta }}^2,{\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	0	1	3	1	2
$(p_1,e_3,1)$	1	2	1	3	3
$(p_2,e_2,0)$	0	1	1	3	0
$(p_3,e_3,0)$	3	1	0	0	4
$(\neg p_1,e_1,1)$	2	2	1	2	0
$(\neg p_1,e_3,1)$	3	2	3	0	1
$(\neg p_2,e_2,0)$	2	3	2	0	3
$(\neg p_3,e_3,0)$	1	3	2	2	0

, respectively. The results of the 5-BSE extended union and intersection, as well as the 5-BSE restricted union and intersection, are detailed in

Table 13. The 5-BSE extended union $({\gamma }^1,{\eta }^1,A^1,5)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,5)$ = $({\gamma }^3,{\eta }^3,A^1\cup A^2,5)$ in Example 5.

$({\mathit{\gamma }}^3,{\mathit{\eta }}^3,{\mathit{A}}^1\cup {\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	3	2	4	1	4
$(p_1,e_2,1)$	2	1	3	4	0
$(p_1,e_3,1)$	1	2	1	3	3
$(p_2,e_1,0)$	2	0	2	0	1
$(p_2,e_2,0)$	0	1	1	3	0
$(p_3,e_3,0)$	3	2	2	3	4
$(\neg p_1,e_1,1)$	0	2	0	1	0
$(\neg p_1,e_2,1)$	1	3	1	0	4
$(\neg p_1,e_3,1)$	3	2	3	0	1
$(\neg p_2,e_1,0)$	2	0	1	4	3
$(\neg p_2,e_2,0)$	2	3	2	0	3
$(\neg p_3,e_3,0)$	1	1	1	0	0

,

Table 14. The 5-BSE extended intersection $({\gamma }^1,{\eta }^1,A^1,5)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,5)$ = $({\gamma }^4,{\eta }^4,A^1\cup A^2,5)$ in Example 5.

$({\mathit{\gamma }}^4,{\mathit{\eta }}^4,{\mathit{A}}^1\cup {\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	0	1	3	0	2
$(p_1,e_2,1)$	2	1	3	4	0
$(p_1,e_3,1)$	1	2	1	3	3
$(p_2,e_1,0)$	2	0	2	0	1
$(p_2,e_2,0)$	0	1	1	3	0
$(p_3,e_3,0)$	2	1	0	0	3
$(\neg p_1,e_1,1)$	2	2	1	2	0
$(\neg p_1,e_2,1)$	1	3	1	0	4
$(\neg p_1,e_3,1)$	3	2	3	0	1
$(\neg p_2,e_1,0)$	2	0	1	4	3
$(\neg p_2,e_2,0)$	2	3	2	0	3
$(\neg p_3,e_3,0)$	1	3	2	2	0

,

Table 15. The 5-BSE restricted union $({\gamma }^1,{\eta }^1,A^1,5)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,5)$ = $({\gamma }^5,{\eta }^5,A^1\cap A^2,5)$ in Example 5.

$({\mathit{\gamma }}^5,{\mathit{\eta }}^5,{\mathit{A}}^1\cap {\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	3	2	4	1	4
$(p_3,e_3,0)$	3	2	2	3	4
$(\neg p_1,e_1,1)$	0	2	0	1	0
$(\neg p_3,e_3,0)$	1	1	1	0	0

and

Table 16. The 5-BSE restricted intersection $({\gamma }^1,{\eta }^1,A^1,5)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,5)$ = $({\gamma }^6,{\eta }^6,A^1\cap A^2,5)$ in Example 5.

$({\mathit{\gamma }}^6,{\mathit{\eta }}^6,{\mathit{A}}^1\cap {\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$(p_1,e_1,1)$	0	1	3	0	2
$(p_3,e_3,0)$	2	1	0	0	3
$(\neg p_1,e_1,1)$	2	2	1	2	0
$(\neg p_3,e_3,0)$	1	3	2	2	0

.

Definition 23.

The OR-operation between two N-BSE sets $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$ is denoted and defined as $({\gamma }^1,{\eta }^1,A^1,N)\tilde{\vee }({\gamma }^2,{\eta }^2,A^2,N)=(\gamma ,\eta ,A^1\times A^2,N)$, where, for all $(a_1,a_2)\in A^1\times A^2$, $a_1\in A^1$, $a_2\in A^2$, and $z\in \mathcal{Z}$,

$$\gamma (a_1,a_2)\left(z\right)=max\{{\gamma }^1\left(a_1\right)\left(z\right),{\gamma }^2\left(a_2\right)\left(z\right)\},$$

and for all $(\neg a_1,\neg a_2)\in \neg A^1\times \neg A^2$, $\neg a_1\in \neg A^1$, $\neg a_2\in \neg A^2$, and $z\in \mathcal{Z}$,

$$\eta (\neg a_1,\neg a_2)\left(z\right)=min\{{\eta }^1(\neg a_1)\left(z\right),{\eta }^2(\neg a_2)\left(z\right)\}.$$

Definition 24.

The AND-operation between two N-BSE sets $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$ is denoted and defined as $({\gamma }^1,{\eta }^1,A^1,N)\tilde{\wedge }({\gamma }^2,{\eta }^2,A^2,N)=(\gamma ,\eta ,A^1\times A^2,N)$, where, for all $(a_1,a_2)\in A^1\times A^2$, $a_1\in A^1$, $a_2\in A^2$, and $z\in \mathcal{Z}$,

$$\gamma (a_1,a_2)\left(z\right)=min\{{\gamma }^1\left(a_1\right)\left(z\right),{\gamma }^2\left(a_2\right)\left(z\right)\},$$

and for all $(\neg a_1,\neg a_2)\in \neg A^1\times \neg A^2$, $\neg a_1\in \neg A^1$, $\neg a_2\in \neg A^2$, and $z\in \mathcal{Z}$,

$$\eta (\neg a_1,\neg a_2)\left(z\right)=max\{{\eta }^1(\neg a_1)\left(z\right),{\eta }^2(\neg a_2)\left(z\right)\}.$$

Example 6.

Consider two 5-BSE sets, $({\gamma }^1,{\eta }^1,A^1,5)$ and $({\gamma }^2,{\eta }^2,A^2,5)$, as presented in Table 11 and Table 12, respectively, in Example 5. The results of the OR-operation and AND-operation are shown in

Table 17. The OR-operation $({\gamma }^1,{\eta }^1,A^1,5)$ $\tilde{\vee }$ $({\gamma }^2,{\eta }^2,A^2,5)$ = $({\gamma }^3,{\eta }^3,A^1\times A^2,5)$ in Example 6.

$({\mathit{\gamma }}^3,{\mathit{\eta }}^3,{\mathit{A}}^1\times {\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$((p_1,e_1,1),(p_1,e_1,1))$	3	2	4	1	4
$((p_1,e_1,1),(p_1,e_3,1))$	3	2	4	3	4
$((p_1,e_1,1),(p_2,e_2,0))$	3	2	4	3	4
$((p_1,e_1,1),(p_3,e_3,0))$	3	2	4	0	4
$((p_1,e_2,1),(p_1,e_1,1))$	2	1	3	4	2
$((p_1,e_2,1),(p_1,e_3,1))$	2	2	3	4	3
$((p_1,e_2,1),(p_2,e_2,0))$	2	1	3	4	0
$((p_1,e_2,1),(p_3,e_3,0))$	3	1	3	4	4
$((p_2,e_1,0),(p_1,e_1,1))$	2	1	3	1	2
$((p_2,e_1,0),(p_1,e_3,1))$	2	2	2	3	3
$((p_2,e_1,0),(p_2,e_2,0))$	2	1	2	3	1
$((p_2,e_1,0),(p_3,e_3,0))$	3	1	2	0	4
$((p_3,e_3,0),(p_1,e_1,1))$	2	2	3	3	3
$((p_3,e_3,0),(p_1,e_3,1))$	2	2	2	3	3
$((p_3,e_3,0),(p_2,e_2,0))$	2	2	2	3	3
$((p_3,e_3,0),(p_3,e_3,0))$	3	2	2	3	4
$((\neg p_1,e_1,1),(\neg p_1,e_1,1))$	0	2	0	1	0
$((\neg p_1,e_1,1),(\neg p_1,e_3,1))$	0	2	0	0	0
$((\neg p_1,e_1,1),(\neg p_2,e_2,0))$	0	2	0	1	0
$((\neg p_1,e_1,1),(\neg p_3,e_3,0))$	0	2	0	1	0
$((\neg p_1,e_2,1),(\neg p_1,e_1,1))$	1	2	1	0	0
$((\neg p_1,e_2,1),(\neg p_1,e_3,1))$	1	2	1	0	1
$((\neg p_1,e_2,1),(\neg p_2,e_2,0))$	1	3	0	1	3
$((\neg p_1,e_2,1),(\neg p_3,e_3,0))$	1	3	1	0	0
$((\neg p_2,e_1,0),(\neg p_1,e_1,1))$	2	0	1	2	0
$((\neg p_2,e_1,0),(\neg p_1,e_3,1))$	2	0	1	0	1
$((\neg p_2,e_1,0),(\neg p_2,e_2,0))$	2	0	1	0	3
$((\neg p_2,e_1,0),(\neg p_3,e_3,0))$	1	0	1	2	0
$((\neg p_3,e_3,0),(\neg p_1,e_1,1))$	1	1	1	0	0
$((\neg p_3,e_3,0),(\neg p_1,e_3,1))$	1	1	1	0	0
$((\neg p_3,e_3,0),(\neg p_2,e_2,0))$	1	1	1	0	0
$((\neg p_3,e_3,0),(\neg p_3,e_3,0))$	1	1	1	0	0

and

Table 18. The AND-operation $({\gamma }^1,{\eta }^1,A^1,5)$ $\tilde{\wedge }$ $({\gamma }^2,{\eta }^2,A^2,5)$ = $({\gamma }^4,{\eta }^4,A^1\times A^2,5)$ in Example 6.

$({\mathit{\gamma }}^4,{\mathit{\eta }}^4,{\mathit{A}}^1\times {\mathit{A}}^2,5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$
$((p_1,e_1,1),(p_1,e_1,1))$	0	1	3	0	2
$((p_1,e_1,1),(p_1,e_3,1))$	1	2	1	0	3
$((p_1,e_1,1),(p_2,e_2,0))$	0	1	1	0	0
$((p_1,e_1,1),(p_3,e_3,0))$	3	1	0	0	4
$((p_1,e_2,1),(p_1,e_1,1))$	0	1	3	1	0
$((p_1,e_2,1),(p_1,e_3,1))$	1	1	1	3	0
$((p_1,e_2,1),(p_2,e_2,0))$	0	1	1	3	0
$((p_1,e_2,1),(p_3,e_3,0))$	2	1	0	0	0
$((p_2,e_1,0),(p_1,e_1,1))$	0	0	2	0	1
$((p_2,e_1,0),(p_1,e_3,1))$	1	0	1	0	1
$((p_2,e_1,0),(p_2,e_2,0))$	0	0	1	0	0
$((p_2,e_1,0),(p_3,e_3,0))$	2	0	0	0	1
$((p_3,e_3,0),(p_1,e_1,1))$	0	1	2	1	2
$((p_3,e_3,0),(p_1,e_3,1))$	1	2	1	3	3
$((p_3,e_3,0),(p_2,e_2,0))$	0	1	1	3	0
$((p_3,e_3,0),(p_3,e_3,0))$	2	1	0	0	3
$((\neg p_1,e_1,1),(\neg p_1,e_1,1))$	2	2	1	2	0
$((\neg p_1,e_1,1),(\neg p_1,e_3,1))$	3	2	3	2	1
$((\neg p_1,e_1,1),(\neg p_2,e_2,0))$	2	3	2	1	3
$((\neg p_1,e_1,1),(\neg p_3,e_3,0))$	1	3	2	2	0
$((\neg p_1,e_2,1),(\neg p_1,e_1,1))$	2	3	1	2	4
$((\neg p_1,e_2,1),(\neg p_1,e_3,1))$	3	3	3	0	4
$((\neg p_1,e_2,1),(\neg p_2,e_2,0))$	2	3	2	0	4
$((\neg p_1,e_2,1),(\neg p_3,e_3,0))$	1	3	2	2	4
$((\neg p_2,e_1,0),(\neg p_1,e_1,1))$	2	2	1	4	3
$((\neg p_2,e_1,0),(\neg p_1,e_3,1))$	3	2	3	4	3
$((\neg p_2,e_1,0),(\neg p_2,e_2,0))$	2	3	2	4	3
$((\neg p_2,e_1,0),(\neg p_3,e_3,0))$	2	3	2	4	3
$((\neg p_3,e_3,0),(\neg p_1,e_1,1))$	2	2	1	2	0
$((\neg p_3,e_3,0),(\neg p_1,e_3,1))$	3	2	3	0	1
$((\neg p_3,e_3,0),(\neg p_2,e_2,0))$	2	3	2	0	3
$((\neg p_3,e_3,0),(\neg p_3,e_3,0))$	1	3	2	2	0

, respectively.

Proposition 1.

Let $({\gamma }^1,{\eta }^1,A,N)$, $({\gamma }^2,{\eta }^2,A,N)$, and $({\gamma }^3,{\eta }^3,A,N)$ be three N-BSE sets. Then,

1. 

$({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A,N)$ $\widetilde{⊑}$ $({\gamma }^1,{\eta }^1,A,N)$.

2. 

$({\gamma }^1,{\eta }^1,A,N)$ $\widetilde{⊑}$ $({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A,N)$.

3. 

If $({\gamma }^1,{\eta }^1,A,N)$ $\widetilde{⊑}$ $({\gamma }^2,{\eta }^2,A,N)$ and $({\gamma }^2,{\eta }^2,A,N)$ $\widetilde{⊑}$ $({\gamma }^3,{\eta }^3,A,N)$, then $({\gamma }^1,{\eta }^1,A,N)$ $\widetilde{⊑}$ $({\gamma }^3,{\eta }^3,A,N)$.

Proof. 

Straightforward.    □

Proposition 2.

Let $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$ be two N-BSE sets. Then,

1. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N)$ is the smallest N-BSE set that contains both $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$.

2. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N)$ is the largest N-BSE set that is contained in both $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$.

Proof. 

Straightforward.    □

Proposition 3.

Let $({\gamma }^1,{\eta }^1,A,N)$ and $({\gamma }^2,{\eta }^2,A,N)$ be two N-BSE sets. Then,

1. 

${({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A,N)}^{\tilde{c}}$ = $({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A,N)$.

2. 

${({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A,N)}^{\tilde{c}}$ = $({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A,N)$.

3. 

${\left({({\gamma }^1,{\eta }^1,A,N)}^{\tilde{c}}\right)}^{\tilde{c}}$ = $({\gamma }^1,{\eta }^1,A,N)$.

4. 

If $({\gamma }^1,{\eta }^1,A,N)$ $\widetilde{⊑}$ $({\gamma }^2,{\eta }^2,A,N)$, then ${({\gamma }^2,{\eta }^2,A,N)}^{\tilde{c}}$ $\widetilde{⊑}$ ${({\gamma }^1,{\eta }^1,A,N)}^{\tilde{c}}$.

5. 

$({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A,N)$ $\widetilde{⊑}$ $({\gamma }^1,{\eta }^1,A,N)$ ${\tilde{\sqcap }}_{\Re }$ ${({\gamma }^1,{\eta }^1,A,N)}^{\tilde{c}}$ $\widetilde{⊑}$ $({\gamma }^1,{\eta }^1,A,N)$ ${\tilde{\bigsqcup }}_{\Re }$ ${({\gamma }^1,{\eta }^1,A,N)}^{\tilde{c}}$ $\widetilde{⊑}$ $({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A,N)$.

6. 

If $({\gamma }^1,{\eta }^1,A,N)$ $\widetilde{⊑}$ $({\gamma }^2,{\eta }^2,A,N)$, then $({\gamma }^1,{\eta }^1,A,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A,N)$ = $({\gamma }^1,{\eta }^1,A,N)$.

7. 

If $({\gamma }^1,{\eta }^1,A,N)$ $\widetilde{⊑}$ $({\gamma }^2,{\eta }^2,A,N)$, then $({\gamma }^1,{\eta }^1,A,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A,N)$ = $({\gamma }^2,{\eta }^2,A,N)$.

Proof. 

Straightforward.    □

Proposition 4.

Let $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$ be two N-BSE sets. Then,

1. 

$\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N){)}^{\tilde{c}}$ = ${({\gamma }^1,{\eta }^1,A^1,N)}^{\tilde{c}}$ ${\tilde{\sqcap }}_{\epsilon }$ ${({\gamma }^2,{\eta }^2,A^2,N)}^{\tilde{c}}$.

2. 

$\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N){)}^{\tilde{c}}$ = ${({\gamma }^1,{\eta }^1,A^1,N)}^{\tilde{c}}$ ${\tilde{\bigsqcup }}_{\epsilon }$ ${({\gamma }^2,{\eta }^2,A^2,N)}^{\tilde{c}}$.

3. 

$\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N){)}^{\tilde{c}}$ = ${({\gamma }^1,{\eta }^1,A^1,N)}^{\tilde{c}}$ ${\tilde{\sqcap }}_{\Re }$ ${({\gamma }^2,{\eta }^2,A^2,N)}^{\tilde{c}}$.

4. 

$\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N){)}^{\tilde{c}}$ = ${({\gamma }^1,{\eta }^1,A^1,N)}^{\tilde{c}}$ ${\tilde{\bigsqcup }}_{\Re }$ ${({\gamma }^2,{\eta }^2,A^2,N)}^{\tilde{c}}$.

5. 

$\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ $\tilde{\vee }$ $({\gamma }^2,{\eta }^2,A^2,N){)}^{\tilde{c}}$ = ${({\gamma }^1,{\eta }^1,A^1,N)}^{\tilde{c}}$ $\tilde{\wedge }$ ${({\gamma }^2,{\eta }^2,A^2,N)}^{\tilde{c}}$.

6. 

$\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ $\tilde{\wedge }$ $({\gamma }^2,{\eta }^2,A^2,N){)}^{\tilde{c}}$ = ${({\gamma }^1,{\eta }^1,A^1,N)}^{\tilde{c}}$ $\tilde{\vee }$ ${({\gamma }^2,{\eta }^2,A^2,N)}^{\tilde{c}}$.

Proof. 

(1) Let $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N)$ = $({\gamma }^3,{\eta }^3,A^1\cup A^2,N)$. Then, $\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N){)}^{\tilde{c}}$ = ${({\gamma }^3,{\eta }^3,A^1\cup A^2,N)}^{\tilde{c}}$ = $({{\gamma }^3}^{\tilde{c}},{{\eta }^3}^{\tilde{c}},A^1\cup A^2,N)$. For all $a\in A^1\cup A^2$ and $z\in \mathcal{Z}$,

$${\gamma }^3\left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^1\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^1\setminus A^2\hfill \\ {\gamma }^2\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^2\setminus A^1\hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},\hfill & \mathrm{if}a\in A^1\cap A^2\hfill \end{array}\right.$$

and for all $\neg a\in \neg A^1\cup \neg A^2$ and $z\in \mathcal{Z}$

$${\eta }^3(\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^1(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^1\setminus \neg A^2\hfill \\ {\eta }^2(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^2\setminus \neg A^1\hfill \\ min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg A^1\cap \neg A^2.\hfill \end{array}\right.$$

Then, for all $a\in A^1\cup A^2$ and $z\in \mathcal{Z}$,

$${{\gamma }^3}^{\tilde{c}}\left(a\right)\left(z\right)={\eta }^3(\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^1(\neg a)\left(z\right),\hfill & \mathrm{if}a\in A^1\setminus A^2\hfill \\ {\eta }^2(\neg a)\left(z\right),\hfill & \mathrm{if}a\in A^2\setminus A^1\hfill \\ min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},\hfill & \mathrm{if}a\in A^1\cap A^2.\hfill \end{array}\right.$$

and for all $\neg a\in \neg A^1\cup \neg A^2$ and $z\in \mathcal{Z}$,

$${{\eta }^3}^{\tilde{c}}(\neg a)\left(z\right)={\gamma }^3\left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^1\left(a\right)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^1\setminus \neg A^2\hfill \\ {\gamma }^2\left(a\right)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^2\setminus \neg A^1\hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg A^1\cap \neg A^2.\hfill \end{array}\right.$$

On the other hand, let ${({\gamma }^1,{\eta }^1,A^1,N)}^{\tilde{c}}$ ${\tilde{\sqcap }}_{\epsilon }$ ${({\gamma }^2,{\eta }^2,A^2,N)}^{\tilde{c}}$ = $({\gamma }^4,{\eta }^4,A^1\cup A^2,N)$. By Definition 18, for all $a\in A^1\cup A^2$ and $z\in \mathcal{Z}$,

$${\gamma }^4\left(a\right)\left(z\right)=\left\{\begin{array}{cc}{{\gamma }^1}^{\tilde{c}}\left(a\right)\left(z\right)={\eta }^1(\neg a)\left(z\right),\hfill & \mathrm{if}a\in A^1\setminus A^2\hfill \\ {{\gamma }^2}^{\tilde{c}}\left(a\right)\left(z\right)={\eta }^2(\neg a)\left(z\right),\hfill & \mathrm{if}a\in A^2\setminus A^1\hfill \\ min\{{{\gamma }^1}^{\tilde{c}}\left(a\right)\left(z\right),{{\gamma }^2}^{\tilde{c}}\left(a\right)\left(z\right)\}=min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},\hfill & \mathrm{if}a\in A^1\cap A^2.\hfill \end{array}\right.$$

and for all $\neg a\in \neg A^1\cup \neg A^2$ and $z\in \mathcal{Z}$,

$${\eta }^4(\neg a)\left(z\right)=\left\{\begin{array}{cc}{{\eta }^1}^{\tilde{c}}(\neg a)\left(z\right)={\gamma }^1\left(a\right)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^1\setminus \neg A^2\hfill \\ {{\eta }^2}^{\tilde{c}}(\neg a)\left(z\right)={\gamma }^2\left(a\right)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^2\setminus \neg A^1\hfill \\ max\{{{\eta }^1}^{\tilde{c}}(\neg a)\left(z\right),{{\eta }^2}^{\tilde{c}}(\neg a)\left(z\right)\}=max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg A^1\cap \neg A^2.\hfill \end{array}\right.$$

Since ${({\gamma }^3,{\eta }^3,A^1\cup A^2,N)}^{\tilde{c}}$ and $({\gamma }^4,{\eta }^4,A^1\cup A^2,N)$ are equivalent for all $a\in A^1\cup A^2$, $\neg a\in \neg A^1\cup \neg A^2$, and $z\in \mathcal{Z}$, the proof follows.

The remaining parts can be demonstrated in the same manner.    □

Proposition 5.

Let $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^1,N)$ be two N-BSE sets. Then,

1. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^1,N)$ = $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^1,N)$.

2. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^1,N)$ = $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^1,N)$.

3. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^1,{\eta }^1,A^1,N)$ = $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^1,{\eta }^1,A^1,N)$ = $({\gamma }^1,{\eta }^1,A^1,N)$.

4. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A^1,N)$ = $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A^1,N)$ = $({\gamma }^{\mathbb{O}},{\eta }^{\mathbb{O}},A^1,N)$.

5. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A^1,N)$ = $({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A^1,N)$ and $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^{\mathbb{W}},{\eta }^{\mathbb{W}},A^1,N)$ = $({\gamma }^1,{\eta }^1,A^1,N)$.

Proof. 

Straightforward.    □

Proposition 6.

Let $({\gamma }^1,{\eta }^1,A^1,N)$ and $({\gamma }^2,{\eta }^2,A^2,N)$ be two N-BSE sets. Then,

1. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N))$ = $({\gamma }^1,{\eta }^1,A^1,N)$.

2. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\epsilon }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N))$ = $({\gamma }^1,{\eta }^1,A^1,N)$.

3. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\Re }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N))$ = $({\gamma }^1,{\eta }^1,A^1,N)$.

4. 

$({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N))$ = $({\gamma }^1,{\eta }^1,A^1,N)$.

Proof. 

(1) Suppose that $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N)$ = $({\gamma }^3,{\eta }^3,A^1\cap A^2,N)$. Then, for all $a\in A^1\cap A^2$ and $z\in \mathcal{Z}$,

$${\gamma }^3\left(a\right)\left(z\right)=min\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},$$

and for all $\neg a\in \neg A^1\cap \neg A^2$ and $z\in \mathcal{Z}$,

$${\eta }^3(\neg a)\left(z\right)=max\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\}.$$

Now, let $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^3,{\eta }^3,A^1\cap A^2,N)$ = $({\gamma }^4,{\eta }^4,A^1\cup (A^1\cap A^2),N)$ = $({\gamma }^4,{\eta }^4,A^1,N)$. Then, for all $a\in A^1\cup (A^1\cap A^2)$ and $z\in \mathcal{Z}$,

$${\gamma }^4\left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^1\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^1\setminus (A^1\cap A^2)\hfill \\ {\gamma }^3\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in (A^1\cap A^2)\setminus A^1=\varnothing \hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^3\left(a\right)\left(z\right)\},\hfill & \mathrm{if}a\in A^1\cap (A^1\cap A^2).\hfill \end{array}\right.$$

$$=\left\{\begin{array}{cc}{\gamma }^1\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^1\setminus (A^1\cap A^2)\hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),min\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\}\},\hfill & \mathrm{if}a\in A^1\cap (A^1\cap A^2).\hfill \end{array}\right.$$

and for all $\neg a\in \neg A^1\cup (\neg A^1\cap \neg A^2)$ and $z\in \mathcal{Z}$,

$${\eta }^4(\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^1(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^1\setminus (\neg A^1\cap \neg A^2)\hfill \\ {\eta }^3(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in (\neg A^1\cap \neg A^2)\setminus \neg A^1=\varnothing \hfill \\ min\{{\eta }^1(\neg a)\left(z\right),{\eta }^3(\neg a)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg A^1\cap (\neg A^1\cap \neg A^2).\hfill \end{array}\right.$$

$$=\left\{\begin{array}{cc}{\eta }^1(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^1\setminus (\neg A^1\cap \neg A^2)\hfill \\ min\{{\eta }^1(\neg a)\left(z\right),max\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\}\},\hfill & \mathrm{if}\neg a\in \neg A^1\cap (\neg A^1\cap \neg A^2).\hfill \end{array}\right.$$

Hence,

$${\gamma }^4\left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^1\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^1\setminus (A^1\cap A^2)\hfill \\ {\gamma }^1\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^1\cap A^2\hfill \end{array}\right.$$

and

$${\eta }^4(\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^1(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^1\setminus (\neg A^1\cap \neg A^2)\hfill \\ {\eta }^1(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^1\cap \neg A^2\hfill \end{array}\right.$$

Therefore, $({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N))$ = $({\gamma }^1,{\eta }^1,A^1,N)$.

The remaining parts can be demonstrated in the same manner.    □

Proposition 7.

Let $({\gamma }^1,{\eta }^1,A^1,N^1)$, $({\gamma }^2,{\eta }^2,A^2,N^2)$, and $({\gamma }^3,{\eta }^3,A^3,N^3)$ be three N-BSE sets and let $\odot \in \{{\tilde{\bigsqcup }}_{\epsilon },{\tilde{\sqcap }}_{\epsilon },{\tilde{\bigsqcup }}_{\Re },{\tilde{\sqcap }}_{\Re }\}$. Then,

1. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$⊙$({\gamma }^2,{\eta }^2,A^2,N^2)$ = $({\gamma }^2,{\eta }^2,A^2,N^2)$⊙$({\gamma }^1,{\eta }^1,A^1,N^1)$.

2. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$⊙$\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$⊙$({\gamma }^3,{\eta }^3,A^3,N^3))$ = $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$⊙$({\gamma }^2,{\eta }^2,A^2,N^2))$⊙$({\gamma }^3,{\eta }^3,A^3,N^3)$.

Proof. 

Straightforward.    □

Proposition 8.

Let $({\gamma }^1,{\eta }^1,A^1,N^1)$, $({\gamma }^2,{\eta }^2,A^2,N^2)$, and $({\gamma }^3,{\eta }^3,A^3,N^3)$ be three N-BSE sets. Then,

1. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$ = $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N^2))$ ${\tilde{\sqcap }}_{\Re }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$.

2. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\Re }$ $\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$ ${\tilde{\bigsqcup }}_{\epsilon }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$ = $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N^2))$ ${\tilde{\bigsqcup }}_{\epsilon }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$.

3. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\epsilon }$ $\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$ = $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^2,{\eta }^2,A^2,N^2))$ ${\tilde{\bigsqcup }}_{\Re }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$.

4. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$ = $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N^2))$ ${\tilde{\sqcap }}_{\epsilon }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$.

5. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$ = $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N^2))$ ${\tilde{\sqcap }}_{\Re }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$.

6. 

$({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\Re }$ $\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$ = $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N^2))$ ${\tilde{\bigsqcup }}_{\Re }$ $\left(\right({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\sqcap }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$.

Proof. 

(4) Suppose that $\left(\right({\gamma }^2,{\eta }^2,A^2,N^2)$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^3,{\eta }^3,A^3,N^3))$ = $({\gamma }^4,{\eta }^4,A^2\cup A^3,max(N^2,N^3))$; then, for all $a\in A^2\cup A^3$ and $z\in \mathcal{Z}$,

$${\gamma }^4\left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^2\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^2\setminus A^3\hfill \\ {\gamma }^3\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in A^3\setminus A^2\hfill \\ min\{{\gamma }^2\left(a\right)\left(z\right),{\gamma }^3\left(a\right)\left(z\right)\},\hfill & \mathrm{if}a\in A^2\cap A^3\hfill \end{array}\right.$$

and for all $\neg a\in \neg A^2\cup \neg A^3$ and $z\in \mathcal{Z}$,

$${\eta }^4(\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^2(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^2\setminus \neg A^3\hfill \\ {\eta }^3(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg A^3\setminus \neg A^2\hfill \\ max\{{\eta }^2(\neg a)\left(z\right),{\eta }^3(\neg a)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg A^2\cap \neg A^3.\hfill \end{array}\right.$$

Let $({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^4,{\eta }^4,A^2\cup A^3,max(N^2,N^3))$ = $({\gamma }^5,{\eta }^5,A^1\cap (A^2\cup A^3)$, $max(N^1$, $max(N^2,N^3)\left)\right)$ = $({\gamma }^5,{\eta }^5,O\cup P,max(N^1,N^2,N^3))$ where $O=A^1\cap A^2$ and $P=A^1\cap A^3$; then, for all $a\in O\cup P$ and $z\in \mathcal{Z}$,

$${\gamma }^5\left(a\right)\left(z\right)=max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^4\left(a\right)\left(z\right)\},$$

and for all $\neg a\in \neg O\cup \neg P$ and $z\in \mathcal{Z}$,

$${\eta }^5(\neg a)\left(z\right)=min\{{\eta }^1(\neg a)\left(z\right),{\eta }^4(\neg a)\left(z\right)\}.$$

Hence, for all $a\in O\cup P$ and $z\in \mathcal{Z}$,

$${\gamma }^5\left(a\right)\left(z\right)=\left\{\begin{array}{cc}max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},\hfill & \mathrm{if}a\in O\setminus P\hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^3\left(a\right)\left(z\right)\},\hfill & \mathrm{if}a\in P\setminus O\hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),min\{{\gamma }^2\left(a\right)\left(z\right),{\gamma }^3\left(a\right)\left(z\right)\}\}\hfill & \mathrm{if}a\in P\cap O\hfill \end{array}\right.$$

and for all $\neg a\in \neg O\cup \neg P$ and $z\in \mathcal{Z}$,

$${\eta }^5(\neg a)\left(z\right)=\left\{\begin{array}{cc}min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg O\setminus \neg P\hfill \\ min\{{\eta }^1(\neg a)\left(z\right),{\eta }^3(\neg a)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg P\setminus \neg O\hfill \\ min\{{\eta }^1(\neg a)\left(z\right),max\{{\eta }^2(\neg a)\left(z\right),{\eta }^3(\neg a)\left(z\right)\}\}\hfill & if\neg a\in \neg P\cap \neg O.\hfill \end{array}\right.$$

On the other hand, let $({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^2,{\eta }^2,A^2,N^2)$ = $({\gamma }^6,{\eta }^6,A^1\cap A^2,max(N^1,N^2))$; then, for all $a\in A^1\cap A^2$ and $z\in \mathcal{Z}$,

$${\gamma }^6\left(a\right)\left(z\right)=max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},$$

and for all $\neg a\in \neg O\cup \neg P$ and $z\in \mathcal{Z}$,

$${\eta }^6(\neg a)\left(z\right)=min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\}.$$

Next, let $({\gamma }^1,{\eta }^1,A^1,N^1)$ ${\tilde{\bigsqcup }}_{\Re }$ $({\gamma }^3,{\eta }^3,A^3,N^3)$ = $({\gamma }^7,{\eta }^7,A^1\cap A^2,max(N^1,N^2))$; then, for all $a\in A^1\cap A^3$ and $z\in \mathcal{Z}$,

$${\gamma }^7\left(a\right)\left(z\right)=max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^3\left(a\right)\left(z\right)\},$$

and for all $\neg a\in \neg O\cup \neg P$ and $z\in \mathcal{Z}$,

$${\eta }^7(\neg a)\left(z\right)=min\{{\eta }^1(\neg a)\left(z\right),{\eta }^3(\neg a)\left(z\right)\}.$$

Now, suppose that $({\gamma }^6,{\eta }^6,A^1\cap A^2,max(N^1,N^2))$ ${\tilde{\sqcap }}_{\epsilon }$ $({\gamma }^7,{\eta }^7,A^1\cap A^3,max(N^1,N^3))$ = $({\gamma }^8,{\eta }^8,O\cup P),max(N^1,N^2,N^3))$ where $O=A^1\cap A^2$ and $P=A^1\cap A^3$; then, for all $a\in O\cup P$ and $z\in \mathcal{Z}$

$${\gamma }^8\left(a\right)\left(z\right)=\left\{\begin{array}{cc}{\gamma }^6\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in O\setminus P\hfill \\ {\gamma }^7\left(a\right)\left(z\right),\hfill & \mathrm{if}a\in P\setminus O\hfill \\ min\{{\gamma }^6\left(a\right)\left(z\right),{\gamma }^7\left(a\right)\left(z\right)\}\hfill & \mathrm{if}a\in P\cap O\hfill \end{array}\right.$$

$$=\left\{\begin{array}{cc}max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},\hfill & \mathrm{if}a\in O\setminus P\hfill \\ max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^3\left(a\right)\left(z\right)\},\hfill & \mathrm{if}a\in P\setminus O\hfill \\ min\{max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^2\left(a\right)\left(z\right)\},max\{{\gamma }^1\left(a\right)\left(z\right),{\gamma }^3\left(a\right)\left(z\right)\}\}\hfill & \mathrm{if}a\in P\cap O\hfill \end{array}\right.$$

and for all $\neg a\in \neg O\cup \neg P$ and $z\in \mathcal{Z}$,

$${\eta }^8(\neg a)\left(z\right)=\left\{\begin{array}{cc}{\eta }^6(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg O\setminus \neg P\hfill \\ {\eta }^7(\neg a)\left(z\right),\hfill & \mathrm{if}\neg a\in \neg P\setminus \neg O\hfill \\ max\{{\eta }^6(\neg a)\left(z\right),{\eta }^7(\neg a)\left(z\right)\}\hfill & \mathrm{if}\neg a\in \neg P\cap \neg O\hfill \end{array}\right.$$

$$=\left\{\begin{array}{cc}min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg O\setminus \neg P\hfill \\ min\{{\eta }^1(\neg a)\left(z\right),{\eta }^3(\neg a)\left(z\right)\},\hfill & \mathrm{if}\neg a\in \neg P\setminus \neg O\hfill \\ max\{min\{{\eta }^1(\neg a)\left(z\right),{\eta }^2(\neg a)\left(z\right)\},min\{{\eta }^1(\neg a)\left(z\right),{\eta }^3(\neg a)\left(z\right)\}\}\hfill & \mathrm{if}\neg a\in \neg P\cap \neg O.\hfill \end{array}\right.$$

Since $({\gamma }^5,{\eta }^5,O\cup P,max(N^1,N^2,N^3))$ and $({\gamma }^8,{\eta }^8,O\cup P,max(N^1,N^2,N^3))$ are equivalent for all $a\in O\cup P$, $\neg a\in \neg O\cup \neg P$, and $z\in \mathcal{Z}$, the proof follows.

The remaining parts can be demonstrated in the same manner.    □

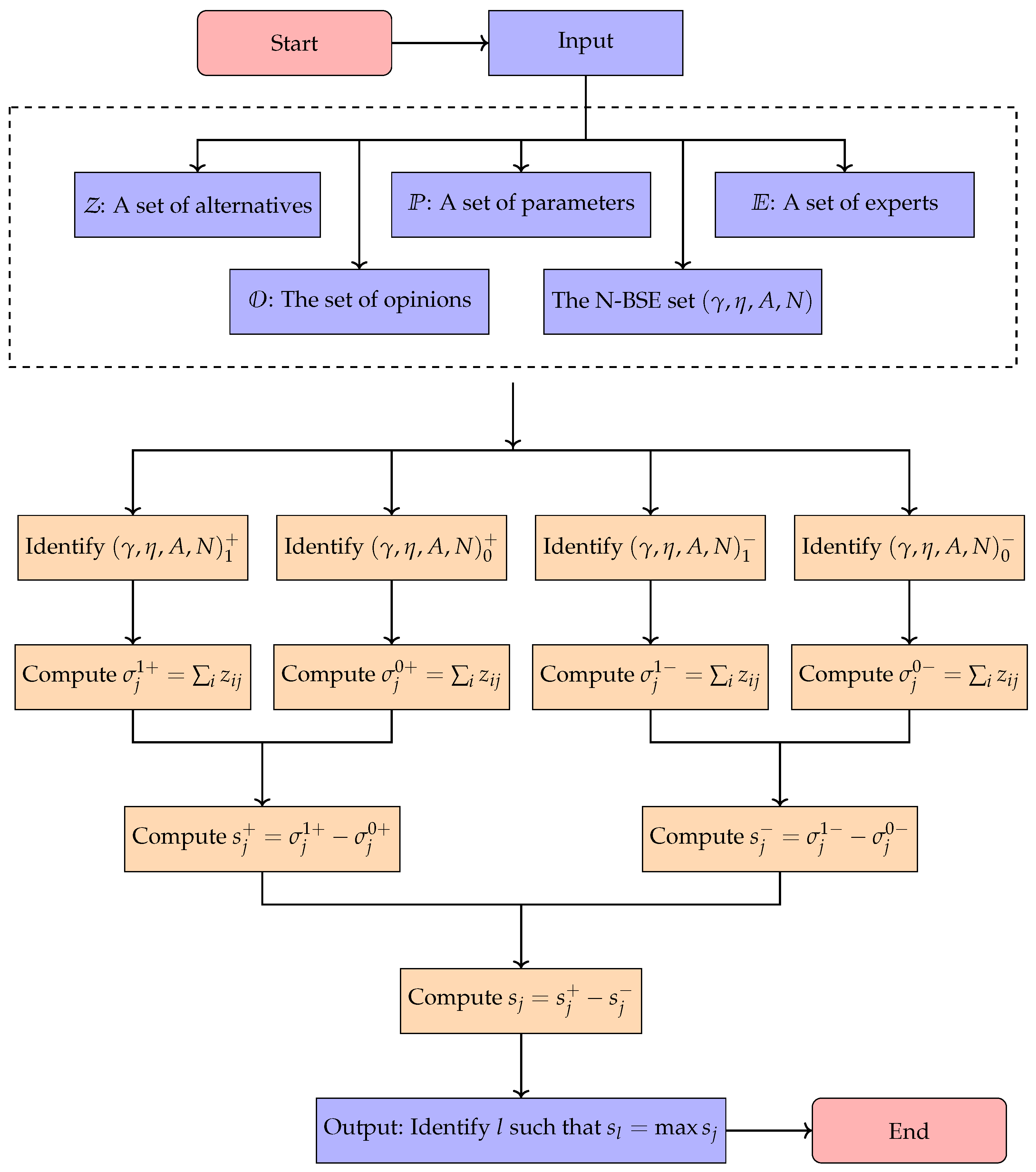
4. Application of N-Bipolar Soft Expert Sets in Multi-Attribute Group Decision-Making

MAGDM is a method in which multiple decision-makers evaluate a set of alternatives based on several criteria. It is particularly useful for addressing complex problems where stakeholders may have conflicting views. By combining different perspectives, MAGDM facilitates the achievement of a consensus. This approach is widely applied in areas such as business, healthcare, engineering, and public policy, where decisions have significant consequences.

In this section, we apply the N-BSE framework to identify optimal solutions in MAGDM scenarios. To demonstrate its practical use, we present a case study on selecting the best sustainable energy solution for different regions, considering both positive and negative aspects of each option.

4.1. Algorithm for Optimal Decision-Making

In this section, we present an algorithm designed to identify the optimal alternative in multi-criteria DM scenarios, where expert evaluations include both positive and negative assessments. The algorithm is based on the concept of N-BSE sets to compute decision scores for each alternative, effectively incorporating both favorable and unfavorable opinions. By aggregating judgments from multiple experts and comparing the resulting net scores, the algorithm ensures a systematic and transparent process for selecting the best option. This method is versatile, and can be applied to a wide range of DM problems, offering an objective and structured approach to selecting the most suitable alternative in complex, multi-attribute environments.

The flowchart of the Algorithm 1 is shown in the Figure 1, which illustrates the steps involved in computing the decision scores and identifying the optimal alternative.

Algorithm 1 Determining the optimal choice using N-BSE sets.

1: Input: (i) $\mathcal{Z}$: A set of alternatives (objects). (ii) $\mathbb{P}$: A set of decision parameters. (iii) $\mathbb{E}$: A set of experts. (iv) $\mathbb{O}=\{0=\mathrm{disagree},1=\mathrm{agree}\}$: The set of opinions. (v) The N-BSE set $(\gamma ,\eta ,A,N)$, where $A\subseteq$ ¥, with $\yen =\mathbb{P}\times \mathbb{E}\times \mathbb{O}$. 2: Procedure: (i) Identify the positive agree N-BSE set ${(\gamma ,\eta ,A,N)}_1^{+}$ and positive disagree N-BSE set ${(\gamma ,\eta ,A,N)}_0^{+}$. (ii) Identify the negative agree N-BSE set ${(\gamma ,\eta ,A,N)}_1^{-}$ and negative disagree N-BSE set ${(\gamma ,\eta ,A,N)}_0^{-}$. (iii) For each j, determine: $$\begin{array}{cc}\hfill {\sigma }_j^{1+}& =\sum _i{z}_{ij}\mathrm{from}{(\gamma ,\eta ,A,N)}_1^{+},\hfill \\ {\sigma }_j^{0+}& \hfill =\sum _i{z}_{ij}\mathrm{from}{(\gamma ,\eta ,A,N)}_0^{+},\\ {\sigma }_j^{1-}& =\sum _i{z}_{ij}\mathrm{from}{(\gamma ,\eta ,A,N)}_1^{-},\hfill \\ {\sigma }_j^{0-}& \hfill =\sum _i{z}_{ij}\mathrm{from}{(\gamma ,\eta ,A,N)}_0^{-}.\end{array}$$ (iv) Compute the scores for each j: $$s_j=s_j^{+}-s_j^{-}\mathrm{where}{s}_j^{+}={\sigma }_j^{1+}-{\sigma }_j^{0+}\mathrm{and}{s}_j^{-}={\sigma }_j^{1-}-{\sigma }_j^{0-}.$$ 3: Output: Identify l such that $s_l=max{s}_j$.

4.2. Case Study: Sustainable Energy Solutions

In addressing global challenges like climate change, organizations play a crucial role in advancing sustainable energy solutions. Selecting the most suitable energy project for implementation is a complex task that requires thorough evaluation. A poorly chosen project could lead to inefficiencies and resource wastage, while the right project can foster energy efficiency and environmental sustainability. This example illustrates the process of selecting an optimal energy project.

Suppose a renewable energy company intends to implement one project from a list of seven proposals: $\mathcal{Z}=\{z_1,z_2,z_3,z_4,z_5,z_6,z_7\}$. The company forms a committee of experienced employees to prepare a report evaluating the proposals based on key parameters: $\mathbb{P}=\{p_1=\text{cost-effectiveness},p_2=\mathrm{energy}\mathrm{efficiency},p_3=\mathrm{environmental}\mathrm{impact}\}$, along with their negative counterparts: $\neg \mathbb{P}=\{\neg p_1=\mathrm{high}\mathrm{cost},\neg p_2=\mathrm{low}\mathrm{energy}\mathrm{efficiency},$ $\neg p_3=\mathrm{negative}\mathrm{environmental}\mathrm{impact}\}$. To finalize the decision, the company shares the report with three energy experts $\mathbb{E}=\{e_1,e_2,e_3\}$ and considers their opinions $\mathbb{O}=\{0=\mathrm{disagree},1=\mathrm{agree}\}$ on the report, as shown in

Table 19. Evaluations of sustainable energy solutions by experts using check-marks.

$\mathit{A}\setminus \mathcal{Z}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$	${\mathit{z}}_6$	${\mathit{z}}_7$
$(p_1,e_1,1)$	$★★★$	$★★$	$★★★★$	$★★$	$★★$	$★★★$	$★★$
$(p_1,e_2,1)$	★	$★★★$	∘	$★★★$	★	$★★★$	$★★★$
$(p_1,e_3,1)$	$★★$	★	$★★★$	$★★★$	★	★	$★★★$
$(p_2,e_1,1)$	$★★★$	$★★$	$★★$	$★★$	★	$★★★$	∘
$(p_2,e_2,1)$	$★★★$	∘	$★★★$	$★★$	$★★★$	∘	$★★$
$(p_2,e_3,1)$	∘	$★★$	$★★★★$	$★★$	$★★$	∘	$★★$
$(p_3,e_1,1)$	$★★★$	$★★★$	★	$★★$	$★★★$	∘	$★★★$
$(p_3,e_2,1)$	$★★$	∘	$★★★$	★	★	$★★★$	$★★$
$(p_3,e_3,1)$	$★★$	$★★★$	$★★★$	$★★★$	$★★$	$★★★$	∘
$(p_1,e_1,0)$	★	$★★$	∘	$★★$	★	∘	$★★$
$(p_1,e_2,0)$	$★★$	★	★	★	$★★$	★	★
$(p_1,e_3,0)$	★	$★★★$	★	∘	$★★★$	$★★$	★
$(p_2,e_1,0)$	∘	★	∘	★	$★★★$	★	∘
$(p_2,e_2,0)$	∘	∘	★	★	★	$★★★★$	$★★$
$(p_2,e_3,0)$	$★★★$	$★★$	∘	$★★$	★	★	★
$(p_3,e_1,0)$	★	★	$★★★$	$★★$	∘	$★★★$	★
$(p_3,e_2,0)$	$★★$	$★★$	★	★	$★★★$	★	$★★$
$(p_3,e_3,0)$	★	∘	★	∘	$★★$	★	$★★★★$
$(\neg p_1,e_1,1)$	∘	★	∘	$★★$	$★★$	★	★
$(\neg p_1,e_2,1)$	$★★$	★	$★★★$	★	$★★$	∘	∘
$(\neg p_1,e_3,1)$	$★★$	$★★$	★	★	$★★$	$★★$	★
$(\neg p_2,e_1,1)$	★	★	$★★$	★	$★★$	∘	$★★★★$
$(\neg p_2,e_2,1)$	∘	$★★$	★	★	★	$★★★$	$★★$
$(\neg p_2,e_3,1)$	$★★★★$	$★★$	∘	$★★$	★	$★★$	$★★$
$(\neg p_3,e_1,1)$	★	★	$★★★$	$★★$	∘	★	∘
$(\neg p_3,e_2,1)$	★	∘	★	$★★$	$★★★$	★	$★★$
$(\neg p_3,e_3,1)$	★	★	★	★	$★★$	★	★
$(\neg p_1,e_1,0)$	$★★★$	$★★$	∘	$★★$	★	$★★★$	$★★$
$(\neg p_1,e_2,0)$	★	$★★$	★	$★★$	$★★$	★	★
$(\neg p_1,e_3,0)$	$★★$	★	$★★★$	$★★★$	∘	★	★
$(\neg p_2,e_1,0)$	$★★$	$★★$	$★★$	$★★$	∘	$★★$	∘
$(\neg p_2,e_2,0)$	$★★★★$	$★★$	$★★$	$★★$	$★★$	∘	★
$(\neg p_2,e_3,0)$	∘	★	$★★★$	$★★$	$★★$	★	$★★$
$(\neg p_3,e_1,0)$	$★★$	$★★★$	★	★	$★★$	★	∘
$(\neg p_3,e_2,0)$	$★★$	★	$★★$	$★★$	∘	$★★$	$★★$
$(\neg p_3,e_3,0)$	$★★$	$★★$	★	★	∘	★	∘

.

The check-marks are translated into numerical values (0, 1, 2, 3, 4) for computation, as shown in Example 1.

Therefore, the experts construct a 5-BSE set $(\gamma ,\eta ,A,5)$, as detailed in

Table 20. Evaluations of sustainable energy solutions by experts using 5-BSE set $(\gamma ,\eta ,A,5)$.

$(\mathit{\gamma },\mathit{\eta },\mathit{A},5)$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$	${\mathit{z}}_6$	${\mathit{z}}_7$
$(p_1,e_1,1)$	3	2	4	2	2	3	2
$(p_1,e_2,1)$	1	3	0	3	1	3	3
$(p_1,e_3,1)$	2	1	3	3	1	1	3
$(p_2,e_1,1)$	3	2	2	2	1	3	0
$(p_2,e_2,1)$	3	0	3	2	3	0	2
$(p_2,e_3,1)$	0	2	4	2	2	0	2
$(p_3,e_1,1)$	3	3	1	2	3	0	3
$(p_3,e_2,1)$	2	0	3	1	1	3	2
$(p_3,e_3,1)$	2	3	3	3	2	3	0
$(p_1,e_1,0)$	1	2	0	2	1	0	2
$(p_1,e_2,0)$	2	1	1	1	2	1	1
$(p_1,e_3,0)$	1	3	1	0	3	2	1
$(p_2,e_1,0)$	0	1	0	1	3	1	0
$(p_2,e_2,0)$	0	0	1	1	1	4	2
$(p_2,e_3,0)$	3	2	0	2	1	1	1
$(p_3,e_1,0)$	1	1	3	2	0	3	1
$(p_3,e_2,0)$	2	2	1	1	3	1	2
$(p_3,e_3,0)$	1	0	1	0	2	1	4
$(\neg p_1,e_1,1)$	0	1	0	2	2	1	1
$(\neg p_1,e_2,1)$	2	1	3	1	2	0	0
$(\neg p_1,e_3,1)$	2	2	1	1	2	2	1
$(\neg p_2,e_1,1)$	1	1	2	1	2	0	4
$(\neg p_2,e_2,1)$	0	2	1	1	1	3	2
$(\neg p_2,e_3,1)$	4	2	0	2	1	2	2
$(\neg p_3,e_1,1)$	1	1	3	2	0	1	0
$(\neg p_3,e_2,1)$	1	0	1	2	3	1	2
$(\neg p_3,e_3,1)$	1	1	1	1	2	1	1
$(\neg p_1,e_1,0)$	3	2	0	2	1	3	2
$(\neg p_1,e_2,0)$	1	2	1	2	2	1	1
$(\neg p_1,e_3,0)$	2	1	3	3	0	1	1
$(\neg p_2,e_1,0)$	2	2	2	2	0	2	0
$(\neg p_2,e_2,0)$	4	2	2	2	2	0	1
$(\neg p_2,e_3,0)$	0	1	3	2	2	1	2
$(\neg p_3,e_1,0)$	2	3	1	1	2	1	0
$(\neg p_3,e_2,0)$	2	1	2	2	0	2	2
$(\neg p_3,e_3,0)$	2	2	1	1	0	1	0

.

For simplicity in the computation process, the experts constructs the tables for positive agree, positive disagree, negative agree, and negative disagree in a straightforward manner, as shown in

Table 21. Tabular representation of a positive agree 5-BSE set ${(\gamma ,\eta ,A,5)}_1^{+}$.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_1^{+}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$	${\mathit{z}}_6$	${\mathit{z}}_7$
$(p_1,e_1,1)$	3	2	4	2	2	3	2
$(p_1,e_2,1)$	1	3	0	3	1	3	3
$(p_1,e_3,1)$	2	1	3	3	1	1	3
$(p_2,e_1,1)$	3	2	2	2	1	3	0
$(p_2,e_2,1)$	3	0	3	2	3	0	2
$(p_2,e_3,1)$	0	2	4	2	2	0	2
$(p_3,e_1,1)$	3	3	1	2	3	0	3
$(p_3,e_2,1)$	2	0	3	1	1	3	2
$(p_3,e_3,1)$	2	3	3	3	2	3	0
${\sigma }_j^{1+}={\sum }_i{z}_{ij}$	${\sigma }_1^{1+}=19$	${\sigma }_2^{1+}=16$	${\sigma }_3^{1+}=23$	${\sigma }_4^{1+}=20$	${\sigma }_5^{1+}=16$	${\sigma }_6^{1+}=16$	${\sigma }_7^{1+}=17$

,

Table 22. Tabular representation of a positive disagree 5-BSE set ${(\gamma ,\eta ,A,5)}_0^{+}$.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_0^{+}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$	${\mathit{z}}_6$	${\mathit{z}}_7$
$(p_1,e_1,0)$	1	2	0	2	1	0	2
$(p_1,e_2,0)$	2	1	1	1	2	1	1
$(p_1,e_3,0)$	1	3	1	0	3	2	1
$(p_2,e_1,0)$	0	1	0	1	3	1	0
$(p_2,e_2,0)$	0	0	1	1	1	4	2
$(p_2,e_3,0)$	3	2	0	2	1	1	1
$(p_3,e_1,0)$	1	1	3	2	0	3	1
$(p_3,e_2,0)$	2	2	1	1	3	1	2
$(p_3,e_3,0)$	1	0	1	0	2	1	4
${\sigma }_j^{0+}={\sum }_i{z}_{ij}$	${\sigma }_1^{0+}=11$	${\sigma }_2^{0+}=12$	${\sigma }_3^{0+}=8$	${\sigma }_4^{0+}=10$	${\sigma }_5^{0+}=16$	${\sigma }_6^{0+}=14$	${\sigma }_7^{0+}=14$

,

Table 23. Tabular representation of a negative agree 5-BSE set ${(\gamma ,\eta ,A,5)}_1^{-}$.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_1^{-}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$	${\mathit{z}}_6$	${\mathit{z}}_7$
$(\neg p_1,e_1,1)$	0	1	0	2	2	1	1
$(\neg p_1,e_2,1)$	2	1	3	1	2	0	0
$(\neg p_1,e_3,1)$	2	2	1	1	2	2	1
$(\neg p_2,e_1,1)$	1	1	2	1	2	0	4
$(\neg p_2,e_2,1)$	0	2	1	1	1	3	2
$(\neg p_2,e_3,1)$	4	2	0	2	1	2	2
$(\neg p_3,e_1,1)$	1	1	3	2	0	1	0
$(\neg p_3,e_2,1)$	1	0	1	2	3	1	2
$(\neg p_3,e_3,1)$	1	1	1	1	2	1	1
${\sigma }_j^{1-}={\sum }_i{z}_{ij}$	${\sigma }_1^{1-}=12$	${\sigma }_2^{1-}=11$	${\sigma }_3^{1-}=12$	${\sigma }_4^{1-}=13$	${\sigma }_5^{1-}=15$	${\sigma }_6^{1-}=11$	${\sigma }_7^{1-}=13$

and

Table 24. Tabular representation of a negative disagree 5-BSE set ${(\gamma ,\eta ,A,5)}_0^{-}$.

${(\mathit{\gamma },\mathit{\eta },\mathit{A},5)}_0^{-}$	${\mathit{z}}_1$	${\mathit{z}}_2$	${\mathit{z}}_3$	${\mathit{z}}_4$	${\mathit{z}}_5$	${\mathit{z}}_6$	${\mathit{z}}_7$
$(\neg p_1,e_1,0)$	3	2	0	2	1	3	2
$(\neg p_1,e_2,0)$	1	2	1	2	2	1	1
$(\neg p_1,e_3,0)$	2	1	3	3	0	1	1
$(\neg p_2,e_1,0)$	2	2	2	2	0	2	0
$(\neg p_2,e_2,0)$	4	2	2	2	2	0	1
$(\neg p_2,e_3,0)$	0	1	3	2	2	1	2
$(\neg p_3,e_1,0)$	2	3	1	1	2	1	0
$(\neg p_3,e_2,0)$	2	1	2	2	0	2	2
$(\neg p_3,e_3,0)$	2	2	1	1	0	1	0
${\sigma }_j^{0-}={\sum }_i{z}_{ij}$	${\sigma }_1^{0-}=18$	${\sigma }_2^{0-}=16$	${\sigma }_3^{0-}=15$	${\sigma }_4^{0-}=17$	${\sigma }_5^{0-}=9$	${\sigma }_6^{0-}=12$	${\sigma }_7^{0-}=9$

, where $z_{ij}$ represents the entries in these tables.

We can easily construct

Table 25. Positive score table.

${\mathit{\sigma }}_{\mathit{j}}^{1+}$	${\mathit{\sigma }}_{\mathit{j}}^{0+}$	${\mathit{s}}_{\mathit{j}}^{+}={\mathit{\sigma }}_{\mathit{j}}^{1+}-{\mathit{\sigma }}_{\mathit{j}}^{0+}$
${\sigma }_1^{1+}=19$	${\sigma }_1^{0+}=11$	$s_1^{+}=8$
${\sigma }_2^{1+}=16$	${\sigma }_1^{0+}=12$	$s_2^{+}=4$
${\sigma }_3^{1+}=23$	${\sigma }_1^{0+}=8$	$s_3^{+}=15$
${\sigma }_4^{1+}=20$	${\sigma }_1^{0+}=10$	$s_4^{+}=10$
${\sigma }_5^{1+}=16$	${\sigma }_1^{0+}=16$	$s_5^{+}=0$
${\sigma }_6^{1+}=16$	${\sigma }_1^{0+}=14$	$s_6^{+}=2$
${\sigma }_7^{1+}=17$	${\sigma }_1^{0+}=14$	$s_7^{+}=3$

by combining the data from Table 21 and Table 22. Similarly,

Table 26. Negative score table.

${\mathit{\sigma }}_{\mathit{j}}^{1-}$	${\mathit{\sigma }}_{\mathit{j}}^{0-}$	${\mathit{s}}_{\mathit{j}}^{-}={\mathit{\sigma }}_{\mathit{j}}^{1-}-{\mathit{\sigma }}_{\mathit{j}}^{0-}$
${\sigma }_1^{1-}=12$	${\sigma }_1^{0-}=18$	$s_1^{-}=-6$
${\sigma }_2^{1-}=11$	${\sigma }_2^{0-}=16$	$s_2^{-}=-5$
${\sigma }_3^{1-}=12$	${\sigma }_3^{0-}=15$	$s_3^{-}=-3$
${\sigma }_4^{1-}=13$	${\sigma }_4^{0-}=17$	$s_4^{-}=-4$
${\sigma }_5^{1-}=15$	${\sigma }_5^{0-}=9$	$s_5^{-}=6$
${\sigma }_6^{1-}=11$	${\sigma }_6^{0-}=12$	$s_6^{-}=-1$
${\sigma }_7^{1-}=13$	${\sigma }_7^{0-}=9$	$s_7^{-}=4$

can be derived from Table 23 and Table 24.

Finally, we can combine the results from Table 25 and Table 26 to construct

Table 27. Final score table.

${\mathit{s}}_{\mathit{j}}^{+}$	${\mathit{s}}_{\mathit{j}}^{-}$	${\mathit{s}}_{\mathit{j}}={\mathit{s}}_{\mathit{j}}^{+}-{\mathit{s}}_{\mathit{j}}^{-}$
$s_1^{+}=8$	$s_1^{-}=-6$	$s_1=14$
$s_2^{+}=4$	$s_2^{-}=-5$	$s_2=9$
$s_3^{+}=15$	$s_3^{-}=-3$	$s_3=18$
$s_4^{+}=10$	$s_4^{-}=-4$	$s_4=14$
$s_5^{+}=0$	$s_5^{-}=6$	$s_5=-6$
$s_6^{+}=2$	$s_6^{-}=-1$	$s_6=3$
$s_7^{+}=3$	$s_7^{-}=4$	$s_7=-1$

.

Based on Table 27, we can observe that the maximum score $max{s}_j=s_3$; thus, the experts will select $z_3$.

5. Comparative Analysis

This section provides a critical analysis of the proposed N-BSE model, emphasizing its advantages, comparing it with existing approaches, and outlining its limitations. The goal is to evaluate the model’s performance within the context of MAGDM, particularly in situations involving expert input and non-binary evaluations.

5.1. Advantages of the Proposed Model

The proposed N-BSE model offers several significant advantages over existing models in the realm of MAGDM. Key benefits include:

• Comprehensive evaluation: incorporates both positive and negative attributes of alternatives, offering a more balanced and complete assessment.
• Expert opinion integration: aggregates diverse evaluations from multiple experts, ensuring robust and well-rounded DM.
• Non-binary evaluation: allows multi-valued evaluations, providing finer distinctions between alternatives and enhancing DM accuracy.
• Flexibility: applicable across various domains like business, engineering, and healthcare, making it versatile for a wide range of DM problems.
• Transparency: the systematic evaluation process and expert aggregation ensure a transparent and explainable DM framework.

5.2. Comparison with Relevant Existing Approaches

In this subsection, we compare the N-BSE model with several existing approaches, focusing on expert input, evaluation types, and the handling of both positive and negative attributes. The models differ in terms of whether expert input is incorporated, whether bipolarity (the distinction between positive and negative attributes) is considered, and whether evaluations are binary (limited to 0 or 1) or multinary (allowing for more nuanced assessments).

The following

Table 28. Comparison of N-BSE model with relevant existing approaches.

Model	Expert Input	Bipolarity	Evaluation Type	Description
S-set [17]	No	Not considered	Binary	Alternatives are evaluated using predefined attributes. Alternatives are assessed in a binary manner.
SE set [53]	Yes	Not considered	Binary	Experts assess alternatives based on binary parameters. The evaluations focus solely on whether attributes of alternatives are satisfied (1) or not (0).
BS set [26]	No	Considered	Binary	Assesses both supportive and contradictory attributes of alternatives using binary values.
BSE set [59]	Yes	Considered	Binary	Combines expert input with bipolarity. Experts evaluate both positive and negative aspects of alternatives, assigning binary values.
N-S set [31]	No	Not considered	Multinary	Extends binary evaluations to multinary scales, allowing for nuanced assessments of alternatives’ attributes.
N-SE set [56]	Yes	Not considered	Multinary	Experts evaluate alternatives using multinary scales, capturing a range of values for attributes.
N-BS set [32]	No	Considered	Multinary	Incorporates both positive and negative evaluations of alternatives using multinary values, providing detailed assessments.
N-BSE set (proposed)	Yes	Considered	Multinary	Combines expert input, bipolarity, and multinary evaluations. Experts assess both positive and negative aspects of alternatives using multinary values, offering comprehensive and detailed DM.

summarizes these models, showing how they vary in terms of expert input, bipolarity, evaluation type, and the specific methodology for assessing alternatives.

5.3. Limitations of the Proposed Model

Despite its advantages, the N-BSE model has certain limitations:

• Expert input dependency: the model relies heavily on expert evaluations, which may introduce subjectivity and prove challenging in contexts with limited expert availability.
• Complex aggregation: aggregating multi-valued expert evaluations can be complex and require sophisticated techniques to ensure consistency and accuracy, especially with large datasets.

6. Conclusions and Future Directions

In this paper, we introduced the N-BSE model, a novel approach to MAGDM that integrates expert input, bipolarity, and non-binary evaluations. The N-BSE model provides a comprehensive framework for handling both positive and negative attributes of alternatives, offering a more balanced and nuanced assessment compared to traditional methods. Through the definition of core operations and the presentation of its algebraic properties, we demonstrated the mathematical foundation of the model and its applicability to real-world DM problems. The model’s versatility was highlighted through a case study on selecting sustainable energy solutions, illustrating its ability to aggregate expert opinions and provide optimal decisions in complex, multi-criteria scenarios. A comparative analysis further emphasized the advantages of the N-BSE model, particularly in its ability to handle non-binary evaluations and incorporate diverse expert viewpoints. Overall, the N-BSE model represents a significant advancement in DM frameworks, offering a robust, transparent, and flexible approach to MAGDM that can be applied across various domains.

In the future, we aim to expand our work to include (1) fuzzy N-BSE sets, (2) intuitionistic fuzzy N-BSE sets, (3) Pythagorean fuzzy N-BSE sets, (4) Fermatean fuzzy N-BSE sets, (5) q-rung orthopair fuzzy N-BSE sets, and other related models.