Memetic-Based Biogeography Optimization Model for the Optimal Design of Mechanical Systems
Abstract
1. Introduction
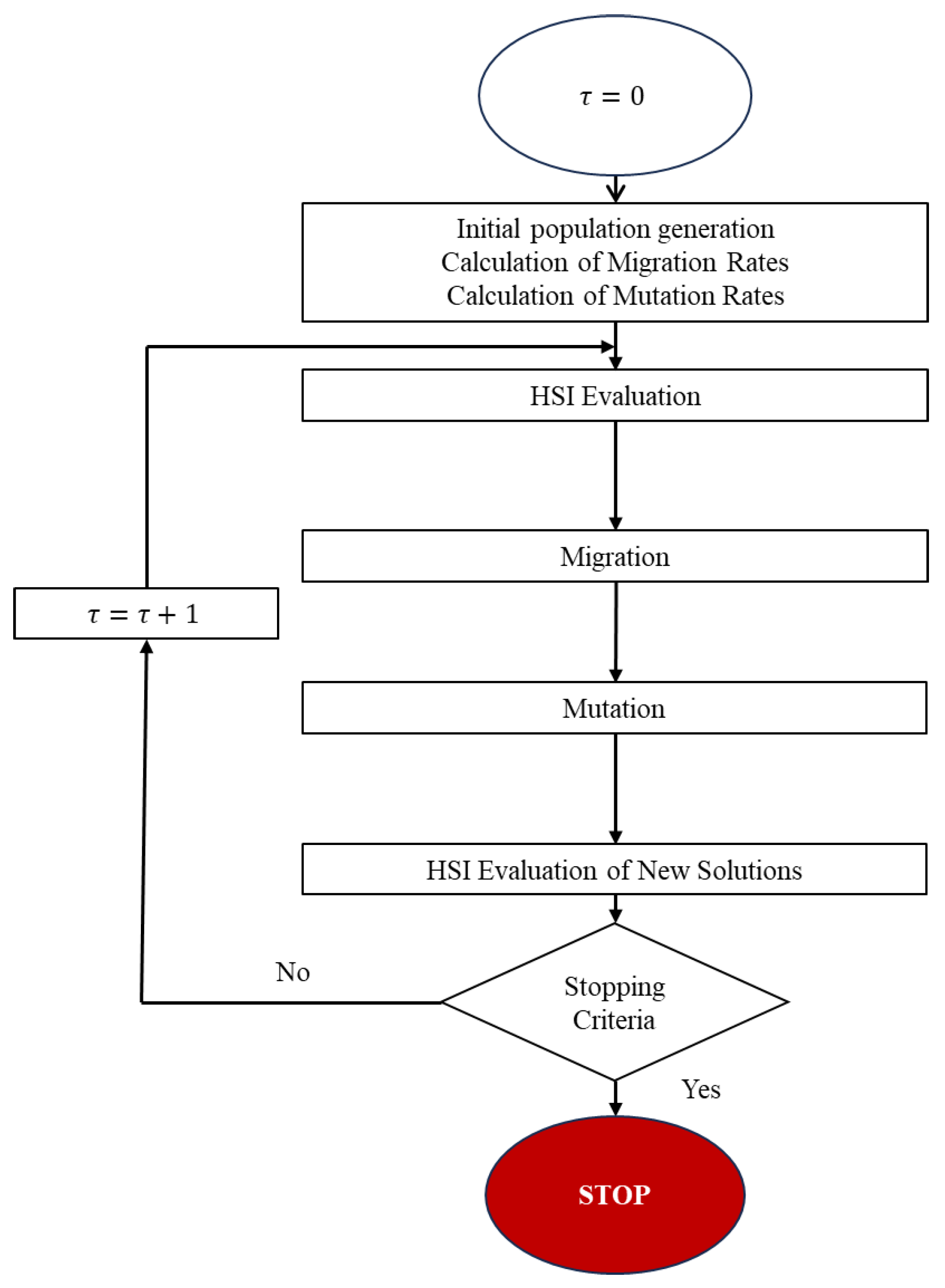
2. BBO Approach Model
2.1. Mathematical Model
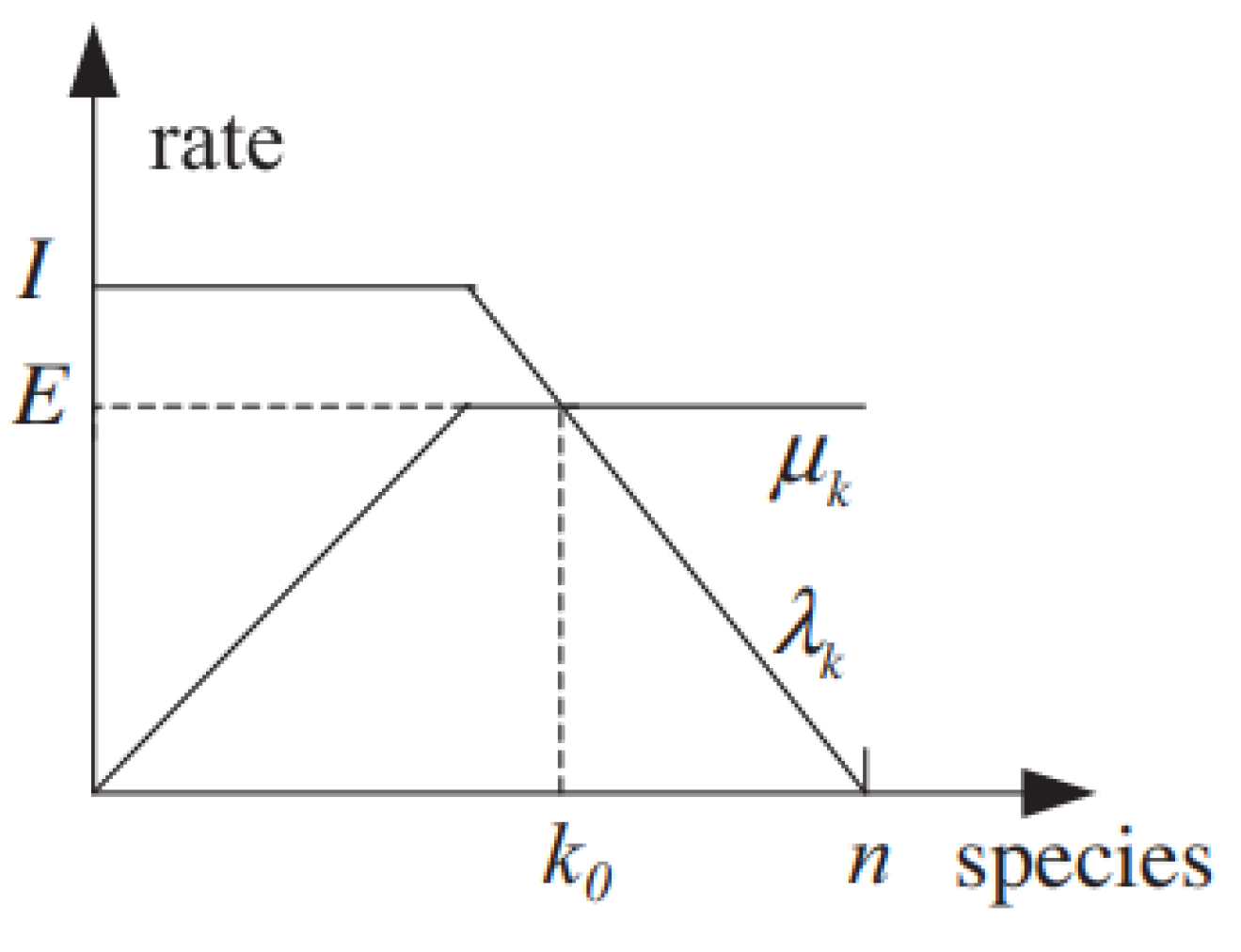
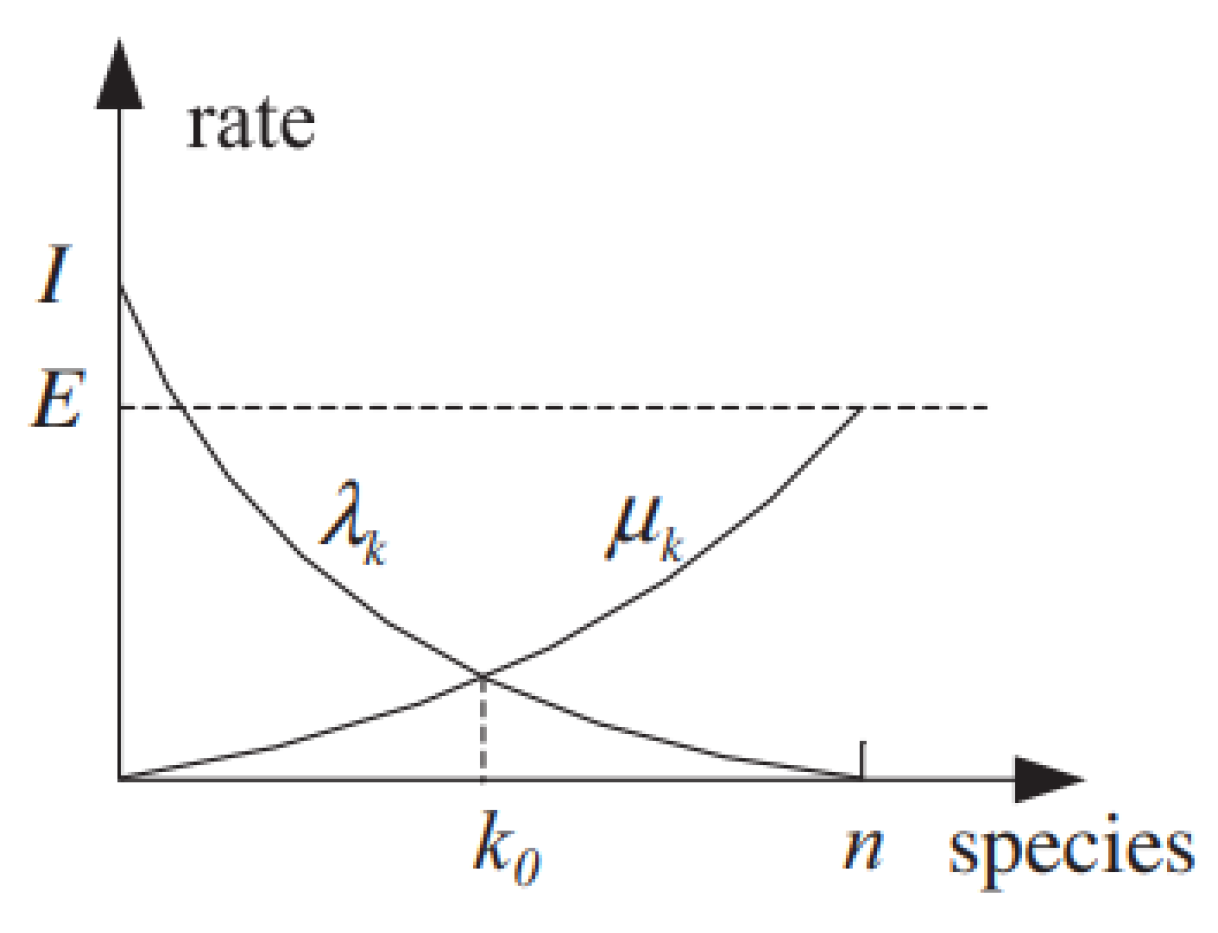
2.2. Migration Operator
| Algorithm 1: Migration’s Pseudocode | |
| 1 | For to do |
| 2 | If then |
| 3 | |
| 4 | Define |
| 5 | End If |
| 6 | End For |
2.3. Mutation Operator
| Algorithm 2: Pseudocode for BBO’s standard mutation | |
| 1 | For to do |
| 2 | If then |
| 3 | |
| 4 | End If |
| 5 | End For |
| Algorithm 3: Pseudocode for differential mutation | |
| 1 | For to do |
| 2 | ) and a dimension () randomly |
| 3 | to do |
| 4 | If then |
| 5 | If or then |
| 6 | |
| 7 | Else |
| 8 | |
| 9 | End If |
| 10 | Else |
| 11 | If or then |
| 12 | |
| 13 | Else |
| 14 | |
| 15 | End If |
| 16 | End If |
| 17 | End For |
| 18 | End For |
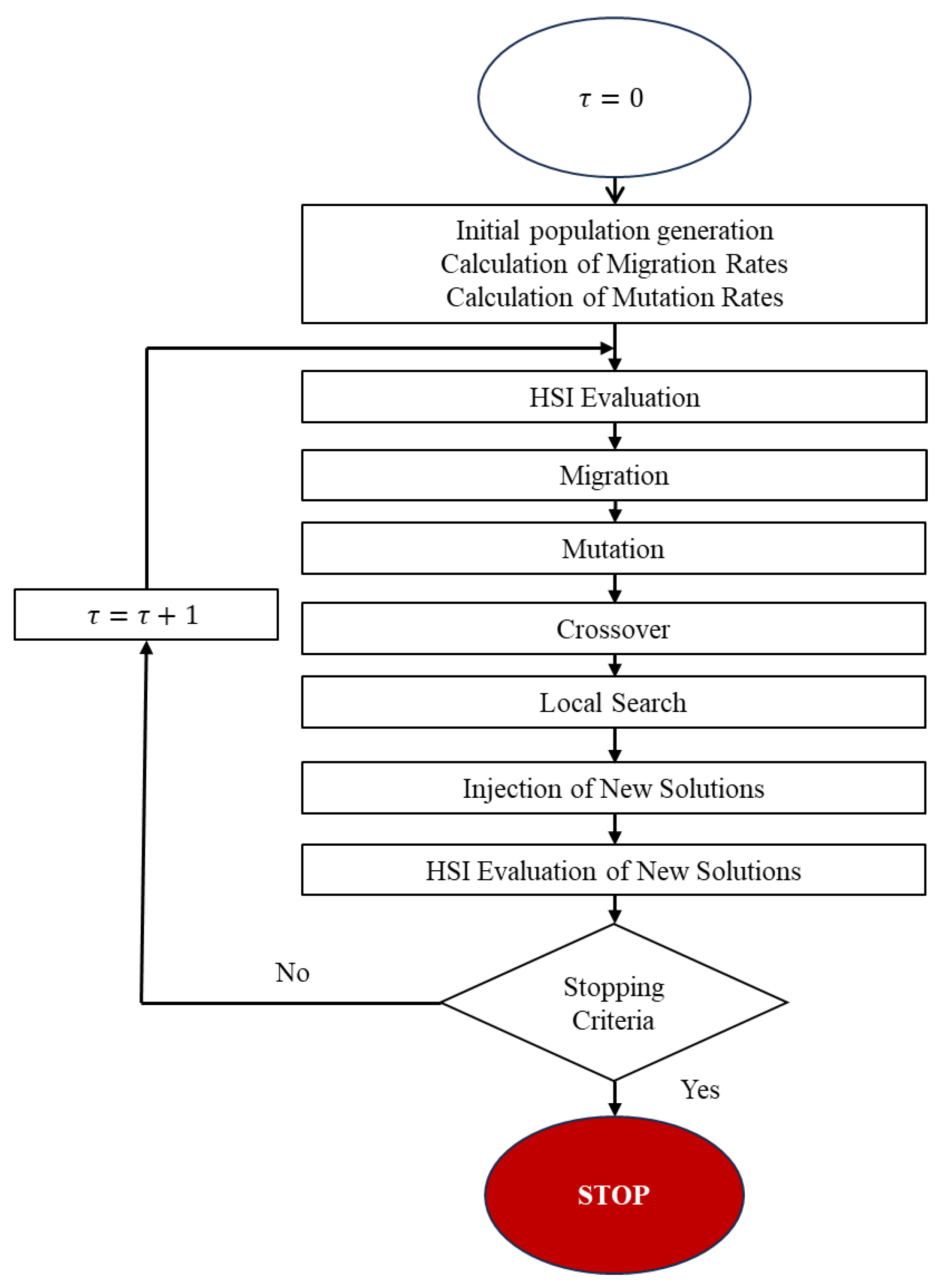
3. Proposed Approach for BBO
3.1. Operators, Modifications, and Hybridization
| Algorithm 4: Hook-Jeeves local search method pseudocode | |
| 1 | ) |
| 2 | For to do |
| 3 | |
| 4 | Perform the first step iteration (Equation (26)) |
| 5 | in BBO algorithm |
| 6 | is better than then |
| 7 | |
| 8 | End If |
| 9 | Save the solution information, |
| 10 | /* Local search loop */ |
| 11 | While stopping criteria are not verified do |
| 12 | Compute the new step value (Equation (27)) |
| 13 | Compute the new solution |
| 14 | If is better than then |
| 15 | |
| 16 | If better than then |
| 17 | |
| 18 | End If |
| 19 | End If |
| 20 | End While |
| 21 | End For |
3.2. Numerical Implementation
4. Case Studies
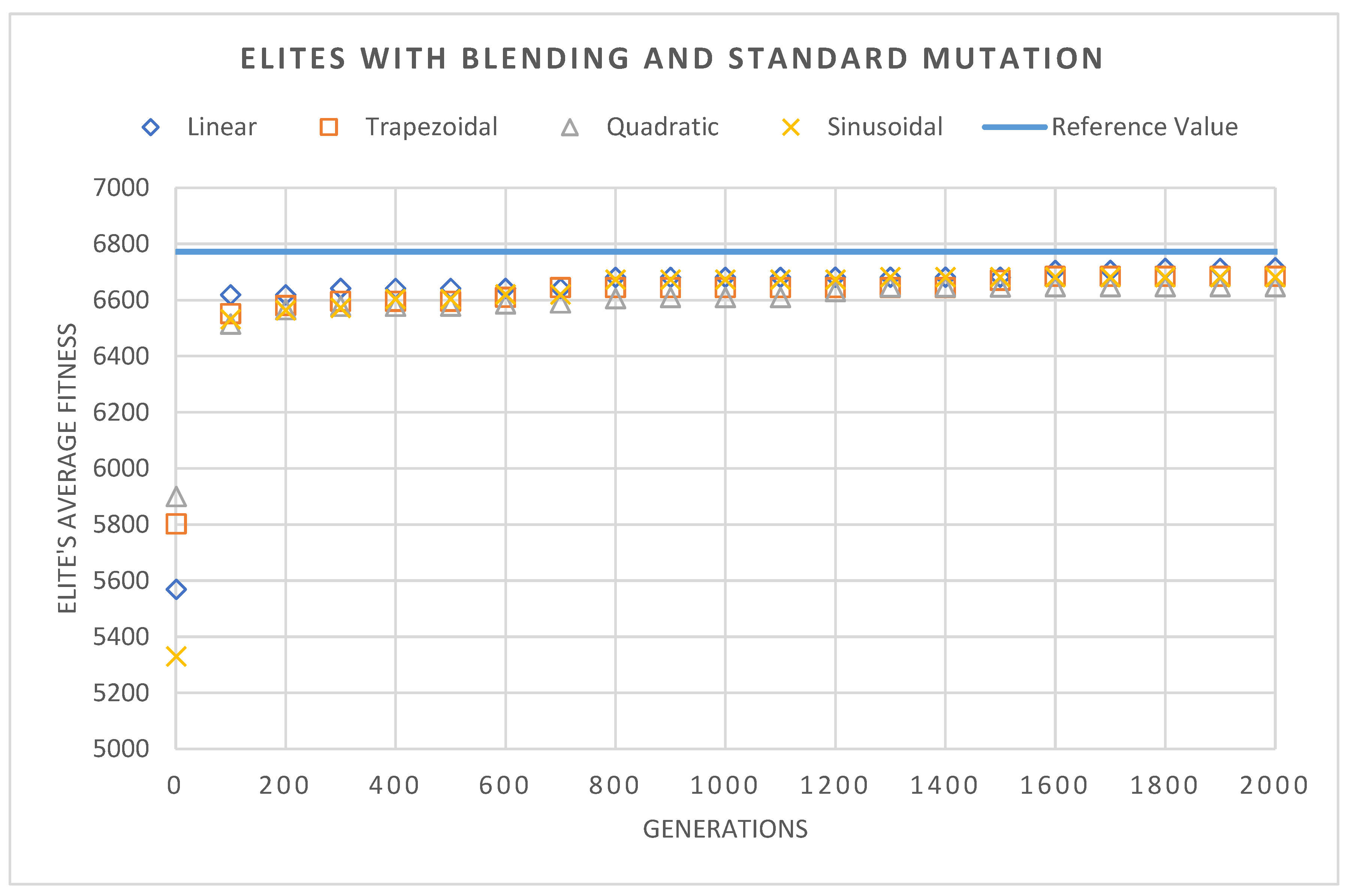
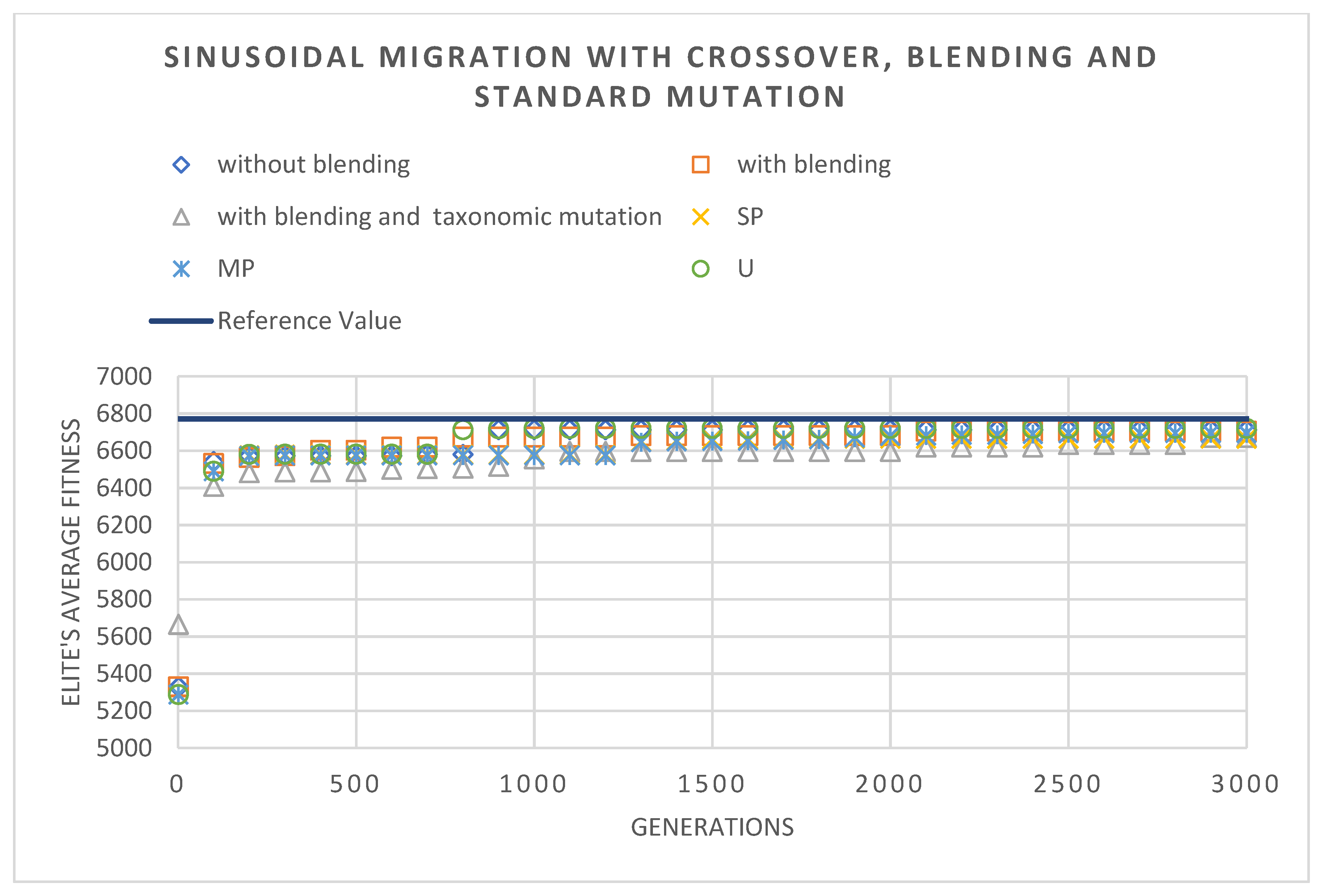
4.1. Case Study 1: Welded Beam Design
Results for the Case Study 1
- The fully hybridized model shows the best results. It is even possible to obtain better results than the reference value [17];
- The Hooke–Jeeves local optimizer was the inclusion with the most impact. In this example, the influence of the crossover was not very significant;
- Standard mutation had the best performance, with and without the use of the blending strategy in migration;
- Blending had an impact, also showing good synergy with the local optimizer and crossover operators;
- The linear migration model obtained the best performance, proving to be more consistent;
- It should be noted that the sinusoidal migration model also obtained good results.
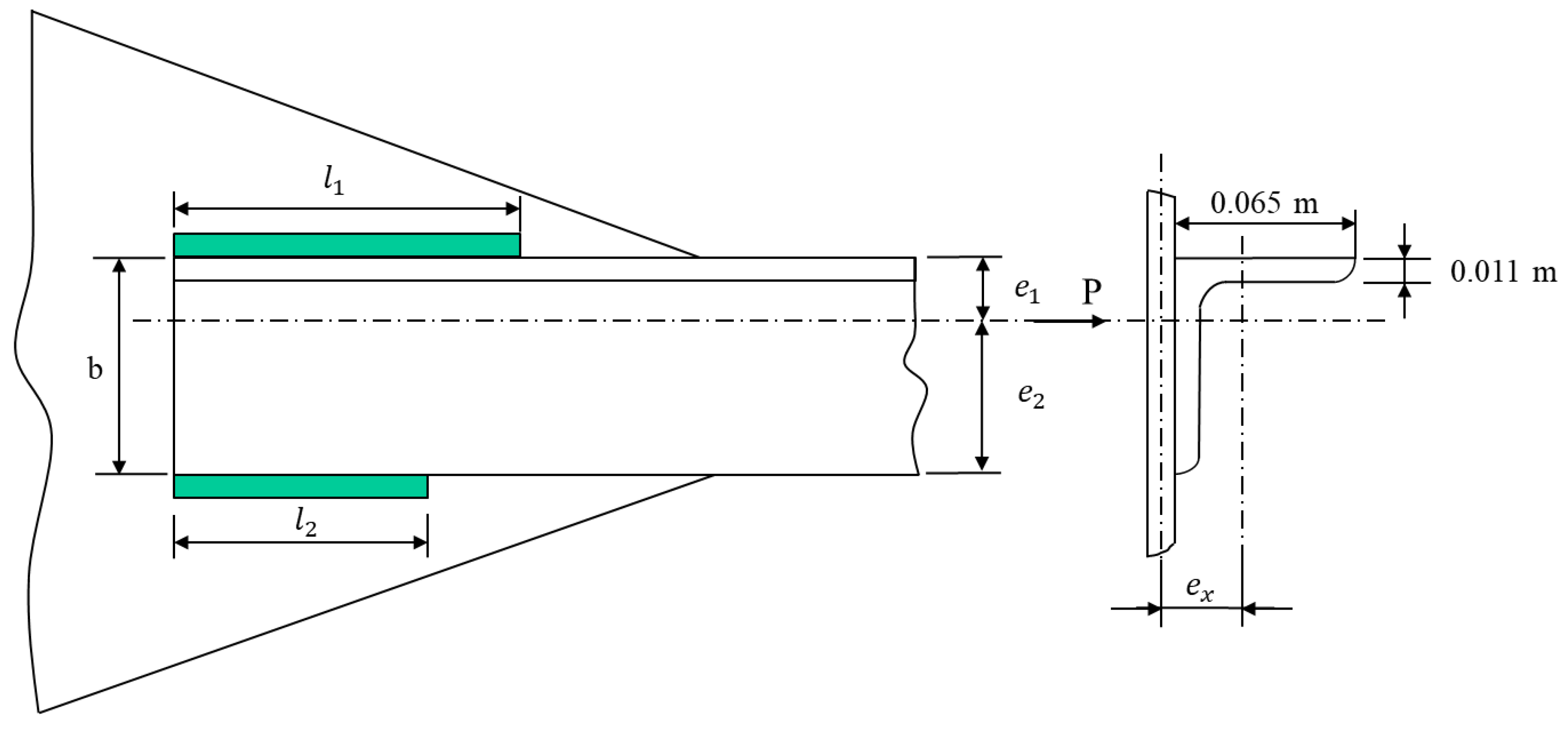
4.2. Case Study 2: Welded Gusset Optimal Design
Results for the Case Study 2
- -
- The fully hybridized model with the different options originally not included in the BBO continued to achieve the best results;
- -
- The inclusion of the crossover operator proved to be a good option, showing good results both with and without the use of the Hooke–Jeeves local optimizer. Both strategies achieved good results;
- -
- The Hooke–Jeeves local optimizer continued to be an advantage, showing several robust results;
- -
- The migration model with blending was an asset. In this example, we can see its impact on synergy with the other hybridization options, especially the Hooke–Jeeves local optimizer;
- -
- The linear migration model was the most prevalent in this case;
- -
- Both mutations achieved good results, but the taxonomic mutation showed worse synergy when integrated with other options, slowing down the algorithm in some cases.
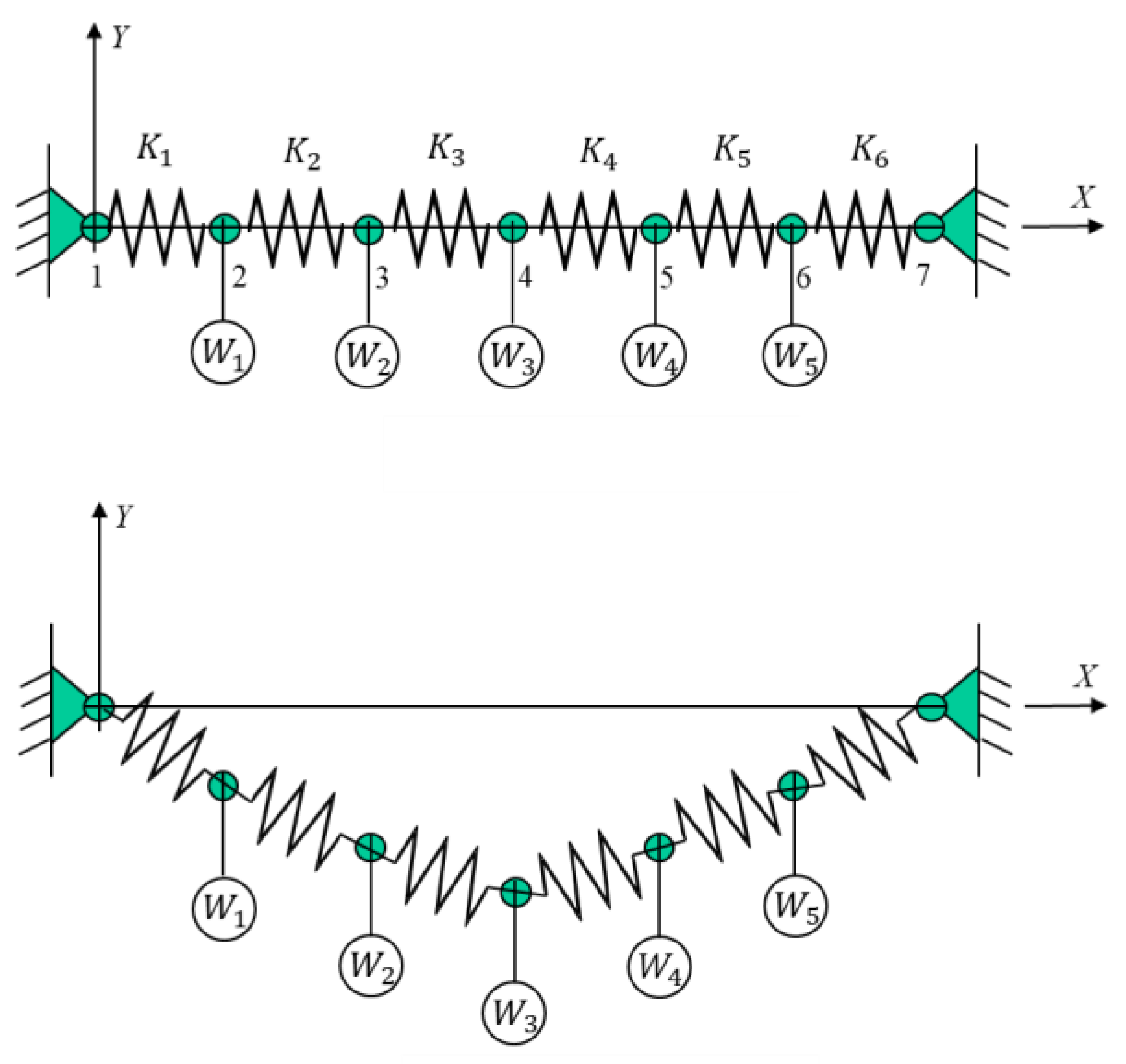
4.3. Case Study 3: Design of Springs and Weights System
Results for the Case Study 3
- -
- The algorithm presented more difficulties in this example but managed to obtain solutions close to the reference value when fully hybridized;
- -
- Both options included (crossover and local optimizer) had an impact, with the local optimizer being the most important;
- -
- The linear model continued to have the best performance, but the other non-linear models obtained the best results in the end;
- -
- Standard mutation obtained the best results due to a problem that differential mutation had with the bad solutions coming from the crossover operators;
- -
- Migration with blending has continued to be an impactful modification, and this example demonstrates it well.
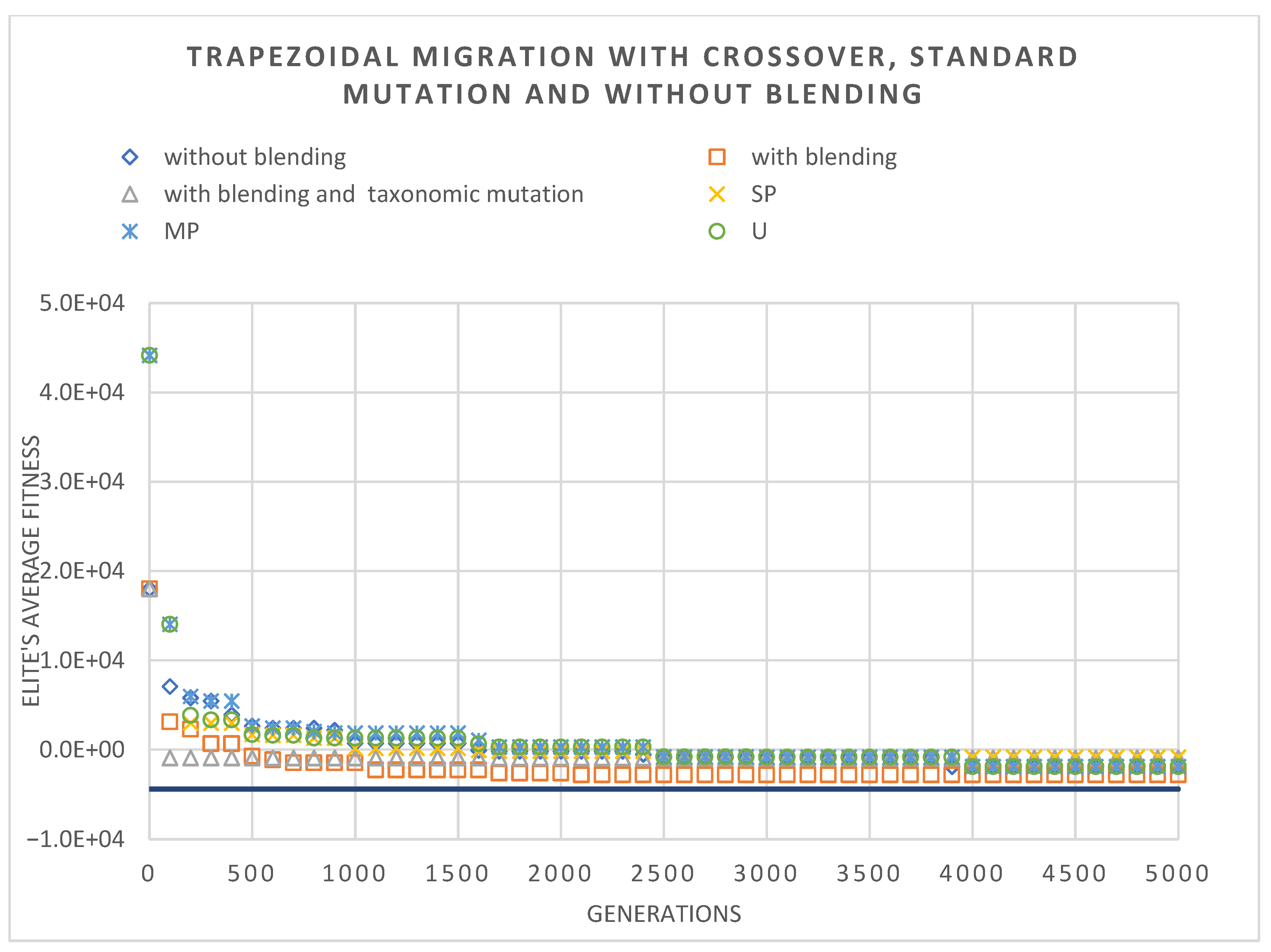
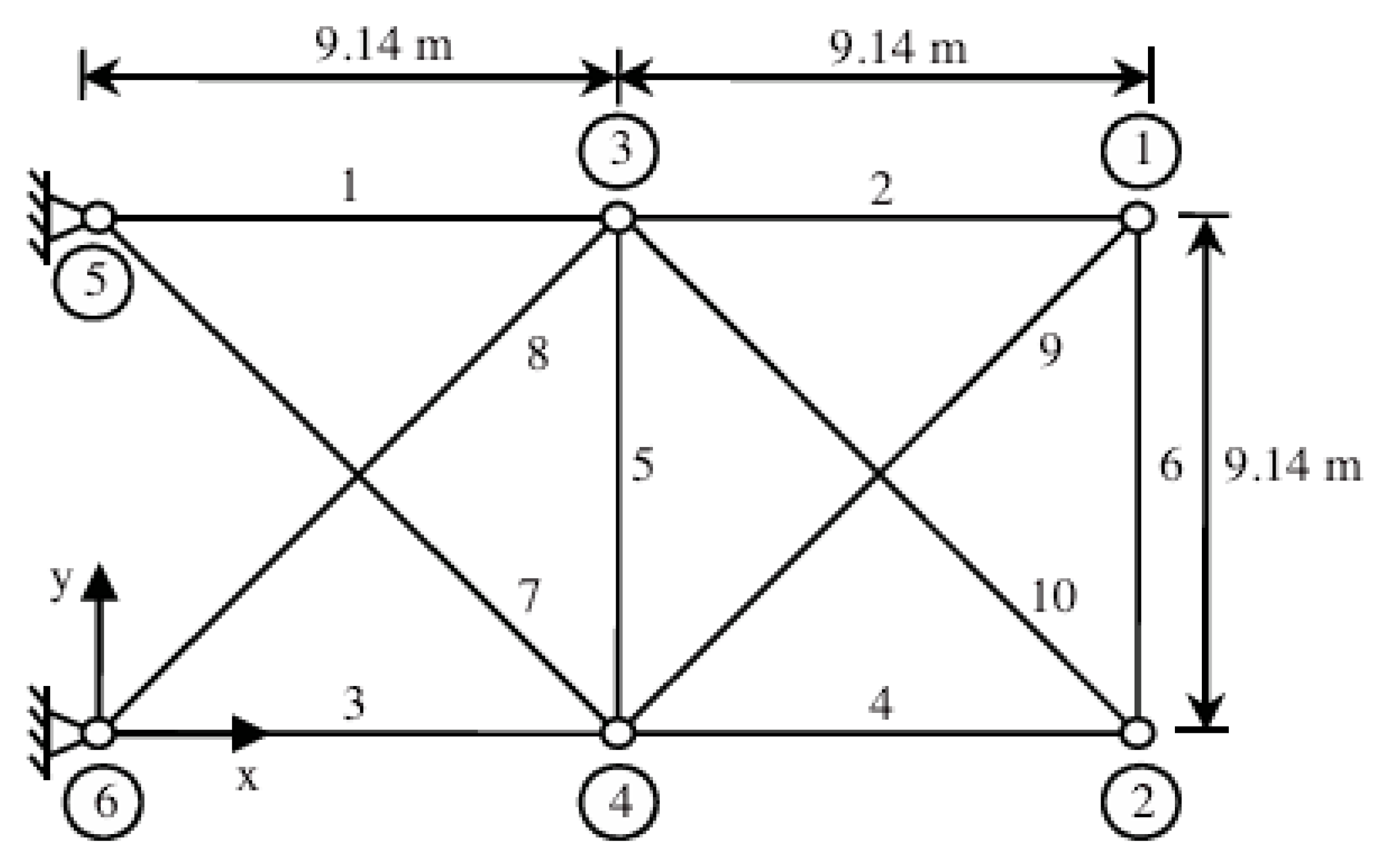
4.4. Case Study 4: The 10-Bar Truss
Results for the Case Study 4
- -
- The inclusion options (crossover and local optimizer) had quite an impact. The fully hybridized algorithm obtained the best results;
- -
- This example has shown that for more complex problems, more complex migration models obtain better results. However, the linear model manages to overcome this advantage in some cases with its good synergy with other techniques;
- -
- The model, without hybridization, struggled to achieve reasonable results;
- -
- The migration model with blending maintained its good performance, especially during tests including other hybridization options;
- -
- The model with standard mutation obtained the best results, but taxonomic mutation also performed well.
5. Statistical Tests
- As observed, there are only five values below the normal significance value (α = 0.05), which means that these tests (marked in bold) were the only ones in which the difference between parameters was significant enough to reject the null hypothesis;
- It can also be seen that local research, on average, has the lowest p-value, so it can be concluded that its introduction has had the greatest impact on the method;
- It is also important to note that the differences between the different migration models were not as significant as the other additions since, on average, the p-value is the highest of all the tests;
- The values obtained in the mutation tests are also very interesting, with the second lowest average p-value, which may be due to the problems that were described in Case Study 3, with the use of the crossover and taxonomic mutation operators, a problem that also arose in Case Study 2, the two case studies with the lowest p-value for mutation.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Holland, J. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Dawkins, R. The Selfish Gene; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- Lamarck, J.B. Zoological Philosophy; Macmillan and Co.: London, UK, 1914. [Google Scholar]
- Mark Baldwin, J. A New Facctor in Evolution. Am. Natl. 1869, 30, 354. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D.; Siarry, P.; Zhile, Y.; Fei, M. Biogeography-Based Optimization: A 10-Year Review. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 391–406. [Google Scholar] [CrossRef]
- Ma, H. An analysis of the equilibrium of migration models for biogeography. Inf. Sci. 2010, 180, 3444–3464. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D. Blended biogeography-based optimization for constrained optimization. Eng. Appl. Artif. Intell. 2011, 24, 517–525. [Google Scholar] [CrossRef]
- Boussaïd, I.; Chatterjee, A.; Siarry, P.-N.M. Biogeography-based optimization for constrained optimization problems. Comput. Oper. Res. 2012, 39, 3293–3304. [Google Scholar] [CrossRef]
- Bi, X.; Wang, J. Constrained Optimization Based on Epsilon Constrained Biogeography-Based Optimization. Int. Conf. Intell. Hum.-Mach. Syst. Cybern. 2012, 2, 369–372. [Google Scholar]
- Ma, H.; Ruan, X.; Pan, Z. Handling multiple objectives with biogography-based optimization. Int. J. Autom. Comput. 2012, 9, 30–36. [Google Scholar] [CrossRef]
- Bi, X.; Wang, J.; Li, B. Multi-objective optimization based in hybrid biogeography-based optimization. Syst. Eng. Electron. 2014, 36, 179–186. [Google Scholar]
- Xu, Z. Study on Multi-Objective Optimization Theory and Application Based on Biogeography Algorithm. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2013. [Google Scholar]
- Kundra, H.; Sood, M. Cross-Country Path Finding using Hybrid approach of PSO and BBO. Internatuinal J. Comput. Appl. 2010, 7, 15–19. [Google Scholar] [CrossRef]
- Albrase, F.; Alroomi, A.; Talaq, J. Optimal Coordination of Directional Overcurrent Relays Using Biogeography-Based Optimization Algorithm. IEEE Trans. Power Deliv. 2015, 30, 1810–1820. [Google Scholar]
- Gong, W.; Cai, Z.; Ling, C. “DE/BBO: A hybrid differential evolution with biogeography.based optimization for global numerical optimization. Soft Comput. 2010, 15, 645–665. [Google Scholar] [CrossRef]
- Boussaid, I.; Chatterjee, A.; Siarry, P.; Ahmed-Nacer, M. Hybridizing Biogeography-Based Optimization With Differential Evolution for Optimal Power Allocation in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2011, 60, 2347–2353. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Hybrid differential evolution with biogeography-based optimization algorithm for solution of economic emission load dispatch problems. Expert Syst. Appl. 2011, 38, 14001–14010. [Google Scholar] [CrossRef]
- Panchal, V.; Jundra, H.; Kaur, A. An Integrated Approach to Biogeography Based Optimization with case based reasoning for retrieving Groundwater Possibility. J. Technol. Eng. Sci. 2010, 1, 32–38. [Google Scholar]
- Wang, L.; Xu, Y. An effective hybrid biogeography-based optimization algorithm for parameter estimation of chaotic systems. Expert Syst. Appl. 2011, 38, 15103–15109. [Google Scholar] [CrossRef]
- Arora, P.; Jundra, H.; Panchal, V. Fusion of Biogeography based optimization and Artificial bee colony for identification of Natural Terrain Features. Int. J. Adv. Comput. Sci. Appl. 2012, 3. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Duan, H.; Shao, M. Hybridizing Harmony Search with Biogeography Based Optimization for Global Numerical Optimization. J. Comput. Theor. Nanosci. 2013, 10, 2312–2322. [Google Scholar] [CrossRef]
- Zhao, B.; Deng, C.; Yang, Y.; Peng, H. Novel Binary Biogeography-Based Optimization Algorithm for the Knapsack Problem. In Proceedings of the International Conference in Swarm Intelligence, Shenzhen, China, 17–20 June 2012. [Google Scholar]
- Conceição António, C.A. A hierarchical genetic algorithm for reliability based design of geometrically non-linear composite structures. Compos. Struct. 2001, 54, 37–47. [Google Scholar] [CrossRef]
- Conceição António, C.A. A multilevel genetic algorithm for optimization of geometrically nonlinear stiffened composite structures. Struc. Multidisc. Optim. 2002, 24, 372–386. [Google Scholar] [CrossRef]
- Wilson, E.O.; MacArthur, R. The Theory of Island Biogeography; Princeton University Press: Princeton, NJ, USA, 1967. [Google Scholar]
- Zheng, Y.; Sueqin, L.; Zhang, M.; Chen, S. Biogeography-Based Optimization: Algorithms and Applications; Science Press Beijing: Beijing, China, 2019. [Google Scholar]
- Hao, J.; Zhao, X.; Ji, Y. A Novel Biogeography-Based Optimization Algorithm with Momentum Migration and Taxonomic Mutation. Adv. Swarm Intell. 2020, 12145, 83–93. [Google Scholar]
- António, C.C. Optimization of Mechanical Systems; Efeitos Gráficos: Porto, Portugal, 2022. [Google Scholar]
- Eshelman, L.; Caruana, A.; Schaffer, J. Biases in the crossover landscape. In Proceedings of the Third International Conference on Genetic Algorithms, Fairfax, VA, USA, 4–7 June 1989; pp. 10–19. [Google Scholar]
- Peixoto, A. Modelo de Otimização Biogeográfico Hibridizado com Algoritmos Meméticos para Conceção Ótima de Sistemas Mecânicos; Faculdade de Engenharia da Universidade do Porto: Porto, Portugal, 2024. [Google Scholar]
- António, C.A.C.; Carneiro, G.M.P.N. Optimization of Mechanical Systems: Optimal Design Applications; Efeitos Gráficos: Porto, Portugal, 2022. [Google Scholar]
- “Welded Beam Design Optimization”, MAPLE. Available online: https://www.maplesoft.com/support/help/maple/view.aspx?path=applications%2FWeldedBeam (accessed on 1 March 2024).
- Gonçalves, H.F.S. Development and Implementation of Memetic Models for the Optimal Design of Mechanical Systems; Faculdade de Engenharia da Universidade do Porto: Porto, Portugal, 2023. [Google Scholar]
- REAE. Decreto-Lei nº 21/86. In Regulamento de Estruturas de Aço para Edifícios; Imprensa Nacional Casa da Moeda: Lisbon, Portugal, 1986. [Google Scholar]
- Vanderplaats, G.N. Numerical Optimization with MATLAB Programming; McGraw Hill: New York, NY, USA, 1984. [Google Scholar]
- Aminifar, F.; Aminifar, F.; Nazarpour, D. Optimal design of truss structures via an augmented genetic algorithm. Turk. J. Eng. Environ. Sci. 2013, 37, 56–68. [Google Scholar]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 674–701. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]








| Migration | Blending | Mutation | Crossover | Strategy | Local Search | Objective | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Linear | No | Standard | No | 0.1793 | 4.6384 | 9.0316 | 0.2113 | 1.8761 | ||
| Linear | No | Taxonomic | No | 1.1000 | 1.1000 | 4.1000 | 1.1000 | 4.7467 | ||
| Quadratic | Yes | Standard | No | 0.1887 | 3.9392 | 8.8488 | 0.2138 | 1.7917 | ||
| Sinusoidal | Yes | Taxonomic | No | 0.2225 | 3.2084 | 8.9869 | 0.2064 | 1.7428 | ||
| Quadratic | No | Standard | Yes | 0.1923 | 3.9511 | 8.8552 | 0.2176 | 1.8252 | ||
| Linear | No | Taxonomic | Yes | 0.1597 | 6.9744 | 9.0712 | 0.2083 | 2.1033 | ||
| Trapezoidal | Yes | Standard | Yes | 0.2118 | 3.3365 | 9.0278 | 0.2057 | 1.7192 | ||
| Trapezoidal | Yes | Taxonomic | Yes | 0.2117 | 3.3369 | 9.0281 | 0.2057 | 1.7192 | ||
| Linear | Yes | Taxonomic | MP | PEbS | No | 0.2115 | 3.3289 | 9.0875 | 0.2090 | 1.7487 |
| Quadratic | Yes | Taxonomic | MP | ISbF | No | 0.2084 | 3.4617 | 8.8805 | 0.2116 | 1.7501 |
| Trapezoidal | Yes | Standard | SP | PEbS | Yes | 0.2117 | 3.3377 | 9.0269 | 0.2057 | 1.7192 |
| Sinusoidal | Yes | Taxonomic | SP | ISbF | Yes | 0.2115 | 3.3425 | 9.0269 | 0.2057 | 1.7192 |
| Migration | Blending | Mutation | Crossover | Strategy | Local Search | Objective | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Linear | No | Standard | No | 5.152 | 5.446 | 383.299 | 240.904 | 3286.891 | ||
| Linear | No | Taxonomic | No | 5.433 | 5.833 | 385.931 | 220.302 | 3382.000 | ||
| Linear | Yes | Standard | No | 5.333 | 5.285 | 377.282 | 240.724 | 3284.266 | ||
| Sinusoidal | Yes | Taxonomic | No | 5.272 | 5.256 | 383.589 | 242.931 | 3299.102 | ||
| Linear | No | Standard | Yes | 5.162 | 4.751 | 400.000 | 250.000 | 3252.320 | ||
| Linear | No | Taxonomic | Yes | 5.370 | 4.460 | 400.000 | 248.257 | 3255.336 | ||
| Linear | Yes | Standard | Yes | 4.957 | 4.935 | 399.908 | 249.939 | 3215.531 | ||
| Quadratic | Yes | Taxonomic | Yes | 5.144 | 5.144 | 385.182 | 246.330 | 3248.703 | ||
| Quadratic | Yes | Standard | SP | PEbS | No | 5.265 | 5.262 | 382.206 | 238.214 | 3266.031 |
| Quadratic | Yes | Standard | U | ISbF | No | 5.243 | 5.241 | 382.236 | 240.257 | 3263.141 |
| Linear | Yes | Standard | U | PEbS | Yes | 4.945 | 4.945 | 400.000 | 250.000 | 3214.375 |
| Linear | Yes | Standard | MP | ISbF | Yes | 4.945 | 4.945 | 400.000 | 250.000 | 3214.375 |
| Migration | Blending | Mutation | Crossover | Strategy | Local Search | Objective | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Linear | No | Standard | No | 10.661 | 21.662 | 32.472 | 42.576 | 52.798 | −1.074 | −6.640 | −8.149 | −8.245 | −6.338 | −2672.011 | ||
| Linear | No | Taxonomic | No | 9.693 | 20.007 | 32.468 | 41.354 | 50.033 | −5.157 | −5.452 | −8.277 | −4.353 | −1.409 | 1365.146 | ||
| Linear | Yes | Standard | No | 10.687 | 21.898 | 32.099 | 42.324 | 51.633 | −4.513 | −8.426 | −11.010 | −9.361 | −5.726 | −4092.193 | ||
| Quadratic | Yes | Taxonomic | No | 9.623 | 21.124 | 31.305 | 41.743 | 51.953 | −6.019 | −9.242 | −10.971 | −9.279 | −6.374 | −3823.344 | ||
| Linear | No | Standard | Yes | 10.661 | 21.662 | 32.472 | 42.576 | 52.798 | −1.074 | −6.640 | −8.149 | −8.245 | −6.338 | −2672.01 | ||
| Trapezoidal | Yes | Standard | Yes | 10.331 | 21.037 | 31.642 | 42.043 | 51.727 | −4.289 | −7.907 | −9.817 | −9.330 | −5.954 | −4415.8 | ||
| Trapezoidal | Yes | Taxonomic | Yes | 10.260 | 20.769 | 31.299 | 41.583 | 51.383 | −4.159 | −7.885 | −9.418 | −8.652 | −5.501 | −4354.79 | ||
| Linear | Yes | Standard | U | PEbS | No | 10.260 | 20.769 | 31.299 | 41.583 | 51.383 | −4.159 | −7.885 | −9.418 | −8.652 | −5.501 | −4354.79 |
| Linear | Yes | Standard | MP | ISbF | No | 10.138 | 21.365 | 31.552 | 41.634 | 51.231 | −4.565 | −6.713 | −8.980 | −8.843 | −5.249 | −4151.46 |
| Quadratic | Yes | Standard | SP | PEbS | Yes | 10.347 | 21.076 | 31.679 | 42.082 | 51.764 | −4.292 | −7.914 | −9.860 | −9.390 | −6.003 | −4416.36 |
| Sinusoidal | Yes | Standard | U | ISbF | Yes | 10.349 | 21.078 | 31.679 | 42.080 | 51.766 | −4.286 | −7.892 | −9.840 | −9.377 | −6.005 | −4416.36 |
| Migration | Blending | Mutation | Crossover | Strategy | Local Search | Objective | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Trapezoidal | No | Standard | No | 0.0156 | 0.0166 | 0.0224 | 0.0183 | 0.000108 | 0.00548 | 0.0135 | 0.02 | 0.00635 | 0.0225 | 4221.072 | ||
| Linear | No | Taxonomic | No | 0.0226 | 0.0226 | 0.0226 | 0.0129 | 0.000315 | 0.0226 | 0.0226 | 0.0226 | 0.00374 | 0.0226 | 5189.495 | ||
| Trapezoidal | Yes | Standard | No | 0.0205 | 0.000506 | 0.0212 | 0.0141 | 0.000407 | 0.0106 | 0.00353 | 0.0204 | 0.0173 | 0.0214 | 3946.545 | ||
| Linear | Yes | Taxonomic | No | 0.0215 | 0.0154 | 0.0177 | 0.0224 | 0.00825 | 0.00695 | 0.0225 | 0.0209 | 0.00915 | 0.021 | 4974.689 | ||
| Quadratic | No | Standard | Yes | 0.00536 | 0.000065 | 0.0226 | 0.0226 | 0.0000645 | 0.0000645 | 0.00531 | 0.0199 | 0.0000645 | 0.0226 | 3002.792 | ||
| Linear | No | Taxonomic | Yes | 0.0205 | 0.0226 | 0.0223 | 0.013 | 0.0000645 | 0.0073 | 0.0225 | 0.00992 | 0.0203 | 0.0226 | 4873.072 | ||
| Trapezoidal | Yes | Standard | Yes | 0.000397 | 0.000065 | 0.0195 | 0.0114 | 0.0000645 | 0.000398 | 0.00353 | 0.0158 | 0.000567 | 0.0197 | 2226.827 | ||
| Sinusoidal | Yes | Taxonomic | Yes | 0.00098 | 0.000065 | 0.0179 | 0.0213 | 0.0000645 | 0.00476 | 0.00437 | 0.0226 | 0.0000645 | 0.0222 | 2908.027 | ||
| Linear | Yes | Taxonomic | MP | PEbS | No | 0.000213 | 0.000065 | 0.0197 | 0.00961 | 0.0000645 | 0.00032 | 0.00352 | 0.0188 | 0.00185 | 0.0171 | 2234.67 |
| Linear | Yes | Taxonomic | SP | ISbF | No | 0.000065 | 0.000065 | 0.0158 | 0.0132 | 0.0000645 | 0.000509 | 0.00366 | 0.0203 | 0.00186 | 0.0168 | 2280.885 |
| Sinusoidal | Yes | Standard | U | PEbS | Yes | 0.000725 | 0.000066 | 0.0226 | 0.0108 | 0.0000651 | 0.000925 | 0.00346 | 0.0166 | 0.00152 | 0.0144 | 2182.267 |
| Quadratic | Yes | Standard | MP | ISbF | Yes | 0.000684 | 0.000065 | 0.0215 | 0.0141 | 0.0000677 | 0.00101 | 0.00348 | 0.0146 | 0.00138 | 0.0152 | 2190.475 |
| Case Study | Test | Test Statistic | p-Value |
|---|---|---|---|
| 1 | Migration | 0.9344 | 0.8171 |
| Mutation | 3 | 0.4652 | |
| Crossover | 4 | 0.3452 | |
| Crossover Operators (PEbS) | 8.4 | 0.01499 | |
| Crossover Operators (ISbF) | 6 | 0.04978 | |
| Local Search | 0 | 0.02771 | |
| 2 | Migration | 2.636 | 0.4512 |
| Mutation | 0 | 0.03125 | |
| Crossover | 5 | 0.5002 | |
| Crossover Operators (PEbS) | 0.6667 | 0.7165 | |
| Crossover Operators (ISbF) | 0.1333 | 0.9355 | |
| Local Search | 0 | 0.02771 | |
| 3 | Migration | 0.5556 | 0.9065 |
| Mutation | 0 | 0.125 | |
| Crossover | 0 | 0.1797 | |
| Crossover Operators (PEbS) | 2 | 0.3679 | |
| Crossover Operators (ISbF) | 4.667 | 0.09697 | |
| Local Search | 0 | 0.1088 | |
| 4 | Migration | 0.5056 | 0.9177 |
| Mutation | 5 | 0.3125 | |
| Crossover | 0 | 0.125 | |
| Crossover Operators (PEbS) | 1.5 | 0.4724 | |
| Crossover Operators (ISbF) | 0.5 | 0.7788 | |
| Local Search | 1 | 0.0625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peixoto, A.C.F.; António, C.A.C. Memetic-Based Biogeography Optimization Model for the Optimal Design of Mechanical Systems. Mathematics 2025, 13, 492. https://doi.org/10.3390/math13030492
Peixoto ACF, António CAC. Memetic-Based Biogeography Optimization Model for the Optimal Design of Mechanical Systems. Mathematics. 2025; 13(3):492. https://doi.org/10.3390/math13030492
Chicago/Turabian StylePeixoto, Arcílio Carlos Ferreira, and Carlos A. Conceição António. 2025. "Memetic-Based Biogeography Optimization Model for the Optimal Design of Mechanical Systems" Mathematics 13, no. 3: 492. https://doi.org/10.3390/math13030492
APA StylePeixoto, A. C. F., & António, C. A. C. (2025). Memetic-Based Biogeography Optimization Model for the Optimal Design of Mechanical Systems. Mathematics, 13(3), 492. https://doi.org/10.3390/math13030492








