On the Integral Representation of Jacobi Polynomials
Abstract
1. Introduction
2. A New Integral Representation of Jacobi Polynomials
2.1. Preliminaries for Jacobi Polynomials
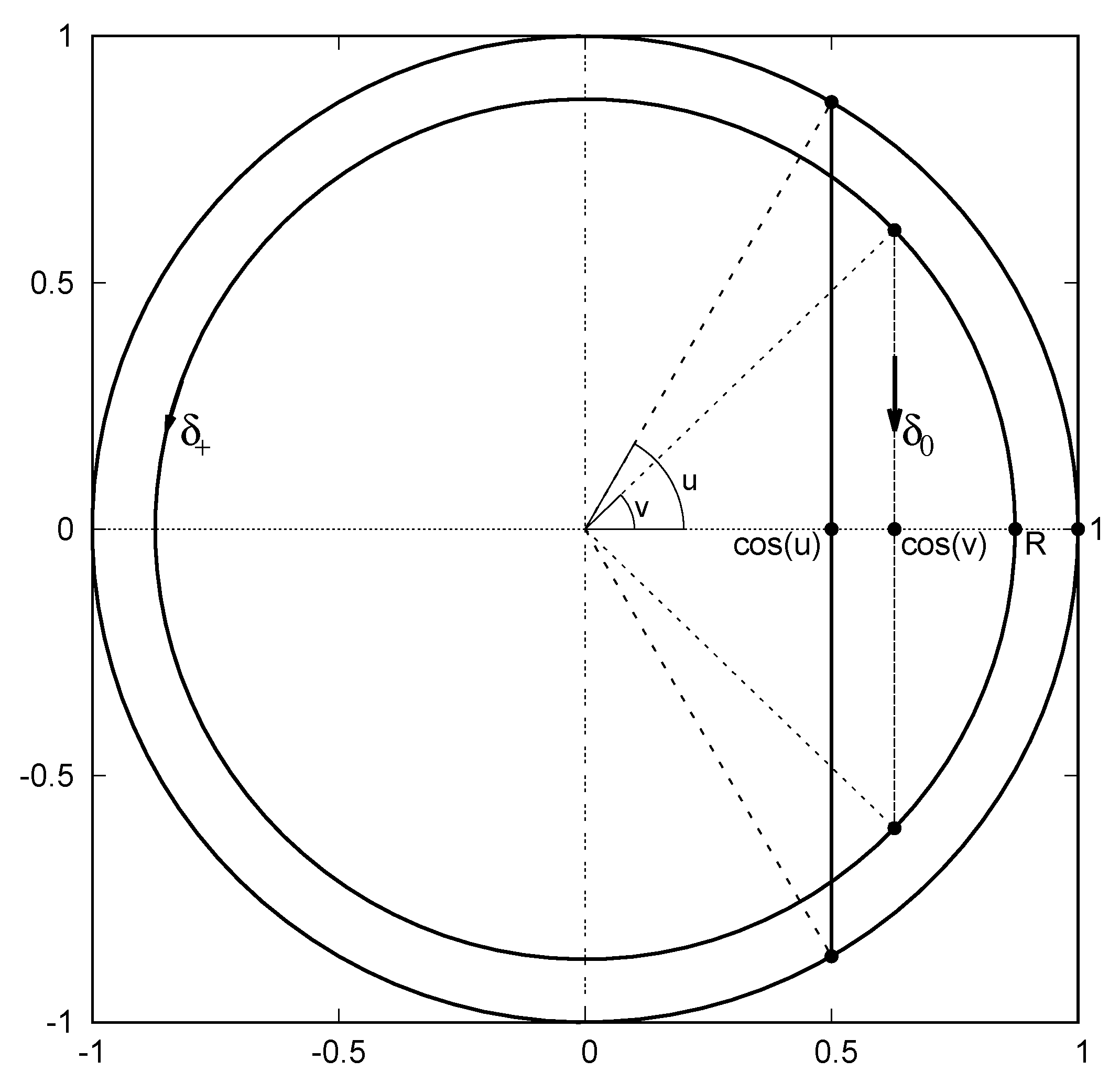
2.2. A New Integral Representation of Jacobi Polynomials
Representation of Jacobi Polynomials in Terms of Gegenbauer Polynomials
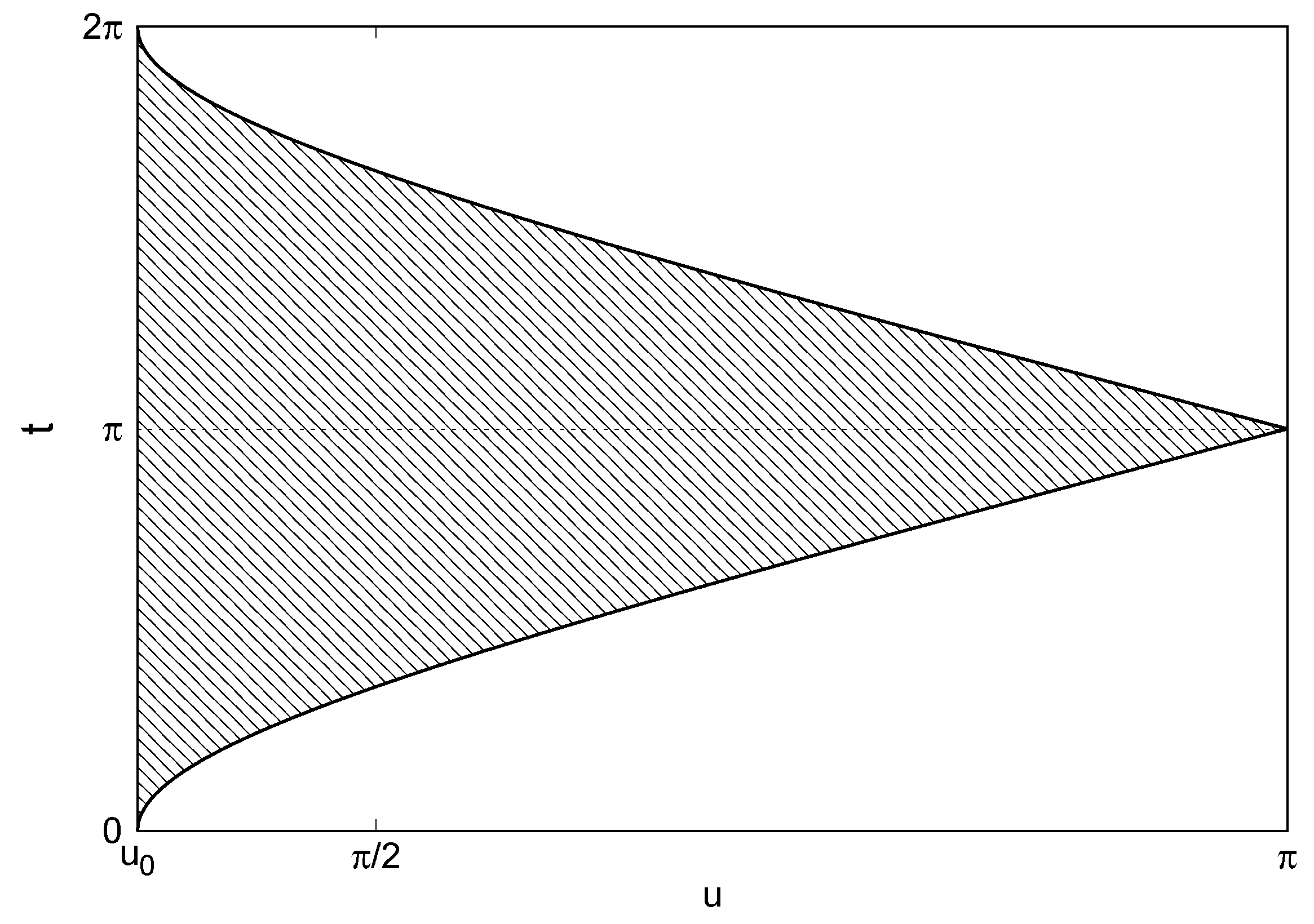
3. Fourier–Jacobi Coefficients
3.1. Extension of the Fourier–Jacobi Coefficients to Negative Index n
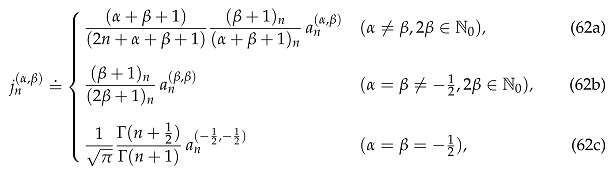 where are the Fourier–Jacobi coefficients defined in (38). Then, for , the corresponding Fourier–Jacobi coefficients with a negative index are given by
where are the Fourier–Jacobi coefficients defined in (38). Then, for , the corresponding Fourier–Jacobi coefficients with a negative index are given by
3.2. Relations Between Coefficients with Different Parameters
3.2.1. Recurrence Relations
3.2.2. Fourier–Jacobi Coefficients of Derivatives and Anti-Derivatives
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Recurrence Relations for the Fourier–Jacobi Coefficients and
References
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods, Scientific Computation; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Gottlieb, D.; Orszag, S.A. Numerical Analysis of Spectral Methods: Theory and Applications; SIAM: Philadelphia, PA, USA, 1977. [Google Scholar]
- Hesthaven, J.S.; Gottlieb, S.; Gottlieb, D. Spectral Methods for Time-dependent Problems; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Colton, D. Jacobi polynomials of negative index and a nonexistence theorem for the generalized axially symmetric potential equation. SIAM J. Appl. Math. 1968, 16, 771–776. [Google Scholar] [CrossRef]
- Erdélyi, A. Singularities of generalized axially symmetric potentials. Comm. Pure Appl. Math. 1956, 9, 403–414. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L.-L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Doha, E.H.; Bhrawy, A.H. Efficient spectral-Galerkin algorithms for direct solution of fourth-order differential equations using Jacobi polynomials. Appl. Numer. Math. 2008, 58, 1224–1244. [Google Scholar] [CrossRef]
- Guo, B. Jacobi spectral approximations to differential equations on the half line. J. Comput. Math. 2000, 18, 95–112. [Google Scholar]
- Duran, A. Spectral Jacobi approximations for Boussinesq systems. Stud. Appl. Math. 2024, 153, e12680. [Google Scholar] [CrossRef]
- Guo, B.-y.; Wang, L.-l. Jacobi approximations in non-uniformly Jacobi-weighted Sobolev spaces. J. Approx. Theory 2004, 128, 1–41. [Google Scholar] [CrossRef]
- Babuška, I.; Guo, B. Optimal estimates for lower and upper bounds of approximation errors in the p-version of the finite element method in two dimensions. Numer. Math. 2000, 85, 219–255. [Google Scholar] [CrossRef]
- Awonusika, R.; Taheri, A. A spectral identity on Jacobi Polynomials and its analytic implications. Canad. Math. Bull. 2018, 61, 473–482. [Google Scholar] [CrossRef]
- Lecoanet, D.; Vasil, G.M.; Burns, K.J.; Brown, B.P.; Oishi, J.S. Tensor calculus in spherical coordinates using Jacobi polynomials. Part-II: Implementation and examples. J. Comput. Phys. X 2019, 3, 100012. [Google Scholar] [CrossRef]
- Tehrani, S.A.; Khorramian, A.N. The Jacobi polynomials QCD analysis for the polarized structure function. J. High Energy Phys. 2007, 2007, 048. [Google Scholar] [CrossRef]
- Domina, M.; Patil, U.; Cobelli, M.; Sanvito, S. Cluster expansion constructed over Jacobi-Legendre polynomials for accurate force fields. Phys. Rev. B 2023, 108, 094102. [Google Scholar] [CrossRef]
- Bergeron, G.; Vinet, L.; Zhedanov, A. Signal Processing, Orthogonal Polynomials, and Heun Equations. In Orthogonal Polynomials; Foupouagnigni, M., Koepf, W., Eds.; Birkhäuser: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Tchiotsop, D.; Wolf, D.; Louis-Dorr, V.; Husson, R. ECG data compression using Jacobi polynomials. Annu. Int. Conf. IEEE Eng. Med Biol. Soc. 2007, 2007, 1863–1967. [Google Scholar] [CrossRef] [PubMed]
- Koornwinder, T.H. The addition formula for Jacobi polynomials I summary of results. Indag. Math. (Proc.) 1972, 34, 188–191. [Google Scholar] [CrossRef]
- Koornwinder, T.H. Jacobi Polynomials and Their Two-Variable Analogues. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 1975. [Google Scholar]
- Braaksma, B.L.J.; Meulenbeld, B. Jacobi polynomials as spherical harmonics. Indag. Math. (Proc.) 1968, 71, 384–389. [Google Scholar] [CrossRef]
- Dijksma, A.; Koornwinder, T.H. Spherical harmonics and the product of two Jacobi polynomials. Indag. Math (Proc.) 1971, 74, 191–196. [Google Scholar] [CrossRef]
- Aomoto, K. Jacobi polynomials associated with Selberg integrals. SIAM J. Math. Anal. 1987, 18, 545–549. [Google Scholar] [CrossRef]
- Feldheim, E. Relations entre les polynomes de Jacobi, Laguerre et Hermite. Acta Math. 1941, 74, 117–138. [Google Scholar] [CrossRef]
- Askey, R.; Fitch, J. Integral representations for Jacobi polynomials and some applications. J. Math. Anal. Appl. 1969, 26, 411–437. [Google Scholar] [CrossRef]
- Chatterjea, S.K. Integral representation for the product of two Jacobi polynomials. J. Lond. Math. Soc. 1964, s1-39, 753–756. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Panda, R. An integral representation for the product of two Jacobi polynomials. J. Lond. Math. Soc. 1976, s2-12, 419–425. [Google Scholar] [CrossRef]
- Szegö, G. Orthogonal Polynomials, IV ed.; Colloquium Publications; AMS: Providence, RI, USA, 1975; Volume 23. [Google Scholar]
- Olver, F.W.J.; Olde Daalhuis, A.B.; Lozier, D.W.; Schneider, B.I.; Boisvert, R.F.; Clark, C.W.; Miller, B.R.; Saunders, B.V.; Cohl, H.S.; McClain, M.A. (Eds.) NIST Digital Library of Mathematical Functions. Release 1.2.3. Available online: http://dlmf.nist.gov/ (accessed on 16 December 2024).
- Askey, R. Jacobi polynomials, I. New proof of Koornwinder’s Laplace type integral representation and Bateman’s bilinear sum. SIAM J. Math. Anal. 1974, 5, 119–124. [Google Scholar] [CrossRef]
- Koelink, H.T. On Jacobi and continuous Hahn polynomials. Proc. Amer. Math. Soc. 1996, 124, 887–898. [Google Scholar] [CrossRef]
- Kvernadze, G. Uniform convergence of Fourier-Jacobi series. J. Approx. Theory 2002, 117, 207–228. [Google Scholar] [CrossRef]
- Chen, S.; Shen, J.; Wang, L.-L. Generalized Jacobi functions and their applications to fractional differential equations. Math. Comput. 2016, 300, 1603–1638. [Google Scholar] [CrossRef]
- Liu, G.; Liu, W.; Duan, B. Estimates for coefficients in Jacobi series for functions with limited regularity by fractional calculus. Adv. Comput. Math. 2024, 50, 68. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Fractional Sturm-Liouville eigen-problems: Theory and numerical approximation. J. Comput. Phys. 2013, 252, 495–517. [Google Scholar] [CrossRef]
- Awonusika, R.O.; Ariwayo, A.G. Descriptions of fractional coefficients of Jacobi polynomial expansions. J. Anal. 2022, 30, 1567–1608. [Google Scholar] [CrossRef]
- Ervin, V.J.; Heuer, N.; Roop, J.P. Regularity of the solution to 1-D fractional order diffusion equations. Math. Comput. 2018, 87, 2273–2294. [Google Scholar] [CrossRef]
- Khosravian-Arab, H.; Almeida, R. Numerical solution for fractional variational problems using the Jacobi polynomials. Appl. Math. Model. 2015, 39, 6461–6470. [Google Scholar] [CrossRef]
- Singh, H.; Pandey, R.K.; Srivastava, H.M. Solving non-lineal fractional variational problems using Jacobi polynomials. Mathematics 2019, 7, 224. [Google Scholar] [CrossRef]
- Muthukumar, P.; Priya, B.G. Numerical solution of fractional delay differential equation by shifted Jacobi polynomials. Int. J. Comput. Math. 2017, 94, 471–492. [Google Scholar] [CrossRef]
- Esmaeili, S.; Shamsi, M.; Luchko, Y. Numerical solution of fractional differential equations with a collocation method based on Müntz polynomials. Comput. Math. Appl. 2011, 62, 918–929. [Google Scholar] [CrossRef]
- Calvetti, D. A stochastic roundoff error analysis for the fast Fourier transform. Math. Comput. 1991, 56, 755–774. [Google Scholar] [CrossRef]
- Bonneux, N. Exceptional Jacobi polynomials. J. Approx. Theory 2019, 239, 72–112. [Google Scholar] [CrossRef]
- Lewanowicz, S. Quick construction of recurrence relations for the Jacobi coefficients. J. Comput. Appl. Math. 1992, 43, 355–372. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Xie, Z. Sharp error bounds for Jacobi expansions and Gegenbauer-Gauss quadrature of analytic functions. SIAM J. Numer. Anal. 2013, 51, 1443–1469. [Google Scholar] [CrossRef]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume 2. [Google Scholar]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials; Chapman and Hall/CHC: New York, NY, USA, 2002. [Google Scholar]
- Friedlander, F.G. Introduction to the Theory of Distributions; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Cuchta, T.; Grow, D.; Wintz, N. Discrete matrix hypergeometric functions. J. Math. Anal. Appl. 2023, 518, 126716. [Google Scholar] [CrossRef]
- Gogovcheva, E.; Boyadjiev, L. Fractional extension of Jacobi polynomials and Gauss hypergeometric function. Fract. Calc. Appl. Anal. 2005, 4, 431–438. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Micheli, E. On the Integral Representation of Jacobi Polynomials. Mathematics 2025, 13, 483. https://doi.org/10.3390/math13030483
De Micheli E. On the Integral Representation of Jacobi Polynomials. Mathematics. 2025; 13(3):483. https://doi.org/10.3390/math13030483
Chicago/Turabian StyleDe Micheli, Enrico. 2025. "On the Integral Representation of Jacobi Polynomials" Mathematics 13, no. 3: 483. https://doi.org/10.3390/math13030483
APA StyleDe Micheli, E. (2025). On the Integral Representation of Jacobi Polynomials. Mathematics, 13(3), 483. https://doi.org/10.3390/math13030483





