Research on the Design and Meshing Performance Analysis of Face Gear Face Gear Meshing Nutation Reducers

Abstract

In view of the problems of the complex design, difficult machining, and high manufacturing cost of a traditional nutation reducer, this paper intends to design a nutation reducer and study its meshing performance. First, the meshing pair is designed by the method of internal and external cutting of the shaper cutter, and the method of face gear tooth surface modification is proposed. Second, based on tooth contact analysis (TCA) and loaded tooth contact analysis (LTCA), the contact performance of the meshing pair is studied. Then, the nutation reducer is improved by using the pair instead of the internal bevel gear pair. Finally, examples are presented to test the feasibility of the improved design. The results show that the improved nutation reducer maintains the advantages of a large transmission ratio and high bearing capacity of the traditional nutation reducer and can make use of the advantages of face gears to further improve its transmission performance. This study can lay a foundation for the further application and popularization of nutation reducers.

1. Introduction

A reducer is an intermediate device connecting a power source and an actuator, and its development has a history hundreds of years long. With the continuous progress of modern technology, especially the rapid development of new energy vehicles and other equipment, the requirements for reducers are increasing day by day. Nowadays, reducers are more inclined to be lightweight, miniaturized, and precise. In this context, nutation reducers with the advantages of a compact structure, small size, and light weight have received extensive attention in the industrial field [1,2,3,4] and have gradually become a hotspot for research and application.

In the past few decades, many scholars have conducted a lot of research on nutation reducers. Yamamori Motoyasu [5] analyzed the nutation transmission mechanism and studied a nutating gear transmission mechanism suitable for automobile devices. Cheng et al. [6] analyzed the transmission ratio calculation formula of several nutation gear transmission types through practical research and proposed two output mechanism schemes. Yu et al. [7] applied nutation drives to gear drives, analyzed the calculation method of torque in cone difference nutation drives, and proposed a new optimization method. Wang et al. [8] proposed a nutation reduction transmission device, and carried out three-dimensional modeling and motion simulation to verify the correctness of the mechanism. Yao et al. [9] applied nutation drives to a nutation reducer with double-sided spiral bevel gears, established a three-dimensional model of the reducer, and carried out simulation analysis. Cai et al. [10] completed the kinematic analysis of an internal bevel gear nutation drive by combining gear meshing principles. Mathur et al. [11] calculated the meshing stiffness of nutation drives and analyzed the elastohydrodynamic lubrication of gears. Saribay et al. [12] proposed a peripheral ring transmission (PMT), studied its contact stress and bending stress, and applied it to the reducer of a helicopter, combining this with structural principles to analyze the changes in gear load and bearing load and analyze the meshing efficiency of the PMT system through the theory of elastohydrodynamic lubrication. The analysis was carried out, and a formula for calculating the meshing efficiency was obtained. The above research deepens the understanding of nutation transmission mechanisms and promotes the practical application and development of nutation deceleration technology.

A nutation reducer has a simple structure and a high reduction ratio. As the core component of the nutating reducer, the meshing bevel gear pair has attracted some scholars to conduct research on its design methods, processing, and manufacturing [13]. Shih et al. [14,15] proposed a unified mathematical model to simulate the end-face-hobbing and end milling processes of a general hypoid gear generator, and studied the relief deviation of the design parameters, including tool parameters, machine tool settings, and auxiliary gears using the polynomial coefficients of surface correction motion. Simon [16,17] used a multi-objective optimization method to propose the optimal tool geometry and machine tool settings, and introduced the optimal tooth profile modification into the teeth of a face-hobbing quasi-hyperbolic gear, with the purpose of reducing tooth contact pressure and transmission errors and reducing the sensitivity of the gear pair to tooth surface errors and the relative positions of mating components. Deng et al. [18] proposed a spiral bevel gear pair using the face-milling method, which can improve the cutting strip width and processing efficiency, and verified the feasibility of this method through processing experiments and measurements of spiral bevel gear pairs. Tang et al. [19] proposed a double-arc tooth logarithmic spiral bevel gear pair (DCAP) with a higher contact/bending strength, better load distribution, and smaller transmission error, and studied four of them. The influence of this typical manufacturing error on the meshing characteristics of bevel gear pairs provides a basic reference for the tolerance design of cycloidal bevel gears. However, there are a limited amount of research results on internal-meshing bevel gear pairs and nutation reducers that utilize internal-meshing bevel gear pairs. The main reasons are as follows: (1) the design of the teeth of the internal bevel gear pair is complex, the machining means are scarce, and the manufacturing cost is high; and (2) there are relatively few application fields for internal bevel gear transmission, and researchers lack the internal driving force for exploration. Nutation reducers have few parts, a simple structure, and a high load. Under the background of the ultimate pursuit of the high load and high speed of reducers for manufacturing equipment in various fields, nutation reducers have unique advantages that other types of reducers do not have. To promote the application of nutation reducers in more fields, further improvements are necessary.

Face gear transmission [20,21,22] is a kind of transmission mode which can realize space interleaving. Figure 1 shows three typical face gear pairs with different shaft angles. The diversity of shaft angles allows the face gears to adapt to a wider range of transmission scenarios. At present, face gear transmission has been matured and applied to the main reducer of armed helicopters [23], and its good meshing performance has attracted extensive attention from researchers. Litvin et al. [24] made a thorough study of the tooth engagement of the face gear and derived the conditions for the tooth root undercut and tooth tip sharpening of the face gears. Zanzi et al. [25] analyzed the face gear by finite element simulation method, and studied its meshing performance deeply, so as to make theoretical preparation for the design and application of face gear. Zhang et al. [26] established the design criteria of offset face gears, the axis of the pinion and the face gear are staggered. Liu et al. [27] proposed an offset face gear and multiple pinion gear transmission, which greatly utilized the advantages of offset face gear. Kawasaki et al. [28] studied helical gears, and obtained the reasonable design parameters. Feng et al. [29] analyzed the involute helical end face gear transmission. Zhu et al. [30] established a torsion-bending-pendulum gear transmission model with multi-state meshing and analyzed its dynamics. Zschippang et al. [31] studied the general generation method of face gears with helix angle, shaft angle and axial offset, and geometrically modified the pinion tooth profile. Peng et al. [32] studied the method of surface-active modification of face gear and reduced the vibration of face gear transmission through modification, which provided theoretical basis for vibration reduction design of face gear pair. Hochrein et al. [33] proposed two methods for calculating the contact stress of face gear drives with arbitrary configurations of helix angles and center offsets, as there are no established calculation standards for face gear transmissions. It can be found from the above documents that domestic and foreign research institutions invest a lot of manpower and material resources to make the design theory and manufacturing method of face gear transmission mature day by day.

Compared to the meshing bevel gear transmission, the face gear transmission has a simple tooth surface design, low error sensitivity, and the face gear can be processed with a gear shaping cutter, which is easy to process and the technology is mature. Therefore, to promote the application of nutation reducers, this paper aims to replace the internal meshing bevel gear pair with a face gear face gear meshing pair for improving the nutation reducer. The specific contents are as follows: In Section 2, a mathematical model for the conjugate meshing of face gear face gear pairs is derived using the method of internal and external cutting of the shaper cutter, and the meshing performance improvement method based on face gear tooth surface modification is proposed. In Section 3, based on TCA and LTCA, the geometric contact performance and load contact performance of face gear meshing pair are further studied to verify the meshing correctness of face gear meshing pair. In Section 4, the improved design of nutation reducer is carried out by replacing the internal meshing bevel gear meshing pair of traditional nutation reducer with the proposed face gear meshing pair. Section 6 summarizes the main conclusions of this study.

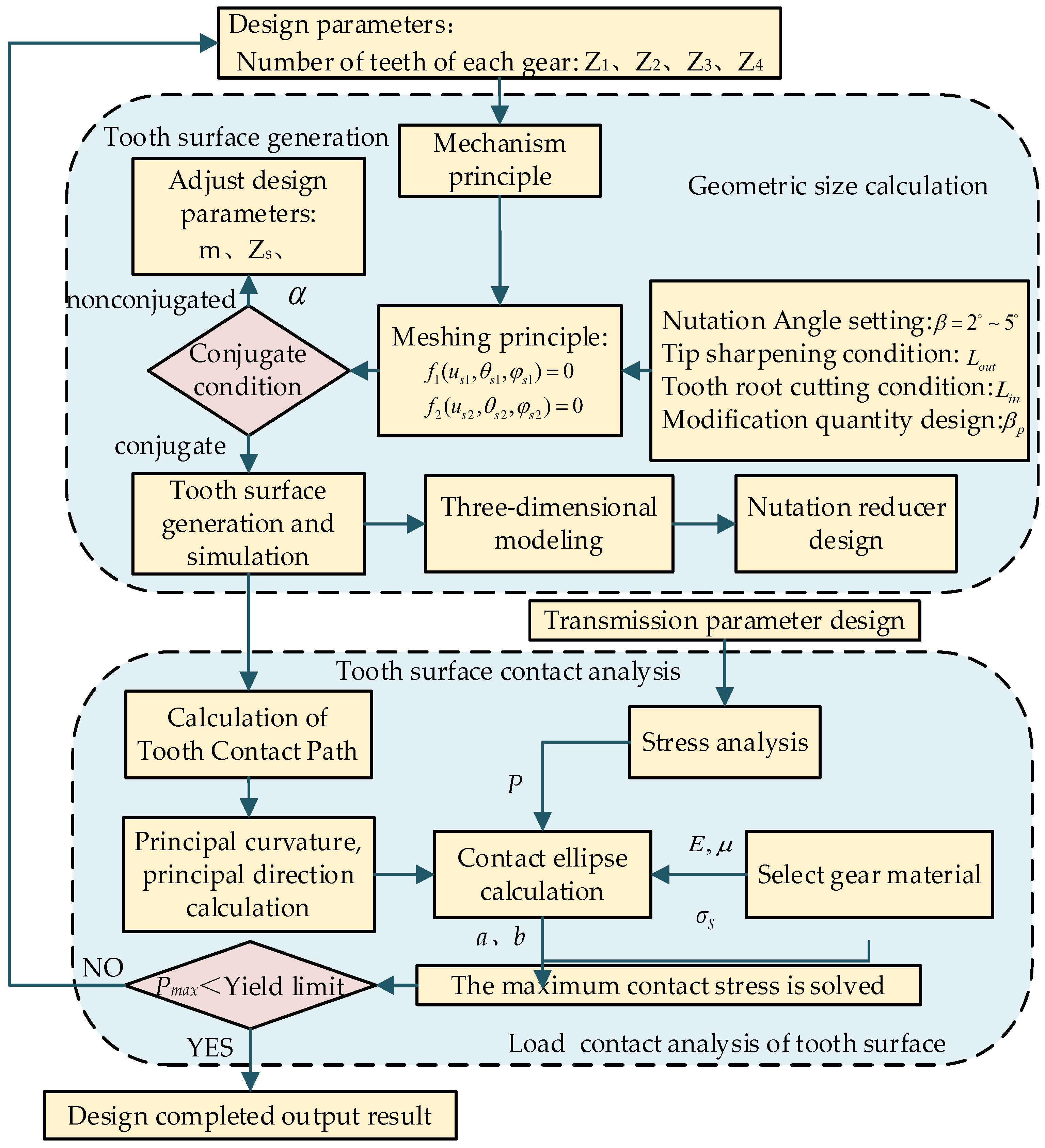
2. Geometric Generation and Modification Design of Nutation Face Gear Tooth

2.1. Design of Shaper Cutter

The tooth profile of the shaper cutter used for machining the face gear blank is the general involute tooth profile, and the tooth shape of the cutter is shown in Figure 2. The plane X₀ = 0 denotes the symmetrical plane of the tooth groove of the shaper cutter, and the other side tooth surface can be obtained according to the symmetry. θ_s0 is used to determine the shaper cutter on the base circle of the groove width of half. θ_s0 denotes the angle from the symmetry line of the cutter slot to the starting point of the involute tooth profile.

The gear shaper cutter satisfies standard involute gear equation such as Equation (1).

$${\theta }_{s0}={\displaystyle \frac{\pi }{2Z_s}}-inv{\alpha }_s$$

(1)

where, invα_s denotes the involute function of the shaper cutter; Z_s denotes the number of teeth of the shaper cutter, and α_s denotes the pressure angle of the shaper cutter.

$${\theta }_s={\theta }_k+{\alpha }_{ks}=\tan {\alpha }_{ks}$$

(2)

where, θ_s denotes the angle between the starting point of the involute of the shaper cutter and any point of the involute; θ_k denotes the spread angle of any point of the involute of the shaper cutter; α_ks denotes the pressure angle of any point of the involute of the shaper cutter.

According to Figure 2, the position vector of the gear shaper profile is Equation (3).

$${\mathit{r}}_{\mathit{s}}\left(u_s,{\theta }_s\right)=\left[\begin{array}{c}{x}_s\\ y_s\\ z_s\\ 1\end{array}\right]=\left[\begin{array}{c}{r}_{bs}[\sin ({\theta }_{s0}+{\theta }_s)-{\theta }_s\cos ({\theta }_{s0}+{\theta }_s)]\\ -r_{bs}[\sin ({\theta }_{s0}+{\theta }_s)-{\theta }_s\cos ({\theta }_{s0}+{\theta }_s)]\\ u_s\\ 1\end{array}\right]$$

(3)

where, r_bs represents the base circle radius of the shaper cutter, μ_s represents the variable in the axial direction of the shaper cutter.

Unit normal vector of shaper cutter is Equation (4).

$${\mathit{n}}_{\mathit{s}}={\displaystyle \frac{{\mathit{r}}_{{\mathit{s}}_{\mathsf{\theta }}}\times {\mathit{r}}_{{\mathit{s}}_{\mathit{u}}}}{\left|{\mathit{r}}_{{\mathit{s}}_{\mathsf{\theta }}}\times {\mathit{r}}_{{\mathit{s}}_{\mathit{u}}}\right|}}=\left[\begin{array}{c}-\cos ({\theta }_s+{\theta }_{s0})\\ -\sin ({\theta }_s+{\theta }_{s0})\\ 0\end{array}\right]$$

(4)

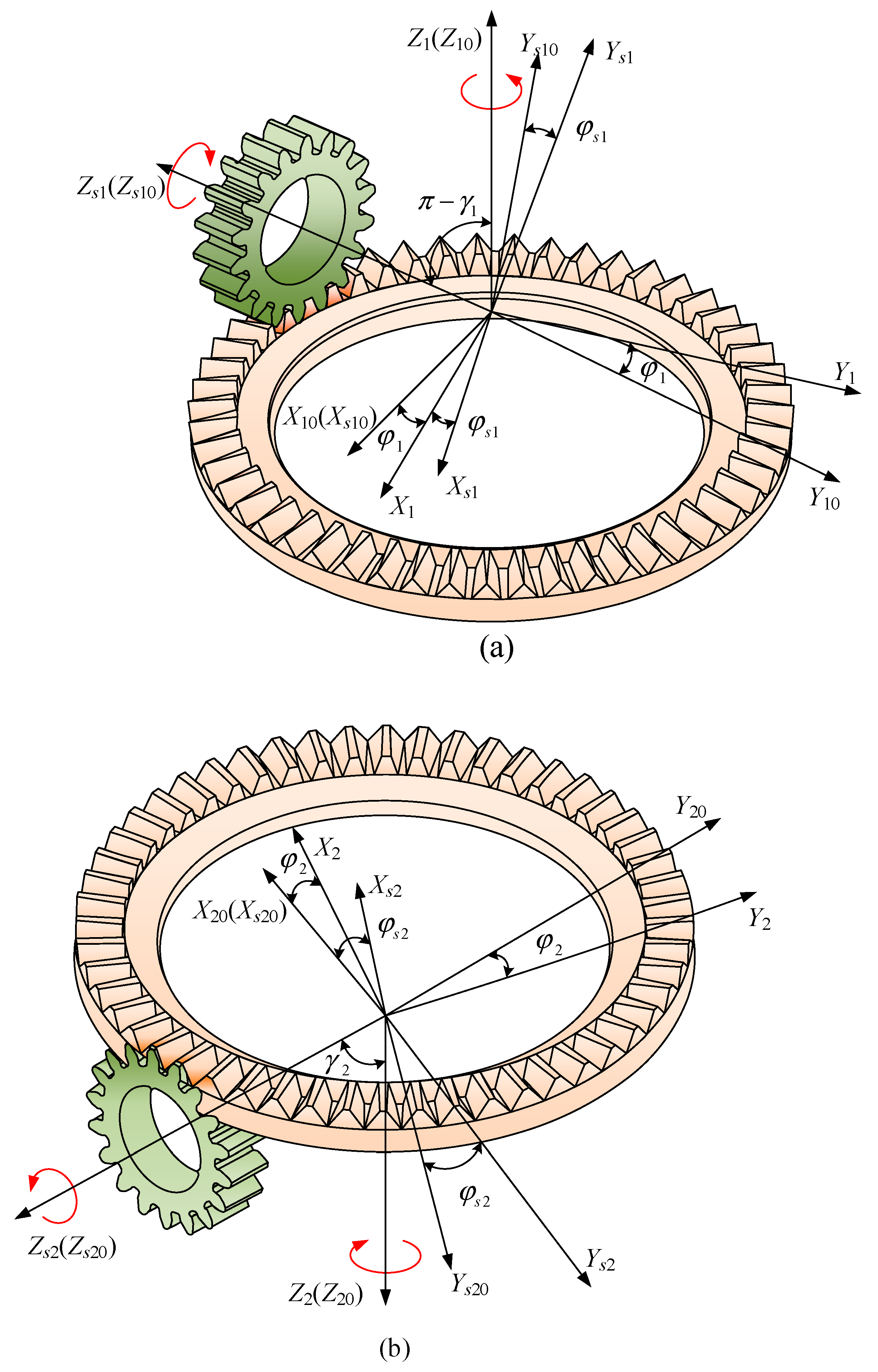
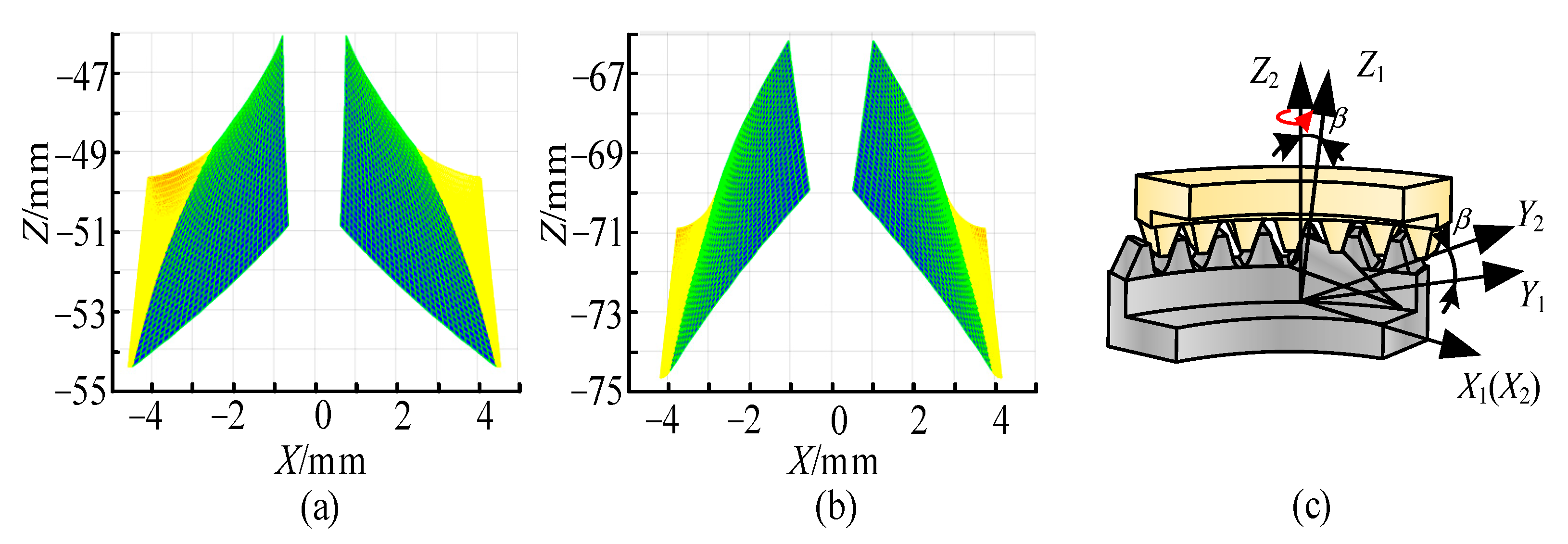
2.2. Generation of Face Gear with Internal and External Meshing

Figure 3 shows face gear with internal and external cut surfaces machined using the internal and external cut method using a shaper cutter. Figure 3a represents the coordinate system for machining external meshing face gear. S₁₀(O₁₀-X₁₀Y₁₀Z₁₀) is fixed coordinate system, Z₁₀ coincides with the rotation axis of the external meshing face gear, S₁(O₁-X₁Y₁Z₁) is connected to the face gear with external meshing, S_s10(O_s10-X_s10Y_s10Z_s10) is fixed coordinate system, Z_s10 coincides with the rotation axis of cutter 1, S_s1(O_s1-X_s1Y_s1Z_s1) is connected to the cutter 1. The origins of the four coordinate systems coincide, Z₁₀ and Z₁ coincide, X_s10 and X₁₀ coincide, Z_s1 and Z_s10 coincide. Z₁₀ and Z_s10 included angle of π-γ₁, φ_s1 denotes the instantaneous rotation angle of cutter 1, φ₁ denotes the instantaneous rotation angle of the external meshing face gear.

Figure 3b represents the coordinate system for machining internal meshing face gear. S₂₀(O₂₀-X₂₀Y₂₀Z₂₀) is fixed coordinate system, Z₂₀ coincides with the rotation axis of the internal meshing face gear, S₂(O₂-X₂Y₂Z₂) is connected to the face gear with internal meshing, S_s20(O_s20-X_s20Y_s20Z_s20) is fixed coordinate system, Z_s20 coincides with the rotation axis of cutter 2, S_s2(O_s2-X_s2Y_s2Z_s2) is connected to the cutter 2. The origins of the three coordinate systems coincide, Z₂₀ and Z₂ coincide, X_s20 and X₂₀ coincide, Z_s2 and Z_s20 coincide. Z₂₀ and Z_s20 included angle of γ₂, φ_s2 denotes the instantaneous rotation angle of cutter 2, φ₂ denotes the instantaneous rotation angle of the internal meshing face gear.

According to the principle of gear meshing, the meshing conditions of the two gear tooth surfaces is written as Equation (5).

$$f\left(u_s,{\theta }_s,{\phi }_s\right)={\mathit{n}}_{\mathit{s}}^{\left(\mathit{s}\right)}·{\mathit{v}}_{\mathit{s}}^{\left(\mathit{sn}\right)}=0$$

(5)

where, v_s^(sn) is the relative velocity of shaper cutter can be determined with the Equation (6).

$${\mathit{v}}_{\mathit{s}}^{\mathit{sn}}={\mathit{\omega }}_{\mathit{s}}^{\mathit{sn}}\times {\mathit{r}}_{\mathit{s}}+{\displaystyle \frac{d\mathit{D}}{dt}}-{\mathsf{\omega }}_{\mathit{s}}\times \mathit{D}={\omega }_s\left[\begin{array}{c}-y_s-{\displaystyle \frac{n_s}{n_n}}{z}_s\cos {\phi }_s\\ x_s+{\displaystyle \frac{n_s}{n_n}}{z}_s\sin {\phi }_s\\ {\displaystyle \frac{n_s}{n_n}}{x}_s\cos {\phi }_s-{\displaystyle \frac{n_s}{n_n}}{y}_s\sin {\phi }_s\end{array}\right]$$

(6)

Here is an example of an externally meshing gear. Substituting equations Equations (4) and (5) into Equation (6), and the meshing equation between the tool and the external meshing face gear is obtained (the same is true for the the internal meshing face gear).

$$f\left(u_s,{\theta }_s,{\phi }_s\right)=r_{bs}\left(1-{\displaystyle \frac{Z_s}{Z_1}}\right)-u_s{\displaystyle \frac{Z_s}{Z_1}}\sin {\gamma }_1\cos \left({\phi }_s+{\theta }_s+{\theta }_{s0}\right)$$

(7)

The transformation matrix (Appendix A) of the external meshing face gear from the coordinate system S_s1 to the coordinate system S₁ can be expressed as Equation (8).

$$\begin{array}{l}{M}_{1S1}=M_{110}{M}_{10S10}{M}_{S10S1}\\ =\left[\begin{array}{cccc}\cos {\phi }_1\cos {\phi }_{s1}-\cos {\gamma }_1\cos {\phi }_1\cos {\phi }_{s1}& -\cos {\gamma }_1\sin {\phi }_1\cos {\phi }_{s1}-\cos {\phi }_1\sin {\phi }_{s1}& -\sin {\gamma }_1\sin {\phi }_1& 0\\ -\sin {\phi }_1\cos {\phi }_{s1}-\cos {\gamma }_1\cos {\phi }_1\sin {\phi }_{s1}& -\cos {\gamma }_1\cos {\phi }_1\cos {\phi }_{s1}+\sin {\phi }_1\sin {\phi }_{s1}& -\sin {\gamma }_1\cos {\phi }_1& 0\\ \sin {\gamma }_1\sin {\phi }_{s1}& \sin {\gamma }_1\cos {\phi }_{s1}& -\cos {\gamma }_1& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

(8)

Similarly, the transformation matrix of the internal meshing face gear from the coordinate system S_s2 to the coordinate system S₂ can be expressed as Equation (9).

$$\begin{array}{l}{M}_{2S2}=M_{220}{M}_{20S20}{M}_{S20S2}\\ =\left[\begin{array}{cccc}\cos {\phi }_2\cos {\phi }_{s2}+\cos {\gamma }_2\cos {\phi }_2\cos {\phi }_{s2}& \cos {\gamma }_2\sin {\phi }_2\cos {\phi }_{s2}-\cos {\phi }_2\sin {\phi }_{s2}& -\sin {\gamma }_2\sin {\phi }_2& 0\\ -\sin {\phi }_2\cos {\phi }_{s2}+\cos {\gamma }_2\cos {\phi }_2\sin {\phi }_{s2}& \cos {\gamma }_2\cos {\phi }_2\cos {\phi }_{s2}+\sin {\phi }_2\sin {\phi }_{s2}& -\sin {\gamma }_2\cos {\phi }_2& 0\\ \sin {\gamma }_2\sin {\phi }_{s2}& \sin {\gamma }_2\cos {\phi }_{s2}& \cos {\gamma }_2& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

(9)

Since the tooth surface of the face gear is formed by the tooth surface envelope of the gear shaper cutter, the expression of normal vector of face gear tooth surface established by the spatial meshing theory can be written as Equation (10).

$${\mathit{n}}_{\mathit{n}}({\theta }_s,{\phi }_s)=L_{nSn}·{\mathit{n}}_{\mathit{s}}(u_s,{\theta }_s)$$

(10)

where, L_nSn denotes a 3 × 3 submatrix of M_nSn (n = 1, 2), same as below.

Thus, by substituting Equations (3), (8) and (9) into Equation (11), the gear tooth surface equation of the internal and external meshing face gear can be obtained.

$${\mathit{r}}_{\mathit{n}}(u_s,{\theta }_s,{\phi }_s)=\left[\begin{array}{c}{x}_n\\ y_n\\ z_n\\ 1\end{array}\right]=M_{nSn}·{\mathit{r}}_{\mathit{s}}(u_s,{\theta }_s)$$

(11)

2.3. Conjugated Conditions of Face Gear Face Gear Pair

As shown in Figure 4, in actual machining, there is a limit meshing point between the gear shaper cutter and the face gear, that is, the working pressure angle cannot be equal to zero. When the working pressure angle is too small, the conjugate tooth profile of the face gear will be cut off by the transition part of the tooth tip of the gear shaper cutter, that is, the root undercut phenomenon occurs; The larger the working pressure angle, the smaller the tooth tip thickness. When the tooth tip thickness reaches a certain position, the tooth tip becomes zero, and the tooth tip becomes sharp.

At the undercut critical point on the shaper cutter and face gear tooth surface, the following relationship exists.

$${\mathit{v}}_{\mathit{s}}^{\left(\mathit{sn}\right)}+{\mathit{v}}_{\mathit{s}}=0$$

(12)

where, ν_s denotes the absolute velocity of the shaper cutter, ν_s^(sn) denotes the relative velocity of the shaper cutter at the meshing point of the face gear.

Considering that Equation (7) is an identity for all time t, differentiate it, and arrange the equations needed to determine the existence of undercut limit lines on the cutter tooth surface [34].

$$\left\{\begin{array}{l}{\mathit{r}}_{\mathit{s}}={\mathit{r}}_{\mathit{s}}({\theta }_s,{\phi }_s)\\ f(u_s,{\theta }_s,{\phi }_s)=0\\ {\displaystyle \frac{\partial f(u_s,{\theta }_s,{\phi }_s)}{\partial t}}=0\end{array}\right.$$

(13)

Simplify Equation (13) to obtain.

$$\Delta =\left|\begin{array}{ccc}{\displaystyle \frac{\partial x_s}{\partial u_s}}& {\displaystyle \frac{\partial x_s}{\partial {\theta }_s}}& -v_x^{(sn)}\\ {\displaystyle \frac{\partial z_s}{\partial u_s}}& {\displaystyle \frac{\partial z_s}{\partial {\theta }_s}}& -v_z^{(sn)}\\ f_{u_s}& f_{{\theta }_s}& -f_{{\phi }_s}{\displaystyle \frac{d{\phi }_s}{dt}}\end{array}\right|=0$$

(14)

where, f_μs, f_θs and f_φs represents partial derivatives of meshing equation with respect to μ_s, θ_s and φ_s, respectively, ∂x_s/∂μ_s = 0, ∂z_s/∂μ_s = 0, ∂x_s/∂θ_s = 0, ∂z_s/∂θ_s = r_bsθ_ssin(θ_s0 + θ_s).

The minimum inner radius of the face gear root without undercutting can be obtained by arranging the above equations and expressed as Equation (15).

$$L_{in}=\sqrt{x^2({\theta }_s^{\prime },{\phi }_s^{\prime })+{(-y({\theta }_s^{\prime },{\phi }_s^{\prime })\sin \gamma +z({\theta }_s^{\prime },{\phi }_s^{\prime })\cos \gamma +r_{bs}\cot \gamma )}^2}$$

(15)

Assuming that a cone at the tooth tip of the face gear is used to cross section the tooth surfaces on both sides of the gear, this cone surface is coaxial with the shaper cutter and tangent to the cylinder with radius r_ds = r_ps − m_s, where r_ps denotes the pitch circle radius of the gear shaper cutter and m_s denotes the shaper cutter module. When r_ds < r_bs, r_ds = r_bs should be taken.

According to the symmetry of the tooth surfaces on both sides of the face gear teeth, the sharp tip position of the tooth tip should be on its symmetry plane, and the coordinates of the sharp point satisfy Equation (16).

$$\left\{\begin{array}{l}x({\theta }_s^{″},{\phi }_s^{”})=0\\ -y({\theta }_s^{″},{\phi }_s^{″})\cot \gamma +{\displaystyle \frac{r_{ds}}{\sin \gamma }}+z({\theta }_s^{″},{\phi }_s^{″})=0\end{array}\right.$$

(16)

Equation (16) x(θ_s″,φ_s″) and z(θ_s″,φ_s″) are substituted into the equation Equation (7), the values of θ_s and φ_s can be calculated. Then substitute the obtained value into Equation (16) and the value of y(θ_s″,φ_s″) is obtained, then the maximum outer radius at which the tooth tip of the face gear does not become sharp is expressed as Equation (17).

$$L_{out}=-y({\theta }_s^{″},{\phi }_s^{″})/\sin \gamma$$

(17)

Conjugation of gear tooth surfaces is based on the concept of envelope. If the meshing equations of the two gears and the cutter are equal, then the two gears are conjugate. Because of the face gear face gear pair, a pair of gears that mesh with each other are formed by external cutting and internal cutting by cutters of the same parameter. Therefore, it is possible to obtain that the meshing of two gears satisfies by Equation (18).

$$f_1(u_s,{\theta }_s,{\phi }_s)=f_2(u_s,{\theta }_s,{\phi }_s)$$

(18)

Simultaneous Equations (7) and (18) conjugate conditions of face gear face gear pairs can be obtained by sorting out.

$${\theta }_s(u_s,{\phi }_s)={\cos }^{-1}\left[{\displaystyle \frac{-r_{bs}\left(\frac{Z_s}{Z_2}\cos {\gamma }_2-\frac{Z_s}{Z_1}\cos {\gamma }_1\right)}{-u_s\left(\frac{Z_s}{Z_2}\sin {\gamma }_2-\frac{Z_s}{Z_1}\sin {\gamma }_1\right)}}\right]-({\phi }_s+{\theta }_{s0})$$

(19)

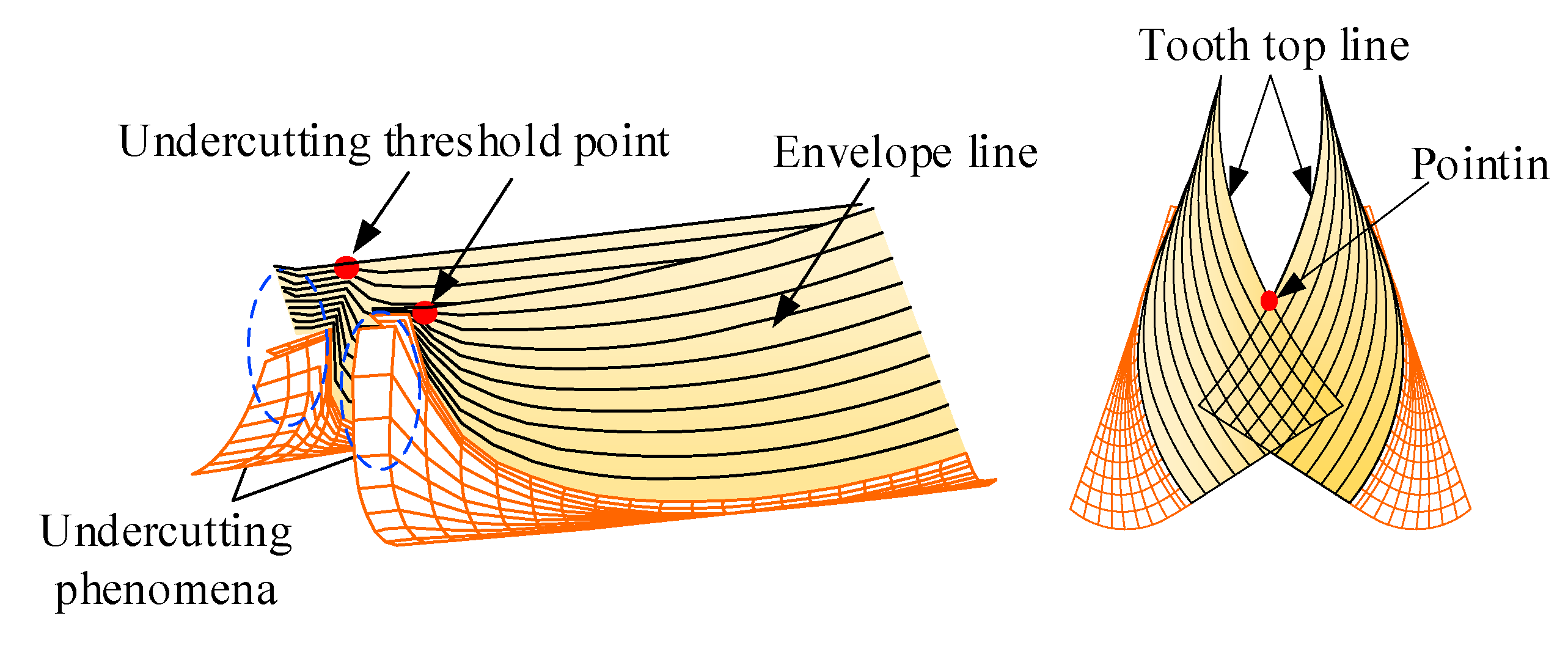
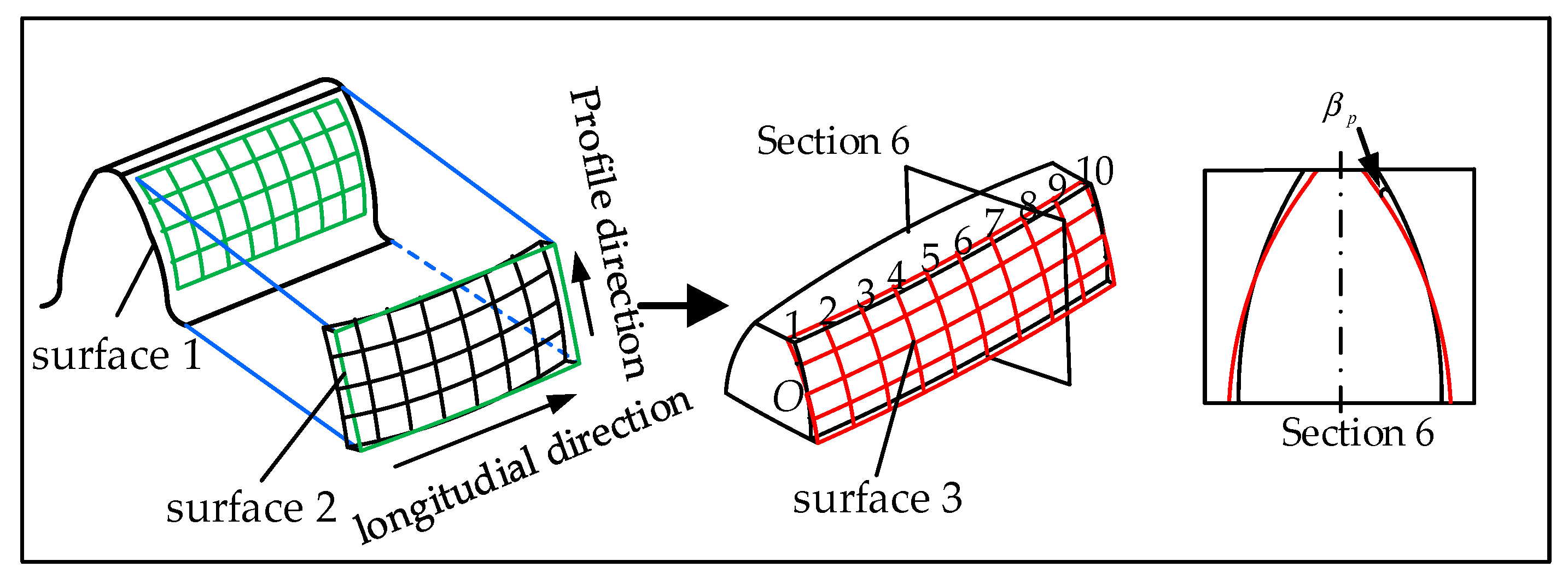
2.4. Tooth Modification Design of Face Gear

By modifying the shaper cutter and machining the face gear with the modified gear shaper cutter, the modified face gear can be obtained. The modification method described in this chapter is based on the original parabola modification, and then rotate the tooth surface by a β_p to improve the tooth root strength and ensuring that there is no interference in the process of gear meshing.

As shown in Figure 5, the shaper cutter tooth surface 1 is modified into tooth surface 2. Based on previous experience, modification parabola y = a_px² is selected, modification amount Δm is calculated, and modification amount Δm is subtracted from the value of x on the coordinate of theoretical tooth surface to obtain a new abscissa x, and the values of y and z are kept unchanged.

$$\Delta m=a_p{x}^2$$

(20)

Then from the tooth surface 2 modification to the final shaper cutter tooth surface 3, the equation of gear involute in rectangular coordinate system is based on the origin of rectangular coordinate system, assuming that the coordinate value at point O coordinate is (x_z,y_z), Equations can be written as Equation (21).

$$x_z^2+y_z^2=r^2$$

(21)

where, r denotes the radius of the indexing circle, r = mz/2.

According to the Equation (22).

$$r_{bs}^2{[\sin ({\theta }_{s0}+{\theta }_0)-{\theta }_s\cos ({\theta }_{s0}+{\theta }_0)]}^2+r_{bs}^2{[\sin ({\theta }_{s0}+{\theta }_0)-{\theta }_s\cos ({\theta }_{s0}+{\theta }_0)]}^2={\left({\displaystyle \frac{mz}{2}}\right)}^2$$

(22)

Translate the origin of the coordinate system to point O and rotate it by angle β_b

$$\left\{\begin{array}{l}{x}^{\prime }=(x-x_z)\cos {\beta }_p+(y-y_z)\sin {\beta }_p+x_z-\Delta m\\ y^{\prime }=(y-y_z)\cos {\beta }_p+(x-x_z)\sin {\beta }_p+y_z\end{array}\right.$$

(23)

The above can be achieved by adjusting the coordinate value (x_z,y_z) and rotation angle β_p at point O. After the coordinate transformation, the modified face gear tooth can be obtained.

3. Geometric Contact Analysis of Face Gear Face Gear Pairs

3.1. TCA

The meshing form of the face gear face gear pair is point contact. In the process of analyzing its meshing characteristics and solving the contact stress, it is necessary to determine the contact trajectory of the face gear during the meshing process. Here, a single pair of face gear face gear meshing is taken as an example to solve and visualize the contact trajectories during the meshing of the external and internal face gears, and to study the influence of installation errors on the contact trajectory.

As shown in Figure 6, coordinate systems S₁ and S_f are rigidly fixed to the external meshing face gear and the frame, coordinate systems S₂ and S_e are rigidly fixed to the internal meshing face gear and the frame, and S_q, S_m, S_k are auxiliary coordinate systems. The installation errors in the nutation drive are mainly: Nutation Angle error Δγ; offset error ΔE; Axial displacement error Δq.

Coordinate transformation is carried out on the internal and external meshing gears obtained in Section 2, and the gears are rotated to the same fixed coordinate system.

$$M_{f1}=\left[\begin{array}{cccc}\cos {\phi }_1^{\prime }& -\sin {\phi }_1^{\prime }& 0& 0\\ \sin {\phi }_1^{\prime }& \cos {\phi }_1^{\prime }& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(24)

$$\begin{array}{l}{M}_{f2}=M_{fm}{M}_{mq}{M}_{qk}{M}_{k2}\\ =\left[\begin{array}{cccc}\cos {\phi }_2^{\prime }& -\sin {\phi }_2^{\prime }& 0& \Delta E\\ \cos ({\gamma }_2+\Delta \gamma )\sin {\phi }_2^{\prime }& \cos ({\gamma }_2+\Delta \gamma )\cos {\phi }_2^{\prime }& -\sin ({\gamma }_2+\Delta \gamma )& -\Delta q\sin ({\gamma }_2+\Delta \gamma )\\ \sin ({\gamma }_2+\Delta \gamma )\sin {\phi }_2^{\prime }& \sin ({\gamma }_2+\Delta \gamma )\cos {\phi }_2^{\prime }& \cos ({\gamma }_2+\Delta \gamma )& \Delta q\cos ({\gamma }_2+\Delta \gamma )\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

(25)

From Figure 6, the tooth surface position vector r_f⁽¹⁾(θ_s1,φ_s1,φ₁′) and the tooth surface unit normal vector n_f⁽¹⁾(θ_s1,φ_s1,φ₁′) of the external meshing face gear in the coordinate system can be obtained as follows:

$$\begin{array}{l}{\mathit{r}}_{\mathit{f}}^{\left(1\right)}({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime })=M_{f1}{\mathit{r}}_1({\theta }_{s1},{\phi }_{s1})\\ {\mathit{n}}_{\mathit{f}}^{\left(1\right)}({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime })=L_{f1}{\mathit{n}}_1({\theta }_{s1},{\phi }_{s1})\end{array}$$

(26)

where, θ_S1 and φ_S1 denote the cutter spread angle and rotation angle, respectively.

When the two face gears are engaged under installation error, in the same coordinate system S_f, the position vector and unit normal vector at the meshing contact point should always coincide, which can be determined.

$$\begin{array}{l}{x}_f^{(1)}\left({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime }\right)=x_f^{(2)}\left({\theta }_{s2},{\phi }_{s2},{\phi }_2^{\prime }\right)\\ y_f^{(1)}\left({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime }\right)=y_f^{(2)}\left({\theta }_{s2},{\phi }_{s2},{\phi }_2^{\prime }\right)\\ z_f^{(1)}\left({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime }\right)=z_f^{(2)}\left({\theta }_{s2},{\phi }_{s2},{\phi }_2^{\prime }\right)\\ n_{xf}^{(1)}\left({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime }\right)=n_{xf}^{(2)}\left({\theta }_{s2},{\phi }_{s2},{\phi }_2^{\prime }\right)\\ n_{yf}^{(1)}\left({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime }\right)=n_{yf}^{(2)}\left({\theta }_{s2},{\phi }_{s2},{\phi }_2^{\prime }\right)\\ n_{zf}^{(1)}\left({\theta }_{s1},{\phi }_{s1},{\phi }_1^{\prime }\right)=n_{zf}^{(2)}\left({\theta }_{s2},{\phi }_{s2},{\phi }_2^{\prime }\right)\end{array}$$

(27)

Only five equations in Equation (27) are independent, so we have a system of five independent nonlinear equations with six unknowns (θ_s1,θ_s2,φ_s1,φ_s2,φ₁′,φ₂′). Assuming φ₂′ is a known parameter, simultaneous equations can be used to find the values of the other five parameters. The contact path can be obtained by substituting them into the tooth surface equations.

Based on the above, φ₁′ can be derived from φ₂′, and the range of values of φ₂′ is given by Equation (28).

$$-{\displaystyle \frac{\pi }{z_2}}\le {\phi }_2^{\prime }\le {\displaystyle \frac{\pi }{z_2}}$$

(28)

The transmission error, Δφ₂′ is expressed by Equation (29).

$$\Delta {\phi }_2^{\prime }={\phi }_2^{\prime }-{\displaystyle \frac{N_1}{N_2}}\left({\phi }_1^{\prime }-{\phi }_1^{″}\right)$$

(29)

where, φ₁″ represents the value when φ₂′ is 0.

3.2. LTCA

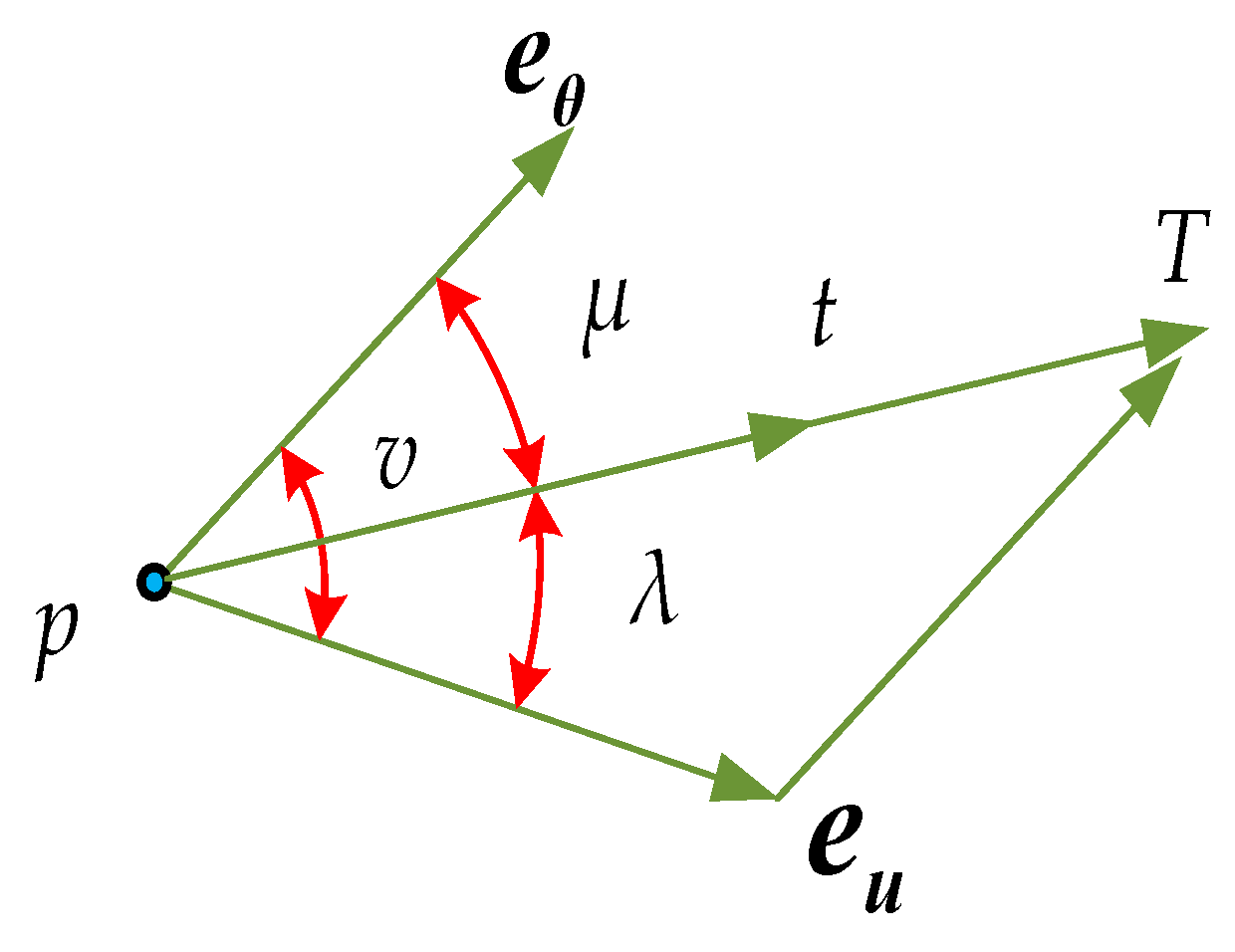
3.2.1. Calculation and Analysis of Principal Curvature and Principal Direction

According to Hertzian elastic contact theory, when calculating the contact stress and deformation of two arbitrarily shaped surfaces, it is essential to know the principal curvature of the surfaces at the contact point.

The position vector p of the surface can be represented by the variables μ, θ.

$$\mathit{r}\left(u,\theta \right)=x\left(u,\theta \right)\mathit{i}+y\left(u,\theta \right)\mathit{j}+z\left(u,\theta \right)\mathit{k}$$

(30)

where, i, j, and k are the unit vector of the surface in the coordinate system.

Assume the vector function of a regular surface is r(u, θ); the unit normal vector n(u, θ) of the surface can be derived from Equation (31) [35].

$$\mathit{n}\left(u,\theta \right)={\displaystyle \frac{\frac{\partial \mathit{r}}{\partial u}\times \frac{\partial \mathit{r}}{\partial \theta }}{\left|\frac{\partial \mathit{r}}{\partial u}\times \frac{\partial \mathit{r}}{\partial \theta }\right|}}$$

(31)

where, μ and λ denote the angles between vectors e_u and e_θ which are variable parameters, while v = a + b is a constant for a given point on the surface.

The first fundamental form of a surface is represented by the metric tensor.

$${\rm I}=d^2{\mathit{r}}^2={\mathit{e}}_{\mathit{u}}^2·{\left(du\right)}^2+2{\mathit{e}}_{\mathit{u}}·{\mathit{e}}_{\mathsf{\theta }}·du·d\theta +{\mathit{e}}_{\mathsf{\theta }}^2·{\left(d\theta \right)}^2$$

(32)

The second fundamental form is also given by the metric tensor.

$$\Pi =d^2\mathit{r}·\mathit{n}={\displaystyle \frac{{\partial }^2\mathit{r}}{\partial u^2}}·\mathit{n}·{\left(du\right)}^2+2{\displaystyle \frac{{\partial }^2\mathit{r}}{\partial u\partial \theta }}·\mathit{n}·du·d\theta +{\displaystyle \frac{{\partial }^2\mathit{r}}{\partial {\theta }^2}}·\mathit{n}·{\left(d\theta \right)}^2$$

(33)

From Figure 7, the tangent vector at point p on the surface can be expressed as [34]:

$$\mathit{T}=a{\mathit{e}}_{\mathit{u}}+b{\mathit{e}}_{\mathsf{\theta }}$$

(34)

where, $e_u={\displaystyle \frac{\frac{\partial r}{\partial u}}{\left|\frac{\partial r}{\partial u}\right|}}$, $e_{\theta }={\displaystyle \frac{\frac{\partial r}{\partial \theta }}{\left|\frac{\partial r}{\partial \theta }\right|}}$.

$$t={\displaystyle \frac{{\mathit{e}}_{\mathit{u}}\sin \mu +{\mathit{e}}_{\mathsf{\theta }}\sin (\nu -\mu )}{\sin \nu }}$$

(35)

where, $t={\displaystyle \frac{T}{\left|T\right|}}$, cosν = e_u∙e_θ, sinν = |e_u × e_θ|.

The equation for normal curvature is derived through a derivative transformation of the equation above.

$$K_n={\displaystyle \frac{\Pi }{{\rm I}}}=A{\sin }^2\mu +2B\sin (\nu -\mu )\sin \mu +C{\sin }^2(\nu -\mu )$$

(36)

where, $A={\displaystyle \frac{L}{{\mathit{r}}_{\mathit{u}}^2{\sin }^2\nu }}$, $B={\displaystyle \frac{M}{\left|{\mathit{r}}_{\mathit{u}}\right|\left|{\mathit{r}}_{\mathsf{\theta }}\right|{\sin }^2\nu }}$, $C={\displaystyle \frac{N}{{\mathit{r}}_{\mathsf{\theta }}^2{\sin }^2\nu }}$.

$$\tan 2\mu ={\displaystyle \frac{C\sin 2\nu -2B\sin \nu }{A-2B\cos \nu +C\cos 2\nu }}$$

(37)

Equation (37) provides two solutions, μ₁ and μ₂, where μ₂ = μ₁ + π/2. By substituting μ₁ and μ₂ into Equation (35), the values of the two principal directions at the contact point of the tooth surface can be determined. Substituting these values into Equation (36),the principal curvatures at the point in the two principal directions can be obtained.

By calculating the curvature of the gear with internal and external meshing surfaces, the principal curvature of the nutation gear at the meshing point can be determined using the formula for principal curvature mentioned above.

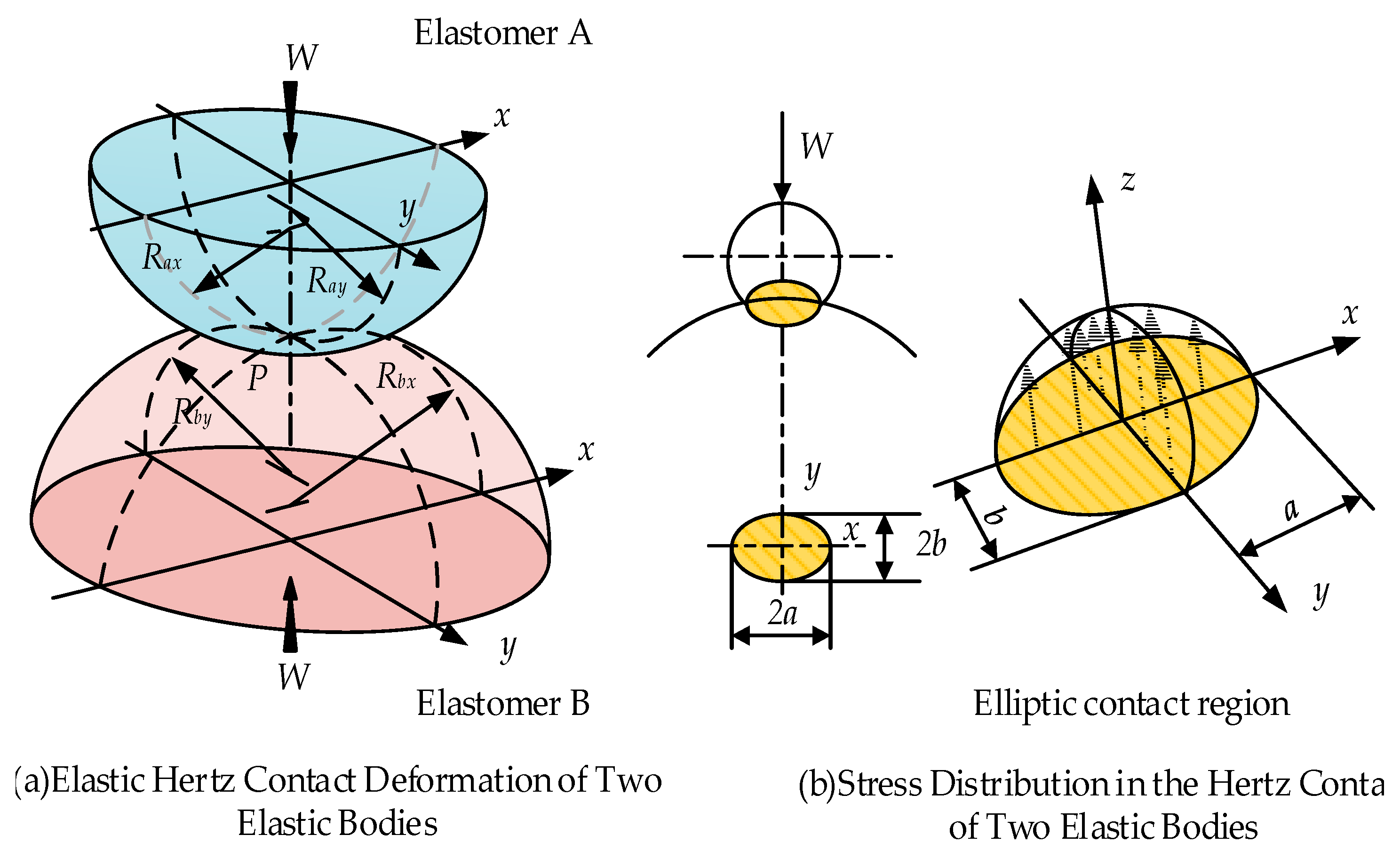
3.2.2. Hertzian Contact Theory

According to Figure 8a,b, there are four planes in Hertzian contact between the curved surfaces, corresponding to the principal curvature surfaces of the two surfaces, respectively. In the contact ellipse, a and b represent the major axis and minor axis of contact, respectively, with the maximum contact stress assumed to be P.

Based on Hertz contact theory analysis, when the elastomers A and B are in contact, the value of a and b in the contact region can be expressed as:

$$\left\{\begin{array}{l}a={\left({\displaystyle \frac{6{\overline{k}}^2\overline{\epsilon }W{R}^{\prime }}{\pi E^{\prime }}}\right)}^{1/3}\\ b={\left({\displaystyle \frac{6\overline{\epsilon }{W}^{\prime }}{\pi \overline{k}{E}^{\prime }}}\right)}^{1/3}\end{array}\right.$$

(38)

where, E′ represents the elastic modulus at the contact point of the ellipse, R′ is the equivalent radius of curvature, $\overline{k}$ is the first elliptic integral, and $\overline{\epsilon }$ is the second elliptic integral.

$$\left\{\begin{array}{l}{\displaystyle \frac{1}{R^{\prime }}}={\displaystyle \frac{1}{R_x}}+{\displaystyle \frac{1}{R_y}}={\displaystyle \frac{1}{R_{ax}}}+{\displaystyle \frac{1}{R_{bx}}}+{\displaystyle \frac{1}{R_{ay}}}+{\displaystyle \frac{1}{R_{by}}}\\ {\displaystyle \frac{1}{E^{\prime }}}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1-{\mu }_A^2}{E_A}}+{\displaystyle \frac{1-{\mu }_B^2}{E_B}}\right)\\ \overline{k}=1.0339{\left({\displaystyle \frac{R_y}{R_x}}\right)}^{0.636}\\ \overline{\epsilon }=1.0003+{\displaystyle \frac{0.5968R_y}{R_x}}\end{array}\right.$$

(39)

μ_A and μ_B are the Poisson’s ratios of elastomers A and B; respectively, while E_A and E_B elastic moduli of elastomers A and B; R_x and R_y radii of curvature in the x- and y-directions, respectively.

The maximum contact stress P is given by Equation (40).

$$P={\displaystyle \frac{3W}{2\pi ab}}$$

(40)

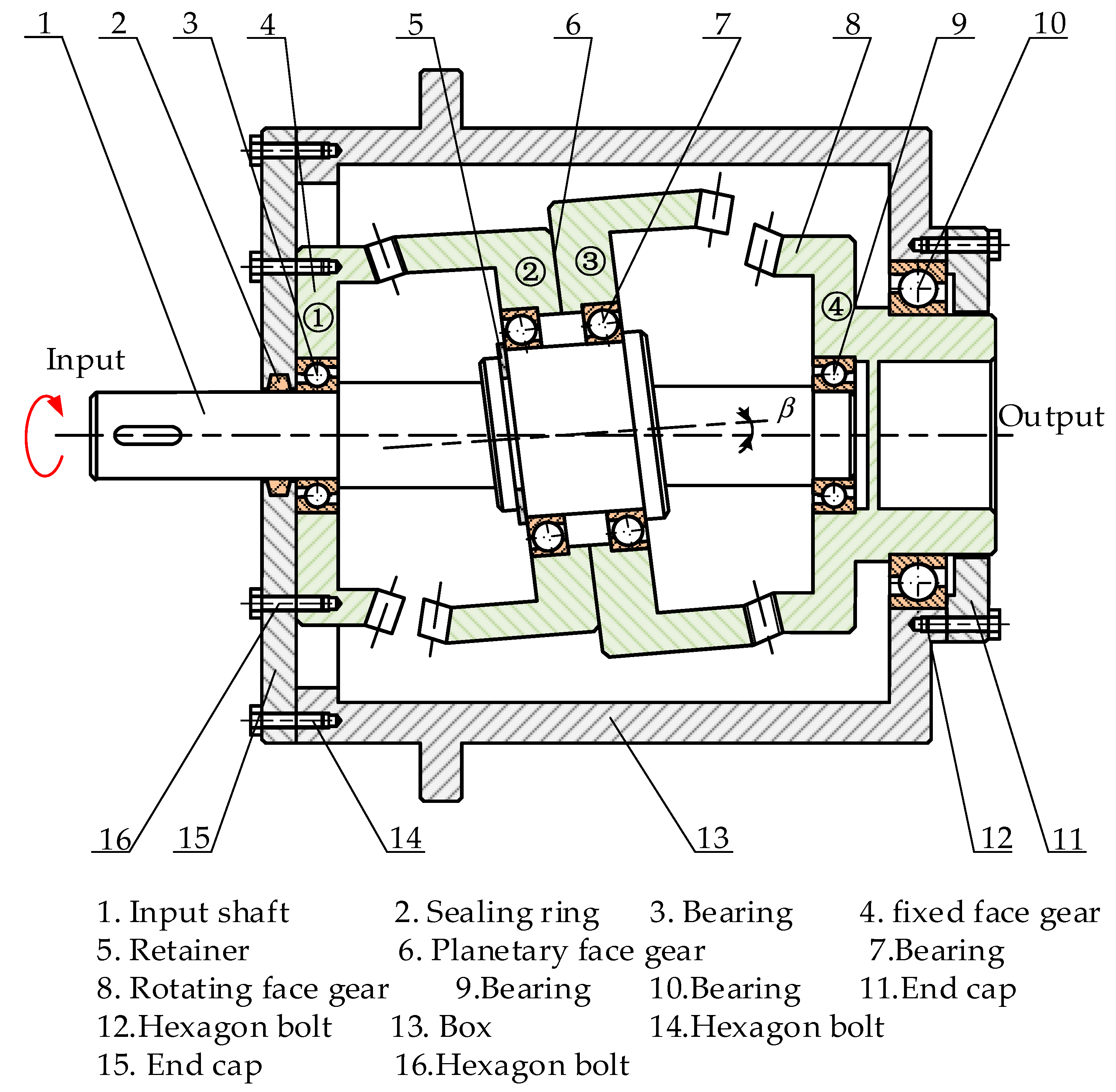
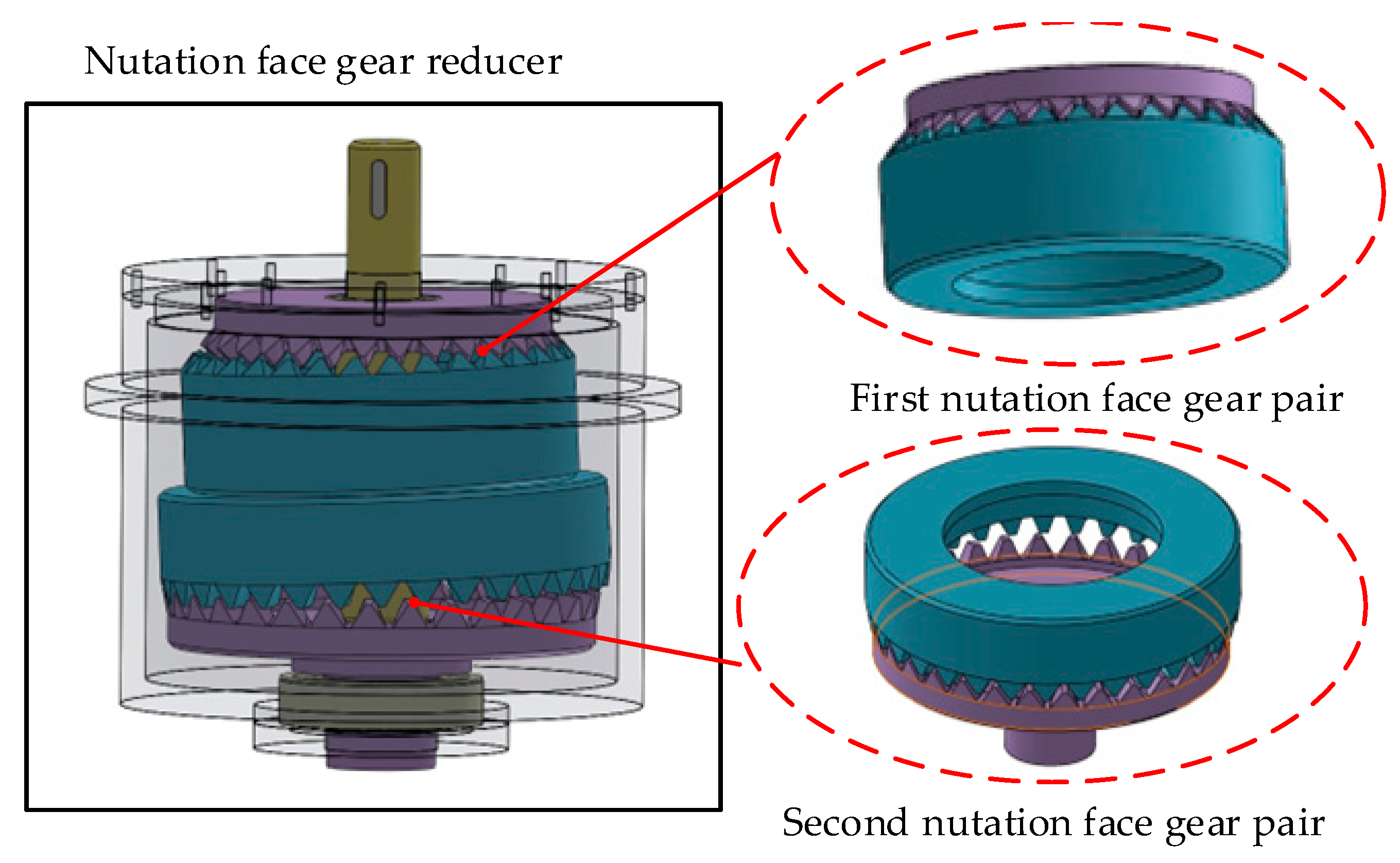
4. Design of Face Gear Face Gear Nutation Reducer

Analysis and Design of Nutation Reducer

As shown in Figure 9, the basic structure of the nutation reducer consists of four main components: the input shaft, the planetary face gear (which is made up of two face gears), the fixed face gear, and the rotating face gear. The input shaft is connected to the planetary face gear through bearings. The fixed face gear is securely attached to the frame, while the rotating face gear is rigidly connected to the output shaft. The angle between the axis of the input shaft and the axis of the inclined shaft segment, where the planetary gear is located, is known as the nutation angle, denoted as β. The transmission ratio of the nutation reducer is calculated as follows.

The rotation angle formed between face gear 1 and face gear 2 during rotation [36,37].

$${\phi }_{21}={\displaystyle \frac{Z_2-Z_1}{Z_2}}·2\pi$$

(41)

The rotation angle formedbetween face gear 3 and face gear 4 during rotation.

$${\phi }_{34}={\displaystyle \frac{Z_3-Z_4}{Z_4}}·2\pi$$

(42)

Due to the fixed connection between face gears 2 and 3, the angle difference is transmitted to face gear 4 through face gear 3. Therefore, the actual angle value of face gear 4 is determined.

$${\phi }_4={\displaystyle \frac{Z_3}{Z_4}}·({\phi }_{21}-{\phi }_{34})$$

(43)

Since face gears 2 and 3 are connected to the input shaft, and face gear 4 is connected to the output shaft, the output angle value is equal to the actual angle value of face gear 4, which defines the transmission ratio of the reducer.

$${\mathit{q}}_{14}={\displaystyle \frac{2\pi }{{\phi }_4}}={\displaystyle \frac{2\pi }{\left(\frac{Z_3}{Z_4}\right)({\phi }_{21}-{\phi }_{34})}}={\displaystyle \frac{Z_2{Z}_4}{Z_2{Z}_4-Z_1{Z}_3}}$$

(44)

In nutation face gear transmission, the planetary face gear rotates around its own axis, exhibiting nutation motion. Based on the structural characteristics of the face gear, when the difference in the number of teeth is no greater than 3, the structural dimensions of the meshing face gears are almost identical. Therefore, in nutation face gear transmission, the number of teeth on each face gear must satisfy the following constraints.

$$\left.\begin{array}{l}1\le Z_2-Z_1\le 3\\ 1\le Z_3-Z_4\le 3\end{array}\right\}$$

(45)

Figure 10 illustrates the face gear nutation reducer. The main body of the nutation reducer consists of two opposing face gear meshing pairs and an input shaft. The output shaft is fixedly connected to the external tangent face gear in the second meshing pair.

Figure 11 presents the detailed flow chart for the design of the nutation reducer in this paper. The first part covers tooth surface generation, while the second part addresses tooth surface contact analysis.

5. Numerical Examples and Discussions

5.1. Generation of Tooth Surface of Face Gear Face Gear Meshing Pair

Face gears differ from conventional gears, and the process of establishing a 3D model for face gears is more complex. First, using the tooth surface equation of the face gear, combined with the parameters in

Table 1. Design parameters of face gear face gear meshing pair.

Design Parameters	External Meshing Face Gear	Internal Meshing Face Gear
Module m/mm	3	3
Tooth count of the hobbing cutter Zs	16	16
Tool pressure angle αs/mm	25	25
Addendum coefficient ha*	1.25	1.25
Teeth number Zn	29	31
Cross axis angle/°	50.31	127.19
Pitch cone angle/°	33.67	143.82
Nutation angle β/°	2.5	2.5
Tooth width b/mm	8	8
Offset error/mm	0.3
Axial displacement error/mm	0.2
Nutation angle error/mm	0.05

, the 3D model of the face gear’s tooth surface was designed using MATLAB. The coordinate values of the tooth surface were obtained by discretizing the surface through a cell-based method. These coordinates were then imported into SolidWorks, where the 3D solid model of the face gear was generated using the solid command. Figure 12 illustrates the generated external meshing face gear, internal meshing face gear, and the seven-tooth contact model of the face gear meshing pair.

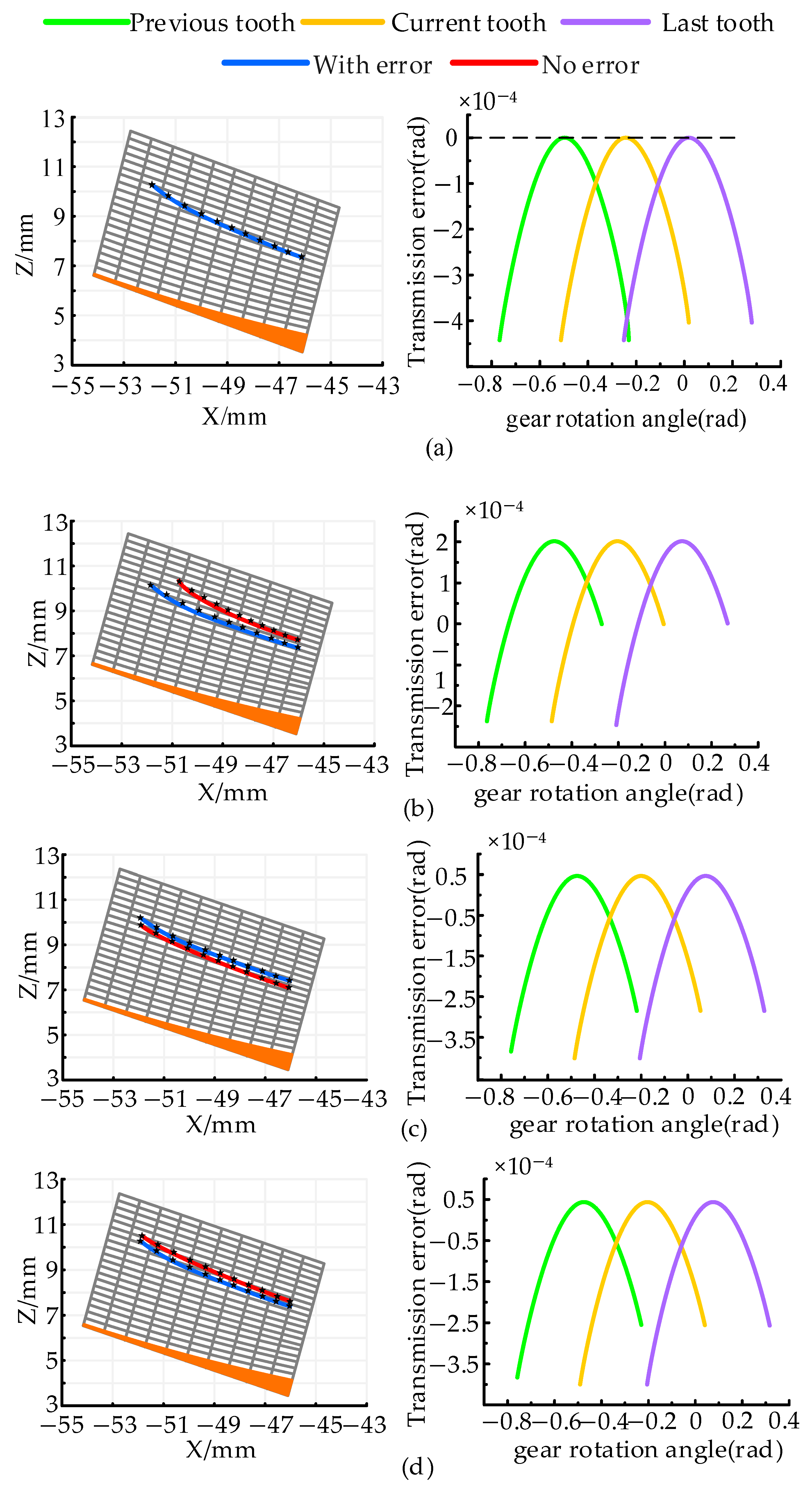
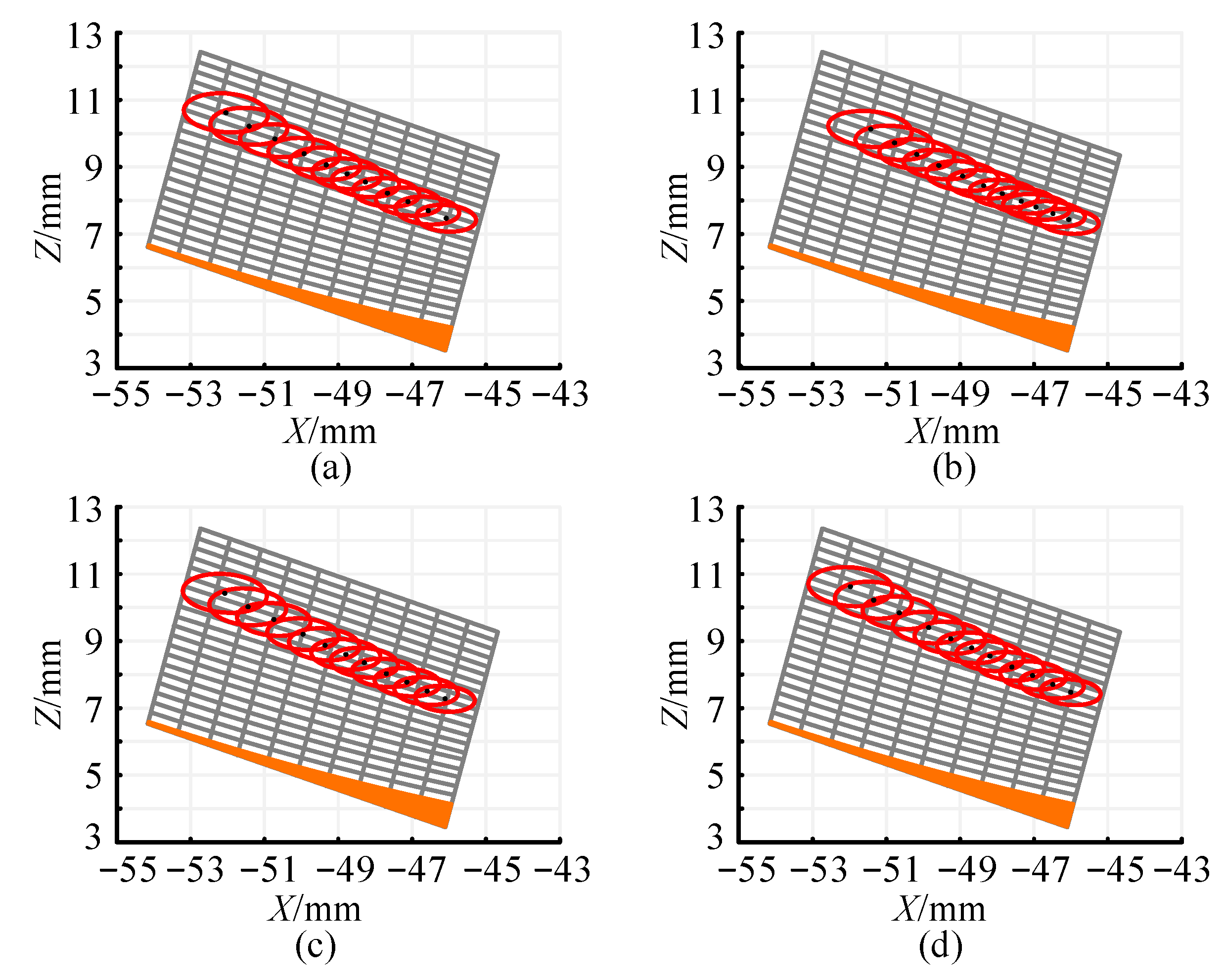
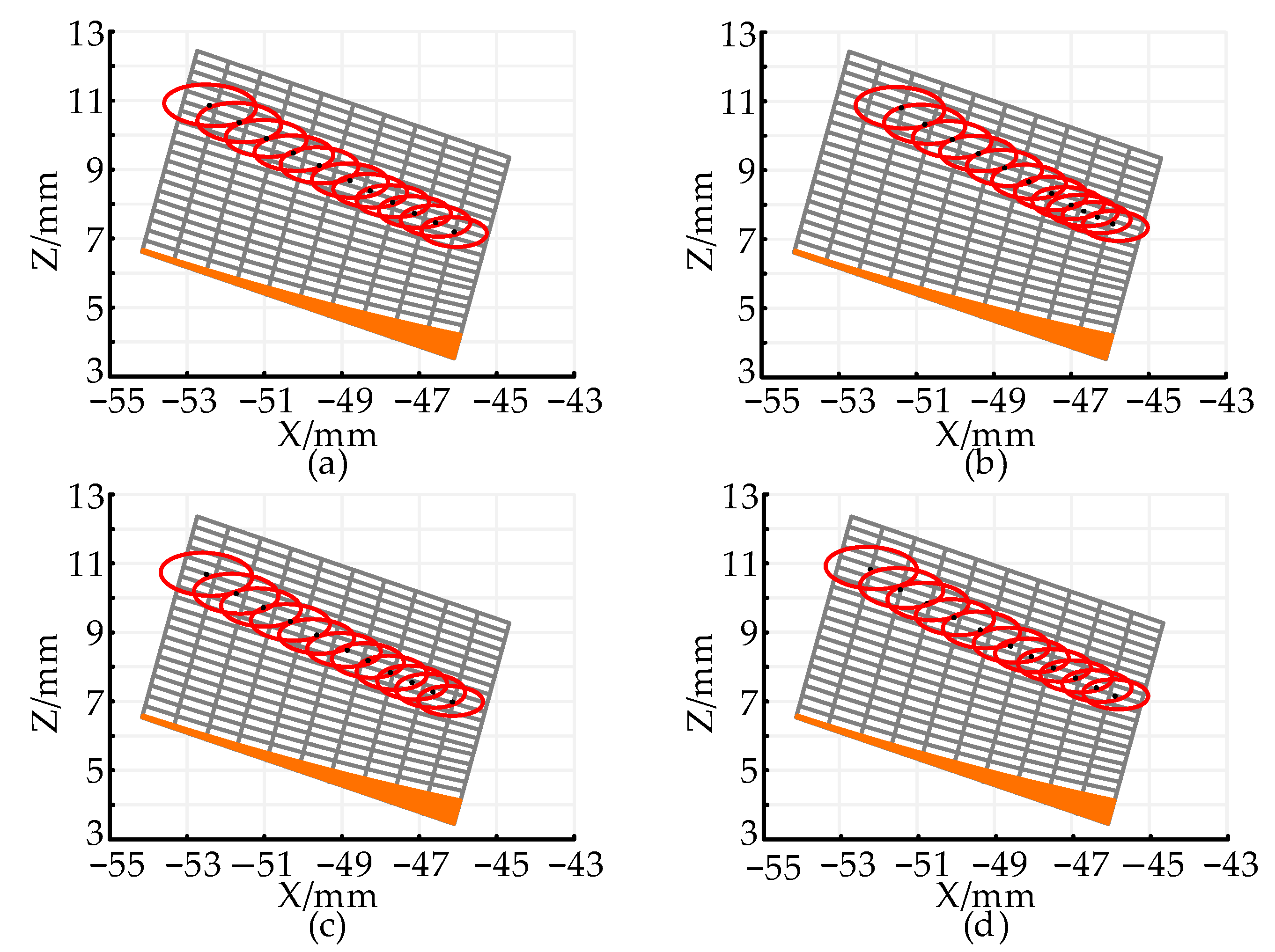
5.2. Analysis of Tooth Contact Path

Figure 13a shows the contact path and transmission error curve of the face gear meshing pair under standard installation. From the figure, it is evident that the transmission error value is 1 × 10⁻⁴ rad, and the contact path extends from the tooth root at the inner diameter to the tooth tip at the outer diameter of the face gear. Figure 13c shows that when the offset error ΔE = 0.5 mm, the transmission error value increases to 1.48 × 10⁻⁴ rad. The contact path shifts slightly towards the tooth tip and inner diameter, compared to the ideal installation position. Figure 13d shows that when the axial displacement error Δq = 0.2 mm, the transmission error value is 1.09 × 10⁻⁴ rad. In this case, the contact path moves towards the root and inner diameter, but the deviation is not significant. Figure 13b shows he case with a angle error Δγ = 0.05°, awhere the transmission error value is 0.86 × 10⁻⁴ rad. Compared to the ideal installation position, the contact path deviates significantly towards the tooth tip and inner diameter, with a noticeable shortening of the contact path. In conclusion, the nutation angle error has the greatest impact on the contact path. Since the contact path is less sensitive to offset and axial displacement errors, the influence of modifications on nutation contact is primarily analyzed through the nutation angle error.

Figure 14 illustrates that the two principal curvatures at the meshing point on the tooth surface of the nutation face gear are positive and negative and can vary accordingly. When the two face gears mesh, one of the tooth surfaces is concave and the other is convex. In Figure 14, K₁ and K₃ represent the principal curvatures of the external meshing face gear, while K₂ and K₄ represent the principal curvatures of the internal meshing face gear. Along the same line of action, the absolute value of the principal curvature at the meshing point of the tooth surface is inversely related to the value of the tool’s rotation angle, with mild fluctuations in the principal curvature. As shown in Figure 14, the nutation angle error has the greatest impact on the variation in the principal curvature, while the offset and axial displacement errors have a lesser effect, consistent with the influence of installation errors on the contact path discussed earlier.

Table 2. Calculation results of hertz elastic contact method.

Contact Point	Major Axis	Minor Axis	Maximum Contact Stress
1	1.802	1.476	1592.08
2	1.888	1.476	1463.18
3	2.000	1.504	1374.02
4	2.108	1.534	1291.12
5	2.214	1.565	1216.65
6	2.518	1.596	1148.90
7	2.420	1.629	1087.09
8	2.523	1.662	1030.06
9	2.625	1.696	976.04
10	2.729	1.731	927.53
11	2.833	1.767	880.98

presents the elastic deformation data at the meshing point of the external meshing face gear, calculated using the Hertz contact method, under the condition of no installation error and no modification. This data includes the values for the major and minor axes of the contact ellipse, as well as the maximum contact stress. When the external meshing face gear contacts the internal meshing face gear, the maximum contact stress on the tooth surface is 1592.08 MPa, and the contact stress gradually decreases along the direction of the contact path.

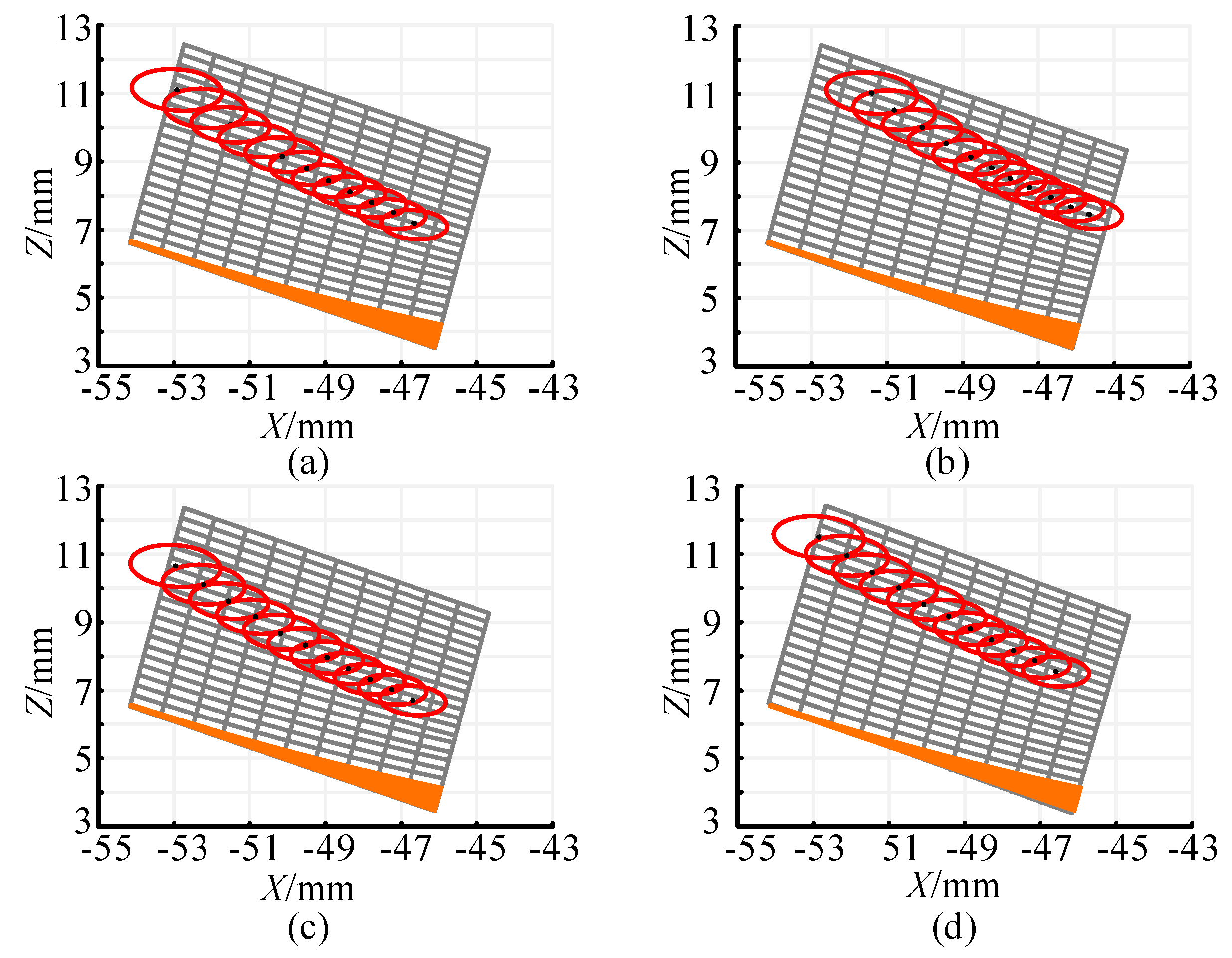
5.3. Tooth Contact Analysis of Face Gear Face Gear Meshing Pair with Modification Machining

Table 3. Parameters of different modification.

	Case1	Case2	Case3	Case4
arabola modification coefficient αp/mm	0.001	0.001	0.001	0.001
Modified coordinates origin xz/mm	0.019	0.019	0.019	0.019
Modified coordinates origin yz/mm	−24.213	−24.213	−24.213	−24.213
Modified rotation angle βp/°	0	−1	−2	−3

lists the modification parameters used in this study. Under the action of load (T_g = 1200 NM), different contact paths for the external meshing face gear can be obtained by modifying (x_z, y_z) and the rotation angle β_p. In this paper, α_p = 0.001 is selected, with no changes to (x_z, y_z), and the value of β_p is modified to 0°, −1°, −2°, and −3°. To compare the effects of different modification coefficients on the actual tooth surface of the face gear, the tooth surfaces corresponding to these values are analyzed. The comparative analysis method is as follows: substitute the different modification parameters into the formula.

Figure 15 shows that when β_p = 0°, he parabolic modification has minimal impact on the contact path, with no significant changes observed.

Figure 16 shows that when β_p = −1°, the contact path extends from the tooth root at the inner diameter to the tooth tip at the outer diameter. The contact path under the four installation conditions is slightly inclined, but the change is not significant. The effective contact path becomes longer with nutation angle error. However, the contact path under offset and axial displacement errors remains largely unchanged, though the contact ellipses increase slightly.

Figure 17 shows that when β_p = −2°, the effective contact path under all four installation conditions becomes noticeably longer. The contact path under nutation angle error shows the most significant change, with the contact path clearly tilting and the contact ellipse increasing.

Figure 18 shows when β_p = −3°, the inclination becomes more pronounced, and the contact path exceeds the tooth surface. The influence of axial bias error and axial displacement error on the contact path is amplified.

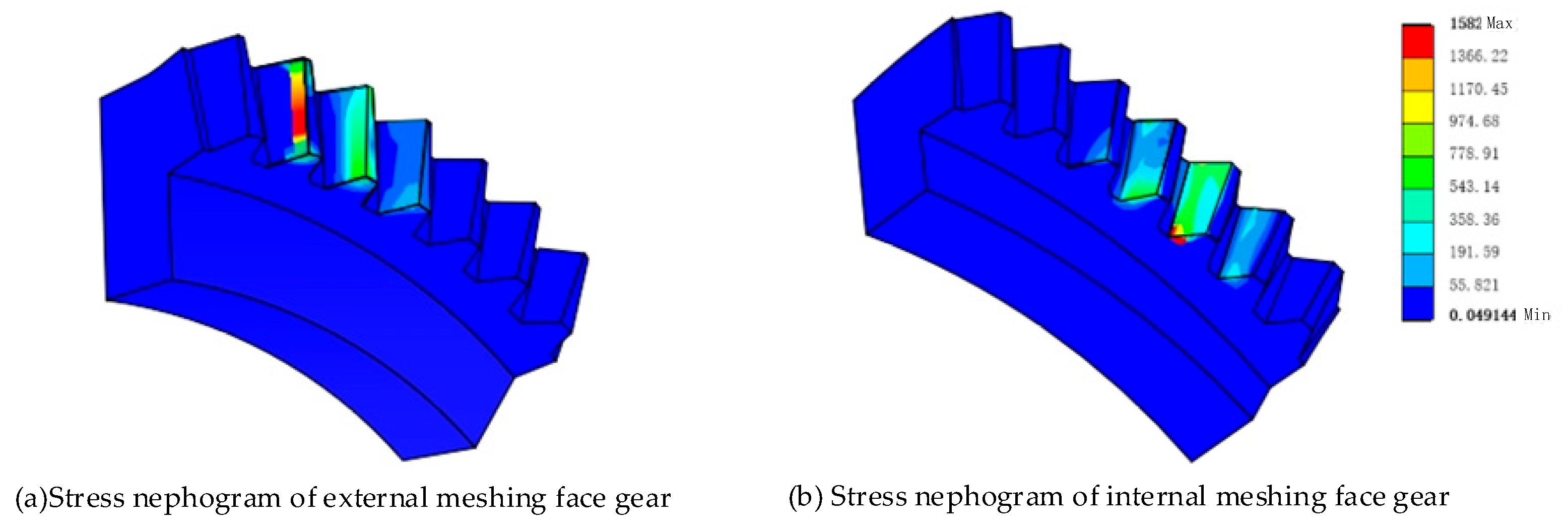
5.4. Contact Stress Analysis

In the meshing process of transmission, under load, the teeth of the nutation face gear will undergo elastic deformation. However, this does not significantly affect the transmission performance. In contrast, if the teeth undergo plastic deformation, the transmission performance will be greatly reduced.

The maximum Mises stresses follow the fourth strength theory in material mechanics, also known as the distortion energy theory, which considers material deformation as the primary form of material failure. Using finite element software, the nutation face gear drive is analyzed, and the maximum Mises stress at the gear tooth contact is obtained to evaluate the performance of the nutation face gear drive.

When using ANSYS to analyze the contact stress of a gear transmission with a small number of teeth, the main steps include pre-processing, solving, and post-processing. The specific steps are as follows:

(1)

Creation of nutating face gear transmission components.

(2)

Selection of materials for the nutation face gear, with material parameters shown in

Table 4. Face gear material parameter values.

Material	Density (kg/m3)	Elastic Modulus (GPa)	Poisson’s Ratio
20Cr2Ni4A	7800	211	0.30

.

(3)

Preliminary meshing of the nutating face gear. After importing the small-tooth differential gear assembly model, redundant contacts may exist that can affect subsequent loading analysis. Therefore, it is necessary to delete the existing contacts first and then perform preliminary meshing to determine if the imported 3D model is suitable for finite element analysis.

(4)

Determination of the connection relationships for the nutating face gear. To determine the size and distribution of contact stress during the re-meshing transmission process, it is necessary to simulate the meshing process, add two rotary connection pairs, and introduce frictional contact at the meshing tooth surfaces to simulate gear tooth engagement.

(5)

Final meshing of the nutating face gear. Since the contact stress of gear meshing is the primary focus of the analysis, the mesh type is defined as tetrahedral.

(6)

Setting of loading conditions for the nutating face gear. A torque of 1200 Nm is applied along the axial direction of the internal gear to simulate the contact behavior of the internal meshing face gear in a new energy vehicle.

(7)

Solution and post-processing for the nutating face gear.

As shown in Figure 19, the maximum contact stress occurs at the tip area of the gear teeth, indicating that this area is prone to contact fatigue failure first. The load condition of the face gear can be improved by modifying the meshing area or increasing the number of teeth. The primary method used in this study is tooth modification.

Figure 20 shows the maximum contact stress of both the external and internal meshing face gears under different modification angles. The calculation results obtained from the analytical method are similar to those obtained from the finite element method (FEM), with the maximum stress error between the two methods being no greater than 10%. This confirms the validity of the constructed force model.

As the modification angle (βp) decreases, the maximum contact stress gradually decreases. When β_p = −1°, he contact stress is significantly reduced. At β_p = −2°, the maximum stress of both the external and internal meshing face gears reaches its minimum value according to both the analytical and FEM methods. However, when β_p = −3°, the maximum contact stress increases again. As shown in Figure 18, the contact ellipse formed by the loading extends beyond the tooth surface boundary, leading to a significant increase in contact stress.

6. Conclusions

This paper proposes a method to improve the nutation reducer by replacing the internal meshing bevel gear pair with a face gear-face gear meshing pair. Based on this approach, a mathematical model for the face gear-face gear meshing pair is established, and the geometric contact analysis of the meshing pair is conducted. The feasibility of this method is verified by simulation results, and a face gear-face gear meshing nutation reducer is ultimately designed. The following conclusions can be drawn from this study:

(1)

The external meshing face gear and the internal meshing face gear, manufactured using the same tool, can conjugate and mesh to form a face gear-face gear pair.

(2)

For the face gear, a modification method based on parabolic modification with an adjustment of the angle β_p is proposed. Compared to simple parabolic modification, this method is more suitable for nutation face gear transmission. The new modification technique improves meshing performance and reduces contact stress. However, when β_p becomes too small, the contact ellipse formed by the load extends beyond the tooth surface boundary, resulting in a surge in contact stress.

(3)

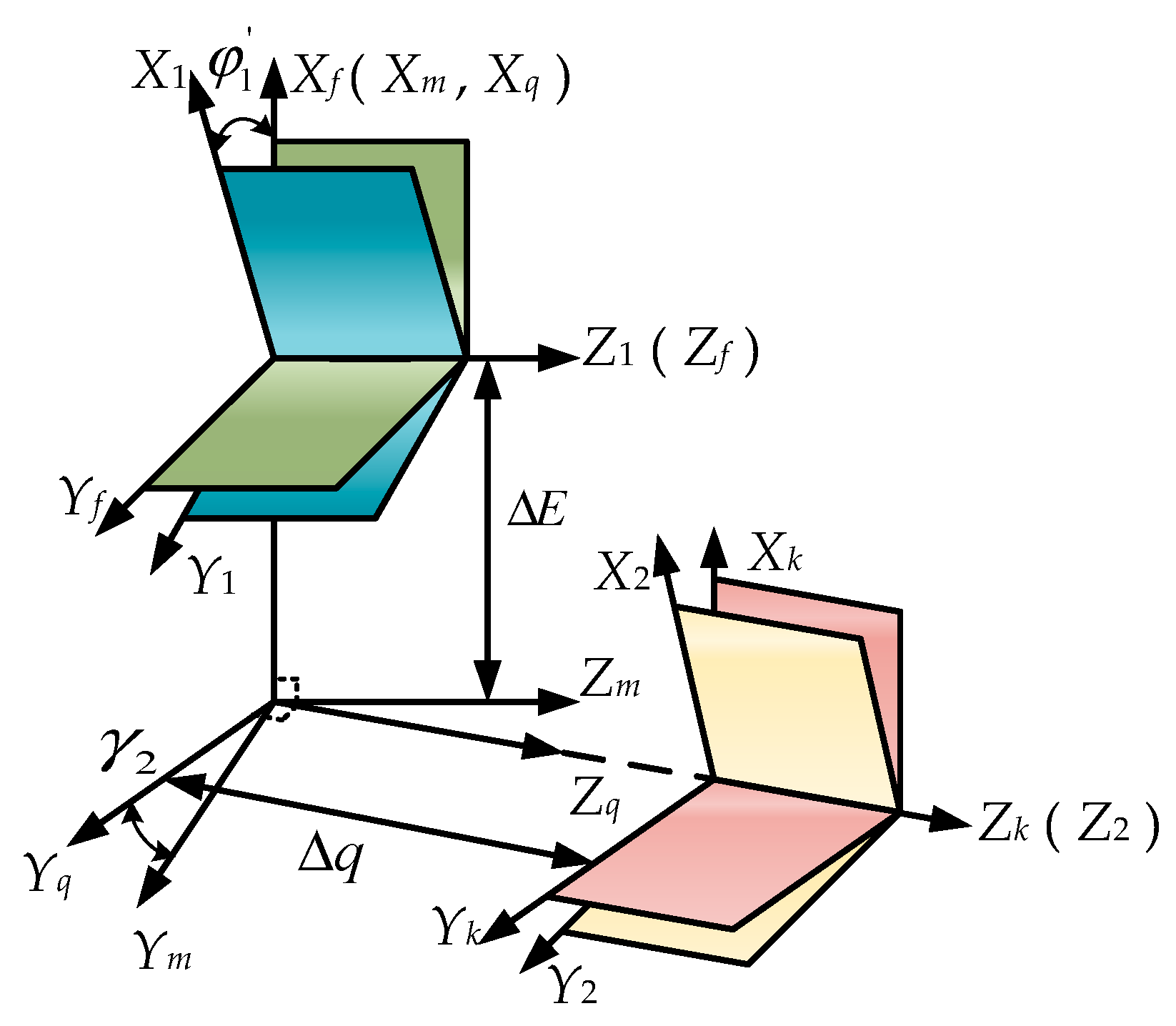
The impact of installation errors on the contact path of the face gear-face gear meshing pair is analyzed. The results show that, compared to axis bias and axial displacement errors, the nutation angle error has the most significant effect on the contact path. This is because the nutation angle error not only directly alters the position and distribution of the contact points but also causes a substantial change in the main curvature of the tooth surface, particularly in the tooth top and outer diameter areas. This has a major impact on the TCA results. Additionally, the nutation angle error has global and cumulative effects, making its influence much greater than other local errors.

(4)

According to the ANSYS contact analysis results, the maximum contact stress occurs at the internal tooth tip area of the face gear. The contact stress distribution is consistent with the calculated value from Hertzian elastic contact theory, as described in Section 5.2. The maximum contact stress is approximately 1500 MPa, indicating that this area is most susceptible to contact fatigue failure. It is also observed that the nutating face gear transmission involves multi-tooth meshing with significant overlap and good power splitting characteristics. However, edge contact occurs, necessitating subsequent tooth surface modifications to resolve the issue.