Abstract
The core issue in handling constrained multi-objective optimization problems (CMOP) is how to maintain a balance between objectives and constraints. However, existing constrained multi-objective evolutionary algorithms (CMOEAs) often fail to achieve the desired performance when confronted with complex feasible regions. Building upon this theoretical foundation, a two-stage archive-based constrained multi-objective evolutionary algorithm (CMOEA-TA) based on genetic algorithms (GA) is proposed. In CMOEA-TA, First stage: The archive appropriately relaxes constraints based on the proportion of feasible solutions and constraint violations, compelling the population to explore more search space. Second stage: Sharing valuable information between the archive and the population, while embedding constraint dominance principles to enhance the feasibility of solutions. In addition an angle-based selection strategy was used to select more valuable solutions to increase the diversity of the population. To verify its effectiveness, CMOEA-TA was tested on 54 CMOPs in 4 benchmark suites and 7 state-of-the-art algorithms were compared. The experimental results show that it is far superior to seven competitors in inverse generation distance (IGD) and hypervolume (HV) metrics.
MSC:
68W50; 65K10; 49K30
1. Introduction
With the advent of artificial intelligence, in real life, many situations involve constraints on multiple objectives. For example, issues such as allocation of water resources [1], vehicle scheduling [2], and route optimization [3,4]. In order to tackle the significant challenges posed by CMOPs [5], an increasing number of constrained multi-objective evolutionary algorithms (CMOEAs [6]) have been proposed over the past 20 years. These algorithms can generally be classified into those based on indicator-based selection mechanisms [7], penalty-based relaxation mechanisms [8], bi-archival memory schemes [9], and decomposition-based approaches [10]. Generally speaking, constrained multi-objective evolutionary algorithms face significant challenges in maintaining a balance between constraints and objectives [11]. Currently, it is difficult to simultaneously address both constraints and the demands of multiple objectives. Constrained Multi-Objective Optimization Problems (CMOPs) are typically defined as:
where is a solution vector. represents the inequality constraints, where p is the number of inequality constraints. represents the equality constraints, where is the number of equality constraints. denotes the decision space and m represents the number of objective functions.
When addressing constraint problems, we need to know the constraint violation of solution x for each constraint. Therefore, the constraint violation of solution x on the j-th constraint is calculated as follows:
In the above formula, serves as a small positive tolerance parameter, which in this paper is set to , aimed at converting equality constraints into inequality constraints. According to Formula (2), the constraint violation of the solution in each objective function is obtained, and then the total constraint violation is calculated as follows:
The total constraint violation of each solution can be obtained using Formula (3). When , x is a feasible solution; otherwise, it is an infeasible solution.
The primary challenge in solving CMOPs is to maintain a balance between objectives and constraints [12]. In some literature, researchers are making extensive efforts to achieve this balance, such as the dual population cooperative evolution framework [13], the multiobjective sorting framework [14], the multistage framework [15], and the archive cooperative evolution framework [16]. In the aforementioned frameworks, the multistage framework and archive cooperative evolution are receiving increasing attention. In a multistage framework, tasks are divided, and appropriate criteria and coping strategies are established at different stages to maintain a balance between constraints and objectives. The cooperative evolution framework of the archive aims to record useful information obtained by the algorithm, helping to obtain a complete constrained Pareto front (CPF) [17]. However, they appear to be somewhat inadequate in dealing with CMOPs with diverse characteristics [18]. These algorithms often tend to focus on searching for feasible solutions, neglecting information about infeasible solutions, which can easily lead the algorithm to local optima [19].
Building on the aforementioned theory, this paper integrates the concept of cooperative archive evolution into a dual-stage framework [15]. Different tasks and response strategies [20] are established at different stages, with a temporary archive mechanism implemented to record useful information obtained by the algorithm at each stage, further enhancing the overall performance of the algorithm. The proposed CMOEA-TA is an evolutionary algorithm based on genetic algorithms. After elite selection generates high-quality parents, high-quality offspring are produced through genetic operators, which promotes the population’s rapid convergence to the optimal solution. The main contributions of this paper are summarized as follows:
- (1)
- A novel two-stage archiving framework is proposed in this paper. In Stage 1, Constraints are appropriately relaxed based on the proportion of feasible solutions and the degree of constraint violation. Simultaneously, under the condition of relaxed constraints, the optimal solution (minimum value) is stored in the archive. In Stage 2, an exchange between the archive and the population is conducted, giving equal consideration to objectives and constraints to enhance the convergence of the population.
- (2)
- A novel constraint learning relaxation mechanism is designed to enhance the algorithm’s exploration capability, prompting the population to attain the complete Pareto front (PF) [21]. At the same time, the archive is continually updated throughout the algorithm’s evolution process, encouraging the algorithm to obtain well-distributed solutions to enhance the convergence and diversity of the population.
- (3)
- Designing a strict constraint dominance principle for parent selection to generate superior offspring and compel the population to achieve the complete CPF. Simultaneously, a balancing mechanism was embedded to select candidate solutions, thereby enhancing the convergence of the population.
- (4)
- To validate the proposed CMOEA-TA, this paper conducted comparative experiments on 54 CMOPs against seven state-of-the-art algorithms. The experimental results indicate that CMOEA-TA significantly outperforms its competitors.
The rest of the work in this paper is arranged as follows. In Section 2, the related work is discussed to elucidate the motivation for this study. In Section 3, the proposed CMOEA-TA is presented in detail. Section 4 describes the experimental study of CMOEA-TA. Finally, Section 5 gives an overall summary and hopes for the future.
2. Related Work and Motivation
This section is divided into two parts. Section 2.1 elaborates on the current state of algorithms balancing constraints and objectives. Section 2.2 introduces the strengths and weaknesses of some algorithms, leading to the motivation for this work. To improve the readability of the paper, Table 1 outlines all the abbreviations.

Table 1.
List of Abbreviations.
2.1. Balancing Constraints and Objectives
To address the balance between objectives and constraints, current CMOEAs can be roughly classified into four categories.
2.1.1. Multi-Stage CMOEAs
This type of algorithm balances constraints and objectives by setting different tasks and responsing strategies at different stages. Wang et al. [22] proposed a two-stage framework called ToP. In the first stage, the weighted vector constrained multi-objective problem is decomposed into constrained single-objective problems, encouraging the population to discover more promising feasible regions. In the second stage, a CMOEA is executed to compel the population to obtain the complete constrained pareto front (CPF) [17]. Fan et al. [23] proposed a novel Push-Pull (PPS) framework mechanism, comprising two stages: the push stage and the pull stage. In the push stage, no constraints are considered, exploring the entire search space, while in the pull stage, constraints are relaxed appropriately to pull infeasible solutions into feasible regions. Tian et al. [12] proposed a two-stage algorithm named CMOEA-MS, which dynamically switches stages during the evolution process to promote a balance between objectives and constraints. Zhang et al. [37] introduced an escape strategy detection mechanism, where the task is to determine whether the population is trapped in a local optimum. If a local optimum is detected, the escape strategy is triggered to facilitate escaping. Tian et al. [25] proposed a multi-stage algorithm named MSCMO, which handles complex constraints one by one and sets corresponding strategies at different stages.
2.1.2. Multi-Population CMOEAs
This second category involves employing a multi-population strategy to balance constraints and objectives. Tian et al. [26] proposed a weak cooperative evolution framework called CCMO, in which two populations play a strong-weak collaboration role, enhancing the population’s ability for external exploration. Ming et al. [27] proposed a multi-task framework called CMOQLMT, which adopts different strategies for different tasks and employs a reinforcement learning mechanism to select corresponding auxiliary tasks. A differential evolution framework named CCMODE [28] is proposed, where constrained single-objective optimization and constrained multi-objective optimization are configured as separate archive populations.
2.1.3. Multi-Ranking CMOEAs
The third category achieves a balance between objectives and constraints through multi-ranking strategies. Wang et al. [38] used pareto dominance and constraint dominance relationships as evaluation metrics to assess the feasibility of algorithms. In [39], a three-objective framework for convergence, diversity, and feasibility was proposed, defining three metrics for evolution within the three-objective framework. Wang et al. [40] proposed a novel metric framework that integrates the metrics of MOEAs with constraint handling techniques, optimizing objectives through metrics and optimizing constraints through constraint handling techniques.
2.1.4. Archive-Based CMOEAs
The fourth category achieves a balance between objectives and constraints through archive-based strategies. Yao et al. [29] proposed a dual-archive framework called C-TAEA, where the CA archive simultaneously optimizes objectives and constraints, enhancing population convergence, while the DA archive only optimizes objectives, enhancing population diversity. Ming et al. [30] proposed a two-stage framework with a single archive called C-TSEA, where the archive assists population evolution, enhancing the algorithm’s exploration capability of feasible regions and facilitating the population’s attainment of a complete CPF. Li et al. [31] proposed a weakly cooperative dual-archive framework called CMOEA-TWC. The driving archive only considers objectives, while the general archive considers both objectives and constraints. The two archives weakly cooperate, sharing useful information to enhance the algorithm’s exploration capability and overall performance.
2.2. Motivation
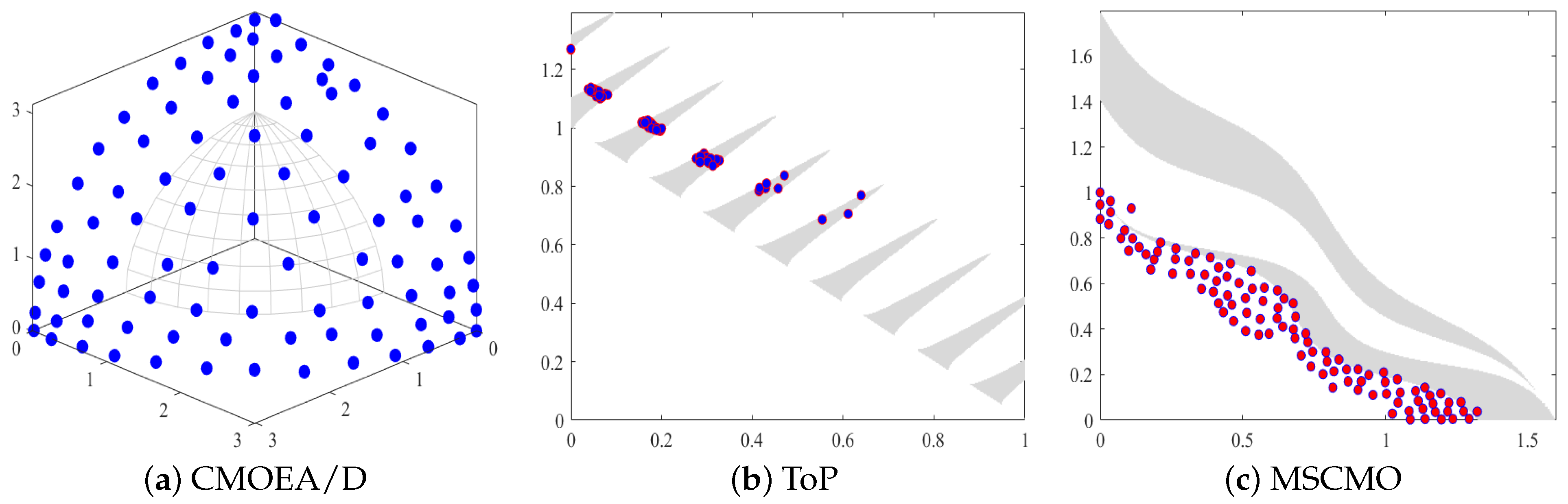
To strike a balance between objectives and constraints, researchers have conducted a significant amount of research. In the initial research stage, Jain et al. [24] proposed the CMOEA/D algorithm, which decomposes constrained multi-objective problems into constrained single-objective subproblems and optimizes these subproblems to obtain a series of evenly distributed solutions. As shown in Figure 1a, although CMOEA/D obtained a relatively evenly distributed set of solutions on LIRCMOP14 [41], the density of the solutions is rather sparse, and it can not guarantee the algorithm to achieve a complete Pareto front. In ToP [22], although constrained multi-objective problems are transformed into constrained single-objective optimization problems by reference vectors, the handling process of subproblems is not sufficiently refined, resulting in slow convergence speed and affecting the overall performance of the algorithm. The performance of ToP on MW2 is illustrated in Figure 1b, where it’s evident that ToP fails to achieve complete convergence and overlooks many feasible regions. In the proposed algorithm MSCMO [25], the process of satisfying the constraints one by one to make the individual a feasible solution is very slow. Therefore, within a limited computational budget, it can not be guaranteed that the solutions will meet all the constraints. As shown in Figure 1c, the distribution of MSCMO [25] on MW12 reveals that the solutions are scattered and there are many infeasible individuals outside the feasible region. It hasn’t fully converged to the pareto front (PF) [21] and hasn’t obtained a complete constrained pareto front (CPF) [17]. Based on the above theory, it can be concluded that achieving a balance between constraints and objectives is extremely important.
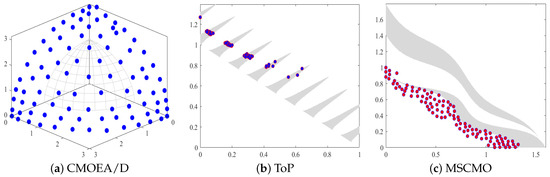
Figure 1.
The obtained feasible and non-dominated solutions of (a). CMOEA/D on LIRCMOP14, (b). ToP on MW2, (c). MSCMO on MW12.
Qiao et al. [32] proposed a multi-population cooperative algorithm called IMTCMO, which assists auxiliary populations to evolve along with the main population, significantly enhancing the algorithm’s performance. However, it neglects the information carried by individuals themselves, resulting in poor migration capability between populations, which easily traps the algorithm into local optima and greatly wastes the algorithm’s exploratory ability and resources. Faced with these challenges, this paper adds an archiving mechanism on top of the existing two-stage approach. As populations evolve continuously, the algorithm records information about solutions and preserves promising individuals, thereby enhancing the convergence of the populations. A balancing mechanism has been embedded in the process of parent selection, thereby enhancing the diversity and convergence of the population. To discover more exploration space and promising solutions, constraints are appropriately relaxed based on the proportion of feasible solutions, preventing the population from getting trapped in local optima and facilitating the population to reach a complete CPF.
3. The Proposed CMOEA-TA
3.1. Framework of CMOEA-TA
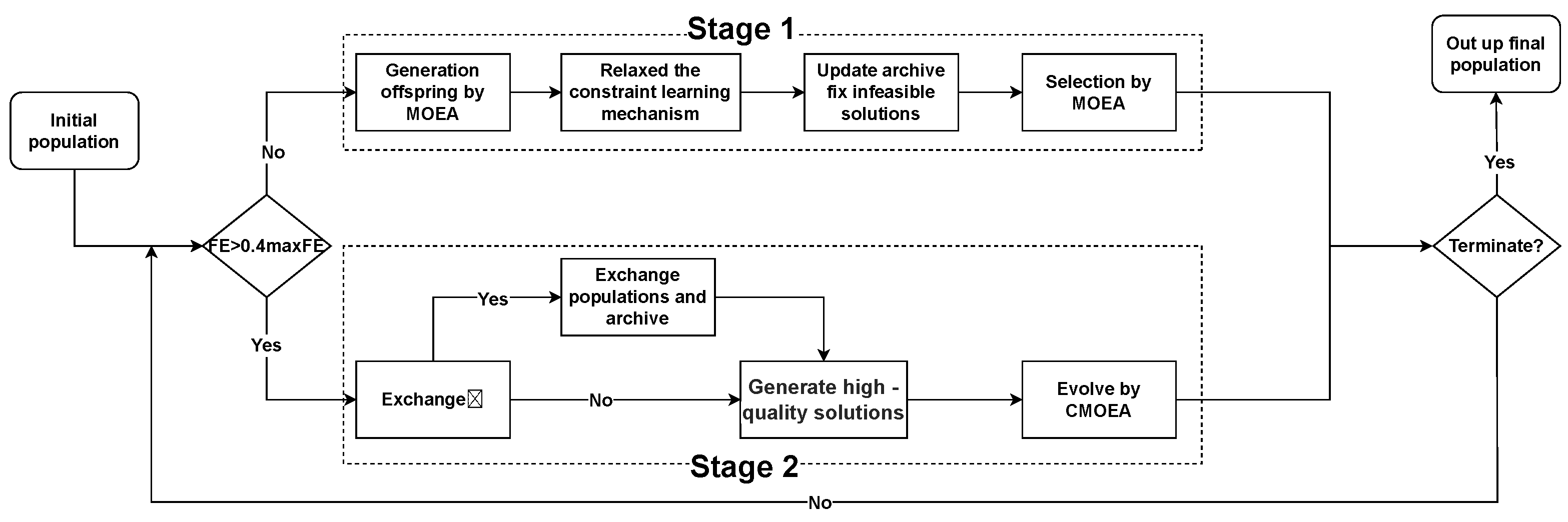
The algorithm in this paper is based on genetic algorithms. Under the algorithm framework designed in this paper, other algorithms can also be used as underlying algorithms, such as swarm optimization, differential evolution, etc. The framework of CMOEA-TA is presented in Algorithm 1. As shown in Algorithm 1, generate an initial population () arbitrarily in the decision space, apply constraint relaxation by factor to obtain the Archive. Compute the minimum constraint violation value in for subsequent . The algorithm then proceeds to iterate within the dual-stage framework we have established. Lines 7 to 13 constitute the first stage of the algorithm. In line 7, the Pareto front of is obtained through non-dominated sorting. In line 8, is combined with to form . In line 9, through an elitist selection mechanism, parents are selected from the merged set and the . In line 10, genetic operators are applied to generate offspring. At this point, our paper introduces the balancing mechanism of DSPCMDE [33], ensuring the convergence of the population with respect to the Pareto front. The specific formula for the balancing parameter is as follows:
At the same time, CDP is used as a prerequisite for selecting parents. The specific formula is as follows:
When the condition is satisfied, solution dominates solution under the constraints. After obtaining the parents (), genetic operators are applied to generate offspring (). Next, the minimum constraint violation value in the offspring is calculated for the next step of updating. After obtaining the new , the population () and offspring () are selected using angle-based environmental selection. At this point, the first stage concludes officially, and the algorithm proceeds to the second stage once the termination conditions are met.
When the algorithm enters the second stage, In line 15, there is an exchange between and , ensuring that the population possesses high-quality candidate solutions. Lines 16 to 17 carry out the same parent selection and offspring generation operations, followed by the execution of elitist environmental selection for the final population . To gain a more intuitive understanding of CMOEA-TA, we present its framework flowchart as shown in Figure 2.
| Algorithm 1 Framework of CMOEA-TA. |
|
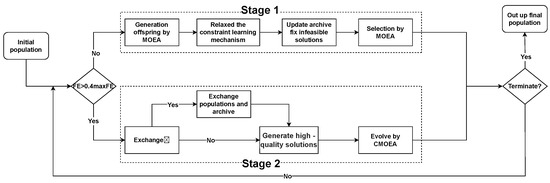
Figure 2.
Framework Flowchart of CMOEA-TA.
3.2. Relaxed the Constraint Learning Mechanism
The relaxed constraint learning mechanism is a commonly used approach aimed at relaxing the constraints of solutions to obtain more useful information from infeasible solutions. The relaxation method typically focuses on constraint violation and the search space, enhancing the exploration of the feasible region and improving the population’s search ability to obtain more solutions. However, during the relaxation process, there is a lack of evaluative indicators to control the boundary search criteria, leading to the unnecessary waste of algorithm resources. Therefore, it is important not only to select high-quality solutions from within the feasible boundary but also to use reference indicators as criteria for scaling the search. The mathematical model of constraint relaxation is as follows:
represents the constraint boundary value for lending, where T and t respectively represent the maximum and current generations. In this process, based on the obtained , the inequality constraints are ignored and forcibly converted into equality constraints, with the aim of introducing more infeasible solutions, increasing the population’s diversity, and promoting its rapid convergence to the unconstrained Pareto front. The motivation for adopting relaxed constraints is as follows: (1) First, in order to increase the utilization of infeasible solutions in the archive and reduce the constraints on feasible solutions, we aim to provide the population with more valuable information. This further enhances the population’s exploratory capabilities, allowing it to find more feasible regions. (2) In the first stage, the purpose of relaxing constraints is to incorporate more infeasible solutions, obtaining more valuable information, and prompting the population to converge from feasible and infeasible regions to CPF. This is aimed at increasing the balance between constraints and objectives, and enhancing the algorithm’s convergence and diversity [37]. This lays the foundation for the migration and interaction in the second stage.
In the selection of relaxation values, we adopt an adaptive relaxation approach. The selection of is subject to constraints such as the proportion of feasible solutions and the degree of constraint violation. When is relatively large, we choose as the relaxation value to introduce more infeasible solutions and reduce their proportion of feasibility. Conversely, when is relatively large, we use as the relaxation value to obtain more information from infeasible solutions and employ constraint-handling techniques to remove redundant solutions.
3.3. The Mechanism of Elite Mating Pool Selection
Algorithm 2 describes the entire process of elite parent selection. First, calculate the number of feasible solutions, denoted as , in set . When the quantity of is greater than N or is less than N, supplement and eliminate using boundary binary tournaments. Otherwise, introduce the balancing mechanism from DSPCMDE to select high-quality solutions from the population and . When is less than a, select two solutions ( and ) from the population, and use Formula (5) from lines 8 to 11 to identify dominated solutions. In this way, the algorithm’s exploration capability is enhanced while maintaining the convergence of the population. If two solutions are mutually non-dominated, select solutions with lower density for supplementation. To provide the population with more exploration space and enhance its diversity. Alternatively, we select two solutions from to perform the above operation.
| Algorithm 2 Elite mating pool selection. |
|
3.4. Updated Archive
Algorithm 3 elaborates on the entire process of updating the archive. Firstly, the number of feasible solutions in the combined population P (Algorithm 1 , ) is determined based on the relaxed constraint conditions. When the number of feasible solutions is less than N, the solutions in P are sorted in ascending order according to Formula (3), and the N-th solution is selected to supplement the update of the archive. When the number of feasible solutions exceeds N, the fitness indicator of SPEA2-CDP [42] is used as the evaluation criterion. By using Formula (10), the fitness of all solutions continues to be calculated, thereby removing redundant inferior solutions. The fitness evaluation formula is as follows:
represents the number of solutions that can dominate x, and is used as an indicator of the convergence strength of x.
Here, represents the crowding degree of solution x. d(x, ) represents the distance from K nearest neighboring solutions to solution x.
| Algorithm 3 UpdatedArchive. |
|
4. Experimental Study
The experimental section introduces the setup of the entire experimental process, elucidates the advantages of CMOEA-TA through IGD [35] and HV [36] metrics, and finally conducts ablation experiments to validate the importance of each innovation.
4.1. Experimental Setup
All experimental setups involved in this paper are as follows:
(1) Test problems
In this study, we employed four commonly used benchmark test suites: MW [43], LIRCMOP [41], ZXH_CF [44], and C_DTLZ [45]. A total of 54 test problems were considered, with the number of objective functions set to their default values without modification.
(2) Performance indicator
The evaluation metrics used in this paper are the most commonly used inverted generational distance (IGD) and hypervolume (HV). A smaller IGD value indicates better performance of the algorithm, while HV behaves inversely; a larger HV value indicates better performance of the algorithm. The black cells in the table represent the best values achieved by algorithms on the test problems.
(3) Compared algorithms
In the experimental comparison process of this paper, seven advanced algorithms were selected, namely ToP [22], C-TAEA [29], CMOEA_MS [12], CMOEA/D [24], TSTI [34], IMTCMO [32] and MSCMO [25]. Among them, C-TAEA, ToP, TSTI, and CMOEA_MS are two-stage algorithms, IMTCMO is an archive-based multi-population algorithm, and MSCMO is a two-stage archive algorithm.
(4) Algorithm parameters
The population size is set to 100, with 100,000 evaluations, and the algorithm runs for 20 iterations. To ensure fairness, the genetic and other parameters of the algorithm are kept unchanged as stated in their paper. Wilcoxon [46] tests are conducted for comparative experimental analysis at a significance level of 0.05. The transition parameter for the two-stage conversion is set to 0.4. The symbols “+”, “−”, and “≈” in the text respectively represent “superior to”, “inferior to”, and “comparable to” our proposed CMOEA-TA, serving to facilitate readers’ quick comparison of performance differences between algorithms. The gray text in all the tables throughout the paper indicates the best values achieved.
(5) Platform and device requirements
The experiments in this paper were conducted using MATLAB software version 2021 or above, and all experiments were performed on the PlatEMO 4.3 [47] platform. The experiments were conducted on computers running Windows 10 or above, with X64-based processors. The analysis plots involved in this paper were created using the 2021 versions of Origin and draw software.
4.2. Comprehensive Analysis of IGD Values
From Table 2, it can be observed that the IGD values of 8 algorithms are listed across 54 test problems in 4 benchmark test suites. It is evident from the table that CMOEA-TA outperforms its competitors significantly in the MW test suite. In the MW test problems, CMOEA-TA achieved 7 best values and outperformed CMOEA/D, ToP, TSTI, MSCMO, CMOEA_MS, CTAEA, and IMTCMO in 10, 9, 8, 9, 12, 10, and 10 test problems, respectively. This is primarily attributed to the application of the constraint learning mechanism, which enhanced its diversity and convergence.

Table 2.
The IGD results (mean and standard deviation) obtained by eight algorithms on the MW, LIRCMOP, ZXH_CF and C_DTLZ problems.
In the LIRCMOP test suites, many infeasible regions are inconsistent with the algorithm’s Pareto front. As a result, many algorithms perform poorly when handling these test suites. In the LIRCMOP test cases, CMOEAD, ToP, TSTI, and CTAEA failed to find the optimal solution, while CMOEA_MS and MSCMO only achieved the best results in one test problem. To accelerate the population’s convergence toward the optimal PF, a strict dominance principle and archiving mechanism were embedded into the original algorithm to enhance its convergence. Compared to the competing algorithms, CMOEA-TA outperformed CMOEAD, ToP, TSTI, MSCMO, CMOEA_MS, CTAEA, and IMTCMO in 14, 14, 14, 8, 12, 4, and 5 test problems, respectively, fully demonstrating CMOEA-TA’s excellent convergence and robustness.
From the ZXH_CFtest problems, it can be seen that although CMOEA-TA did not perform satisfactorily in some test problems, overall, CMOEA-TA not only outperformed seven competing algorithms in 12, 16, 4, 11, 10, 11, and 10 test problems but also achieved the best results in 5 test problems, further validating the effectiveness of CMOEA-TA.
The purpose of the C_DTLZ test suite is to evaluate the performance of algorithms in many multi-objective scenarios. To handle ultra-high-dimensional objective scenarios, an archive update mechanism was embedded to filter higher-quality solutions. As seen from Table 2, CMOEA-TA significantly outperforms its competitors in the C_DTLZ test suite, demonstrating its strong capability in handling numerous multi-objective test problems. This further proves that CMOEA-TA possesses strong diversity and convergence. ToP did not find feasible solutions in five test problems, while CMOEA-TA achieved the best performance in 8 test problems.
In terms of comprehensive IGD values, CMOEA-TA demonstrates superior performance across 46, 46, 32, 36, 45, 44, and 35 test problems when compared to the other seven competing algorithms. However, in 3, 0, 3, 0, 0, 5, and 12 test problems, the seven competing algorithms outperform CMOEA-TA. This analysis reveals that while CMOEA-TA may not always achieve optimal performance in certain test problems, it consistently delivers significantly better results than its competitors across the majority of test cases.
4.3. Comprehensive Analysis of HV Values
From Table 3, we can see that the HV values of eight algorithms on 54 test problems. In the MW test set, CMOEA-TA achieved the best performance on 7 test problems, while ToP failed to find feasible solutions for the MW1 and MW10 test problems, demonstrating CMOEA-TA’s strong search capability, which enhances the algorithm’s diversity. CMOEA-TA outperformed the seven competing algorithms in 10, 9, 7, 9, 12, 10, and 11 test problems, indicating that embedding the dominance principle is the most effective choice, enabling the algorithm to exhibit superior diversity and robustness compared to its competitors.

Table 3.
The HV results (mean and standard deviation) obtained by eight algorithms on the MW, LIRCMOP, ZXH_CF and C_DTLZ problems.
On the LIRCMOP and ZXH_CF test suites, many algorithms struggled to achieve satisfactory results due to the presence of significant infeasible regions and discrete feasible regions on these two test suites. For example, in the LIRCMOP6 test problem, there are some large and discontinuous infeasible regions. Algorithms with weaker search capabilities cannot traverse these large infeasible regions, resulting in the failure to find feasible solutions. In contrast, CMOEA-TA was able to navigate through these infeasible regions and successfully find feasible solutions, demonstrating its robustness.
In the ZXH_CF test suite, CMOEA-TA demonstrated its superior performance by outperforming seven comparison algorithms in 12, 16, 4, 11, 10, 10, 11, and 10 test problems, while the seven competing algorithms surpassed CMOEA-TA in only 1, 0, 4, 0, 1, 2, and 4 test problems. This highlights the impressive superiority of CMOEA-TA. In the C_DTLZ test suite, among the 10 test problems, ToP failed to find feasible solutions for 2 problems, whereas CMOEA-TA attained the best performance in seven cases, significantly outperforming its competitors in terms of solution quality and robustness.
Looking at the 54 test problems in total, CMOEA-TA outperforms seven competitors in 45, 46, 32, 36, 43, 44, and 35 of the test problems. The seven competitors perform similarly to CMOEA-TA in 7, 3, 16, 17, 9, 6, and 8 of the test problems.
Therefore, based on the aforementioned quantitative analysis, it is evident that although CMOEA-TA may perform poorly on some test problems, overall, CMOEA-TA significantly outperforms its competitors, further demonstrating its advantages in diversity and convergence compared to the competing algorithms.
4.4. Performance Analysis
In this section, we conducted performance testing and analysis on CMOEA-TA. From Table 4, we can observe the Wilcoxon [46] test results of CMOEA-TA compared to seven competitors. In the table, , , and p-value respectively indicate superior to, inferior to, and approximate to competitors. ToP failed to find feasible solutions in some test problems and did not outperform or approximate CMOEA-TA in any test problem. While other competitors have all found feasible solutions, their Wilcoxon values are significantly lower compared to CMOEA-TA. Even though IMTCMO has the highest Wilcoxon value among the competitors, CMOEA-TA is noticeably superior to IMTCMO.

Table 4.
Wilcoxon test results with respect to and HV on the 54 test problems.
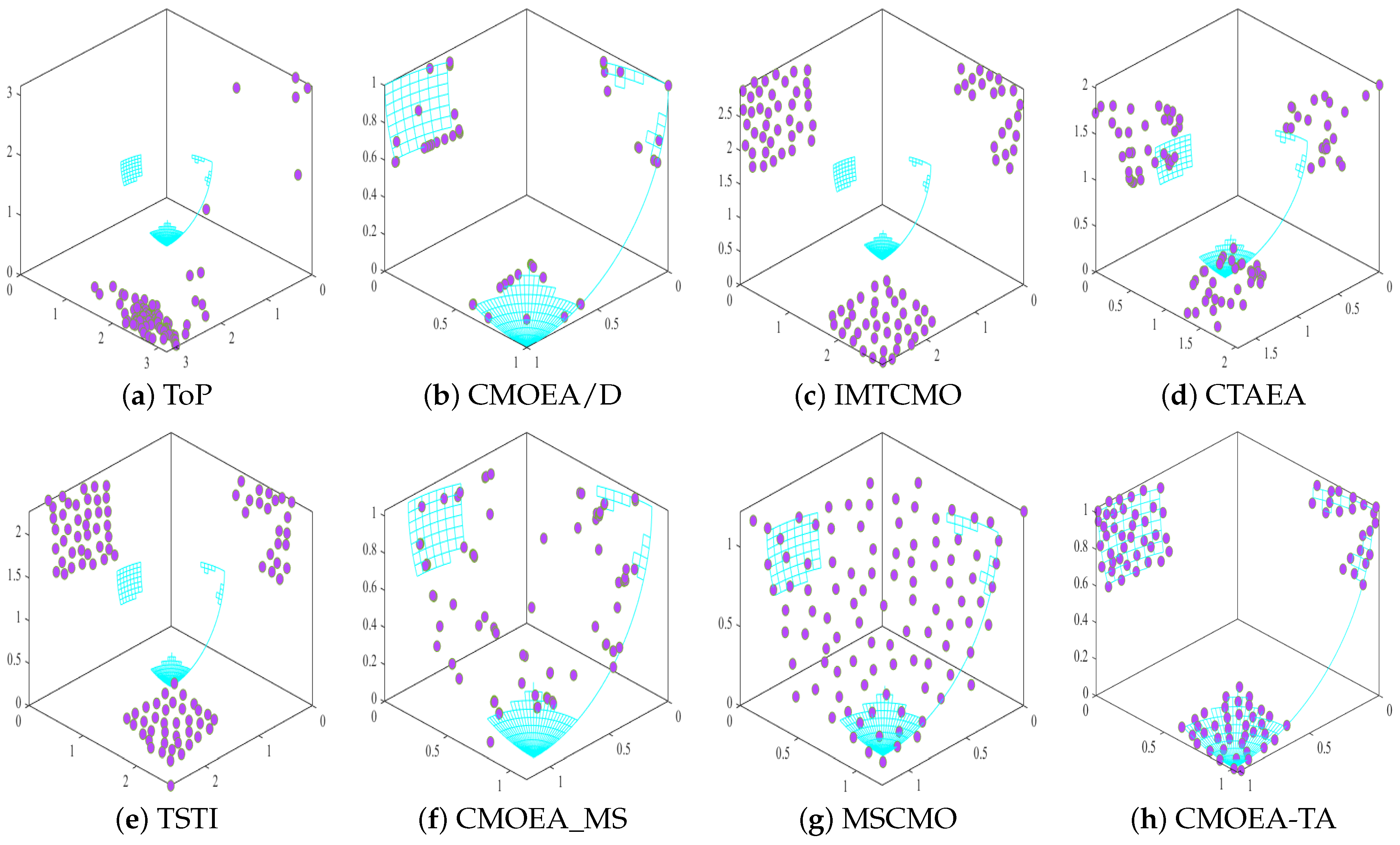
From Figure 3, we can observe the Pareto Front (PF) of eight algorithms on the ZXH_CF10 test problem. It is clear that ToP, IMTCMO, and TSTI did not find solutions on the PF, and most of the solutions found by CMOEA/D, CTAEA, MSCMO, and CMOEA_MS were not on the PF. In contrast, CMOEA-TA not only found all solutions on the PF but also distributed them evenly across it. Therefore, considering Table 4 and Figure 3 collectively, CMOEA-TA significantly outperforms the competitors.
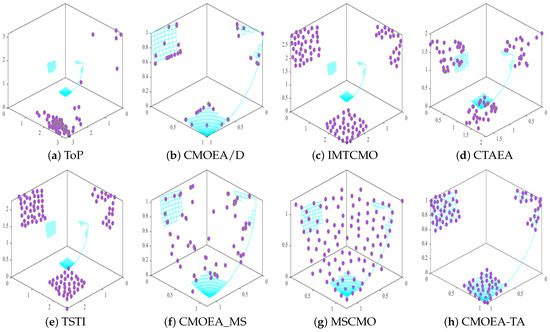
Figure 3.
The Pareto Front (PF) plot obtained in ZXH_CF10 test problem.
4.5. Real-World Problems Analysis
To better highlight the applicability of CMOEA-TA, we compare CMOEA-TA with seven competitors on 15 real-world engineering problems in this section. Since CMOEA does not have a PF on real-world problems, HV is used as its evaluation metric in this paper.
As shown in Table 5, the HV values of 8 CMOEAs on RWMOP1-15 are presented. It can be observed that CMOEA/D and ToP outperform CMOEA-TA only on RWMOP13 and RWMOP15, respectively. CMOEA_MS outperforms CMOEA-TA only on RWMOP1 and RWMOP6, while IMTCMO outperforms CMOEA-TA only on RWMOP7 and RWMOP10. In contrast, CMOEA-TA outperforms CMOEA/D, ToP, TSTI, MSCMO, CMOEA_MS, CTAEA, and IMTCMO on 14, 13, 14, 14, 12, 14, and 13 test problems, respectively.

Table 5.
The HV results (mean and standard deviation) obtained by eight algorithms on the real-world problems.
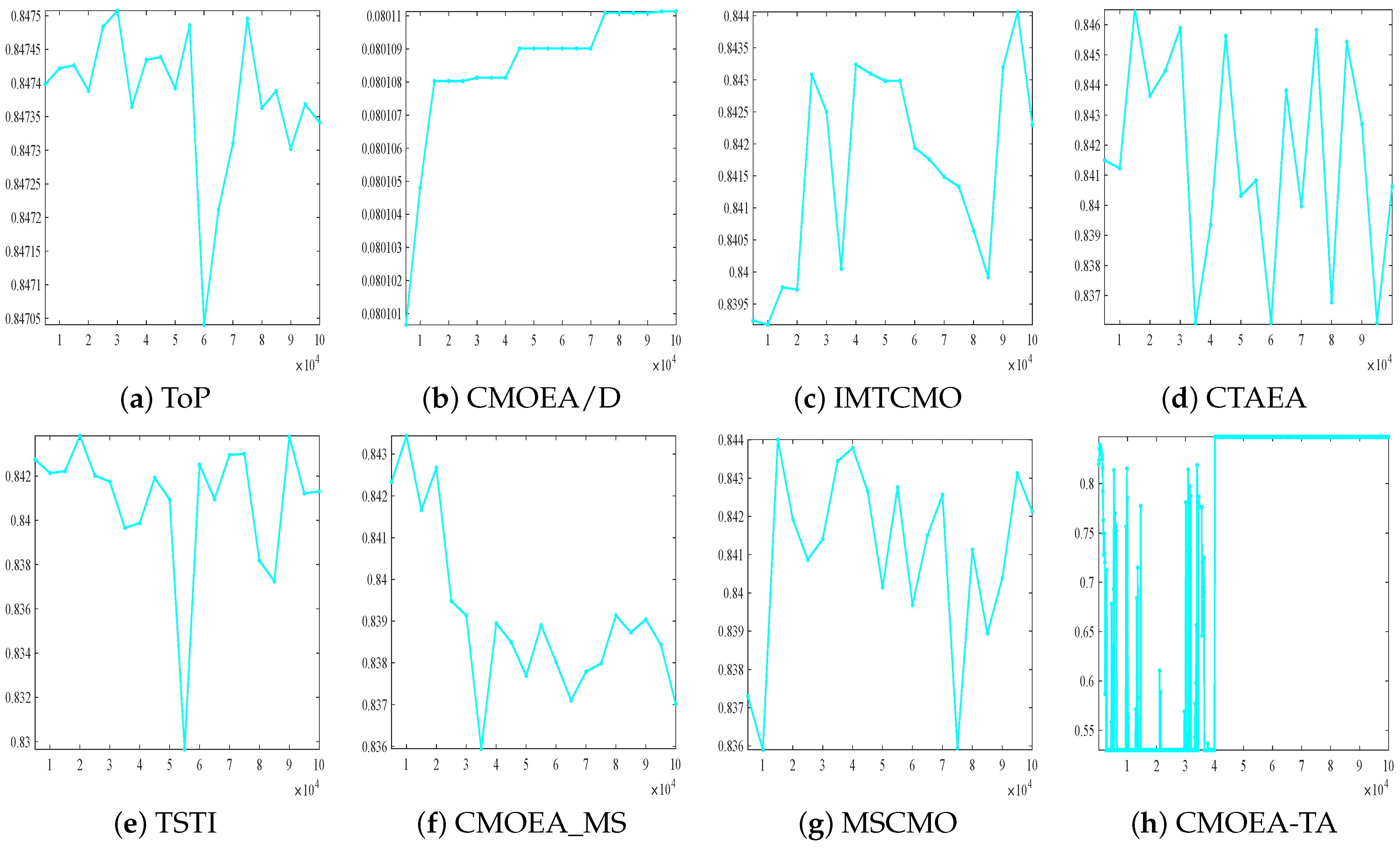
To better highlight the superiority of CMOEA-TA, Figure 4 shows the HV plots of eight CMOEAs on RWMOP10. It is clear that CMOEA-TA reaches the optimal value the earliest, with a higher HV indicating stronger algorithm performance. In contrast, the other competitors fail to consistently maintain the optimal value throughout the evaluation process, and their HV values fluctuate significantly. Only CMOEA/D maintains the optimal value, but its HV value is too low, indicating poor algorithm performance. Therefore, based on the analysis of Table 5 and Figure 4, it can be concluded that CMOEA-TA outperforms its competitors.
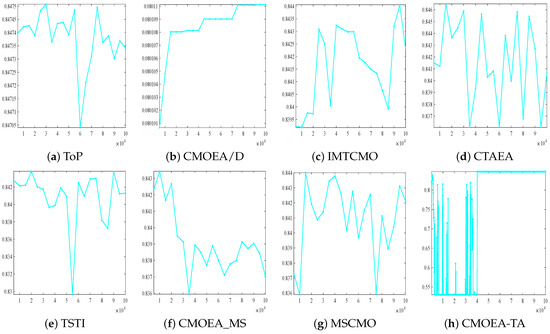
Figure 4.
The hypervolume(HV) plot obtained in RWMOP10 test problem.
4.6. Effectiveness of Core Components of CMOEA-TA
In this section, in order to further validate the effectiveness of the innovation, four variants (namely, CMOEA-TA1-4) were designed and compared with CMOEA-TA, with detailed information shown in Table 6.

Table 6.
List of Variant Abbreviations.
From Table 7, we can observe the IGD values of CMOEA-TA and its four variants on the MW benchmark problem. CMOEA-TA1 and CMOEA-TA2 failed to find feasible solutions on three test problems, validating the importance of the two-stage framework and archiving mechanism. CMOEA-TA3 performs worse than CMOEA-TA on 14 test problems, further validating the effectiveness of the balancing mechanism. CMOEA-TA4 performs worse than CMOEA-TA on 8 test problems, indicating the irreplaceable role of the relaxed constraint mechanism in its design. Table 8 presents the HV values of the four variants and CMOEA-TA across 14 test cases, where CMOEA-TA outperforms the four variants on 7, 7, 14, and 8 test problems respectively. In summary, both the framework and innovative mechanisms we proposed have achieved remarkable results, further validating the effectiveness of CMOEA-TA.

Table 7.
The IGD results (mean and standard deviation) of CMOEA-TA and four variants of it on MW test suite.

Table 8.
The HV results (mean and standard deviation) of CMOEA-TA and four variants of it on MW test suite.
To validate the effectiveness of the proposed genetic algorithm-based framework on other evolutionary algorithms, we embedded swarm optimization and differential evolution algorithms as underlying algorithms into the CMOEA-TA framework, forming two independent variants (CMOEA-TA(SO) and CMOEA-TA(DE)).
As shown in Table 9, the IGD values of variants CMOEA-TA(SO) and, CMOEA-TA(DE) and the seven CMOEAs on test instances C_DTLZ clearly indicate that the CMOEA-TA(SO) and CMOEA-TA(DE) variants achieved optimal values on 9 and 5 test problems, respectively, demonstrating that CMOEA-TA has strong applicability when faced with other underlying algorithms. Looking at the HV values in Table 10, the CMOEA-TA(SO) outperforms the seven competitors on 9, 7, 7, 8, 8, 10, and 9 test problems, while the CMOEA-TA(DE) variant outperforms them on 4, 5, 2, 4, 3, 6, and 5 test problems. Therefore, both the IGD and HV metrics show that CMOEA-TA(SO) and CMOEA-TA(DE) outperform the competitors, further validating the effectiveness and applicability of the proposed genetic algorithm-based CMOEA-TA.

Table 9.
The IGD results (mean and standard deviation) of CMOEA-TA(SO), CMOEA-TA(DE) variants, and their seven CMOEAs on the C_DTLZ test suite.

Table 10.
The HV results (mean and standard deviation) of CMOEA-TA(SO), CMOEA-TA(DE) variants, and their seven CMOEAs on the C_DTLZ test suite.
5. Conclusions
In this research work, a two-stage archive-based framework based on genetic algorithms was designed to handle CMOP. In the first stage, a learning relaxation mechanism is introduced, where the relaxation of constraint values is adaptively adjusted based on the feasible ratio and the degree of constraint violation. Feasible solutions obtained are stored in an archive, which is continuously updated throughout the algorithm iterations. In the second stage, the relaxation of constraints is eliminated, and the balance between constraints and objectives is considered to ensure the feasibility of the algorithm. When selecting parents, a strict dominance constraint strategy is implemented to ensure the production of high-quality offspring.
The experimental results show that CMOEA-TA outperforms seven other competing algorithms across 54 test problems. Quantitatively, CMOEA-TA demonstrates superior performance in terms of HV and IGD on the majority of test problems, showing stronger convergence and diversity, which proves its robustness and effectiveness in solving CMOPs. Furthermore, the algorithm exhibits strong practicality when applied to 15 real-world engineering problems.
A limitation of CMOEA-TA is its preference for feasible solutions, which often leads to suboptimal results when dealing with large infeasible regions and sparse areas, as observed in the case of the LIR-CMOP problem, for example. Therefore, in future work, increasing the utilization of infeasible solution information and enhancing interaction with the archive will be key research directions.
Author Contributions
Conceptualization, K.Z. and J.C.; Methodology, J.C.; Software, J.C.; Validation, J.C. and K.Z.; Formal analysis, J.C.; Investigation, J.C.; Resources, K.Z.; Data curation, K.Z. and J.C.; Writing—original draft, K.Z., J.C., H.Z. and S.Z.; Writing—review & editing, K.Z., J.C., H.Z. and S.Z.; Visualization, J.C.; Supervision, K.Z. and J.C.; Project administration, K.Z.; Funding acquisition, K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zarei, F.; Arashpour, M.; Mirnezami, S.A.; Shahabi-Shahamiri, R.; Ghasemi, M. Multi-skill resource-constrained project scheduling problem considering overlapping: Fuzzy multi-objective programming approach to a case study. Int. J. Constr. Manag. 2024, 24, 820–833. [Google Scholar] [CrossRef]
- Li, X.; Peng, Y.; Tian, Q.; Feng, T.; Wang, W.; Cao, Z.; Song, X. A decomposition-based optimization method for integrated vehicle charging and operation scheduling in automated container terminals under fast charging technology. Transp. Res. Part E Logist. Transp. Rev. 2023, 180, 103338. [Google Scholar] [CrossRef]
- Ding, L.; Shi, C.; Zhou, J. Collaborative route optimization and resource management strategy for multi-target tracking in airborne radar system. Digit. Signal Process. 2023, 138, 104051. [Google Scholar] [CrossRef]
- Farahmand-Tabar, S.; Afrasyabi, P. Multi-modal Routing in Urban Transportation Network Using Multi-objective Quantum Particle Swarm Optimization. In Applied Multi-Objective Optimization; Springer: Berlin/Heidelberg, Germany, 2024; pp. 133–154. [Google Scholar]
- Wang, Q.; Li, T.; Meng, F.; Li, B. A framework for constrained large-scale multi-objective white-box problems based on two-scale optimization through decision transfer. Inf. Sci. 2024, 665, 120411. [Google Scholar] [CrossRef]
- Hao, L.; Peng, W.; Liu, J.; Zhang, W.; Li, Y.; Qin, K. Competition-based two-stage evolutionary algorithm for constrained multi-objective optimization. Math. Comput. Simul. 2025, 230, 207–226. [Google Scholar] [CrossRef]
- Falcón-Cardona, J.G.; Coello, C.A.C. Convergence and diversity analysis of indicator-based multi-objective evolutionary algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; pp. 524–531. [Google Scholar]
- Wang, F.; Huang, M.; Yang, S.; Wang, X. Penalty and prediction methods for dynamic constrained multi-objective optimization. Swarm Evol. Comput. 2023, 80, 101317. [Google Scholar] [CrossRef]
- Gu, Q.; Liu, R.; Hui, Z.; Wang, D. A constrained multi-objective optimization algorithm based on coordinated strategy of archive and weight vectors. Expert Syst. Appl. 2024, 244, 122961. [Google Scholar] [CrossRef]
- Alwuthaynani, M.M.; Abdallah, Z.S.; Santos-Rodriguez, R. A robust class decomposition-based approach for detecting Alzheimer’s progression. Exp. Biol. Med. 2023, 248, 2514–2525. [Google Scholar] [CrossRef] [PubMed]
- Kawachi, T.; Kushida, J.i.; Hara, A.; Takahama, T. Efficient parameter-free adaptive penalty method with balancing the objective function value and the constraint violation. Int. J. Comput. Intell. Stud. 2021, 10, 127–160. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Su, Y.; Zhang, X.; Tan, K.C.; Jin, Y. Balancing objective optimization and constraint satisfaction in constrained evolutionary multiobjective optimization. IEEE Trans. Cybern. 2021, 52, 9559–9572. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, H.; Tian, Y.; Li, C.; Yue, D. Cooperative constrained multi-objective dual-population evolutionary algorithm for optimal dispatching of wind-power integrated power system. Swarm Evol. Comput. 2024, 87, 101525. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Zhang, T.; Meuser, C.; von Unwerth, T. Multi-Objective Operating Parameters Optimization for the Start Process of Proton Exchange Membrane Fuel Cell Stack with Non-Dominated Sorting Genetic Algorithm II. J. Electrochem. Soc. 2024, 171, 034506. [Google Scholar] [CrossRef]
- Zhou, T.; He, P.; Niu, B.; Yue, G.; Wang, H. A novel competitive constrained dual-archive dual-stage evolutionary algorithm for constrained multiobjective optimization. Swarm Evol. Comput. 2023, 83, 101417. [Google Scholar] [CrossRef]
- Bao, Q.; Wang, M.; Dai, G.; Chen, X.; Song, Z.; Li, S. An archive-based two-stage evolutionary algorithm for constrained multi-objective optimization problems. Swarm Evol. Comput. 2022, 75, 101161. [Google Scholar] [CrossRef]
- Zhong, X.; Yao, X.; Gong, D.; Qiao, K.; Gan, X.; Li, Z. A dual-population-based evolutionary algorithm for multi-objective optimization problems with irregular Pareto fronts. Swarm Evol. Comput. 2024, 87, 101566. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, S.X.; Zheng, S.Y. A diverse/converged individual competition algorithm for computationally expensive many-objective optimization. Appl. Intell. 2024, 54, 2564–2581. [Google Scholar] [CrossRef]
- Su, T.V.; Hang, D.D. Second-order optimality conditions in locally Lipschitz multiobjective fractional programming problem with inequality constraints. Optimization 2023, 72, 1171–1198. [Google Scholar] [CrossRef]
- Fan, C.; Wang, J.; Xiao, L.; Cheng, F.; Ai, Z.; Zeng, Z. A coevolution algorithm based on two-staged strategy for constrained multi-objective problems. Appl. Intell. 2022, 52, 17954–17973. [Google Scholar] [CrossRef]
- Yeste, P.; Melsen, L.A.; García-Valdecasas Ojeda, M.; Gámiz-Fortis, S.R.; Castro-Díez, Y.; Esteban-Parra, M.J. A Pareto-Based Sensitivity Analysis and Multiobjective Calibration Approach for Integrating Streamflow and Evaporation Data. Water Resour. Res. 2023, 59, e2022WR033235. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y. Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces. IEEE Trans. Evol. Comput. 2019, 23, 870–884. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Li, H.; Wei, C.; Zhang, Q.; Deb, K.; Goodman, E. Push and pull search for solving constrained multi-objective optimization problems. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Ma, H.; Wei, H.; Tian, Y.; Cheng, R.; Zhang, X. A multi-stage evolutionary algorithm for multi-objective optimization with complex constraints. Inf. Sci. 2021, 560, 68–91. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2020, 25, 102–116. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Gao, L. Adaptive auxiliary task selection for multitasking-assisted constrained multi-objective optimization [feature]. IEEE Comput. Intell. Mag. 2023, 18, 18–30. [Google Scholar] [CrossRef]
- Wang, J.; Liang, G.; Zhang, J. Cooperative differential evolution framework for constrained multiobjective optimization. IEEE Trans. Cybern. 2018, 49, 2060–2072. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-archive evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2018, 23, 303–315. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Zhen, H.; Li, S.; Wang, L.; Liao, Z. A simple two-stage evolutionary algorithm for constrained multi-objective optimization. Knowl.-Based Syst. 2021, 228, 107263. [Google Scholar] [CrossRef]
- Li, Y.; Feng, X.; Yu, H. A constrained multiobjective evolutionary algorithm with the two-archive weak cooperation. Inf. Sci. 2022, 615, 415–430. [Google Scholar] [CrossRef]
- Qiao, K.; Liang, J.; Yu, K.; Yue, C.; Lin, H.; Zhang, D.; Qu, B. Evolutionary constrained multiobjective optimization: Scalable high-dimensional constraint benchmarks and algorithm. IEEE Trans. Evol. Comput. 2023, 28, 965–979. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.; Luo, Y.; Yue, C. Dynamic selection preference-assisted constrained multiobjective differential evolution. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 2954–2965. [Google Scholar] [CrossRef]
- Dong, J.; Gong, W.; Ming, F.; Wang, L. A two-stage evolutionary algorithm based on three indicators for constrained multi-objective optimization. Expert Syst. Appl. 2022, 195, 116499. [Google Scholar] [CrossRef]
- Hakimazari, M.; Baghoolizadeh, M.; Sajadi, S.M.; Kheiri, P.; Moghaddam, M.Y.; Rostamzadeh-Renani, M.; Rostamzadeh-Renani, R.; Hamooleh, M.B. Multi-objective optimization of daylight illuminance indicators and energy usage intensity for office space in Tehran by genetic algorithm. Energy Rep. 2024, 11, 3283–3306. [Google Scholar] [CrossRef]
- Shen, X.; Yao, X.; Gong, D.; Tu, H. Multi-objective optimization and integrated indicator-driven two-stage project recommendation in time-dependent software ecosystem. Inf. Softw. Technol. 2024, 170, 107433. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Q.; Lin, Q. A constrained multiobjective evolutionary algorithm with detect-and-escape strategy. IEEE Trans. Evol. Comput. 2020, 24, 938–947. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y.; Song, W. A new fitness function with two rankings for evolutionary constrained multiobjective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5005–5016. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, M.; Wang, J.; Zhang, Z.; Xiang, Y.; Zhang, J. Tri-goal evolution framework for constrained many-objective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3086–3099. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y.; Wang, B.C. Indicator-based constrained multiobjective evolutionary algorithms. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5414–5426. [Google Scholar] [CrossRef]
- Cetina-Quiñones, A.; Bassam, A.; Medina-Carril, D.; Chan-Dzib, E.; Hernandez Bautista, A. Multi-objective optimization of energo-enviro-economic indicators of an outdoor swimming pool heating system: An approach with advanced computational techniques. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 186. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK Report. 2001, 103. [Google Scholar] [CrossRef]
- Jin, L.; Kazemi, M.; Comodi, G.; Papadimitriou, C. Assessing battery degradation as a key performance indicator for multi-objective optimization of multi-carrier energy systems. Appl. Energy 2024, 361, 122925. [Google Scholar] [CrossRef]
- Xie, Y.; Li, J.; Li, Y.; Zhu, W.; Dai, C. Two-stage evolutionary algorithm with fuzzy preference indicator for multimodal multi-objective optimization. Swarm Evol. Comput. 2024, 85, 101480. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, H.L.; Yang, S. An adaptive parental guidance strategy and its derived indicator-based evolutionary algorithm for multi-and many-objective optimization. Swarm Evol. Comput. 2024, 84, 101449. [Google Scholar] [CrossRef]
- Desai, S.A.; Monika, s. An empirical study on application of Wilcoxon signed rank test in statistical process control when process target is fixed. Int. J. Manag. IT Eng. 2018, 8, 130–136. [Google Scholar]
- Tian, Y.; Zhu, W.; Zhang, X.; Jin, Y. A practical tutorial on solving optimization problems via PlatEMO. Neurocomputing 2023, 518, 190–205. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).