Abstract
A generalization of the efficient interpolation of periodic Green’s functions is presented for a multilayer medium hosting transverse electric current densities and transverse equivalent magnetic current densities at different interfaces. The mathematical model is realized in terms of Maxwell’s equations for multilayer media with isolated electric and magnetic equivalent current densities for large values of spectral variables or small values of spatial variables. This fact enables the use of Mixed Potential Integral Equation (MPIE) approaches in the spectral domain and provides asymptotic behaviors for Green’s functions of vector and scalar potentials for both electric and magnetic sources. Consequently, the singular behaviors of the Green’s functions around the source point are obtained as the spatial counterpart of the proposed spectral asymptotic behaviors. Thus, regularized multilayer periodic Green’s functions are obtained, which can be efficiently interpolated over the entire unit cell using Chebyshev’s polynomials.
MSC:
78-10; 65D05; 41A60; 45E10
1. Introduction
In the design and analysis of electromagnetic devices such as frequency selective surfaces (FSSs) [1], reflectarrays/transmitarrays [2], leaky wave antennas [3], and metasurface antennas [4], efficient electromagnetic analysis tools for multilayer periodic structures are required. In the design of these devices, it is common practice to assume that each element of the antenna or FSS is located in a periodic environment. This is known as the local periodicity assumption [2].
There are mature methods to analyze multilayer periodic structures based on Finite Elements (FEMs) [5,6,7] and the Finite Difference Time Domain (FDTD) [8,9]. However, these methods involve volumetric meshes of the multilayer medium to face domain integral computations or iterative recurrence relations with slow convergence. A method to avoid domain integrals consists of using the Boundary Element Method (BEM). The BEM is known for its main advantage, which enables working with boundary integrals instead of some domain integrals by means of Green’s functions of the structure under study [10]. This fact is very advantageous since the dimensionality of the problem is reduced. In the past half-century, the BEM has been gradually developed from a single theory to engineering applications in areas such as crack propagation [11,12], acoustic fields [13,14], and cathodic protection [15], etc. We highlight efficient versions of the BEM, such as the Isogeometric Boundary Element Method with Reciprocity Duality (IG-DRBEM) [16] or the Scaled Coordinate Transformation Method in Boundary Elements (SCTBEM) [17], where the problem is addressed in its entirety only through contour integrals involving Green’s functions and their derivatives. Either way, an efficient computation of Green’s functions is required to implement BEMs.
A well-established method of analysis for multilayer periodic structures is the boundary element approach, commonly known in electromagnetics as the method of moments (MoM) [18,19,20,21]. This method is suitable since the multilayer medium is modeled by transverse dyadic (i.e., tensor of order 2) Green’s functions and the volumetric mesh of the multilayer medium is avoided. These transverse dyadic Green’s functions relate transverse electric and magnetic fields to their sources, which are transverse electric current densities and equivalent magnetic current densities [22]. However, in the case of periodic structures, one has to deal with the computation of infinite double sums of discrete samples of spectral dyadic Green’s functions of the non-periodic multilayer medium. Although accurate and stable techniques exist to provide the multilayer Green’s functions in the spectral domain in closed form [23,24], the infinite double sums converge slowly and their computations involve prohibitive consumption of CPU time.
Fortunately, preprocessing techniques exist to efficiently interpolate the Green’s functions in terms of Chebyshev polynomials after extracting the known singular behavior around the source point [19,25]. Moreover, Kummer’s transformation and Ewald’s method [26,27,28] are used in [19] for the fast computation of the sampling of the multilayer Green’s functions in the spatial domain for the interpolation process. However, the approaches shown in [19,25] only consider transverse electric current densities on ‘layouts’ embedded in the multilayer medium (i.e., transverse equivalent magnetic current densities or transverse electric fields on slots or apertures are not considered). In this work, we will present a generalization of these approaches to extract the singular behavior and interpolate the resulting regularized multilayer periodic Green’s functions when the multilayer medium hosts both transverse electric current densities and transverse equivalent magnetic current densities at different interfaces of the multilayer medium.
For this purpose, we use the asymptotic behaviors of the multilayer dyadic Green’s functions in the spectral domain for large values of spectral variables [24]. These asymptotic behaviors will show that the multilayer medium with electric current densities and equivalent magnetic current densities behaves like a multilayer medium with isolated sources. This fact will enable the MPIE formulation of the multilayer Green’s functions [29] to generalize the efficient interpolation proposed in [19,25].
Figure 1 shows a multilayer periodic structure that hosts transverse electric current densities (with x- and y-components) and transverse equivalent magnetic current densities (with x- and y-components) at different interfaces of the multilayer medium, where represents the total number of interfaces containing sources. Note that the z-axis is orthogonal to the multilayer medium. Consider periodic transverse electric current densities hosted at the th interface () and transverse equivalent magnetic current densities hosted at the th interface (). The multilayer substrate consists of isotropic and homogeneous layers with thickness and complex electric permittivity and real magnetic permeability (), where and are the vacuum permittivity and permeability, respectively, and are the relative permittivity and permeability of the homogeneous pth layer, respectively, and is the imaginary unit. Although layers with permittivity and permeability are considered, all the relations shown in this work are valid for the typical dielectric multilayer media of electromagnetic devices by completing . The lower limit of the multilayer substrate is either a ground plane or free space. The periodic structure in Figure 1 is illuminated by a linearly polarized plane wave with an arbitrary polarization direction, and the incidence direction is provided by spherical angular coordinates and .
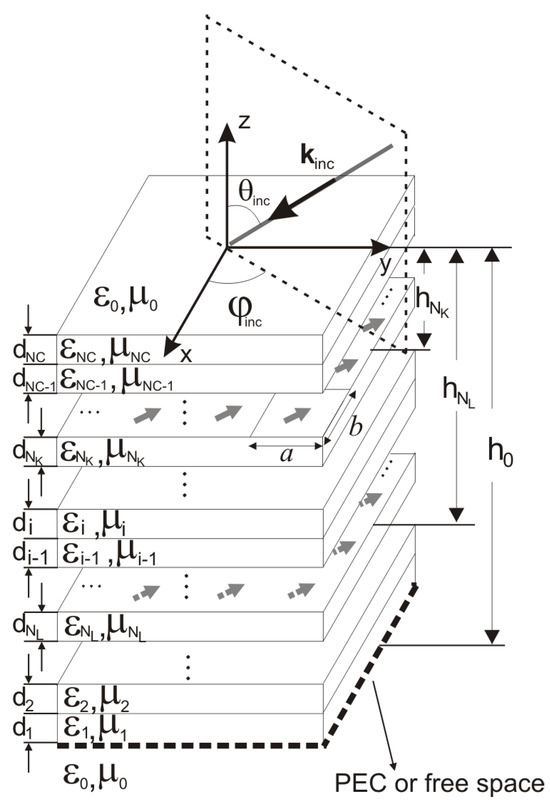
Figure 1.
Multilayer periodic structure with as the periodic cell size. The transverse electric current densities (solid gray arrows) are located at the interfaces, and the transverse equivalent magnetic current densities (dashed gray arrows) are located at the interfaces. Note that the z-axis is orthogonal to the multilayer medium.
2. Relationship Between Sources and Fields in a Non-Periodic Multilayer Medium
Since the computation of the periodic multilayer Green’s functions in the spatial domain involves infinite double sums of discrete samples of spectral Green’s functions of the non-periodic multilayer medium, in this section, we briefly review the general algorithm shown in [23] for the computation of the transverse dyadic Green’s functions of the non-periodic multilayer medium in the spectral domain for isotropic and homogeneous layers. In a similar way to that shown in [23], let us consider the non-periodic multilayer medium of the periodic structure shown in Figure 1 but with only transverse electric current densities hosted at the interfaces () (i.e., transverse equivalent magnetic current densities are not considered).
In the following, we shall make extensive use of the two-dimensional Fourier Transform, which can be defined for square-integrable functions on , i.e., those functions such that
Definition 1.
Let be a complex-valued square-integrable function. The two-dimensional Fourier Transform is defined as
Particularly for periodic functions, which are the specific focus of our work, the square integrability is not satisfied, and the Fourier Transform becomes a distribution. In fact, it is an infinite sum of shifted Dirac delta distributions multiplied by coefficients that happen to be the coefficients of the Fourier series:
with
The square integrability of f on is thus replaced by square integrability on the unit cell . The original function can be reconstructed from the Fourier coefficients through
The square integrability condition in the unit cell will be satisfied for all the functions considered in this work (electric and magnetic fields, currents, etc.) since they will always be bounded in the unit cell.
For the case of Green’s functions, they always have singularities, so their Fourier Transform must be understood in the context of tempered distributions (see, for instance, [30]).
The following theorem can be stated:
Theorem 1.
Let be the two-dimensional Fourier Transform of the transverse electric fields (with x- and y-components) in the region of the multilayer medium (see Figure 1). Let us denote and . Then, the two-dimensional Fourier Transform of the transverse electric field, , in the region has the following expression:
where and , with λ being the working free space wavelength.
Proof.
Let us consider Maxwell’s equations in the frequency domain for the ith layer (i.e., region ).
where and f is the working frequency.
Since the multilayer medium is not limited in the x and y directions, we apply the two-dimensional Fourier Transform with respect to the x- and y-coordinates to (7) and (8). The resulting expressions for the components of the fields are provided by
Solving and in (11) and (14) and substituting the resulting expressions in (9), (10), (12), and (13) yields a linear system of differential equations. This system of differential equations can be written in matrix form as
where
satisfying
with . Equations (15) and (16) are coupled differential linear equations. In order to decouple them, we differentiate with respect to z in (15) and substitute (16), obtaining in the region
Since , the two-dimensional Fourier Transform of the transverse electric field provided in Theorem 1 satisfies (20). □
Once Theorem 1 has been demonstrated, we can state the following Lemma:
Corollary 1.
Consider a non-periodic multilayer medium with isotropic and homogeneous layers with only transverse electric current densities hosted at the interfaces (). Let be the two-dimensional Fourier Transform of the transverse electric current density at the ith interface . The following system of equations is satisfied:
where , and where the rest of the matrices are defined in Appendix A.
Proof.
Let be the two-dimensional Fourier Transform of the transverse magnetic fields (with x- and y-components). According to (15), can be calculated in the region as
where (19) has been taken into account to calculate the inverse matrix of . The continuity condition of the transverse magnetic fields leads to
where denotes the unit vector along the z-coordinate. Substituting (22) into (23) leads to the system of equations provided in (21). □
It is important to note that, from (21), the transverse electric field at the th or th interface can be solved in terms of the rest of the transverse electric fields when this interface does not host a transverse electric current density. In this way, we can iteratively solve the transverse electric field at the th or th interface in order to obtain a reduced system of equations. Bearing this in mind, we can state the following:
Lemma 1
(Mesa, Marqués & Horno ’91). Consider a non-periodic multilayer medium with isotropic and homogeneous layers with only transverse electric current densities hosted at the interfaces (). The following reduced system of equations is satisfied:
with and where
The matrices and are computed by means of the following downward recurrent algorithm:
and where the matrices and are computed by means of the following upward recurrent algorithm:
The recurrent algorithms are initialized with the matrices , , and .
For the proof of Lemma 1, we suggest referring to [23].
The expression shown in (24) relates the spectral version of the transverse electric current density on the th interface with the spectral version of the transverse electric fields on the th, th, and th interfaces.
However, (21) and (24) have been obtained under the assumption of only transverse electric current densities hosted at the interfaces (). Let us now consider the interfaces with transverse electric current densities (electric sources hosted at the th interface ()) and the interfaces with transverse equivalent magnetic current densities (magnetic sources hosted at the th interface ()), which is the initially posed problem. It is known that fictitious sources can be considered in each interface from their transverse electric fields and transverse magnetic fields (see, for example, [22]) using the relations and (where and denote the two-dimensional Fourier Transform of the transverse magnetic field and the transverse magnetic current density on the th interface, respectively). Another approach is to use the relations and to consider fictitious transverse magnetic and electric fields on the interface. In this work, we will consider fictitious transverse electric fields, , and fictitious electric current densities, , on the interfaces that host equivalent magnetic currents (th interface). These fictitious and also satisfy the expression provided in (24). However, since the fictitious electric fields are built from magnetic current densities (i.e., ) and the fictitious electric current densities are built from magnetic fields (i.e., ), in this case, plays the role of the source and plays the role of the field. So, the following corollary can be stated, which is a direct application of the previous considerations to Lemma 1:
Corollary 2.
Consider a non-periodic multilayer medium with isotropic and homogeneous layers where transverse electric current densities are hosted at the interfaces () and transverse magnetic current densities are hosted at the interfaces (, ). Then, the following reduced system of equations is satisfied as follows:
where and .
Since the th interface that hosts equivalent magnetic current density and transverse magnetic fields is considered, we use the expression provided in (24) for the th, th, and th interfaces using the fictitious field, , and current density, , and the non-fictitious fields , , , and the non-fictitious current densities , , , . So, the systems of equations provided by (30) and (31) lead to
Since , , and play the role of sources and , , , , and play the role of fields, we pass the source terms to the right-hand side of the equations, resulting in the following equivalent system of equations:
The rest of the equations in the system of equations provided in (24) are kept unchanged. The matrix provided in (37) can be obtained in terms of the matrix as follows:
We would like to point out that the independent terms of the system of equations provided by (37)–(39) play the role of sources. In this way, the fictitious current density and the fields , , , and can be obtained by inversion of the coefficient matrix of the system of equations and by matrix multiplication of this inverse matrix and the independent terms of the system of equations.
3. Asymptotic Behavior of the Spectral Transverse Dyadic Green’s Function of a Non-Periodic Multilayer Medium
Below, we will show the behavior of the system of equations provided by (37)–(39). Let us state the following Lemma:
Lemma 2.
Consider a non-periodic multilayer medium with transverse magnetic current densities hosted at the interface . Consider also another non-periodic multilayer medium with transverse electric current densities hosted at the interfaces . For high values of spectral variables and , , the following reduced system of equations is satisfied:
Proof.
When , the variable . This fact leads to and consequently , and . According to Appendix A, we can see that (where is the Frobenius norm) when the spectral variables . According to (26), (27), (29), and (31), this fact leads to and , where , , , , and [24]. This last fact leads to and when and , respectively, when the spectral variables . In this way, the system of equations provided in (32) and (33) is decoupled for large values of spectral variables (i.e., a multilayer medium that hosts electric and equivalent magnetic current densities behaves as multilayer media with isolated sources when ). This fact implies that the system of equations provided by (37)–(39) satisfies the relations provided in (44) and (45) for each interface that hosts either a transverse equivalent magnetic current density (i.e., fictitious transverse electric field) or a transverse electric current density. □
Since and play the role of sources, we can express the fictitious current density and the transverse electric fields in terms of source terms as follows:
where (40) has been considered. If the spatial counterparts of and are calculated from (46) and (47), convolutions between the spatial versions of and and between the spatial versions of and are obtained. Since and play the role of sources, the spatial versions of and play the role of dyadic Green’s functions. Moreover, since the multilayer medium behaves as multilayer media with isolated sources, we can apply the MPIE approach for an isolated transverse electric current density on the th interface or an isolated transverse electric field on a slot or aperture at the th interface. In order to relate the MPIE approach with and , we use the spectral version of MPIE Green’s functions for isolated transverse electric current densities (see (13)–(15) in [31]) and the dual version for isolated transverse equivalent magnetic current densities.
Theorem 2.
Let us consider a multilayer medium as depicted in Figure 1. Let be the two-dimensional Fourier Transform of the dyadic Green’s function of the transverse electric field for transverse electric current densities at the th interface. Let also be the two-dimensional Fourier Transform of the dyadic Green’s function of the fictitious transverse electric current densities for fictitious transverse electric field at the th interface. Then, the relations between the dyadic Green’s functions and the Green’s functions of mixed potential are provided by
where . and are spectral versions of Green’s functions for the magnetic scalar potential and the x-component of the electric vector potential, respectively, at the th interface. and are spectral versions of Green’s functions for the electric scalar potential and the x-component of the magnetic vector potential, respectively, at the th interface.
Proof.
Let us prove it for the case of Green’s functions of magnetic vector potential, , and electric scalar potential, . The proof for the case of Green’s functions of electric vector potential, , and magnetic scalar potential, , can be made by the conventional duality theorem.
Consider a multilayer medium with isolated transverse current densities hosted at the th interface. In the region , the following relation between mixed potentials and the electric field is satisfied:
where Lorentz’s Gauge has been assumed (i.e., ). Let us consider the relations between the fields and the isolated transverse current densities hosted at the th interface:
where
and
The dyadic Green’s function of the vector potential has been chosen to be consistent with Sommerfeld’s choice of potentials (p. 258, [32]). Substituting (51)–(54) in (50) and retaining the x- and y-components of the dyadic Green’s function of the electric field leads to
According to (p. 145, [33]), when there is a transverse electric current density, the Green’s function of the scalar potential and the components of the dyadic magnetic vector potential satisfy the expression
Once Theorem 2 has been demonstrated, we state the next Lemma:
Lemma 3.
Consider a non-periodic multilayer medium with transverse magnetic current densities hosted at the interface . For high spectral variables and , , the asymptotic behavior of the two-dimensional Fourier Transform of Green’s functions of magnetic scalar potential, , and the x-component of vector electric potential, , are provided by
where . and are provided by
Proof.
In [25], the asymptotic behaviors of and were provided as functions of , which were proportional to , where and were obtained from the effective medium concept of the two adjacent layers to the th interface. In order to generalize this asymptotic behavior for spectral Green’s functions and , we consider the asymptotic behavior of the matrix for high values of spectral variables . Since when , we can conclude that from (28) and (30). Moreover, if we consider in the expression of provided in (A2) in Appendix A for high values of the argument of the hyperbolic cotangent function and we take into account (25), we deduce the following asymptotic behavior for :
where is the identity matrix and is also a matrix defined in Appendix A in terms of the spectral variables and . By applying the effective medium concept in a similar way to that shown in [25], we obtain
where . From the Taylor expansion of , , and in (70) and (71) with respect to up to , we obtain the expressions provided in (67) and (68) for and .
4. Efficient Computation of Transverse Dyadic Green’s Functions in a Periodic Multilayer Medium
In this section, the computation of the spatial counterpart of for periodic structures, , is shown. This computation can be carried out by a double infinite sum of discrete samples of in the spectral domain as follows:
where is the periodic cell and and , with and the angular spherical coordinates of the incident plane wave (see Figure 1). From now on, x and y represent the Cartesian coordinates of the observation point, and and represent the Cartesian coordinates of the source point, assuming the source point is in the th interface and the observation point is in the th interface.
In the previous section, we showed that with exponential decay when [24]. Therefore, the systems of equations provided in (32) and (33) are decoupled for large values of the spectral variables (i.e., and with exponential decay when if and ). This fact ensures exponential convergence of infinite double sums shown in (72) when . However, when , the infinite double sums are slowly convergent. So, it is preferable to use the MPIE approach when . Let represent the periodic multilayer Green’s functions for scalar and vector potential: and if (i.e., the th interface hosts transverse electric current densities), and and if (i.e., the th interface hosts transverse equivalent magnetic current densities), respectively. Let represent and if , and and if , respectively. According to [19,25], the computation of also involves double infinite sums of discrete samples of spectral Green’s functions:
Bearing in mind the asymptotic behaviors shown in (65) and (66) for , and the asymptotic behaviors provided in [25] for , when , we can apply Kummer’s transformation [25] as follows:
where . In (74), the first infinite double sums are truncated for , where typically a value of is enough. The other asymptotic infinite double sums can be efficiently computed by means of Ewald’s method as in [19,25] since the asymptotic spectral Green’s function, , behaves as a function that is proportional to (where represents either or ). In our context, Ewald’s method can be stated by the following theorem:
Theorem 3
(Ewald’s method). Define , and . Then,
where the function is the complementary error function [34].
Note that, while the double infinite sum on the left-hand side is slowly convergent, the sums on the right-hand side are rapidly convergent (see [28,35,36]).
According to [37], it is recommended that the parameter E appearing in (75) is selected inside the interval . According to (65) and (66), and [25], this behavior leads to a type of function that is suitable for applying Ewald’s method.
Although (72) and (74) provide efficient computation of and , greater CPU time savings can be obtained by means of interpolation of Green’s functions in terms of Chebyshev polynomials [19].
In order to achieve highly accurate interpolation of , the extraction of the known singular behavior around the source point should be carried out before the interpolation process [19,25]. According to the properties of the Fourier Transform, this singular behavior can be obtained from the Fourier Transform of the asymptotic behavior when of the spectral function as follows:
where and is either or , depending on whether plays the role of or . The results shown in (76) can be obtained by using Equation (4.302) of [38]. So, in a similar manner as shown in [19], we can define a regularization function as follows:
Bearing in mind the definition of the regularization function, the regularization of in the whole unit cell can be conducted by the extraction of the regularization function at the source points placed at the corners of the unit cell [19].
We would like to point out that this regularization does not take into account possible quasi-singularities that may arise from images of the source point through thin layers adjacent to the th interface (for example, possible glues used to bond the different dielectric layers). In that case, the regularization function can be completed by a term that models quasi-singular behavior by means of the discrete complex image method (DCIM) [39], as proposed in [19].
Once the regularized Green’s functions are available, an accurate interpolation of and when can be conducted in terms of Chebyshev polynomials in the whole unit cell as follows:
where stands for the rth Chebyshev polynomial of the first kind. The coefficients and the matrix can be obtained by using Equation (26) of [19]. Once these coefficients are available, the efficient computation of () can be conducted by means of (80), while the efficient computation of can be conducted by
where is provided by using the approximations in (79).
5. Results
In this section, we will show different results obtained at a frequency GHz from the analysis of the scattering of a periodic multilayer medium under a normal incident plane wave with a periodic cell of . The results are obtained by considering the multilayer medium lower limit by free space and composed of nine commercial low-loss dielectric layers. The multilayer medium of our analysis uses Rohacell® layers () as separators between printed layers, and Diclad® 880 (), Arlon® layer (), Rogers® (), and glass () as printed layers. All the layers are 3 mm thick. This multilayer medium hosts transverse current densities at interfaces and transverse equivalent magnetic current densities at interfaces.
Figure 2 shows the normalized values of the components of the matrix and with respect to the maximum values as a function of . In Figure 2, an exponential decay is observed, as expected from the discussion in the previous section. In fact, reductions of 3 and 5 orders of magnitude are demonstrated, respectively, for the components of and with respect to their maximum values when . On the other hand, Figure 3a shows the relative error between , (, and ) and their respective asymptotic behaviors. Similar results are obtained for and in Figure 3b. These asymptotic behaviors have been obtained according to [25] for and , and obtained by (65) and (66) for and . In Figure 3, a relative error of 0.001 is reached when . All these facts mean that the choice of in (74) and truncation of the infinite double sums in (74) with fewer than 90 terms retained are sufficient to provide accurate results.
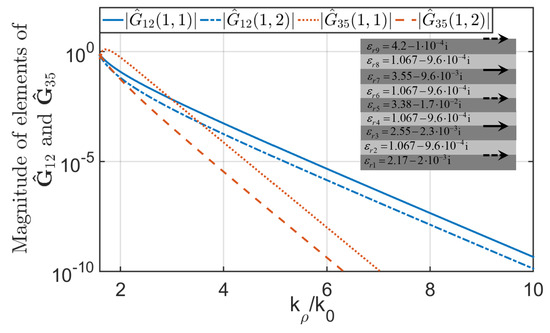
Figure 2.
Normalized values of the magnitude of the components of the matrix and with respect to maximum values as a function of . The inset explains the layout of the different layers with the corresponding values of the permittivity and the presence of transverse electric current densities (solid gray arrows) or transverse equivalent magnetic current densities (dashed gray arrows).
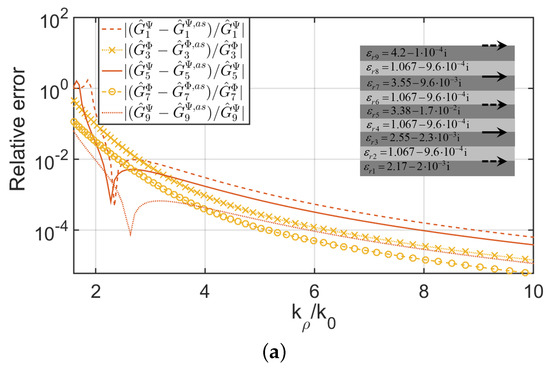
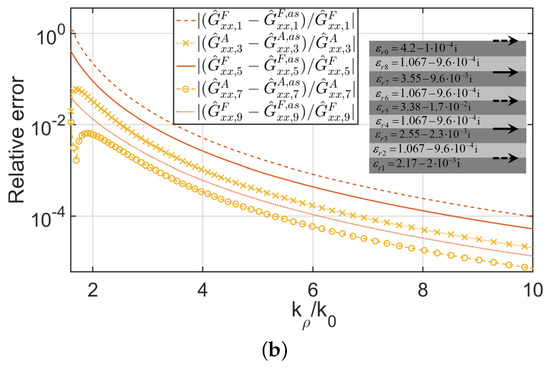
Figure 3.
Relative error between Green’s function in the spectral domain and asymptotic behavior provided in (65) and (66), and [25] (a) for , and (b) for , (, and ). The inset explains the layout of the different layers with the corresponding values of the permittivity and the presence of transverse electric current densities (solid gray arrows) or transverse equivalent magnetic current densities (dashed gray arrows).
Figure 4a shows the relative error for the computation of periodic multilayer Green’s functions and (, and ) of scalar potentials by means of (74) using Ewald’s method, and by the direct computation of (73). Figure 4b shows the relative error for the computation of periodic multilayer Green’s functions and (, and ). In Figure 4a,b, the relative error is always below 0.004. We would like to point out that roughly 16 million terms were retained in the computation of (73), while fewer than 90 terms were retained when Kummer’s transformation and Ewald’s method were applied.
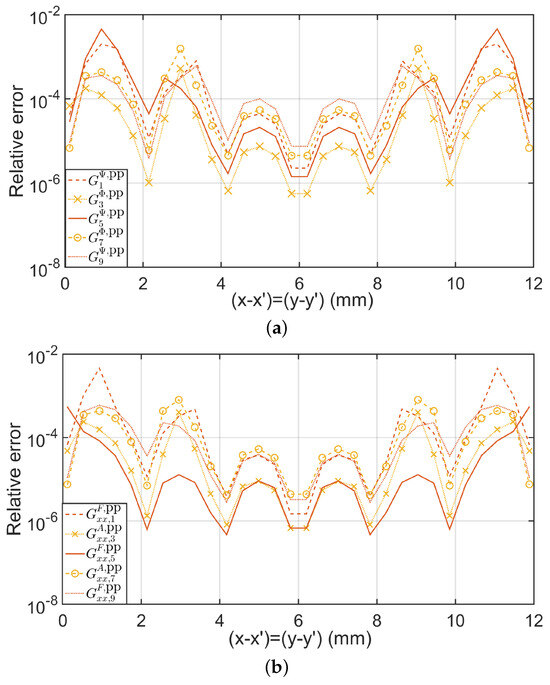
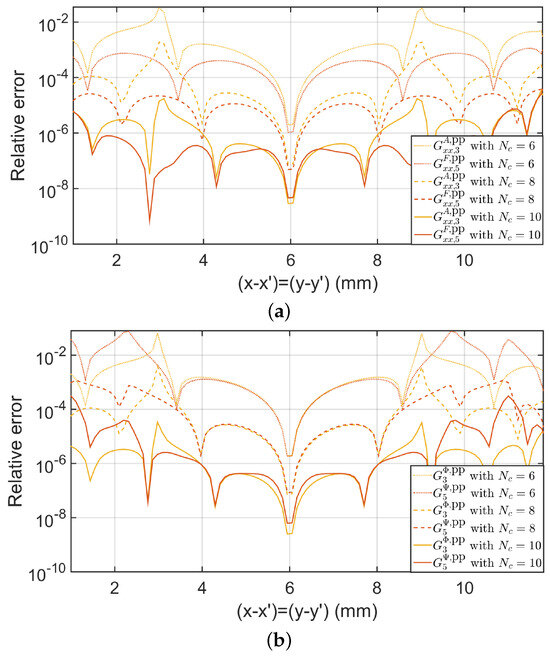
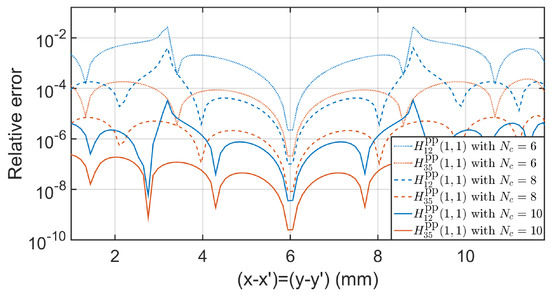
Finally, Figure 5 shows the relative error between the computations of the diagonal component of and by the exact formula (72) and by Chebyshev interpolation (80), while Figure 6a shows the relative error between the computations of and by (74) (Kummer’s transformation and Ewald’s method are used) and by means of Chebyshev interpolation of regularized Green functions (81). Figure 6b also shows the relative error between and by (74) (Kummer’s transformation and Ewald’s method are used) and by means of Chebyshev interpolation of regularized Green functions (81). In Figure 5 and Figure 6, the relative errors for different values of , and 10 are compared. These comparisons clearly show that the relative error is reduced in a geometric way as increases (see [40]), providing a relative error of roughly 0.001 for along the values on the periodic cell. We would like to point out that the CPU time reduction in the computation of the results shown in Figure 5 and Figure 6 for using (79)–(81), with respect to the use of (72) and (74), is roughly by a factor of 100. This CPU time gain justifies the effort of judicious interpolation in the spatial domain in terms of 2-D Chebyshev polynomials after extracting the singular behavior of the Green’s functions around the source points.
6. Conclusions
A generalization of efficient interpolation of multilayer periodic Green’s functions for a multilayer medium that hosts both transverse electric current densities and transverse equivalent magnetic current densities in different interfaces was presented. The multilayer medium behaves as multilayer media with isolated electric and equivalent magnetic current densities for large values of spectral variables. This fact enabled the use of MPIE approaches in the spectral domain, providing the asymptotic behaviors of Green’s functions for magnetic scalar potential and the x-component of electric vector potential by using the effective medium concept as shown in [25] These proposed asymptotic behaviors produce relative errors below 0.001 when . Thus, the knowledge of singular behaviors of Green’s functions around the source point is obtained as the spatial counterpart of the proposed asymptotic behaviors in the spectral domain. Finally, regularized multilayer periodic Green’s functions were obtained and efficiently interpolated in the whole unit cell, providing relative errors below 0.001 and a CPU time reduction by a factor of 100 compared to that obtained by Kummer’s transformation and Ewald’s method.
We would like to point out that the indicated efficient interpolation of the multilayer periodic Green’s functions covers applications such as the analysis and design of frequency electromagnetic devices like selective surfaces (FSSs), reflectarrays/transmitarrays, leaky wave antennas, metamaterials, and metasurface antennas, where all these devices hold layouts and/or apertures/slots that can be modeled by transverse electric current densities and/or equivalent magnetic current densities, respectively. In the analysis and design of these devices, it is common practice to employ the local periodicity assumption, where each element in the device, with dimensions close to the working wavelength (i.e., ), is considered as located in a periodic environment. In future works, the efficient interpolation will be extended to the case of periodic multilayer structures with anisotropic dielectric layers, thus enabling the analysis and design of devices with novel materials such as layers of liquid crystals, graphene, ferromagnetic layers, etc.
Author Contributions
Conceptualization, R.F. and J.G.; methodology, R.F.; software, R.F.; validation, R.F.; formal analysis, R.F. and J.G.; investigation, R.F. and J.G.; resources, R.F. and J.G.; writing—original draft preparation, R.F.; writing—review and editing, R.F. and J.G.; visualization, R.F. and J.G.; supervision, J.G.; project administration, J.G.; funding acquisition, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the ’Diputación de Jaén’, through the ’Instituto de Estudios Gienenses’ under the project entitled ’Sistema de medida de bajo coste para testeo de antenas con drones en escenarios reales en la provincia de Jaén’.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MPIE | Mixed Potential Integral Equation |
| FSS | Frequency Selective Surface |
| MoM | Method of Moments |
| DCIM | Discrete Complex Image Method |
References
- Munk, B.A. Frequency Selective Surfaces; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
- Huang, J.; Encinar, J.A. Reflectarray Antennas; IEEE Press/Wiley: Piscataway, NJ, USA, 2008. [Google Scholar]
- Minatti, G.; Caminita, F.; Casaletti, M.; Maci, S. Spiral leaky wave antennas based on modulated surface impedance. IEEE Trans. Antennas Propag. 2011, 59, 4436–4444. [Google Scholar] [CrossRef]
- Minatti, G.; Maci, S.; De Vita, P.; Freni, A.; Sabbadini, M. A circularly-polarized isoflux antenna based on anisotropic metasurface. IEEE Trans. Antennas Propag. 2012, 59, 4498–5009. [Google Scholar] [CrossRef]
- De la Rubia, V.; Zapata, J.; González, M.A. Finite element analysis of periodic structures without constrained meshes. IEEE Trans. Antennas Propagat. 2008, 56, 3020–3028. [Google Scholar] [CrossRef]
- Eibert, T.F.; Erdemli, Y.E.; Volakis, J.L. Hybrid finite element-fast spectral domain multilayer boundary integral modeling of doubly periodic structures. IEEE Trans. Antennas Propag. 2003, 51, 2517–2520. [Google Scholar] [CrossRef]
- Liu, J.; Liu, N.; Liu, Q.H. Microscopic Modeling of Metasurfaces by the Mixed Finite Element Numerical Mode-Matching Method. IEEE Trans. Microw. Theory Tech. 2020, 68, 469–478. [Google Scholar] [CrossRef]
- Yang, F.; Rahmat-Samii, Y. Electromagnetic Band Gap Structures in Antenna Engineering; University Press: Cambridge, UK, 2008. [Google Scholar]
- ElMahgoub, K.; Yang, F.; Elsherbeni, A.Z. FDTD/GSM Analysis of Multilayered Periodic Structures With Arbitrary Skewed Grid. IEEE Trans. Microw. Theory Tech. 2011, 59, 3264–3271. [Google Scholar] [CrossRef]
- Cheng, A.H.D.; Cheng, D.T. Heritage and early history of the boundary element method. Eng. Anal. Bound. Elem. 2005, 29, 268–302. [Google Scholar] [CrossRef]
- Kolk, K.; Weber, W.; Kuhn, G. Investigation of 3D crack propagation problems via fast BEM formulations. Comput. Mech. 2005, 37, 32–40. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, C. Novel special crack-tip elements for interface crack analysis by an efficient boundary element method. Eng. Fract. Mech. 2020, 239, 107302. [Google Scholar] [CrossRef]
- Wu, Y.; Dong, C.; Yang, H. Isogeometric indirect boundary element method for solving the 3D acoustic problems. J. Comput. Appl. Math. 2020, 363, 273–299. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, B.; Chen, L. Non-iterative reconstruction of time-domain sound pressure and rapid prediction of large-scale sound field based on IG-DRBEM and POD-RBF. J. Sound. Vib. 2014, 573, 118226. [Google Scholar] [CrossRef]
- Abootalebi, O.; Kermanpur, A.; Shishesaz, M.; Golozar, M. Optimizing the electrode position in sacrificial anode cathodic protection systems using boundary element method. Corros. Sci. 2010, 52, 678–687. [Google Scholar] [CrossRef]
- Yu, B.; Cao, G.; Meng, Z.; Gong, Y.; Dong, C. Three-dimensional transient heat conduction problems in FGMs via IG-DRBEM. Comput. Methods Appl. Mech. Eng. 2021, 384, 113958. [Google Scholar] [CrossRef]
- Jim, R.; Yu, B.; Ren, S.; Yao, W. A novel SCTBEM with inversion-free Padé series expansion for 3D transient heat transfer analysis in FGMs. Comput. Methods Appl. Mech. Eng. 2025, 433, 117546. [Google Scholar]
- Harrington, R.F. Field Computation by Moment Methods; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Florencio, R.; Boix, R.R.; Encinar, J.A. Fast and Accurate MoM Analysis of Periodic Arrays of Multilayered Stacked Rectangular Patches with Application to the Design of Reflectarray Antennas. IEEE Trans. Antennas Propag. 2015, 63, 2558–2571. [Google Scholar] [CrossRef]
- Camacho, M.; Boix, R.R.; Medina, F. NUFFT for the Efficient Spectral Domain MoM Analysis of a Wide Variety of Multilayered Periodic Structures. IEEE Trans. Antennas Propag. 2019, 67, 6551–6563. [Google Scholar] [CrossRef]
- Florencio, R.; Somolinos, A.; González, I.; Cátedra, M.F. BICGSTAB-FFT Method of Moments with NURBS for Analysis of Planar Generic Layouts Embedded in Large Multilayer Structures. Electronics 2020, 9, 1476. [Google Scholar] [CrossRef]
- Collin, R.E. Field Theory of Guided Waves; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Mesa, F.; Marqués, R.; Horno, M. A general algorithm for computing the bidimensional spectral Green’s dyads in multilayered complex bianisotropic media: The equivalent boundary method. IEEE Trans. Microw. Theory Tech. 1991, 39, 1640–1649. [Google Scholar] [CrossRef]
- Boix, R.R.; Alexopóulos, N.G.; Horno, M. Efficient numerical computation of the spectral transverse dyadic Green’s functions in stratified anisotropic media. J. Electromagn. Waves Appl. 1996, 10, 1047–1083. [Google Scholar] [CrossRef]
- Valerio, G.; Baccarelli, P.; Paulotto, S.; Frezza, F.; Galli, A. Regularization of mixed-potential layered-media Green’s functions for efficient interpolation procedures in planar periodic structures. IEEE Trans. Antennas Propag. 2009, 57, 122–134. [Google Scholar] [CrossRef]
- Valerio, G.; Baccarelli, P.; Burghignoli, P.; Galli, A. Comparative analysis of acceleration techniques for 2-D and 3-D Green’s functions in periodic structures along one and two directions. IEEE Trans. Antennas Propag. 2007, 55, 1630–1643. [Google Scholar] [CrossRef]
- Park, M.J.; Nam, S. Efficient calculation of the Green’s function for multilayered planar periodic structures. IEEE Trans. Antennas Propag. 1998, 46, 1582–1583. [Google Scholar] [CrossRef][Green Version]
- Jordan, K.E.; Richter, G.E.; Sheng, P. An efficient numerical evaluation of the Green’s function for the Helmholtz operator in periodic structures. J. Comput. Phys. 1986, 63, 222–235. [Google Scholar] [CrossRef]
- Michalski, K.A.; Mosig, J.R. Multilayered media Green’s functions in integral equation formulations. IEEE Trans. Antennas Propag. 1997, 45, 508–519. [Google Scholar] [CrossRef]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics, I: Functional Analysis; Academic Press: New York, NY, USA, 1972; Volume 3. [Google Scholar]
- Florencio, R.; Boix, R.R.; Encinar, J.A. Enhanced MoM analysis of the scattering by periodic strip gratings in multilayered substrates. IEEE Trans. Antennas Propag. 2013, 61, 5088–5099. [Google Scholar] [CrossRef]
- Sommerfeld, A. Partial Differential Equations in Physics; Academic Press: New York, NY, USA, 1949. [Google Scholar]
- Itoh, T. Numerical Techniques for Microwave and Millimeter-Wave Passive Structures; John Wiley and Sons: New York, NY, USA, 1989. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions, 9th ed.; Dover Publications: New York, NY, USA, 1970. [Google Scholar]
- Capolino, F.; Wilton, D.R.; Johnson, W.A. Efficient Computation of the 2D Green’s Function for 1D Periodic Layered Structures Using the Ewald Method. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, San Antonia, TX, USA, 16–21 June 2002. [Google Scholar]
- Capolino, F.; Wilton, D.R.; Johnson, W.A. Efficient computation of the 3D Green’s function for the Helmholtz operator for a linear array of point sourcesusing the Ewald method. J. Comput. Phys. 2007, 223, 250–261. [Google Scholar] [CrossRef][Green Version]
- Fructos, A. Cálculo Eficiente de Funciones de Green Periódicas y no Periódicas en Medios Homogéneos y en Medios Multicapa. Doctoral Dissertation, University of Seville, Sevilla, Spain, 2010. [Google Scholar]
- Dudley, D.G. Mathematical Foundations for Electromagnetic Theory; IEEE Press: New York, NY, USA, 1994. [Google Scholar]
- Aksun, M.I. A robust approach for the derivation of closed–form Green’s functions. IEEE Trans. Microw. Theory Tech. 1996, 44, 651–658. [Google Scholar] [CrossRef]
- Trefethen, L.N. Approximation Theory and Approximation Practice; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).