On the Pricing of Vulnerable Foreign Equity Options with Stochastic Volatility in an Intensity-Based Model
Abstract
1. Introduction
2. Model
- (1)
- The payoff of foreign equity call struck in foreign currency:
- (2)
- The payoff of foreign equity call struck in domestic currency:
3. The Valuation of Vulnerable Foreign Equity Options
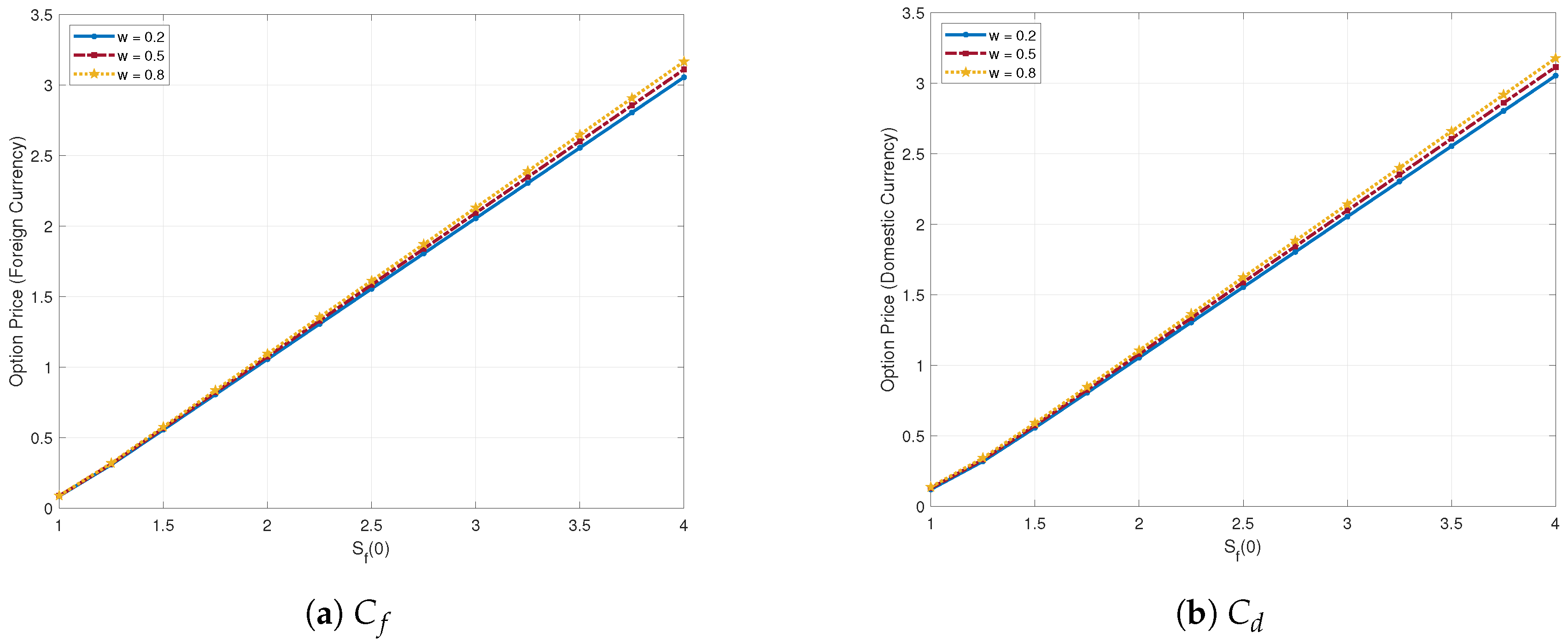
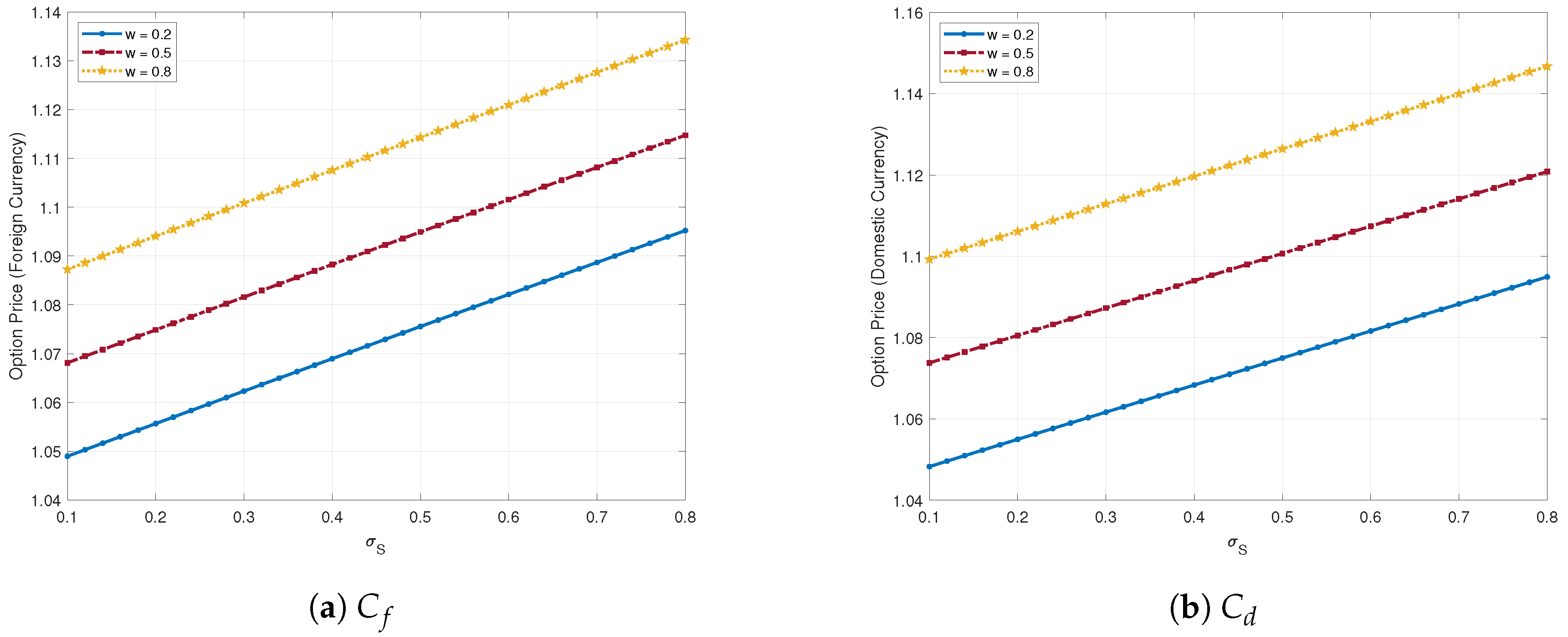
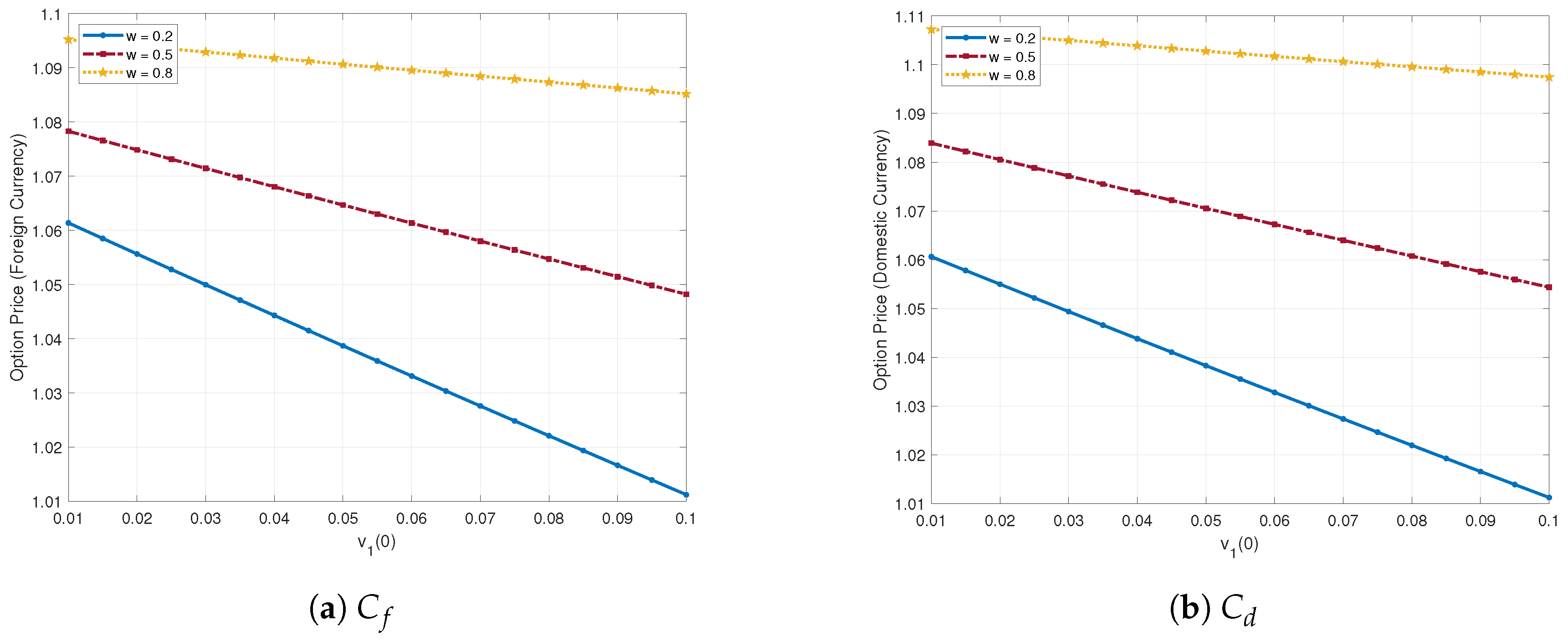
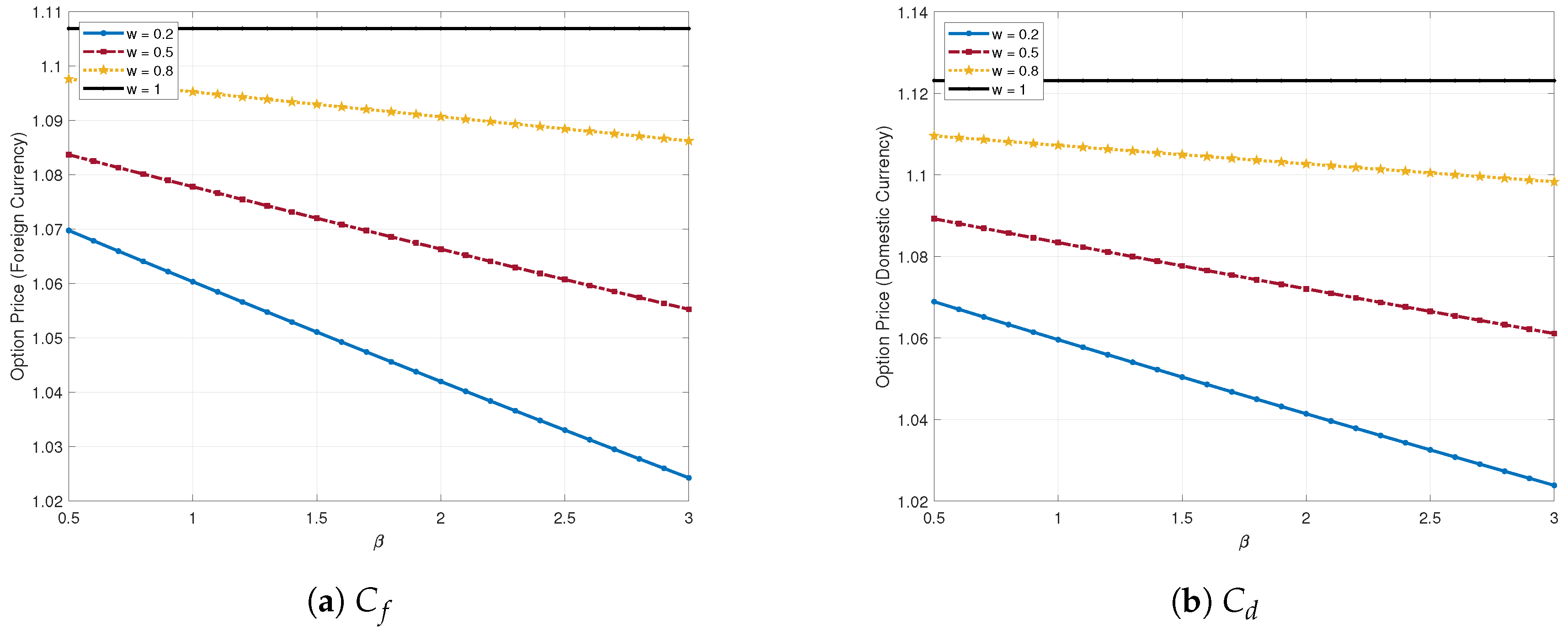
4. Numerical Examples
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Johnson, H.; Stulz, R. The pricing of options with default risk. J. Financ. 1987, 42, 267–280. [Google Scholar] [CrossRef]
- Klein, P. Pricing Black-Scholes options with correlated credit risk. J. Bank. Financ. 1996, 20, 1211–1229. [Google Scholar] [CrossRef]
- Jarrow, R.; Turnbull, S. Pricing options on financial securities subject to default risk. J. Financ. 1995, 50, 53–86. [Google Scholar] [CrossRef]
- Lando, D. On Cox processes and credit risky securities. Rev. Deriv. Res. 1998, 2, 99–120. [Google Scholar] [CrossRef]
- Kwok, Y.K.; Wong, H.Y. Currency-translated foreign equity options with path dependent features and their multi-asset extensions. Int. J. Theor. Appl. Financ. 2000, 3, 257–278. [Google Scholar] [CrossRef]
- Huang, S.C.; Hung, M.W. Pricing foreign equity options under Lévy processes. J. Futur. Mark. Futur. Options Other Deriv. Prod. 2005, 25, 917–944. [Google Scholar] [CrossRef]
- Ma, J. Pricing Foreign Equity Options with Stochastic Correlation and Volatility. Ann. Econ. Financ. 2009, 10, 303–327. [Google Scholar]
- Sun, Q.; Xu, W. Pricing foreign equity option with stochastic volatility. Phys. A Stat. Mech. Its Appl. 2015, 437, 89–100. [Google Scholar] [CrossRef]
- Fan, K.; Shen, Y.; Siu, T.K.; Wang, R. Pricing foreign equity options with regime-switching. Econ. Model. 2014, 37, 296–305. [Google Scholar] [CrossRef]
- Xu, W.; Wu, C.; Li, H. Foreign equity option pricing under stochastic volatility model with double jumps. Econ. Model. 2011, 28, 1857–1863. [Google Scholar] [CrossRef]
- Ma, Y.; Pan, D.; Shrestha, K.; Xu, W. Pricing and hedging foreign equity options under Hawkes jump–diffusion processes. Phys. A Stat. Mech. Its Appl. 2020, 537, 122645. [Google Scholar] [CrossRef]
- Kim, D.; Yoon, J.H.; Kim, G. Closed-form pricing formula for foreign equity option with credit risk. Adv. Differ. Equ. 2021, 2021, 332. [Google Scholar] [CrossRef]
- Kim, G. A Simplified Approach to the Pricing of Vulnerable Options with Two Underlying Assets in an Intensity-Based Model. Axioms 2023, 12, 1105. [Google Scholar] [CrossRef]
- Fard, F.A. Analytical pricing of vulnerable options under a generalized jump–diffusion model. Insur. Math. Econ. 2015, 60, 19–28. [Google Scholar] [CrossRef]
- Wang, X. Analytical valuation of vulnerable European and Asian options in intensity-based models. J. Comput. Appl. Math. 2021, 393, 113412. [Google Scholar] [CrossRef]
- Shephard, N.G. From characteristic function to distribution function: A simple framework for the theory. Econom. Theory 1991, 7, 519–529. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, G. Analytically Pricing a Vulnerable Option under a Stochastic Liquidity Risk Model with Stochastic Volatility. Mathematics 2024, 12, 2642. [Google Scholar] [CrossRef]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| T | 1 | 0.06 | |
| 2 | 0.05 | ||
| 1 | −0.5 | ||
| 0.2 | 0.02 | ||
| 0 | 0.03 | ||
| 0.03 | 0.06 | ||
| 1.1 | 0.3 | ||
| 0.02 | 0.2 | ||
| 2 | 0.2 | ||
| 0.02 | 0.06 | ||
| 2 | 0.01 | ||
| a | 0.02 | 1.25 | |
| b | 2 | w | 0.4 |
| 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, J.; Kim, G. On the Pricing of Vulnerable Foreign Equity Options with Stochastic Volatility in an Intensity-Based Model. Mathematics 2025, 13, 400. https://doi.org/10.3390/math13030400
Jeon J, Kim G. On the Pricing of Vulnerable Foreign Equity Options with Stochastic Volatility in an Intensity-Based Model. Mathematics. 2025; 13(3):400. https://doi.org/10.3390/math13030400
Chicago/Turabian StyleJeon, Junkee, and Geonwoo Kim. 2025. "On the Pricing of Vulnerable Foreign Equity Options with Stochastic Volatility in an Intensity-Based Model" Mathematics 13, no. 3: 400. https://doi.org/10.3390/math13030400
APA StyleJeon, J., & Kim, G. (2025). On the Pricing of Vulnerable Foreign Equity Options with Stochastic Volatility in an Intensity-Based Model. Mathematics, 13(3), 400. https://doi.org/10.3390/math13030400






