Selkov’s Dynamic System of Fractional Variable Order with Non-Constant Coefficients
Abstract
1. Introduction
2. Statement of the Problem
3. Adams–Bashforth–Multon Method
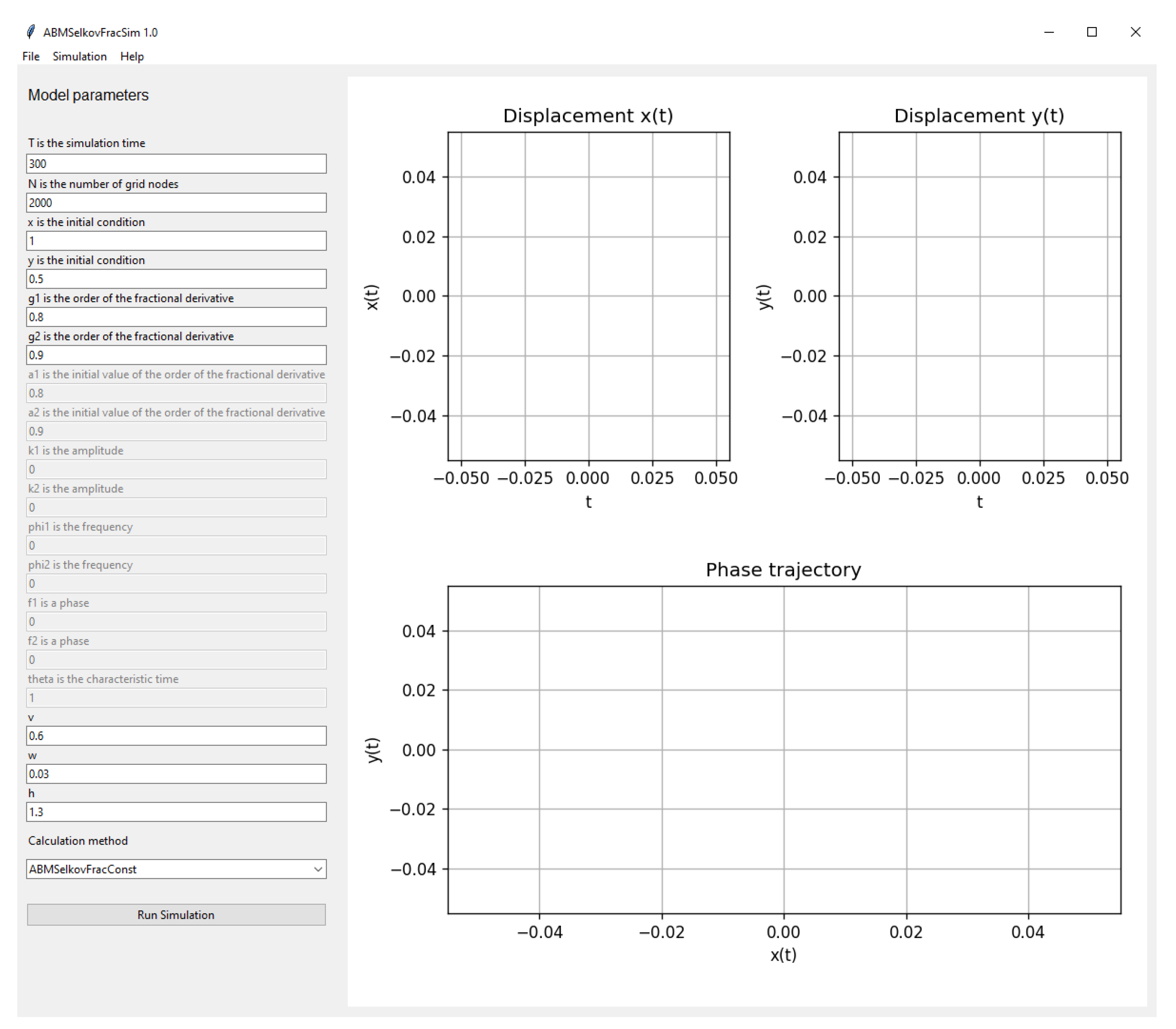
4. Software Package ABMSelkovFracSim
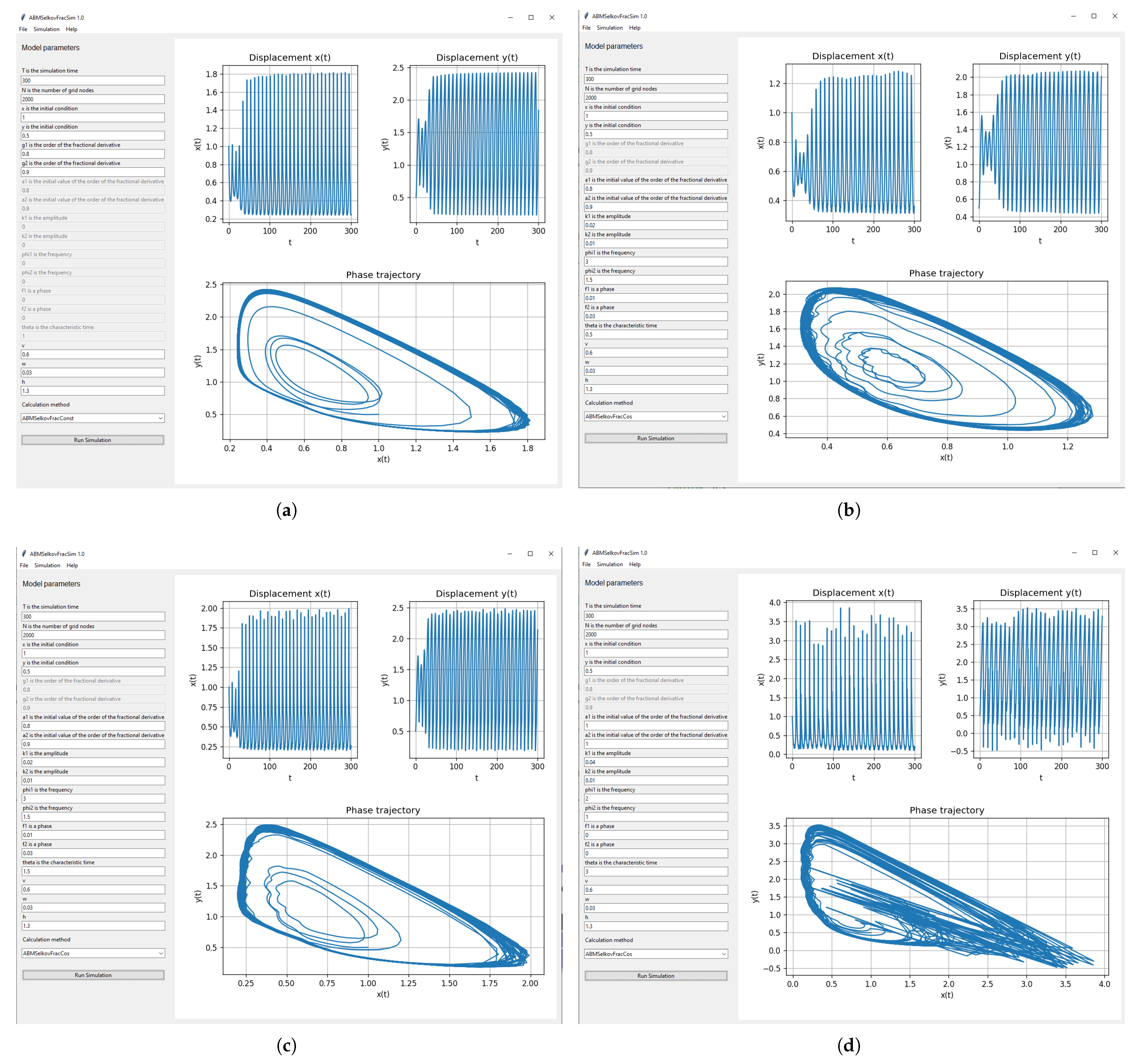
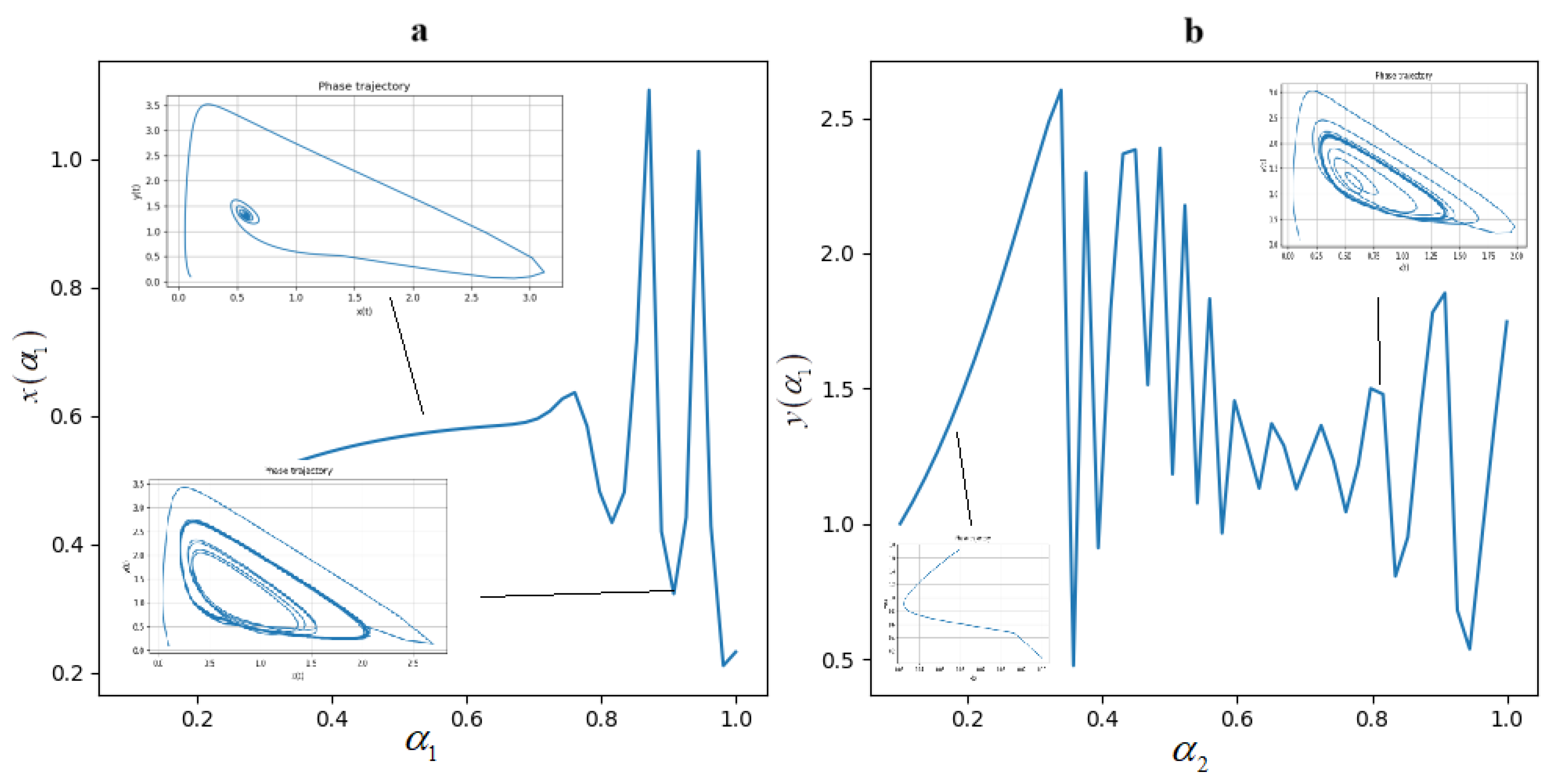
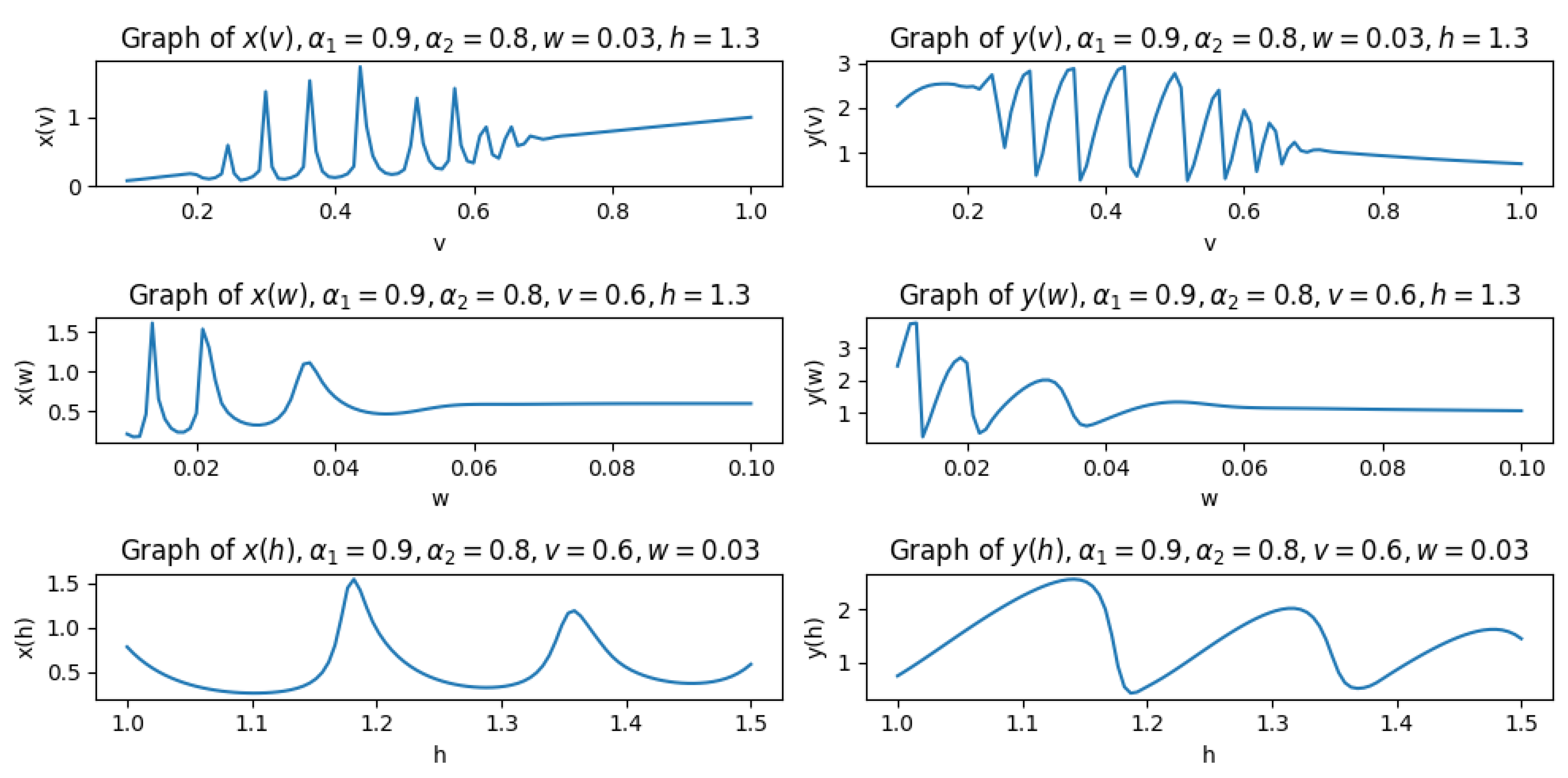
5. Simulation Results
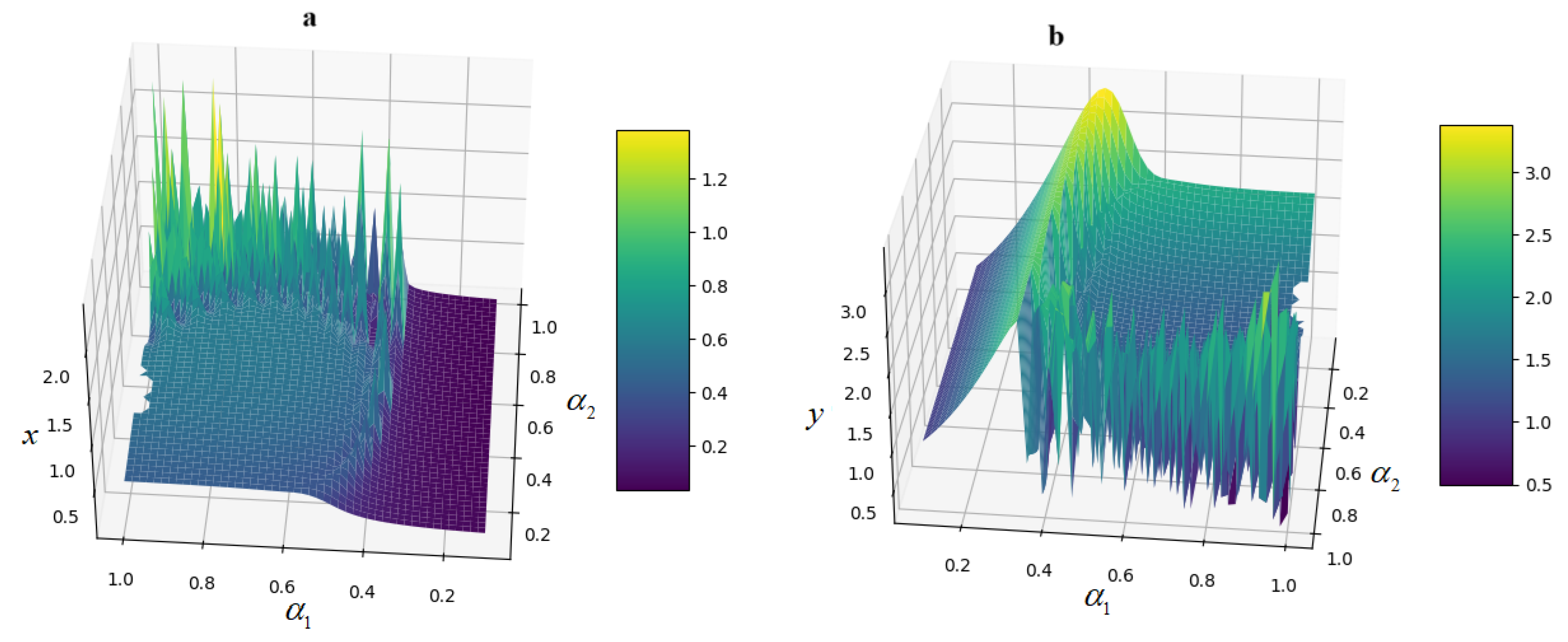
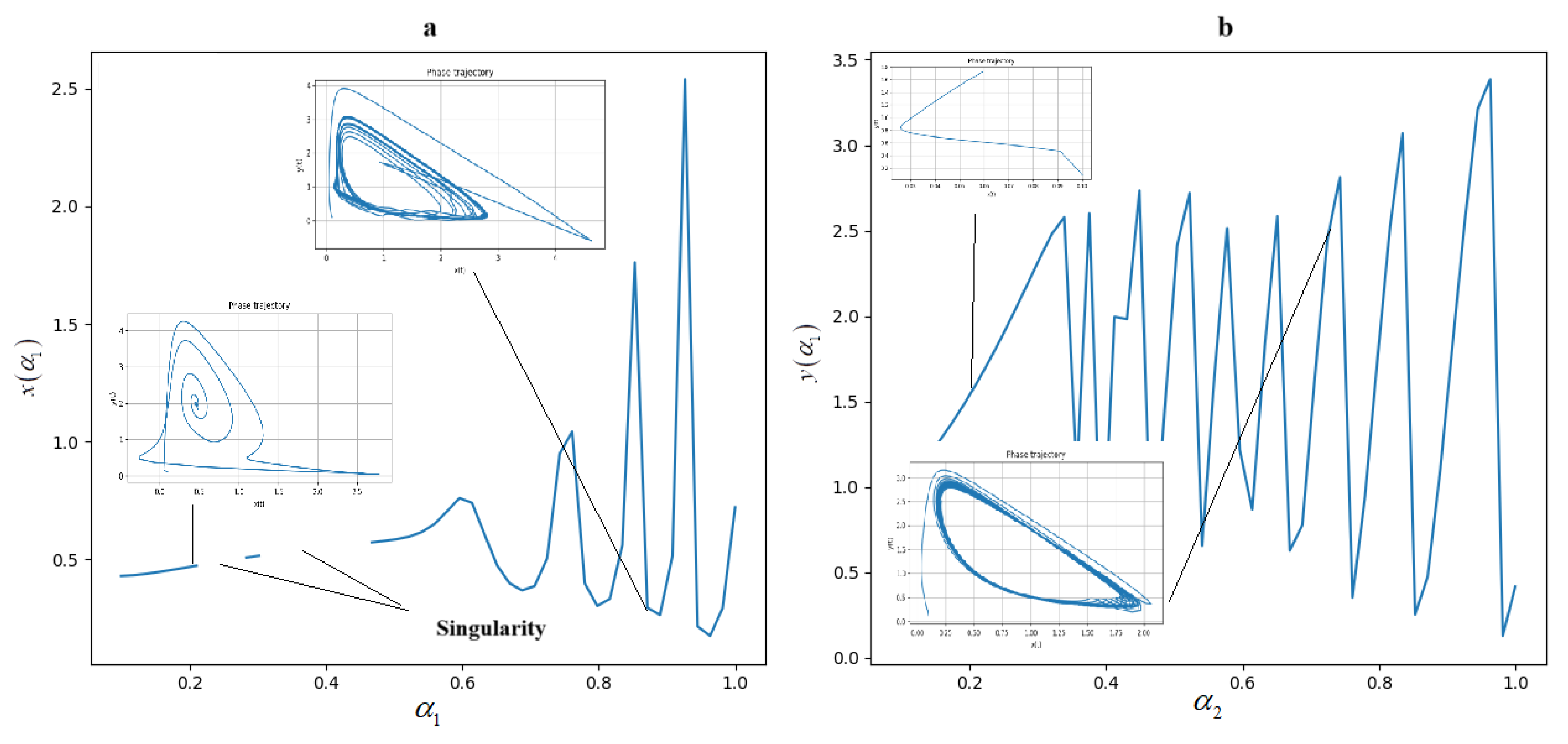
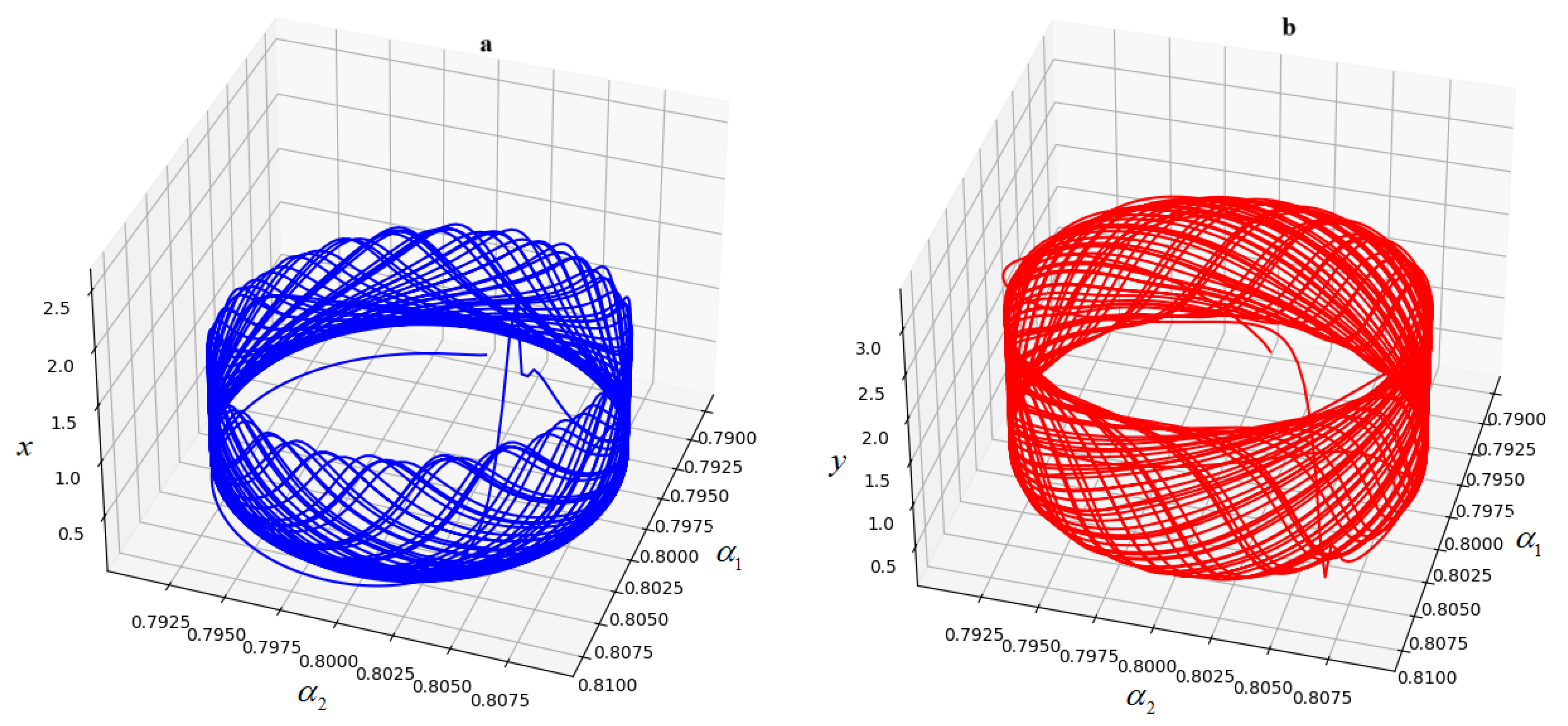
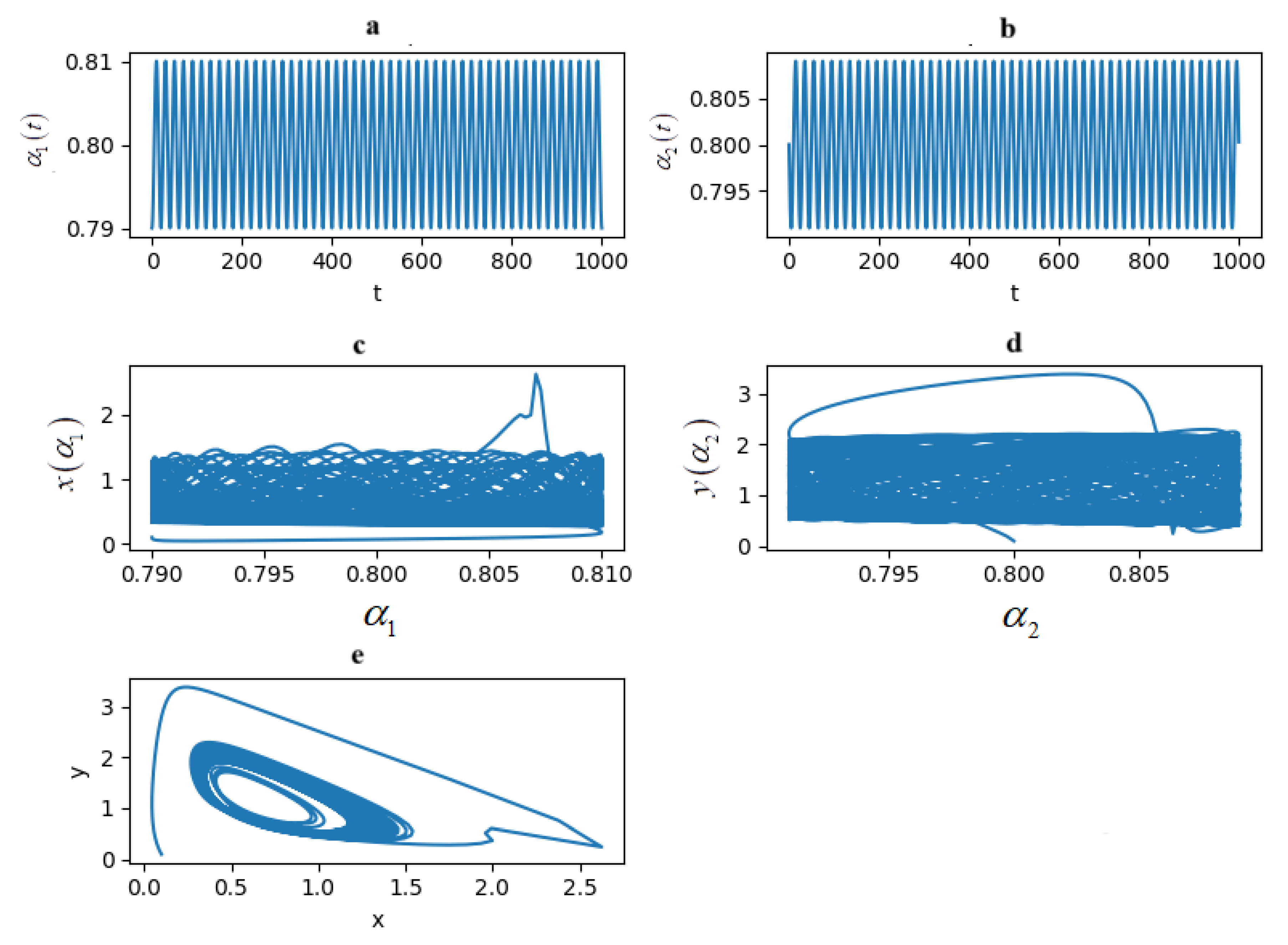
6. Bifurcation Diagrams
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Selkov, E.E. Self-oscillations in glycolysis. I. A simple kinetic model. Eur. J. Biochem. 1968, 4, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Makovetsky, V.I.; Dudchenko, I.P.; Zakupin, A.S. Auto oscillation model of microseism’s sources. Geosist. Pereh. Zon. 2017, 4, 37–46. [Google Scholar]
- Parovik, R.; Rakhmonov, Z.; Zunnunov, R. Modeling of fracture concentration by Sel’kov fractional dynamic system. E3S Web Conf. EDP Sci. 2020, 196, 02018. [Google Scholar] [CrossRef]
- Parovik, R.I. Studies of the Fractional Selkov Dynamical System for Describing the Self-Oscillatory Regime of Microseisms. Mathematics 2022, 10, 4208. [Google Scholar] [CrossRef]
- Rabotnov, Y.N. Elements of Hereditary Solid Mechanics; Mir: Moscow, Russia, 1980; p. 387. [Google Scholar]
- Hoffmann, X.R.; Marián, B. Memory-induced complex contagion in epidemic spreading. New J. Phys. 2019, 21, 033034. [Google Scholar] [CrossRef]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- Volterra, V. Functional Theory, Integral and Integro-Differential Equations; Dover Publications: New York, NY, USA, 2005; p. 288. [Google Scholar]
- Nakhushev, A.M. Fractional Calculus and Its Applications; Fizmatlit: Moscow, Russia, 2003; p. 272. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204, p. 523. [Google Scholar]
- Parovik, R.I. Selkov Dynamic System with Variable Heredity for Describing Microseismic Regimes. In Solar-Terrestrial Relations and Physics of Earthquake Precursors: Proceedings of the XIII International Conference; Springer Nature Switzerland AG: Cham, Switzerland, 2023; pp. 166–178. [Google Scholar]
- Parovik, R.I. Qualitative analysis of Selkov’s fractional dynamical system with variable memory using a modified Test 0–1 algorithm. Vestn. KRAUNC. Fiz.-Mat. Nauki. 2023, 45, 9–23. [Google Scholar]
- Shaw, Z.A. Learn Python the Hard Way; Addison-Wesley Professional: New York, NY, USA, 2024; p. 306. [Google Scholar]
- Van Horn, B.M., II; Nguyen, Q. Hands-On Application Development with PyCharm: Build Applications Like a Pro with the Ultimate Python Development Tool; Packt Publishing Ltd.: Birmingham, UK, 2023; p. 652. [Google Scholar]
- Novozhenova, O.G. Life And Science of Alexey Gerasimov, One of the Pioneers of Fractional Calculus in Soviet Union. Fract. Calc. Appl. Anal. 2017, 20, 790–809. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Aguilar, J.F.G.; Hernández, M.M. Space-Time Fractional Diffusion-Advection Equation with Caputo Derivative. Abstr. Appl. Anal. 2014, 2014, 283019. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A Review on Variable-Order Fractional Differential Equations: Mathematical Foundations, Physical Models, Numerical Methods and Applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A R. Soc. Publ. 2020, 476, 20190498. [Google Scholar] [CrossRef] [PubMed]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Yang, C.; Liu, F. A computationally effective predictor-corrector method for simulating fractional order dynamical control system. ANZIAM J. 2005, 47, 168–184. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 016. [Google Scholar] [CrossRef]
- Bao, B.; Hu, J.; Cai, J.; Zhang, X.; Bao, H. Memristor-induced mode transitions and extreme multistability in a map-based neuron model. Nonlinear Dyn. 2023, 111, 3765–3779. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Li, Q.; Raut, R.V.; Townsend, A. Beyond expectations: Residual dynamic mode decomposition and variance for stochastic dynamical systems. Nonlinear Dyn. 2024, 112, 2037–2061. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. On the implementation of the 0–1 test for chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
- Fouda, J.S.A.E.; Bodo, B.; Sabat, S.L.; Effa, J.Y.A. Modified 0–1 test for chaos detection in oversampled time series observations. Int. J. Bifurc. Chaos 2014, 24, 1450063. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parovik, R. Selkov’s Dynamic System of Fractional Variable Order with Non-Constant Coefficients. Mathematics 2025, 13, 372. https://doi.org/10.3390/math13030372
Parovik R. Selkov’s Dynamic System of Fractional Variable Order with Non-Constant Coefficients. Mathematics. 2025; 13(3):372. https://doi.org/10.3390/math13030372
Chicago/Turabian StyleParovik, Roman. 2025. "Selkov’s Dynamic System of Fractional Variable Order with Non-Constant Coefficients" Mathematics 13, no. 3: 372. https://doi.org/10.3390/math13030372
APA StyleParovik, R. (2025). Selkov’s Dynamic System of Fractional Variable Order with Non-Constant Coefficients. Mathematics, 13(3), 372. https://doi.org/10.3390/math13030372





