Abstract
The boundary shape function method (BSFM) and the variational iteration method (VIM) are merged together to seek the analytic solutions of nonlinear boundary value problems. The boundary shape function method transforms the boundary value problem to an initial value problem (IVP) for a new variable. Then, a modified variational iteration method (MVIM) is created by applying the VIM to the resultant IVP, which can achieve a good approximate solution to automatically satisfy the prescribed mixed-boundary conditions. By using the Picard iteration method, the existence of a solution is proven with the assumption of the Lipschitz condition. The MVIM is equivalent to the Picard iteration method by a back substitution. Either by solving the nonlinear equations or by minimizing the error of the solution or the governing equation, we can determine the unknown values of the parameters in the MVIM. A nonlocal BSFM is developed, which then uses the MVIM to find the analytic solution of a nonlocal nonlinear boundary value problem. In the second part of this paper, a new splitting–linearizing method is developed to expand the analytic solution in powers of a dummy parameter. After adopting the Liapunov method, linearized differential equations are solved sequentially to derive an analytic solution. Accurate analytical solutions are attainable through a few computations, and some examples involving two boundary layer problems confirm the efficiency of the proposed methods.
Keywords:
nonlinear boundary value problem; boundary shape function method; splitting–linearizing method; modified variational iteration method; Liapunov method MSC:
45G10; 65L05; 65R20
1. Introduction
Many computational methods are available to solve the boundary value problems (BVPs) [1,2,3,4,5]. The existence of solution to the BVP requires a priori bounds on the derivatives of the potential solution. The lower and upper solutions provide a priori bounds on the solutions with different Nagumo growth conditions [6,7,8,9,10,11].
The Picard iteration method is a conventional functional iteration method that is simply used to seek the analytical solution of nonlinear ordinary differential equations (ODEs). In order to improve the slow convergence of the Picard iteration method and enhance its accuracy, the variational iteration method (VIM) was proposed and modified [12,13,14,15,16]. The VIM as a modification of the Picard iteration method is a powerful method for analytically solving nonlinear scientific and engineering problems [17,18].
As stated in [19], Liapunov developed a dummy parameter technique to investigate the conditions of stability of the Hill equation [20]:
where for some as a periodic funtion. Liapunov recast Equation (1) to:
where is a dummy parameter. When , Equation (2) recovers to Equation (1). The analytic solution of Equation (1) can be determined as the sum of a convergent power series of the parameter :
Substituting Equation (3) for into Equation (1) and equating equal powers of yields the following:
which is a recurrent formula to sequentially determine from of the previous step solution. By starting from and subjecting to , Liapunov proved that
where M is an upper bound of , and the convergent solution of Equation (1) was obtained:
We will call the above technique the Liapunov method.
The homotopy perturbation method is proposed via homotopy [21], which is rather general and valid for nonlinear differential equations. Above all, homotopy is constructed by introducing an embedding parameter. Even the Liapunov method did not mention the concept of homotopy and apply it to the nonlinear ODE; its use of the perturbed parameter in the analysis of the series solution of is indeed a precursor of the homotopy perturbation method. Currently, there exist many homotopy perturbation techniques for solving two-point boundary value problems [22,23,24].
Previously, the variational iteration method [12] was applied to solve the initial value problem (IVP). Khuri and Sayfy [25] extended the variational iteration method to the Dirichlet-type boundary value problem by using two Lagrange multipliers in the correct functional. The specific advantages of the present approach obtained by merging the boundary shape function method with the variational iteration method (VIM), which is named a modified variational iteration method (MVIM), are that the specified boundary conditions are automatically and exactly satisfied. When the method of Khuri and Sayfy is not applicable, the present approach can easily treat the mixed and nonlocal boundary value problems. For these mixed and nonlocal boundary conditions, there is not a simple way to identify the two Lagrange multipliers in the correct functional.
An extra advantage is that there exist free parameters for the new variable, which can be adopted to minimize the absolute error of the analytic solution, such that we can obtain a more accurate analytic solution. When the boundary shape function method (BSFM) is used in the nonlinear BVP [26], its numerical solution can be obtained. However, the analytic form of the solution cannot be obtained by the BSFM individually.
On the other hand, the VIM is designed for the IVP, not for BVP. How to effectively apply the VIM to a large class of nonlinear BVPs endowed with complicated boundary conditions to derive the analytic solution is still a great challenge. This motivates us to develop the new version of the VIM for an effective method to seek the analytic solution of a nonlinear BVP. When the BSFM is combined with the VIM, we can simply derive the analytic solution of a nonlinear BVP.
We are going to cover a nonlocal boundary value problem based on the concept of the nonlocal boundary shape function method. In the field of variational iteration methods, work treating nonlocal boundary value problems using the VIM is rare.
The outline of this paper is given as follows. For second-order nonlinear boundary value problems (BVPs) with the Dirichlet boundary conditions, we clarify the existence of a solution in Section 2 by considering the transformation of the BVP to an initial value problem (IVP). We take an example in Section 3 to explore the slow convergence of the Picard iteration method. In Section 4, we derive the boundary shape function method for the nonlinear BVPs under mixed-boundary conditions. In Section 5, with the aid of the boundary shape function, we can transform the nonlinear BVP with the mixed-boundary and/or nonlocal boundary conditions to an initial value problem with unknown right-hand values appearing in the ODE for the new variable. Then, a modified VIM (MVIM) is developed, and the methods to compute the right-hand values are depicted. Some examples are tested in Section 6. In Section 7, we develop a linearized Liapunov method for seeking the analytic solutions. Some examples using the linearized Liapunov method are tested in Section 8. Finally, the conclusions are drawn in Section 9.
2. The Existence of Solutions
We consider a second-order nonlinear ordinary differential equation (ODE) endowed with the Dirichlet boundary conditions:
Later, more complex boundary conditions will be considered in Section 4 and Section 5, nonlocal boundary conditions will be addressed in Section 5.4, and a multi-point BVP is solved in Example 7.
2.1. Existence Theorem
Theorem 1.
there exist m roots for α, where α is a parameter to denote the right-hand value of a new variable , given by
in which . R is a nonlinear function of α derived from Equation (7).
In , if is continuous and satisfies
then the nonlinear BVP (7) and (8) may have m solutions when in the following nonlinear equation:
Proof.
Suppose that is transformed to by Equation (11), where are given initial conditions for the new variable , and the right-hand value is to be determined. It is obvious that automatically satisfies the boundary conditions and in Equation (8),
where and were used.
It follows from Equations (7) and (11) that
which is an IVP with the ODE continuously depending on an unknown value of the parameter .
Let
be a two-dimensional IVP system. We have
based on Equation (9), we can derive the Lipschitz condition:
According to [27,28], the existence of the solutions and is guaranteed. Now, applying the Picard iteration method to Equations (14) and (15) generates the following:
Considering and and starting from and , the iteration converges to the true solution and , which depends on the parameter continuously through the function g in Equation (12). Enforcing , we can obtain a nonlinear Equation (10) for . Solving this equation for , it is possible that there exist no solution, one solution, two solutions, etc. □
To prove the existence of a solution of the BVP, it is of utmost importance to construct the nonlinear function , which might be an implicit function of , by using the numerical integration method. However, by using the analytic method, the function is explicit. Then, we can solve the nonlinear equation to determine and the number of analytic solutions. In Appendix A, we demonstrate this process by giving an example.
Zhou and Shen [29] employed the Nagumo condition and the lower and upper solutions technique to prove the existence of a unique solution to Equations (7) and (8). Generally, the existence of a solution was discussed using different Nagumo growth conditions, assuming that
on and
where . The key point is finding a positive function as the bound of and proving Equation (20). Because Equations (7) and (8) are transformed to an IVP in Equations (12) and (13), according to the theory of ODE [27,28], the Lipschitz condition guarantees the unique solution of . The Lipschitz condition is weaker than the Nagumo condition; hence, the most practical boundary value problem can be treated by the presented technique to transform the BVP to an IVP.
2.2. Application to an Example
The following example demonstrates an application of Theorem 1:
whose exact solution is
Upon letting
and are satisfied automatically, where and . We take to simplify the notation. We come to an IVP for the new variable :
The solution is
Taking leads to
Equation (28) is a special case of Equation (10) with . In Appendix A, another comment of Equation (10) is given. The MVIM solution of Equation (25) is provided.
3. Slow Convergence of the Picard Iteration Method
The Picard iteration method can be applied to the nonlinear ODE system [27]:
where . Note that any solution to Equation (31) will satisfy the following integral equation:
It is useful to prove the existence of solution to Equation (31) via successive approximation deduced from Equation (32):
This iteration generates a sequence of successive approximations of the real solution .
For the example in Equation (25) written as
where , starting from and and through five iterations in the Picard method in Equations (18) and (19), we can derive
imposing , is obtained as follows:
Notice that the boundary conditions and are exactly satisfied by in Equation (36).
In Figure 1, we compare Equations (36) and (23), and the maximum error (ME) is . In order to enhance the accuracy, more computations to generate more terms are needed, which compensate for the slow convergence of the Picard iteration method.
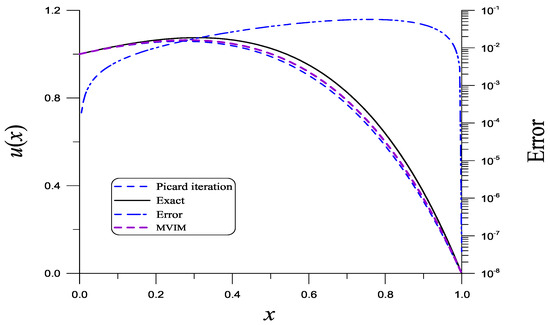
In Appendix A, we will solve Equations (21) and (22) again by using a modified variational iteration method (MVIM).
4. Boundary Shape Function Method
Next, we impose the mixed-boundary conditions on Equation (7) as follows:
From now on, we propose a newly modified VIM (MVIM) for seeking an analytic solution of Equations (7) and (37) using the following results.
Theorem 2.
Two shape functions satisfy the following:
Proof.
Refer to [30] for the proof of the existence of and . □
Theorem 3.
Proof.
Refer to [30] for the proof of this theorem. □
The exact solution must satisfy the mixed-boundary conditions in Equation (37), and in this sense, is one member of the boundary shape function.
Based on Theorem 3, we can transform to a new variable by
where
The initial values are given as follows:
In general, we take . Equations (43) and (45) constitute an initial value problem (IVP) with and as unknown parameters in G given by Equation (42). We introduce and to simplify the notations.
To demonstrate the transformation process step-by-step, we consider a benchmark BVP given as follows:
The first step determines the shape functions and by satisfying the following:
It is easily deduced to and . The second step transforms to as follows:
The boundary values and are satisfied automatically. The third step derives a new ODE for :
which together with the given initial values in Equation (45) constitute an initial value problem (IVP) for . is a parameter in the ODE (46). By applying the VIM to IVP (46) and (45), is a parameter when the trial solution is derived sequentially by starting from the initial function .
5. A Modified Variational Iteration Method
Based on the variational iteration method, we develop a new methodology for finding the analytic solution of Equations (7) and (37) in this section.
5.1. Variational Iteration Method
In order to accelerate the convergence speed of the Picard iteration method, we consider the variational iteration method (VIM) [12], which is more efficient than the Picard iteration method. According to the VIM for the differential Equation (7), a correct functional is given as follows:
where
is a Lagrange multiplier.
However, we find that the iteration (47) cannot exactly fulfill Equation (37) unless some extra techniques are developed. We improve this drawback below by transforming the BVP to an initial value problem (IVP) and then applying the VIM to the resultant IVP, namely a modified variational iteration method (MVIM).
5.2. A Modified VIM
The following integral formula will be used later.
Lemma 1.
For any integrable function , we have the following:
Proof.
Let
Then, we have
The proof is completed. □
When is obtained by the MVIM, can be obtained by applying Equations (41) and (42), which automatically satisfies the mixed-boundary conditions in Equation (37).
Theorem 4.
For Equation (43), the MVIM starting from an initial guess can be derived as follows:
Proof.
Applying Lemma 1, we have the following integral relation:
such that Equation (50) can be written as follows:
Upon noting that and , we can prove Equation (51). □
In the MVIM, does not exactly satisfy the ODE in Equation (43): , because of ; hence, Equation (53), then Equation (51) is an approximation of Equation (43).
Inserting Equation (48) into Equation (47) and adopting a similar derivation to that in Theorem 4, the VIM can be written as follows:
A strong form of the VIM, like Equation (53) for , is as follows:
Remark 1.
Upon comparing Equations (51) and (54), the current MVIM applied to Equation (43) is different from the VIM, which is applied to Equation (7). In the MVIM of Equation (51), we have the freedom to chose and , inserting the resultant into Equation (41) to obtain the solution , which fulfills Equation (37) automatically. In contrast, in the VIM of Equation (54), and cannot be chosen freely, which must satisfy in Equation (37). Moreover, the resultant is not guaranteed to satisfy in Equation (37). It may need to solve some nonlinear algebraic equations to adjust the values of and , such that can be satisfied nearly. It is not an easy task for searching the higher-order analytic solution of the mixed-type BVP by applying the original VIM to Equations (7) and (37).
Remark 2.
Notice that the standard VIM [12] is applied to Equation (7) with the specified initial conditions and ; hence, upon giving the initial guessed function , we can find the subsequent analytic solutions by sequentially inserting into Equation (54). In contrast, the present MVIM is worked using Equation (51) for the new ODE in Equation (43), which is started from any initial guessed function . In doing so, the MVIM is easily tailored to automatically satisfy the boundary conditions given in Equation (37). When the standard VIM is applied to solve the nonlinear BVP, it encounters the difficulty that and are unknown. To satisfy the boundary conditions given in Equation (37), in the VIM, some coupled nonlinear algebraic equations must be solved to determine the two unknowns of C and D. This process might be complicated and expensive. In this regard, the MVIM is better than the VIM.
Theorem 5.
For Equation (43), the MVIM is equivalent to the back substitution of the Picard iteration method.
Proof.
Let ; Equation (43) can be expressed as a two-dimensional ODE system:
where we suppose that the initial values are and .
A slight modification of the Picard iteration method via back substitution is that we can insert Equation (59) for into Equation (58), which results in the following:
Using Lemma 1, it leads to the following:
5.3. Determination of the Right-Hand Values
In Equation (42), we let
to simplify the notations. Therefore, in view of Equations (43) and (51), the solution depends on and . Solving these two nonlinear algebraic equations in Equation (62), we can determine and , whose procedures are complicated when we seek a higher-order analytic solution.
To overcome the inefficiency in solving the nonlinear algebraic equations, we develop other efficient methods to determine and as follows. Because depends on and , by inserting
into Equation (51), and also depend on and . Then, calculated from Equation (41) also depends on and . Next, we search for the optimal values of and by minimizing the absolute error of the solution compared to the exact one:
where denotes the exact solution. If is not available, we can minimize the absolute error of the governing equation.
For the minimization problem in Equation (63), the 2D golden section search algorithm [31] was used to find the optimal values of and .
We insert the derived analytic solution into the governing equation and define the following minimization problem:
which measures the error to fit the governing equation. For the minimization problem in Equation (64), the 2D golden section search algorithm [31] was used to find the optimal values of and .
5.4. Nonlocal Boundary Conditions
Next, more complicated nonlocal boundary conditions are considered for Equation (7):
where and are weight functions.
Theorem 6.
Proof.
We first prove Equation (65). Applying to Equation (70) and using the linear property of , we have
which, with the aid of the first equations in Equations (68) and (69), becomes
6. Example Testing for the MVIM
We assess the performance of the newly developed methodology of the MVIM by testing some examples.
Example 1.
We consider a nonlinear BVP with the mixed-boundary condition at the left boundary:
whose exact solution is
Imposing , we can derive
Obviously, is a solution, which leads to , then the exact solution is obtained via Equation (71). For this example, we can derive the exact solution by using the MVIM.
Example 2.

Let us consider the following singular boundary value problem [32]:
with the exact solution . The term is singular at .
The first-order approximate solution obtained by Lu [32] based on the VIM is as follows:
We give a detailed analysis of this example when we solve it using the MVIM. Let and ; based on Equations (45), (41), and (42) with , we have
where we suppose that the unknown right-hand value is , and is taken in Equation (45). In the iteration, the starting initial guess is . Inserting Equation (74) into Equation (72), we can derive a new ODE:
The MVIM in Equation (51), starting from a restricted and with , leads to the following first-order approximation:
Imposing , we can solve
Inserting it into Equation (72), we search for the optimal value of A by minimizing the absolute error of the governing equation in Equation (72):
Notice that in the minimization problem with a single unknown value A, we can adopt the so-called interval reduction method to find the proper value of A. First, we select a large interval and list the data of in the computer. We can observe where the minimal point locates, then we reduce the interval to a smaller one to involve that minimal point. We carry out the same procedure a few times to find an accurate value of A.
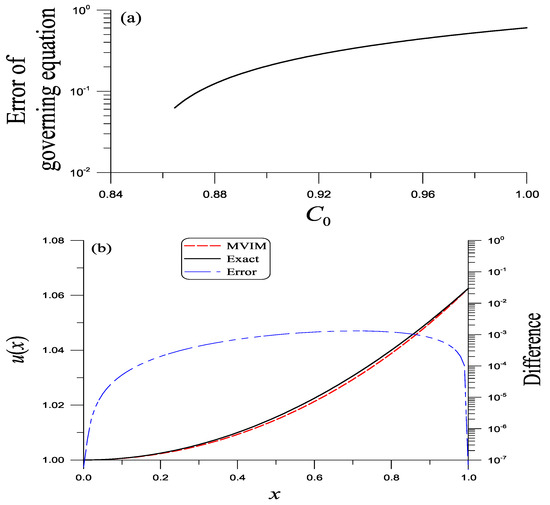
In Figure 2a, we plot the error of the governing equation to the value of A, which shows that there exists a minimal value at ; thus, . Based on this value, we compare the solution obtained from the MVIM to the exact one in Figure 2b, whose ME is .

Figure 2.
For the singular equation in Example 2 solved using the modified variational iteration method, we show (a) the error of governing equation, and (b) a comparison of solutions and the errors.
From Table 1, we can observe that the analytic solution obtained by the first-order MVIM is much more accurate than that obtained by Lu [32], whose results are under-estimated.

Table 1.
For Example 2, comparing the approximate solutions obtained using the MVIM and by Lu [32] to the exact one.
Notice that A and B in Equation (51) can be regarded as free parameters since they do not influence the new ODE: . For this example, we take , not . For the latter case, we will derive Equation (73) again, which does not improve the accuracy for the first-order solution.
Next, we apply Equation (63) to determine the optimal value of α. We begin with , and up to the first-order, we obtain the following:
The optimal value is , which is slightly different from obtained above. ME is , which is more accurate than that calculated from Equation (77) with ME = .
Example 3.
We consider the Airy-type boundary value problem [32,33]:
where is a given constant. Due to the stiffness when , the Lie-group shooting method [5] fails to solve this problem. We consider .
We seek a variable transformation as follows:
Starting from and from Equation (51), we can derive the following:
Similarly, we can derive the following:
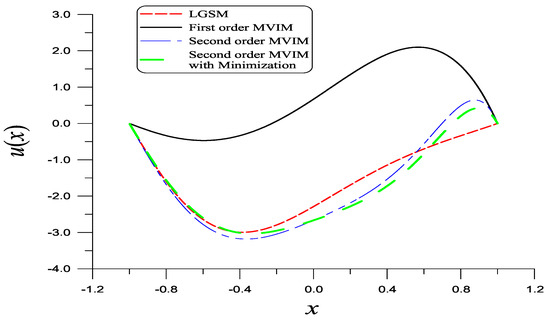
By imposing , we can obtain . In Figure 3, we compare the solutions obtained from the MVIM to that obtained using the Lie-group shooting method (LGSM) [5].

Figure 3.
For the stiff equation in Example 3 solved using the modified variational iteration method and solving a nonlinear algebric equation and with a minimization technique, we compare the solutions to that obtained using the LGSM.
Example 4.
Let us consider [5,34,35]:
where
There are two solutions, of which
is the first solution.
Similarly, we can derive the following:
It can be checked that exactly satisfies the boundary conditions and .
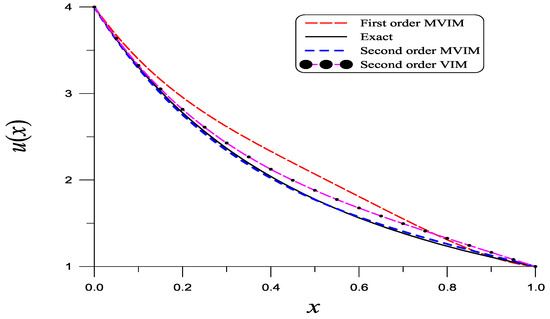
In , there exists a free parameter α. Therefore, we apply Equation (63) to determine α in Equation (86). The optimal value is . As shown in Figure 4, the current solution based on the second-order MVIM with the minimization technique is quite close to the exact one, whose ME is . In Figure 4, we compare the analytic solutions of the MVIM to the exact solution in Equation (85), of which we can observe that the second-order solution is more accurate than the first-order solution and tends to the exact solution.

Figure 4.
For a nonlinear equation of Example 4 solved by the modified variational iteration method with a minimization technique, we compare the solutions obtained using MVIM and VIM to the exact one.
To compare with the traditional VIM, we begin with
where B is determined to meet the right-hand condition in Equation (84). Through laborious work, we can derive the following:
is obtained by considering . The result is plotted in Figure 4 with ME = 0.115, which is less accurate than ME = obtained by the MVIM by about one order.
Example 5.
We consider a more difficult nonlinear BVP with a mixed-boundary condition given on the right-boundary:
of which the exact solution is given by Equation (85).
Let and . It follows from Equations (41) and (42) that
where and are adopted. The new ODE for is Equation (43) with the following function:
Starting from and inserting Equation (89) for H into Equation (51) yields
where . Notice that in , cannot be replaced by γ; otherwise, the right-boundary condition will not be satisfied. Indeed, and are calculated from Equation (90).
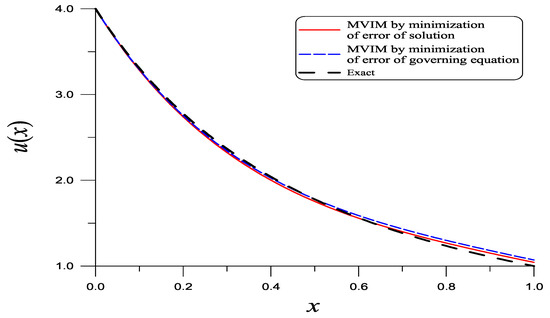
For this problem, it is hard to solve the coupled nonlinear algebraic equations to obtain and . Therefore, we apply Equation (63) to determine γ in Equation (90). The optimal value is . As shown in Figure 5 by a solid line, the current solution based on the second-order MVIM with the minimization of the error of the solution is quite close to the exact one, whose ME is .

Figure 5.
For a nonlinear equation of Example 5 solved using the modified variational iteration method with the minimization of the error of solution and the minimization of the error of governing equation, we compare the solutions to the exact solution.
Next, we search for the optimal value of γ by minimizing the absolute error of the governing equation in Equation (88):
The optimal value is , which is slightly larger than in the above. As shown in Figure 5 by a dashed line, the solution based on the second-order MVIM with the minimization of the error of governing equation is also close to the exact one, whose ME is .
A Nonlocal BVP
For Equation (83), we extend the result to the following nonlocal BVP:
The corresponding nonlocal shape functions are given as follows:
We begin with
where the value of B can be optimized to minimize the absolute error of the analytic solution. Then, we have the following:
Let
we come to the first-order analytic solution:
We can check that satisfies the nonlocal boundary conditions in Equation (93).
When B is determined by
the optimal value is . From Table 2, we can observe that the first-order analytic solution obtained by the MVIM with a nonlocal modification is quite accurate. As shown in Figure 6, these two curves are close, with ME = 0.1369.

Table 2.
For a nonlocal BVP, we compare the approximate solutions obtained by the MVIM to the exact one.
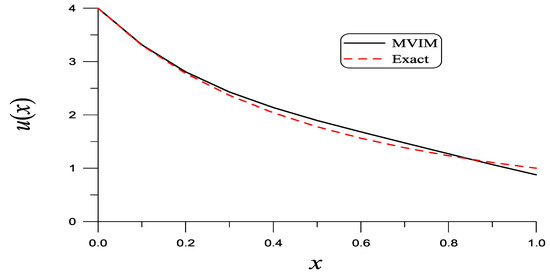
Figure 6.
For a nonlinear nonlocal BVP solved using the modified variational iteration method with the minimization of the error of solution, we compare the first-order analytic solution to the exact one.
7. Linearized Liapunov Method for Seeking Analytic Solutions
Before the application of the Liapunov method to solve the nonlinear BVP, we are required to linearize the transformed IVP for Equation (43), which is assumed to have the following form:
where and are nonlinear functions of , and a, b, and c are constants.
According to Equation (45), we can take a suitable initial guess of . To simplify the new analytic method, we decompose Equation (100) as follows:
where is a constant weight factor. Starting from the initial guess , one solves the following linearized ODE:
to seek a higher-order analytic solution. This technique is termed a decomposition–linearization method, advocated by Liu et al. [36] as a basis to treat the analytic solution of the nonlinear ODE.
Inserting
into Equation (102) and equating the coefficients preceding , we can derive the following:
We found that the solutions to the above series of ODEs are easily derived. Then, we can fast find the analytic solution of the nonlinear BVP.
8. Examples Testing for the Linearized Liapunov Method
The background of the linearized Liapunov method is a decomposition–linearization technique, which is executed on the nonlinear ODE by simplifying it to a linear ODE around a zero-th order solution . Previously, the decomposition–linearization technique was combined with the homotopy perturbation method in [36] to treat the nonlinear differential/integral equations and nonlinear jerk equations. It can be seen that Equation (104) can be sequentially used to find the analytic solutions step-by-step by merely executing twice integrations with the integrand, being a function of the previous step’s solution. The reason to generate this powerful method is that we introduced a dummy parameter in the linearized Equation (102), then in the solution in Equation (103). Below, we will test the performance of the linearized Liapunov method.
Example 6.

To explain the process of the decomposition–linearization technique, we rewrite Equation (83) to an equivalent form:
the term is moved to the right-hand side:
We select a reference solution , then we linearize the nonlinear term on the left-hand side to a linear term . At the same time, on the right-hand side is approximated by ; hence, we have the following:
Apparently, it is a second-order linear ODE when is a given constant, and is a given function.
We consider the following boundary conditions for Equation (83):
Equation (85) is the first solution of this boundary value problem.
We give the zeroth-order solution of as follows:
Let
where is to be determined, and A and B are parameters whose values are to be optimized.
Differentiating Equation (106) with respect to x, inserting and using Equation (108), we can derive the following:
Then, we have
where
Inserting Equation (109) into Equation (83) and directly considering its linearization around , we have
where
Sequentially solving the above linear IVPs to derive and inserting them into Equation (103) with , an analytic solution of can be achieved; then, is obtained from Equation (109).
For the first-order solution, we can derive
where
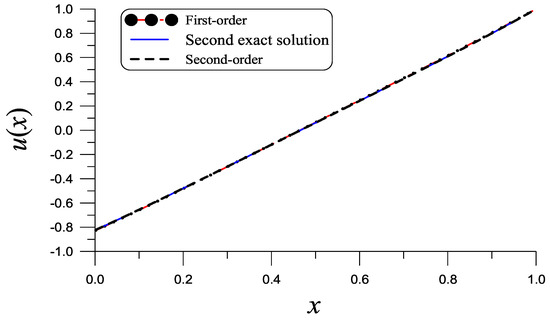
The parameters are , , and , and the first-order solution is close to the exact one obtained by the Lie-group shooting/boundary shape function method [37], which is the second solution for Equations (83) and (105) and is different from that in Equation (85). As shown in Figure 7 by a dashed-dotted line, the first-order solution is quite accurate with ME = .

Figure 7.
For Example 6 solved using the Liapunov technique and a splitting–linearizing method, we compare the first-order and second-order solutions to the exact solution.
Through some manipulations, the second-order solution can be derived as follows:
where
We take , and , and the second-order solution denoted by a dashed line is quite close to the exact one. As shown in Figure 7, the second-order solution is more accurate than the first-order solution with ME = .
In Table 3, we tabulate the values of governed by Equation (83) but with different boundary conditions to those in Equation (105), and we compare them to the exact one. It can be seen that the second-order solution is more accurate than that obtained from the first-order solution with ME = .

Table 3.
For Example 6, we compare the values of and with different x values to the exact one.
Note that if we do not consider the linearization in Equation (111), we can derive
which, by equating the coefficients preceding , leads to the following:
Obviously, Equation (119) is equivalent to Equation (113) by taking , and Equation (120) with an extra term is more complex than Equation (114) by taking . We find that the second-order solution obtained from Equations (118) and (119) by and is less accurate than that in Equation (116) with ME = .
To compare with the homotopy perturbation method [21], Equation (83) is written in a homotopy form:
Inserting
into Equation (121) and equating the coefficients preceding , we can derive the following:
We found that the solutions to the above series of ODEs are not easily derived when because the number of terms in is greater than eight; hence, the computation of would be required significant work.
We begin with
which satisfies the left boundary condition in Equation (105). Through a lengthy derivation, we come to the following:
Example 7.

Let us consider a three-point boundary value problem:
which has an exact solution:
The two shape functions are given by and , and the variable transformation is given as follows:
such that automatically satisfies Equation (127). Let
and inserting into the derivative of Equation (129), we can obtain
where and . Based on Equation (129), we have
where
We give the zeroth-order solution of as follows:
Inserting Equation (130) into Equation (126) and considering its linearization around , we have
where
By the same token, we can derive the following:
For the second-order solution, we can derive
where
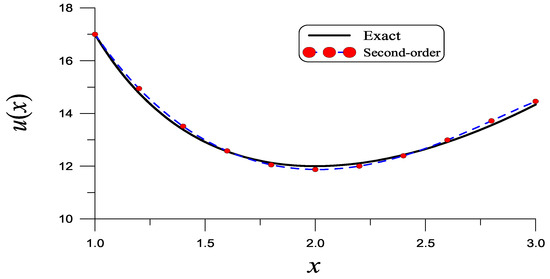
We take , , and . The second-order solution is close to the exact one in Equation (128), as shown in Figure 8 with the maximum relative error (MRE) = . Table 4 reveals that the present analytic solutions are quite accurate.

Figure 8.
For Example 7 of a three-point BVP solved using the Liapunov technique and a splitting–linearizing method, we compare the second-order solution to the exact solution.

Table 4.
For example 7 with different x values, we list the exact solution, second-order solution, and RE.
Example 8.
The boundary layer theory explains very well the steady-state flow over a flat plate at a zero incidence angle. Based on the assumption of incompressibility and the conservation of momentum, the laminar flow satisfies the following:
In above, X and Y are the coordinates attached to the plate in the horizontal and perpendicular directions, and U and V are the velocity components of the flow in the X and Y directions, respectively. The fluid density ρ is assumed to be a constant.
The shear stress is governed by the Newtonian fluid:
where is a constant. The corresponding boundary conditions are given by
where the plate is moving at a constant speed in the direction parallel to an oncoming flow with a constant speed . After introducing a similarity variable and a stream function:
with
we can obtain
which is subjected to the boundary conditions:
In above, is the velocity ratio. When , we have a reverse flow attached near the boundary. When , the speed of the oncoming fluid is larger than that of the plate. When , the speed of the moving plate is faster than the speed of the oncoming fluid. The term is a constant related to the situation of suction if it is negative or injection if it is positive.
Since the boundary layer problem is an important issue in practical applications of fluid mechanics, we take them as an application of the proposed method. We concern those which can be transformed to the second-order nonlinear boundary value problems. Many more boundary layer problems are governed by third-order nonlinear boundary value problems, which cannot be treated as second-order nonlinear boundary value problems.
In this case, we consider a third-order nonlinear boundary value problem [38] for depicting a simple boundary layer problem of a fluid:
Previously, Chang et al. [38] employed a Lie-group-shooting method to solve the problem of Blasius flow, obtaining
which was also obtained by Cortell [39].
No matter which case is considered, we are concerned with the following value:
which corresponds to
We begin with the zeroth-order solutions:
where α and β are determined, respectively, by matching the right-hand boundary conditions for Blasius flow and for Sakidis flow.
Inserting
into
yields
After inserting into the above equations with , for the Blasius flow, we can derive the following:
By taking , is found by solving . This value of α is very close to that in Equation (134). Figure 9 compares the analytic solution to the exact one obtained by RK4, whose ME = is quite small.

Figure 9.
For the Blasius boundary layer problem solved using the Liapunov technique and the linearization method, we compare the analytic solution to the exact solution.
After inserting into Equations (144)–(147) up to , for the Sakidis flow, we can derive the following:
By taking , is found by solving . The value of α is obtained from Equation (148) by inserting as follows:
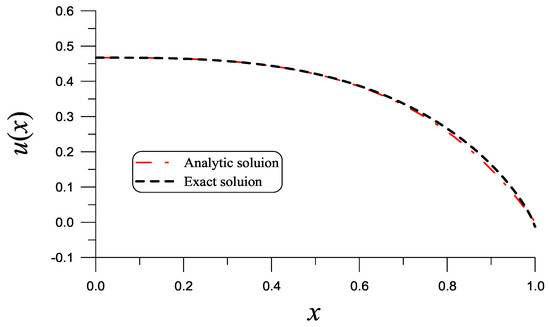
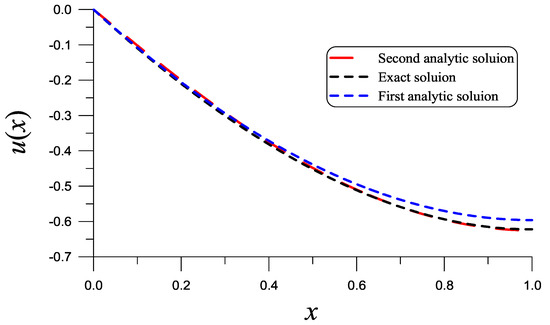
was obtained by Zheng et al. [40] through a more complicated process. Figure 10 compares the analytic solution to the exact one obtained by the Lie-group shooting/boundary shape function method [37], whose ME = is quite small.

Figure 10.
For the Sakidis boundary layer problem solved using the Liapunov technique and the linearization method, we compare the analytic solution to the exact solution.
To obtain a faster convergence solution for the Sakidis boundary layer problem, Equation (142) is expressed for by
where
We attempt to compute .
We linearize Equation (149) with respect to to
It follows that by equating the coefficients preceding :
After inserting into the above equations, we can derive a faster convergence solution for the Sakidis flow up to :
By taking , is found by solving . The value is very close to that of obtained by Zheng et al. [40]. Here, with , we obtained a higher-order analytic solution to ; in Equation (148), only was obtained by taking k up to . Figure 10 compares the second analytic solution to the exact one obtained by the Lie-group shooting/boundary shape function method [37], whose ME = is improved compared to that obtained by the first analytic solution.
Example 9.
To further clarify the versality of the splitting–linearizing Lyapunov method, we consider a highly nonlinear BVP:
whose exact solution is
Let
where the left condition is considered. We suppose that is unknown, such that
where A is to be determined. Equation (150) can be written as
We suppose that
satisfying , where b and λ are parameters. Then, we have
where b is selected such that the constant term in Equation (155) is zero.
Now, we recast Equation (153) to
where μ is a dummy parameter. Then, the analytic solution is determined by
where are to be determined.
Inserting Equation (158) into Equation (157) and equating the coefficients preceding , , we can derive the following:
Let us define
It follows from Equations (161), (152), and (158) with and that
where we have replaced λ in the first two terms by to control the raising part of the curve.
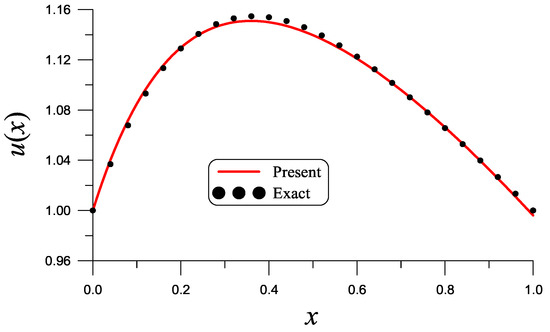
We take and , and is obtained via the interval reduction method. The first-order approximate analytic solution is quite close to the exact one in Equation (151), as shown in Figure 11 with ME = .

Figure 11.
For Example 9, we compare the first-order approximate analytic solution obtained using the linearized Lyapunov method to the exact one.
9. Conclusions
We have proven that the back substitution of the Picard iteration method for the second-order nonlinear ODE is equivalent to the variational iteration method. According to the new idea of the boundary shape function method, we have developed a novel modified variational iteration method (MVIM) for second-order nonlinear BVPs with mixed-boundary conditions. The main contributions of the present paper are the introduction of a boundary shape function and then the transform from to to seek the analytic solution. If is solved, automatically satisfies the specified mixed-boundary conditions. We have transformed the nonlinear BVP with the mixed-boundary conditions to the initial value problem of a nonlinear ODE with the parameters of the unknown right-hand values of the new variable. The unique solution of the transformed IVP was proven with the Lipschitz condition, and the MVIM can find the analytic solution very fast. Two methods were developed to determine the unknown values of the parameters. One is solving nonlinear algebraic equations, and the other is the minimization of the error of the solution and the minimization of the error of the governing equation. We found that the minimizing techniques were better than that solving the nonlinear algebraic equations based on efficiency and accuracy. The examples showed that the novel MVIM and the Liapunov method, together with the splitting–linearizing method based on the boundary shape function, are accurate and effective. Up to the second-order analytic solution, the accuracy is acceptable.
There exist many nonlinear boundary value problems with analytic solutions. In the present paper, we only consider very restricted type nonlinear boundary value problems. Since boundary layer problems of fluid mechanics are an important issue, we take them as an application of the proposed method. We were only concerned with those which could be transformed to second-order nonlinear boundary value problems; many more boundary layer problems are governed by third-order nonlinear boundary value problems. Also, discontinuous-type nonlinear boundary value problems are not addressed here, which might be pursued in the near future.
Author Contributions
Methodology, C.-S.L.; Validation, B.L. and C.-L.K.; Formal analysis, C.-L.K.; Writing—original draft, C.-S.L.; Writing—review & editing, B.L. and C.-L.K. All authors have read and agreed to the published version of the manuscript.
Funding
The NSTC 113-2221-E-019-043-MY3 granted by the National Science and Technology Council, who partially supported this study, is gratefully acknowledged.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Some comments are given for Equation (10). It is known that even for a linear BVP with the Dirichlet boundary conditions, there are different situations for the existence of the solution. Like that for
with the following variable transformation:
where and , we can derive a specific case of Equation (10):
Depending on the given values of and c, there are four possible cases for the existence of the solution of :
We can guarantee the unique solution of upon giving the initial conditions and :
which depends continuously on the parameter . However, the existence of depends on the value of determined by b and c in Equation (A1).
For the example given in Equations (21) and (22), we have obtained the exact solution in Equation (30) by exactly solving Equations (25) and (26). Instead of the exact solution, we employ the MVIM to seek an approximate analytic solution. By taking and , . Starting from and through four iterations in the MVIM, we can derive
where . By imposing , we can obtain the following:
Upon deriving , is given as follows:
In , we replace by to preserve the right-boundary condition.
In Figure 1, we compare it to the exact one in Equation (23), whose ME is and is more accurate than that obtained using the Picard iteration method. Moreover, the MVIM converges faster than the Picard iteration method, which spent five iterations with ME = .
It can be seen that in Equation (A4) is quite complicated. Next, we apply Equation (63) to determine the optimal value of . We begin with and
Up to the third-order analytic solution, we can obtain the following:
where and the optimal value is . The ME is , which is more accurate than the fourth-order solution in Equation (A5), as compared in Table A1. Both Equations (A6) and (A5) can exactly fulfill the boundary conditions.

Table A1.
For the example in Equations (21) and (22), we compare the approximate solutions obtained using the MVIM with Equations (A5)–(A7) to the exact one.
| x | Exact | Equation (A6) | Equation (A5) | Equation (A7) |
|---|---|---|---|---|
| 0 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| 0.1 | 1.03753 | 1.05255 | 1.03468 | 1.03025 |
| 0.2 | 1.06402 | 1.08885 | 1.05740 | 1.04716 |
| 0.3 | 1.07501 | 1.10347 | 1.06351 | 1.04601 |
| 0.4 | 1.06482 | 1.09023 | 1.04724 | 1.02132 |
| 0.5 | 1.02626 | 1.04222 | 1.00164 | 0.966968 |
| 0.6 | 0.950319 | 0.951926 | 0.918457 | 0.876260 |
| 0.7 | 0.825678 | 0.811284 | 0.788167 | 0.741986 |
| 0.8 | 0.638204 | 0.611764 | 0.599927 | 0.556525 |
| 0.9 | 0.370281 | 0.344429 | 0.341633 | 0.311926 |
| 1.0 | 0 | 0 | 0 |
By using the VIM in Equation (54) to solve Equations (21) and (22), we find that it is quite complicated, since we start from a nonzero function:
which satisfies the left-boundary condition in Equation (22), while a is to be determined by matching the right-boundary condition in Equation (22). Through a lengthy computation up to the third-order analytic solution, we can obtain the following:
where and is solved from . The ME is , which is less accurate than the third-order solution in Equation (A6), as compared in Table A1. The values of obtained using the VIM are under-estimated, and the right-boundary condition is not precisely satisfied.
Instead of solving to obtain a, which is quite complicated, we seek the optimal value of a by
When the optimal value is obtained, the ME reduces to . However, at this moment, the error of the right-boundary condition increases to .
Notice that in the minimization problem with a single unknown value a, we can adopt the so-called interval reduction method to find the proper value of a. First, we select a large interval and list the data of in the computer. We can observe where the minimal point locates, then we reduce the interval to a smaller one to involve that minimal point. We carry out the same procedure a few times, then we can find a quite accurate value of a.
It is apparent that the MVIM is better than the VIM. When the MVIM satisfies the boundary conditions automatically, the VIM does not satisfy the right-boundary condition.
Appendix B
In this appendix, we apply the MVIM to solve a singularly perturbed BVP [41]:
Starting from and using Equation (51), we can derive the fourth-order solution:
and by imposing , we can obtain
We take , and upon comparing the analytic solution to the exact solution (A10), the ME is .
When we apply Equation (63) to determine in Equation (A11) with , the optimal value is . The current solution based on the fourth-order MVIM with the minimization technique is quite close to the exact one, whose ME is , which is more accurate than that calculated using Equations (A11) and (A12) with ME = .
References
- Cash, J.R. On the numerical integration of nonlinear two-point boundary value problems using iterated deferred corrections, Part 1: A survey and comparison of some one-step formulae. Comput. Math. Appl. 1986, 12, 1029–1048. [Google Scholar] [CrossRef]
- Cash, J.R. On the numerical integration of nonlinear two-point boundary value problems using iterated deferred corrections, Part 2: The development and analysis of highly stable deferred correction formulae. SIAM J. Numer. Anal. 1988, 25, 862–882. [Google Scholar] [CrossRef]
- Cash, J.R.; Wright, R.W. Continuous extensions of deferred correction schemes for the numerical solution of nonlinear two-point boundary value problems. Appl. Numer. Math. 1998, 28, 227–244. [Google Scholar] [CrossRef]
- Ascher, U.M.; Mattheij, R.M.M.; Russell, R.D. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Liu, C.S. The Lie-group shooting method for nonlinear two-point boundary value problems exhibiting multiple solutions. Comput. Model. Eng. Sci. 2006, 13, 149–163. [Google Scholar]
- Cabada, A.; Pouso, R.L. Existence theory for functional p-Laplacian equations with variable exponents. Nonlinear Anal. 2003, 52, 557–572. [Google Scholar] [CrossRef]
- Cabada, A.; O’Regan, D.; Pouso, R.L. Second order problems with functional conditions including Sturm-Liouville and multipoint conditions. Math. Nachr. 2008, 281, 1254–1263. [Google Scholar] [CrossRef]
- Mawhin, J.; Thompson, H.B. Bounding surfaces and second order quasilinear equations with compatible nonlinear functional boundary conditions. Adv. Nonlinear Stud. 2011, 11, 157–172. [Google Scholar] [CrossRef]
- Erbe, L.H. Nonlinear boundary value problems for second order differential equations. J. Diff. Equ. 1970, 7, 459–472. [Google Scholar] [CrossRef]
- Mawhin, J.; Schmitt, K. Upper and lower solutions and semilinear second order elliptic equations with non-linear boundary conditions. Proc. Roy. Soc. Edinburgh 1984, 97, 199–207. [Google Scholar] [CrossRef]
- De Coster, C.; Habets, P. Two-Point Boundary Value Problems: Lower And Upper Solutions; Elsevier: New York, NY, USA, 2006. [Google Scholar]
- He, J.H. Variational iteration method – a kind of non-linear analytical technique: Some examples. Int. J. Non-linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method for autonomous ordinary systems. Appl. Math. Comput. 2000, 114, 115–123. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. A modified variational iteration method for strongly nonlinear problems. Nonlinear Sci. Lett. A 2010, 1, 183–192. [Google Scholar]
- Turkyilmazoglu, M. An optimal variational iteration method. Appl. Math. Lett. 2011, 24, 762–765. [Google Scholar] [CrossRef]
- Wang, X.; Atluri, S.N. A unification of the concepts of the variational iteration, Adomian decomposition and Picard iteration methods; and a local variational iteration method. Comput. Model. Eng. Sci. 2016, 111, 567–585. [Google Scholar]
- Chang, S.H. Convergence of variational iteration method applied to two-point diffusion problems. Appl. Math. Model. 2016, 40, 6805–6810. [Google Scholar] [CrossRef]
- Chang, S.H. A variational iteration method involving Adomian polynomials for a strongly nonlinear boundary value problem. East Asian J. Appl. Math. 2019, 9, 153–164. [Google Scholar]
- Farkas, M. Periodic Motions; Springer: New York, NY, USA, 1994. [Google Scholar]
- Liapunov, A.M. Sur une série dans la théorie des équations différentielles linéaires du second ordre à coefficients périodiques. Zap. Akad. Nauk Fiz.-Mat. Otd. 8th series 1902, 13, 1–70. [Google Scholar]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phy. Lett. A 2006, 350, 87–88. [Google Scholar] [CrossRef]
- Noor, M.A.; Mohyud-Din, S.T. Homotopy perturbation method for solving sixth-order boundary value problems. Comput. Math. Appl. 2008, 55, 2953–2972. [Google Scholar] [CrossRef]
- Chun, C.; Sakthivel, R. Homotopy perturbation technique for solving two-point boundary value problems–comparison with other methods. Comput. Phy. Communi. 2010, 181, 1021–1024. [Google Scholar] [CrossRef]
- Khuri, S.A.; Sayfy, A. Generalizing the variational iteration method for BVPs: Proper setting of the correction functional. Appl. Math. Lett. 2017, 68, 68–75. [Google Scholar] [CrossRef]
- Liu, C.S.; Chang, C.W. Boundary shape function method for nonlinear BVP, automatically satisfying prescribed multipoint boundary conditions. Bound. Value Prob. 2020, 2020, 139. [Google Scholar] [CrossRef]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Reid, W.T. Ordinary Differential Equations; John Wiley & Son: New York, NY, USA, 1971. [Google Scholar]
- Zhou, Z.; Shen, J. A second-order boundary value problem with nonlinear and mixed boundary conditions: Existence, uniqueness, and approximation. Abstr. Appl. Anal. 2010, 2010, 287473. [Google Scholar] [CrossRef]
- Liu, C.S.; Chang, J.R. Boundary shape functions methods for solving the nonlinear singularly perturbed problems with Robin boundary conditions. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 797–806. [Google Scholar] [CrossRef]
- Rani, G.S.; Jayan, S.; Nagaraja, K.V. An extension of golden section algorithm for n-variable functions with MATLAB code. IOP Conf. Ser. Mater. Sci. Eng. 2018, 577, 012175. [Google Scholar] [CrossRef]
- Lu, J. Variational iteration method for solving two-point boundary value problems. J. Comput. Appl. Math. 2007, 207, 92–95. [Google Scholar] [CrossRef]
- Adomian, G.; Elrod, M.; Rach, R. A new approach to boundary value equations and application to a generalization of Airy’s equation. J. Math. Anal. Appl. 1989, 140, 554–568. [Google Scholar] [CrossRef]
- Ha, S.N. A nonlinear shooting method for two-point boundary value problems. Comput. Math. Appl. 2001, 42, 1411–1420. [Google Scholar] [CrossRef]
- Ha, S.N.; Lee, C.R. Numerical study for two-point boundary value problems using Green’s functions. Comput. Math. Appl. 2002, 44, 1599–1608. [Google Scholar] [CrossRef]
- Liu, C.S.; Kuo, C.L.; Chang, C.W. Decomposition-linearization-sequential homotopy methods for nonlinear differential/integral equations. Mathematics 2024, 12, 3557. [Google Scholar] [CrossRef]
- Liu, C.S.; Chang, C.W. Lie-group shooting/boundary shape function methods for solving nonlinear boundary value problems. Symmetry 2022, 14, 778. [Google Scholar] [CrossRef]
- Chang, C.W.; Chang, J.R.; Liu, C.S. The Lie-group shooting method for solving classical Blasius flat-plate problem. Comput. Mater. Contin. 2008, 7, 139–153. [Google Scholar]
- Cortell, R. Numerical solutions of the classical Blasius flat-plate problem. Appl. Math. Comput. 2005, 170, 706–710. [Google Scholar] [CrossRef]
- Zheng, L.C.; Chen, X.H.; Chang, X.X. Analytical approximants for a boundary layer flow on a stretching moving surface with a power velocity. Int. J. Appl. Mech. Eng. 2004, 9, 795–802. [Google Scholar]
- Khuri, S.A.; Sayfy, A. Self-adjoint singularly perturbed boundary value problems: An adaptive variational approach. Math. Meth. Appl. Sci. 2013, 36, 1070–1079. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).