An Improved Whale Optimization Algorithm for the Integrated Scheduling of Automated Guided Vehicles and Yard Cranes
Abstract
1. Introduction
- A more comprehensive model for the YAAISP is proposed in this paper, in which AGVs’ bi-directional flow, coordinated operations of import and export container tasks, and container task constraints relationship are considered simultaneously.
- A specific encoding and decoding method is developed for the YAAISP, ensuring the feasibility of all encoding schemes without the need for adjustments or discarding, expanding the search space for potential solutions.
- An IWOA algorithm is proposed to solve the YAAISP, and population initialization with inverse learning and a random differential mutation strategy are implemented to enhance the diversity of solutions, effectively preventing the algorithm from getting trapped in local optima. The nonlinear convergence factor and adaptive weight strategy are used to dynamically adjust the weights, thereby accelerating the convergence speed of the algorithm.
2. Literature Review
2.1. YC Scheduling Problem
2.2. AGV Scheduling Problem
2.3. Integrated Scheduling Problem
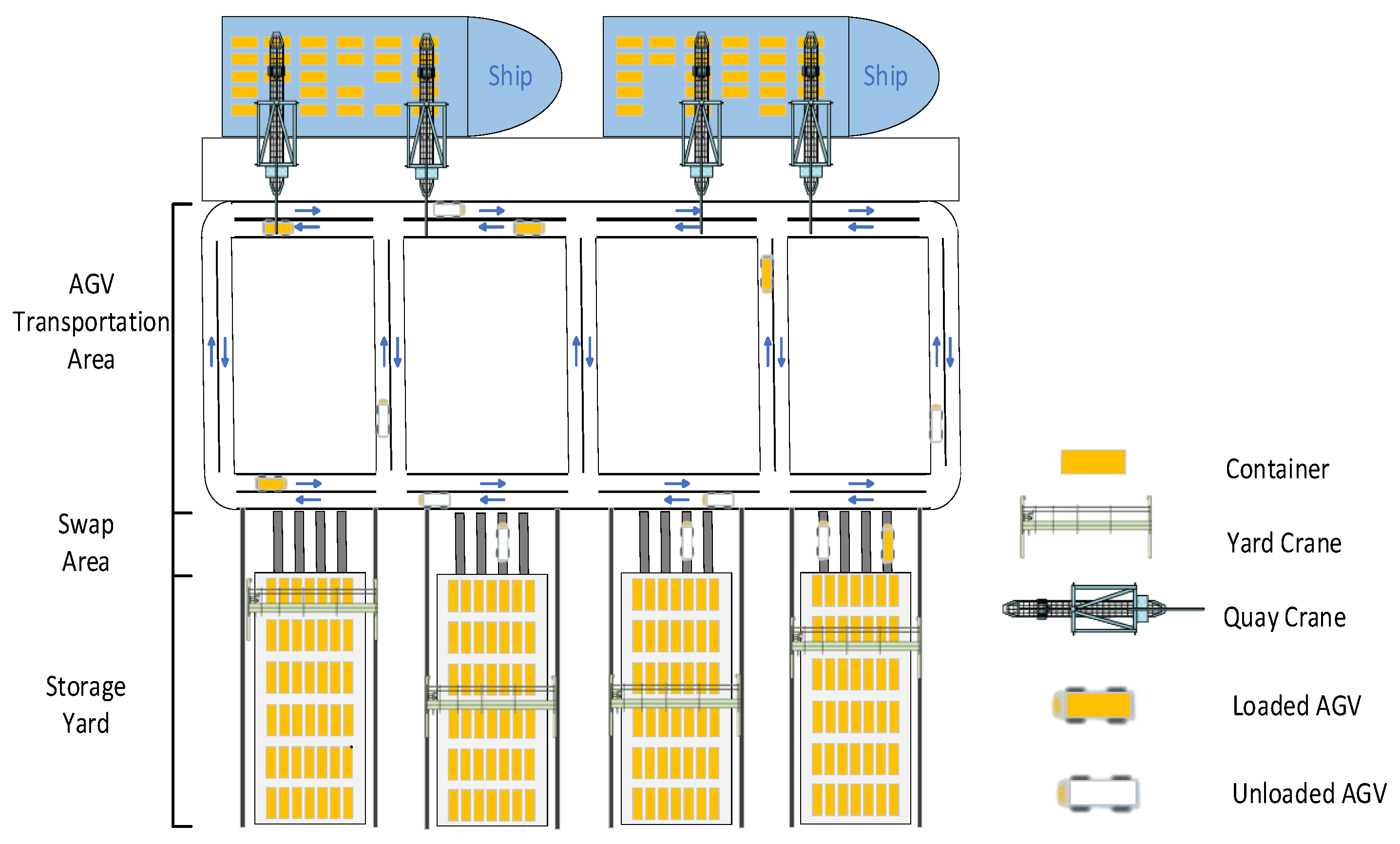
3. Problem Description and Formulation
3.1. Problem Statement
3.2. Notations
3.3. Assumptions
- The loading and unloading points for all container tasks are known;
- The initial positions of the AGVs are known;
- Each AGV can only transport one container task at a time;
- Each container task can only be assigned to one AGV at a time;
- The working time of YCs processing a container task is evenly distributed between (40, 60);
- The efficiency of QCs is high enough to ignore the time of QCs handling container tasks;
- The constraints relationship between each container task is known, and the lower container must wait for the upper container to move before it can be operated.
3.4. Mathematical Modeling
4. IWOA Algorithm for YAAISP
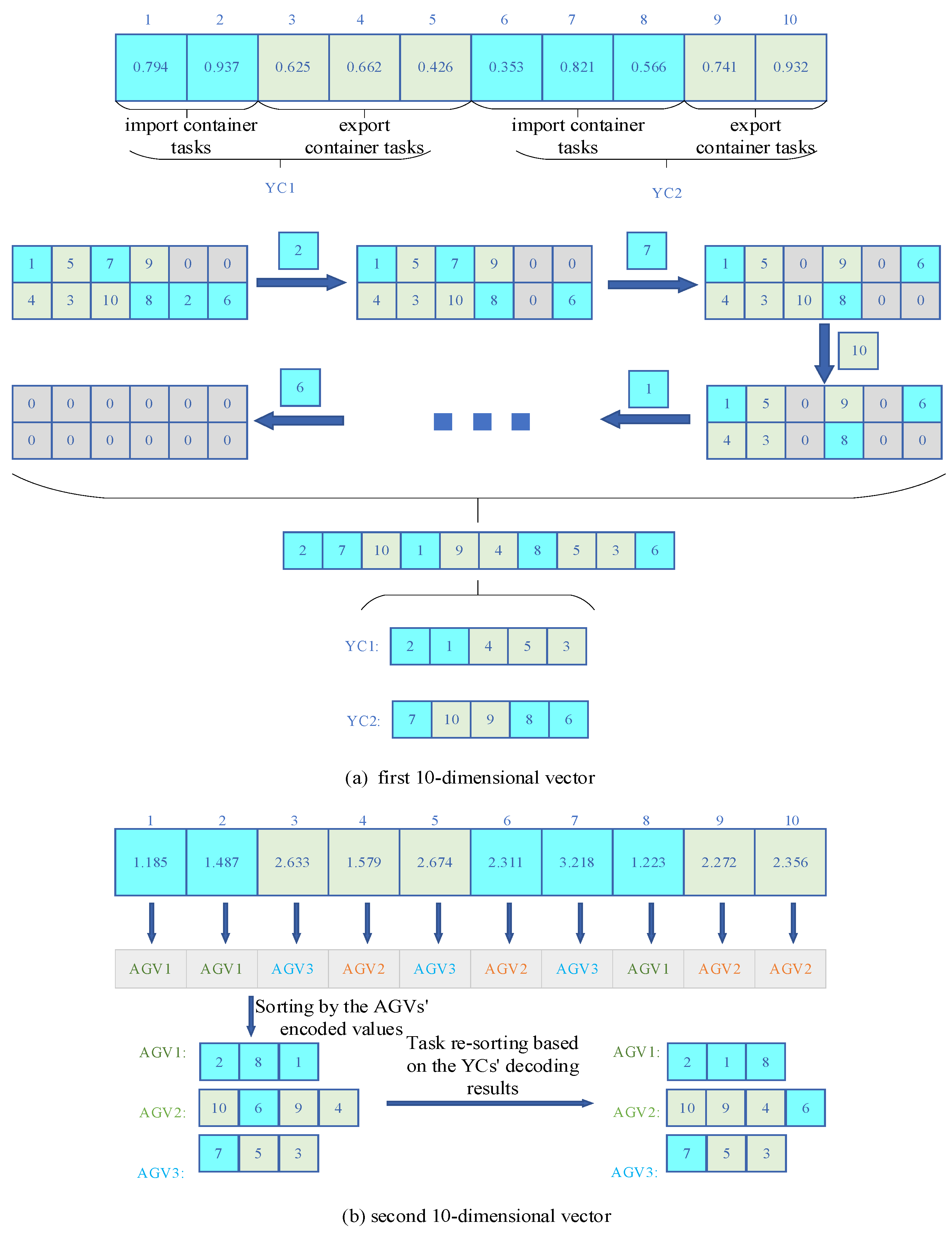
4.1. Solution Representation
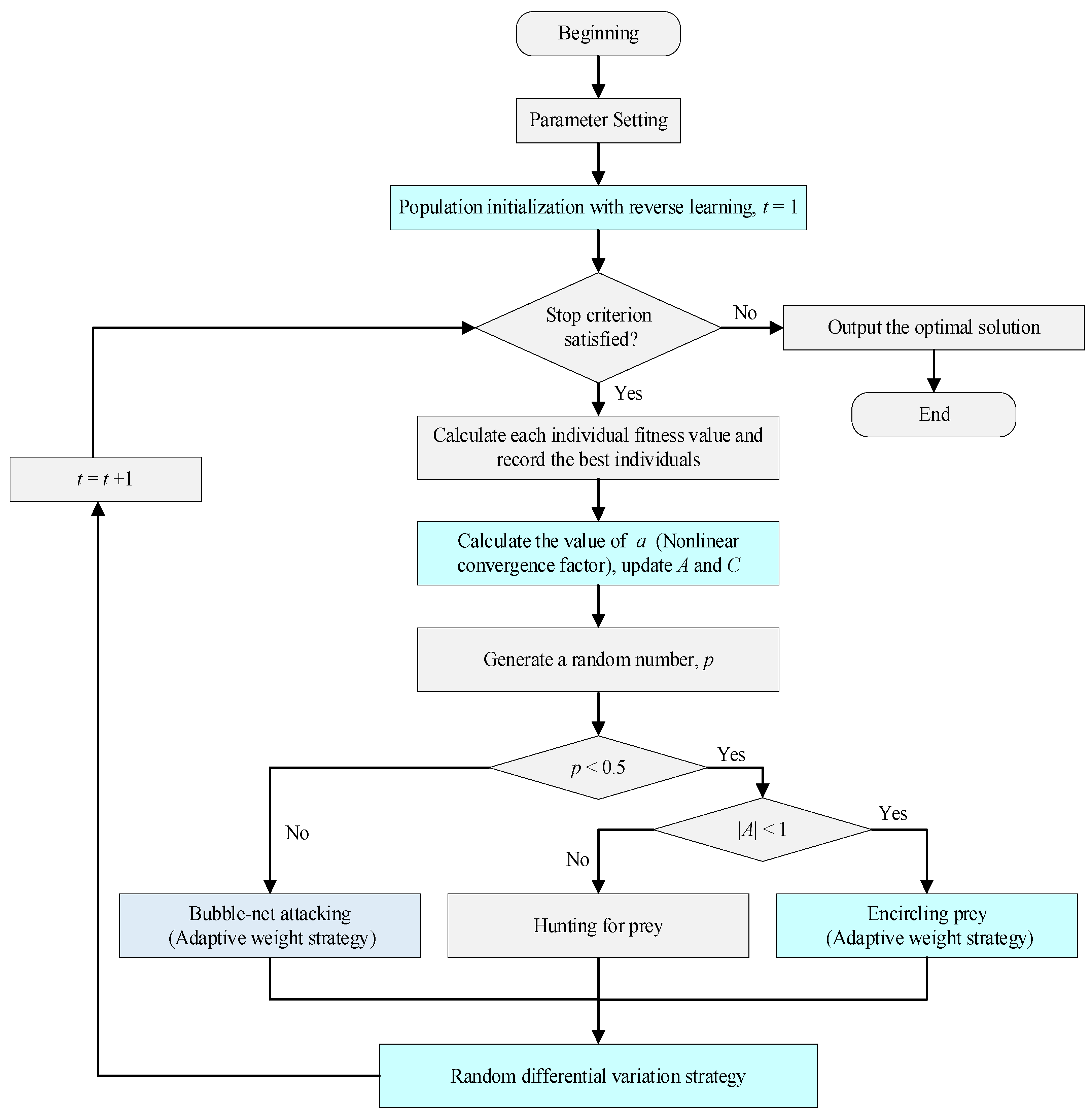
4.2. Standard WOA Algorithm
- Encircling prey
- Bubble-net attacking
- Hunting for prey
4.3. Proposed IWOA Algorithm
- Population initialization with reverse learning
- Nonlinear convergence factor
- Adaptive weight and random differential mutation strategy
5. Validation and Results Analysis
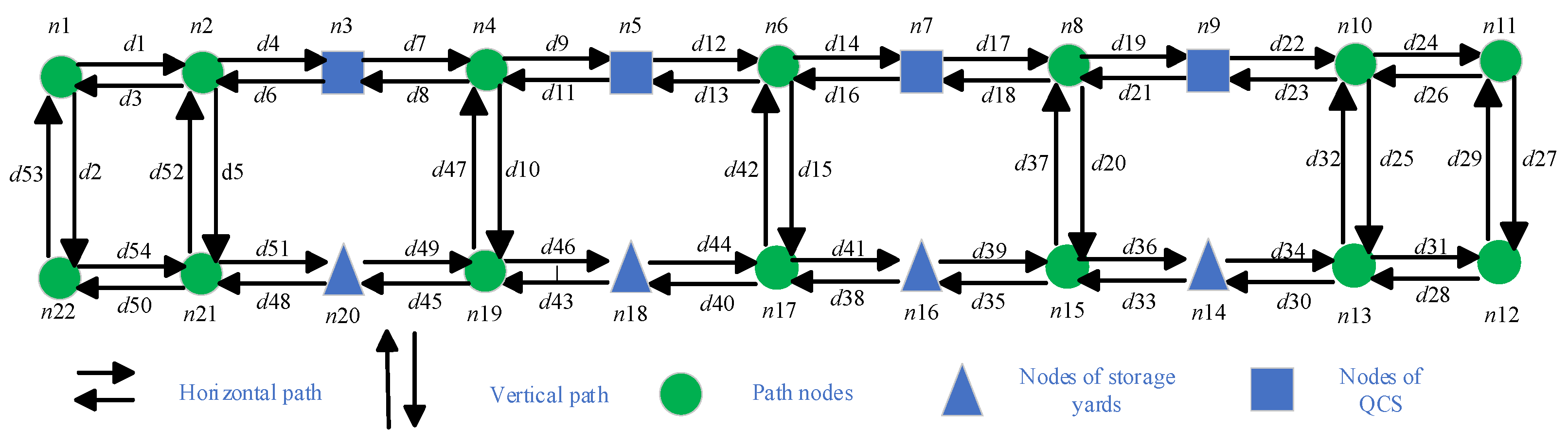
5.1. Instance Generation
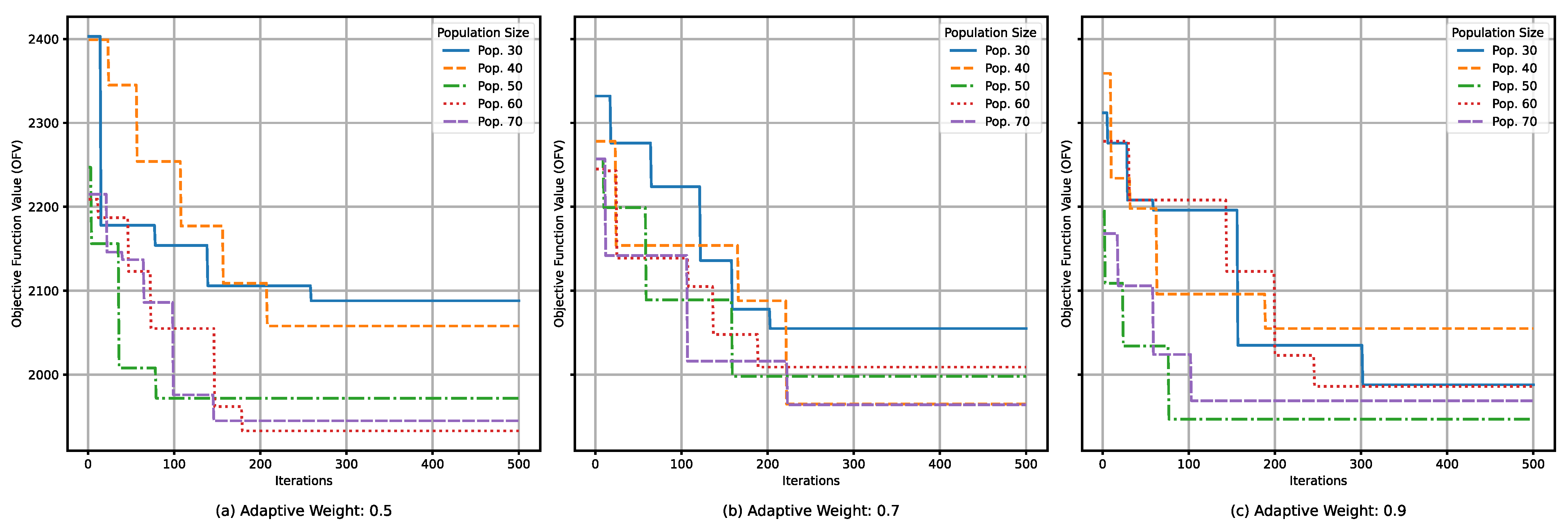
5.2. Parameter Setting
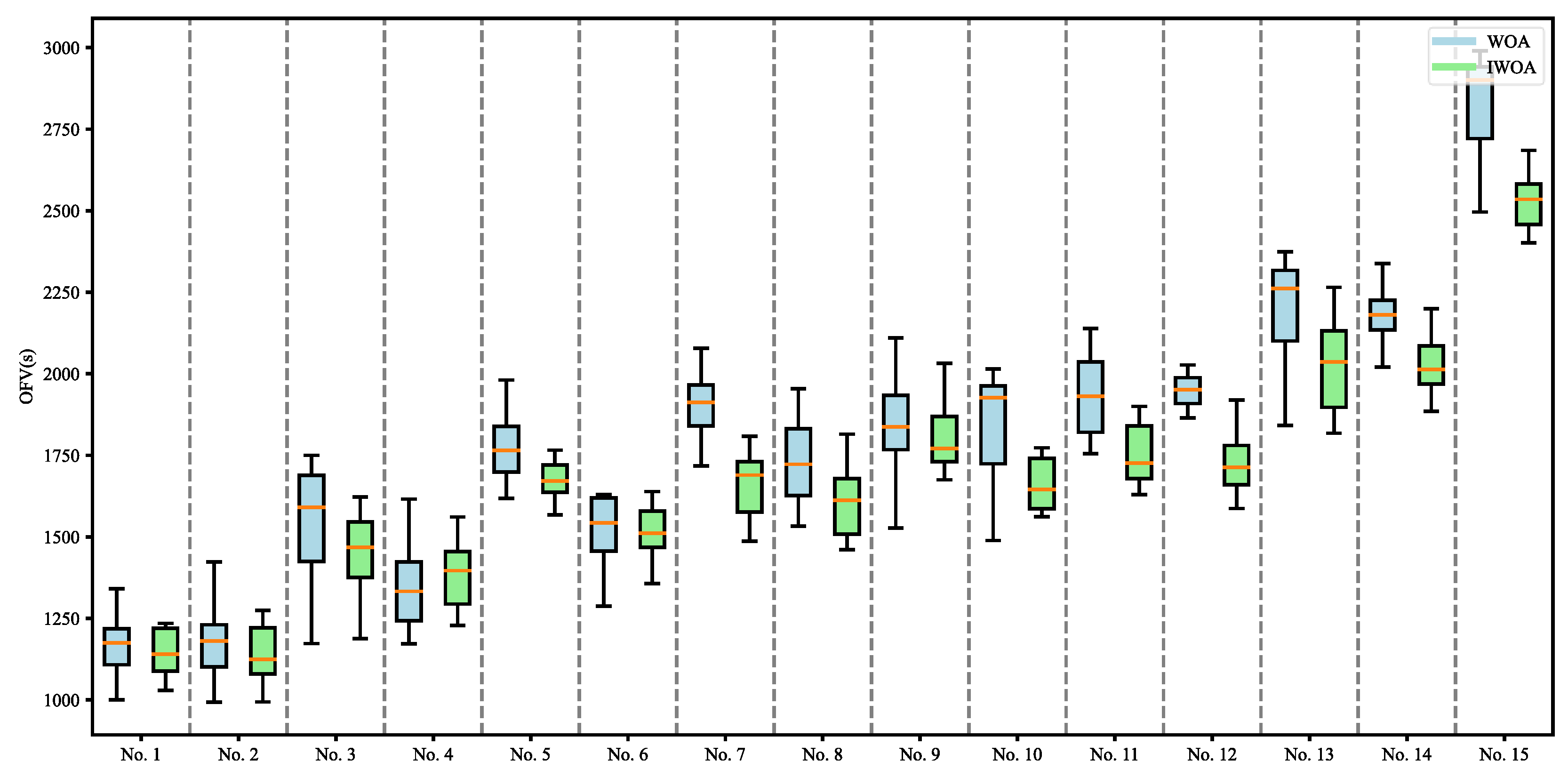
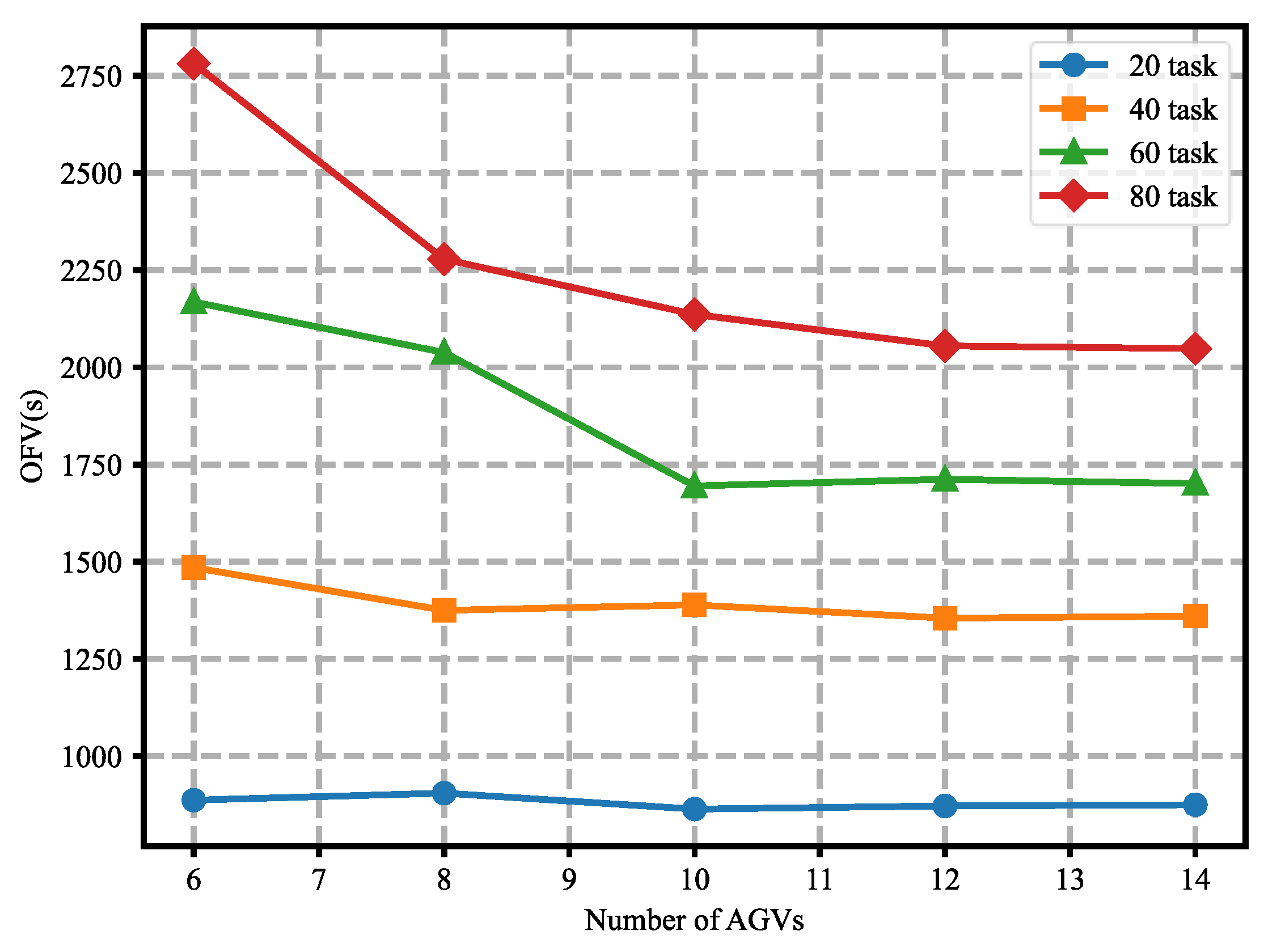
5.3. Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ACTs | Automated Container Terminals |
| AGVS | Automated Guided Vehicles |
| YCs | Yard Cranes |
| QCs | Quay Cranes |
| YAAISP | Integrated Scheduling Problem of Yard Cranes and Automated Guided Vehicles |
| IWOA | Improved Whale Optimization Algorithm |
| WOA | Whale Optimization Algorithm |
| MIP | Mixed-Integer Programming |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| GWO | Grey Wolf Optimizer |
| OFV | Objective Function Value |
| OFVIS(IWOA) | The OFV obtained by the WOA algorithm under integrated scheduling |
| OFVNIS(IWOA) | The OFV obtained by the IWOA algorithm under non-integrated scheduling |
| OFVIS(WOA) | The OFV obtained by the WOA algorithm under integrated scheduling |
| OFVCPLEX | The OFV obtained by the CPLEX solver under integrated scheduling |
| GAP1 | The difference between the IWOA OFV under non-integrated scheduling and the CPLEX OFV under integrated scheduling |
| GAP2 | The difference rate between the OFV of the IWOA and the CPLEX under integrated scheduling |
| GAP3 | The difference rate between the OFV of the IWOA and the WOA solver under integrated scheduling |
References
- Aslam, S.; Michaelides, M.P.; Herodotou, H. Internet of Ships: A Survey on Architectures, Emerging Applications, and Challenges. IEEE Internet Things J. 2020, 7, 9714–9727. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A.; Roodbergen, K.J. Storage Yard Operations in Container Terminals: Literature Overview, Trends, and Research Directions. Eur. J. Oper. Res. 2014, 235, 412–430. [Google Scholar] [CrossRef]
- Vanelslander, T.; Sys, C.; Lam, J.S.L.; Ferrari, C.; Roumboutsos, A.; Acciaro, M.; Macário, R.; Giuliano, G. A Serving Innovation Typology: Mapping Port-Related Innovations. Transp. Rev. 2019, 39, 611–629. [Google Scholar] [CrossRef]
- Cao, J.X.; Lee, D.-H.; Chen, J.H.; Shi, Q. The Integrated Yard Truck and Yard Crane Scheduling Problem: Benders’ Decomposition-Based Methods. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 344–353. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Song, Y.; Xie, H.; Zhu, Z.; Ji, R. Predicting Energy Consumption of Chiller Plant Using WOA-BiLSTM Hybrid Prediction Model: A Case Study for a Hospital Building. Energy Build. 2023, 300, 113642. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Wang, C.-N.; Thanh Tam Nguyen, T.; Dang, T.-T.; Pan, Y.-J. Hybridizing WOA with PSO for Coordinating Material Handling Equipment in an Automated Container Terminal Considering Energy Consumption. Adv. Eng. Inform. 2024, 60, 102410. [Google Scholar] [CrossRef]
- Shaheen, H.I.; Rashed, G.I.; Yang, B.; Yang, J. Optimal Electric Vehicle Charging and Discharging Scheduling Using Metaheuristic Algorithms: V2G Approach for Cost Reduction and Grid Support. J. Energy Storage 2024, 90, 111816. [Google Scholar] [CrossRef]
- Ng, W.C. Crane Scheduling in Container Yards with Inter-Crane Interference. Eur. J. Oper. Res. 2005, 164, 64–78. [Google Scholar] [CrossRef]
- Saini, S.; Roy, D.; De Koster, R. A Stochastic Model for the Throughput Analysis of Passing Dual Yard Cranes. Comput. Oper. Res. 2017, 87, 40–51. [Google Scholar] [CrossRef]
- Zheng, F.; Man, X.; Chu, F.; Liu, M.; Chu, C. Two Yard Crane Scheduling With Dynamic Processing Time and Interference. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3775–3784. [Google Scholar] [CrossRef]
- Chen, L.; Langevin, A. Multiple Yard Cranes Scheduling for Loading Operations in a Container Terminal. Eng. Optim. 2011, 43, 1205–1221. [Google Scholar] [CrossRef]
- Galle, V.; Barnhart, C.; Jaillet, P. Yard Crane Scheduling for Container Storage, Retrieval, and Relocation. Eur. J. Oper. Res. 2018, 271, 288–316. [Google Scholar] [CrossRef]
- He, J.; Chang, D.; Mi, W.; Yan, W. A Hybrid Parallel Genetic Algorithm for Yard Crane Scheduling. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 136–155. [Google Scholar] [CrossRef]
- He, J.; Tan, C.; Zhang, Y. Yard Crane Scheduling Problem in a Container Terminal Considering Risk Caused by Uncertainty. Adv. Eng. Inform. 2019, 39, 14–24. [Google Scholar] [CrossRef]
- Li, J.; Yang, J.; Xu, B.; Yin, W.; Yang, Y.; Wu, J.; Zhou, Y.; Shen, Y. A Flexible Scheduling for Twin Yard Cranes at Container Terminals Considering Dynamic Cut-Off Time. J. Mar. Sci. Eng. 2022, 10, 675. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Wang, L.; Li, S. Flexible Yard Crane Scheduling for Mixed Railway and Road Container Operations in Sea-Rail Intermodal Ports with the Sharing Storage Yard. Transp. Res. Part E Logist. Transp. Rev. 2024, 190, 103714. [Google Scholar] [CrossRef]
- Kim, K.H.; Bae, J.W. A Look-Ahead Dispatching Method for Automated Guided Vehicles in Automated Port Container Terminals. Transp. Sci. 2004, 38, 224–234. [Google Scholar] [CrossRef]
- Rashidi, H.; Tsang, E.P.K. A Complete and an Incomplete Algorithm for Automated Guided Vehicle Scheduling in Container Terminals. Comput. Math. Appl. 2011, 61, 630–641. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y. Modelling of Dual-Cycle Strategy for Container Storage and Vehicle Scheduling Problems at Automated Container Terminals. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 49–64. [Google Scholar] [CrossRef]
- Ma, X.; Bian, Y.; Gao, F. An Improved Shuffled Frog Leaping Algorithm for Multiload AGV Dispatching in Automated Container Terminals. Math. Probl. Eng. 2020, 2020, 1260196. [Google Scholar] [CrossRef]
- Angeloudis, P.; Bell, M.G.H. An Uncertainty-Aware AGV Assignment Algorithm for Automated Container Terminals. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 354–366. [Google Scholar] [CrossRef]
- Xu, W.; Guo, S.; Li, X.; Guo, C.; Wu, R.; Peng, Z. A Dynamic Scheduling Method for Logistics Tasks Oriented to Intelligent Manufacturing Workshop. Math. Probl. Eng. 2019, 2019, 7237459. [Google Scholar] [CrossRef]
- Dang, Q.-V.; Singh, N.; Adan, I.; Martagan, T.; Van De Sande, D. Scheduling Heterogeneous Multi-Load AGVs with Battery Constraints. Comput. Oper. Res. 2021, 136, 105517. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, Y.; Hu, Y.; Ren, W. A Dynamic Scheduling Method for Self-Organized AGVs in Production Logistics Systems. Procedia CIRP 2021, 104, 381–386. [Google Scholar] [CrossRef]
- Li, D.; Tang, J.; Zhou, B.; Cao, P.; Hu, J.; Leung, M.-F.; Wang, Y. Toward Resilient Electric Vehicle Charging Monitoring Systems: Curriculum Guided Multi-Feature Fusion Transformer. IEEE Trans. Intell. Transp. Syst. 2024, 25, 21356–21366. [Google Scholar] [CrossRef]
- Aljanabi, M.R.; Borna, K.; Ghanbari, S.; Obaid, A.J. SVD-Based Adaptive Fuzzy for Generalized Transportation. Alex. Eng. J. 2024, 94, 377–396. [Google Scholar] [CrossRef]
- Shao, Q.; Miao, J.; Liao, P.; Liu, T. Dynamic Scheduling Optimization of Automatic Guide Vehicle for Terminal Delivery under Uncertain Conditions. Appl. Sci. 2024, 14, 8101. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, Y.; Tian, Y. Integrated Optimization of Automated Guided Vehicles and Yard Cranes Considering Charging Constraints. Eng. Optim. 2023, 56, 1748–1766. [Google Scholar] [CrossRef]
- Zhou, C.; Lee, B.K.; Li, H. Integrated Optimization on Yard Crane Scheduling and Vehicle Positioning at Container Yards. Transp. Res. Part E Logist. Transp. Rev. 2020, 138, 101966. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, W.; Duan, J.; Qin, J. Cooperative Scheduling of AGV and ASC in Automation Container Terminal Relay Operation Mode. Math. Probl. Eng. 2021, 2021, 5764012. [Google Scholar] [CrossRef]
- Chen, X.; He, S.; Zhang, Y.; Tong, L.C.; Shang, P.; Zhou, X. Yard Crane and AGV Scheduling in Automated Container Terminal: A Multi-Robot Task Allocation Framework. Transp. Res. Part C Emerg. Technol. 2020, 114, 241–271. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Sheu, J.-B. Integrated Scheduling Optimization of AGV and Double Yard Cranes in Automated Container Terminals. Transp. Res. Part B Methodol. 2024, 179, 102871. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y.; Mendes, A.B. Modelling of Integrated Vehicle Scheduling and Container Storage Problems in Unloading Process at an Automated Container Terminal. Comput. Ind. Eng. 2016, 94, 32–44. [Google Scholar] [CrossRef]
- Ma, M.; Yu, F.; Xie, T.; Yang, Y. A Hybrid Speed Optimization Strategy Based Coordinated Scheduling between AGVs and Yard Cranes in U-Shaped Container Terminal. Comput. Ind. Eng. 2024, 198, 110712. [Google Scholar] [CrossRef]
- Zhao, M. An Improved PSO-GWO Algorithm With Chaos and Adaptive Inertial Weight for Robot Path Planning. Front. Neurorobotics 2021, 15, 770361. [Google Scholar]
- Yuan, Q.; Sun, R.; Du, X. Path Planning of Mobile Robots Based on an Improved Particle Swarm Optimization Algorithm. Processes 2022, 11, 26. [Google Scholar] [CrossRef]


| Notations | Description |
|---|---|
| Indices: | |
| Parameters: | |
| Y | |
| Driving speed of the AGVs | |
| Set of container tasks pairs (i, j) such that i must precede j in handling by same YC | |
| M | A large integer value |
| Variables: | |
| Time when the AGV starts executing container task i | |
| Completion time taken by the AGV to transport container i | |
| Time for the handling container task i on the YC | |
| Time when YC y starts processing task i | |
| Time for YC y to complete task i | |
| Arriving time of the AGV to transport container i | |
| Binary variable that equals 1 if container task i is allocated to AGV a for transporting, otherwise 0 | |
| Binary variable that equals 1 if container task j is transported immediately before i on AGV a, 0 otherwise | |
| Binary variable that equals 1 if container task j is handling immediately before i on YC y, otherwise 0 | |
| Binary variable that equals 1 if container task i is handling before j, otherwise 0 |
| w | CPU Runtimes(s) | ||||
|---|---|---|---|---|---|
| Pop. 30 | Pop. 40 | Pop. 50 | Pop. 60 | Pop. 70 | |
| 0.5 | 31.88 | 41.07 | 59.78 | 75.41 | 94.56 |
| 0.7 | 36.67 | 43.66 | 55.23 | 74.28 | 95.34 |
| 0.9 | 32.22 | 41.28 | 53.64 | 77.54 | 95.78 |
| No. | Problem Size | Integrated Solution (CPLEX) | Non-Integrated Solution (IWOA) | Integrated Solution (IWOA) | |||||
|---|---|---|---|---|---|---|---|---|---|
| T × Y × Q × A * | OFV (s) | Times (s) | OFV (s) | Times (s) | GAP1 | OFV (s) | Times (s) | GAP2 | |
| 1 | 4 × 1 × 2 × 1 | 336 | 36.03 | 342 | 3.61 | 1.78% | 339 | 2.44 | 0.89% |
| 2 | 5 × 1 × 2 × 1 | 389 | 55.34 | 397 | 4.79 | 2.06% | 393 | 3.60 | 1.03% |
| 3 | 6 × 1 × 2 × 1 | 467 | 80.66 | 477 | 5.58 | 2.14% | 475 | 4.73 | 1.71% |
| 4 | 7 × 1 × 2 × 2 | 469 | 220.35 | 475 | 5.66 | 1.28% | 474 | 6.88 | 1.06% |
| 5 | 8 × 1 × 2 × 2 | 502 | 355.45 | 517 | 7.05 | 2.99% | 510 | 7.04 | 1.59% |
| 6 | 9 × 2 × 2 × 2 | 545 | 519.37 | 566 | 8.12 | 3.85% | 554 | 7.42 | 1.65% |
| 7 | 11 × 2 × 2 × 3 | 599 | 658.66 | 639 | 8.77 | 6.68% | 613 | 8.16 | 2.34% |
| 8 | 13 × 2 × 2 × 3 | 628 | 711.45 | 658 | 10.96 | 4.78% | 644 | 8.71 | 2.55% |
| 9 | 15 × 2 × 2 × 3 | 675 | 957.82 | 727 | 11.53 | 7.70% | 691 | 9.22 | 2.37% |
| 10 | 16 × 2 × 3 × 4 | 741 | 1172.93 | 793 | 11.87 | 7.02% | 762 | 9.69 | 2.83% |
| 11 | 17 × 2 × 3 × 4 | 812 | 1502.09 | 865 | 12.59 | 5.30% | 835 | 10.28 | 2.83% |
| 12 | 19 × 2 × 3 × 5 | 846 | 1804.56 | 899 | 13.78 | 6.26% | 877 | 11.15 | 3.66% |
| 13 | 21 × 2 × 3 × 5 | 904 | 1895.52 | 973 | 15.09 | 7.63% | 939 | 13.73 | 3.87% |
| 14 | 23 × 2 × 3 × 6 | 923 | 2087.85 | 998 | 15.97 | 8.13% | 958 | 13.96 | 3.80% |
| 15 | 24 × 2 × 3 × 6 | 1057 | 2219.37 | 1145 | 17.02 | 8.32% | 1108 | 15.01 | 4.82% |
| No. | Problem Size | WOA | IWOA | GAP3 (%) | ||
|---|---|---|---|---|---|---|
| T × Y × Q × A * | OFV (s) | Time (s) | OFV (s) | Time (s) | ||
| 1 | 25 × 2 × 2 × 5 | 1211 | 17.89 | 1135 | 18.46 | 6.27% |
| 2 | 25 × 2 × 3 × 5 | 1189 | 18.56 | 1101 | 19.35 | 7.40% |
| 3 | 35 × 2 × 3 × 5 | 1547 | 22.48 | 1456 | 24.41 | 5.88% |
| 4 | 35 × 2 × 4 × 7 | 1382 | 24.96 | 1296 | 26.04 | 6.22% |
| 5 | 45 × 3 × 3 × 7 | 1780 | 28.01 | 1691 | 30.12 | 5.00% |
| 6 | 45 × 3 × 4 × 8 | 1621 | 32.19 | 1562 | 34.01 | 3.64% |
| 7 | 55 × 3 × 2 × 9 | 1819 | 35.86 | 1688 | 38.16 | 7.29% |
| 8 | 55 × 3 × 3 × 10 | 1774 | 37.47 | 1629 | 39.98 | 8.17% |
| 9 | 65 × 3 × 4 × 10 | 1877 | 40.28 | 1778 | 43.65 | 5.27% |
| 10 | 65 × 3 × 3 × 11 | 1846 | 40.79 | 1697 | 44.01 | 8.06% |
| 11 | 75 × 4 × 3 × 11 | 1902 | 43.64 | 1765 | 47.23 | 7.20% |
| 12 | 75 × 4 × 4 × 12 | 1873 | 45.92 | 1726 | 49.08 | 7.79% |
| 13 | 85 × 4 × 3 × 12 | 2214 | 51.79 | 2113 | 56.19 | 4.56% |
| 14 | 85 × 4 × 4 × 13 | 2187 | 53.48 | 2028 | 58.74 | 7.27% |
| 15 | 100 × 4 × 4 × 13 | 2550 | 58.67 | 2314 | 72.42 | 9.25% |
| No. | Problem Size | GA | GWO | PSO | IWOA | ||||
|---|---|---|---|---|---|---|---|---|---|
| T × Y × Q × A * | OFV (s) | Time (s) | OFV (s) | Time (s) | OFV (s) | Time (s) | OFV (s) | Time (s) | |
| 1 | 30 × 3 × 4 × 6 | 1185 | 19.87 | 1130 | 18.69 | 1086 | 20.85 | 982 | 22.02 |
| 2 | 30 × 4 × 4 × 6 | 1078 | 21.11 | 1096 | 20.06 | 1102 | 21.08 | 950 | 23.67 |
| 3 | 40 × 3 × 4 × 7 | 1347 | 23.15 | 1392 | 23.78 | 1335 | 24.12 | 1194 | 27.18 |
| 4 | 40 × 4 × 4 × 7 | 1201 | 23.94 | 1229 | 24.81 | 1198 | 24.76 | 1129 | 28.44 |
| 5 | 50 × 3 × 4 × 8 | 1577 | 26.89 | 1478 | 29.08 | 1553 | 28.17 | 1342 | 34.75 |
| 6 | 50 × 4 × 4 × 8 | 1469 | 34.02 | 1401 | 34.87 | 1478 | 35.93 | 1297 | 39.96. |
| 7 | 60 × 3 × 4 × 9 | 1784 | 37.09 | 1765 | 38.46 | 1806 | 36.58 | 1649 | 42.07 |
| 8 | 60 × 4 × 4 × 9 | 1602 | 38.84 | 1649 | 40.16 | 1686 | 38.02 | 1564 | 45.89 |
| 9 | 70 × 3 × 4 × 10 | 1994 | 42.14 | 2005 | 41.89 | 2019 | 40.48 | 1836 | 47.98 |
| 10 | 70 × 4 × 4 × 10 | 1735 | 43.75 | 1806 | 43.88 | 1785 | 41.79 | 1642 | 50.74 |
| 11 | 80 × 3 × 4 × 11 | 2311 | 48.52 | 2208 | 49.61 | 2324 | 45.86 | 1994 | 54.72 |
| 12 | 80 × 4 × 4 × 11 | 2158 | 50.83 | 1989 | 50.37 | 2206 | 49.66 | 1798 | 56.29 |
| 13 | 90 × 3 × 4 × 12 | 2499 | 53.98 | 2485 | 54.26 | 2456 | 53.01 | 2256 | 60.87 |
| 14 | 90 × 4 × 4 × 12 | 2258 | 57.29 | 2179 | 58.84 | 2207 | 56.08 | 2046 | 64.02 |
| 15 | 100 × 4 × 4 × 13 | 2598 | 63.96 | 2622 | 62.95 | 2561 | 63.86 | 2314 | 72.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, S.; Lou, P.; Hu, J.; Zeng, Y.; Fan, C. An Improved Whale Optimization Algorithm for the Integrated Scheduling of Automated Guided Vehicles and Yard Cranes. Mathematics 2025, 13, 340. https://doi.org/10.3390/math13030340
Gong S, Lou P, Hu J, Zeng Y, Fan C. An Improved Whale Optimization Algorithm for the Integrated Scheduling of Automated Guided Vehicles and Yard Cranes. Mathematics. 2025; 13(3):340. https://doi.org/10.3390/math13030340
Chicago/Turabian StyleGong, Shuaishuai, Ping Lou, Jianmin Hu, Yuhang Zeng, and Chuannian Fan. 2025. "An Improved Whale Optimization Algorithm for the Integrated Scheduling of Automated Guided Vehicles and Yard Cranes" Mathematics 13, no. 3: 340. https://doi.org/10.3390/math13030340
APA StyleGong, S., Lou, P., Hu, J., Zeng, Y., & Fan, C. (2025). An Improved Whale Optimization Algorithm for the Integrated Scheduling of Automated Guided Vehicles and Yard Cranes. Mathematics, 13(3), 340. https://doi.org/10.3390/math13030340







