Rank-Based Copula-Adjusted Mann–Kendall (R-CaMK)—A Copula–Vine Framework for Trend Detection and Sensor Selection in Spatially Dependent Environmental Networks
Abstract
1. Introduction
2. Literature Review
3. Data—Simulated and Real
3.1. Simulated Data—Full Protocol
- Number of sites (n = 8) for simulation experiments (so results generalise with the seven NSW sites).
- Time length (T = 80) (comparable to real data).
- Marginal parameters drawn from a small set {0, 0.2, 0.5} to reflect weak-to-moderate persistence.
- chosen to produce realistic annual maxima variability, draw once per scenario as σbase × LogNormal(sdlog = 0.25), with σbase = 1.0 (seeded).
- Vine copula structures drawn from families that permit tail dependence (Student-t and Clayton) to emulate hydrological extremes for some scenarios; the Gaussian copula is used in other scenarios.
- This modular generator preserves marginal behaviour and allows controlled exploration of dependence effects on MK inference and selection.
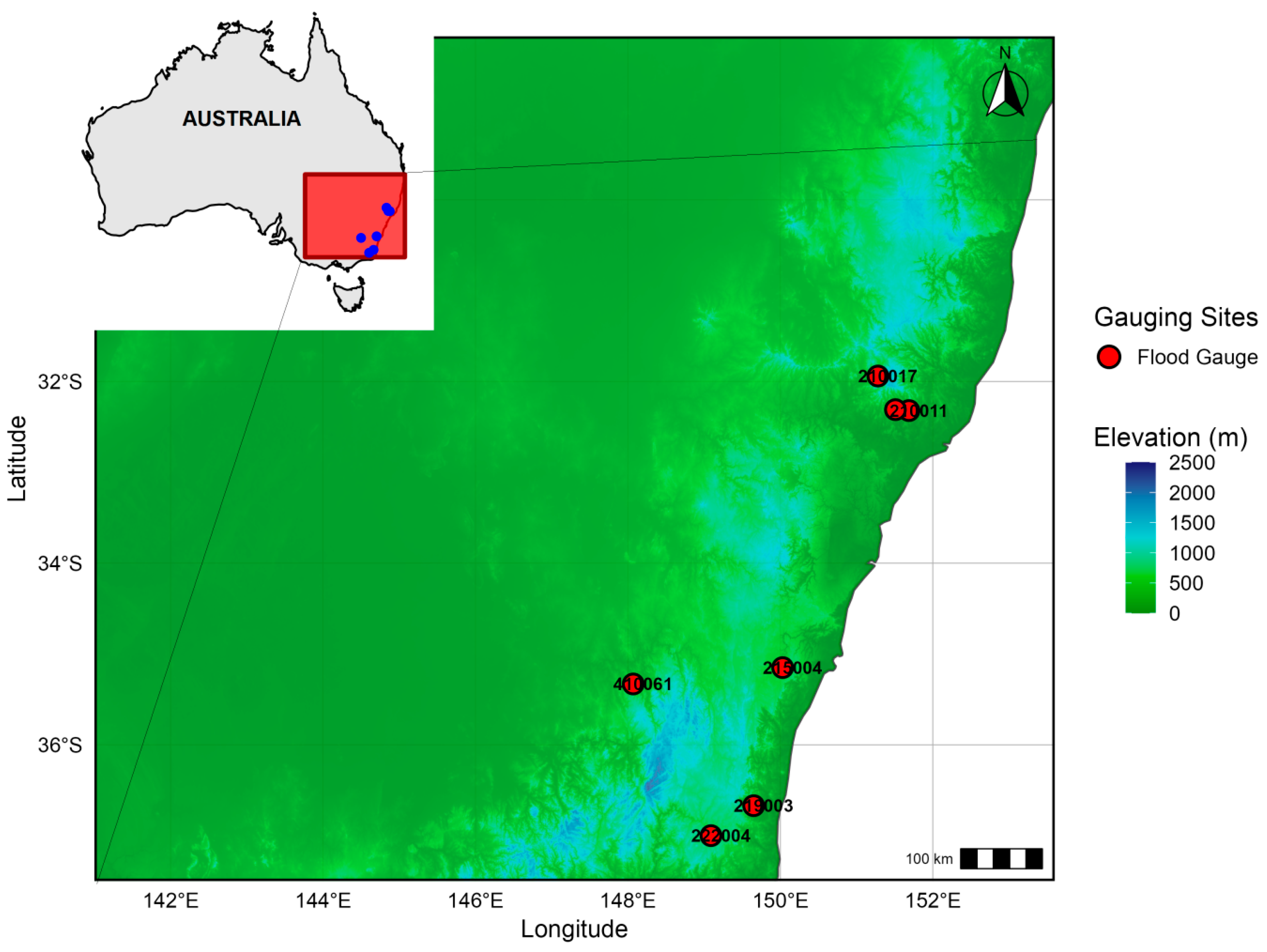
3.2. Real Data—New South Wales (NSW) Gauging Sites
4. Methodology—Mathematical Framework
4.1. Mann–Kendall S as a U-Statistic and Hájek Projection
4.2. Detrending and Marginal Temporal Modelling
4.2.1. Detrending
4.2.2. Marginal Temporal Dependence: AR(1) Fit
4.2.3. Variance Inflation and Effective Sample Size
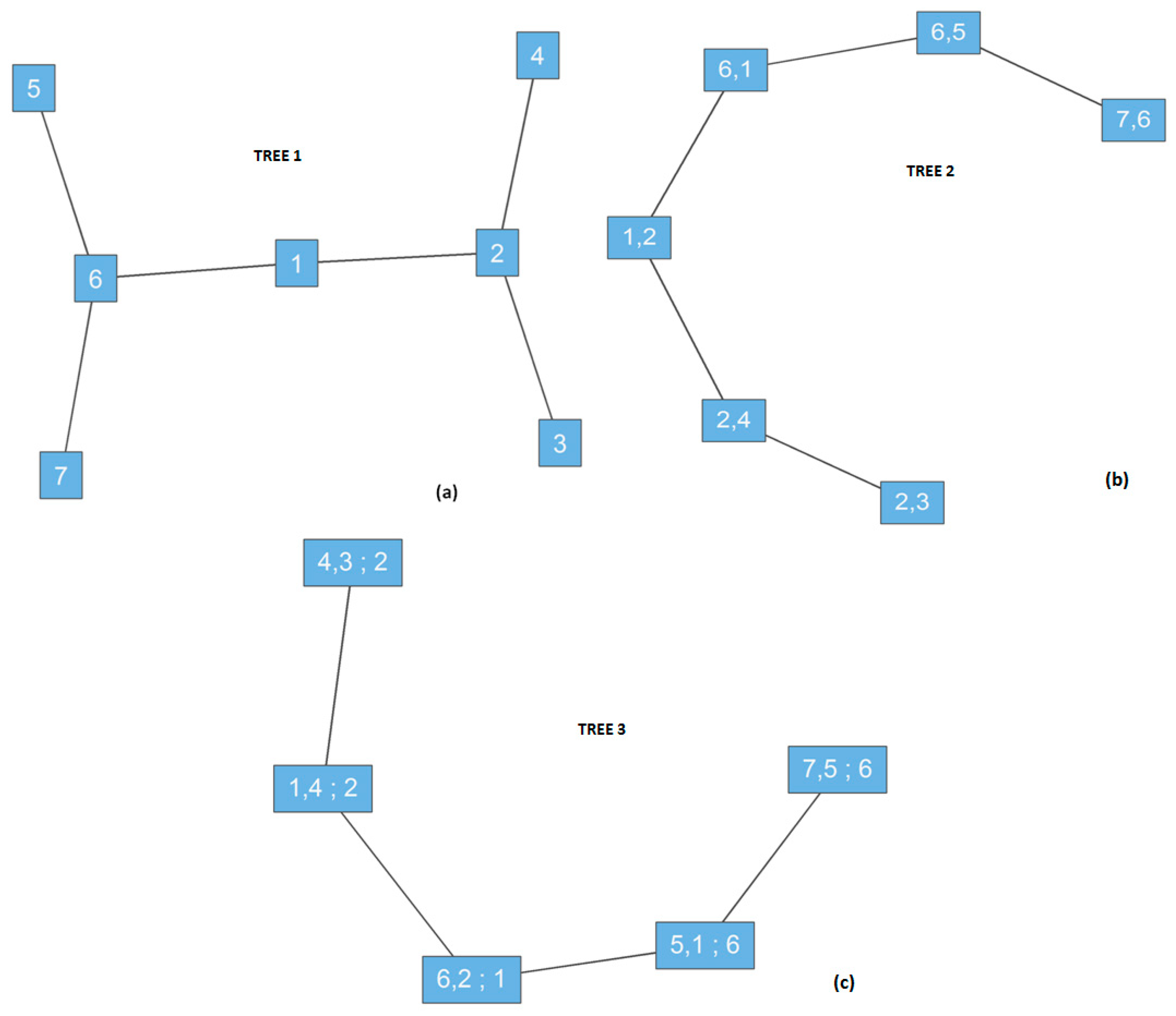
4.3. Rank Transforms and Copula/Vine Modelling of Cross-Site Dependence
4.4. Parametric Spatial Bootstrap for Var(Sj) and Empirical p-Values
- Simulate independent uniforms from (if vine implement RVineSim; if Gaussian, sample and set .
- Convert to Gaussian scores .
- Form innovations .
- Simulate AR(1) margins under null trend:
- Apply the observed missing mask Mt: set simulated values to NA where observed data are NA.
- Compute on the masked replicate using the same detrending and ranking code as for the observed series.
4.5. Detection Score and Integer Linear Programming (ILP) Sensor Selection
4.5.1. Detection Score
4.5.2. ILP Formulation
5. Results and Discussion
5.1. Overview and Organisation of Results
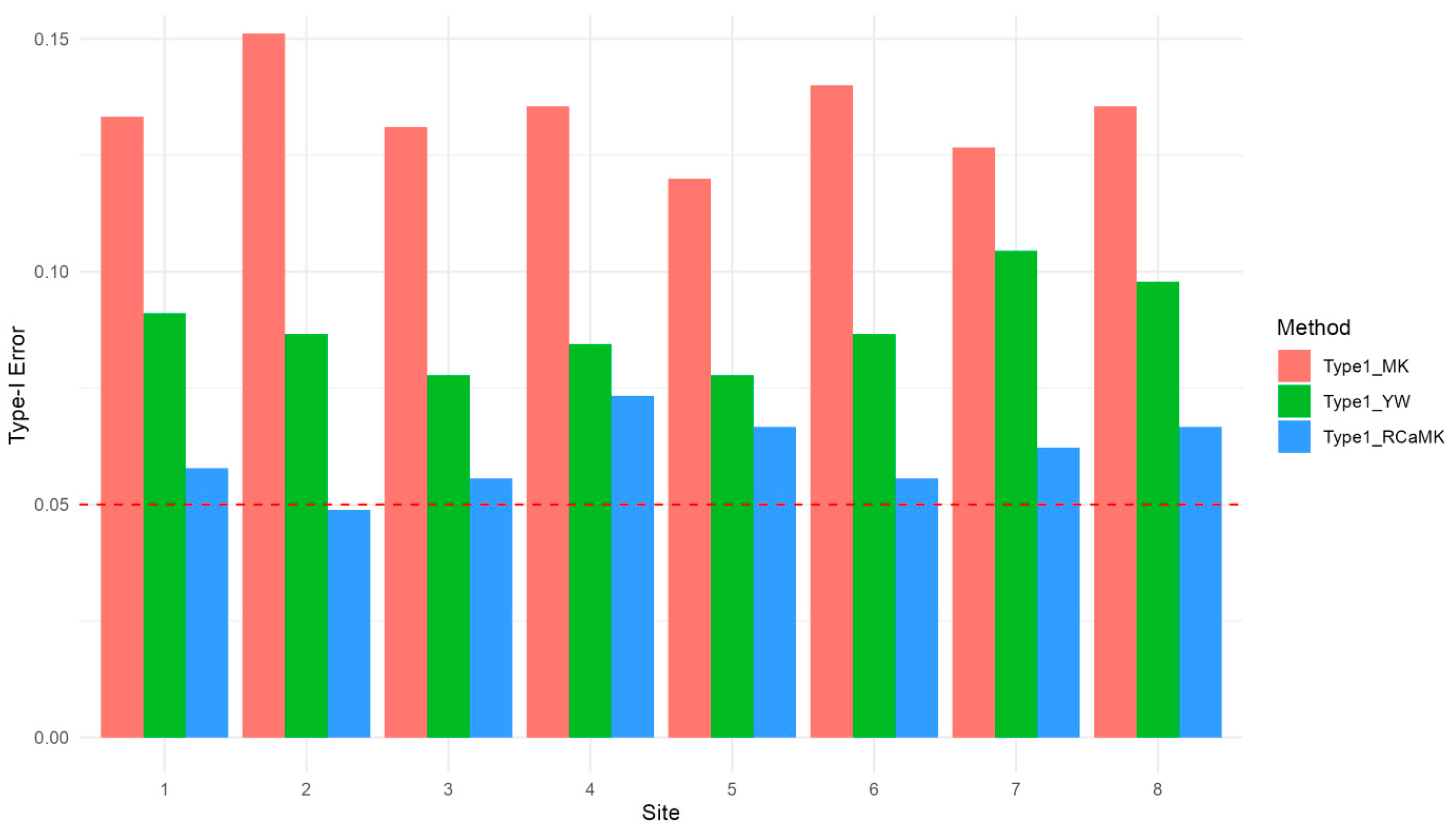
5.2. Simulation Experiments—Type-I Control
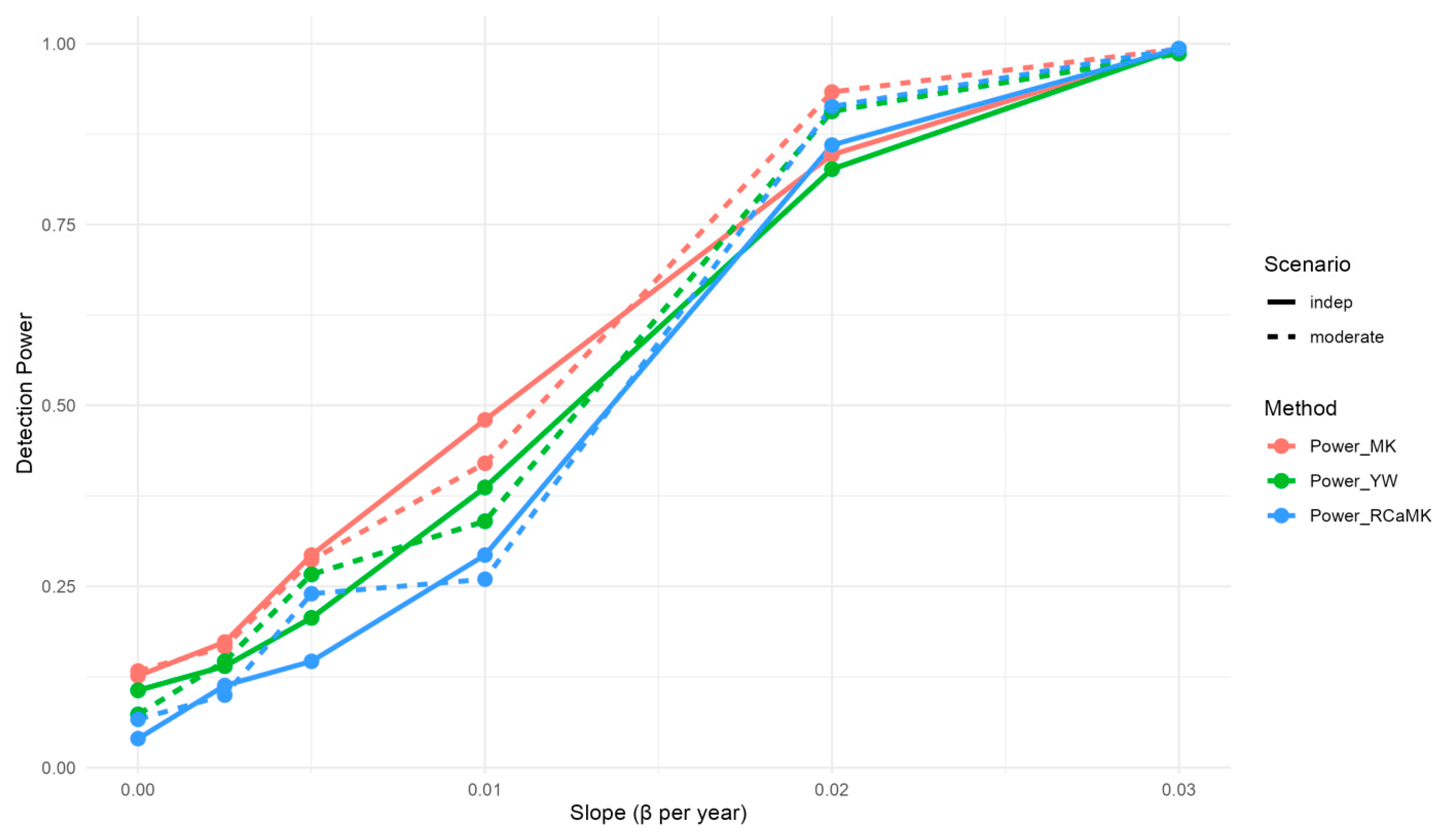
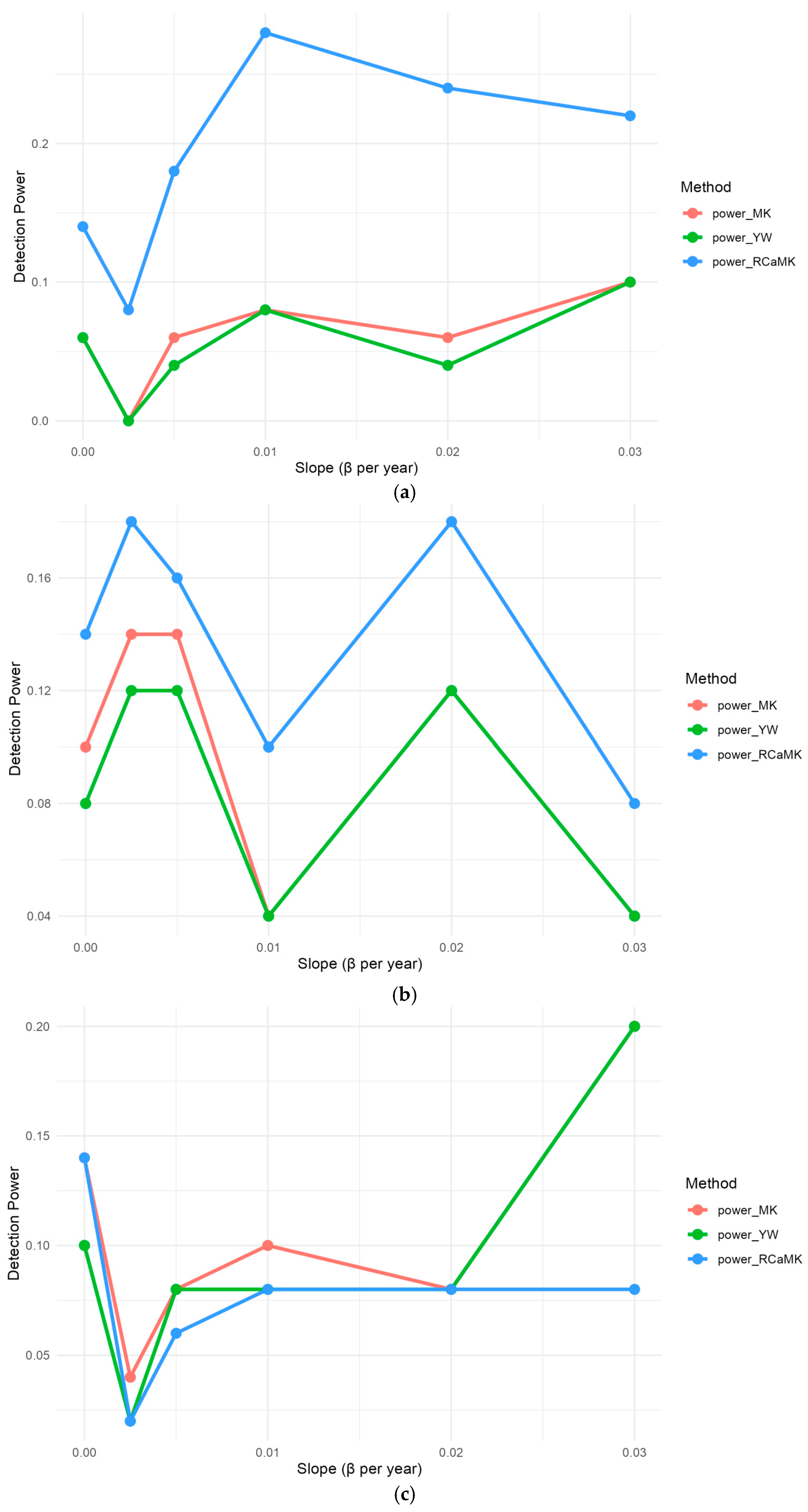
5.3. Simulation Experiments—Empirical Power
5.4. Implications for Hydrological Inference
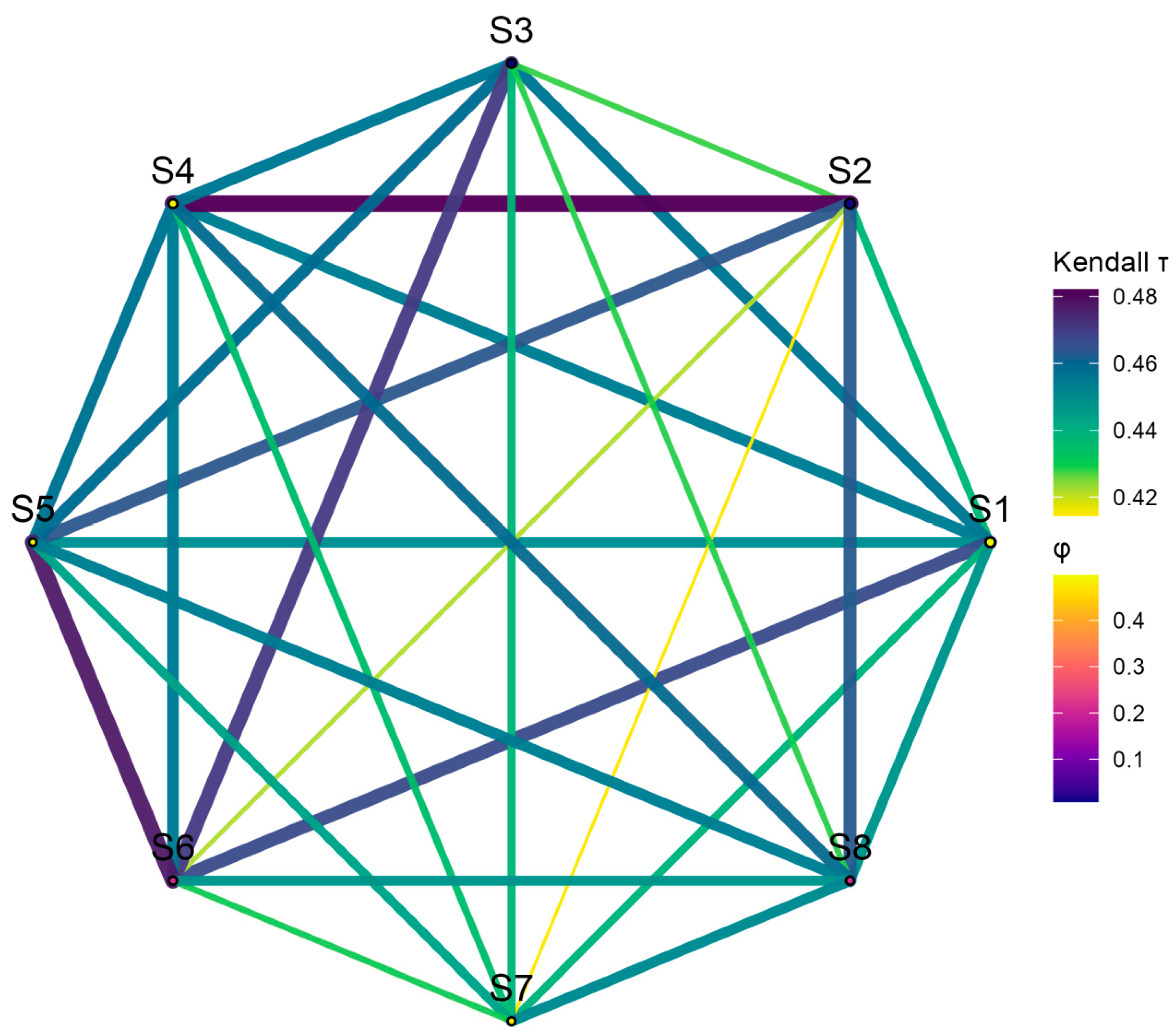
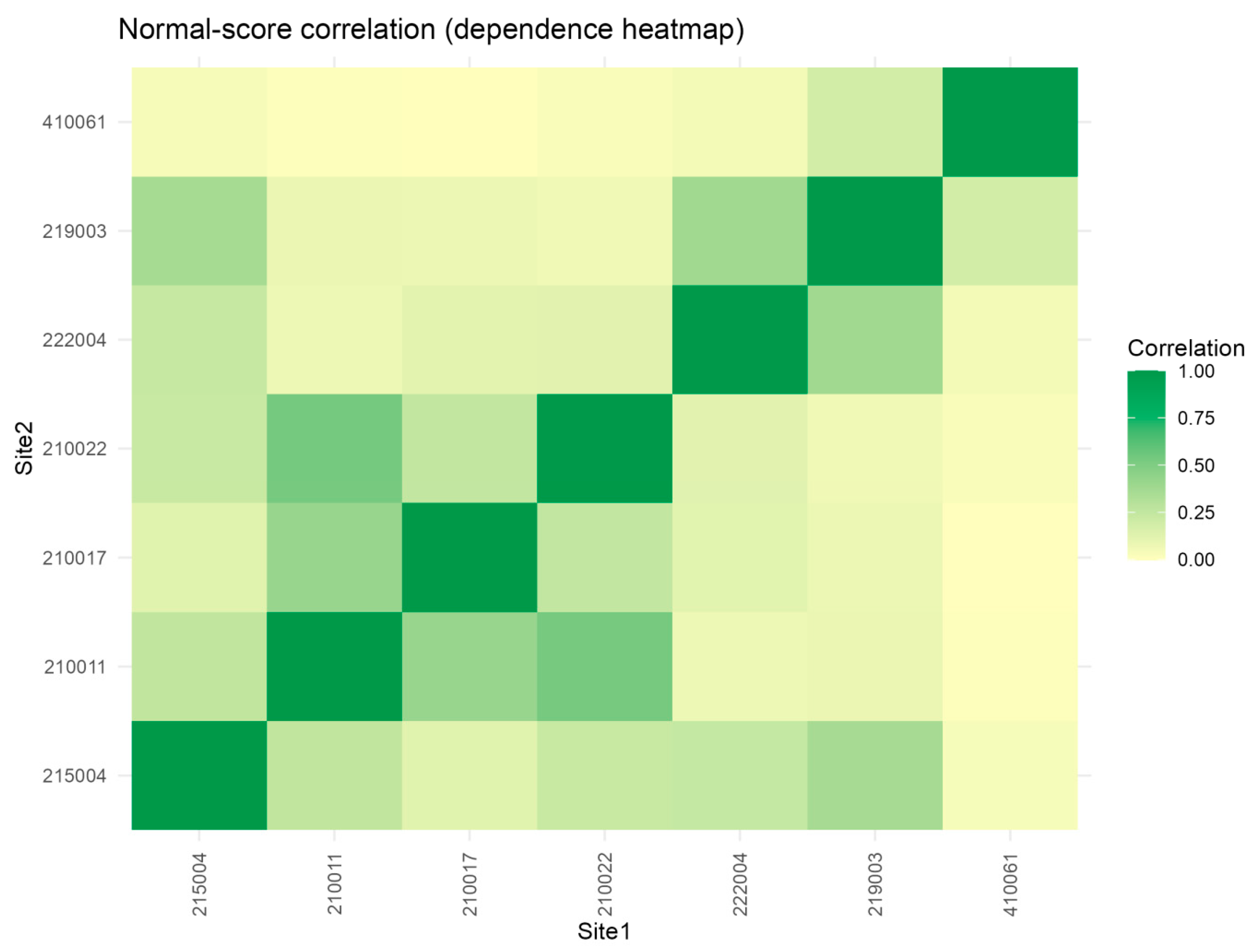
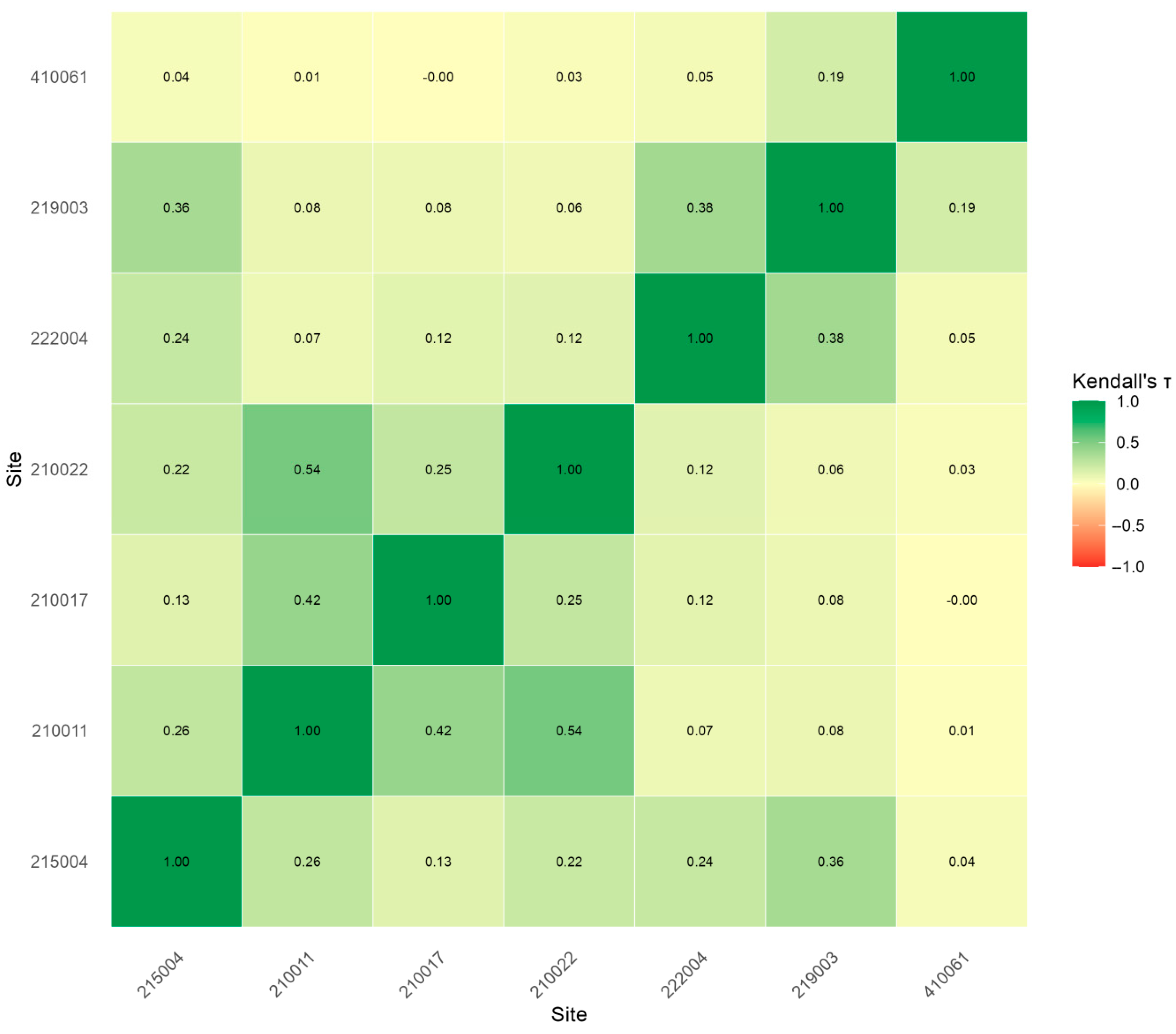
5.5. NSW Empirical Application—Per-Site Inference and Dependence Structure
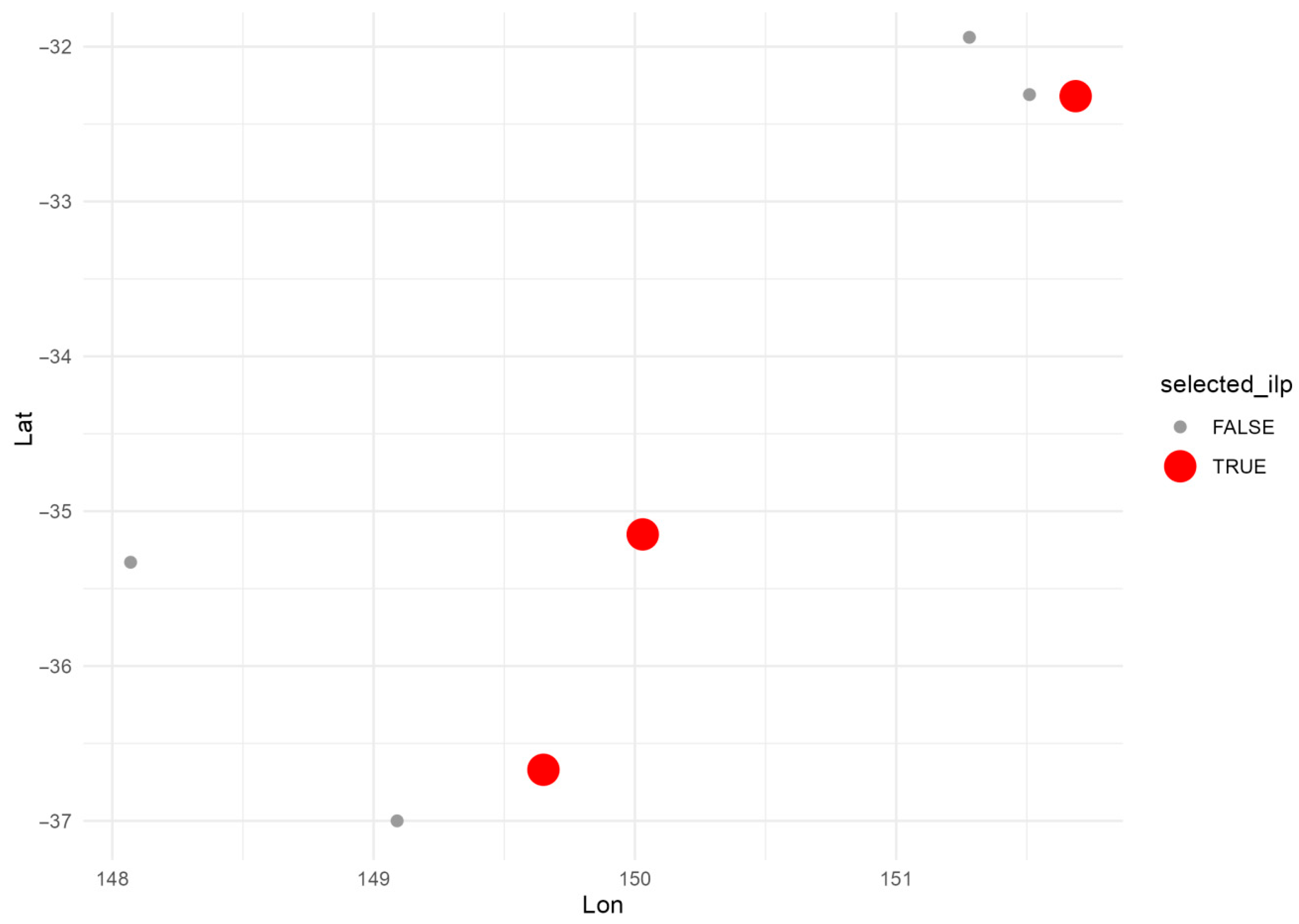
5.6. Sensor Selection—ILP Insights and Robustness
- Site 219003 (wj = 0.00797): largest absolute slope (β = −1.63), moderate variance, yielding the highest individual score.
- Site 210022 (wj = 0.00504): strong positive trend (β = 1.31), providing contrast to negative-trend sites.
- Site 215004 (wj = 0.00270): second-largest negative slope (β = −0.86), geographically distinct from 219003.
5.7. Limitations and Practical Recommendations
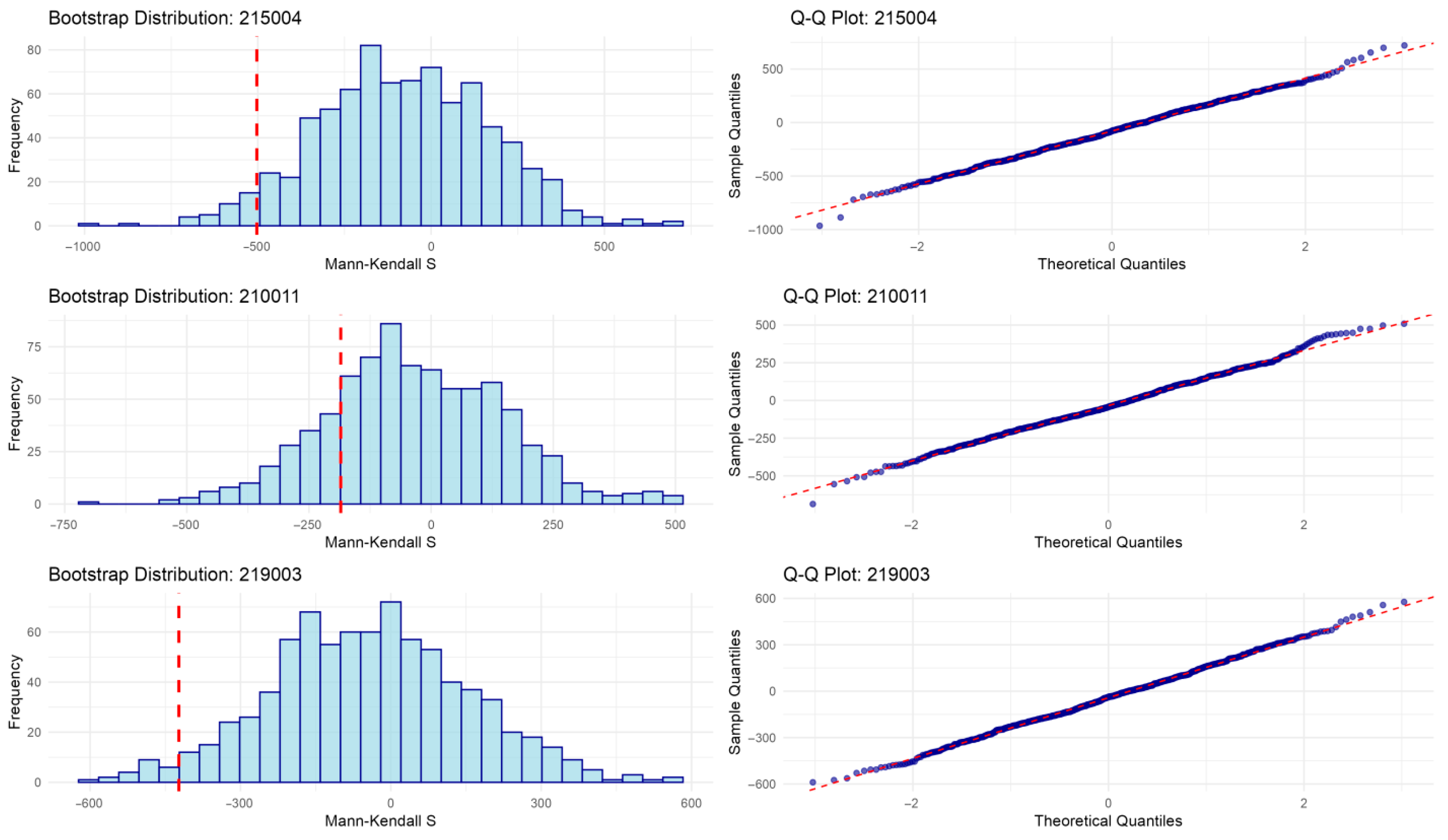
- Conduct bootstrap diagnostics (Figure 8) to verify approximate normality of S under the null; severe departures signal model mis-specification (e.g., non-Gaussian margins and non-stationary dependence).
- Use ILP sensor selection (Figure 9) when budgets constrain monitoring—maximising wj ensures efficient allocation of resources to high-information sites.
- Report both p_emp and p_MK (Table 6a,b) to quantify dependence-adjustment magnitude; large discrepancies indicate strong spatial coupling requiring copula-based inference.
5.8. Implications for Management and Adaptation
6. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
References
- Ishak, E.H.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Evaluating the non-stationarity of Australian annual maximum flood. J. Hydrol. 2013, 494, 134–145. [Google Scholar] [CrossRef]
- Ishak, E.; Rahman, A. Detection of changes in flood data in Victoria, Australia from 1975 to 2011. Hydrol. Res. 2015, 46, 763–776. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Griffin: Williamstown, MA, USA, 1976. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Kimuya, A.M.; Kinyua, D.M.; Memeu, D.M. Development of integrated machine learning model for estimation of spatial distribution of particulate matter pollutant in air. Environ. Res. Commun. 2025, 7, 085020. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Bedford, T.; Cooke, R.M. Probability density decomposition for conditionally dependent random variables modeled by vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Czado, C.; Nagler, T. Vine copula based modeling. Annu. Rev. Stat. Its Appl. 2022, 9, 453–477. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Gürbüz, F.; İspirli, M.N. Multivariate modeling of flood characteristics using Vine copulas. Environ. Earth Sci. 2020, 79, 459. [Google Scholar] [CrossRef]
- Mollaienia, M.R.; Mousavi, Z.A.; Mohammadi, M. Flood modeling in the Qarasu River catchment using four-dimensional vine copulas. J. Clim. Res. 2024, 1403, 101–118. [Google Scholar]
- Zhao, F.; Yi, P.; Wang, Y.; Wan, X.; Wang, S.; Song, C.; Xue, Y. Trivariate Frequency Analysis of Extreme Sediment Events of Compound Floods Based on Vine Copula: A Case Study of the Middle Yellow River in China. J. Hydrol. Eng. 2025, 30, 05024027. [Google Scholar] [CrossRef]
- Czado, C. Analyzing Dependent Data with Vine Copulas; Lecture Notes in Statistics; Springer: Cham, Switzerland, 2019; p. 222. [Google Scholar]
- Brechmann, E.C.; Schepsmeier, U. Modeling dependence with C-and D-vine copulas: The R package CDVine. J. Stat. Softw. 2013, 52, 1–27. [Google Scholar] [CrossRef]
- Chebana, F. Multivariate Frequency Analysis of Hydro-Meteorological Variables: A Copula-Based Approach; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Lai, W.C.; Goh, K.L. Copulas and tail dependence in finance. In Handbook of Financial Econometrics, Mathematics, Statistics, and Machine Learning; World Scientific Publishing: Singapore, 2021; pp. 2499–2524. [Google Scholar]
- Dewick, P.R.; Liu, S. Copula modelling to analyse financial data. J. Risk Financ. Manag. 2022, 15, 104. [Google Scholar] [CrossRef]
- Yang, J.; Yao, J. Estimation of multivariate design quantiles for drought characteristics using joint return period analysis, Vine copulas, and the systematic sampling method. J. Water Clim. Change 2023, 14, 1551–1568. [Google Scholar] [CrossRef]
- Pouliasis, G.; Torres-Alves, G.A.; Morales-Napoles, O. Stochastic modeling of hydroclimatic processes using vine copulas. Water 2021, 13, 2156. [Google Scholar] [CrossRef]
- Gontara, E.; Chebana, F. Mixture copula parameter estimation with metaheuristic algorithms, comparative study under hydrological context. Stoch. Environ. Res. Risk Assess. 2025, 39, 1307–1326. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Review of dependence modeling in hydrology and water resources. Prog. Phys. Geogr. 2016, 40, 549–578. [Google Scholar] [CrossRef]
- Xu, P.; Wang, D.; Wang, Y.; Singh, V.P. A stepwise and dynamic c-vine copula–based approach for nonstationary monthly streamflow forecasts. J. Hydrol. Eng. 2022, 27, 04021043. [Google Scholar] [CrossRef]
- Duan, H.; Yu, J.; Wei, L. Measurement and Forecasting of Systemic Risk: A Vine Copula Grouped-CoES Approach. Mathematics 2024, 12, 1233. [Google Scholar] [CrossRef]
- Acar, E.F.; Czado, C.; Lysy, M. Flexible dynamic vine copula models for multivariate time series data. Econom. Stat. 2019, 12, 181–197. [Google Scholar] [CrossRef]
- Zhao, Z.; Shi, P.; Zhang, Z. Modeling multivariate time series with copula-linked univariate d-vines. J. Bus. Econ. Stat. 2022, 40, 690–704. [Google Scholar] [CrossRef]
- Xiong, X.; Cribben, I. Beyond linear dynamic functional connectivity: A vine copula change point model. J. Comput. Graph. Stat. 2023, 32, 853–872. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1993. [Google Scholar]
- van der Vaart, A.W. Asymptotic Statistics; Cambridge Series in Statistical and Probabilistic Mathematics 3; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Kvam, P.; Vidakovic, B.; Kim, S.J. Nonparametric Statistics with Applications to Science and Engineering with R; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Jiang, Y.; Liu, C.; Zhang, H. Finite sample valid inference via calibrated bootstrap. arXiv 2024, arXiv:2408.16763. [Google Scholar] [CrossRef]
- Prates, M.O.; Azevedo, D.R.; MacNab, Y.C.; Willig, M.R. Non-separable spatio-temporal models via transformed multivariate Gaussian Markov random fields. J. R. Stat. Soc. Ser. C Appl. Stat. 2022, 71, 1116–1136. [Google Scholar] [CrossRef]
- Xu, K.; Wikle, C.K. Estimation of parameterized spatio-temporal dynamic models. J. Stat. Plan. Inference 2007, 137, 567–588. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Y.; Phoon, K.K. Non-parametric modelling and simulation of spatiotemporally varying geo-data. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 77–97. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Xue, F. A review of Bayesian spatiotemporal models in spatial epidemiology. ISPRS Int. J. Geo-Inf. 2024, 13, 97. [Google Scholar] [CrossRef]
- Healy, D.; Tawn, J.; Thorne, P.; Parnell, A. Inference for extreme spatial temperature events in a changing climate with application to Ireland. J. R. Stat. Soc. Ser. C Appl. Stat. 2025, 74, 275–299. [Google Scholar] [CrossRef]
- Krause, A.; Singh, A.; Guestrin, C. Near-optimal sensor placements in Gaussian processes: Theory, efficient algorithms and empirical studies. J. Mach. Learn. Res. 2008, 9, 235–284. [Google Scholar]
- Calamita, A. Location Problems with Covering Constraints: Models and Solution Approaches for the Telecommunications. Doctoral Thesis, Sapienza University of Rome, Rome, Italy, 2024. [Google Scholar]
- Silva, C.A.; Wilcamango-Salas, R.; Melo, J.D.; López-Lezama, J.M.; Muñoz-Galeano, N. Optimal Placement of Wireless Smart Concentrators in Power Distribution Networks Using a Metaheuristic Approach. Energies 2025, 18, 4604. [Google Scholar] [CrossRef]
- Vlasenko, I.; Nikolaidis, I.; Stroulia, E. The smart-condo: Optimizing sensor placement for indoor localization. IEEE Trans. Syst. Man Cybern. Syst. 2014, 45, 436–453. [Google Scholar] [CrossRef]
- Renard, B.; Lang, M.; Bois, P.; Dupeyrat, A.; Mestre, O.; Niel, H.; Sauquet, E.; Prudhomme, C.; Parey, S.; Paquet, E.; et al. Regional methods for trend detection: Assessing field significance and regional consistency. Water Resour. Res. 2008, 44, W08419. [Google Scholar] [CrossRef]
- Koldasbayeva, D.; Tregubova, P.; Gasanov, M.; Zaytsev, A.; Petrovskaia, A.; Burnaev, E. Challenges in data-driven geospatial modeling for environmental research and practice. Nat. Commun. 2024, 15, 10700. [Google Scholar] [CrossRef]
- Khosravi, K.; Farooque, A.A.; Karbasi, M.; Ali, M.; Heddam, S.; Faghfouri, A.; Abolfathi, S. Enhanced water quality prediction model using advanced hybridized resampling alternating tree-based and deep learning algorithms. Environ. Sci. Pollut. Res. 2025, 32, 6405–6424. [Google Scholar] [CrossRef]
- Latif, S.; Simonovic, S.P. Parametric Vine copula framework in the trivariate probability analysis of compound flooding events. Water 2022, 14, 2214. [Google Scholar] [CrossRef]
- Paprotny, D.; ’t Hart, C.M.P.; Morales-Nápoles, O. Evolution of flood protection levels and flood vulnerability in Europe since 1950 estimated with vine-copula models. Nat. Hazards 2025, 121, 6155–6184. [Google Scholar] [CrossRef]
- Siamaki, M.; Safavi, H.R.; Klaho, M.H. Extraction of intensity-duration for short-term extreme rainfalls from daily and yearly extreme rainfalls using copula functions. Theor. Appl. Climatol. 2024, 155, 5759–5777. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Weinmann, P.E.; Kuczera, G.; Ball, J. Streamflow data preparation for regional flood frequency analysis: Lessons from southeast Australia. Australas. J. Water Resour. 2010, 14, 17–32. [Google Scholar] [CrossRef]
- Rima, L.; Haddad, K.; Rahman, A. Generalised Additive Model-Based Regional Flood Frequency Analysis: Parameter Regression Technique Using Generalised Extreme Value Distribution. Water 2025, 17, 206. [Google Scholar] [CrossRef]
- Afrin, N.; Rahman, A.; Sharafati, A.; Ahamed, F.; Haddad, K. Ensemble machine learning (EML) based regional flood frequency analysis model development and testing for south-east Australia. J. Hydrol. Reg. Stud. 2025, 59, 102320. [Google Scholar] [CrossRef]
- Oorschot, J.; Segers, J.; Zhou, C. Tail inference using extreme U-statistics. Electron. J. Stat. 2023, 17, 1113–1159. [Google Scholar] [CrossRef]
- Bücher, A.; Staud, T. Limit theorems for non-degenerate U-statistics of block maxima for time series. Electron. J. Stat. 2024, 18, 2850–2885. [Google Scholar] [CrossRef]
- Berkelaar, M.; Eikland, K.; Notebaert, P. Open Source (Mixed-Integer) Linear Programming System Software, Version 5.5; lpsolve: San Diego, CA, USA, 2004.
- Cheng, T.; Vatter, T.; Nagler, T.; Chen, K. Vine Copulas as Differentiable Computational Graphs. arXiv 2025, arXiv:2506.13318. [Google Scholar] [CrossRef]
| Scenario | n Sites | T (Years) | AR(1) φ Values | Kendall’s τ Range | Slope Grid (βj) | MC Reps |
|---|---|---|---|---|---|---|
| 1 | 8 | 80 | {0, 0.2, 0.5} | 0.0 (indep.) | {0} | 2000 |
| 2 | 8 | 80 | {0, 0.2, 0.5} | 0.1–0.3 | {0} | 2000 |
| 3 | 8 | 80 | {0, 0.2, 0.5} | 0.4–0.6 | {0} | 2000 |
| 4 | 8 | 80 | {0, 0.2, 0.5} | 0.7–0.9 | {0} | 2000 |
| 5 | 8 | 80 | {0, 0.2, 0.5} | 0.0–0.9 | subset with βj ≠ 0 (e.g., ±0.01 ±0.02 per year) | 1000 |
| Site ID | Latitude (°) | Longitude (°) | T (Years) | Catchment Remarks |
|---|---|---|---|---|
| 215004 | −35.15 | 150.03 | 89 | Coastal/Upper Catchment |
| 210011 | −32.32 | 151.6867 | 87 | Coastal Plain |
| 210017 | −31.94 | 151.28 | 78 | Coastal/Small Catchment |
| 210022 | −32.31 | 151.51 | 78 | Coastal/Near Headwaters |
| 222004 | −37 | 149.09 | 77 | Southern NSW |
| 219003 | −36.67 | 149.65 | 75 | Inland River Basin |
| 410061 | −35.33 | 148.07 | 71 | Upland River Basin |
| Site ID | Mean (m3/s) | Std Dev (m3/s) | Skewness | CV (Std Dev/Mean) |
|---|---|---|---|---|
| 215004 | 183.15 | 151.62 | 1.75 | 0.83 |
| 210011 | 346.32 | 309.9 | 1.6 | 0.9 |
| 210017 | 23.65 | 26.07 | 2.26 | 1.11 |
| 210022 | 199.1 | 142.78 | 1.26 | 0.72 |
| 222004 | 77.66 | 96.05 | 3.58 | 1.24 |
| 219003 | 242.21 | 276.08 | 2.8 | 1.14 |
| 410061 | 53.99 | 57.72 | 3.14 | 1.07 |
| Site | Type1_MK | Type1_YW | Type1_RCaMK |
|---|---|---|---|
| 1 | 0.133 | 0.091 | 0.058 |
| 2 | 0.151 | 0.087 | 0.049 |
| 3 | 0.131 | 0.078 | 0.056 |
| 4 | 0.136 | 0.084 | 0.073 |
| 5 | 0.12 | 0.078 | 0.067 |
| 6 | 0.14 | 0.087 | 0.056 |
| 7 | 0.127 | 0.104 | 0.062 |
| 8 | 0.136 | 0.098 | 0.067 |
| Scenario | Type-I Error (α = 0.05) | Power (β = 0.02) | Notes |
|---|---|---|---|
| Vine, Tail Families Enabled (Tcc ≥ 30) | 0.05–0.07 | 0.90–0.93 | Nominal control and robust power |
| Vine, Gaussian Only | 0.08–0.12 | 0.80–0.85 | Upward bias under strong/ tail dependence |
| Gaussian Fallback (Tcc < 30) | 0.07–0.09 | 0.70–0.80 | More conservative and reduced power |
| Gaussian Copula w/Matrix Repair | 0.06–0.10 | 0.70–0.80 | No inflation and conservative under repair |
| (a) | |||||||
| SiteID | βOLS | βTS | Sobs | nobs | |||
| 210011 | −0.0082 | 0.6415 | 0.0455 | 316.52 | 205 | 87 | |
| 210017 | −0.2653 | −0.0208 | −0.1137 | 27.52 | −95 | 78 | |
| 210022 | 1.3054 | 1.1516 | 0.1139 | 136.52 | 441 | 78 | |
| 215004 | −0.8552 | −0.6566 | 0.138 | 153.43 | −360 | 89 | |
| 219003 | −1.6253 | −1.1934 | −0.0048 | 266.58 | −369 | 75 | |
| 222004 | −0.3678 | −0.0656 | −0.0909 | 92.28 | −78 | 77 | |
| 410061 | 0.0315 | −0.2916 | −0.0538 | 57.34 | −284 | 71 | |
| (b) | |||||||
| SiteID | VarS_boot | p_emp | p_mk_uncorrected | VIF | n_eff_yuewang | p_yuewang | wj |
| 210011 | 66,221.6 | 0.373 | 0.452 | 1 | 87 | 0.45232 | 0.00003 |
| 210017 | 41,429.1 | 0.667 | 0.682 | 1 | 78 | 0.6819 | 0.0013 |
| 210022 | 67,173.3 | 0.12 | 0.057 | 1 | 78 | 0.05708 | 0.00504 |
| 215004 | 100,279.7 | 0.307 | 0.202 | 1 | 89 | 0.20203 | 0.0027 |
| 219003 | 41,606.7 | 0.08 | 0.091 | 1 | 75 | 0.09143 | 0.00797 |
| 222004 | 43,073.9 | 0.693 | 0.732 | 1 | 77 | 0.73155 | 0.00177 |
| 410061 | 36,089.2 | 0.133 | 0.159 | 1 | 71 | 0.15864 | 0.00017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddad, K. Rank-Based Copula-Adjusted Mann–Kendall (R-CaMK)—A Copula–Vine Framework for Trend Detection and Sensor Selection in Spatially Dependent Environmental Networks. Mathematics 2025, 13, 3762. https://doi.org/10.3390/math13233762
Haddad K. Rank-Based Copula-Adjusted Mann–Kendall (R-CaMK)—A Copula–Vine Framework for Trend Detection and Sensor Selection in Spatially Dependent Environmental Networks. Mathematics. 2025; 13(23):3762. https://doi.org/10.3390/math13233762
Chicago/Turabian StyleHaddad, Khaled. 2025. "Rank-Based Copula-Adjusted Mann–Kendall (R-CaMK)—A Copula–Vine Framework for Trend Detection and Sensor Selection in Spatially Dependent Environmental Networks" Mathematics 13, no. 23: 3762. https://doi.org/10.3390/math13233762
APA StyleHaddad, K. (2025). Rank-Based Copula-Adjusted Mann–Kendall (R-CaMK)—A Copula–Vine Framework for Trend Detection and Sensor Selection in Spatially Dependent Environmental Networks. Mathematics, 13(23), 3762. https://doi.org/10.3390/math13233762




