Optimal Design of Integrated Energy Systems Based on Reliability Assessment
Abstract
1. Introduction
- Stochastic, reliability-driven design workflow: Uncertainty representation, sequential Monte Carlo (MC), cross-domain indices, and a normalized aggregation are linked into a single ranking rule for siting and sizing.
- Compact index for transparent trade-offs: The CRI provides a single, monotone score across planning priorities; lower values indicate better overall reliability and autonomy.
- Reproducible campus-scale case study: The step-by-step procedure and results show how the workflow guides DER siting and sizing toward an improved configuration.
2. Materials and Methods
2.1. Reliability-Driven Design Framework for Small IESs
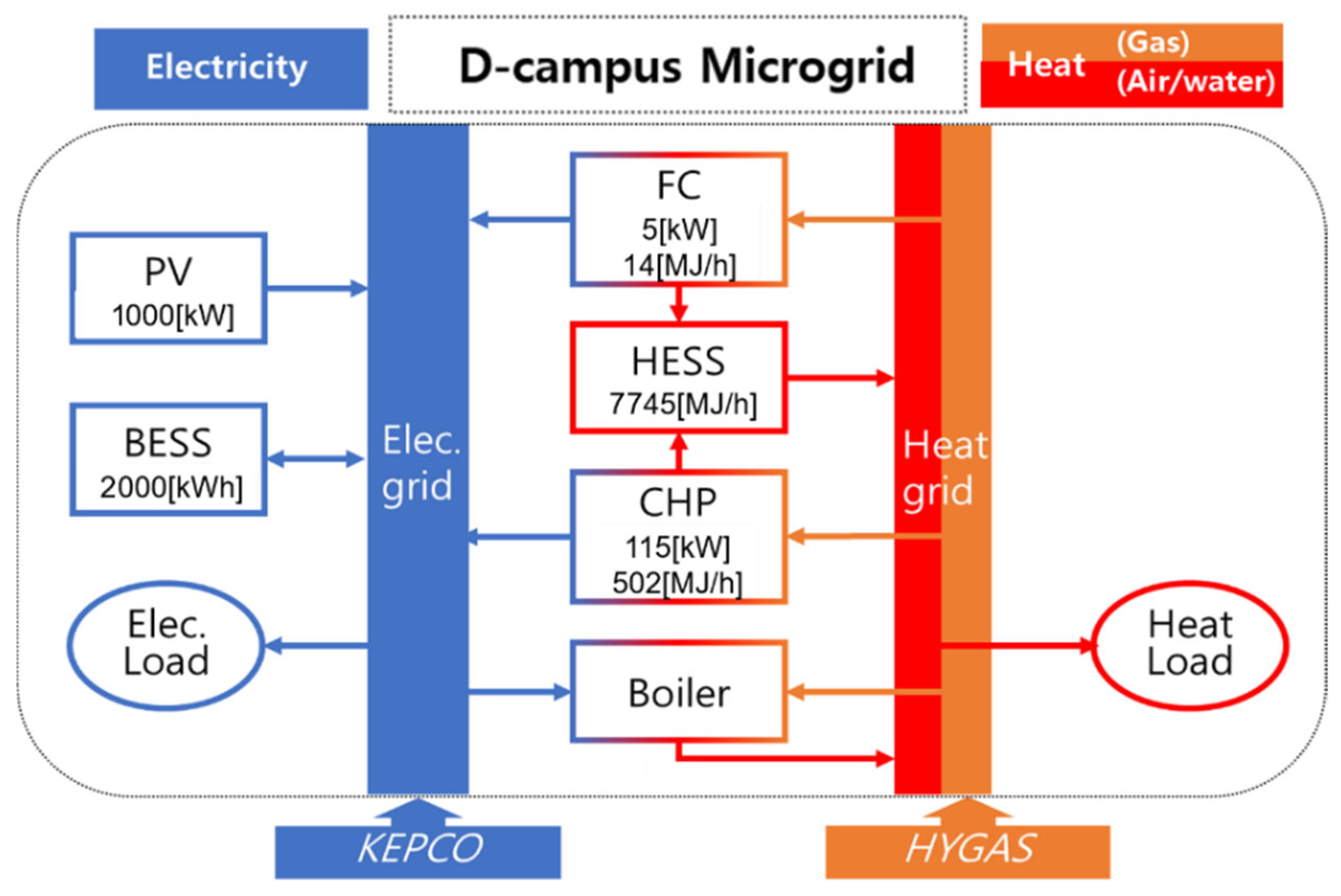
2.1.1. Configuration and Operational Concept of the IES
2.1.2. Probabilistic Reliability Modeling and Metrics Formulation
2.1.3. Mathematical Mapping and Objective
2.2. System Overview and Simulation Setup for Case Study
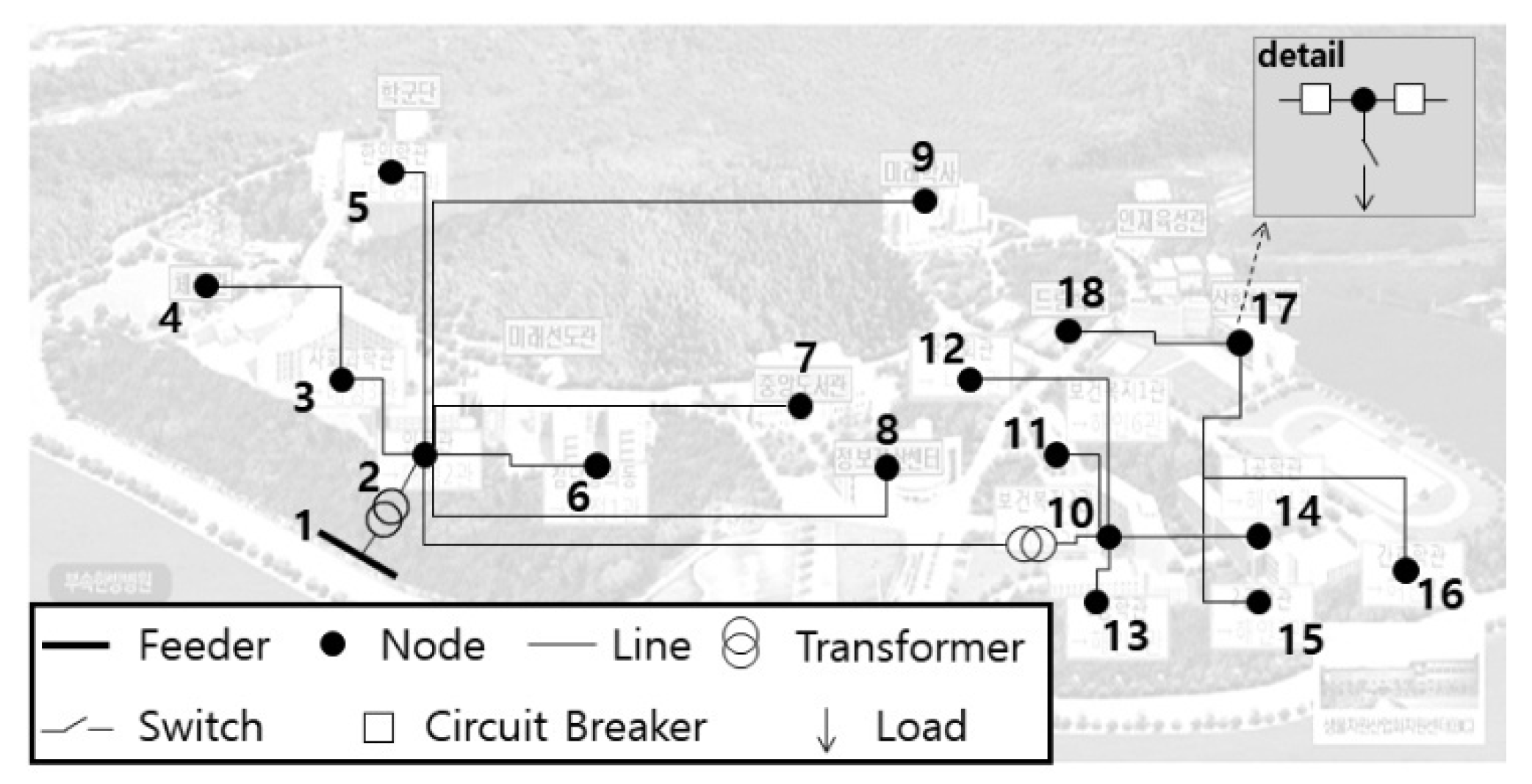
2.2.1. System Description
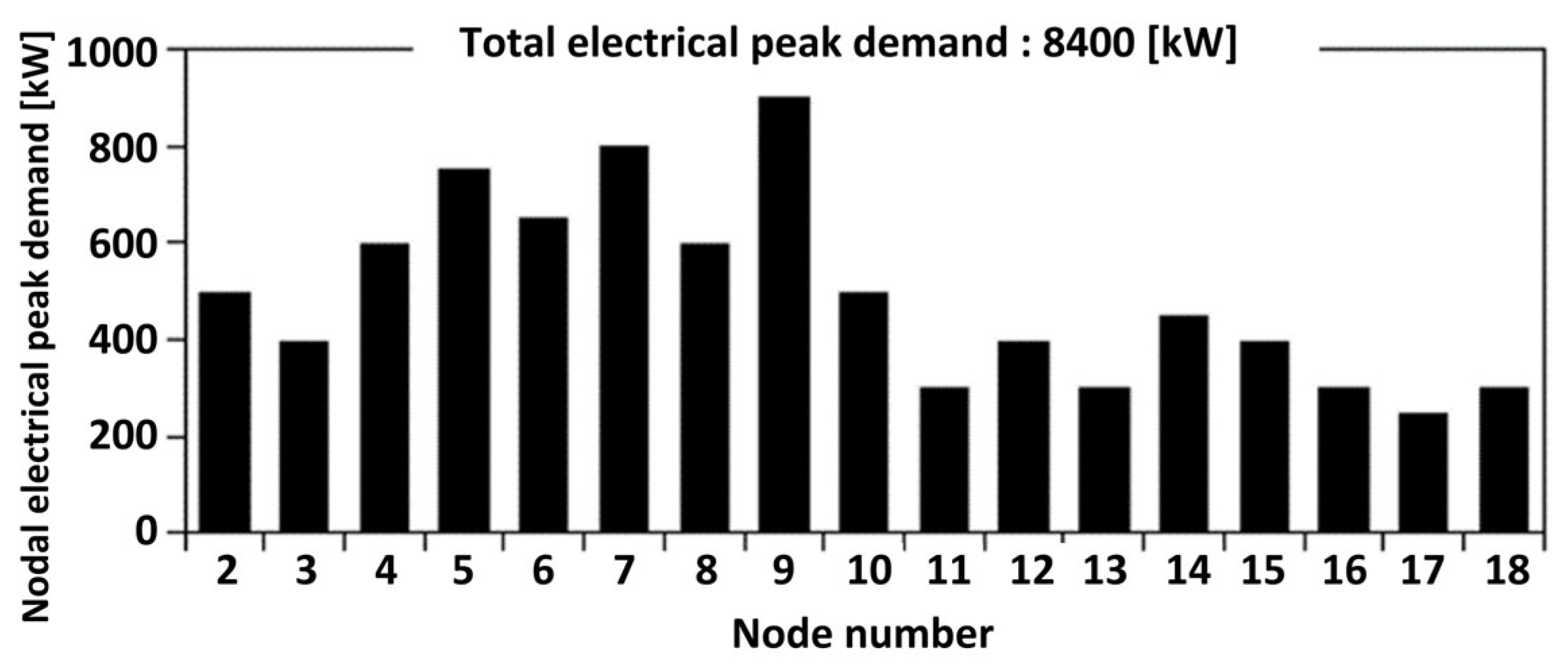
2.2.2. Simulation Conditions for the Reliability Assessment
| Scenario | Electric DERs’ Capacity | Electric DERs’ Location | Heat DERs’ Capacity | Heat DERs’ Location | |||||
|---|---|---|---|---|---|---|---|---|---|
| PV [kWe] | BESS [kWhe] | FC [kWe] | CHP [kWe] | FC [MJt/h] | HESS [MJt] | CHP [MJt/h] | |||
| 1 | 1000 | 2000 | 5 | 115 | Distributed across all nodes (FC, CHP are fixed at Node 17) | 14 | 7745 | 502 | Heat grid near Node 17 |
| 2 | Node 2 | ||||||||
| 3 | Node 17 | ||||||||
| 4 | 300 | 400 | 35 | 800 | Node 2 | - | - | - | |
| 5 | 500 | 1500 | 130 | 3000 | |||||
| 6 | 300 | 400 | 35 | 800 | Node 17 | 5 | 1549 | 3492 | |
| 7 | 500 | 1500 | 130 | 3000 | 7 | 5809 | 13,096 | ||
2.2.3. Reliability Parameters
- Failure Rate : the frequency with which the component experiences failure [failures/year];
- Repair Rate : the frequency of successful repairs [repairs/year];
- Unavailability : the probability of the component being unavailable for operation at any random time [p.u.].
| Component | Failure Rate [Failures/Year] | Repair Rate [Repairs/Year] | Unavailability [p.u.] |
|---|---|---|---|
| Transformer | 0.015 | 200 | 7.5 × 10−5 |
| Circuit Breaker | 0.006 | 50 | 1.2 × 10−4 |
| Switch | 0.001 | 100 | 1.0 × 10−5 |
| Underground Cable | 0.020 | 10 | 2.0 × 10−3 |
| PV | 0.050 | 150 | 3.3 × 10−4 |
| CHP | 0.030 | 100 | 3.0 × 10−4 |
| FC | 0.040 | 120 | 3.3 × 10−4 |
| Gas Boiler | 0.025 | 200 | 1.25 × 10−4 |
| BESS | 0.020 | 250 | 8.0 × 10−5 |
| HESS | 0.010 | 300 | 3.3 × 10−5 |
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IES(s) | Integrated Energy System(s) |
| LOLP | Loss of Load Probability |
| EENS | Expected Energy Not Supplied |
| SSR | Self-Sufficiency Rate |
| CRI | Composite Reliability Index |
| PV | Photovoltaic |
| CHP | Combined Heat and Power |
| BESS | Battery Energy Storage System |
| HESS/TES | Heat (Thermal) Energy Storage (system) |
| EMS | Energy Management System |
| MC | Monte Carlo (simulation) |
| DER | Distributed Energy Resources |
| FC | Fuel Cell |
| LNG | Liquefied Natural Gas |
| TOU | Time-of-Use (tariff) |
| p.u. | per unit |
| DAS | Day-Ahead Scheduling |
| RTS | Real-Time Scheduling |
Appendix A. EMS Operating Modes and Scheduling Logic for the D-Campus IES
Appendix A.1. Tariff Scheme
| Demand Charge | Energy Charge | |
|---|---|---|
| LNG | No charge | Single [$/MJ] |
| Electricity | Single [$/kW] | TOU [$/kWh] |
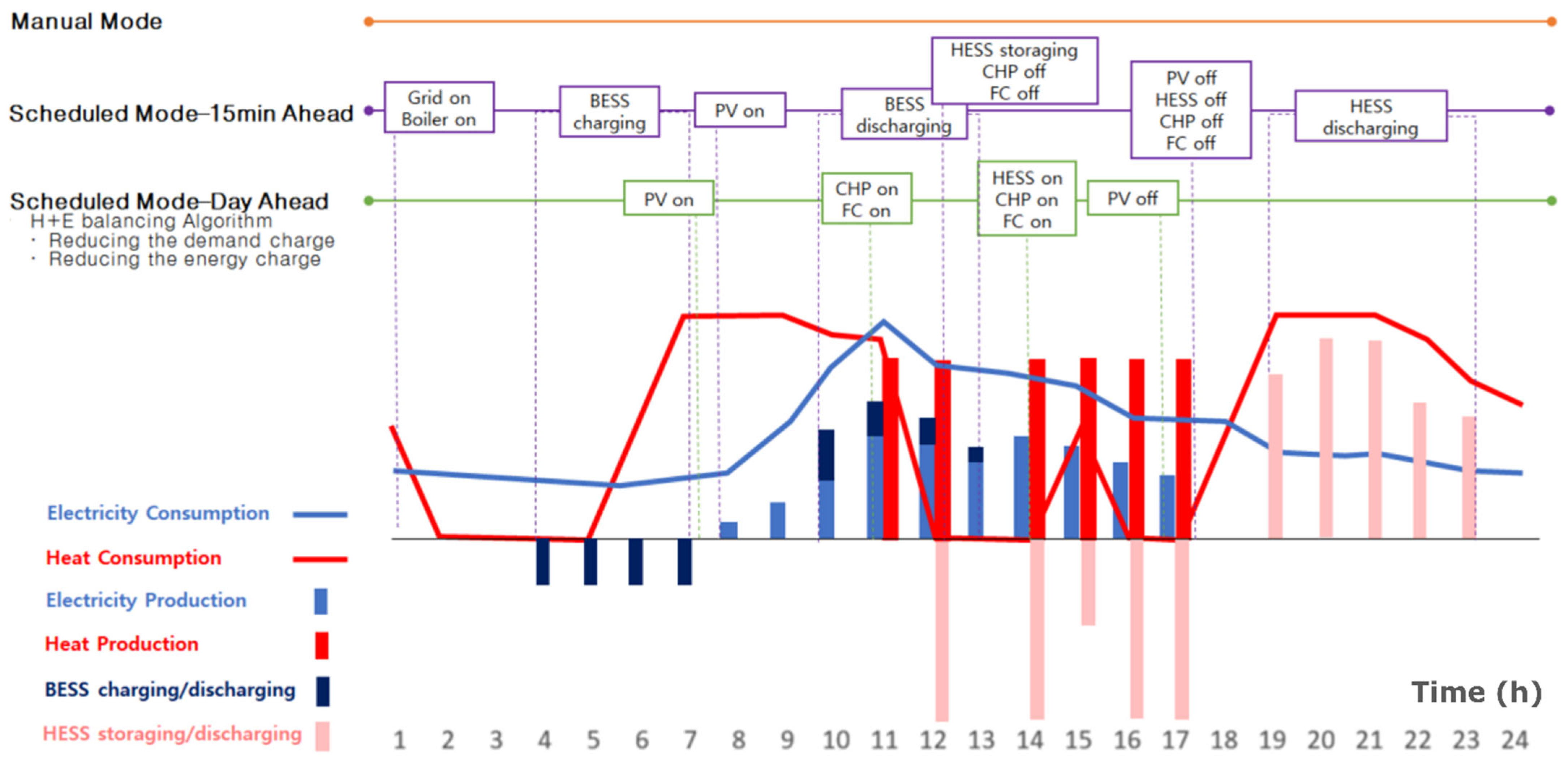
Appendix A.2. EMS Operating Modes
Appendix A.3. Scheduled-Mode Flow in Pseudocode
| Algorithm A1. Peak-Cut Scheduling |
| begin Peak-Cut do determine current net power, heat demand, and device states if net power is greater than peak target then dispatch combined heat and power within limits to reduce net power dispatch fuel cell within limits to reduce net power compute remaining excess over peak target after these dispatches set battery discharge to the minimum of the remaining excess and the available battery capability else set battery discharge to zero and keep generators at feasible baseline end if compute heat produced by combined heat and power and fuel cell if produced heat is greater than heat demand then charge thermal storage within its remaining capacity set boiler heat to zero else if produced heat plus available thermal storage discharge is less than heat demand then discharge thermal storage within limits supply the remaining heat with the gas boiler else discharge thermal storage only as needed and set boiler heat to zero end if compute residual electric demand and set grid import accordingly update battery state of charge and thermal storage state end for end Peak-Cut |
| Algorithm A2. Energy-Conservation Scheduling |
| begin Energy-Conservation identify the set of peak price hours from the time-of-use tariff do belongs to the set of peak price hours then operate combined heat and power in the efficiency region within limits operate fuel cell in the efficiency region within limits discharge battery within power and energy limits discharge thermal storage as available to reduce auxiliary electric heating set battery charge and thermal storage charge to zero else keep generators at feasible baseline within limits if price is low or on-site surplus exists then charge battery within limits else set battery charge to zero end if store surplus cogenerated heat by charging thermal storage within limits set thermal storage discharge to zero end if compute heat from generators and thermal storage set boiler heat to the remaining unmet heat demand, not below zero compute residual electric demand and set grid import accordingly update battery state of charge and thermal storage state end for end Energy-Conservation |
| Algorithm A3. Integration of Peak-Cut and Energy-Conservation |
| begin Integration do combine generator outputs from Peak-Cut and Energy-Conservation to satisfy both objectives combine battery actions to respect power and energy limits and to meet the stricter requirement combine thermal storage actions to satisfy heat balance with minimum boiler use recompute grid import and boiler heat to satisfy final electric and thermal balances enforce all operational constraints including ramp limits and storage bounds end for end Integration |
Appendix B. Monte Carlo Procedure and Reliability Metrics
Appendix B.1. Monte Carlo Procedure
Appendix B.2. Notation
- Demand: ;
- Available on-site supply subject to limits: ;
- Imports subject to limits: ;
- Unmet demand (shortage): .
Appendix B.3. Scenario-Level Metrics
Appendix B.4. Monte Carlo Estimators (Final Indices)
Appendix B.5. Consistency with Main-Text Equations
References
- Lei, Y.; Wang, J.; Wan, C.; Chen, C.; Song, Y. A new reliability assessment approach for integrated energy systems: Using hierarchical decoupling optimization framework and impact-increment based state enumeration method. Appl. Energy 2018, 210, 1237–1250. [Google Scholar] [CrossRef]
- Chen, J.; Yang, Y.; Bie, Z.; Lin, Y.; Li, Z.; Li, G. Fast analytical method for reliability evaluation of electricity-gas integrated energy system considering dispatch strategies. Appl. Energy 2019, 242, 260–272. [Google Scholar] [CrossRef]
- Fu, X.; Bie, Z.; Jiang, Q.; Zhang, C.; Song, Y. Estimating the failure probability in an integrated energy system considering correlations among failure patterns. Energy 2019, 178, 656–666. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, Y.; Sun, H.; Wang, Z. Reliability evaluation of electricity-gas-heat multi-energy consumption based on user experience. Int. J. Electr. Power Energy Syst. 2021, 130, 106926. [Google Scholar] [CrossRef]
- Cao, M.; Tang, Y.; Xue, Y.; Wang, J. Reliability tracing of the integrated energy system using the improved Shapley value. Energy 2022, 260, 124997. [Google Scholar] [CrossRef]
- Wang, S.; Zhai, J.; Hui, H.; Ding, Y.; Song, Y. Operational reliability of integrated energy systems considering gas flow dynamics and demand-side flexibilities. IEEE Trans. Ind. Inform. 2024, 20, 1360–1373. [Google Scholar] [CrossRef]
- Xie, T.; Ma, K.; Zhang, G.; Zhang, K.; Li, H. Optimal scheduling of multi-regional energy system considering demand response union and shared energy storage. Energy Strategy Rev. 2024, 53, 101413. [Google Scholar] [CrossRef]
- Wang, B.; Wang, X.; Wang, Z.; Wei, C.; Zhang, X.-P.; Zhou, M.; Gao, J.; Han, Z. A four-stage fast reliability assessment framework for renewables-dominated strong power systems with large-scale energy storage by temporal decoupling and contingencies filtering. Appl. Energy 2024, 362, 123035. [Google Scholar] [CrossRef]
- Li, M.; Li, M.; Wu, Q.; Xu, X.; Shen, J. Cascading failure simulation and analysis method in integrated electric and gas system based on energy circuit. Electr. Power Syst. Res. 2024, 235, 110844. [Google Scholar] [CrossRef]
- Wang, S.; Hui, H.; Ding, Y.; Song, Y. Long-term reliability evaluation of integrated electricity and gas systems considering distributed hydrogen injections. Appl. Energy 2024, 356, 122374. [Google Scholar] [CrossRef]
- Niu, L.; Zhao, Z.; Tan, J.; Zhao, Y.; Zhang, F.; Xiao, N.; He, Y.; Xie, S.; Jing, R.; Lin, J.; et al. A dynamic reliability assessment framework for integrated energy systems: A new methodology to address cascading failures. Adv. Appl. Energy 2025, 17, 100203. [Google Scholar] [CrossRef]
- Son, E.-T.; Kim, D.-M.; Lee, K.-S.; Kim, M.-S.; Hwang, S.-W. A microgrid model for the integrated operation of heat and electricity. In Proceedings of the CIRED Workshop, Ljubljana, Slovenia, 7–8 June 2018. [Google Scholar]
- Billinton, R.; Allan, R.N. Reliability Evaluation of Power Systems, 2nd ed.; Plenum Press: New York, NY, USA, 1996; pp. 68–70. [Google Scholar] [CrossRef]
- Nishimura, A.; Kitagawa, S.; Hirota, M.; Hu, E. Assessment on energy self-sufficiency rate for building integrated photovoltaics and fuel cell system in Japan. Smart Grid Renew. Energy 2017, 8, 195–211. [Google Scholar] [CrossRef]
- Ribeiro, P.F.; da Silva, M.L.P.; Carneiro, O.; de Almeida, A.T. A new composite index of reliability of supply in industrial systems with distributed generation. Int. J. Electr. Power Energy Syst. 2012, 43, 109–119. [Google Scholar] [CrossRef]
- Son, E.-T.; Bae, I.-S.; Kim, S.-Y.; Kim, D.-M. Resilience-Oriented Framework for Microgrid Planning in Distribution Systems. Energy 2022, 15, 2145. [Google Scholar] [CrossRef]
- Son, E.-T. Resilience-Oriented Distribution System Planning Under the Proliferation of Renewable Energy. Ph.D. Thesis, Dongshin University, Naju, Republic of Korea, January 2022. [Google Scholar]
- Allan, R.N.; Billinton, R.; Sjarief, I.; Goel, L.; So, K.S. A Reliability Test System for Educational Purposes—Basic Distribution System Data and Results. IEEE Trans. Power Syst. 1991, 6, 813–820. [Google Scholar] [CrossRef]
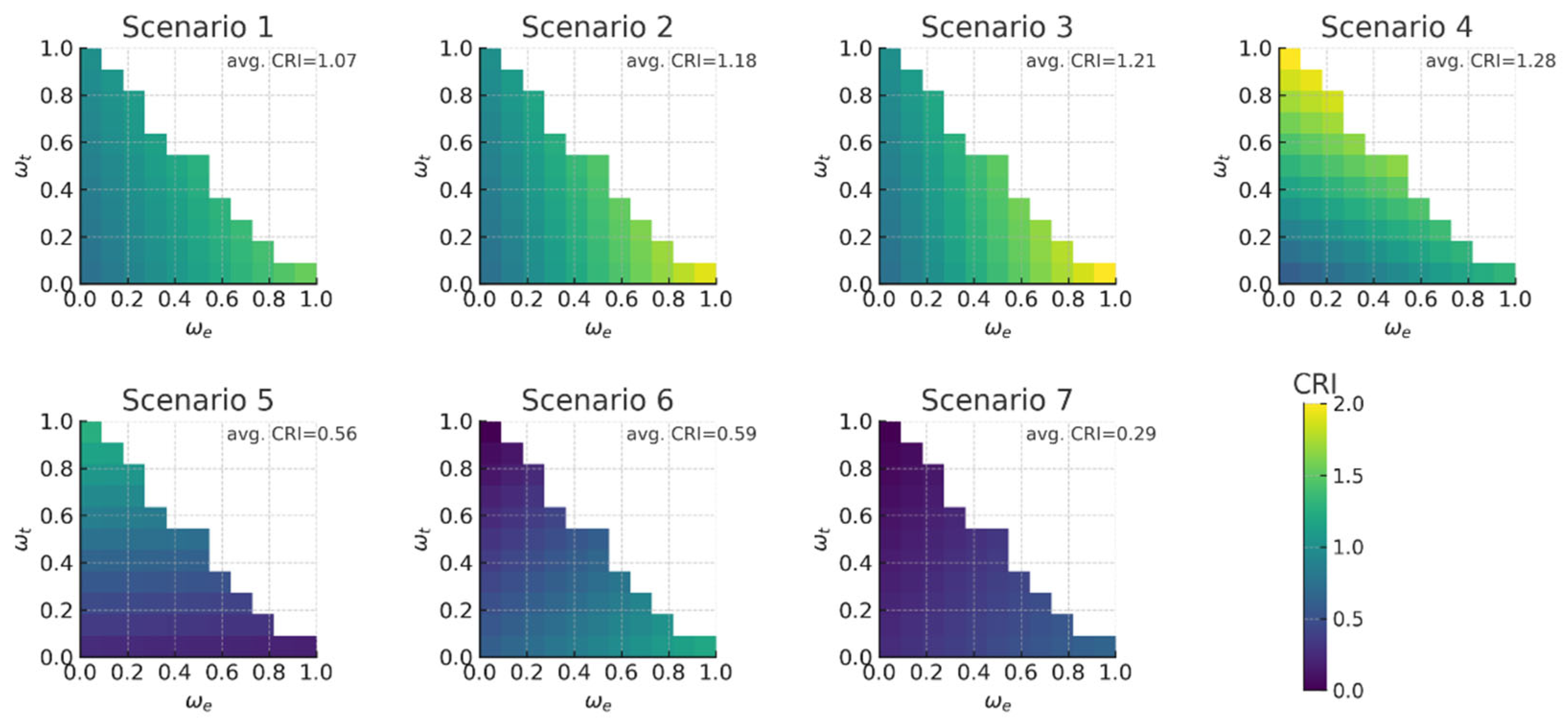
| Scenario | [%] | [MWh/year] | SSR [p.u.] | CRI ) |
|---|---|---|---|---|
| 1 | 0.194 9.258 | 91.769 0.000 | 0.252 | 1.138 |
| 2 | 0.240 9.247 | 114.543 0.000 | 0.252 | 1.287 |
| 3 | 0.263 9.258 | 114.988 0.000 | 0.252 | 1.324 |
| 4 | 0.183 9.281 | 70.042 2.020 | 0.393 | 1.304 |
| 5 | 0.034 9.258 | 6.194 0.527 | 0.748 | 0.527 |
| 6 | 0.183 0.023 | 57.752 0.000 | 0.393 | 0.662 |
| 7 | 0.137 0.000 | 14.861 0.000 | 0.745 | 0.337 |
| Scenario | CRI | ||||
|---|---|---|---|---|---|
| 1 | 1.006 | 1.085 | 1.138 | 1.217 | 1.271 |
| 2 | 1.079 | 1.196 | 1.287 | 1.403 | 1.494 |
| 3 | 1.098 | 1.223 | 1.324 | 1.449 | 1.549 |
| 4 | 1.304 | 1.374 | 1.304 | 1.374 | 1.304 |
| 5 | 0.641 | 0.634 | 0.527 | 0.520 | 0.413 |
| 6 | 0.483 | 0.542 | 0.662 | 0.721 | 0.841 |
| 7 | 0.232 | 0.272 | 0.337 | 0.377 | 0.442 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-M.; Bae, I.-S.; Rhee, J.-H.; Song, W.-C.; Bae, S. Optimal Design of Integrated Energy Systems Based on Reliability Assessment. Mathematics 2025, 13, 3734. https://doi.org/10.3390/math13233734
Kim D-M, Bae I-S, Rhee J-H, Song W-C, Bae S. Optimal Design of Integrated Energy Systems Based on Reliability Assessment. Mathematics. 2025; 13(23):3734. https://doi.org/10.3390/math13233734
Chicago/Turabian StyleKim, Dong-Min, In-Su Bae, Jae-Ho Rhee, Woo-Chang Song, and Sunghyun Bae. 2025. "Optimal Design of Integrated Energy Systems Based on Reliability Assessment" Mathematics 13, no. 23: 3734. https://doi.org/10.3390/math13233734
APA StyleKim, D.-M., Bae, I.-S., Rhee, J.-H., Song, W.-C., & Bae, S. (2025). Optimal Design of Integrated Energy Systems Based on Reliability Assessment. Mathematics, 13(23), 3734. https://doi.org/10.3390/math13233734










