Investigations on the Chaos in the Generalized Double Sine-Gordon Planar System: Melnikov’s Approach and Applications to Generating Antenna Factors
Abstract
1. Introduction
2. A Fresh Model—A Few Simulations
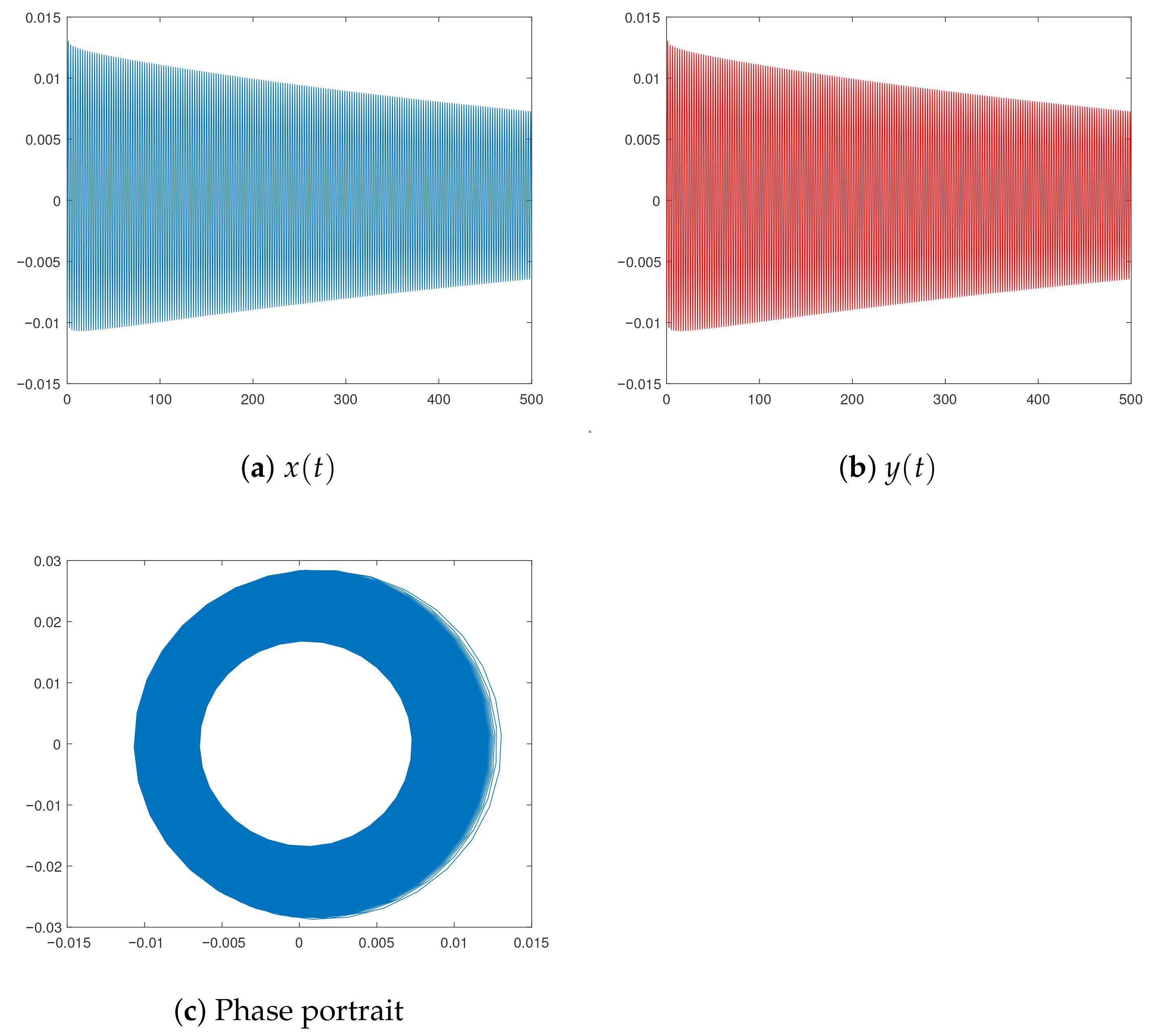
2.1. The Case , , ,
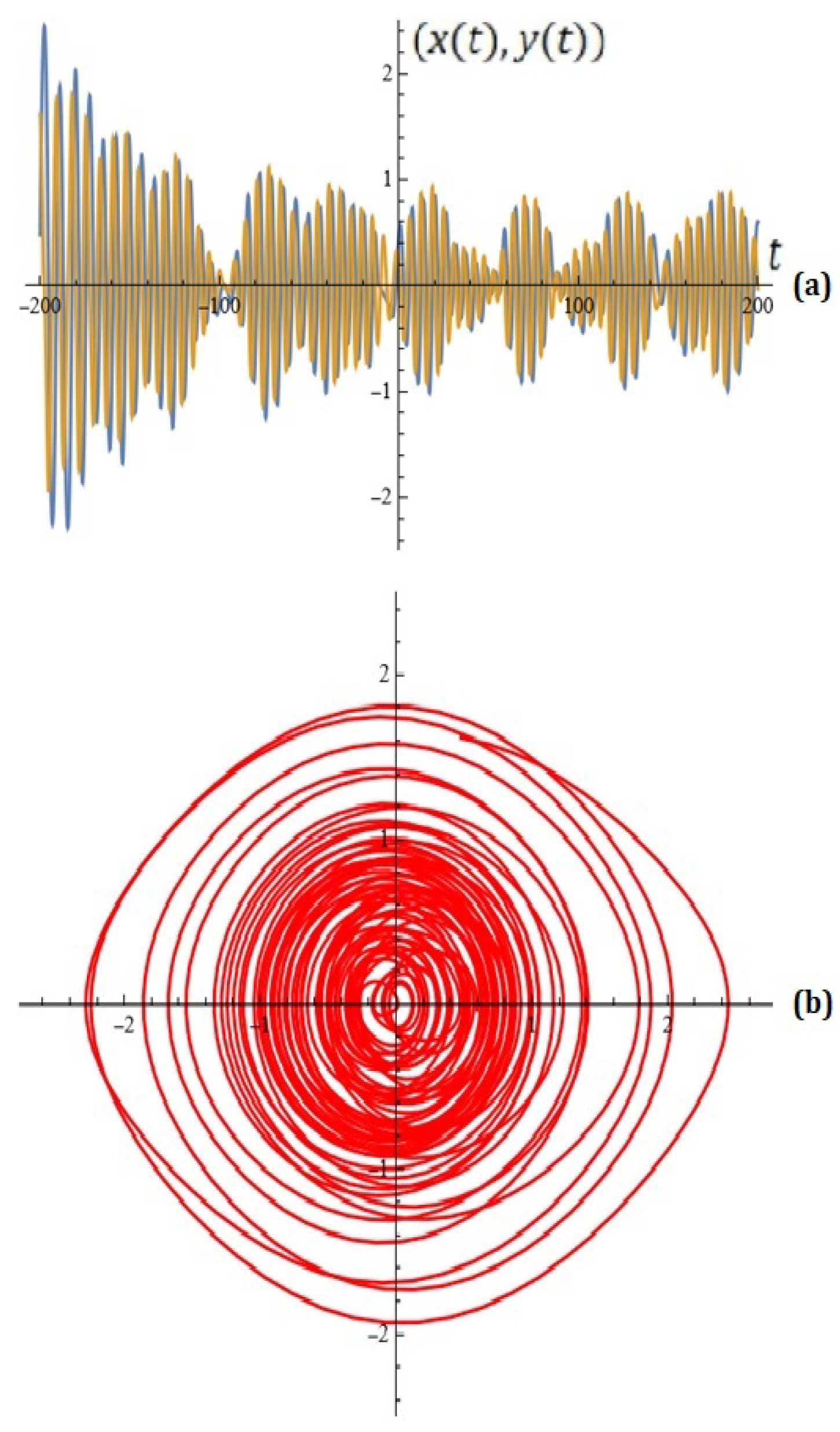
- (a)
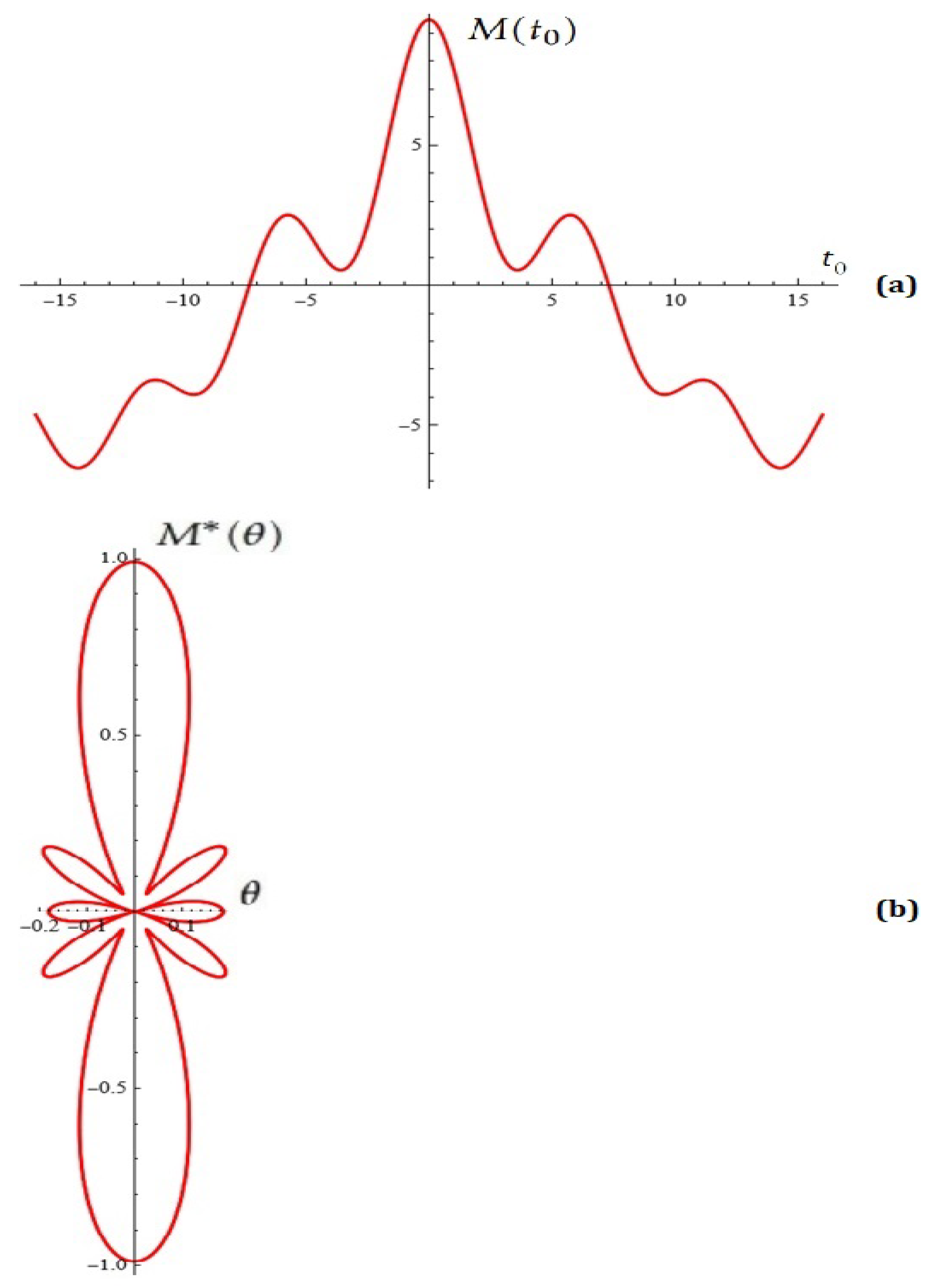
- For and , from (9) for the Melnikov function, we obtain
- (b)
- For and , from (9) for the Melnikov function, we obtain
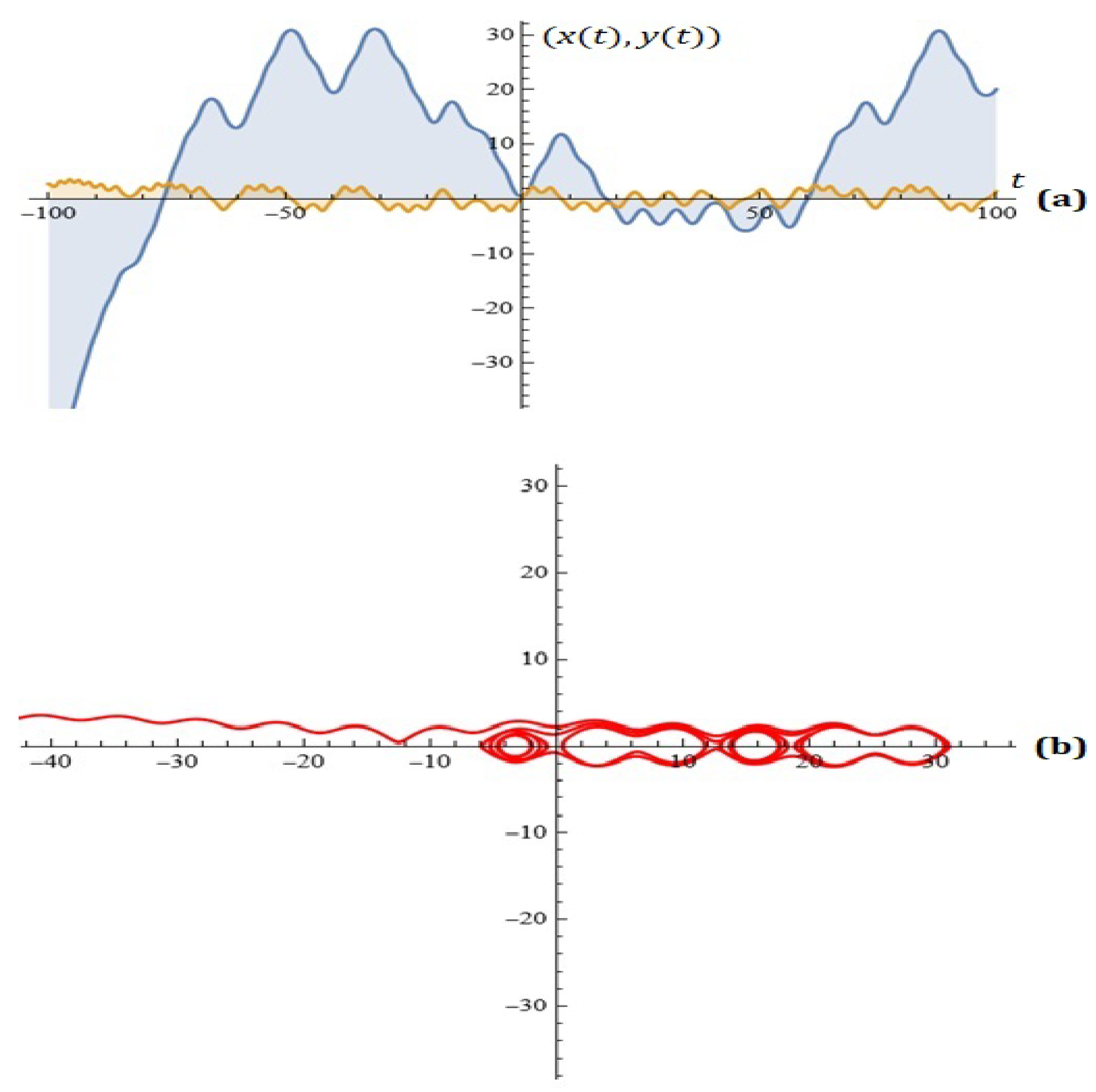
2.2. The Case , , ,
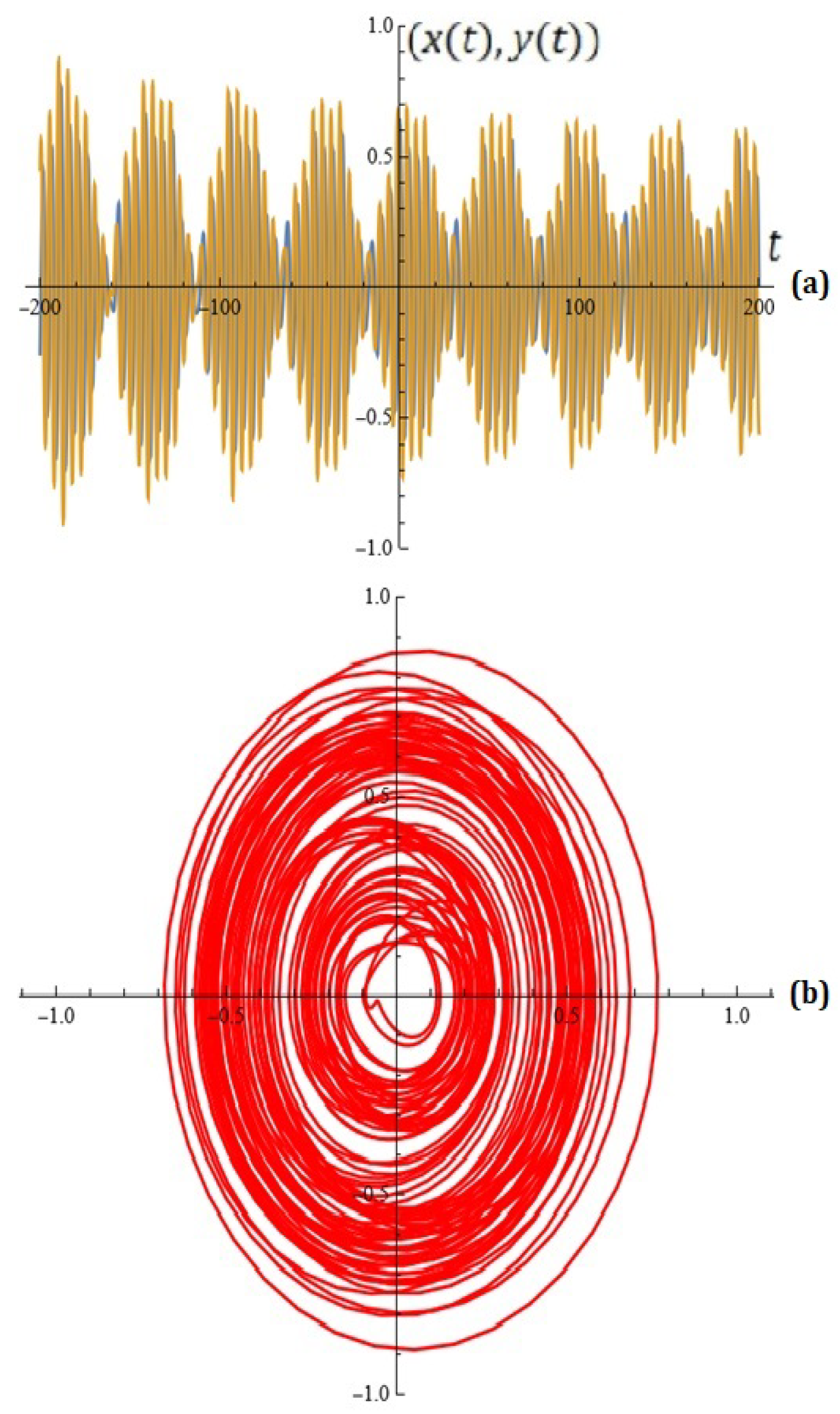
- (a)
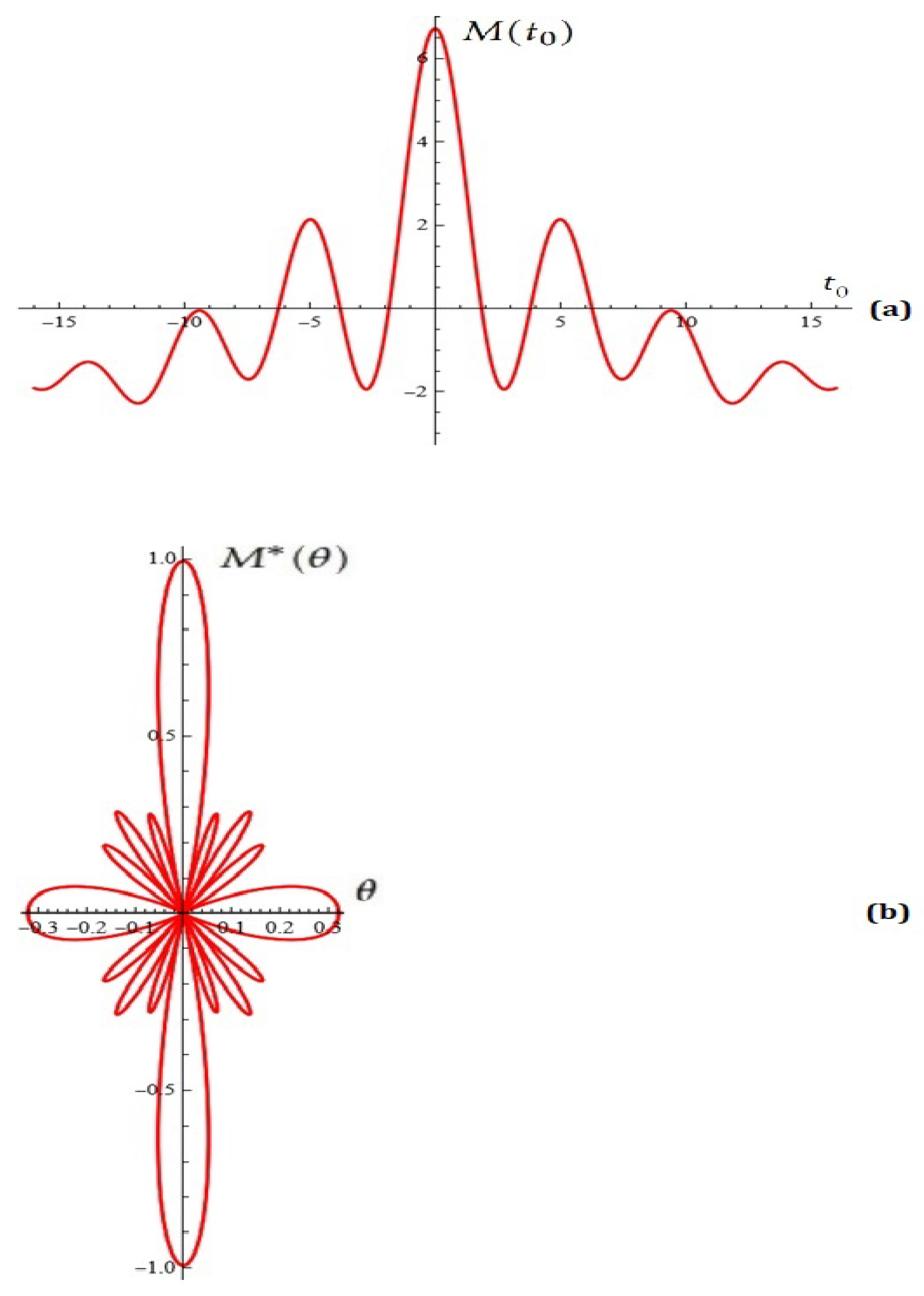
- For and , from (11) for the Melnikov function, we obtain
- (b)
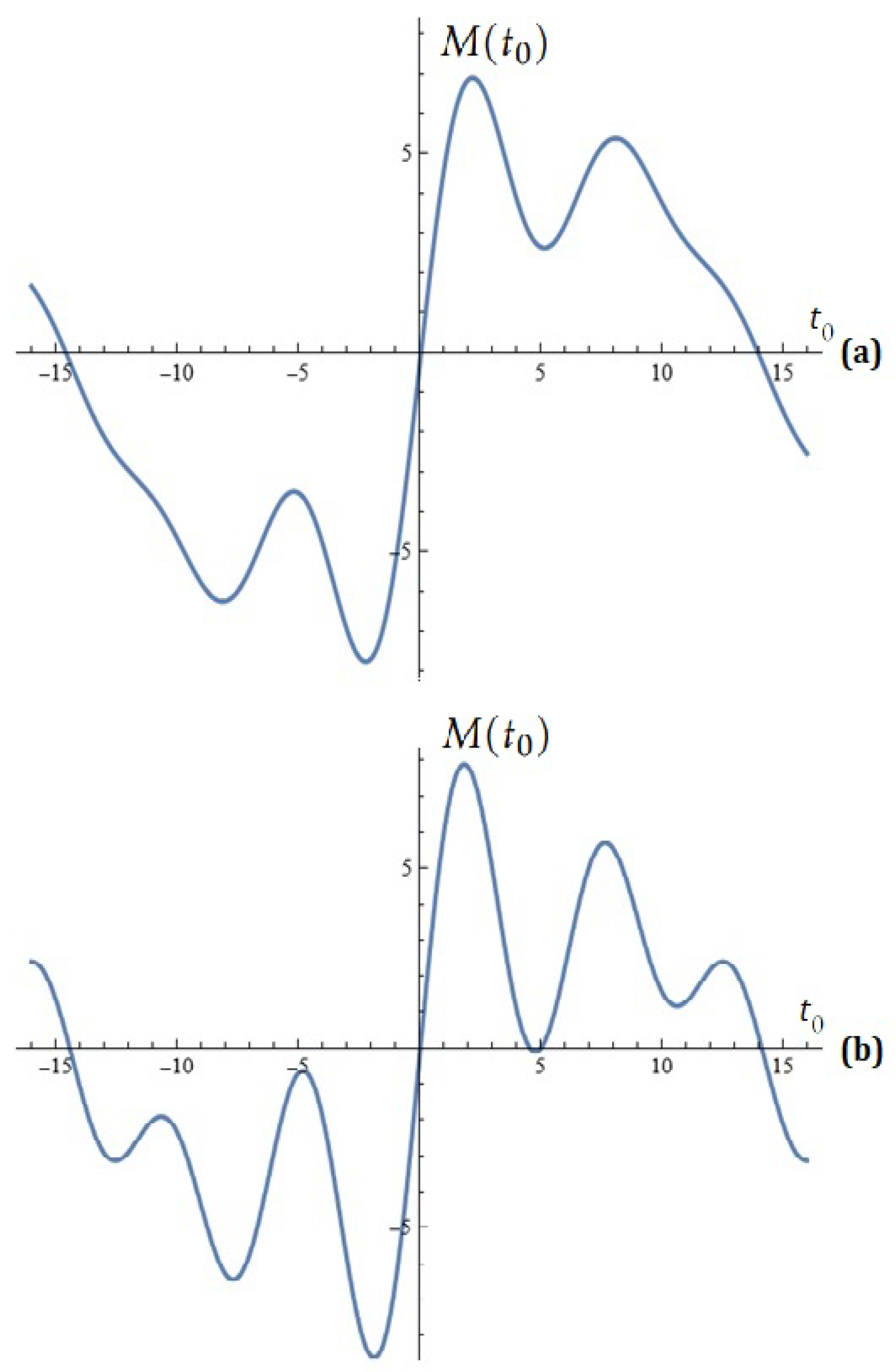
- In our previous publications, we discussed a possible application of the Melnikov functions in the modeling and synthesis of radiation antenna diagrams.
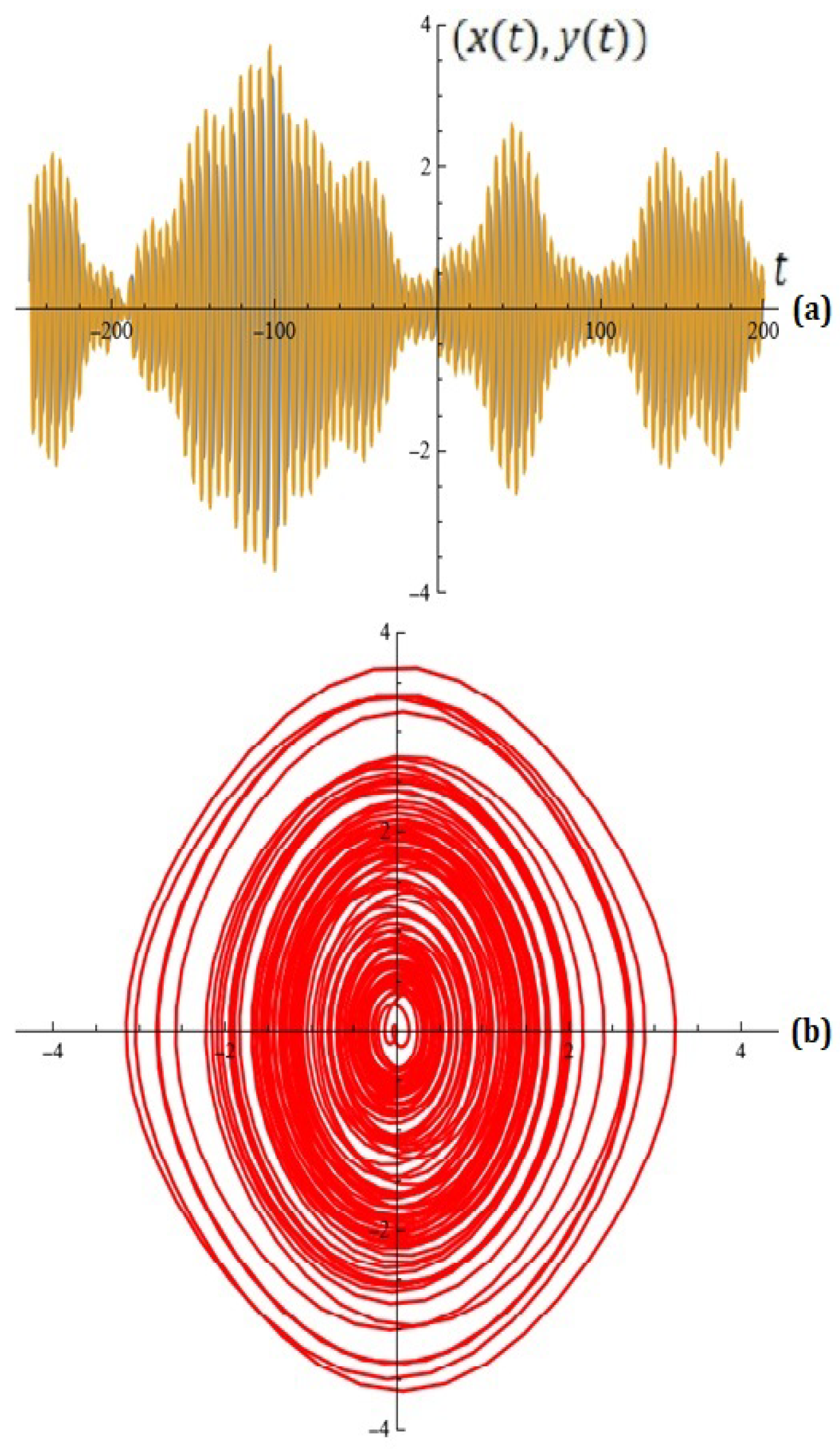
- (a)
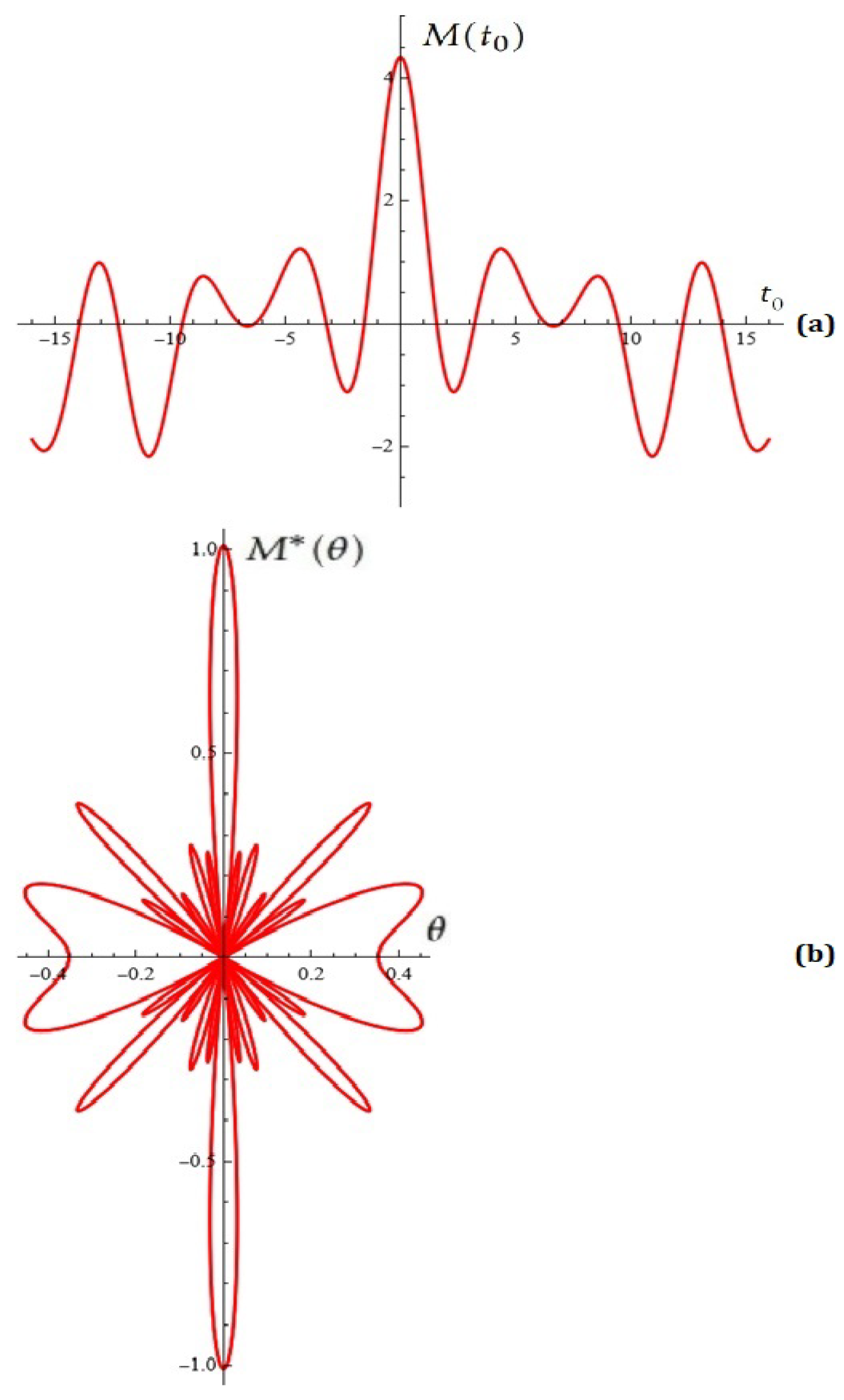
- For and , from (11) for the Melnikov function, we obtain
- (b)
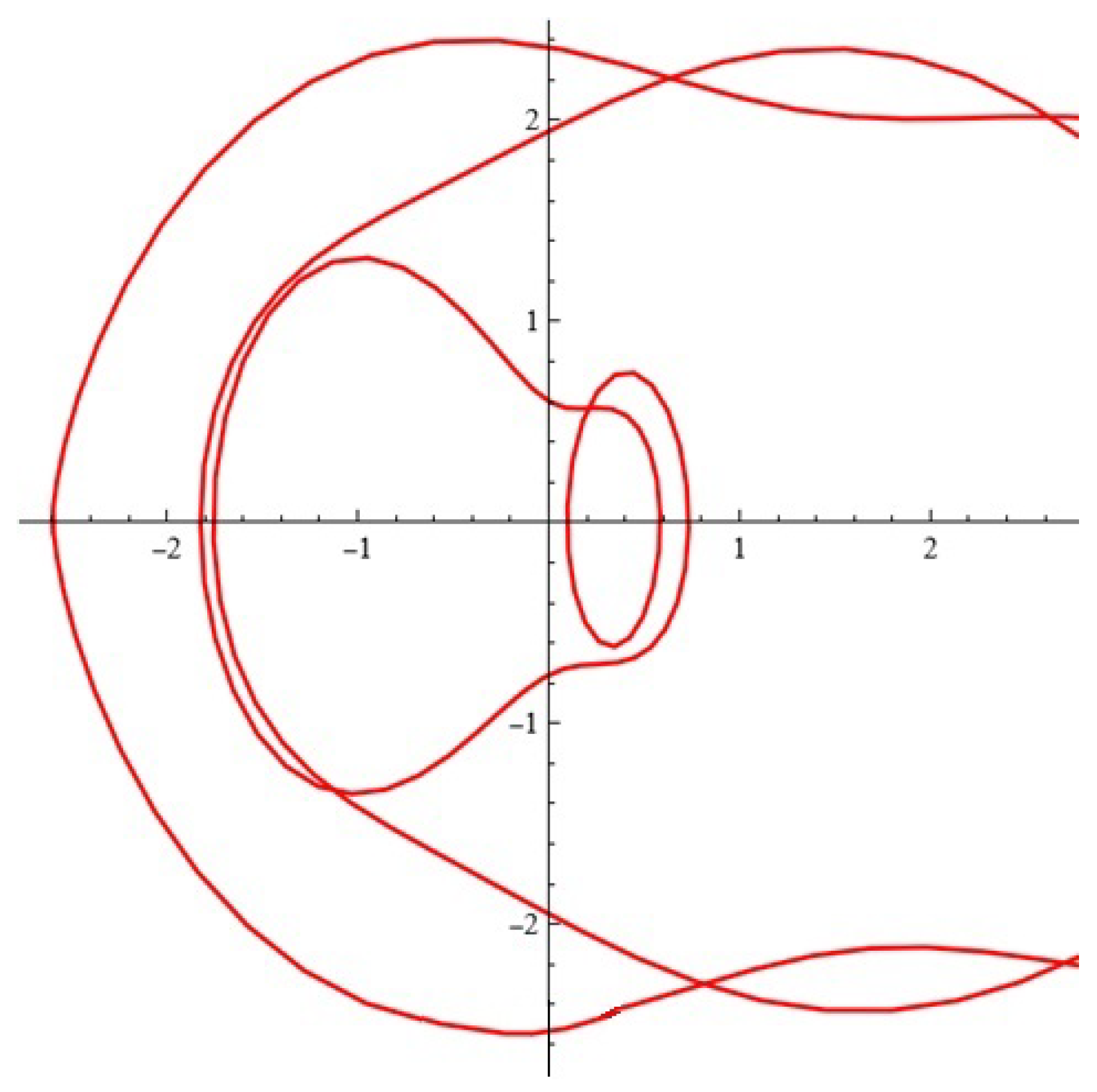
- For ; ; ; and , the Melnikov antenna factor based on (13) is depicted in Figure 7b.
- (a)
- For and , from (11) for the Melnikov function, we obtain
- (b)
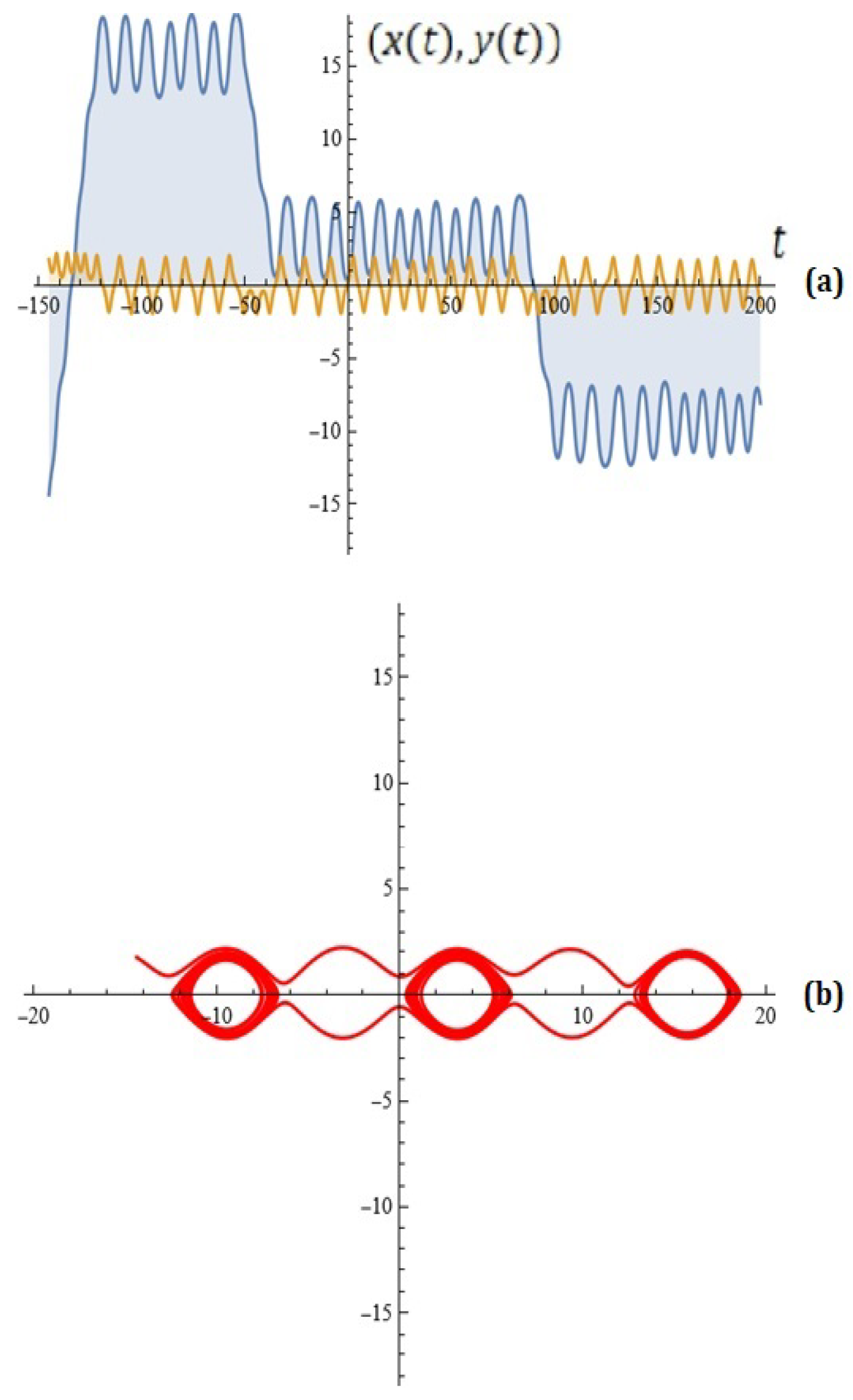
- For ; ; ; and the Melnikov antenna factor based on (14) is depicted in Figure 8b.
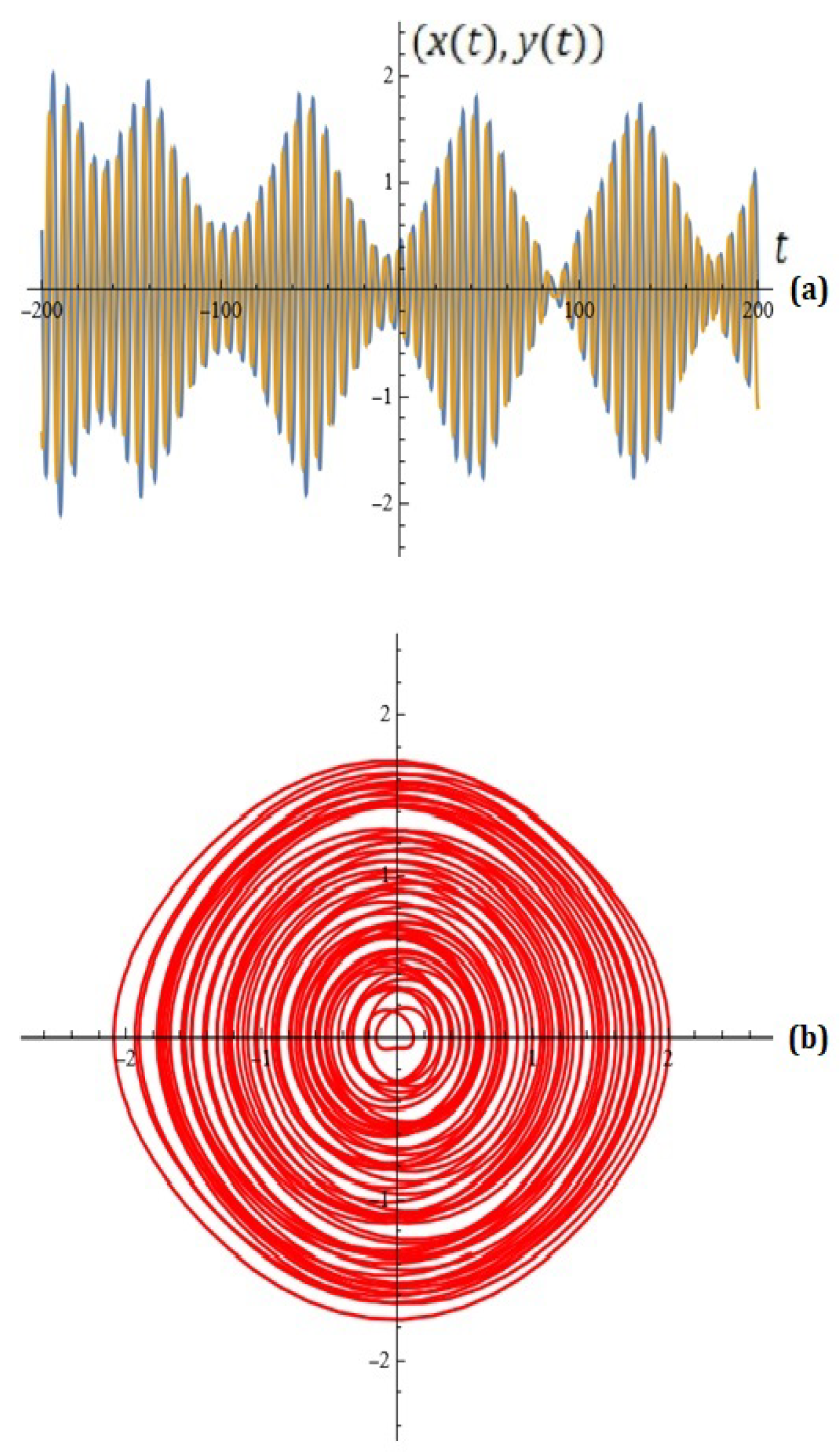
3. Probabilistic Constructions for Model Dynamics
3.1. Reformulation of the Problem
3.2. Discussion on the Possible Control on the Perturbation
4. Conclusions
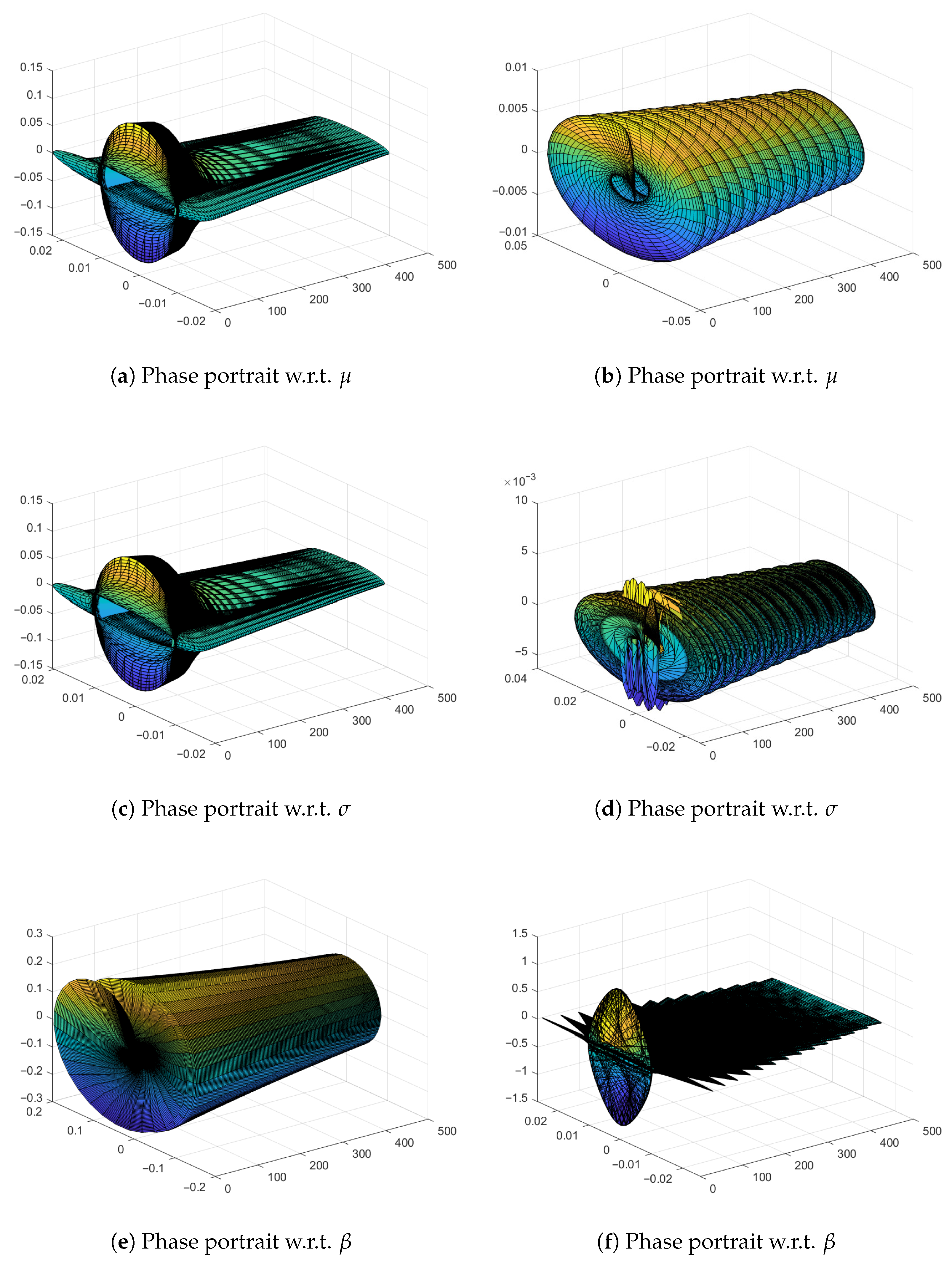
- (a)
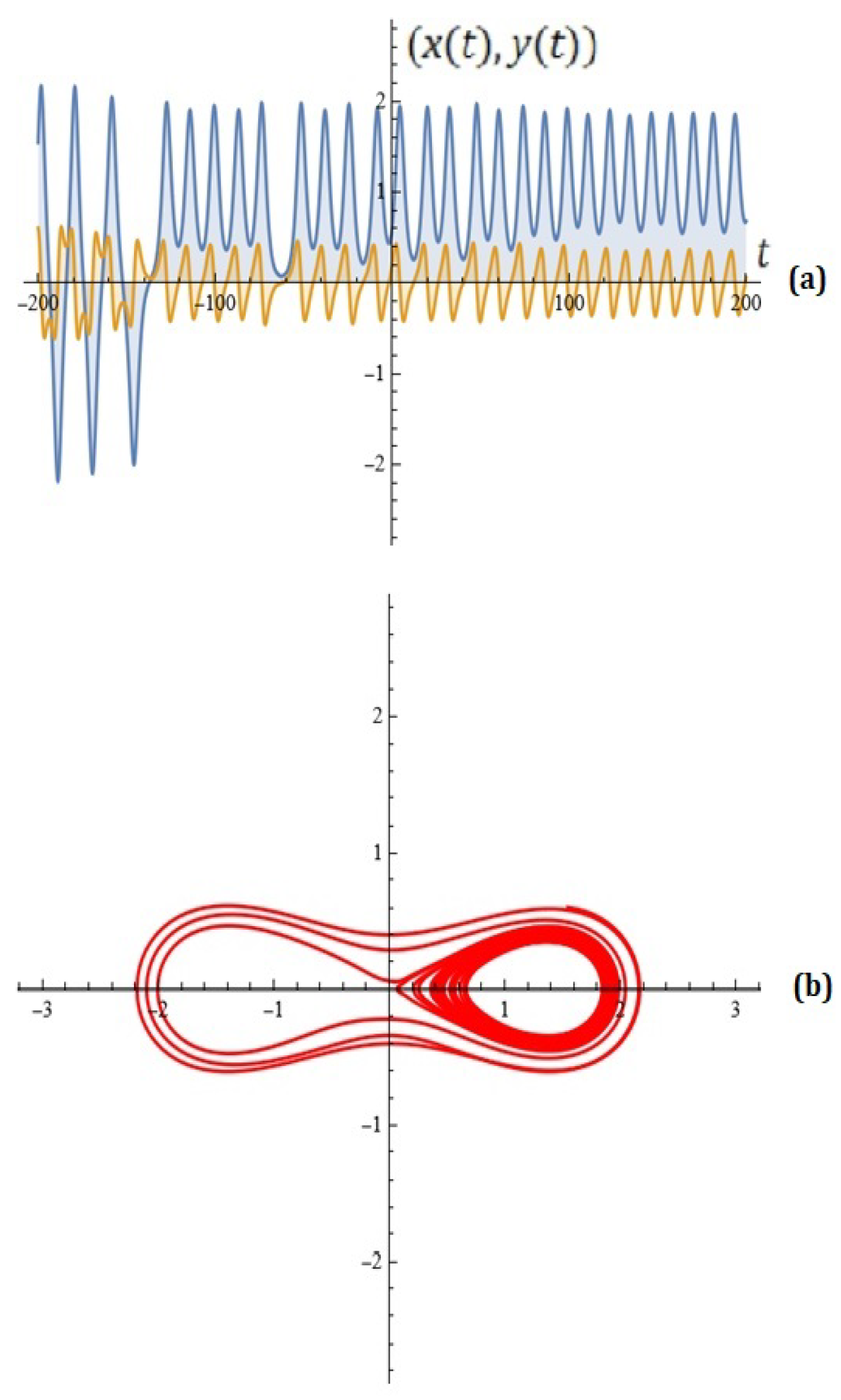
- For what values of the parameters are the dynamics depicted in Figure 16 obtained?
- (b)
- Draw the corresponding conclusions.
- (a)
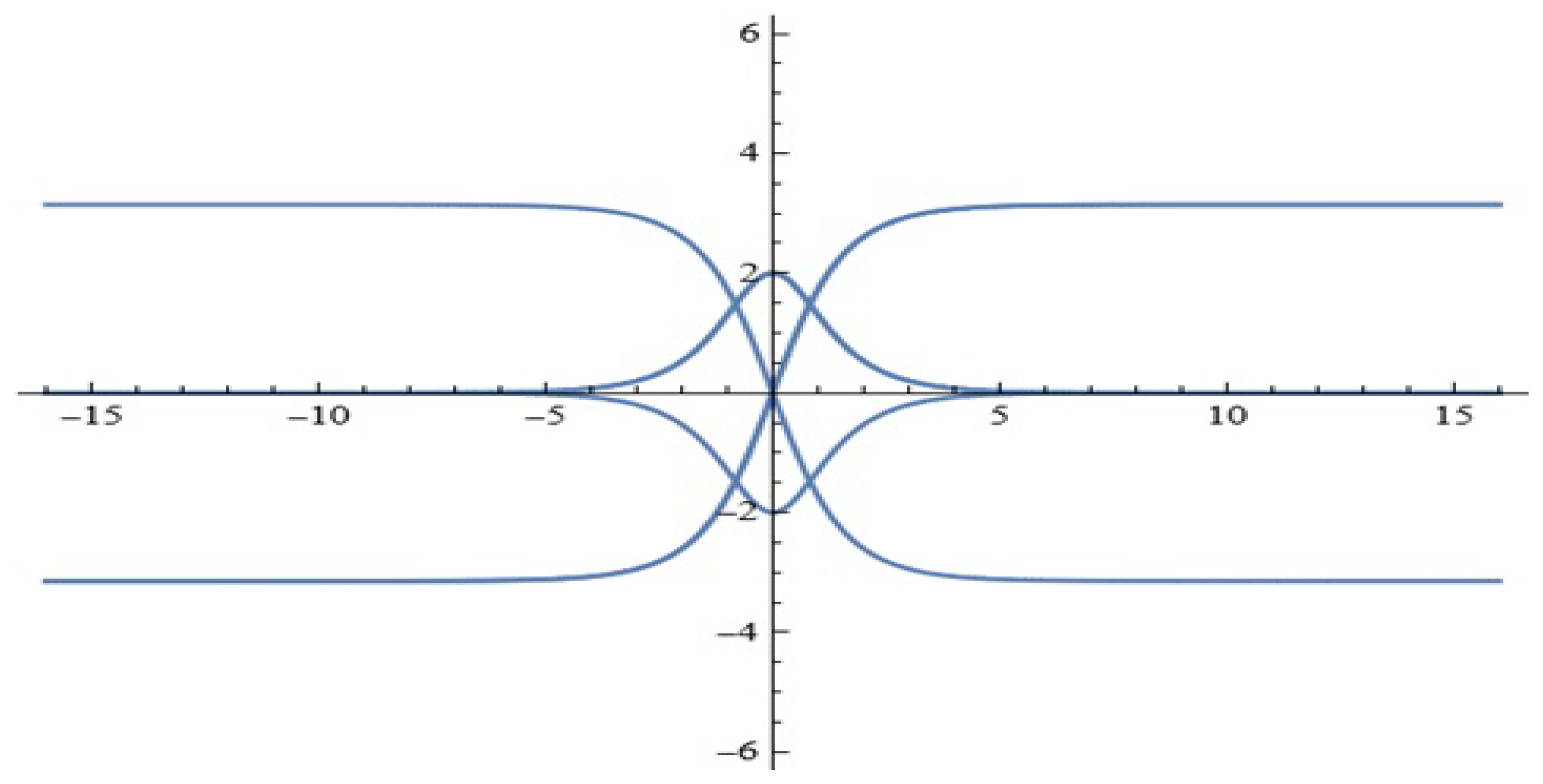
- For what value of the parameter () is the phase portrait depicted in Figure 17 obtained?
- (b)
- Show a chaotic phase portrait/sensitive dependence for parameters above this threshold;
- (c)
- Draw the corresponding conclusions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bullough, R.; Coudrey, P. Nonlinear Evolution Equations Solvable by the Inverse Spectral Transform; Calogero, F., Ed.; Pitman: London, UK, 1978. [Google Scholar]
- Bullough, R.K.; Caudrey, P.J.; Gibbs, H.M. Solitons; Bullough, R.K., Caudrey, P.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Fu, Z.-T.; Liu, S.-K.; Liu, S.-D. Exact Solutions to Triple sine-Gordon Equation. Commun. Theor. Phys. 2005, 43, 1023–1026. [Google Scholar] [CrossRef]
- Tricomi, F. Integratione di un’ equazione differenziale presentatasi in elettrotecnica. Ann. Sc. Norm. Super. Pisa Cl. Sci. 1933, 2, 1–20. [Google Scholar]
- Stoker, J.J. Nonlinear Vibration in Mechanical and Electrical Systems; Interscience: New York, NY, USA, 1950. [Google Scholar]
- Levi, M.; Hoppensteadt, F.; Miranker, W. Dynamics of the Josephson junction. Q. Appl. Math. 1978, 35, 167–198. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer: New York, NY, USA, 1991. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Sanjuan, M.A.F. The effect of nonlinear damping on the universal escape oscillator. Int. J. Bifurcat. Chaos 1999, 9, 735–744. [Google Scholar] [CrossRef]
- Vitanov, N. On travelling waves and double-periodic structures in two-dimensional sine-Gordon systems. J. Phys. A Math. Gen. 1996, 29, 5195–5207. [Google Scholar] [CrossRef]
- Vitanov, N.; Martinov, N. On the solitary waves in the sine-Gordon model of the two-dimensional Josephson junction. Z. Phys. B 1996, 100, 129–135. [Google Scholar] [CrossRef]
- Martinov, N.; Vitanov, N. Running wave solutions of the two-dimensional sine-Gordon equation. J. Phys. A Math. Gen. 1992, 25, 3609–3613. [Google Scholar] [CrossRef]
- McKean, H.P. The sine-Gordon and sinh-Gordon equations in the circle. Commun. Pure Appl. Math. 1981, 34, 197–257. [Google Scholar]
- Zine, Y. Hyperbolic sine-Gordon model beyond the first threshold. arXiv 2025, arXiv:2504.07944v2. [Google Scholar] [CrossRef]
- Joaquin, P. Sinh-Gordon Type Equations for CMC Surfaces; Universidad de Granada: Granada, Spain, 2011; pp. 145–156. [Google Scholar]
- Seong, K. Exponential ergodicity for the stochastic hyperbolic sine-Gordon equation on the circle. arXiv 2023, arXiv:2308.01378. [Google Scholar] [CrossRef]
- Castro, J.; Alvarez, J. Melnikov-Type Chaos of Planar Systems with Two Discontinuities. Int. J. Bifurcat. Chaos 2015, 25, 1550027. [Google Scholar] [CrossRef]
- Levkov, D.G.; Maslov, V.E.; Nugaev, E.Y. Chaotic Solitons in Driven Sine-Gordon Model. Chaos Solitons Fractals 2020, 139, 110079. [Google Scholar] [CrossRef]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263–379. [Google Scholar] [CrossRef]
- Salerno, M. A mechanical analog for the double sine-Gordon equation. Phys. D Nonlinear Phenom. 1985, 17, 227–234. [Google Scholar] [CrossRef]
- Salam, F.M.A.; Sastry, S.S. The complete dynamics on the forced Josephson junction circuit: The regions of chaos. In Chaos in Nonlinear Dynamical Systems; Chandra, J., Ed.; SIAM: Philadelphia, PA, USA, 1984; pp. 43–55. [Google Scholar]
- Genchev, Z.G.; Ivanov, Z.G.; Todorov, B.N. Effect of a Periodic Perturbation on Radio Frequency Model of Josephson Junction. IEEE Trans. Circuits Syst. 1983, 30, 633–636. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. Method for solving the sine-Gordon equation. Phys. Rev. Lett. 1973, 30, 1262–1264. [Google Scholar] [CrossRef]
- Kumar, P.; Holland, R.R. Quasi solitons: A case study of the double sine-Gordon equations. In Nonlinear Problems: Present and Future; Bishop, A.R., Campbell, D.K., Nicolaenko, B., Eds.; North-Holland Mathematics Studies: Amsterdam, The Netherlands, 1982; Volume 61, pp. 229–235. [Google Scholar]
- Kitchenside, P.W.; Mason, A.L.; Bullough, R.K.; Caudrey, P.J. Perturbation theory of the double sine-Gordon equation. In Proceedings of the Symposium on Nonlinear (Soliton) Structure and Dynamics in Condensed Matter, Oxford, UK, 27–29 June 1978; Bishop, A.R.B., Schneider, T., Eds.; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Pagano, S.; Soerensen, M.P.; Christiansen, P.L.; Parmentier, R.D. Stability of fluxon motion in long Josephson junctions at high bias. Phys. Rev. B 1988, 38, 4677–4687. [Google Scholar] [CrossRef] [PubMed]
- Salerno, M.; Samuelsen, M.R. Internal oscillation frequencies and anharmonic effects for the double sine-Gordon kink. Phys. Rev. B 1989, 39, 4500–4503. [Google Scholar] [CrossRef]
- Bishop, A.R.; Flesch, R.; Forest, M.G.; McLaughlin, D.W.; Overman, E.A., II. Correlations between chaos in a perturbed sine-Gordon equation and a truncated model system. SIAM J. Math. Anal. 1990, 21, 1511–1536. [Google Scholar] [CrossRef]
- Golbabai, A.; Arabshahi, M.M. On the behavior of high-order compact approximations in the one-dimensional sine-Gordon equation. Phys. Scr. 2011, 83, 015015. [Google Scholar] [CrossRef]
- Siovitz, I.; Gluck, A.-M.E.; Deller, Y.; Schmutz, A.; Klein, F.; Strobel, H.; Oberthaler, M.K.; Gasenzer, T. Double sine-Gordon class of universal coarsening dynamics in a spin-1 Bose gas. Phys. Rev. A 2024, 112, 023304. [Google Scholar] [CrossRef]
- Afshar, B.; Peyravi, M.; Bamba, K.; Moradpour, H. A Double-Sine-Gordon Early Universe. arXiv 2024, arXiv:2409.10402. [Google Scholar] [CrossRef]
- Melnikov, V.K. On the stability of the center for time periodic perturbations. Trans. Mosc. Math. Soc. 1963, 12, 3–52. [Google Scholar]
- Bartuccelli, M.; Christiansen, P.L.; Pedersen, N.F.; Salerno, M. “Horseshoe chaos” in the space-independent double sine-Gordon system. Wave Motion 1986, 8, 581–594. [Google Scholar]
- Christiansen, P.L.; Parmentier, R.D.; Skovgaard, O. Coherence and Chaos Phenomena in Josephson Oscillators for Superconducting Electronics; Technical Report; U.S. Army European Research Office: London, UK, 1989. [Google Scholar]
- Bruhn, B.; Koch, B. Homoclinic and heteroclinic bifurcations in rf SQUIDs. Z. Naturforsch. A 1988, 43, 930–938. [Google Scholar] [CrossRef]
- Zheng, H.; Xia, Y.; Pinto, M. Chaotic motion and control of the driven-damped double sine-Gordon equation. Discret. Contin. Dyn. Syst. B 2022, 27, 7151–7167. [Google Scholar] [CrossRef]
- Forest, M.G.; Pagano, S.; Parmentier, R.D.; Christiansen, P.L.; Soerensen, M.P.; Sheu, S.-P. Numerical evidence for global bifurcations leading to switching phenomena in long Josephson junctions. Wave Motion 1990, 12, 213–226. [Google Scholar] [CrossRef]
- Fu, Z.-T.; Liu, S.-K.; Liu, S.-D. Exact Jacobian elliptic function solutions to the double sine-Gordon equation. Z. Naturforsch. A 2005, 60, 301–312. [Google Scholar]
- Iliev, A.; Kyurkchiev, N. Nontrivial Methods in Numerical Analysis: Selected Topics in Numerical Analysis; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2010; ISBN 978-3-8433-6793-6. [Google Scholar]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Dynamics of a new class of extended escape oscillators: Melnikov’s approach, possible application to antenna array theory. Math. Inform. 2024, 67, 1–15. [Google Scholar] [CrossRef]
- Soltis, J.J. New Gegenbauer-like and Jacobi-like polynomials with applications. J. Franklin Inst. 1993, 330, 635–639. [Google Scholar] [CrossRef]
- Golev, A.; Terzieva, T.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Simulation on a generalized oscillator model: Web-based application. C. R. L’Acad. Bulg. Sci. 2024, 77, 230–237. [Google Scholar] [CrossRef]
- Makrelov, I.; Kyurkchiev, N.; Tamburov, S. Two two-sided methods for simultaneous determination of all roots of trigonometric and exponential polynomials. Proc. Sci. Works Univ. Plovdiv Math. 1985, 23, 289–298. [Google Scholar]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Branzov, T. A note on the dynamics of modified rf-SQUIDs: Simulations and possible control over oscillations. Mathematics 2025, 13, 722. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Studying Homoclinic Chaos in a Class of Piecewise Smooth Oscillators: Melnikov’s Approach, Symmetry Results, Simulations and Applications to Generating Antenna Factors Using Approximation and Optimization Techniques. Symmetry 2025, 17, 1144. [Google Scholar] [CrossRef]
- Dolph, C.L. A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level. Proc. IRE 1946, 34, 335–348. [Google Scholar] [CrossRef]
- Tu, L.; Ng, B.P. Exponential and generalized Dolph-Chebyshev functions for flat-top array beam pattern synthesis. Multidimens. Syst. Signal Process. 2013, 24, 119–132. [Google Scholar]
- Apostolov, P. An addition to binomial array antenna theory. Prog. Electromagn. Res. Lett. 2023, 113, 113–117. [Google Scholar] [CrossRef]
- Hutu, F.; Cauet, S.; Coirault, P. Antenna arrays principle and solutions: Robust control approach. Int. J. Comput. Commun. Control 2008, 3, 161–171. [Google Scholar] [CrossRef]
- Hutu, F.; Cauet, S.; Coirault, P. Robust synchronization of different coupled oscillators: Application to antenna arrays. J. Frankl. Inst. 2009, 346, 413–430. [Google Scholar] [CrossRef]
- Heath, T.; Kerr, R.R.; Hopkins, G.D. Two-dimensional, nonlinear oscillator array antenna. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005; pp. 1104–1115. [Google Scholar]
- Iordache, M.; Paillot, J.M.; Dumitrescu, I.; Ionita, M. Analysis of coupled oscillators applied to antenna arrays. Ann. Univ. Craiova Electr. Eng. Ser. 2010, 34, 25–28. [Google Scholar]
- Apostolov, P.S. Linear equidistant antenna array with improved selectivity. IEEE Trans. Antennas Propag. 2011, 59, 3940–3943. [Google Scholar] [CrossRef]
- Gachev, M. Synthesis of Antenna Grids with Optimal Directivity Chart. Ph.D. Thesis, VMEI, Sofia, Bulgaria, 1981. [Google Scholar]
- Joseph, S.K.; Schoebel, J. Designing antenna arrays using signal processing, image processing and optimization toolboxes of MATLAB. In MATLAB-Modelling, Programming and Simulations; Leite, E.P., Ed.; InTech: Rijeka, Croatia, 2010; pp. 1–20. [Google Scholar]
- Vinogradova, J.; Couillet, R.; Hachem, W. Statistical inference in large antenna arrays under unknown noise pattern. IEEE Trans. Signal Process. 2013, 61, 5723–5737. [Google Scholar] [CrossRef]
- Fiks, G.E.; Fiks, I.S. Optimal statistical antenna synthesis using the near-zone field. Radiophys. Quantum Electron. 2009, 52, 435. [Google Scholar] [CrossRef]
- Cheng, D.K. Optimization techniques for antenna arrays. Proc. IEEE 1971, 59, 1664–1674. [Google Scholar] [CrossRef]
- Fu, Z.-T.; Liu, S.-K.; Liu, S.-D. Exact solutions to double and triple sinh-Gordon equations. Z. Naturforsch. A 2004, 59, 933–937. [Google Scholar] [CrossRef]
- Khare, A. A QES band-structure problem in one dimension. Phys. Lett. A 2001, 288, 69–72. [Google Scholar] [CrossRef]
- Khare, A.; Habib, S.; Saxena, A. Exact thermodynamics of the double sinh-Gordon theory in (1+1)-dimensions. Phys. Rev. Lett. 1997, 79, 3797–3801. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Nonlinear Partial Differential Equations; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Habib, S.; Khare, A.; Saxena, A. Statistical mechanics of double sinh-Gordon kinks. Phys. D 1998, 123, 341–356. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyurkchiev, N.; Zaevski, T.; Iliev, A. Investigations on the Chaos in the Generalized Double Sine-Gordon Planar System: Melnikov’s Approach and Applications to Generating Antenna Factors. Mathematics 2025, 13, 3700. https://doi.org/10.3390/math13223700
Kyurkchiev N, Zaevski T, Iliev A. Investigations on the Chaos in the Generalized Double Sine-Gordon Planar System: Melnikov’s Approach and Applications to Generating Antenna Factors. Mathematics. 2025; 13(22):3700. https://doi.org/10.3390/math13223700
Chicago/Turabian StyleKyurkchiev, Nikolay, Tsvetelin Zaevski, and Anton Iliev. 2025. "Investigations on the Chaos in the Generalized Double Sine-Gordon Planar System: Melnikov’s Approach and Applications to Generating Antenna Factors" Mathematics 13, no. 22: 3700. https://doi.org/10.3390/math13223700
APA StyleKyurkchiev, N., Zaevski, T., & Iliev, A. (2025). Investigations on the Chaos in the Generalized Double Sine-Gordon Planar System: Melnikov’s Approach and Applications to Generating Antenna Factors. Mathematics, 13(22), 3700. https://doi.org/10.3390/math13223700







