Triple-Stream Contrastive Deep Embedding Clustering via Semantic Structure
Abstract
1. Introduction
- We propose a novel triple-stream deep clustering framework termed TCSS, which leverages the interaction and fusion among three complementary streams (raw, weakly augmented, and strongly augmented) to enrich structural information in both the contrastive and clustering modules.
- We introduce a novel dynamic clustering structure factor as a degree-of-freedom regulator in the self-training loss, capturing intrinsic geometric relations in the embedding space and adaptively guiding cluster formation.
- We design two structure alignment strategies, local (via k-nearest-neighbor alignment) and global (via centroid alignment), along with a clustering-aware negative instance selection mechanism to refine the learned semantic structure.
- Extensive experiments on multiple benchmark datasets validate that TCSS consistently outperforms recent state-of-the-art deep clustering methods.
2. Related Works
2.1. Self-Training Deep Clustering
2.2. Deep Contrastive Clustering
3. Proposed Method
3.1. Motivation and Distinction from Dual-Stream Models
- Lack of a cluster-oriented multiview setting. In dual-stream frameworks, both streams follow the contrastive setup and are treated equally, leaving no spatial anchor in the representation space. As a result, instance representations can vary sharply under augmentations, especially for samples near cluster boundaries.
- Limited inter-view interaction in the clustering head. Due to the two-stream design, most methods only enforce inter-view consistency and intra-view redundancy reduction, without enabling genuine cross-dimensional interactions across views.
- Weak modeling of spatial structure. Each instance forms a single augmented pair per batch, corresponding to a “hyper-line segment” in the representation space. Interactions thus occur only among such segments, limiting cross-view intersections.
- Implicit misalignment in inter-view contrastive mechanisms. Dimension-wise contrastive losses can distort cluster structures when stream-specific cluster distributions are not aligned. For instance, if the a-view of an instance belongs to class i but its b-view falls into class j, the contrastive loss may exaggerate this inconsistency.
- Anchor-based stabilization and cross-view negative sampling. TCSS designates the source sample as an anchor stream and introduces a cross-view negative sampling strategy (Section 3.2.3) together with a soft-label alignment loss (Equation (7), Section 3.3). This stabilizes sample-space representations while maintaining augmentation diversity, improving clustering robustness.
- Triple-stream information fusion and distribution alignment. TCSS employs a Triple-stream fusion strategy with a corresponding distribution alignment loss (Equation (7)) to enhance representation consistency across views.
- Enhanced spatial structural expressiveness. Each training batch forms a “hyper-triangle” in the representation space, where each vertex represents one stream. This extends inter-view interaction from a line to a plane, enriching the model’s spatial representation capacity.
- Cluster-center alignment for stable self-training. A cluster-center alignment loss enforces consistent soft assignments across views, resolving the inter-view alignment issue and improving clustering stability.
3.2. Triple-Stream Contrastive Learning
3.2.1. Introduction of Contrastive Learning
3.2.2. Triple-Stream Contrastive Learning
3.2.3. Tag Bank for Clustering
3.3. Triple-Stream Clustering Learning
3.3.1. Introduction of Self-Training Clustering
3.3.2. Clustering with Triple-Stream
3.3.3. Clustering Structure Factor
- Dependence on crowding. As noted in [25], the proper value of should depend on the degree of crowding—a phenomenon where low-dimensional embeddings become compressed due to dimensionality mismatch with the input space. The literature explicitly recommends adapting to the crowding level, as fixed values perform worse in experiments.
- Scaling effect. From Equation (4), acts as a similarity-scaling factor. A smaller yields heavier distribution tails, producing compact intra-cluster and dispersed inter-cluster structures, whereas a larger flattens the distribution and weakens cluster boundaries.
- Lack of task adaptivity. While can be fixed or learned, the fixed setting lacks flexibility and relies on heuristics, whereas a learnable can cause instability. More critically, neither directly reflects the evolving cluster structure.
3.4. Triple-Stream Structure Alignment
3.4.1. Cluster-Centroid Alignment
3.4.2. Neighbor Alignment
3.5. Overall Loss and Training Strategy
| Algorithm 1: TCSS Algorithm |
| input: Dataset D, strong and weak augmentation denoted as , model structure: backbone , contrastive head , clustering heads for views
|
4. Experiments
4.1. Datasets Evaluation Metrics
- CIFAR-10&CIFAR-100 [51]: CIFAR-10 is a natural image dataset with 50,000/10,000 (train/test) samples from 10 classes for training and testing, respectively. CIFAR-100 contains 20 super-classes, which can be further divided into 100 classes. Moreover, it has the same number of samples and image size (32 × 32) as CIFAR-10. Please note that we use the 20 super-classes as the ground-truth during experiments.
- STL-10 [52]: STL-10 is an ImageNet-sourced dataset containing 5000/8000 (train/test) images with a size of 96 × 96 from each of 10 classes.
- ImageNet-10&ImageNet-Dogs [11]: ImageNet-10 is a subset of ImageNet with 10 classes, each of which consists of 1300 samples with varying image sizes. ImageNet-Dogs is constructed similarly to ImageNet-10, but it selects a total of 19,500 dog images of 15 breeds from the ImageNet dataset.
4.2. Implementations
4.3. Compared to Other Methods
4.4. Clustering Quality
4.5. Analysis of Training Cost
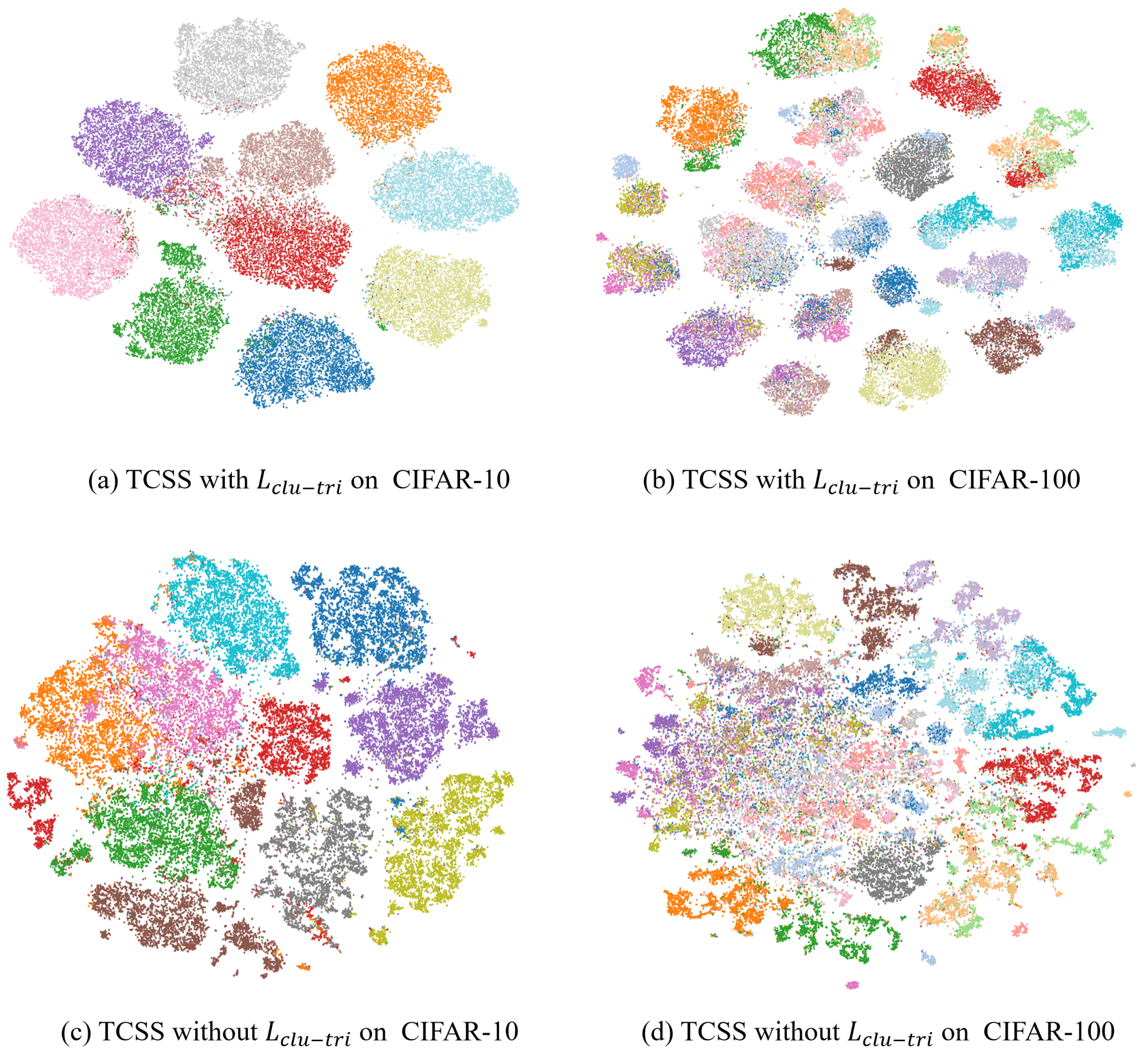
4.6. Ablation Studies
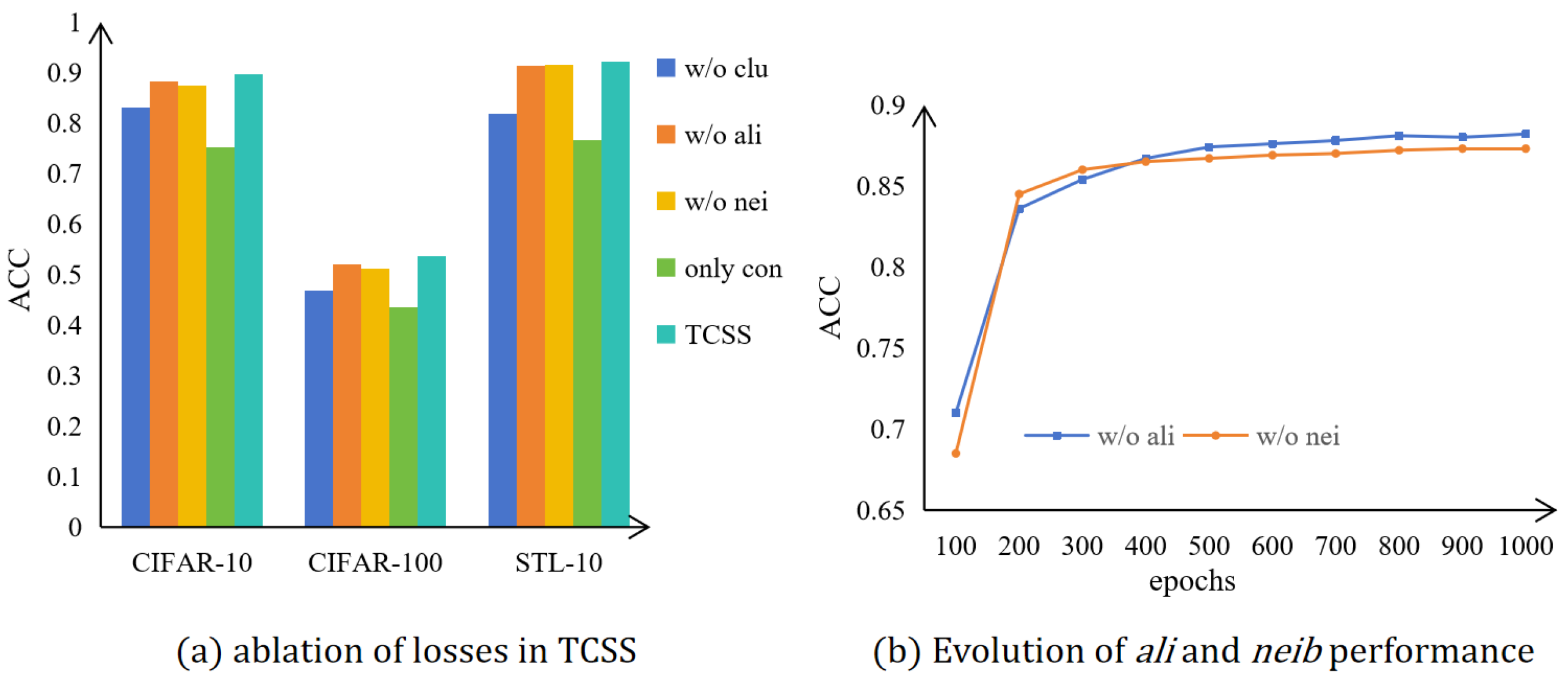
4.6.1. Ablation of Losses
4.6.2. Ablation of Triple-Augmented-View on TCSS
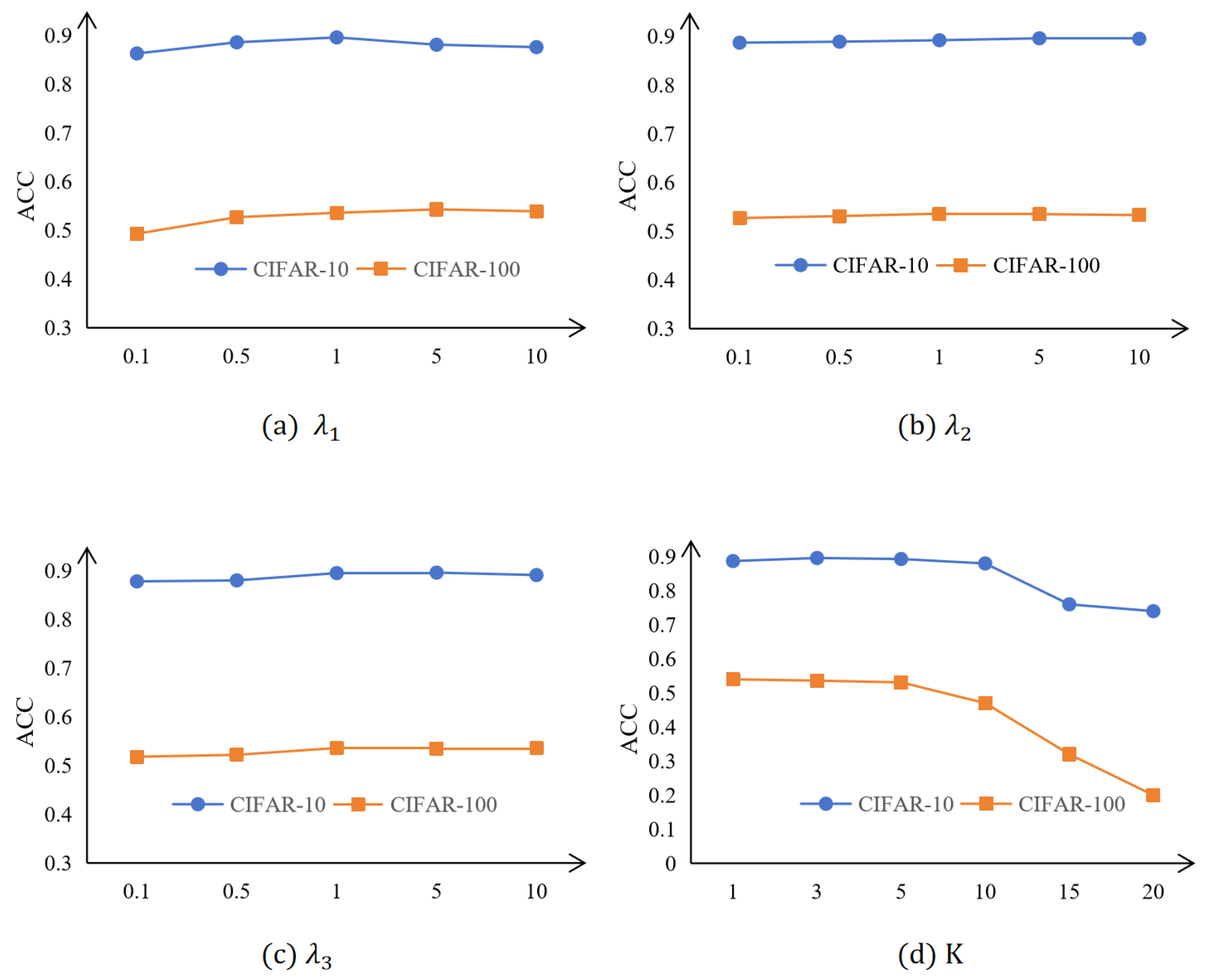
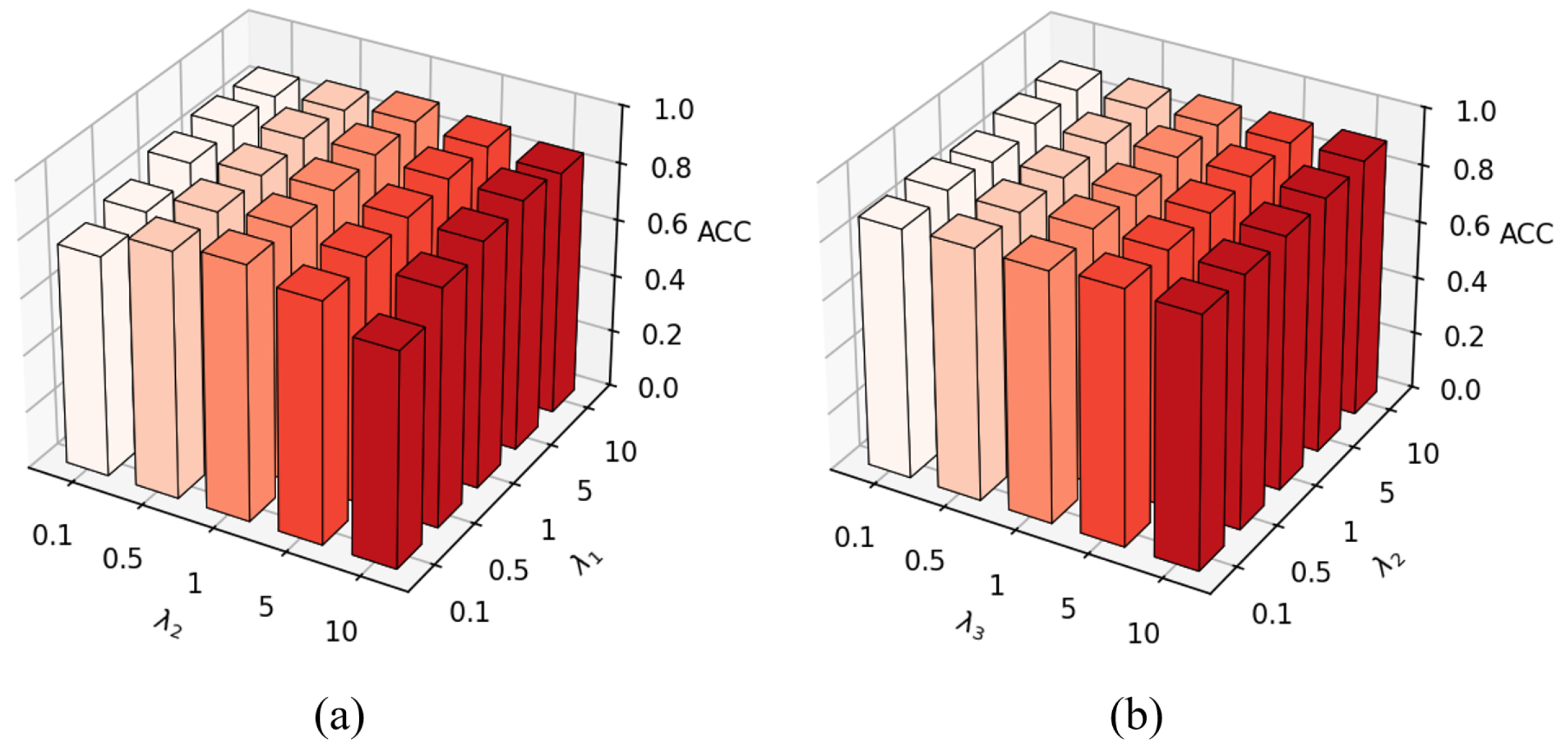
4.6.3. Sensitivity of Hyperparameters
4.6.4. Influence of Clustering Loss with Different Settings of
4.6.5. Investigation of Boosting Strategies
5. Discussion
5.1. Extension of TCSS to Non-Image Domains
5.2. Relation to Multimodal and Text-Guided Clustering
5.3. Summary of Extensibility
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TCSS | Triple-stream Contrastive Deep Embedding Clustering via Semantic Structure |
| CL | Contrastive Learning |
| STC | Self-Training Clustering module |
References
- Yang, H.F.; Yin, X.N.; Cai, J.H.; Yang, Y.Q.; Luo, A.L.; Bai, Z.R.; Zhou, L.C.; Zhao, X.J.; Xun, Y.L. An in-depth exploration of LAMOST unknown spectra based on density clustering. Res. Astron. Astrophys. 2023, 23, 055006. [Google Scholar] [CrossRef]
- Xun, Y.; Wang, Y.; Zhang, J.; Yang, H.; Cai, J. Higher-order embedded learning for heterogeneous information networks and adaptive POI recommendation. Inf. Process. Manag. 2024, 61, 103763. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965; Volume 1, pp. 281–297. [Google Scholar]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. Adv. Neural Inf. Process. Syst. 2001, 14, 1–8. [Google Scholar]
- Zhou, S.; Xu, H.; Zheng, Z.; Chen, J.; Bu, J.; Wu, J.; Wang, X.; Zhu, W.; Ester, M. A comprehensive survey on deep clustering: Taxonomy, challenges, and future directions. arXiv 2022, arXiv:2206.07579. [Google Scholar] [CrossRef]
- Károly, A.I.; Fullér, R.; Galambos, P. Unsupervised clustering for deep learning: A tutorial survey. Acta Polytech. Hung. 2018, 15, 29–53. [Google Scholar] [CrossRef]
- Min, E.; Guo, X.; Liu, Q.; Zhang, G.; Cui, J.; Long, J. A survey of clustering with deep learning: From the perspective of network architecture. IEEE Access 2018, 6, 39501–39514. [Google Scholar] [CrossRef]
- Saunshi, N.; Plevrakis, O.; Arora, S.; Khodak, M.; Khandeparkar, H. A theoretical analysis of contrastive unsupervised representation learning. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 5628–5637. [Google Scholar]
- Caron, M.; Bojanowski, P.; Joulin, A.; Douze, M. Deep clustering for unsupervised learning of visual features. In Proceedings of the 2018 European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 132–149. [Google Scholar]
- Yang, J.; Parikh, D.; Batra, D. Joint unsupervised learning of deep representations and image clusters. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5147–5156. [Google Scholar]
- Chang, J.; Wang, L.; Meng, G.; Xiang, S.; Pan, C. Deep Adaptive Image Clustering. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5880–5888. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised deep embedding for clustering analysis. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 478–487. [Google Scholar]
- Yang, L.; Cheung, N.M.; Li, J.; Fang, J. Deep clustering by gaussian mixture variational autoencoders with graph embedding. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6440–6449. [Google Scholar]
- Van Gansbeke, W.; Vandenhende, S.; Georgoulis, S.; Proesmans, M.; Van Gool, L. Scan: Learning to classify images without labels. In Proceedings of the 16th European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 268–285. [Google Scholar]
- Caron, M.; Misra, I.; Mairal, J.; Goyal, P.; Bojanowski, P.; Joulin, A. Unsupervised learning of visual features by contrasting cluster assignments. Adv. Neural Inf. Process. Syst. 2020, 33, 9912–9924. [Google Scholar]
- Zhang, H.; Zhan, T.; Basu, S.; Davidson, I. A framework for deep constrained clustering. Data Min. Knowl. Discov. 2021, 35, 593–620. [Google Scholar] [CrossRef]
- Wu, J.; Long, K.; Wang, F.; Qian, C.; Li, C.; Lin, Z.; Zha, H. Deep Comprehensive Correlation Mining for Image Clustering. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8149–8158. [Google Scholar]
- Huang, J.; Gong, S.; Zhu, X. Deep Semantic Clustering by Partition Confidence Maximisation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 14–19 June 2020; pp. 8846–8855. [Google Scholar]
- Tao, Y.; Takagi, K.; Nakata, K. Clustering-friendly representation learning via instance discrimination and feature decorrelation. arXiv 2021, arXiv:2106.00131. [Google Scholar] [CrossRef]
- Deng, X.; Huang, D.; Chen, D.H.; Wang, C.D.; Lai, J.H. Strongly augmented contrastive clustering. Pattern Recognit. 2023, 139, 109470. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, D.; Wang, C.D.; Lai, J.H. Deep image clustering with contrastive learning and multi-scale graph convolutional networks. Pattern Recognit. 2024, 146, 110065. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, Y.; Wang, S.; Fan, J.; Guo, W. Wasserstein embedding learning for deep clustering: A generative approach. IEEE Trans. Multimed. 2024, 26, 7567–7580. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, H.; Zhu, X.; Chen, Y. Deep contrastive clustering via hard positive sample debiased. Neurocomputing 2024, 570, 127147. [Google Scholar] [CrossRef]
- Liu, Z.; Song, P. Deep low-rank tensor embedding for multi-view subspace clustering. Expert Syst. Appl. 2024, 237, 121518. [Google Scholar] [CrossRef]
- Van Der Maaten, L. Learning a parametric embedding by preserving local structure. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics, Clearwater Beach, FL, USA, 16–18 April 2009; pp. 384–391. [Google Scholar]
- Li, F.; Qiao, H.; Zhang, B. Discriminatively boosted image clustering with fully convolutional auto-encoders. Pattern Recognit. 2018, 83, 161–173. [Google Scholar] [CrossRef]
- Han, K.; Vedaldi, A.; Zisserman, A. Learning to discover novel visual categories via deep transfer clustering. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8401–8409. [Google Scholar]
- Guo, X.; Gao, L.; Liu, X.; Yin, J. Improved deep embedded clustering with local structure preservation. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, VIC, Australia, 19–25 August 2017; pp. 1753–1759. [Google Scholar]
- Guo, X.; Zhu, E.; Liu, X.; Yin, J. Deep embedded clustering with data augmentation. In Proceedings of the 10th Asian Conference on Machine Learning, Beijing, China, 14–16 November 2018; pp. 550–565. [Google Scholar]
- Li, P.; Zhao, H.; Liu, H. Deep fair clustering for visual learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 14–19 June 2020; pp. 9070–9079. [Google Scholar]
- Gunari, A.; Kudari, S.V.; Nadagadalli, S.; Goudnaik, K.; Tabib, R.A.; Mudenagudi, U.; Jamadandi, A. Deep visual attention based transfer clustering. In Advances in Computing and Network Communications: Proceedings of CoCoNet 2020; Springer: Singapore, 2021; Volume 2, pp. 357–366. [Google Scholar]
- Rabbani, S.B.; Medri, I.V.; Samad, M.D. Deep clustering of tabular data by weighted Gaussian distribution learning. Neurocomputing 2025, 623, 129359. [Google Scholar] [CrossRef]
- Zeng, L.; Yao, S.; Liu, X.; Xiao, L.; Qian, Y. A clustering ensemble algorithm for handling deep embeddings using cluster confidence. Comput. J. 2025, 68, 163–174. [Google Scholar] [CrossRef]
- Wang, S.; Yang, J.; Yao, J.; Bai, Y.; Zhu, W. An overview of advanced deep graph node clustering. IEEE Trans. Comput. Soc. Syst. 2023, 11, 1302–1314. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 2020 International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Chen, X.; Fan, H.; Girshick, R.; He, K. Improved baselines with momentum contrastive learning. arXiv 2020, arXiv:2003.04297. [Google Scholar] [CrossRef]
- Geiping, J.; Garrido, Q.; Fernandez, P.; Bar, A.; Pirsiavash, H.; LeCun, Y.; Goldblum, M. A Cookbook of Self-Supervised Learning. arXiv 2023, arXiv:2304.12210. [Google Scholar] [CrossRef]
- Li, J.; Zhou, P.; Xiong, C.; Hoi, S.C. Prototypical contrastive learning of unsupervised representations. arXiv 2020, arXiv:2005.04966. [Google Scholar]
- Li, Y.; Hu, P.; Liu, Z.; Peng, D.; Zhou, J.T.; Peng, X. Contrastive clustering. In Proceedings of the 2021 AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 8547–8555. [Google Scholar]
- Li, Y.; Yang, M.; Peng, D.; Li, T.; Huang, J.; Peng, X. Twin contrastive learning for online clustering. Int. J. Comput. Vis. 2022, 130, 2205–2221. [Google Scholar] [CrossRef]
- Zhang, F.; Li, L.; Hua, Q.; Dong, C.R.; Lim, B.H. Improved deep clustering model based on semantic consistency for image clustering. Knowl.-Based Syst. 2022, 253, 109507. [Google Scholar] [CrossRef]
- Wang, X.; Qi, G.J. Contrastive learning with stronger augmentations. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5549–5560. [Google Scholar] [CrossRef] [PubMed]
- Luo, F.; Liu, Y.; Gong, X.; Nan, Z.; Guo, T. EMVCC: Enhanced multi-view contrastive clustering for hyperspectral images. In Proceedings of the 32nd ACM International Conference on Multimedia, Melbourne, VIC, Australia, 28 October–1 November 2024; pp. 6288–6296. [Google Scholar]
- Wei, X.; Hu, T.; Wu, D.; Yang, F.; Zhao, C.; Lu, Y. ECCT: Efficient contrastive clustering via pseudo-Siamese vision transformer and multi-view augmentation. Neural Netw. 2024, 180, 106684. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Deng, X.; Chen, D.H.; Wen, Z.; Sun, W.; Wang, C.D.; Lai, J.H. Deep clustering with hybrid-grained contrastive and discriminative learning. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 9472–9483. [Google Scholar] [CrossRef]
- Huang, D.; Chen, D.H.; Chen, X.; Wang, C.D.; Lai, J.H. Deepclue: Enhanced deep clustering via multi-layer ensembles in neural networks. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 1582–1594. [Google Scholar] [CrossRef]
- Kulatilleke, G.K.; Portmann, M.; Chandra, S.S. SCGC: Self-supervised contrastive graph clustering. Neurocomputing 2025, 611, 128629. [Google Scholar] [CrossRef]
- Shi, F.; Wan, S.; Wu, S.; Wei, H.; Lu, H. Deep contrastive coordinated multi-view consistency clustering. Mach. Learn. 2025, 114, 81. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 702–703. [Google Scholar]
- Niu, C.; Shan, H.; Wang, G. Spice: Semantic pseudo-labeling for image clustering. IEEE Trans. Image Process. 2022, 31, 7264–7278. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Coates, A.; Ng, A.; Lee, H. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 215–223. [Google Scholar]
- Radford, A. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the NIPS 2017 Workshop, Long Beach, CA, USA, 8–9 December 2017. [Google Scholar]
- Kingma, D.P. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy layer-wise training of deep networks. Adv. Neural Inf. Process. Syst. 2006, 19, 1–8. [Google Scholar]
- Qiu, L.; Zhang, Q.; Chen, X.; Cai, S. Multi-level cross-modal alignment for image clustering. In Proceedings of the 38th AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 14695–14703. [Google Scholar]
- Cai, S.; Qiu, L.; Chen, X.; Zhang, Q.; Chen, L. Semantic-enhanced image clustering. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 6869–6878. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Lee, S.; Park, T.; Lee, K. Soft contrastive learning for time series. arXiv 2023, arXiv:2312.16424. [Google Scholar]
- Eldele, E.; Ragab, M.; Chen, Z.; Wu, M.; Kwoh, C.K.; Li, X.; Guan, C. Time-series representation learning via temporal and contextual contrasting. arXiv 2021, arXiv:2106.14112. [Google Scholar] [CrossRef]
- Khoeini, A.; Peng, S.; Ester, M. Informed Augmentation Selection Improves Tabular Contrastive Learning. In Proceedings of the 29th Pacific-Asia Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 June 2025; pp. 306–318. [Google Scholar]
- Onishi, S.; Meguro, S. Rethinking data augmentation for tabular data in deep learning. arXiv 2023, arXiv:2305.10308. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, P.; Liu, K.; Wang, P.; Fu, Y.; Lu, C.T.; Aggarwal, C.C.; Pei, J.; Zhou, Y. A comprehensive survey on data augmentation. IEEE Trans. Knowl. Data Eng. 2025, 1–20. [Google Scholar] [CrossRef]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the 2021 International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]




| Aspect | SM 3 | CSD 3 | CSIS 3 | SE 3 | AP 3 | Perf. 1,3 (NMI/ACC/ARI) 2 |
|---|---|---|---|---|---|---|
| CC-2021 [39] | weak, weak | None | Consistency | hyper-line segment | Existence | 0.705, 0.790, 0.637 |
| IDFD-2021 [19] | weak, weak | None | Independence | hyper-line segment | Nonexistence | 0.711, 0.815, 0.663 |
| DCSC-2022 [41] | weak, weak | None | Consistency | hyper-line segment | Existence | 0.704, 0.798, 0.644 |
| DeepCluE-2024 [46] | weak, weak | None | Consistency | hyper-line segment | Existence | 0.727, 0.764, 0.646 |
| IcicleGCN-2024 [21] | weak, weak | None | Consistency | hyper-line segment | Existence | 0.729, 0.807, 0.660 |
| TCSS | raw, weak, strong | Yes | Fusion + Alignment | hyper-triangle | Nonexistence | 0.834, 0.896, 0.787 |
| Datasets | CIFAR-10 | CIFAR-100 | STL-10 | ImageNet-10 | ImageNet-Dogs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Meric | NMI | ACC | ARI | NMI | ACC | ARI | NMI | ACC | ARI | NMI | ACC | ARI | NMI | ACC | ARI |
| K-Means [3] | 0.087 | 0.229 | 0.049 | 0.084 | 0.130 | 0.028 | 0.125 | 0.192 | 0.061 | 0.119 | 0.241 | 0.057 | 0.055 | 0.105 | 0.020 |
| SC [4] | 0.103 | 0.247 | 0.085 | 0.090 | 0.136 | 0.022 | 0.098 | 0.159 | 0.048 | 0.151 | 0.274 | 0.076 | 0.038 | 0.111 | 0.013 |
| AE [57] | 0.239 | 0.314 | 0.169 | 0.100 | 0.165 | 0.048 | 0.250 | 0.303 | 0.161 | 0.210 | 0.317 | 0.152 | 0.104 | 0.185 | 0.073 |
| VAE [56] | 0.245 | 0.291 | 0.167 | 0.108 | 0.152 | 0.040 | 0.200 | 0.282 | 0.146 | 0.193 | 0.334 | 0.168 | 0.107 | 0.179 | 0.079 |
| JULE [10] | 0.192 | 0.272 | 0.138 | 0.103 | 0.137 | 0.033 | 0.182 | 0.277 | 0.164 | 0.175 | 0.300 | 0.138 | 0.054 | 0.138 | 0.028 |
| DCGAN [53] | 0.265 | 0.315 | 0.176 | 0.120 | 0.151 | 0.045 | 0.210 | 0.298 | 0.139 | 0.225 | 0.346 | 0.157 | 0.121 | 0.174 | 0.078 |
| DEC [12] | 0.257 | 0.301 | 0.161 | 0.136 | 0.185 | 0.050 | 0.276 | 0.359 | 0.186 | 0.282 | 0.381 | 0.203 | 0.122 | 0.195 | 0.079 |
| DAC [11] | 0.396 | 0.522 | 0.306 | 0.185 | 0.238 | 0.088 | 0.366 | 0.470 | 0.257 | 0.394 | 0.527 | 0.302 | 0.219 | 0.275 | 0.111 |
| DCCM [17] | 0.496 | 0.623 | 0.408 | 0.285 | 0.327 | 0.173 | 0.376 | 0.482 | 0.262 | 0.608 | 0.710 | 0.555 | 0.321 | 0.383 | 0.182 |
| PICA [18] | 0.591 | 0.696 | 0.512 | 0.310 | 0.337 | 0.171 | 0.611 | 0.713 | 0.531 | 0.802 | 0.870 | 0.761 | 0.352 | 0.352 | 0.201 |
| CC [39] | 0.705 | 0.790 | 0.637 | 0.431 | 0.429 | 0.266 | 0.764 | 0.850 | 0.726 | 0.859 | 0.893 | 0.822 | 0.445 | 0.429 | 0.274 |
| SPICE [50] | 0.734 | 0.838 | 0.705 | 0.448 | 0.468 | 0.294 | 0.817 | 0.908 | 0.812 | 0.840 | 0.921 | 0.836 | 0.498 | 0.546 | 0.362 |
| TCL [40] | 0.790 | 0.865 | 0.752 | 0.529 | 0.531 | 0.357 | 0.799 | 0.868 | 0.757 | 0.875 | 0.895 | 0.837 | 0.518 | 0.549 | 0.381 |
| DCSC [41] | 0.704 | 0.798 | 0.644 | 0.452 | 0.469 | 0.293 | 0.792 | 0.865 | 0.749 | 0.867 | 0.904 | 0.838 | 0.462 | 0.443 | 0.299 |
| SACC [20] | 0.765 | 0.851 | 0.724 | 0.448 | 0.443 | 0.282 | 0.691 | 0.759 | 0.626 | 0.877 | 0.905 | 0.843 | 0.455 | 0.437 | 0.285 |
| DeepCluE [46] | 0.727 | 0.764 | 0.646 | 0.472 | 0.457 | 0.288 | - | - | - | 0.882 | 0.924 | 0.856 | 0.448 | 0.416 | 0.273 |
| IcicleGCN [21] | 0.729 | 0.807 | 0.660 | 0.459 | 0.461 | 0.311 | - | - | - | 0.904 | 0.955 | 0.905 | 0.456 | 0.415 | 0.279 |
| DHCL [45] | 0.710 | 0.801 | 0.654 | 0.432 | 0.446 | 0.275 | 0.726 | 0.821 | 0.680 | - | - | - | 0.495 | 0.511 | 0.359 |
| TCSS | 0.834 | 0.896 | 0.787 | 0.511 | 0.536 | 0.383 | 0.845 | 0.922 | 0.822 | 0.910 | 0.938 | 0.907 | 0.597 | 0.647 | 0.502 |
| Std. | ±0.006 | ±0.019 | ±0.021 | ±0.017 | ±0.021 | ±0.013 | ±0.005 | ±0.013 | ±0.006 | ±0.019 | ±0.026 | ±0.031 | ±0.036 | ±0.026 | ±0.017 |
| p-value | 0.0287 | 0.0324 | 0.0351 | 0.0071 | 0.0063 | 0.0068 | 0.0198 | 0.0215 | 0.0242 | 0.0335 | 0.0389 | 0.0412 | 0.0234 | 0.0276 | 0.0251 |
| Methods 1 | Parameter Count 2 | Training Cost 2 |
|---|---|---|
| TCL [40] | 22.21 M 3 | 17.63 H |
| SACC [20] | 22.21 M 3 | 18.56 H |
| SPICE [50] | 22.19 M | 23.40 H |
| IcicleGCN [21] | 25.1 M | 21.14 H |
| TCSS | 22.13 M | 20.42 H |
| Augmentations | NMI | ACC | ARI |
|---|---|---|---|
| W + W | 0.701 | 0.813 | 0.639 |
| W + R | 0.689 | 0.794 | 0.612 |
| W + S | 0.757 | 0.851 | 0.710 |
| W + W + S | 0.827 | 0.889 | 0.764 |
| W + S + R (TCSS) | 0.834 | 0.896 | 0.787 |
| S + S + R | 0.668 | 0.767 | 0.595 |
| S + S + W | 0.625 | 0.749 | 0.574 |
| w/o tri-clu | 0.771 | 0.862 | 0.732 |
| Datasets | STL-10 | CIFAR-100 | ImageNet-Dogs | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Meric | NMI | ACC | ARI | NMI | ACC | ARI | NMI | ACC | ARI |
| 0.768 | 0.863 | 0.721 | 0.441 | 0.463 | 0.285 | 0.386 | 0.413 | 0.298 | |
| 0.782 | 0.886 | 0.745 | 0.461 | 0.480 | 0.317 | 0.438 | 0.461 | 0.397 | |
| learned | 0.791 | 0.881 | 0.749 | 0.453 | 0.474 | 0.321 | 0.445 | 0.487 | 0.408 |
| -CF | 0.818 | 0.893 | 0.758 | 0.475 | 0.491 | 0.318 | 0.503 | 0.559 | 0.412 |
| -TCSS | 0.845 | 0.922 | 0.822 | 0.511 | 0.536 | 0.383 | 0.597 | 0.647 | 0.502 |
| Datasets | CIFAR-10 | ImageNet-Dogs | ||||
|---|---|---|---|---|---|---|
| Boosting Strategy | NMI | ACC | ARI | NMI | ACC | ARI |
| w/o boosting | 0.793 | 0.882 | 0.756 | 0.579 | 0.630 | 0.467 |
| TCSS-tag | 0.834 | 0.896 | 0.787 | 0.597 | 0.647 | 0.502 |
| TCSS-semi | 0.889 | 0.937 | 0.872 | 0.654 | 0.685 | 0.536 |
| SPICE-self | 0.734 | 0.838 | 0.705 | 0.498 | 0.546 | 0.362 |
| SPICE-semi | 0.865 | 0.926 | 0.852 | 0.504 | 0.554 | 0.343 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, A.; Cai, J.; Yang, H.; Xun, Y.; Zhao, X. Triple-Stream Contrastive Deep Embedding Clustering via Semantic Structure. Mathematics 2025, 13, 3578. https://doi.org/10.3390/math13223578
Zheng A, Cai J, Yang H, Xun Y, Zhao X. Triple-Stream Contrastive Deep Embedding Clustering via Semantic Structure. Mathematics. 2025; 13(22):3578. https://doi.org/10.3390/math13223578
Chicago/Turabian StyleZheng, Aiyu, Jianghui Cai, Haifeng Yang, Yalin Xun, and Xujun Zhao. 2025. "Triple-Stream Contrastive Deep Embedding Clustering via Semantic Structure" Mathematics 13, no. 22: 3578. https://doi.org/10.3390/math13223578
APA StyleZheng, A., Cai, J., Yang, H., Xun, Y., & Zhao, X. (2025). Triple-Stream Contrastive Deep Embedding Clustering via Semantic Structure. Mathematics, 13(22), 3578. https://doi.org/10.3390/math13223578






