Investigation of a Biochemical Model with Recycling in Case of Negative Cooperativity
Abstract
1. Introduction
2. Analysis for g = 0—Negative Cooperativity
3. Numerical Analysis
4. Conclusions
- (1)
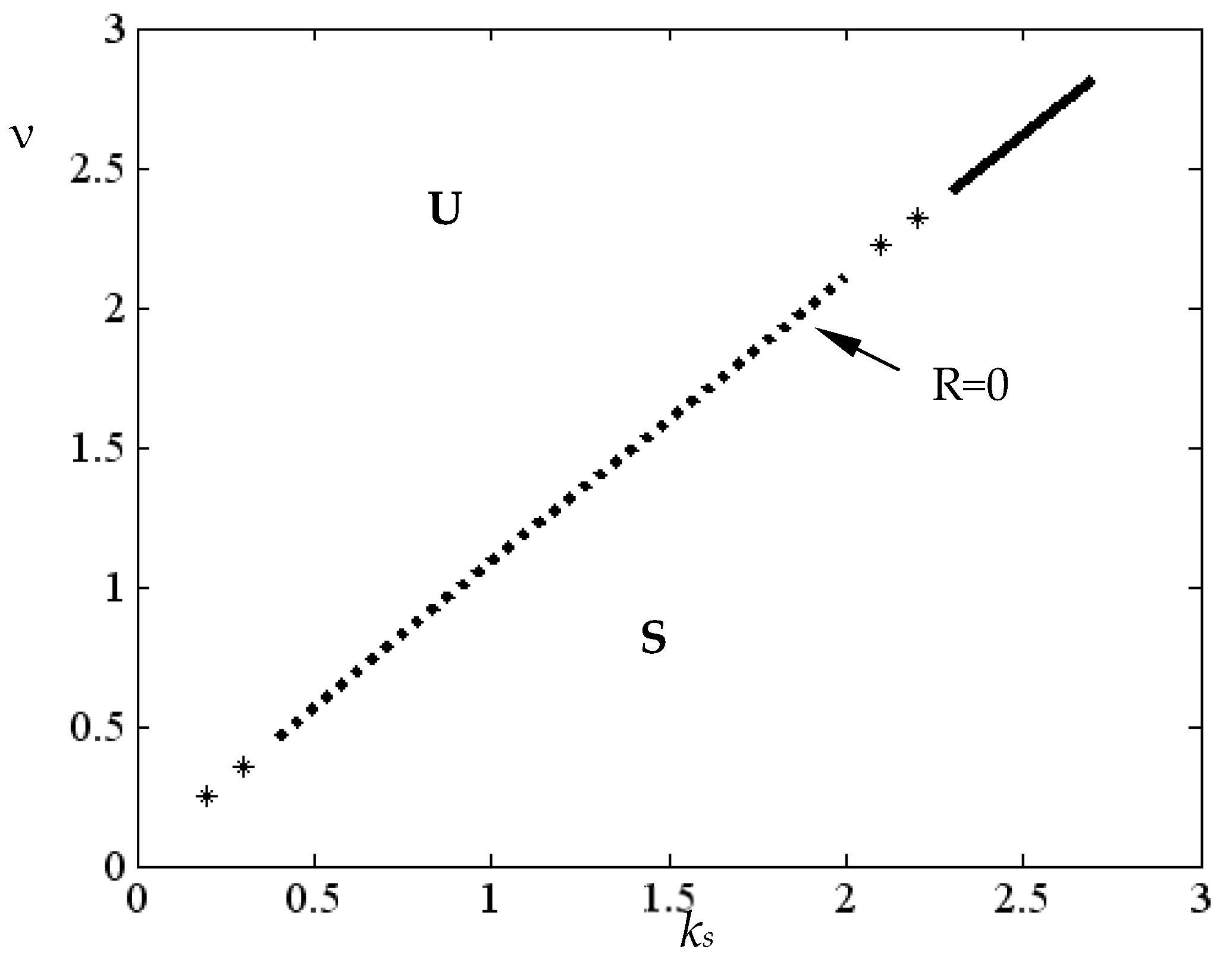
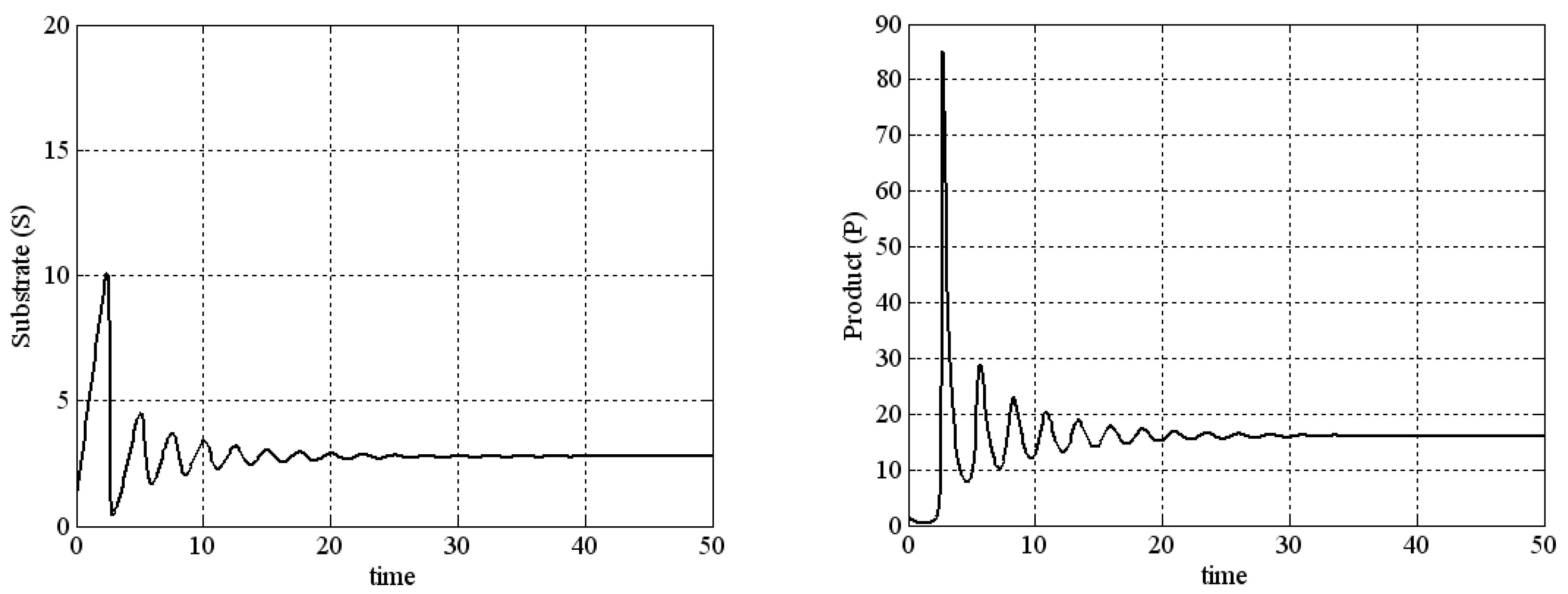
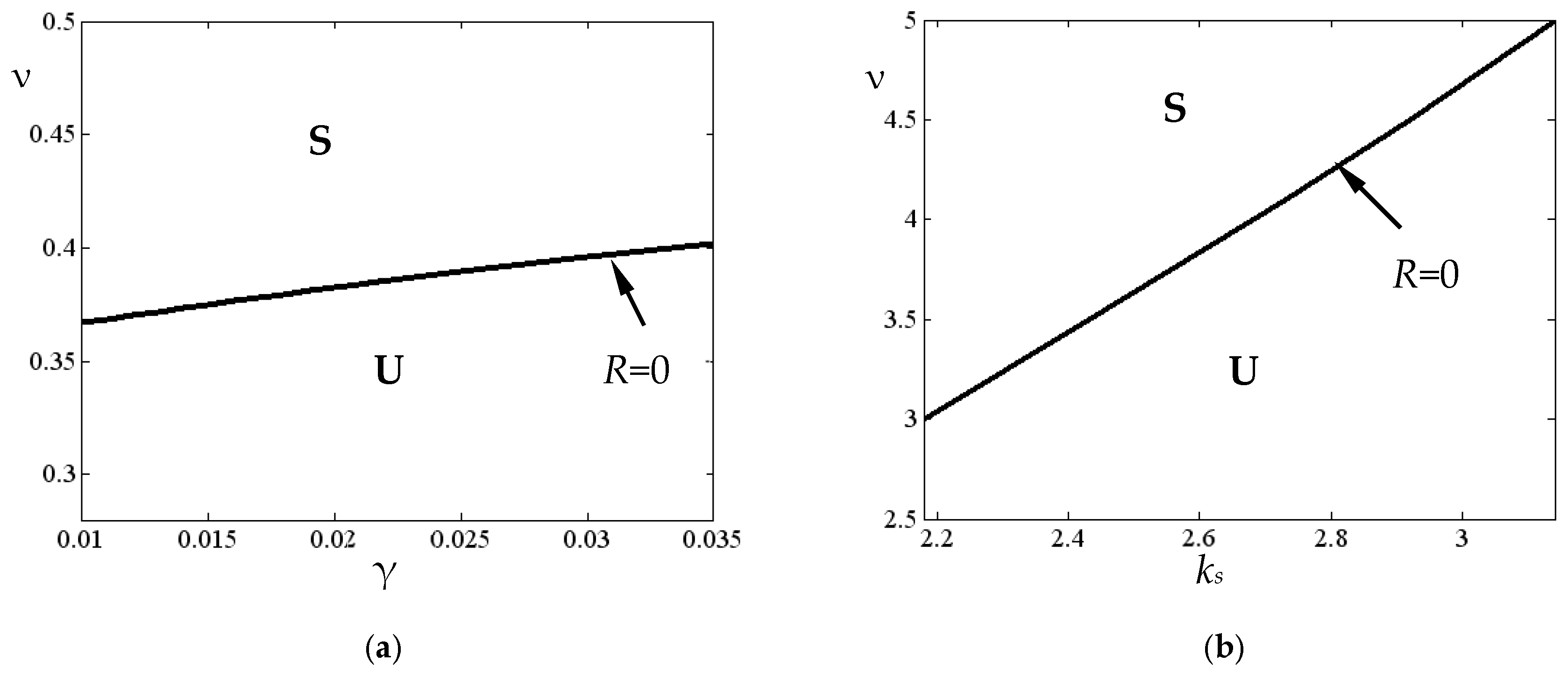
- When and are smaller than , , , and , it is structurally unstable, i.e., ;
- (2)
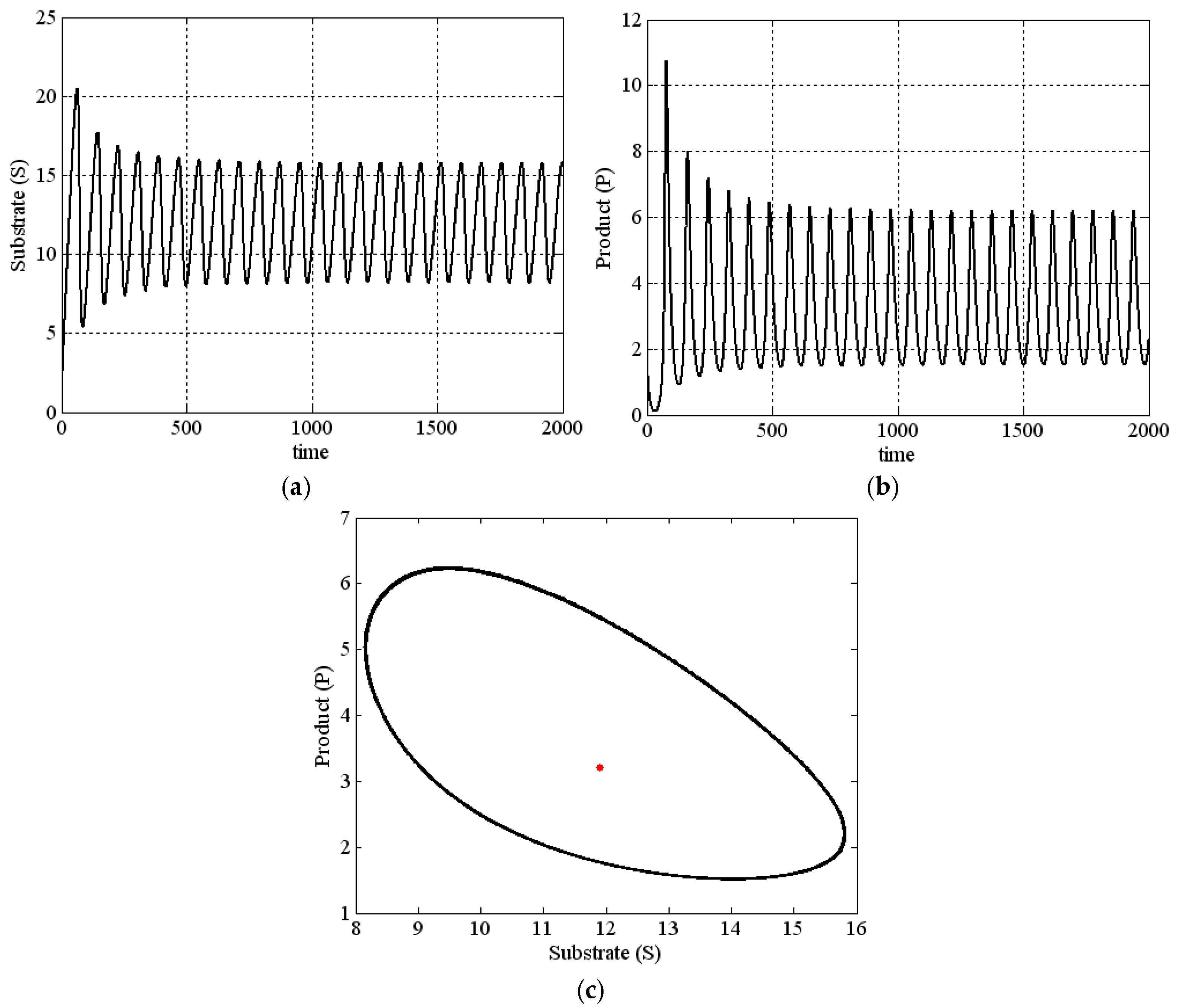
- For , , , and , it has an unstable limit cycle () and an external stable limit cycle (). Note that the same behavior (when and ) occurs for and which are larger than 2.3, , , and . Here, the boundary of stability is safe;
- (3)
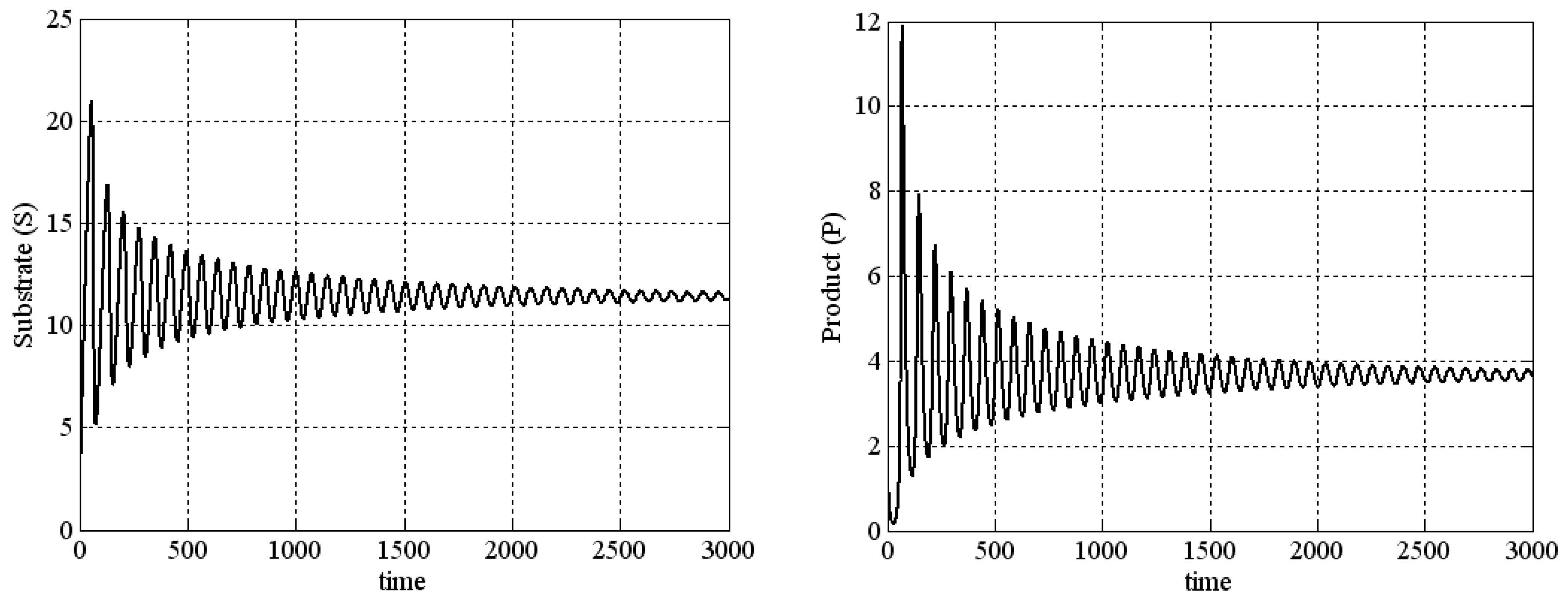
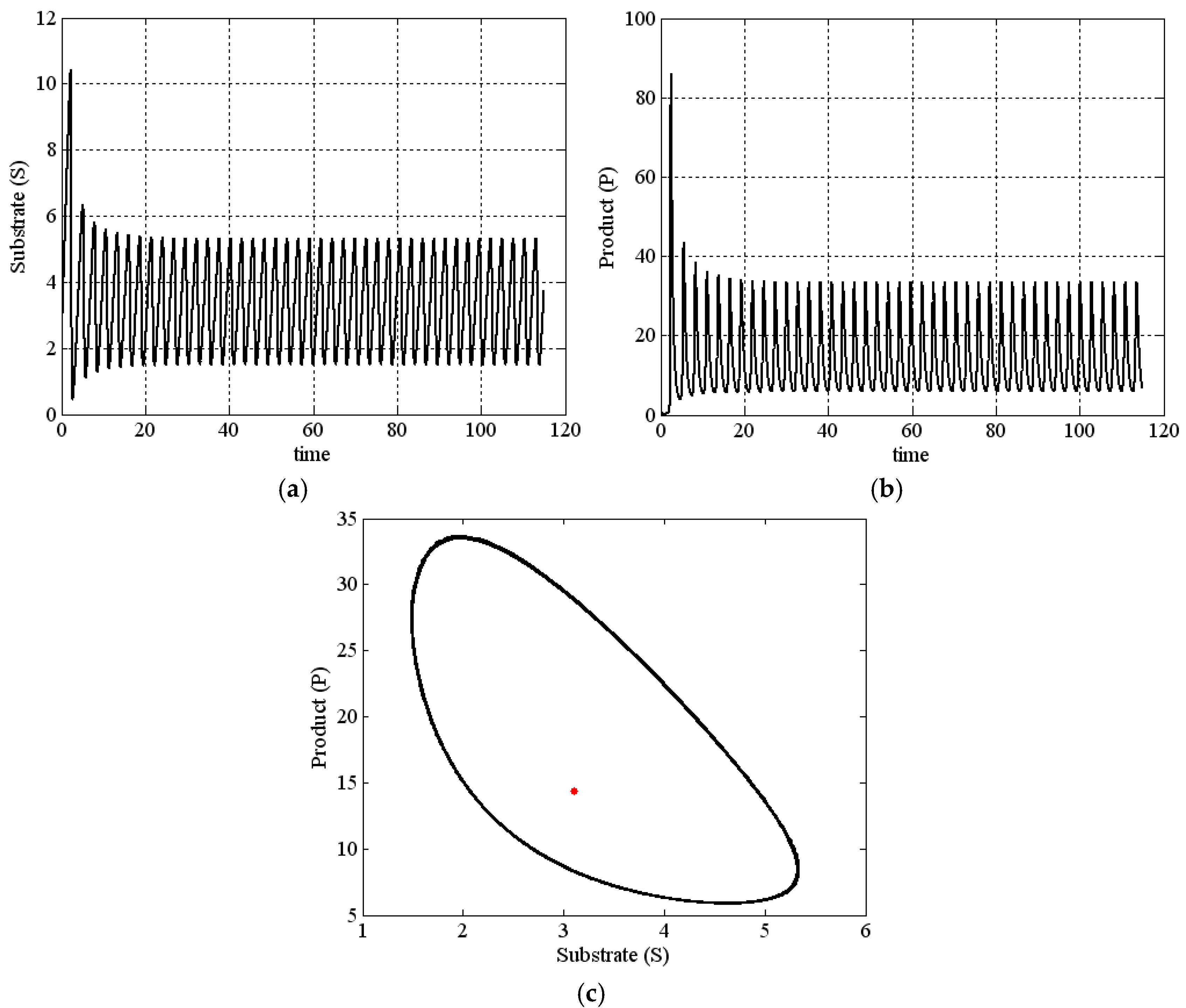
- When , , , , and , it has an external unstable limit cycle (), as the boundary of stability is dangerous.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
- (i)
- , and ;
- (ii)
- , and ;
- (iii)
- , and .

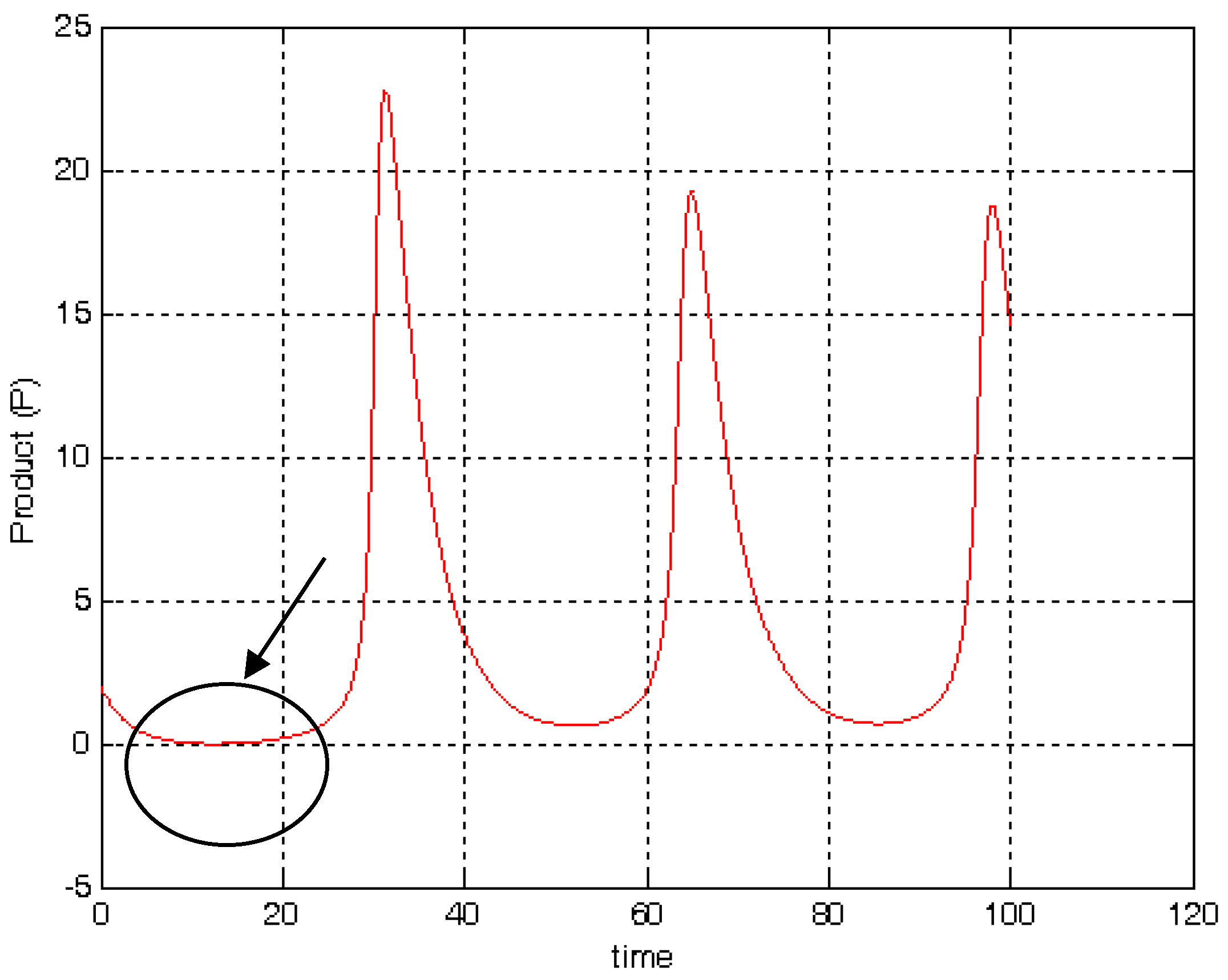
Appendix C
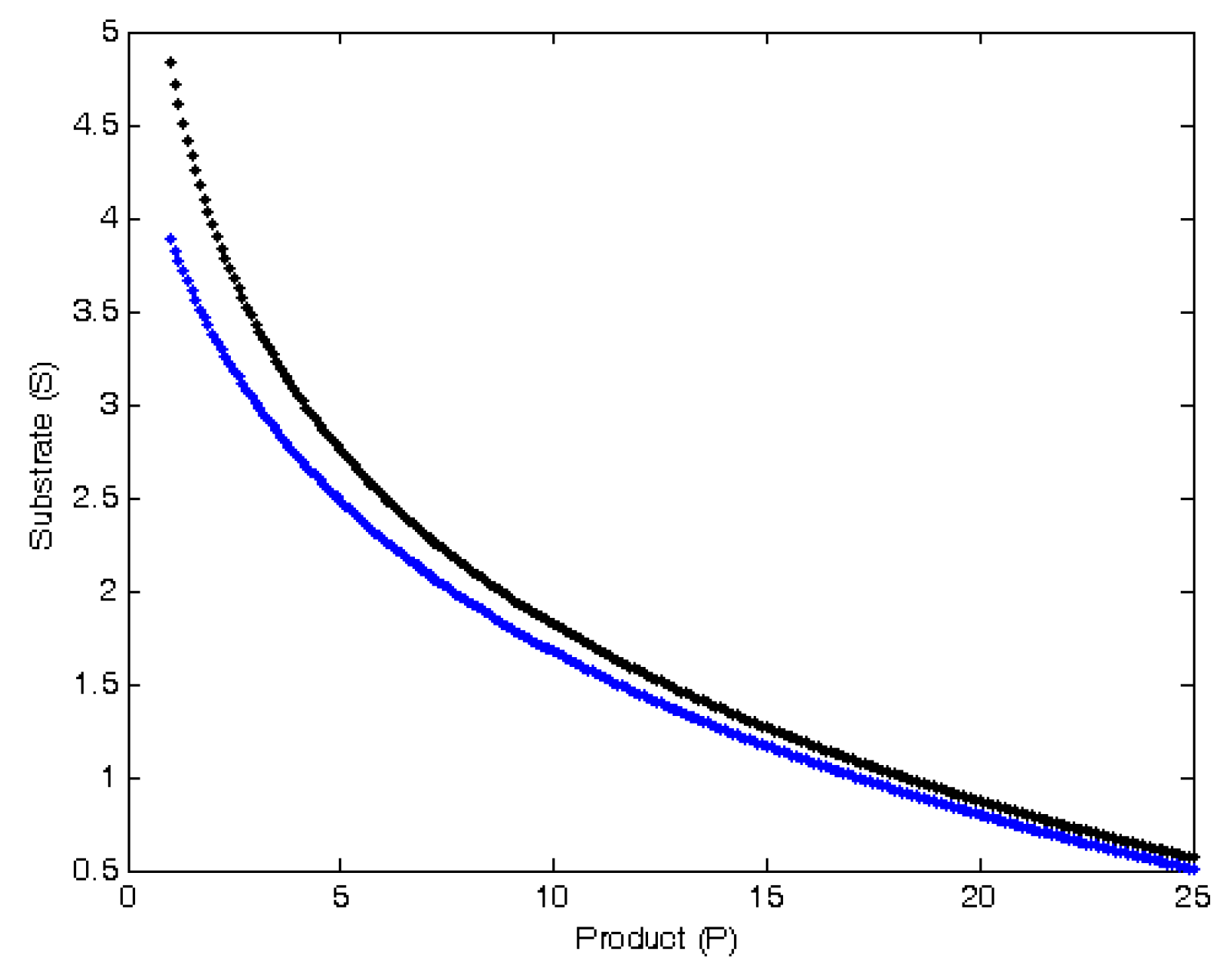
Appendix D
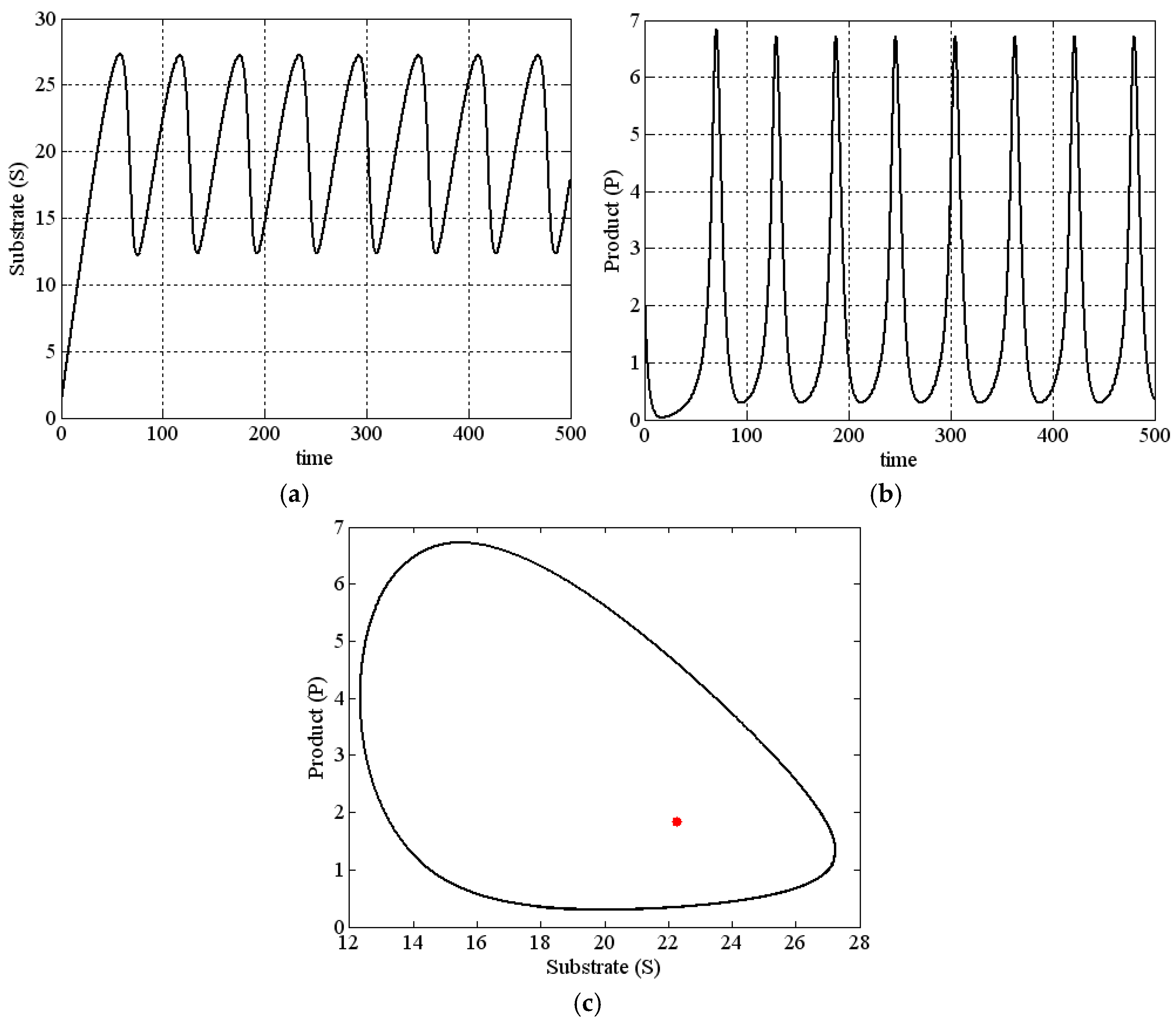
References
- Prigogine, I. The End of Certainty. Time, Chaos and the New Laws of Nature; The Free Press: New York, NY, USA, 1997. [Google Scholar]
- Rubin, A.; Riznichenko, G. Mathematical Biophysics; Springer: New York, NY, USA, 2014. [Google Scholar]
- Shao, P.; Shateyi, S. Stability analysis of SEIRS epidemic model with nonlinear incidence rate function. Mathematics 2021, 9, 2644. [Google Scholar] [CrossRef]
- Blanchini, F.; Giordano, G. Polyhedral Lyapunov functions structurally ensure global asymptotic stability of dynamical networks if the Jacobian is non-singular. Automatica 2017, 86, 183–191. [Google Scholar] [CrossRef][Green Version]
- Nikolov, S.; Lai, X.; Liebal, U.; Wolkenhauer, O.; Vera, J. Integration of sensitivity and bifurcation analysis to detect critical biochemical processes in cell signalling pathway. Int. J. Syst. Sci. 2010, 41, 81–105. [Google Scholar] [CrossRef]
- Jan, A.; Shah, R.; Ahmad, H.; Bilal, H.; Almohsen, B. Dynamic behavior of enzyme kinetics cooperative chemical reactions. AIP Adv. 2024, 14, 035139. [Google Scholar] [CrossRef]
- Nikolov, S. Modelling and analysis of miRNA regulation. BIOMATH 2014, 3, 1407231. [Google Scholar] [CrossRef][Green Version]
- Arnold, V.; Kozlov, V.; Neishtadt, A. Mathematical Aspects of Classical and Celestial Mechanics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Landa, P. Regular and Chaotic Oscillations; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Broer, H.; Takens, F. Dynamical Systems and Chaos; Springer: New York, NY, USA, 2011. [Google Scholar]
- Nayfeh, A.; Mook, D. Nonlinear Oscillations; John Wiley & Sons Inc.: New York, NY, USA, 1995. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 2002. [Google Scholar]
- Goldbeter, A. Biochemical Oscillations and Cellular Rhythms. The Molecular Bases of Periodic and Chaotic Behaviour; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Chen, L.; Wang, R.; Li, C.; Kazuyki, A. Modeling Biomolecular Networks in Cells, Structures and Dynamics; Springer: London, UK, 2010. [Google Scholar]
- Dumortier, F.; Llibre, J.; Artés, J.C. Qualitative Theory of Planar Differential Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Nguyen, L.; Kholodenko, B. Feedback regulation in cell signalling: Lessons for cancer therapeutics. Semin. Cell Dev. Biol. 2016, 50, 85–94. [Google Scholar] [CrossRef]
- Shilnikov, L.; Shilnikov, A.; Turaev, D.; Chua, L. Methods of Qualitative Theory in Nonlinear Dynamics; Part II; World Scientific: London, UK, 2001. [Google Scholar]
- Andronov, A.; Witt, A.; Chaikin, S. Theory of Oscillations; Addison-Wesley: Reading, MA, USA, 1966. [Google Scholar]
- Wu, Y.; Zhang, M.; Mao, J. Bifurcation of limit cycles at a nilpotent critical point in a septic Lyapunov system. J. Appl. Anal. Comput. 2020, 10, 2575–2591. [Google Scholar] [CrossRef]
- Cao, D.; Zhang, W. Global bifurcations and chaotic dynamics for a string-beam coupled system. Chaos Solitons Fractals 2008, 37, 858–875. [Google Scholar] [CrossRef]
- Xing, R.; Xiao, M.; Zhang, Y.; Qiu, J. Stability and Hopf bifurcation analysis of an (n+m)-neuron double-ring neural network model with multiple time delay. J. Syst. Sci. Complex. 2022, 35, 159–178. [Google Scholar] [CrossRef]
- Nikolov, S. Stability and Andronov-Hopf bifurcation of a system with three time delays. J. Math. 2013, 2013, 347071. [Google Scholar] [CrossRef]
- Nikolov, S.; Santos, G.; Wolkenhauer, O.; Vera, J. Model-based phenotypic signatures governing the dynamics of the stem and semi-differentiated cell populations in dysplastic colonic crypts. Bull. Math. Biol. 2018, 80, 360–384. [Google Scholar] [CrossRef] [PubMed]
- Seydel, R. Practical Bifurcation and Stability Analysis, 3rd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Zhdanov, V. Periodic perturbation of genetic oscillations. Chaos Solitons Fractals 2012, 45, 577–587. [Google Scholar] [CrossRef]
- Nikolov, S.; Wolkenhauer, O.; Vera, J. Tumors as chaotic attractors. Mol. BioSyst. 2014, 10, 172–179. [Google Scholar] [CrossRef] [PubMed]
- Nikolov, S.; Dimitrov, A.; Vera, J. Hierarchical levels of biological systems and their integration as a principal cause for tumour occurrence. Nonlinear Dyn. Psychol. Life Sci. 2019, 23, 315–329. [Google Scholar]
- Vera, J.; Lischer, C.; Nenov, M.; Nikolov, S.; Lai, X.; Eberhardt, M. Mathematical modelling in biomedicine: A primer for the curious and the skeptic. Int. J. Mol. Sci. 2021, 22, 547. [Google Scholar] [CrossRef]
- Ahrends, R.; Ota, A.; Kovary, K.; Kudo, T.; Ouk Park, B.; Teruel, M. Controlling low rates of cell differentiation through noise and ultrahigh feedback. Science 2014, 344, 1384–1389. [Google Scholar] [CrossRef]
- Nikolov, S.; Wolkenhauer, O.; Vera, J.; Nenov, M. The role of cooperativity in a p53-miR34 dynamical mathematical model. J. Theor. Biol. 2020, 495, 110252. [Google Scholar] [CrossRef]
- Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste; Gauthier-Villars: Paris, France, 1892; Tome I. (In French) [Google Scholar]
- Hopf, E. Abzweigung Einer Periodischen Lösung von Einer Stationären Lösung Eines Differential Systems. Ber. Math.-Phys. Kl Sächs. Akad. Wiss. Leipz. 1942, 94, 1–22. (In German) [Google Scholar]
- Andronov, A.; Leontovich, E.; Gordon, I.; Maier, A. Theory of Bifurcations of Dynamic Systems on a Plane; Israel Program for Scientific Translations: Jerusalem, Israel, 1971. [Google Scholar]
- Marsden, J.; McCracken, M. The Hopf Bifurcation and Its Applications; Springer: New York, NY, USA, 1976. [Google Scholar]
- Hassard, B.; Kazarinoff, N.; Wan, Y.-H. Theory and Applications of Hopf Bifurcation; London Mathematical Society Lecture Note Series; Cambridge University Press: New York, NY, USA, 1981; Volume 41. [Google Scholar]
- Minorsky, N. Nonlinear Oscillations; Van Nostrand: Princeton, NJ, USA, 1962. [Google Scholar]
- Kuznetsov, Y. Elements of Bifurcation Theory, 3rd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 2004. [Google Scholar]
- Bautin, N. Behaviour of Dynamical Systems Near the Boundary of Stability; Nauka: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Leonov, G.; Kuznetsova, O. Lyapunov quantities and limit cycles of two-dimensional dynamical systems. Analytical methods and symbolic computation. Regul. Chaotic Dyn. 2010, 15, 354–377. [Google Scholar] [CrossRef]
- Nikolov, S.; Vassilev, V. Assessing the non-linear dynamics of a Hopf-Langford type system. Mathematics 2021, 9, 2340. [Google Scholar] [CrossRef]
- Artés, J.; Llibre, J.; Schlomiuk, D. The Geometry of quadratic differential systems with a weak focus of second order. Int. J. Bifurc. Chaos Appl. Sci. Engrg. 2006, 16, 3127–3194. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Kudryashova, E. Cycles of two-dimensional systems: Computer calculations, proofs, and experiments. Vestn. St. Petersburg Univ. Math. 2008, 41, 216–250. [Google Scholar] [CrossRef]
- Llibre, J.; Novaes, D.; Teixeira, M. Maximum number of limit cycles for certain piecewise linear dynamical systems. Nonlinear Dyn. 2015, 82, 1159–1175. [Google Scholar] [CrossRef]
- Goldbeter, A. Computational approaches to cellular rhythms. Nature 2002, 420, 238–245. [Google Scholar] [CrossRef]
- Goldbeter, A. Dissipative structures in biological systems: Bistability, oscillations, spatial patterns and waves. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2018, 376, 20170376. [Google Scholar] [CrossRef]
- Tyson, J.; Novak, B. A dynamical paradigm for molecular cell biology. Trends Cell Biol. 2020, 30, 504–515. [Google Scholar] [CrossRef]
- Goldbeter, A.; Lefever, R. Dissipative structures for an allosteric model: Application to glycolytic oscillations. Biophys. J. 1972, 12, 1302–1315. [Google Scholar] [CrossRef]
- Goldbeter, A.; Nicolis, G. An allosteric enzyme model with positive feedback applied to glycolytic oscillations. Prog. Theor. Biol. 1976, 4, 65–160. [Google Scholar]
- Goldbeter, A.; Dupont, G. Allosteric regulation, cooperativity, and biochemical oscillations. Biophys. Chem. 1990, 37, 341–353. [Google Scholar] [CrossRef]
- Decroly, O.; Goldbeter, A. Birhythmicity, chaos, and other patterns of temporal self-organization in a multiply regulated biochemical system. Proc. Natl. Acad. Sci. USA 1982, 79, 6917–6921. [Google Scholar] [CrossRef]
- Segel, L.; Goldbeter, A. Scaling in biochemical kinetics: Dissection of a relaxation oscillator. J. Math. Biol. 1994, 32, 147–160. [Google Scholar] [CrossRef]
- Goldbeter, A. Oscillatory enzyme reactions and Michaelis-Menten kinetics. FEBS Lett. 2013, 587, 2778–2784. [Google Scholar] [CrossRef] [PubMed]
- Koshland, D.; Hamadani, K. Proteomics and models for enzyme cooperativity. J. Biol. Chem. 2002, 277, 46841–46844. [Google Scholar] [CrossRef] [PubMed]
- Seydoux, F.; Malhotra, O.; Bernhard, S.; Stark, G. Half-site reactivity. CRC Crit. Rev. Biochem. 1974, 2, 227–257. [Google Scholar] [CrossRef]
- Levitzki, A.; Koshland Jr, D. The role of negative cooperativity and half-of-the-sites reactivity in enzyme regulation. In Current Topics in Cellular Regulation; Academic Press: Cambridge, MA, USA, 1976; Volume 10, pp. 1–40. [Google Scholar]
- Koshland, D.E., Jr. The structural basis of negative cooperativity: Receptors and enzymes. Curr. Opin. Struct. Biol. 1996, 6, 757–761. [Google Scholar] [CrossRef]
- Seifert, F.; Golbik, R.; Brauer, J.; Lilie, J.; Schröder-Tittmann, K.; Hinze, E.; Korotchkina, L.; Patel, M.S.; Tittmann, K. Direct kinetic evidence for half-of-the-sites reactivity in the E1 component of the human pyruvate dehydrogenase multienzyme complex through alternating sites cofactor activation. Biochemistry 2006, 45, 12775–12785. [Google Scholar] [CrossRef]
- Bush, E.C.; Clark, A.E.; DeBoever, C.M.; Haynes, L.E.; Hussain, S.; Ma, S.; McDermott, M.M.; Novak, A.M.; Wentworth, J.S. Modeling the role of negative cooperativity in metabolic regulation and homeostasis. PLoS ONE 2012, 7, e48920. [Google Scholar] [CrossRef]
- Ha, S.; Ferrell Jr., J. Thresholds and ultrasensitivity from negative cooperativity. Science 2016, 352, 990–993. [Google Scholar] [CrossRef]
- Morán, F.; Goldbeter, A. Onset of birhthmicity in a regulated biochemical system. Biophys. Chem. 1984, 20, 149–156. [Google Scholar] [CrossRef]
- Cui, Q.; Karplus, M. Allostery and cooperativity revisited. Protein Sci. 2008, 17, 1295–1307. [Google Scholar] [CrossRef]
- Kister, J.; Poyart, C.; Edestein, S. Oxygen-organophosphate linkage in hemoglobin A. The double-hump effect. Biophys. J. 1987, 52, 527–535. [Google Scholar] [CrossRef] [PubMed]
- Moltagh, H.; Wrabi, J.; Li, J.; Hilser, V. The ensemble nature of allostery. Nature 2014, 508, 331–339. [Google Scholar]
- Connors, K. Chemical Kinetics. The Study of Reaction Rates in Solution; VCH Publishers, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Monod, J.; Wyman, J.; Changeux, J. On the nature of allosteric transitions: A plausible model. J. Mol. Biol. 1965, 12, 88–118. [Google Scholar] [CrossRef] [PubMed]
- Semenov, S.N.; Kraft, L.J.; Ainla, A.; Zhao, M.; Baghbanzadeh, M.; Campbell, V.E.; Kang, K.; Fox, J.M.; Whitesides, G.M. Autocatalytic, bistable, oscillatory networks of biologically relevant organic reactions. Nature 2016, 537, 656–660. [Google Scholar] [CrossRef]
- Parks, P.; Hahn, V. Stability Theory; Prentice Hall: New York, NY, USA, 1993. [Google Scholar]
- Lancaster, P. Theory of Matrices with Applications; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- Bautin, N.; Leontovich, E. Methods and Approaches for Investigation of Two Dimensional Dynamical Systems; Nauka: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Andronov, A.; Pontryagin, L. Systems grossieres. Dokladi Academii Nauk USSR 1937, 14, 247–251. [Google Scholar]
- Leontovich, E.; Mayer, A. On trajectories which definite the qualitative separation of sphere of trajectories. Dokladi Academii Nauk USSR 1937, 14, 251–254. [Google Scholar]
- Nikolov, S.; Yankulova, E.; Wolkenhauer, O.; Petrov, V. Principal difference between stability and structural stability (robustness) as used in systems biology. Nonlinear Dyn. Psychol. Life Sci. 2007, 11, 413–433. [Google Scholar]
- Olsman, N.; Goentoro, L. Allosteric proteins as logarithmic sensors. Proc. Natl. Acad. Sci. USA 2016, 113, E4423–E4430. [Google Scholar] [CrossRef]


| 0.248 | 0.2 | 0 |
| 0.356 | 0.3 | 0 |
| 0.46 | 0.4 | 0.13 |
| 0.675 | 0.6 | 0.31 |
| 0.883 | 0.8 | 0.55 |
| 1.09048 | 1 | 0.8 |
| 1.1938 | 1.1 | 0.93 |
| 1.2969 | 1.2 | 1 |
| 1.60398 | 1.5 | 1.2 |
| 2.1135 | 2 | 0.33 |
| 2.4168 | 2.3 | −1.3 |
| 2.618 | 2.5 | −3.1 |
| 2.8189 | 2.7 | −5.6 |
| 3 | 2.1763 | −6.31 |
| 3.5 | 2.43109 | −8.71 |
| 4.0 | 2.676 | −11.51 |
| 4.1 | 2.72419 | −12.12 |
| 4.5 | 2.9131 | −14.71 |
| 5 | 3.143 | −18.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolov, S.G.; Vassilev, V.M.; Nenov, M.I. Investigation of a Biochemical Model with Recycling in Case of Negative Cooperativity. Mathematics 2025, 13, 260. https://doi.org/10.3390/math13020260
Nikolov SG, Vassilev VM, Nenov MI. Investigation of a Biochemical Model with Recycling in Case of Negative Cooperativity. Mathematics. 2025; 13(2):260. https://doi.org/10.3390/math13020260
Chicago/Turabian StyleNikolov, Svetoslav G., Vassil M. Vassilev, and Momchil I. Nenov. 2025. "Investigation of a Biochemical Model with Recycling in Case of Negative Cooperativity" Mathematics 13, no. 2: 260. https://doi.org/10.3390/math13020260
APA StyleNikolov, S. G., Vassilev, V. M., & Nenov, M. I. (2025). Investigation of a Biochemical Model with Recycling in Case of Negative Cooperativity. Mathematics, 13(2), 260. https://doi.org/10.3390/math13020260






