Analytical Solution for Steady-State Seepage Field of Foundation Pit During Water Curtain Leakage
Abstract
1. Introduction
2. Two-Dimensional Steady-State Seepage Modelling of Pits During Water Curtain Leakage
3. Model Solution
3.1. Separation of Variables Method for Solving the Seepage Field
3.2. Seepage at Curtain Leaks
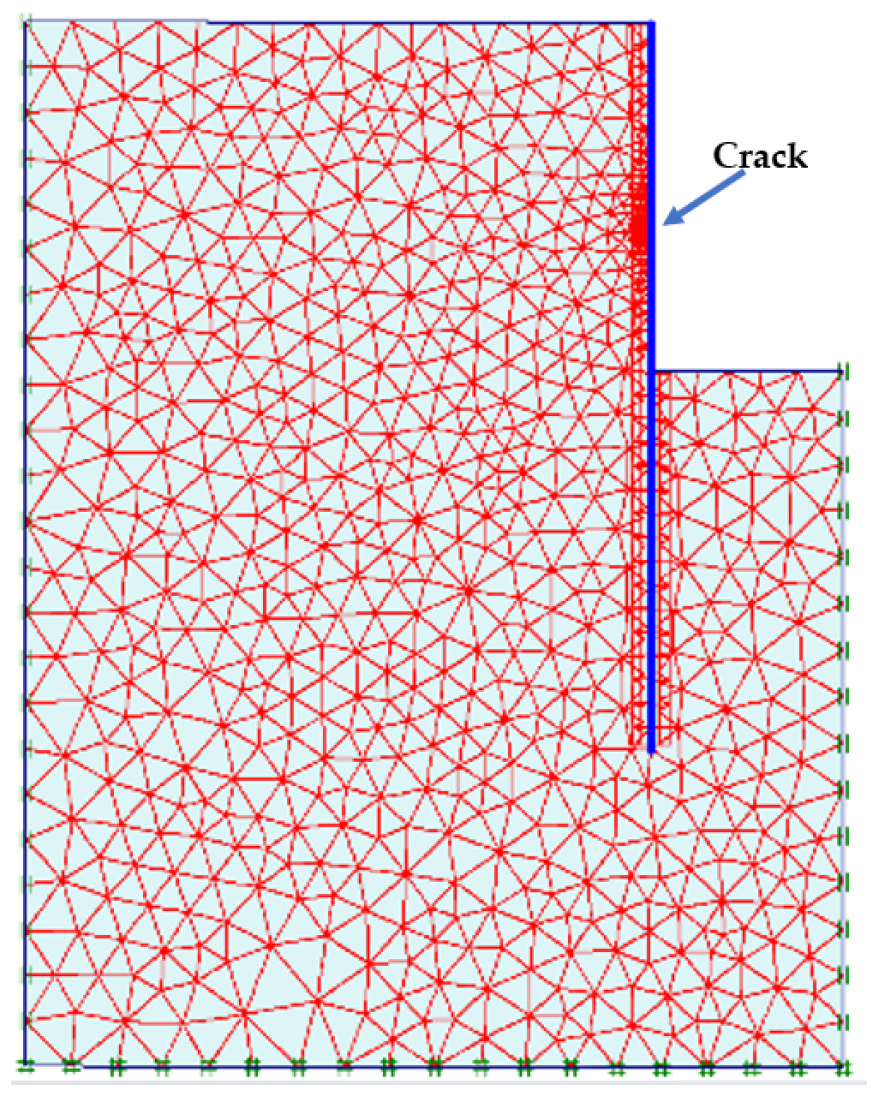
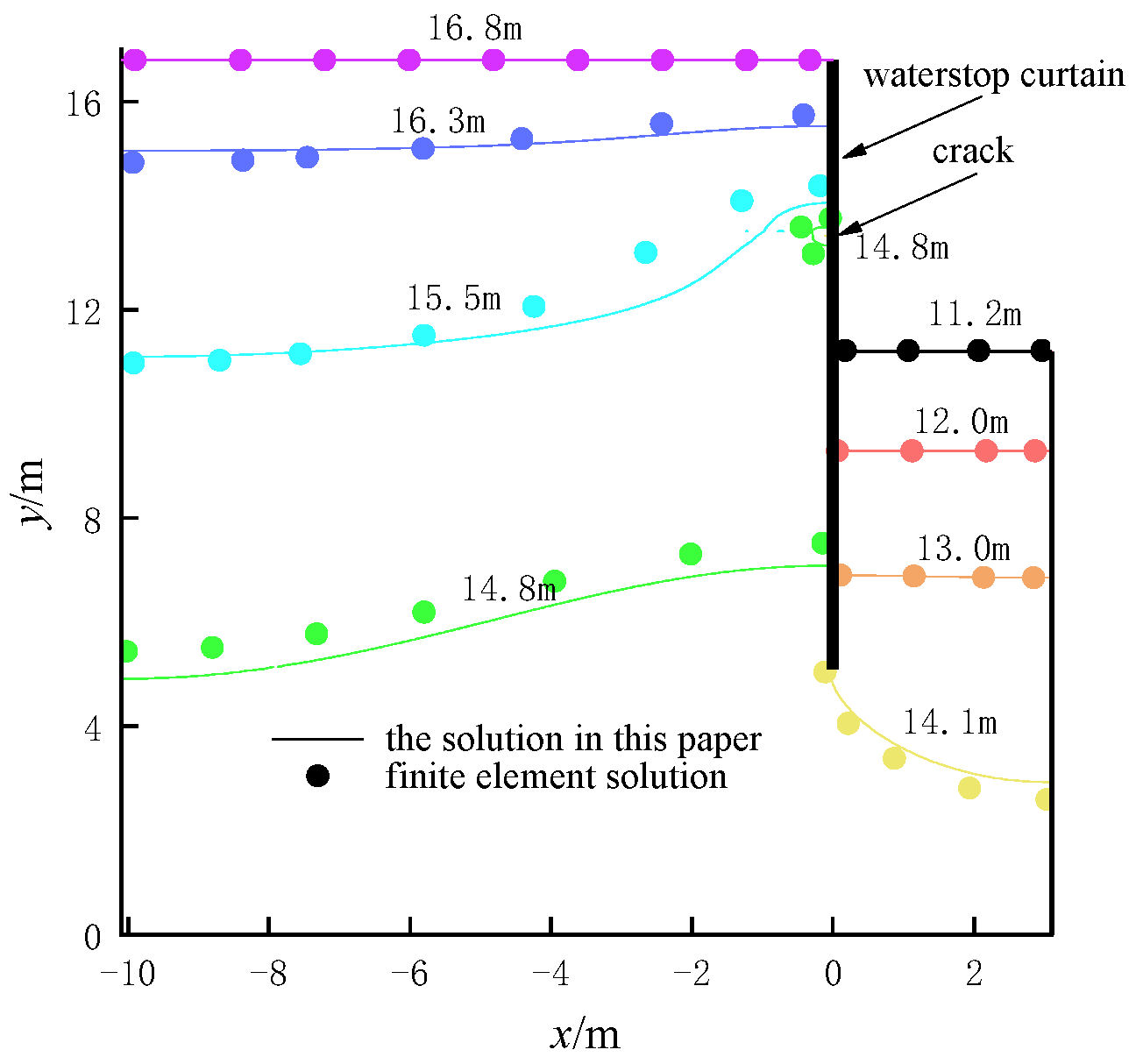
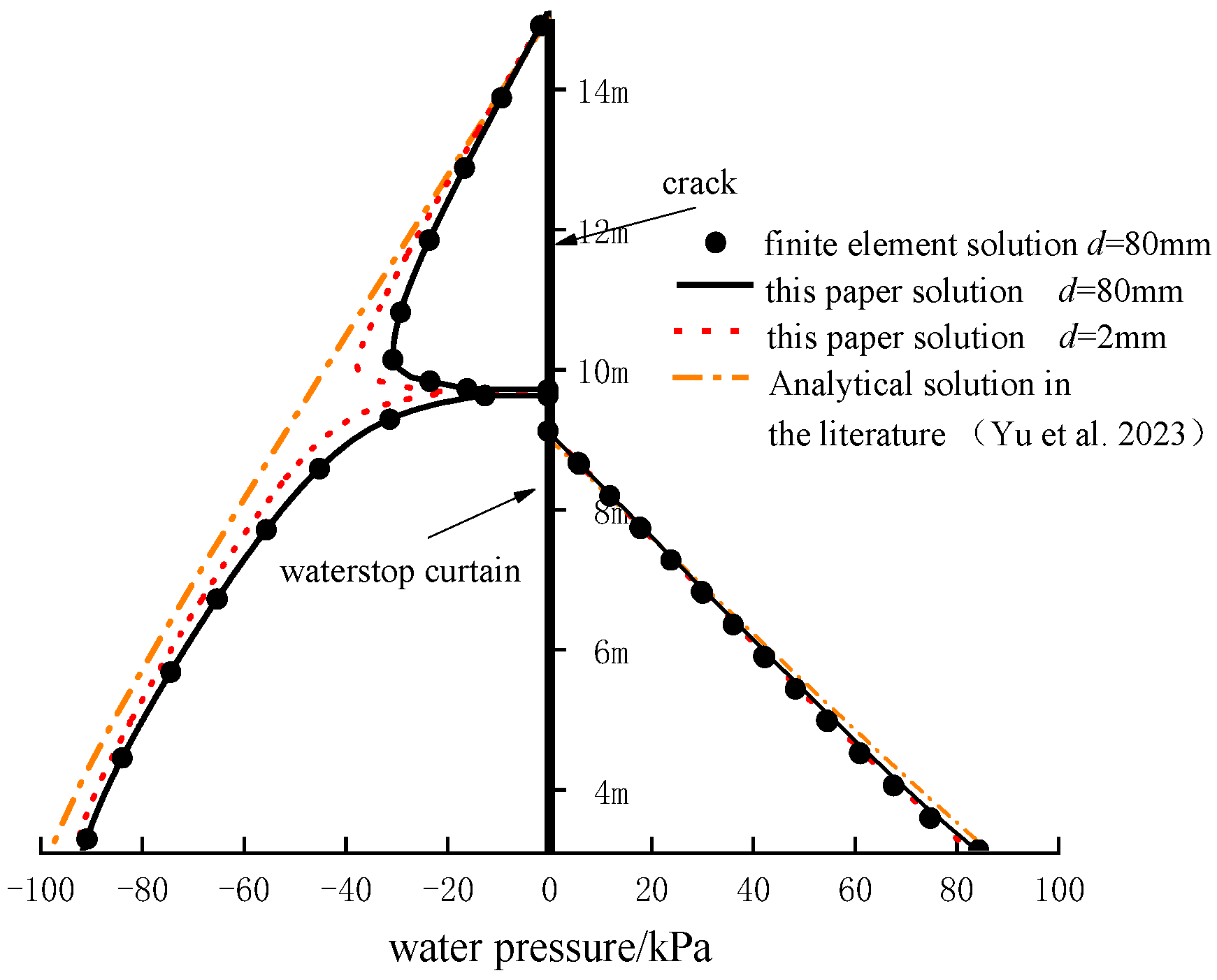
4. Analytical Solution Verification and Analysis
4.1. Comparative Validation of Pit Head Calculation Results
4.2. Comparative Validation of Water Pressure Calculation Results
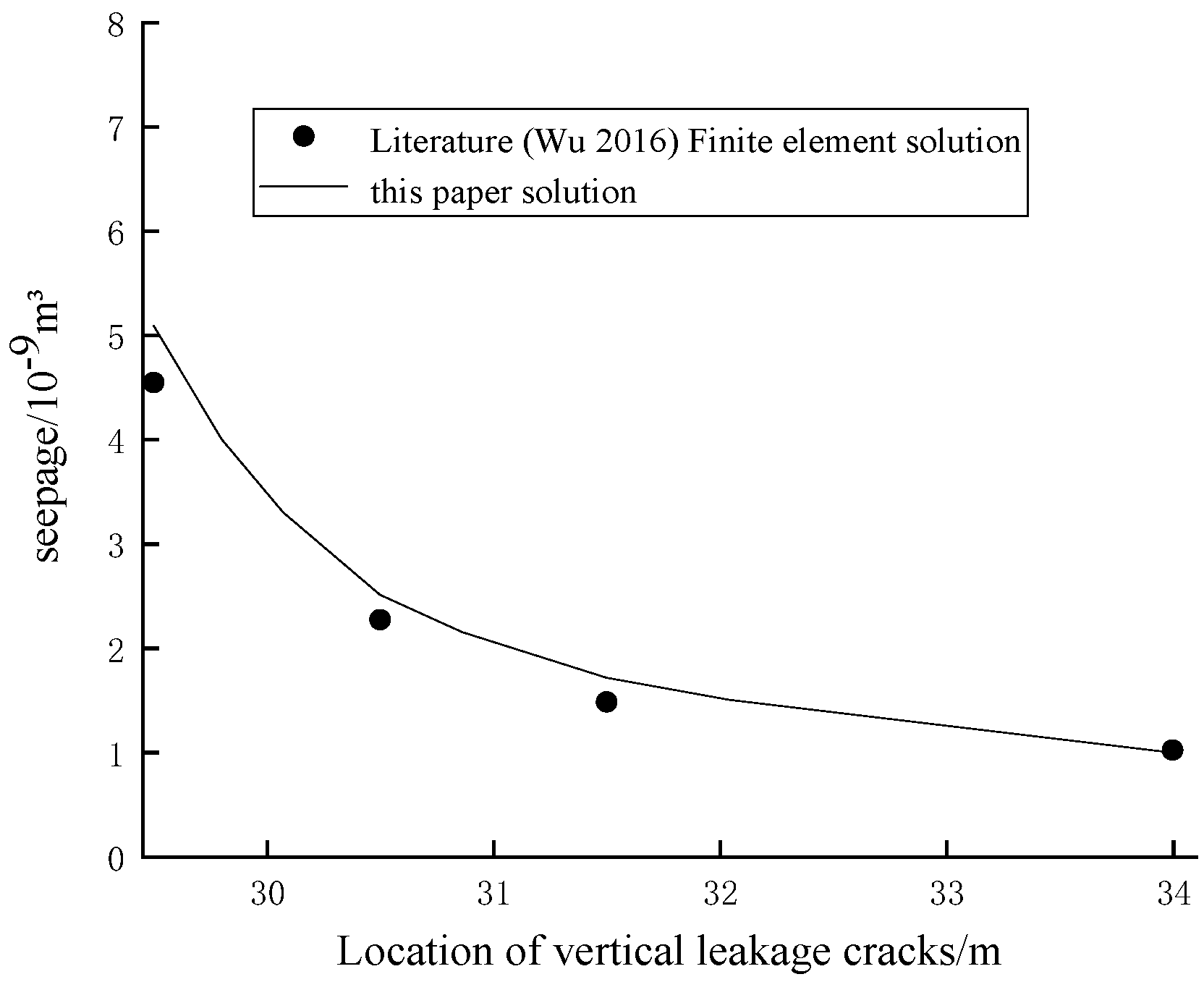
4.3. Comparative Validation of Seepage Flow Calculation Results at Stop Curtain Leaks
5. Parametric Analysis
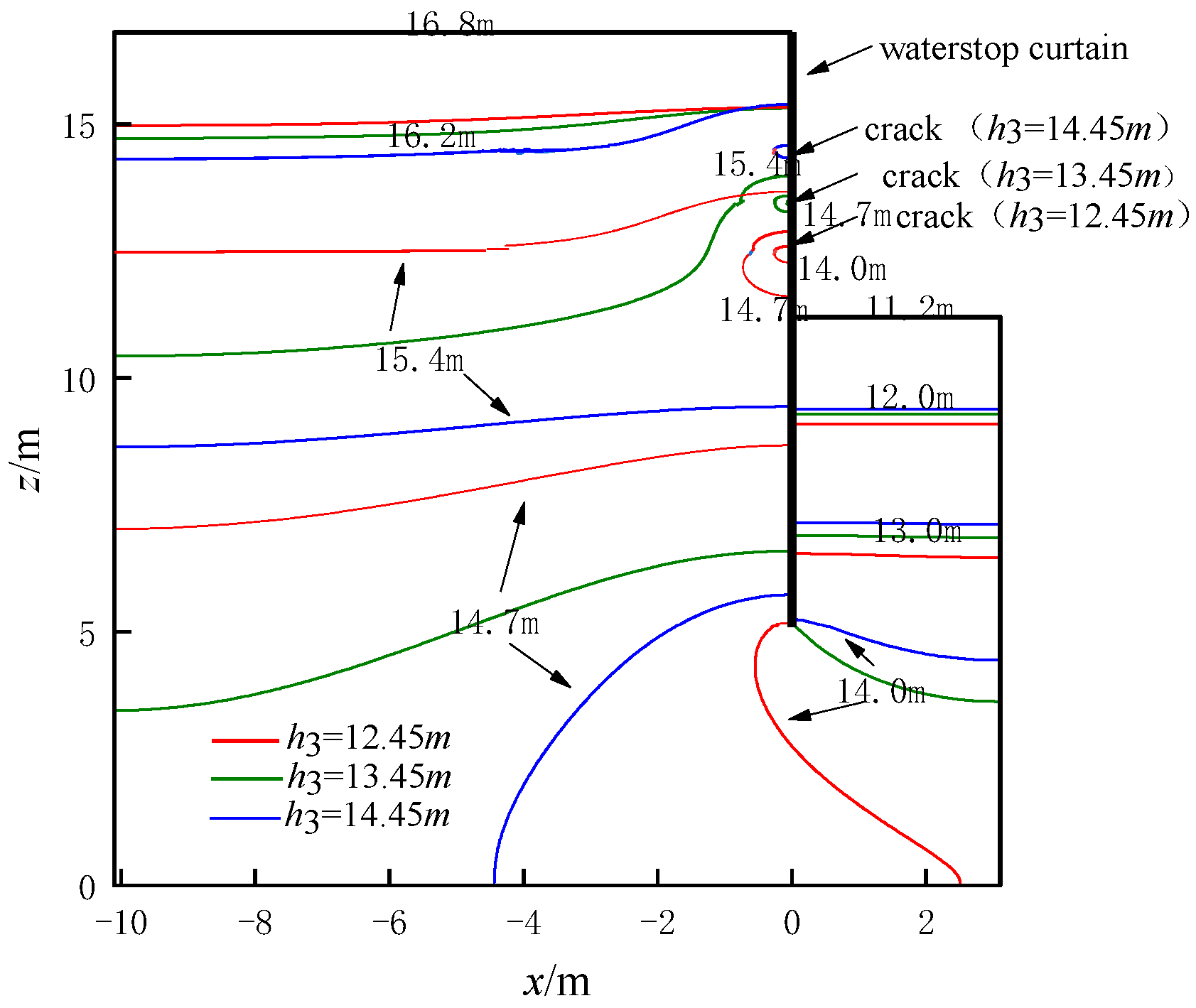
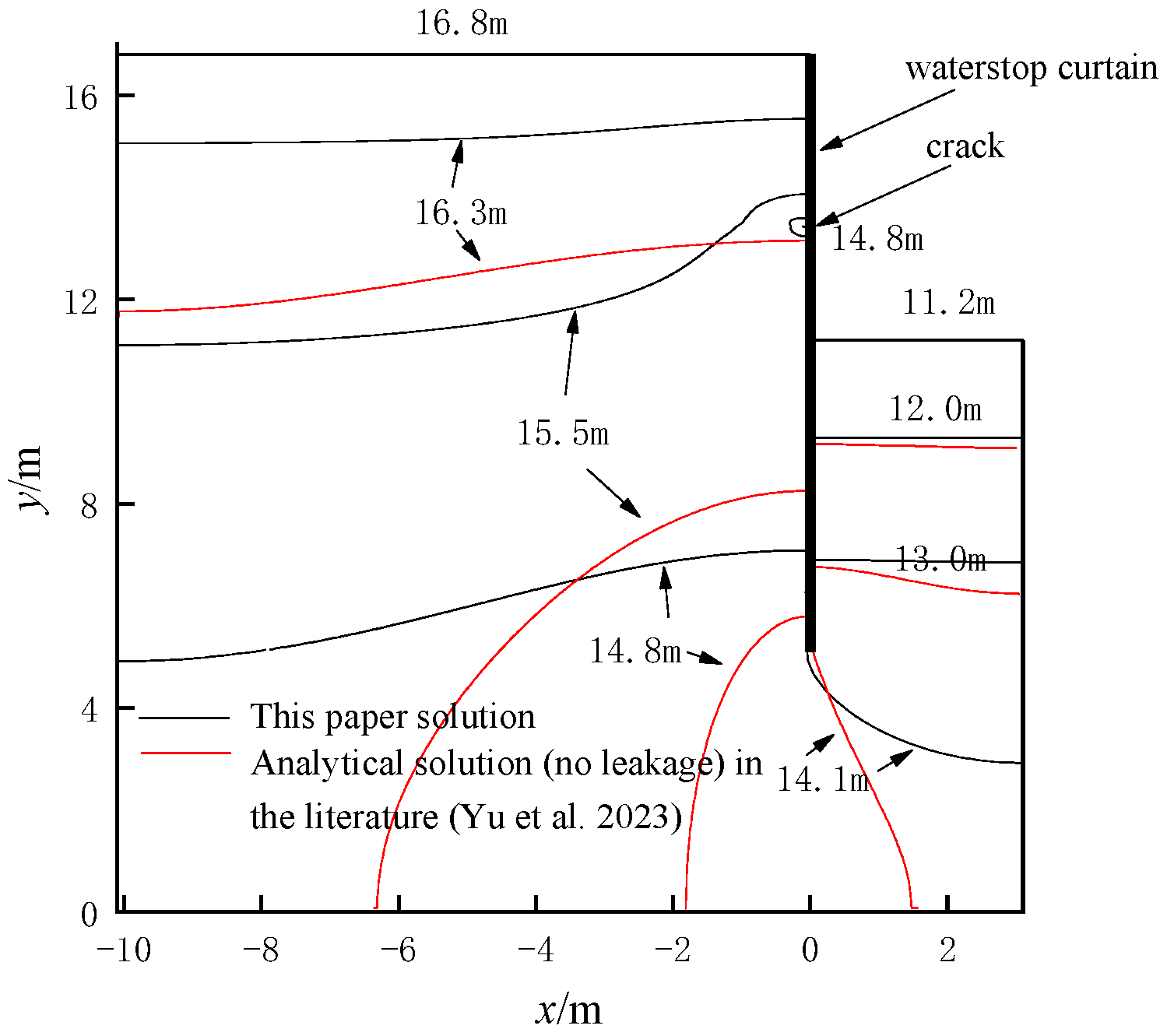
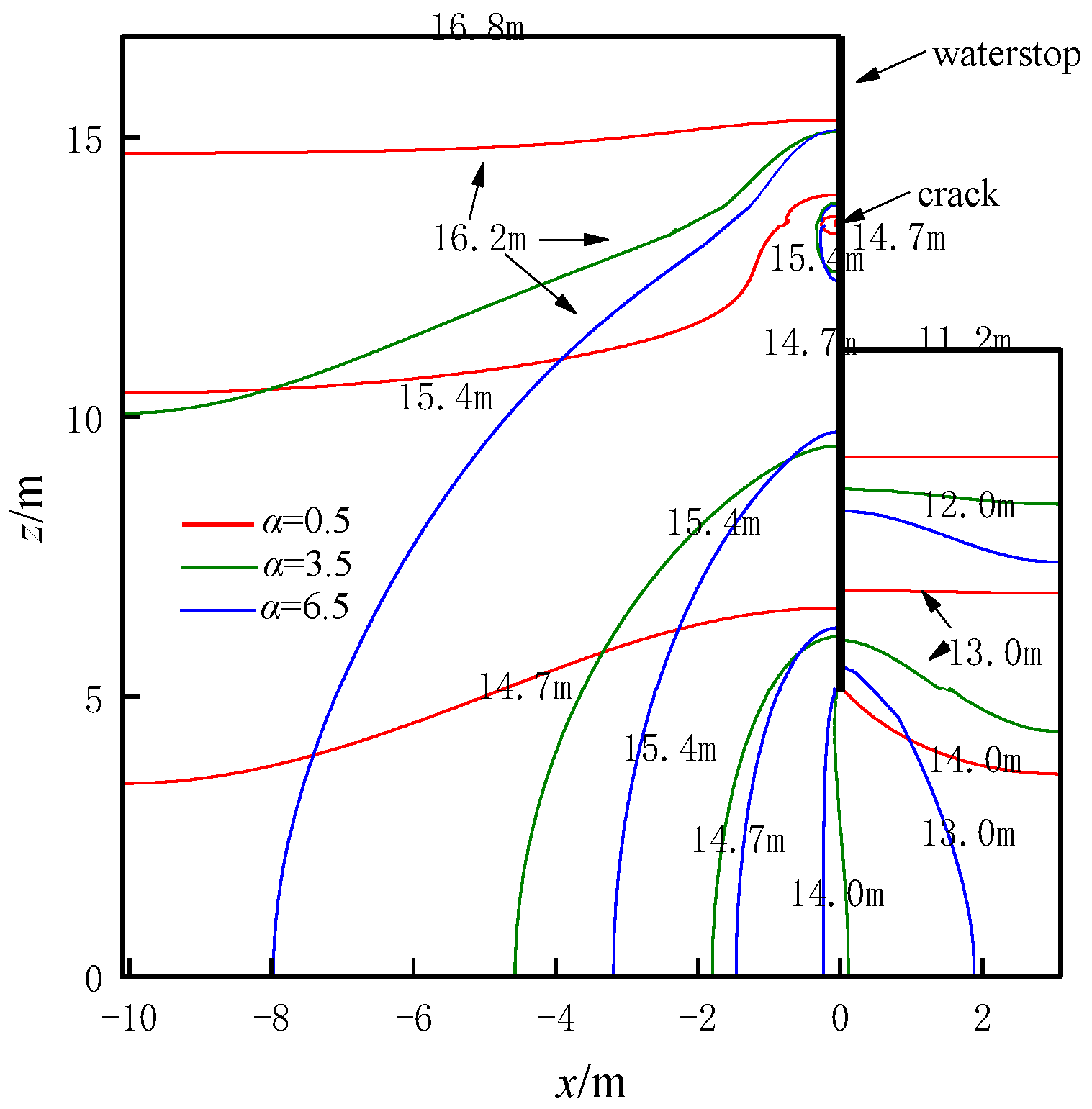
5.1. Pit Head Analysis
- (1)
- The effect of change in d2 (vertical leakage crack width) on the head distribution around the pit.
- (2)
- The effect of changes in h3 (location of vertical leakage cracks) on the head distribution around the pit.
- (3)
- The solution in this paper is analysed in comparison with the finite element solution when there is no leakage in the water-stop curtains.
- (4)
- The effect of changes in α (ratio of vertical to horizontal hydraulic conductivity) on the head distribution around the pit.
5.2. Water Pressure Analysis of Water Curtains
- (1)
- The effect of variation in d2 (vertical leakage crack width) on water pressure around pit stop curtains.
- (2)
- The effect of change in α (ratio of vertical to horizontal hydraulic conductivity) on water pressure around the pit stop curtain.
5.3. Analysis of Seepage Flow at Stop Curtain Leaks
6. Conclusions
- (1)
- The calculated results for head, water pressure on the stop curtain, and seepage flow at the stop curtain leakage obtained in this paper are consistent with those of the numerical software, thus verifying the correctness of the solution in this paper. The solution proposed in this paper is much better than the other existing solutions in terms of accuracy.
- (2)
- Compared with numerical methods, the analytical method used in this paper has many advantages: it eliminates the cumbersome modelling process, is more efficient, and has a function expression that can express the influencing factors more directly.
- (3)
- Working according to the analytical solution of this paper, the influence of the permeability coefficient, the location of seepage cracks, and the width of seepage cracks on the head around the pit, the water pressure on the stop curtain and seepage flow at the leakage of the stop curtain are analysed. The results of the analyses show the influence of some factors and some laws. These can be used in practice to improve the prediction of seepage from water-stop curtains and to reduce adverse effects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.X.; Shen, S.L.; Yuan, D.J. Characteristics of dewatering induced drawdown curve under blocking effect of retaining wall in the aquifer. J. Hydraul. Eng. 2016, 539, 554–566. [Google Scholar] [CrossRef]
- Wu, H.N.; Xu, Y.S.; Shen, S.L.; Chai, J.C. Long-term settlement behaviour of ground around shield tunnel due to leakage of water in the soft deposit of Shanghai. Front. Archit. Civ. Eng. China 2011, 5, 194–198. [Google Scholar] [CrossRef]
- Shen, S.L.; Wu, H.N.; Cui, Y.J.; Yin, Z.Y. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai. Tunn. Undergr. Space Technol. 2014, 40, 309–323. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, S. Risk identification of retaining structure leakage in foundation pits based on measured data. Chin. J. Geotech. Eng. 2008, 30 (Suppl. 1), 667–671. [Google Scholar]
- Xie, Z.F. Optimization and Comparison of Dewatering Method and Waterproof Curtain in Deep-Buried Foundation Pit; Shanghai Jiao Tong University: Shanghai, China, 2019. [Google Scholar]
- Pujades, E.; Carrera, J.; Vazquez-Sune, E.; Jurado, A.; Vilarrasa, V.; Mascuñano-Salvador, E. Hydraulic characterization of diaphragm walls for cut and cover tunnelling. Eng. Geol. 2012, 125, 1–10. [Google Scholar] [CrossRef]
- Pujades, E.; Orban, P.; Bodeux, S.; Archambeau, P.; Erpicum, S.; Dassargues, A. Underground pumped storage hydropower plants using open pit mines: How do groundwater exchanges influence the efficiency? Appl. Energy 2017, 190, 135–146. [Google Scholar] [CrossRef]
- Lu, Z.P. Study of security in subway excavation concerning the influence of the seepage in diaphragm wall. Chin. J. Undergr. Space Eng. 2010, 6, 400–405. [Google Scholar]
- Liu, X.-X.; Shen, S.-L.; Xu, Y.-S.; Yin, Z.-Y. Analytical approach for time-dependent groundwater inflow into shield tunnel face in confined aquifer. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 655–673. [Google Scholar] [CrossRef]
- Conway, B.D. Land subsidence and earth fissures in south-central and southern Arizona, USA. Hydrogeol. J. 2016, 24, 649–655. [Google Scholar] [CrossRef]
- Wu, Y.X.; Lyu, H.M.; Han, J.; Shen, S.-L. Dewatering-induced building settlement around a deep excavation in soft deposit in Tianjin, China. J. Geotech. Geoenviron. Eng. 2019, 145, 05019003. [Google Scholar] [CrossRef]
- Shaqour, F.M.; Hasan, S.E. Groundwater control for construction purposes: A case study from Kuwait. Env. Geol. 2008, 53, 1603–1612. [Google Scholar] [CrossRef]
- Pacheco-Martínez, J.; Hernandez-Marín, M.; Burbey, T.J.; González-Cervantes, N.; Ortíz-Lozano, J.Á.; Zermeño-De-Leon, M.E.; Solís-Pinto, A. Land subsidence and ground failure associated to groundwater exploitation in the Aguascalientes Valley. México Eng. Geol. 2013, 164, 172–186. [Google Scholar] [CrossRef]
- Faunt, C.C.; Sneed, M.; Traum, J.; Brandt, J.T. Water availability and land subsidence in the Central Valley, California, USA. Hydrogeol. J. 2016, 24, 675–684. [Google Scholar] [CrossRef]
- Gambolati, G.; Freeze, R.A. Mathematical simulation of the subsidence of Venice: 1. Theory. Water Resour. Res. 1973, 9, 721–733. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidations. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Gambolati, G.; Gatto, P.; Freeze, R.A. Mathematical simulation of the subsidence of Venice 2: Results. Water Resour. Res. 1974, 10, 563–577. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Carrera, J.; Jurado, A.; Pujades, E.; Vázquez-Suné, E. A methodology for characterizing the hydraulic effectiveness of an annular low-permeability barrier. Eng. Geol. 2011, 120, 68–80. [Google Scholar] [CrossRef]
- Wu, Y.X.; Lyu, H.M.; Shen, S.L.; Zhou, A. A three-dimensional fluid-solid coupled numerical modeling of the barrier leakage below the excavation surface due to dewatering. Hydrogeol. J. 2020, 28, 1–15. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Liu, G.F.; Sheng, Y.Q. Analysis and evaluation of the sealing effect of the rock-socketed underground diaphragm in deep foundation pit. Rock Soil Mech. 2013, 34, 2905–2910. [Google Scholar]
- Qiu, M.M.; Yang, G.L.; Duan, J.Y.; Zhang, P.R. Effect of groundwater leakage of row-pile supporting structure on deformation rule of foundation pit in sandy soil site. J. Water Resour. Water Eng. 2020, 31, 194–200. [Google Scholar]
- Guo, J.Z.; Cui, Z.L.; Wu, T.K.; Li, Z.S.; Li, Q.H.; Cheng, X.S. Refinement and application of variable particle-size methods in 3D discrete element modelling for large-scale problems. Build. Struct. 2022, 52 (Suppl. 2), 2443–2450. [Google Scholar]
- Pang, Z.Y.; Cui, W.H. Research and Practice on Identifying Defects of Waterproof Curtain for Excavation Engineering Based on Changes of Seepage Field. Urban Rapid Rail Transit. 2016, 29, 99–105+119. [Google Scholar]
- France, P.W. Finite element analysis of three-dimensional groundwater flow problems. J. Hydrol. 1974, 21, 381–398. [Google Scholar] [CrossRef]
- Wu, Y.X.; Shen, S.L.; Yin, Z.Y.; Xu, Y.S. Characteristics of groundwater seepage with cut-off wall in gravel aquifer. II: Numerical analysis. Can. Geotech. J. 2015, 52, 1539–1549. [Google Scholar] [CrossRef]
- Zeng, C.F.; Sun, H.Y.; Xue, X.L.; Song, W.W.; Lei, Y.; Chen, Q.N. Responses of adjacent building pile foundation to dewatering in the multi-aquifer system. China Civ. Eng. J. 2023, 56, 164–173+183. [Google Scholar]
- Xue, X.L.; Liao, H.; Zeng, C.F.; Liu, Y.S.; Zeng, X. Barrier effects of existing underground structures on deformation of strata induced by dewatering of foundation pits. Chin. J. Geotech. Eng. 2023, 45, 103–111. [Google Scholar]
- Zeng, C.F.; Bai, N.; Yuan, Z.C.; Xue, X.L.; Mei, G.X. Effect of buried depth of adjacent structure on the foundation pit deformation during pre-excavation dewatering. J. China Univ. Min. Technol. 2022, 51, 283–292. [Google Scholar]
- Wu, Y.X. Method of the Barrier Effect of the Waterproof Curtain on Groundwater Seepage During Dewatering in Aquifers; Shanghai Jiao Tong University: Shanghai, China, 2016. [Google Scholar]
- Yu, J.; Li, D.K.; Hu, Z.W.; Zheng, J.F. Analytical solution of steady seepage field of foundation pit considering the thickness of retaining wall. Chin. J. Geotech. Eng. 2023, 45, 1402–1411. [Google Scholar]
- Thushara, A.M.; Nagaratnam, S. Simple solutions for square and rectangular cofferdam seepage problems. Can. Geotech. J. 2018, 56, 730–745. [Google Scholar]
- Yu, J.; Yang, X.X.; Deng, P.B.; Chen, W.B. Analytical Solution for a Steady Seepage Field of a Foundation Pit in Layered Soil. Int. J. Geomech. 2022, 22, 04022160. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J. Plaxis Introductory: Student Pack and Tutorial Manual; Taylor Fransis: Abingdon-on-Thames, UK, 2010; ISBN 10:9076016100. [Google Scholar]
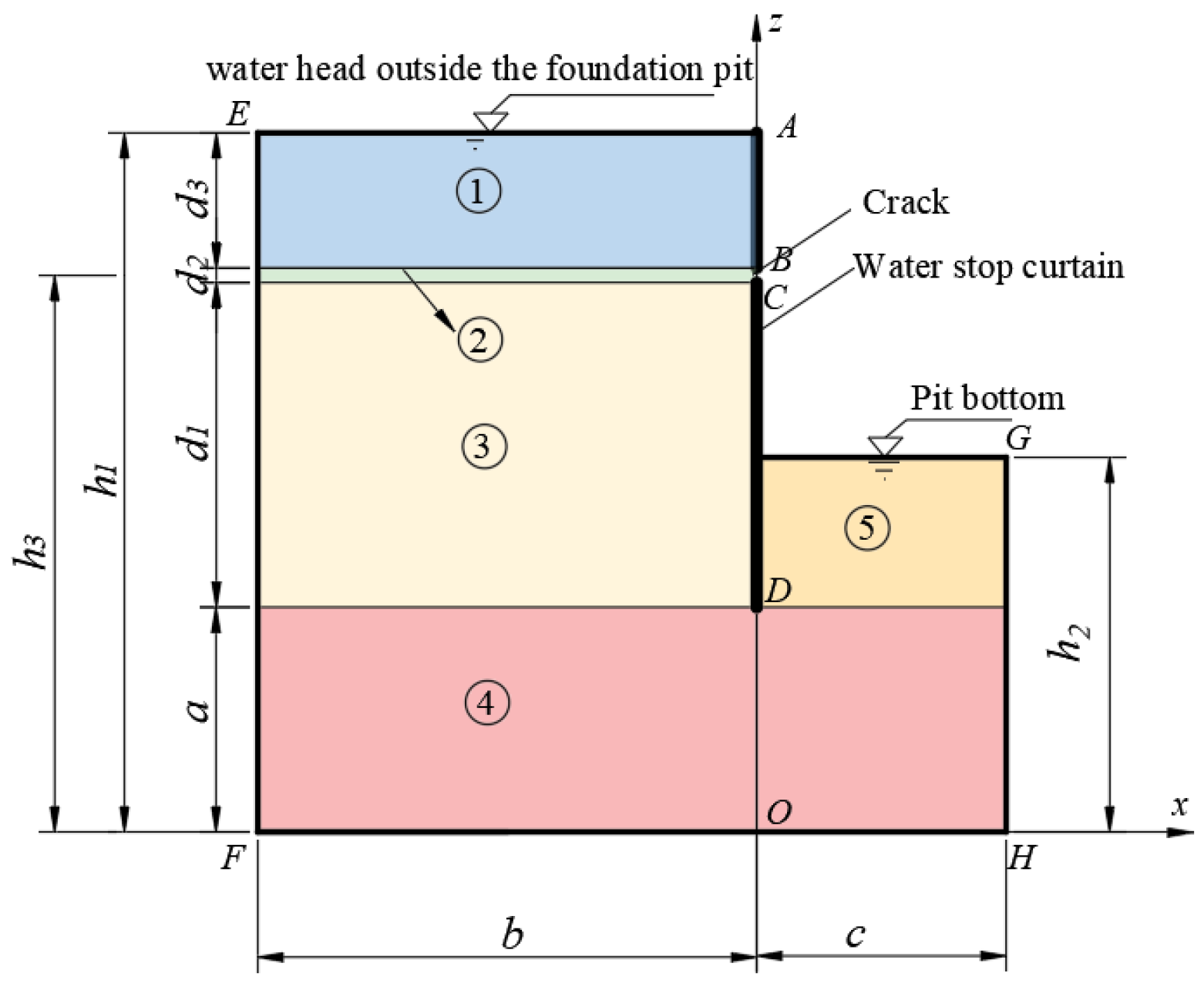

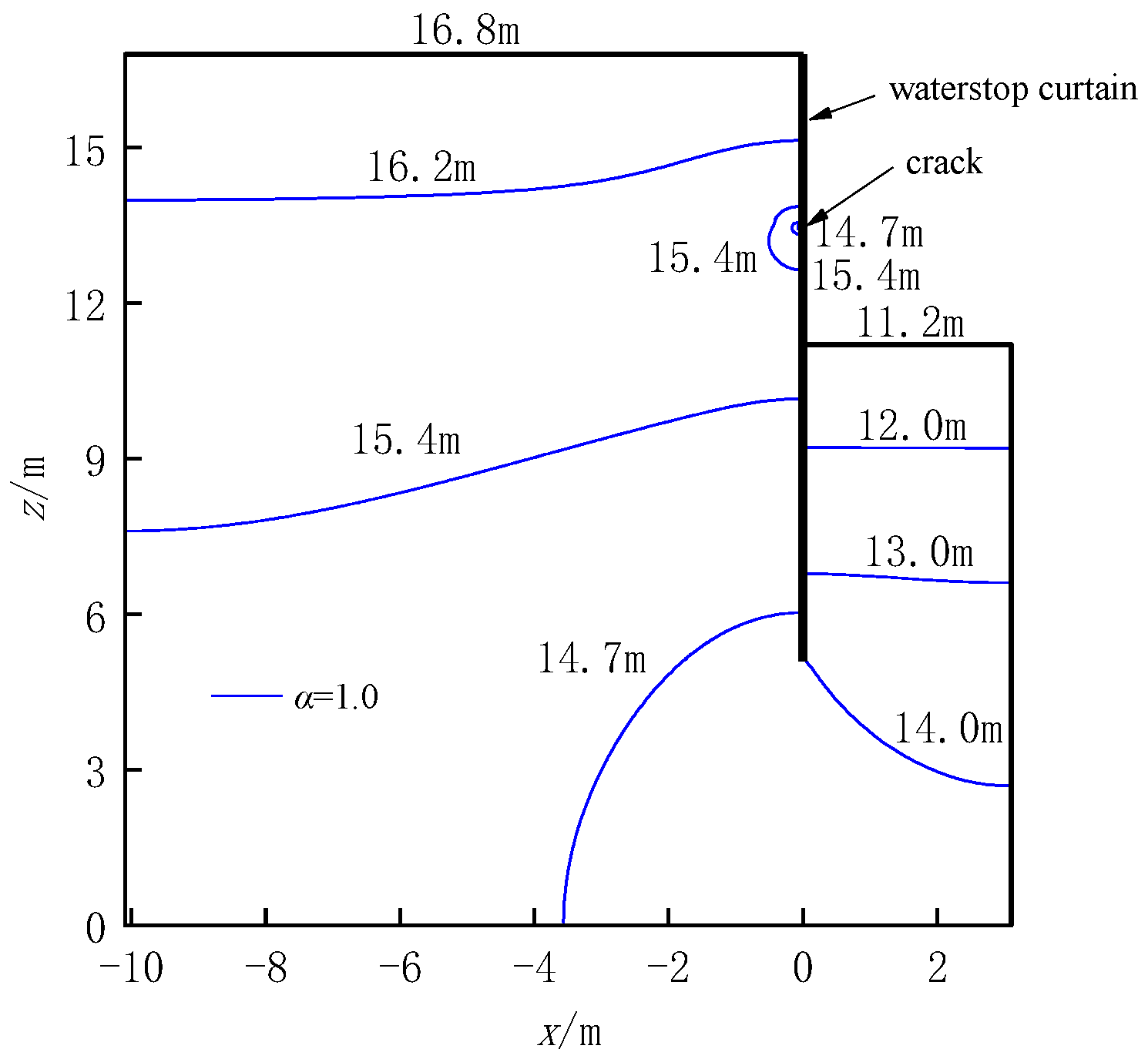
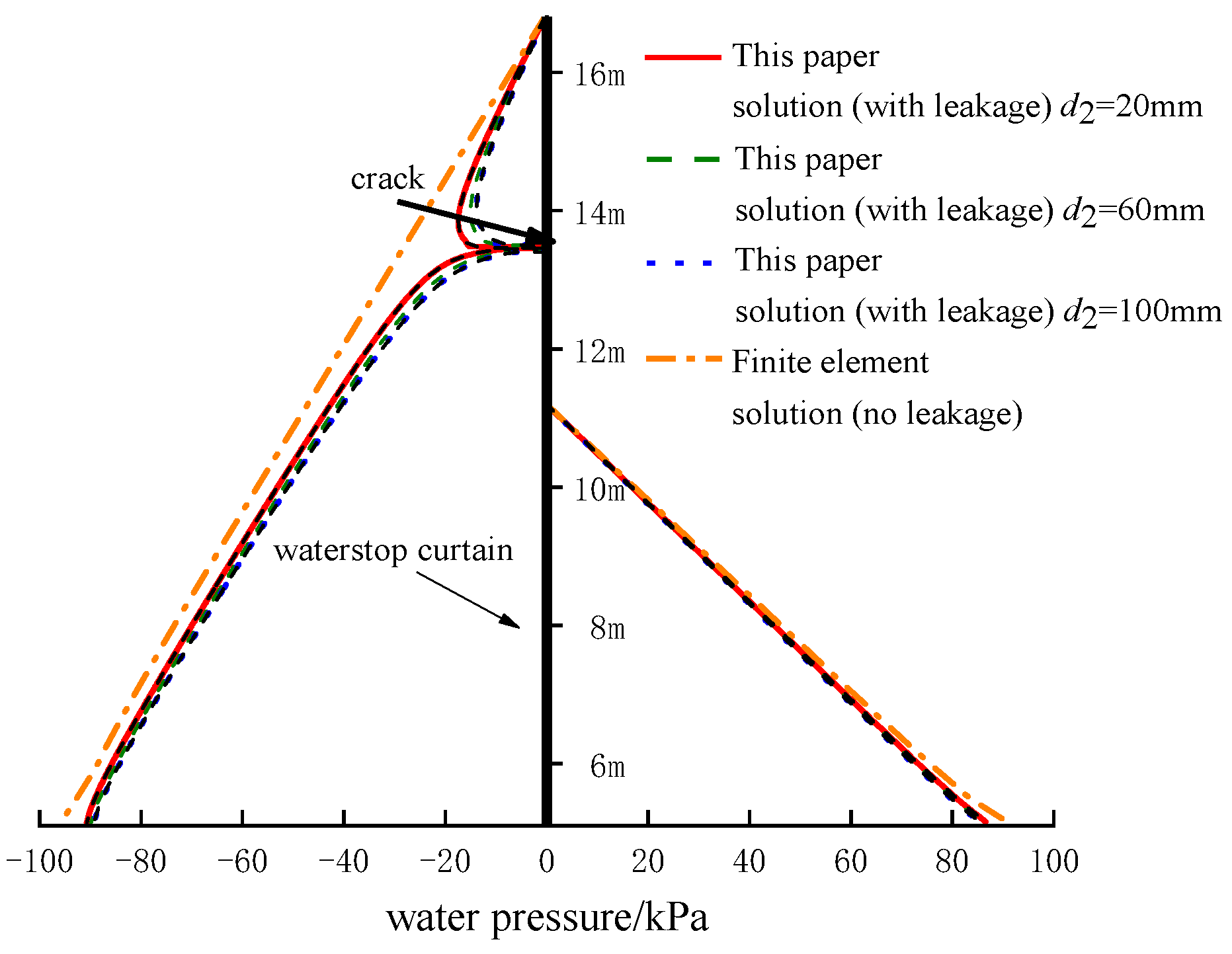
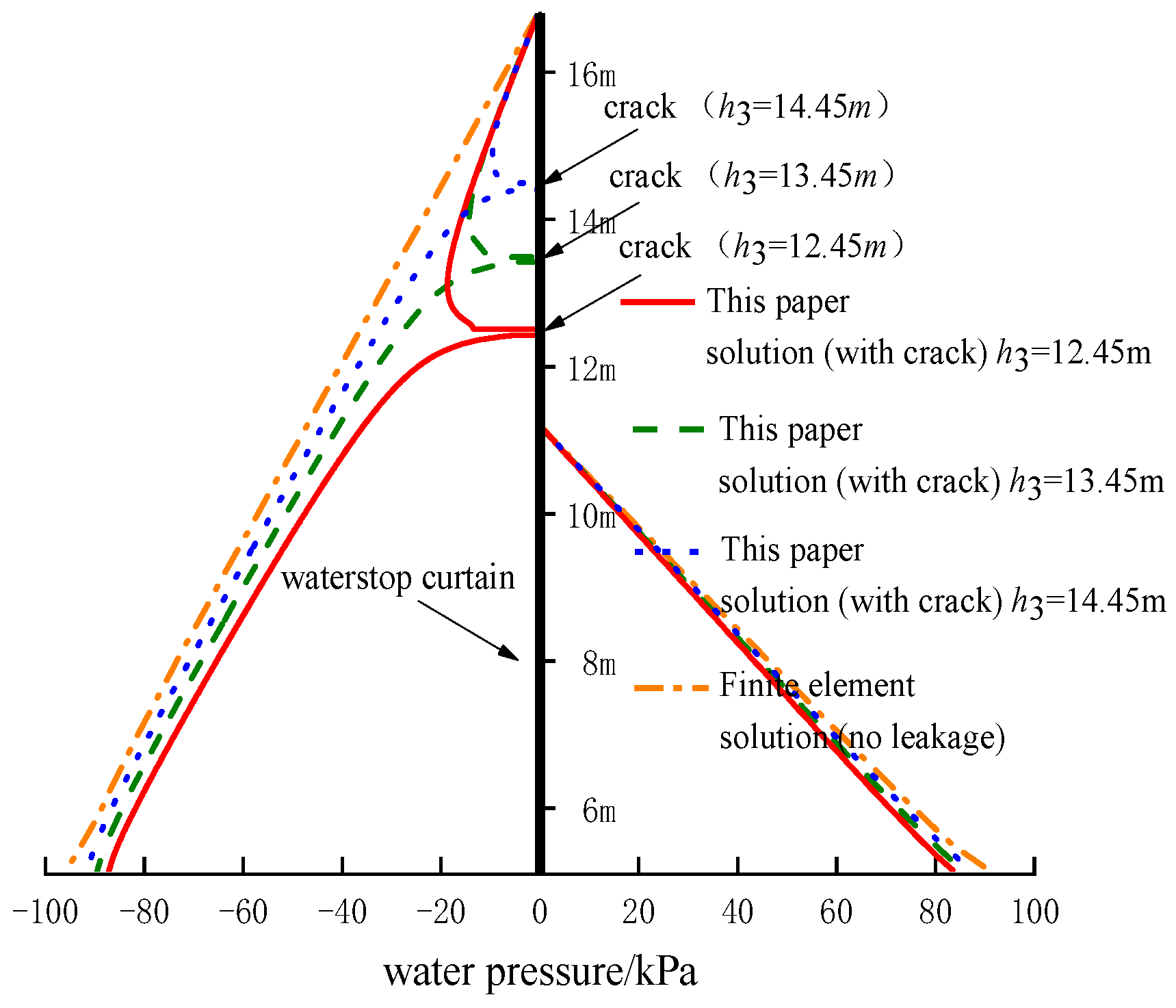

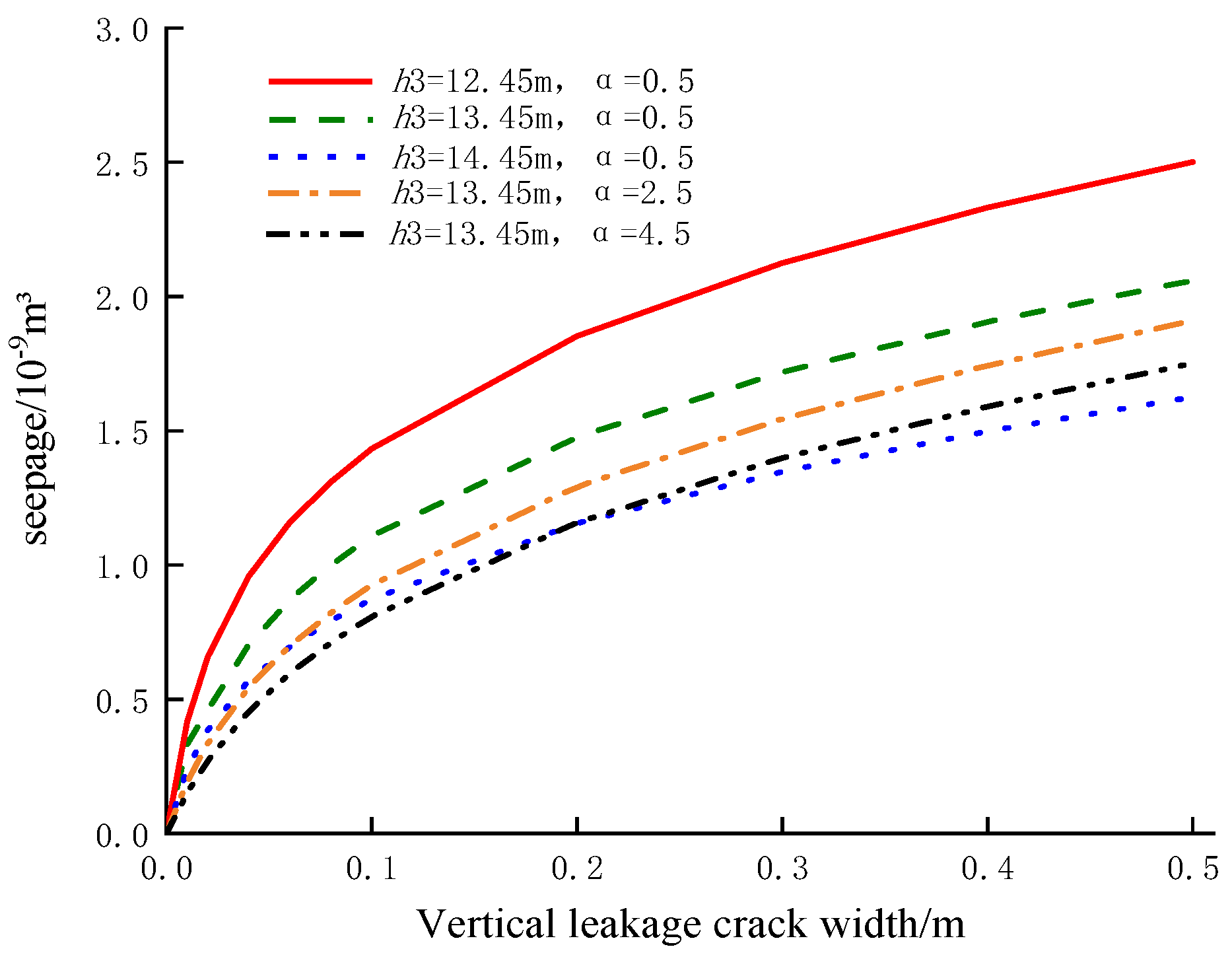
| b/m | c/m | h1/m | h2/m | a/m | h3/m | d2/mm | k/m/s | kh/kv |
|---|---|---|---|---|---|---|---|---|
| 10 | 3 | 16.8 | 11.2 | 5 | 13.45 | 80 | 1.00 × 10−9 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Zhang, W.; Li, D. Analytical Solution for Steady-State Seepage Field of Foundation Pit During Water Curtain Leakage. Mathematics 2025, 13, 203. https://doi.org/10.3390/math13020203
Yu J, Zhang W, Li D. Analytical Solution for Steady-State Seepage Field of Foundation Pit During Water Curtain Leakage. Mathematics. 2025; 13(2):203. https://doi.org/10.3390/math13020203
Chicago/Turabian StyleYu, Jun, Weijie Zhang, and Dongkai Li. 2025. "Analytical Solution for Steady-State Seepage Field of Foundation Pit During Water Curtain Leakage" Mathematics 13, no. 2: 203. https://doi.org/10.3390/math13020203
APA StyleYu, J., Zhang, W., & Li, D. (2025). Analytical Solution for Steady-State Seepage Field of Foundation Pit During Water Curtain Leakage. Mathematics, 13(2), 203. https://doi.org/10.3390/math13020203





