A Spectral Approach to Solve High-Order Ordinary Differential Equations: Improved Operational Matrices for Exponential Jacobi Functions

Abstract

This paper presents a novel numerical approach to handling ordinary differential equations (ODEs) with initial conditions (ICs) by introducing generalized exponential Jacobi functions (GEJFs). These GFJFs satisfy the associated ICs. A crucial part of this approach is using the spectral collocation method (SCM) and building operational matrices (OMs) for the ordinary derivatives (ODs) of GEJFs. These lead to efficient and accurate computations. The suggested algorithm’s convergence and error analysis is proved. We present numerical examples to demonstrate the applicability of the approach.

1. Introduction

In the realm of mathematical modeling, initial value problems (IVPs) play a pivotal role in representing a wide array of physical, biological, and engineering phenomena. The numerical solutions (NUMSs) of IVPs are essential for obtaining approximate solutions (APPSs) when analytical methods prove intractable. Differernt numerical methods have been developed to obtain APPSs for ODEs. One common method is to turn the differential equation (DE) into a system of algebraic equations. Foundational texts such as Shen et al. [1] give a full picture of the powerful spectral methods paradigms. The literature presents a wide array of basis functions for this purpose, encompassing both non-orthogonal and orthogonal polynomials.

Among the non-orthogonal polynomials, Bernstein polynomials have been effectively employed for high-order ordinary differential equations (ODEs) [2,3], whereas alternative methods have utilized bases such as Bernoulli polynomials [4] and cubic Hermite splines [5]. Investigations have examined additional non-classical polynomials, including generalized Fibonacci and Vieta–Fibonacci polynomials, to address fractional and singular issues [6,7].

However, orthogonal polynomials are very common because they can obtain approximating solutions. The Jacobi polynomials (JPs) family is a flexible and unifying base for many spectral methods. JPs and Romanovski–Jacobi polynomials, in their broader applications, have been employed to develop resilient Galerkin and matrix methods for a range of complex DEs [8,9,10]. The strength of this family also comes from its important special cases. For example, Gegenbauer polynomials have been effectively utilized in time-fractional cable problems [11]. Chebyshev polynomials are used in many numerical methods, such as solving singular Lane–Emden equations [12], making Petrov–Galerkin schemes for beam equations [13], and making hybrid methods for nonlinear PDEs [14]. These ideas have been expanded to include specialized bases, such as airfoil polynomials for complex fluid models [15]. In addition to the Jacobi family, similar methods have used Chebyshev wavelets [16] and radial basis functions [17]. These various methods have made it possible to accurately solve other types of DEs, such as the Lane–Emden type [18,19] and the first Painlevé equation [20].

Orthogonal JPs possess numerous advantageous properties that render them highly effective in the NUMSs of various types of ODEs, particularly through spectral methods. The primary attributes of JPs include orthogonality, exponential precision, and the incorporation of two parameters that facilitate versatility in setting the APPSs. In the development of various computational techniques, the usefulness of these characteristics is visible. For the development of Jacobi–Galerkin methods, which provide a strong framework for solving complex differential equations, the orthogonality of JPs is essential [21]. Another useful technique creates OMs for derivatives that function well by utilizing the properties of JPs. This approach streamlines the process of converting a DE into an algebraic system as demonstrated in [22,23].

Orthogonal functions (OFs) have garnered significant interest in addressing different types of DEs. The primary attribute of this strategy is its ability to reduce these problems to the handling of a system of algebraic equations, significantly simplifying the problem. For example, researchers have created fractional-order Legendre functions [24] and shifted fractional-order Jacobi functions to effectively address systems of FDEs [25]. Another significant advancement was the proposal of Exponential Jacobi Polynomials (EJPs) for high-order ODEs to solve problems on semi-infinite intervals [26]. These were later expanded to develop new algorithms for partial DEs in unbounded domains [27,28].

This work aims to expand the use of the novel OFs derived from EJPs to address IVPs, named GEJFs that satisfy the given ICs, to develop an SCM capable of addressing the following IVPs:

$$D^n\mathcal{Y}\left(\check{\mathfrak{t}}\right)=F(\check{\mathfrak{t}},\mathcal{Y}\left(\check{\mathfrak{t}}\right),D\mathcal{Y}\left(\check{\mathfrak{t}}\right),D^2\mathcal{Y}\left(\check{\mathfrak{t}}\right),\dots ,D^{n-1}\mathcal{Y}\left(\check{\mathfrak{t}}\right)),0<\check{\mathfrak{t}}<\infty ,$$

(1)

subject to the ICs

$${\mathcal{Y}}^{\left(j\right)}\left(0\right)={\beta }_j,j=0,1,\dots ,n-1.$$

(2)

In this work, we introduce a novel methodology to solve Equations (1) and (2) by establishing new Galerkin OMs for ODEs based on the basis vectors of GEJFs. To the best of our knowledge, the literature has never used this strategy for addressing ODEs, utilizing the OM of the suggested basis vector, which is presented. This novel technique enables the effective mending and attainment of NUMSs for this class of ODEs.

This article is structured as follows: Section 2 delineates particular characteristics of the JPs and EJFs. Section 3 focuses on the development of innovative OMs for the ODs of GEJFs. In Section 4, we analyze the application of freshly generated OMs in conjunction with the SCM as a numerical approach to solve (1) and (2). The evaluation of the error estimate for the NUMS obtained from this innovative method is elaborated in Section 5. Section 6 provides numerical examples and comparisons with alternative approaches from the literature to illustrate the effectiveness of the proposed strategy. In Section 7, we summarize the key findings and draw implications from our research.

2. Jacobi Polynomials and Exponential Jacobi Functions

This section presents some elementary properties of JPs and EJFs. Additionally, we propose and characterize a new type of OF, called GEJFs.

2.1. Analytical Framework: JP Basis Functions

The JPs, ${\mathcal{P}}_n^{({\varsigma }_1,{\varsigma }_2)}\left(x\right),{\varsigma }_1,{\varsigma }_2>-1$, satisfy the orthogonality relation [29]

$${\int }_{-1}^1{w}^{{\varsigma }_1,{\varsigma }_2}\left(x\right){\mathcal{P}}_n^{({\varsigma }_1,{\varsigma }_2)}\left(x\right){\mathcal{P}}_m^{({\varsigma }_1,{\varsigma }_2)}\left(x\right)dx=\left\{\begin{array}{cc}0,\hfill & m\ne n,\hfill \\ h_n^{({\varsigma }_1,{\varsigma }_2)},\hfill & m=n,\hfill \end{array}\right.$$

where $w^{{\varsigma }_1,{\varsigma }_2}\left(x\right)={(1-x)}^{{\varsigma }_1}{(1+x)}^{{\varsigma }_2}$, and $h_n^{({\varsigma }_1,{\varsigma }_2)}={\displaystyle \frac{2^{\lambda }\Gamma (n+{\varsigma }_1+1)\Gamma (n+{\varsigma }_2+1)}{n!(2n+\lambda )\Gamma (n+\lambda )}},\lambda ={\varsigma }_1+{\varsigma }_2+1$.

The analytical form of ${\mathcal{P}}_i^{({\varsigma }_1,{\varsigma }_2)}\left(x\right)$ can be written as follows ([30], p. 436):

$${\mathcal{P}}_i^{({\varsigma }_1,{\varsigma }_2)}\left(x\right)=\sum _{k=0}^i{c}_k^{\left(i\right)}{(1-x)}^k,$$

(3)

where

$$c_k^{\left(i\right)}={\displaystyle \frac{{(-1)}^k{({\varsigma }_1+1)}_i{(i+\lambda )}_k}{2^k(i-k)!k!{({\varsigma }_1+1)}_k}}.$$

(4)

Alternatively, the expression for ${(1-x)}^k$ in relation to ${\mathcal{P}}_r^{({\varsigma }_1,{\varsigma }_2)}\left(x\right)$ has the following form ([30], p. 441):

$${(1-x)}^k=\sum _{r=0}^k{b}_r^{\left(k\right)}{\mathcal{P}}_r^{({\varsigma }_1,{\varsigma }_2)}\left(x\right),$$

(5)

where

$$b_r^{\left(k\right)}={\displaystyle \frac{{(-1)}^r{2}^{k}k!{({\varsigma }_1+1)}_k(2r+\lambda )}{(k-r)!{({\varsigma }_1+1)}_r{(r+\lambda )}_{k+1}}}.$$

(6)

Additionally, using the following relation ([30], p. 437):

$${\mathcal{P}}_r^{({\varsigma }_1,{\varsigma }_2)}(-x)={(-1)}^r{\mathcal{P}}_r^{({\varsigma }_2,{\varsigma }_1)}\left(x\right),$$

it is easy to see that

$${(1+x)}^k=\sum _{r=0}^k{\overline{b}}_r^{\left(k\right)}{\mathcal{P}}_r^{({\varsigma }_1,{\varsigma }_2)}\left(x\right),$$

(7)

where

$${\overline{b}}_r^{\left(k\right)}={\displaystyle \frac{2^{k}k!{({\varsigma }_2+1)}_k(2r+\lambda )}{(k-r)!{({\varsigma }_2+1)}_r{(r+\lambda )}_{k+1}}}.$$

(8)

2.2. Introducing EJFs and GEJFs

The so-called EJFs, ${\mathcal{J}}_n^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)={\mathcal{P}}_n^{({\varsigma }_1,{\varsigma }_2)}(1-2e^{-\check{\mathfrak{t}}/\ell }),\check{\mathfrak{t}}\in [0,\infty )$, have the following analytical form [26]

$${\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)=\sum _{k=0}^i{\widehat{c}}_k^{\left(i\right)}{e}^{-\check{\mathfrak{t}}k/\ell },{\widehat{c}}_k^{\left(i\right)}=2^k{c}_k^{\left(i\right)}.$$

(9)

These functions satisfy the following orthogonal relation [26]:

$${\int }_0^{\infty }{w}_e^{{\varsigma }_1,{\varsigma }_2}\left(\check{\mathfrak{t}}\right){\mathcal{J}}_n^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right){\mathcal{J}}_m^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)d\check{\mathfrak{t}}=\left\{\begin{array}{cc}{\displaystyle \frac{\ell }{2^{\lambda }}}{h}_n^{({\varsigma }_1,{\varsigma }_2)},\hfill & m=n,\hfill \\ 0,\hfill & m\ne n,\hfill \end{array}\right.$$

where $w_e^{{\varsigma }_1,{\varsigma }_2}\left(\check{\mathfrak{t}}\right)=e^{-\check{\mathfrak{t}}({\varsigma }_1+1)/\ell }{(1-e^{-\check{\mathfrak{t}}/\ell })}^{{\varsigma }_2}$. In addition, they satisfy the following recurrence relation [26]

$$e^{-\check{\mathfrak{t}}/\ell }{\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)={\alpha }_{1,i}{\mathcal{J}}_{i+1}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\alpha }_{2,i}{\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\alpha }_{3,i}{\mathcal{J}}_{i-1}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),$$

(10)

where

$${\alpha }_{1,i}=-{\displaystyle \frac{(i+1)(i+\lambda )}{(2i+\lambda )(2i+\lambda +1)}},{\alpha }_{2,i}={\displaystyle \frac{({\varsigma }_1+1)(\lambda -1)+2i^2+2i\lambda }{(2i+\lambda )(2i+\lambda +1)}},{\alpha }_{3,i}=-{\displaystyle \frac{({\varsigma }_1+i)({\varsigma }_2+i)}{(2i+\lambda -1)(2i+\lambda )}}.$$

(11)

Additionally, ${\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$ has the following special value ([26], p. 437):

$${\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(0\right)={\mathcal{P}}_i^{({\varsigma }_1,{\varsigma }_2)}(-1)={\displaystyle \frac{{(-1)}^i{({\varsigma }_2+1)}_i}{i!}}.$$

(12)

The following lemma is needed throughout the paper.

Lemma 1. 

The function ${\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$ can be written in the following form:

$${\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)=\sum _{k=0}^i{\mathcal{B}}_k^{\left(i\right)}{(1-e^{-\check{\mathfrak{t}}/\ell })}^k,{\mathcal{B}}_k^{\left(i\right)}={\displaystyle \frac{{(-i-\beta )}_{i-k}{(i+\lambda )}_k}{k!(i-k)!}}.$$

(13)

Proof. 

Using Formula (9),

$${\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)=\sum _{k=0}^i{(-1)}^k{\widehat{c}}_k^{\left(i\right)}{(1-e^{-\check{\mathfrak{t}}/\ell }-1)}^k=\sum _{k=0}^i{\widehat{c}}_k^{\left(i\right)}\sum _{r=0}^k{(-1)}^r\left({\displaystyle \genfrac{}{}{0pt}{}{k}{r}}\right){(1-e^{-\check{\mathfrak{t}}/\ell })}^r.$$

(14)

By expanding and collecting similar terms—and after some manipulation—Equation (14) takes the form (13).    □

The following inversion formulae given in Lemma 2 are needed throughout the paper.

Lemma 2. 

The expressions of $e^{-\check{\mathfrak{t}}k/\ell }$ and ${(1-e^{-\check{\mathfrak{t}}/\ell })}^k$, $k=0,1,2,\dots ,$ have the following expansions:

$$e^{-\check{\mathfrak{t}}k/\ell }=\sum _{r=0}^k{d}_r^{\left(k\right)}{\mathcal{J}}_r^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),d_r^{\left(k\right)}=2^{-k}{b}_r^{\left(k\right)},$$

(15)

and

$${(1-e^{-\check{\mathfrak{t}}/\ell })}^k=\sum _{r=0}^k{\widehat{d}}_r^{\left(k\right)}{\mathcal{J}}_r^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),{\widehat{d}}_r^{\left(k\right)}=2^{-k}{\overline{b}}_r^{\left(k\right)}.$$

(16)

Proof. 

The proof is a direct consequence of Formulas (5) and (7), by replacing x with $(1-2e^{-\check{\mathfrak{t}}}/\ell )$.    □

The proof of Corollary 1 is a direct consequence of (10) and (16).

Corollary 1. 

$$e^{-\check{\mathfrak{t}}/\ell }{(1-e^{-\check{\mathfrak{t}}/\ell })}^k=\sum _{r=0}^{k+1}{\mathcal{M}}_r^{\left(k\right)}{\mathcal{J}}_r^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),$$

(17)

where

$${\mathcal{M}}_r^{\left(k\right)}={\alpha }_{1,r-1}{\widehat{d}}_{r-1}^{\left(k\right)}+{\alpha }_{2,r}{\widehat{d}}_r^{\left(k\right)}+{\alpha }_{3,r+1}{\widehat{d}}_{r+1}^{\left(k\right)},{\widehat{d}}_{-1}^{\left(k\right)}={\widehat{d}}_{k+1}^{\left(k\right)}=0.$$

New GEJFs ${\{{\varphi }_{n,j}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)\}}_{j\ge 0}$ are introduced,

$${\varphi }_{n,j}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)={(1-e^{-\check{\mathfrak{t}}/\ell })}^n{\mathcal{J}}_j^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),$$

(18)

which satisfy that $D^q{\varphi }_{n,j}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(0\right)=0,q=0,1,\dots ,n-1,$ and the orthogonality relation

$${\int }_0^{\infty }{\widehat{w}}_{e,n}^{{\varsigma }_1,{\varsigma }_2}\left(\check{\mathfrak{t}}\right){\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right){\varphi }_{n,j}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)d\check{\mathfrak{t}}=\left\{\begin{array}{cc}{\displaystyle \frac{\ell }{2^{\lambda }}}{h}_i^{({\varsigma }_1,{\varsigma }_2)},\hfill & i=j,\hfill \\ 0,\hfill & i\ne j,\hfill \end{array}\right.$$

(19)

where ${\widehat{w}}_{e,n}^{{\varsigma }_1,{\varsigma }_2}\left(\check{\mathfrak{t}}\right)={\displaystyle \frac{1}{{(1-e^{-\check{\mathfrak{t}}/\ell })}^{2n}}}{w}_e^{{\varsigma }_1,{\varsigma }_2}\left(\check{\mathfrak{t}}\right)$.

Remark 1. 

Since

$${\varphi }_{0,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)={\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),$$

${\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$ is a generalization of ${\mathcal{J}}_i^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$.

3. OM for Ods of ${\mathit{\varphi }}_{\mathit{n},\mathit{i}}^{({\mathit{\varsigma }}_{\mathit{1}},{\mathit{\varsigma }}_{\mathit{2}},\ell )}\left(\check{\mathfrak{t}}\right)$

In this section, the main theorem is presented, which provides the OM for Ods of the vector

$${\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)={[{\varphi }_{n,0}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),{\varphi }_{n,1}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),\dots ,{\varphi }_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)]}^T.$$

(20)

Theorem 1. 

The first derivative of ${\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$ for all $i\ge 0$, can be written in the form

$$D{\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)=\sum _{j=0}^i{\Theta }_{i,j}^{{\varsigma }_1,{\varsigma }_2}(n,\ell ){\varphi }_{n,j}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+Q_{n,i}\left(\check{\mathfrak{t}}\right),$$

(21)

where ${\displaystyle Q_{n,i}\left(\check{\mathfrak{t}}\right)={\displaystyle \frac{n}{\ell }}{\mathcal{B}}_0^{\left(i\right)}\sum _{r=0}^n{\mathcal{M}}_r^{(n-1)}{\mathcal{J}}_r^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)}$,  and 

$${\Theta }_{i,j}^{{\varsigma }_1,{\varsigma }_2}\left(n\right)={\displaystyle \frac{1}{\ell }}\sum _{k=0}^{i-j}{\delta }_{k+j}(k+j+n+1){\mathcal{M}}_j^{(k+j-1)}{\mathcal{B}}_{k+j}^{\left(i\right)},$$

(22)

where ${\delta }_0=0,{\delta }_j=1,j\ge 1$.

Proof. 

In view of (13), we obtain

$$\begin{array}{cc}\hfill D{\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)& ={\displaystyle \frac{1}{\ell }}{e}^{-\check{\mathfrak{t}}/\ell }\sum _{k=0}^i{\mathcal{B}}_k^{\left(i\right)}(k+n){(1-e^{-\check{\mathfrak{t}}/\ell })}^{k+n-1}\hfill \\ & ={\displaystyle \frac{1}{\ell }}{e}^{-\check{\mathfrak{t}}/\ell }\sum _{k=1}^i{\mathcal{B}}_k^{\left(i\right)}(k+n){(1-e^{-\check{\mathfrak{t}}/\ell })}^{k+n-1}+{\displaystyle \frac{n}{\ell }}{\mathcal{B}}_0^{\left(i\right)}{e}^{-\check{\mathfrak{t}}/\ell }{(1-e^{-\check{\mathfrak{t}}/\ell })}^{n-1}\hfill \\ & ={\displaystyle \frac{1}{\ell }}{e}^{-\check{\mathfrak{t}}/\ell }\sum _{k=0}^{i-1}{\mathcal{B}}_{k+1}^{\left(i\right)}(k+n+1){(1-e^{-\check{\mathfrak{t}}/\ell })}^{k+n}+{\displaystyle \frac{n}{\ell }}{\mathcal{B}}_0^{\left(i\right)}{e}^{-\check{\mathfrak{t}}/\ell }{(1-e^{-\check{\mathfrak{t}}/\ell })}^{n-1}.\hfill \end{array}$$

(23)

Using Corollary 1, we get

$$D{\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)={\displaystyle \frac{1}{\ell }}{(1-e^{-\check{\mathfrak{t}}/\ell })}^n\sum _{k=0}^{i-1}{\mathcal{B}}_{k+1}^{\left(i\right)}(k+n+1)\sum _{r=0}^{k+1}{\mathcal{M}}_r^{\left(k\right)}{\mathcal{J}}_r^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\displaystyle \frac{n}{\ell }}{\mathcal{B}}_0^{\left(i\right)}\sum _{r=0}^n{\mathcal{M}}_r^{(n-1)}{\mathcal{J}}_r^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right).$$

(24)

Then, expanding and collecting similar terms leads to (21).    □

Now, we have reached the main desired result in this section, the mentioned OM of the vector (20), which is a direct consequence of Theorem 1 as follows:

Corollary 2. 

The mth derivative of the vector ${\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$ has the form

$${\displaystyle \frac{d^m{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)}{d{t}^m}}=G_n^m{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\mathbf{{\rm Y}}}_{n,\aleph }^{\left(m\right)}\left(\check{\mathfrak{t}}\right),$$

(25)

with ${\mathbf{{\rm Y}}}_{n,\aleph }^{\left(m\right)}\left(\check{\mathfrak{t}}\right)={\displaystyle \sum _{k=0}^{m-1}}{G}_n^k{\mathit{Q}}_{n,\aleph }^{(m-k-1)}\left(\check{\mathfrak{t}}\right)$, where ${\mathit{Q}}_{n,\aleph }\left(\check{\mathfrak{t}}\right)={\left[Q_{n,0}\left(\check{\mathfrak{t}}\right),Q_{n,1}\left(\check{\mathfrak{t}}\right),\dots ,Q_{n,\aleph }\left(\check{\mathfrak{t}}\right)\right]}^{T}and{G}_n={\left(g_{i,j}\left(n\right)\right)}_{0\le i,j\le \aleph }$ is a matrix of order $(\aleph +1)\times (\aleph +1)$, which can be expressed explicitly as

$$\left(\begin{array}{cccccc}{\Theta }_{0,0}^{{\varsigma }_1,{\varsigma }_2}(n,\ell )& 0& \dots & \dots & \dots & 0\\ \\ {\Theta }_{1,0}^{{\varsigma }_1,{\varsigma }_2}(n,\ell )& {\Theta }_{1,1}^{{\varsigma }_1,{\varsigma }_2}(n,\ell )& 0& \dots & \dots & 0\\ ⋮& & \ddots & & & ⋮\\ {\Theta }_{i,0}^{{\varsigma }_1,{\varsigma }_2}(n,\ell )& \dots & {\Theta }_{i,i}^{{\varsigma }_1,{\varsigma }_2}(n,\ell )& 0& \dots & 0\\ ⋮& & & \ddots & & ⋮\\ ⋮& & & & \ddots & 0\\ {\Theta }_{\aleph ,0}^{{\varsigma }_1,{\varsigma }_2}(n,\ell )& \dots & \dots & \dots & \dots & {\Theta }_{\aleph ,\aleph }^{{\varsigma }_1,{\varsigma }_2}(n,\ell )\end{array}\right),$$

(26)

where

$$g_{i,j}\left(n\right)=\left\{\begin{array}{cc}{\Theta }_{i,j}^{{\varsigma }_1,{\varsigma }_2}(n,\ell ),\hfill & i\ge j,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

4. Numerical Handling for IVP (1) and (2)

Here, we utilize the OM obtained in Corollary 2 to derive NUMSs for (1) and (2).

4.1. Homogeneous ICs

Suppose we have homogeneous initial conditions (HICs), i.e., ${\beta }_j=0,j=0,1,2,\dots ,n-1$. We propose the APPS to $\mathcal{Y}\left(\check{\mathfrak{t}}\right)$ as

$${\displaystyle \mathcal{Y}\left(\check{\mathfrak{t}}\right)\simeq {\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)=\sum _{i=0}^{\aleph }{c}_i{\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)={\mathit{A}}^T{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),}$$

(27)

where $\mathit{A}={\left[c_0,c_1,\dots ,c_{\aleph }\right]}^T$, and the unknown constants $c_i,i=0,1,\dots ,\aleph ,$ are to be determined.

Corollary 2 enables us to obtain

$$D^m{\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)={\mathit{A}}^T{G}_n^m{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\mathbf{{\rm Y}}}_{n,\aleph }^{\left(m\right)}\left(\check{\mathfrak{t}}\right),m=1,2,\dots ,n-1.$$

(28)

In this method, using the approximations (27) and (28) allows one to write the residual of Equation (1) as

$$\begin{array}{cc}\hfill {\mathfrak{R}}_{n,\aleph }\left(\check{\mathfrak{t}}\right)=& {\mathit{A}}^T{G}_n^n{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\mathbf{{\rm Y}}}_{n,\aleph }^{\left(n\right)}\left(\check{\mathfrak{t}}\right)\hfill \\ & -F(\check{\mathfrak{t}},{\mathit{A}}^T{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),{\mathit{A}}^T{G}_n{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\mathbf{{\rm Y}}}_{n,\aleph }^{\left(1\right)}\left(\check{\mathfrak{t}}\right),\dots ,{\mathit{A}}^T{G}_n^{n-1}{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+{\mathbf{{\rm Y}}}_{n,\aleph }^{(n-1)}\left(\check{\mathfrak{t}}\right)).\hfill \end{array}$$

(29)

We suggest a spectral approach, referred to as GEJFCOPMM using SCM and the computed previous OMs. The collocation points for GEJFCOPMM are the $(\aleph +1)$ zeros whose form

$${\check{\mathfrak{t}}}_{\aleph ,j}=-\ell ln\left({\displaystyle \frac{1-x_{\aleph ,j}}{2}}\right),j=0,1,\dots ,\aleph ,$$

(30)

where ${\mathcal{P}}_{\aleph +1}^{({\varsigma }_1,{\varsigma }_2)}\left(x_{\aleph ,j}\right)={\mathcal{J}}_{\aleph +1}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left({\check{\mathfrak{t}}}_{\aleph ,j}\right)=0$, such that

$${\mathfrak{R}}_{n,\aleph }\left({\check{\mathfrak{t}}}_{i,\aleph }\right)=0,i=0,1,...,\aleph .$$

(31)

By solving (31) using Newton’s iterative method, we obtain the unknown constants $c_i,i=0,1,\dots ,\aleph ,$ and the desired NUMS (27) is computed.

4.2. Nonhomogeneous ICs

Here, GEJFCOPMM is developed to solve (1) and (2) by transforming it into an equivalent form with HICs. This transformation has the form

$$\overline{\mathcal{Y}}\left(\check{\mathfrak{t}}\right)=\mathcal{Y}\left(\check{\mathfrak{t}}\right)-q_n\left(\check{\mathfrak{t}}\right),q_n\left(\check{\mathfrak{t}}\right)=\sum _{i=0}^{n-1}{\displaystyle \frac{{\beta }_i}{i!}}{\check{\mathfrak{t}}}^i,$$

(32)

which leads to

$$D^n\overline{\mathcal{Y}}\left(\check{\mathfrak{t}}\right)=-D^n{q}_n\left(\check{\mathfrak{t}}\right)+F(\check{\mathfrak{t}},\overline{\mathcal{Y}}\left(\check{\mathfrak{t}}\right)+q_n\left(\check{\mathfrak{t}}\right),D(\overline{\mathcal{Y}}\left(\check{\mathfrak{t}}\right)+q_n\left(\check{\mathfrak{t}}\right)),D^2(\overline{\mathcal{Y}}\left(\check{\mathfrak{t}}\right)+q_n\left(\check{\mathfrak{t}}\right)),\dots ,D^{n-1}(\overline{\mathcal{Y}}\left(\check{\mathfrak{t}}\right)+q_n\left(\check{\mathfrak{t}}\right))),0\le \check{\mathfrak{t}}<\infty ,$$

(33)

where

$${\overline{\mathcal{Y}}}^{\left(m\right)}\left(0\right)=0,m=0,1,\dots ,n-1.$$

(34)

Then,

$${\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)={\overline{\mathcal{Y}}}_{\aleph }\left(\check{\mathfrak{t}}\right)+q_n\left(\check{\mathfrak{t}}\right).$$

(35)

Remark 2. 

The algorithm presented here is used to solve multiple numerical examples in Section 6. The computations were performed using Mathematica 13.3 on a computer system equipped with an Intel(R) Core(TM) i9-10850 CPU operating at 3.60 GHz, featuring 10 cores and 20 logical processors. The algorithmic steps for solving the ODEs using GEJFCOPMM are expressed in Algorithm 1.

Algorithm 1 GEJFCOPMM algorithm

Step 1. Given ${\varsigma }_1,{\varsigma }_2,\ell ,\aleph$ and ${\beta }_j,j=0,\dots ,n-1$.

Step 2. Define the basis ${\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$, the vectors $\mathit{A},{\mathbf{\Phi }}_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)$ and compute the elements of $(\aleph +1)(\aleph +1)$ matrix $G_n$.

Step 3. Evaluate ${\mathit{A}}^T{G}_n^m,{\mathbf{{\rm Y}}}_{n,\aleph }^{\left(m\right)}\left(\check{\mathfrak{t}}\right),m=1,...,n.$

Step 4. Define ${\mathfrak{R}}_{n,\aleph }\left(\check{\mathfrak{t}}\right)$ as in Equation (29).

Step 5. List ${\mathfrak{R}}_{n,\aleph }\left({\check{\mathfrak{t}}}_{i,\aleph }\right)=0,i=0,1,...,\aleph ,$ defined in Equation (31).

Step 6. Use Mathematica’s built-in numerical solver to obtain the solution to the system of equations in [Output 5].

Step 7. Evaluate ${\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)$ defined in Equation (27) (In the case of homogeneous ICs).

Step 8. Evaluate $q_n\left(\check{\mathfrak{t}}\right)$ and ${\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)$ defined in Equation (35) (In the case of Nonhomogeneous ICs).

Remark 3. 

For interested readers, we utilized several built-in functions in Mathematica 13.3 for our numerical implementation of the provided algorithms. Below is a summary of the tools used, along with concise information about each function.

• Array: For creating and manipulating arrays, which are used to hold coefficients and OMs throughout the computations.
• NSolve: For finding NUMSs to nonlinear algebraic equations; it is utilized to compute the zeros of ${\mathcal{P}}_{\aleph +1}^{({\varsigma }_1,{\varsigma }_2)}\left(x\right)$.
• FindRoot: For solving equations by finding roots; it is essential in handling the nonlinear aspects of our system, using a zero initial approximation.
• JacobiP: For generating ${\varphi }_{n,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\tau \right)$, which serve as basis functions that provide the foundation for approximating the solution in our collocation method.
• D: To compute ordinary derivatives to determine the defined residuals.
• Table: For generating lists and arrays of values based on specified formulas, particularly for collocation points and other parameterized data.

5. Convergence and Error Analysis (CEA)

In this part, we present the CEA of GEJFCOPMM. In this respect, we consider the space

$$S_{n,\aleph }=Span\{{\varphi }_{n,0}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),{\varphi }_{n,1}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right),...,{\varphi }_{n,\aleph }^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)\}.$$

Additionally, the absolute error (AE) between $\mathcal{Y}\left(\check{\mathfrak{t}}\right)$ and its approximation ${\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)$ can be defined by

$$E_{\aleph }\left(\check{\mathfrak{t}}\right)=\left|\mathcal{Y}\left(\check{\mathfrak{t}}\right)-{\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)\right|.$$

(36)

In the paper, the error obtained by GEJFCOPMM is analyzed by using the the weighted $L_2$ norm

$$\parallel E_{\aleph }{\parallel }_2={\parallel \mathcal{Y}-{\mathcal{Y}}_{\aleph }\parallel }_2={\left({\int }_0^{\infty }{\widehat{w}}_{e,n}^{{\varsigma }_1,{\varsigma }_2}\left(\check{\mathfrak{t}}\right){|\mathcal{Y}\left(\check{\mathfrak{t}}\right)-{\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)|}^{2}d\check{\mathfrak{t}}\right)}^{1/2},$$

(37)

and the $L_{\infty }$ (MAE) norm

$$\parallel E_{\aleph }{\parallel }_{\infty }=\parallel \mathcal{Y}-{\mathcal{Y}}_{\aleph }{\parallel }_{\infty }=\underset{0\le \check{\mathfrak{t}}\le L}{max}|\mathcal{Y}\left(\check{\mathfrak{t}}\right)-{\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)|.$$

(38)

The following lemma is need to prove Theorem 2:

Lemma 3. 

Consider the zeros $x_{\aleph ,k},{\check{\mathfrak{t}}}_{\aleph ,k},k=0,1,\dots ,\aleph$; then, there exists a constant M such that

$$|\check{\mathfrak{t}}-{\check{\mathfrak{t}}}_{\aleph ,k}|<M\ell |x-x_{\aleph ,k}|.$$

(39)

Proof. 

In view of (30), we have

$$|\check{\mathfrak{t}}-{\check{\mathfrak{t}}}_{\aleph ,k}| =|-\ell ln\left({\displaystyle \frac{1-x}{2}}\right)+\ell ln\left({\displaystyle \frac{1-x_{\aleph ,k}}{2}}\right)|=\ell |ln\left({\displaystyle \frac{1-x}{1-x_{\aleph ,k}}}\right)|.$$

(40)

Consider the function $f\left(x\right)=ln\left({\displaystyle \frac{1-x}{1-x_{\aleph ,k}}}\right),x\in (-1,1)$. Using the mean value theorem, we get

$$f\left(x\right)=f^{\prime }\left({\zeta }_x\right)(x-x_{\aleph ,k}),{\zeta }_x\in (x_{\aleph ,k},x);$$

(41)

then,

$$\left|f\left(x\right)\right|\le M|x-x_{\aleph ,k}|,M=\underset{-1\le x\le 1}{max}\left|f^{\prime }\left(x\right)\right|.$$

(42)

Applying the inequality (42) to (40), we obtain

$$|\check{\mathfrak{t}}-{\check{\mathfrak{t}}}_{\aleph ,k}|\le \ell M|x-x_{\aleph ,k}|,$$

(43)

which completes the proof of the lemma. □

Theorem 2. 

Assume that $\mathcal{Y}\left(\check{\mathfrak{t}}\right)={(1-e^{-\check{\mathfrak{t}}/\ell })}^{n}u\left(\check{\mathfrak{t}}\right)$, and ${\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)$ has the form (27) and represents the best possible approximation (BPA) for $\mathcal{Y}\left(\check{\mathfrak{t}}\right)$ out of $S_{n,\aleph }$. Then, there is a constant K such that

$$\parallel E_{\aleph }{\parallel }_{\infty }\le {\displaystyle \frac{K}{2^{\lambda -1}}}{\left({\displaystyle \frac{e}{2}}\right)}^{\aleph }{(\aleph +1)}^{q-\aleph -1},$$

(44)

and

$$\parallel E_{\aleph }{\parallel }_2\le {\displaystyle \frac{K}{2^{\lambda -1}}}\sqrt{{\displaystyle \frac{\Gamma ({\varsigma }_1+1)\Gamma ({\varsigma }_2+1)}{\Gamma (\lambda +1)}}}{\left({\displaystyle \frac{e}{2}}\right)}^{\aleph }{(\aleph +1)}^{q-\aleph -1},$$

(45)

where $q=max\{{\varsigma }_1,{\varsigma }_2,-1/2\}<\aleph +1$, $K={(\ell M)}^{\aleph +1}\underset{\check{\mathfrak{t}}\in [0,\infty )}{max}\left|{\displaystyle \frac{d^{\aleph +1}u\left({\eta }_{\check{\mathfrak{t}}}\right)}{d{\check{\mathfrak{t}}}^{\aleph +1}}}\right|,{\eta }_{\check{\mathfrak{t}}}\in [0,\infty )$ and the constant M is a constant given by Lemma 3.

Proof. 

Using Theorem 3.3 in ([31], p. 109), $u\left(\check{\mathfrak{t}}\right)$ takes the form

$$u\left(\check{\mathfrak{t}}\right)=u_{\aleph }\left(\check{\mathfrak{t}}\right)+{\displaystyle \frac{\underset{\check{\mathfrak{t}}\in [0,\infty )}{max}\left|{\displaystyle \frac{d^{\aleph +1}u\left({\eta }_{\check{\mathfrak{t}}}\right)}{d{\check{\mathfrak{t}}}^{\aleph +1}}}\right|}{(\aleph +1)!}}\prod _{k=0}^{\aleph }(\check{\mathfrak{t}}-{\check{\mathfrak{t}}}_k),{\eta }_{\check{\mathfrak{t}}}\in [0,\infty ),$$

(46)

where $u_{\aleph }\left(\check{\mathfrak{t}}\right)$ (has the form of Equation (3.1) in ([31], p. 108)) is the interpolating polynomial for $u\left(\check{\mathfrak{t}}\right)$ at the points ${\check{\mathfrak{t}}}_k,k=0,1,\dots ,\aleph ,$ that satisfy ${\mathcal{J}}_{\aleph +1}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left({\check{\mathfrak{t}}}_k\right)=0$, such that $\aleph >q-1$. In view of Lemma 3, we have

$$|u\left(\check{\mathfrak{t}}\right)-u_{\aleph }\left(\check{\mathfrak{t}}\right)|\le {\displaystyle \frac{K}{(\aleph +1)!}}\left|\prod _{k=0}^{\aleph }(x-x_k)\right|.$$

(47)

Then, we get

$$\parallel u-u_{\aleph }{\parallel }_{\infty }\le {\displaystyle \frac{K}{(\aleph +1)!}}\parallel \prod _{k=0}^{\aleph }(x-x_k){\parallel }_{\infty }={\displaystyle \frac{K}{(\aleph +1)!c_{\aleph +1}^{\aleph +1}}}{\parallel {\mathcal{P}}_{\aleph +1}^{({\varsigma }_1,{\varsigma }_2)}\parallel }_{\infty },$$

(48)

where $c_{\aleph +1}^{\aleph +1}={\displaystyle \frac{\Gamma (2\aleph +\lambda +2)}{2^{\aleph +1}(\aleph +1)!\Gamma (\aleph +\lambda +1)}}$ is the leading coefficient of ${\mathcal{P}}_{\aleph +1}^{({\varsigma }_1,{\varsigma }_2)}\left(\check{\mathfrak{t}}\right)$. In view of formula ([29], Formula (7.32.2)),

$$\parallel {\mathcal{P}}_{\aleph +1}^{({\varsigma }_1,{\varsigma }_2)}{\parallel }_{\infty }\simeq {(\aleph +1)}^q,$$

(49)

we get

$$\parallel u-u_{\aleph }{\parallel }_{\infty }\le K{\displaystyle \frac{2^{\aleph +1}\Gamma (\aleph +\lambda +1){(\aleph +1)}^q}{\Gamma (2\aleph +\lambda +2)}}.$$

(50)

By using [32],

$$\Gamma (\mathfrak{m}+\lambda )=\mathcal{O}({\mathfrak{m}}^{\lambda -1}\mathfrak{m}!),\left(2\mathfrak{m}\right)!={\displaystyle \frac{1}{\sqrt{\pi }}}{4}^{\mathfrak{m}}\mathfrak{m}!\Gamma (\mathfrak{m}+1/2),\mathfrak{m}!=\mathcal{O}\left(\sqrt{2\pi \mathfrak{m}}{\left({\displaystyle \frac{\mathfrak{m}}{e}}\right)}^{\mathfrak{m}}\right),$$

(51)

the inequality (50) takes the form

$$\parallel u-u_{\aleph }{\parallel }_{\infty }\le {\displaystyle \frac{K}{2^{\lambda -1}}}{\left({\displaystyle \frac{e}{2}}\right)}^{\aleph }{(\aleph +1)}^{q-\aleph -1}.$$

(52)

Now, consider $\mathcal{Y}\left(\check{\mathfrak{t}}\right)\simeq Y_{\aleph }\left(\check{\mathfrak{t}}\right)={(1-e^{-\check{\mathfrak{t}}/\ell })}^n{u}_{\aleph }\left(\check{\mathfrak{t}}\right)$; so,

$$\parallel \mathcal{Y}-Y_{\aleph }{\parallel }_{\infty }\le {\parallel u-u_{\aleph }\parallel }_{\infty }\le {\displaystyle \frac{K}{2^{\lambda -1}}}{\left({\displaystyle \frac{e}{2}}\right)}^{\aleph }{(\aleph +1)}^{q-\aleph -1}.$$

(53)

Since the APPS ${\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)\in S_{n,\aleph },$ represents the BPA to $\mathcal{Y}\left(\check{\mathfrak{t}}\right)$, we have

$$\parallel \mathcal{Y}-{\mathcal{Y}}_{\aleph }{\parallel }_{\infty }\le {\parallel \mathcal{Y}-h\parallel }_{\infty },\forall h\in S_{n,\aleph },$$

(54)

and

$$\parallel \mathcal{Y}-{\mathcal{Y}}_{\aleph }{\parallel }_2\le {\parallel \mathcal{Y}-h\parallel }_2,\forall h\in S_{n,\aleph }.$$

(55)

So,

$$\parallel \mathcal{Y}-{\mathcal{Y}}_{\aleph }{\parallel }_{\infty }\le {\parallel \mathcal{Y}-Y_{\aleph }\parallel }_{\infty }\le {\displaystyle \frac{K}{2^{\lambda -1}}}{\left({\displaystyle \frac{e}{2}}\right)}^{\aleph }{(\aleph +1)}^{q-\aleph -1},$$

(56)

and

$$\parallel \mathcal{Y}-{\mathcal{Y}}_{\aleph }{\parallel }_2^2\le \parallel \mathcal{Y}-Y_{\aleph }{\parallel }_2^2\le \parallel u-u_{\aleph }{\parallel }_2^2 = {\int }_0^{\infty }{\widehat{w}}_{e,n}^{{\varsigma }_1,{\varsigma }_2}\left(\check{\mathfrak{t}}\right){|u\left(\check{\mathfrak{t}}\right)-u_{\aleph }\left(\check{\mathfrak{t}}\right)|}^{2}d\check{\mathfrak{t}}.$$

(57)

Using inequality (52) leads to

$$\parallel \mathcal{Y}-{\mathcal{Y}}_{\aleph }{\parallel }_2\le {\displaystyle \frac{K}{2^{\lambda -1}}}\sqrt{{\displaystyle \frac{\Gamma ({\varsigma }_1+1)\Gamma ({\varsigma }_2+1)}{\Gamma (\lambda +1)}}}{\left({\displaystyle \frac{e}{2}}\right)}^{\aleph }{(\aleph +1)}^{q-\aleph -1}.$$

(58)

□

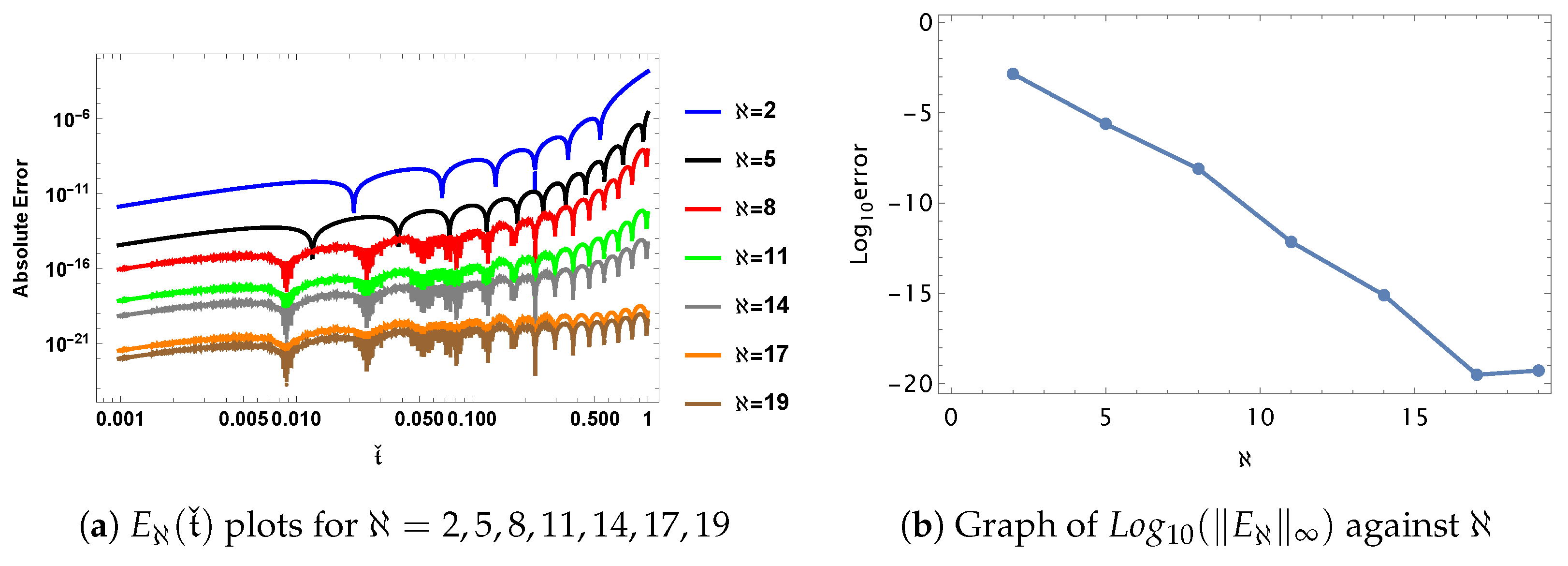
The following implication demonstrates that the acquired inaccuracies converge rapidly.

Corollary 3. 

For all $\aleph >q-1$, we have

$$\parallel E_{\aleph }{\parallel }_{\infty }=\mathcal{O}\left({(e/2)}^{\aleph }{\aleph }^{q-\aleph -1}\right),$$

(59)

and

$$\parallel E_{\aleph }{\parallel }_2=\mathcal{O}\left({(e/2)}^{\aleph }{\aleph }^{q-\aleph -1}\right).$$

(60)

The next theorem emphasizes the stability of error, i.e., making an estimation for error propagation.

Theorem 3. 

For any two successive approximations of $\mathcal{Y}\left(\check{\mathfrak{t}}\right)$, we get

$$|{\mathcal{Y}}_{\aleph +1}-{\mathcal{Y}}_{\aleph }| \lesssim \mathcal{O}\left({(e/2)}^{\aleph }{\aleph }^{q-\aleph -1}\right),\aleph >q-1,$$

(61)

where ≲ means that a generic constant d exists, such that $|{\mathcal{Y}}_{\aleph +1}-{\mathcal{Y}}_{\aleph }{| \le d(e/2)}^{\aleph }{\aleph }^{q-\aleph -1}$.

Proof. 

We have

$$|{\mathcal{Y}}_{\aleph +1}-{\mathcal{Y}}_{\aleph }| = |{\mathcal{Y}}_{\aleph +1}-\mathcal{Y}+\mathcal{Y}-{\mathcal{Y}}_{\aleph }| \le |\mathcal{Y}-{\mathcal{Y}}_{\aleph +1}| + |\mathcal{Y}-{\mathcal{Y}}_{\aleph } | \le \parallel E_{\aleph +1}{\parallel }_{\infty }+{\parallel E_{\aleph }\parallel }_{\infty }.$$

(62)

By considering (59), we can obtain (61). □

6. Numerical Simulations

In this part, numerical examples are given to demonstrate that GEJFCOPMM has high efficiency. In these examples,

Table 1. MAEs for Problem 1 using different values for ${\varsigma }_1,{\varsigma }_2$ and ℵ and $\ell =1$.

${\mathit{\varsigma }}_1$	${\mathit{\varsigma }}_2$	$\mathit{Errors}$	$\mathit{\aleph }=2$	$\mathit{\aleph }=5$	$\mathit{\aleph }=8$	$\mathit{\aleph }=11$	$\mathit{\aleph }=14$	$\mathit{\aleph }=17$
0	0	$\parallel E_{\aleph }{\parallel }_{\infty }$	1.31 $\times {10}^{-2}$	2.12 $\times {10}^{-3}$	4.25 $\times {10}^{-5}$	5.15 $\times {10}^{-7}$	1.05 $\times {10}^{-9}$	6.83 $\times {10}^{-10}$
		$\parallel E_{\aleph }{\parallel }_2$	1.11 $\times {10}^{-2}$	1.22 $\times {10}^{-3}$	4.15 $\times {10}^{-5}$	4.15 $\times {10}^{-7}$	1.01 $\times {10}^{-9}$	6.81 $\times {10}^{-10}$
		CPU time	0.231	0.442	0.622	0.831	0.886	0.922
1	1	$\parallel E_{\aleph }{\parallel }_{\infty }$	1.21 $\times {10}^{-2}$	2.22 $\times {10}^{-3}$	4.35 $\times {10}^{-5}$	5.31 $\times {10}^{-7}$	1.20 $\times {10}^{-9}$	6.85 $\times {10}^{-10}$
		$\parallel E_{\aleph }{\parallel }_2$	2.17 $\times {10}^{-2}$	2.12 $\times {10}^{-3}$	4.25 $\times {10}^{-5}$	5.25 $\times {10}^{-7}$	1.10 $\times {10}^{-9}$	6.82 $\times {10}^{-10}$
		CPU time	0.223	0.434	0.625	0.840	0.871	0.901
−1/2	1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	2.22 $\times {10}^{-2}$	1.32 $\times {10}^{-3}$	3.15 $\times {10}^{-5}$	4.11 $\times {10}^{-7}$	1.23 $\times {10}^{-9}$	6.80 $\times {10}^{-10}$
		$\parallel E_{\aleph }{\parallel }_2$	1.13 $\times {10}^{-2}$	1.12 $\times {10}^{-3}$	2.15 $\times {10}^{-5}$	4.01 $\times {10}^{-7}$	1.21 $\times {10}^{-9}$	6.79 $\times {10}^{-10}$
		CPU time	0.227	0.417	0.630	0.829	0.885	0.919
1/2	−1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	2.23 $\times {10}^{-2}$	4.12 $\times {10}^{-3}$	3.85 $\times {10}^{-5}$	4.81 $\times {10}^{-7}$	2.70 $\times {10}^{-9}$	6.78 $\times {10}^{-10}$
		$\parallel E_{\aleph }{\parallel }_2$	2.21 $\times {10}^{-2}$	4.02 $\times {10}^{-3}$	3.75 $\times {10}^{-5}$	4.77 $\times {10}^{-7}$	2.68 $\times {10}^{-9}$	6.77 $\times {10}^{-10}$
		CPU time	0.253	0.425	0.651	0.834	0.891	0.981

,

Table 2. Comparison of AE between the two methods EJOM [26] and $GEJFCOPMM$ for Problem 1.

	Analytical	$\mathit{GEJFCOPMM} (\mathit{\aleph }=12,\mathit{\ell }=1)$			EJOM [26] $(\mathit{\aleph }=20,\mathit{\ell }=1)$
$\check{\mathfrak{t}}$		${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=-\mathbf{0}.\mathbf{5}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}.\mathbf{5}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=-\mathbf{0}.\mathbf{5}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}.\mathbf{5}$
0.0	1.0000000	1.0000000	1.0000000	1.00000000	1.00000000	1.00000000	1.00000000
0.1	0.99004983	0.99004982	0.99004984	0.99004981	0.99004988	0.99004994	0.99004993
0.2	0.96078943	0.96078944	0.96078942	0.96078942	0.96078946	0.96078942	0.96078934
0.3	0.91393118	0.91393117	0.91393116	0.91393117	0.91393112	0.91393112	0.91393120
0.4	0.85214378	0.85214377	0.85214376	0.85214377	0.85214382	0.85214381	0.85214376
0.5	0.77880078	0.77880077	0.77880076	0.77880079	0.77880085	0.77880096	0.77880099
0.6	0.69767632	0.69767633	0.69767634	0.69767631	0.69767618	0.69767594	0.69767596
0.7	0.61262639	0.61262638	0.61262637	0.61262636	0.61262644	0.61262662	0.61262661
0.8	0.527292424	0.527292425	0.527292426	0.527292424	0.52729252	0.52729272	0.52729269
0.9	0.44485806	0.44485805	0.44485803	0.44485802	0.44485807	0.44485772	0.44485769
1.0	0.36787944	0.36787946	0.36787947	0.36787948	0.36787939	0.36787915	0.36787921

,

Table 3. Errors obtained for Problem 2 using different values for ${\varsigma }_1,{\varsigma }_2$ and ℵ and $\ell =1$.

${\mathit{\varsigma }}_1$	${\mathit{\varsigma }}_2$	$\mathit{Errors}$	$\mathit{\aleph }=2$	$\mathit{\aleph }=6$	$\mathit{\aleph }=10$	$\mathit{\aleph }=14$	$\mathit{\aleph }=18$	$\mathit{\aleph }=20$
0	0	$\parallel E_{\aleph }{\parallel }_{\infty }$	2.11 $\times {10}^{-2}$	1.32 $\times {10}^{-4}$	2.35 $\times {10}^{-6}$	4.25 $\times {10}^{-9}$	1.10 $\times {10}^{-10}$	5.10 $\times {10}^{-11}$
		$\parallel E_{\aleph }{\parallel }_2$	1.01 $\times {10}^{-2}$	1.12 $\times {10}^{-4}$	2.15 $\times {10}^{-6}$	3.15 $\times {10}^{-9}$	1.01 $\times {10}^{-10}$	4.12 $\times {10}^{-11}$
		CPU time	0.253	0.443	0.810	0.879	0.936	0.996
1	1	$\parallel E_{\aleph }{\parallel }_{\infty }$	2.35 $\times {10}^{-2}$	3.31 $\times {10}^{-4}$	4.15 $\times {10}^{-6}$	4.35 $\times {10}^{-9}$	4.15 $\times {10}^{-10}$	6.11 $\times {10}^{-11}$
		$\parallel E_{\aleph }{\parallel }_2$	2.31 $\times {10}^{-2}$	2.52 $\times {10}^{-4}$	3.15 $\times {10}^{-6}$	4.25 $\times {10}^{-9}$	1.25 $\times {10}^{-10}$	5.15 $\times {10}^{-11}$
		CPU time	0.249	0.457	0.821	0.888	0.945	0.995
−1/2	1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	4.01 $\times {10}^{-2}$	4.12 $\times {10}^{-4}$	3.25 $\times {10}^{-6}$	5.75 $\times {10}^{-9}$	5.15 $\times {10}^{-10}$	6.86 $\times {10}^{-11}$
		$\parallel E_{\aleph }{\parallel }_2$	3.10 $\times {10}^{-2}$	4.02 $\times {10}^{-4}$	2.75 $\times {10}^{-6}$	5.65 $\times {10}^{-9}$	2.15 $\times {10}^{-10}$	6.85 $\times {10}^{-11}$
		CPU time	0.255	0.456	0.836	0.899	0.949	0.998
1/2	−1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	4.21 $\times {10}^{-2}$	4.31 $\times {10}^{-4}$	5.45 $\times {10}^{-6}$	4.65 $\times {10}^{-9}$	5.80 $\times {10}^{-10}$	7.15 $\times {10}^{-11}$
		$\parallel E_{\aleph }{\parallel }_2$	1.61 $\times {10}^{-2}$	1.72 $\times {10}^{-4}$	2.85 $\times {10}^{-6}$	6.15 $\times {10}^{-9}$	5.13 $\times {10}^{-10}$	6.92 $\times {10}^{-11}$
		CPU time	0.259	0.450	0.844	0.897	0.956	0.995

,

Table 4. Comparison of AE between the two methods EJOM [26] and $GEJFCOPMM$ for Problem 2.

	$\mathit{GEJFCOPMM}(\mathit{\aleph }=20,\mathit{\ell }=1)$			EJOM [26] $(\mathit{\aleph }=24,\mathit{\ell }=1)$
$\check{\mathfrak{t}}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=-\mathbf{0}.\mathbf{5}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}.\mathbf{5}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=-\mathbf{0}.\mathbf{5}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}$	${\mathbf{\varsigma }}_{\mathbf{1}}={\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0}.\mathbf{5}$
0.0	0	0	0	0	0	0
1.0	$4.780\times {10}^{-14}$	$3.890\times {10}^{-14}$	$2.317\times {10}^{-14}$	$3.007\times {10}^{-8}$	$2.107\times {10}^{-8}$	$2.707\times {10}^{-8}$
2.0	$2.308\times {10}^{-14}$	$4.217\times {10}^{-14}$	$4.357\times {10}^{-14}$	$2.353\times {10}^{-8}$	$4.976\times {10}^{-8}$	$5.067\times {10}^{-8}$
3.0	$5.481\times {10}^{-14}$	$5.652\times {10}^{-14}$	$4.982\times {10}^{-14}$	$3.180\times {10}^{-8}$	$5.733\times {10}^{-8}$	$5.028\times {10}^{-8}$
4.0	$1.117\times {10}^{-14}$	$1.223\times {10}^{-14}$	$1.121\times {10}^{-14}$	$9.386\times {10}^{-8}$	$2.368\times {10}^{-8}$	$6.252\times {10}^{-9}$
5.0	$1.112\times {10}^{-14}$	$2.227\times {10}^{-14}$	$2.311\times {10}^{-14}$	$9.514\times {10}^{-9}$	$6.890\times {10}^{-9}$	$1.667\times {10}^{-8}$
6.0	$3.127\times {10}^{-14}$	$3.007\times {10}^{-14}$	$3.018\times {10}^{-14}$	$1.007\times {10}^{-9}$	$4.581\times {10}^{-9}$	$3.294\times {10}^{-9}$
7.0	$1.112\times {10}^{-14}$	$1.717\times {10}^{-14}$	$1.126\times {10}^{-14}$	$6.591\times {10}^{-10}$	$1.593\times {10}^{-10}$	$9.366\times {10}^{-9}$
8.0	$5.521\times {10}^{-14}$	$5.423\times {10}^{-14}$	$5.326\times {10}^{-14}$	$1.070\times {10}^{-9}$	$3.543\times {10}^{-9}$	$1.079\times {10}^{-8}$
9.0	$4.960\times {10}^{-11}$	$4.892\times {10}^{-11}$	$4.563\times {10}^{-11}$	$1.375\times {10}^{-9}$	$5.259\times {10}^{-9}$	$1.136\times {10}^{-8}$
10.0	$2.107\times {10}^{-10}$	$2.107\times {10}^{-10}$	$2.107\times {10}^{-10}$	$6.492\times {10}^{-10}$	$5.976\times {10}^{-9}$	$1.153\times {10}^{-8}$

,

Table 5. Errors obtained for Problem 3 using different values for ${\varsigma }_1,{\varsigma }_2$ and ℵ and $\ell =1$.

${\mathit{\varsigma }}_1$	${\mathit{\varsigma }}_2$	$\mathit{Errors}$	$\mathit{\aleph }=2$	$\mathit{\aleph }=5$	$\mathit{\aleph }=8$	$\mathit{\aleph }=11$	$\mathit{\aleph }=14$	$\mathit{\aleph }=17$
0	0	$\parallel E_{\aleph }{\parallel }_{\infty }$	1.01 $\times {10}^{-3}$	2.12 $\times {10}^{-6}$	3.15 $\times {10}^{-9}$	4.35 $\times {10}^{-12}$	2.10 $\times {10}^{-15}$	4.30 $\times {10}^{-18}$
		$\parallel E_{\aleph }{\parallel }_2$	1.00 $\times {10}^{-3}$	2.05 $\times {10}^{-6}$	3.11 $\times {10}^{-9}$	4.25 $\times {10}^{-12}$	2.09 $\times {10}^{-15}$	4.20 $\times {10}^{-18}$
		CPU time	0.248	0.456	0.666	0.871	0.889	0.949
1	1	$\parallel E_{\aleph }{\parallel }_{\infty }$	2.31 $\times {10}^{-3}$	1.32 $\times {10}^{-6}$	3.45 $\times {10}^{-9}$	4.55 $\times {10}^{-12}$	2.16 $\times {10}^{-15}$	4.80 $\times {10}^{-18}$
		$\parallel E_{\aleph }{\parallel }_2$	2.29 $\times {10}^{-3}$	1.30 $\times {10}^{-6}$	3.41 $\times {10}^{-9}$	4.52 $\times {10}^{-12}$	2.12 $\times {10}^{-15}$	4.78 $\times {10}^{-18}$
		CPU time	0.251	0.451	0.659	0.881	0.901	0.962
−1/2	1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	3.11 $\times {10}^{-3}$	1.32 $\times {10}^{-6}$	3.35 $\times {10}^{-9}$	4.45 $\times {10}^{-12}$	2.60 $\times {10}^{-15}$	4.70 $\times {10}^{-18}$
		$\parallel E_{\aleph }{\parallel }_2$	3.08 $\times {10}^{-3}$	1.27 $\times {10}^{-6}$	3.31 $\times {10}^{-9}$	4.41 $\times {10}^{-12}$	2.58 $\times {10}^{-15}$	4.68 $\times {10}^{-18}$
		CPU time	0.249	0.458	0.655	0.879	0.896	0.958
1/2	−1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	4.11 $\times {10}^{-3}$	2.72 $\times {10}^{-6}$	2.75 $\times {10}^{-9}$	5.15 $\times {10}^{-12}$	3.11 $\times {10}^{-15}$	4.70 $\times {10}^{-18}$
		$\parallel E_{\aleph }{\parallel }_2$	4.05 $\times {10}^{-3}$	2.52 $\times {10}^{-6}$	2.61 $\times {10}^{-9}$	5.01 $\times {10}^{-12}$	3.06 $\times {10}^{-15}$	4.61 $\times {10}^{-18}$
		CPU time	0.259	0.461	0.661	0.899	0.906	0.971

,

Table 6. Comparison between the methods [33,34,35,36] and $GEJFCOPMM$ for Problem 3.

GEJFCOPMM $(\aleph =\mathbf{17},{\mathbf{\varsigma }}_{\mathbf{1}}=\mathbf{2},{\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0},\ell =\mathbf{1})$	SC3COMM [36] $(\aleph =\mathbf{22})$	SC3CM [36] $(\aleph =\mathbf{22})$	VIM [33]	QBSM [34]	BSCM [35]
1.14 $\times {10}^{-19}$	4.542 $\times {10}^{-15}$	2.123 $\times {10}^{-14}$	1.10 $\times {10}^{-1}$	1.29 $\times {10}^{-5}$	4.08 $\times {10}^{-7}$

,

Table 7. Errors obtained for Problem 4 using different values for ${\varsigma }_1,{\varsigma }_2$ and ℵ and $\ell =2$.

${\mathit{\varsigma }}_1$	${\mathit{\varsigma }}_2$	$\mathit{Errors}$	$\mathit{\aleph }=2$	$\mathit{\aleph }=5$	$\mathit{\aleph }=8$	$\mathit{\aleph }=11$	$\mathit{\aleph }=14$	$\mathit{\aleph }=17$
0	0	$\parallel E_{\aleph }{\parallel }_{\infty }$	1.21 $\times {10}^{-2}$	3.22 $\times {10}^{-5}$	3.75 $\times {10}^{-8}$	5.15 $\times {10}^{-11}$	3.15 $\times {10}^{-14}$	4.60 $\times {10}^{-17}$
		$\parallel E_{\aleph }{\parallel }_2$	1.10 $\times {10}^{-2}$	3.15 $\times {10}^{-5}$	3.71 $\times {10}^{-8}$	5.05 $\times {10}^{-11}$	3.09 $\times {10}^{-14}$	4.55 $\times {10}^{-17}$
		CPU time	0.352	0.552	0.699	0.901	0.981	1.062
1	1	$\parallel E_{\aleph }{\parallel }_{\infty }$	1.23 $\times {10}^{-3}$	2.42 $\times {10}^{-6}$	2.55 $\times {10}^{-9}$	3.45 $\times {10}^{-12}$	1.26 $\times {10}^{-15}$	4.84 $\times {10}^{-18}$
		$\parallel E_{\aleph }{\parallel }_2$	1.20 $\times {10}^{-3}$	2.40 $\times {10}^{-6}$	1.99 $\times {10}^{-9}$	3.33 $\times {10}^{-12}$	1.22 $\times {10}^{-15}$	4.52 $\times {10}^{-18}$
		CPU time	0.356	0.558	0.701	0.922	0.991	1.052
−1/2	1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	4.21 $\times {10}^{-3}$	3.12 $\times {10}^{-6}$	2.21 $\times {10}^{-9}$	5.15 $\times {10}^{-12}$	4.61 $\times {10}^{-15}$	3.52 $\times {10}^{-18}$
		$\parallel E_{\aleph }{\parallel }_2$	4.17 $\times {10}^{-3}$	3.07 $\times {10}^{-6}$	2.11 $\times {10}^{-9}$	5.01 $\times {10}^{-12}$	4.58 $\times {10}^{-15}$	3.44 $\times {10}^{-18}$
		CPU time	0.359	0.560	0.711	0.937	0.992	1.072
1/2	−1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	3.15 $\times {10}^{-2}$	3.71 $\times {10}^{-5}$	1.76 $\times {10}^{-8}$	4.35 $\times {10}^{-11}$	4.15 $\times {10}^{-14}$	5.72 $\times {10}^{-17}$
		$\parallel E_{\aleph }{\parallel }_2$	3.13 $\times {10}^{-2}$	3.69 $\times {10}^{-5}$	1.62 $\times {10}^{-8}$	4.20 $\times {10}^{-11}$	4.11 $\times {10}^{-14}$	5.63 $\times {10}^{-17}$
		CPU time	0.360	0.581	0.711	0.944	0.999	1.079

,

Table 8. Comparison between the methods SCJ [37] and $GEJFCOPMM$ for Problem 4.

$\check{\mathfrak{t}}$	Absolute Errors
	$\mathit{GEJFCOPMM}$	SJC [37]
	$(\aleph =\mathbf{17},{\mathbf{\varsigma }}_{\mathbf{1}}=\mathbf{2},{\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{0},\ell =\mathbf{2})$	$(\aleph =\mathbf{18})$
0.0	0.0000	1.991 $\times {10}^{-18}$
0.1	1.12 $\times {10}^{-20}$	3.037 $\times {10}^{-17}$
0.2	5.31 $\times {10}^{-20}$	4.353 $\times {10}^{-17}$
0.3	6.71 $\times {10}^{-20}$	1.908 $\times {10}^{-17}$
0.4	4.17 $\times {10}^{-20}$	6.418 $\times {10}^{-17}$
0.5	3.21 $\times {10}^{-20}$	5.204 $\times {10}^{-18}$
0.6	2.07 $\times {10}^{-20}$	8.326 $\times {10}^{-17}$
0.7	1.34 $\times {10}^{-19}$	1.110 $\times {10}^{-16}$
0.8	2.66 $\times {10}^{-19}$	1.110 $\times {10}^{-16}$
0.9	2.43 $\times {10}^{-19}$	1.110 $\times {10}^{-16}$
1.0	1.13 $\times {10}^{-19}$	1.110 $\times {10}^{-16}$

,

Table 9. Errors obtained for Problem 5 using different values for ${\varsigma }_1,{\varsigma }_2$ and ℵ and $\ell =2$.

${\mathit{\varsigma }}_1$	${\mathit{\varsigma }}_2$	$\mathit{Errors}$	$\mathit{\aleph }=2$	$\mathit{\aleph }=6$	$\mathit{\aleph }=10$	$\mathit{\aleph }=14$	$\mathit{\aleph }=18$	$\mathit{\aleph }=22$
0	0	$\parallel E_{\aleph }{\parallel }_{\infty }$	1.32 $\times {10}^{-2}$	2.44 $\times {10}^{-4}$	4.51 $\times {10}^{-6}$	5.32 $\times {10}^{-9}$	6.98 $\times {10}^{-13}$	7.11 $\times {10}^{-15}$
		CPU time	0.263	0.451	0.824	0.889	0.946	1.057
1	1	$\parallel E_{\aleph }{\parallel }_{\infty }$	3.45 $\times {10}^{-2}$	3.15 $\times {10}^{-4}$	2.19 $\times {10}^{-6}$	2.65 $\times {10}^{-9}$	4.77 $\times {10}^{-13}$	6.58 $\times {10}^{-15}$
		CPU time	0.268	0.453	0.834	0.899	0.986	1.110
−1/2	1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	1.11 $\times {10}^{-2}$	2.32 $\times {10}^{-4}$	2.55 $\times {10}^{-6}$	4.15 $\times {10}^{-9}$	5.25 $\times {10}^{-13}$	7.06 $\times {10}^{-15}$
		CPU time	0.275	0.483	0.874	0.902	0.990	1.115
1/2	−1/2	$\parallel E_{\aleph }{\parallel }_{\infty }$	4.21 $\times {10}^{-2}$	4.31 $\times {10}^{-4}$	5.45 $\times {10}^{-6}$	4.65 $\times {10}^{-9}$	5.80 $\times {10}^{-10}$	7.15 $\times {10}^{-11}$
		CPU time	0.271	0.489	0.881	0.932	0.995	1.120

and

Table 10. Comparison between residual errors obtained by the methods RBF-DQ [17] and $GEJFCOPMM$ for Problem 5.

$\check{\mathfrak{t}}$	Residual Errors
	$\mathit{GEJFCOPMM}$	RBF-DQ [17]
	$(\aleph =\mathbf{22},{\mathbf{\varsigma }}_{\mathbf{1}}=\mathbf{1}.\mathbf{5},{\mathbf{\varsigma }}_{\mathbf{2}}=\mathbf{1},\ell =\mathbf{2})$	$(\aleph =\mathbf{30})$
0.0	0.0000	0.0000
0.1	1.22 $\times {10}^{-21}$	7.40 $\times {10}^{-16}$
0.2	2.21 $\times {10}^{-21}$	1.49 $\times {10}^{-15}$
0.5	5.31 $\times {10}^{-20}$	4.36 $\times {10}^{-15}$
1.0	4.42 $\times {10}^{-20}$	1.30 $\times {10}^{-17}$
1.5	3.72 $\times {10}^{-19}$	3.29 $\times {10}^{-13}$
2.0	4.52 $\times {10}^{-18}$	1.51 $\times {10}^{-13}$

are given, in which the computed errors to obtain some NUMSs ${\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)$ are presented; additionally, the comparisons between GEJFCOPMM and other techniques in [17,26,33,34,35,36,37] are given. In these tables, excellent computational results are obtained. In addition, they confirm that GEJFCOPMM gives more accurate results than the other techniques. Additionally, Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show that the exact solutions and APPSs in the presented examples are in excellent agreement.

Problem 1. 

Consider the nonlinear Emden–Fowler equation

$$\begin{array}{cc}& D^2\mathcal{Y}\left(\check{\mathfrak{t}}\right)+{\displaystyle \frac{6}{\check{\mathfrak{t}}}}D\mathcal{Y}\left(\check{\mathfrak{t}}\right)+14\mathcal{Y}\left(\check{\mathfrak{t}}\right)+4\mathcal{Y}\left(\check{\mathfrak{t}}\right)ln\mathcal{Y}\left(\check{\mathfrak{t}}\right)=0,\check{\mathfrak{t}}\ge 0,\\ & \mathcal{Y}\left(0\right)=1,\mathit{and}{\mathcal{Y}}^{\prime }\left(0\right)=0.\end{array}\}$$

(63)

The exact solution is $\mathcal{Y}\left(\check{\mathfrak{t}}\right)=e^{-{\check{\mathfrak{t}}}^2}$. The application of GEJFCOPMM gives the proposed solution in the form

$${\displaystyle {\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)=\sum _{i=0}^{\aleph }{c}_i{\varphi }_{2,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+1.}$$

(64)

Figure 1 shows $\mathcal{Y}\left(\check{\mathfrak{t}}\right)$, ${\mathcal{Y}}_{17}\left(\check{\mathfrak{t}}\right)$, and $E_{17}\left(\check{\mathfrak{t}}\right)$ using ${\varsigma }_1=1,{\varsigma }_2=-0.5,\ell =1$, and $\aleph =17$, which leads to an accuracy of $7.8\times {10}^{-11}$. Table 1 shows that the application of $GEJFCOPMM$ using various values of ${\varsigma }_1$ and ${\varsigma }_2$ and $\ell =1$ leads to an accuracy of ${10}^{-10}$. Table 2 also shows a comparison of the AE between our method at $\aleph =12$ and the EJOM method at $\aleph =20$ as mentioned in [26]. Notably, the results demonstrate that $GEJFCOPMM$ achieves significantly better error performance compared to the EJOM method, confirming its superiority.

Problem 2. 

Consider the DE

$$\begin{array}{cc}& D^2\mathcal{Y}\left(\check{\mathfrak{t}}\right)+{\displaystyle \frac{8}{\check{\mathfrak{t}}}}D\mathcal{Y}\left(\check{\mathfrak{t}}\right)+{\mathcal{Y}}^2\left(\check{\mathfrak{t}}\right)=\mathit{erf}{\left(\check{\mathfrak{t}}\right)}^2-{\displaystyle \frac{4e^{-{\check{\mathfrak{t}}}^2}({\check{\mathfrak{t}}}^2-4)}{\sqrt{\pi }\check{\mathfrak{t}}}},\check{\mathfrak{t}}\ge 0,\\ & \mathcal{Y}\left(0\right)=0,{\mathcal{Y}}^{\prime }\left(0\right)={\displaystyle \frac{2}{\sqrt{\pi }}},\end{array}\}$$

(65)

where the exact solution is $\mathcal{Y}\left(\check{\mathfrak{t}}\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^{\check{\mathfrak{t}}}{e}^{-x^2}dx$. The application of GEJFCOPMM gives the proposed solution in the form

$${\displaystyle {\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)=\sum _{i=0}^{\aleph }{c}_i{\varphi }_{2,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+\frac{2\check{\mathfrak{t}}}{\sqrt{\pi }}.}$$

(66)

Table 3 shows that the results from different values of ${\varsigma }_1$, ${\varsigma }_2$, ℵ, and $\ell =1$ have an accuracy that reaches $5\times {10}^{-11}$ at $\aleph =20$. Additionally, Figure 2 shows $\mathcal{Y}\left(\check{\mathfrak{t}}\right)$, ${\mathcal{Y}}_{20}\left(\check{\mathfrak{t}}\right)$, and $E_{20}\left(\check{\mathfrak{t}}\right)$ using ${\varsigma }_1=2,{\varsigma }_2=0.5,\ell =1$, which leads to an accuracy of $5.42\times {10}^{-11}$. Additionally, a comparison between Figure 4 in [26] (using ${\varsigma }_1=-0.5,{\varsigma }_2=0.5,\ell =1$, and $\aleph =24$) and Figure 3 (using ${\varsigma }_1=-0.5,{\varsigma }_2=0.5,\ell =1$, and $\aleph =20$) shows that the AE obtained by applying our method provides better accuracy than that of [26] and reduces the computational efforts. Table 4 also shows a comparison of the AE between our method using $\aleph =20$ and the EJOM method [26] using $\aleph =24$. Notably, the results demonstrate that $GEJFCOPMM$ achieves significantly better error performance compared to the EJOM method, confirming its superiority.

Problem 3. 

Consider the DE

$$\begin{array}{cc}& D^3\mathcal{Y}\left(\check{\mathfrak{t}}\right)+{\displaystyle \frac{6}{\check{\mathfrak{t}}}}{D}^2\mathcal{Y}(\check{\mathfrak{t}})+{\displaystyle \frac{6}{{\check{\mathfrak{t}}}^2}}D\mathcal{Y}\left(\check{\mathfrak{t}}\right)=6({\check{\mathfrak{t}}}^6+2{\check{\mathfrak{t}}}^3+10)e^{-3\mathcal{Y}\left(\check{\mathfrak{t}}\right)},\check{\mathfrak{t}}\in [0,1],\\ & \mathcal{Y}\left(0\right)=0,{\mathcal{Y}}^{\left(1\right)}\left(0\right)=0,{\mathcal{Y}}^{\left(2\right)}\left(0\right)=0,\end{array}\}$$

(67)

where $g\left(\check{\mathfrak{t}}\right)$ is selected, such that $\mathcal{Y}\left(\check{\mathfrak{t}}\right)=ln({\check{\mathfrak{t}}}^3+1)$. The application of GEJFCOPMM gives the proposed solution in the form

$${\displaystyle {\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)=\sum _{i=0}^{\aleph }{c}_i{\varphi }_{3,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)}$$

(68)

and leads to obtaining the numerical results that are summarized in Table 5, and comparisons between GEJFCOPMM and other methods, SC3COMM and SC3CM [36], VIM [33], QBSM [34], and BSCM [35], are presented in Table 6. Additionally, Figure 4a shows the rapid convergence of APPS to the exact solution. Furthermore, Figure 4b shows the log-errors, which demonstrate that the solutions obtained are stable and converge.

Problem 4. 

Consider the DE

$$\begin{array}{cc}& D^5\mathcal{Y}\left(\check{\mathfrak{t}}\right)+\mathcal{Y}\left(\check{\mathfrak{t}}\right)D^4\mathcal{Y}\left(\check{\mathfrak{t}}\right)=g\left(\check{\mathfrak{t}}\right),\check{\mathfrak{t}}\in [0,1],\\ & {\mathcal{Y}}^{\left(i\right)}\left(0\right)=0,i=0,1,2,3,4,\end{array}\}$$

(69)

where $g\left(\check{\mathfrak{t}}\right)$ is selected, such that $\mathcal{Y}\left(\check{\mathfrak{t}}\right)={\check{\mathfrak{t}}}^{5}cos\check{\mathfrak{t}}$. The application of GEJFCOPMM gives the proposed solution in the form

$${\displaystyle {\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)=\sum _{i=0}^{\aleph }{c}_i{\varphi }_{5,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)}$$

(70)

and provides Table 7, which illustrates that the varying parameters ${\varsigma }_1$ and ${\varsigma }_2$ significantly influence the accuracy and convergence of the solutions, which is essential for understanding the behavior of the solution being studied. Furthermore, Table 8 provides a comparison between the SCJ method [37] and the $GEJFCOPMM$ approach, confirming the superiority of $GEJFCOPMM$. Figure 5 illustrates the relationship between the NUMSs and their corresponding errors for the specified parameter values ℵ. By depicting both the solutions and their errors, the figure enables a thorough analysis of the performance of the employed numerical method. Additionally, observing how the solutions converge as ℵ varies provides instructive information about the stability and reliability of the results.

Problem 5. 

Consider the DE

$$\begin{array}{cc}& D^2\mathcal{Y}\left(\check{\mathfrak{t}}\right)+{\displaystyle \frac{2}{\check{\mathfrak{t}}}}\mathcal{Y}\left(\check{\mathfrak{t}}\right)+sin\left(\mathcal{Y}\left(\check{\mathfrak{t}}\right)\right)=0,\check{\mathfrak{t}}\in [0,2],\\ & \mathcal{Y}\left(0\right)=1,{\mathcal{Y}}^{\left(1\right)}\left(0\right)=0,\end{array}\}$$

(71)

where the explicit exact solution is not available; so, the following error norm is used to check the accuracy in this case:

$$\parallel E_{\aleph }{\parallel }_{\infty }=\underset{\check{\mathfrak{t}}\in [0,2]}{max}{R}_{\aleph }\left(\check{\mathfrak{t}}\right),$$

(72)

where $R_{\aleph }\left(\check{\mathfrak{t}}\right)$ is the absolute residual error defined as follows:

$$R_{\aleph }\left(\check{\mathfrak{t}}\right)=|D^2{\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)+{\displaystyle \frac{2}{\check{\mathfrak{t}}}}{\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)+sin\left({\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)\right)|.$$

The application of GEJFCOPMM gives the proposed solution in the form

$${\displaystyle {\mathcal{Y}}_{\aleph }\left(\check{\mathfrak{t}}\right)=\sum _{i=0}^{\aleph }{c}_i{\varphi }_{2,i}^{({\varsigma }_1,{\varsigma }_2,\ell )}\left(\check{\mathfrak{t}}\right)+1}$$

(73)

and provides Table 9, which demonstrates the high efficiency of the $GEJFCOPMM$. Additionally, Table 10 compares the RBF-DQ method [17] with the $GEJFCOPMM$ approach, confirming the superiority of the latter. Figure 6 presents the NUMSs ${\mathcal{Y}}_3\left(\check{\mathfrak{t}}\right)$ and ${\mathcal{Y}}_7\left(\check{\mathfrak{t}}\right)$, along with the residual errors $R_{20}\left(\check{\mathfrak{t}}\right)$ and $R_{22}\left(\check{\mathfrak{t}}\right)$. By illustrating these solutions and errors, the figure facilitates a comprehensive analysis of the performance of $GEJFCOPMM$.

Remark 4. 

In view of the presented CPU time (in seconds), our approach has efficient performance. The calculations show that the memory consumption was excellent. For example, Table 7 shows that the calculated CPU time using $\aleph =8$ is 25% slower than $\aleph =5$ and moreover requires an increase of 21% of memory consumption of RAM compared to the $\aleph =5$ calculation. The numerical examples and comparisons provided in our paper highlight the superior accuracy and efficiency of our algorithm, solidifying its potential for solving ODEs effectively. In contrast, the methods described in [17,26,33,34,35,36,37] did not provide the CPU time or memory usage data. However, our analysis suggests that our approach performs better than these referenced methods.

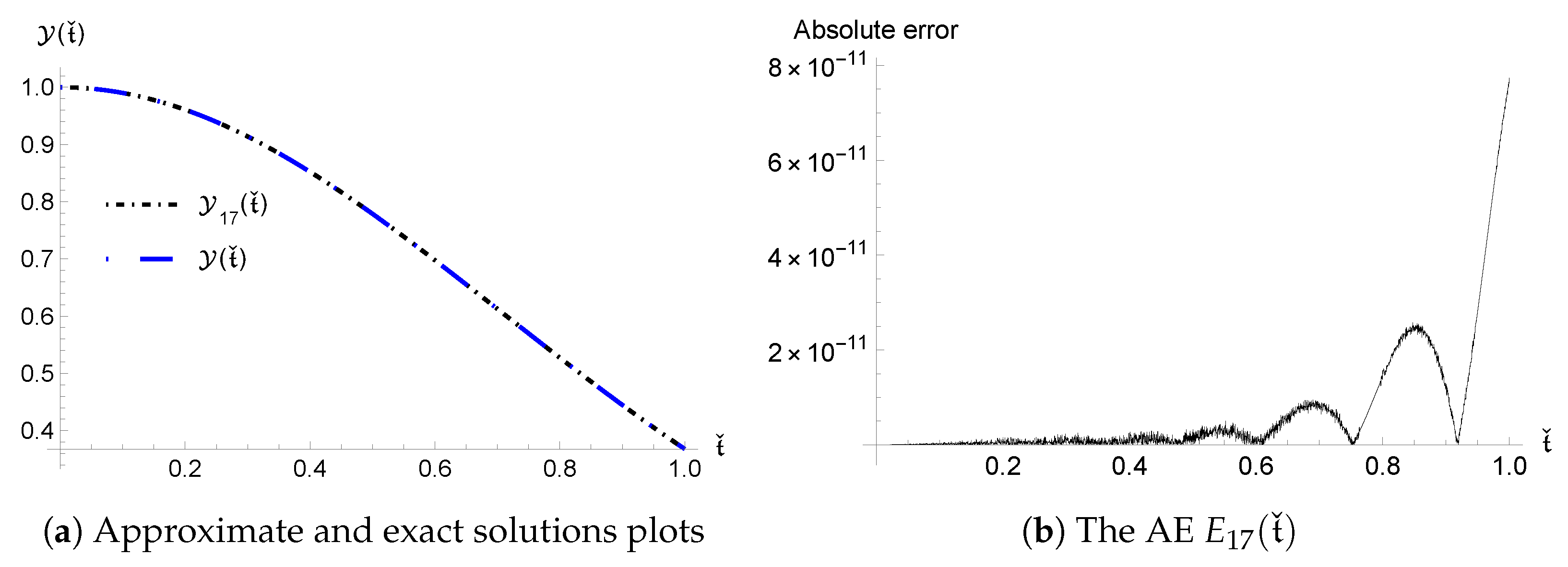
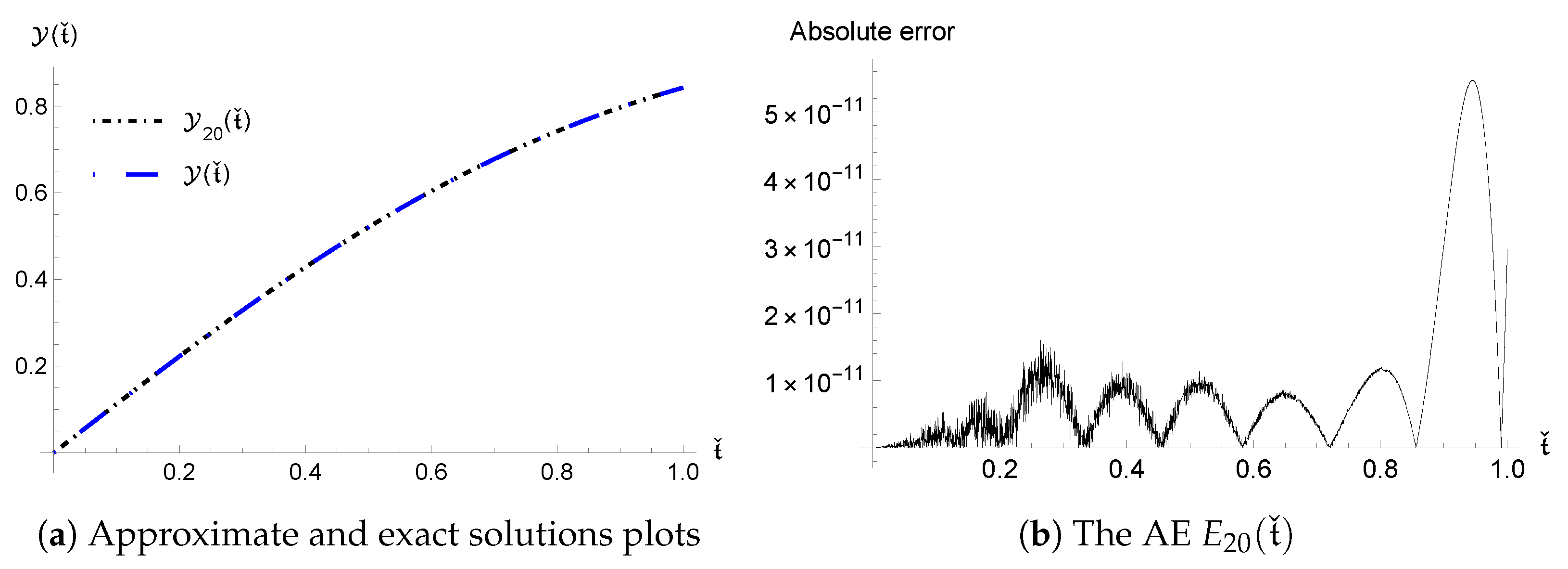
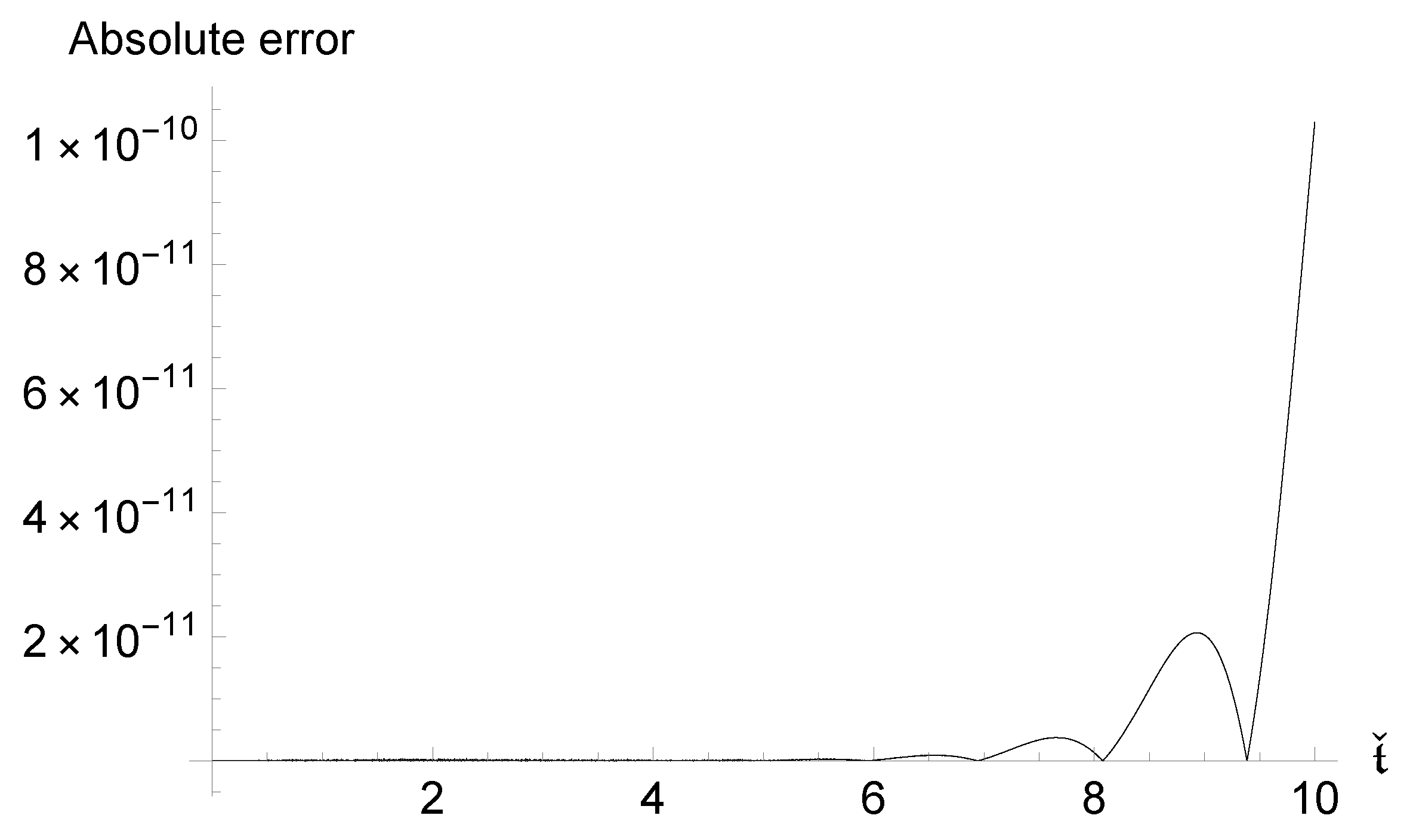
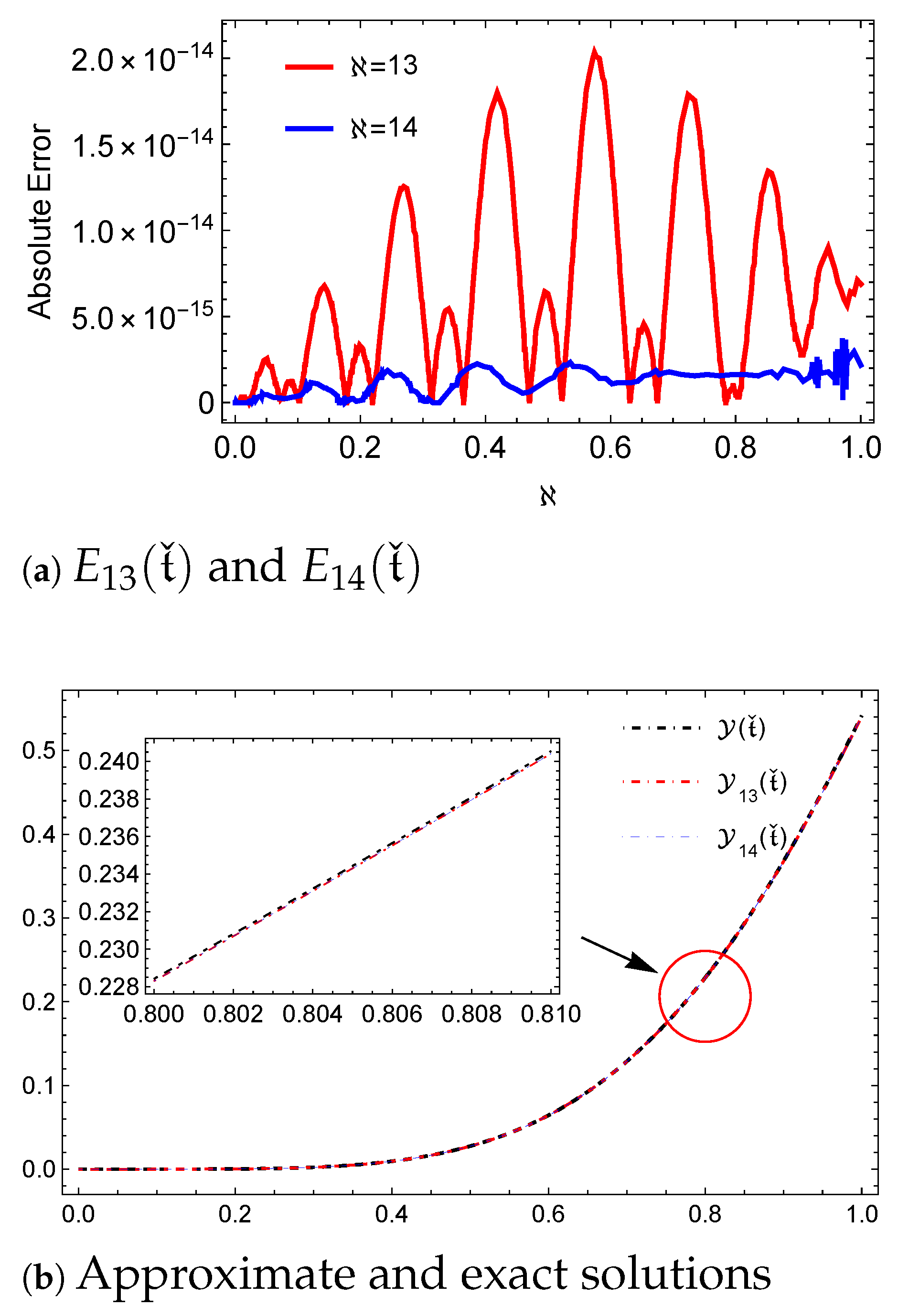
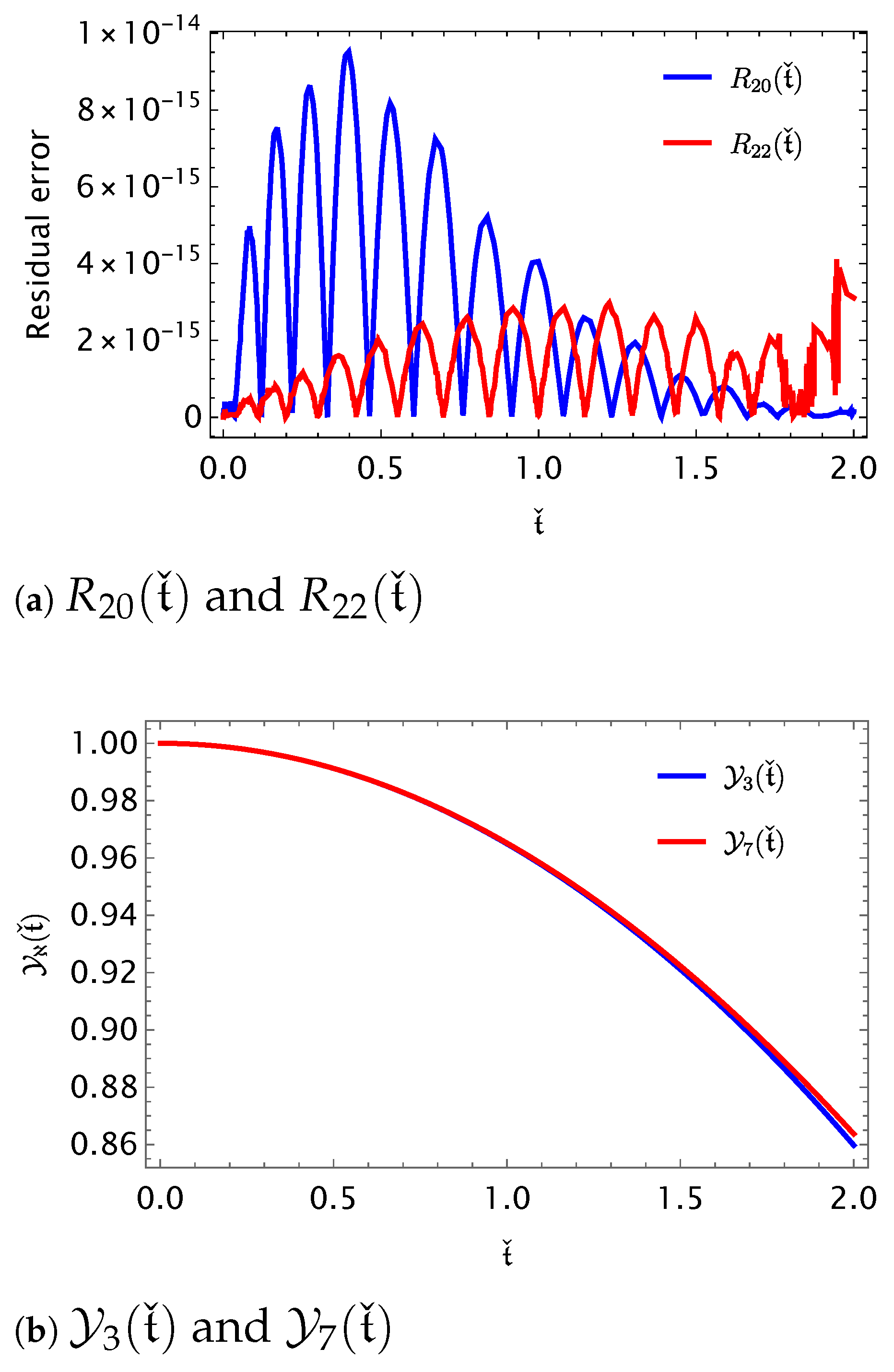
7. Conclusions

In this work, we have introduced GEJFs that satisfy HC. Moreover, by utilizing the computed OMs with the SCM, GEJFCOPMM is established. GEJFCOPMM gives high-accuracy NUMSs and efficiency. For future work, we have identified several potential research avenues. First, we intend to extend the GEJFCOPMM framework to address boundary value problems, which bring with them special difficulties and opportunities for further development. Additionally, we believe that the theoretical findings presented in this paper can be adapted to handle other types of DEs, including PDEs and systems of DEs. Furthermore, exploring the application of GEJFs in real-world scenarios, such as in engineering and physics, could provide valuable insights and validate the robustness of our approach. We also encourage further investigation into the enhancement of OMs for various function classes to broaden the applicability of our method.