Joint Power Allocation Algorithm Based on Multi-Agent DQN in Cognitive Satellite–Terrestrial Mixed 6G Networks

Abstract

The Cognitive Satellite–Terrestrial Network (CSTN) is an important infrastructure for the future development of 6G communication networks. This paper focuses on a potential communication scenario, where satellite users (SUs) dominate and are selected as the primary users, and terrestrial base station users (TUs) are the secondary users. Additionally, each terrestrial base station owns multiple antennae, and the interference of TUs to SUs in the CSTN is limited to a low level or below. In this paper, based on the observation of diversity and the time-varying characteristics of a variety of user requirements, a multi-agent deep Q-network algorithm under interference limitation (MADQN-IL) was proposed, where the power of each antenna in the base station is allocated to maximize the total system throughput while meeting the interference constraints in the CSTN. In our proposed MADQN-IL, the base stations play the role of intelligent agents, and each agent selects the antenna power allocation and cooperates with other agents through sharing system states and the total rewards. Through a simulation comparison, it was discovered that the MADQN-IL algorithm can achieve a higher system throughput than the adaptive resource adjustment (ARA) algorithm and the fixed power allocation methods.

1. Introduction

Space–Air–Ground Integrated Networks (SAGINs), which integrate space and aerial networks with terrestrial wireless systems, play a crucial role in enabling the emerging sixth-generation (6G) wireless networks [1,2,3]. Within this framework, Cognitive Satellite–Terrestrial Networks (CSTNs) serve as valuable networks, making use of the broad coverage and the resilient disaster tolerance of satellite networks to improve spectrum utilization. There are four main technical challenges to using CSTNs: the network architecture and topology, communication protocols and transmission technologies, and security and reliability, as well as resource management and optimization. Among them, numerous studies have proposed various methods to effectively manage CSTN communication resources to enhance system performance.

To integrate the advantages of dynamic spectrum utilization and satellite communication, Ref. [4] proposed a multi-level, sliced sensing architecture and designed the workflow by combining satellites and spectrum sensing. Ref. [5] investigated a CSTN, where both the ST (secondary transmitter) and the SR (secondary receiver) can cooperate with the PU (primary user) in order to improve the PU performance. Ref. [6] proposed a framework for joint optimization, aiming to enhance the system speed by optimizing cooperative beamforming and resource allocation simultaneously, where optimization was achieved through adaptive user scheduling and a cooperative access backhaul strategy leveraging ground 5G base stations (BSs).

In CSTNs, power allocation is critical; it must avoid interfering with satellite users while boosting the terrestrial throughput. Radio frequency congestion intensifies the satellite–terrestrial interference [7], demanding precise control of terrestrial power. Additionally, the cooperative NOMA scheme in [8]—where dynamic power adjustment lets secondary terrestrial networks improve their performance without disrupting the primary satellite networks—further underscores the need for research into terrestrial power allocation strategies.

Some Refs. [9,10,11,12] have investigated the power allocation problem from various mathematical analysis perspectives, such as the convex theory, adaptive methods, and minimum mean square error (MMSE) techniques. Ref. [9] formulated a power allocation optimization problem to maximize the secure energy efficiency and solved it using an iterative algorithm based on a specialized binary search algorithm, successive convex approximation, and S-procedure techniques. Ref. [10] studied the energy-efficient power allocation in CSTNs by formulating the power allocation schemes as optimization problems under the interference constraint and obtained the optimal transmit power by transforming the original concave–convex problem to an equivalent convex problem via the Charnes–Cooper transformation. Ref. [11] considered an overlay satellite–terrestrial network employing an adaptive power-splitting factor; this approach benefits the Internet of Things (IoT) network while guaranteeing a certain quality of service (Qos) of the satellite network. Ref. [12] addressed the joint optimization of hybrid beamforming, user scheduling, and resource allocation in an integrated terrestrial–satellite network (ITSN) and achieved performance gains in the system sum rate and energy efficiency based on the MMSE criterion and logarithmic linearization.

Additionally, allocation algorithms in other networks offer valuable insights. For instance, studies on imperfect-orthogonality-aware scheduling in LPWANs, which balance resource efficiency and interference management [13], provide guidance for the secure, scalable power allocation in CSTNs. These works emphasize the importance of accounting for non-ideal signal characteristics, representing another promising direction in resource allocation research relevant to CSTN optimization.

Besides mathematical methods, game-theory methods have also been widely adopted for resource allocation problems in CSTN scenarios [14,15,16,17]. Ref. [14] transformed the power allocation for caching, computing, and communication in a terrestrial–satellite system into a Nash bargaining game and obtaining the optimal solution by dual decomposition. Ref. [15] constructed a joint spectrum access and power control game and proposed a learning-based distributed spectrum access algorithm inspired by trial-and-error learning which outperforms the original algorithm. Ref. [16] proposed a two-layer hierarchical game framework for a multi-terrestrial BS CSTN scenario and imported a Stackelberg game to model the competition between satellites and BSs, thereby ensuring fairness in resource trading and achieving a win–win outcome for both networks. Ref. [17] designed a distributed power control algorithm to achieve the Nash equilibrium as well as guarantee the SINR requirements of satellite links, and this algorithm outperforms the existing typical algorithms in terms of the system throughput and coverage speed.

However, traditional methods require the construction of complex models, which are often inflexible and difficult to adapt to the dynamic CSTN environment. By leveraging deep reinforcement learning technology (DRL), the speed and effectiveness of resource optimization can be significantly enhanced [18,19,20]. Ref. [18] proposed an enhanced meta-critic learning algorithm in satellite-assisted communications, which is better than the prior actor–critic and meta-learning methods in efficiently scheduling resources and adapting to dynamic wireless environments. Ref. [19] employed a multi-agent DRL approach based on non-orthogonal multiple access (NOMA) to achieve a lower latency and higher energy efficiency in the integrated satellite–terrestrial networks. Ref. [20] proposed a DRL-based beam pattern and bandwidth allocation scheme to match the non-uniform and time-varying traffic demands. Notably, Ref. [21] explores the potential of large language models (LLMs) in optimizing data flows and real-time decision-making within integrated satellite–aerial–terrestrial networks, offering insights for a more adaptive power allocation in dynamic CSTNs.

Future extensions will consider multi-orbit constellations and diverse service scenarios, while analyzing the impacts of user density and terrain on algorithm performance.

However, the existing DRL-based research faces a critical gap: the current works either focus on single-agent settings, neglect satellite–terrestrial interference constraints, or lack dedicated multi-agent coordination mechanisms for power allocation. For instance, ref. [20] employs multi-agent DRL but prioritizes latency and energy efficiency over power optimization under satellite interference, where Ref. [22] focuses on beam and bandwidth allocation with limited consideration to terrestrial BS power management. Therefore, a multi-agent framework is required to balance the terrestrial throughput and satellite interference through coordinated power allocation.

In summary, this paper proposes a multi-agent deep reinforcement learning algorithm (MADQN-IL) for base station power allocation in CSTNs, which integrates interference constraints into the multi-agent DQN framework to balance the terrestrial throughput and satellite interference mitigation. The simulation results validate the algorithm’s effectiveness, demonstrating that it not only achieves the target of enhancing the system throughput to the desired level but also outperforms the existing approaches in maximizing the throughput under interference constraints. The paper is organized as follows: Section 2 presents the system model; Section 3 details the MADQN-IL design; Section 4 analyzes the simulation results; and Section 5 concludes with future work.

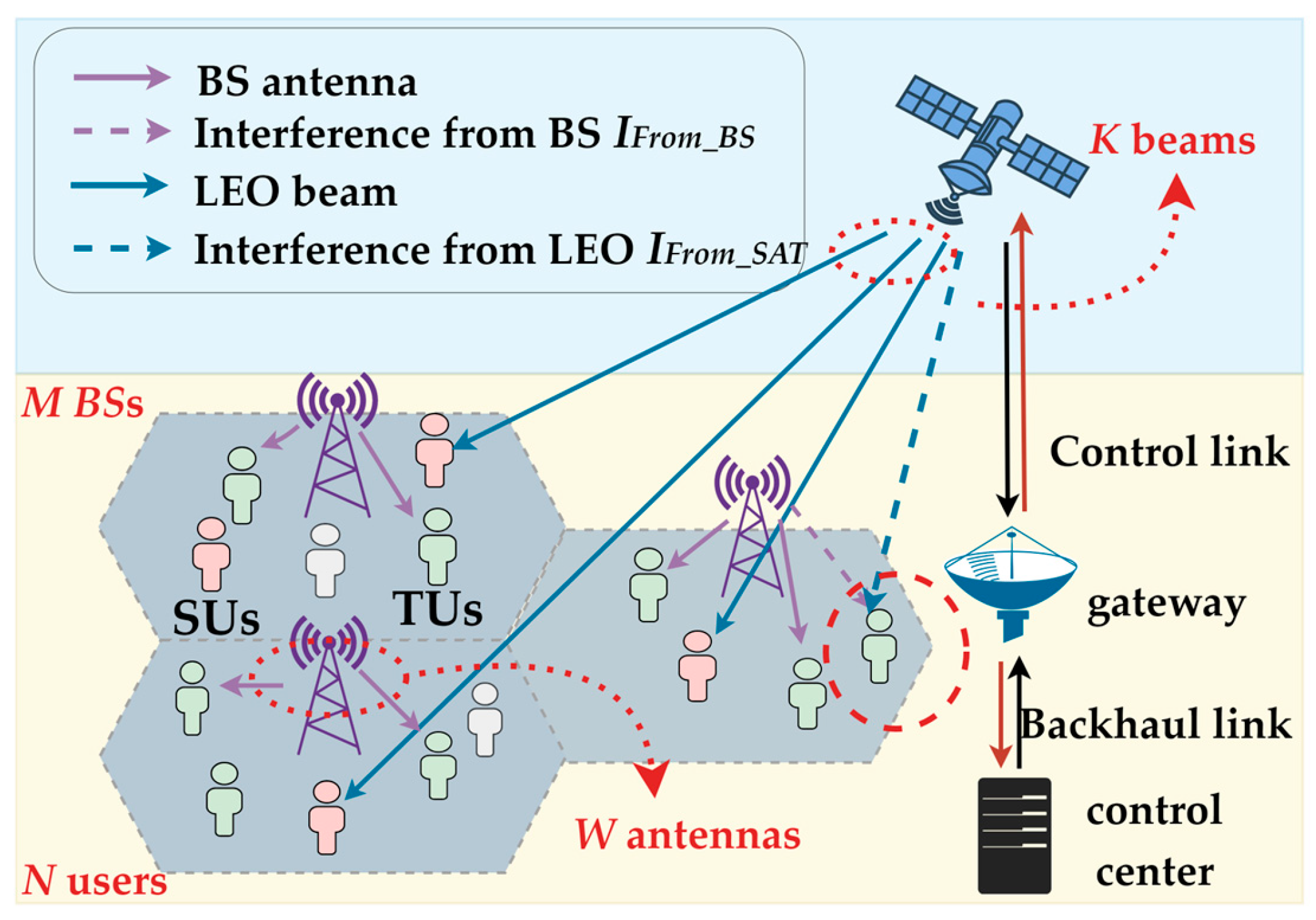
2. System Model

As shown in Figure 1, the system comprises M terrestrial base stations (BSs), one low Earth orbit (LEO) satellite equipped with K spot beams, and N ground users. Each BS is equipped with W antennae and provides downlink services to terrestrial users (TUs). The LEO satellite communicates with the terrestrial network through a gateway, which is connected to a control center via a backhaul link. Users are categorized into three parts, satellite users (SUs) served by the LEO satellite, terrestrial users (TUs) served by the BSs, and unserved users. The system employs a time division multiplexing mechanism to optimize resource allocation among users.

Co-channel interference arises from both the LEO satellite (denoted as $I_{From\_SAT}$) and BSs ($I_{From\_BS}$), as explicitly illustrated in Figure 1 and formulated in Equations (7) and (8), respectively. This integrated architecture enables coordinated resource allocation and interference management across domains.

The association relationship between BSs and users is represented by the BS antenna–user matching matrix $A^{BS}\in C^{M\times N}$, which is a binary matrix of size M × N. The association matrix $A^{BS}$ is defined as follows:

$$A^{BS}=\left[\begin{array}{ccc}{a}_{1,1}^{bs}& \dots & a_{1,N}^{bs}\\ ⋮& \ddots & ⋮\\ a_{M,1}^{bs}& \dots & a_{M,N}^{bs}\end{array}\right]$$

(1)

where, if $a_{m,n}^{bs}=1$, BS m in the current time slot provides services to user n; otherwise, it does not provide services.

The channel gain matrix between users and BSs is represented by $H^{BS}\in C^{M\times N}$, and the matrix element $h_{m,w,n}^{bs}$ is the channel gain between antenna w and user n in BS m. Referring to the definition of 3GPP [23], the offset angle $\phi (m,w,n)$ between BS m’s antenna w and user n determines the BS transmitting antenna gain, denoted as $G_T^{bs}[\phi (m,w,n)]$:

$$G_T^{bs}[\phi (m,w,n)]={10}^{{\displaystyle \frac{G_{T\max }^{bs}}{10}}+\max \{-0.6{[{\displaystyle \frac{\phi (m,w,n)}{{\phi }_{3dB}}}]}^2,-{\displaystyle \frac{A_M}{10}}\}}$$

(2)

where ${\phi }_{3dB}$ is the 3 dB bandwidth, $G_{T\max }^{bs}$ is the maximum transmission gain, and $A_M$ is the ratio of the maximum radiation direction power flux density of the main lobe to the maximum power flux density in the opposite direction. And $L_{m,n}^{bs}$ is the free space loss, shown as follows:

$$L_{m,n}^{bs}(dB)=32.44+20\lg (d_{m,n})+20\lg (F)$$

(3)

where F is the system center frequency (in megahertz MHz), and $d_{m,n}$ is the distance from BS m to the user. Therefore, the channel gain of antenna w and user n is expressed as follows:

$$h_{m,w,n}^{bs}={(G_T^{bs}[\phi (m,w,n)]\cdot L_{m,n}^{bs})}^{{\displaystyle \frac{1}{2}}}$$

(4)

The transmit power allocated to the channel by BS m is $p_m^{BS}$, which satisfies the constraint whereby transmit powers across all channels do not exceed the maximum power that the BS can provide:

$$p_m^{BS}=[p_{m,1}^{bs},\dots ,p_{m,w}^{bs},\dots ,p_{m,W}^{bs}]$$

(5)

Now, consider the channel capacity provided by the antenna w of BS m to user n, expressed as follows:

$$C_{m,w,n}^{bs}=B\cdot {\log }_2(1+{\displaystyle \frac{p_{m,w}^{bs}|h_{m,w,n}^{bs}{|}^2}{n_0\cdot B+I_{m,w,n}^{bs}}})$$

(6)

where B is the bandwidth shared by all BSs in the LEO-assisted network, where $p_{m,w}^{bs}$ is the power allocated to the antenna w of BS m and $n_0$ is the power spectral density of Gaussian noise.

The interference received by terrestrial users is $I_{m,w,n}^{bs}=I_{From\_SAT}+I_{From\_BS}$. For a user n within the coverage range of BS m, the received signal consists of three parts: the desired signal, co-channel interference, and additive white Gaussian noise. The interference includes both interference $I_{From\_SAT}$ from all satellite users and interference $I_{From\_BS}$ from the other users under the same BS m. The terrestrial network operates in the same frequency band as the satellite users, and the maximum transmission power of the BS is allocated across its w antennae of the BS for use. If the user is associated with the BS, the interference to user n comes from the sum of the interference from the other antennae under the same BS. For users not associated with the BS located within the coverage range of the BS, their interference $I_{From\_BS}$ they received comes from all users served by that BS. $I_{From\_SAT}$ and $I_{From\_BS}$ are then denoted by

$$I_{From\_SAT}={\displaystyle \sum _{k=1}^K{p}_k^{sat}|h_{k,n}^{sat}{|}^2}$$

(7)

$$I_{From\_BS}=\left\{\begin{array}{cc}{\displaystyle \sum _{w=1}^W{p}_{m,w}^{bs}|h_{m,w,n}^{bs}{|}^2},& \mathrm{users}\mathrm{not}\mathrm{served}\\ {\displaystyle \sum _{w’=1,w’\ne w}^W{p}_{m,w’}^{bs}|h_{m,w’,n}^{bs}{|}^2},& \mathrm{users}\mathrm{served}\mathrm{by}\mathrm{BS}m\mathrm{with}\mathrm{antenna}w\end{array}\right.$$

(8)

Terrestrial BS users are secondary users in the cognitive satellite–terrestrial system. Therefore, for terrestrial BS users, the primary objective is to guarantee that the aggregate interference from BSs to satellite users does not exceed the predefined threshold value. The interference imposed by BS users on satellites for those within the BS coverage range can be expressed as $I_{BS\_to\_LEO}$. To safeguard the service for satellite users and maintain the reliable communication of satellite users, it is essential to satisfy the constraint $I_{BS\_to\_LEO}\le I_{th}$, where $I_{th}$ is a predefined fixed constant. The expression of $I_{BS\_to\_LEO}$ is given by the following:

$$I_{BS\_to\_LEO}=\max p_{m,w}^{bs}|h_{m,w,n}^{bs}{|}^2,w=1,2,\dots ,W$$

(9)

The arrival of user requests in the system is modeled as a Poisson process. Due to the heterogeneous spatial distribution of terrestrial services, the mean arrival rate of each user’s service requests exhibits temporal variations over a certain period. In a specific time slot, the demand of the N user constitutes a user demand matrix $R=\{r_1,r_2,\dots ,r_n\}$, where $r_n$ represents the instantaneous data rate requirement of user n.

Considering the limited computational and storage resources on the satellite, each user’s demand R is temporarily stored in a limited-length resource demand pool on the satellite side. When a user’s demand in a specific time slot is not immediately satisfied, the unmet portion is queued and retained for up to a predefined number of consecutive time slots, known as the Time to Live (TTL) consecutive time slots. If a data packet remains in the queue beyond its TTL limit, it is discarded. User demands are modeled as a temporal traffic matrix F of dimension N × TTL as illustrated in Figure 2, where F is represented as follows:

$$F=\left[\begin{array}{ccc}{f}_{1,1}& \dots & f_{1,TTL}\\ ⋮& \ddots & ⋮\\ f_{N,1}& \dots & f_{N,TTL}\end{array}\right]$$

(10)

where $f_{n,t}$ means the demand of user n in the slot t. The total pending demand R for user n in the storage pool is the cumulative sum of each row in F, as illustrated in Figure 2.

When the allocated service rate falls below the user’s actual demand, it may cause idle and wasted resources that could have been used for other users or tasks and cause the system to overload. Therefore, the throughput of user n in the time slot t is expressed as follows:

$$Throughpu{t}_t^n=\min [C_{m,w,n}^{bs},r_n]$$

(11)

Thus, the optimization problem aims to maximize the total system throughput, and is formulated as follows:

$$\max T{h}_{all}=\max {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{n=1}^{N}Throughpu{t}_t^n}}$$

(12)

where the transmission power of each antenna in the BS needs to be less than the maximum transmission power $P_{\max }^{BS}$ of the BS, $p_{m,w}^{bs}\le P_{\max }^{BS}$. And each user can be associated with at most one BS, ${\displaystyle \sum _{m=1}^M{a}_{m,n}^{bs}}\le 1$. One antenna only can serve at most one TU, and each BS can serve at most W TUs, ${\displaystyle \sum _{n=1}^N{a}_{m,n}^{bs}}\le W$. Furthermore, the interference $I_{BS\_to\_LEO}$ of the BS to satellite users within its range needs to be less than the maximum interference threshold, $I_{BS\_to\_LEO}\le I_{th}$.

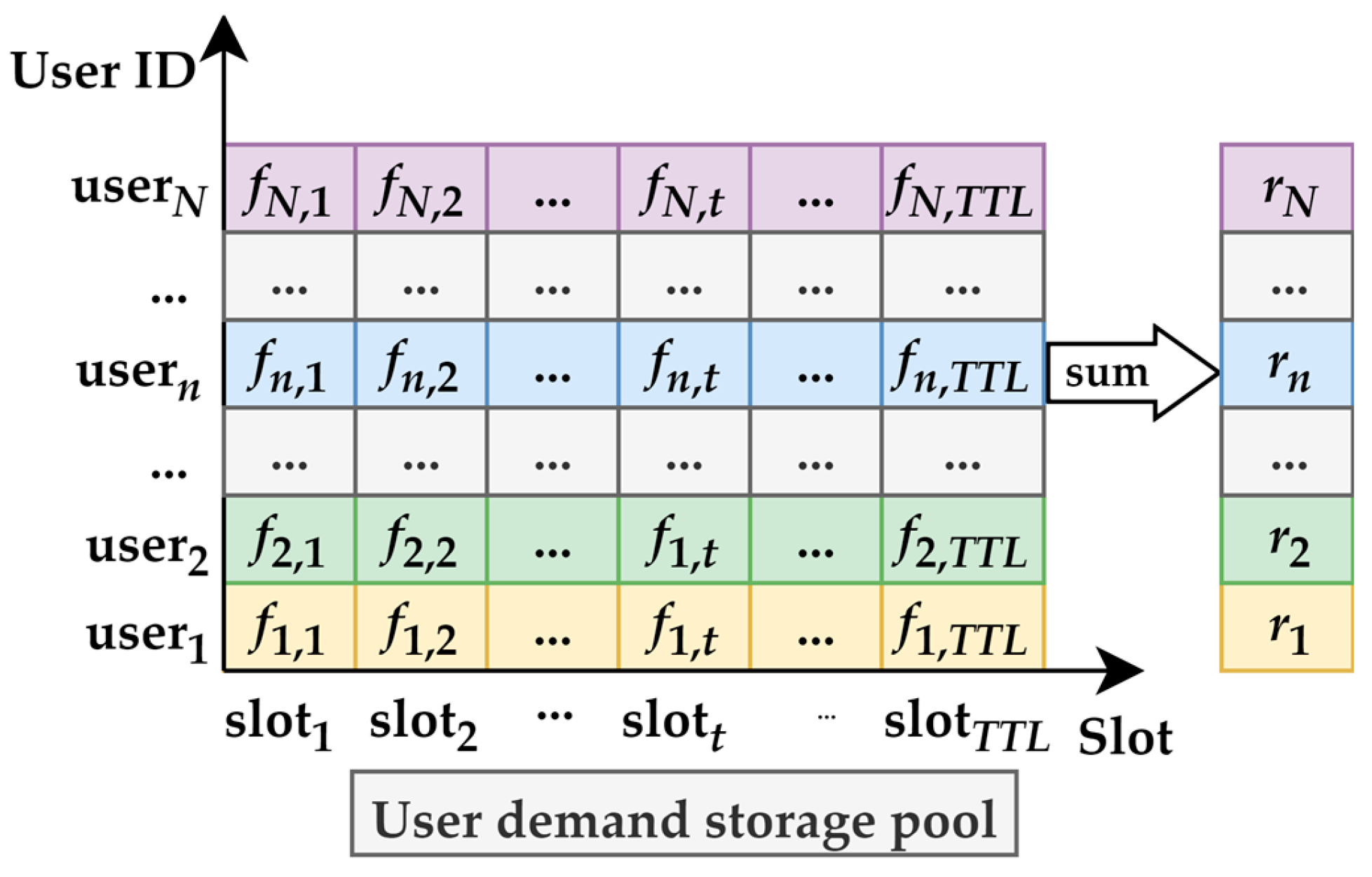
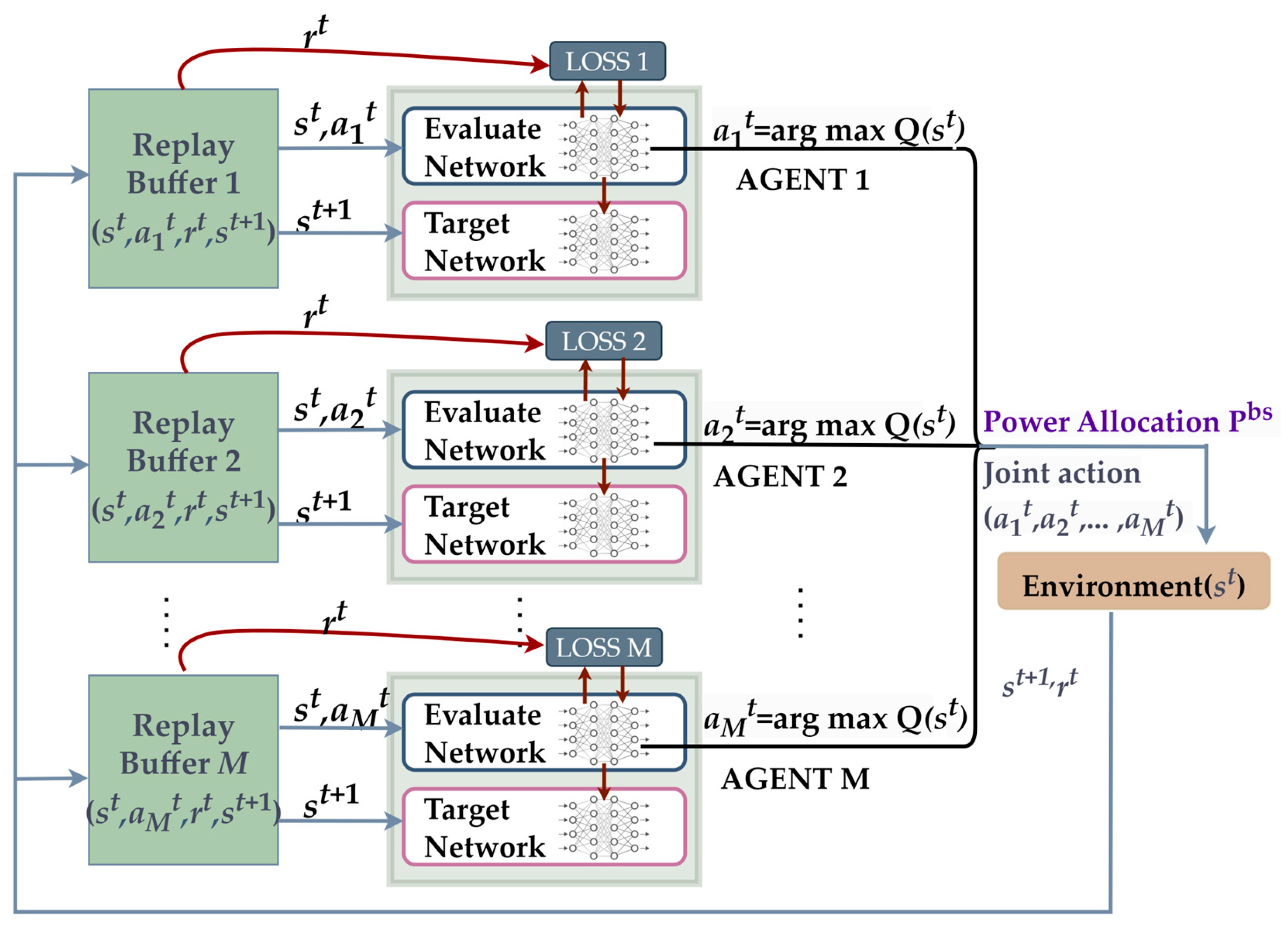
3. MADQN-IL Scheme

First, the association among terrestrial BS users is established using the demand-maximizing approach in our proposed MADQN-IL scheme. Specifically, BS determines the SUs and serves other terminals by calculating the distance from the TUs within the BS; then, BS will select TUs in descending order of their data demands; and, finally, the association matrix is obtained. This association process between BSs and terminals in our proposed scheme is illustrated below. The Algorithm 1 first takes input such as the terminal locations and base station radius. It then distinguishes between terminals served by satellites and those served by base stations, calculates the distances, and establishes associations based on user needs. Finally, it computes the offset angles for terminal–antenna matching and outputs the base station–terminal correlation matrix X.

Algorithm 1 Ground base station terminal association algorithm

1. Input: Input the location of the terminal to the BS{posBS, posUser}, BS radius{RBS}, satellite correlation situation{ASAT}, user request{F}. 2. Determine the terminals that have been served by the satellite based on the satellite beam patter {nSat}. BS will serve other terminals {nBS}. 3. Calculate the distance from the terminal to the BS and determine the terminals within the BS{$n_m^{bs}$, m = 1, 2, …, M}. 4. Determine the terminals associated with the BS based on user needs from high to low, and obtain the BS user association matrix ABS. 5. for m = 0 to M − 1 do 6.        Calculate the offset angle between the terminal and antenna, and complete the matching pattern between the terminal and antenna within the BS size(X) = N × M × W: 7. end for 8. Output: BS terminal correlation matrix X.

After the correlation matrix is generated by this association algorithm, the proposed multi-agent deep Q-network with interference limitation (MADQN-IL) is applied to dynamically optimize the transmit power of the antennae for BSs for maximizing the throughput of the terrestrial network for BS terminals while ensuring that the interference to satellite terminals remains below the threshold. In terms of the DRL fundamental elements, this framework models the M terrestrial BSs as M intelligent agents and uses the current user request matrix $S^t=F$ as the state. And the action space for each agent consists of discrete power allocation choices for each beam of the BS $Actio{n}^t=\{P_1^{BS},P_2^{BS},\dots ,P_M^{BS}\}$. Then, with the interaction with the CSTN environment, each agent will receive a shared reward Re, which is calculated as follows:

$$Re=\left\{\begin{array}{c}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{n=1}^{N}Throughpu{t}_t^n}},I_{BS\_to\_LEO}\le I_{th}\\ -\eta ,I_{BS\_to\_LEO}>I_{th}\end{array}\right.$$

(13)

When the interference caused by terrestrial BS users to satellite users is within the interference threshold $I_{th}$, the reward is the throughput size of the system within that time slot; and, when the interference caused by terrestrial BS users to satellite users exceeds the threshold value $I_{th}$, if the condition is not satisfied, a large penalty term $\eta$ is set to ensure that the network training meets the interference threshold.

Based on the idea mentioned above, our proposed multi-agent framework is depicted in Figure 3. All agents share aggregated states and a global reward, while each maintains an independent network and experience replay buffer for learning the individual power allocation policies. Notably, each agent’s independent network follows a double Q-network (DDQN) structure, separating the action selection and value evaluation to avoid Q-value overestimation. Additionally, the shared reward mechanism integrates a penalty factor for interference exceeding the predefined thresholds, adapting to the CSTN scenario’s interference constraints.

To promote coverage and ensure the convergence of neural networks, each agent is equipped with two networks, i.e., the evaluation network and the target network. The evaluation network’s parameters are periodically synchronized with the target network at regular intervals. The current network is used to learn the Q-value and use the target network to calculate the target value.

The Q value of the evaluate network is represented as $\mathrm{Q}(s_t,a_t^m;{\omega }_m)$, where ${\omega }_m$ represents the parameters of the m-th evaluate network and $a_t^m$ denotes the action taken by BS m in response to the current global state $s_t$. Likewise, the target Q value of the target network and the parameters are represented as $\widehat{\mathrm{Q}}(s_t,a_t^m;{\overline{\omega }}_m)$ and ${\overline{\omega }}_m$.

The Q-value function is updated according to the following rule:

$${\mathrm{Q}}_{t+1}(s_t,a_t^m;{\omega }_m)=(1-\alpha )Q_t(s_t,a_t^m;{\omega }_m)+\alpha (r_t+\gamma \underset{a_{t+1}^m}{\max }{\mathrm{Q}}_t(s_{t+1},a_{t+1}^m;{\omega }_m))$$

(14)

where α is the learning rate, representing the speed of the agent’s strategy learning; and γ is the discount factor, representing the extent to which the agent values future rewards.

Throughout the training iteration of MADQN-IL, each agent first acquires the user demand matrix $S^t=F$ from the environment. Next, actions are selected via the ε-greedy strategy, defined in the following equation:

$$a_m^t=\left\{\begin{array}{cc}\mathrm{random}\mathrm{choice}& \mathrm{with}\mathrm{probability}\epsilon \\ \arg \underset{a}{\max }\mathrm{Q}(s_t,a_t^m;{\omega }_m)& \mathrm{with}\mathrm{probability}1-\epsilon \end{array}\right.$$

(15)

where $\epsilon \in [0,1]$ represents the exploration parameter. During the initial phases of training, ε is initialized with a higher value to encourage the extensive environment exploration. Then, $\epsilon$ is gradually decreased as the understanding of the environment increases, which can shift the policy from exploration toward exploitation, thereby enhancing the utilization of the learned knowledge.

After the selected action is executed, the environment transitions to the new state. The agent collects the current state, action, reward, and the next state into an experience tuple $(s_t,a_m^t,r_t,s_{t+1})$ which is stored in the resource replay pool.

The target function value $y_{\mathrm{t}}^m$ is represented by the current state reward $r_t$ and the previous output of the target network, and is given as follows:

$$y_{\mathrm{t}}^m=r_t+\gamma \widehat{\mathrm{Q}}(s_{t+1},\underset{a}{\max }\mathrm{Q}(s_{t+1},a_t^m;{\omega }_m);{\overline{\omega }}_m)$$

(16)

where $\gamma \in [0,1]$ represents the discount factor. After accumulating sufficient experience, the agent randomly samples a mini-batch of tuples to update the network parameters.

At the start, the network is not well-trained, and the Q value approximated by the eval Q-network exhibits a notable discrepancy from the target Q-value. The network’s loss function adopts the mean square error (MSE) loss function, which is used to represent the difference between the predicted value $\mathrm{Q}(s_t,a_t^m;{\omega }_m)$ of the evaluate network and the target value $y_{\mathrm{t}}^m$. The MSE loss function is given by the following:

$$L({\omega }_m)={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{(y_t^m-\mathrm{Q}(s_t,a_t^m;{\omega }_m))}^2}$$

(17)

where T is the time slot length of one episode. After calculating the loss function, the Adam optimizer is used to update the neural network parameters through back propagation. The update formula for the Adam optimizer is as follows:

$${\omega }_{t+1}={\omega }_t-\alpha \cdot {\displaystyle \frac{m_t}{\sqrt{V_t+\sigma }}}$$

(18)

$$V_t={\beta }_2\cdot V_{t-1}+(1-{\beta }_2)g_t^2$$

(19)

$$m_t={\beta }_1\cdot m_{t-1}+(1-{\beta }_1)\cdot g_t$$

(20)

$$g_t={\displaystyle \frac{\partial L({\omega }_t)}{\partial {\omega }_t}}$$

(21)

Among them, ${\beta }_1$ and ${\beta }_2$ are the historical first-order momentum retention rates and decay rates for the first-order moment estimates. $m_t$ and $m_{t-1}$ are the first-order momentum of the current step and the first-order momentum of the previous step. α is the learning rate. A minimum value ε is used to avoid situations where the denominator is 0. $g_t$ is the gradient obtained by taking the derivative of network parameters for the loss function.

The process of the MADQN-IL algorithm is shown below (Algorithm 2). MADQN-IL initializes with neural network parameters and replay memories, then runs episodes where each base station selects power-allocation actions based on the observed states and correlation matrices, storing the interaction data. Once sufficient data is collected, it trains agents by updating networks with sampled batches, ultimately outputting trained parameters and optimized power strategies. The maximum antenna power is set to ${\displaystyle \frac{P_{max}^{BS}}{W}}$ and uniformly divided into L levels where L represents the number of layers for power classification. Each BS antenna has $\{0,{\displaystyle \frac{P_{max}^{BS}}{L\cdot W}},{\displaystyle \frac{2\cdot P_{max}^{BS}}{L\cdot W}},\dots ,{\displaystyle \frac{(L-1)\cdot P_{max}^{BS}}{L\cdot W}},{\displaystyle \frac{P_{max}^{BS}}{W}}\}$ choices. To meet the service quality of BS users, the minimum antenna power that can provide services to terminals is set to 0.1 × $P_{max}^{BS}$. For any power level below this threshold, the antenna power is set to zero.

Algorithm 2 MADQN-IL algorithm for power allocation of base station antennae

1. Input: Input M neural network parameters and M replay memories. 2. for episode = 1 to Ep do 3.        Initialize the environment. 4.        for step = l to Max_step do 5.        Obtain observation status s = {F}. 6.        Obtain the correlation matrix X between the BS antenna and the terminal through Algorithm 1. 7.        for m = 1 to M do 8.             Selection of antenna power allocation combination for BS m, $P_m=b_{max}^{BS}$ 9.        end for 10.      BS network execution action a = {P1, P2, …, PM}. Obtain reward r and the next state s: 11.      Calculate the channel capacity provided by each BS to serve the BS terminals based on the power allocation decisions of X and BS. 12.      Calculate the maximum interference of ground terminals on satellite users IBS, and compare it with the threshold requirements Ith. Then determine reward size. 13.      Update the requirement storage pool to obtain the next state s. 14.      for m = 1 to M do 15.           The quadruple $(s_t,a_m^t,r_t,s_{t+1})$ will be stored in Memory m. 16.      end for 17.      If the number of quadruples stored in Memory is greater than the starting number of training, start training: 18.           for m = 1 to M do 19.                  Sample a random batch from Memory m. 20.                  Calculate loss function. 21.                  Each agent updates the current Q-network m. 22.                  Update the target network parameters m at a certain frequency. 23.          end for 24.    end for 25. end for Output: Train neural network parameters and BS power allocation strategies.

The deep neural network in the MADQN-IL scheme adopts a fully connected feedforward architecture, which includes one input layer, two hidden layers, and one output layer. The dimensionality of the input layers is the number of states in the algorithm, which is the number of terminals multiplied by TTL. The output layer dimension is the number of actions in Algorithm 2, which varies depending on the allocation of resources.

The output of each layer of the network is activated using the ReLU activation function, which is then used as the input for the next layer of the network. The ReLU function is essentially a function that takes the maximum value. Compared with activation functions such as sigmoid and tanh, it has advantages such as no gradient vanishing problem, good sparsity, high efficiency, and fast convergence. The ReLU activation function is $f(x)=\max (0,x)$.

4. Results and Discussion

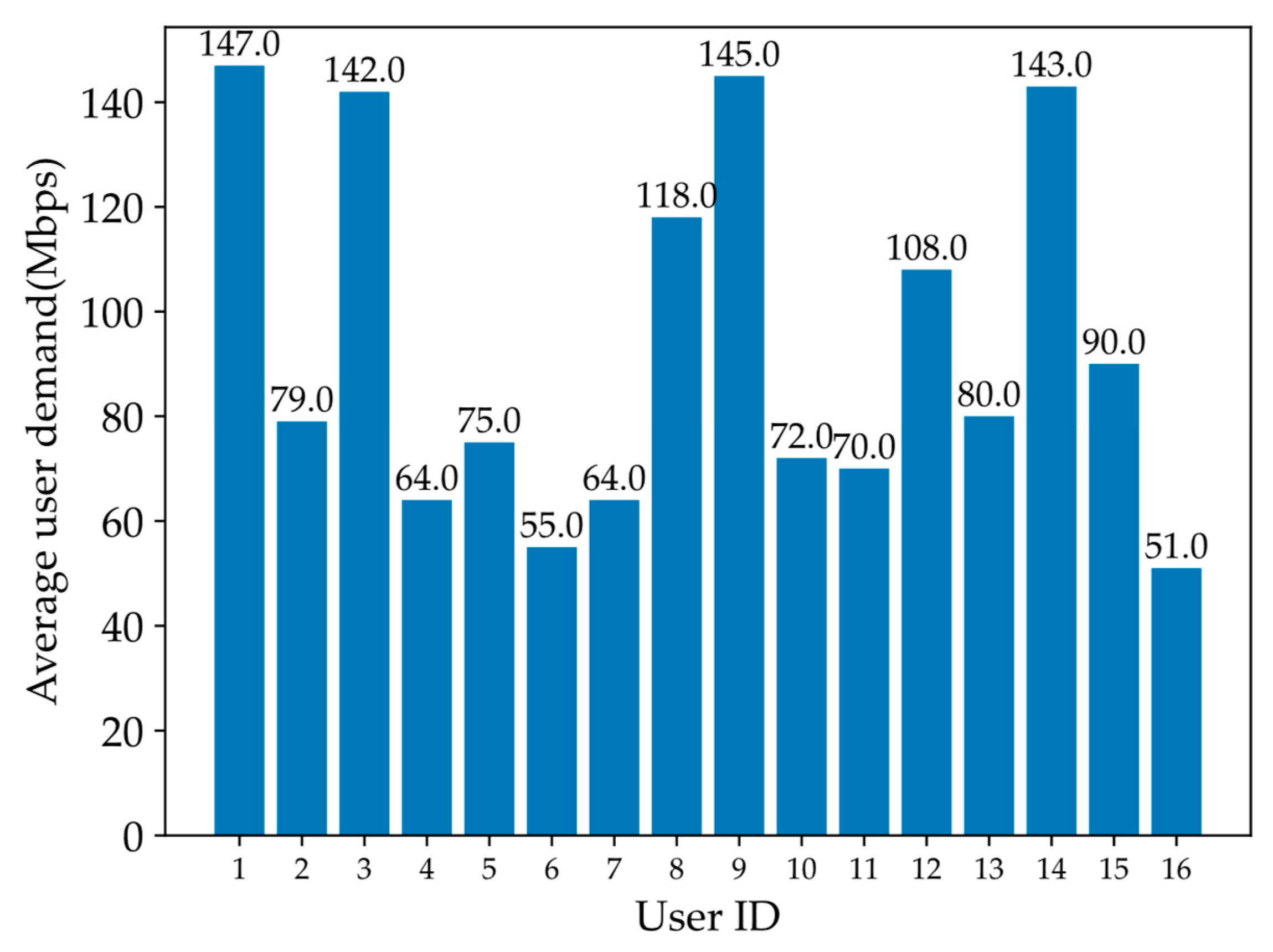
4.1. Simulation Environment Settings

The simulation validation was conducted under a cognitive satellite–terrestrial integrated network scenario, which uses one low earth orbit (LEO) satellite and three multi-antenna BSs in the system, which use time-division multiplexing to provide downlink services to 16 terrestrial users. The satellites employ beam hopping technology, dynamically activating 4 out of its available beams in each time slot. The total transmitting power is equally allocated among the active beams. Each BS has three antennae, and the maximum power of each antenna is one-third of the BS power. Each BS selects its own antenna power allocation scheme according to the environment and the decisions other BSs made.

All simulations are implemented using PyCharm 2023.3, with the algorithm developed based on the PyTorch 2.6.0+cu118 framework. The hardware environment includes an NVIDIA GeForce RTX 4060 Laptop GPU (with CUDA 12.0 support) and a 13th Gen Intel(R) Core(TM) i7-13700H CPU, ensuring the efficient computation of the dynamic network scenarios.

The system center operates at a communication frequency of 20 GHz and is allocated a total bandwidth of 500 MHz. The distribution of terrestrial terminal positions follows a two-dimensional Poisson Point Process (PPP). The terminals follow a uniform distribution within a given range, and their distances follow an exponential distribution. The data rate requirement is modeled as a Poisson-distributed random variable, and the Poisson mean of each user’s data rate requirement is uniformly distributed between 50 Mbps and 150 Mbps. As shown in Figure 4, there is a significant difference in the mean demand of each user, reflecting the variability of user needs. Given the fluctuating nature of user demands over time, the Poisson mean for each user updated a change at every 200 time intervals.

The other parameters are shown in

Table 1. Environmental parameters of satellite terrestrial integrated network.

Parameters	Values
BS radius R	10 km
Maximum transmission power ($P^{BS}$)	22 dBW
Max transmission gain ($G_{T,max}^{BS}$)	20 dBi
3dB bandwidth (${\phi }_{3dB}$)	30°
Noise power ($B=500$ MHz)	−117 dBW
Noise interference threshold ($I_{th}$)	−123 dBW
Time slot length $(T_{slot}$)	2 ms
Data packet time to live (TTL)	40

and Table 2 (the same as in Ref. [22]).

The specific parameters for network training are as follows:

Table 2. General network training parameters.

Parameters	Value
Training steps	250
Learning rate α	0.00001
Greedy factor ε	0.9
Discount factor γ	0.95
Update frequency	200
Memory size	10,000
Training episodes	4000
Batch size	512
Sampling interval	20
Number of networks	3
Input numbers	640
Number of neurons	128/128/128/125

Table 2. General network training parameters.

Parameters	Value
Training steps	250
Learning rate α	0.00001
Greedy factor ε	0.9
Discount factor γ	0.95
Update frequency	200
Memory size	10,000
Training episodes	4000
Batch size	512
Sampling interval	20
Number of networks	3
Input numbers	640
Number of neurons	128/128/128/125

4.2. Simulation Results

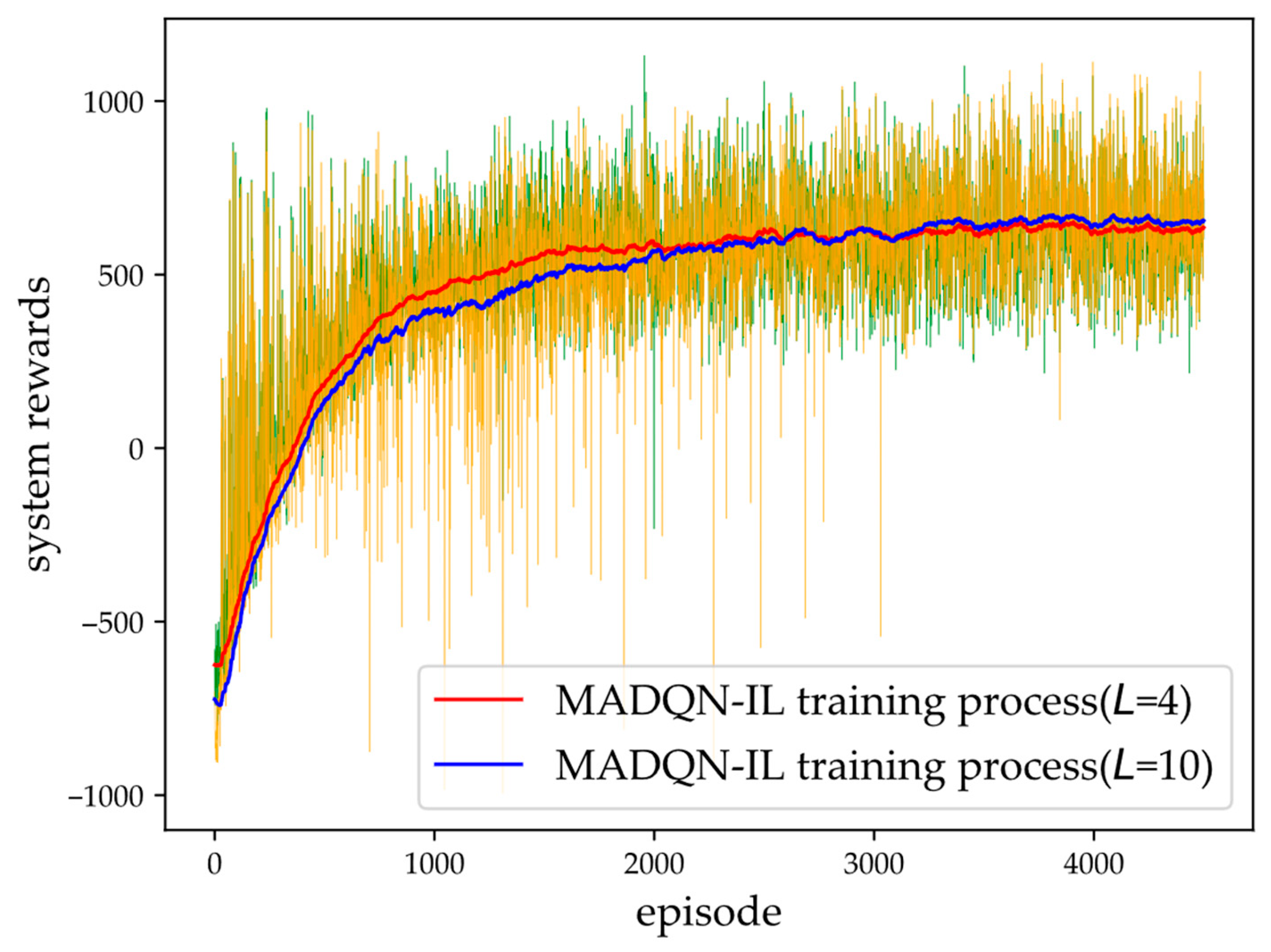
4.2.1. Network Training Convergence Result

After undergoing 3000 rounds of training, the system’s reward reaches a plateau, indicating that the network has converged, and MADQN-IL (L = 10) converges to a slightly higher final value than MADQN-IL (L = 4), as shown in Figure 5.

4.2.2. Test Results

(1)

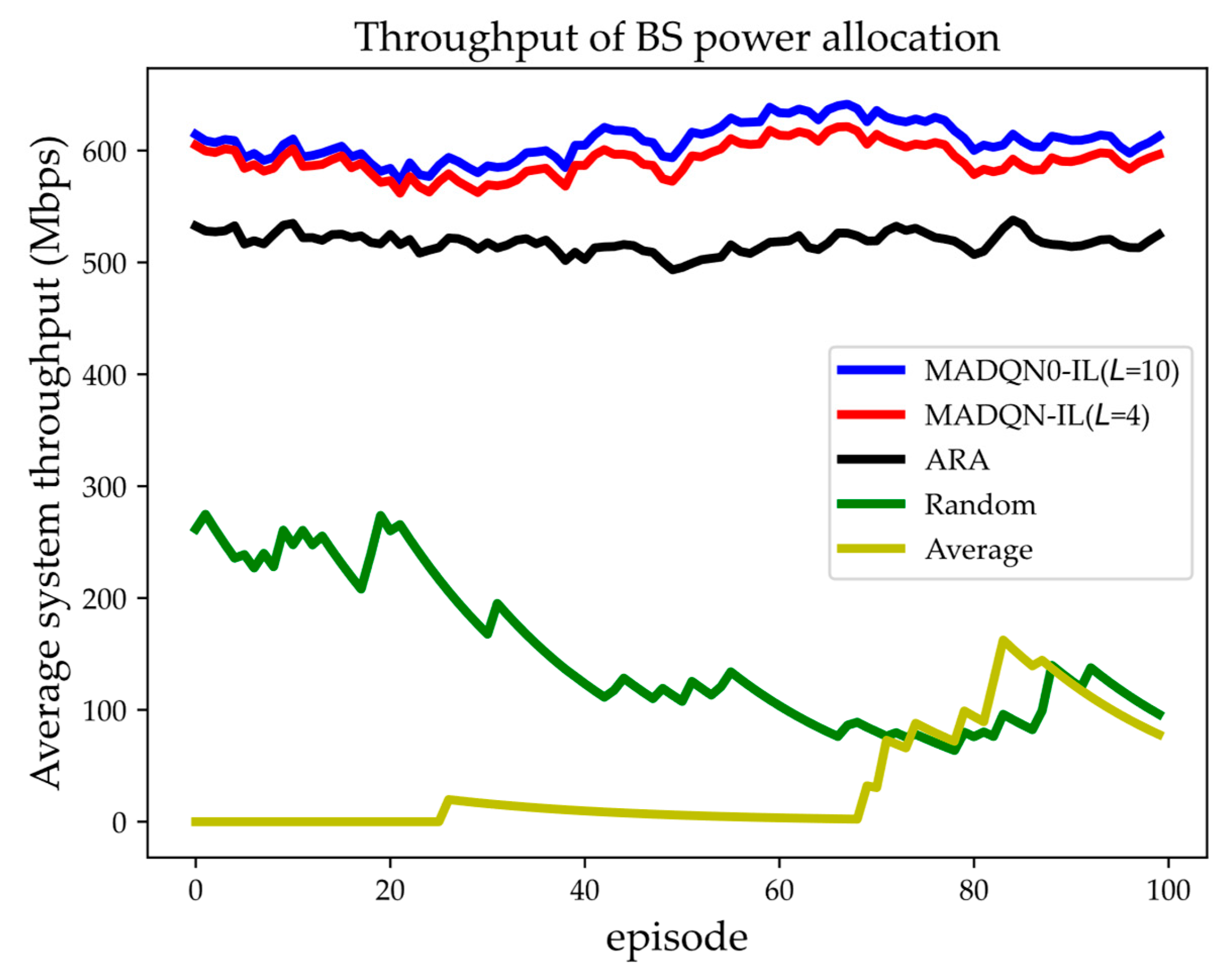
Comparison of Throughput of Different Algorithms with Fixed BS Power

The BS’s maximum transmission power is set to 24 dBW; each algorithm undergoes 100 rounds of testing, as shown in Figure 6. Other comparison methods besides MADQN-IL are introduced as follows:

(i)

ARA [22]: This algorithm iteratively decreases the antenna transmit power in fixed-step increments, converging to the point where the interference constraint is satisfied.

(ii)

Random power allocation: This randomly selects the power size for each BS antenna.

(iii)

Average power allocation: Each BS antenna transmits information with an equal distribution of BS power.

For the benchmark selection, we prioritized methods fitting the CSTN dynamics. The state-of-the-art DRL (MADDPG, PPO, etc.) struggles with our discrete power quantization and dynamic interference, while traditional optimization relies on static models ill-suited to CSTN variability. Hence, we compared random/average allocation and ARA—a CSTN-relevant method—to better highlight our approach’s strengths.

The aggregate results depicted in Figure 6 are summarized in

Table 3. Average throughput of BS power allocation.

Algorithms	Average Throughput
MADQN-IL (L = 10)	609.01 Mbps
MADQN-IL (L = 4)	590.89 Mbps
ARA power allocation	517.27 Mbps
Random power allocation	112.63 Mbps
Average power allocation	49.19 Mbps

. We compared other algorithms in terms of system throughput. More precisely, it outperforms ARA by 14% to 17%. Additionally, as the level of power quantization rises, the BS is capable of allocating power to the antenna with greater precision. Consequently, the throughput achieved by the MADQN-IL algorithm with L = 10 is marginally higher than that of the MADQN-IL algorithm with L = 4.

(2)

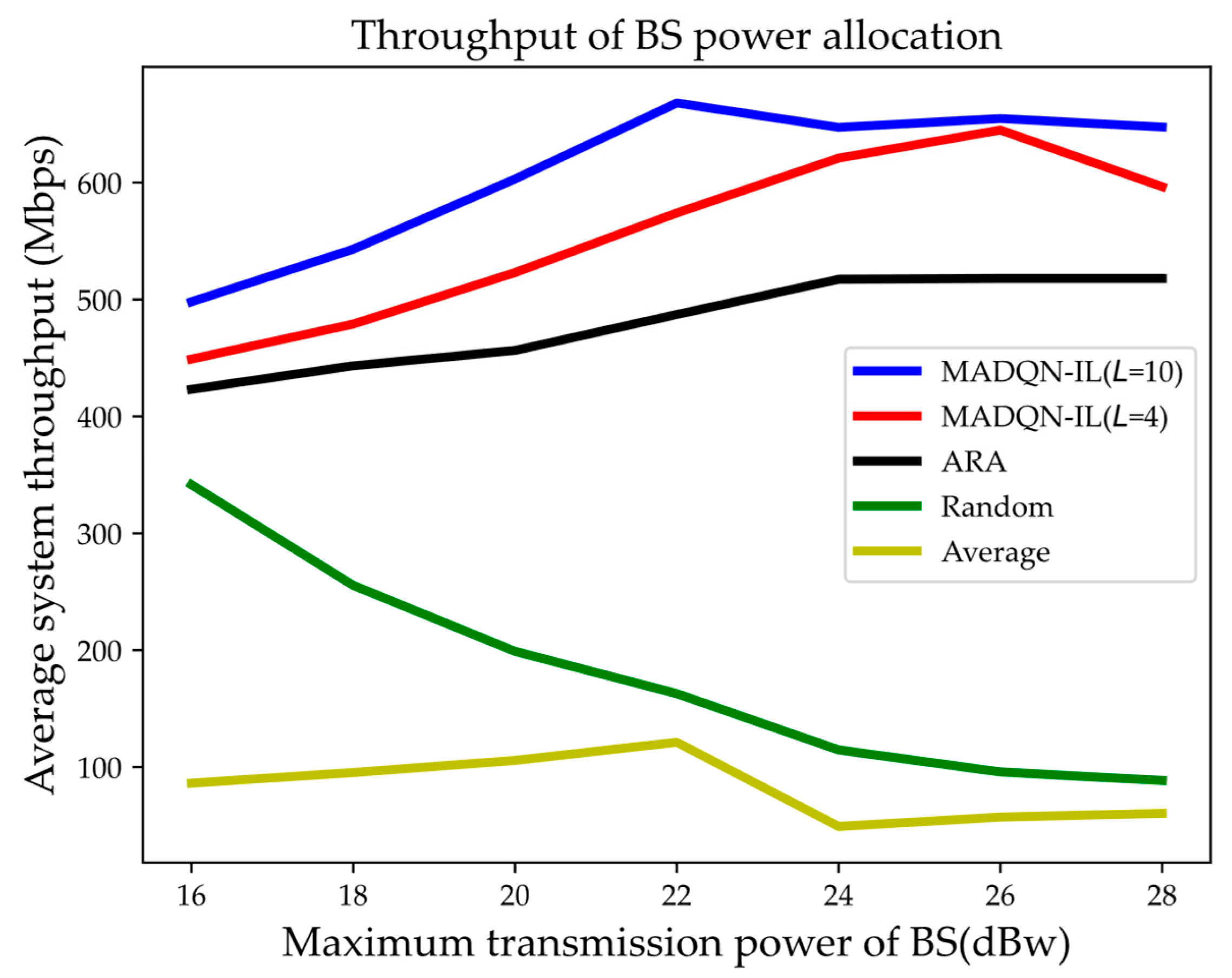
Comparison of Throughput of Different Algorithms when BS Power Changes

When the BS’s maximum transmission power ranges from 16 dBW to 28 dBW, the comparison of various algorithms is shown in Figure 7. As the BS’s maximum power increases, both our MADQN-IL algorithm and the ARA algorithm exhibit a strong adaptability to environmental changes, ensuring that the system throughput increases monotonically.

However, the other two benchmark algorithms fail to dynamically adjust their strategies. As the power increases, they struggle to meet interference constraints, leading to a decline in the system throughput. Consequently, their performance suffers. In contrast, the MADQN-IL (L = 10) algorithm consistently achieves the highest throughput even when the environment changes. Moreover, MADQN-IL (L = 10) exhibits a significant performance improvement compared to MADQN-IL (L = 4) when the power is between 16 and 24. As the power increases, the performance gap between the two methods narrows.

Notably, the simulation parameters—16 terrestrial users, 3 BSs, 1 LEO satellite, BS power range of 16–28 dBW, and user demand fluctuations (50–150 Mbps with 200-interval updates)—mirror typical real-world CSTN scenarios, encompassing dynamic user demands, variable transmission power, and strict satellite–terrestrial interference constraints. MADQN-IL’s consistent outperformance across these ranges highlights its robustness and generalization capability with varying network scales and environmental conditions.

(3)

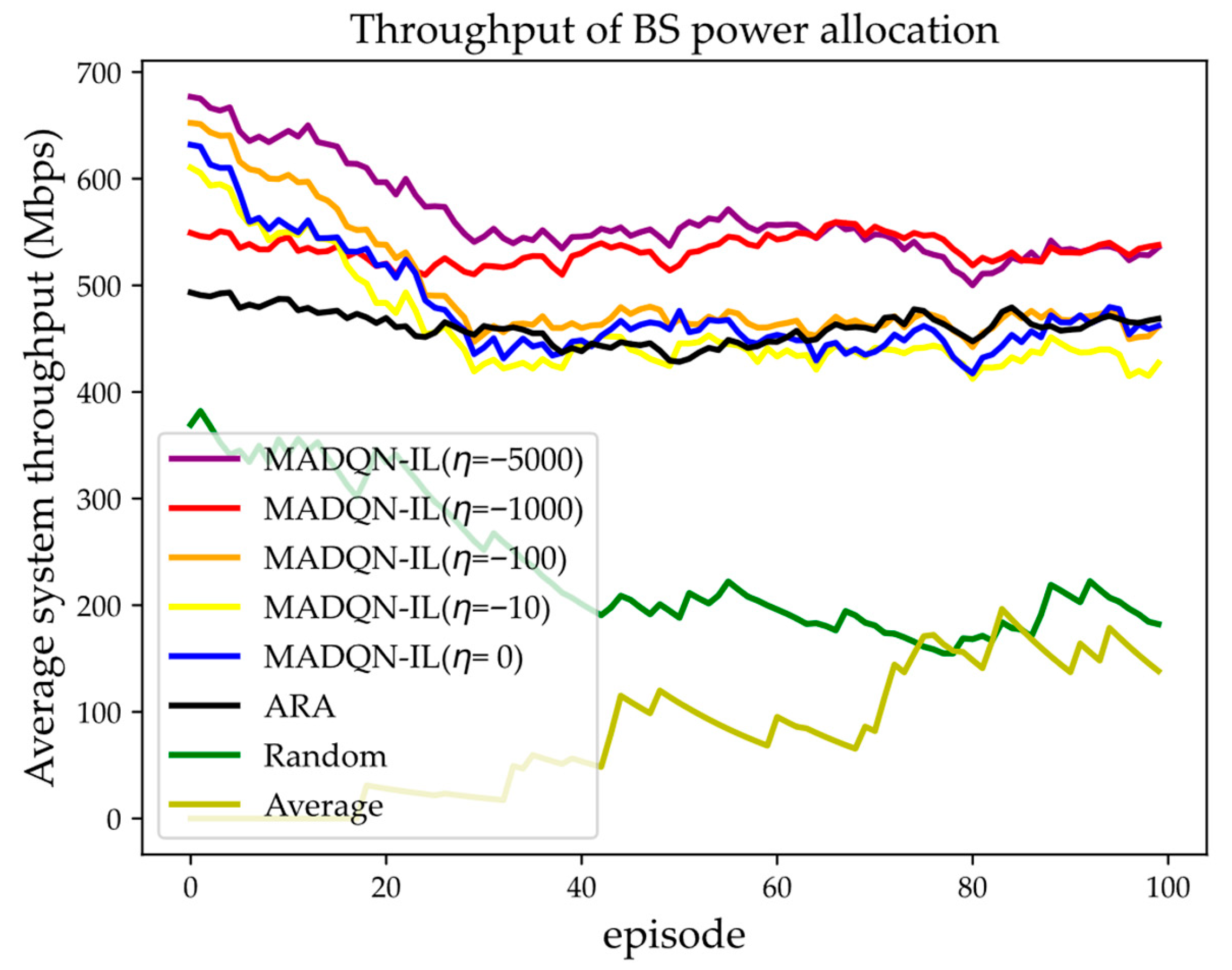
Comparison of Throughput of Different Algorithms with Different Interference-Penalty Factors ($\eta$)

Figure 8 illustrated the average system throughput of MADQN-IL (with a quantization level L = 10 and power at 20 dBW) under different interference-penalty factors ($\eta$), along with benchmark methods. When $\eta$ is 0, MADQN-IL has a high but fluctuating throughput. As $\eta$ decreases to −10, −100, −1000, and −5000, the throughput changes. A penalty of $\eta$ = −1000 gives MADQN-IL the best performance, outperforming benchmarks like ARA, Random, and Average power allocation. Moreover, while a penalty of $\eta$ = −5000 further increases the penalty magnitude compared to $\eta$ = −1000, it brings little additional gain in throughput. Therefore, considering the balance between performance improvement and complexity, a penalty factor of $\eta$ = −1000 is selected.

The results underscore the critical role of the interference-penalty $\eta$ factor in MADQN-IL. A stronger penalty leads to better power-allocation decisions for a higher throughput. MADQN-IL with an appropriate $\eta$ outperforms benchmarks, validating the penalty mechanism. Future work could optimize $\eta$ for better performance and stability in complex environments. The observed relationship between the penalty magnitude and throughput provides actionable insights for tuning $\eta$ to enhance performance and stability in complex environments.

5. Conclusions

This paper mainly addresses the resource allocation challenges of BS user association and antenna power management in a cognitive satellite–terrestrial integrated network, leveraging a multi-agent deep reinforcement learning algorithm MADQN-IL.

(1)

Based on the current research status of satellite–terrestrial integrated networks and the research content of the relevant literature, we established a cognitive satellite–terrestrial integrated network architecture and downlink communication process. The study of resource optimization problems takes the unbalanced and time-varying nature of terrestrial user service demands into consideration, which is more in line with the diversified and variable characteristics of services in satellite–terrestrial integrated networks.

(2)

To address the cognitive radio demands of satellite–terrestrial integrated networks, a MADQN-IL algorithm is proposed for power allocation in BSs. Through collaborative decision making, multiple agents optimize system performance while simplifying the neural network structure, which can improve the throughput under interference suppression conditions. The simulation verification of the terrestrial network DRL resource allocation algorithm shows that the MADQN-IL algorithm demonstrates higher system throughput performance in interference limitation compared to the ARA and fixed power allocation algorithms.