Oscillation Controlling in Nonlinear Motorcycle Scheme with Bifurcation Study
Abstract
1. Introduction
2. Description of the Non-Perturbative Approach (NPA)
- The method deals with weakly nonlinear oscillators.
- The initial conditions are fixed with no changes.
- To obtain better accuracy, the initial amplitude must be less than unity.
3. Application of NPA: Equivalent Equation of a Dynamic Motorcycle
| Symbol | Description |
| The equivalent mass of rider and motorcycle | |
| The equivalent damping coefficient | |
| The equivalent stiffness through a linear and nonlinear spring | |
| Displacement, velocity, and acceleration, respectively. | |
| The equivalent natural frequency | |
| The equivalent damping factor | |
| Cubic nonlinear duffing factor | |
| Quintic nonlinear duffing factor | |
| External excited force | |
| Excitation forcing frequency coefficient |
3.1. Validation of NPA
3.2. Stability Analysis for NPA
3.3. Demonstrates the Time History at Various Parameters and the Polar Plot
4. The Vibrating Dynamic of the Motorcycle via the PDPPF Controller
4.1. Motion Equations Within the Control Process
4.2. Time Histories and Phase-Planes via Numerical Simulation
4.3. Mathematical Treatment
- (i)
- Primary resonance:
- (ii)
- Internal resonance:
- (iii)
- Simultaneous resonance: Any combination of the above resonance cases is considered as simultaneous resonance.
4.4. Frequency–Response Equations
4.5. Stability of the Problem
5. Simulation of the Results
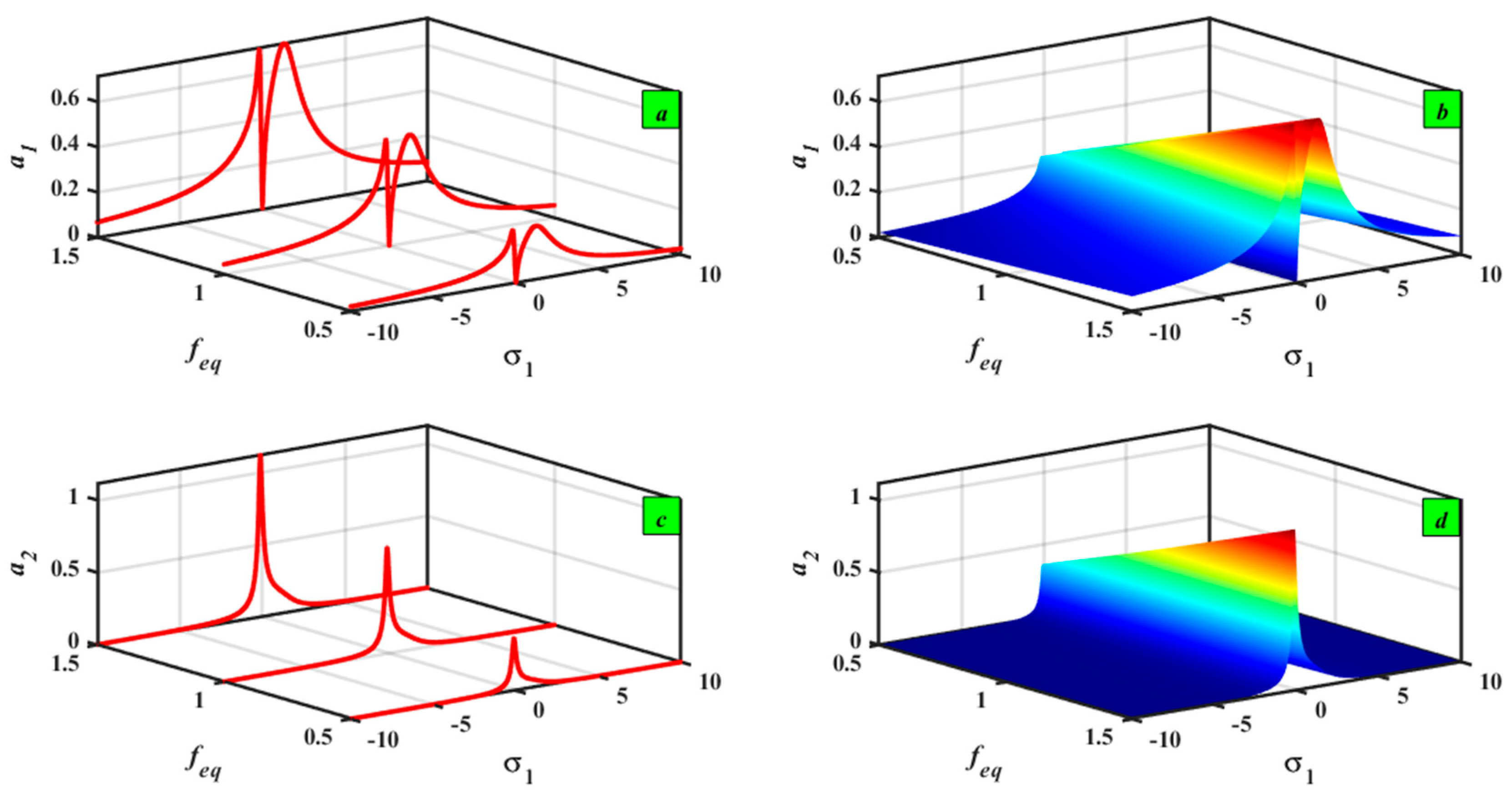
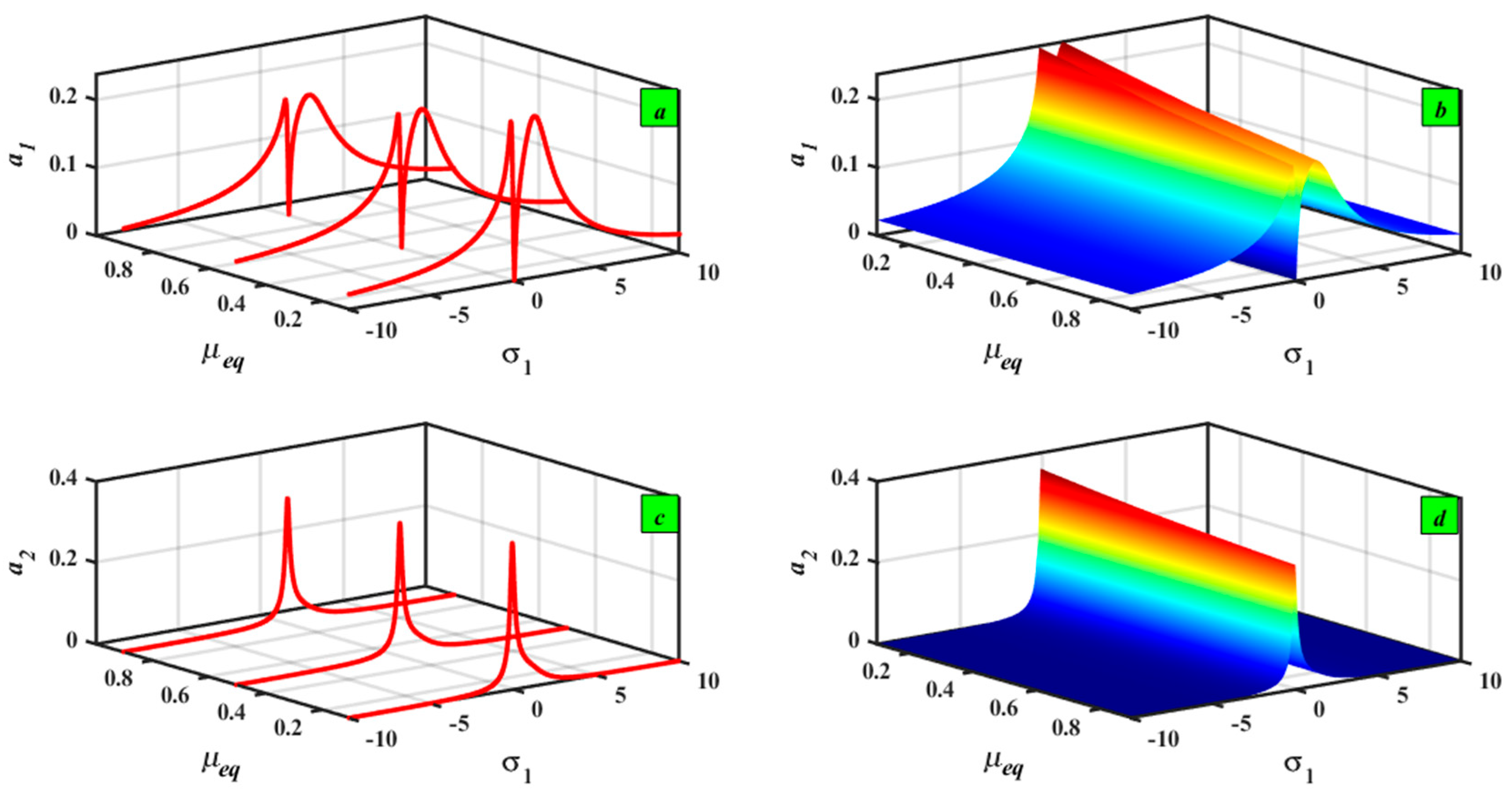
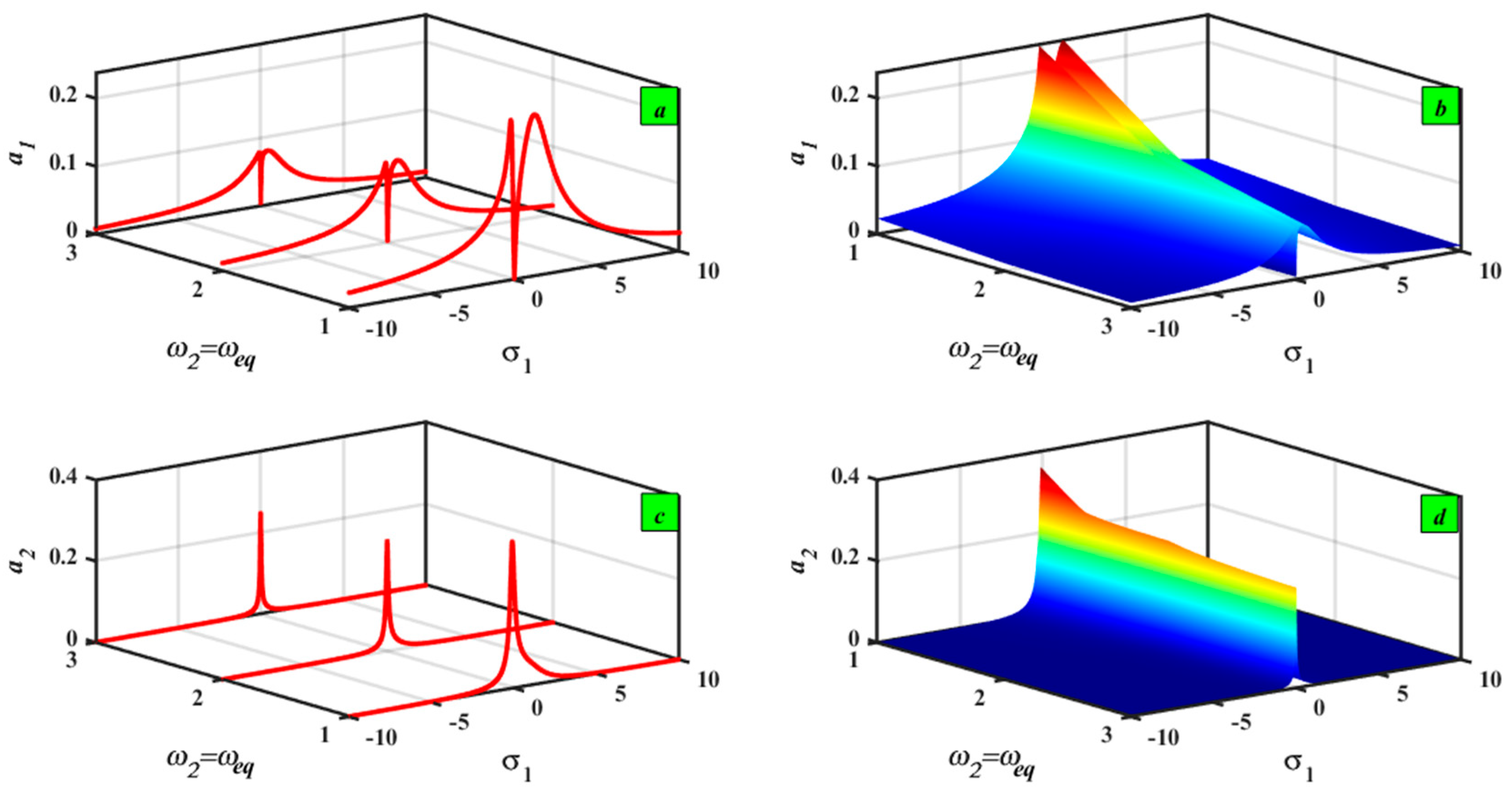
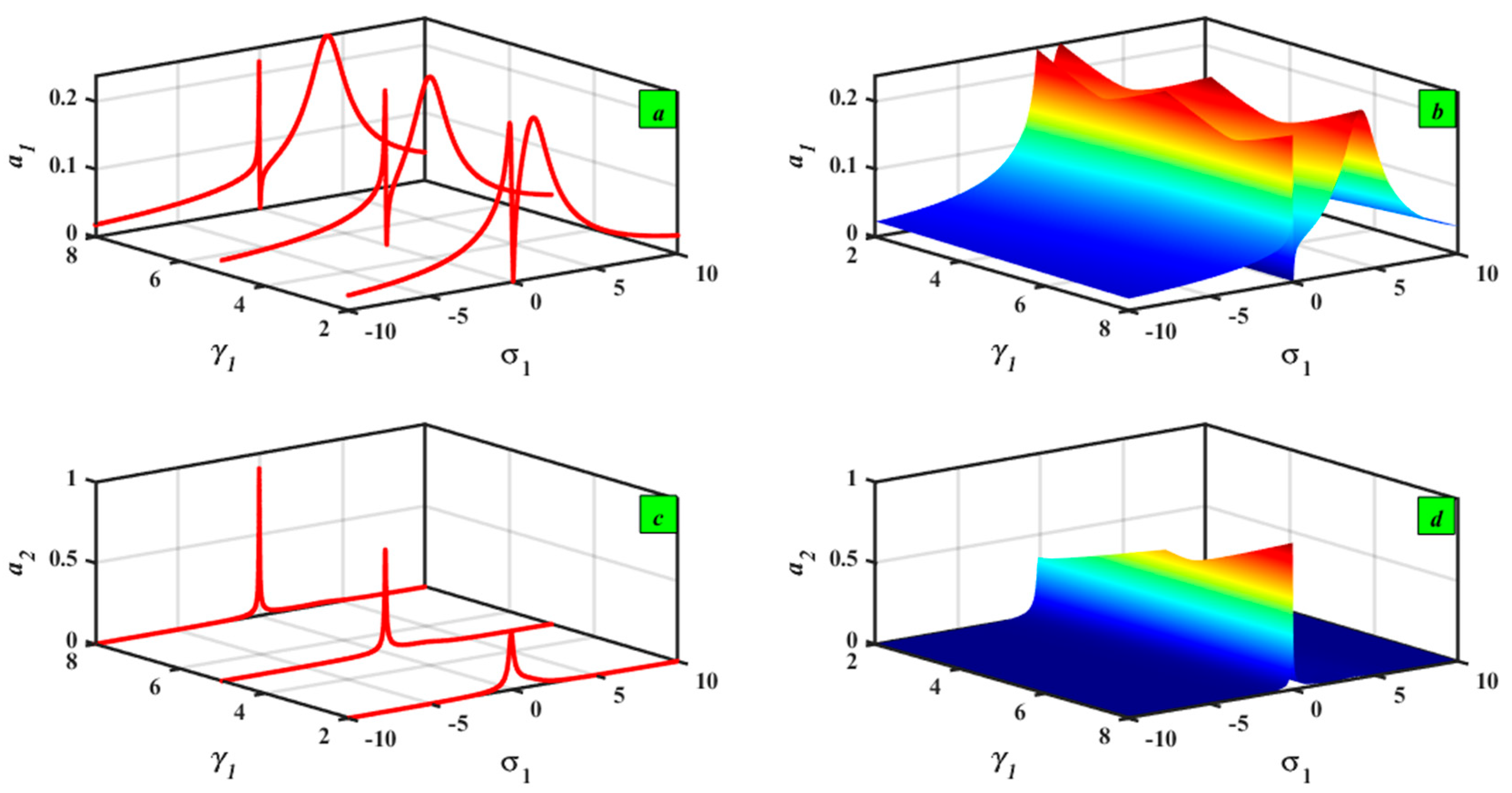
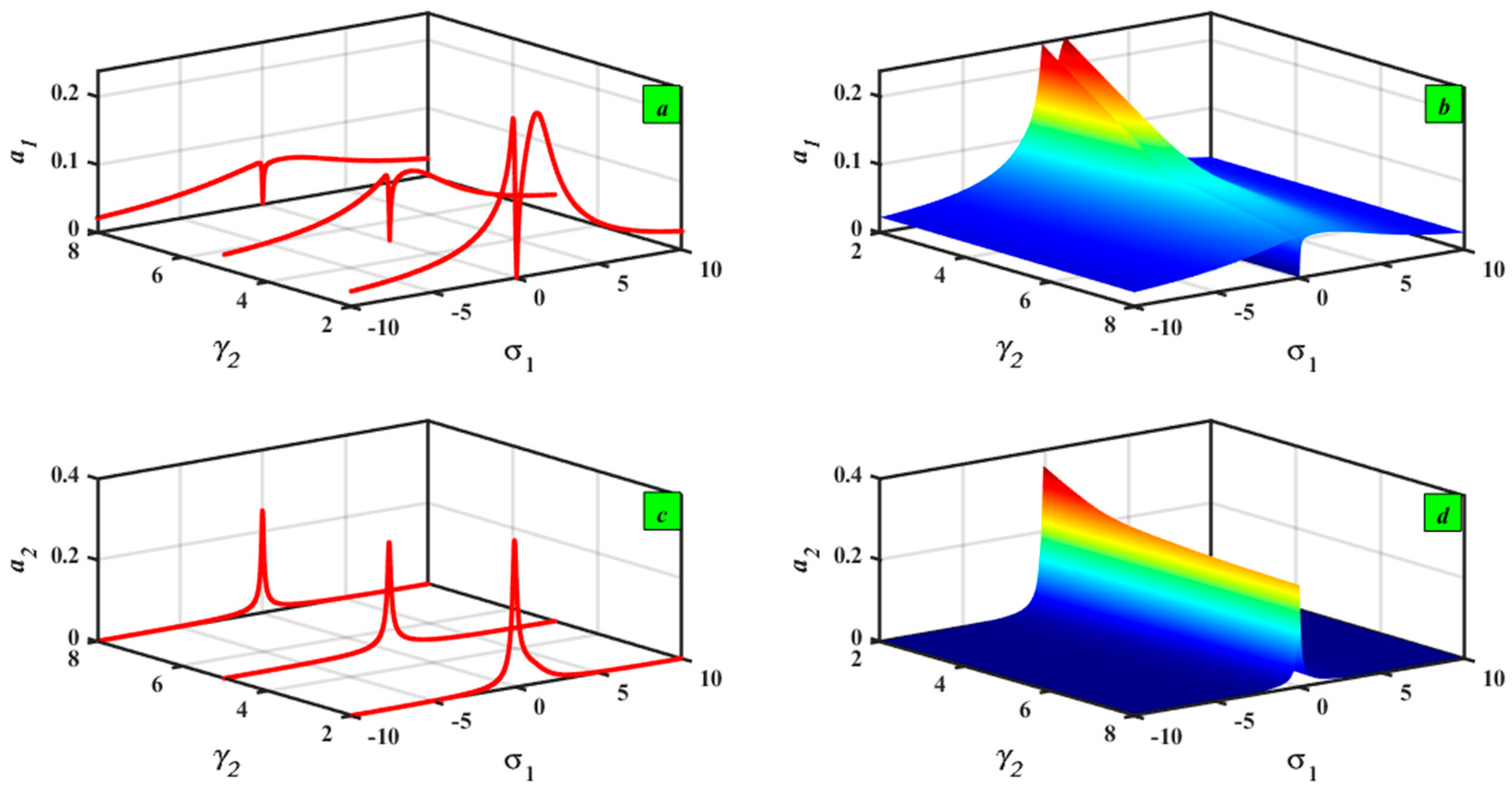
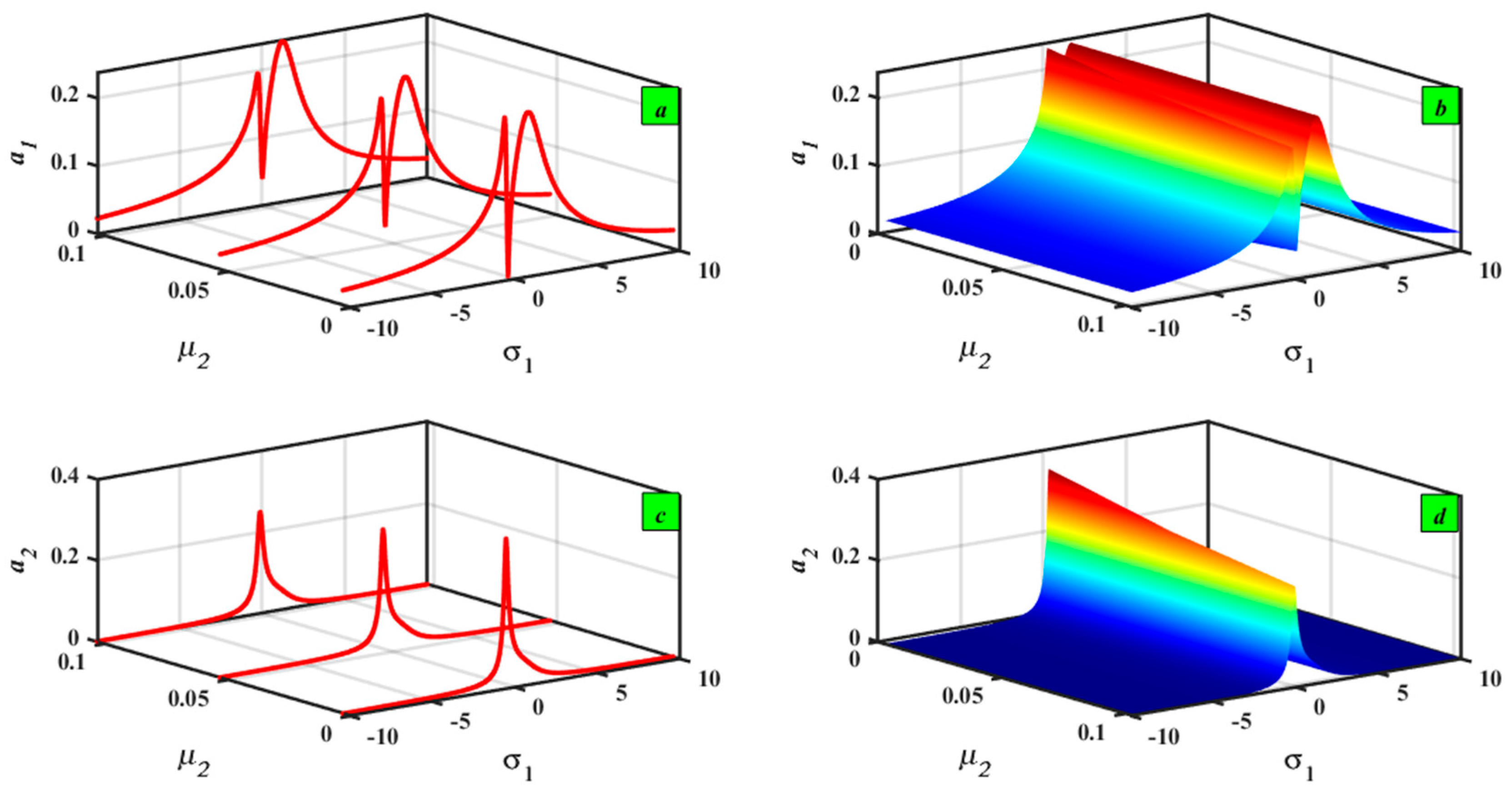
5.1. Frequency–Response Curves (FRCs) Description
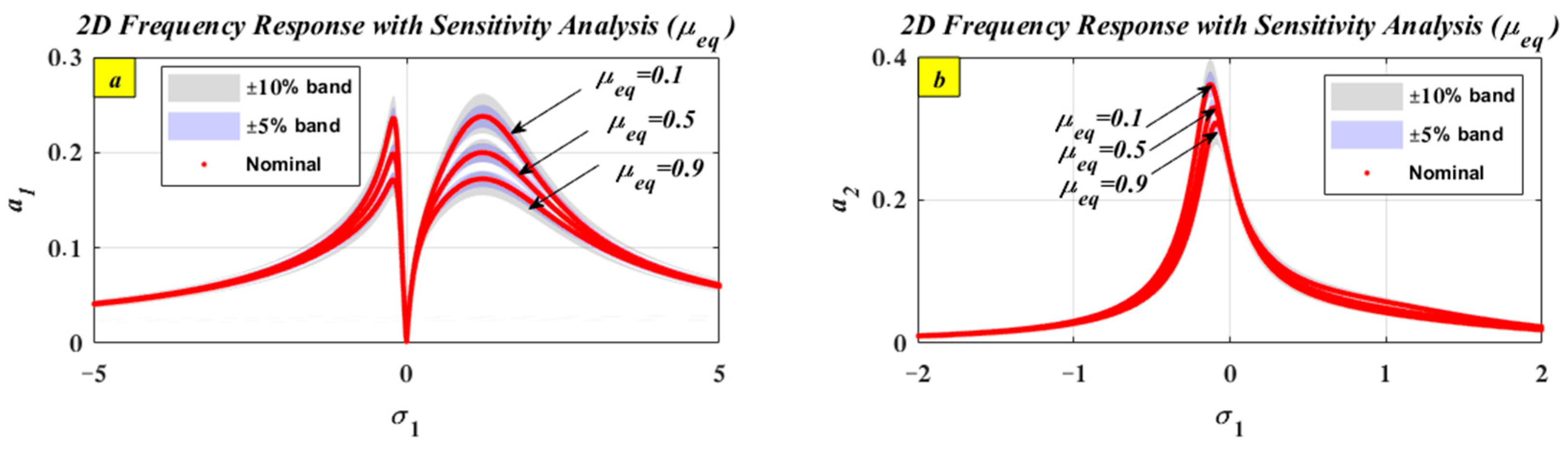
5.2. Sensitivity Analysis with ±5% and ±10%
5.3. Comparison Description
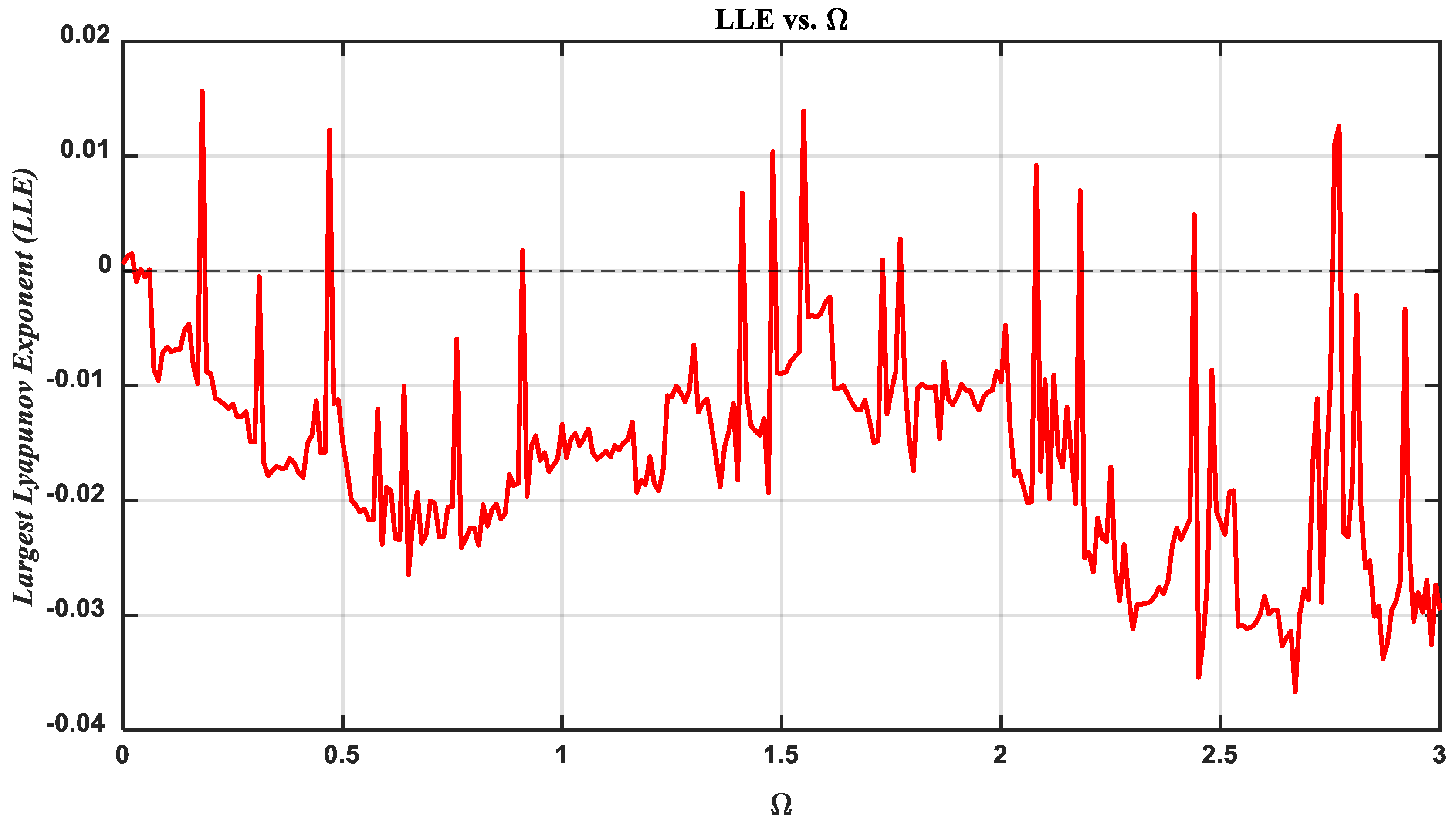
5.4. Bifurcation and Chaotic Motion Description
6. Conclusions
- To suppress the resulting dangerous vibrations, a novel proportional derivative positive position feedback (PDPPF) control strategy was proposed, combining the strengths of PD and PPF controllers.
- Comparative analysis showed that the PDPPF controller reduced peak vibration amplitudes by up to 99.93% near resonant frequencies, outperforming standalone PD and PPF controllers under the same conditions.
- The PDPPF controller offered a highly effective solution for enhancing ride comfort and structural integrity in motorcycle suspension systems, especially under resonant excitation.
- The numerical and analytical solutions, validated through MATLAB simulations, confirmed the accuracy and reliability of the proposed approach, demonstrating good agreement between both methods. These findings underscore the effectiveness of the PDPPF control technique in addressing vibration issues and ensuring stability in dynamic systems.
- The PDPPF control approach provided a viable method for enhancing ride comfort, stability, and component longevity in motorcycle suspension systems.
- The bifurcation diagram illustrated these transitions, offering valuable insights into how small changes in system parameters can induce significant shifts in behavior. This understanding is crucial for predicting and controlling instability, chaotic dynamics, and limit cycles, which are typical in nonlinear systems.
- Overall, this investigation contributed valuable insights into the control and analysis of dynamic systems with resonant behavior, offering practical implications for the design and optimization of engineering applications, particularly in systems prone to vibration-related challenges. Future work could extend this approach to other types of resonant systems, exploring additional control strategies and optimization techniques.
- The 99.93% suppression predicted in simulations should be interpreted as a theoretical upper bound under the idealized assumptions of the model. In practical scenarios, physical constraints such as actuator saturation, energy limitations, and sensor noise will limit the achievable performance. Nevertheless, the results confirm the mathematical effectiveness of the PDPPF strategy and its potential for substantial vibration reduction in real-world applications.
7. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 53, 1034–1062. [Google Scholar] [CrossRef]
- Tseng, T.; Hrovat, D. Some characteristics of optimal vehicle suspensions based on quarter-car models. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 2232–2237. [Google Scholar]
- Hrovat, D. Survey of advanced suspension developments and related optimal control applications. Automatica 1997, 33, 1781–1817. [Google Scholar] [CrossRef]
- Attia, T.; Vamvoudakis, K.G.; Kochersberger, K.; Bird, J.; Furukawa, T. Simultaneous dynamic system estimation and optimal control of vehicle active suspension. Veh. Syst. Dyn. 2019, 57, 1467–1493. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. Design of static output feedback and structured controllers for active suspension with quarter-car model. Energies 2021, 14, 8231. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. Comparative Study on Effects of Input Configurations of Linear Quadratic Controller on Path Tracking Performance under Low Friction Condition. Actuators 2023, 12, 153. [Google Scholar] [CrossRef]
- Yang, M.; Peng, C.; Li, G.; Wang, Y.; Ma, S. Event-triggered H∞ control for active semi-vehicle suspension system with communication constraints. Inf. Sci. 2019, 486, 101–113. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Zhang, C. Robust fault-tolerant H∞ output feedback control of active suspension and dynamic vibration absorber with finite-frequency constraint. IET Intell. Transp. Syst. 2020, 14, 1935–1945. [Google Scholar] [CrossRef]
- Du, H.; Zhang, N. Fuzzy control for nonlinear uncertain electrohydraulic active suspensions with input constraint. IEEE Trans. Fuzzy Syst. 2008, 17, 343–356. [Google Scholar] [CrossRef]
- Gad, A.S.; El-Zoghby, H.; Oraby, W.; El-Demerdash, S.M. Application of a Preview Control with an MR Damper Model Using Genetic Algorithm in Semi-Active Automobile Suspension; Technical Paper No. 2019-01-5006; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Huang, Y.; Na, J.; Wu, X.; Liu, X.; Guo, Y. Adaptive control of nonlinear uncertain active suspension systems with prescribed performance. ISA Trans. 2015, 54, 145–155. [Google Scholar] [CrossRef]
- Pan, H.; Sun, W.; Jing, X.; Gao, H.; Yao, J. Adaptive tracking control for active suspension systems with non-ideal actuators. J. Sound Vib. 2017, 399, 2–20. [Google Scholar] [CrossRef]
- Su, X. Master–slave control for active suspension systems with hydraulic actuator dynamics. IEEE Access 2017, 5, 3612–3621. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, C.; Liu, Y.J.; Wang, R.; Tong, S. Performance improvement of active suspension constrained system via neural network identification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7089–7098. [Google Scholar] [CrossRef]
- Liu, Y.; Zuo, L. Energy-flow-driven (EFD) semi-active suspension control. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 2120–2125. [Google Scholar]
- Enders, E.; Burkhard, G.; Munzinger, N. Analysis of the influence of suspension actuator limitations on ride comfort in passenger cars using model predictive control. Actuators 2020, 9, 77. [Google Scholar] [CrossRef]
- Shao, X.; Naghdy, F.; Du, H. Reliable fuzzy H∞ control for active suspension of in-wheel motor driven electric vehicles with dynamic damping. Mech. Syst. Signal Process. 2017, 87, 365–383. [Google Scholar] [CrossRef]
- Slaski, G.; Gudra, A.; Borowicz, A. Analysis of the influence of additional unsprung mass of in-wheel motors on the comfort and safety of a passenger car. Arch. Automot. Eng.–Arch. Motoryz. 2014, 65, 51–64. [Google Scholar]
- Choi, S.B.; Lee, H.S.; Park, Y.P. H8 control performance of a full-vehicle suspension featuring magnetorheological dampers. Veh. Syst. Dyn. 2002, 38, 341–360. [Google Scholar] [CrossRef]
- Sohn, J.W.; Oh, J.S.; Choi, S.B. Design and novel type of a magnetorheological damper featuring piston bypass hole. Smart Mater. Struct. 2015, 24, 035013. [Google Scholar] [CrossRef]
- Pham, T.P.; Sename, O.; Dugard, L. Real-time damper force estimation of vehicle electrorheological suspension: A nonlinear parameter varying approach. IFAC-Pap. Online 2019, 52, 94–99. [Google Scholar] [CrossRef]
- Kawamoto, Y.; Suda, Y.; Inoue, H.; Kondo, T. Modeling of electromagnetic damper for automobile suspension. J. Syst. Des. Dyn. 2007, 1, 524–535. [Google Scholar] [CrossRef]
- Parker, R.G.; Wu, X. Parametric instability of planetary gears having elastic continuum ring gears. J. Vib. Acoust. 2012, 134, 041011. [Google Scholar] [CrossRef]
- Yildirim, T.; Ghayesh, M.H.; Li, W.; Alici, G. Design and development of a parametrically excited nonlinear energy harvester. Energy Convers. Manag. 2016, 126, 247–255. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Kumar, V.; Shaw, S.W.; Turner, K.L. The non-linear dynamics of electromagnetically actuated micro beam resonators with purely parametric excitations. Int. J. Non-Linear Mech. 2013, 55, 79–89. [Google Scholar] [CrossRef]
- Genter, S.; Paul, O. Parylene-C as an Electret Material for Micro Energy Harvesting. Ph.D. Thesis, Universität Freiburg, Breisgau, Germany, 2019. [Google Scholar]
- Mbong, T.D.; Siewe, M.S.; Tchawoua, C. Controllable parametric excitation effect on linear and nonlinear vibrational resonances in the dynamics of a buckled beam. Commun. Nonlinear Sci. Numer. Simul. 2018, 54, 377–388. [Google Scholar] [CrossRef]
- El-Sayed, A.T.; Bauomy, H.S. NIPPF versus ANIPPF controller outcomes on semi-direct drive cutting transmission system in a shearer. Chaos Solitons Fractals 2022, 156, 111778. [Google Scholar] [CrossRef]
- Bauomy, H.S.; El-Sayed, A.T. A new six-degrees of freedom model designed for a composite plate through PPF controllers. Appl. Math. Model. 2020, 88, 604–630. [Google Scholar] [CrossRef]
- Bauomy, H.S.; El-Sayed, A.T. Act of nonlinear proportional derivative controller for MFC laminated shell. Phys. Scr. 2020, 95, 095210. [Google Scholar] [CrossRef]
- Bauomy, H.S.; El-Sayed, A.T. Nonlinear saturation controller simulation for reducing the high vibrations of a dynamical system. Math. Biosci. Eng. 2022, 19, 3487–3508. [Google Scholar] [CrossRef]
- Piantini, S.; Pierini, M.; Delogu, M.; Baldanzini, M.; Franci, A.; Mangini, M.; Peris, A. Injury Analysis of Powered Two-Wheeler versus Other Vehicle Urban Accidents. In Proceedings of the 2016 IRCOBI Conference, Malaga, Spain, 14–16 September 2016; IRCOBI: Malaga, Spain, 2016. [Google Scholar]
- Prochowski, L.; Pusty, T. Charakterystyka Obrotu i Unoszenia Motocykla po Uderzeniu w Bok Samochodu. In The Archives of Automotive Engineering; Archiwum Motoryzacji: Warszawa, Poland, 2012. [Google Scholar]
- Wypadki Drogowe w Polsce w 2019 roku; Technical Report; Biuro Ruchu Drogowego Zespół Profilaktyki i Analiz: Warszawa, Poland, 2020.
- Stan Bezpiecze’ Nstwa Ruchu Drogowego Oraz Działania Realizowane w Tym Zakresie w 2019r. Available online: https://www.krbrd.gov.pl/baza-wiedzy/raporty-o-stanie-brd/ (accessed on 18 August 2021).
- Dukalski, P.; B˛edkowski, B.; Parczewski, K.; Wn ˛ek, H.; Urba’s, A.; Augustynek, K. Dynamics of the vehicle rear suspension system with electric motors mounted in wheels. Eksploat. I Niezawodn. Maint. Reliab. 2019, 21, 125–136. [Google Scholar] [CrossRef]
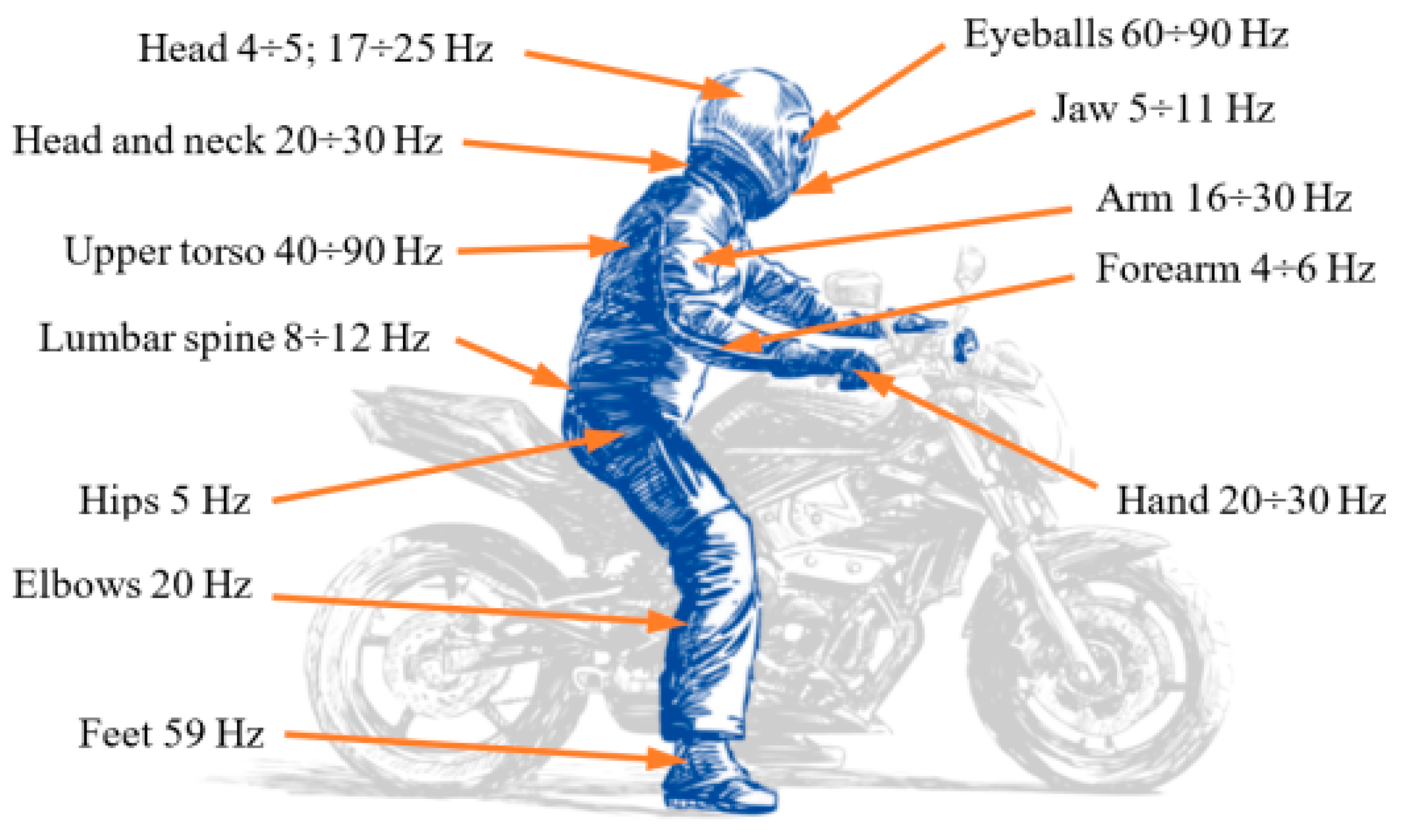
- Nader, M.; Korzeb, J. Przeglad ˛ Biomechanicznych Modeli do Oceny Oddziaływania Drga ’n na Organizm Ludzki, Materiały III Krajowego Sympozjum, Komputerowe Systemy Wspomagania Prac Inzynierskich w Przemy’sle i Transporcie; Politechnika Radomska: Zakopane, Poland, 1999; pp. 219–234. [Google Scholar]
- Shivakumara, B.S.; Sridhar, V. Study of Vibration and Its Effect on Health of the Motorcycle Rider. Online J. Health Allied Sci. 2010, 9, 9. [Google Scholar]
- Di Massa, G.; Pagano, S.; Strano, S.; Terzo, M. A Mono-axial Wheel Force Transducer for the Study of the Shimmy Phenomenon. In Proceedings of the World Congress on Engineering, London, UK, 3–5 July 2013. [Google Scholar]
- Grzegozek, W.; Weigel-Millert, K. Analiza możliwości wykorzystania badań stanowiskowych do oceny stabilności pojazdu jednośladowego. Arch. Automot. Eng. Arch. Motoryz. 2015, 67, 165–173. [Google Scholar]
- Slusarczyk, P. Analiza Modelowa Stateczno’sci Pojazdu Jedno’sladowego, Czasopismo Techniczne; Wyd, P.K., Ed.; Zeszyt 7-M: Kraków, Poland, 2004; pp. 165–173. [Google Scholar]
- D˛ebowski, A. Analiza Mozliwo’sci Ograniczenia Drga ’n Skr˛etnych w Układzie Kierowniczym Motocykla. Ph.D. Thesis, Military University of Technology, Warszawa, Poland, 2019. [Google Scholar]
- Sharp, R.S. The stability and control of motorcycles. J. Mech. Eng. Sci. 1971, 13, 313–329. [Google Scholar] [CrossRef]
- Sharp, R.S. The Influence of Frame Flexibility on the Lateral Stability of Motorcycles. J. Mech. Eng. Sci. 1974, 16, 117–120. [Google Scholar] [CrossRef]
- Sharp, R.S.; Alstead, C.J. The influence of structural flexibilities on the straight-running stability of motorcycles. Veh. Syst. Dyn. 1980, 9, 327–357. [Google Scholar] [CrossRef]
- Kane, T.R. The Effect of Frame Flexibility on High Speed Weave of Motorcycles; SAE Technical Paper 780306; SAE International: Warrendale, PA, USA, 1978. [Google Scholar]
- Cossalter, V. Motorcycle Dynamics; LULU: Morrisville, NC, USA, 2006. [Google Scholar]
- Cossalter, V.; Lot, R.; Massaro, M. An Advanced Multibody Code for Handling and Stability Analysis of Motorcycles; Springer Meccanica: Berlin/Heidelberg, Germany, 2011; Volume 46, pp. 943–958. [Google Scholar]
- De Falco, D.; Di Massa, G.; Pagano, S.; Strano, S. Wheel Force Transducer for Shimmy Investigation. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2015. [Google Scholar]
- Sharp, R.S.; Limbeer, D.J.N. On steering wobble oscillations of motorcycles. J. Mech. Eng. Sci. 2004, 14, 1449–1456. [Google Scholar] [CrossRef]
- Abohamer, M.K.; Awrejcewicz, J.; Amer, T.S. Modeling and analysis of a piezoelectric transducer embedded in a nonlinear damped dynamical system. Nonlinear Dyn. 2023, 111, 8217–8234. [Google Scholar] [CrossRef]
- Bauomy, H.S.; EL-Sayed, A.T.; Amer, T.S.; Abohamer, M.K. Negative derivative feedback control and bifurcation in a two-degree-of-freedom coupled dynamical system. Chaos Solitons Fractals 2025, 193, 116138. [Google Scholar] [CrossRef]
- Saeed, N.A.; EL-Shourbagy, S.M.; Kamel, M.; Raslan, K.R.; Awrejcewicz, J.; Gepreel, K.A. On the Resonant Vibrations Control of the Nonlinear Rotor Active Magnetic Bearing Systems. Appl. Sci. 2022, 12, 8300. [Google Scholar] [CrossRef]
- Saeed, N.A.; Kandil, A. Lateral vibration control and stabilization of the quasiperiodic oscillations for rotor-active magnetic bearings system. Nonlinear Dyn. 2019, 98, 1191–1218. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, G.; Yu, K.; Gao, X.; Wang, D.; Ge, M. Attitude Control and Vibration Suppression Using PD + CPPF Compound Control Strategy. Adv. Guid. Navig. Control 2022, 845, 6934–6944. [Google Scholar]
- Saeed, N.A.; Awwad, E.M.; Abdelhamid, T.; EL-Meligy, M.A.; Sharaf, M. Adaptive versus Conventional Positive Position Feedback Controller to Suppress a Nonlinear System Vibrations. Symmetry 2021, 13, 255. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Perturbation Methods; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- He, J.H. An improved amplitude-frequency formulation for nonlinear oscillators. Int. J. Nonlinear Sci. Numer. Simul. 2008, 9, 211–212. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Insightful and comprehensive formularization of frequency-amplitude formula for strong or singular nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control 2023, 42, 89–109. [Google Scholar] [CrossRef]
- El-Dib, Y.O. The damping Helmholtz -Rayleigh-Duffing oscillator with the non-perturbative approach. Math. Comput. Simul. 2022, 194, 552–562. [Google Scholar] [CrossRef]
- Moatimid, G.M.; El-Sayed, A.T.; Salman, H.F. Different controllers for suppressing oscillations of a hybrid oscillator via non-perturbative analysis. Sci. Rep. 2024, 14, 307. [Google Scholar] [CrossRef] [PubMed]
- Moatimid, G.M.; Amer, T.S.; Galal, A.A. Studying highly nonlinear oscillators using the non-perturbative methodology. Sci. Rep. 2023, 13, 20288. [Google Scholar] [CrossRef] [PubMed]
- Moatimid, G.M.; Amer, T.S.; Galal, A.A. Inspection of some extremely nonlinear oscillators using an inventive. J. Vib. Eng. Technol. 2024, 12 (Suppl. S2), S1211–S1221. [Google Scholar] [CrossRef]
























Nonlinear ODE | Linear ODE | Absolute Error | |
|---|---|---|---|
| 0 | 0.01 | 0.01 | 0 |
| 5 | 0.0797433 | 0.0793304 | 0.0004129 |
| 10 | −0.0506181 | −0.0510558 | 0.0004377 |
| 15 | −0.0477873 | −0.0468101 | 0.0009772 |
| 20 | 0.0649539 | 0.0659082 | 0.0009543 |
| 25 | −0.0414129 | −0.0413779 | 3.5 × 10−5 |
| 30 | 0.0488045 | 0.048411 | 0.0003935 |
| 35 | 0.00247337 | 0.00105323 | 0.00142014 |
| 40 | −0.0459552 | −0.0445459 | 0.0014093 |
| 45 | 0.0657408 | 0.0663284 | 0.0005876 |
| 50 | −0.0443966 | −0.0452382 | 0.0008416 |
| 55 | 0.00798973 | 0.00931482 | 0.00132509 |
| 60 | 0.0177671 | 0.0174413 | 0.0003258 |
| 65 | −0.0597973 | −0.0593512 | 0.0004461 |
| 70 | 0.0622374 | 0.0625057 | 0.0002683 |
| 75 | −0.0281102 | −0.0282766 | 0.0001664 |
| 80 | −0.0174564 | −0.0174284 | 2.8 × 10−5 |
| 85 | 0.0495248 | 0.0494664 | 5.84 × 10−5 |
| 90 | −0.0627916 | −0.0626233 | 0.0001683 |
| 95 | 0.0435045 | 0.0438188 | 0.0003143 |
| 100 | −0.00163407 | −0.00324607 | 0.001612 |
| Controller | Peak Amplitude | Reduction % | Settling Time (s) |
|---|---|---|---|
| No Control | 0.95 | ــــــــــــــ | 150 |
| PD | 0.17 | 82.11% | 150 |
| PPF | 0.014 | 98.53% | 117.53 |
| PDPPF | 0.000675 | 99.93% | 23.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bauomy, H.S.; EL-Sayed, A.T. Oscillation Controlling in Nonlinear Motorcycle Scheme with Bifurcation Study. Mathematics 2025, 13, 3120. https://doi.org/10.3390/math13193120
Bauomy HS, EL-Sayed AT. Oscillation Controlling in Nonlinear Motorcycle Scheme with Bifurcation Study. Mathematics. 2025; 13(19):3120. https://doi.org/10.3390/math13193120
Chicago/Turabian StyleBauomy, Hany Samih, and Ashraf Taha EL-Sayed. 2025. "Oscillation Controlling in Nonlinear Motorcycle Scheme with Bifurcation Study" Mathematics 13, no. 19: 3120. https://doi.org/10.3390/math13193120
APA StyleBauomy, H. S., & EL-Sayed, A. T. (2025). Oscillation Controlling in Nonlinear Motorcycle Scheme with Bifurcation Study. Mathematics, 13(19), 3120. https://doi.org/10.3390/math13193120







