Abstract
Chaotic systems appear in a wide range of natural and engineering contexts, making the design of reliable and flexible control strategies a crucial challenge. This work proposes a robust control scheme based on the Fractional-Order Backstepping Control (FOBC) method for the stabilization of non-commensurate fractional-order chaotic systems subject to bounded uncertainties and external disturbances. The method is developed through a rigorous stability analysis grounded in the Mittag–Leffler function, enabling the step-by-step stabilization of each subsystem. By incorporating fractional-order derivatives into carefully selected Lyapunov candidate functions, the proposed controller ensures global system stability. The performance of the FOBC approach is validated on fractional-order versions of the Duffing–Holmes system and the Rayleigh oscillator, with the results compared against those of a fractional-order PID (FOPID) controller. Numerical evaluations demonstrate the superior performance of the proposed strategy: the error dynamics converge rapidly to zero, the system exhibits strong robustness by restoring state variables to equilibrium quickly after disturbances, and the method achieves low energy dissipation with a high error convergence speed. These quantitative indices confirm the efficiency of FOBC over existing methods. The integration of fractional-order dynamics within the backstepping framework offers a powerful, robust, and resilient approach to stabilizing complex chaotic systems in the presence of uncertainties and external perturbations.
Keywords:
chaotic systems; fractional-order systems; control and stabilization; backstepping control; Mittag–Leffler principle MSC:
93-10
1. Introduction
Numerous natural phenomena exhibit dramatic changes on a large scale while also displaying intricate, fine-scale irregularities. Such complex behaviors can be effectively captured by mathematical models of chaotic systems. The dynamics of these systems have proven valuable in many applications, ranging from biological systems [1,2,3] to telecommunications [4,5], electrical circuits [6,7], viscoelastic materials [8,9], image encryption [10], chaotic oscillators [11], energy [12], medicine [13], physics [14], and chemical reactors [15,16,17].
One of the major challenges in dealing with chaotic systems is ensuring their stability around a desired operating point or equilibrium. The most common method for analyzing stability is Lyapunov’s approach, which has been adapted to handle chaotic systems as well. Moreover, the Mittag–Leffler stability concept offers an alternative framework by extending Lyapunov’s method with fractional derivatives and integrals [18,19,20]. This criterion has proven to be a highly effective tool for studying the stability of fractional-order chaotic systems (FOCSs). To stabilize FOCSs, researchers have explored a variety of control strategies. The field has evolved rapidly, with classical and nonlinear control techniques, as well as artificial intelligence-based methods, drawing significant interest. Selecting the right controller is crucial; for example, PI controllers have been used to stabilize certain FOCSs by managing unstable fixed points [21], and the design problem of a finite-time bounded tracking controller for a class of fractional-order systems with state delays is studied in [22].
In the literature, a wide range of control strategies have been developed for chaotic systems, including both classical and modern techniques. Controlling nonlinear fractional-order dynamics when uncertainties are present has been investigated in studies such as [23]. An adaptive sliding-mode control method was proposed for optimizing chaotic supply chain systems in [24], and impulsive control for wireless text data transmission in FOCSs was demonstrated in [25]. In addition, comprehensive investigations into stabilization via backstepping control were presented in [20], while hybrid approaches that integrate fuzzy logic and neural networks have also yielded promising results [26,27,28].
Backstepping control, in particular, has emerged as a promising tool for stabilizing nonlinear systems, making it highly suitable for our study on FOCS stabilization. For example, ref. [29] explored backstepping for the synchronization and stabilization of FOCSs; however, their work was confined to systems with identical fractional orders and limited to a state dimension of three, thus restricting its broader application. Similarly, ref. [30] developed a backstepping strategy for dual-mass MEMS gyroscopes under event-triggered conditions, but the approach does not easily extend to other FOCSs.
Other studies, such as [31], have examined uncertain nonlinear fractional-order n-dimensional systems, but often assume commensurate orders, limiting their real-world applicability. In [32], the research was centered on linear systems with uniform fractional orders, whereas [33] focused solely on Rössler-type systems. Likewise, ref. [34] proposed a backstepping method for FOCS synchronization that was restricted to three-dimensional cases, thereby impeding its extension to more complex systems.
While many studies emphasize the diverse applications of chaotic dynamics, fewer works provide in-depth discussions on the control methodologies themselves. To address this imbalance, the present work places greater focus on control-oriented references, highlighting the growing interest in fractional-order control frameworks for handling nonlinear and uncertain dynamics.
Although data-driven schemes such as sigmoid PID controllers [35,36], BELBIC PID controllers [37], and neuroendocrine PID controllers [38] have shown promising performance in various contexts, they often lack a rigorous analytical foundation and may require extensive tuning or training data. In contrast, the Fractional-Order Backstepping approach is rooted in model-based design, providing a systematic step-by-step framework that leverages Lyapunov stability analysis and the Mittag–Leffler function to guarantee robust stabilization even under parameter uncertainties and external disturbances [39,40,41,42]. This analytical tractability forms a key gap between the proposed method and data-driven controllers, offering formal guarantees of stability that purely data-driven schemes cannot always ensure. Furthermore, the choice of fractional-order control is well justified by their proven success in a variety of recent engineering applications, such as load frequency control in photovoltaic-integrated two-area power systems [43], automatic voltage regulator (AVR) systems [44], and wind turbine generator systems [45], among others. These applications demonstrate the versatility and effectiveness of fractional-order controllers, thereby supporting their use in the challenging context of chaotic system stabilization considered in this paper.
In this paper, we aim to fill these gaps by investigating the control of non-commensurate fractional-order chaotic (NFOC) systems under uncertainties and external disturbances using Fractional-Order Backstepping Control (FOBC). Our main contribution lies in developing a generalized control framework that does not assume identical fractional orders. By employing the Mittag–Leffler stability criterion along with carefully chosen candidate functions incorporating fractional derivatives, we achieve a comprehensive stability analysis of the overall system.
The main contribution of this study, which sets it apart from previous works, is the development of a Fractional-Order Backstepping Control strategy that robustly stabilizes non-commensurate fractional-order chaotic systems in the presence of uncertainties and disturbances, without relying on simplifying assumptions. The proposed method fully preserves the nonlinear dynamics of the system and demonstrates its effectiveness even when the fractional orders used in simulation are significantly less than one.
Overall, this study introduces a generalized and robust control approach tailored for fractional-order systems. The FOBC strategy is thoroughly developed and applied to the regulation of NFOC systems in the presence of uncertainties and external disturbances. To validate the effectiveness of the proposed method, we successfully demonstrate the stabilization and control of two well-known chaotic systems: the Duffing–Holmes system and the Rayleigh oscillator, considering their fractional-order dynamics under perturbations. Furthermore, a comparative study with the Fractional-Order PID (FOPID) controller highlights the superior performance of the proposed FOBC approach in terms of stabilization speed, robustness, energy dissipation, and resilience against disturbances.
The rest of the paper is structured as follows: Section 2 introduces the fundamental concepts of fractional calculus and outlines the key principles of stability analysis. Section 3 details the core contributions of this work, focusing on the control and stabilization of a general class of NFOC systems in the presence of uncertainties and external disturbances. Section 4 presents numerical simulations alongside a discussion of the obtained results. Finally, Section 5 concludes the paper by summarizing the main findings and contributions.
2. Background on Fractional-Order Calculus
Despite being recognized as a mathematical concept for centuries, fractional-order calculus has only recently started to attract substantial interest for its industrial applications. By incorporating operators that allow differentiation and integration to be carried out at non-integer orders, this field broadens and enriches the traditional framework of classical calculus.
2.1. Fractional-Order Operators
In fractional calculus, the main operator—represented as —is defined as follows:
In this context, a and t set the boundaries for the operation, while denotes the fractional order, which can take any real value. There are three primary definitions of this operator commonly cited in the literature: those by Caputo, Grunwald–Letnikov, and Riemann–Liouville [46,47,48].
- Caputo’s Definition: The fractional derivative in Caputo’s definition is given by
- The Grunwald–Letnikov Definition: An alternative fractional-order derivative is formulated as follows:
- The Riemann–Liouville Definition: The fractional derivative in this framework is given bywhere , , , , is a causal function, and is the Gamma function, given by
To simplify our discussion, we will refer to the fractional-order operator as throughout the rest of the sections.
2.2. Stability Analysis of FOCSs
Ensuring the stability of dynamical systems—particularly those exhibiting chaotic behavior—is a fundamental aspect of their analysis. Among the many available approaches, the Lyapunov criterion remains one of the most widely used methods for assessing stability. Additionally, the Mittag–Leffler criterion plays a crucial role, especially in the context of fractional-order systems, where conventional methods may fall short.
2.2.1. Lyapunov Stability
Let us consider a nonlinear system defined by
where , s, and t are a nonlinear function, a sate vector, and the time, respectively. The Lyapunov approach is the standard method for analyzing stability in both linear and nonlinear systems. It uses a Lyapunov function , which is a scalar function that decreases over time along system trajectories.
If is an equilibrium point of Equation (6), and for the system reduces to an integer-order system, then the stability of the system is determined by a Lyapunov function . If V is continuous and differentiable, and if it satisfies , in D, and in D, then is stable. Moreover, if in D, then the equilibrium is asymptotically stable. The function V is known as a Lyapunov candidate function [49].
2.2.2. Stability in the Mittag–Leffler Criterion
This criterion is specifically adapted for fractional-order differential equations, where system dynamics include memory and hereditary properties.
Lemma 1
([19]). For a function that is real, continuous, and differentiable, and given that , where n is a natural number and , the fractional derivative satisfies the following condition:
Particularly, when ,
Theorem 1
([19]). For and , assuming that , the system described by Equation (6) remains stable under the control input if
For , where n is a natural number, if , then the system governed by the control law is asymptotically stable according to the Mittag–Leffler stability principle.
3. Methods
In this section, we present the design procedure of the proposed Fractional-Order Backstepping Control (FOBC) strategy for the stabilization of a class of non-commensurate fractional-order chaotic systems subject to uncertainties and external perturbations. The method is developed in a step-by-step manner following the backstepping framework, where each subsystem is stabilized progressively. To guarantee the overall stability of the closed-loop system, the construction relies on the Mittag–Leffler stability principle, which is particularly suited to fractional-order dynamics. Careful selection of Lyapunov candidate functions at each stage plays a central role in the design, ensuring that the stabilization objectives are systematically achieved while accounting for the effects of modeling uncertainties and external disturbances.
3.1. System Overview and Problem Statement
Many real-world phenomena exhibit chaotic behavior and are often modeled as nonlinear systems. By incorporating fractional-order dynamics, we can achieve a more precise representation of these systems. Notably, a considerable subset of them is formulated in strict-feedback form, which includes several well-known chaotic models such as the Van der Pol oscillator, Chen’s system, Liu’s system, Chua’s circuit, and the Rössler system.
A proposed class of these fractional-order chaotic systems can be generally expressed as follows:
where t is the time, , with , and representing the system states. The vector captures the system’s state history, while denotes the control signal to be designed. The terms and account for bounded parameter uncertainties and external disturbances, respectively ( and , with ). Additionally, and are known smooth nonlinear functions, where the condition ensures that the fractional orders remain within the range .
This proposed class of fractional-order chaotic systems is a general nonlinear, strict-feedback, fractional-order system that
- Exhibits memory effects due to fractional derivatives;
- Allows for step-by-step stabilization via backstepping;
- Incorporates uncertainties and disturbances;
- Provides a unified framework that can represent many well-known chaotic systems under realistic operating conditions.
The general class of fractional-order chaotic systems proposed in Equation (10) is designed to capture a wide range of nonlinear and chaotic dynamics while explicitly accounting for fractional derivatives, parameter uncertainties, and external disturbances. This structure establishes a flexible modeling framework that can represent many well-known chaotic systems as special cases.
- Van der Pol oscillator: The Van der Pol system is a second-order nonlinear oscillator characterized by a self-sustained oscillation with nonlinear damping. In the general model, this corresponds to the case where , with and defining the linear and nonlinear damping terms, and capturing the coupling between and . By introducing fractional derivatives, the system generalizes the classical Van der Pol dynamics to a fractional-order setting.
- Chen’s system: Chen’s system, a well-known three-dimensional chaotic system, can be expressed in the proposed form with . Here, and encode the linear and bilinear interactions among states , while the fractional derivative orders introduce memory effects that extend the classical integer-order Chen system.
- Liu’s system: Similarly, Liu’s system (another three-dimensional chaotic attractor with a close relation to the Chen and Lorenz systems) can be represented within this framework by selecting appropriate nonlinear functions, and . The proposed class accommodates its structure naturally, with fractional orders offering an additional degree of freedom to control stability and chaos intensity.
- Chua’s circuit: Chua’s circuit is a nonlinear electronic system that exhibits rich chaotic behavior. Its dynamics include piecewise-linear nonlinearities, which can be modeled by the functions in the proposed formulation. Fractional derivatives further enhance the description by incorporating hereditary and memory properties often observed in physical circuits.
- Rössler system: The Rössler attractor, characterized by its simple but chaotic spiral structure, is another three-dimensional system that fits as a subclass of (10). The bilinear terms in the Rössler equations map naturally to the terms in the proposed model, while nonlinear drift terms appear in the . Fractional orders extend this system into a richer class of dynamics.
This study aims to develop a Fractional-Order Backstepping Control (FOBC) strategy to guarantee the stability of system (10) using the Mittag–Leffler stability framework.
The control of FOCSs using the proposed FOBC approach is illustrated in Figure 1.
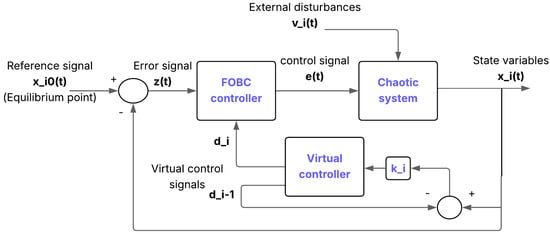
Figure 1.
A summary diagram illustrating the stabilization of NFOC systems using FOBC.
3.2. Design of Fractional-Order Backstepping Control for FOCSs
Using a fractional-order controller instead of an integer-order controller offers several advantages. It provides a powerful way to represent memory effects, increases the system’s degrees of freedom, and enables more accurate modeling of physical systems. Additionally, it enhances robustness against uncertainties, strengthens security in communication systems, and is particularly well suited for encryption applications [50].
To achieve effective control of FOCSs, the following control theorem is presented, combining fractional-order calculus with the backstepping approach. This method ensures both the control and stabilization of the system.
Theorem 2.
The control law that guarantees the asymptotic stabilization of the system states in (10), ensuring that , is given by
Here, () represents the designed virtual controls, while the constants () are predefined parameters.
The variable transformation is given by . For , it is defined as .
Proof of Theorem 2.
Step 1: By setting the variable equal to in system (10), we obtain the first subsystem for :
For this initial subsystem, we choose as the control input and as the virtual control input. We then define as the difference between and , which gives us the relationship . As a result, Equation (12) can be rewritten as follows:
Let the initial Lyapunov function candidate for subsystem (13) be
Since the uncertainties and external disturbances are bounded signals, and based on Lemma 1, taking the fractional-order derivative of Equation (14) results in the following inequality:
By substituting Equation (13) into inequality (15), we obtain inequality (16):
For the stability condition based on the Mittag–Leffler criterion to be satisfied, must be chosen according to the form given in Equation (17).
This gives the following result:
In the next step, the coupled term will be eliminated, and we ensure that while driving the error state towards zero. According to Theorem 1, the virtual control plays a crucial role in ensuring that the state converges to zero over time, thereby improving the stability of subsystem (13).
Step 2: For the second subsystem, labeled as , we follow a similar approach, which leads to
Let us define as the error between the current control and the virtual control , i.e., . Rearranging this equation gives .
By substituting this expression into Equation (19), we get
A possible Lyapunov function for the combined first and second subsystems can be defined as follows:
Note that [47] .
Lemma 1 states that the fractional-order time derivative of this function is given by
Substituting Equation (20) into inequality (22) yields inequality (23):
According to Theorem 1, as time progresses, the state gradually approaches zero, guaranteeing the stability of the second subsystem (20). This is achieved by choosing in the following form:
By substituting Equation (24) into Equation (23), we obtain Equation (25).
The coupled term will be eliminated in the next step by ensuring that the error state converges to zero.
If , then the second subsystem will be asymptotically stable.
Similarly, a Lyapunov function, as defined in Equation (26), can be introduced, and the corresponding virtual control law (27) can be derived for any subsystem, where .
where
Step (n-1):
As a result, the fractional-order global candidate Lyapunov function and the corresponding virtual control for the subsystem are defined by Equations (28) and (29), respectively.
Step (n): In the final step, we construct the full Lyapunov function for the entire system as follows:
Equation (30) yields
With a simple rearrangement of the constants, Equation (31) takes the following form:
Using the second equation from system (10), expression (31) transforms into
To ensure that (33) remains negative, the global control must be chosen as defined in Equation (34):
This requirement transforms inequality (33) into the following form:
Expression (35) will be negative if , and it indicates that the overall control law (34) guarantees the convergence of the states to zero in a steady state, as stated in Theorem 1. Consequently, this also means that the system states will converge to the origin, following the definition of . □
The constants are selected by the designer to ensure that the desired temporal performance criteria are satisfied.
The methodology can also be presented as pseudocode (Algorithm 1):
| Algorithm 1: FOBC for Stabilization of Chaotic Systems | |
| Input: Non-commensurate fractional-order chaotic system with uncertainties and disturbances Output: Control input ensuring stabilization | |
| 1. | Initialize system states , , …, |
| 2. | Define control objective: as |
| 3. | For each subsystem to n do |
| a. Choose Lyapunov candidate function | |
| b. Compute fractional derivative | |
| c. Design virtual control law for | |
| d. Update composite Lyapunov function | |
| 4. | Derive final control law for last subsystem |
| 5. | Verify stability using Mittag–Leffler principle |
| 6. | Apply to system and simulate |
| 7. | Evaluate performance: |
| - Error convergence to zero | |
| - Robustness against disturbances | |
| - Energy dissipation | |
| - Convergence speed | |
| End Algorithm | |
4. Results
In this section, we explore the controlling of two FOCSs using the Fractional-Order Backstepping method compared with FOPID controller. The FOPID controller can take the following form:
where is the control signal; is the error signal between the reference signal and the output; is the proportional gain, is integration gain, is the integration fractional order, is the derivation gain, and is the derivation fractional order.
Our objective is to ensure these systems reach stability around their equilibrium points. The first system is a modified fractional variant of the Duffing–Holmes system, while the second is a proposed non-commensurate fractional-order form of the Rayleigh oscillator.
To assess the effectiveness of our approach, we run simulations in Matlab/Simulink (MATLAB R17a). The simulations are conducted over a total duration of 1 s with a time step of 0.001 s.
To evaluate the effectiveness of the proposed control strategy, several performance criteria are considered in this section.
- First, we examine the stability of the closed-loop system around the origin , which reflects the ability of the controller to achieve asymptotic stabilization.
- Second, the error convergence speed is assessed, defined as , where is the reference signal and x is the system output.
- Third, the instantaneous energy consumption is measured through , providing insight into the energy required for stabilization at each instant.
- Finally, we consider the normalized cumulative energy, given by where denotes the cumulative energy over time. These criteria together allow for a comprehensive assessment of the stability, robustness, energy efficiency, and convergence characteristics of the proposed control method.
4.1. Control of the Fractional-Order Duffing-Holmes System
Let us examine the widely recognized forced Duffing–Holmes (DH) system model, as outlined below [51].
In this system, represents the state variables, while denotes the applied force, and .
To rewrite the system in a fractional-order form, we introduce the following state variables: , , , and . These definitions are subject to the constraints and . The fractional orders used in this study are , , , and . Under this transformation, system (37) can be expressed in the following form:
with .
The initial conditions are chosen as follows: ; ; ; .
The uncertainties and external disturbances for , which begin to affect the system at time , modify the system’s behavior such that it can be represented in the following form:
with and , where the maximum values are quantified and bounded as and , and the selected parameters of the control signal should be as follows:
Figure 2a displays a 3D phase portrait of the uncontrolled Fractional-Order Duffing–Holmes (FODH) system without uncertainties or external disturbances, highlighting the trajectories of the state variables for . In contrast, Figure 2b shows uncontrolled FODH system state variables without uncertainties and external disturbances, revealing how these factors affect the trajectories of the state variables for .
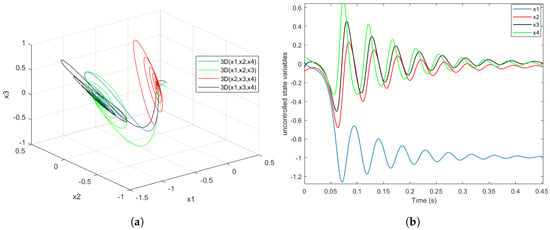
Figure 2.
(a) Three-dimensional phase portrait of uncontrolled FODH system without uncertainties and external disturbances. (b) Uncontrolled FODH system state variables without uncertainties and external disturbances.
System (39) is written in the same form as system (10), where for , while and for . Additionally, and . According to Theorem 2, the FOBC signal that stabilizes system (38) is given by
For FOBC, the chosen values are , , , and . The values of the FOPID controller are selected as:, , , , and .
Figure 3 illustrates the decline in the evolution of all states over time t.
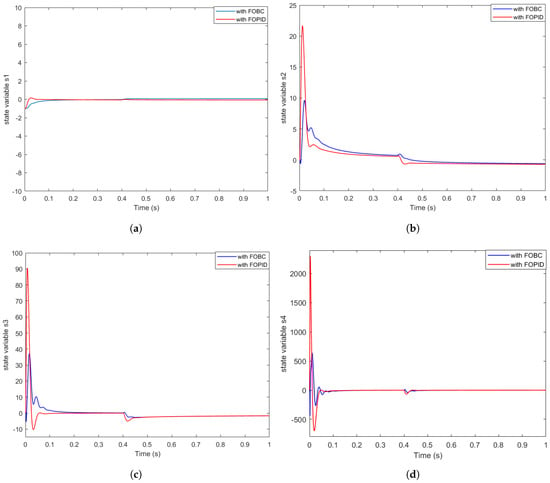
Figure 3.
Controlled state variables of FODH system with initial conditions under uncertainties and external disturbances using FOBC and FOPID controllers: (a) state variable ; (b) state variable ; (c) state variable ; (d) state variable .
Figure 4 presents a zoomed-in view of the controlled states of the FODH system under both FOBC and FOPID controllers.
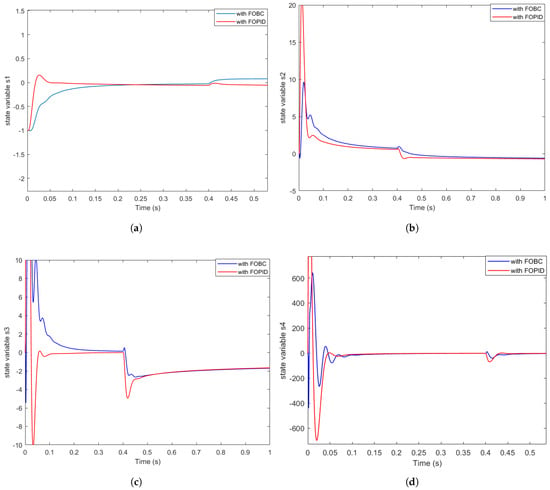
Figure 4.
Zoomed-in view of controlled state variables of FODH system with initial conditions under uncertainties and external disturbances using FOBC and FOPID controllers: (a) zoomed-in view of state variable ; (b) zoomed-in view of state variable ; (c) zoomed-in view of state variable ; (d) zoomed-in view of state variable .
Also, both the FOBC and FOPID control signals are depicted in Figure 5 and both their instantaneous and normalized energy dissipation are illustrated in Figure 6.

Figure 5.
(a) FOBC and FOPID Control signals for controlling and stabilizing the FODH system. (b) Zoomed-in view of the FOBC and FOPID control signals.
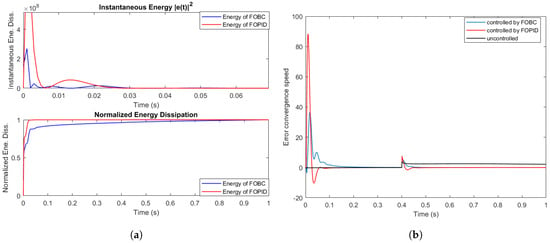
Figure 6.
(a) Instantaneous and normalized energy dissipation plots of FOBC and FOPID controllers. (b) Controlled and uncontrolled error convergence speed of FODH system.
Figure 4 and Figure 5 clearly illustrate the dynamic behavior of the state variables of the FODH system under the influence of the proposed control strategy, namely Fractional-Order Backstepping Control (FOBC). It can be observed that all state variables gradually converge to the equilibrium point, indicating successful asymptotic stabilization. This result highlights the effectiveness of the controller in suppressing chaotic behavior and achieving precise system regulation.
Moreover, the proposed approach demonstrates strong robustness in the presence of uncertainties and external disturbances. At time , both internal uncertainties and external disturbances are introduced into the system. As shown in the trajectories, this causes a momentary disruption in the system’s stability. However, the state variables quickly return to the equilibrium point, thanks to the corrective action provided by the FOBC signal. This rapid recovery emphasizes the controller’s ability to compensate for perturbations in real time, making it well suited for uncertain and dynamic environments.
4.2. Control of the Fractional-Order Rayleigh Oscillator
The Rayleigh oscillator is a classic example of a nonlinear dynamical system that exhibits self-sustained oscillations due to its inherent energy balance mechanisms. Originally introduced by Lord Rayleigh to model the oscillations of a clarinet reed, this oscillator has since been applied to various physical and engineering systems [52].
The standard form of the Rayleigh differential equation is
where
- x represents the system’s state variable (e.g., displacement);
- and denote the first and second derivatives of x with respect to time (velocity and acceleration);
- is a parameter that controls the nonlinearity and the strength of the damping or energy input ();
- is the natural frequency of the system ().
This equation describes a system where the damping term changes sign depending on the velocity . For small velocities, the term provides negative damping (energy input), while for larger velocities, it provides positive damping (energy dissipation), leading to the emergence of a stable limit cycle characteristic of self-sustained oscillations. To implement the proposed Fractional-Order Backstepping Control approach, we first introduce a non-commensurate fractional-order dynamic model of the system, referred to as the Fractional-Order Rayleigh Oscillator (FORO). This is achieved through the following variable transformation: . System (40) becomes
where , and is the control signal.
The uncertainties and external disturbances , for , begin to influence the system at time , altering its dynamics. As a result, the system can be modeled by the following set of fractional-order differential equations:
where , , , , , , , .
Here, the maximum values are quantified and bounded as and ; ; ; and , and the selected parameters of the control signal should be as follows: ; ; ; and .
This formulation captures the impact of both internal uncertainties and external disturbances on the system’s fractional-order dynamics.
For instance, under the initial conditions (; ), simulations can reveal the transition from transient behaviors to the establishment of a limit cycle. These simulations are instrumental in understanding the oscillator’s response under various conditions and in validating analytical predictions. For FOBC, the chosen values are , , , and . The values of the FOPID controller are selected as follows: , , , = 50.1039, and = 0.95.
Figure 7a shows a 3D phase portrait of the uncontrolled FORO oscillator in the absence of uncertainties and external disturbances, highlighting the trajectories of the state variables for . In contrast, Figure 7b depicts Uncontrolled FORO oscillator state variables without uncertainties and external disturbances, demonstrating how these factors affect the trajectories of the state variables for .
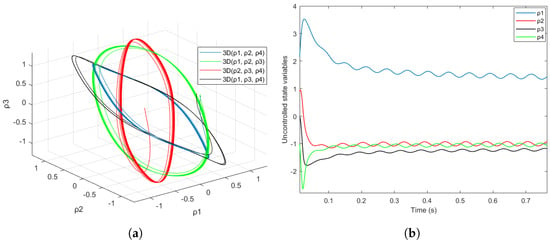
Figure 7.
(a) Three-dimensional phase portrait of the uncontrolled FORO oscillator without uncertainties and external disturbances. (b) Uncontrolled FORO oscillator state variables without uncertainties and external disturbances.
Figure 8 illustrates the decreasing trend of all states over time t.
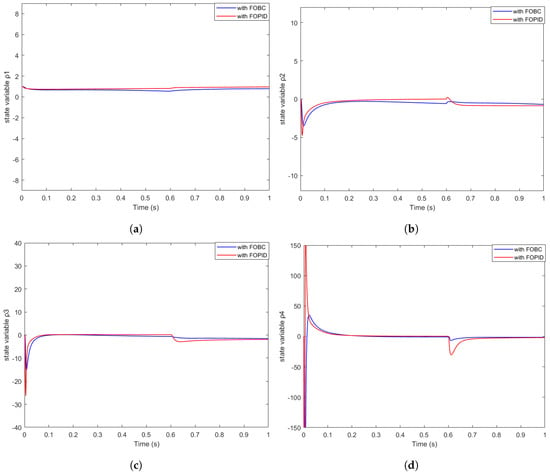
Figure 8.
Controlled state variables of FORO system with initial conditions under uncertainties and external disturbances using FOBC and FOPID controllers: (a) state variable ; (b) state variable ; (c) state variable ; (d) state variable .
Figure 9 presents a zoomed-in view of the controlled states of the FORO oscillator under both the FOBC and FOPID controllers.
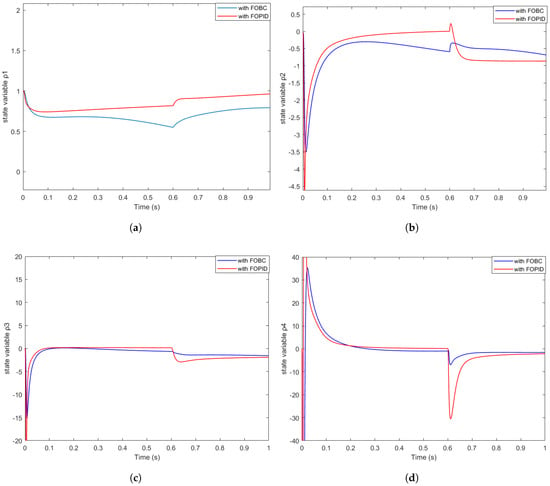
Figure 9.
Zoomed-in view of controlled state variables of FODH system with initial conditions under uncertainties and external disturbances using FOBC and FOPID controllers: (a) zoomed-in view of state variable ; (b) zoomed-in view of state variable ; (c) zoomed-in view of state variable ; (d) zoomed-in view of state variable .
The corresponding control signals of both FOBC and FOPID are depicted in Figure 10.
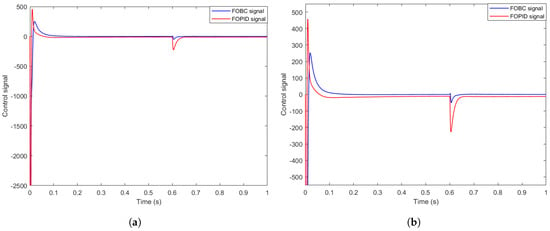
Figure 10.
(a) FOBC and FOPID control signals for controlling and stabilizing the FORO oscillator. (b) Zoomed-in view of the FOBC and FOPID control signals.
The instantaneous and normalized energy dissipation of FOBC and FOPID controllers, in terms of controlled and uncontrolled error convergence speed, are illustrated in Figure 11.
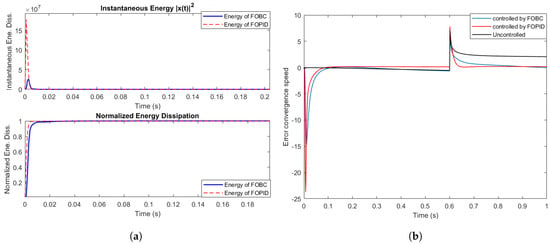
Figure 11.
(a) Instantaneous and normalized energy dissipation plot of FOBC and FOPID controllers. (b) Controlled and uncontrolled error convergence speed.
Figure 8 and Figure 9 illustrate the dynamic response of the FORO oscillator under the proposed Fractional-Order Backstepping Control (FOBC) in comparison with the FOPID controller. Under FOBC, the state trajectories converge smoothly and steadily toward the equilibrium point, confirming the controller’s capability to suppress chaotic oscillations and achieve asymptotic stability with high precision. This highlights the efficiency of the FOBC design relative to the FOPID controller, which shows slower convergence and greater sensitivity to parameter variations.
The superiority of FOBC becomes even more evident when uncertainties and external disturbances are applied at . Although the system momentarily deviates from equilibrium, the FOBC quickly restores the state trajectories to the desired point, demonstrating strong robustness and adaptability. In contrast, the FOPID controller requires more time to re-stabilize the system and consumes more energy in the process. These results clearly validate the resilience of the FOBC approach and its advantage over conventional FOPID control in stabilizing non-commensurate fractional-order chaotic systems.
4.3. Discussion
- Parameter Sensitivity Analysis: To further validate the effectiveness of the proposed FOBC scheme, a parameter sensitivity analysis was carried out. In this study, the control parameters of the FOBC were carefully selected while explicitly accounting for bounded uncertainties and external perturbations, ensuring robustness under practical conditions. For comparison, the FOPID controller was tuned using the coefficients , which were adjusted to provide the best achievable performance under the same scenarios. Different sets of initial conditions and fractional derivative orders were also considered to examine the sensitivity of both controllers to variations in the system’s configuration. The results highlight that FOBC maintains stability and reliable performance despite parameter fluctuations and disturbances, whereas the FOPID controller demonstrates more sensitivity to parameter variations, particularly under uncertain or perturbed operating conditions.
- Computational Complexity Analysis: In addition to parameter sensitivity, a computational complexity assessment was conducted to evaluate the practical feasibility of the proposed method. The analysis focused on robustness, low energy consumption, and error convergence speed in comparison with the FOPID controller. Particular attention was given to the computational requirements for fractional-order derivative calculations, the influence of the number of state variables, and the performance of the method when the values of the fractional order are significantly less than one. The results indicate that the FOBC approach achieves faster error convergence and reduced energy dissipation while preserving robustness against disturbances, even in high-dimensional or strongly fractional systems. Although FOBC requires additional computations due to the step-by-step backstepping structure, this overhead remains manageable and is outweighed by the significant improvements in robustness and stabilization efficiency relative to the FOPID controller.
These simulation results demonstrate that the FOBC strategy not only achieves effective stabilization under ideal conditions, but also maintains strong performance in the presence of significant disturbances. The system states converge rapidly and reliably to equilibrium, confirming the robustness and efficiency of the proposed approach for controlling non-commensurate fractional-order chaotic systems. Compared with the FOPID controller, FOBC exhibits clear superiority by offering higher robustness against uncertainties, lower energy consumption, and a faster error convergence rate, making it a more powerful and resilient control solution.
5. Conclusions
Chaotic dynamical systems are inherently diverse and complex, with their nonlinear nature posing significant challenges for researchers developing advanced control strategies. In this study, we introduce a robust and efficient method for stabilizing non-commensurate fractional-order chaotic systems affected by uncertainties and external disturbances using an FOBC approach. The proposed strategy is grounded in the Mittag–Leffler stability criterion and employs a carefully constructed Lyapunov-like candidate function that integrates fractional derivative terms, ensuring both stability and effective disturbance rejection.
To evaluate the performance of the proposed approach, it was applied to two representative case studies, the Fractional-Order Duffing–Holmes system and the Rayleigh oscillator, both subjected to internal and external perturbations, and compared against the FOPID controller. The simulation results show that the proposed control law effectively stabilizes chaotic behavior under a wide range of initial conditions and disturbances, while also demonstrating clear superiority over the FOPID controller in terms of stabilization speed, robustness, low energy dissipation, and resilience to perturbations. These findings confirm the reliability and effectiveness of the FOBC strategy for controlling complex nonlinear chaotic systems in the presence of uncertainties.
Author Contributions
Writing—Original Draft, A.D., M.A.A. and H.D.; Methodology, A.D. and R.D.; Software, A.D.; Investigation, A.A. and Y.A.; Resources, H.D.; Data Curation, A.D.; Funding Acquisition, Y.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2504).
Data Availability Statement
All data generated or analyzed in this study are included in the article. Additional information is available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, Y.; Li, Z.; Sun, J. Three-Variable Chaotic Oscillatory System Based on DNA Strand Displacement and Its Coupling Combination Synchronization. IEEE Trans. Nanobiosci. 2020, 19, 434–445. [Google Scholar] [CrossRef]
- Deng, A.; Chen, M.; Chen, G.; Zhang, L.; Cai, Y.; Wang, L.; Wang, D.; Gao, X.; Zhou, J. A hybrid encryption scheme of DNA and chaotic precoding for IMDD-FBMC systems. Opt. Commun. 2023, 529, 129076. [Google Scholar] [CrossRef]
- Stankevich, N.V.; Bobrovskii, A.A.; Shchegoleva, N.A. Chaos and Hyperchaos in Two Coupled Identical Hindmarsh—Rose Systems. Regul. Chaotic Dyn. 2024, 29, 120–133. [Google Scholar] [CrossRef]
- Li, R.G.; Wu, H.N. Adaptive synchronization control with optimization policy for fractional-order chaotic systems between 0 and 1 and its application in secret communication. ISA Trans. 2019, 92, 35–48. [Google Scholar] [CrossRef] [PubMed]
- Gokyildirim, A.; Akgul, A.; Calgan, H.; Demirtas, M. Parametric fractional-order analysis of Arneodo chaotic system and microcontroller-based secure communication implementation. AEU—Int. J. Electron. Commun. 2024, 175, 155080. [Google Scholar] [CrossRef]
- Liu, Y. Circuit implementation and finite-time synchronization of the 4D Rabinovich hyperchaotic system. Nonlinear Dyn. 2012, 67, 89–96. [Google Scholar] [CrossRef]
- Wu, J.; Li, C.; Ma, X.; Lei, T.; Chen, G. Simplification of Chaotic Circuits With Quadratic Nonlinearity. IEEE Trans. Circuits Syst. 2022, 69, 1837–1841. [Google Scholar] [CrossRef]
- Sha, X.; Lu, A.; Zhang, N. Analysis of layered soil under general time-varying loadings by fractional-order viscoelastic model. Appl. Math. Model. 2024, 126, 232–248. [Google Scholar] [CrossRef]
- Liang, Y.; Zhou, F.; Cao, X.; Wang, L.; Liu, H.; Zhu, S. Scattering of plane SH waves by a circular tunnel in nonlocal fractional-order viscoelastic half-space. Soil Dyn. Earthq. Eng. 2023, 170, 107934. [Google Scholar] [CrossRef]
- Zareai, D.; Balafar, M.; FeiziDerakhshi, M. EGPIECLMAC: Efficient grayscale privacy image encryption with chaos logistics maps and Arnold Cat. Evol. Syst. 2023, 14, 993–1023. [Google Scholar] [CrossRef]
- Cavlak, Y.; Ateş, A.; Abualigah, L.; Elaziz, M.A. Correction to: Fractional-order chaotic oscillator-based Aquila optimization algorithm for maximization of the chaotic with Lorentz oscillator. Neural Comput. Appl. 2024, 36, 10–45. [Google Scholar] [CrossRef]
- Bouarroudj, N.; Houam, Y.; Djari, A.; Feliu-Batlle, V.; Lakhdari, A.; Benlahbib, B. A Linear Quadratic Integral Controller for PV-Module Voltage Regulation for the Purpose of Enhancing the Classical Incremental Conductance Algorithm. Energies 2023, 16, 4532. [Google Scholar] [CrossRef]
- Kuptsov, P.V.; Ishbulatov, Y.M.; Karavaev, A.S.; Stankevich, N.V. Verification of Chaos in a Human Cardiovascular System Model. Regul. Chaotic Dyn. 2025, 30, 291–305. [Google Scholar] [CrossRef]
- Carlos, L.; Lambruschini, P.; Rider, J.R.; Guillermo, H.C. Dynamics near the edge-of-chaos in a fiber laser model. Phys. Lett. A 2023, 481, 128995. [Google Scholar]
- Berezowski, M.; Grabski, A. Chaotic and non-chaotic mixed oscillations in a logistic system with delay and heat-integrated tubular chemical reactor. Chaos Solitons Fractals 2002, 14, 97–103. [Google Scholar] [CrossRef]
- Li, A.; Yao, Y.; Tang, X.; Liu, P.; Zhang, Q.; Li, Q.; Li, P.; Zhang, F.; Wang, Y.; Tao, C.; et al. Experimental and computational investigation of chaotic advection mixing in laminar rectangular stirred tanks. Chem. Eng. J. 2024, 485, 149956. [Google Scholar] [CrossRef]
- Yadav, V.K.; Das, S.; Bhadauria, B.S.; Singh, A.K.; Srivastava, M. Stability analysis, chaos control of a fractional order chaotic chemical reactor system and its function projective synchronization with parametric uncertainties. Chin. J. Phys. 2017, 55, 594–605. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag–Leffler stability of frac- tional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Ding, D.; Qi, D.; Wang, Q. Non-linear Mittag–Leffler stabilisation of commensurate fractional-order non-linear systems. IET Control Theory Appl. 2015, 9, 681–690. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Stabilization of a class of fractional order chaotic systems via backstepping approach. Chaos Solitons Fractals 2017, 98, 56–62. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Stabilization of Unstable Fixed Points of Chaotic Fractional Order Systems by a State Fractional PI Controller. Eur. J. Control 2008, 14, 247–257. [Google Scholar] [CrossRef]
- Wu, J.; Xie, H.; Li, T.; He, W.; Xi, T.; Liang, X. Design of a Finite-Time Bounded Tracking Controller for Time-Delay Fractional-Order Systems Based on Output Feedback. Mathematics 2025, 13, 200. [Google Scholar] [CrossRef]
- Aghababa, M.P. Design of a chatter-free terminal sliding mode controller for nonlinear fractional-order dynamical systems. Int. J. Control 2013, 86, 1744–1756. [Google Scholar] [CrossRef]
- Xu, X.; Lee, S.-D.; Kim, H.-S.; You, S.-S. Management and optimisation of chaotic supply chain system using adaptive sliding mode control algorithm. Int. J. Prod. Res. 2021, 59, 2571–2587. [Google Scholar] [CrossRef]
- Megherbi, O.; Hamiche, H.; Bettayeb, M. Implementation of a wireless text data transmission based on the impulsive control of fractional-order chaotic systems. Comput. Electr. Eng. 2024, 116, 109224. [Google Scholar] [CrossRef]
- Djeddi, A.; Dib, D.; Azar, A.T.; Abdelmalek, S. Fractional order unknown inputs fuzzy observer for TS systems. Mathematics 2019, 7, 984. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Huang, X. Exponential Stabilization of Delayed Chaotic Memristive Neural Networks Via Aperiodically Intermittent Control. Int. J. Bifurc. Chaos 2020, 30, 2050029. [Google Scholar] [CrossRef]
- Dalir, M.; Bigdeli, N. An Adaptive neuro-fuzzy backstepping sliding mode controller for finite time stabilization of fractional-order uncertain chaotic systems with time-varying delays. Int. J. Mach. Learn. Cybern. 2021, 12, 1949–1971. [Google Scholar] [CrossRef]
- Chen, T.; Yang, H.; Yuan, J. Event-Triggered Adaptive Neural Network Backstepping Sliding Mode Control for Fractional Order Chaotic Systems Synchronization With Input Delay. IEEE Access 2021, 9, 100868–100881. [Google Scholar] [CrossRef]
- Li, F.; Luo, S.; Yang, G.; Ouakad, H.M. Dynamical analysis and accelerated adaptive backstepping funnel control for dual-mass MEMS gyroscope under event trigger. Chaos Solitons Fractals 2023, 168, 113116. [Google Scholar] [CrossRef]
- Adeleh, A.J.; Seyed, M.A.; Mohsen, H.N. Adaptive type-2 fuzzy backstepping control of uncertain fractional-order nonlinear systems with unknown dead-zone. Appl. Math. Model. 2019, 69, 506–532. [Google Scholar] [CrossRef]
- Luo, R.; Liu, S.; Song, Z.; Zhang, F. Fixed-time control of a class of fractional-order chaotic systems via backstepping method. Chaos Solitons Fractals 2023, 167, 113076. [Google Scholar] [CrossRef]
- Aib, Y.; Feng, Z.; Wang, H. Fixed-Time Adaptive Fuzzy Anti-Synchronization Control of Hyperchaotic Rössler System Based on Backstepping Method. Int. J. Fuzzy Syst. 2023, 25, 2501–2513. [Google Scholar]
- Sun, J.; Shan, Z.; Liu, P.; Wang, Y. Backstepping Synchronization Control for Three-Dimensional Chaotic Oscillatory System via DNA Strand Displacement. IEEE Trans. Nanobiosci. 2023, 22, 511–522. [Google Scholar] [CrossRef]
- Sahin, A.K.; Cavdar, B.; Ayas, M.S. An adaptive fractional controller design for automatic voltage regulator system: Sigmoid-based fractional-order PID controller. Neural Comput. Appl. 2024, 36, 14409–14431. [Google Scholar] [CrossRef]
- Suid, M.H.; Ahmad, M.A. Optimal tuning of sigmoid PID controller using Nonlinear Sine Cosine Algorithm for the Automatic Voltage Regulator system. ISA Trans. 2022, 128, 265–286. [Google Scholar] [CrossRef] [PubMed]
- Safari, A.; Sorouri, H.; Oshnoei, A. The Regulation of Superconducting Magnetic Energy Storages with a Neural-Tuned Fractional Order PID Controller Based on Brain Emotional Learning. Fractals Fract. 2024, 8, 365. [Google Scholar] [CrossRef]
- Ghazali, M.R.B.; Ahmad, M.A.B.; Raja Ismail, R.M.T.B. Adaptive safe experimentation dynamics for data-driven neuroendocrine-PID control of MIMO systems. IETE J. Res. 2022, 68, 1611–1624. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, H.H. Neural Network-Based Adaptive Fractional-Order Backstepping Control of Uncertain Quadrotors with Unknown Input Delays. Fractals Fract. 2023, 7, 232. [Google Scholar] [CrossRef]
- Zirkohi, M.M. Robust adaptive backstepping control of uncertain fractional-order nonlinear systems with input time delay. Math. Comput. Simul. 2022, 196, 251–272. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Zou, Y. Adaptive Backstepping Control for Fractional-Order Nonlinear Systems with External Disturbance and Uncertain Parameters Using Smooth Control. IEEE Trans. Syst. Man, Cybern. 2021, 51, 7860–7869. [Google Scholar] [CrossRef]
- Bigdeli, N.; Ziazi, H.A. Finite-time fractional-order adaptive intelligent backstepping sliding mode control of uncertain fractional-order chaotic systems. J. Frankl. Inst. 2017, 354, 160–183. [Google Scholar] [CrossRef]
- Ekinci, S.; Izci, D.; Turkeri, C.; Ahmad, M.A. Spider Wasp Optimizer-Optimized Cascaded Fractional-Order Controller for Load Frequency Control in a Photovoltaic-Integrated Two-Area System. Mathematics 2024, 12, 3076. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Kozyra, J.; Kutsyk, A.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kasha, L.; Lishchuk, A. AVR Fractional-Order Controller Based on Caputo–Fabrizio Fractional Derivatives and Integral Operators. Energies 2024, 17, 5913. [Google Scholar] [CrossRef]
- Paducel, I.; Safirescu, C.O.; Dulf, E.-H. Fractional Order Controller Design for Wind Turbines. Appl. Sci. 2022, 12, 8400. [Google Scholar] [CrossRef]
- Djari, A.; Bouden, T.; Vinagre, B.M. Design of Fractional-order Sliding Mode Controller (FSMC) for a class of Fractional-order Non-linear Commensurate Systems using a Particle Swarm Optimization (PSO) Algorithm. J. Control Eng. Appl. Inform. 2014, 16, 46–55. [Google Scholar]
- Djari, A.; Bouden, T.; Vinagre, B.M. Optimal Fractional-order Sliding Mode Controller (OFSMC) Design for a class of Fractional-order Nonlinear SIMO Systems using PSO Algorithm. J. Control Eng. Appl. Inform. 2016, 18, 14–25. [Google Scholar]
- Fu, D.-X.; Feng, Y.-Y.; Zhu, Z.-W.; Hou, M.-M.; Wang, J. Boundary Feedback Control of a Cascade System of Fractional PDE-ODEs. Fractal Fract. 2025, 9, 514. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. Learning Control: Applications in Robotics and Complex Dynamical Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 93–102. [Google Scholar]
- Rashidnejad, Z.; Karimaghaee, P. Synchronization of a class of uncertain chaotic systems utilizing a new finite-time fractional adaptive sliding mode control. Chaos Solitons Fractals 2020, 5, 100042. [Google Scholar] [CrossRef]
- Mohammadpour, S.; Binazadeh, T. Robust finite-time synchronization of uncertain chaotic systems: Application on Duffing-Holmes system and chaos gyros. Syst. Sci. Control Eng. 2018, 6, 28–36. [Google Scholar] [CrossRef]
- Sun, Z.; Xue, Q.; Zhao, N. Chimera states in fractional-order coupled Rayleigh oscillators. Commun. Nonlinear Sci. Numer. Simul. 2024, 135, 108083. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).