Command-Filter-Based Velocity-Free Tracking Control of an Electrohydraulic System with Adaptive Disturbance Compensation
Abstract
1. Introduction
- (1)
- This paper proposes a command-filter-based velocity-free tracking controller for electrohydraulic servo systems without a velocity sensor. The controller employs cascaded observers to estimate the unmeasured velocity state and compensate for both matched and mismatched disturbances. Command filters streamline the design process, while filtering error compensation terms prevent filter error accumulation from cascaded implementations.
- (2)
- Compared to the LESO utilized in [11,12,13,14,15,16,17,18] and the AESO employed in [18,19,20], this paper constructs a cascaded-AESO framework based on a smooth nonlinear function. This framework enables simultaneous estimation of unknown system state and disturbances while avoiding observation peaking and discontinuities from abrupt gain variations, thus preventing potential system instability.
2. Nonlinear Model of Electrohydraulic Servo Systems
3. Command-Filter-Based Velocity-Free Tracking Controller Design
3.1. Model Analysis and Issues to Be Addressed
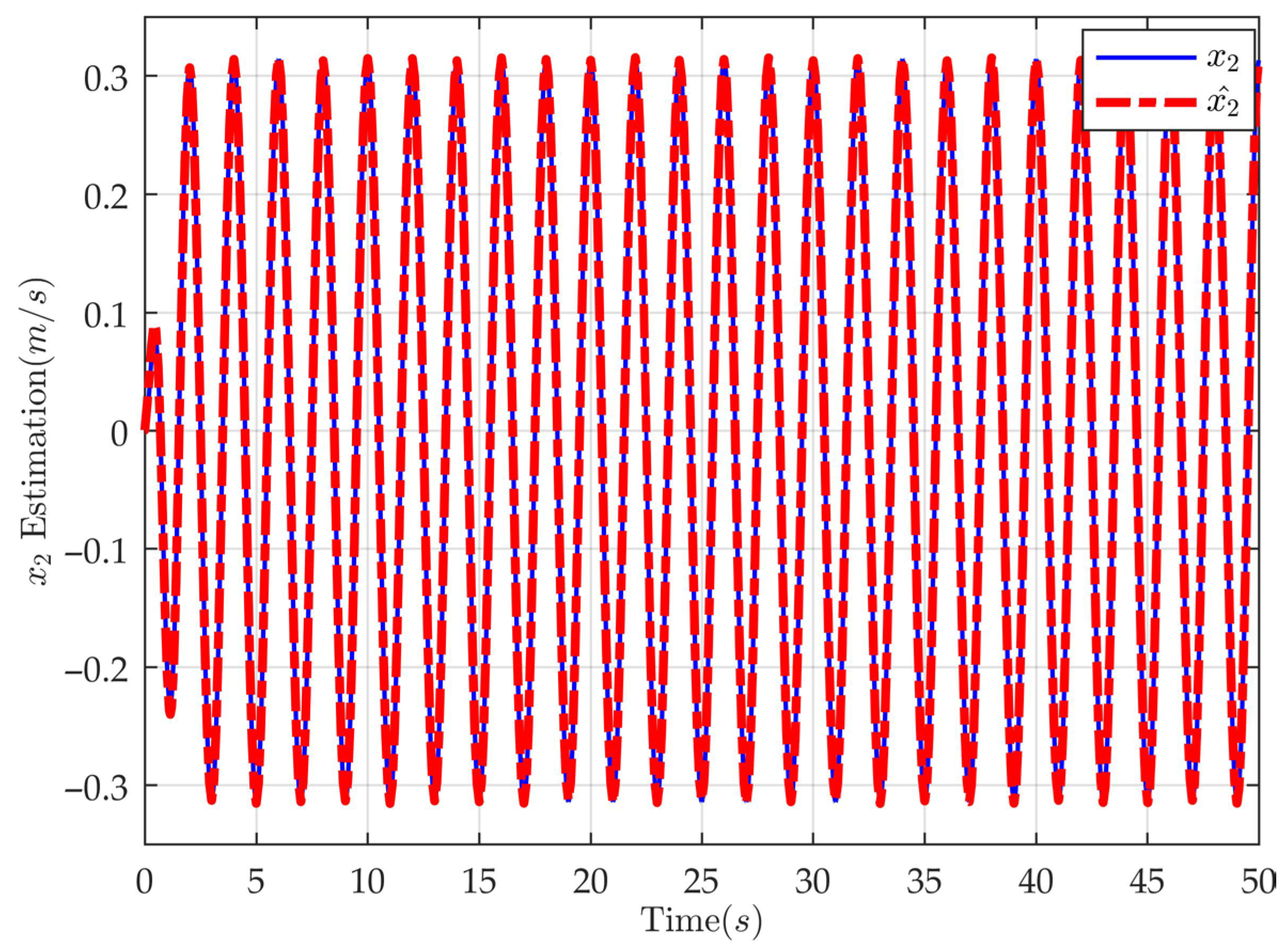
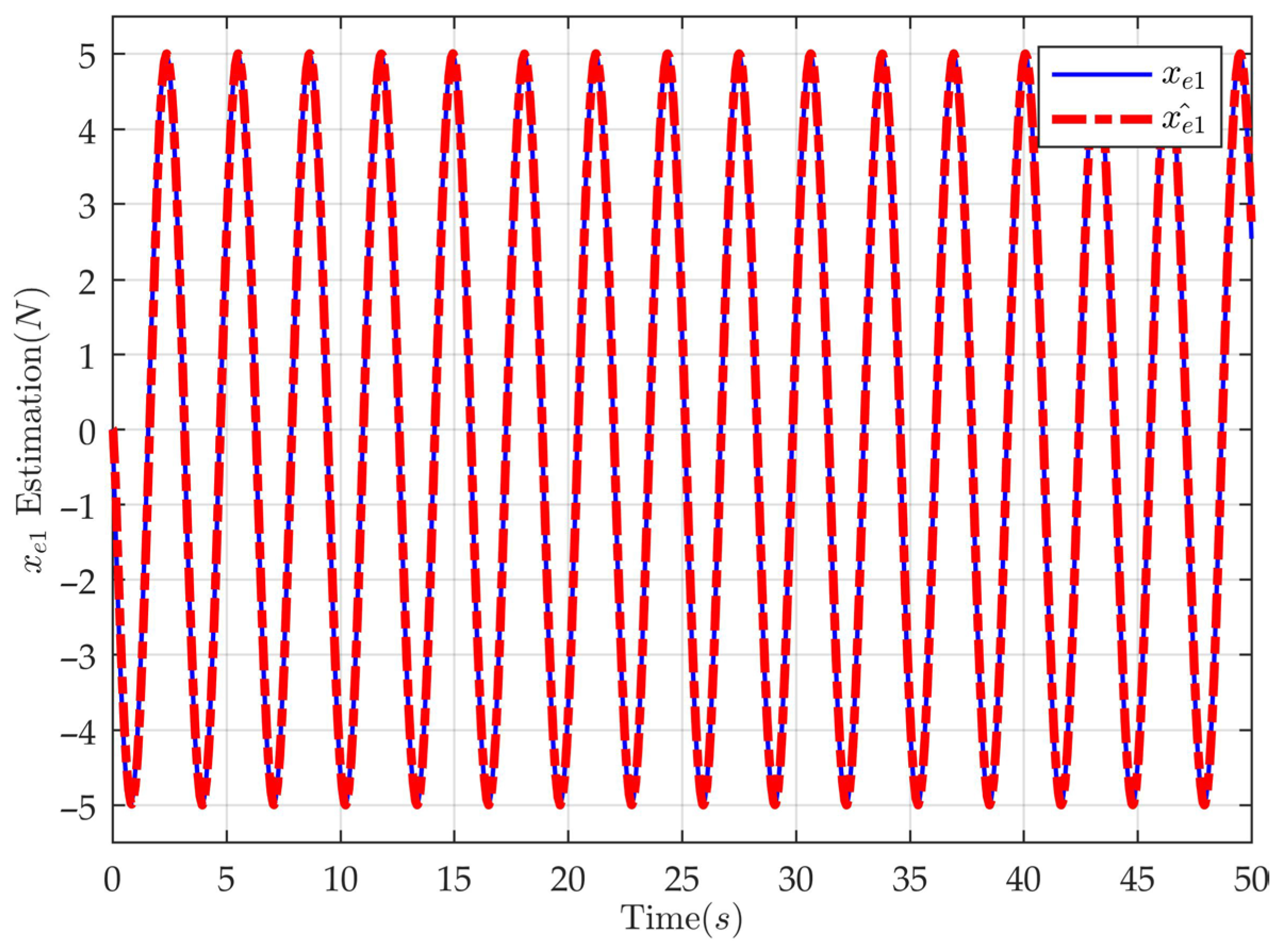
3.2. Cascaded AESO Design
3.3. Controller Design
3.4. Main Result and Stability Analysis
- (1)
- The proposed controller guarantees bounded tracking error in the electrohydraulic servo system and bounded estimation error in the cascaded AESO.
- (2)
- The proposed controller ensures boundedness of all closed-loop signals.
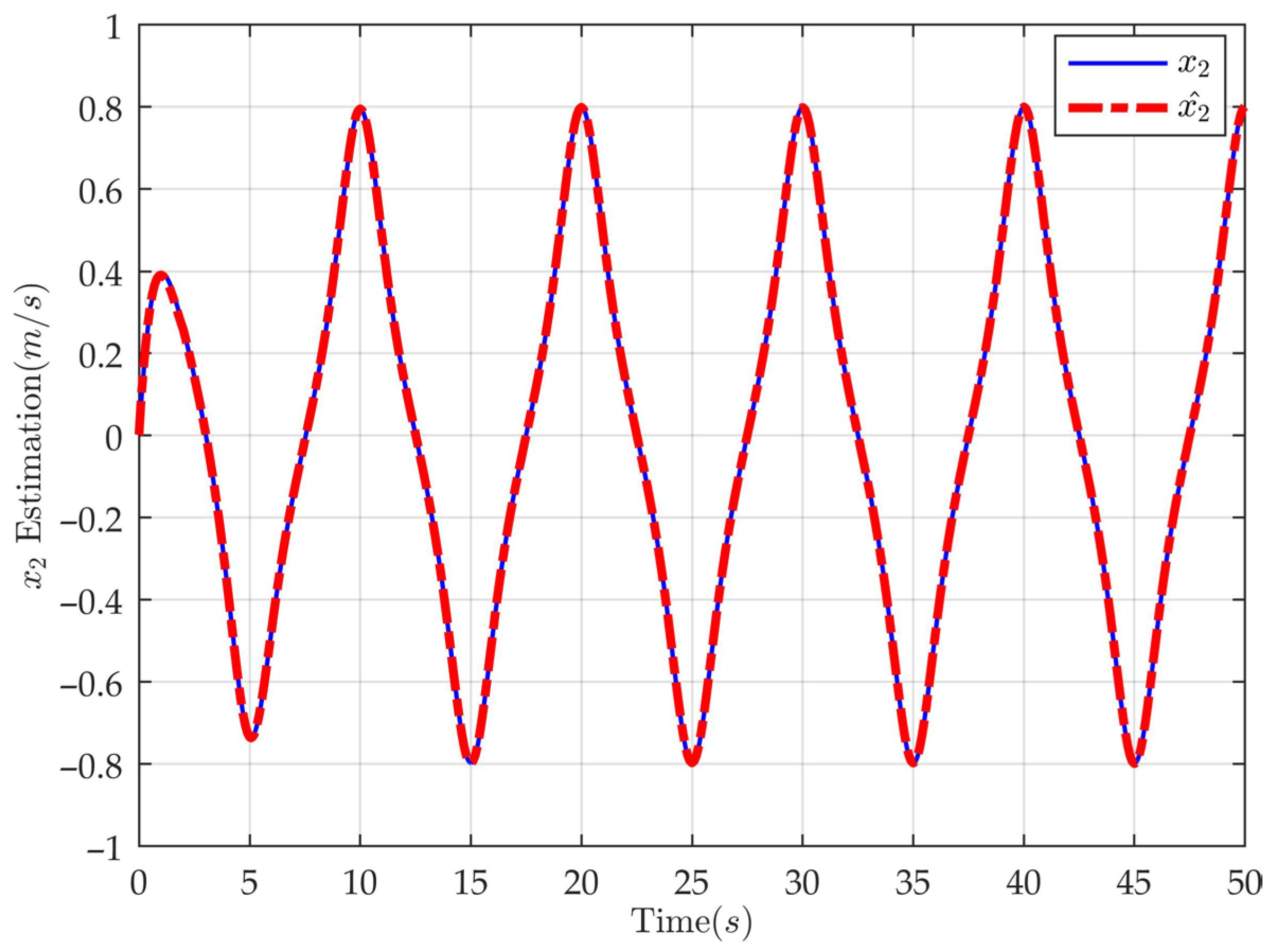
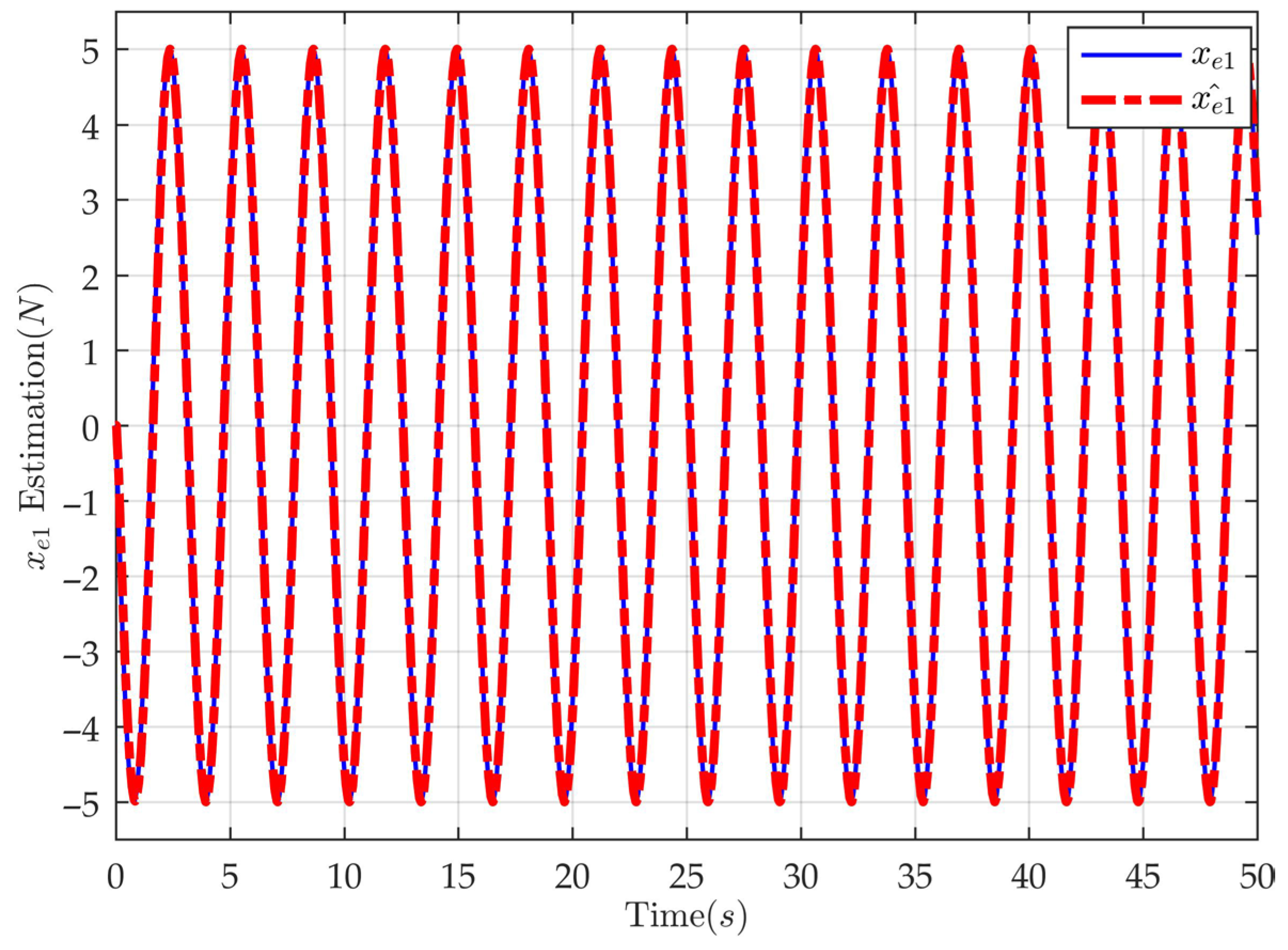
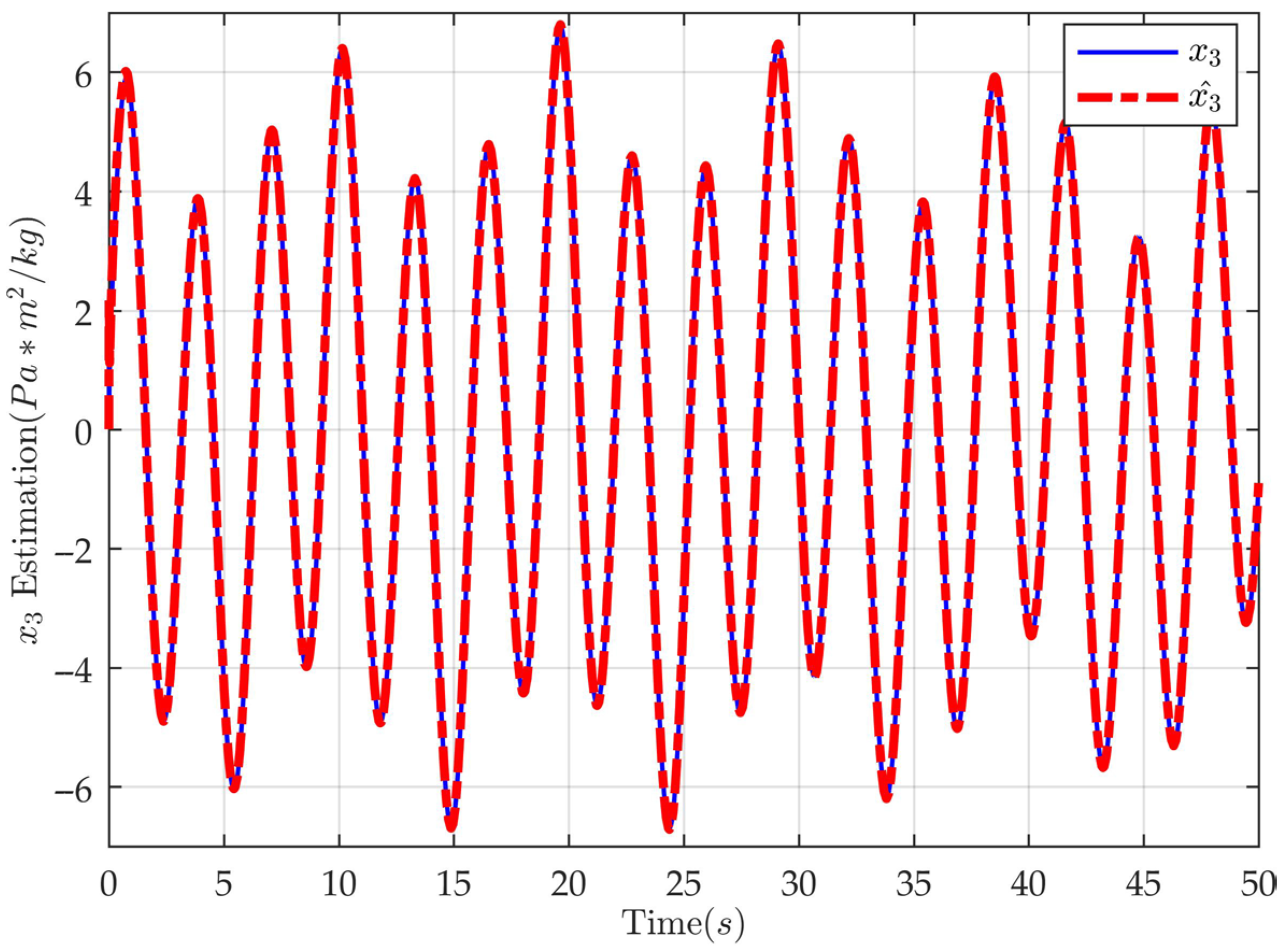
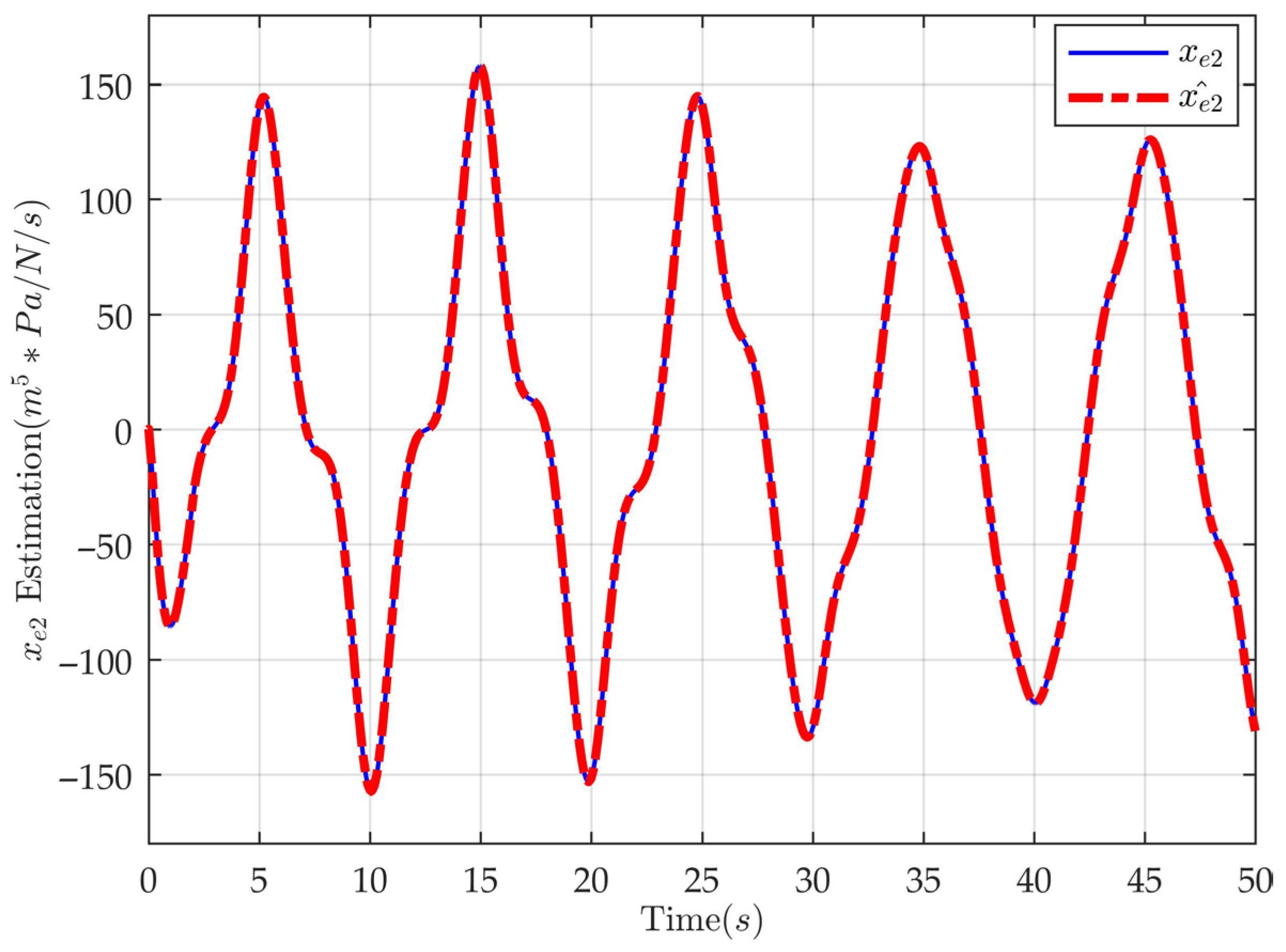
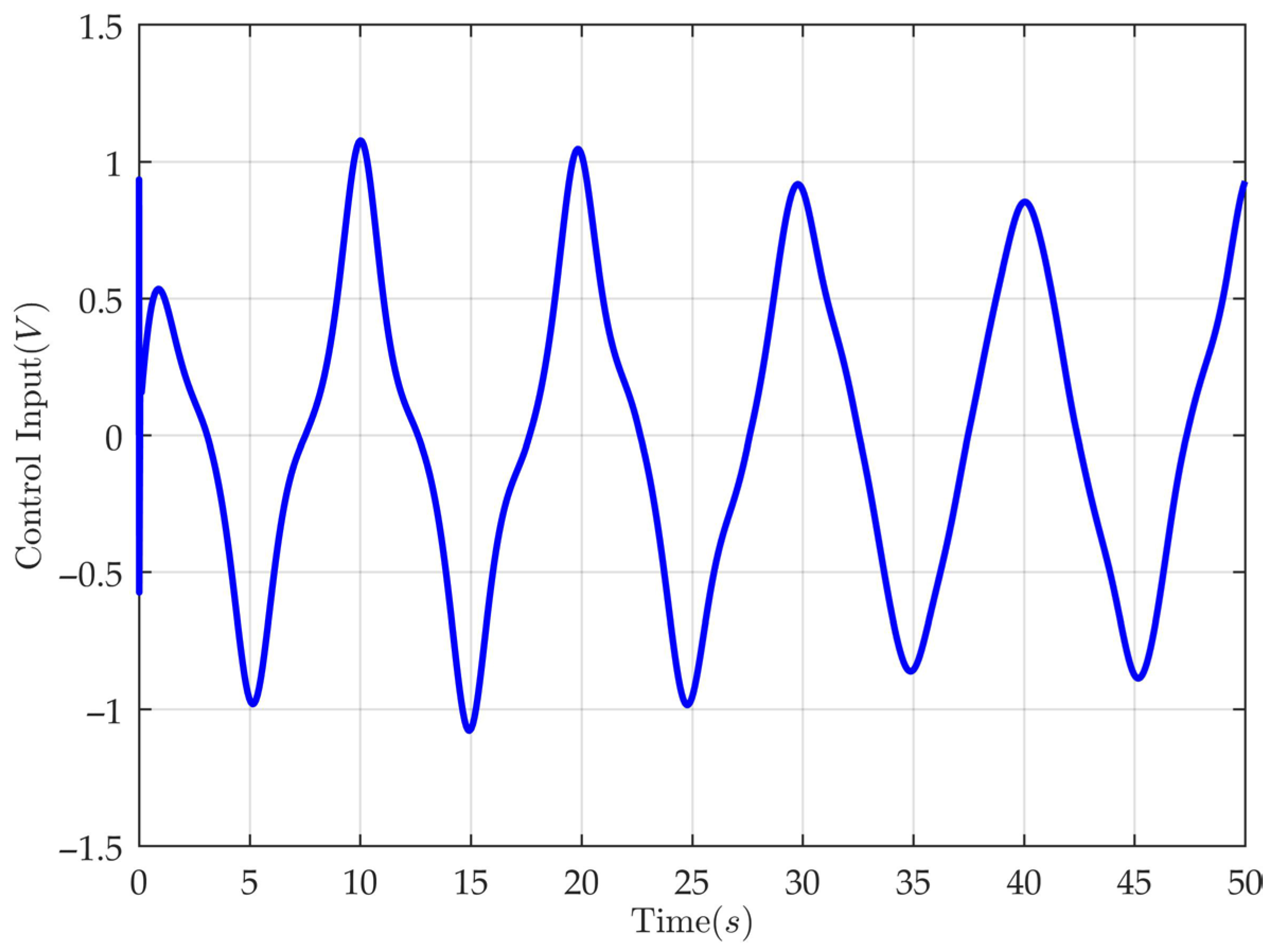
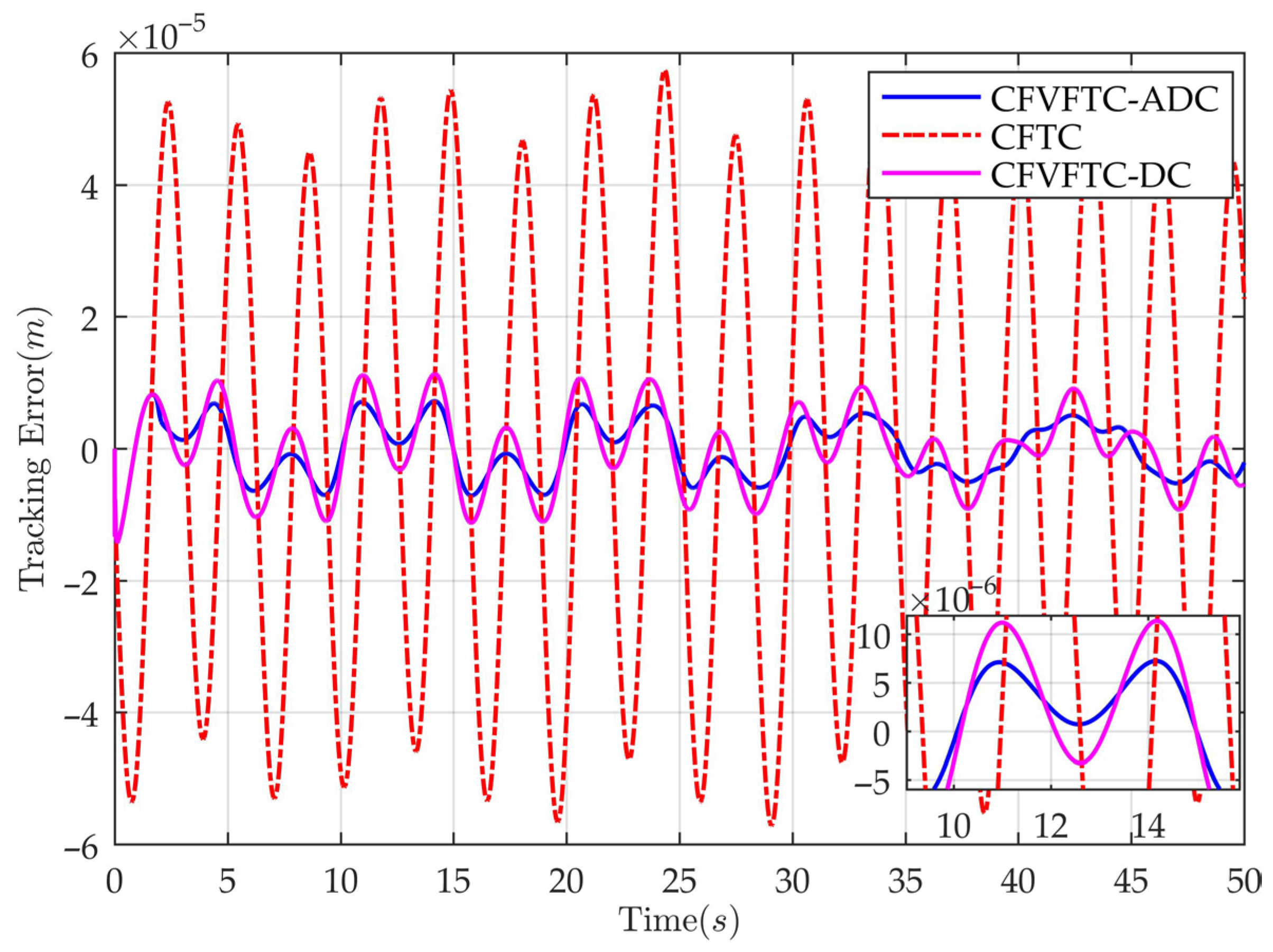
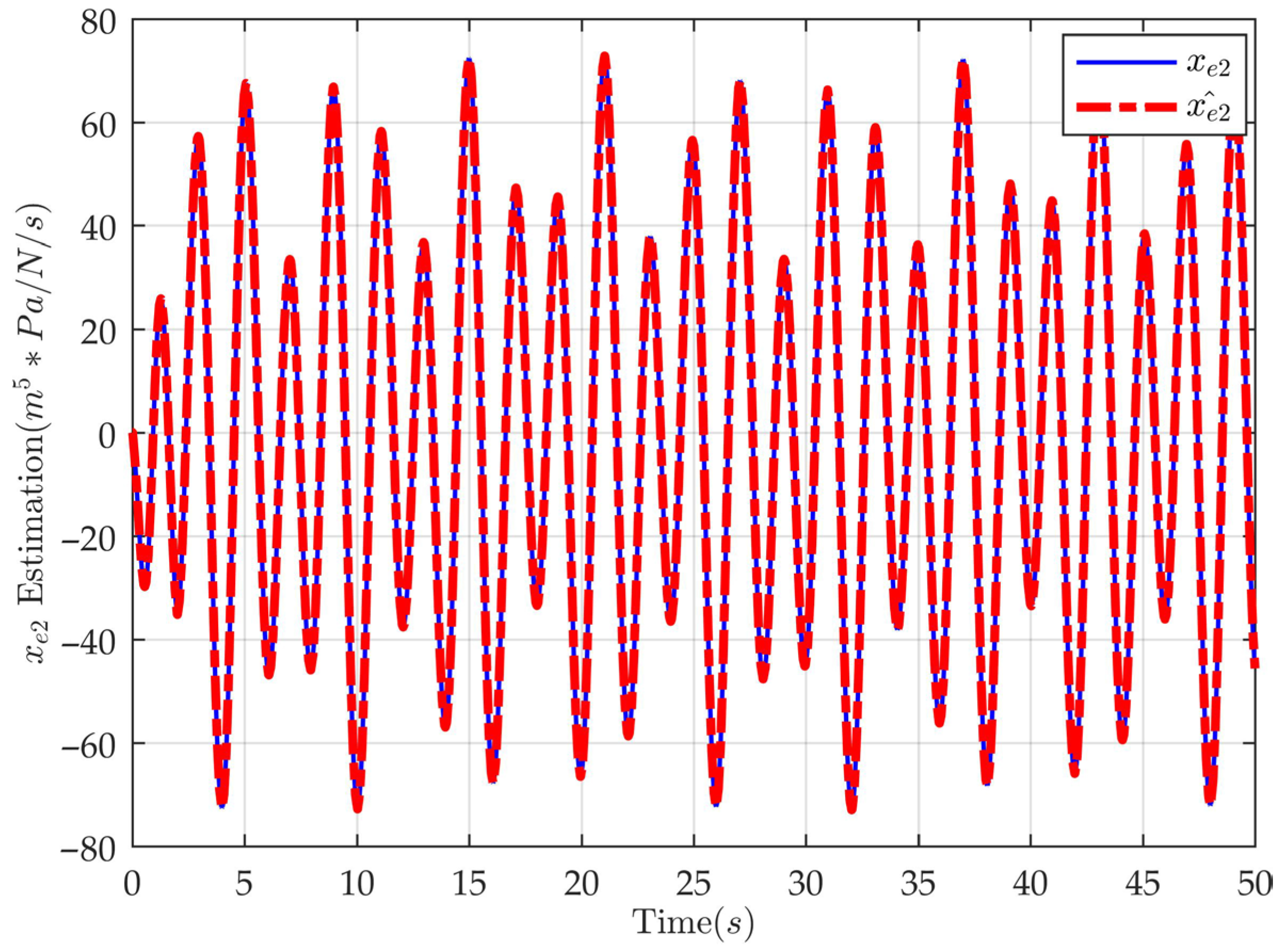
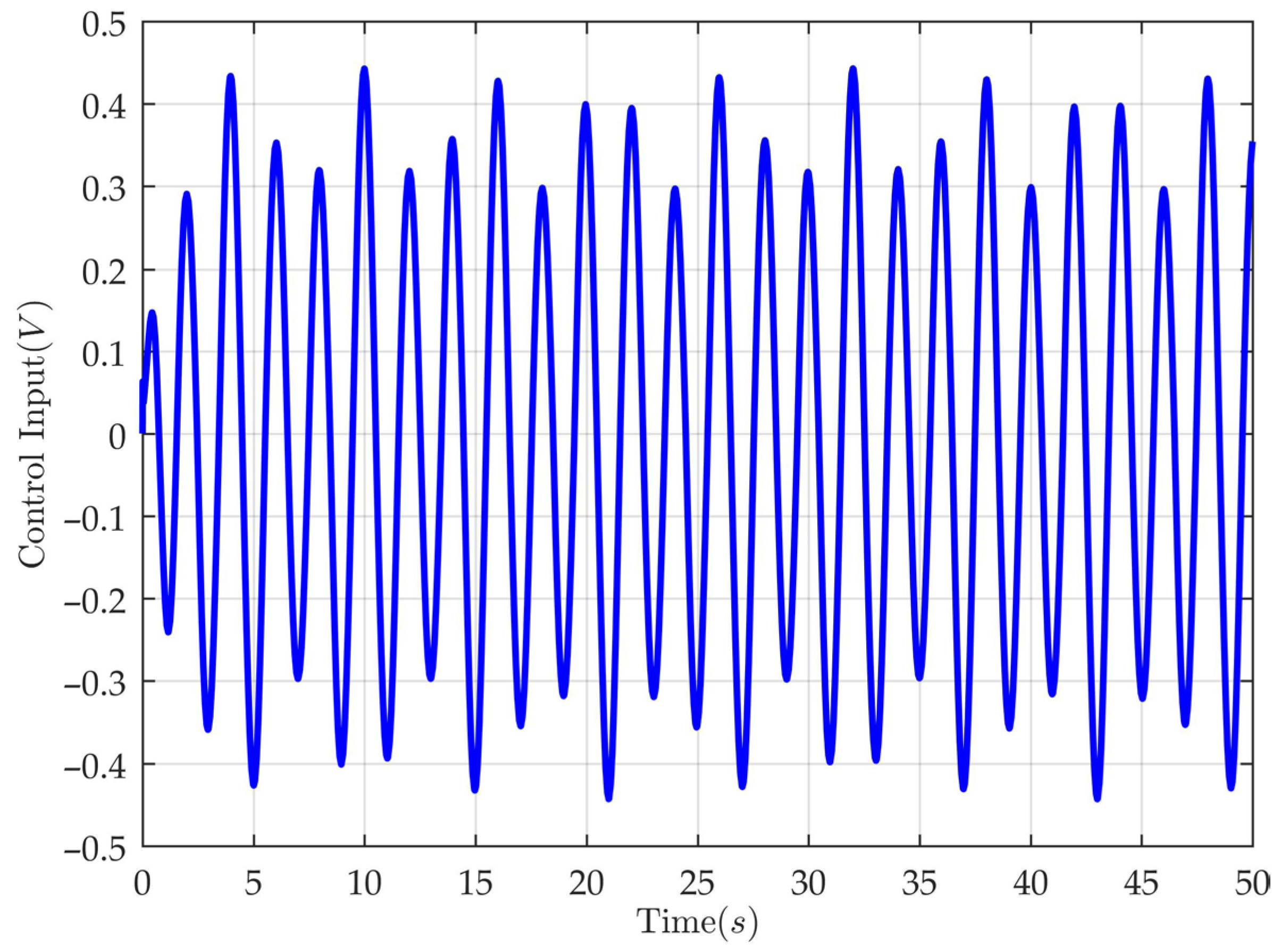
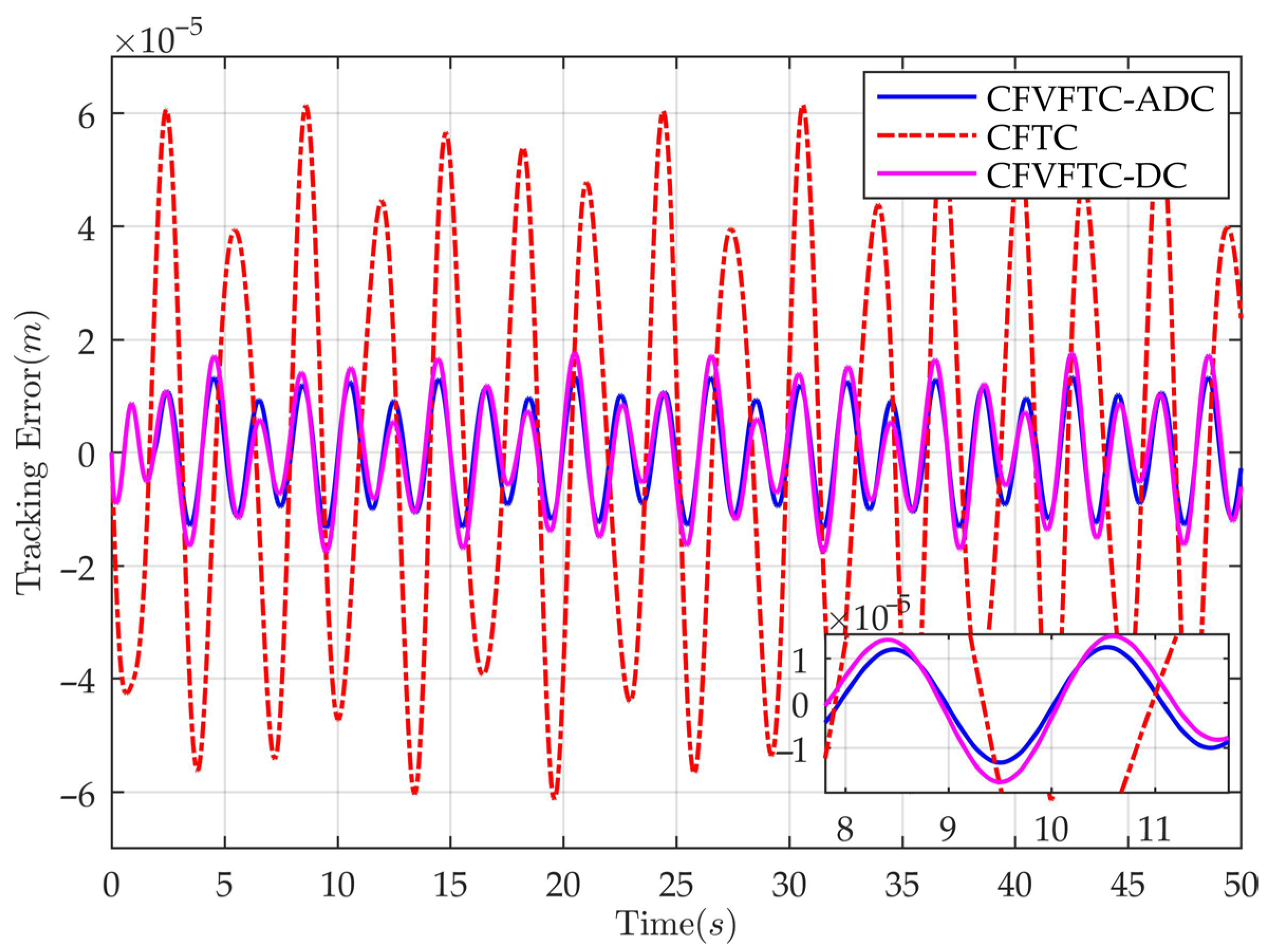
4. Simulation and Comparative Analysis
- (1)
- CFVFTC-ADC (Command-filter-based velocity-free tracking controller with adaptive disturbance compensation): The proposed controller has its parameters set as follows: , , , , , and .
- (2)
- CFTC (Command-filter-based tracking controller): Compared with the proposed controller, this controller differs by numerically obtaining the system velocity state while lacking disturbance compensation capability. For fair comparison, controller parameter settings are maintained identically to those of CFVFTC-ADC.
- (3)
- CFVFTC-DC (Command-filter-based velocity-free tracking controller with disturbance compensation): In contrast to the proposed controller, this controller utilizes a conventional LESO for disturbance and state estimation. For a fair comparison, all controller parameters except the observer gains remain consistent with those of the CFVFTC-ADC. The LESO parameters are set as follows: , .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Patre, P.M.; MacKunis, W.; Dupree, K.; Dixon, W.E. Modular Adaptive Control of Uncertain Euler–Lagrange Systems with Additive Disturbances. IEEE Trans. Automat. Contr. 2011, 56, 155–160. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Deng, W.; Yao, J. Precision Motion Control for Electro-Hydraulic Axis Systems under Unknown Time-Variant Parameters and Disturbances. Chin. J. Aeronaut. 2024, 37, 463–471. [Google Scholar] [CrossRef]
- Sun, W.; Pan, H.; Gao, H. Filter-Based Adaptive Vibration Control for Active Vehicle Suspensions with Electrohydraulic Actuators. IEEE Trans. Veh. Technol. 2016, 65, 4619–4626. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Tomizuka, M. High-Gain-Observer-Based Integral Sliding Mode Control for Position Tracking of Electrohydraulic Servo Systems. IEEE/ASME Trans. Mechatron. 2017, 22, 2695–2704. [Google Scholar] [CrossRef]
- Pan, H.; Sun, W. Nonlinear Output Feedback Finite-Time Control for Vehicle Active Suspension Systems. IEEE Trans. Ind. Inf. 2019, 15, 2073–2082. [Google Scholar] [CrossRef]
- Ahn, K.K.; Nam, D.N.C.; Jin, M. Adaptive Backstepping Control of an Electrohydraulic Actuator. IEEE/ASME Trans. Mechatron. 2014, 19, 987–995. [Google Scholar] [CrossRef]
- Kaddissi, C.; Kenné, J.-P.; Saad, M. Indirect Adaptive Control of an Electrohydraulic Servo System Based on Nonlinear Backstepping. IEEE/ASME Trans. Mechatron. 2011, 16, 1171–1177. [Google Scholar] [CrossRef]
- Sun, W.; Gao, H.; Yao, B. Adaptive Robust Vibration Control of Full-Car Active Suspensions with Electrohydraulic Actuators. IEEE Trans. Contr. Syst. Technol. 2013, 21, 2417–2422. [Google Scholar] [CrossRef]
- Li, X.; Xia, H. A New Extended State Observer with Low Sensitivity to High Frequency Noise and Low Gain Power. IFAC-PapersOnLine 2020, 53, 4929–4934. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W. Active Disturbance Rejection Adaptive Control of Hydraulic Servo Systems. IEEE Trans. Ind. Electron. 2017, 64, 8023–8032. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S.; Yu, X. Composite Super-Twisting Sliding Mode Control Design for PMSM Speed Regulation Problem Based on a Novel Disturbance Observer. IEEE Trans. Energy Convers. 2021, 36, 2591–2599. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhang, O.; Zhao, Y.; Chen, W.; Gao, Y. Adaptive Disturbance Observer-Based Fixed-Time Tracking Control for Uncertain Robotic Systems. IEEE Trans. Ind. Electron. 2024, 71, 14823–14831. [Google Scholar] [CrossRef]
- Chen, J.; Shuai, Z.; Zhang, H.; Zhao, W. Path Following Control of Autonomous Four-Wheel-Independent-Drive Electric Vehicles via Second-Order Sliding Mode and Nonlinear Disturbance Observer Techniques. IEEE Trans. Ind. Electron. 2021, 68, 2460–2469. [Google Scholar] [CrossRef]
- Lakomy, K.; Madonski, R.; Dai, B.; Yang, J.; Kicki, P.; Ansari, M.; Li, S. Active Disturbance Rejection Control Design with Suppression of Sensor Noise Effects in Application to DC–DC Buck Power Converter. IEEE Trans. Ind. Electron. 2022, 69, 816–824. [Google Scholar] [CrossRef]
- Ma, Z.; Xiao, Y.; Wang, P.; Zhao, Y. Linear-Extended-State-Observer Based Pinning Control of Nonlinear Multi-Robots System. IEEE Access 2020, 8, 144522–144528. [Google Scholar] [CrossRef]
- Wang, C.; Quan, L.; Jiao, Z.; Zhang, S. Nonlinear Adaptive Control of Hydraulic System with Observing and Compensating Mismatching Uncertainties. IEEE Trans. Contr. Syst. Technol. 2018, 26, 927–938. [Google Scholar] [CrossRef]
- Pu, Z.; Yuan, R.; Yi, J.; Tan, X. A Class of Adaptive Extended State Observers for Nonlinear Disturbed Systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Zhao, L.; Cheng, H.; Xia, Y.; Liu, B. Angle Tracking Adaptive Backstepping Control for a Mechanism of Pneumatic Muscle Actuators via an AESO. IEEE Trans. Ind. Electron. 2019, 66, 4566–4576. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, Z.; Yu, X.; Qiu, J.; Rudas, I.J.; Gao, H.; Qu, D. Adaptive Extended State Observer-Based Velocity-Free Servo Tracking Control with Friction Compensation. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2–11. [Google Scholar] [CrossRef]
- Yang, X.; Deng, W.; Yao, J. Neural Adaptive Dynamic Surface Asymptotic Tracking Control of Hydraulic Manipulators with Guaranteed Transient Performance. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7339–7349. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Zhu, W.; Deng, W.; Zhao, X.; Yao, J. Adaptive Motion Control for Electro-Hydraulic Servo Systems with Appointed-Time Performance. IEEE/ASME Trans. Mechatron. 2025. early access. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, J.; Feng, J.; Wang, Z.; Zhuang, G. Command Filter-Based Adaptive Fuzzy Control for Nonlinear Systems with Unknown Control Directions. IEEE Trans. Syst. Man Cybern, Syst. 2019, 51, 1945–1953. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, L.; Yu, H.; Lin, C. Barrier Lyapunov Functions-Based Command Filtered Output Feedback Control for Full-State Constrained Nonlinear Systems. Automatica 2019, 105, 71–79. [Google Scholar] [CrossRef]
- Zheng, X.; Yu, X.; Jiang, J.; Yang, X. Practical Finite-Time Command Filtered Backstepping with Its Application to DC Motor Control Systems. IEEE Trans. Ind. Electron. 2024, 71, 2955–2964. [Google Scholar] [CrossRef]
- Li, M.; Li, S.; Ahn, C.K.; Xiang, Z. Adaptive Fuzzy Event-Triggered Command-Filtered Control for Nonlinear Time-Delay Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 1025–1035. [Google Scholar] [CrossRef]
- Shen, Q.; Shi, P. Distributed Command Filtered Backstepping Consensus Tracking Control of Nonlinear Multiple-Agent Systems in Strict-Feedback Form. Automatica 2015, 53, 120–124. [Google Scholar] [CrossRef]
- Hao, R.; Wang, H.; Liu, S.; Yang, M.; Tian, Z. Multi-Objective Command Filtered Adaptive Control for Nonlinear Hydraulic Active Suspension Systems. Nonlinear Dyn. 2021, 105, 1559–1579. [Google Scholar] [CrossRef]
- Wan, Y.; Yue, W.; Gao, X.; Chen, Q.; Xu, R. Adaptive Finite-Time Prescribed Performance Tracking Control for Hydraulic Servo Systems with Friction Compensation. Neurocomputing 2024, 564, 126967. [Google Scholar] [CrossRef]
- Yang, X.; Deng, W.; Yao, J. Disturbance-Observer-Based Adaptive Command Filtered Control for Uncertain Nonlinear Systems. ISA Trans. 2022, 130, 490–499. [Google Scholar] [CrossRef]
- Xi, R.; Zhang, H.; Liang, Q.; Liu, X. Command Filtered Adaptive Tracking Control for a Class of Random Nonlinear Systems. IEEE Trans. Circuits Syst. II 2023, 70, 2087–2091. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.-G.; Yu, J. Command-Filter-Approximator-Based Adaptive Control for Uncertain Nonlinear Systems and Its Application in PMSMs. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6828–6835. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, H.; Shen, H.; Xu, S.; Park, J.H. Command-Filter-Based Predefined-Time Control for State-Constrained Nonlinear Systems Subject to Preassigned Performance Metrics. IEEE Trans. Automat. Contr. 2024, 69, 7801–7807. [Google Scholar] [CrossRef]
- Merritt, H. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Krstic, M.; Kanellakopoulos, I.; Kokotovic, P. Nonlinear and Adaptive Control Design; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Doostmohammadian, M.; Meskin, N. Finite-Time Stability Under Denial of Service. IEEE Syst. J. 2021, 15, 1048–1055. [Google Scholar] [CrossRef]
- Fortuna, L.; Muscato, G. A Roll Stabilization System for a Monohull Ship: Modeling, Identification, and Adaptive Control. IEEE Trans. Contr. Syst. Technol. 1996, 4, 18–28. [Google Scholar] [CrossRef]
- Longo, D.; Muscato, G.; Nunnari, G. Neural network system identification for a low pressure non-linear dynamical subsystem onboard the alicia II climbing robot. IFAC Proc. Vol. 2003, 36, 369–374. [Google Scholar] [CrossRef]
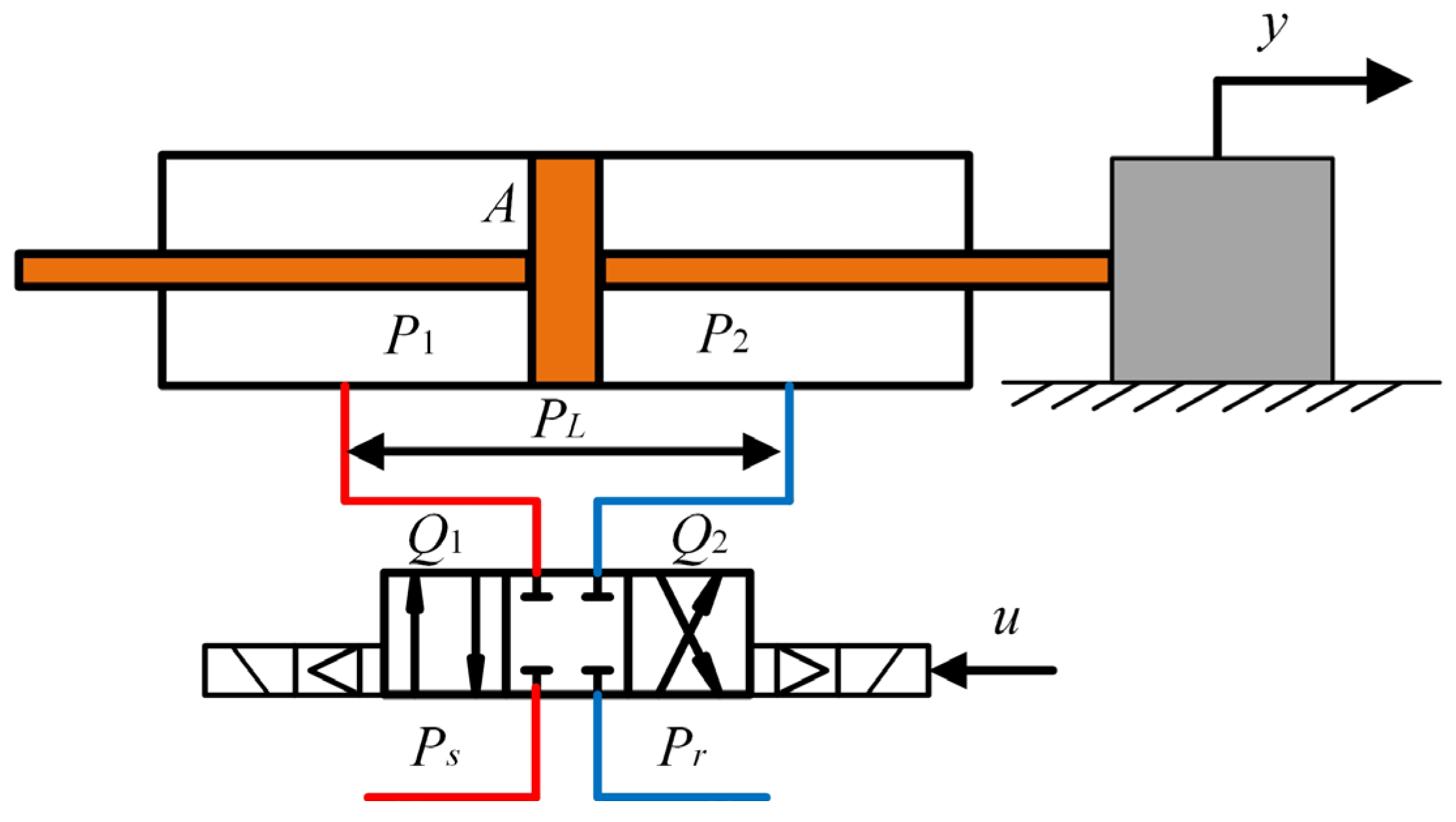
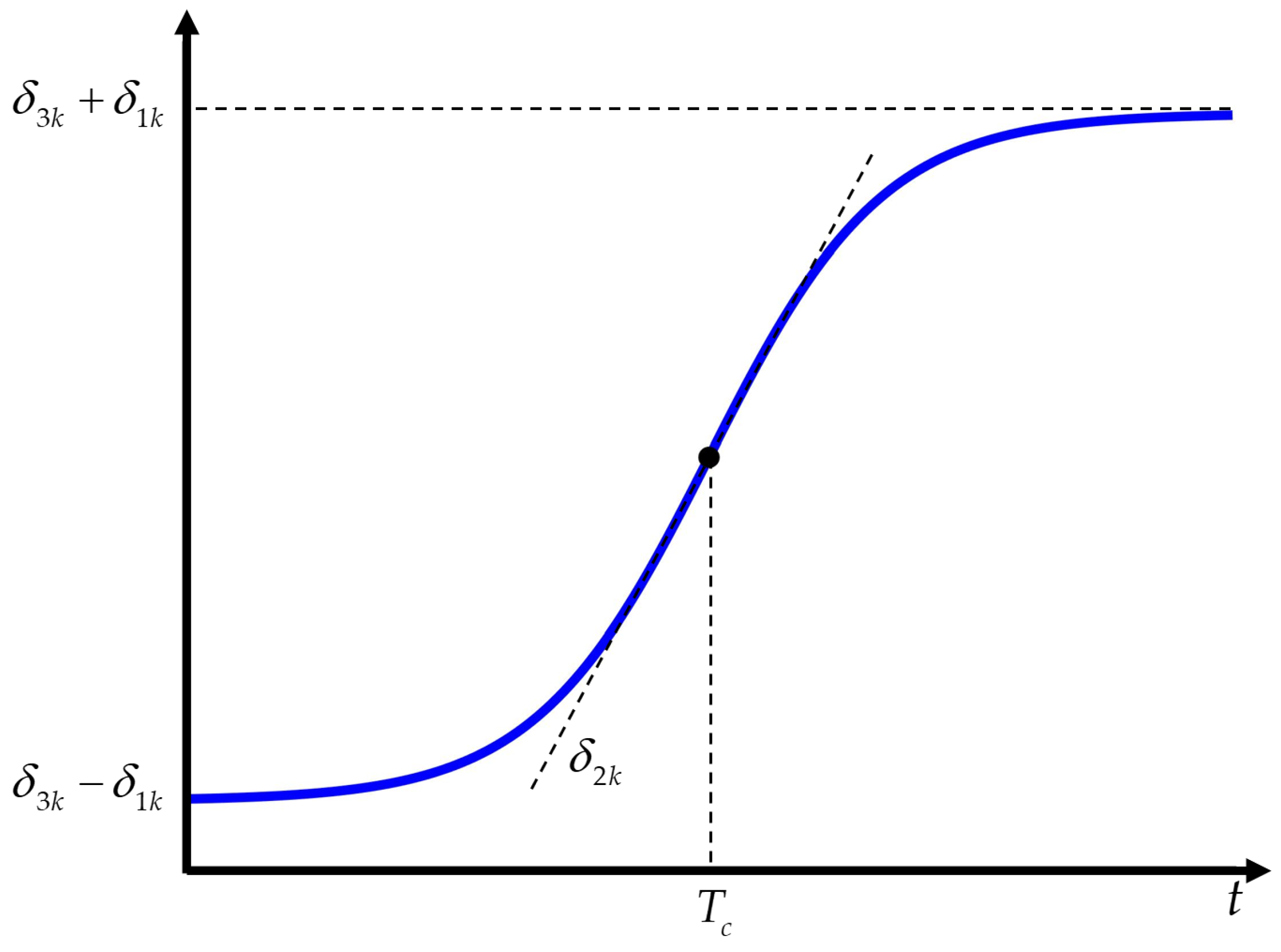
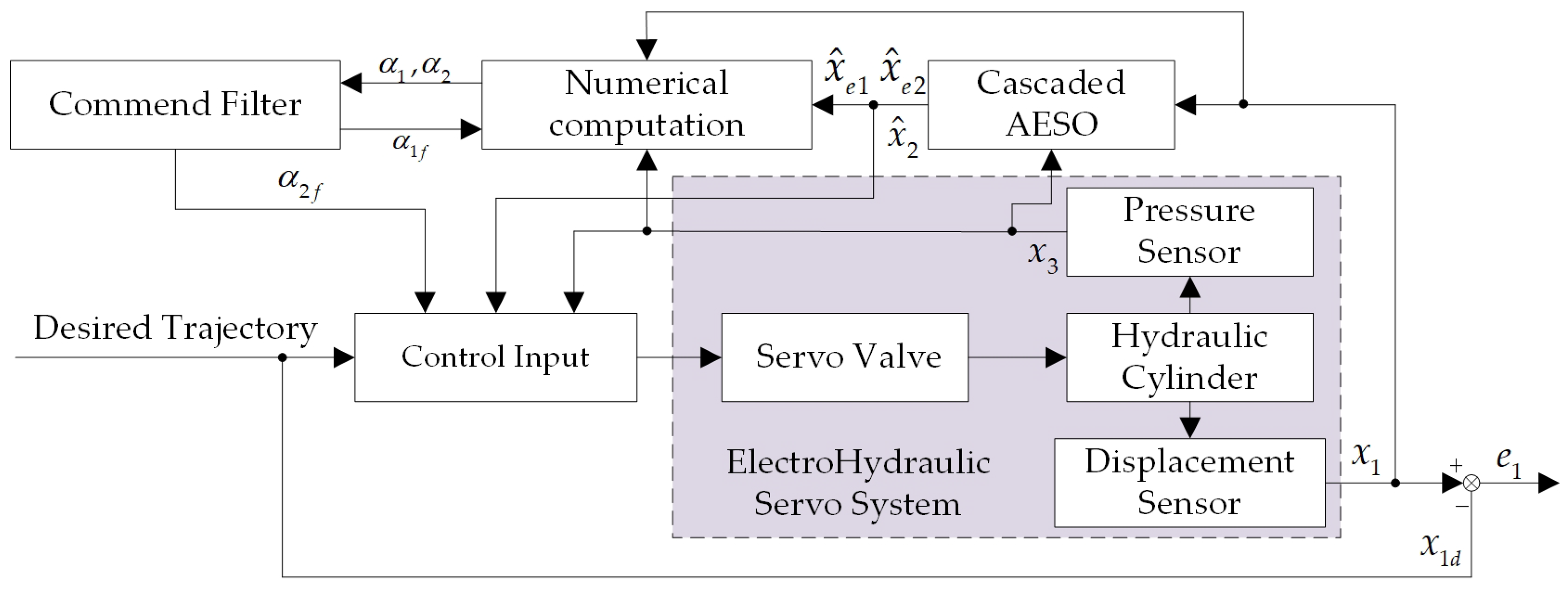
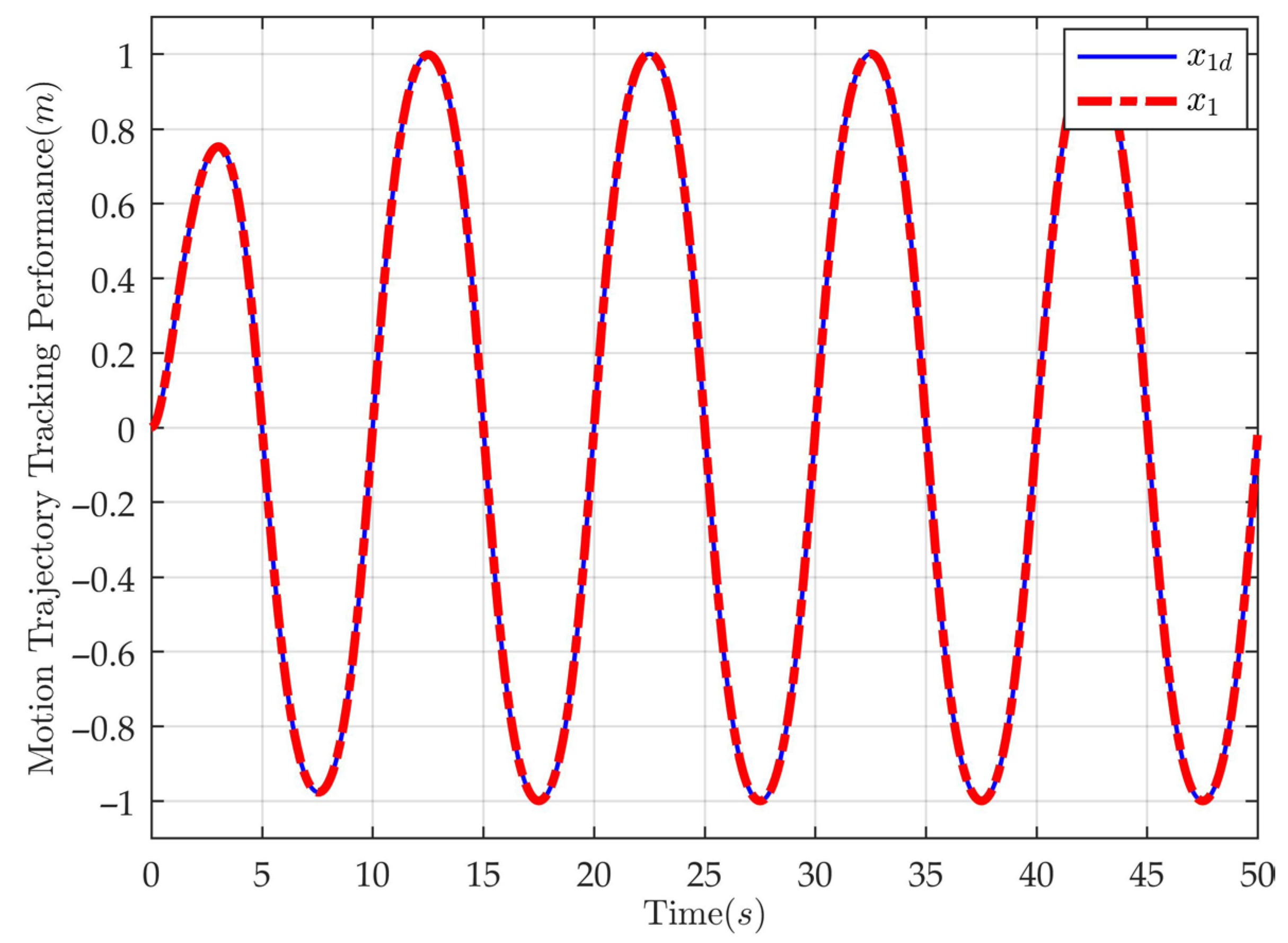



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m (kg) | 40 | Ps (MPa) | 7 |
| Pr (MPa) | 0 | A (m2) | 2 × 10−4 |
| B (N·s/m) | 80 | Vt (m3) | 2 × 10−3 |
| (MPa) | 200 | kt () | 9.25 × 10−8 |
| (m5/(N·s)) | 7 × 10−12 |
| Metrics (m) | |||
|---|---|---|---|
| CFVFTC-ADC | −1.476 × 10−7 | −6.721 × 10−7 | 4.315 × 10−6 |
| CFTC | −2.507 × 10−7 | −4.551 × 10−7 | 3.626 × 10−5 |
| CFVFTC-DC | −1.502 × 10−7 | −2.765 × 10−9 | 5.943 × 10−6 |
| Metrics (m) | |||
|---|---|---|---|
| CFVFTC-ADC | −3.647 × 10−8 | −1.190 × 10−7 | 8.065 × 10−6 |
| CFTC | −1.410 × 10−7 | −4.963 × 10−7 | 3.655 × 10−5 |
| CFVFTC-DC | −3.686 × 10−8 | −1.047 × 10−7 | 9.223 × 10−6 |
| No. | Detailed Description |
|---|---|
| 1 | A novel cascaded AESO structure is developed, enabling simultaneous estimation of the system velocity state along with both matched and mismatched disturbances. |
| 2 | A smooth time-varying function is constructed to formulate the AESO gains, replacing the conventional piecewise function approach. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Yang, X.; Deng, W.; Lu, C.; Yao, J. Command-Filter-Based Velocity-Free Tracking Control of an Electrohydraulic System with Adaptive Disturbance Compensation. Mathematics 2025, 13, 3081. https://doi.org/10.3390/math13193081
Zhao G, Yang X, Deng W, Lu C, Yao J. Command-Filter-Based Velocity-Free Tracking Control of an Electrohydraulic System with Adaptive Disturbance Compensation. Mathematics. 2025; 13(19):3081. https://doi.org/10.3390/math13193081
Chicago/Turabian StyleZhao, Gaoyang, Xiaowei Yang, Wenxiang Deng, Chuanjie Lu, and Jianyong Yao. 2025. "Command-Filter-Based Velocity-Free Tracking Control of an Electrohydraulic System with Adaptive Disturbance Compensation" Mathematics 13, no. 19: 3081. https://doi.org/10.3390/math13193081
APA StyleZhao, G., Yang, X., Deng, W., Lu, C., & Yao, J. (2025). Command-Filter-Based Velocity-Free Tracking Control of an Electrohydraulic System with Adaptive Disturbance Compensation. Mathematics, 13(19), 3081. https://doi.org/10.3390/math13193081







