Abstract
Dynamic path generation in complex transportation networks is essential for intelligent transportation systems. Traditional methods, such as shortest path algorithms or heuristic-based models, often fail to capture real-world travel behaviors due to their reliance on simplified assumptions and limited ability to handle long-range dependencies or non-linear patterns. To address these limitations, we propose PathGen-LLM, a large language model (LLM) designed to learn spatial–temporal patterns from historical paths without requiring handcrafted features or graph-specific architectures. Exploiting the structural similarity between path sequences and natural language, PathGen-LLM converts spatiotemporal trajectories into text-formatted token sequences by encoding node IDs and timestamps. This enables the model to learn global dependencies and semantic relationships through self-supervised pretraining. The model integrates a hierarchical Transformer architecture with dynamic constraint decoding, which synchronizes spatial node transitions with temporal timestamps to ensure physically valid paths in large-scale road networks. Experimental results on real-world urban datasets demonstrate that PathGen-LLM outperforms baseline methods, particularly in long-distance path generation. By bridging sequence modeling and complex network analysis, PathGen-LLM offers a novel framework for intelligent transportation systems, highlighting the potential of LLMs to address challenges in large-scale, real-time network tasks.
Keywords:
complex networks; deep learning; data-driven complex system modeling; path generation; spatiotemporal data MSC:
90B06
1. Introduction
With the acceleration of urbanization, urban spaces continue to expand, and transportation networks exhibit characteristics of large scale, multi-level hierarchy, and complex connectivity. These complex networks give rise to intricate travel behaviors such as long-distance commuting and multi-modal transfers, posing challenges for modeling travel behaviors, particularly in path generation. Travel paths describe how travelers move from origin to destination over time and are represented by an ordered sequence of nodes, links, and timestamps within a transportation network. The goal of path generation is to convert travel demands—origin, destination, and departure time—into specific routes [1]. This process serves as the core component of travel behavior modeling and influences how traffic flow distributes over space and time [2]. Accurate path generation models support various applications: providing personalized navigation that aligns with real behavioral patterns [3], evaluating travel behaviors for transportation planning [4,5], or supplying accurate data for micro-simulations [6]. Consequently, path generation has attracted significant attention from researchers in network science and intelligent transportation domains [7].
Traditional path generation models assume travelers make fully rational decisions, choosing optimal paths based on predefined rules and objectives like distance or time. Representative approaches include graph-theoretical methods like Dijkstra and A* search [8,9], which generate deterministic routes directly from link features within the network. To address dynamic and stochastic traffic conditions, extensions such as the dynamic Dijkstra and stochastic shortest path algorithms have been developed [10,11], incorporating time-varying weights or probability distributions [12]. However, these models often fail to reflect real-world behaviors, especially non-rational aspects like habit dependency and information asymmetry [13]. Additionally, their computational complexity increases exponentially with network size, posing scalability issues for large-scale networks [1,14].
The development of intelligent transportation and big data has enabled the collection of massive real-world trajectory datasets, creating opportunities to develop data-driven path generation models that accurately capture real-world behaviors. Deep learning models, with their ability to handle nonlinear relationships between variables, have been applied to path generation. Existing deep learning-based models fall into two categories: history data-driven and feature-driven models. History data-driven models learn node transition probabilities from historical trajectories using LSTM or RNN but show limited generalization for unseen origin–destination (OD) pairs [15,16]. Feature-driven models combine travel data with network features to model path generation logic [17,18]. They apply to OD pairs not covered by training data but may introduce biases due to manual priors, leading to discrepancies with actual behaviors, especially under dynamically complex traffic scenarios [19].
In recent years, large language models (LLMs) have shown promise in sequence generation and complex relationship modeling, with applications expanding to transportation tasks like travel demand forecasting and trajectory generation [20,21,22]. While the structural isomorphism between path data and natural language—both consisting of discrete elements (nodes/words) arranged in sequences—provides a basic rationale for applying LLMs to transportation, the fundamental alignment extends far beyond mere sequence modeling capabilities. This similarity allows paths to be tokenized into textual sequences encoding node IDs, timestamps, and route logic, enabling LLMs to learn real travel patterns directly from massive historical trajectories without reliance on handcrafted features. The self-attention mechanism in LLMs effectively addresses the critical long-range dependency challenge in path generation, where traditional sequence models suffer from exponential information decay across extended paths. More importantly, when scaled to sufficient parameter scales, LLMs exhibit emergent abilities that enable genuine generalization to unseen OD pairs by extracting and recombining path fragments from global network knowledge, rather than merely memorizing training paths [23]. This capability is essential for practical applications where historical data cannot cover all possible travel scenarios. Additionally, LLMs naturally model both spatial transitions and temporal dynamics as a unified sequence, avoiding the error accumulation inherent in traditional approaches that predict node sequences and timestamps separately. The text-based nature of LLM processing further provides exceptional flexibility for incorporating diverse contextual information—such as real-time traffic updates—without architectural modifications, making the framework readily extensible to increasingly complex urban scenarios. This comprehensive alignment justifies the adoption of full-scale LLMs despite their higher computational costs, particularly for applications requiring high-fidelity path simulations in large-scale networks.
This paper addresses efficiency and authenticity challenges in path generation for complex networks by proposing an end-to-end framework named PathGen-LLM. By creating a “path-to-text” semantic mapping system, it transforms node sequences and timestamps into natural language token sequences. This approach enables the model to capture traveler behavior patterns directly from path data without relying on manually defined features. Using the hierarchical Transformer architecture adapted for complex networks and dynamic constraint decoding mechanisms, the model achieves rapid and precise path generation based on OD pairs and departure times. The main contributions of this study are as follows:
- Leveraging the structural similarity between path data and natural language, we use a “path-to-text” mapping system to apply LLMs’ semantic modeling capabilities to spatiotemporal sequence analysis, constructing a path generation framework for large-scale complex networks.
- PathGen-LLM does not require historical data for specific OD pairs to be present in the training set. Instead, it captures universal travel patterns through self-supervised learning from global path corpora that comprehensively cover the network structure, enabling generalization to unseen OD pairs.
- Integrating rotary position embedding (RoPE) position encoding, grouped query attention (GQA), and dynamic constraint decoding mechanisms, PathGen-LLM ensures simultaneous spatial–temporal path generation. Generated paths comply with network traversal rules and match statistical characteristics of historical passage times.
- Our study validates the path generation capability of PathGen-LLM in ultra-large-scale scenarios using real-world Beijing traffic network and travel data.
2. Related Work
2.1. Traditional Path Generation Models
Traditional path generation models are based on the assumption of fully rational decision-making, where travelers select globally optimal paths based on predefined objectives such as travel time or cost minimization. Under this assumption, the path generation problem is modeled as a shortest path problem in graph theory. Dijkstra serves as a benchmark method in this domain [8], employing a greedy strategy and a priority queue structure to iteratively expand the nearest unvisited node from the starting point, thereby calculating the shortest path from the origin to all nodes within the network. The A* search algorithm enhances Dijkstra by introducing heuristic functions (e.g., the Euclidean distance to the destination) to dynamically adjust search directions, thereby reducing computational overhead [9]. For large-scale road networks, bidirectional search technology is often combined with Dijkstra or A* algorithms [24]. By initiating searches from both the origin and destination simultaneously and merging paths at the convergence point, this approach significantly improves computational efficiency.
The demand for path generation under dynamic traffic environments has spurred various algorithmic extensions. Dynamic Dijkstra algorithms handle real-time traffic changes by maintaining a retroactive priority queue and an adjacency matrix update mechanism: when the travel time of a road segment changes, the algorithm first identifies affected nodes, then updates network topology based on the adjacency matrix, gradually correcting relevant path costs [11,25]. The D* algorithm adopts a backward search strategy, starting from the target point and updating path costs in reverse [10]. Through incremental optimization, it reduces the computational overhead associated with dynamic adjustments. For stochastic dynamic routing problems, Hall [11] modeled travel times of road segments as time-varying random variables, proposing a path generation framework based on dynamic programming. Sever et al. [26] further formalized this into a discrete-time Markov decision process (MDP), designing approximate dynamic programming algorithms using value function approximation and network hierarchical clustering techniques to balance solution quality and computational efficiency.
Despite the diverse implementation schemes derived from traditional models, inherent limitations become increasingly apparent in complex urban networks: firstly, the fully rational assumption struggles to capture non-rational characteristics of real-world travel behaviors, such as habitual route preferences and decisions under information asymmetry [13,27]; secondly, the algorithm’s time complexity grows exponentially with network size, facing severe scalability issues in ultra-large-scale networks with millions of nodes [1,14].
2.2. Deep Learning-Based Path Generation Models
Deep learning-based path generation models can be divided into two categories: history data-driven models and feature-driven models. One category of methods aims to model statistical patterns by mining historical path data. Crivellari [28] utilized LSTM to capture sequence dependencies within historical trajectories, directly predicting subsequent node transition probabilities. Chen [15] proposed a regional aggregation strategy by merging adjacent links into semantic domains and enhancing the model’s spatial awareness by integrating directional vectors and grid coordinates among other multi-source information and employed beam search to generate physically feasible paths. The STF-RNN model developed by Al-Molegi et al. [16] automatically extracted trajectory features through stacked spatiotemporal-based gated recurrent units, avoiding the need for manual feature engineering. Guo et al. [29] addressed sparse trajectory scenarios and introduced a transfer learning-based approach for modeling regional path preferences by first dividing the road network into functional areas using spectral clustering, then learning cross-regional transition patterns to solve path generation issues for long-tail OD pairs. While these methods can replicate historical path patterns, their generalization ability is limited by training data coverage, making it difficult to generate reasonable paths for unseen OD pairs.
Another category integrates external features such as path data and road network attributes to achieve path generation. These methods explore the relationship between network features—such as link hierarchy, capacity, and contextual path characteristics—and travel paths, enabling path generation between OD pairs lacking historical travel data. Wu et al. [17] proposed the CSSRNN model, introducing topological constraints and multitask learning in an RNN framework to achieve path generation without relying on historical data. Wang et al. [30] developed the MTNet framework, encoding road meta-knowledge (e.g., lane count, speed limit) into learnable graph embeddings and improving result authenticity and efficiency via meta-learning strategies. Jain et al. [18] designed the NeuroMLR model, dividing route generation into two stages: modeling transition probabilities and route searching. By utilizing Lipschitz embedding to capture the geometric structure of network topology and graph convolutional networks (GCNs) for node reachability inference, they significantly improved the model’s generalization capability for unseen nodes. Xiong et al.’s [31] RoPT model integrated destination-aware position encoding in the Transformer architecture, allowing the self-attention mechanism to dynamically adjust the spatial direction during path generation. Cao et al. [32] propose holistic semantic representation (HOSER), a trajectory generation framework leveraging holistic semantic representation to model human mobility patterns across multi-level road networks and multi-granularity trajectories. HOSER demonstrates strong generalization in few-shot/zero-shot learning scenarios. Wang et al. [33] focused on travel time prediction, proposing DeepTTE, which captures spatial correlations through geographic convolution fusion of geographical information and handles temporal dependencies with recurrent units, achieving accurate travel time predictions. Despite improving model versatility by fusing features and enabling path generation between OD pairs without historical data, these methods still face two limitations: firstly, they rely on manually preset feature engineering, potentially overlooking implicit traveler preferences; secondly, most methods predict node order and timestamps independently, failing to fully consider their spatiotemporal correlation.
2.3. Large Language Models in Transportation
In recent years, large language models have provided new technical approaches for transportation spatiotemporal sequence analysis with their powerful sequence modeling capabilities. In the domain of time-series forecasting, Ren et al. [34] proposed the TPLLM framework, which extracts dynamic features of road networks through spatial–temporal graph embedding layers and combines low-rank adaptation (LoRA) fine-tuning techniques, demonstrating superior accuracy over traditional time-series models in traffic flow prediction tasks. Li et al. [21] encoded multi-source urban data, such as GPS trajectories and POI distributions, into spatiotemporal instructions with UrbanGPT using instruction tuning to enable LLMs to perform cross-modal reasoning, achieving joint optimization of travel demand forecasting and traffic state estimation. Yuan et al. [35] developed the UniST framework by employing a multi-scenario pretraining strategy to uniformly represent heterogeneous spatiotemporal data like road traffic and crowd movement as semantically enriched token sequences, validating the potential of large models in cross-task transfer learning.
In the area of spatial trajectory modeling, Zhang et al. [22] adopted a pretraining–fine-tuning paradigm to process human mobility data: during the pretraining phase, they learned continuous vector representations of trajectory point coordinates; during the fine-tuning phase, they utilized multi-layer perceptrons for user profiling and regional function analysis. Huang et al. [36] experimented with converting vehicle routing problems into natural language constraints by designing structured prompt templates to guide LLMs in generating drivable routes compliant with traffic rules. Wang et al. [37] encoded historical travel paths into discrete token sequences by leveraging the long-term memory characteristics of LLMs to simulate the limited rational decision-making process of humans, achieving significant improvements in daily path selection predictions. Marcelyn et al. [38] employed retrieval-augmented generation (RAG) technology to integrate historical trajectory similarity searches, realizing personalized path recommendations that are contextually aware and dynamically adaptive, although their accuracy still lags behind existing path generation algorithms.
However, current applications of LLMs in path generation face notable limitations; most research remains at the level of prompt engineering and workflow optimization, failing to fully unlock the potential of LLMs in spatiotemporal sequence generation, particularly lacking systematic solutions for end-to-end path generation. Additionally, many studies are based on small-scale road networks, lacking validation in real-world complex transportation systems.
In summary, while existing works have advanced path generation, critical challenges persist in complex networks: Fully rational assumptions fail to capture real-world behaviors. Data-driven methods struggle with generalization for unseen OD pairs, and LLMs lack end-to-end solutions for spatiotemporal consistency. These gaps highlight the need for innovative frameworks that address authenticity in large-scale scenarios, as proposed by this study through PathGen-LLM.
3. Problem Formulation
We define the traffic network as a directed graph , where is a finite set of traffic zones, representing aggregated geographical regions; is the set of road network nodes, corresponding to intersections or key link points; is the set of directed links, where each link denotes a one-way connection from node to node ; is the set of connectors, where each connector denotes an access link connecting traffic zone to node .
A travel path from origin zone to destination zone , departing at time , is represented as a sequence of spatiotemporal states:
where denotes the arrival time at node and is the arrival time at the destination zone. The path captures both spatial transitions (node sequences) and temporal dynamics (arrival times), forming a spatiotemporal trajectory through the network.
This study addresses the path generation problem in complex traffic networks, aiming to construct spatiotemporal paths that seamlessly integrate spatial connectivity and temporal consistency. Given an OD pair of traffic zones and a departure time , the goal is to develop a model that generates a feasible path:
where each node transition adheres to the directed links in the road network, while the arrival times satisfy for .
4. Methodology
PathGen-LLM is a framework for efficient path generation in complex networks, and it comprises four core components:
- Path-to-Text Data Construction: It converts path data into natural language-like sequences using standardized tokens for zones, nodes, and timestamps, enabling LLM processing.
- Graph-Adaptive Transformer Architecture: It is a decoder-only neural network integrated with RoPE, grouped query attention, and Flash Attention, and it is optimized for modeling spatiotemporal dependencies in complex networks.
- Two-Stage Training Pipeline: It combines self-supervised pretraining and task-specific fine-tuning. Pretraining uses next-token predictions to learn general network representations, while fine-tuning on instruction–data pairs adapts the model to generate paths for specific OD pairs.
- Integrated Inference Framework: It is a hybrid decoding strategy combining reachability-constrained token generation, cyclic path validation, and computational caching to ensure validity and efficiency in large-scale networks.
The framework leverages the structural similarity between path sequences and text data, allowing LLMs to learn implicit route choice patterns from real-world trajectory data, thereby addressing the limitations of traditional econometric methods in accuracy, scalability, and granularity.
4.1. Path-to-Text Data Construction
4.1.1. Mapping Paths to Natural Language Sequences
Although route data shares structural similarities with natural language data, large language models cannot directly process structured route data. To bridge this gap, we convert geometric path representations into natural language-like sequences that encode traffic zones, nodes, and temporal information.
First, unique tokens are created for traffic zones and nodes by formatting their IDs as [zone_ <ID>] and [node_<ID>], respectively. This ensures each zone/node maps to a distinct token in the model’s vocabulary. Then, time information is converted into the total number of seconds in a day to form a continuous numerical representation, where, for example, 07:00:00 is encoded as 25,200 s. Finally, each spatial–temporal state along the route—comprising a zone/node ID and its corresponding timestamp—is then serialized using two special delimiters: <sep> to connect an entity ID with its timestamp and <next> to separate consecutive states. As shown in Figure 1, a route leaving zone 6 at 7:00 AM; passing through nodes 15, 17, 25, and 29; and arriving at zone 7 at 7:08:16 AM is encoded as shown below.
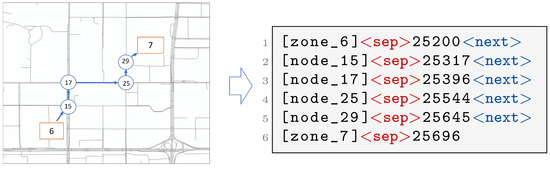
Figure 1.
Example of the path-to-text mapping mechanism of textual encoding for paths.
This sequence-based encoding transforms paths into token streams that align with the input format requirements of LLMs, enabling the model to learn spatial–temporal dependencies through language modeling techniques.
4.1.2. Vocabulary Construction
Given the clear semantic boundaries in zone/node IDs and timestamp components, our vocabulary avoids subword tokenization. Instead, it directly incorporates complete entity IDs and time fragments as atomic tokens: (1) Zone/node tokens represent unique tokens for each [zone_<ID>] and [node_<ID>] and are based on the road network’s topological structure. (2) Time tokens serve as single-digit numerical tokens (e.g., 0, 1,…, 9) to construct the numerical representation of the total number of seconds in a day, enabling the encoding of time information as a discrete sequence representing values ranging from 0 to 86,399. (3) Special tokens serve as task-specific delimiters (<sep>, <next>), instruction templates, and formatting markers to standardize input/output structures. All tokens are predefined according to the road network topology and data schema, eliminating the need for dynamic vocabulary learning during training. This design ensures semantic clarity and computational efficiency, as each token directly maps to a meaningful spatial–temporal unit without ambiguous subword segmentation.
4.2. Model Architecture
The proposed path generation model employs a decoder-only Transformer architecture, as illustrated in Figure 2. The design addresses two critical characteristics of transportation networks: temporal dependency and spatial structural constraints. The integration of RoPE with grouped-query attention mechanisms enables effective capture of complex network connectivity relationships. Simultaneously, the sigmoid-weighted linear unit (SiLU) activation function coordinated with Flash Attention optimization ensures precise modeling of complex time–cost patterns during long-sequence processing while maintaining computational efficiency.
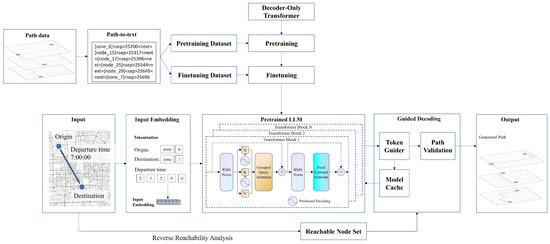
Figure 2.
Architecture of the PathGen-LLM model.
4.2.1. Hierarchical Transformer
The architecture employs a decoder-centric design that omits the encoder module to prioritize computational efficiency in sequence generation tasks. Input sequences are first mapped into token embeddings through vocabulary projection, followed by positional information encoding via RoPE. Distinct from conventional absolute positional encoding, RoPE parametrizes positional relationships through rotation matrices, decomposing high-dimensional token embeddings into orthogonal 2D subspaces [39]. This trigonometric rotational operation implicitly encodes the sequential order of node visitation, providing the model with the positional context necessary to learn temporal dependencies and sequential node relationships from the training data.
To address the challenges of extended path sequences and complex node interactions in complex networks, the architecture replaces traditional multi-head attention with grouped-query attention. This mechanism partitions queries into multiple groups while sharing key-value computations across each group, achieving significant computational complexity reduction without compromising attention precision [40]. This efficiency improvement makes the model especially well-suited for processing long-path sequences containing dozens of nodes, as commonly encountered in complex networks in megacities.
4.2.2. Activation Functions and Computational Efficiency Optimization
The feedforward neural network module within each decoder layer employs the SiLU activation function, which is defined as
This function synergizes the smooth saturation properties of the sigmoid function with the linear region advantages of ReLU. By preserving gradient responsiveness in negative-value regions, the SiLU mitigates general gradient vanishing issues in deep networks while preventing ’dead neuron’ phenomena during training.
To address memory bottlenecks in long-sequence generation, the architecture integrates Flash Attention optimization. Specifically, Flash Attention computes attention weights block by block, storing only softmax normalization factors rather than full attention matrices [41]. During backpropagation, intermediate results are regenerated on the fly, achieving significant improvements in training and inference efficiency without sacrificing precision. This optimization proves critical for processing path sequences containing thousands of nodes and timestamps, ensuring real-time generation capability.
4.3. Two-Stage Training Pipeline
We devise a two-phase training pipeline that leverages conventional large language model training methodologies. This pipeline aims to extract universal network features through self-supervised pretraining on path data, followed by instruction-based fine-tuning to incorporate domain-specific constraints for optimal OD path generation.
4.3.1. Pretraining
The pretraining phase focuses on the unsupervised next-token prediction task, where the model takes a tokenized path sequence as input, processes the first n tokens, and aims to predict the (n + 1)-th token. This learning process is based on the self-attention mechanism of the Transformer architecture, enabling the model to capture dependencies between tokens within the sequence. Through training on a large volume of path sequences, the model implicitly learns the topological structure of the road network, models the statistical patterns of travel times across different links, and adapts to the formatting conventions of tokenized paths—such as using ‘<sep>’ to separate nodes and timestamps or ‘<next>’ to indicate state transitions. The training data for this phase do not need to cover all OD pairs but must include at least one valid traversal record for every link and node in the network, ensuring that the model acquires a comprehensive understanding of the entire network’s structural characteristics. This enables the model to develop an internal representation of the spatiotemporal logic of the transportation system, grasp the fundamental principles of path generation, and establish a strong foundation for generalization ability, which will later support the instruction fine-tuning phase.
4.3.2. Fine-Tuning
The instruction fine-tuning phase adapts the pretrained model to OD path generation tasks, enabling synthesis of physically plausible and behaviorally realistic routes conditioned on the origin, destination, and departure time. This stage constructs instruction–response pairs where natural language commands map to textual path sequences, as shown in Listing 1.
| Listing 1. An example of instruction–response pairs for OD path generation task. |
 |
Fine-tuning employs a weighted cross-entropy loss function with a double penalty for node/zone ID prediction errors:
where for node/zone ID tokens and otherwise, with representing the one-hot encoded ground-truth labels and representing the model’s predicted probability distribution. This weighting scheme prioritizes the accuracy of topological connectivity, effectively preventing the generation of discontinuous paths. Through this process, the model learns to map abstract OD pairs and temporal constraints to concrete node sequences, enforce strict temporal monotonicity across all nodes, and maintain compliance with segmented traversal-time distributions.
4.4. Inference Framework
To enhance the accuracy and efficiency of path generation in complex road networks, PathGen-LLM employs an inference framework integrating guided decoding, path validation, and model cache mechanisms, aiming to improve the proportion of generated paths accurately reaching the destination zone and the efficiency of large-scale inference.
In directed graph networks, generated paths may fail to reach the destination zone due to constraints such as one-way road restrictions or invalid detours. To address this, PathGen-LLM introduces guided decoding during inference through a reachable node constraint set. Specifically, reverse reachability analysis is first performed based on historical path data to construct a Reachable Node Set from any node to the destination zone, which is a set of all nodes that can reach the destination zone via compliant paths. When the model receives an input instruction containing the origin, destination, and departure time, it first parses the zone ID corresponding to the target destination and generates a candidate node set conforming to road network traffic rules for the current decoding step based on the Reachable Node Set. During the token generation phase, the token-level constraint module restricts the model’s output to only allow node IDs from the compliant candidate set to be selected, thus avoiding generating invalid paths that enter dead ends or deviate from the destination direction.
A Route Validation module is introduced to address the issue of cyclic paths caused by repeated visits to the same node during model generation. This module monitors the generated node sequence during inference and maintains a set of visited nodes to detect in real time whether the currently generated node already exists in the historical path. If repeated generation of the same node ID is detected, indicating a repeated node visit, it triggers a path backtracking mechanism to delete the path segment between two visits to the same node. Additionally, the Route Validation module checks whether the node order complies with the directed edge constraints of the road network to ensure that the generated path conforms to the actual road network structure.
To improve the generation efficiency of the model in large-scale complex road networks, PathGen-LLM adopts two methods: parallel processing and intermediate result reuse. First, a beam search-based parallel implementation is used for batch parallel decoding to generate paths between multiple OD pairs simultaneously. Second, a model cache strategy based on node sequences and timestamps is designed to store the logit distribution of generated path nodes. When a new path and a historical path satisfy three conditions simultaneously: (1) The access order of five consecutive nodes is completely consistent. Here, “consistent” refers to the identity of both node IDs and their sequential order. Specifically, if there exist consecutive subsequences and satisfying , then their access order is considered consistent. (2) The time difference between the first corresponding nodes in the five consecutive subsequences does not exceed 10 min, i.e., , where k and l are the indices of the first node in the consistent subsequence. (3) The target destinations are the same, i.e., . Then the model directly reuses the subsequent path generation results of and terminates the independent decoding process of . This mechanism reduces redundant computations by leveraging the spatiotemporal similarity of travel demands.
5. Experiments and Results
5.1. Dataset
To validate the performance of PathGen-LLM, this study selected taxi and subway path datasets from Beijing, as well as taxi path data from Porto as experimental data. These three datasets are referred to as the BJ-taxi dataset, the BJ-subway dataset, and the Porto dataset, respectively, and their statistical characteristics are presented in Table 1. BJ-taxi path data were sourced from anonymized GPS trajectory data of taxis in Beijing during June 2023, specifically covering four Wednesdays (June 7, 14, 21, and 28) during the morning peak hours (7:00 to 9:00). The data-processing steps included the following: first, removing data from the empty driving phase of taxis and retaining only passenger-carrying trajectory records; second, deleting discontinuous trajectory data with time intervals exceeding 30 s; and finally, mapping the points of trajectories to corresponding traffic zones using a hidden Markov model [42] to construct a complete path dataset.

Table 1.
Dataset statistics.
Subway path data were based on anonymized mobile phone base station communication records during the morning peak hours (6:00 to 9:00) from 20 to 24 May 2024. The deployment of base stations within subway stations allowed for the identification of passengers’ arrival times at stations, thereby extracting subway travel paths. In modeling the subway network, each line at each station was represented as an independent node. For example, a station with three lines for transfer functions was split into three nodes. The connection relationships between nodes were represented by links, including regular links connecting different stations and transfer links used for transfers within the same station. Transfer link travel times were calculated based on transfer distances. For discontinuous path data, if the number of skipped stations was less than three, missing segments were completed using Dijkstra’s algorithm to find the shortest travel-time path; otherwise, those records were discarded. For data security and privacy protection, the original anonymized data of the BJ-Taxi and B]-Subway were processed in a restricted-access environment. Only after generating security-compliant data were they used for subsequent processing. The Porto dataset is an open-source dataset that records taxi trajectory data in Porto from January to June 2013, and it has been processed into a route dataset [32].
5.2. Baselines
This study selects three baselines: Dijkstra, NeuroMLR, and HOSER. Dijkstra assumes that travelers follow a fully rational decision-making logic, generating paths with the objective of minimizing travel time [8]. NeuroMLR is a deep learning-based path generation model that operates in three stages: first, it employs GCNs to extract geometric features of the road network topology while ensuring node embedding stability through Lipschitz constraints; second, it estimates the link transition probability distribution based on traffic state features reduced via principal component analysis (PCA); finally, it utilizes an improved version of Dijkstra’s algorithm to search for the shortest path that satisfies reachability constraints [18].
HOSER generated paths based on graph attention networks (GATs) and multi-granularity spatial–temporal modeling [32]. It first extracts hierarchical network features via GATs, then models trajectories from local transitions to regional patterns, and finally uses reinforcement learning to align multi-level decisions for destination-consistent path generation.
5.3. Experiment Settings
To evaluate the model’s generalization capability on unseen origin–destination (OD) pairs, this study partitions the datasets by OD pairs into the training and testing sets. Specifically, of the OD pairs corresponding to path data are used for model training, while the remaining are reserved for testing to validate the model’s performance in scenarios involving unseen OD pairs.
Two versions of PathGen-LLM with different parameter scales are tested: PathGen-LLM-1B (1.3 billion parameters) and PathGen-LLM-7B (7 billion parameters). PathGen-LLM-1B includes a 28-layer Transformer module with 1536 hidden units per layer, while PathGen-LLM-7B also employs a 28-layer Transformer architecture but increases the hidden unit size to 3584 per layer.
Model training was conducted on a server equipped with eight NVIDIA A100 GPUs, each featuring 80 GB of memory. The hyperparameters of the two versions of PathGen-LLM are listed in Table 2 and categorized into two types: model architecture parameters and training parameters. During the pretraining phase, the AdamW optimizer was employed with the cross-entropy loss function as the training objective. The learning rate was set to for a single epoch. To balance training efficiency and numerical stability, the model utilized FP16/BF16 mixed-precision computation, which was combined with gradient scaling and dynamic loss scaling strategies. The token-level batch size was configured as 262,144, which is equivalent to a distributed training setup where eight GPUs process eight batches in parallel, with each batch containing 4096 tokens. For the instruction fine-tuning phase, the AdamW optimizer was retained, but the learning rate was reduced to to mitigate overfitting risks. The training duration was extended to three epochs, and the batch size was adjusted to 128 to accommodate the task-specific data scale.

Table 2.
Model parameters.
5.4. Evaluation Metrics
To evaluate model performance, the following metrics are employed:
(1) Next-Token Accuracy (NTA): This metric assesses the performance of large language models [43,44]. It is defined as the ratio of correctly predicted tokens to the total number of predicted tokens during the next-token prediction task in the pretraining phase.
(2) Node Sequence Accuracy: This study employs precision, recall, and the F1-score to evaluate the spatial accuracy of paths generated by the model [18,31]. By removing timestamps from the path data, the node sequence between origin–destination (OD) pairs can be extracted. Let denote the node sequence generated by the model, and let denote the ground truth. The formulas for precision, recall, and the F1-score are defined as follows:
(3) Travel Time Error: We calculate the mean absolute error (MAE) and root mean squared error (RMSE) between the model’s predicted arrival times and the ground-truth values to analyze the accuracy of time prediction [33]. These metrics are defined as follows:
where N denotes the total number of evaluated paths, represents the generated arrival time for the i-th path, and is the corresponding ground-truth arrival time.
5.5. Model Performance Comparison
Table 3 presents the performance comparison of all models; for each dataset, the best-performing metric values are bolded, while the second-best ones are underlined. Overall, all models demonstrate superior performance on the BJ-subway dataset compared to the BJ-taxi dataset and Porto dataset, particularly in node sequence prediction. This is primarily attributed to the subway networks having fewer nodes and links, resulting in simpler passenger route-choice patterns where most travelers select the shortest paths. However, in travel time prediction, no model achieves significantly higher accuracy on railway paths due to uncertainties in waiting and transfer times. This contrasts with the BJ-taxi dataset, where travel time predictions benefit from more deterministic mobility patterns.

Table 3.
Model performance comparison.
In all datasets, the two versions of PathGen-LLM outperform all baselines. On the BJ-taxi and Porto datasets, the next-token accuracy of both versions of PathGen-LLM is around 95%, while the BJ-subway dataset sees accuracies above 98%. This is partly due to the presence of predictable special delimiters in path text data, but more importantly, it demonstrates the effectiveness of pretraining. The model fully captures statistical patterns in the training data, providing robust support for handling spatiotemporal sequence data in complex networks. Among all models, the traditional Dijkstra algorithm performs the worst. On the BJ-taxi and Porto datasets, its F1-scores are 63.67% and 57.50%, respectively, which validates that many travelers do not travel along the shortest path due to reasons such as incomplete information mastery, avoidance of toll roads, and concerns about the reliability of travel time. In contrast, for rail travel, where these factors are less influential, the proportion of passengers choosing shortest paths increases significantly, raising Dijkstra’s F1 to 85.79%. NeuroMLR performs better than Dijkstra, indicating that deep learning methods can learn real travel patterns from path data, while HOSER performs even better, especially in terms of the precision metric. PathGen-LLM-1B further improves deep learning models. In the BJ-taxi, BJ-subway, and Porto datasets, its F1-scores are 5.53%, 1.04%, and 0.38% higher than those of HOSER, respectively, which verifies the ability of LLMs to capture complex path patterns through self-supervised learning. Additionally, the MAE and RMSE of PathGen-LLM-1B in predicting travel time are lower than those of NeuroMLR and HOSER, demonstrating that synchronous modeling of node sequences and time intervals mitigates error accumulation for more accurate temporal predictions. PathGen-LLM-7B achieves the best overall performance. Compared to the 1B version, the 7B version has improvements in all metrics, indicating that expanding the parameter scale can enhance the model’s capability, especially with significant gains in large-scale complex networks.
Notably, PathGen-LLM generally exhibits higher recall than precision across most datasets, while the baselines typically show the opposite trend. This discrepancy is most pronounced in the BJ-taxi and Porto datasets, where PathGen-LLM’s generative nature leads to slightly longer paths. In the BJ-subway dataset, where paths are generally more direct, the difference between precision and recall is minimal. This discrepancy arises from PathGen-LLM’s nature as an end-to-end generative model. During node transition prediction, it preferentially selects popular nodes (e.g., arterial roads), leading to detours. Additionally, its dynamic constraint decoding mechanism may introduce redundant paths to bypass dead ends or one-way streets. Consequently, the generated path lengths exceed ground-truth values, resulting in lower precision relative to recall. In contrast, the HOSER, NeuroMLR, and Dijkstra algorithms prioritize shorter paths during route search, potentially pruning segments and missing detour nodes present in true paths. This leads to an underestimation of path lengths, causing recall to fall below precision.
To evaluate the impact of path distance, we test the models’ F1-scores and travel time errors across different distance intervals, with results shown in Figure 3 and Figure 4. Figure 3 presents the results on the BJ-taxi dataset. PathGen-LLM outperforms all baselines across all distance ranges, demonstrating the proposed model’s superiority and stability. As path distance increases, the number of possible route branches grows, raising the complexity of path generation. Consequently, all models exhibit performance degradation with longer paths, but PathGen-LLM shows significantly slower decay. For short paths with fewer than 20 nodes, PathGen-LLM improves the F1-score by 3.31% over HOSER and reduces the RMSE by 13.28 s. However, for long paths exceeding 80 nodes, the F1-score improvement reaches 5.57%, while RMSE decreases by 229.08 s. This highlights PathGen-LLM’s advantage in generating long-distance paths. Comparing the two PathGen-LLM variants, the 7B version achieves greater performance gains on long paths than short ones, indicating that scaling up LLM parameters enhances long-sequence modeling capabilities more significantly.
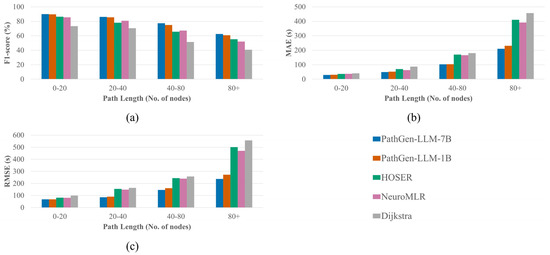
Figure 3.
Impact of path length on model performance in the BJ-taxi dataset: (a) F1-Score; (b) MAE; (c) RMSE.
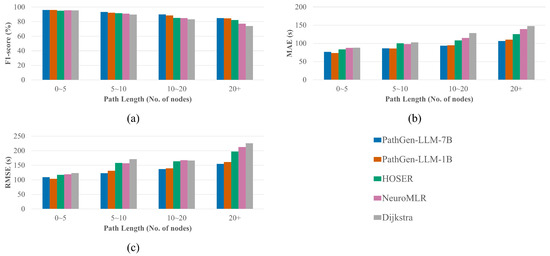
Figure 4.
Impact of path length on model performance in the BJ-subway dataset: (a) F1-Score; (b) MAE; (c) RMSE.
Figure 4 compares model performance on the BJ-subway dataset of varying lengths. For short paths with fewer than five nodes, most passengers choose shortest paths, resulting in minimal performance differences between models. As path distance increases, PathGen-LLM’s advantages emerge—a trend consistent with the taxi dataset—but the performance gap between PathGen-LLM and baselines narrows. On the rail dataset, PathGen-LLM-7B shows no significant improvement over the 1B version, suggesting that the smaller model already captures rail travel patterns effectively, with diminishing returns from parameter scaling.
5.6. Ablation Studies
To evaluate the contributions of key components in the path-to-text data construction and model architecture, we conducted ablation experiments on the BJ-taxi dataset, as summarized in Table 4. The baseline is the 1B version of PathGen-LLM with full pretraining and token design. The model labeled w/o special tokens removes task-specific delimiters such as <sep> and <next> that standardize input and output formats. The model labeled alternate temporal encoding converts time information into the hh:mm:ss format and uses two-digit numerical tokens to handle minute/second timestamp components. The model labeled w/o pretraining removes the pretraining phase with the unsupervised next-token prediction task.

Table 4.
Ablation study results.
The results show that each module contributes to the model’s performance. Among them, pretraining has the most significant impact. After removing this phase, the model’s F1-score decreases by 9.7%, while the RMSE of travel time prediction increases by 53.63 s. This underscores the foundational role of pretraining in learning generalizable sequence patterns and contextual relationships, which are essential for downstream task-specific fine-tuning to effectively adapt to the path generation task. After removing special tokens, the model’s F1-score decreases by 3.03%, while the RMSE increases by 4.56 s. This is because special delimiters like <sep> and <next> clearly define the association boundaries between nodes and timestamps, as well as the logical segments of state sequences. They help the model clearly identify prediction targets and reduce decoding ambiguities. When time information is converted into the hh:mm:ss format, the model’s F1-score decreases by 0.71%, while the RMSE increases by 11.33 s. This is because the continuous second-based encoding simplifies the time vocabulary (only requiring single-digit tokens of 0–9) and better aligns with the continuous nature of time. Additionally, errors in single digits have a smaller impact on overall time.
5.7. Hyperparameter Sensitivity Analysis
We systematically evaluated the impact of learning rate, fine-tuning batch size, the number of fine-tuning epochs, and parameter size on model performance in BJ-taxi, with the experimental results shown in Figure 5. Figure 5a–d illustrate the influence of hyperparameters on the model’s F1-score, while Figure 5e–h present the corresponding RMSE values. In our hyperparameter sensitivity analysis, we tested different learning rate configurations, maintaining a 10:1 ratio between pretraining and fine-tuning phases. For instance, when the pretraining learning rate is 1 , the fine-tuning learning rate is 1 . Experiments show that a learning rate of 1 performs best in both the F1-score and RMSE. An excessively high learning rate makes it difficult for the model to converge stably, while an overly low learning rate leads the model to underfitting, resulting in decreased performance. When the fine-tuning batch size increases from 32 to 128, the model’s performance gradually improves. However, when the batch size increases to 256, its F1-score slightly decreases. This may be because a large batch size reduces the frequency of gradient updates, leading to a decline in the model’s sensitivity to local features. Thus, 128 is the optimal batch size configuration. In the experiment on the number of fine-tuning epochs, after the number of epochs reaches three, the model’s performance basically stabilizes. The marginal gains from further increasing the number of epochs are limited, and there is a risk of overfitting. In the comparative experiments on parameter scales, we added a 0.5B version of the PathGen-LLM model, which consists of a 24-layer Transformer module with 896 hidden units per layer. Compared with the 1B version, the 0.5B version of PathGen-LLM shows a 7.22% decrease in F1-score and a 35.9 s increase in RMSE. Its performance does not show advantages over HOSER and NeuroMLR. In contrast, the 7B version outperforms both the 1B and 0.5B versions in all metrics. This demonstrates the importance of the parameter scale for large models.
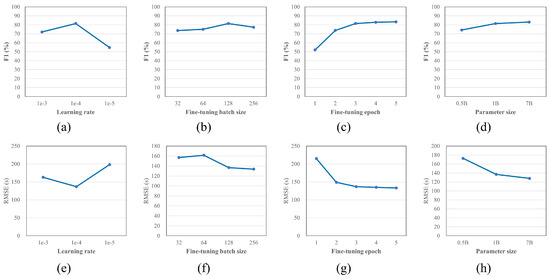
Figure 5.
Effects of hyperparameters on the F1-score and RMSE: (a) Learning Rate (F1-Score); (b) Fine-Tuning Batch Size (F1-Score); (c) Fine-Tuning Epoch (F1-Score); (d) Parameter Size (F1-Score); (e) Learning Rate (RMSE); (f) Fine-Tuning Batch Size (RMSE); (g) Fine-Tuning Epoch (RMSE); (h) Parameter Size (RMSE).
5.8. Inference Efficiency
Table 5 presents the time required for each model to generate a single path across three datasets. Consistent with previous observations, the traditional Dijkstra algorithm maintains the highest inference efficiency. Among deep learning-based models, NeuroMLR remains more efficient than HOSER, while PathGen-LLM-1B achieves inference speeds comparable to NeuroMLR across all datasets, outperforming HOSER in efficiency while delivering superior predictive performance. In contrast, PathGen-LLM-7B exhibits significantly longer inference times than all other models, reflecting the computational overhead of its larger parameter scale. This trend shows a trade-off: higher performance tends to come with longer latency. However, PathGen-LLM-1B performs nearly as fast as NeuroMLR. This confirms its practical viability for real-world use, even with its LLM-based architecture.

Table 5.
Model inference speed comparison (seconds per path).
5.9. Discussion
5.9.1. LLM Scale and Performance Trade-Offs
The experimental results demonstrate PathGen-LLM’s superior performance in path generation, particularly for long-distance routes. However, as a full-scale LLM, its computational demands present legitimate concerns. To evaluate this trade-off, we tested a 0.5B parameter version of PathGen-LLM, which showed a 7.22% decrease in F1-score and a 35.9 s increase in RMSE compared to the 1B version, performing no better than traditional models like NeuroMLR.
This reveals a critical insight: LLMs’ distinctive capabilities in path generation emerge primarily at sufficient scale. As shown in Section 5.5, the performance gap between PathGen-LLM variants and baselines widens substantially with path complexity. For paths exceeding 80 nodes, PathGen-LLM-1B improves the F1-score by 5.57% over HOSER and reduces the RMSE by 229.08 s, with the 7B version delivering even greater gains. This scaling behavior aligns with research on emergent abilities in LLMs [23].
Three factors justify the computational cost: (1) Emergent abilities enable genuine generalization to unseen OD pairs by learning underlying network connectivity. When scaled to sufficient parameter sizes, LLMs exhibit emergent abilities that enable genuine generalization to novel scenarios such as real-time traffic disruptions by extracting and recombining path fragments from global network knowledge. This capacity is critical for practical applications where historical data cannot cover all possible travel scenarios and where the model must adapt to dynamic changes. (2) Integrated modeling of spatial and temporal dynamics eliminates error propagation from multi-stage approaches. (3) PathGen-LLM-1B achieves comparable inference speed to NeuroMLR while delivering superior accuracy. For applications requiring high-fidelity path simulations in megacities—where travel behavior is highly variable—full-scale LLMs provide significant value that outweighs their costs, especially given the diminishing performance of traditional methods on long-distance routes.
5.9.2. Model Interpretability and Behavioral Validity
While PathGen-LLM demonstrates strong performance in generating realistic paths, we acknowledge that the interpretability of LLM-based path generation remains an open challenge—a limitation shared across many large language model applications [45]. Unlike traditional shortest path algorithms that follow explicit optimization criteria, PathGen-LLM learns complex behavioral patterns from historical data through self-supervised learning, making its decision process inherently less transparent.
However, it is essential to recognize that PathGen-LLM’s outputs are rooted in the statistical regularities of real trajectory data. As validated by previous research and our experiments, travelers frequently deviate from shortest paths due to factors like incomplete network knowledge, habitual preferences, or risk aversion to congestion [13,27]. By learning from massive historical paths, the model aligns with these behaviors even when deviating from shortest paths—this empirical consistency, while not fully transparent, provides foundational validity. The model operates through a two-stage learning process: during pretraining, it internalizes the underlying topology and connectivity patterns of the transportation network; during fine-tuning, it learns to follow path generation instructions while respecting network constraints. At the inference time, PathGen-LLM generates paths through a step-by-step process where each node selection represents the highest probability transition based on both learned network knowledge and the current context. This mechanism, combined with our dynamic constraint decoding that prevents invalid transitions, ensures physically plausible paths that align with observed human behavior.
Enhancing model interpretability represents an important direction for future work, which can further enhance the model’s utility in decision-support applications. Potential approaches could include attention visualization to understand which historical patterns influence specific path decisions or counterfactual analysis to examine how path selections change with modified inputs. However, in the context of path generation for transportation planning, we believe that PathGen-LLM provides valuable capabilities for generating high-fidelity path simulations that reflect real-world behavior patterns.
5.9.3. Data Dependency and Generalization Limitations
As a data-driven model, PathGen-LLM inherently depends on comprehensive historical path data to learn network connectivity patterns. Within our framework, nodes and links in the road network are treated as discrete tokens, with no explicit topological attributes directly provided to the model. Instead, the model learns about network connectivity indirectly, deriving this knowledge from the co-occurrence patterns of nodes and links in the historical trajectories it is trained on. This means that the model’s understanding of the network is entirely rooted in the path data it has observed during training.
This data-driven nature has clear implications for generalization. For instance, if a node or link was never visited in training data, the model will lack knowledge of its connectivity—this can lead to suboptimal or invalid paths when such elements are encountered during inference. While our methodology requires training data to cover all network nodes and links, in practical scenarios, some network elements might not be adequately represented in historical data, particularly for newly constructed roads or infrequently used paths. Similarly, the model’s generalization is confined to the specific network it was trained on. While it can generate reasonable paths for unseen OD pairs within this known network, it cannot be directly applied to entirely new cities or networks with unobserved topological structures. This data dependency has both strengths and limitations: it eliminates the need for manual feature engineering of road attributes but restricts applicability to unseen networks.
Addressing generalization to novel networks is a critical direction for future work. One promising approach is integrating explicit network attributes with LLM capabilities—for example, using multi-agent reinforcement learning frameworks that simulate dynamic interactions between vehicles and environmental feedback. Such methods could enable the model to learn generalizable routing rules from network attributes, reducing reliance on historical path data and improving transferability to unseen networks.
6. Conclusions and Future Work
This study focuses on path generation in complex transportation networks, proposing PathGen-LLM—a framework based on large language models that leverages self-supervised learning to extract spatiotemporal sequence features from massive historical path data, enabling effective path generation for unseen OD pairs. Unlike traditional methods, PathGen-LLM employs a “path-to-text” mapping system to convert node IDs, timestamps, and other information into natural language-like token sequences. This allows the model to directly capture traveler behavior patterns from path data without relying on manually engineered features. By integrating a hierarchical Transformer architecture with dynamic constraint decoding, PathGen-LLM efficiently generates paths that conform to both road network rules and statistical characteristics of historical travel times while ensuring physical plausibility.
Experimental results demonstrate that PathGen-LLM achieves superior performance on real-world taxi and subway path datasets in Beijing, as well as the Porto taxi dataset, particularly for long-distance paths. Compared to the classical Dijkstra algorithm and the deep learning models, PathGen-LLM not only improves path prediction accuracy but also exhibits higher precision in travel time estimation. Notably, increasing the parameter scale—from 1.3 billion (PathGen-LLM-1B) to 7 billion (PathGen-LLM-7B)—further enhances performance, especially in large-scale complex networks, where its advantages in handling long-range dependencies and complex spatiotemporal patterns become more pronounced.
While PathGen-LLM demonstrates promising results, PathGen-LLM has room for improvement, including its reliance on comprehensive path data for network connectivity learning and the need for enhanced interpretability of its decision-making processes. Building on these insights, future work will focus on advancing its generalization to unseen networks and enhancing model transparency through attention visualization and counterfactual analysis. Additionally, optimizing inference efficiency via model compression will accelerate its deployment in real-world complex transportation systems, further unlocking its potential for intelligent transportation applications.
Author Contributions
Conceptualization, X.L. and K.X.; methodology, X.L. and S.B.; software, S.B. and H.X.; validation, X.L. and K.X.; formal analysis, X.L. and S.B.; investigation, X.L., Y.Y. and S.B.; resources, X.L., K.X. and H.W.; data curation, H.X. and Y.Y.; writing—original draft preparation, X.L.; writing—review and editing, S.B. and K.X.; visualization, X.L. and S.B.; supervision, K.X. and H.W.; project administration, X.L. and K.X.; funding acquisition, Y.Y., K.X. and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 72288101. And The APC was funded by the National Natural Science Foundation of China, grant number 72288101.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The authors have obtained permission to use the processed data for research purposes; however, the use of the raw data is subject to privacy restrictions.
Acknowledgments
During the preparation of this manuscript/study, the authors used ChatGPT-4.5 for the purposes of improving grammar, clarity, conciseness, and overall readability. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
Author Shengguang Bai was employed by the company Learnable.ai. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Bast, H.; Delling, D.; Goldberg, A.V.; Müller-Hannemann, M.; Pajor, T.; Sanders, P.; Wagner, D.; Werneck, R.F. Route Planning in Transportation Networks; Technical Report MSR-TR-2014-4; Microsoft Research; One Microsoft Way: Redmond, WA, USA, 2014. [Google Scholar]
- Sheffi, Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods; Prentice-Hall: Hoboken, NJ, USA, 1984. [Google Scholar]
- Tyagi, N.; Singh, J.; Singh, S. A Review of Routing Algorithms for Intelligent Route Planning and Path Optimization in Road Navigation. In Proceedings of the Recent Trends in Product Design and Intelligent Manufacturing Systems; Deepak, B., Bahubalendruni, M.R., Parhi, D., Biswal, B.B., Eds.; Springer: Singapore, 2023; pp. 851–860. [Google Scholar]
- Ghamami, M.; Kavianipour, M.; Zockaie, A.; Hohnstadt, L.R.; Ouyang, Y. Refueling infrastructure planning in intercity networks considering route choice and travel time delay for mixed fleet of electric and conventional vehicles. Transp. Res. Part C Emerg. Technol. 2020, 120, 102802. [Google Scholar] [CrossRef]
- Huang, W.; Hu, J.; Huang, G.; Lo, H.K. A three-layer hierarchical model-based approach for network-wide traffic signal control. Transp. B Transp. Dyn. 2023, 11, 1912–1942. [Google Scholar] [CrossRef]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wiessner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2575–2582. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, Z.; Yang, L.; Teng, F.; Li, T. A survey of route recommendations: Methods, applications, and opportunities. Inf. Fusion 2024, 108, 102413. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, SSC-4, 100–107. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. D* Lite. In Proceedings of the 18th National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July–1 August 2002; pp. 182–188. [Google Scholar]
- Hall, R.W. The Fastest Path through a Network with Random Time-Dependent Travel Times. Transp. Sci. 1986, 20, 182–188. [Google Scholar] [CrossRef]
- Huang, W.; Wang, J. The Shortest Path Problem on a Time-Dependent Network with Mixed Uncertainty of Randomness and Fuzziness. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3194–3204. [Google Scholar] [CrossRef]
- González Ramírez, H.; Leclercq, L.; Chiabaut, N.; Becarie, C.; Krug, J. Travel time and bounded rationality in travellers’ route choice behaviour: A computer route choice experiment. Travel Behav. Soc. 2021, 22, 59–83. [Google Scholar] [CrossRef]
- Zheng, G.; Chai, W.K.; Katos, V. A dynamic spatial–temporal deep learning framework for traffic speed prediction on large-scale road networks. Expert Syst. Appl. 2022, 195, 116585. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Xiao, F.; Peng, D.; Zhang, C.; Hong, B. Route Planning by Merging Local Edges into Domains with LSTM. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 505–510. [Google Scholar] [CrossRef]
- Al-Molegi, A.; Jabreel, M.; Ghaleb, B. STF-RNN: Space Time Features-based Recurrent Neural Network for predicting people next location. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Wu, H.; Chen, Z.; Sun, W.; Zheng, B.; Wang, W. Modeling trajectories with recurrent neural networks. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; IJCAI’17. pp. 3083–3090. [Google Scholar]
- Jain, J.; Bagadia, V.; Manchanda, S.; Ranu, S. NEUROMLR: Robust & reliable route recommendation on road networks. In Proceedings of the 35th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 6–14 December 2021. NIPS ’21. [Google Scholar]
- van der Pol, M.; Currie, G.; Kromm, S.; Ryan, M. Specification of the Utility Function in Discrete Choice Experiments. Value Health 2014, 17, 297–301. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Li, C.; Tang, H.; Ge, Y.; Shan, Y.; Li, G. ST-LLM: Large Language Models Are Effective Temporal Learners. In Proceedings of the Computer Vision—ECCV 2024: 18th European Conference, Milan, Italy, 29 September–4 October 2024; Proceedings, Part LVII. Springer: Berlin/Heidelberg, Germany, 2024; pp. 1–18. [Google Scholar] [CrossRef]
- Li, Z.; Xia, L.; Tang, J.; Xu, Y.; Shi, L.; Xia, L.; Yin, D.; Huang, C. UrbanGPT: Spatio-Temporal Large Language Models. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; KDD ’24. pp. 5351–5362. [Google Scholar] [CrossRef]
- Zhang, R.; Han, L.; Sun, L.; Liu, Y.; Wang, J.; Lv, W. Regions are Who Walk Them: A Large Pre-trained Spatiotemporal Model Based on Human Mobility for Ubiquitous Urban Sensing. arXiv 2023, arXiv:2311.10471. [Google Scholar] [CrossRef]
- Wei, J.; Tay, Y.; Bommasani, R.; Raffel, C.; Zoph, B.; Borgeaud, S.; Yogatama, D.; Bosma, M.; Zhou, D.; Metzler, D.; et al. Emergent Abilities of Large Language Models. Trans. Mach. Learn. Res. 2022. [Google Scholar] [CrossRef]
- Dantzig, G.B. Linear Programming and Extensions; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Sunita; Garg, D. Dynamizing Dijkstra: A solution to dynamic shortest path problem through retroactive priority queue. J. King Saud Univ.-Comput. Inf. Sci. 2021, 33, 364–373. [Google Scholar] [CrossRef]
- Sever, D.; Zhao, L.; Dellaert, N.; Demir, E.; Van Woensel, T.; De Kok, T. The dynamic shortest path problem with time-dependent stochastic disruptions. Transp. Res. Part C Emerg. Technol. 2018, 92, 42–57. [Google Scholar] [CrossRef]
- Liu, D.; Li, D.; Gao, K.; Song, Y.; Zhang, T. Enhancing choice-set generation and route choice modeling with data- and knowledge-driven approach. Transp. Res. Part C Emerg. Technol. 2024, 162, 104618. [Google Scholar] [CrossRef]
- Crivellari, A.; Beinat, E. LSTM-Based Deep Learning Model for Predicting Individual Mobility Traces of Short-Term Foreign Tourists. Sustainability 2020, 12, 349. [Google Scholar] [CrossRef]
- Guo, C.; Yang, B.; Hu, J.; Jensen, C. Learning to Route with Sparse Trajectory Sets. In Proceedings of the 2018 IEEE 34th International Conference on Data Engineering (ICDE), Paris, France, 16–19 April 2018; pp. 1073–1084. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Li, K.; Yuan, H. A Deep Generative Model for Trajectory Modeling and Utilization. Proc. VLDB Endow. 2022, 16, 973–985. [Google Scholar] [CrossRef]
- Xiong, Z.; Wang, Y.; Tian, Y.; Liu, L.; Zhu, S. RoPT: Route-Planning Model with Transformer. Appl. Sci. 2025, 15, 4914. [Google Scholar] [CrossRef]
- Cao, J.; Zheng, T.; Guo, Q.; Wang, Y.; Dai, J.; Liu, S.; Yang, J.; Song, J.; Song, M. Holistic semantic representation for navigational trajectory generation. In Proceedings of the Thirty-Ninth AAAI Conference on Artificial Intelligence and Thirty-Seventh Conference on Innovative Applications of Artificial Intelligence and Fifteenth Symposium on Educational Advances in Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025. AAAI’25/IAAI’25/EAAI’25. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J.; Cao, W.; Li, J.; Zheng, Y. When will you arrive? estimating travel time based on deep neural networks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence and Thirtieth Innovative Applications of Artificial Intelligence Conference and Eighth AAAI Symposium on Educational Advances in Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. AAAI’18/IAAI’18/EAAI’18. [Google Scholar]
- Ren, Y.; Chen, Y.; Liu, S.; Wang, B.; Yu, H.; Cui, Z. TPLLM: A Traffic Prediction Framework Based on Pretrained Large Language Models. arXiv 2024, arXiv:cs.LG/2403.02221. [Google Scholar] [CrossRef]
- Yuan, Y.; Ding, J.; Feng, J.; Jin, D.; Li, Y. UniST: A Prompt-Empowered Universal Model for Urban Spatio-Temporal Prediction. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; KDD ’24. pp. 4095–4106. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, G.; Sukhatme, G.S. Can Large Language Models Solve Robot Routing? arXiv 2024, arXiv:cs.CL/2403.10795. [Google Scholar]
- Wang, L.; Duan, P.; He, Z.; Lyu, C.; Chen, X.; Zheng, N.; Yao, L.; Ma, Z. AI-Driven Day-to-Day Route Choice. arXiv 2024, arXiv:cs.LG/2412.03338. [Google Scholar]
- Marcelyn, S.C.; Gao, Y.; Zhang, Y.; Gao, X.; Chen, G. PathGPT: Leveraging Large Language Models for Personalized Route Generation. arXiv 2025, arXiv:cs.IR/2504.05846. [Google Scholar] [CrossRef]
- Su, J.; Ahmed, M.; Lu, Y.; Pan, S.; Bo, W.; Liu, Y. RoFormer: Enhanced transformer with Rotary Position Embedding. Neurocomputing 2024, 568, 127063. [Google Scholar] [CrossRef]
- Ainslie, J.; Lee-Thorp, J.; de Jong, M.; Zemlyanskiy, Y.; Lebrón, F.; Sanghai, S. GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints. arXiv 2023, arXiv:cs.CL/2305.13245. [Google Scholar]
- Dao, T.; Fu, D.; Ermon, S.; Rudra, A.; Ré, C. FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness. In Proceedings of the Advances in Neural Information Processing Systems; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2022; Volume 35, pp. 16344–16359. [Google Scholar]
- Newson, P.; Krumm, J. Hidden Markov map matching through noise and sparseness. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; GIS ’09. pp. 336–343. [Google Scholar] [CrossRef]
- Shlegeris, B.; Roger, F.; Chan, L.; McLean, E. Language Models Are Better Than Humans at Next-token Prediction. Trans. Mach. Learn. Res. 2024. [Google Scholar] [CrossRef]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 6–12 December 2020. NIPS ’20. [Google Scholar]
- Singh, C.; Inala, J.P.; Galley, M.; Caruana, R.; Gao, J. Rethinking Interpretability in the Era of Large Language Models. arXiv 2024, arXiv:cs.CL/2402.01761. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).