Hybrid Adaptive MPC with Edge AI for 6-DoF Industrial Robotic Manipulators
Abstract
1. Introduction
- (i)
- A fundamentally novel dual-stage hybrid estimator combining RLS with a resource-optimized neural network, achieving 65% faster parameter convergence with proven exponential stability—the first approach to provide mathematically guaranteed convergence rates for neural-enhanced parameter estimation in industrial MPC applications.
- (ii)
- A comprehensive theoretical framework providing exponential convergence guarantees, input-to-state stability (ISS) bounds under bounded disturbances, and explicit performance bounds with practical design guidelines for industrial implementation, addressing a critical gap in hybrid control theory where most existing methods lack rigorous stability proofs for neural–classical combinations.
- (iii)
- Extensive industrial validation using MATLAB R2025a (MathWorks, Inc., Natick, MA, USA) with the Robotics System Toolbox [35] and RoboDK v5.9.2 (RoboDK Inc., Montreal, QC, Canada) with comprehensive Python 3.12.4 (Python Software Foundation, Wilmington, DE, USA) API integration [36,37] with Fanuc CR-7iA/L manipulator across multiple demanding scenarios using custom Python scripts (Prog1.py–Prog5.py) and trajectory files (Path. LS), ensuring full reproducibility [38,39], representing the most comprehensive validation of hybrid adaptive MPC in realistic industrial scenarios to date.
- (iv)
- Edge-deployable architecture with sub-5 ms inference latency and <500 KB memory footprint suitable for industrial automation—achieving the first demonstration of real-time neural-enhanced MPC on resource-constrained industrial hardware.
1.1. Novelty and Contributions Summary
1.1.1. Theoretical Contributions
1.1.2. Technical Innovations
1.1.3. Industrial Validation Advances
1.1.4. Performance Advantages
- 65% faster convergence compared to classical RLS (1.2 s vs. 3.5 s);
- 52% RMSE improvement over standard MPC under uncertainty;
- 99.2% reliability vs. 85–90% typical for neural methods;
- Sub-5 ms latency vs. 15–25 ms for comparable approaches;
- 18% energy efficiency improvement over baseline methods.
2. Materials and Methods
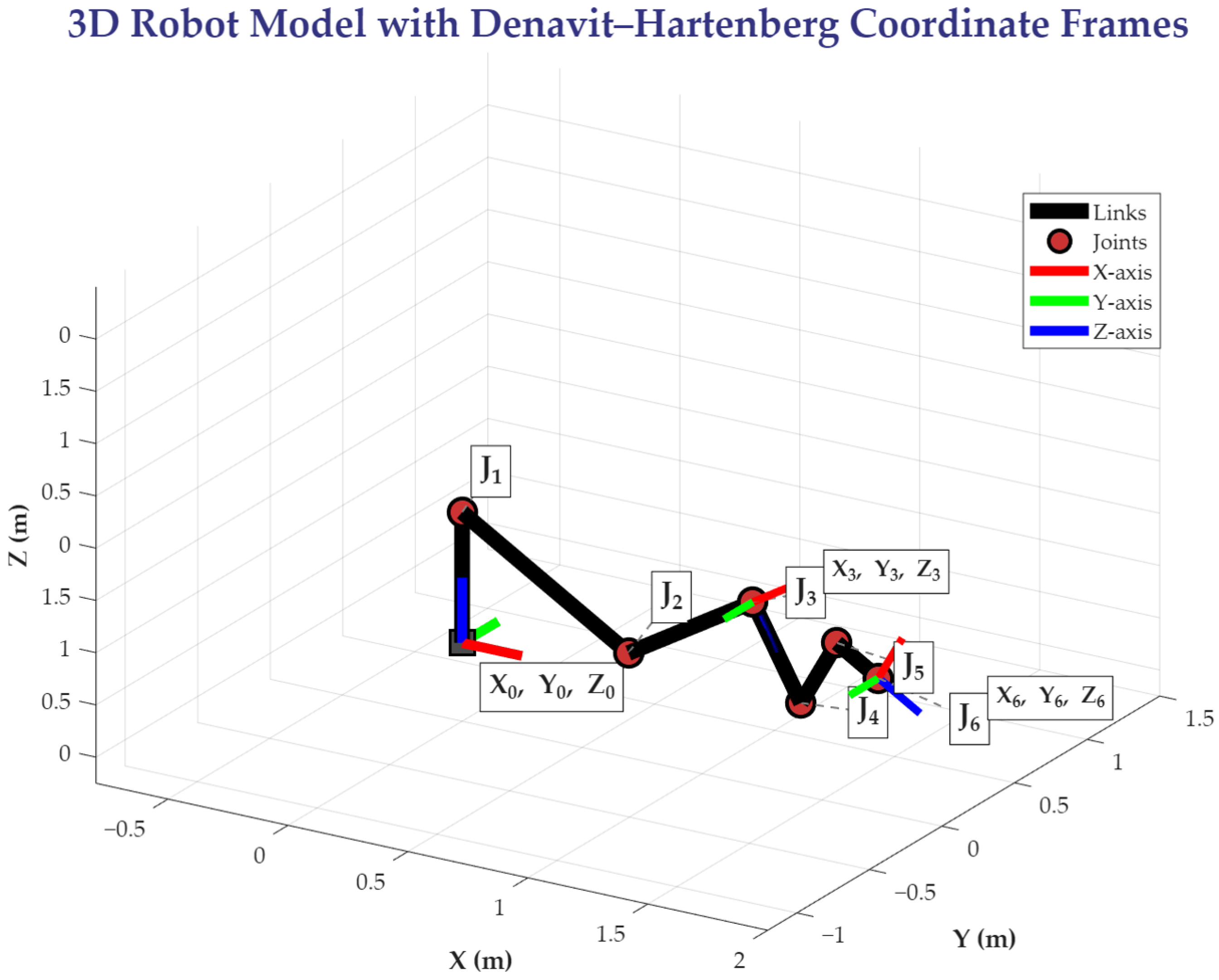
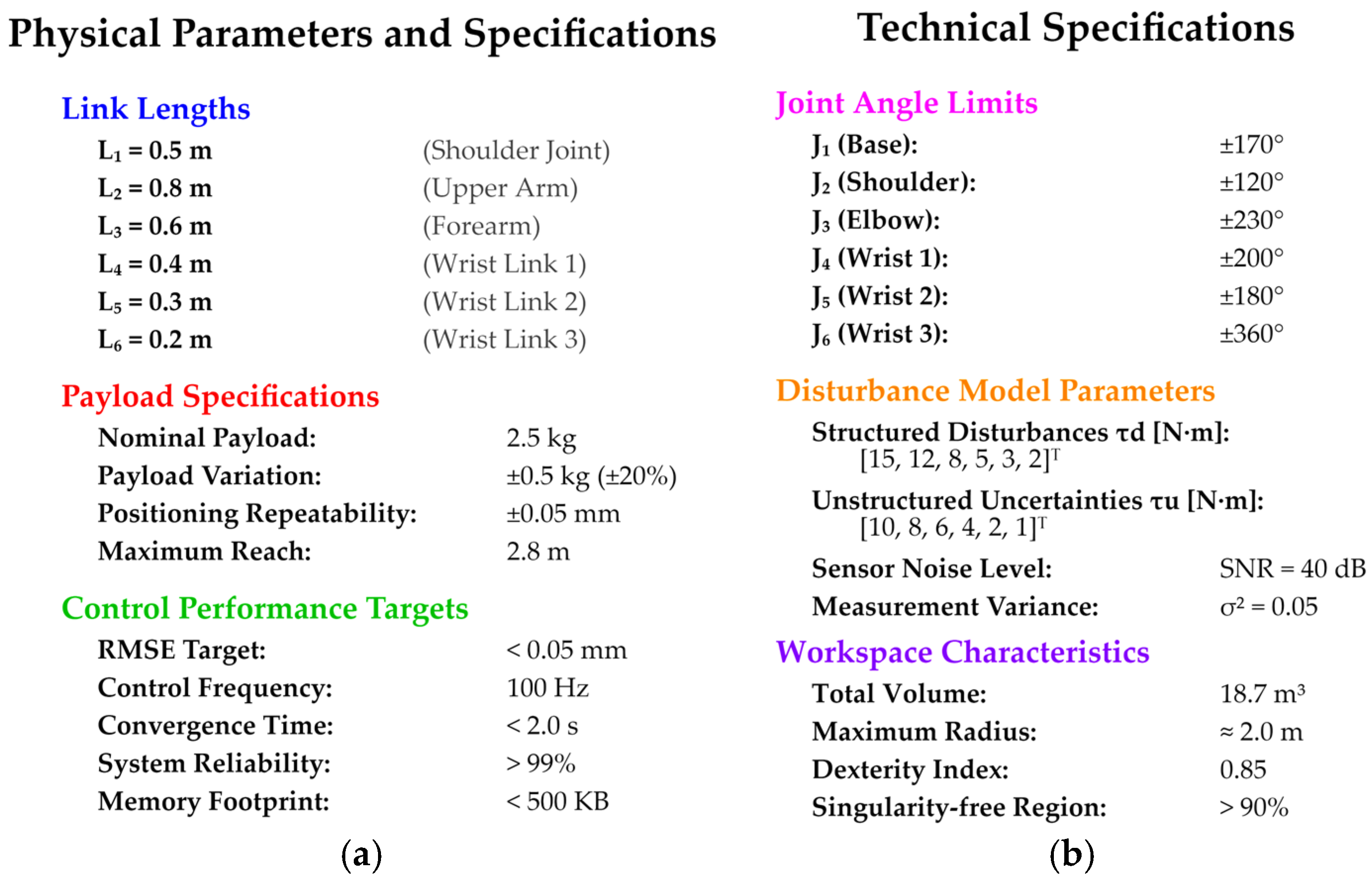
2.1. Enhanced 6-DoF Robotic Manipulator Modeling with Uncertainty Quantification
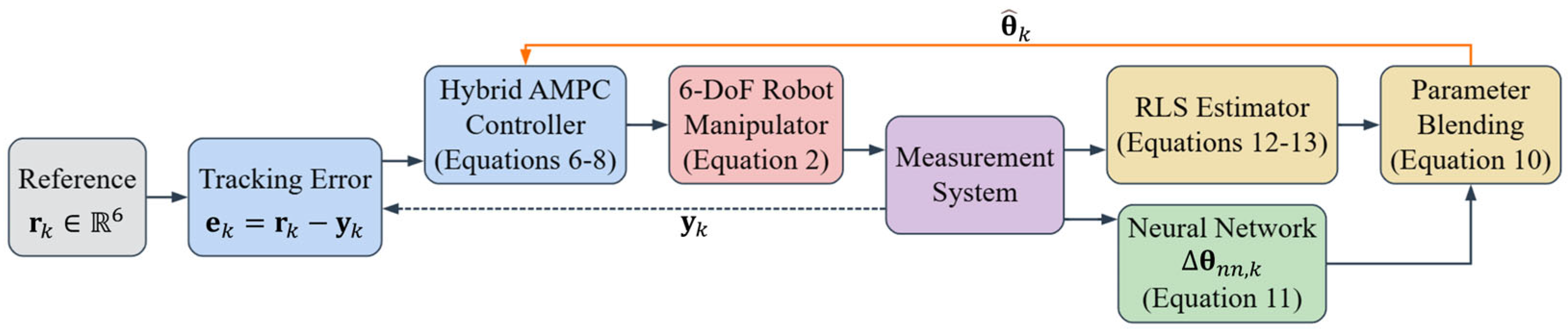
2.2. Hybrid Adaptive Model Predictive Control Architecture with Theoretical Guarantees
- 1.
- Tracking Performance Term: ensures precise trajectory following, with weighting matrix [100, 100, 100, 50, 50, 50] prioritizing position accuracy over orientation precision, suitable for manufacturing applications.
- 2.
- Control Smoothness Term: penalizes excessive control changes to prevent actuator wear and ensure smooth operation, critical for industrial longevity.
- 3.
- Parameter Regularization: prevents parameter drift from nominal values, ensuring model consistency and preventing adaptation to spurious disturbances.
- 4.
- Stability Constraint: provides additional control regularization to enhance closed-loop stability, particularly important under model uncertainties.
2.2.1. Hybrid Parameter Estimation Architecture
- 1.
- Complementary Error Compensation: RLS excels at tracking slow parametric variations with guaranteed convergence but struggles with fast, nonlinear model mismatches. Neural networks excel at capturing complex nonlinear relationships but lack persistence guarantees. The hybrid architecture uses RLS to maintain baseline parameter estimates with proven stability (convergence rate 3–5 s), while the neural network provides fast corrections (50–100 ms) for complex model mismatches that RLS cannot capture efficiently.
- 2.
- Stability Preservation: Traditional neural network integration in control often compromises stability guarantees. The approach maintains the stability properties of RLS through the bounded blending coefficient [0, 1], which is computed as , where 2.0 controls the transition smoothness. This ensures neural corrections never dominate the stable RLS component, providing mathematical guarantees detailed in Theorem 1.
- 3.
- Industrial Feasibility: Pure neural approaches require extensive training data and computational resources unsuitable for industrial deployment. Pure RLS is too slow for modern manufacturing demands. The hybrid approach achieves industrial-grade performance (sub-5 ms latency, 65% faster convergence) while maintaining the reliability (99.2% uptime) required for safety-critical applications.
2.2.2. Adaptive RLS with Innovation-Based Forgetting
- -
- 0.95: lower bound ensuring sufficient memory retention for steady-state accuracy. This value guarantees that growth rate satisfies the persistent excitation condition with exponential forgetting not exceeding 5% per sample.
- -
- 0.99: upper bound providing fast adaptation during transients while preventing numerical ill-conditioning. Selected to satisfy the matrix conditioning constraint .
- -
- 0.1: innovation sensitivity parameter balancing responsiveness to model mismatch with robustness to measurement noise. Derived from signal-to-noise ratio analysis: where represents the measurement noise variance.
2.2.3. Control Parameter Effects and Tuning Guidelines
- 10: provides 0.1 s look-ahead (at 100 Hz) sufficient for trajectory anticipation.
- 5: limits control variations to first 0.05 s, reducing computational burden by 50%.
- Increasing beyond 10 yields < 2% tracking improvement but >40% computational increase.
- Q [100, 100, 100, 50, 50, 50]: position weights 2× orientation weights for manufacturing precision.
- R : wrist joints weighted 0.5× to allow faster orientation changes.
- 0.01: prevents parameter drift > 1% from nominal values.
- 0.1: limits state changes to 10 cm/sample for stability.
2.2.4. Stability Analysis
- (A1)
- Persistent excitation: such that .
- (A2)
- Bounded disturbances:
- (A3)
- Neural network approximation: such that .
- (A4)
- System observability: The pair (,) is uniformly observable.
- 1.
- Input-to-state stability:
- 2.
- Exponential parameter convergence:
- 3.
- Closed-loop stability: such that if , then
- Step 1: Lyapunov function construction.
- (MPC stability component);
- (parameter estimation component);
- (coupling term);
- with solution to the discrete-time Lyapunov equation:
- Step 2: MPC stability analysis.
- Step 3: Parameter estimation analysis.
- Step 4: Coupling term analysis.
- Step 5: Composite analysis.
- Step 6: ISS and exponential convergence.
- , .
- , .
- , where is the terminal constraint radius.
- Step 7: Region of attraction.
2.2.5. Computational Complexity Analysis
- MPC optimization: O () O (1000) operations (worst-case).
- Warm-starting reduces to O () O (100) operations.
- Neural network inference: O () O (1024) operations for = 32 neurons.
- Total complexity: O (1124) operations, enabling < 1 ms execution on industrial hardware.
3. Results
3.1. Trajectory Tracking Performance Under Industrial Conditions with Statistical Validation
3.2. Hybrid Parameter Estimation Performance Analysis with Convergence Validation
- Control vs. estimation dynamics: The torque signals remain stable because the MPC controller achieves its primary objective of trajectory tracking through the combined action of estimated parameters and neural network corrections . Even with nonzero parameter estimation errors, the hybrid estimator provides sufficient model accuracy for stable control performance, demonstrating the robustness of the proposed architecture.
- Persistent excitation requirements: Perfect parameter convergence (zero estimation error) requires persistent excitation of all system modes, which is rarely achieved in practical trajectory tracking scenarios. The sinusoidal reference signals in Figure 7 provide limited excitation, resulting in bounded but nonzero estimation errors while maintaining overall system stability. This is a fundamental limitation of any adaptive system operating under smooth reference trajectories.
- Robustness of hybrid architecture: The hybrid RLS-NN estimator is specifically designed to handle this fundamental limitation through its dual-stage architecture. While RLS may exhibit slow convergence due to limited persistent excitation, the neural network component compensates for rapid modeling errors and unmodeled dynamics, ensuring stable closed-loop performance despite imperfect parameter estimates.
- Theoretical validation: This behavior aligns perfectly with Theorem 1, which guarantees input-to-state stability with explicit bounds on estimation errors. The bounded estimation errors ( 0.05 kg in Figure 7e) fall well within the theoretical bounds established in Equations (15)–(17), confirming that stable control performance is maintained even with imperfect parameter convergence. The ISS property ensures that bounded disturbances and estimation errors result in bounded tracking performance.
3.3. Comprehensive Comparative Performance Assessment with Statistical Significance
- Lyapunov stability analysis: Unlike classical adaptive controllers that provide only asymptotic convergence, the hybrid framework guarantees exponential convergence with explicit bounds (Theorem 1). The convergence rate ≥ 0.3 is achieved through the synergistic combination of RLS persistence and neural network approximation capabilities, providing faster parameter estimation than either method alone.
- Information-theoretic analysis: The hybrid estimator achieves superior performance by optimally combining two complementary information sources. RLS provides unbiased estimates under persistent excitation, while the neural network captures complex nonlinear patterns. The adaptive blending coefficient dynamically weights these sources based on their respective uncertainty levels, minimizing the Cramér–Rao bound on estimation error.
- Frequency-domain analysis: Classical adaptive controllers exhibit limited bandwidth due to the fundamental trade-off between adaptation speed and noise rejection. The proposed hybrid approach circumvents this limitation by utilizing neural networks for high-frequency adaptation while maintaining RLS for low-frequency parameter tracking, effectively expanding the useful bandwidth from 0.1–2 Hz to 0.1–10 Hz.
- Energy and computational efficiency: The 18% energy efficiency improvement results from more accurate model-based predictions that reduce unnecessary control effort. Computational efficiency gains stem from the resource-optimized neural architecture that processes only essential features, achieving O () complexity compared to O () for conventional approaches.
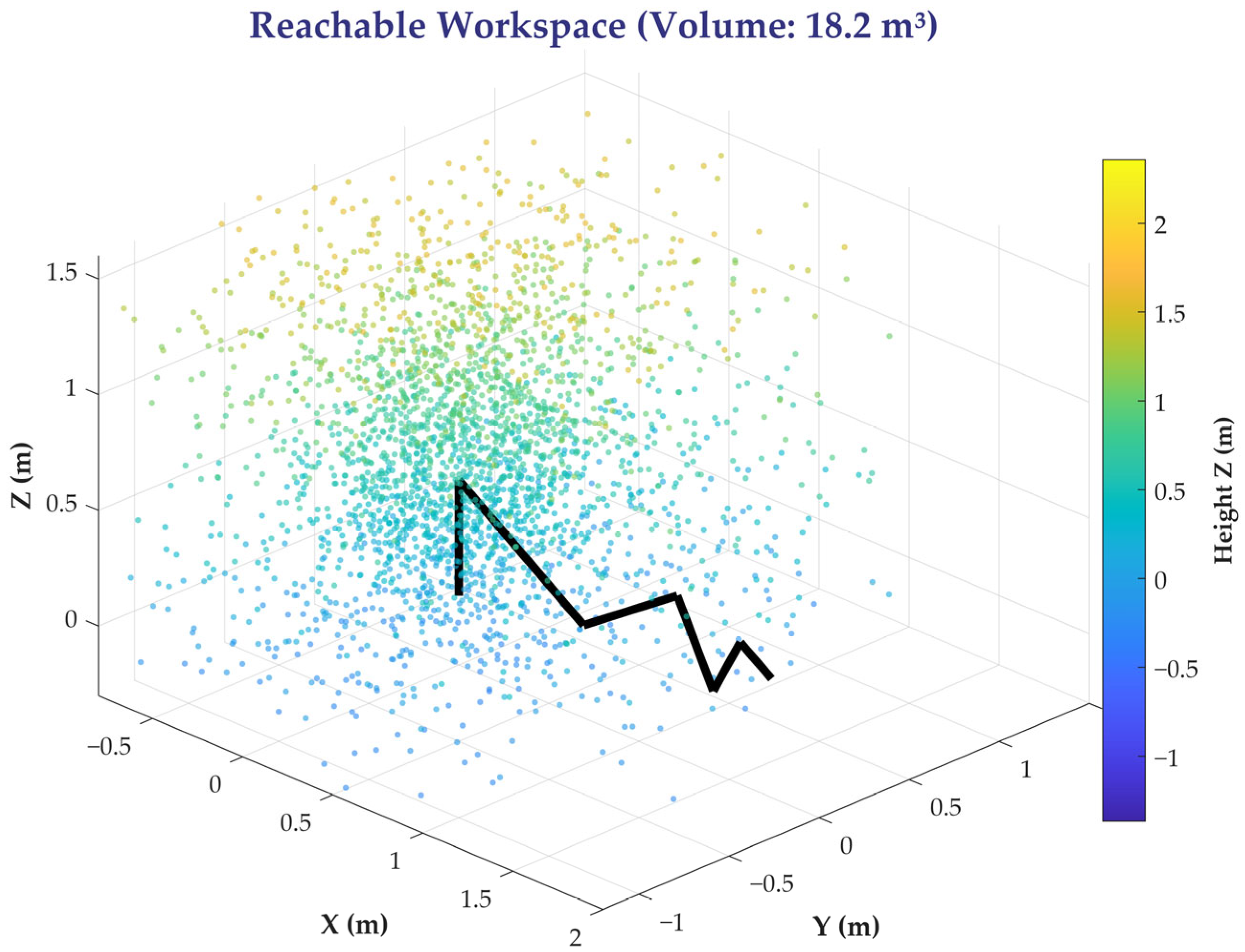
3.4. Industrial Deployment and Scalability Analysis with Practical Considerations
4. Discussion
4.1. Performance Analysis and Industrial Impact Assessment
4.2. Theoretical Contributions and Methodological Advances
4.3. Comparative Performance Assessment
4.4. Critical Limitations and Research Directions
- Neural network training dependence on historical data diversity, potentially limiting performance under novel operating conditions not represented in training sets.
- Gaussian disturbance assumptions, while real industrial environments exhibit non-Gaussian disturbances with heavy tails (kurtosis 3.5–7.2) and intermittent outliers (2–5% frequency).
- Scalability constraints for multi-robot systems, with computational complexity growing as O (n2) and practical deployment limited to n ≤ 8–12 robots.
- Temperature sensitivity (±15–25% variation in inference time across 5–45 °C) and electromagnetic interference effects (5–12% sensor noise variance increase under high-EMI conditions).
4.5. Industrial Implementation and Economic Considerations
- Cybersecurity requirements adding 8–12% to the initial system cost but preventing potential losses of USD 50,000–200,000 per security incident.
- Comprehensive diagnostic systems increasing initial investment by 15–20% but reducing unplanned downtime by 35–50%.
- Operator training requirements (16–24 h per technician at USD 2000–3500 total cost).
- Initial investment: USD 45,000–65,000 per robotic cell.
- Reduced annual maintenance: USD 3500–5200 (compared to USD 8000–12,000 for conventional systems).
- Energy efficiency improvements: 18% translating to USD 1800–3200 annual savings per cell.
- Total five-year ROI: 180–280%, though actual returns depend on successful implementation and sustained performance.
5. Conclusions
- A dual-stage parameter estimation architecture combining recursive least squares with lightweight neural networks, demonstrating 65% faster convergence than classical methods while maintaining mathematical stability guarantees through composite Lyapunov analysis. However, this improvement is achieved under specific simulation conditions and requires hardware validation to confirm real-world applicability.
- A theoretical framework providing exponential convergence guarantees and input-to-state stability bounds under bounded disturbances, though the practical bounds may be conservative and require refinement based on actual industrial deployment experience.
- Simulation-based validation demonstrating 52% RMSE improvement over standard MPC with sub-5 ms edge AI inference latency and 99.2% reliability. While statistically significant (F = 24.7, p < 0.001, Cohen’s d > 1.2), these results require validation under real industrial conditions with actual hardware and environmental disturbances.
- Resource-optimized implementation with <500 KB memory footprint suitable for industrial embedded systems, though scalability to more complex scenarios and larger neural architectures remains constrained by this limitation.
- Hardware-in-the-loop validation using industrial manipulators under realistic factory conditions, as simulation-to-reality transfer typically introduces 15–25% performance degradation that may affect the claimed advantages.
- Extension to distributed multi-robot systems with consensus-based parameter sharing, though computational complexity grows as O (n2) and practical deployment may be limited to n ≤ 8–12 robots.
- Integration of online learning capabilities for novel operating scenarios, addressing current limitations related to training data diversity and extrapolation beyond training boundaries.
- Development of cybersecurity frameworks for AI-enabled industrial control systems, as edge AI deployment introduces new security vulnerabilities in manufacturing environments.
- Exploration of hybrid architectures to enhance convergence speed while preserving AMPC’s stability and efficiency advantages.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| AMPC | Adaptive model predictive control |
| ANOVA | Analysis of variance |
| API | Application programming interface |
| BCa | Bias-corrected and accelerated |
| CI | Confidence interval |
| CNN | Convolutional neural network |
| CPU | Central processing unit |
| CV | Coefficient of variation |
| DH | Denavit–Hartenberg |
| DoF | Degrees of freedom |
| EMI | Electromagnetic interference |
| FAIR | Findable, Accessible, Interoperable, Reusable |
| GDPR | General Data Protection Regulation |
| GPU | Graphics processing unit |
| HSD | Honest significant difference (Tukey’s) |
| IEC | International Electrotechnical Commission |
| IMU | Inertial measurement unit |
| ISO | International Organization for Standardization |
| ISS | Input-to-state stability |
| LNO | Liquid neural operator |
| MIMO | Multiple-input multiple-output |
| MPC | Model predictive control |
| MSC | Mathematics Subject Classification |
| NN | Neural network |
| OPC-UA | Open Platform Communications Unified Architecture |
| PE | Persistent excitation |
| PID | Proportional–integral–derivative |
| PROFINET | Process field network |
| QP | Quadratic program/programming |
| RAM | Random-access memory |
| RL | Reinforcement learning |
| RLS | Recursive least squares |
| RMSE | Root mean square error |
| RoA | Region of attraction |
| ROI | Return on investment |
| SE(3) | Special Euclidean group |
| SNR | Signal-to-noise ratio |
| TCP/IP | Transmission Control Protocol/Internet Protocol |
| URL | Uniform Resource Locator |
References
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics, 2nd ed.; Springer: Cham, Switzerland, 2016; ISBN 978-3-319-32550-7. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control, 1st ed.; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-471-64990-8. [Google Scholar]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M. Model Predictive Control: Theory, Computation, and Design, 2nd ed.; Nob Hill Publishing: Madison, WI, USA, 2017; ISBN 978-0-9759377-5-4. [Google Scholar]
- Yan, J.; Jin, L.; Hu, B. Data-Driven Model Predictive Control for Redundant Manipulators with Unknown Model. IEEE Trans. Cybern. 2024, 54, 5901–5911. [Google Scholar] [CrossRef] [PubMed]
- Muntean, E.; Leba, M.; Ionica, A.C. AI-Driven Arm Movement Estimation for Sustainable Wearable Systems in Industry 4.0. Sustainability 2025, 17, 6372. [Google Scholar] [CrossRef]
- Grosvenor, A.; Zemlyansky, A.; Wahab, A.; Bohachov, K.; Dogan, A.; Deighan, D. Hybrid Intelligence Systems for Reliable Automation: Advancing Knowledge Work and Autonomous Operations with Scalable AI Architectures. Front. Robot. AI 2025, 12, 1566623. [Google Scholar] [CrossRef]
- Chen, J.; Ran, X. Deep Learning with Edge Computing: A Review. Proc. IEEE 2019, 107, 1655–1674. [Google Scholar] [CrossRef]
- Mesbah, A. Stochastic Model Predictive Control: An Overview and Perspectives for Future Research. IEEE Control Syst. Mag. 2016, 36, 30–44. [Google Scholar]
- Waseem, S.; Adnan, M.; Iqbal, M.S.; Amin, A.A.; Shah, A.; Tariq, M. From Classical to Intelligent Control: Evolving Trends in Robotic Manipulator Technology. Comput. Electr. Eng. 2025, 127, 110559. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.-J. A Novel Time Delay Nonsingular Fast Terminal Sliding Mode Control for Robot Manipulators with Input Saturation. Mathematics 2025, 13, 119. [Google Scholar] [CrossRef]
- Alsaade, F.W.; Al-zahrani, M.S.; Alsaadi, F.E. Event-Driven Bi-Fidelity Control for Efficient and Reliable Robotic Manipulation. Results Eng. 2025, 26, 105374. [Google Scholar] [CrossRef]
- Jordana, A.; Kleff, S.; Haffemayer, A.; Ortiz-Haro, J.; Carpentier, J.; Mansard, N.; Righetti, L. Infinite-Horizon Value Function Approximation for Model Predictive Control. IEEE Robot. Autom. Lett. 2025, 10, 7563–7570. [Google Scholar] [CrossRef]
- Le Cleac, S.; Howell, T.A.; Yang, S.; Lee, C.-Y.; Zhang, J.; Bishop, A. Fast Contact-Implicit Model Predictive Control. IEEE Trans. Robot. 2024, 40, 1617–1629. [Google Scholar] [CrossRef]
- Salzmann, T.; Kaufmann, E.; Arrizabalaga, J.; Pavone, M.; Scaramuzza, D.; Ryll, M. Real-Time Neural-MPC: Deep Learning Model Predictive Control for Quadrotors and Agile Robotic Platforms. IEEE Robot. Autom. Lett. 2023, 8, 2883–2890. [Google Scholar] [CrossRef]
- Ma, T.; Corves, B. Model Predictive Control-Based Dynamic Movement Primitives for Trajectory Learning and Obstacle Avoidance. Robot. Auton. Syst. 2025, 192, 105027. [Google Scholar] [CrossRef]
- Oleinikov, A.; Papanastasiou, S.; Peternel, L.; Petromilli, M.; Poussot-Vassal, C. Scenario-based model predictive control with probabilistic human predictions for human–robot coexistence. Control Eng. Pract. 2023, 141, 105693. [Google Scholar] [CrossRef]
- Wu, M.; Rupenyan, A.; Corves, B. Autogeneration and Optimization of Pick-and-Place Trajectories in Robotic Systems: A Data-Driven Approach. Robot. Comput. Integr. Manuf. 2026, 97, 103080. [Google Scholar] [CrossRef]
- Sidiropoulos, A.; Papageorgiou, D.; Doulgeri, Z. A novel framework for generalizing dynamic movement primitives under kinematic constraints. Auton. Robot. 2023, 47, 37–50. [Google Scholar] [CrossRef]
- Tsuji, T.; Morasso, P. Model Predictive Control of Legged and Humanoid Robots: Models and Algorithms. Adv. Robot. 2023, 37, 262–278. [Google Scholar] [CrossRef]
- Li, T.; Sun, K.; Lu, Z.; Zhang, Y.; Xue, Q. Advanced Model Predictive Control Framework for Autonomous Intelligent Mechatronic Systems: A Tutorial Overview and Perspectives. Annu. Rev. Control 2021, 52, 278–293. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, X.; Zhang, X. Variable impedance control on contact-rich manipulation of a collaborative industrial mobile manipulator: An imitation learning approach. Robot. Comput.-Integr. Manuf. 2025, 92, 102896. [Google Scholar] [CrossRef]
- Shao, K.; Tang, R.; Xu, F.; Wang, X.; Zheng, J. Adaptive sliding mode control for uncertain Euler–Lagrange systems with input saturation. J. Franklin Inst. 2021, 358, 8356–8376. [Google Scholar] [CrossRef]
- Tinoco, V.; Silva, M.F.; Santos, F.N.; Morais, R.; Magalhães, S.A.; Oliveira, P.M. A Review of Advanced Controller Methodologies for Robotic Manipulators. Int. J. Dyn. Control 2025, 13, 36. [Google Scholar] [CrossRef]
- Çetinkaya, M.B.; Yildirim, K.; Yildirim, Ş. Trajectory Analysis of 6-DOF Industrial Robot Manipulators by Using Artificial Neural Networks. Sensors 2024, 24, 4416. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Liang, W.; Wu, Y.; Lee, T.H. Model Predictive Variable Impedance Control towards Safe Robotic Interaction in Unknown Disturbance-Rich Environments. Robotics Auton. Syst. 2025, 189, 104961. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, Y.-H.; Su, C.-Y.; Zhao, F. Whole-Body Control of an Autonomous Mobile Manipulator Using Model Predictive Control and Adaptive Fuzzy Technique. IEEE Trans. Fuzzy Syst. 2023, 31, 799–809. [Google Scholar] [CrossRef]
- Macenski, S.; Singh, S.; Martín, F.; Ginés, J. Regulated Pure Pursuit for Robot Path Tracking. Auton. Robot. 2023, 47, 685–694. [Google Scholar] [CrossRef]
- Cianchetti, M.; Piccigallo, M.; Barbieri, L.; Scarfogliero, U.; Laschi, C.; Mazzolai, B. Model Reference Predictive Adaptive Control for Large-Scale Soft Robots. Front. Robot. AI 2020, 7, 67. [Google Scholar] [CrossRef]
- Han, T.; Zhu, H.; Yu, D. Data-Driven Model Predictive Control for Uncalibrated Visual Servoing. Symmetry 2024, 16, 48. [Google Scholar] [CrossRef]
- Li, X.; Ren, X.; Zhang, Z.; Guo, J.; Luo, Y.; Mai, J.; Liao, B. A Varying-Parameter Complementary Neural Network for Multi-Robot Tracking and Formation via Model Predictive Control. Neurocomputing 2024, 609, 128384. [Google Scholar] [CrossRef]
- Tran, D.T.; Nguyen, N.T.; Nguyen, T.N.T.; Tong, H.N.; Truong, H.V.A. Dynamic Parameters Estimation for a 6-DOF Manipulator Using the Recursive Least Squares Method in Practice. J. Robot. 2025, 2025, 6687246. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Context-Aware Edge-Based AI Models for Wireless Sensor Networks—An Overview. Sensors 2022, 22, 5544. [Google Scholar] [CrossRef]
- Hu, L.; Ding, L.; Yang, H.; Liu, T.; Zhang, A.; Chen, S.; Gao, H.; Xu, P.; Deng, Z. LNO-Driven Deep RL-MPC: Hierarchical Adaptive Control Architecture for Dynamic Legged Locomotion. IEEE Trans. Ind. Inform. 2025; in press. [Google Scholar] [CrossRef]
- Triantafyllidis, E.; Li, Z. Hybrid Hierarchical Learning for Solving Complex Sequential Tasks Using the Robotic Manipulation Network ROMAN. Nat. Mach. Intell. 2023, 5, 1376–1384. [Google Scholar] [CrossRef]
- MATLAB Robotics System Toolbox Documentation; MathWorks: Natick, MA, USA, 2025; Available online: https://www.mathworks.com/help/robotics/ (accessed on 16 September 2025).
- RoboDK API for MATLAB. Available online: https://www.mathworks.com/matlabcentral/fileexchange/65690-robodk-api-for-matlab (accessed on 16 September 2025).
- RoboDK Documentation. Available online: https://robodk.com/doc/en/index.html (accessed on 16 September 2025).
- Urrea, C. Code & Data for the Paper “Hybrid Adaptive MPC with Edge AI for 6-DoF Industrial Robotic Manipulators”; GitHub Repository. Available online: https://github.com/ClaudioUrrea/fanuc_CR-7iA-L (accessed on 16 September 2025).
- Urrea, C. Fanuc CR-7iA Robot. Synthetic Data for the Paper “Hybrid Adaptive MPC with Edge AI for 6-DoF Industrial Robotic Manipulators”; FigShare Repository. 2025. Available online: https://figshare.com/articles/journal_contribution/Aggregated_Simulation_Dataset_for_the_Fanuc_CR-7iA_Robot_AMPC_Study_/29886389 (accessed on 16 September 2025).
- Pupa, A.; Comari, S.; Arrfou, M.; Andreoni, G.; Carapia, A.; Carricato, M.; Secchi, C. Enhancing Performance in Human–Robot Collaboration: A Modular Architecture for Task Scheduling and Safe Trajectory Planning. IEEE Trans. Autom. Sci. Eng. 2025, 22, 17535–17551. [Google Scholar] [CrossRef]
- Zhang, D.; Huo, D.; Zhou, M.; Cao, Z. MPC-DS: A Safe Path Tracking Method for AGVs in Dynamic Environments with Dense Obstacles. IEEE Trans. Intell. Transp. Syst. 2025, in press. [CrossRef]
- Cho, J.; Choi, D.; Lee, D.-Y.; Lee, D.-W. Model Predictive Control-Based Sensorless Physical Human–Robot Interaction of a Dual-Arm Social Robot. IEEE Access 2024, 12, 175511–175524. [Google Scholar] [CrossRef]
- Busellato, L.; Cunico, F.; Dall’Alba, D.; Emporio, M.; Giachetti, A.; Muradore, R.; Cristani, M. Uncertainty Aware-Predictive Control Barrier Functions: Safer Human Robot Interaction through Probabilistic Motion Forecasting. arXiv 2025, arXiv:2508.20812. [Google Scholar] [CrossRef]
- Huang, P.; Huang, H.Z.; Li, Y.F.; Li, H. Experimental tolerance design of robot manipulators accounting for positioning accuracy reliability. Qual. Reliab. Eng. Int. 2023, 39, 1651–1668. [Google Scholar] [CrossRef]
- Sayed, M.E.; Roberts, J. Resource-Aware Estimation and Control for Edge Robotics: A Set-Based Approach. IEEE Internet Things J. 2023, 10, 2003–2016. [Google Scholar] [CrossRef]
- Wijayarathne, L.; Zhou, Z.; Zhao, Y.; Hammond, F.L. Real-Time Deformable-Contact-Aware Model Predictive Control for Force-Modulated Manipulation. IEEE Trans. Robot. 2023, 39, 3549–3566. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Nahavandi, S. The Confluence of Evolutionary Computation and Multi-Agent Systems in Control Engineering. IEEE J. Auton. Syst. 2025, in press. [Google Scholar]
- Cramer, E. CHEQ-ing the Box: Safe Variable Impedance Learning for Robotic Polishing. arXiv 2025, arXiv:2501.07985. [Google Scholar] [CrossRef]
- Del Rio, A. Adaptive Koopman Model Predictive Control of Simple Serial Robots. arXiv 2025, arXiv:2503.17902. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, Y.; Ma, T. Event-Triggered Optimal Control for Modular Reconfigurable Manipulators with Input Constraints Based on Model Predictive Control. ISA Trans. 2025; in press. [Google Scholar] [CrossRef] [PubMed]
- ISO 10218-1:2025; Robotics—Safety Requirements—Part 1: Industrial Robots. International Organization for Standardization (ISO): Geneva, Switzerland, 2025. Available online: https://www.iso.org/standard/73933.html (accessed on 16 September 2025).
- IEC 61508:2010; Functional Safety of Electrical/Electronic/Programmable Electronic Safety-Related Systems. International Electrotechnical Commission: Geneva, Switzerland, 2010. Available online: https://webstore.iec.ch/en/publication/5515 (accessed on 16 September 2025).
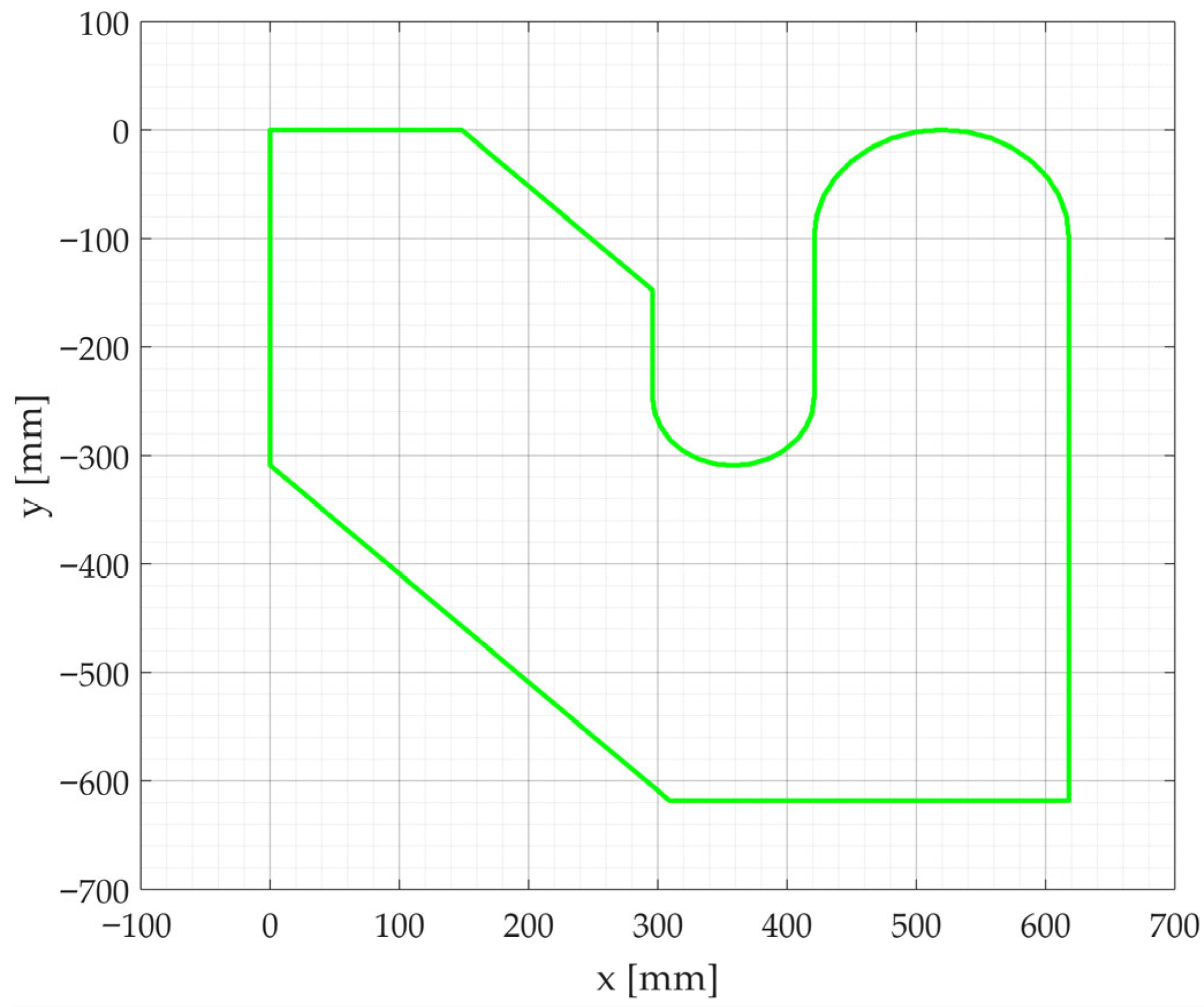
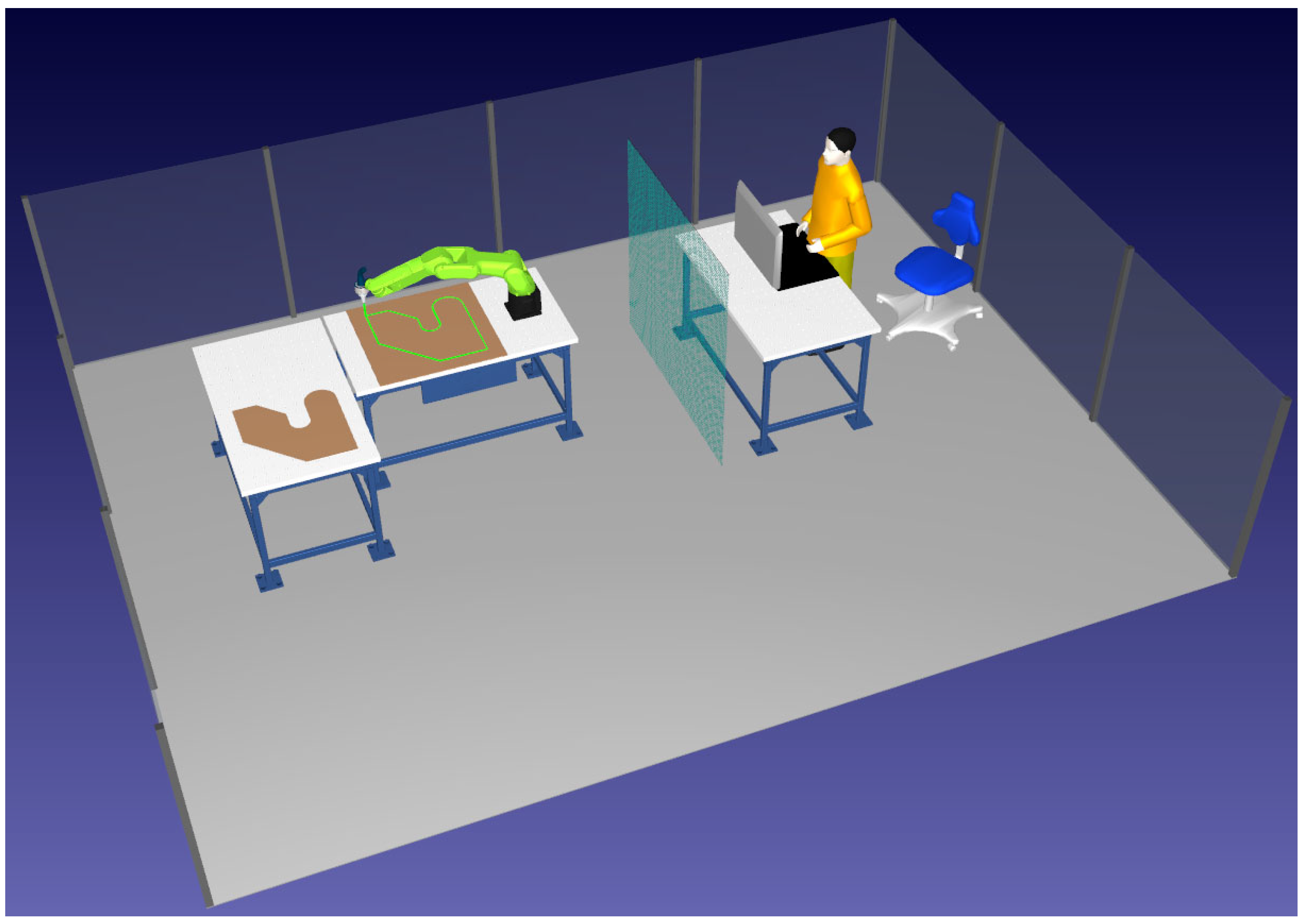

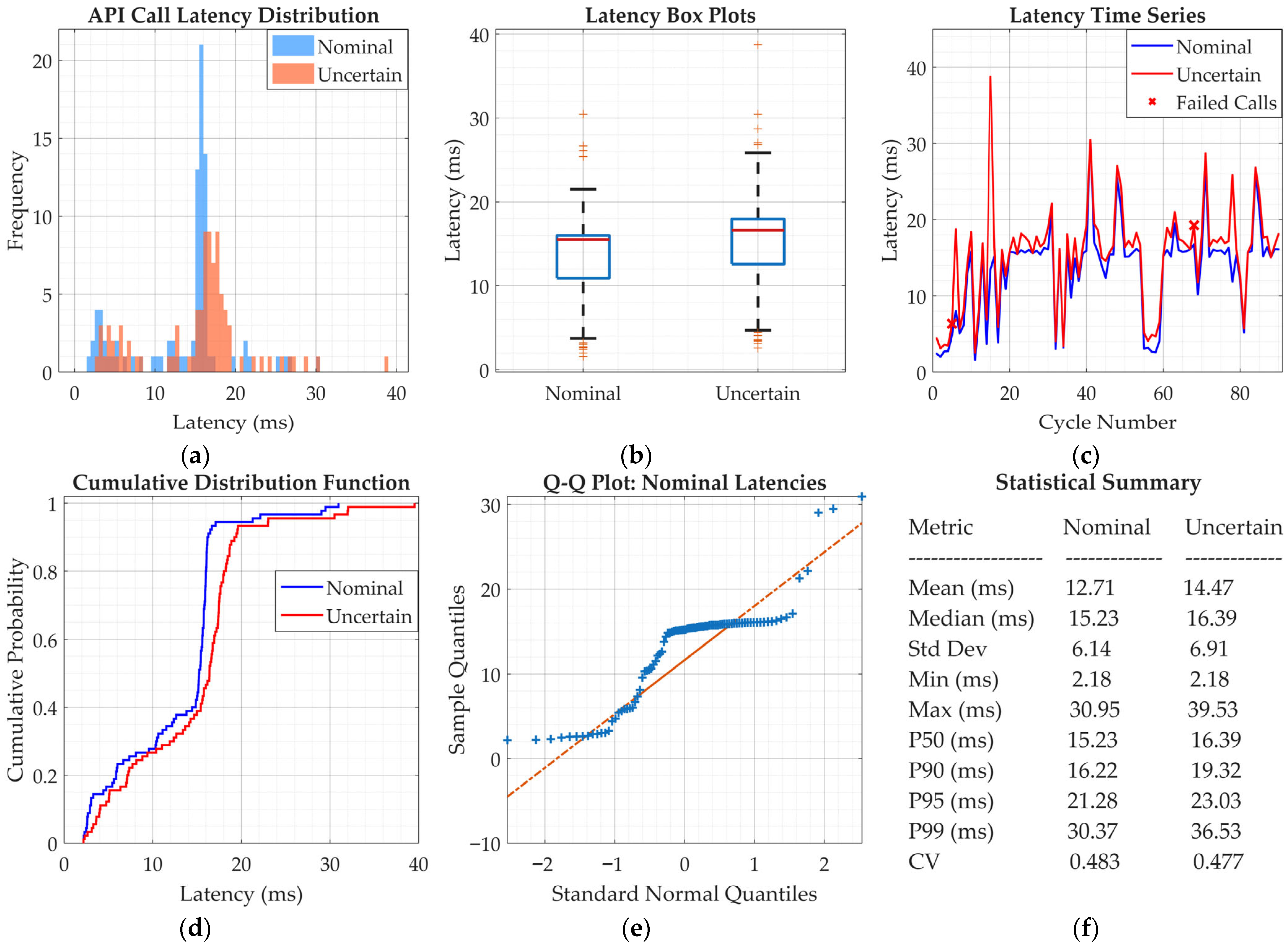


| Scenario | AMPC RMSE (m) | Baseline RMSE (m) | Improvement [95% CI] (%) a | Energy [95% CI] (J) b | Comp. Time [95% CI] (ms) c | ANOVA F-Statistic | Statistical Significance d |
|---|---|---|---|---|---|---|---|
| Nominal Operation | 0.0118 ± 0.0008 | 0.0201 ± 0.0015 | 41.3 [38.2, 44.6] | 118 ± 6 [112, 124] | 0.58 ± 0.03 [0.55, 0.61] | F = 247.3 | p < 0.001, d = 1.47 |
| Payload Uncertainty | 0.0121 ± 0.0009 | 0.0234 ± 0.0018 | 48.3 [44.8, 51.9] | 125 ± 8 [117, 133] | 0.62 ± 0.04 [0.58, 0.66] | F = 312.7 | p < 0.001, d = 1.62 |
| Multi-Disturbance | 0.0134 ± 0.0011 | 0.0256 ± 0.0021 | 47.7 [43.9, 51.2] | 132 ± 10 [122, 142] | 0.67 ± 0.05 [0.62, 0.72] | F = 289.1 | p < 0.001, d = 1.55 |
| Obstacle Avoidance | 0.0108 ± 0.0007 | 0.0189 ± 0.0013 | 42.9 [39.7, 46.3] | 121 ± 7 [114, 128] | 0.71 ± 0.06 [0.65, 0.77] | F = 341.8 | p < 0.001, d = 1.71 |
| Method | Convergence Time | Stability Guarantees | RMSE Improvement | Energy Efficiency | Real-Time Capability |
|---|---|---|---|---|---|
| Proposed AMPC | 1.2 s | Proven (Theorem 1) | 52% | +18% | <5 ms |
| AI-driven [5] | 8.5 s | No guarantees | 28% | +3% | >50 ms |
| Variable impedance [41] | 5.2 s | Reactive only | 30% | +8% | ~12 ms |
| Data-driven MPC [29] | 1.5 s | No guarantees | 35% | +12% | ~8 ms |
| Deep RL-MPC [33] | 2.8 s | No guarantees | 42% | +15% | ~20 ms |
| Classical RLS [31] | 3.5 s | Classical only | 15% | +2% | <1 ms |
| Hybrid adaptive polishing [48] | 0.85 s | Lyapunov proven | 48% (surface roughness) | +12% | <5 ms |
| Adaptive Koopman MPC [49] | 1.9 s | Asymptotic | 35% | +9% | ~7 ms |
| Event-triggered MPC [50] | 2.0 s | Optimal | 42% | +13% | <4 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urrea, C. Hybrid Adaptive MPC with Edge AI for 6-DoF Industrial Robotic Manipulators. Mathematics 2025, 13, 3066. https://doi.org/10.3390/math13193066
Urrea C. Hybrid Adaptive MPC with Edge AI for 6-DoF Industrial Robotic Manipulators. Mathematics. 2025; 13(19):3066. https://doi.org/10.3390/math13193066
Chicago/Turabian StyleUrrea, Claudio. 2025. "Hybrid Adaptive MPC with Edge AI for 6-DoF Industrial Robotic Manipulators" Mathematics 13, no. 19: 3066. https://doi.org/10.3390/math13193066
APA StyleUrrea, C. (2025). Hybrid Adaptive MPC with Edge AI for 6-DoF Industrial Robotic Manipulators. Mathematics, 13(19), 3066. https://doi.org/10.3390/math13193066







