A SEIQRS Model for Interbank Financial Risk Contagion and Rescue Strategies in Complex Networks
Abstract
1. Introduction
2. Construction of an Empirical Interbank Network
2.1. Methodology
2.2. Preliminaries
2.2.1. Theoretical Foundations of Scale-Free Networks and Power-Law Degree Distributions
2.2.2. Network Reconstruction via the Minimum-Density Method
2.3. Network Characteristics Analysis and Estimation Results
3. SEIQRS Dynamics Model
3.1. Model Assumptions
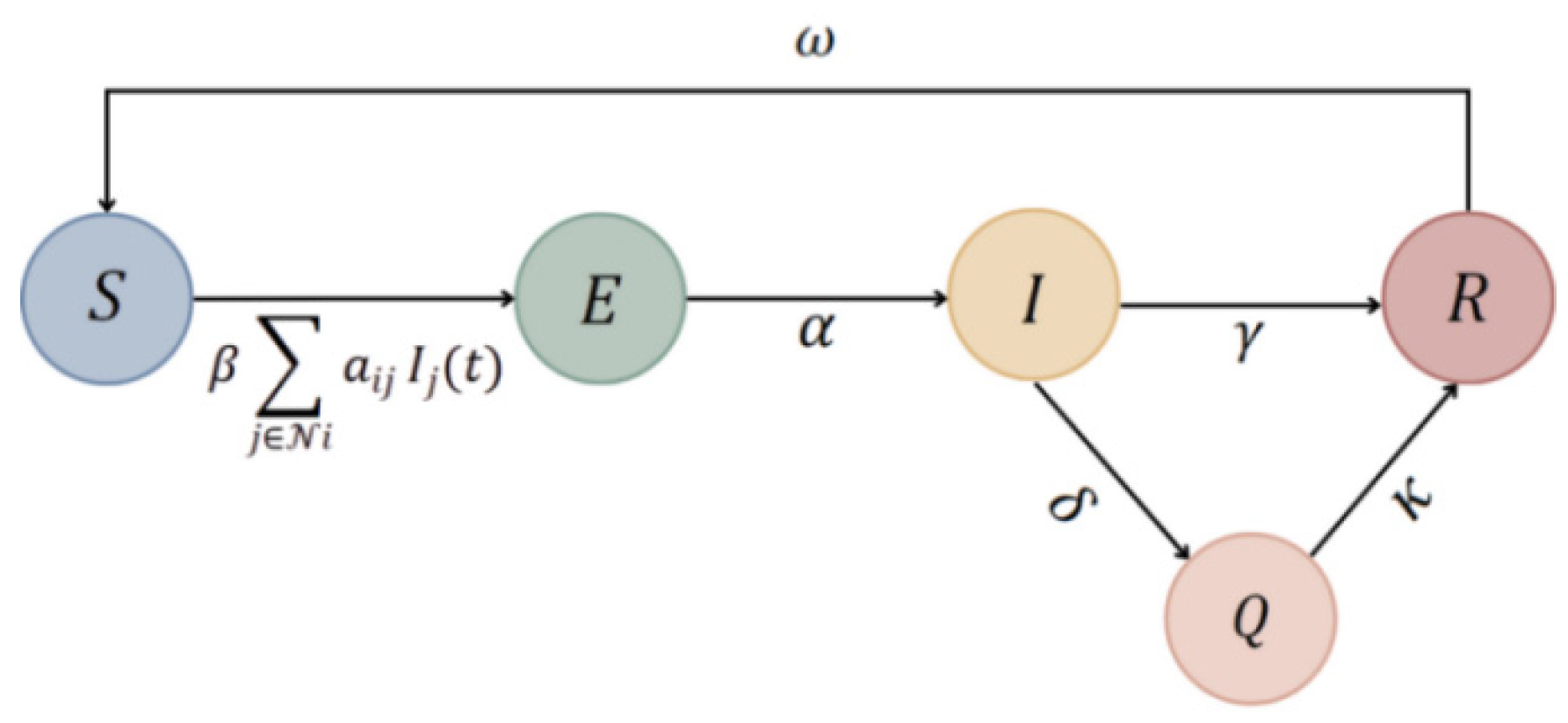
3.2. Model Description
3.3. Heterogeneous Mean-Field Approximation
3.4. Mathematical Analysis of the SEIQRS Model Under Heterogeneous Mean Fields
3.4.1. Basic Reproduction Number in HMF Form (Next-Generation Method)
3.4.2. Local Stability of the Disease-Free Equilibrium (DFE)
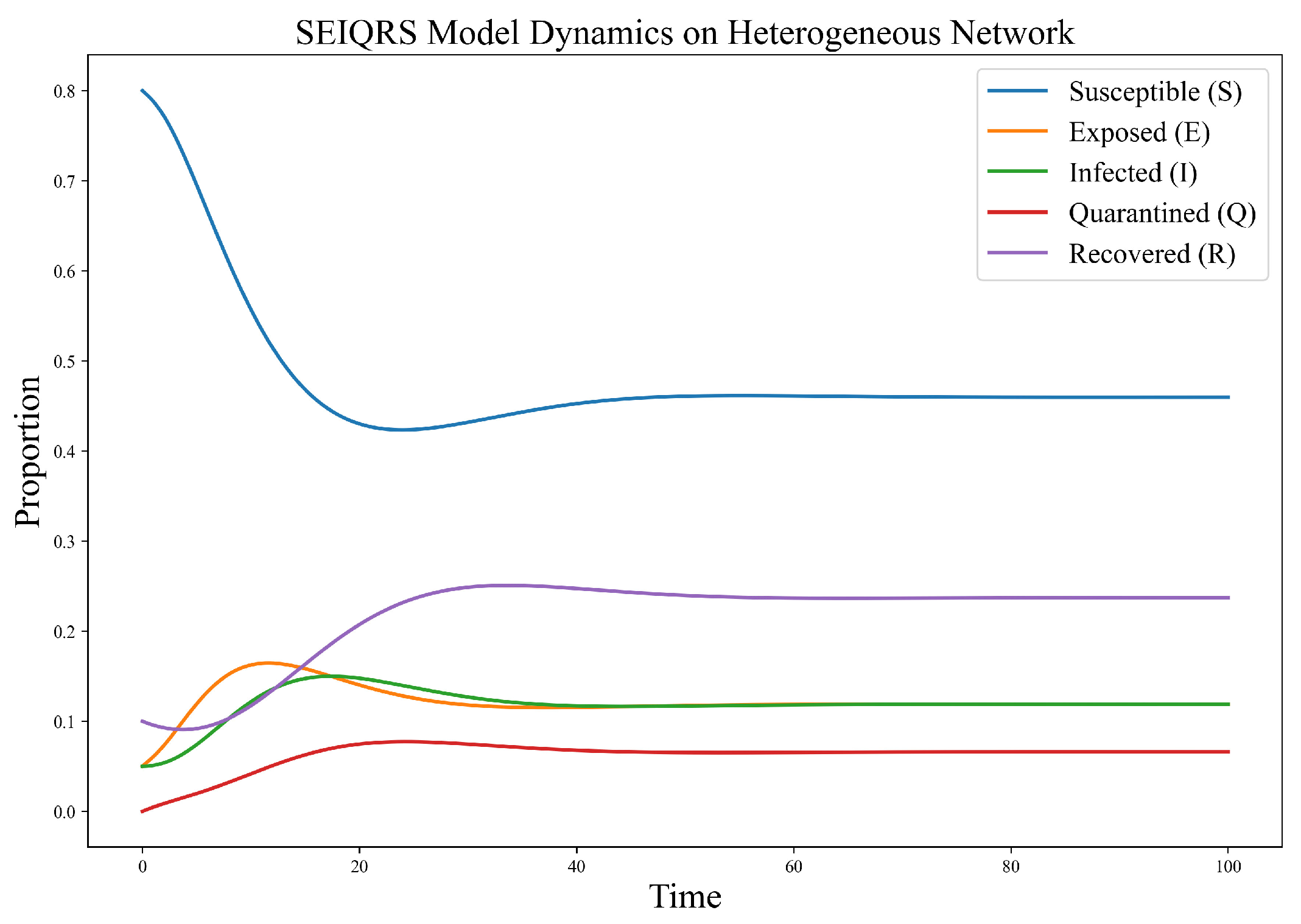
3.5. Numerical Simulation
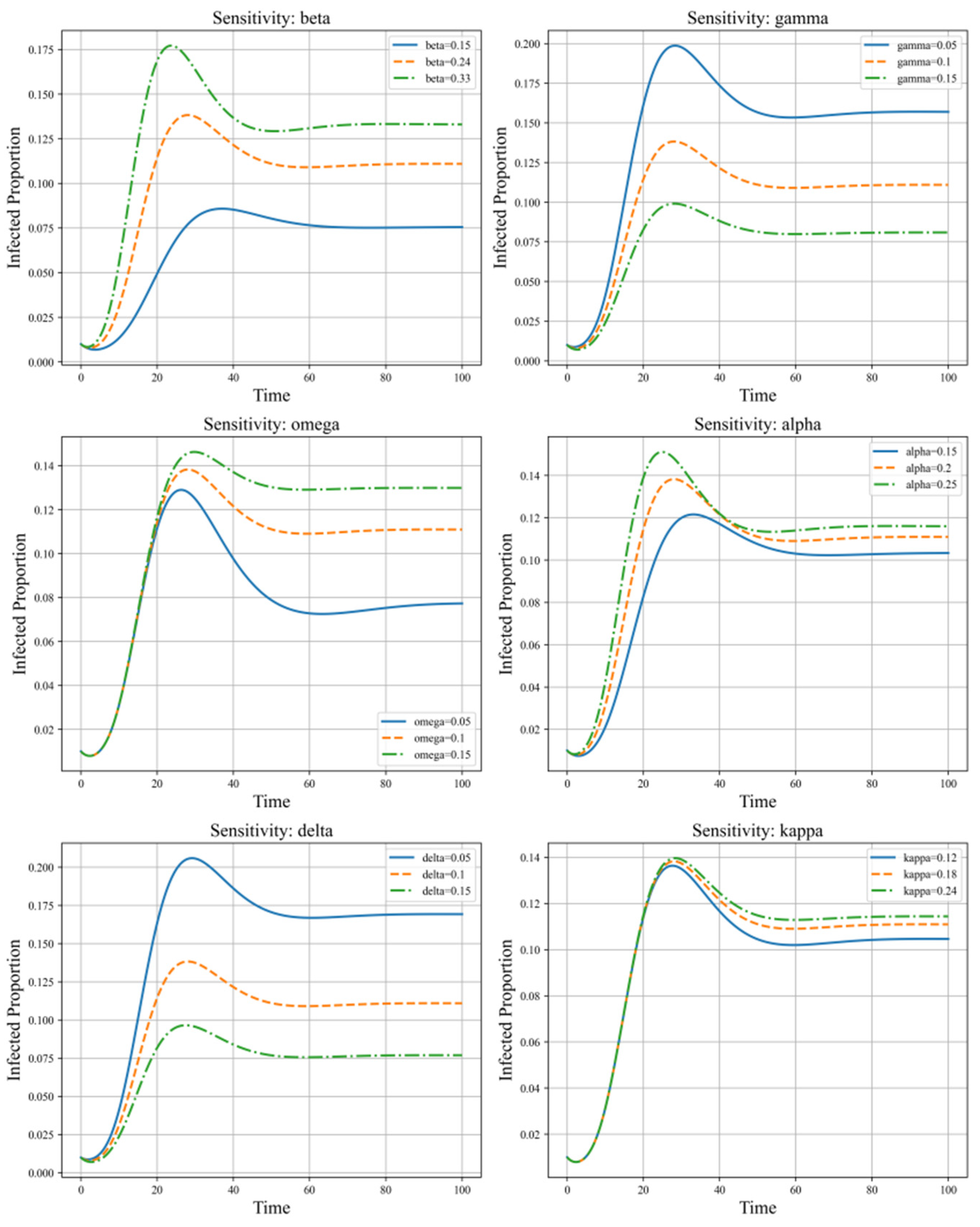
3.6. Sensitivity Analysis
4. Simulation of Rescue Strategies
4.1. Assumptions
4.2. Parameters and Rescue-Strategy Design
4.3. The Impact of Rescue Timing on Strategy Effectiveness
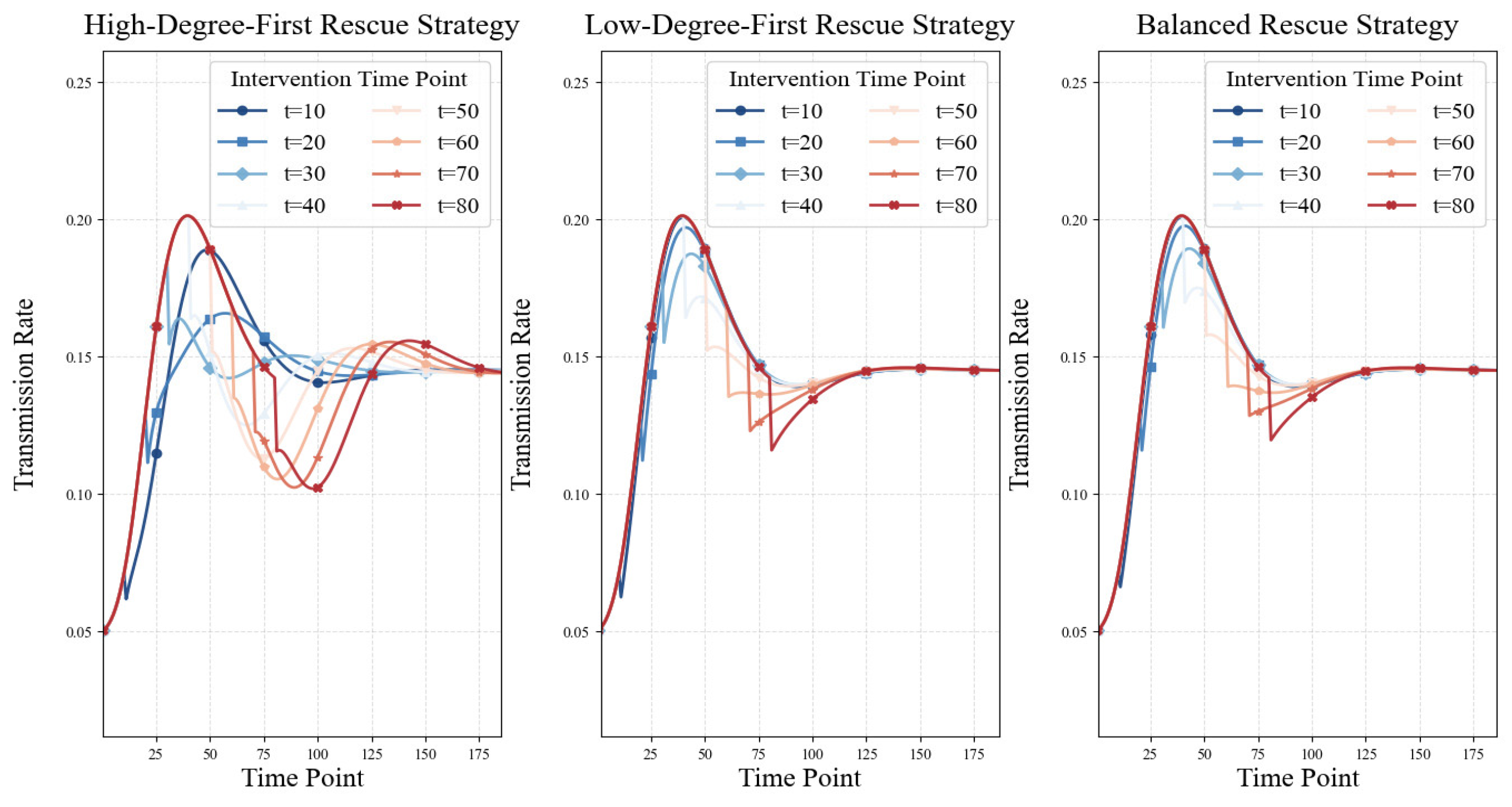
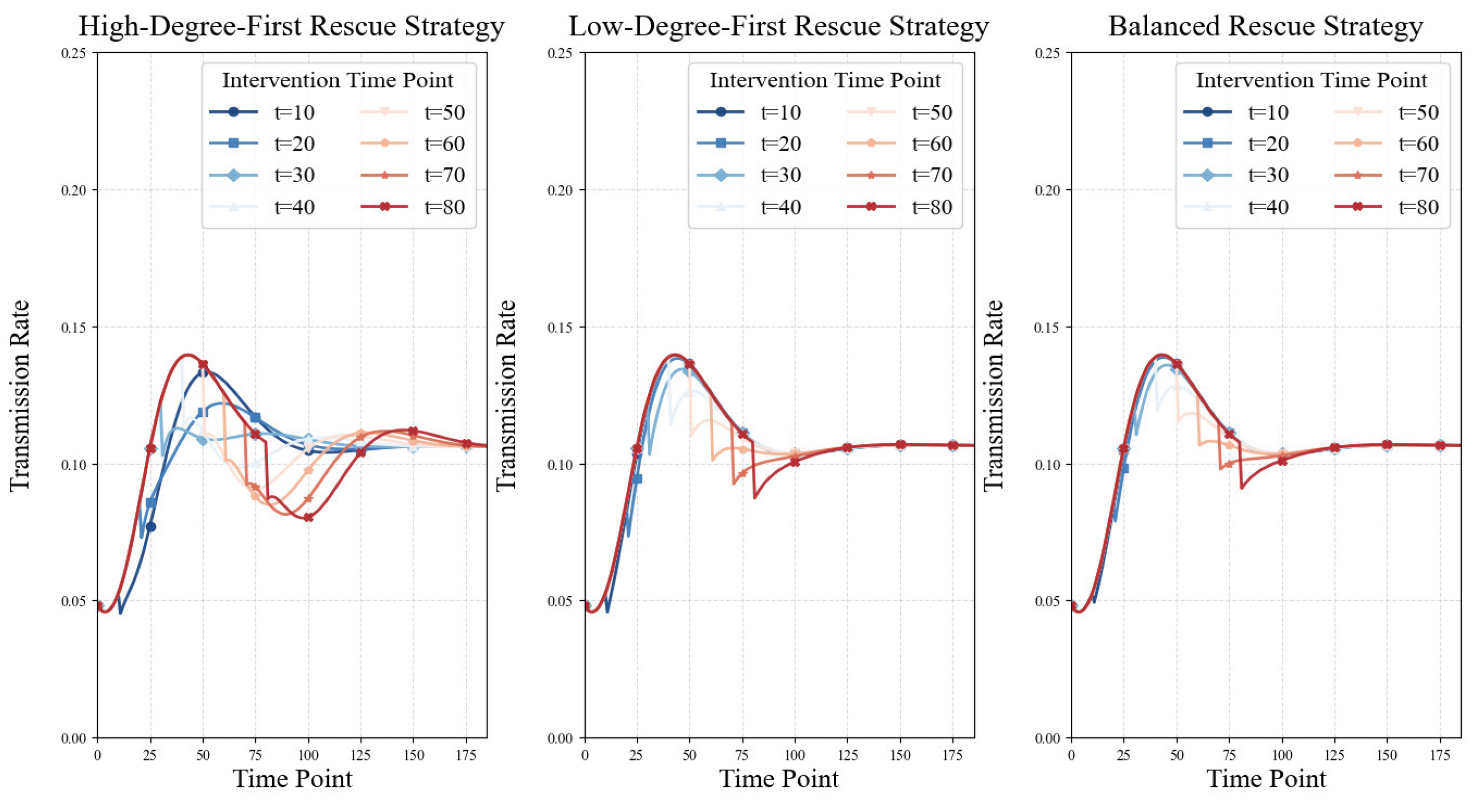
4.3.1. Impact of Rescue Timing on the Transmission Rate
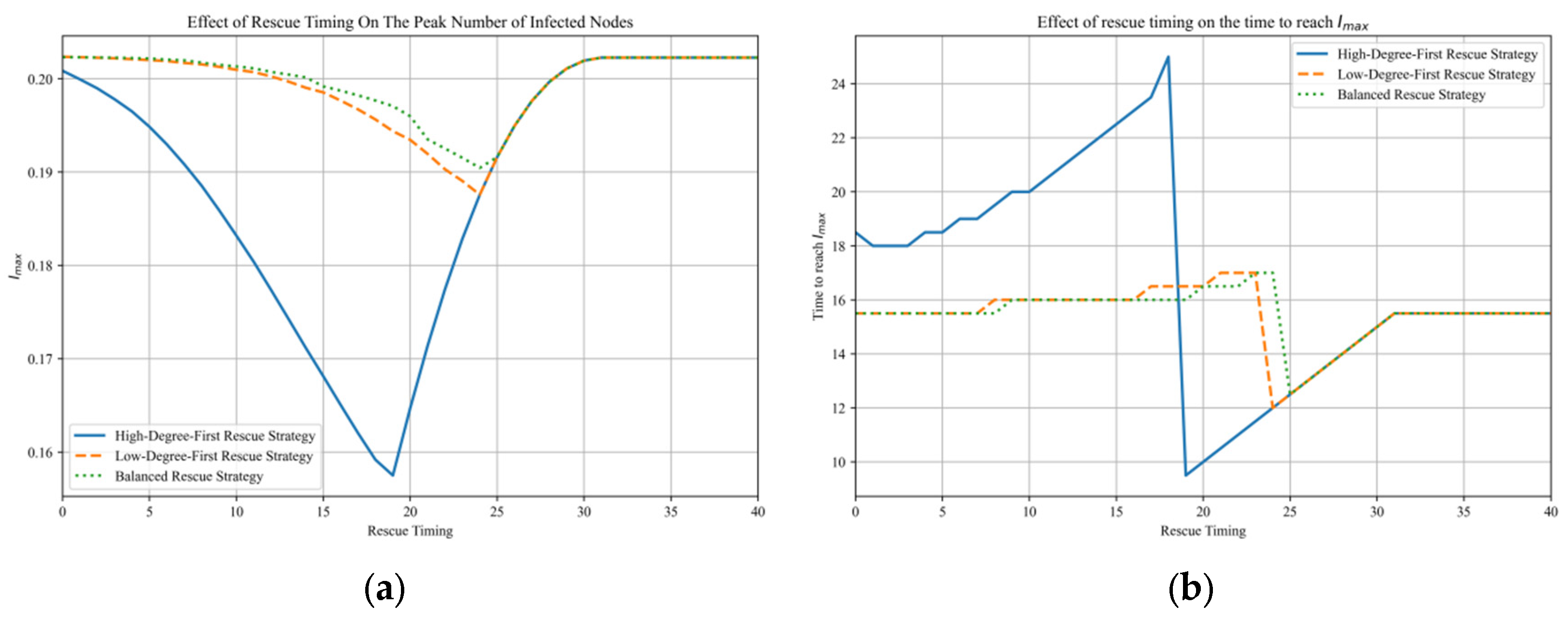
4.3.2. Impact of Rescue Timing on Strategy Effectiveness and the Optimal Rescue Time Point
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allen, F.; Babus, A.; Carletti, E. Financial Connections and Systemic Risk; National Bureau of Economic Research: Cambridge, MA, USA, 2010. [Google Scholar]
- Hüser, A.C. Too interconnected to fail: A survey of the interbank networks literature. Netw. Theory Financ. 2015, 1, 1–50. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Teng, Y.; Ma, S.; Qian, Q.; Wang, G. SEIR-diffusion modeling and stability analysis of supply chain finance based on blockchain technology. Heliyon 2024, 10, e24981. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.S. A Study of Risk Contagion in Selected Global Equity Markets Based on a Complex Network Contagion Model. Master’s Thesis, Fujian University of Technology, Fuzhou, China, 2023. [Google Scholar]
- Shi, X.Y.; Gao, H.L. SEIQR Infectious Disease Model with Media Effects and Age Structure. Appl. Math. 2025, 38, 435–445. [Google Scholar]
- Tian, Z.W.; Wang, L.; Liu, C. Information Dissemination Mechanism Analysis and Model Construction of Micro-blog Based on Complex Network. Inf. Sci. 2015, 33, 15–21. [Google Scholar]
- Tong, M.; He, Y. Systemic Risk and Liquidity Rescue in Complex Financial Networks: A Study Based on China’s Large-value Payment System. J. Financ. Res. 2012, 39, 20–33. [Google Scholar]
- Xu, T. Research on Contagion in Interbank Market and Control Strategies Based on the Integration of Complex Network and Multi-Agent. Ph.D. Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Krapivsky, P.L.; Redner, S.; Leyvraz, F. Connectivity of growing random networks. Phys. Rev. Lett. 2000, 85, 4629. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.F.; Mu, X.Y. Systemic Financial Risk Contagion in Bank Interbank Lending Based on Complex Network. Ningxia Soc. Sci. 2023, 4, 135–140. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.H.; Li, X.H. Contagion and Bailout Strategy in Complex Financial Networks—SIRS Model on the Chinese Scale-free Financial Network. Financ. Trade Econ. 2017, 38, 101–114. [Google Scholar]
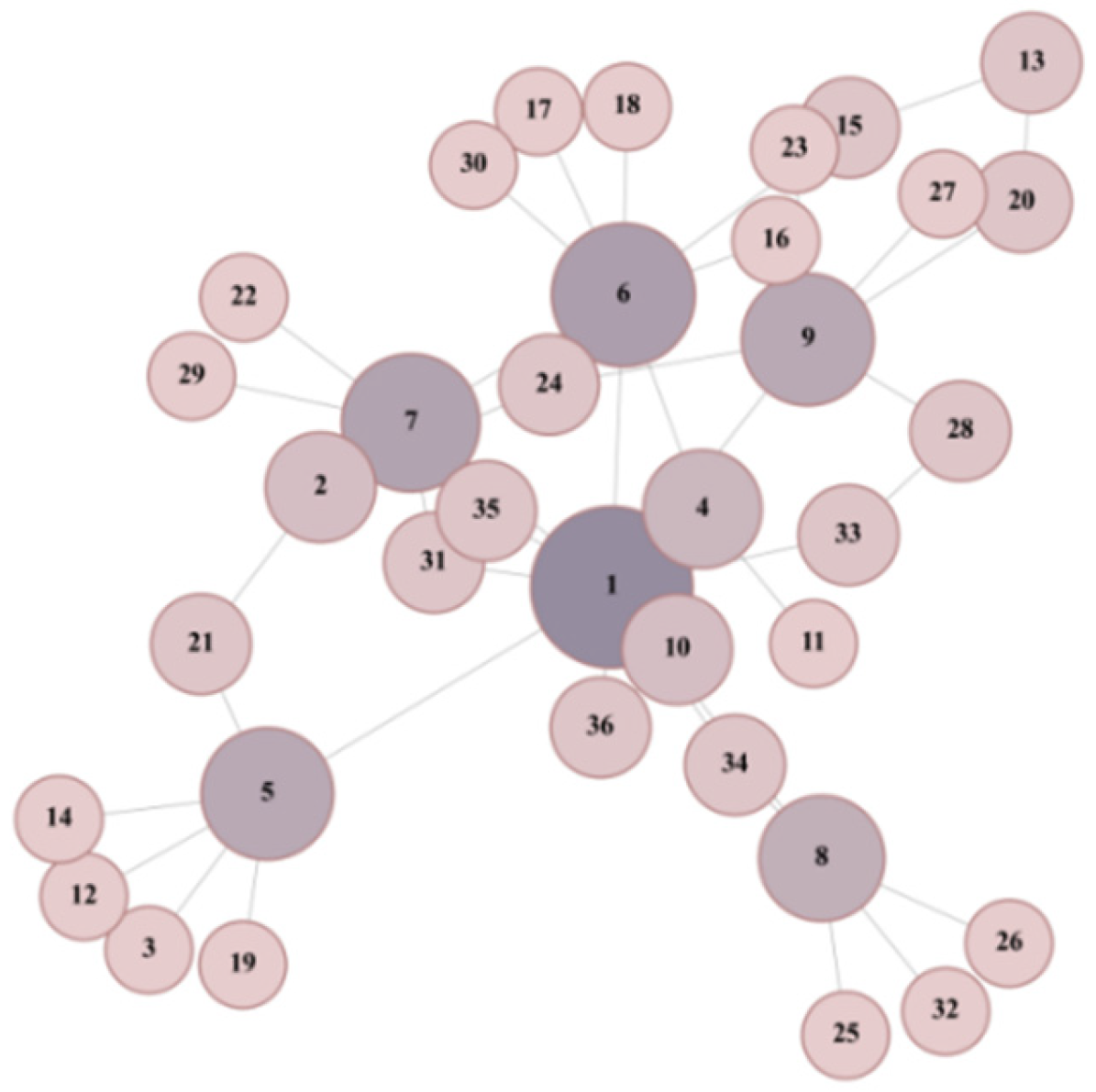
| No. | Bank Name | No. | Bank Name | No. | Bank Name |
|---|---|---|---|---|---|
| 1 | ABC | 13 | SHBANK | 25 | CDCB |
| 2 | ICBC | 14 | BOB | 26 | LZYH |
| 3 | CCB | 15 | PSBC | 27 | CQBANK |
| 4 | BOC | 16 | JSBANK | 28 | XMBANK |
| 5 | CIB | 17 | CZBANK | 29 | ZZBANK |
| 6 | BCM | 18 | NBBANK | 30 | QDCCB |
| 7 | SPDB | 19 | HZCB | 31 | QDRCB |
| 8 | CMBC | 20 | NJCB | 32 | QLBANK |
| 9 | CMB | 21 | CQRCB | 33 | CSRCB |
| 10 | CEB | 22 | SHRCB | 34 | RFRCB |
| 11 | HXBANK | 23 | CSCB | 35 | XABANK |
| 12 | SPABANK | 24 | BOSZ | 36 | SZRCB |
| Symbol | Definition | Description |
|---|---|---|
| Susceptible | A financial institution not yet hit by risk, but can be infected via network connections. | |
| Exposed | A financial institution that has encountered risk but is not yet infectious; enters I after a latent period. | |
| Infectious | A financial institution currently experiencing risk and capable of transmitting it to others. | |
| Quarantined | A financial institution isolated by regulators and temporarily unable to spread risk. | |
| Recovered | A financial institution that has recovered from risk but may lose immunity and become susceptible again over time. | |
| Transmission Rate | The probability per contact that an infectious bank infects an undistressed bank. | |
| Exposed-to-infectious Transition Rate | The rate at which exposed banks become infectious. | |
| Quarantine Rate | The rate at which infectious banks are isolated by regulators. | |
| Natural Recovery Rate | The rate at which infectious banks recover on their own without quarantine. | |
| Quarantine-Recovery Rate | The rate at which quarantined banks recover and become immune. | |
| Immunity-Loss Rate | The rate at which recovered banks lose immunity and return to the susceptible state. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Liu, Y. A SEIQRS Model for Interbank Financial Risk Contagion and Rescue Strategies in Complex Networks. Mathematics 2025, 13, 3059. https://doi.org/10.3390/math13193059
Sun B, Liu Y. A SEIQRS Model for Interbank Financial Risk Contagion and Rescue Strategies in Complex Networks. Mathematics. 2025; 13(19):3059. https://doi.org/10.3390/math13193059
Chicago/Turabian StyleSun, Bo, and Yujia Liu. 2025. "A SEIQRS Model for Interbank Financial Risk Contagion and Rescue Strategies in Complex Networks" Mathematics 13, no. 19: 3059. https://doi.org/10.3390/math13193059
APA StyleSun, B., & Liu, Y. (2025). A SEIQRS Model for Interbank Financial Risk Contagion and Rescue Strategies in Complex Networks. Mathematics, 13(19), 3059. https://doi.org/10.3390/math13193059





