An Approach for Sustainable Supplier Segmentation Using Adaptive Network-Based Fuzzy Inference Systems
Abstract
1. Introduction
- i.
- Lack of supervised learning capabilities using historical data: Despite the diversity of techniques explored for supplier segmentation, none of the existing models incorporate a supervised learning procedure based on historical supplier performance [3,6]. This limitation hinders the use of data from periodic supplier assessments to refine cause-and-effect relationships between input and output variables. While current models rely heavily on Multi-criteria Decision Making (MCDM) methods, they remain static and cannot be tuned or updated through accumulated historical evidence.
- ii.
- Inability to capture nonlinear relationships among segmentation criteria: As MCDM methods typically produce a global ranking for each alternative based on weighted combinations of inputs, they are limited to linear aggregation and fail to represent nonlinear cause-and-effect dynamics. However, in supplier evaluation, many relationships are inherently nonlinear (e.g., x = y/z and x = z · y2),which makes such methods inadequate for contexts where complex interactions exist among sustainability indicators [21].
- iii.
- Absence of an inference rule base to support decision-making: Current sustainable supplier segmentation models also lack a structured rule base to guide the decision process. Without such a mechanism, decision-making becomes less transparent, harder to justify, and more dependent on expert judgment, which can introduce subjectivity and inconsistency.
2. Theoretical Framework
2.1. Sustainable Supplier Segmentation
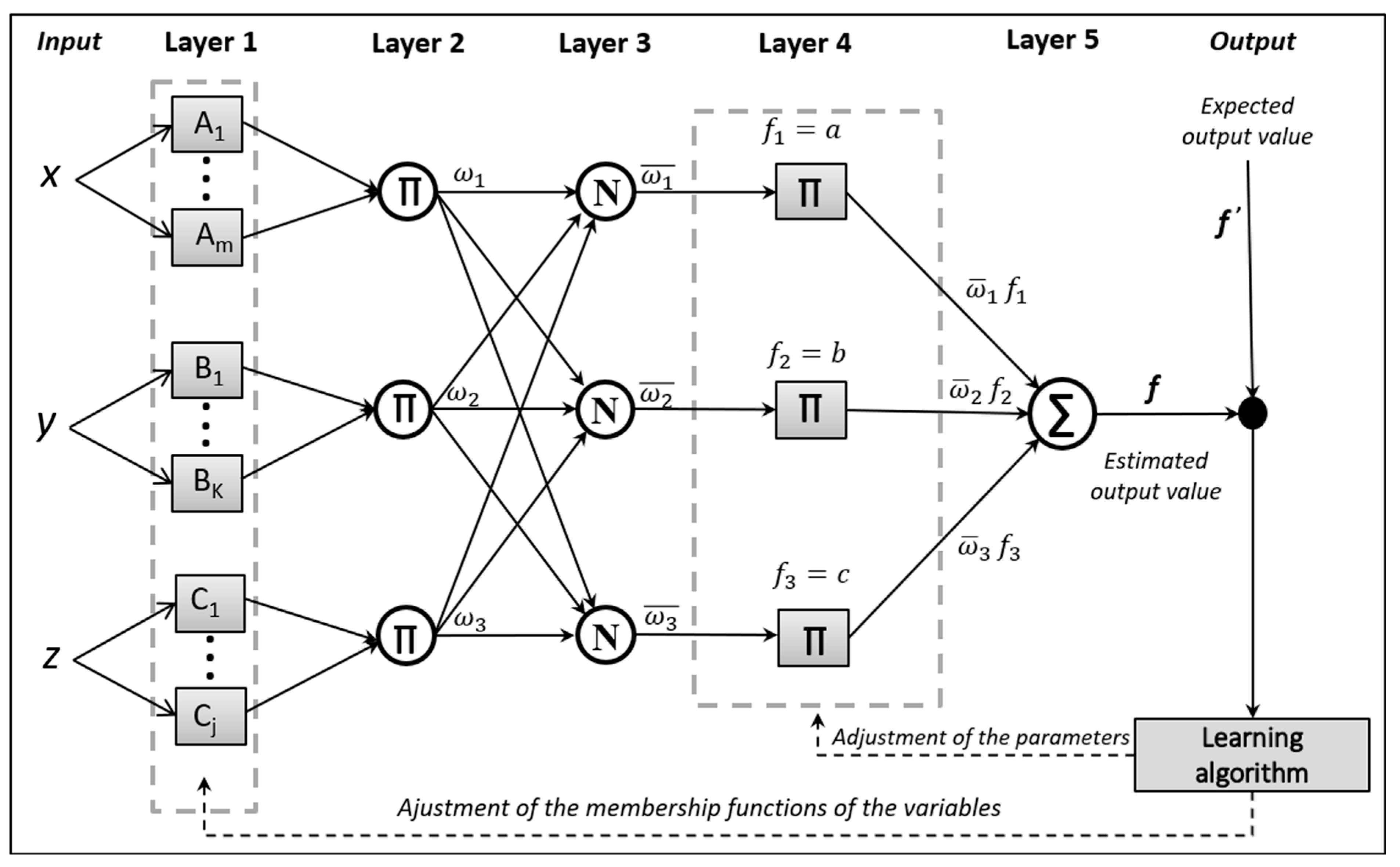
2.2. Adaptive Neuro-Fuzzy Inference Systems
- (a)
- Layer 1: In this layer, the input values (x and y) in crisp format are converted into fuzzy set equivalents. Their function can be given as:
- (b)
- Layer 2: This layer combines all of the previous layer’s nodes to establish the logical relationships among the activated membership functions. This layer represents the antecedent part of the decision-making rules, which realizes operations of “AND” or “OR”. The equation that represents the realized operation for this combination layer is given by:
- (c)
- Layer 3: This layer normalizes the weights of the activated rules. Equation (3) describes the procedure.
- (d)
- Layer 4: This is the layer of the adaptive nodes that represents the rule consequents. These consequents generate outputs for each activated rule according to Equation (4). A linear function or a constant function can produce the consequent value. The output value of this layer is calculated by the simple product of the consequent of each rule () and the weight of the rule activated in the third layer.
- (e)
- Layer 5: This layer is composed of a fixed node that calculates a weighted sum of the previous layer’s outputs, as represented by Equation (5).
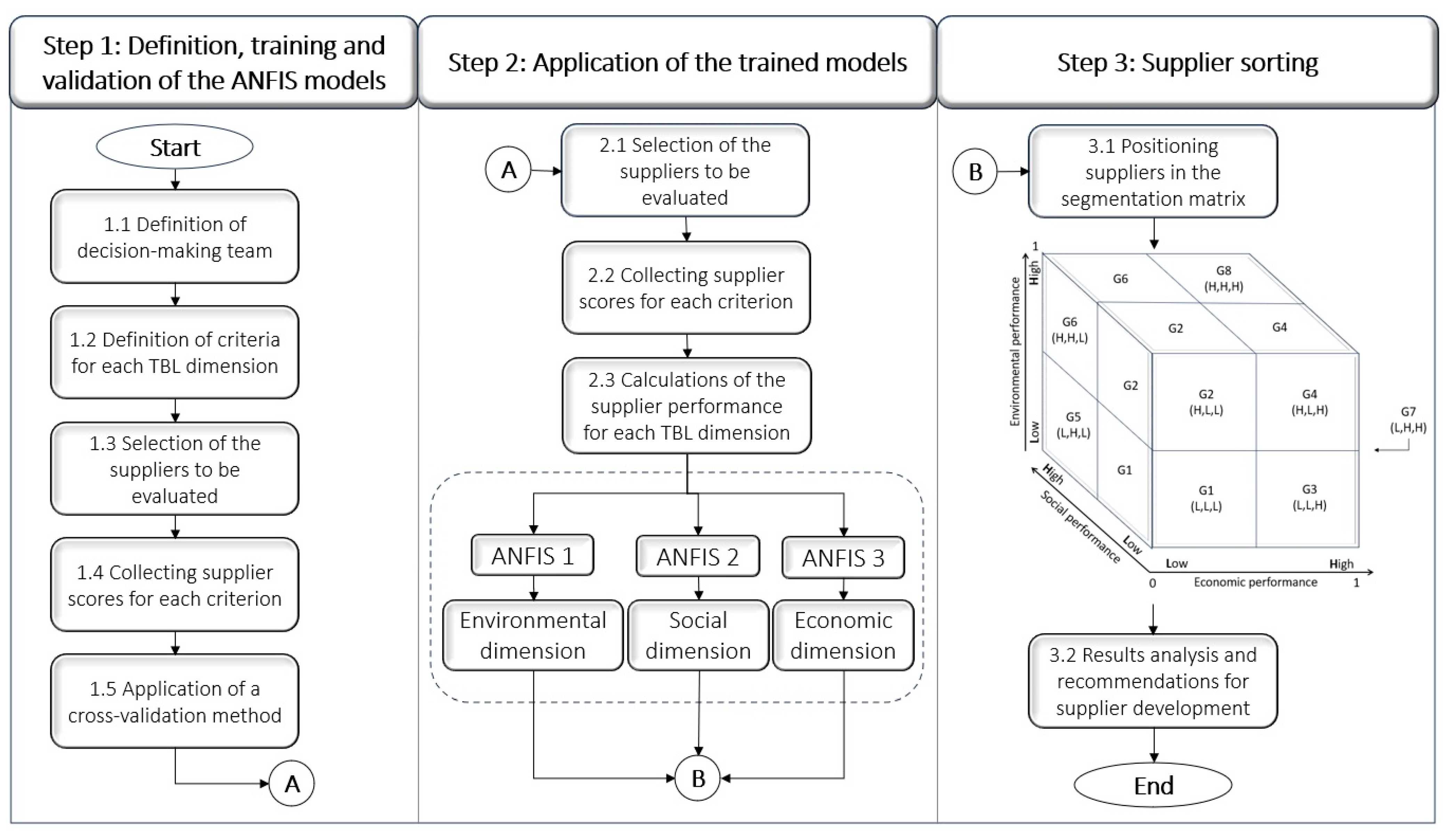
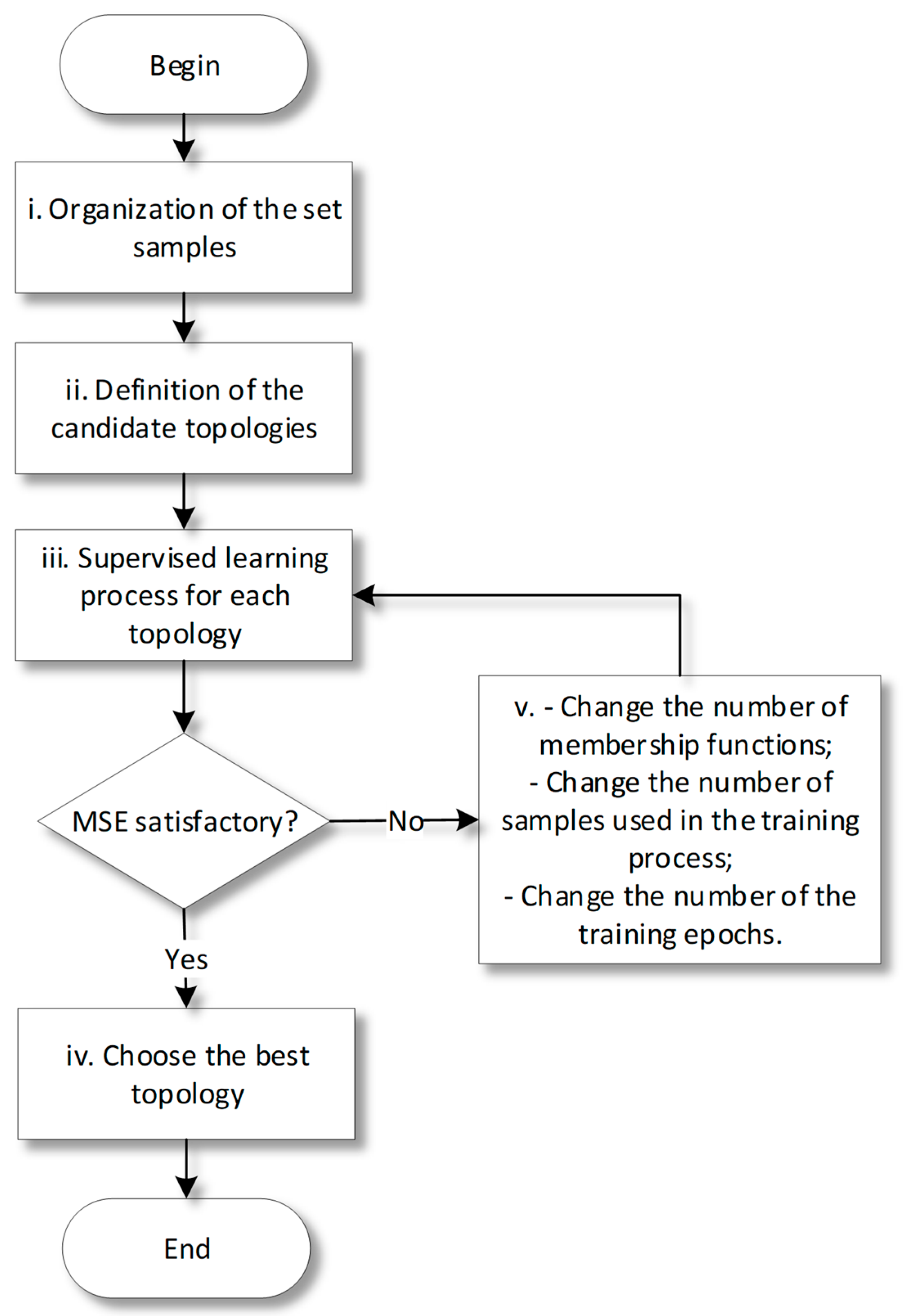
3. The Proposed Model for Sustainable Supplier Segmentation
- Changing the number of membership functions, which affects the granularity of the fuzzy inference process;
- Increasing the number of training samples to enhance the model’s learning capacity.
- Adjusting the number of training epochs will allow the model to have more iterations to converge.
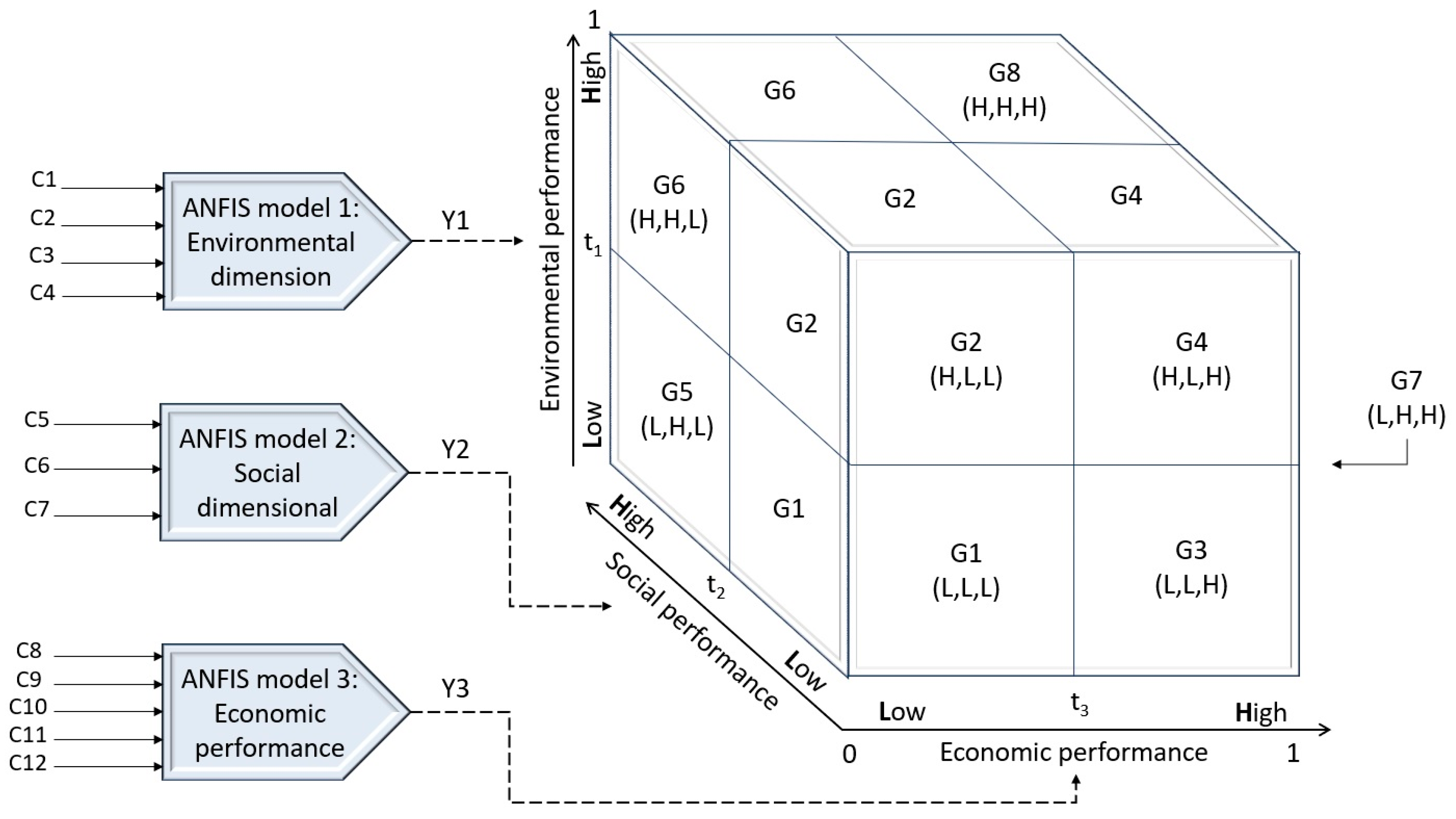
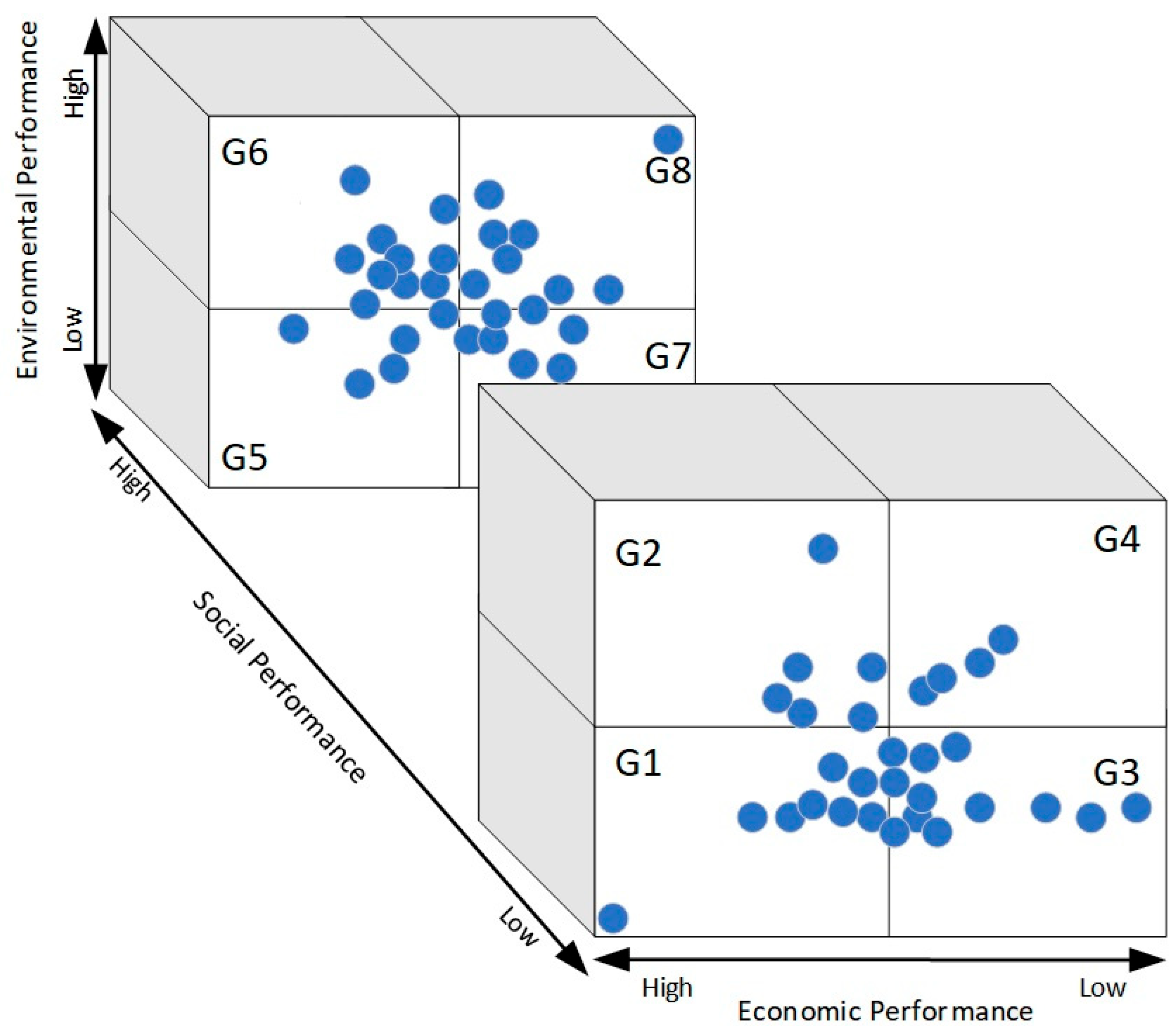
- (a)
- G1 (L, L, L)—This group consists of the suppliers with the worst performance evaluations, or those with poor economic, environmental, and social performance. The suppliers in this group should be substituted if possible [53]. Otherwise, supplier development programs should be implemented to achieve improved supplier performance in the three dimensions of the TBL.
- (b)
- G2 (H, L, L)—This group consists of suppliers that have achieved good environmental performance and poor economic and social performance. The suppliers in this segment generally focus on efficient use of natural resources and controlling and preventing pollution.
- (c)
- G3 (L, L, H)—This group consists of suppliers with good economic performance and poor social and environmental performance. They operate their supply chains with a focus on profits and are not concerned with environmental and social issues.
- (d)
- G4 (H, L, H)—This group comprises suppliers with satisfactory economic and environmental performance, but poor social performance. They generally reduce costs through their efficient use of energy and natural resources.
- (e)
- G5 (L, H, L)—This group consists of suppliers with good social performance and poor economic and environmental performance. They are focused on social justice. They emphasize diversity in their labor, human rights, a reduction in inequality, and the quality of life of their employees.
- (f)
- G6 (H, H, L)—This group consists of suppliers with poor economic performance and good social and environmental performance. They emphasize using just a portion of natural resources in domestic and international spheres.
- (g)
- G7 (L, H, H)—This group comprises suppliers with good social and economic performance and poor environmental performance. These suppliers seek to reduce costs, considering the social needs of society. They have ethical standards and ensure just business practices that protect the human rights of their employees.
- (h)
- G8 (H, G, G)—This group consists of sustainable suppliers with good social, economic, and environmental performance. They focus on improving their products and the quality of life of people, prioritizing environmental activities, and maximizing renewable natural resources at the least possible cost.
4. Application Case Study
4.1. Presentation of the Company
4.2. Application of the Proposed Model
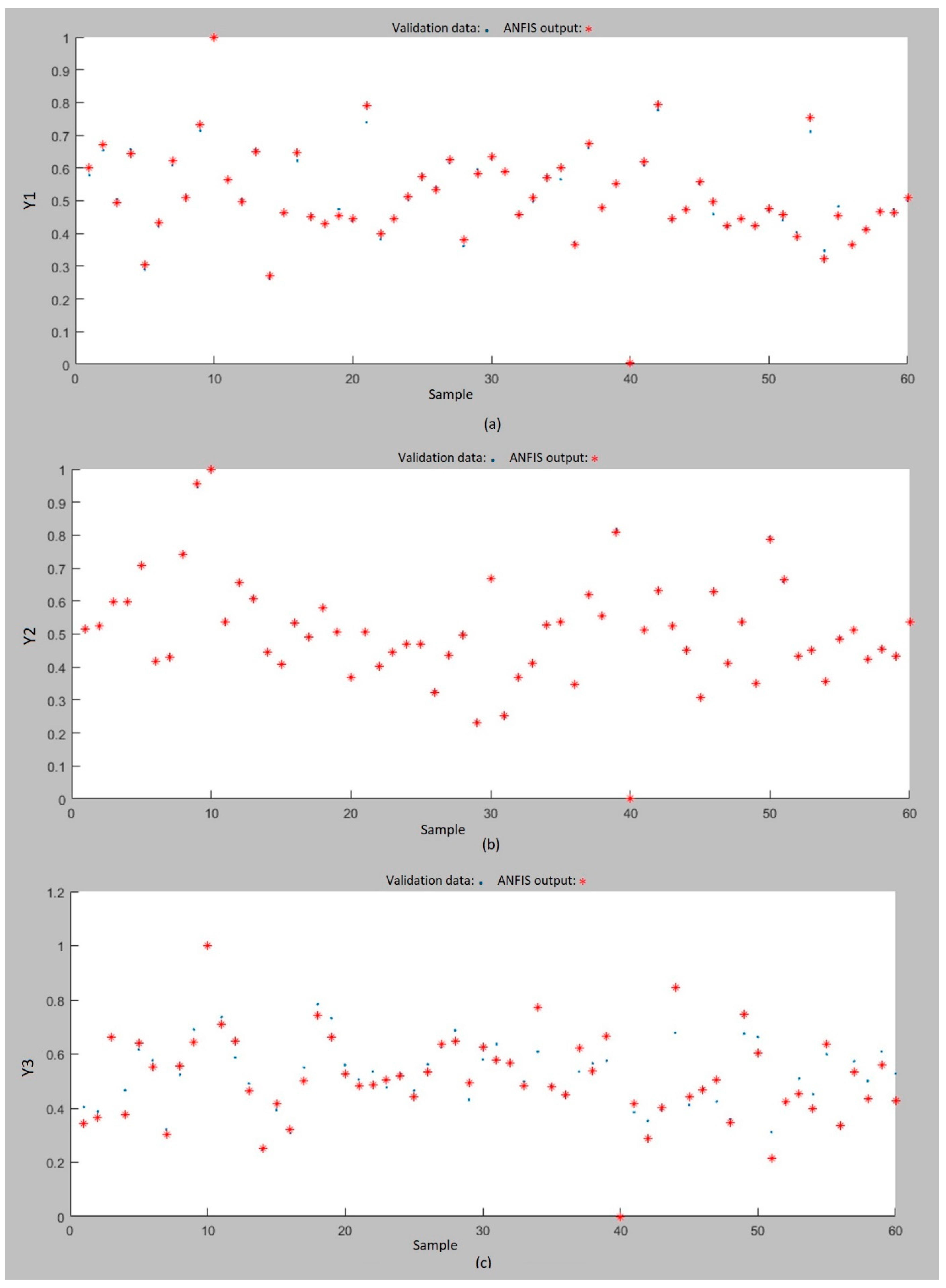
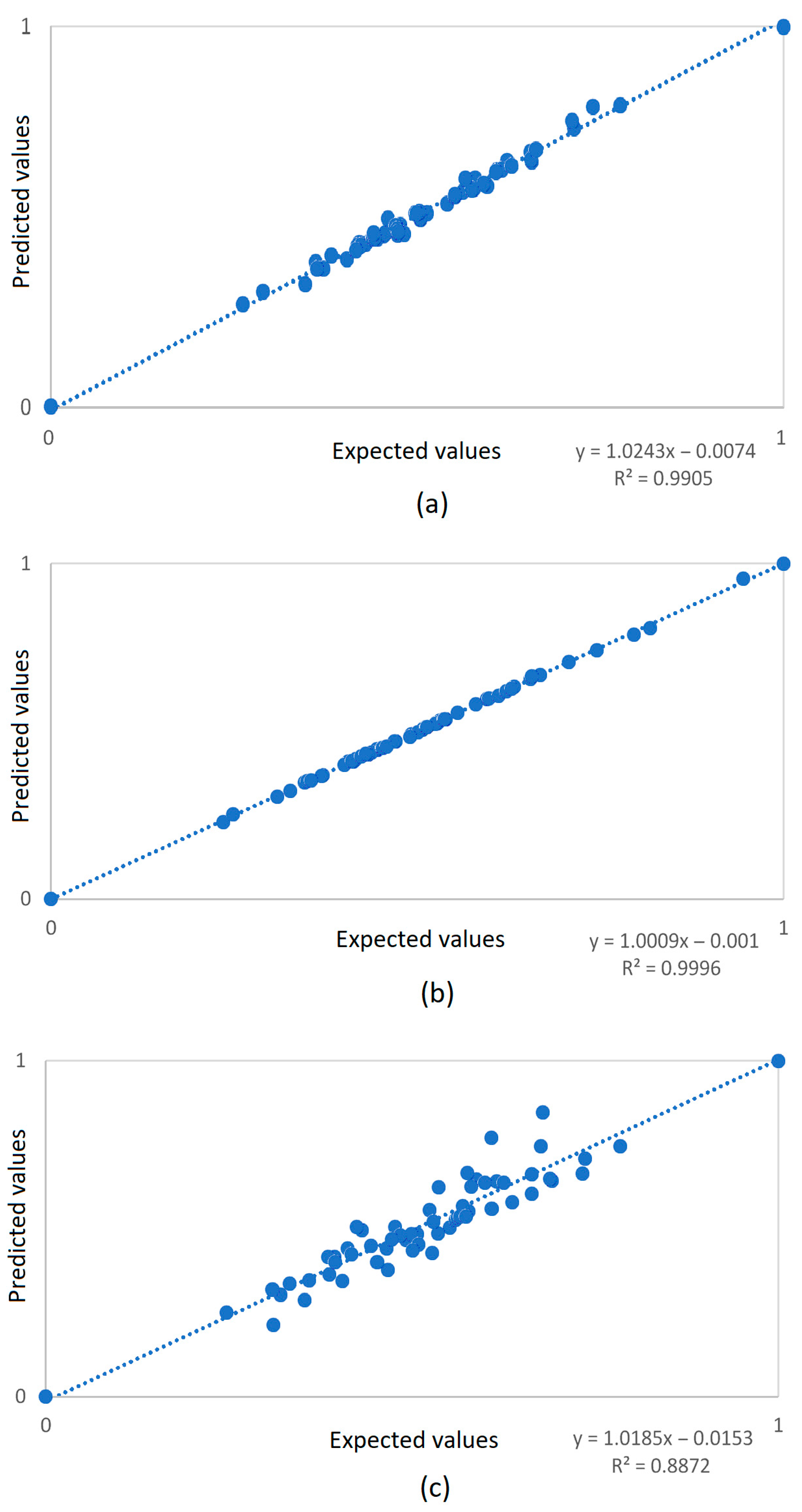
4.2.1. Stage 1: Definition, Training, and Validation of the ANFIS Models
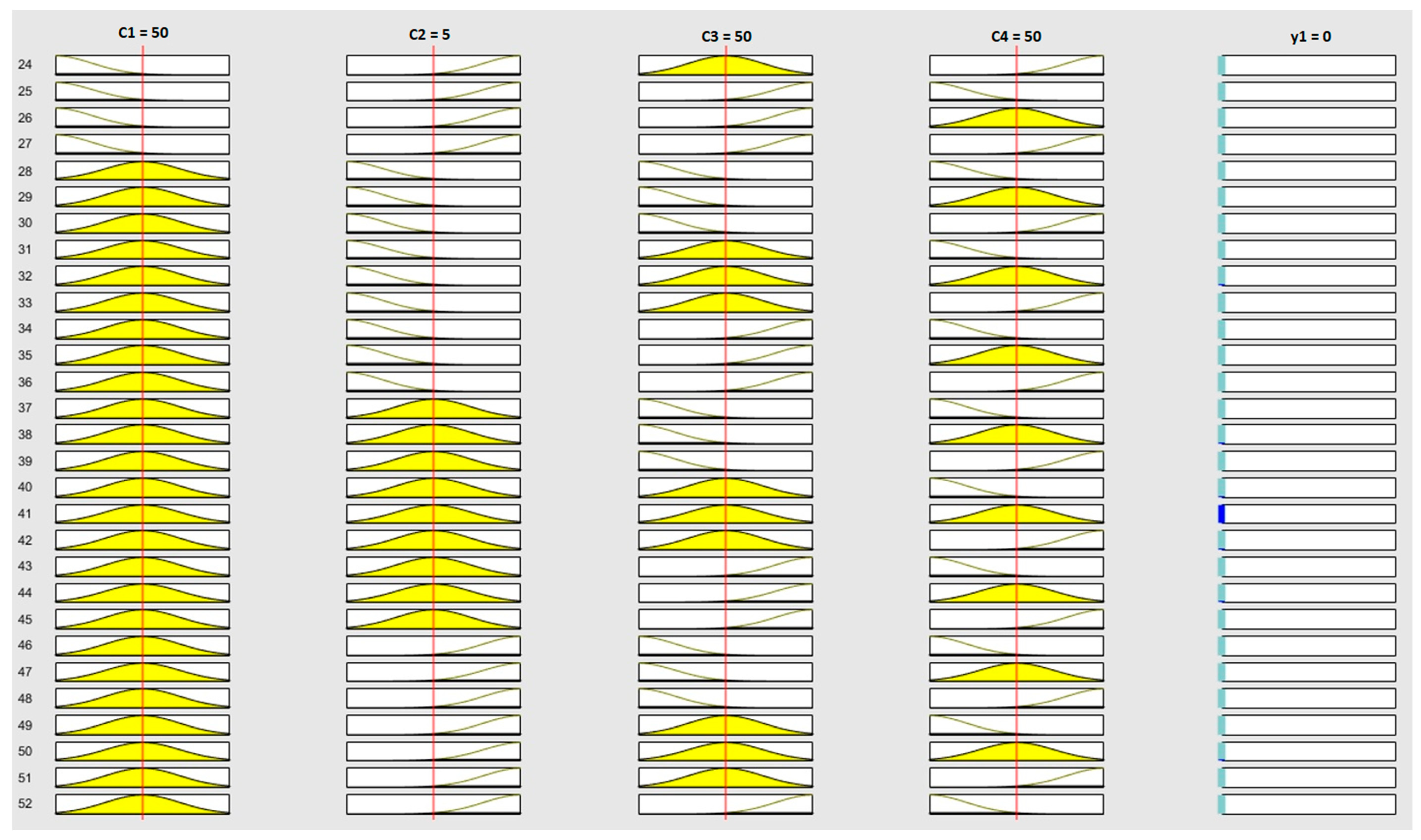
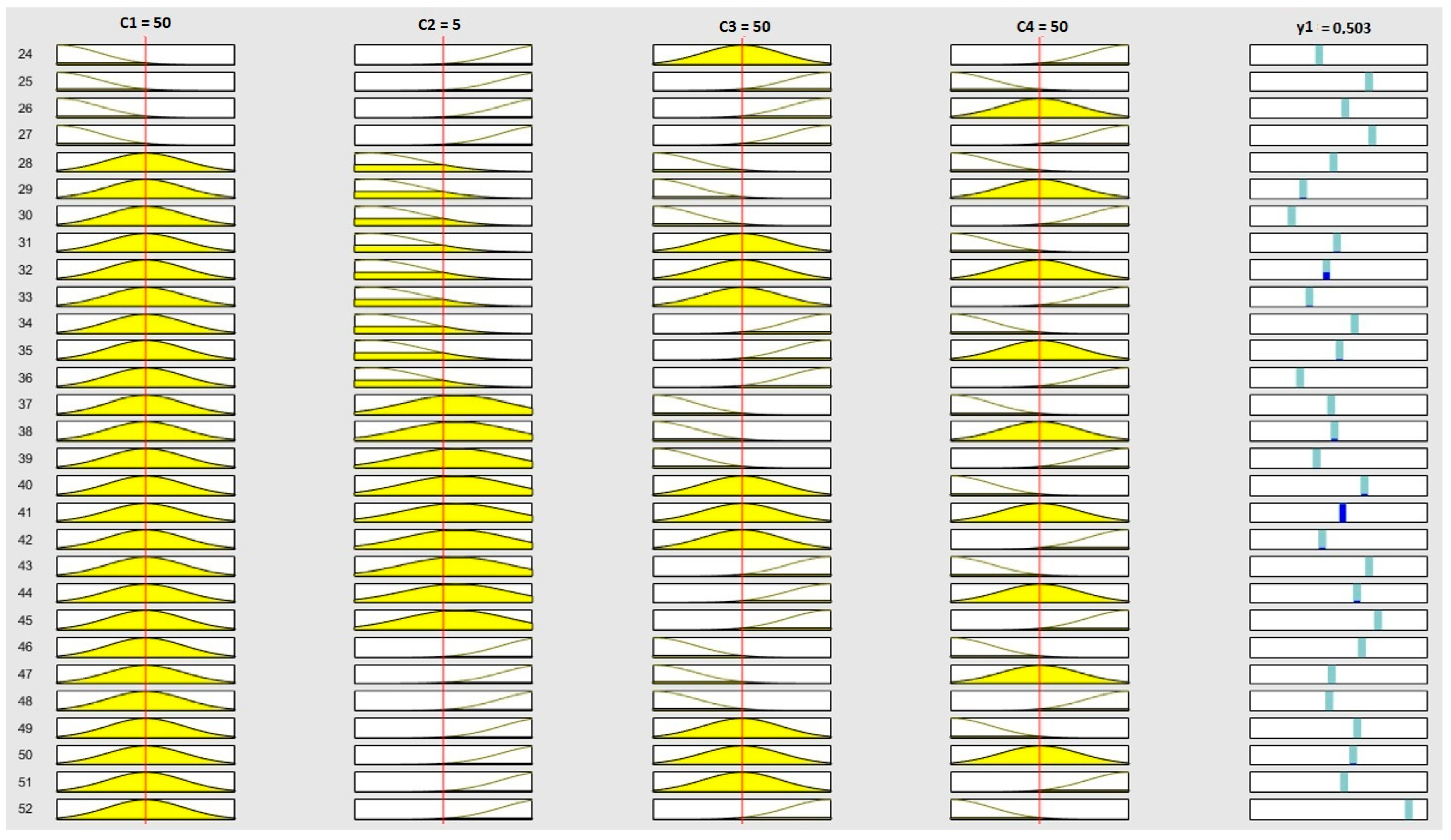
4.2.2. Stage 2: Application of the ANFIS Models
4.2.3. Stage 3: Supplier Categorization
4.3. Contributions and Implications
5. Statistical Test Results
6. Conclusions
- i.
- Model based on supervised learning and nonlinear modeling: Using a supervised learning method, this is the first supplier segmentation model that uses historical performance data to automatically adjust the relationships between the input variables, capturing nonlinear interactions among criteria.
- ii.
- Transparency and interpretability through decision rules: The supervised learning process allows the incorporation of available knowledge about supplier performance into the inference rules. This makes the outputs produced by the ANFIS models easily interpretable and allows identification of which decision rules produced specific results.
- iii.
- Identification of appropriate ANFIS topological parameters: This study also contributes by determining appropriate topological parameters to achieve accurate results. These guidelines provide practical support for researchers and practitioners developing computational solutions based on ANFIS for supplier evaluation, ensuring computational efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
| ANFIS | Adaptive Network-based Fuzzy Inference System |
| ANP | Analytic Network Process |
| BWM | Best Worst Method |
| Cj | j-th criterion |
| DEA | Data Envelopment Analysis |
| DEMATEL | Decision Making Trial and Evaluation Laboratory |
| DM | Decision Maker |
| ELECTREE | ÉLimination Et Choix Traduisant la REalité (em francês) |
| MAUT | Multi-attribute Utility Theory |
| MCDM | Multi-criteria Decision Making |
| MSE | Mean Squared Error |
| PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluation |
| RMSE | Root Mean Square Error |
| Si | i-th supplier |
| TBL | Triple Bottom Line |
| TOPSIS | Technique for Order of Preference by Similarity to the Ideal Solution |
| VIKOR | Vlsekriterijumska Optimizacija I KOmpromisno Resenje |
| Ym | Output of the m-th model |
Appendix A
| Economic Criteria | Environmental Criteria | Social Criteria |
|---|---|---|
|
|
|
References
- Finger, G.W.S.; Lima, F.R., Jr. A Hesitant Fuzzy Linguistic QFD Approach for Formulating Sustainable Supplier Development Programs. Int. J. Prod. Econ. 2022, 247, 108428. [Google Scholar] [CrossRef]
- Bai, C.; Kusi-Sarpong, S.; Khan, S.A.; Vazquez-Brust, D. Sustainable Buyer–Supplier Relationship Capability Development: A Relational Framework and Visualization Methodology. Ann. Oper. Res. 2021, 304, 1–34. [Google Scholar] [CrossRef]
- Shiralkar, K.; Bongale, A.; Kumar, S. Nos with Decision Making Methods for Supplier Segmentation in Supplier Relationship Management: A Literature Review. Mater. Today Proc. 2022, 50, 1786–1792. [Google Scholar] [CrossRef]
- Zimmer, K.; Fröhling, M.; Schultmann, F. Sustainable Supplier Management: A Review of Models Supporting Sustainable Supplier Selection, Monitoring and Development. Int. J. Prod. Res. 2016, 54, 1412–1442. [Google Scholar] [CrossRef]
- Resende, C.H.L.; Lima, F.R., Jr.; Carpinetti, L.C.R. Decision-Making Models for Formulating and Evaluating Supplier Development Programs: A State-of-the-Art Review and Research Paths. Transp. Res. Part E Logist. Transp. Rev. 2023, 180, 103340. [Google Scholar] [CrossRef]
- Borges, W.V.; Lima, F.R., Jr.; Peinado, J.; Carpinetti, L.C.R. A Hesitant Fuzzy Linguistic TOPSIS Model to Support Supplier Segmentation. J. Contemp. Adm. 2022, 26, e210133. [Google Scholar] [CrossRef]
- Rezaei, J.; Lajimi, H.F. Segmenting Supplies and Suppliers: Bringing Together the Purchasing Portfolio Matrix and the Supplier Potential Matrix. Int. J. Logist. Res. Appl. 2019, 22, 419–436. [Google Scholar] [CrossRef]
- Day, M.; Magnan, G.M.; Moeller, M.M. Evaluating the Bases of Supplier Segmentation: A Review and Taxonomy. Ind. Mark. Manag. 2010, 39, 625–639. [Google Scholar] [CrossRef]
- Borges, W.V.; Lima, F.R., Jr. Decision Support Models for Supplier Segmentation: A Systematic Literature Review. In Proceedings of the 10th Brazilian Congress of Production Engineering (ConBRepro), Online, 2–4 December 2020. [Google Scholar]
- Torres-Ruiz, A.; Ravindran, R. Multiple Criteria Framework for the Sustainability Risk Assessment of a Supplier Portfolio. J. Clean. Prod. 2018, 172, 4478–4493. [Google Scholar] [CrossRef]
- Rius-Sorolla, G.; Estelles-Miguel, S.; Rueda-Armengot, C. Multivariable Supplier Segmentation in Sustainable Supply Chain Management. Sustainability 2020, 12, 4556. [Google Scholar] [CrossRef]
- Coşkun, S.S.; Kumru, M.; Kan, N.M. An Integrated Framework for Sustainable Supplier Development Through Supplier Evaluation Based on Sustainability Indicators. J. Clean. Prod. 2022, 335, 130287. [Google Scholar] [CrossRef]
- Mavi, R.K.; Zarbakhshnia, N.; Mavi, N.K.; Kazemi, S. Clustering Sustainable Suppliers in the Plastics Industry: A Fuzzy Equivalence Relation Approach. J. Environ. Manag. 2023, 345, 118811. [Google Scholar] [CrossRef]
- Rahiminia, M.; Razmi, J.; Shahrabi Farahani, S.; Sabbaghnia, A. Cluster-Based Supplier Segmentation: A Sustainable Data-Driven Approach. Mod. Supply Chain Res. Appl. 2023, 5, 209–228. [Google Scholar] [CrossRef]
- Taghipour, A.; Fooladvand, A.; Khazaei, M.; Ramezani, M. Criteria Clustering and Supplier Segmentation Based on Sustainable Shared Value Using BWM and PROMETHEE. Sustainability 2023, 15, 8670. [Google Scholar] [CrossRef]
- Ahamed, N.; Dey, G.; Ahmed, T.; Rahman, R.; Taqi, H.M.M.; Ahmed, S. Embracing Sustainability in Green Supplier Evaluation: A Novel Integrated Multi-Criteria Decision-Making Framework. Contemp. Math. 2024, 5, 1891–1917. [Google Scholar] [CrossRef]
- Li, Y.; Tsang, Y.; Lee, C.; Wu, C. Multi-Criteria Group Decision Analytics for Sustainable Supplier Relationship Management in a Focal Manufacturing Company. J. Clean. Prod. 2024, 476, 143690. [Google Scholar] [CrossRef]
- Messaoudi, L.; Mahdhi, M. Integrating Hierarchical Clustering and Stochastic Multi-Objective Decision-Making for Optimized Decision Processes. In Proceedings of the International Conference on Decision Aid Sciences and Applications, Manama, Bahrain, 11–12 December 2024; pp. 1–5. [Google Scholar]
- Paybarjay, H.; Lajimi, H.F.; Zolfani, S.H. An Investigation of Supplier Development Through Segmentation in Sustainability Dimensions. Environ. Dev. Sustain. 2024, 26, 14369–14403. [Google Scholar] [CrossRef]
- Azadi, M.; Moghaddas, Z.; Farzipoor, R. Assessing Resilience and Sustainability of Suppliers: An Extension and Application of Data Envelopment Analytical Hierarchy Process. Ann. Oper. Res. 2025, 346, 705–750. [Google Scholar] [CrossRef]
- Lima, F.R., Jr.; Carpinetti, L.C.R. An Adaptive Network-Based Fuzzy Inference System to Supply Chain Performance Evaluation Based on SCOR® Metrics. Comput. Ind. Eng. 2020, 139, 106191. [Google Scholar] [CrossRef]
- Bamakan, S.M.H.; Faregh, N.; ZareRavasan, A. Di-ANFIS: An Integrated Blockchain–IoT–Big Data-Enabled Framework for Evaluating Service Supply Chain Performance. J. Comput. Des. Eng. 2021, 8, 676–690. [Google Scholar] [CrossRef]
- Nzamba, Y.; Lima, F.R.; Nascimento, M.C.; Batista, Á.A.S.; Tonon, L. Um Panorama dos Modelos de Tomada de Decisão para Segmentação de Fornecedores. Cad. Pedagógico 2024, 21, e11451. [Google Scholar] [CrossRef]
- Akman, G. Evaluating Suppliers to Include Green Supplier Development Programs via Fuzzy C-Means and VIKOR Methods. Comput. Ind. Eng. 2015, 86, 69–82. [Google Scholar] [CrossRef]
- Aloini, D.; Dulmin, R.; Mininno, V.; Zerbino, P. Leveraging Procurement Related Knowledge Through a Fuzzy-Based DSS: A Refinement of Purchasing Portfolio Models. J. Knowl. Manag. 2019, 23, 1077–1104. [Google Scholar] [CrossRef]
- Bianchini, A.; Benci, A.; Pellegrini, M.; Rossi, J. Supply Chain Redesign for Lead-Time Reduction Through Kraljic Purchasing Portfolio and AHP Integration. Benchmarking Int. J. 2019, 26, 1194–1209. [Google Scholar] [CrossRef]
- Boujelben, M.A. A Unicriterion Analysis Based on the PROMETHEE Principles for Multicriteria Ordered Clustering. Omega 2017, 69, 126–140. [Google Scholar] [CrossRef]
- Demir, L.; Akpinar, M.E.; Araz, C.; Ilgin, M.A. A Green Supplier Evaluation System Based on a New Multi-Criteria Sorting Method: VIKORSORT. Expert Syst. Appl. 2018, 114, 479–487. [Google Scholar] [CrossRef]
- Duc, D.A.; Van, L.H.; Yu, V.F.; Chou, S.Y.; Hien, N.V.; Chi, N.T.; Toan, D.V.; Dat, L.Q. A Dynamic Generalized Fuzzy Multi-Criteria Group Decision Making Approach for Green Supplier Segmentation. PLoS ONE 2021, 16, e0245187. [Google Scholar] [CrossRef]
- Haghighi, P.S.; Moradi, M.; Salahi, M. Supplier Segmentation Using Fuzzy Linguistic Preference Relations and Fuzzy Clustering. Int. J. Intell. Syst. Appl. 2014, 6, 76–82. [Google Scholar] [CrossRef][Green Version]
- Jharkharia, S.; Das, C. Low Carbon Supplier Development: A Fuzzy C-Means and Fuzzy Formal Concept Analysis Based Analytical Model. Benchmarking Int. J. 2019, 26, 73–96. [Google Scholar] [CrossRef]
- Kaur, H.; Singh, S.P. Multi-Stage Hybrid Model for Supplier Selection and Order Allocation Considering Disruption Risks and Disruptive Technologies. Int. J. Prod. Econ. 2021, 231, 107830. [Google Scholar] [CrossRef]
- Keskin, F.D.; Kaymaz, Y. Machine Learning in Supply Chain Management: A Risk-Based Supplier Segmentation Application. In Business Studies and New Approaches; Unvan, Y.A., Ed.; Livre de Lyon: Lyon, France, 2021; pp. 139–161. [Google Scholar]
- Lima, F.R., Jr.; Carpinetti, L.C.R. Combining SCOR® Model and Fuzzy TOPSIS for Supplier Evaluation and Management. Int. J. Prod. Econ. 2016, 174, 128–141. [Google Scholar] [CrossRef]
- Lo, S.C.; Sudjatmika, F.V. Solving Multi-Criteria Supplier Segmentation Based on the Modified FAHP for Supply Chain Management: A Case Study. Soft Comput. 2016, 20, 4981–4990. [Google Scholar] [CrossRef]
- Matshabaphala, N.M.; Grobler, J. Supplier Segmentation: A Case Study of Mozambican Cassava Farmers. S. Afr. J. Ind. Eng. 2021, 32, 196–209. [Google Scholar]
- Medeiros, M.; Ferreira, L. Development of a Purchasing Portfolio Model: An Empirical Study in a Brazilian Hospital. J. Prod. Plan. Control 2018, 29, 571–585. [Google Scholar] [CrossRef]
- Nasiri, G.R.; Miandoabchi, E.; Javadi, M. Developing a Two-Stage Decision-Making Method for Selecting and Clustering Suppliers Based on the Resilience Criteria. Group Decis. Negot. 2025, 34, 7–34. [Google Scholar] [CrossRef]
- Osiro, L.; Lima, F.R., Jr.; Carpinetti, L.C.R. A Fuzzy Logic Approach to Supplier Evaluation for Development. Int. J. Prod. Econ. 2014, 153, 95–112. [Google Scholar] [CrossRef]
- Parkouhi, S.V.; Ghadikolaei, A.S.; Lajimi, H.F. Resilient Supplier Selection and Segmentation in Grey Environment. J. Clean. Prod. 2019, 207, 1123–1137. [Google Scholar] [CrossRef]
- Rajesh, G.; Raju, R. A Fuzzy Inference Approach to Supplier Segmentation for Strategic Development. S. Afr. J. Ind. Eng. 2021, 32, 44–55. [Google Scholar]
- Restrepo, R.; Villegas, J.G. Supplier Evaluation and Classification in a Colombian Motorcycle Assembly Company Using Data Envelopment Analysis. Acad. Rev. Lat. Adm. 2019, 32, 159–180. [Google Scholar]
- Rezaei, J.; Ortt, R. Multi-Criteria Supplier Segmentation Using a Fuzzy Preference Relation Based AHP. Eur. J. Oper. Res. 2013, 225, 75–84. [Google Scholar] [CrossRef]
- Rezaei, J.; Ortt, R. Supplier Segmentation Using Fuzzy Logic. Ind. Mark. Manag. 2013, 42, 507–517. [Google Scholar] [CrossRef]
- Rezaei, J.; Kadzinski, M.; Vana, C.; Tavasszy, L. Embedding Carbon Impact Assessment in Multi-Criteria Supplier Segmentation Using ELECTRE TRI-rC. Ann. Oper. Res. 2017, 312, 1445–1467. [Google Scholar] [CrossRef]
- Rezaei, J.; Wang, J.; Tavasszy, L. Linking Supplier Development to Supplier Segmentation Using Best Worst Method. Expert Syst. Appl. 2015, 42, 9152–9164. [Google Scholar] [CrossRef]
- Santos, L.F.O.M.; Osiro, L.; Lima, R.H.P. A Model Based on 2-Tuple Fuzzy Linguistic Representation and Analytic Hierarchy Process for Supplier Segmentation Using Qualitative and Quantitative Criteria. Expert Syst. Appl. 2017, 79, 53–64. [Google Scholar] [CrossRef]
- Segura, M.; Maroto, C. A Multiple Criteria Supplier Segmentation Using Outranking and Value Function Methods. Expert Syst. Appl. 2017, 69, 87–100. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Özkana, G.; Inal, M. Comparison of Neural Network Application for Fuzzy and ANFIS Approaches for Multi-Criteria Decision-Making Problems. Appl. Soft Comput. 2014, 24, 232–238. [Google Scholar] [CrossRef]
- Mavi, R.K.; Mavi, N.K.; Goh, M. Modeling Corporate Entrepreneurship Success with ANFIS. Oper. Res. 2017, 17, 213–238. [Google Scholar]
- Xue, G.; Chang, Q.; Wang, J.; Zhang, K.; Pal, N.R. An Adaptive Neuro-Fuzzy System with Integrated Feature Selection and Rule Extraction for High-Dimensional Classification Problems. IEEE Trans. Fuzzy Syst. 2023, 31, 2167–2181. [Google Scholar] [CrossRef]
- Lajimi, H.F. Sustainable Supplier Segmentation: A Practical Procedure. In Strategic Decision Making for Sustainable Management of Industrial Networks; Rezaei, J., Ed.; Springer: Cham, Switzerland, 2021; pp. 119–137. [Google Scholar]
- Pedroso, C.B.; Tate, W.L.; Silva, A.L.; Carpinetti, L.C.R. Supplier Development Adoption: A Conceptual Model for Triple Bottom Line (TBL) Outcomes. J. Clean. Prod. 2021, 314, 127886. [Google Scholar] [CrossRef]
- Bai, C.; Rezaei, J.; Sarkis, J. Multicriteria Green Supplier Segmentation. IEEE Trans. Autom. Sci. Eng. 2017, 64, 515–528. [Google Scholar] [CrossRef]
- Akkoç, S. An Empirical Comparison of Conventional Techniques, Neural Networks and the Three Stages Hybrid Adaptive Neuro Fuzzy Inference System (ANFIS) Model for Credit Scoring Analysis: The Case of Turkish Credit Card Data. Eur. J. Oper. Res. 2012, 222, 168–178. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, S.; Wang, L.; Yang, Y.; Hapashi, K. An Evaluation Model of Supply Chain Performances Using 5DBSC and LMBP Neural Network Algorithm. J. Bionic Eng. 2013, 10, 383–395. [Google Scholar] [CrossRef]
- Montgomery, D.; Runger, G. Applied Statistics and Probability for Engineers; Hoboken: Wiley, NJ, USA, 2018. [Google Scholar]
| [6] | [10] | [11] | [12] | [13] | [14] | [15] | [16] | [17] | [18] | [19] | [20] | Our Study | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Does it offer support for sustainable supplier segmentation? | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Does it have a supervised learning process? | No | No | No | No | No | No | No | No | No | No | No | No | Yes |
| Is segmentation based on economic, environmental, and social dimensions? | No | No | No | Yes | Yes | No | No | No | Yes | No | Yes | No | Yes |
| Is there compensation among the TBL dimensions or criteria? | Yes | Yes | Yes | No | Yes | Yes | Yes | Yes | No | Yes | No | Yes | No |
| Does it have the capacity to model nonlinear relationships between inputs and outputs? | No | No | No | No | No | No | No | No | No | No | No | No | Yes |
| Does the model include decision rules? | No | No | No | No | No | No | No | No | No | No | No | No | Yes |
| Proposed by | Decision-Making Techniques | Segmentation Dimensions | Supply Chain Management Strategy | ||||
|---|---|---|---|---|---|---|---|
| Traditional | Green | Agile | Resilient | Sustainable | |||
| [4] | Fuzzy c-means and VIKOR | Does not adopt segmentation dimensions | X | ||||
| [16] | TOPSIS and Fuzzy DEMATEL | Does not adopt segmentation dimensions | X | ||||
| [25] | Fuzzy inference | Supplier attractiveness and strength of the relationship | X | ||||
| [20] | DEA and AHP | Does not adopt segmentation dimensions | X | X | |||
| [2] | Rough Sets, VIKOR, and fuzzy c-means | Supplier capabilities and willingness | X | ||||
| [26] | AHP | Profit impact and supply risk | X | ||||
| [6] | Hesitant Fuzzy Linguistic-TOPSIS | Supplier capabilities and willingness | X | ||||
| [27] | PROMETHEE | Supplier capabilities and willingness | X | ||||
| [12] | ANP, PROMETHEE, and cluster analysis | Economic, environmental, and social | |||||
| [28] | VIKORSORT | Does not adopt segmentation dimensions | X | ||||
| [29] | Fuzzy logic | Supplier capabilities and willingness | X | ||||
| [30] | Fuzzy-AHP and Fuzzy c-means | Supplier capabilities and willingness | X | ||||
| [31] | Fuzzy c-means and Fuzzy formal concept analysis | Supplier investment decisions and supplier collaboration decisions | X | ||||
| [32] | DEA | Does not adopt segmentation dimensions | X | ||||
| [33] | K-means | Does not adopt segmentation dimensions | X | ||||
| [17] | Bayesian best-worst method and Canopy-K-Means clustering algorithm | Economic, environmental, and social | X | ||||
| [34] | Fuzzy-TOPSIS | Cost and delivery performance | X | ||||
| [35] | Fuzzy-AHP | Supplier capabilities and willingness | X | ||||
| [36] | K-means | Does not adopt segmentation dimensions | X | ||||
| [13] | Fuzzy-AHP and Fuzzy equivalence relation | Economic, environmental, social, and risk | X | ||||
| [37] | Fuzzy-TOPSIS | Profit impact and supply risk | X | ||||
| [18] | Stochastic multi-objective programming | Profit, capability, and willingness | X | ||||
| [38] | BWM and K-means | The model does not rely on predefined segmentation dimensions | X | ||||
| [39] | Fuzzy inference | Potential for partnership and delivery performance | X | ||||
| [40] | Grey DEMATEL and Grey Simple Additive Weighting technique | Resiliency enhancer and resiliency reducer | X | ||||
| [19] | BWM and Grey Simple Additive Weighting | Economic, environmental, and social | X | ||||
| [14] | BWM and K-means | Profit impact and supply risk | X | ||||
| [41] | Fuzzy inference | Agility capability and business excellence | X | ||||
| [42] | DEA | Diversity, efficiency, and cross efficiency | X | ||||
| [7] | BWM | Supplier capabilities and supplier willingness | X | ||||
| [43] | Fuzzy preference relation-based AHP | Supplier capabilities and supplier willingness | X | ||||
| [44] | AHP | Supplier capabilities and supplier willingness | X | ||||
| [45] | ELECTRE TRI-rC | Supplier capabilities and supplier willingness | X | ||||
| [46] | BWM | Supplier capabilities and supplier willingness | X | ||||
| [11] | Procedure based on the arithmetic mean | Profit impact and supply risk | X | ||||
| [47] | AHP and Fuzzy 2-tuple | Supplier capabilities and supplier willingness | X | ||||
| [48] | AHP, PROMETHEE, and MAUT | Critical performance and strategic performance | X | ||||
| [15] | BWM and PROMETHEE | Critical performance and strategic performance of suppliers | X | ||||
| [10] | AHP | Supplier risks, country risks, and risk management practice | X | ||||
| Performance Dimension | Supplier Development Strategies | Supplier Groups |
|---|---|---|
| Environmental |
| G1, G3, G5, and G7 |
| Social |
| G1, G2, G3, and G4 |
| Economic | G1, G2, G5, and G6 |
| Suppliers | Supplier Scores on Each Criterion (Inputs) | Output (Y1) | |||
|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | ||
| S1 | 100 | 6 | 48 | 62 | 0.5845 |
| S2 | 93 | 9 | 8 | 51 | 0.5453 |
| S3 | 69 | 2 | 69 | 62 | 0.5024 |
| S4 | 90 | 9 | 59 | 70 | 0.6215 |
| S5 | 76 | 5 | 11 | 94 | 0.3797 |
| : | : | : | : | : | : |
| S200 | 68 | 6 | 35 | 59 | 0.4987 |
| Description of the Parameters | Tested Functions and Values |
|---|---|
| Membership function type: determines the quantitative representation and behavior of input variables. | Triangular, trapezoidal, and Gaussian functions [22,51]. |
| Consequent type: determines the type of the output for each activated rule. | Linear functions and constant values [21,49,50]. |
| Number of fuzzy membership functions: determines the partition granularity of the fuzzy input variables. | 3, 4, and 5 functions [51,56]. |
| Fuzzy operator: responsible for aggregation operations among the degrees of activated membership functions. | Minimum and algebraic product operators [21,50]. |
| Candidate Topology | Number of Inference Rules | Membership Function Type | Consequent Type | Number of Fuzzy Membership Functions | Fuzzy Operator | Training MSE | Training RMSE | Validation MSE | Validation RMSE |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 81 | Triangular | Crisp | 3 | Minimum | 2.738 × 10−4 | 1.654 × 10−2 | 3.518 × 10−3 | 5.933 × 10−2 |
| 2 | 81 | Triangular | Crisp | 3 | Product | 4.277 × 10−6 | 2.068 × 10−3 | 3.820 × 10−4 | 1.955 × 10−2 |
| 3 | 256 | Triangular | Crisp | 4 | Minimum | 2.719 × 10−11 | 5.215 × 10−6 | 2.885 × 10−3 | 5.371 × 10−2 |
| 4 | 256 | Triangular | Crisp | 4 | Product | 5.659 × 10−12 | 2.379 × 10−6 | 1.056 × 10−2 | 1.028 × 10−1 |
| 5 | 625 | Triangular | Crisp | 5 | Minimum | 8.425 × 10−12 | 2.902 × 10−6 | 2.641 × 10−2 | 1.624 × 10−1 |
| 6 | 625 | Triangular | Crisp | 5 | Product | 3.557 × 10−12 | 1.886 × 10−6 | 6.540 × 10−2 | 2.557 × 10−1 |
| 7 | 81 | Triangular | Linear | 3 | Minimum | 2.597 × 10−15 | 5.096 × 10−8 | 1.073 × 10−2 | 1.036 × 10−1 |
| 8 | 81 | Triangular | Linear | 3 | Product | 5.239 × 10−15 | 7.238 × 10−8 | 2.269 × 10−3 | 4.764 × 10−2 |
| 9 | 256 | Triangular | Linear | 4 | Minimum | 2.606 × 10−15 | 5.105 × 10−8 | 4.776 × 10−3 | 6.911 × 10−2 |
| 10 | 256 | Triangular | Linear | 4 | Product | 6.729 × 10−15 | 8.205 × 10−8 | 1.058 × 10−2 | 1.029 × 10−1 |
| 11 | 625 | Triangular | Linear | 5 | Minimum | 5.544 × 10−15 | 7.444 × 10−8 | 2.667 × 10−2 | 1.633 × 10−1 |
| 12 | 625 | Triangular | Linear | 5 | Product | 8.285 × 10−15 | 9.099 × 10−8 | 4.669 × 10−2 | 2.161 × 10−1 |
| 13 | 81 | Trapezoidal | Crisp | 3 | Minimum | 6.117 × 10−4 | 2.473 × 10−2 | 4.336 × 10−2 | 2.082 × 10−1 |
| 14 | 81 | Trapezoidal | Crisp | 3 | Product | 5.414 × 10−4 | 2.326 × 10−2 | 1.340 × 10−1 | 3.660 × 10−1 |
| 15 | 256 | Trapezoidal | Crisp | 4 | Minimum | 8.607 × 10−6 | 2.933 × 10−3 | 8.072 × 10−2 | 2.840 × 10−1 |
| 16 | 256 | Trapezoidal | Crisp | 4 | Product | 1.028 × 10−9 | 3.206 × 10−5 | 1.270 × 10−1 | 3.564 × 10−1 |
| 17 | 625 | Trapezoidal | Crisp | 5 | Minimum | 1.285 × 10−11 | 3.584 × 10−6 | 9.416 × 10−2 | 3.069 × 10−1 |
| 18 | 625 | Trapezoidal | Crisp | 5 | Product | 6.073 × 10−12 | 2.464 × 10−6 | 1.321 × 10−1 | 3.634 × 10−1 |
| 19 | 81 | Trapezoidal | Linear | 3 | Minimum | 9.499 × 10−15 | 9.746 × 10−8 | 2.353 × 10−2 | 1.534 × 10−1 |
| 20 | 81 | Trapezoidal | Linear | 3 | Product | 1.224 × 10−14 | 1.106 × 10−7 | 2.769 × 10−2 | 1.664 × 10−1 |
| 21 | 256 | Trapezoidal | Linear | 4 | Minimum | 7.910 × 10−14 | 2.811 × 10−7 | 4.623 × 10−2 | 2.150 × 10−1 |
| 22 | 256 | Trapezoidal | Linear | 4 | Product | 6.299 × 10−14 | 2.509 × 10−7 | 5.915 × 10−2 | 2.432 × 10−1 |
| 23 | 625 | Trapezoidal | Linear | 5 | Minimum | 4.237 × 10−14 | 2.058 × 10−7 | 9.806 × 10−2 | 3.131 × 10−1 |
| 24 | 625 | Trapezoidal | Linear | 5 | Product | 4.415 × 10−14 | 2.101 × 10−7 | 1.183 × 10−1 | 3.439 × 10−1 |
| 25 | 81 | Gaussian | Crisp | 3 | Minimum | 8.543 × 10−5 | 9.241 × 10−3 | 1.428 × 10−3 | 3.778 × 10−2 |
| 26 | 81 | Gaussian | Crisp | 3 | Product | 2.381 × 10−5 | 4.879 × 10−3 | 2.380 × 10−4 | 1.543 × 10−2 |
| 27 | 256 | Gaussian | Crisp | 4 | Minimum | 1.626 × 10−11 | 4.032 × 10−6 | 1.565 × 10−3 | 3.956 × 10−2 |
| 28 | 256 | Gaussian | Crisp | 4 | Product | 1.594 × 10−11 | 3.991 × 10−6 | 1.032 × 10−2 | 1.016 × 10−1 |
| 29 | 625 | Gaussian | Crisp | 5 | Minimum | 8.993 × 10−12 | 2.999 × 10−6 | 1.198 × 10−2 | 1.094 × 10−1 |
| 30 | 625 | Gaussian | Crisp | 5 | Product | 2.690 × 10−12 | 1.640 × 10−6 | 7.195 × 10−2 | 2.682 × 10−1 |
| 31 | 81 | Gaussian | Linear | 3 | Minimum | 1.535 × 10−15 | 3.918 × 10−8 | 4.037 × 10−3 | 6.354 × 10−2 |
| 32 | 81 | Gaussian | Linear | 3 | Product | 1.376 × 10−14 | 1.173 × 10−7 | 7.782 × 10−3 | 8.822 × 10−2 |
| 33 | 256 | Gaussian | Linear | 4 | Minimum | 1.833 × 10−15 | 4.281 × 10−8 | 3.658 × 10−3 | 6.048 × 10−2 |
| 34 | 256 | Gaussian | Linear | 4 | Product | 1.235 × 10−14 | 1.111 × 10−7 | 1.351 × 10−2 | 1.162 × 10−1 |
| 35 | 625 | Gaussian | Linear | 5 | Minimum | 3.656 × 10−15 | 6.045 × 10−8 | 1.296 × 10−2 | 1.138 × 10−1 |
| 36 | 625 | Gaussian | Linear | 5 | Product | 2.567 × 10−14 | 1.602 × 10−7 | 4.822 × 10−2 | 2.196 × 10−1 |
| Candidate Topology | Number of Inference Rules | Membership Function Type | Consequent Type | Number of Fuzzy Membership Functions | Fuzzy Operator | Training MSE | Training RMSE | Validation MSE | Validation RMSE |
|---|---|---|---|---|---|---|---|---|---|
| 37 | 81 | Triangular | Crisp | 3 | Minimum | 3.075 × 10−4 | 1.754 × 10−2 | 5.539 × 10−4 | 2.354 × 10−2 |
| 38 | 81 | Triangular | Crisp | 3 | Product | 7.921 × 10−6 | 2.814 × 10−3 | 1.349 × 10−5 | 3.673 × 10−3 |
| 39 | 256 | Triangular | Crisp | 4 | Minimum | 1.063 × 10−4 | 1.031 × 10−2 | 3.618 × 10−4 | 1.902 × 10−2 |
| 40 | 256 | Triangular | Crisp | 4 | Product | 1.697 × 10−6 | 1.303 × 10−3 | 2.178 × 10−5 | 4.667 × 10−3 |
| 41 | 625 | Triangular | Crisp | 5 | Minimum | 8.705 × 10−6 | 2.950 × 10−3 | 2.077 × 10−2 | 1.441 × 10−1 |
| 42 | 625 | Triangular | Crisp | 5 | Product | 2.850 × 10−10 | 1.688 × 10−5 | 8.717 × 10−3 | 9.336 × 10−2 |
| 43 | 81 | Triangular | Linear | 3 | Minimum | 8.052 × 10−7 | 8.973 × 10−4 | 1.389 × 10−4 | 1.179 × 10−2 |
| 44 | 81 | Triangular | Linear | 3 | Product | 9.466 × 10−8 | 3.077 × 10−4 | 5.206 × 10−5 | 7.215 × 10−3 |
| 45 | 256 | Triangular | Linear | 4 | Minimum | 3.210 × 10−14 | 1.792 × 10−7 | 1.606 × 10−4 | 1.267 × 10−2 |
| 46 | 256 | Triangular | Linear | 4 | Product | 4.448 × 10−15 | 6.669 × 10−8 | 9.201 × 10−5 | 9.592 × 10−3 |
| 47 | 625 | Triangular | Linear | 5 | Minimum | 6.219 × 10−16 | 2.494 × 10−8 | 7.544 × 10−3 | 8.686 × 10−2 |
| 48 | 625 | Triangular | Linear | 5 | Product | 1.308 × 10−15 | 3.617 × 10−8 | 1.153 × 10−2 | 1.074 × 10−1 |
| 49 | 81 | Trapezoidal | Crisp | 3 | Minimum | 7.520 × 10−5 | 8.672 × 10−3 | 1.167 × 10−4 | 1.080 × 10−2 |
| 50 | 81 | Trapezoidal | Crisp | 3 | Product | 7.542 × 10−5 | 8.684 × 10−3 | 1.171 × 10−4 | 1.082 × 10−2 |
| 51 | 256 | Trapezoidal | Crisp | 4 | Minimum | 2.845 × 10−4 | 1.687 × 10−2 | 5.836 × 10−2 | 2.416 × 10−1 |
| 52 | 256 | Trapezoidal | Crisp | 4 | Product | 1.105 × 10−4 | 1.051 × 10−2 | 4.418 × 10−4 | 2.102 × 10−2 |
| 53 | 625 | Trapezoidal | Crisp | 5 | Minimum | 1.218 × 10−4 | 1.104 × 10−2 | 2.826 × 10−1 | 5.316 × 10−1 |
| 54 | 625 | Trapezoidal | Crisp | 5 | Product | 1.076 × 10−4 | 1.037 × 10−2 | 6.911 × 10−2 | 2.629 × 10−1 |
| 55 | 81 | Trapezoidal | Linear | 3 | Minimum | 9.025 × 10−7 | 9.500 × 10−4 | 1.946 × 10−3 | 4.411 × 10−2 |
| 56 | 81 | Trapezoidal | Linear | 3 | Product | 1.542 × 10−7 | 3.927 × 10−4 | 5.054 × 10−4 | 2.248 × 10−2 |
| 57 | 256 | Trapezoidal | Linear | 4 | Minimum | 1.836 × 10−13 | 4.285 × 10−7 | 1.012 × 10−3 | 3.181 × 10−2 |
| 58 | 256 | Trapezoidal | Linear | 4 | Product | 7.792 × 10−14 | 2.791 × 10−7 | 1.052 × 10−3 | 3.243 × 10−2 |
| 59 | 625 | Trapezoidal | Linear | 5 | Minimum | 8.016 × 10−8 | 2.831 × 10−4 | 4.529 × 10−2 | 2.128 × 10−1 |
| 60 | 625 | Trapezoidal | Linear | 5 | Product | 8.016 × 10−8 | 2.831 × 10−4 | 4.978 × 10−2 | 2.231 × 10−1 |
| 61 | 81 | Gaussian | Crisp | 3 | Minimum | 7.841 × 10−5 | 8.855 × 10−3 | 1.242 × 10−4 | 1.114 × 10−2 |
| 62 | 81 | Gaussian | Crisp | 3 | Product | 6.943 × 10−6 | 2.635 × 10−3 | 1.125 × 10−5 | 3.354 × 10−3 |
| 63 | 256 | Gaussian | Crisp | 4 | Minimum | 2.093 × 10−5 | 4.575 × 10−3 | 5.461 × 10−5 | 7.390 × 10−3 |
| 64 | 256 | Gaussian | Crisp | 4 | Product | 7.844 × 10−7 | 8.857 × 10−4 | 9.769 × 10−6 | 3.126 × 10−3 |
| 65 | 625 | Gaussian | Crisp | 5 | Minimum | 5.196 × 10−7 | 7.208 × 10−4 | 1.142 × 10−1 | 3.379 × 10−1 |
| 66 | 625 | Gaussian | Crisp | 5 | Product | 1.194 × 10−9 | 3.455 × 10−5 | 3.517 × 10−3 | 5.930 × 10−2 |
| 67 | 81 | Gaussian | Linear | 3 | Minimum | 7.606 × 10−7 | 8.721 × 10−4 | 2.097 × 10−4 | 1.448 × 10−2 |
| 68 | 81 | Gaussian | Linear | 3 | Product | 1.781 × 10−8 | 1.335 × 10−4 | 1.088 × 10−4 | 1.043 × 10−2 |
| 69 | 256 | Gaussian | Linear | 4 | Minimum | 3.571 × 10−14 | 1.890 × 10−7 | 5.159 × 10−5 | 7.183 × 10−3 |
| 70 | 256 | Gaussian | Linear | 4 | Product | 2.344 × 10−14 | 1.531 × 10−7 | 8.415 × 10−5 | 9.173 × 10−3 |
| 71 | 625 | Gaussian | Linear | 5 | Minimum | 1.448 × 10−15 | 3.805 × 10−8 | 1.921 × 10−3 | 4.383 × 10−2 |
| 72 | 625 | Gaussian | Linear | 5 | Product | 4.698 × 10−15 | 6.854 × 10−8 | 1.287 × 10−2 | 1.134 × 10−1 |
| Candidate Topology | Number of Inference Rules | Membership Function Type | Consequent Type | Number of Fuzzy Membership Functions | Fuzzy Operator | Training MSE | Training RMSE | Validation MSE | Validation RMSE |
|---|---|---|---|---|---|---|---|---|---|
| 73 | 81 | Triangular | Crisp | 3 | Minimum | 1.385 × 10−9 | 3.720 × 10−5 | 9.198 × 10−3 | 9.593 × 10−2 |
| 74 | 81 | Triangular | Crisp | 3 | Product | 1.065 × 10−11 | 3.264 × 10−6 | 8.355 × 10−3 | 9.142 × 10−2 |
| 75 | 256 | Triangular | Crisp | 4 | Minimum | 1.542 × 10−11 | 3.927 × 10−6 | 3.852 × 10−2 | 1.962 × 10−1 |
| 76 | 256 | Triangular | Crisp | 4 | Product | 2.761 × 10−12 | 1.661 × 10−6 | 1.358 × 10−1 | 3.685 × 10−1 |
| 77 | 625 | Triangular | Crisp | 5 | Minimum | 3.018 × 10−11 | 5.495 × 10−6 | 1.183 × 10−1 | 3.439 × 10−1 |
| 78 | 625 | Triangular | Crisp | 5 | Product | 3.212 × 10−12 | 1.791 × 10−6 | 2.199 × 10−1 | 4.690 × 10−1 |
| 79 | 81 | Triangular | Linear | 3 | Minimum | 6.159 × 10−16 | 7.846 × 10−8 | 1.215 × 10−2 | 1.102 × 10−1 |
| 80 | 81 | Triangular | Linear | 3 | Product | 5.302 × 10−16 | 7.282 × 10−8 | 1.175 × 10−2 | 1.084 × 10−1 |
| 81 | 256 | Triangular | Linear | 4 | Minimum | 9.885 × 10−16 | 9.943 × 10−8 | 4.131 × 10−2 | 2.031 × 10−1 |
| 82 | 256 | Triangular | Linear | 4 | Product | 6.336 × 10−15 | 7.958 × 10−8 | 6.981 × 10−2 | 2.641 × 10−1 |
| 83 | 625 | Triangular | Linear | 5 | Minimum | 2.984 × 10−15 | 5.462 × 10−8 | 1.165 × 10−1 | 3.414 × 10−1 |
| 84 | 625 | Triangular | Linear | 5 | Product | 2.704 × 10−15 | 5.200 × 10−8 | 1.551 × 10−1 | 3.938 × 10−1 |
| 85 | 81 | Trapezoidal | Crisp | 3 | Minimum | 2.777 × 10−05 | 5.267 × 10−3 | 8.711 × 10−2 | 2.950 × 10−1 |
| 86 | 81 | Trapezoidal | Crisp | 3 | Product | 1.101 × 10−05 | 3.318 × 10−3 | 6.174 × 10−2 | 2.484 × 10−1 |
| 87 | 256 | Trapezoidal | Crisp | 4 | Minimum | 4.329 × 10−12 | 2.080 × 10−6 | 1.829 × 10−1 | 4.277 × 10−1 |
| 88 | 256 | Trapezoidal | Crisp | 4 | Product | 1.545 × 10−12 | 1.243 × 10−6 | 2.093 × 10−1 | 4.576 × 10−1 |
| 89 | 625 | Trapezoidal | Crisp | 5 | Minimum | 2.511 × 10−7 | 5.011 × 10−4 | 2.033 × 10−1 | 4.509 × 10−1 |
| 90 | 625 | Trapezoidal | Crisp | 5 | Product | 2.510 × 10−7 | 5.010 × 10−4 | 2.398 × 10−1 | 4.897 × 10−1 |
| 91 | 81 | Trapezoidal | Linear | 3 | Minimum | 9.025 × 10−15 | 9.497 × 10−8 | 5.713 × 10−2 | 2.390 × 10−1 |
| 92 | 81 | Trapezoidal | Linear | 3 | Product | 8.604 × 10−15 | 9.272 × 10−8 | 6.371 × 10−2 | 2.523 × 10−1 |
| 93 | 256 | Trapezoidal | Linear | 4 | Minimum | 1.327 × 10−14 | 1.152 × 10−7 | 1.783 × 10−1 | 4.221 × 10−1 |
| 94 | 256 | Trapezoidal | Linear | 4 | Product | 2.253 × 10−14 | 1.500 × 10−7 | 1.936 × 10−1 | 4.398 × 10−1 |
| 95 | 625 | Trapezoidal | Linear | 5 | Minimum | 1.427 × 10−14 | 1.194 × 10−7 | 2.023 × 10−1 | 4.497 × 10−1 |
| 96 | 625 | Trapezoidal | Linear | 5 | Product | 8.294 × 10−15 | 9.102 × 10−8 | 2.257 × 10−1 | 4.751 × 10−1 |
| 97 | 81 | Gaussian | Crisp | 3 | Minimum | 5.132 × 10−10 | 2.266 × 10−5 | 4.202 × 10−3 | 6.484 × 10−2 |
| 98 | 81 | Gaussian | Crisp | 3 | Product | 1.453 × 10−11 | 3.811 × 10−6 | 1.680 × 10−2 | 1.296 × 10−1 |
| 99 | 256 | Gaussian | Crisp | 4 | Minimum | 2.169 × 10−11 | 4.657 × 10−6 | 1.340 × 10−2 | 1.157 × 10−1 |
| 100 | 256 | Gaussian | Crisp | 4 | Product | 1.657 × 10−12 | 1.287 × 10−6 | 1.482 × 10−1 | 3.850 × 10−1 |
| 101 | 625 | Gaussian | Crisp | 5 | Minimum | 3.195 × 10−11 | 5.650 × 10−6 | 6.921 × 10−2 | 2.630 × 10−1 |
| 102 | 625 | Gaussian | Crisp | 5 | Product | 1.295 × 10−12 | 1.138 × 10−6 | 2.443 × 10−1 | 4.943 × 10−1 |
| 103 | 81 | Gaussian | Linear | 3 | Minimum | 2.978 × 10−16 | 1.726 × 10−8 | 2.958 × 10−3 | 5.436 × 10−2 |
| 104 | 81 | Gaussian | Linear | 3 | Product | 1.556 × 10−14 | 1.247 × 10−7 | 1.383 × 10−2 | 1.176 × 10−1 |
| 105 | 256 | Gaussian | Linear | 4 | Minimum | 9.274 × 10−16 | 9.629 × 10−8 | 1.391 × 10−2 | 1.179 × 10−1 |
| 106 | 256 | Gaussian | Linear | 4 | Product | 1.584 × 10−14 | 1.258 × 10−7 | 6.808 × 10−2 | 2.608 × 10−1 |
| 107 | 625 | Gaussian | Linear | 5 | Minimum | 2.448 × 10−15 | 4.948 × 10−8 | 4.646 × 10−2 | 2.155 × 10−1 |
| 108 | 625 | Gaussian | Linear | 5 | Product | 1.723 × 10−14 | 1.312 × 10−7 | 1.536 × 10−1 | 3.920 × 10−1 |
| Null hypothesis: H0: µD = Alternative hypothesis: H1: µD ≠ Test statistic: T0 = Rejection region (for two-tailed test): t0 < − or t0 > Reject H0 if the p-value is <α |
| Model | Sample Set | Shapiro–Wilk | |
|---|---|---|---|
| Statistic | p-Value | ||
| ANFIS 1 | Expected values | 0.984 | 0.629 |
| Predicted values | 0.975 | 0.252 | |
| ANFIS 2 | Expected values | 0.965 | 0.087 |
| Predicted values | 0.965 | 0.087 | |
| ANFIS 3 | Expected values | 0.993 | 0.982 |
| Predicted values | 0.993 | 0.976 | |
| Model | Levene Statistic | p-Values |
|---|---|---|
| ANFIS 1 | 0.122 | 0.728 |
| ANFIS 2 | 0.000 | 0.990 |
| ANFIS 3 | 0.568 | 0.453 |
| Model | Mean | Standard Deviation | Mean Standard Error | T | p-Value |
|---|---|---|---|---|---|
| ANFIS 1 | −0.00493 | 0.01473 | 0.0019 | −2.593 | 0.012 |
| ANFIS 2 | 0.00051 | 0.00313 | 0.0004 | 1.251 | 0.216 |
| ANFIS 3 | 0.00592 | 0.05455 | 0.00704 | 0.841 | 0.404 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saugo, R.A.; Lima Junior, F.R.; Carpinetti, L.C.R.; Duarte, A.P.; Peinado, J. An Approach for Sustainable Supplier Segmentation Using Adaptive Network-Based Fuzzy Inference Systems. Mathematics 2025, 13, 3058. https://doi.org/10.3390/math13193058
Saugo RA, Lima Junior FR, Carpinetti LCR, Duarte AP, Peinado J. An Approach for Sustainable Supplier Segmentation Using Adaptive Network-Based Fuzzy Inference Systems. Mathematics. 2025; 13(19):3058. https://doi.org/10.3390/math13193058
Chicago/Turabian StyleSaugo, Ricardo Antonio, Francisco Rodrigues Lima Junior, Luiz Cesar Ribeiro Carpinetti, Ana Paula Duarte, and Jurandir Peinado. 2025. "An Approach for Sustainable Supplier Segmentation Using Adaptive Network-Based Fuzzy Inference Systems" Mathematics 13, no. 19: 3058. https://doi.org/10.3390/math13193058
APA StyleSaugo, R. A., Lima Junior, F. R., Carpinetti, L. C. R., Duarte, A. P., & Peinado, J. (2025). An Approach for Sustainable Supplier Segmentation Using Adaptive Network-Based Fuzzy Inference Systems. Mathematics, 13(19), 3058. https://doi.org/10.3390/math13193058







