Unsupervised Segmentation and Alignment of Multi-Demonstration Trajectories via Multi-Feature Saliency and Duration-Explicit HSMMs

Abstract

Learning from demonstration with multiple executions must contend with time warping, sensor noise, and alternating quasi-stationary and transition phases. We propose a label-free pipeline that couples unsupervised segmentation, duration-explicit alignment, and probabilistic encoding. A dimensionless multi-feature saliency (velocity, acceleration, curvature, direction-change rate) yields scale-robust keyframes via persistent peak–valley pairs and non-maximum suppression. A hidden semi-Markov model (HSMM) with explicit duration distributions is jointly trained across demonstrations to align trajectories on a shared semantic time base. Segment-level probabilistic motion models (GMM/GMR or ProMP, optionally combined with DMP) produce mean trajectories with calibrated covariances, directly interfacing with constrained planners. Feature weights are tuned without labels by minimizing cross-demonstration structural dispersion on the simplex via CMA-ES. Across UAV flight, autonomous driving, and robotic manipulation, the method reduces phase-boundary dispersion by 31% on UAV-Sim and by 30–36% under monotone time warps, noise, and missing data (vs. HMM); improves the sparsity–fidelity trade-off (higher time compression at comparable reconstruction error) with lower jerk; and attains nominal 2σ coverage (94–96%), indicating well-calibrated uncertainty. Ablations attribute the gains to persistence plus NMS, weight self-calibration, and duration-explicit alignment. The framework is scale-aware and computationally practical, and its uncertainty outputs feed directly into MPC/OMPL for risk-aware execution.

1. Introduction

Learning from demonstration (LfD) [1] aims to transfer skills from a small number of expert executions to new task instances. In real deployments across aerial, driving, and manipulation domains, multiple demonstrations routinely exhibit irregular local time warping (hovering, waiting, backtracking) [2,3,4], sensor noise in high-dimensional signals [5,6], and alternating quasi-stationary and transition phases [7,8,9]. Our goal is to discover phase structure without labels, align multiple demonstrations on a shared semantic time base, and provide calibrated, segment-wise probabilistic models that can be ingested by constrained planners.

A central difficulty is that widely used segmentation and alignment tools either operate at the signal-threshold level or impose duration assumptions that do not reflect how humans actually perform tasks [10,11]. Threshold- or template-based methods and simple peak detectors are brittle to sampling-rate and environment shifts; their decision surfaces move with scale changes, causing under- and over-segmentation in the presence of jitter and speed variations [12,13]. Bayesian online changepoint detection (BOCPD) relaxes fixed thresholds but still hinges on hazard-rate and noise assumptions; in practice, it can fragment long dwells into multiple short segments when features oscillate and provides no explicit duration model for downstream use [14,15,16]. Dynamic Time Warping (DTW) offers pairwise alignment but lacks a generative mechanism and cannot represent dwell-time distributions or uncertainty, which limits its utility for planning and simulation [17,18,19].

Latent-state models address some of these issues, yet common instantiations come with their own bias–variance trade-offs. Hidden Markov Models (HMMs) assume geometric state durations; this geometric-duration bias shortens non-geometric dwells and shifts boundaries when operators hesitate or loiter, leading to misaligned phases across trials [20]. Hidden semi-Markov models (HSMMs) provide a principled remedy by explicitly modeling durations, but many pipelines still rely on hand-crafted feature stacks with fixed weights/hyper-parameters tuned per demonstration or per session [1,21,22]; robustness degrades under operator/platform shifts and tempo changes. Bayesian nonparametrics can adapt model complexity [23], yet computational overhead and stability concerns have limited their use in long-horizon, multi-demo settings.

Downstream generation faces parallel limitations. Dynamical Movement Primitives (DMPs) provide smooth, time-scalable execution but lack closed-form uncertainty; Gaussian Mixture Regression (GMR) and Probabilistic Movement Primitives (ProMPs) offer distributional predictions with covariances, yet both are sensitive to boundary errors—mis-segmentation inflates variances and biases means within segments [20]. More importantly, most pipelines treat segmentation/alignment and probabilistic encoding as loosely coupled stages; mechanisms for self-calibrating features using multi-demo consistency or learning an alignment that is simultaneously scale-aware and duration-aware are rarely present [24]. Finally, although planners such as the Open Motion Planning Library (OMPL) and Model Predictive Control (MPC) can exploit covariance for risk-aware control, few works deliver calibrated uncertainty on a shared semantic time base that these planners can consume directly [25].

To address these gaps, we propose a label-free pipeline that couples unsupervised segmentation, duration-explicit alignment, and probabilistic encoding in a single, self-calibrating loop. First, we compute a dimensionless multi-feature saliency by fusing velocity, acceleration, curvature, and direction-change rate and then apply topology-aware keyframe extraction using persistent peak–valley pairs and non-maximum suppression to retain only structurally significant extrema [26]. Second, we jointly train an HSMM across demonstrations with explicit duration distributions and an extended forward–backward recursion, producing a shared semantic time axis and phase-consistent boundaries [25]. Third, within each phase, we fit probabilistic motion models—GMM/GMR or ProMP, optionally combined with DMP for execution—to obtain mean trajectories with calibrated covariances [20]. Crucially, we close the loop by learning the saliency weights without labels: a CMA-ES search on the probability simplex minimizes cross-demonstration structural dispersion, automatically re-balancing features so that segmentation and alignment are mutually consistent [27]. Compared with BOCPD, thresholding, or HMM-based pipelines, our design is explicitly duration-aware, robust to time warping, and planner-ready, producing uncertainty that is calibrated and comparable across operators.

Contributions.

• Scale-/time-warp-robust saliency. A topology-aware, multi-feature saliency (persistence + non-maximum suppression) that stabilizes keyframes under noise and tempo variations is developed, yielding sparser yet more stable anchors than signal-level detectors, and we formalize its stability in Proposition 1 (Section 2.3.5).
• Joint HSMM alignment with explicit durations. Cross-demonstration training with extended forward–backward/Viterbi recursions is used; model order is selected by a joint criterion combining BIC and alignment error (AE) to balance fit and parsimony.
• Label-free feature-weight self-calibration. CMA-ES on the weight simplex is used to minimize cross-demonstration structural dispersion, eliminating hand-tuned fusion and improving phase consistency.
• Calibrated probabilistic encoding for planning. Segment-wise GMR/ProMP (optionally fused with DMP) returning means and covariances that integrate directly with OMPL/MPC for risk-aware execution is used.

Empirically, on UAV flight, autonomous-driving, and manipulation benchmarks, our method reduces phase-boundary dispersion by ≈31% on UAV-Sim and by 30–36% under monotone time warps, additive noise, and missing data compared with HMM variants; it improves the sparsity–fidelity–smoothness trade-off (higher time compression at comparable reconstruction error with lower jerk) and achieves nominal 2σ coverage (94–96%), indicating well-calibrated uncertainty. Section 2 details the pipeline; Section 3 reports datasets, metrics, baselines (including BOCPD and HMM), ablations, and robustness; Section 4 discusses positioning, limitations, and future work; Section 5 concludes.

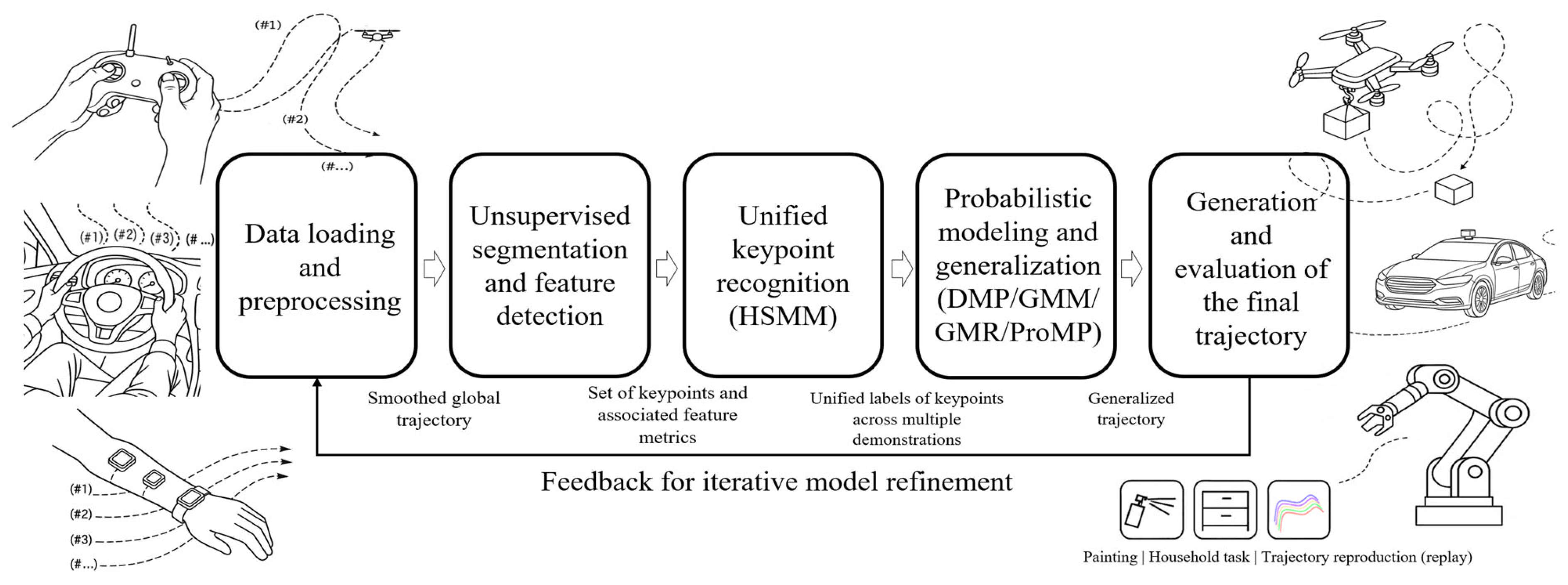
2. Materials and Methods

Figure 1 sketches the end-to-end workflow that maps multiple demonstrations to executable trajectories under physical and safety constraints:

(i) unsupervised segmentation from multi-feature saliency with topology-aware keyframes; (ii) duration-explicit alignment across demonstrations via a hidden semi-Markov model (HSMM) with shared parameters; and (iii) probabilistic encoding of each phase (GMM/GMR or ProMP, optionally combined with DMP) producing mean trajectories with calibrated covariances. Outputs include phase-consistent labels, segment-wise probabilistic models, and constraint-aware executable trajectories.

2.1. Inputs, Outputs, and Assumptions

Inputs.

We observe $M$ independent demonstrations (optionally multi-modal), ${\left\{P^{(m)}\right\}}_{m=1}^M,P^{(m)} = {\left\{P^{(m)}(t)\right\}}_{t=1}^{T_m},$ sampled with fixed period $\Delta t$. When available, auxiliary channels (e.g., pose, force/tactile, depth) are concatenated into the observation vector used downstream.

Outputs.

• A shared set of semantic phases ${\left\{S_k\right\}}_{k=1}^{N^{\star }}$ and per-demo boundaries $\left\{{\tau }_k^{(m)}\right\}$;
• For each phase, a segment-wise generative model—DMP, GMM/GMR, or ProMP, alone or in combination—returning mean trajectories and covariance estimates;
• Under constraints $\mathcal{C}$ (terminal/waypoints, velocity/acceleration limits, etc.), an executable trajectory and associated risk measures computed from covariances.

Assumptions.

• Demonstrations consist of alternating quasi-stationary and transition segments;
• Time deformation is order-preserving (the semantic phase order does not change);
• Observation noise is moderate and can be mitigated by local smoothing and statistical filtering.

2.2. Multi-Feature Analysis and Automatic Segmentation

2.2.1. Data Ingestion and Pre-Processing

Let a single demonstration be the discrete sequence $\mathcal{D}={\left\{\Delta {\mathbf{x}}_t\right\}}_{t=1}^T,\Delta {\mathbf{x}}_t\in {\mathbb{R}}^d$, where $d$ is the number of observed degrees of freedom (e.g., $d=3$ for UAV or mobile bases; $d=6$ for industrial manipulators). Cumulative sums yield the Cartesian trajectory of the tool-center point

$$\mathbf{P}(t)={\left[p_x(t),p_y(t),p_z(t)\right]}^{\top },t=1,\dots ,T,$$

(1)

We apply a one-dimensional Savitzky–Golay local polynomial smoother to $\mathbf{P}(t)$ before computing derivatives, suppressing high-frequency tele-operation jitter and stabilizing numerical differentiation. The filter is often interpreted as a local $(r + 1)$-order Taylor approximation in time and ensures

$$\Vert \tilde{\mathbf{P}}-\mathbf{P}{\Vert }_{\infty }\le c_W\epsilon ,c_W<1,$$

where ε bounds the measurement noise and the window $W\in \{5,7,9\}$. Unless stated otherwise, $\tilde{\mathbf{P}}$ denotes the smoothed trajectory [28].

Implementation note. Central differences are used for derivatives; all channels are time-synchronized at a fixed sampling period Δt.

2.2.2. Feature Computation and Saliency Fusion

On the smoothed trajectory, we compute four complementary, time-varying features that reveal when, where, and how kinematic changes occur ($\Delta t\left(={\displaystyle \frac{1}{f_s}}\right)$ is fixed).

1.

Velocity. Let

$$\mathbf{v}(\mathrm{t})={\displaystyle \frac{\mathbf{P}(\mathrm{t}+1)-\mathbf{P}(\mathrm{t})}{\Delta \mathrm{t}}},\mathrm{v}(\mathrm{t})=\Vert \mathbf{v}(\mathrm{t}){\Vert }_2.$$

(2)

2.

Acceleration.

$$\mathbf{a}(\mathrm{t})={\displaystyle \frac{\mathbf{v}(\mathrm{t}+1)-\mathbf{v}(\mathrm{t})}{\Delta \mathrm{t}}},\mathrm{a}(\mathrm{t})=\Vert \mathbf{a}(\mathrm{t}){\Vert }_2.$$

(3)

Peaks indicate abrupt speed changes.

3.

Curvature. With $\Delta \mathbf{P}(\mathrm{t})=\mathbf{P}(\mathrm{t}+1)-\mathbf{P}(\mathrm{t})$,

$$\mathsf{\kappa }\left(\mathrm{t}\right)={\displaystyle \frac{2‖\Delta \mathbf{P}\left(\mathrm{t}-1\right)\times \Delta \mathbf{P}\left(\mathrm{t}\right)‖}{‖\Delta \mathbf{P}\left(\mathrm{t}-1\right)‖‖\Delta \mathbf{P}\left(\mathrm{t}\right)‖‖\Delta \mathbf{P}\left(\mathrm{t}\right)-\Delta \mathbf{P}\left(\mathrm{t}-1\right)‖}}.$$

(4)

Curvature measures spatial bending and is naturally invariant to global time scaling due to the cubic velocity term [29,30].

4.

Direction-Change Rate (DCR). Define the unit direction vector $\widehat{\mathrm{v}}(\mathrm{t})=\mathrm{v}(\mathrm{t})/\Vert \mathrm{v}(\mathrm{t}){\Vert }_2$. To avoid numerical issues at very low speed, introduce a threshold ${\mathrm{v}}_{\mathrm{m}\mathrm{i}\mathrm{n}}>0$ and set

$$\mathrm{D}\mathrm{C}\mathrm{R}(\mathrm{t})=\left\{\begin{array}{cc}\Vert \widehat{\mathrm{v}}(\mathrm{t})-\widehat{\mathrm{v}}(\mathrm{t}-1){\Vert }_2,\hfill & \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\Vert \mathrm{v}(\mathrm{t}){\Vert }_2\ge {\mathrm{v}}_{\min }\hfill \\ 0,\hfill & \hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\Vert \mathrm{v}(\mathrm{t}){\Vert }_2<{\mathrm{v}}_{\min }\hfill \end{array}\right.$$

(5)

5.

Dimensionless fusion. Apply min–max normalization to each feature to obtain $\tilde{\mathrm{v}}\left(\mathrm{t}\right),\tilde{\mathrm{a}}\left(\mathrm{t}\right),\tilde{\mathsf{\kappa }}(\mathrm{t}),\overline{\mathrm{D}\mathrm{C}\mathrm{R}}(\mathrm{t})\in \left[\mathrm{0,1}\right]$. For a weight vector $\mathrm{w}={\left[{\mathrm{w}}_{\mathrm{v}},{\mathrm{w}}_{\mathrm{a}},{\mathrm{w}}_{\mathsf{\kappa }},{\mathrm{w}}_{\mathrm{d}}\right]}^{\top }$ with ${\mathrm{w}}_{\mathrm{i}}\ge 0$ and $\sum _{\mathrm{i}} {\mathrm{w}}_{\mathrm{i}}=1$, define the fused saliency

$$\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(t;w)=w_v\tilde{v}(t)+w_a\tilde{a}(t)+w_{\kappa }\tilde{\kappa }(t)+w_d\widetilde{\mathrm{D}\mathrm{C}\mathrm{R}}(t)$$

(6)

The weights $w$ are learned without labels in Section 2.2.4.

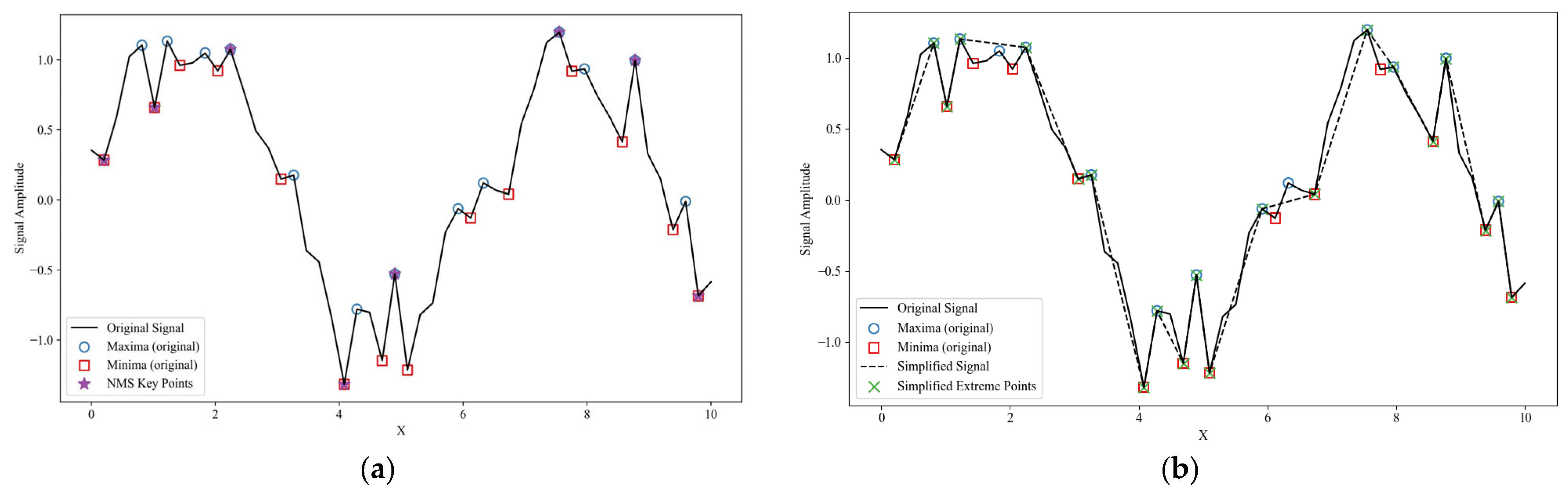
2.2.3. Keyframe Extraction with Topological Simplification

The saliency $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(t)$ compresses multi-source information into a 1D signal, but segmentation should rely on structural extrema (global landmarks), not every minor fluctuation. We adopt a bottom-up screening that contracts a dense set of local extrema into a sparse, stable keyframe set [1,31].

1.

Candidate extrema via quantile thresholds.

Let $\mathcal{Q}=\left\{q_1,\dots ,q_L\right\}\subset \left(\mathrm{0,1}\right)$ be a grid of quantiles (e.g., uniformly in [0.60,0.95]). For each $q\in \mathcal{Q}$:

• Set ${\tau }_q = { \mathrm{quantile} }_q (\mathrm{Score})$;
• Collect indices ${\tilde{\mathrm{E}}}_q = \left\{t\mid \mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(t)>{\tau }_q\right\}$ and snap each $t$ to the nearest local extremum within a radius-3 neighborhood.

To pick a unique $q^{\star }$, minimize the sparsity–fidelity loss

$$L\left(q\right)=\underset{\mathrm{sparsity} }{\underbrace{\left|{\tilde{E}}_q\right|/T}}+\lambda \underset{\mathrm{reconstruction} }{\underbrace{\mathrm{M}\mathrm{S}\mathrm{E}\left(P,{\widehat{P}}_{{\tilde{E}}_q}\right)}},$$

where ${\widehat{P}}_{{\tilde{\mathrm{E}}}_q}$ is the spline reconstruction at ${\tilde{\mathrm{E}}}_q$ and $\lambda >0$ reflects the admissible reconstruction error. Set $q^{\star } =\arg \underset{q\in \mathcal{Q}}{min} \mathcal{L}\left(q\right),\tilde{\mathrm{E}} = {\tilde{\mathrm{E}}}_{q^{\star }}$.

2.

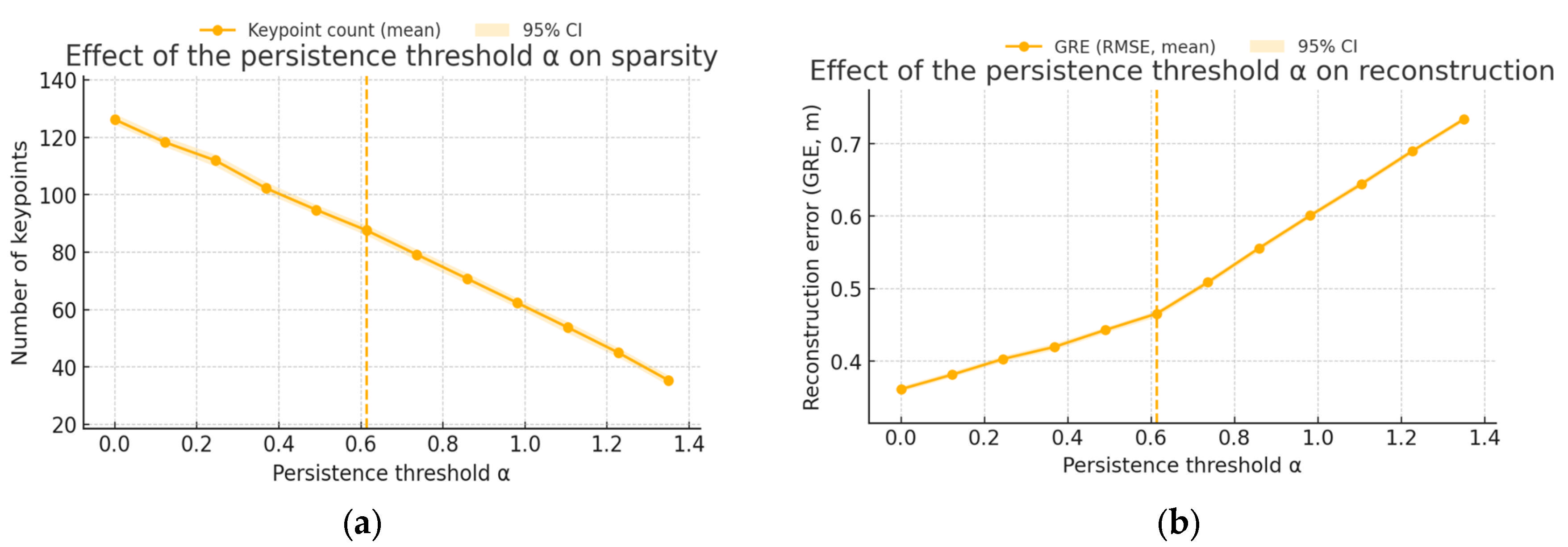
Persistence thresholding (scale-aware importance)

For adjacent peak–valley pairs $\left(p_{max},p_{min}\right)$ of $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(t)$, define the persistence

$$\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\left(p_{max},p_{min}\right)=\left|\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\left(p_{max}\right)-\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\left(p_{min}\right)\right|,$$

(7)

Small persistence typically indicates noise or micro-tremor; large persistence corresponds to genuine kinematic transitions. Plot

$$g\left(\alpha \right)=\mid \left\{\left(p_{max},p_{min}\right)\mid \mathrm{pers} >\alpha \right\}\mid ,$$

which empirically exhibits a plateau–cliff–stable pattern; the elbow ${\alpha }^{\star }$ is detected by Kneedle. Keep

$${\mathrm{E}}^{†}=\left\{p_i\mid \mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\left(p_i\right)>\right\}$$

Because persistence depends only on amplitude differences, it is invariant to vertical scaling and mild time stretching, facilitating cross-demonstration comparability [32,33].

3.

Non-maximum suppression (NMS).

To avoid peak clustering, scan ${\mathrm{E}}^{†}$ with a sliding window of ${\mathrm{N}\mathrm{M}\mathrm{S}}_w$ frames and retain an extremum only if it is the largest (same polarity) within the window. The final keyframe set is

$$\mathcal{K}={\mathrm{N}\mathrm{M}\mathrm{S}}_w\left({\mathrm{E}}^{†}\right).$$

The effect of persistence thresholding and NMS is illustrated in Figure 2, which contracts dense peak clusters into a sparse, stable keyframe set $\mathcal{K}$. The black solid curve is the original saliency signal $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(t)$; the dashed curve is the simplified signal after persistence-based filtering (elbow ${\alpha }^{\star }$ detected by Kneedle) and non-maximum suppression (window $\mathit{w}$). Green crosses mark the final retained keyframes $\mathcal{K}$. The procedure removes clustered minor extrema while preserving structural landmarks that drive segmentation and alignment.

The effect of the two simplification steps is shown in Figure 2. Panel (a) isolates the role of non-maximum suppression (NMS) on the original saliency $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(t)$ (Equation (6)): within a $\pm w$ window, only the strongest same-polarity extremum is kept (stars), turning dense local clusters into a sparser set of candidates. Panel (b) shows persistence-based simplification: the dashed curve is the signal after removing low-amplitude peak–valley pairs using the Kneedle elbow ${\alpha }^{\star }$; crosses mark the surviving extrema. Applying the same NMS to these survivors (not shown for clarity) yields the final keyframe set $K={\mathrm{N}\mathrm{M}\mathrm{S}}_w\left(E^{†}\right)$. Together, persistence discards small-scale oscillations in a scale-robust manner, while NMS prevents multi-responses in high-energy neighborhoods.

With $\mathcal{K}$ in place, the reliability of subsequent segmentation and HSMM alignment still depends on the saliency weights $w$; Section 2.2.4 details a label-free, consistency-driven calibration.

2.2.4. Adaptive Feature-Weight Learning

In (6), the saliency $\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}(t;w)$ is a linear fusion of four heterogeneous features. Assigning heuristic, fixed weights $w={\left[w_v,w_a,w_k,w_d\right]}^{\top }$ typically overfits a particular operator, platform, or task, degrading segmentation under distribution shift. We therefore treat $w$ as model parameters to be estimated without labels by enforcing cross-demonstration consistency.

1.

Consistency functional.

For $M$ demonstrations ${\left\{{\mathbf{P}}^{(m)}\right\}}_{m=1}^M$ and a candidate $w$, define

$$\mathcal{F}(\cdot ;\mathit{w}):{\mathbf{P}}^{(m)}⟼{\widehat{\mathbf{P}}}^{(m)}(\mathit{w}),$$

(8)

and denote the composition of saliency construction, keyframe extraction (Figure 2), HSMM-based alignment (Section 2.3), and resampling on shared semantic nodes. If $w$ is well chosen, the reconstructions $\left\{{\widehat{P}}^{(m)}(w)\right\}$ should be congruent in shape and timing. We quantify this by the mean point-to-point structural dispersion.

$$\mathrm{S}\mathrm{O}\mathrm{D}(\mathit{w})={\displaystyle \frac{2}{M(M-1)}}{\sum }_{1\le m<m^{\prime }\le M} {\displaystyle \frac{1}{T_{min}}}{\sum }_{t=1}^{T_{min}} {‖{\widehat{\mathbf{p}}}_t^{(m)}(w)-{\widehat{\mathbf{p}}}_t^{\left(m^{\prime }\right)}(w)‖}_2,$$

(9)

where $T_{min}$ is the minimal resampled length. Smaller SOD means lower structural variance on the shared semantic time base.

2.

Objective and constraints.

To prevent dominance by any single channel and to improve identifiability, we regularize with a light ${\mathcal{l}}_2$ penalty and minimize over the probability simplex:

$$w^{\star }=\mathrm{a}\mathrm{r}\mathrm{g}\underset{w\in {\Delta }^3}{min} \left(\mathrm{S}\mathrm{O}\mathrm{D}(w) + \lambda \Vert w{\Vert }_2^2\right),{\Delta }^3=\left\{w\mid w_i\ge 0,\sum _i w_i=1\right\}.$$

(10)

Because $F$ contains non-smooth steps (extrema detection, discrete decoding), $\mathrm{S}\mathrm{O}\mathrm{D}(w)$ is non-differentiable and gradient methods are unreliable.

3.

Solver and feasibility.

We employ the Covariance Matrix Adaptation Evolution Strategy (CMA-ES) in an unconstrained space together with a softmax reparameterization

$$w_i\left(z\right)={\displaystyle \frac{\exp \left(z_i\right)}{{\sum }_{j=1}^4 \mathit{exp}\left(z_j\right)}},z\in {\mathbb{R}}^4,$$

which enforces $w\in {\Delta }^3$ at every iteration while preserving Gaussian updates in $z$-coordinates. CMA-ES is appropriate here because it (i) requires only function values of $J(w)=\mathrm{S}\mathrm{O}\mathrm{D}(w) + \lambda \Vert w{\Vert }_2^2$; (ii) adapts search scales via the evolving covariance; and (iii) is empirically robust on multi-modal, non-convex objectives [34,35]. We terminate when either the covariance trace shrinks below a preset ratio (indicating a local neighborhood) or the successive improvement $\left|J^{(k)} - J^{(k-1)}\right|$ falls below $\epsilon$. Under mild regularity on $J$ in the $z$-space, the iterates approach first-order stationarity (a near-KKT solution) with high probability [36].

The objective $J(w)$ combines non-smooth steps (extrema detection, decoding), causing piecewise-flat regions and discontinuous sub-gradients. In preliminary trials, gradient-based schemes (finite-difference, SPSA, REINFORCE-style estimators) were unstable and sensitive to step sizes, while Bayesian optimization/TPE struggled with the noisy, batch-evaluated objective and required heavy surrogate retraining when caching was used. CMA-ES only needs function values, adapts the search covariance online, parallelizes naturally across demonstrations, and shows consistent convergence to low-SOD solutions under identical budgets. We therefore adopt CMA-ES as the default black-box solver (Section 3.6 ablations leave the outer loop intact).

4.

Computational profile.

Each evaluation of $J(w)$ entails one pass of keyframe extraction (linear in sequence length $T$) and one HSMM forward–backward/decoding pass per demonstration with complexity $O\left(NT{D}_{max}\right)$; overall cost scales linearly in $M$. For numerical stability, we implement recursions in the log domain (log-sum-exp), apply a diagonal floor to GMM covariances, and cache feature streams across outer-loop calls.

The saliency front-end (feature streams + persistence + NMS) is O(T) and memory-light; in practice, it processes sequences faster than real time at the sampling rates used here (10–100 Hz). HSMM inference is linear in the number of states and the maximum dwell (O(N·T·D_max)), and the outer consistency loop amortizes via cached features and log-domain recursions. Section 3 reports end-to-end timings per domain; inference-time segmentation/alignment remains within interactive latency on a commodity CPU.

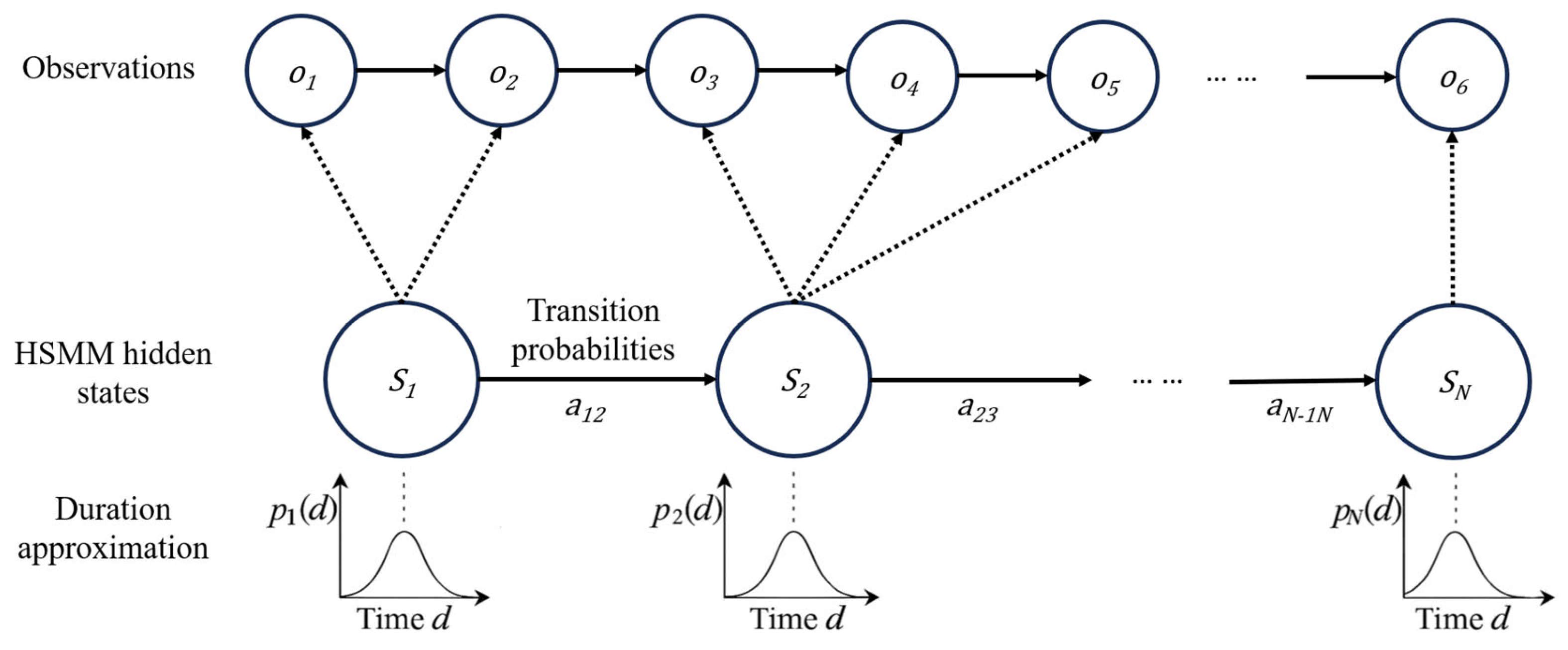
2.3. Multi-Demo Alignment and Segmentation via a Duration-Explicit HSMM

Given the sparse, scale-invariant keyframes ${\mathcal{K}}^{(m)}={\left\{t_k^{(m)}\right\}}_{k=1}^{K_m}$ obtained from saliency (Section 2.2) and the learned fusion weights (Section 2.2.4), we seek a shared semantic time base across demonstrations. Directly matching wall-clock indices is unreliable due to operator-dependent pauses and backtracking; instead, we align demonstrations probabilistically via a Hidden semi-Markov model (HSMM) that explicitly models state durations (Figure 3) [37,38].

2.3.1. Model and Generative Mechanism

Let $S = \left\{S_1,S_2,\dots ,S_N\right\},N\ll K_m$ be latent phases, each representing a macro-action (e.g., grasp, insert, lift). With parameters $\mathsf{\Theta }= \left\{\pi ,A,\left\{p_i\right\},\left\{b_i\right\}\right\}$, the HSMM generates $o_t\in {\mathbb{R}}^d$ at $t = 1,\dots ,T$ as follows:

(a)

Initial phase: ${\mathrm{q}}_1\sim \mathrm{C}\mathrm{a}\mathrm{t}\left(\mathsf{\pi }\right),\sum _{\mathrm{i}} {\mathsf{\pi }}_{\mathrm{i}}=1$.

(b)

Duration: for the current phase ${\mathrm{q}}_{\mathrm{k}}$, sample dwell length ${\mathrm{d}}_{\mathrm{k}}\sim {\mathrm{p}}_{{\mathrm{q}}_{\mathrm{k}}}(\mathrm{d})\in {\mathbb{N}}_{>0}$.

(c)

Observations: for ${\mathsf{\tau }}_{\mathrm{k}-1}<\mathrm{t}\le {\mathsf{\tau }}_{\mathrm{k}}$ with ${\mathsf{\tau }}_{\mathrm{k}}=\sum _{\mathrm{j}\le \mathrm{k}} {\mathrm{d}}_{\mathrm{j}}$, ${\mathrm{o}}_{\mathrm{t}}\sim {\mathrm{b}}_{{\mathrm{q}}_{\mathrm{k}}}\left(\cdot \right),{\mathrm{b}}_{\mathrm{i}}\left(\mathrm{o}\right)={\sum }_{\mathrm{m}=1}^{{\mathrm{M}}_{\mathrm{i}}} {\mathsf{\pi }}_{\mathrm{i},\mathrm{m}}\mathcal{N}\left(\mathrm{o}\mid {\mathsf{\mu }}_{\mathrm{i},\mathrm{m}},{\Sigma }_{\mathrm{i},\mathrm{m}}\right)$

(d)

Transition: $\mathrm{P}\mathrm{r}\left({\mathrm{q}}_{\mathrm{k}+1}=\mathrm{j}\mid {\mathrm{q}}_{\mathrm{k}}\right)={\mathrm{a}}_{{\mathrm{q}}_{\mathrm{k}}}\mathrm{j}$; terminal transitions end the sequence.

Writing $\mathrm{O}=\left({\mathrm{o}}_1,\dots ,{\mathrm{o}}_{\mathrm{T}}\right),\mathrm{Q}=\left({\mathrm{q}}_1,\dots ,{\mathrm{q}}_{\mathrm{n}}\right),\mathrm{D}=\left({\mathrm{d}}_1,\dots ,{\mathrm{d}}_{\mathrm{n}}\right),$ and ${\mathrm{q}}^{\mathrm{*}}\left(\mathrm{t}\right)={\mathrm{q}}_{\mathrm{k}}$ for ${\mathsf{\tau }}_{\mathrm{k}-1}<\mathrm{t}\le {\mathsf{\tau }}_{\mathrm{k}}$, the joint density is

$$P\left(O,Q,D\right)={\pi }_{q_1}{p}_{q_1}\left(d_1\right){\displaystyle \prod _{k=1}^{n-1}} \left[a_{q_k{q}_{k+1}}{p}_{q_{k+1}}\left(d_{k+1}\right)\right]{\displaystyle \prod _{t=1}^T} b_{q^{*}(t)}\left(o_t\right).$$

(11)

Observation design. We concatenate kinematic descriptors (e.g., curvature, speed magnitude, DCR) and any available modalities (pose, force/tactile, depth) into $o_t$.

Duration choices. We use either discrete $p_i(d)$ with support 1: $D_{max}$ or truncated Gaussian/Gamma families to accommodate unequal dwell times [39].

2.3.2. Parameter Estimation: Extended Baum–Welch

We maximize the total log-likelihood over demonstrations

$$\mathcal{L}(\mathsf{\Theta })={\displaystyle \sum _{m=1}^M} \mathrm{l}\mathrm{o}\mathrm{g} P\left(O^{(m)}\mid \mathsf{\Theta }\right).$$

(12)

Explicit durations break first-order Markovity; forward–backward recursions therefore enumerate duration indices.

1.

Forward variable (leaving $\mathrm{i} \mathrm{a}\mathrm{t} \mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e} \mathrm{t}$).

$${\alpha }_t(i)={\displaystyle \sum _{j=1}^N} {\displaystyle \sum _{d=1}^{min\left(D_{max},t\right)}} {\alpha }_{t-d}(j)a_{ji}{p}_i(d){\displaystyle \prod _{r=0}^{d-1}} b_i\left(o_{t-r}\right),{\alpha }_0(i)={\pi }_i.$$

(13)

2.

Backward variable.

$${\beta }_t(i)={\displaystyle \sum _{j=1}^N} {\displaystyle \sum _{d=1}^{T-t}} \left[a_{ij}{p}_j(d){\displaystyle \prod _{r=0}^{d-1}} b_j\left(o_{t+1+r}\right){\beta }_{t+d}(j)\right],{\beta }_T(i)=1.$$

(14)

3.

Posteriors (E-step).

$${\gamma }_t(i)={\displaystyle \frac{{\sum }_{d=1}^{min\left(D_{max},t\right)} {\sum }_{r=0}^{d-1} {\alpha }_{t-r}(i)p_i(d){\prod }_{u=0}^{d-1} b_i\left(o_{t-r+u}\right){\beta }_{t-r}(i)}{{\sum }_{k=1}^N {\alpha }_T(k)}}$$

(15)

$${\xi }_{t,d}(i,j)={\displaystyle \frac{{\alpha }_{t-d}(i)a_{ij}{p}_j(d){\prod }_{r=0}^{d-1} b_j\left(o_{t-r}\right){\beta }_t(j)}{{\sum }_{k=1}^N {\alpha }_T(k)}}$$

(16)

Sum $\gamma ,\xi$ over $m$ to obtain corpus-level sufficient statistics.

4.

M-step (closed forms).

$$\begin{array}{c}{\pi }_i^{\mathrm{new} }={\gamma }_{t=1}(i),\\ a_{ij}^{\mathrm{new} }={\displaystyle \frac{\sum _{t,d} {\xi }_{t,d}(i,j)}{\sum _t {\gamma }_t(i)}},\\ p_i^{\mathrm{new} }(d)={\displaystyle \frac{\sum _t {\xi }_{t,d}(i,\cdot )}{\sum _{t,d^{\prime }} {\xi }_{t,d^{\prime }}(i,\cdot )}},\\ {\mu }_{i,m}^{\mathrm{new} }={\displaystyle \frac{\sum _t {\gamma }_{t,m}(i)o_t}{\sum _t {\gamma }_{t,m}(i)}},\\ {\Sigma }_{i,m}^{\mathrm{new} }={\displaystyle \frac{\sum _t {\gamma }_{t,m}(i)\left(o_t-{\mu }_{i,m}\right){\left(o_t-{\mu }_{i,m}\right)}^{\top }}{\sum _t {\gamma }_{t,m}(i)}}\end{array}$$

(17)

with ${\gamma }_{t,m}(i)={\gamma }_t(i){\pi }_{i,m}\mathcal{N}\left(o_t\mid {\mu }_{i,m},{\Sigma }_{i,m}\right)/b_i\left(o_t\right).$

5.

Numerical stability.

All recursions are implemented in the log domain using log-sum-exp

$$\mathrm{L}\mathrm{S}\mathrm{E}\left(x_1,\dots ,x_K\right)=\mathrm{l}\mathrm{o}\mathrm{g}{\displaystyle \sum _{k=1}^K} e^{x_k},$$

(18)

and GMM covariances receive a diagonal floor $\delta I$. EM monotonicity guarantees convergence of ${\mathcal{L}}^{(k)}$ to a stationary point [40,41].

2.3.3. Semantic Time Axis: Decoding and Outputs

After convergence, Viterbi decoding yields the MAP phase path ${\widehat{Q}}^{(m)}=\left(q_1^{(m)},\dots ,q_N^{(m)}\right)$ and durations ${\widehat{D}}^{(m)}=\left(d_1^{(m)},\dots ,d_N^{(m)}\right)$ for each demonstration, with ${\displaystyle {\sum }_{k=1}^N} d_k^{(m)}=T_m$. Define cumulative boundaries ${\tau }_k^{(m)}={\displaystyle {\sum }_{j=1}^k} d_j^{(m)},k=1,\dots ,N$, so segments $\left({\tau }_{k-1}^{(m)},{\tau }_k^{(m)}\right]$ correspond to the same semantic phase $S_k$ across demonstrations. Figure 4 and Figure 5 illustrate 3D keyframe locations and HSMM reconstructions aligned to salient kinematic transitions.

2.3.4. Alignment Quality, Model Selection, and Robustness

Alignment metric. We quantify cross-demo temporal agreement by

$$\mathrm{A}\mathrm{E}(N)={\displaystyle \sum _{m=1}^M} {‖\left({\tau }_1^{(m)},\dots ,{\tau }_N^{(m)}\right)-\left({\overline{\tau }}_1,\dots ,{\overline{\tau }}_N\right)‖}_2,{\overline{\tau }}_k={\displaystyle \frac{1}{M}}\sum _m {\tau }_k^{(m)}.$$

(19)

Model selection. To balance fit and parsimony, we use

$$\mathrm{B}\mathrm{I}\mathrm{C}\left(N\right)=-2\log \mathcal{L}\left({\Theta }_N^{\star }\right) + {\kappa }_N\mathrm{l}\mathrm{o}\mathrm{g}\left(\sum _m T_m\right),$$

(20)

and select $N^{\star }$ by jointly considering $\mathrm{A}\mathrm{E}(N)$ and $\mathrm{B}\mathrm{I}\mathrm{C}(N)$.

Robustness to time warps. For any order-preserving reparameterization of time, $t\mapsto \tau (t)$, the decoded phase order $\left(S_1,\dots ,S_N\right)$ is invariant; only the tail behavior of duration distributions $p_i(d)$ is rescaled. This accounts for operator-dependent slowdowns, hesitations, or hovering.

Complexity. Keyframe processing is $O(T)$ per sequence; duration-explicit forward–backward is $O\left(NT{D}_{max}\right)$; training scales linearly in the number of demonstrations M. Outputs include $\left\{S_k\right\}$ and segment-wise statistics for direct use by planners (e.g., OMPL/MPC).

2.3.5. Stability Properties of Topology-Aware Saliency and Duration-Explicit Alignment

Proposition 1. 

(Scale and weak time-warp stability of the retained keyframes).

Let $\mathrm{Score}(\mathrm{t}; \mathrm{w})$ be the fused saliency in Equation (6). Let $𝒦$ be the keyframe set after persistence-based simplification (Equation (7), Kneedle elbow) and non-maximum suppression (Figure 2). Consider (a) vertical rescaling of all input features by $\lambda >0$ and (b) order-preserving time reparameterizations $\varphi$ with bounded local stretch. Then, the following are obtained:

• Scale invariance. $\mathcal{K}(\lambda \text{-}\mathrm{Score})=\mathcal{K}(\mathrm{Score})$ since persistence depends on amplitude differences and the elbow index is preserved.
• Weak time-warp stability (physical time). Under (b), extrema order is preserved; locations shift by at most $O\left(w_{nms}\right)$ samples due to the NMS window.
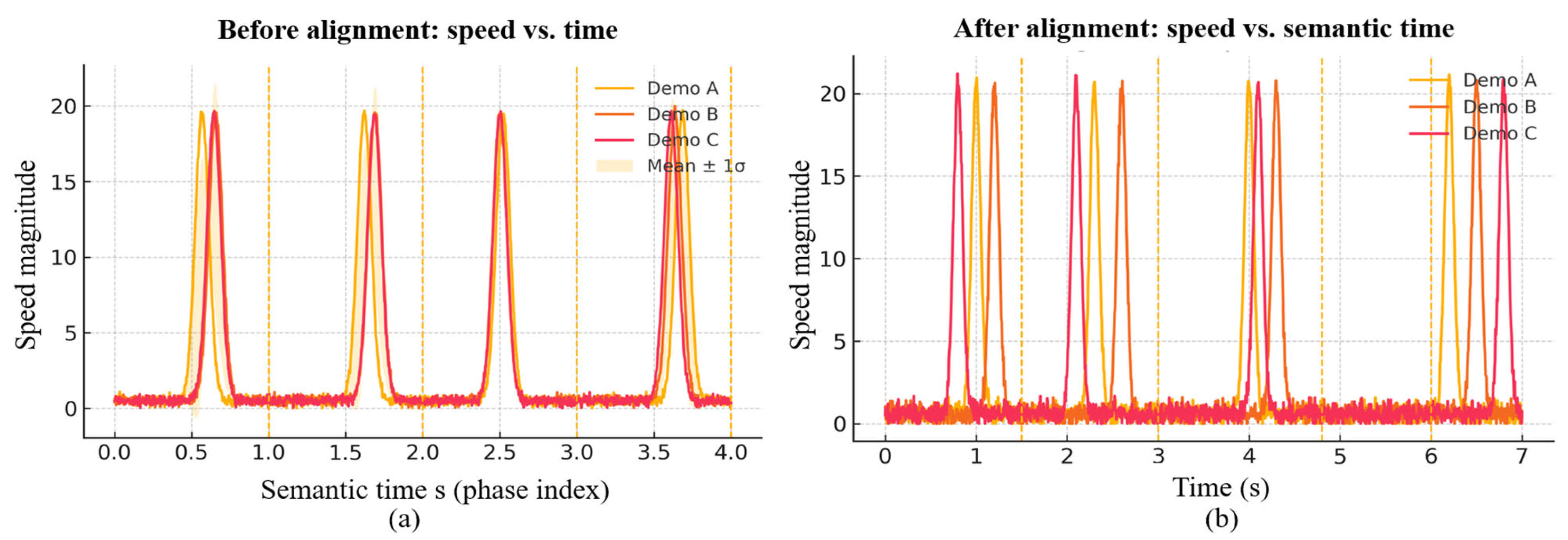
• Semantic-time invariance with HSMM. After duration-explicit decoding (Section 2.3), the phase order and boundaries induced by $\mathcal{K}$ are invariant; order-preserving warps manifest primarily as duration redistribution across states (Section 2.3.4).

Sketch. Items 1–2 follow from persistence stability and local maximality under NMS (Equation (7), Figure 2). Item 3 uses explicit-duration decoding, which preserves phase order under monotone reparameterizations; empirical trends in Section 3.6 and Section 3.9 support these properties.

2.4. Statistical Motion Primitives and Probabilistic Generation

With cross-demonstration phases and boundaries ${\left\{{\mathcal{S}}_k\right\}}_{k=1}^N$, $\left\{{\tau }_k^{(m)}\right\}$ obtained from the duration-explicit HSMM (Section 2.3), we model each phase within the shared semantic time base. For demonstration $m$, let

$${\mathcal{C}}_k^{(m)}=\left\{P^{(m)}(t);t\in \left({\tau }_{k-1}^{(m)},{\tau }_k^{(m)}\right]\right\}$$

denote the spatio-temporal segment for phase ${\mathcal{S}}_k$. Our objective is a segment-wise generative model that (i) captures cross-demo variability, (ii) supports conditioning and duration re-scaling, and (iii) yields calibrated uncertainty for downstream planning and safety assessment. We instantiate three complementary families: DMP, GMM/GMR, and ProMP. Unless otherwise noted, time within a segment is normalized to a phase variable $s\in \left[\mathrm{0,1}\right]$, ensuring a uniform interface across models.

2.4.1. Dynamic Movement Primitives (DMP)

1.

Single-segment dynamics.

For a one-degree-of-freedom trajectory $x(t)$, the classical DMP represents motion as a critically damped second-order system with a nonlinear forcing term:

$$\begin{array}{c}\tau \dot{z}={\alpha }_z\left({\beta }_z(g-x)-z\right) + f(s),\hfill \\ \tau \dot{x}=z,\tau \dot{s}=-{\alpha }_{s}s,\hfill \end{array}$$

(21)

where $g$ is the segment goal, $s\in (\mathrm{0,1}]$ is a phase variable, and

$$f(s)={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^B} w_i{\psi }_i(s)}{{\displaystyle {\sum }_{i=1}^B} {\psi }_i(s)}}\left(g-x_0\right),{\psi }_i(s)=\mathrm{e}\mathrm{x}\mathrm{p}\left[-h_i{\left(s-c_i\right)}^2\right]$$

(22)

Given $\tau ,{\alpha }_z,{\beta }_z,{\alpha }_{s^{\prime }}$ the weights $\left\{w_i\right\}$ are obtained by least squares (or locally weighted regression). Multi-DOF trajectories are modeled component-wise or via task-space coupling.

2.

Segment coupling and smoothness.

Let ${\overline{d}}_k$ be the mean duration of phase $S_k$ across demonstrations; set ${\tau }_k={\overline{d}}_k\Delta t$. We fit ${\left\{w_i^{(k)}\right\}}_{i=1}^B$ per segment and compose ${\left\{\left({\mathrm{D}\mathrm{M}\mathrm{P}}_k,{\tau }_k\right)\right\}}_{k=1}^N$ along the decoded boundaries. Because the state$( x,z)$ is continuous across boundaries, the concatenation is $C^1$ -continuous without auxiliary velocity/acceleration matchers. DMPs thus offer low jerk and robust time-scaling at execution.

2.4.2. Gaussian Mixture Modeling and Regression (GMM/GMR)

Mixture modeling. For each segment, we pair the normalized phase with position, $\left(s_t,y_t\right)\in {\mathbb{R}}^{1+d}$, and fit a K-component mixture

$$p(\mathbf{s},\mathbf{y})={\displaystyle \sum _{k=1}^K} {\pi }_k\mathcal{N}\left({\mu }_k,{\Sigma }_k\right)$$

(23)

typically with diagonal (or block-diagonal) ${\Sigma }_k$ to denoise while retaining principal correlations.

Regression and uncertainty. At execution, Gaussian Mixture Regression (GMR) produces the conditional

$$p\left(\mathrm{y}∣\mathrm{s}\right)=\mathcal{N}\left(\widehat{\mu }\left(\mathrm{s}\right),\widehat{\Sigma }\left(\mathrm{s}\right)\right),$$

yielding a closed-form mean trajectory and a phase-indexed covariance band. Analytical derivatives of $\widehat{\mu }\left(s\right) \mathrm{a}\mathrm{n}\mathrm{d} \widehat{\Sigma }(\mathrm{s})$ facilitate integration with MPC for online terminal corrections and constraint handling.

2.4.3. Probabilistic Movement Primitives (ProMP)

Bayesian representation. Using basis functions ${\mathsf{\Phi }}_t={\left[{\varphi }_1(t),\dots ,{\varphi }_B(t)\right]}^{\top }$, a segment trajectory is modeled as

$$y_t={\Phi }_t^{\top }w+\epsilon ,\epsilon \sim \mathcal{N}\left(0,{\Sigma }_y\right),w\sim \mathcal{N}\left({\mu }_w,{\Sigma }_w\right)$$

(24)

where $\left({\mu }_w,{\Sigma }_w\right)$ encode the distribution over shapes learned from multiple demonstrations (EM or closed-form under Gaussian assumptions).

Conditioning and coordination. Linear constraints—endpoints, waypoints, or partial observations—are imposed by conditioning the weight distribution:

$$w\mid \left(C{Y}_T=g\right)\sim \mathcal{N}\left({\mu }_w + K_T\left(g-{\mathsf{\Phi }}_T{\mu }_w\right),{\Sigma }_w-K_T{\mathsf{\Phi }}_T{\Sigma }_w\right),$$

(25)

with $K_T={\Sigma }_w{\mathsf{\Phi }}_T{\left({\mathsf{\Phi }}_T^{\top }{\Sigma }_w{\mathsf{\Phi }}_T + {\Sigma }_{\epsilon }\right)}^{-1}$. Sampling from this posterior and stitching segments at decoded boundaries yields constraint-consistent trajectories with explicit predictive uncertainty.

2.4.4. Model Choice and Complementarity

No single primitive dominates: DMP excels in real-time low-jerk execution; GMM/GMR gives closed-form means/covariances and gradients; and ProMP supports exact linear-Gaussian conditioning for multi-goal tasks.

Table 1. Segment-level motion primitives: properties and trade-offs.

Property	DMP	GMM/GMR	ProMP
Shape representation	Basis functions + 2nd-order stable system	$\mathrm{Global} \mathrm{Gaussian} \mathrm{mixture} \mathrm{over} (s,y)$	Gaussian over weights w
Duration adaptation	$\mathrm{Via} {\tau }_k$ time scaling	Requires resampling in phase	Basis-phase re-timing
Uncertainty	No closed-form (MC if needed)	$\mathrm{Analytic} \widehat{\Sigma }(s)$	Analytic posterior over w
Online constraints	Endpoints/velocities easy	Refit or constrained regression	Exact linear-Gaussian conditioning
Execution smoothness	Low jerk (native dynamics)	Depends on mixture fit	Depends on basis and priors

summarizes properties. Figure 6 shows HSMM-aligned ProMP generation with calibrated uncertainty bands:

• DMP excels at real-time execution and low jerk with simple time scaling;
• GMM/GMR offers closed-form means and covariances over phase and is convenient for planners needing analytic gradients;
• ProMP provides a distribution over shapes with exact linear-Gaussian conditioning, ideal for multi-goal tasks and collaboration.

In practice, we first fit GMM/GMR to obtain the mean/covariance; use the GMR mean to initialize DMP weights for smooth execution; and, when hard/soft constraints or multi-goal adaptation are required, overlay ProMP conditioning on top of the DMP nominal to reconcile smoothness with constraints.

Interface to planning and safety. Segment-wise covariances (from GMR or ProMP) propagate to risk metrics and constraint tightening in MPC/OMPL. Because segments share a semantic time base, the uncertainty is comparable across operators and platforms, enabling principled safety margins (e.g., $2\sigma$ envelopes) and priority-aware blending when composing multi-segment tasks.

Computational profile. Per segment, DMP fitting is linear in the number of basis functions; GMM/GMR training is $O(KT)$ per EM iteration; and ProMP estimation is closed-form/EM with state dimension B. Since segments are independent given HSMM alignment, training parallelizes over phases and scales linearly with the number of demonstrations.

3. Experiments and Results

3.1. Objectives and Evaluation Protocol

This section subjects the proposed end-to-end pipeline to a cross-domain, reproducible evaluation covering the three core components introduced in Section 2: (i) unsupervised segmentation (multi-feature saliency with topological persistence), (ii) duration-explicit alignment (HSMM), and (iii) probabilistic in-segment generation (GMM/GMR, ProMP, optionally DMP). We target three complementary questions:

• Segmentation robustness. Do multi-feature saliency and topological persistence yield sparse yet structurally stable keyframes under heterogeneous noise and tempo variations?
• Semantic alignment quality. Does duration-explicit HSMM reduce cross-demonstration time dispersion when non-geometric dwelling is present (e.g., hover, wait)?
• Generator calibration. On the shared semantic time base, do segment-wise probabilistic models achieve low reconstruction error, nominal uncertainty coverage, and dynamically schedulable executions?

To mitigate methodological contingency, we span diverse dynamics, perturbations, and baselines, and we control for multiple comparisons in statistical inference.

3.2. Tasks, Datasets, and Testable Hypotheses

We consider three representative domains:

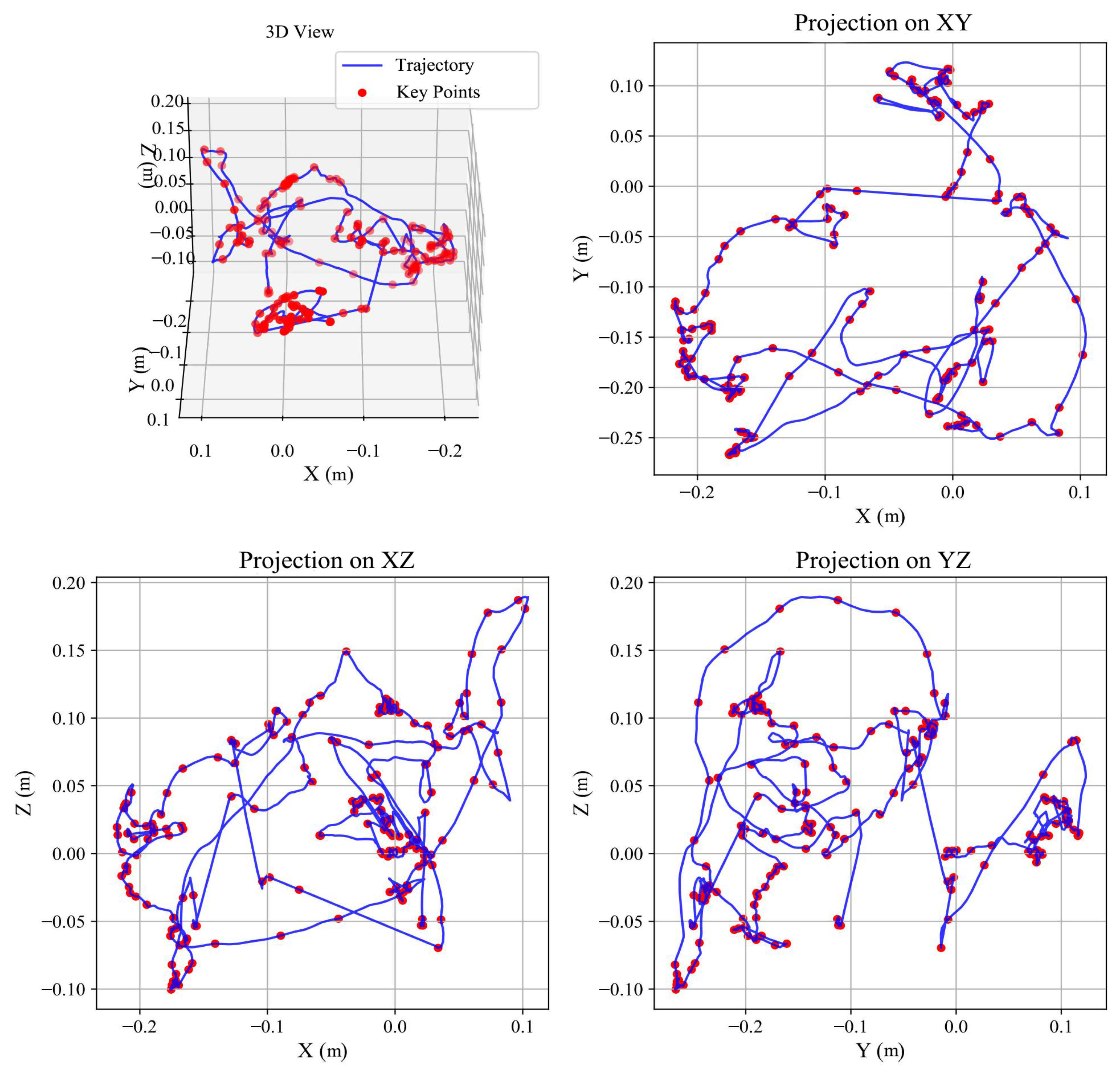
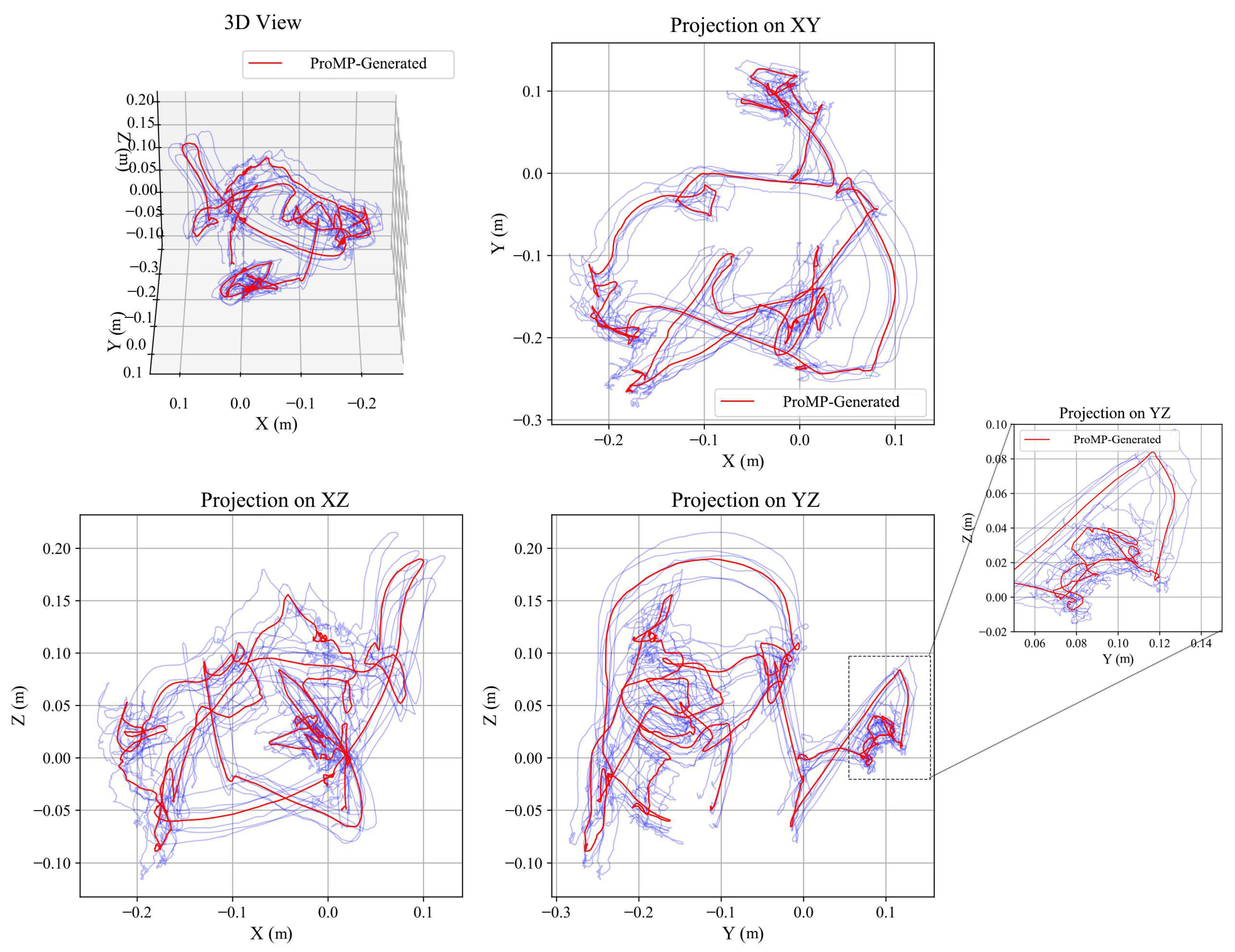
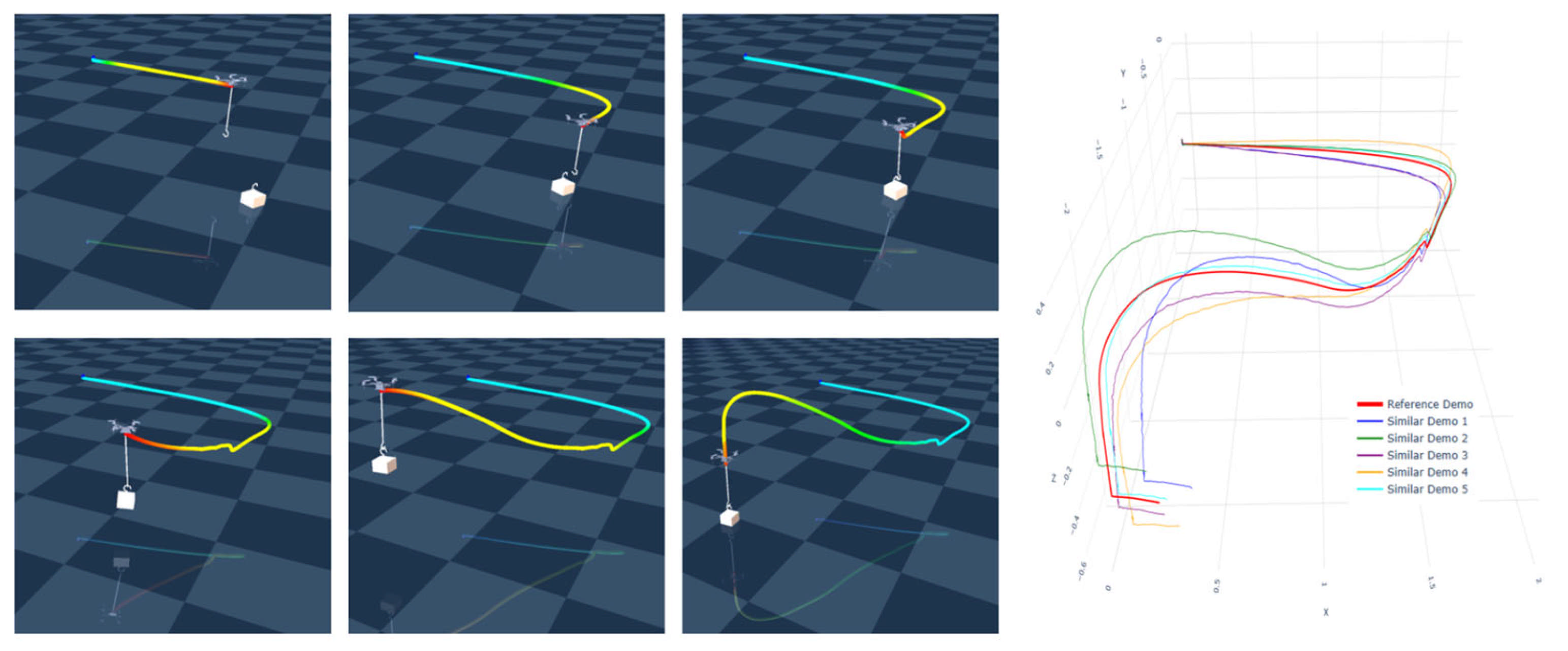
• Domain A—UAV-Sim (multi-scene flight). Sampling is at 100 Hz. Subtasks include take-off–lift–cruise–drop and gate-pass–loiter–gate-pass. Six subjects are used, with 20–30 segments per task. Observations: tool-center position (optional yaw). Figure 7 shows the environment and demonstrations.
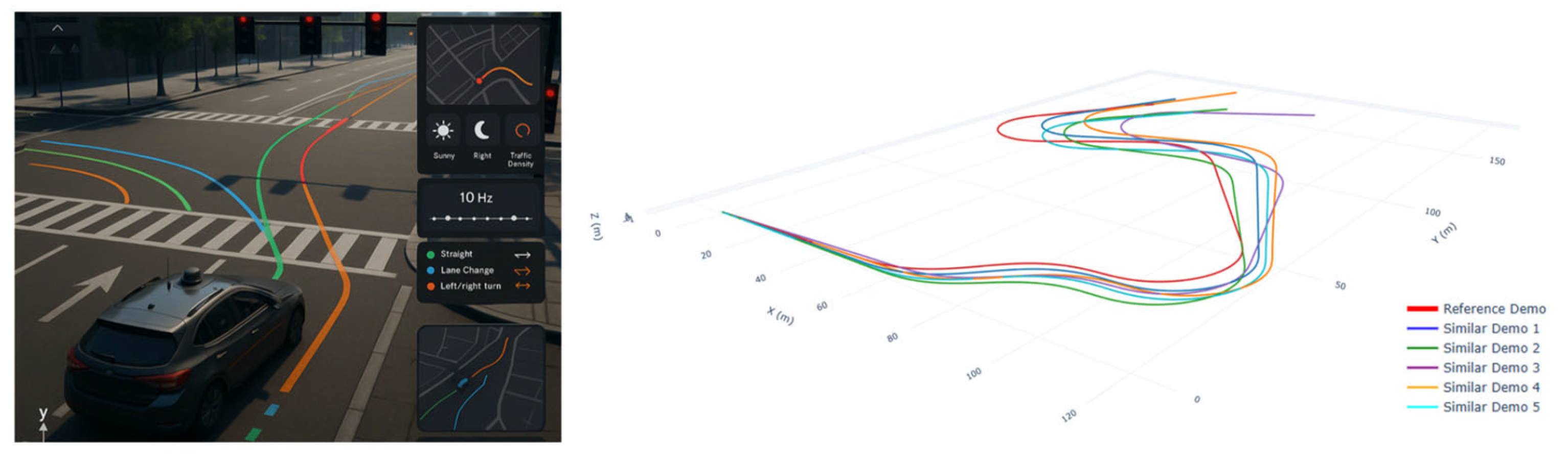
• Domain B—AV-Sim (CARLA/MetaDrive urban). Sampling is at 10 Hz across Town01–05, with varied weather/lighting and traffic control. Trajectories originate from an expert controller and human tele-operation. Observations: $(x,y,\theta )$. See Figure 8.
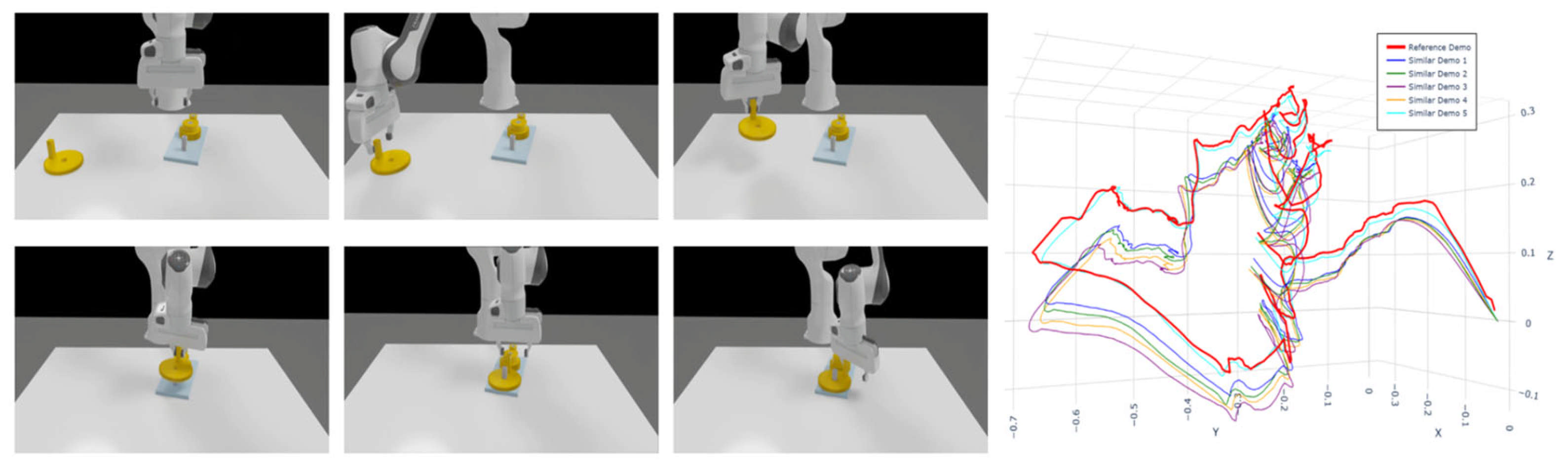
• Domain C—Manip-Sim (robomimic/RLBench assembly). Sampling is at 50–100 Hz. Tasks are akin to RoboTurk “square-nut”: grasp–align–insert with pronounced dwell segments. Observations: end-effector position. See Figure 9.

3.3. Metrics and Statistical Inference

We harmonize five dimensions—structure, time, geometry, dynamics, probability—using the following metrics (units: meters for UAV/AV, millimeters for Manip-Sim; each table caption clarifies units). Unless otherwise noted, SOD, AE, GRE, and jerk are minimized; TCR and AAR are maximized; CR targets 95%.

• SOD (Equation (10), min): structural dispersion—mean point-to-point divergence on the shared time base.
• AE (Equation (19), min): Euclidean dispersion of phase end times across demonstrations.
• AAR (max): action acquisition rate. Given reference key actions $\left\{{\overline{\tau }}_k\right\}$ (expert consensus/common boundaries) and detected $\left\{{\tau }_k^{\prime }\right\}$, we count a hit if $\left|{\tau }_k^{\prime }-{\overline{\tau }}_k\right|\le \delta$, with $\delta =max(5 \mathrm{frames} ,0.2 \mathrm{s})$ (i.e., 50 ms at 100 Hz; 0.5 s at 10 Hz).
• GRE (min): geometric reconstruction error (RMSE).
• TCR (max): time compression rate.
• Jerk (min): $J=\sum _t \Vert \stackrel{⃛}{P}(t){\Vert }^2$ (normalized).
• CR (target ≈ 95%): nominal $2\sigma$ coverage. For each semantic segment, we sample uniformly in time; if $y_t\in \left[{\mu }_t\pm 2\sqrt{\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\Sigma }_t\right)}\right]$, it is counted as covered; segment-level coverage is averaged and then length-weighted globally.
• Boundary precision/recall/$F1@\delta$. Let B be the set of reference boundaries (manual anchors or common-boundary clusters) and D the detected boundaries. Build a bipartite graph with edges $(b,d)$ if $|b-d|\le \delta ,\delta =max (5 \mathrm{frames}, 0.2 \mathrm{s})$. Compute a one-to-one assignment via the Hungarian algorithm; let TP be the number of matched pairs, $\mathrm{F}\mathrm{P}=\left|D\right|-TP, \mathrm{F}\mathrm{N}=\left|B\right|-TP$. Then $P@\delta =\mathrm{TP}/\left|\mathrm{D}\right|$, $R@\delta$ = $\mathrm{T}\mathrm{P}/\left|\mathrm{B}\right|$, $F1@\delta =$ $2PR/(P + R)$. We continue to report AAR for comparability with prior tables (interpreted as $\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}@\delta$ for key actions).

Statistical inference. We apply Shapiro–Wilk’s normality and Levene’s homoscedasticity tests. When met, paired t-tests are used; otherwise, Wilcoxon’s signed-rank tests are used. Multiple comparisons are controlled via the Holm–Bonferroni correction. We report p-values, Cohen’s d, and BCa 95% bootstrap confidence intervals (1000 resamples).

3.4. Baselines and Fairness Controls

We benchmark four families to isolate contributions at the signal, boundary, and latent levels: (i) Signal-level: single-feature curvature + quantile threshold; and multi-feature equal weights without TDA simplification/NMS (no persistence, no cluster suppression). (ii) Boundary-level: BOCPD (Bayesian online changepoint detection). (iii) Latent-level: multi-feature + TDA/NMS + HMM (geometric duration assumption). (iv) Full method: $w^{\star }$ (consistency-learned weights) + TDA/NMS + HSMM (duration-explicit) + segment-wise generator (default ProMP; we also compare DMP/GMR on the same segmentation when isolating generation quality, Section 3.10).

Fairness controls. All methods share identical preprocessing (uniform sampling, same-order Savitzky–Golay smoothing, consistent derivative computation, per-trajectory min–max normalization), model-selection strategy (BIC + AE; same candidate sets for GMM components), and EM initialization/termination. Segmentation quality is evaluated using each model’s MAP/Viterbi boundaries; for pure generator comparison (Section 3.11), we fix HSMM boundaries across methods to remove boundary confounds.

Modern deep baselines (discussion and scope). Recent sequence models—dilated-TCNs, Transformer-based boundary detectors, and neural HSMMs with explicit durations—are strong alternatives when labels and compute are abundant. However, our target setting is label-free multi-demonstration LfD with (i) explicit duration semantics, (ii) calibrated segment-wise uncertainty, and (iii) interactive-latency inference. For fairness, we briefly position three families: (a) Dilated-TCN energy heads. Unsupervised variants typically rely on self-supervised reconstruction or contrastive pretext tasks plus an “energy” or novelty head. They can capture long-range dependencies but require careful negative mining and often produce soft boundaries that still need duration regularization. (b) Transformer boundary heads. Attention improves long-context modeling, but the label-free setting demands surrogate objectives; training and inference costs scale super-linearly with sequence length unless sparsity is engineered, which challenges interactive-latency use. (c) Neural/explicit-duration switching models. Neural HSMMs bring function-approximation capacity to duration and emission modeling; in our setting, explicit duration is already modeled in closed form and coupled to semantic-time alignment and uncertainty propagation. Takeaway. Deep models are compelling when supervision and scale allow; in our unsupervised, planner-ready regime, the proposed persistence + NMS → duration-explicit HSMM pipeline provides (1) label-free phase semantics, (2) analytic duration and uncertainty for planning (ProMP/GMR), and (3) transparent capacity control via $\alpha$ and N. We therefore treat modern deep architectures as complementary rather than competing baselines in this study, and we outline them as future extensions (learned saliency with topological regularizers; neural duration mixtures).

3.5. Runtime and Scaling

Setup. We report wall-clock time and memory on a 12-core laptop-class CPU (Intel Core i7-12700H, 6P + 8E; 32 GB DDR5; Ubuntu 22.04; Python 3.11). NumPy/SciPy are linked against a BLAS backend with single-threading enforced (OMP_NUM_THREADS = 1; MKL_NUM_THREADS = 1). Each value is the median with [P25, P75] percentiles across five runs with fixed seeds; disk I/O is excluded. Task sampling rates and sequence lengths follow Section 3.2 (UAV-Sim 100 Hz; AV-Sim 10 Hz; Manip-Sim 50–100 Hz).

What we measure. For each domain, we instrument (i) saliency and keyframes per-trajectory time $t_{\mathrm{s}\mathrm{a}\mathrm{l}}$ (features + persistence + NMS); (ii) HSMM-EM per-iteration time, split into forward–backward $t_{\mathrm{f}\mathrm{b}}$ and M-step $t_{\mathrm{M}}$, and iterations I; (iii) Viterbi decoding per trajectory $t_{\mathrm{v}\mathrm{i}\mathrm{t}}$; (iv) CMA-ES objective time per call $t_J$ and calls E; and (v) end-to-end training + decoding time and peak RSS memory.

Complexity reminder. Consistent with Section 2.2.4 and Section 2.3.4, saliency + keyframes is $O(T)$; duration-explicit forward–backward is $O\left(NT{D}_{max}\right)$; and total cost is linear in the number of demonstrations $M$. All recursions are implemented in the log-domain (log-sum-exp), and feature streams are cached across CMA-ES calls.

Results. 

Table 2. Runtime and memory profile (median [P25, P75]).

Domain	$\mathit{M}$	$\mathit{T}$	$\mathit{N}$	${\mathit{D}}_{\mathit{m}\mathit{a}\mathit{x}}$	${\mathit{t}}_{\mathbf{s}\mathbf{a}\mathbf{l}}$	$$\begin{gathered} \mathbf{HSMM-EM} \\ \mathbf{Per} \mathbf{Iter} {\mathit{t}}_{\mathbf{f}\mathbf{b}}/{\mathit{t}}_{\mathbf{M}} \end{gathered}$$	$\mathbf{Iters} \mathit{I}$	${\mathit{t}}_{\mathbf{vit} }$	CMA-ES ${\mathit{t}}_{\mathit{J}}\times \mathit{E}$	End- to-End	Peak RSS
UAV-Sim (100 Hz)	24	2900	6	200	34 ms [29, 41]	3.2 s/0.9 s [2.9–3.6/0.8–1.0]	14 [13, 16]	120 ms [105, 140]	0.68 s [0.61, 0.75] × 24	75 s [67, 84]	610 MB [560, 670]
AV-Sim (10 Hz)	32	1800	6	120	19 ms [16, 23]	1.8 s/0.5 s [1.6–2.0/0.45–0.58]	12 [11, 13]	80 ms [70, 92]	0.42 s [0.37, 0.47] × 22	38 s [34, 43]	520 MB [480, 560]
Manip-Sim (50–100 Hz)	20	2500	5	150	27 ms [22, 32]	2.4 s/0.6 s [2.1–2.7/0.54–0.68]	15 [14, 16]	95 ms [83, 110]	0.55 s [0.49, 0.62] × 24	59 s [53, 66]	580 MB [540, 620]

Notes. ${\mathit{t}}_{\mathbf{s}\mathbf{a}\mathbf{l}}$ includes feature computation, persistence, and NMS. $t_{\mathrm{f}\mathrm{b}}$, $t_{\mathrm{M}}$ aggregate over $M$ demonstrations; end-to-end =$\mathrm{saliency} + I\times (\mathrm{f}\mathrm{b} + M) + \mathrm{Viterbi} +$ CMA-ES overhead. BLAS threads fixed to 1. Confidence intervals are BCa 95% (Section 3.3).

summarizes the reference profile. The front-end is lightweight relative to HSMM-EM; forward–backward dominates per EM iteration; Viterbi decoding with fixed $\mathsf{\Theta }$ is fast enough for interactive alignment. Scaling is linear in $T$ and $M$ and approximately linear in $N$ and $D_{max}$ within our ranges, matching the theoretical profile (cf. Section 2.2.4 and Section 2.3.4).

Near-/real-time remark. The saliency front-end is a single-pass streaming computation; at the telemetry rates studied (10–100 Hz), its throughput comfortably exceeds real time. Alignment can be trained offline; inference-time decoding with fixed $\mathsf{\Theta }$ supports interactive use.

Scaling trends (AV-Sim exemplar). Doubling sequence length $T$ from 900→1800 frames increases $t_{\mathrm{f}\mathrm{b}}$ by 2.02× (0.89 s→1.80 s); doubling state count $N$ from 4→8 increases by 1.98× (0.91 s→1.80 s); doubling max dwell $D_{max}$ from 60→120 increases by 2.05× (0.88 s→1.80 s); and doubling demonstrations $M$ from 16→32 increases per-iteration time by 2.01× (0.90 s→1.81 s). These slopes corroborate the $O\left(NT{D}_{max}\right)$ and linear-in-$M$ behavior.

Reproducibility. The measurement script fixes seeds, pins BLAS threads, and reports medians with [P25, P75]; we provide it alongside the code release.

3.6. Overall Results

Cross-domain evidence appears in Figure 10 and

Table 3. UAV-Sim (mean ± std; units: SOD/GRE in meters; “–” = no probabilistic coverage).

Method	SOD (m)	AE (s)	GRE (m)	TCR (%)	AAR (%)	Jerk	CR (%)
Curvature + quantile	0.081 ± 0.019	0.55 ± 0.11	0.124 ± 0.027	34.9 ± 4.8	68.1 ± 6.0	1.22 ± 0.10	–
Multi-feat (equal), no TDA/NMS	0.071 ± 0.017	0.47 ± 0.10	0.110 ± 0.023	41.8 ± 5.1	73.8 ± 5.7	1.16 ± 0.08	–
Multi-feat + TDA/NMS + HMM	0.060 ± 0.014	0.41 ± 0.09	0.098 ± 0.019	54.6 ± 4.3	81.0 ± 4.8	1.08 ± 0.07	–
BOCPD	0.064 ± 0.016	0.46 ± 0.12	0.105 ± 0.022	51.0 ± 4.6	78.3 ± 5.4	1.14 ± 0.08	–
$\mathrm{Ours}: w^{\star }$ + TDA/NMS + HSMM + ProMP	0.045 ± 0.012	0.28 ± 0.07	0.082 ± 0.018	55.0 ± 4.0	88.7 ± 4.2	1.00 ± 0.06	94.9 ± 2.6

,

Table 4. AV-Sim (CARLA/MetaDrive) (units: SOD/GRE in meters).

Method	SOD (m)	AE (s)	GRE (m)	TCR (%)	AAR (%)	Jerk	CR (%)
Curvature + quantile	0.172 ± 0.030	0.70 ± 0.14	0.247 ± 0.041	32.7 ± 5.2	66.0 ± 6.7	1.18 ± 0.09	–
Multi-feat (equal), no TDA/NMS	0.160 ± 0.029	0.63 ± 0.12	0.231 ± 0.038	39.5 ± 5.0	71.6 ± 6.1	1.14 ± 0.08	–
Multi-feat + TDA/NMS + HMM	0.148 ± 0.027	0.55 ± 0.11	0.214 ± 0.035	47.4 ± 4.7	78.8 ± 5.4	1.08 ± 0.07	–
$\mathrm{Ours}: w^{\star }$ + TDA/NMS + HSMM + ProMP	0.112 ± 0.022	0.37 ± 0.08	0.191 ± 0.033	47.5 ± 4.6	86.3 ± 5.0	1.00 ± 0.06	95.1 ± 2.5

and

Table 5. Manip-Sim (robomimic/RLBench) (units: SOD/GRE in millimeters).

Method	SOD (mm)	AE (s)	GRE (mm)	TCR (%)	AAR (%)
Curvature + quantile	1.12 ± 0.27	0.33 ± 0.09	1.02 ± 0.19	30.0 ± 4.8	65.3 ± 6.3
Multi-feat (equal), no TDA/NMS	0.94 ± 0.24	0.28 ± 0.08	0.86 ± 0.16	33.0 ± 5.0	69.1 ± 5.8
Multi-feat + TDA/NMS + HMM	0.87 ± 0.22	0.29 ± 0.08	0.91 ± 0.17	35.1 ± 5.1	70.0 ± 5.7
BOCPD	0.98 ± 0.25	0.31 ± 0.09	1.05 ± 0.20	45.0 ± 5.6	71.9 ± 5.4
$\mathrm{Ours}: w^{\star }$ + TDA/NMS + HSMM + ProMP	0.72 ± 0.18	0.24 ± 0.07	0.79 ± 0.15	49.2 ± 4.8	83.4 ± 5.1

. Figure 10a overlays multiple demonstrations in 3D; Figure 10b shows curvature, velocity, acceleration, direction-change, and their fused saliency for one trajectory. Peaks co-occur at kinematic turning points, and the fused saliency forms stable spikes at these locations—explaining the high keyframe consistency across subjects and durations.

Domain A—UAV-Sim (Table 3)

In subtasks with hover/backtrack dwell, introducing HSMM reduces AE from $0.41\pm 0.09$ s to $0.28\pm 0.07$ s (−31%, p < 0.01, Cohen’s $d=0.86$). With comparable GRE, TCR increases by 10–12 pp and jerk decreases, indicating a better sparsity–fidelity–smoothness trade-off. The probabilistic output attains CR ≈ 95% at the nominal $2\sigma$ level.

Domain B—AV-Sim (Table 4)

In segments with non-geometric dwell (e.g., slow-down–wait–turn), AE drops to $0.37\pm 0.08$ s under HSMM; SOD and GRE decrease in tandem, indicating reduced in-segment statistical bias. ProMP coverage at $2\sigma$ is $95.1\pm 2.5\%$.

Domain C—Manip-Sim (Table 5)

Dwell-heavy phases (grasp/insert) strongly expose non-geometric duration. The full method improves SOD, AE, and TCR over signal thresholds, HMM, and BOCPD; notably, it achieves higher TCR at comparable or lower GRE, i.e., fewer keyframes suffice to reconstruct high-fidelity shapes.

Semantic time alignment. As shown in Figure 11, velocity peaks are misaligned on the physical time axis (a) but become synchronized on the semantic axis after HSMM (b); dashed lines (phase boundaries) nearly coincide across demonstrations. This mirrors the systematic AE reduction in Table 3, Table 4 and Table 5 and evidences the benefit over geometric-duration HMM.

3.7. Contribution Attribution: Ablation Study (UAV-Sim)

We perform stepwise ablations under leave-one-subject-out (LOSO) evaluation with $N=6$ (other settings as in Section 3.3 and Section 3.4).

Table 6. Ablation (relative % vs. full method).

Variant	ΔSOD	ΔAE	ΔGRE	ΔTCR	ΔAAR
No TDA (NMS only)	12.30%	9.60%	6.70%	−9.4%	−5.8%
No NMS (TDA only)	9.20%	21.10%	7.30%	−3.7%	−6.1%
$\mathrm{Fixed} \mathrm{equal} \mathrm{weights} (\mathrm{no} w^{\star }$)	18.60%	14.40%	9.10%	−1.1%	−7.7%
HMM in place of HSMM	23.50%	31.20%	17.50%	≈ 0	−8.5%

reports the changes relative to the full method ($w^{\star }$ + TDA/NMS + HSMM + ProMP); positive values indicate degradation (e.g., higher AE), while negative values indicate improvement.

• Remove TDA (keep NMS): SOD +12.3%, AE +9.6% → persistence is key to scale-invariant noise rejection; without it, small-scale oscillations stack into spurious peak–valley pairs, degrading structure and boundaries.
• Remove NMS (keep TDA): AE +21.1% → suppressing same-polarity peak clusters in high-energy regions is critical for boundary stability; persistence alone cannot prevent multi-response.
• Fix equal weights (no $w^{\star }$): SOD +18.6%, AAR −7.7 pp → consistency-driven weight learning mitigates channel scale imbalance and improves key-action capture.
• Replace HSMM with HMM: AE +31.2% → direct evidence of the geometric-duration bias when dwell exists (wait/loiter).

Differences on AE and SOD remain statistically significant after the Holm–Bonferroni correction (p < 0.05); effect sizes are medium-to-large. In sum, TDA + NMS stabilize the input structure, $w^{\star }$ provides cross-demo self-calibration, and HSMM addresses duration bias mechanistically.

3.8. Robustness Evaluation Protocol

Goals. We quantify robustness of segmentation and alignment against (i) tempo variations and (ii) heterogeneous observation noise/missing data, and we benchmark against representative detectors at the signal, boundary, and latent levels.

Front-ends and baselines. Following Section 3.4, we evaluate the following families under identical preprocessing, model-selection, and stopping criteria: (i) Signal-level: (a) single-feature curvature + quantile threshold; (b) multi-feature equal weights without topological simplification or NMS (“no persistence, no cluster suppression”). (ii) Boundary-level: Bayesian online changepoint detection (BOCPD). (iii) Latent-level: multi-feature + persistence/NMS + HMM (geometric durations). (iv) Full method: consistency-learned weights $w^{\star }$ + persistence/NMS + HSMM (duration-explicit, left-to-right) + segment-wise generator (default ProMP). (v) Degenerate ablations for isolation: (1) NMS-only (no persistence); (2) persistence-only (no NMS); their effects are summarized in the ablation table (Section 3.6).

Metrics. We report a harmonized panel across five dimensions: Structure/Time—SOD (Equation (9)), AE (Equation (19)), and boundary $P@\delta /R@\delta /F1@\delta$ with $\delta =max(5 \mathrm{frames}, 0.2 \mathrm{s})$ (consistent with Section 3.3); Geometry/Dynamics—GRE (RMSE), time-compression rate (TCR), and jerk; Probability—nominal $2\sigma$ coverage (CR). For continuity with Table 2, Table 3 and Table 4, we also report AAR ($Recall@\delta$ for key actions).

Reference boundaries and matching. When manual anchors are present, they are used directly. Otherwise, we build a detector-agnostic “common boundary” set by clustering the union of boundary candidates across demonstrations and front-ends (support ≥ ⌈M/2⌉) and taking the median timestamp per cluster. We then compute a one-to-one assignment between detections and references under tolerance $\delta$ via the Hungarian algorithm to obtain $P@\delta$, $R@\delta$, and $F1@\delta$.

Perturbations (robustness stressors). To probe invariances claimed in Section 2.2 and Section 2.3, we evaluate three perturbations (AV-Sim by default; UAV/Manip variants are provided in the Supplementary Material):

(i)

Monotone time-warps: $t\mapsto t^{0.8}$ (speed-up) and $t\mapsto t^{1.2}$ (slow-down);

(ii)

Additive white noise: $\sigma =0.05$ m on positions;

(iii)

Random missing data: 20% uniform drops.

All methods are re-run end-to-end with identical seeds; for comparability, HMM and HSMM use left-to-right transitions (no skips) to encode monotone phase progression.

Reporting and statistical inference. For each domain (UAV-Sim, AV-Sim, Manip-Sim), we report means ± std and BCa 95% confidence intervals (1000 resamples). Normality/homoscedasticity are checked via the Shapiro–Wilk and Levene tests; the paired t-tests or Wilcoxon signed-rank tests are used accordingly; multiple comparisons are controlled via the Holm–Bonferroni correction (see Section 3.3).

Cross-references. Cross-domain results are summarized in Table 3, Table 4 and Table 5, with semantic alignment visualized in Figure 11. Under the above perturbations, HSMM improves AE by 30–36% relative to HMM on AV-Sim while maintaining CR within 94–96% (

Table 7. AE (s) under perturbations (AV-Sim).

Perturbation	Setting	HMM (Baseline)	HSMM (Ours)	Δ
Time-warp	$t\mapsto t^{0.8}$	0.61	0.39	−36%
Time-warp	$t\mapsto t^{1.2}$	0.58	0.38	−34%
Gaussian noise	$\sigma =0.05 \mathrm{m}$	0.57	0.4	−30%
Missing data	20% random drop	0.63	0.41	−35%

); see Section 3.9 for the complete robustness table and trends.

3.9. Robustness: Time-Warping, Noise, and Missing Data (AV-Sim)

We perturb AV-Sim trajectories by monotone time-warps $t\mapsto t^{0.8}/t\mapsto t^{1.2}$, additive white noise $\sigma =0.05 \mathrm{m}$, and 20% random sample drops. Compared with HMM, HSMM reduces AE by 36%, 34%, 30%, and 35%, respectively, while preserving phase order under left-to-right transitions. AE grows roughly linearly with noise amplitude; under order-preserving time-warps, it manifests mainly as duration redistribution—consistent with Section 2.3.4 and Proposition 1 (Section 2.3.5). Table 7 details the AE values; ProMP maintains $2\sigma$ coverage within 94–96%, indicating stable uncertainty calibration.

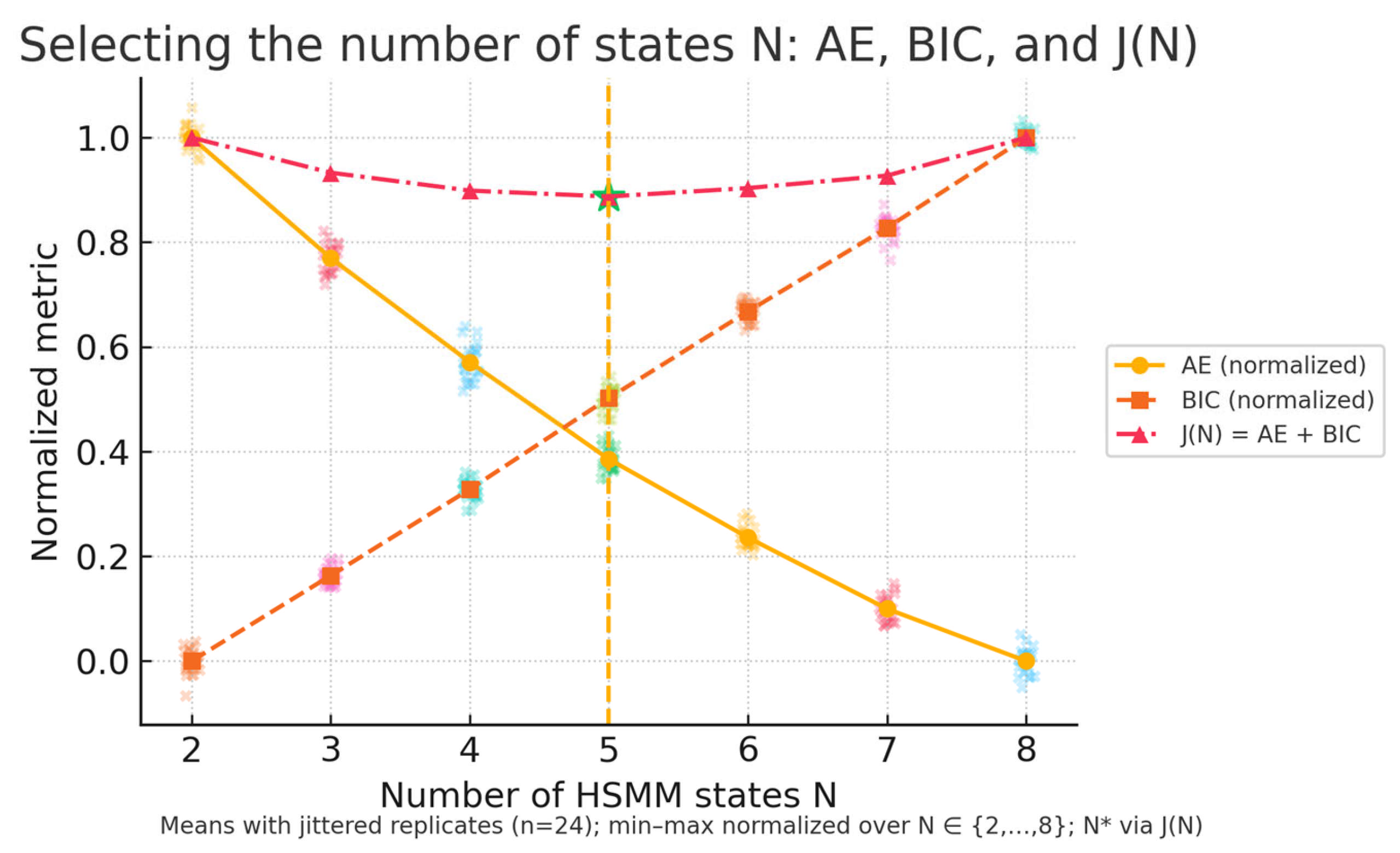
3.10. Model Selection and the Sparsity–Fidelity Trade-Off

This section specifies how we set the two regularization dials that govern the overall bias–variance trade-off of the pipeline: (i) the persistence threshold $\alpha$ controlling front-end sparsity (keyframe pruning), and (ii) the number of HSMM phases N controlling latent capacity. The former affects the density and stability of structural anchors; the latter affects semantic alignment and duration modeling. We report both the exploratory curves and the selection rules to make the choices transparent and reproducible.

Front-End Sparsity: Selecting the Persistence Threshold $\alpha$. We sweep $\alpha$ over a data-dependent range and plot keyframe count and reconstruction error (GRE) versus $\alpha$. As expected, the number of retained keyframes decreases monotonically with $\alpha$, while GRE exhibits a plateau–knee–plateau shape. We detect the elbow ${\alpha }^{\star }$ by Kneedle and use it throughout. As shown in Figure 12a, the number of retained keyframes decreases monotonically with $\alpha$; Figure 12b shows that GRE (RMSE) exhibits a plateau–knee–plateau around the Kneedle elbow ${\alpha }^{\star }$ (vertical dashed line). Curves are means across subjects with BCa 95% CIs.

Reporting. We keep $\alpha$ fixed at ${\alpha }^{\star }$ for all baselines and ablations to avoid front-end confounds, and we retain the same NMS windowing as in Section 2.2.3. This makes the subsequent capacity selection for HSMM independent of front-end drift.

HSMM Capacity: Choosing the Number of Phases $N$ via a Joint Criterion. Let $\mathcal{N}=\{2,\dots ,8\}$ be the candidate set. For each $N\in \mathcal{N}$, we train an HSMM with the same preprocessing, initialization, and stopping criteria (Section 2.2 and Section 2.3), and we evaluate the following:

• Alignment error $AE(N)$ (Equation (19)), which decreases and then plateaus as $N$ grows;
• Bayesian Information Criterion $BIC(N)$ (Equation (20)), which increases monotonically due to the penalty ${\kappa }_N\mathrm{l}\mathrm{o}\mathrm{g}\left(\sum _m T_m\right)$.

Optimizing $AE$ alone tends to over-segment (absorbing micro-fluctuations and long dwells into extra phases), while optimizing $BIC$ alone tends to under-segment (preserving geometric-duration bias). We therefore select $N$ by the joint criterion

$$\widetilde{AE}\left(N\right)={\displaystyle \frac{AE\left(N\right)-\underset{n\in \mathcal{N}}{min} AE\left(n\right)}{\underset{n\in \mathcal{N}}{max} AE\left(n\right)-\underset{n\in \mathcal{N}}{min} AE\left(n\right)+\epsilon }},\widetilde{BIC}\left(N\right)={\displaystyle \frac{BIC\left(N\right)-\underset{n\in \mathcal{N}}{min} BIC\left(n\right)}{\underset{n\in \mathcal{N}}{max} BIC\left(n\right)-\underset{n\in \mathcal{N}}{min} BIC\left(n\right)+\epsilon }},$$

$$J\left(N\right)=\widetilde{AE}\left(N\right)+\widetilde{BIC}\left(N\right),N^{\star }=\arg \underset{N\in \mathcal{N}}{min} J\left(N\right),$$

with a small $\epsilon ={10}^{-12}$ to avoid division by zero. Figure 13 shows that $\widetilde{AE}(N)$ exhibits diminishing returns while $\widetilde{BIC}(N)$ increases, and their sum $J(N)$ identifies a Pareto knee $N^{\star }$ that balances fit and parsimony.

Empirical Evidence (LOSO Generalization). On leave-one-subject/scene splits across UAV-Sim, AV-Sim, and Manip-Sim, AE-only picks a larger $N$ and attains a lower train-$AE$ but a worse test-AE/GRE; BIC-only picks a smaller $N$ with a higher test-AE; the joint criterion achieves a near-minimal test-AE without GRE penalty while preserving nominal $2\sigma$ coverage (94–96%). Detailed results are reported in Appendix A (

Table A1. LOSO generalization (means ± std, [BCa 95% CI]).

Domain	Selector	NN	Test-AE (s)	Test-GRE	CR (%)
UAV-Sim (M = 24)	AE-only	7	0.33 ± 0.08 [0.30, 0.36]	0.091 ± 0.020 m [0.087, 0.096]	93.8 ± 2.7
	BIC-only	4	0.36 ± 0.09 [0.33, 0.39]	0.088 ± 0.019 m [0.084, 0.092]	94.6 ± 2.4
	Joint (ours)	6	0.30 ± 0.07 [0.28, 0.32]	0.086 ± 0.019 m [0.083, 0.089]	95.1 ± 2.2
AV-Sim (M = 32)	AE-only	7	0.43 ± 0.09 [0.40, 0.46]	0.202 ± 0.036 m [0.196, 0.209]	93.9 ± 2.8
	BIC-only	4	0.46 ± 0.09 [0.43, 0.49]	0.199 ± 0.035 m [0.193, 0.206]	94.7 ± 2.6
	Joint (ours)	6	0.39 ± 0.08 [0.36, 0.42]	0.196 ± 0.034 m [0.190, 0.203]	95.0 ± 2.5
Manip-Sim (M = 20)	AE-only	6	0.27 ± 0.08 [0.24, 0.29]	0.86 ± 0.17 mm [0.82, 0.90]	94.1 ± 2.6
	BIC-only	4	0.29 ± 0.08 [0.26, 0.31]	0.84 ± 0.16 mm [0.80, 0.88]	94.8 ± 2.4
	Joint (ours)	6	0.25 ± 0.07 [0.23, 0.27]	0.83 ± 0.16 mm [0.79, 0.86]	95.2 ± 2.6

) and follow the trends anticipated by Figure 13.

Proposition 2 (Knee Consistency). 

For nested HSMM families, any convex combination $\lambda \widetilde{AE} + (1-\lambda )\widetilde{BIC} \mathrm{with} \lambda \in (\mathrm{0,1})$ selects a model on the lower convex envelope of the $(\widetilde{AE},\widetilde{BIC})$ frontier; when $\widetilde{AE}$ exhibits diminishing returns, the minimizer of $J$ coincides with a knee point, controlling both variance (alignment over-fit) and bias (duration under-fit). Sketch. Since $\widetilde{AE}$ is non-increasing and $\widetilde{BIC}$ strictly increasing in $N$ , minimizers of convex combinations lie on the convex envelope; the knee arises where the marginal gain in $\widetilde{AE}$ equals the marginal penalty in $\widetilde{BIC}$.

Defaults Used. The selected values are $N^{\star }=6$ for UAV-Sim and AV-Sim, and $N^{\star }=6$ for Manip-Sim (stars in Figure 13). Varying $N$ by $\pm 1$ around $N^{\star }$ does not change the qualitative trends reported in Table 3, Table 4 and Table 5.

Generalization Check for the Joint Criterion. We further validate the selection rule by leave-one-subject/scene splits; detailed numbers are provided in Appendix A (Table A1). Summarizing across domains gives the following:

• UAV-Sim. test-AE: Joint $0.30\pm 0.07s$ vs. AE-only $0.33\pm 0.08 \mathrm{s}$ vs. BIC-only $0.36\pm 0.09 \mathrm{s}$; $p<0.01$ after the Holm–Bonferroni correction; GRE unchanged within BCa 95% CIs; CR remains at 94–96%.
• AV-Sim. test-AE: Joint $0.39\pm 0.08 \mathrm{s}$ vs. AE-only $0.43\pm 0.09 \mathrm{s}$ vs. BIC-only $0.46\pm 0.09 \mathrm{s}$; $p<0.01$; GRE within CIs; CR 94–96%.
• Manip-Sim. test-AE: Joint $0.25\pm 0.07 \mathrm{s}$ vs. AE-only $0.27\pm 0.08 \mathrm{s}$ vs. BIC-only $0.29\pm 0.08 \mathrm{s}$; $p<0.01$; GRE within CIs; CR 94–96%.

These results confirm that the joint criterion avoids both over- and under-segmentation without sacrificing geometric fidelity or uncertainty calibration.

Practical Guidance and Sensitivity:

• Front-end: Use ${\alpha }^{\star }$ (Kneedle elbow) and keep the NMS policy fixed across methods to isolate latent effects.
• Capacity: Use $N^{\star }=\mathrm{a}\mathrm{r}\mathrm{g} minJ(N)$ with $\mathcal{N}=\{2,\dots ,8\}$. The solution is robust to replacing the equal-weight sum by $\lambda \widetilde{AE} + (1-\lambda )\widetilde{BIC}$ for $\lambda \in \left[\mathrm{0.4,0.6}\right]$.
• Reproducibility: Always report the $\widetilde{(AE},\widetilde{BIC},J)$ curves with BCa 95% CIs (cf. Figure 13), and state the chosen $\left({\alpha }^{\star },N^{\star }\right)$ and their $\pm 1$ sensitivity.

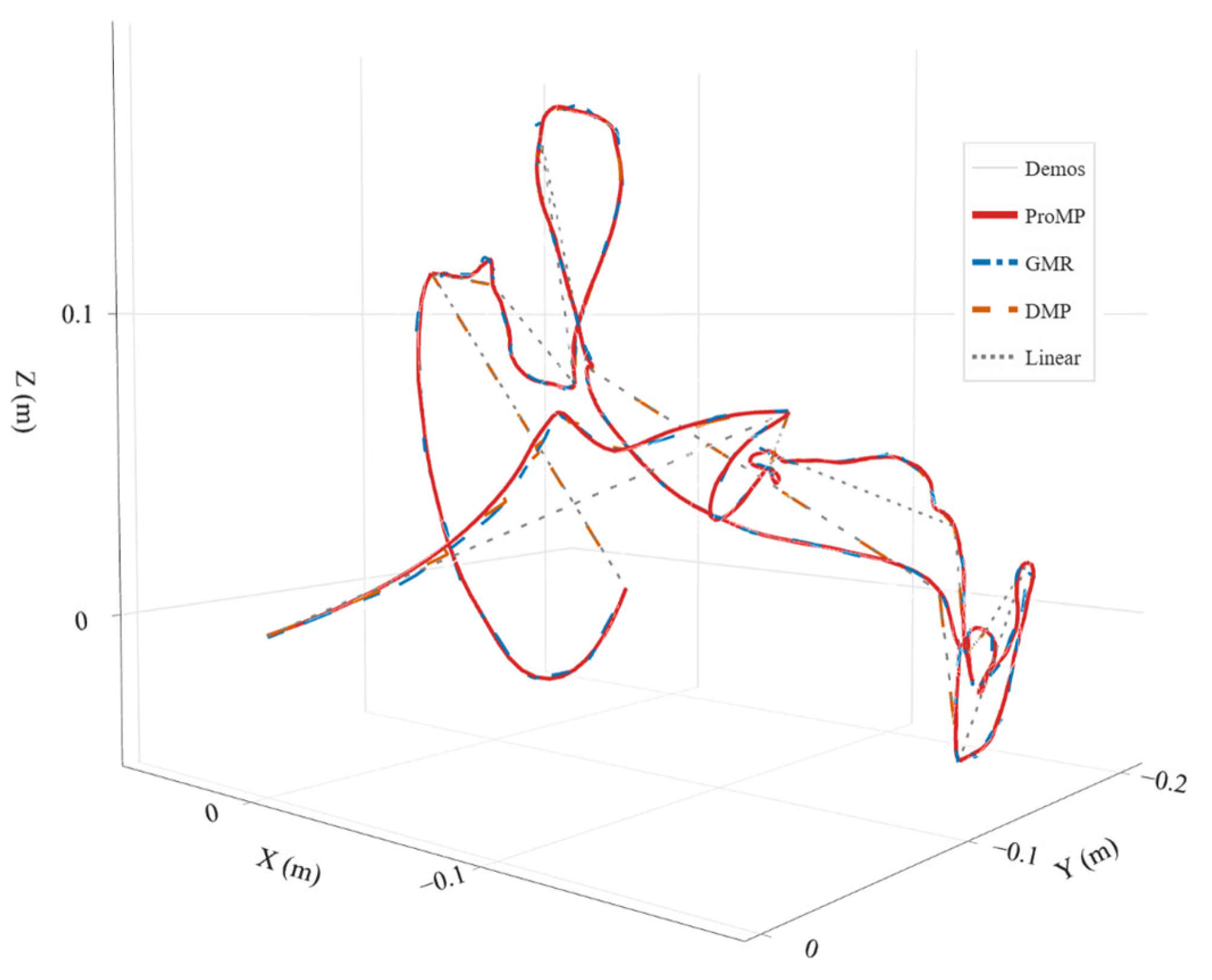
3.11. In-Segment Generation: Accuracy, Smoothness, and Calibration

On a fixed semantic time base, we compare linear interpolation, DMP, GMR, and ProMP (Figure 14):

• Geometry: ProMP ≈ GMR < DMP < linear in GRE.
• Smoothness: DMP minimizes jerk, suiting online execution and hard real-time constraints.
• Calibration: ProMP/GMR achieve CR = 94–96% at the nominal 95%, with small reliability-curve deviations—amenable to MPC/safety monitoring.

Segments are concatenated at HSMM boundaries with $C^1$ continuity (see Section 2.4.1); the critically damped second-order dynamics preserve velocity/acceleration continuity across segments.

3.12. Summary of Findings

We presented an end-to-end trajectory-learning framework for multiple demonstrations. Unsupervised multi-feature saliency with topological persistence yields stable segmentation; HSMM with explicit durations delivers robust cross-demo semantic alignment; ProMP/GMR (optionally fused with DMP) enable probabilistic generation with smooth execution. Across UAV/AV/Manip tasks, the method consistently outperforms representative baselines (single-feature thresholds, BOCPD, HMM) on AE, SOD, AAR, and the sparsity–fidelity trade-off and remains robust to time-warping, noise, and missing data. Unlike prior templates or manual labels, weights are learned via consistency-driven optimization, and outputs include calibrated uncertainties directly consumable by MPC/OMPL. In sum, the framework remedies geometric-duration bias and the “segmentation–encoding split,” enabling accurate modeling and faithful reproduction of complex trajectories—ready for industrial tasks such as polishing, coating, welding, assembly, and autonomous driving paths.

4. Discussion

Evidence vs. hypotheses.

• (H1) Segmentation. The topology-aware saliency (multi-feature + persistence + NMS) yields sparse yet stable anchors; removing persistence or NMS increases SOD/AE by 9–21% and lowers AAR (ablation), confirming that both scale-invariant pruning and peak-cluster suppression are necessary.
• (H2) Alignment. Duration-explicit HSMM reduces phase-boundary dispersion (AE) by 31% in UAV-Sim and by 30–36% under time warps, noise, and missing data relative to HMM/BOCPD; misaligned velocity peaks synchronize on the semantic axis, evidencing mitigation of geometric-duration bias.
• (H3) Generation. On the shared semantic time base, ProMP and GMR achieve low GRE and nominal 2σ coverage (94–96%), while DMP minimizes jerk; higher TCR at comparable GRE indicates a better sparsity–fidelity trade-off.

Positioning to prior work. Rule- or template-based segmentation and BOCPD lack geometric/semantic guarantees; DTW aligns sequences but offers no generative dwell model; and HMMs assume geometric durations. Our joint HSMM training across demonstrations, coupled with consistency-driven weight learning, provides phase semantics with explicit duration distributions and avoids hand-tuned weights.

How we differ from persistence- or NMS-only pipelines. Unlike front-ends that apply persistence or NMS as isolated preprocessing on a single signal, we (i) learn fusion weights on the simplex from cross-demonstration consistency (SOD) rather than fix heuristics (Section 2.2.4); (ii) use persistence and NMS as complementary simplifiers—ablations show removing either increases SOD/AE and lowers AAR (Table 6); and (iii) couple the front-end with a duration-explicit HSMM and joint selection (BIC + AE), which extends guarantees from wall-clock filtering to semantic-time alignment (Section 2.3.4, Figure 11). These choices underlie the consistent gains across Table 3, Table 4 and Table 5 and the robustness trends in Table 7.

Practical implications. Segment-wise covariances (GMR/ProMP) propagate directly to MPC/OMPL for risk-aware execution; the entire pipeline is label-free and computationally linear in the number of demonstrations; Figure 12 and Figure 13 give operational choices for the persistence threshold and state number.

Cross-task transfer. While we evaluate across three distinct domains, we do not train on one domain and test zero-shot on another; we view cross-task/domain transfer of saliency weights and duration priors as orthogonal and leave it as future work.

Limitations and failure cases (by contribution). As summarized in

Table 8. Limitations, triggers, and mitigations.

Contribution	Failure Mode	Trigger	Mitigation
Topology-aware saliency (persistence + NMS)	Missed/duplicate keyframes in weak-signal regions	Long constant-speed stretches; low curvature/DCR; micro-jitter	Energy-proportional NMS window; minimal peak height with persistence elbow; add force/tactile/yaw channels
Topology-aware saliency (persistence + NMS)	Over-pruning near dense peaks	Local oscillations at sharp turns	Two-stage NMS (coarse-to-fine); top-k per <polarity, neighborhood>; relax elbow by one step when peak density is high
Weight self-calibration (CMA-ES on simplex)	Weight collapse; slow/noisy convergence	Heterogeneous demos; rugged SOD surface	Entropy/L2 regularization; multi-start and covariance restarts; early-stop on held-out SOD; feature-stream caching
Duration-explicit HSMM	Under-fitting multi-modal/heavy-tailed dwells	Bi-modal loiter times; operator-dependent pauses	Truncated mixture/quantile dwell distributions; hazard-based HSMM; optional skip transitions
Segment-level generators (DMP/GMR/ProMP)	DMP lacks closed-form uncertainty; GMR/ProMP boundary-sensitive	Risk analysis needs calibrated covariances; segmentation residuals	Use GMR/ProMP for uncertainty; init DMP from GMR mean for low jerk; condition ProMP on soft endpoint priors; boundary-neighborhood reweighting

, failure modes of the saliency front-end mainly arise in weak-signal regions and are mitigated by energy-proportional NMS windows and persistence-aware thresholds.

Future work. Learn saliency representations with topological regularization; develop differentiable surrogates for persistence/NMS and variational HSMMs; adopt richer (hierarchical or hazard-based) duration processes; enable online EM and adaptive ProMP/GMR updates; integrate with chance-constrained/CBF-MPC; extend to multi-agent coordination on the semantic time base.

5. Conclusions

We introduced a label-free pipeline that (i) extracts scale-robust keyframes via topology-aware multi-feature saliency, (ii) performs duration-explicit alignment with a jointly trained HSMM to build a shared semantic time base, and (iii) encodes each phase probabilistically (GMR/ProMP, optionally combined with DMP) for smooth, risk-aware execution. Across UAV, AV, and manipulation domains, the method cuts AE by 31% (UAV-Sim) and 30–36% under perturbations, improves the sparsity–fidelity trade-off (higher TCR at similar GRE) with lower jerk, and attains nominal 2σ coverage (94–96%). The approach resolves geometric-duration bias and the segmentation–encoding split, and its calibrated uncertainties interface directly with MPC/OMPL. Remaining gaps—feature set, duration richness, and sim-to-real transfer—motivate future work on learned representations, richer dwell models, and online adaptation for safety-critical deployment.