A Review of XAI Methods Applications in Forecasting Runoff and Water Level Hydrological Tasks

Abstract

Modern artificial intelligence methods are increasingly applied in hydrology, particularly for forecasting water inflow into reservoirs. However, their limited interpretability constrains practical deployment in critical water resource management systems. Explainable AI offers solutions aimed at increasing the transparency of models, which makes the topic relevant in the context of developing sustainable and trusted AI systems in hydrology. Articles published in leading scientific journals in recent years were selected for the review. The selection criteria were the application of XAI methods in hydrological forecasting problems and the presence of a quantitative assessment of interpretability. The main attention is paid to approaches combining LSTM, GRU, CNN, and ensembles with XAI methods such as SHAP, LIME, Grad-CAM, and ICE. The results of the review show that XAI mechanisms increase confidence in AI forecasts, identify important meteorological features, and allow analyzing parameter interactions. However, there is a lack of standardization of interpretation, especially in problems with high-dimensional input data. The review emphasizes the need to develop robust, unified XAI approaches that can be integrated into next-generation hydrological models.

1. Introduction

A primary objective in contemporary hydrology is the accurate forecasting of hydrological variables. Such forecasts are essential for predicting the state of water and ice regimes in rivers, lakes, and reservoirs. Hydrological forecasts are classified by lead-time parameter. It determines the time interval between the preparation of the forecast and the moment of occurrence of the forecasted state. Forecasts with a lead time of 1 to 10 days are considered short-term, and forecasts with a lead time of several weeks to several months are considered long-term. The ultra-long-term forecasts are determined by a lead time of 1 year or more. Hydrological forecasts can be classified according to the content (subject of forecasting). It is common to distinguish water regime forecasts (including water level, flow, and inflow), ice regime forecasts (including freezing and opening of water bodies, and ice thickness), and water quality forecasts (including the degree of pollution of a water body by industrial waste). A distinction is also made between the local and territorial hydrological forecasts and forecasts by the type of water body considered (plain rivers, mountain rivers, lakes, and reservoirs).

The significance of hydrological forecasts is underscored by the influence of water and ice regimes on various industrial sectors: firstly, the productivity of the pulp and paper, textile, and metallurgical industries, and hydropower production; additionally, water transport—restrictions on movement due to low water levels or reservoir icing; moreover, agriculture—the impact of water levels in rivers on the crop yields of adjacent territories and the life of the population (consequences of floods during spring floods). In particular, accurate forecasting of water inflow to the reservoir of hydroelectric power plants (HPPs) plays an important role. Changes in water inflow to the reservoir affect the following processes within the framework of the functioning of the HPP:

• planning of hydroelectric power station operating modes;
• efficient water consumption and minimization of idle discharges;
• regulation of water levels in the upper and lower pools of the reservoir.

The need to control hydroelectric power station generation on hourly and shorter intervals within a day determines the importance of short-term (1–10 days in advance) forecasts of water inflow to the reservoir. The task of short-term forecasting of water inflow is associated with analyzing many different factors and parameters that have a high degree of heterogeneity.

Inflow forecasts are made using hydrological models. The first hydrological models were mathematical models of individual components of the hydrological cycle (water infiltration into the soil, rainfall runoff, snowmelt runoff, etc.). These models were developed during the 1910–1920s and were based solely on empirical observations.

Then, in the 1930s–1940s, a model of a single hydrograph was developed and physically substantiated. It made it possible to move from purely empirical methods to the creation of generalized models substantiated physically [1].

In the 1970s–1980s, many conceptual models were proposed for the physical and mathematical modeling of river runoff formation (models with lumped and distributed parameters, variable contributing area models) [2]. During this period, the use of remote sensing data from satellites of the Earth’s surface in hydrological models began.

In the 1990s–2000s, the development of geographic information systems (GIS) and digital elevation models gave rise to certain events. They served as an impetus for the development of more detailed modern physical and mathematical hydrological models (Soil Water Assessment Tool (SWAT) [3], Physically based land surface model SWAP [4], ECOMAG [5], MIKE SHE [6], and GEOtop [7]). At the same time, two approaches became widespread: first, an approach based on the representation of the area of a river basin in the form of representative elementary areas and volumes [8]; the representative elementary catchments [9].

Modern hydrological models used to forecast inflow use data on precipitation, evaporation, air temperature, soil conditions, snow reserves, as well as relief, the presence of vegetation, and its types in the catchment area as input parameters [10]. At the same time, strict requirements for temporal and spatial resolution and specific pre-processing are imposed on the listed data [11].

An alternative to mathematical and physical models of inflow forecasting is models based on the use of artificial intelligence (AI). Recent reviews on hydrological forecasting have drawn several key conclusions [12,13]. It is indicated that over the past 10–15 years, the frequency of using various AI models in such problems has significantly increased. At the same time, the types of implemented models have also changed. Early studies used Support Vector Regressor (SVR), Fuzzy logic models, along with statistical models of Linear Regression and ARMA/ARIMA, to forecast water inflows and outflows to water bodies [14,15,16]. Later studies started implementing ensemble machine learning models, artificial neural networks (ANNs) of various structures: convolutional neural networks (CNNs), transformer ANN [17], long short-term memory (LSTM) [18,19,20], etc., as well as hybrid approaches (SVR with cooperation search [21], LSTM with encoder–decoder [18] or attention mechanism [22], and wavelet-neural network [23]).

The use of models based on AI algorithms (especially various ANNs) has found wide application in problems of forecasting hydrological quantities. Models based on data analysis using ANNs and deep machine learning methods achieve higher accuracy compared to physically based hydrological models. Examples of problems of short-term runoff forecasting [24], inflow [25,26,27], and streamflow [28,29] confirm this. However, the high accuracy of AI models is often accompanied by their opacity. Such models operate as “black-box models”, making decisions based on internal representations that are not directly interpretable. This significantly limits their application in critical areas such as hydropower and water management, which require not only predictive accuracy but also explainability for verification, auditing, and decision-making by the operators.

Against this background, the direction of explainable artificial intelligence (XAI) is developing actively. It is aimed at increasing the interpretability of models and understanding the factors that influence the result. The tasks of XAI include the construction of interpretable architectures, post-processing of model results for the purpose of explanation, visualization of feature contributions, and the formation of confidence intervals for forecasts. The use of XAI is especially relevant for hydrological models. These models must handle high-dimensional data, strong seasonality, and spatial heterogeneity.

This paper presents a systematic review of modern XAI approaches applied to short- and medium-term hydrological forecasting tasks such as inflow, runoff, and streamflow. The focus is on the applicability of XAI methods to various model types and their practical use in engineering. Moreover, open issues concerning interpretability under uncertainty are of particular importance.

The scientific novelty of the work lies in:

• The systematic classification of XAI methods for hydrological forecasting by interpretability type (ante-hoc/post-hoc), level (global/local), and intended function (interpretation, control, and trust);
• Identifying methodological limitations in current XAI applications dealing with multidimensional time series and spatial data;
• Formulating directions for advancing XAI in hydrology, including metrics for interpretability assessment and semantic, engineering-oriented visualization interfaces.

The paper is structured as follows: Section 2 describes the criteria for selecting publications for the review; Section 3 presents the features of hydrological forecasting problems; Section 4 is devoted to the systematization of XAI methods and their application in existing studies; Section 5 discusses the relationship between explainability and confidence; Section 6 formulates directions for further research; Section 7 provides conclusions.

2. Article Selection Criteria and Methodology

This review was conducted as a systematic literature review (SLR) and reported in accordance with the PRISMA 2020 guidelines [30]. It focuses on identifying current approaches to improving the interpretability of AI models in hydrological forecasting applications.

Particular attention is paid to publications considering forecasting the following target variables: water inflow to a reservoir (reservoir inflow); river runoff; water level in rivers and reservoirs (streamflow, water level).

2.1. Search Sources

The search for publications was conducted in the following indexed databases: Scopus, Web of Science, IEEE Xplore, MDPI, ScienceDirect, and SpringerLink. Open repositories (ResearchGate) and systematic reviews were also used as metasearch sources.

We used curated bibliographic indexes (Scopus, Web of Science, IEEE Xplore, MDPI, ScienceDirect, and SpringerLink) to ensure stable coverage definitions, transparent deduplication, and replicable queries. Database such as Google Scholar was not used as a primary source because it is not a curated index and mixes journal, conference, and preprint versions with non-refereed items, which reduces the auditability of the SLR protocol.

2.2. Keywords and Search Syntax

The following keywords were used to retrieve relevant articles: (“streamflow forecasting” OR “reservoir inflow” OR “runoff prediction”) AND (“machine learning” OR “deep learning” OR “artificial intelligence”) AND (“explainable AI” OR “interpretable AI” OR “SHAP” OR “LIME”).

The search was limited to articles published in the period 2020–2025, primarily in Q1–Q2 journals in the following categories: Hydrology, Water Science, Energy, Power Engineering, and AI Applications.

We limited the search to 2020–2025 to capture the period in which hydrology-specific applications of the modern XAI family, e.g., Shapley additive explanation (SHAP), local interpretable model-agnostic explanations (LIME), Gradient-weighted Class Activation Mapping (Grad-CAM), Individual Conditional Expectation (ICE) probabilistic XAI, and attention-augmented neural architectures became prevalent in forecasting tasks, enabling methodologically consistent comparison across studies.

2.3. Inclusion and Exclusion Criteria

Such articles were accepted for consideration that:

• contain a description of AI models applied to hydrological forecasting problems;
• apply or analyze explainability methods (XAI)—SHAP, LIME, Grad-CAM, ICE, etc.;
• contain both qualitative and quantitative verification of forecasts, e.g., root mean squared error (RMSE), mean absolute error (MAE), and interpretability metrics (if available);
• are published in peer-reviewed journals (including preprints).

The following articles were filtered out:

• those without containing descriptions of AI models;
• those without any explicit connection with the tasks of forecasting hydrological quantities;
• those that do not use XAI or do not attempt to interpret the model.

Additionally, the review uses publications that reveal the essence of hydrological forecasting methods and their development.

We recorded counts at each stage (identification, screening, eligibility, and inclusion) and the reason for each eligibility exclusion. These are summarized in Figure 1.

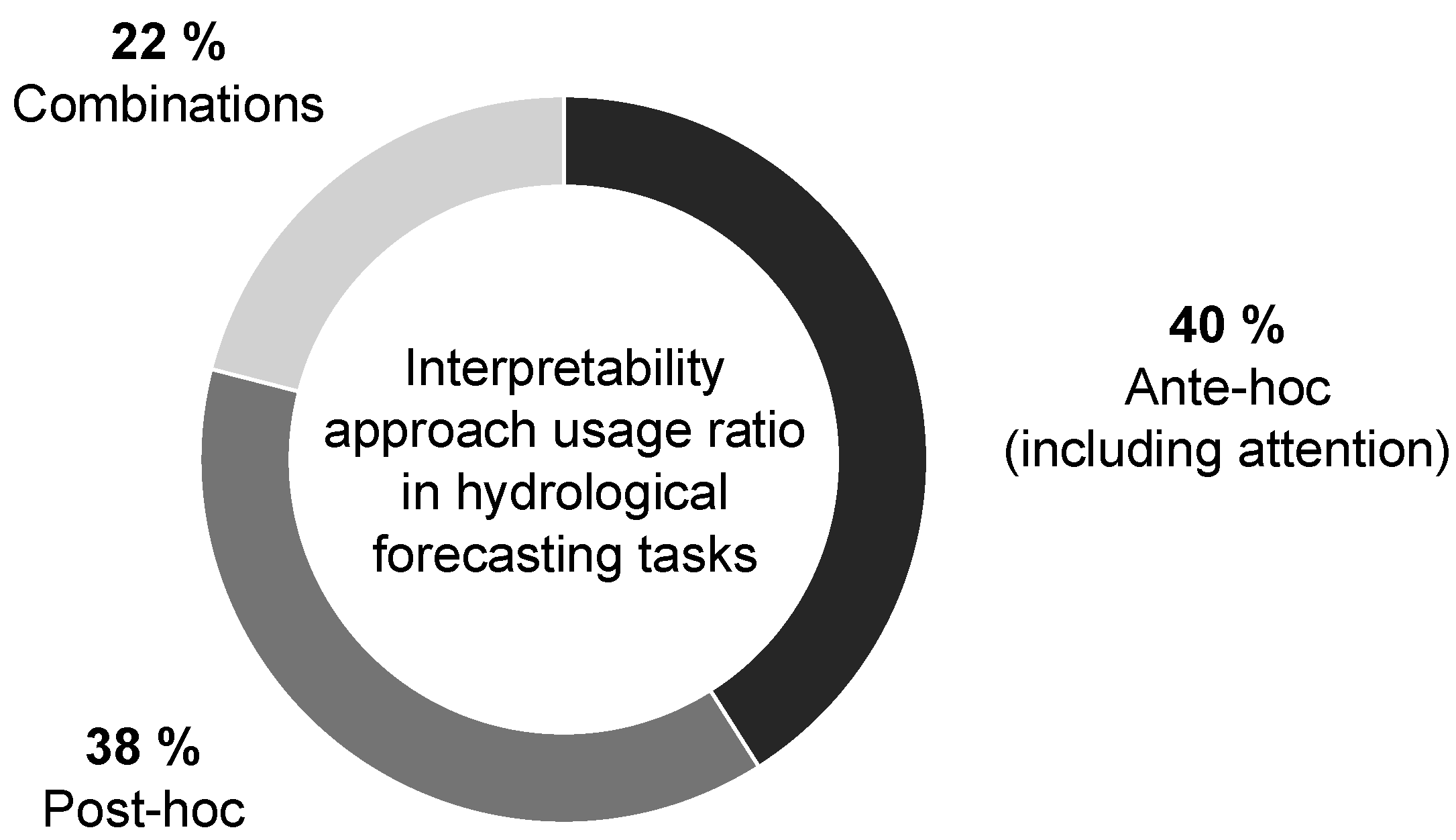
2.4. Selection Results

Following PRISMA 2020, we identified 154 records across databases; after removing 5 duplicates, 149 records were screened by title/abstract. Of these, 52 were excluded at screening. Ninety-seven full-text reports were assessed for eligibility; none were unretrievable. Fourteen reports were excluded at the eligibility stage (reason recorded as “no AI/XAI forecasting model representation”), leaving 83 studies included in the review. The following explains the numbers in detail (Figure 1):

• 29 use post-hoc XAI methods (SHAP, LIME, Grad-CAM, and ICE);
• 31 use ante-hoc approaches, mainly attention mechanisms;
• 23 combine both approaches.
• The most frequently used AI models include the following:

  ◦

  LSTM and GRU for working with time series;

  ◦

  CNN and Transformers (including the attention);

  ◦

  XGBoost, Random Forest, and other ensembles;

  ◦

  hybrid architectures combining wavelet transforms, filtering, and neural networks.

The key articles among those analyzed in this review, devoted to the application of XAI in hydrological forecasting problems, are presented in

Table 1. The most representative articles about XAI applications in the current review.

Ref.	Authors	Title	Explainable Approach
[31]	Hu H., Yang K., Yang Z.	Adaptive Reservoir Inflow Forecasting Using Variational Mode Decomposition and Long Short-Term Memory	Amplitude–frequency decomposition based on attention coefficients
[32]	Lei K. Chang, J., Long R., Wang Y., Zhang H.	Cascade Hydropower Station Risk Operation under the Condition of Inflow Uncertainty	Confidence intervals of the forecast based on the method of constructing scenario trees
[33]	Zhou F., Wang Z., Chen D., Zhang K.	Reservoir Inflow Forecasting in Hydropower Industry: A Generative Flow-Based Approach	Confidence intervals with probability distribution of attention coefficients
[34]	Wang S., Peng H., Hu Q., Jiang M.	Analysis of Runoff Generation Driving Factors Based on Hydrological Model and Interpretable Machine Learning Method	SHAP values for the XGBoost model
[35]	Yang R., Wu J., Gan G., Guo R., Zhang H.	Combining Physical Hydrological Model with Explainable Machine Learning Methods to Enhance Water Balance Assessment in Glacial River Basins	SHAP values for the hybrid physically supported model
[36]	Mushtaq H., Akhtar T., Hashmi M.Z.U.R., Masood A., Saeed F.	Hydrologic Interpretation of Machine Learning Models for 10-Daily Streamflow Simulation in Climate Sensitive Upper Indus Catchments	SHAP values for detailing the contribution of features to results
[37]	Xiang X., Guo S., Cui Z., Wang L., Xu C.-Y.	Improving Flood Forecast Accuracy Based on Explainable Convolutional Neural Network by Grad-CAM Method	Grad-CAM for visualizing the importance of CNN inputs
[38]	Xu Y., Lin K., Hu C., Wang S., Wu Q., Zhang J., Xiao M., Luo Y.	Interpretable Machine Learning on Large Samples for Supporting Runoff Estimation in Ungauged Basins	Heatmaps based on SHAP values for the XGBoost model

.

2.5. Limitation

We did not produce cross-study accuracy or interpretability tables because the included studies differ in targets, lead times, basins/climates, inputs, modeling choices, and reported metrics, making aggregation non-comparable. For interpretability, no standardized “score” is consistently reported; explanation outcomes are configuration- and context-dependent. Our synthesis, therefore, emphasizes taxonomy, use-cases, and reporting guidelines rather than head-to-head rankings.

3. Key Characteristics of Inflow Forecasting Task

Forecasting of water inflow to reservoirs and other water bodies is a task of modeling dynamic hydrological processes based on temporal and spatially distributed data. Considering modern hydropower, water management, and risk management, the accuracy and timeliness of such forecasts are critical. They are meant for prompt regulation of water levels, optimization of power generation, and preventing emergencies.

3.1. Types of Forecasts and Forecasting Horizons

Types of forecasts and forecasting horizons:

• Short-term ones refer to time periods from a few hours to a few days. They are essential for warning and managing emergency situations, such as floods and high water, allowing for rapid protective measures to be taken. These forecasts are also useful for run-of-the-river hydroelectricity regarding the compensation of energy fluctuations in national energy systems.
• Medium-term ones cover a time interval from a few weeks to a month. They are useful for optimizing the operation of irrigation and electricity production.
• Long-term ones extend over a period of months or even years. These forecasts are essential for strategic water resources planning, assessing the storage capacity of reservoirs, and for major investment decisions in hydrotechnical infrastructure.

3.2. Complexity and Multidimensionality of Input Data

The target variable, water inflow, depends on many interrelated factors. These can be grouped into meteorological, hydrological, geophysical, geospatial, and climatic categories. Meteorological data include precipitation, temperature, pressure, humidity, and solar radiation. Hydrological data include retrospective values of water level, discharge, snow cover, and runoff delay. Geophysical and geographical data include relief, soil type, vegetation, area, and structure of the water basin. Climate data include El Niño-Southern Oscillation (ENSO), North Atlantic Oscillation (NAO), and Arctic Oscillation (AO) data, seasonal patterns.

The data come from different sources:

• Hydrometeorological stations and posts (heterogeneous in density and frequency of observations);
• Numerical Weather Prediction (NWP) models;
• Satellite remote sensing data;
• Manual measurements and historical series (archives of hydrometeorological services and energy companies).

3.3. Multiscale Nature of the Task

The complexity of the model is caused, among other things, by the multiscale nature of the forecasting task. The multiscale nature of the task of forecasting hydrological variables is manifested:

• in time (from minute and hourly intervals to seasonal cycles);
• in space (from observation points to basins with an area of thousands of km²);
• in data structure (from scalar time series to graphs and spatiotemporal matrices).

This places special demands on the model architecture, such as support for temporal memory (LSTM, gated recurrent units—GRUs), working with spatial structure (CNN, graph convolution network—GCN, attention over map), robustness to sparse and noisy data, and the ability to adapt the model to the characteristics of new territories without retraining.

3.4. Data-Related Issues

Climate change influences the stationarity of time series and changes in land use but also different water abstractions, as well as the occurrence of changes in watershed management schemes through changes in water uses, cause model parameters to change and become difficult to estimate.

Additional features in the problems of forecasting hydrological variables are caused by the features of the initial data:

• Sparseness of the observation network (low spatial coverage of posts and stations);
• Mixed data format (combination of numerical models, retrospectives, manual measurements, and images);
• Seasonal instability of values (snow reserves, floods, evaporation, and soil freezing);
• Lack of direct observation of key parameters (soil moisture, snow cover structure).

To compensate for the lack of data, the following measures are used:

• Indirect indicators (previous runoff as an indicator of humidity);
• Wavelet decompositions of time series;
• Methods of aggregation and reconstruction of missing values.

3.5. Implications for XAI

This problem structure emphasizes the need for model explainability. It is impossible to interpret a forecast without understanding the feature importances in each season and region. Engineers and operators must trust the model in conditions where data are incomplete or if it changes in real time. XAI tools must take into account seasonality, geographic specificity, and hydropower plant operating constraints. Therefore, XAI tasks in the context of inflow forecasting include not only the assessment of feature contributions but also:

• Identifying critical factors in small data environments;
• Explanation of transient regimes (e.g., sudden changes in precipitation);
• Construction of confidence intervals and scenario trees for risk assessment.

Figure 2 shows a common pipeline for hydrological variables forecasting using AI models with XAI.

The studies devoted to inflow forecasting emphasize the importance of using historical values of flows, levels, and discharges in rivers that form the catchment area of the forecasted reservoir. Another factor that has a significant impact on the accuracy of forecasts is the consideration of snow storage parameters as input features of the forecast models.

In studies [39,40,41,42,43,44], inflow forecasting is performed using the input parameters described above in addition to the results of Numerical Weather Prediction models. The forecast variable and input parameters used to obtain the forecast in the studies considered are presented in

Table 2. Input parameters for inflow prediction.

Reference	Target Variable	Input Parameters
[39]	Inflow into the reservoir (1–7 days)	Historical inflow values; decomposed time series components
[40]	Inflow to the reservoir (online)	Historical inflow values, precipitation, and coded inflow extremes
[41]	Inflow into the reservoir (1 day)	Precipitation and temperature forecast data from The European Centre for Medium-Range Weather Forecasts (ECMWF) and National Centers for Environmental Prediction (NCEP) models, snow storage, and soil moisture parameters
[42]	Inflow into the reservoir (1 month)	Climate and meteorological data from ENSO and AO, solar flux data, and historical inflow values
[43]	Inflow into the reservoir (1 month)	Historical inflow values, climate and meteorological data from ENSO, Southern Oscillation Index (SOI), and DMI
[44]	Inflow into the reservoir (1 day)	Climate and meteorological data from ENSO, AO, and NAO; precipitation; lagged variables

.

Since historical meteorological and hydrological data are among the main input parameters for inflow forecasting models, the inflow forecasting problem faces data source-related difficulties. The spatial sparseness of the locations of meteorological stations and hydrological posts recording the parameters required for forecasting makes it difficult to process such data. Another challenge is the application of such data to the targeted areas, which may be remote from existing meteorological and hydrological posts. National databases obtained by averaging the results of various numerical weather forecasting models and hydrological parameters provide data on a coordinate grid with a very wide step of about 0.5–1.0 geographic degrees or more.

To obtain the necessary data in the territory under consideration, the following approaches are used:

• Installation of additional meteorological and hydrological posts in the territories under consideration;
• Approximation of data obtained from functioning meteorological stations and hydroposts [45,46];
• Use of Earth remote sensing data (satellite images) [47,48,49].

In addition to the difficulties in obtaining initial data of the required spatial and temporal resolution for the territories under consideration, there is another problem. This problem is related to the dependence of the predicted hydrological parameters on seasonal and regional factors.

The influence of seasonal and regional factors on the amount of inflow can be traced using the example of steppe territories. In this area, the preceding autumn moisture, the nature of snowmelt, and precipitation during the snowmelt period play a major role. Additionally, for such territories, the moisture saturation of the soil is an important parameter, since a larger volume of precipitation can be absorbed into the soil. For mountainous territories, a sharp increase in the accuracy of the forecast can be achieved by taking into account the characteristics of the snow cover. The reason is that in rocky terrain, the largest water reserves are localized in the snow cover [50].

Obtaining direct data on snow cover characteristics or soil moisture in real time is extremely difficult. It requires installing a large number of additional sensors directly in the area under consideration. However, the use of AI models together with the use of data indirectly describing the above parameters allows increasing the accuracy of forecasts. Studies [51,52] show the possibility of considering soil moisture through the amount of previous runoff, precipitation (snow/rain) when training the LSTM model.

The use of AI-based models to account for data that are extremely difficult to obtain directly improves the accuracy of inflow forecasting. The studies analyzed in the review [13] and the studies presented above, including [39,40,41,42,43,44], highlight the most used AI models for inflow forecasting. So, the most common LSTM and hybrid approaches combine different ANNs with heuristic algorithms and wavelet transform.

Despite the high accuracy of the forecast results obtained using AI methods, they are poorly substantiated and often cause mistrust and bias from the end user’s side. Increasing trust in the intermediate and final results of AI models is associated with the development of explainability and transparency at all stages of the functioning of the models used.

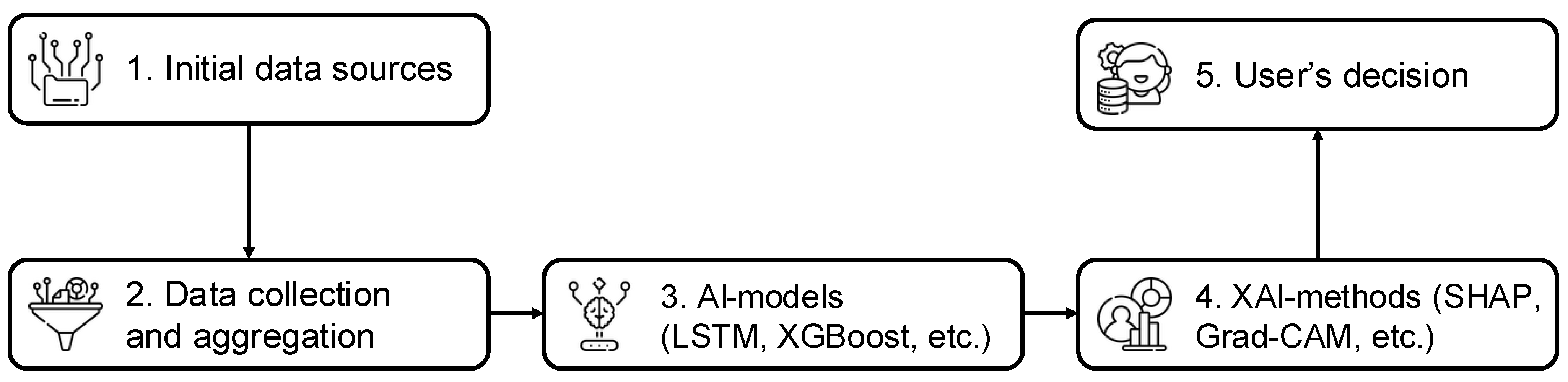
4. Methods of Explainability of Artificial Intelligence

XAI methods in tasks of water inflow forecasting perform a key function: They ensure transparency of decision-making by the AI model. Thereby, they increase the confidence in the forecast results on the part of engineers, dispatchers, and operators of water management systems.

4.1. Classification of Interpretability Approaches

We distinguish two families:

(i)

Post-hoc XAI: external or model-agnostic methods applied to an already trained predictor to explain its behavior (e.g., SHAP, LIME, ICE, anchors, counterfactuals, and Grad-CAM);

(ii)

Ante-hoc interpretability aids: intrinsic signals or transparent models whose parameters/structure are interpretable by design (e.g., attention mechanisms, monotonic constraints, linear/logistic models, shallow trees, and GAM-style additivity). In this paper, we use the term “XAI” strictly for post-hoc methods; attention and other intrinsic signals are reported as ante-hoc aids that may be corroborated by XAI.

Classification of XAI methods is presented in

Table 3. Post-hoc XAI and ante-hoc interpretability methods classification.

XAI Method	Type	Explanation Tool
SHAP	Post-hoc	Individual quantitative contribution of each feature to the result
LIME	Post-hoc	Approximation of the forecast by a simple interpretable model
ICE	Post-hoc	Feature–result curves
Anchors	Post-hoc	The rules and conditions that determine the outcome
Counterfactual explanations	Post-hoc	Recommendations for changing the values of attributes
Attention mechanisms *	Ante-hoc	Feature importances based on weight coefficients

* Attention weights are intrinsic importance signals; they do not evaluate model behavior externally. We therefore report them as ante-hoc aids and recommend corroboration by post-hoc XAI.

.

4.2. Ante-Hoc Approaches

Some of the models do not require the use of methods meant to improve interpretability (transparency, explainability). For example, linear and logistic regression models, shallow decision trees, and their ensembles are easily interpretable by their nature. And the user can evaluate the validity and rationale of the outputs by repeating the steps of the algorithm independently. However, to explain the results of more complex models, such as ensembles of deep decision trees and various artificial neural networks, special methods for interpreting the results are required.

Attention Mechanisms

Another method for determining the feature importances used in AI models, which is mainly used to explain the results of artificial neural networks, is called attention mechanisms. Attention mechanisms are model-intrinsic signals that highlight inputs the network focuses on; they are not XAI in the post-hoc sense. Their interpretive value should be validated by external (post-hoc) methods when used for hydrological reasoning. However, some studies [53,54,55,56] cite the results of implementing attention mechanisms as an example of increasing the interpretability of results obtained using artificial neural networks.

Attention mechanisms for artificial neural networks represent a tool for selecting significant features. They provide weights that reflect the degree of significance of the model inputs for its outputs in terms of specific instances of the original data. One example of using attention mechanisms for artificial neural networks is transformers. Transformers are a specialized architecture of artificial neural networks based on attention mechanisms that do not contain convolutions and recurrent layers. The use of transformers has provided significant progress in the performance of neural network models when processing long sequences (time series, text).

In the study [57], the query, key, and value matrices are used to determine the attention coefficients of the model for inflow forecasting:

$$Att\left(Q,K,V\right)=Soft \max \left({\displaystyle \frac{Q{K}^T}{\sqrt{d_{att}}}}\right)\cdot V,$$

(1)

where the scaling of attention mechanisms on values V is based on the relationships between keys K and queries Q. Here, V represents the output of a specific variable, such as flow, while K represents the output of an interrelated variable, such as rainfall. Similarly, Q represents the output of the task-shared module, which combines the outputs of a single variable and passes them into the feedforward neural network (FNN).

4.3. Post-Hoc Methods

Often, methods of a posteriori explanation are used to explain the results obtained using complex artificial intelligence models. Such models allow to explain how an already learned model makes decisions. A post-hoc method of interpretability of AI models is divided into two groups: methods of global interpretation and methods of local interpretation.

Methods of global interpretation of AI models are aimed at a general explanation of the model results. Most often, methods of global interpretation present an explanation of the results in the form of probability distributions, confidence intervals, most probable values, etc. Among the methods of global interpretation, the following are distinguished [58,59]:

• quantitative assessment of the joint influence of features on the model results (H-statistic);
• decomposition of a complex predictive model function into simpler components (functional decomposition);
• assessment of the influence of a feature on the results of a model when changing the order of the features used (permutation feature importance);
• using simpler and more interpretable models to predict the results of the original model (global surrogate models).

Local Interpretation Methods

Local interpretation methods of AI models are aimed at explaining the results of the model obtained for a specific instance of initial data. Thus, local interpretation methods provide an analysis of the performance of the predictive model in a particular case, without offering a general explanation of the model’s performance. Among the local interpretation methods, the following are distinguished [59]:

• Local Interpretable Model-Agnostic Explanation;
• SHapley Additive exPlanations;
• Scoped rules (anchors);
• Individual conditional expectation curves;
• Counterfactual explanations.

Such methods as scoped rules (anchors), individual conditional expectation curves, and counterfactual explanations present information about the model solution in the form of defining rules, conditions, or key values. The SHAP and LIME methods describe the solutions obtained by the model in the form of a quantitative contribution of each of the considered features or their combination.

The SHAP method is based on game theory. For each model, it calculates the contribution of each feature to the prediction, taking into account all possible combinations of features. SHAP explanations are described mathematically as follows [60,61,62,63]:

For a predictor $f:R^M\to R$ and an instance x, the Shapley value of feature i is as follows:

$$\begin{array}{c}{\varphi }_i\left(x\right)={\displaystyle \sum _{S\subseteq F\setminus \left\{i\right\}}}{\displaystyle \frac{\left|S\right|!\hspace{0.17em}\left(M-\left|S\right|-1\right)!}{M!}}\left(f_x\left(S\cup \left\{i\right\}\right)-f_x\left(S\right)\right),\end{array}$$

(2)

where M is the number of features; S is the subset not containing i; $f_x\left(S\right)=\left[f\left(X\right)∣X_S=x_S\right]$ is the model output averaged over a background dataset for features not in S; x_S is the values of x on S; ${\varphi }_i\left(x\right)$ is the contribution of feature i at x.

The additive form is $f\left(x\right)={\varphi }_0+{\sum }_{i=1}^M{\varphi }_i\left(x\right)$, where ${\varphi }_0=E\left[f\left(X\right)\right]$ is the baseline. In practice, KernelSHAP estimates $f_x\left(S\right)$ by weighted sampling over a background set, while TreeSHAP computes exact values for tree ensembles.

The LIME method approximates a “black” model in the neighborhood of prediction using a simple model (e.g., linear regression). Mathematical description of the LIME method for creating linear models that approximate the original model [59,64,65,66] is the following:

LIME fits an interpretable surrogate g in around x by

$$\begin{array}{c}{g}^{*}\left(x\right)=\arg \underset{g\in \mathcal{G}}{\min }{\displaystyle \sum _{z\in Z}}{\pi }_x\left(z\right)\hspace{0.17em}l\left(f\left(z\right),g\left(z\right)\right)+\mathsf{\Omega }\left(g\right)\end{array}$$

(3)

where Z is a set of perturbed samples near x (neighborhood samples); ${\pi }_x\left(z\right)$ is a locality kernel (e.g., $\mathit{exp}\left[-D{\left(x,z\right)}^2/{\sigma }^2\right]$); $l$ is a pointwise loss (e.g., squared error); $\mathsf{\Omega }\left(g\right)$ is penalizes model complexity (e.g., sparsity); $\mathcal{G}$ is a class of interpretable models; $D\left(\cdot ,\cdot \right)$ distance; $\mathsf{\sigma }$ locality width; $\mathsf{\Omega }$ complexity penalty; $\theta$ surrogate parameters. For a sparse linear surrogate $g\left(z\right)={\theta }_0+{\sum }_{j\in S}{\theta }_j{z}_j$, the explanation is the coefficient vector $\theta$ on the locally important features S.

4.4. Advantages and Disadvantages of XAI Methods

The considered methods for interpreting the results of AI-based models have both positive and negative aspects that limit their applicability.

The main advantage of ante-hoc interpretable AI models is that they are completely transparent and do not require explanations. However, such models are less accurate. These models are often used as surrogate models to explain complex architectures.

Attention mechanisms (in LSTM, Transformers, and Seq2Seq) allow the model to “focus” on the most relevant parts of the input signal. The main advantage of attention mechanisms is the embeddedness of this interpretation method in the interpreted model. Thus, when using attention mechanisms, the need for additional external algorithms and models to explain the result of the original model is reduced. However, the disadvantages of attention mechanisms are high sensitivity to changes in the original data, assessment of the importance of only individual features without taking into account the effect of the combined influence of several features, and dependence on the model used. Attention weights do not always correlate with the “understanding” of the model; reinterpretation is possible.

The ICE method provides clear dependencies of the model results on the changes in feature values. These dependencies are useful in identifying heterogeneous relationships between features and results. However, this method does not allow for analyzing the influence of more than one feature at a time. Constructing multiple curves leads to overload and a decrease in the informativeness of the graph.

Considering hydrological forecasts, the ICE method is applied to explain and assess the impact of water retention or evaporation.

Applying the LIME method allows achieving a high understanding of the results by using easily interpretable models to explain the model. However, this method has difficulties with the instability of explanations and their incorrectness when the complexity of the model is incorrectly determined or incorrectly configured.

Application area of LIME for explaining hydrological forecasts: rapid interpretation of the causes of anomalous forecasts, such as sudden precipitation events

There are two main advantages of the SHAP method: first is the ability to determine the distributed contribution of all features to the model result; second is the ability to compare explanations of the model results on different subsets of data. The disadvantages of the SHAP method include high computing power requirements, the need for access to source data to explain the model results, and the high degree of influence of irrelevant data on the results of the explanation.

The scope of SHAP for explaining hydrological forecasts: analysis of the influence of precipitation, temperature, and snow storage on the inflow in different seasons.

For practitioner access,

Table 4. Practitioner-oriented synthesis by task, model family, and interpretability tool.

Hydrological Task (Typical Horizon)	Typical Model Families Seen in the Corpus	Interpretability Tool Used in Practice	Typical Inputs Noted	Practitioner Takeaway (Recurring Across Studies)
Reservoir inflow (1–10 days; 2–4 weeks)	LSTM/GRU; hybrids (e.g., VMD-LSTM); ensembles; Transformers in some cases	SHAP, ICE; probabilistic XAI (scenario trees, intervals); attention as ante-hoc aid	Lagged inflow/streamflow; precipitation; temperature; snow proxies; sometimes climate indices	Precipitation and lagged flow dominate short-horizon drivers; snow/temperature thresholds matter in nival/glacial regimes; confidence intervals useful for risk-aware operation.
Streamflow/runoff	XGBoost/Random Forest; LSTM/GRU; Transformers (emerging)	SHAP (local/global summaries); occasional Grad-CAM for spatial CNN inputs	Precipitation, evaporation; land use/slope; seasonal factors	Climate/season stratification changes driver ranks; SHAP often confirms hydrologic plausibility (e.g., slope–precipitation synergies, temperature thresholds).
Water level	CNN; CNN-LSTM-attention; Seq2Seq with attention	Grad-CAM (spatial focus); attention (ante-hoc)	Precipitation; upstream inflow; evaporation; spatial tiles	Spatial hot-spots align with storm periods and contributing areas; combine attention with post-hoc checks for robustness.

summarizes task–model–XAI pairings and key takeaways;

Table 5. XAI methods at a glance for hydrological forecasting.

Method	Works Best with	Outputs	Common Pitfalls
SHAP	Tree ensembles; tabular time series; also used with DL via Kernel/Deep variants	Local and aggregated feature attributions; seasonal/segment analysis	Background set sensitivity; compute cost
LIME	Local diagnosis around single predictions	Sparse local surrogate with feature weights	Kernel width sensitivity; locality mismatch
ICE	Monotone/threshold behavior checks	Feature–response curves by instance/aggregate	One-feature-at-a-time; crowding of curves
Grad-CAM	CNNs on spatial inputs	Saliency maps over input space	Layer/variant dependence

provides method-level guidance and minimal reporting fields. These tables synthesize our existing results without implying cross-paper performance rankings.

5. Explainability and Trust in Inflow Forecasting Problems Using AI Models

The use of AI models in systems of critical industries, such as inflow forecasting in hydrology, is associated with a number of risks and vulnerabilities:

• Retraining models under data limitations;
• Leak of “future” data;
• Use of incorrect (unfair) dependencies;
• Uncontrolled data generalization.

One of the main risks of using AI is the risk of overfitting predictive models. Overfitting occurs when using small amounts of data in combination with simple AI architectures, such as an LSTM without regularization. In this case, the implemented model remembers the data used for training too accurately, losing its generalization ability, which leads to a decrease in accuracy when using test data. Also, when training predictive models incorrectly, data from the test sample can be partially used at the model training stage. In this case, the model “peeps” and, accordingly, overestimates the results of the accuracy assessment metrics. Problems associated with overfitting and “peeping” when training an LSTM model with a large number of parameters under limited data conditions are considered in the study [67].

The use of incorrect dependencies leads to the formation of model forecasts based on random or statistically unrelated dependencies, including physically unsubstantiated ones. Even though in such a case the forecast may be highly accurate, its substantiation and verification are impossible, which reduces confidence in the results. The study [68] reflects the importance of assessing the correctness of the dependencies between the input parameters and the predicted variable.

Unsupervised generalization occurs when pre-trained models are used in different conditions, such as applying an AI model to forecast the inflow of a water body located in another basin. The lack of adaptation of the model used to new conditions and data can lead to the formation of erroneous forecasts. The study [69] provides a methodology for using additional statistical descriptors to avoid incorrect generalization of dependencies of different water catchment basins.

To mitigate the above-described risks and vulnerabilities associated with the use of AI in the inflow forecasting tasks of hydrology, explainable artificial intelligence (XAI) methods are used. In studies devoted to the application of such methods [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81], XAI methods are understood as techniques that allow black-box models to reveal their internal logic using:

• Determining the contribution of each input parameter to the formation of the forecast;
• Accompanying each predicted value with a confidence interval.

Thus, the XAI methods presented in the analyzed studies can be divided into two groups: ante-hoc approaches and post-hoc approaches. Ante-hoc approaches include approaches related to the use of interpretable AI models, such as linear regression, shallow decision trees, and Bayesian models. Post-hoc approaches include approaches related to ontological matching of input parameters (SHAP, LIME, Grad-CAM, etc.).

A separate direction considered in the context of increasing the explainability of the results of AI models is the use of attention mechanisms in LSTM architectures.

Table 6. Application examples of feature importance evaluation methods for inflow prediction.

Reference	XAI Method	Explanation
[70]	LSTM attention mechanism	Assignment of different weighting coefficients expressing the influence of wavelet components on the forecast result at different time intervals
[71]	LSTM attention mechanism + binary masks for selecting input parameters depending on the season	Selection of input data to make a forecast based on the use of an attention mechanism. Additionally, the creation of binary masks for input parameters based on the importance of the contribution of features to the forecast
[72]	Spatial LSTM attention mechanism + temporal LSTM attention mechanism	An assessment based on a graph structure represents the topological relationships between the considered watershed points and is used to assess the contribution of a data source to the forecast result A temporal LSTM attention mechanism based on the outputs of the hidden layer of the model used to assess the influence of periodicity and seasonality
[73]	Spatial graph LSTM attention mechanism + temporal LSTM attention mechanism + DropEdge mechanism	The DropEdge mechanism used to limit overfitting and improve the generalization ability of the model. It removes part of the edges of the model graph during its training Assessment of the influence of periodicity and seasonality by means of a temporal LSTM attention mechanism based on the outputs of the hidden layer of the model
[74]	Dual attention mechanisms (temporal and features) + heatmap visualization	A temporal convolutional network with dual attention mechanisms used to estimate the contribution of each feature and time step Heat maps used to visualize the contribution.
[75]	Temporal LSTM attention mechanism, SHAP	Sensitivity analysis of selected “energy” features
[76]	Temporal–spatial LSTM attention mechanism	The analysis of the contribution of data from each sensor to the predicted value expressed by a matrix of weighting coefficients
[77]	Feature selection protocol (Relief F) + multi-objective optimization	A formed rating of the importance of geological and hydrological indicators
[78]	Variational mode decomposition (VMD), mode extraction	To justify the forecast, the user is provided with data on the influence of parameters in the form of an amplitude-frequency decomposition
[79]	Confidence intervals of the forecast	The method of constructing scenario trees used to determine the confidence intervals of the forecast
[80]	Temporal LSTM attention mechanism with probability distribution construction, confidence intervals	Estimated probability distribution of the hidden layer output for different time intervals and the given forecast with confidence intervals for risk assessment.
[81]	Rolling-feedback approach	Step-by-step adaptation of the forecast performed, taking into account previous and current inflow values
[82]	Quartile regression, introduction of forecasting rules	The data sample divided into “normal” and “extreme” conditions, on the basis of which clear rules for explaining the forecast are formed
[83]	Multi-head attention mechanism	Local features of the data taken into account when extracting time features of the input parameters
[84]	Seq2Seq attention mechanism, wavelet transform	The Attention layer receives the decoder states and all the encoder states as input, then the alignment layer determines the relationship between the input and output parameters

presents examples of the application of methods for assessing the importance of the features used in problems of inflow forecasting in hydrology.

Most modern studies aimed at forecasting inflow and other hydrological quantities focus on ante-hoc methods and attention mechanisms [33,70,71,72,73,74,75,76,80,81]. The attention family remains the most popular ante-hoc tool. Studies include various methods for embedding attention mechanisms into forecast models (including the use of graph structures and the combination of temporal and spatial attention mechanisms).

The use of post-hoc models in their pure form to improve the interpretability of forecasts of hydrological variables is considered in studies [34,35,36,37,38,57,82,83].

The authors of [84] used SHAP to assess the contribution of various meteorological factors to changes in water quality in the considered reservoirs. Specifically, SHAP is used to interpret the gradient boosting model, which uses time series of temperature, humidity, precipitation, and water level as input data. As a result of applying SHAP, the authors provided average numerical estimates reflecting the influence of the parameters on the forecast result of the target variable. A similar approach is presented in [82]. Here, the authors used averaged SHAP values to determine the feature importances in the XGBoost model to forecast excess water levels in reservoirs and flooding of adjacent territories.

The main drawback of these studies is that the given significance estimates themselves do not help to interpret the forecast. They are used only to exclude insignificant features from consideration. The studies do not provide an analysis of the forecast results for specific data, indicating the individual contribution of certain features to the final result.

The study [35] presented the results of applying SHAP to interpret water balance forecasts using various approaches combining physical and black-box models. The authors of the study presented the results of assessing the contribution of features using SHAP for each of the considered features at each point of the test data set. In addition to the SHAP values for each point of the test data set, the authors provided average estimates of the SHAP values for each feature within four different models (ANN, LSTM, Random Forest, and XGBoost). Also, to obtain more detailed explanations of the forecast results, the authors considered the forecast errors. Additionally, they analyzed them using the SHAP values, dividing the data set into four quartiles. Within each quartile, the influence of each feature on the increase and decrease in the forecast error relative to the median error was determined. The study draws conclusions about the contribution of features to the forecast results and the magnitude of the forecast error, broken down by quartiles.

In [34], SHAP is used to interpret river runoff forecasts using SWAT and XGBoost models. The authors presented the results of SHAP values for each of the features used in the model, including average values. Based on the analysis of SHAP values, it was concluded that there are characteristic threshold values for the slope of the territory, temperature, and solar radiation that determine the forecast values of the inflow calculated by the model. Also, the analysis of the obtained SHAP values helped to identify synergies between groups of parameters for different local basins:

• relationship between the precipitation volume and slope of territories;
• relationship between the type of land use, housing density, and precipitation volumes.

The authors of [37] demonstrated the results of using Grad-CAM. It is meant to visualize the importance of spatial features used in a model for predicting the water level in a reservoir with the help of a CNN. Based on the results of the analysis, scatter diagrams of the significance of the parameters precipitation, evaporation, and inflow are presented. The authors also analyzed changes in the feature importances over several time intervals of forecasts for 8 variations of the forecast model. Based on the results of the analysis, a conclusion was made about the greatest contribution of the parameters precipitation and inflow discharge, regardless of the type of water level increase.

In [38], SHAP values are analyzed to interpret river runoff estimates using the XGBoost model in unexplored areas. Based on the SHAP values calculated for a number of features, a heat map is formed. It determines the average contribution of features to river runoff level estimates for river basins in tropical, arid, temperate, cold, and polar climates. The most significant features for the interpreted models are precipitation and evaporation (for tropical, arid, and temperate climates), snow reserves, and solid precipitation (for cold and polar climates). The obtained explanations of the model results confirm its physicality and adequacy in the problem of river runoff value estimation.

The use of ICE together with SHAP and LIME for interpreting the results of snowmelt-based river flow assessment models is described in [83]. When analyzing the constructed PD and ICE graphs, it was determined that the accounting for changes in individual parameters of the models is adequate. Constructed on the basis of RandomForest, it coincides with the hydrological dependencies between precipitation, snow storage, and river flow in mountainous areas. SHAP and LIME were also used for a detailed explanation of the model results on the time interval corresponding to the drought period. Using SHAP, the features that make the greatest contribution to the model results were determined. Then, based on the most significant feature, LIME prediction curves were constructed for each model. Based on this multi-stage analysis, the authors determined that certain features explain low values of river flow assessment in dry months. Namely, lower values of the predictor–response relationship level in relation to the parameters identified as the most significant according to the SHAP values.

Another example of using SHAP values to explain the results of the XGBoost model for simulating a river flow in India is presented in [36]. To interpret the results of the developed model, the authors detailed the contribution of each feature to the final result for each test data point. The distribution of SHAP values is also considered to estimate the average contribution of features depending on seasonality (the month under examination). The proposed approach allowed the authors of the study to determine that there is an obvious temperature threshold (the critical threshold for snowmelt), which has a significant impact on the model results. This impact is especially strong for the minimum temperature during runoff formation from glaciers and snow storage in the Indus and Chenab basins.

Post-hoc explanations of the results of AI models in the reviewed studies are presented mostly by the SHAP method [34,35,36,38,75,77,84]. Some studies provide examples of using Grad-CAM, ICE, and LIME [35,83], including in combination with SHAP. The probabilistic explanation of forecasts approach (probabilistic XAI) is also used. Within the framework of it, operators are provided with forecast confidence intervals, probability, and spectral distributions of input parameters. It is especially important for risk management [31,32,79]. The distribution of the XAI methods used in the articles reviewed is presented in Figure 3.

At present, there is no unified system for assessing the interpretability of forecast models. Each of the described approaches to explaining the results of forecast models uses its own indicators. Thus, only qualitative assessments of model explainability are currently feasible, but not a quantitative comparison of different methods for explaining results.

Figure 4 presents the correspondence between the applied XAI methods, the architectures of the models used for prediction, and the objectives of the interpretation results. All the above-mentioned is based on the analyzed publications.

6. Directions of Further Development

Analysis of modern publications shows active implementation of XAI tools in hydrological variable forecasting models. However, the wide application of XAI in critical engineering problems is still limited by a number of conceptual and practical barriers. Below are the key areas requiring further scientific development.

6.1. Developing Unified Interpretability Metrics

Nowadays, there exist different methods and approaches to interpreting the results of artificial intelligence forecasting models, and they are being developed even more. However, there is no unified approach to qualitative assessment and explanation of the results. The studies use various authors’ metrics for assessing the influence of features and initial data on the forecast results, visualization methods, and even when the same interpretation methods are used. Due to this, a complete and objective comparison of the research results is almost impossible. Therefore, a relevant and recommended direction for further research is the development of a number of unified metrics and visualization methods. All of them should be useful for assessing the interpretability of model forecasts, similar to the metrics for assessing the accuracy of forecasts (RMSE, MAE, and R2).

The following metrics can be considered as a relevant set of metrics for a unified assessment of interpretability:

• Stability—stability of explanations with small input changes;
• Fidelity—the degree of correspondence between the explanation and the actual solution of the model;
• Consistency—similarity of explanations for models with the same behavior;
• Sparsity—compactness of explanation without loss of meaning.

Such metrics could form the basis of XAI benchmark platforms for hydrology.

Once these criteria (stability, fidelity, consistency, and sparsity) are reported consistently on common datasets and protocols, quantitative comparisons will become feasible; until then, cross-paper tables risk conflating incomparable settings.

In operations—stability maps to robustness under sparse/noisy data; fidelity to trustworthy local diagnosis; consistency to basin transfer; sparsity to real-time feasibility—we recommend reporting these alongside RMSE/MAE.

6.2. Post-Hoc and Ante-Hoc Sharing

Most studies observe the use of either attention mechanisms embedded in the model architecture (ante-hoc) or additional external methods such as SHAP or LIME (post-hoc). Combining two approaches potentially improves the accuracy and explainability of forecast models. In particular, the introduction of post-hoc explanations on top of already interpreted attention mechanisms can provide a deeper understanding of the contribution of various factors.

The following combinations of ante-hoc and post-hoc methods might be considered:

• Use of attention mechanisms as a primary interpretation of the feature importances for the model, followed by SHAP analysis to determine the individual contribution of each significant feature;
• Construction of surrogate models from attention-weighted input subsets;
• Interpretation of attention maps using ICE graphs or rules (anchors).

6.3. Adapting XAI to High-Dimensional Data

Forecasting of hydrological parameters is associated with features that have multidimensional spatial, temporal, and seasonal dependencies. In connection with these features, it is necessary to develop XAI methods capable of:

• identify synergistic features (joint influence);
• process graph structures and spatiotemporal data;
• interpret the outputs of models such as GCN, spatial–temporal LSTM, and transformers.

A number of reviewed studies presented approaches using graph structures and multi-level attention mechanisms. Further development of this direction is relevant and important for the tasks of forecasting hydrological variables.

6.4. Spatial and Seasonal Stability of XAI

In practice, we recommend season-wise and basin-transfer audits of SHAP/attention distributions with rank-stability reporting to document explanation robustness.

Along with the validation of forecast models, it is necessary to validate the models used to explain the forecast results. This is performed in order to assess the stability of the obtained forecast results. In the context of forecasting hydrological variables, it is necessary to validate not only different sets of initial data used in training and testing the model. Another important task is to conduct spatial validation, assessing the stability and adequacy of explanations when testing forecast models on data from different water basins. When adapting forecast models to new catchments and regions with different climatic features, the applied XAI methods should provide:

• XAI spatial validation methods;
• assessment of explanation transferability;
• analysis of the stability of attention/SHAP values by seasons and regions.

6.5. Physical Meaningfulness of Explanations

One of the main problems of artificial intelligence models in hydrology remains the lack of physical justification for their forecasts. It is necessary to integrate physical and hydrological patterns not only into the structure of forecast models. It is also necessary to use XAI methods that allow interpreting forecasts based on known hydrological patterns. Operational checks should include simple physics-aware tests (e.g., monotonic precipitation–inflow relations within wet seasons; snowmelt thresholds) to filter implausible explanations. Promising areas may include:

• development of physics-aware XAI that imposes constraints on acceptable explanations;
• integration of expert ontologies (for example, “if precipitation + snow reserve > threshold—forecast for level increase”);
• generating explanations in the form of rules or causal diagrams that are understandable to engineers.

6.6. Practical Implications

Table 7. Limitations, challenges, and implementation.

Limitation	Hydrological Challenge	Implementation
Stability of explanations under data perturbations (SHAP/LIME/attention).	Sparse/noisy gauges and changing input coverage	Bootstrap explanations; stratify SHAP/attention summaries by season and basin; report rank-correlation stability with small perturbations
Fidelity of local surrogates (LIME) and post-hoc additivity assumptions (SHAP)	Nonlinear, regime-dependent responses (snowmelt vs. rain)	Tune LIME locality kernel by regime; verify SHAP additivity with ICE spot-checks on key features and seasons; flag mismatches as potential model misuse
Consistency across models and basins	Transfer to new catchments/climates	Basin-transfer tests for explanations; compare attribution patterns for models with matched accuracy; report a consistency score across basins
Computational cost of explanations	Real-time or near-real-time operation	Use TreeSHAP for ensembles; pre-compute attributions on seasonal prototypes; cache top-k features; employ lightweight ICE for on-the-fly diagnostics; schedule full explanations offline
Lack of physical meaningfulness	Trustworthy operation decisions	Apply physics-aware constraints/ontologies (e.g., monotonic precipitation-to-inflow within regime) and reject explanations violating known hydrologic relations
Explanations ignore forecast uncertainty	Risk-aware reservoir operation	Pair explanations with predictive intervals/scenario trees; attribute drivers of interval width or exceedance risk (probabilistic XAI)

presents the limitations, challenges, and implementations for hydrological forecasting.

6.7. Accounting for Uncertainty and Confidence Intervals

The development of probabilistic XAI approaches that provide confidence intervals and scenario trees of forecasts allows for considering risks and increasing the sustainability of decisions. Probabilistic approaches and approaches that represent different forecast scenarios have already been presented in the studies reviewed. However, further research on their effectiveness and adequacy in critically important tasks of forecasting hydrological variables is still required.

Thus, forecasting models should not only predict inflows but also indicate how confident the model is in the forecast. The development of probabilistic XAI will allow:

• transmit forecasts with confidence intervals;
• assess risk based on interpretable factors;
• generate scenario trajectories that take into account the range of weather conditions and model uncertainty.

For decision support, explanations should accompany predictive intervals, indicating which drivers widen or shrink risk bounds relevant to spill or gate scheduling.

6.8. Semantic XAI Interfaces

In most of the reviewed studies, the interpretation of the forecast results is limited to numerical values of feature contributions or heat maps. However, to incorporate XAI into decision support systems (DSS), the following are necessary:

• visualization interfaces: heat maps, scenario trees, dynamics of contributions over time;
• semantic explanations: generating texts in an engineering style, using domain terms;
• integration with SCADA/ASUE: explanation of anomalies and support for decisions on the operational horizon.

Based on the conducted review, a number of directions for further consideration of the application of methods were formed. Their main idea is to interpret the results of artificial intelligence models in the problems of forecasting hydrological quantities.

6.9. Operational Applicability

By applicability to operations, we refer to explanation patterns that translate into plant and basin decisions: SHAP/ICE-based drivers for pre-release and flood warning, attention-based temporal focus for gate scheduling, and probabilistic XAI for confidence-aware operation. The included literature contains operationally framed examples, such as risk-aware cascade operation under inflow uncertainty, hydropower-industry inflow forecasting with industrial data, and dam-level forecasting relevant to HPP reservoir management; we cite these here to make the link explicit. Detailed plant-internal case studies are scarce in open sources due to confidentiality and safety-critical constraints.

7. Conclusions

This paper presents a review of 83 publications devoted to the application of explainable artificial intelligence (XAI) methods in hydrological forecasting. It classifies modern XAI approaches—both ante-hoc and post-hoc—and compares their use across various model architectures such as LSTM, CNN, XGBoost, and hybrid models. Moreover, their capabilities and limitations were analyzed, and finally, promising research directions in the field of XAI application in hydrological forecasting problems were formulated. Integration of XAI into engineering interfaces (DSS, SCADA) requires further development, which explains the limited number of fully documented industrial case studies in the open literature; our focus is to consolidate the method–decision mapping that enables such integration.

This review consolidates how explainable AI is being used in hydrological forecasting and what it can reliably tell operators and researchers.

Overarching insights:

• Post-hoc methods—especially SHAP for tabular time series and Grad-CAM for spatial features—currently dominate hydrological XAI; ante-hoc signals such as attention can aid interpretation but should be corroborated by post-hoc analysis.
• When scrutinized seasonally and by regime, explanations frequently align with hydrologic reasoning (e.g., precipitation/temperature drivers, snowmelt thresholds, lagged-flow memory), and they help diagnose model failure modes and data issues.
• XAI is most informative when embedded in the modeling workflow (feature design, sanity checks, and stress tests) rather than used as an after-the-fact visualization.

Key gaps:

• Lack of standardized protocols and shared benchmarks prevents fair cross-study comparisons of both accuracy and interpretability.
• Limited spatiotemporal validation (basin transfer, seasonal stratification, and climate-zone reporting) makes generalization uncertain.
• Physics-aware and causally consistent explanations remain rare; risks of spurious associations persist under data scarcity.
• Uncertainty-aware XAI (explaining predictive intervals and risk) is underreported; extremes and flood regimes are insufficiently probed.
• Multimodal fusion (in situ plus remote sensing) and human-in-the-loop evaluation for decision support are still immature.

Future directions:

• Benchmarks and protocols: curate public hydrological datasets with fixed train/validation/test splits and reporting checklists; evaluate XAI configurations on identical folds.
• Evaluation of explanations: report stability, fidelity, consistency, and sparsity alongside RMSE/MAE/NSE/KGE; analyze explanation drift across seasons and basins.
• Physics-aware XAI: encode monotonicity and energy-/mass-balance constraints; pair post-hoc methods with hybrid (theory-guided) models to enforce hydrologic plausibility.
• Spatiotemporal generalization: require basin-transfer tests, seasonal stratification, and climate-class breakdowns for explanations and accuracy.
• Uncertainty and risk: develop probabilistic XAI that attributes drivers of predictive intervals and tail risk relevant to operations (e.g., spill and exceedance probabilities).
• Decision-centric tooling: counterfactual and “what-if” analyses for reservoir operation policies; online monitoring of explanation drift in DSS/SCADA.
• Governance and deployment: document background datasets, XAI hyperparameters, and audit trails to meet traceability needs in water management and hydropower settings.

Overall, the integration of XAI into hydrological AI systems is essential to improve trust, decision quality, and resilience to uncertainty. The combination of XAI approaches aligned with physical processes and engineering expertise will be a key element of future intelligent water management systems.