Evolutionary Optimisation of Runge–Kutta Methods for Oscillatory Problems

Abstract

We propose a new strategy for constructing Runge–Kutta (RK) methods using evolutionary computation techniques, with the goal of directly minimising global error rather than relying on traditional local properties. This approach is general and applicable to a wide range of differential equations. To highlight its effectiveness, we apply it to two benchmark problems with oscillatory behaviour: the (2+1)-dimensional nonlinear Schrödinger equation and the N-Body problem (the latter over a long interval), which are central in quantum physics and astronomy, respectively. The method optimises four free coefficients of a sixth-order, eight-stage parametric RK scheme using a novel objective function that compares global error against a benchmark method over a range of step lengths. It overcomes challenges such as local minima in the free coefficient search space and the absence of derivative information of the objective function. Notably, the optimisation relaxes standard RK node bounds ($c_i\in [0,1]$), leading to improved local stability, lower truncation error, and superior global accuracy. The results also reveal structural patterns in coefficient values when targeting high eccentricity and non-sinusoidal problems, offering insight for future RK method design.

1. Introduction

Even though the class of Runge–Kutta (RK) methods has been well established and studied for decades, a complete determination of all their coefficient values based on their performance remains unresolved to this day, except for RK methods with a small number of stages. This is due to the large number and the strong nonlinearity of the conditions that must be satisfied to achieve high-order accuracy. The main approach to address this complexity is to predetermine a set of coefficients, often by setting them to zero, to simplify the resulting system enough to be solvable [1] and, to the same end, to consider additional simplifying assumptions [2].

Traditionally, once the order conditions have been satisfied, the remaining free coefficients are used to satisfy other local properties, such as increased phase-lag order and/or amplification error order, phase fitting, amplification error fitting, exponential/trigonometric fitting, and minimisation of the local truncation error, among others. The problems considered here, the (2+1)-dimensional nonlinear Schrödinger (NLS) equation, the Two-Body (TB) problem and its generalisation, i.e., the N-Body (NB) problem, all exhibit oscillatory and periodic behaviour. As such, methodologies targeting oscillatory and/or periodic systems have been widely applied. For example, a phase- and amplification-fitted Runge–Kutta–Nyström pair has been derived in [3] for the numerical solution of oscillatory systems. For the same type of problems, Abdulsalam et al. [4] developed a multistep Runge–Kutta–Nyström method with frequency-dependent coefficients. More specific problem approaches have been adopted as well, and trigonometrically-fitted methods have been developed for the Schrödinger equation in [5] and orbital problems in [6]. Further minimisation of the local truncation error coefficients or other quantities, e.g., the Lagrangian of the system, has also been investigated [7], while invariant domain preserving and mass conservative explicit Runge–Kutta methods have also been developed [8]. Finally, explicit integrators that obey local multisymplectic conservation laws, based on partitioned Runge–Kutta methods, have been investigated in [9].

However, a key limitation of these classical approaches is their reliance on local properties. That is, they ensure the method performs well locally, perhaps by integrating simple problems, based on the assumption that acquiring certain local features implies good global behaviour. This assumption, although common, is not always verified for complex or long-time integration problems. The global error in the real problem remains the ultimate metric for assessing a method’s performance, and this is the approach we adopt here. Rather than analysing local accuracy or stability conditions, we directly target the global error of the problem.

For this reason, we consider a parametric explicit RK method with eight stages and sixth-order accuracy, which has four free coefficients and can be optimised to efficiently solve the NLS, TB, and NB problems. In a previous work [10], we attempted to optimise this method for the NLS equation only. However, several significant barriers were encountered: the highly nonlinear behaviour of the optimisation landscape, the presence of local minima in the free coefficient space, the expensive computation of the global error via time integration, and the black-box nature of the objective function, due to the absence of derivative information. These factors make a systematic investigation of the optimisation problem particularly difficult and suggest the need for non-traditional approaches.

Utilising artificial intelligence methodologies to solve scientific and engineering problems is increasingly common; see [11] and references therein. Computational intelligence techniques [12], and in particular evolutionary computation (EC) methods [13], are well-suited for optimising parametric numerical methods. Particle swarm optimisation (PSO) is among the most prominent of these methods [14], and differential evolution techniques are also gaining popularity [15]. There is research that involves combining optimisation and RK methods, but not with the ultimate goal of developing an optimised RK method. For example, in [16], the RK method is used to define the update rule in a metaheuristic optimiser. Notwithstanding, there have been limited applications of EC techniques to optimise finite difference schemes and even fewer for Runge–Kutta methods, despite the fact that the complex nature and size of the system of nonlinear equations would benefit from such techniques. Babaei in [17] develops new RK methods for the solution of initial value problems; however, the process does not involve any order conditions. Neelan and Nair [18] developed hyperbolic Runge–Kutta methods with an optimised stability region using evolutionary algorithms. Optimisation of parametric RK methods has also been achieved using differential evolution by Kovalnogov et al. in [19] and by Jerbi et al. in [20].

In this article, we use the particle swarm optimisation algorithm [21] to determine the optimal values of the four free coefficients in our parametric RK method [10]. PSO, which continues to evolve, is well-suited to overcoming the aforementioned obstacles [22], as it does not require derivative information and allows for efficient global exploration of the coefficient space. It also provides a systematic way to experiment with otherwise impractical constraints, such as relaxing the node bounds $c_i\in [0,1]$ to a more general interval $c_i\in [a,b]\supset [0,1]$. The use of PSO not only enhances the ability to identify effective RK coefficients but also enables the discovery of optimal methods tailored to real-world problems in quantum physics, astronomy, and related fields.

In summary, the main contributions of this article are the formulation of an evolutionary optimisation framework for Runge–Kutta methods that targets global accuracy rather than local properties, the introduction of a benchmark-based objective function, the relaxation of conventional coefficient bounds to enhance stability and error properties, and the identification of structural patterns in optimal coefficients for highly oscillatory regimes.

The structure of this paper is as follows:

• In Section 2, we introduce the Runge–Kutta framework, formulate the parametric optimisation problem, and describe the implementation of the evolutionary computation methods;
• In Section 3, we present the numerical problems used for training and testing the methods;
• In Section 4, we report the optimal Runge–Kutta coefficients obtained for each training problem;
• In Section 5, we analyse the error and stability properties of the resulting methods;
• In Section 6, we present numerical results evaluating the performance of the optimised methods;
• In Section 7, we discuss key trends and implications of the results;
• In Section 8, we summarise the main contributions.

2. Evolutionary Optimisation of Parametric RK Methods

2.1. Overview of Runge–Kutta Methods

The problems under investigation fall under the same category of initial value problems, presented in the autonomous form:

$$\begin{array}{c}{\displaystyle \frac{du}{dt}=f\left(u\right)}\hfill \\ u\left(0\right)=u_0\hfill \end{array}$$

(1)

where u implicitly contains t and potentially x and y and all derivatives with respect to variables other than t, if they exist, which can be semi-discretised via finite differences or replaced by a theoretical solution if available. The resulting problem can, in that case, be solved using the method of lines.

An s-stage explicit Runge–Kutta method for the solution of Equation (1) is presented below:

$$\left\{\begin{array}{c}{u}_{n+1}=u_n+h{\displaystyle \sum _{i=1}^s}{b}_i{k}_i\hfill \\ k_i=f(t_n+c_{i}h,u_n+h{\displaystyle \sum _{j=1}^{i-1}}{a}_{ij}{k}_j),i=1,\dots ,s\hfill \end{array}\right.or\begin{array}{cc}c& A\\ & b\end{array}$$

(2)

where $A=\left[a_{ij}\right]\in {\mathbb{R}}^{s\times s}$ is strictly lower triangular, $b={\left[b_i\right]}^T\in {\mathbb{R}}^s$ (weights), $c=\left[c_i\right]\in {\mathbb{R}}^s$ (nodes), and all coefficients $a_{ij},b_i,c_i\in \mathbb{R}$, for $i=1,2,\dots ,s$ and $j=1,2,\dots ,i-1$, define the method [2]. Here, $h=\Delta t$ is the step length in time, and f is defined in the form $u^{\prime }=f(x,y,t,u)$.

2.2. Parametric Runge–Kutta Method

We consider a general parametric method, which was developed in [10] for the solution of Equation (1). It is an eight-stage, sixth-order explicit RK method and has 10 fixed coefficients, namely $c_3={\displaystyle \frac{1}{6}}$, $c_6={\displaystyle \frac{1}{2}}$, $c_8=1$, $b_2=0$, $b_3=0$, $a_{42}=0$, $a_{52}=0$, $a_{62}=0$, $a_{72}=0$, $a_{82}=0$, while 29 coefficients depend on one or more of $\left\{c_2,c_4,c_5,c_7\right\}$, which serve as the four degrees of freedom in the optimisation.

In [10], we attempted to optimise the method using a standard optimisation technique, with a progressively decreasing step length $\Delta c$ from $0.1$ to $0.001$ for all four free coefficients $c_2,c_4,c_5,c_7$. The optimisation yielded the following results as optimal: $\left\{c_2=0.007\right.$, $c_4=0.208$, $c_5=0.441$, $\left.c_7=0.915\right\}$. Using evolutionary optimisation, we will identify improved variants of the method described above, illustrating the limitations of conventional optimisation in finding globally optimal values.

2.3. The Optimisation Problem

The objective of the optimisation is to explore the free coefficient space thoroughly and efficiently across a range of step lengths to ensure that the optimal RK method performs well across all step lengths. Many setups were successful, with varying efficiencies. For example, when a reliable benchmark method exists across all accuracy levels and can act as a benchmark, then it is useful to optimise the mean ratio of the errors of the method under development to those of the benchmark method.

We define the objective function C as the mean ratio of the maximum norm of the global error produced by the new method over that of the benchmark method, averaged over several runs with different step lengths. Formally, the objective function is defined as

$$\underset{c_2,c_4,c_5,c_7}{\mathrm{minimise}}C={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{{\Vert E_i\Vert }_{\infty }}{{\Vert {\overline{E}}_i\Vert }_{\infty }}}$$

(3)

C: The objective function to be minimised. It represents the average relative error of the new method compared with the benchmark method with the same stages and order.

• N: The total number of runs, each corresponding to a specific step length $h_i$.
• ${\Vert E_i\Vert }_{\infty }$: The maximum norm of the global error of the new method in the i-th run.
• ${\Vert {\overline{E}}_i\Vert }_{\infty }$: The maximum norm of the global error of the benchmark method in the i-th run.

The benchmark method is only run once per run. We chose the optimal method developed in [10], also presented in Section 4, to act as the benchmark method, due to its consistent performance across all step lengths.

In order to ensure a uniformly good performance for all accuracies, we select a range of different step lengths $h_i$ that produce results with varying accuracies, avoiding both excessively large (unstable) and excessively small (round-off dominated) values. The best results were obtained from the geometric sequence:

$$h_i={\displaystyle \frac{2}{5}}·2^{-(i-1)},i=1,\dots ,6,t\in [0,2.5],\mathrm{for} \mathrm{the} \mathrm{NLS} \mathrm{Equation} \left(10\right)$$

(4a)

$$h_i=2^{-{\displaystyle \frac{i-1}{2}}},i=1,\dots ,10,t\in [0,100],\mathrm{for} \mathrm{the} \mathrm{Two-Body} \mathrm{problem} \left(17\right)$$

(4b)

Several variations were also examined, but the above combinations provided the most reliable results over a set of individual runs.

Each run involves solving a problem using both the new and the benchmark methods under identical conditions (e.g., same problem, same step length). The global error is measured as the maximum absolute difference between the numerical and exact (or reference) solution over time. By averaging the ratio ${\Vert E_i\Vert }_{\infty }/{\Vert {\overline{E}}_i\Vert }_{\infty }$ across all N runs, we obtain a scalar performance measure C that reflects the overall accuracy of the new method relative to the benchmark. A value of $C<1$ indicates that the new method, on average, outperforms the benchmark in terms of maximum global error.

For optimising the four coefficients to perform well when integrating the NLS Equation (10), described in Section 3.1, we use the same equation over a shorter interval as a training problem, in contrast to the test problem.

To improve the performance of the methods in the N-Body problem (19), described in Section 3.3, instead of using it as a training problem and test problem, we select the Two-Body problem (17), described in Section 3.2, to tune the coefficients, as it is computationally cheaper yet shares similar dynamics. We experimented with three different eccentricities, but $e=0.05$ yielded the best results, as it is the dominant eccentricity in our problem, as explained in Section 3.3.

Alternatively, we tested the following objective function:

$$\underset{c_2,c_4,c_5,c_7}{\mathrm{minimise}}C={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{{\Vert E_i\Vert }_{\infty }}{h_i^{\widehat{p}}}}$$

(5)

where $\widehat{p}$ is the experimental order of accuracy, although it can be empirically tuned, as its purpose in the above formula is to balance the scale of the ratios within the objective function (an equivalent objective function was proposed in [20]). However, despite offering independence from a benchmark method, the function was less consistent and required fine-tuning of the parameter $\widehat{p}$ for comparable results, so it was not adopted in our main optimisation.

We have one main boundary constraint for all coefficients $c_i\in [0,1]$, which is the typical constraint when developing Runge–Kutta methods. However, this constraint offers limited practical benefit for the problems studied. As we will show, removing this bound allows for smaller maximum global error, lower local error constants, and larger stability intervals, all simultaneously. The efficient implementation of PSO allows this type of experimentation with different setups, enabling the removal of traditional constraints that are not essential. Even when bounds are enforced, PSO yields better results than classical optimisation techniques.

To conclude, we present the optimisation problem under investigation below:

• Minimise the objective function C, defined in (3),
• with respect to the four coefficients $c_2,c_4,c_5,c_7$,
• in combination with the step lengths defined in (4),
• subject to $c_i\in [0,1]$ (optional).

2.4. Implementation of Particle Swarm Optimisation

Because the goal is to minimise the global error, and the objective function lacks derivative information, derivative-based methods are inapplicable. For instance, optimisation methods such as gradient descent could be considered; however, the absence of derivative information and the problem’s strong nonlinearity render derivative-free approaches more appropriate. This motivates the use of derivative-free global optimisation strategies, such as evolutionary computation methods.

Particle Swarm Optimisation (PSO), inspired by the social behaviour of bird flocks and fish schools, is a population-based stochastic method that iteratively improves candidate solutions (in our case, quadruples of free coefficients) through individual experience and social learning. PSO is a well-established and widely used optimisation technique, known for its robustness, simplicity, and flexibility across diverse problem domains. We selected PSO for its balance between exploration and exploitation and relatively few control parameters [21,22,23]. Its straightforward tuning requirements and fast convergence behaviour further support its practical appeal. Additionally, its structure naturally supports parallel evaluation of candidates, which is beneficial given the computational cost of calculating the global error via time integration. While other evolutionary methods, such as differential evolution, have been applied in similar optimisation problems, PSO best meets our requirements for efficiency, robustness, and ease of integration into the optimisation framework.

We used a standard PSO algorithm described by the update rules below (Algorithm 1).

Algorithm 1 Neighbourhood-Best PSO with Adaptive Parameters

The position of particle i at iteration $t+1$ is updated as $${\mathbf{x}}_i^{t+1}={\mathbf{x}}_i^t+{\mathbf{v}}_i^{t+1}$$ (6) The velocity is updated according to $${\mathbf{v}}_i^{t+1}={\omega }^t{\mathbf{v}}_i^t+c_1{r}_1\left({\mathbf{p}}_{i,\mathrm{best}}-{\mathbf{x}}_i^t\right)+c_2{r}_2\left({\mathbf{p}}_{\mathrm{neigh},i}-{\mathbf{x}}_i^t\right)$$ (7) where ${\omega }^t$ is the inertia weight at iteration t; $c_1$ and $c_2$ are the cognitive and social acceleration coefficients; $r_1,r_2\sim U(0,1)$ are independent uniform random numbers drawn for each particle and dimension at every iteration; ${\mathbf{p}}_{i,\mathrm{best}}$ is the best position found by particle i; ${\mathbf{p}}_{\mathrm{neigh},i}$ is the best position found in the neighbourhood of particle i; $N^t$ is the neighbourhood size at iteration t. The inertia weight is adapted at each iteration as $${\omega }^{t+1}=\left\{\begin{array}{cc}min\left(max(2{\omega }^t,{\omega }_{min}),{\omega }_{max}\right),\hfill & \mathrm{if}\mathrm{stallCounter}<2\hfill \\ min\left(max(0.5{\omega }^t,{\omega }_{min}),{\omega }_{max}\right),\hfill & \mathrm{if}\mathrm{stallCounter}>5\hfill \\ {\omega }^t,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$ (8) where ${\omega }_{min}$ and ${\omega }_{max}$ bound the inertia range, and stallCounter counts consecutive iterations without improvement. The neighbourhood size $N^t$ is adapted as $$N^{t+1}=\left\{\begin{array}{cc}{N}_{min},\hfill & \mathrm{if}\mathrm{improvement}\mathrm{found}\hfill \\ min(N_{max},N^t+N_{min}),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$ (9) where $N_{min}$ and $N_{max}$ are the minimum and neighbourhood sizes, respectively.

In all experiments, the parameters were set as follows: $c_1=1.49$, $c_2=1.49$, ${\omega }_{min}=0.1$, ${\omega }_{\mathrm{init}}={\omega }_{max}=1.1$, $N_{init}=N_{min}=S/4$, and $N_{max}$ equal to the swarm size S. These choices follow commonly recommended guidelines about parameter values, such as the cognitive and social acceleration coefficients [23,24] and update rules, specifically the inertia and neighbourhood update rules [25], while accommodating the specific requirements of our problems. For example, there are numerous articles and surveys advocating for the use of neighbourhoods in the PSO algorithm [26,27]. Other authors propose even more advanced variants [28,29], however, we prefer the technique described above, which accommodates ease of integration without compromising on efficiency or robustness.

The population size is now generally expected to be much larger than the 20–50 particles suggested in early PSO studies, as observed in many applications [30]. In our study, the criteria for selecting a population size S are, in order of priority: (i) achieving the lowest possible objective-function values among the best solutions, (ii) maintaining solution diversity, and (iii) if these two are comparable, maximising the computational efficiency of the optimisation process. We analysed the sensitivity of these criteria with respect to $S=1000,2000,4000$ when training for the Two-Body problem (e = 0.05) for the step lengths in (4a) and objective function (5), based on nine independent runs per population size in this representative test configuration. The analysis revealed equivalent objective function values with means ${\mu }_1=0.00214$, ${\mu }_2=0.00256$, ${\mu }_4=0.00207$ and standard deviations ${\sigma }_1=0.00040$, ${\sigma }_2=0.00050$, ${\sigma }_4=0.00055$ for $S=1000$, 2000, 4000 respectively. The deciding factor in selecting the population size was the diversity of the solutions: the average pairwise Euclidean distances were $d_1=0.114$, $d_2=0.520$, and $d_4=0.344$, indicating that the solutions for $S=2000$ were more spread out and less prone to clustering in a narrow region. Furthermore, for $S=4000$, the system exhibited instability due to high memory usage from parallelisation. Thus, $S=2000$ provided the most robust and diverse results. For completeness, the average number of function evaluations was $c_1=1.93\times {10}^5$, $c_2=2.90\times {10}^5$, and $c_4=8.02\times {10}^5$.

Nonetheless, it was necessary to reinitiate the population between runs, as this alone could redirect the swarm to more optimal regions of the search space. Each run converged in approximately 100–300 iterations, which resulted naturally without imposing any hard iteration limit, with a maximum of 50 stall iterations, where the best solution has not changed by more than the function tolerance, which is set to machine epsilon, approximately $2.2\times {10}^{-16}$ for our machine.

During the exploration phase of the optimisation, we observed that the optimal solution exhibited high mobility across the search space, overcoming local barriers and valleys. Different settings and initial populations led to distinct optimal solutions, and this behaviour further indicates the complex nature of the optimisation problem.

More than 20 runs were attempted for each of the four problems, the NLS Equation (10), and the Two-Body problem (17) with three different eccentricities, $e=0.00$, $e=0.05$, and $e=0.25$. The solution derived from each of these runs was tested over the full interval for either the NLS Equation (10) or the N-Body problem (19), depending on the problem for which it was optimised. All experiments were conducted on a computer with an Intel i9 processor (14 cores) and 32 GB of RAM. MATLAB R2024b was used for numerical computations, and Maple 2024 was used for symbolic computations.

Before presenting the optimised coefficients obtained from the training process, we first introduce the numerical problems used in both the optimisation and testing stages.

3. Training and Test Problems

We now describe the numerical problems used to train and test the methods, namely the (2+1)-dimensional nonlinear Schrödinger equation, the Two-Body problem and the N-Body problem.

3.1. (2+1)-Dimensional Nonlinear Schrödinger (NLS) Equation

We consider the (2+1)-dimensional nonlinear Schrödinger (NLS) equation of the form:

$$\begin{array}{c}i{u}_t+a{u}_{xx}+b{u}_{yy}+c{\left|u\right|}^{2}u+du=0\hfill \\ u(x,y,t=0)=u_0(x,y)\hfill \end{array}$$

(10)

where $i=\sqrt{-1}$, $a,b,c,d\in \mathbb{R}$, $u(x,y,t):{\mathbb{R}}^3\to \mathbb{C}$ is a complex function of the spatial variables $x,y$ and the temporal variable t, and $u_0(x,y):{\mathbb{R}}^2\to \mathbb{C}$. The term $i{u}_t$ governs temporal evolution, the terms $a{u}_{xx}$ and $b{u}_{yy}$ describe spatial dispersion in the x and y directions, respectively, and the nonlinear term ${c\left|u\right|}^{2}u$ arises in physical applications such as Bose–Einstein condensates and optical beam propagation [31].

Equation (10) has a dark soliton solution given by

$$u(x,y,t)=\sqrt{-{\displaystyle \frac{\gamma }{c}}}tanh\left(\sqrt{{\displaystyle \frac{\gamma }{2\beta }}}\left(k_{1}x+l_{1}y-2at+{\xi }_0\right)\right){\mathrm{e}}^{i\left(k_{2}x+l_{2}y-c_{2}t+{\eta }_0\right)}$$

(11)

where $\beta =a{k}_1^2+b{l}_1^2$, $\gamma =c_2+d-a{k}_2^2-b{l}_2^2$, and we select $a=1$, $b=1$, $c=-1$, $d=1$, $k_1=1$, $k_2=1$, $l_1=0$, $l_2=0$, $c_2=2$, ${\xi }_0=0$, ${\eta }_0=0$ [32].

The analytical solution of the above special case is

$$u(x,y,t)=\sqrt{2}tanh\left(x-2t\right){\mathrm{e}}^{i\left(x-2t\right)}$$

(12)

and the density is given by

$${\left|u(x,y,t)\right|}^2=2{\left|tanh\left(x-2t\right)\right|}^2$$

Furthermore, the solution $u(x,y,t)$ of Equation (10) satisfies the mass conservation law [33]:

$$M\left[u\right]\left(t\right)=\underset{{\mathbb{R}}^2}{\int }{\left|u(x,y,t)\right|}^{2}dxdy\equiv M\left[u\right]\left(0\right)$$

(13)

For the numerical solution of Equation (10),

$$\begin{array}{c}\mathrm{let}(x,y,t)\in [x_L,x_U]\times [y_L,y_U]\times [0,T]\mathrm{and}\hfill \\ u_{l,m}^n\mathrm{denotes} \mathrm{an} \mathrm{approximation} \mathrm{of}u(x_l,y_m,t_n),\mathrm{where}\hfill \\ x_l=x_L+l\Delta x,l=0,1,\dots ,L-1,L={\displaystyle \frac{x_U-x_L}{\Delta x}}+1,\Delta x>0\hfill \\ y_m=y_L+m\Delta y,m=0,1,\dots ,M-1,M={\displaystyle \frac{y_U-y_L}{\Delta y}}+1,\Delta y>0\hfill \\ t_n=nh,n=0,1,\dots ,N-1,N={\displaystyle \frac{T}{h}}+1,h>0\hfill \end{array}$$

(14)

We use the method of lines for $(x,y,t)\in [-20,30]\times [-1,1]\times [0,T]$ for the integration of problem (10), where $T=2.5$ for the training problem, and $T=5$ for the test problem. Even shorter training intervals could yield good results, but not consistently, and the resulting RK methods may lack sufficient stability characteristics. As we are interested in the RK method’s performance, we use Equation (12) to evaluate both the initial and boundary conditions and the second derivatives $u_{xx}$ and $u_{yy}$ of the same equation. The maximum global solution error and the maximum relative mass error of the numerical solution are defined by Equations (15) and (16) respectively.

For the NLS equation, if $u_{l,m}^n$ is the numerical approximation, $u(x_l,y_m,t_n)$, we define the maximum global solution error as

$$\Vert E_{\infty }\Vert =\underset{l,m,n}{max}\left(\right|u_{l,m}^n-u(x_l,y_m,t_n)\left|\right)$$

(15)

and the maximum relative mass error over the region D as

$$\underset{n}{max}\left(\left|{\displaystyle \frac{M_D^n-M_D^0}{M_D^0}}\right|\right)$$

(16)

where $M_D^n$ is approximating $M\left[u\right]\left(t_n\right)$ over $D=[-20,30]\times [-1,1]$ for $t\in [0,T]$, and $M_D^0$ is approximating $M\left[u\right]\left(0\right)$ over the same region D.

3.2. Two-Body Problem

The classical planar Newtonian Two-Body problem is used as a training problem to tune the four free coefficients before testing it on the N-Body problem.

In Cartesian form:

$$\left\{\begin{array}{c}{u}_1^{″}=-{\displaystyle \frac{u_1}{r^3}},u_2^{″}=-{\displaystyle \frac{u_2}{r^3}}\hfill \\ u_1\left(0\right)=1-e,u_1^{\prime }\left(0\right)=0\hfill & \hfill \\ u_2\left(0\right)=0,u_2^{\prime }\left(0\right)=\sqrt{{\displaystyle \frac{1+e}{1-e}}}\hfill & \hfill \end{array}\right.$$

(17)

where $r=\sqrt{u_1^2+u_2^2}$ and e is the orbital eccentricity.

The theoretical solution is provided by:

$$\left\{\begin{array}{cc}{u}_1\left(t\right)=cos\left(\theta \right)-e\hfill & \hfill \\ u_2\left(t\right)=\sqrt{1-e^2}sin\left(\theta \right)\hfill & \hfill \end{array}\right.$$

(18)

where $\theta$ can be found by solving the equation $\theta -esin\left(\theta \right)-t=0$ [34].

As we consider the Two-Body problem a training problem, we select a relatively short interval of integration: $t\in [0,100]$. We tested the trained methods in the Two-Body problem for $t\in [0,1000]$ and the N-Body problem, as described in the next section.

3.3. N-Body Problem

The N-Body problem is the problem that investigates the movement of N bodies under Newton’s law of motion. It is expressed by the system

$$\begin{array}{c}{\displaystyle u_i^{″}=G\sum _{j=1,j\ne 0}^N\frac{m_j(\overrightarrow{u_j}-\overrightarrow{u_i})}{|\overrightarrow{u_j}-\overrightarrow{u_i}{|}^3},i=1,2,\dots ,N}\hfill \end{array}$$

(19)

where G is the gravitational constant, $m_j$ is the mass of body j, and $\overrightarrow{u_i}$ and $\overrightarrow{u_i^{″}}$ denote the vectors of the position and acceleration of body i, respectively.

We solve the five outer body problem, a specific configuration of the N-Body problem. This system consists of the Sun and the four inner planets (denoted as Sun+4), the four outermost planets, and Pluto.

Table 1. Five outer body problems: The basic properties of the bodies, their orbits, and their initial position and velocity, where Sun+4 denotes the Sun and the four inner planets.

Body	Mass (Solar Masses)	Orbital Ecc.	Rev. Period (Years)	Init. Position	Init. Velocity
				0	0
Sun+4	1.00000597682	-	-	0	0
				0	0
				−3.5023653	0.00565429
Jupiter	0.000954786104043	0.0484	11.86	−3.8169847	−0.00412490
				−1.5507963	−0.00190589
				9.0755314	0.00168318
Saturn	0.000285583733151	0.0541	29.46	−3.0458353	0.00483525
				−1.6483708	0.00192462
				8.3101420	0.00354178
Uranus	0.0000437273164546	0.0472	84.01	−16.2901086	0.00137102
				−7.2521278	0.00055029
				11.4707666	0.00288930
Neptune	0.0000517759138449	0.0086	164.79	−25.7294829	0.00114527
				−10.8169456	0.00039677
				−15.5387357	0.00276725
Pluto	$1/(1.3\times {10}^8)$	0.2488	248.59	−25.2225594	−0.00170702
				−3.1902382	−0.00136504

shows the masses (relative to the solar mass), the orbital eccentricities and revolution periods (in Earth years), and the initial position and velocity components of the six bodies. The distances are in astronomical units, and the gravitational constant is $G=2.95912208286\times {10}^{-4}$.

As analytical solutions are unavailable, we compare against reference high-precision numerical results, produced by applying the 10-stage implicit Runge–Kutta method of Gauss with 20th algebraic order, for $t\in [0,{10}^6]$ (about 2738 years), following the procedure described in [35].

Table 1 implies that the dominant eccentricity of the bodies with the highest frequencies, or lowest revolution periods, that is, Jupiter, Saturn, and Uranus, is $e\approx 0.05$. This observation motivates our choice of training eccentricity, as further explained in Section 6. Additional methodologies for investigating the performance and behaviour of the methods in astronomical problems can be found in [36].

4. Optimal RK Coefficients

Table 2. Coefficients of developed methods. Entries where $c_i\notin [0,1]$ are bolded.

Method	${\mathit{c}}_2$	${\mathit{c}}_4$	${\mathit{c}}_5$	${\mathit{c}}_7$
Original [10]	0.0070000000000000	0.2080000000000000	0.4410000000000000	0.9150000000000000
NLS	0.1846192563425903	0.2247603817048323	0.5706075347944812	1.0582458651706454
NLS in $[0,1]$	0.0092477488555108	0.2166123597181641	0.5440778163831921	0.9805511474091542
TB I ($e=0$)	−0.0094525465942426	−0.1057207949231992	0.4183913927663807	1.5601765389027689
TB Ib in $[0,1]$	0.1366360718492776	0.0408398027965382	0.1818797871926411	0.5520864798690709
TB II ($e=0.05$)	0.0157893424540159	−0.1580319415439770	0.3356276745332045	0.8364470804118889
TB IIb in $[0,1]$	0.0010067780917901	0.2592782871426017	0.4231941925978401	0.6844694952540733
TB III ($e=0.25$)	0.0955480567625531	0.3901353596573214	0.1789726462498607	0.2883289058072621

lists the optimal coefficient values obtained for each training problem. These include the nonlinear Schrödinger equation and the Two-Body problem with eccentricities $e=0.00$, $0.05$, and $0.25$ for both bounded ($c_i\in [0,1]$) and unbounded cases. For comparison, the Original method from [10] is also included.

In total, seven new optimised RK methods were constructed:

• NLS (unbounded) and NLS in [0, 1] (bounded),
• TB I, TB II, TB III (unbounded, trained for $e=0.00$, $0.05$, and $0.25$),
• TB Ib, TB IIb (bounded counterparts of TB I and TB II).

Notably, the coefficients of the bounded NLS method are relatively close to those of the Original method, while the unbounded version differs significantly. The unbounded Two-Body methods (TB I and TB II) also show substantial deviations from their bounded counterparts (TB Ib and TB IIb). In contrast, TB III, trained on a problem with high eccentricity $e=0.25$, naturally satisfies $c_i\in [0,1]$ and therefore has no bounded variant.

These variations in coefficient values reflect the complex, nonlinear relationship between the free parameters and the global behaviour of the method. They also illustrate the influence of the training problem, particularly the solution’s eccentricity and oscillatory character, on the structure of the optimal coefficients.

5. Error and Stability Analysis

In this section, we present the local truncation error and stability analysis.

5.1. Error Analysis

The local truncation error analysis of the parametric method defined in Equation (2) and Section 2.2, based on the Taylor expansion series of the difference ${\tau }_{n+1}=u^{n+1}-u\left(t_{n+1}\right)$, yields the principal term of the local truncation error, which is given by

$${\tau }_{n+1}=p_7{\displaystyle \frac{d^{7}u}{d{t}^7}}{h}^7+𝒪\left(h^8\right)$$

(20)

where

$$\begin{array}{cc}\hfill p_7=& -{\left(64\left(30c_4^3-35c_4^2+11c_4-1\right)\right)}^{-1}\hfill \\ \hfill & {\left(\left(10c_4{c}_5{c}_7-5c_4{c}_5-5c_4{c}_7-5c_5{c}_7+3c_4+3c_5+3c_7-2\right)\right)}^{-1}\hfill \\ \hfill & 25(\left(\left(c_7-{\displaystyle \frac{3}{5}}\right)c_5^2+\left(-{\displaystyle \frac{151c_7}{210}}+{\displaystyle \frac{53}{126}}\right)c_5+{\displaystyle \frac{218c_7}{1575}}-{\displaystyle \frac{218}{2625}}\right)c_4^4\hfill \\ \hfill & +\left(\left(-{\displaystyle \frac{37c_7}{30}}+{\displaystyle \frac{23}{30}}\right)c_5^2+\left({\displaystyle \frac{2977c_7}{3150}}-{\displaystyle \frac{26933}{47250}}\right)c_5+{\displaystyle \frac{5801}{47250}}-{\displaystyle \frac{3107c_7}{15750}}\right)c_4^3\hfill \\ \hfill & +\left(\left({\displaystyle \frac{124c_7}{225}}-{\displaystyle \frac{397}{1125}}\right)c_5^2+\left(-{\displaystyle \frac{7019c_7}{15750}}+{\displaystyle \frac{1451}{5250}}\right)c_5+{\displaystyle \frac{527c_7}{5250}}-{\displaystyle \frac{3053}{47250}}\right)c_4^2\hfill \\ \hfill & +\left(\left(-{\displaystyle \frac{118c_7}{1125}}+{\displaystyle \frac{232}{3375}}\right)c_5^2+\left({\displaystyle \frac{694c_7}{7875}}-{\displaystyle \frac{439}{7875}}\right)c_5+{\displaystyle \frac{328}{23625}}-{\displaystyle \frac{166c_7}{7875}}\right)c_4\hfill \\ \hfill & +\left({\displaystyle \frac{8c_7}{1125}}-{\displaystyle \frac{16}{3375}}\right)c_5^2+\left({\displaystyle \frac{92}{23625}}-{\displaystyle \frac{16c_7}{2625}}\right)c_5+{\displaystyle \frac{4c_7}{2625}}-{\displaystyle \frac{8}{7875}})\hfill \end{array}$$

(21)

indicating global accuracy of order six. The $p_7$ values for the newly developed methods are presented in Table 3.

5.2. Stability Analysis

For the analysis of the (absolute) stability of method (2), we consider the problem

$$u^{\prime }=\lambda u,\lambda \in \mathbb{C}$$

(22)

Applying method (2) to the above equation, we obtain the numerical solution $u_{n+1}=R\left(v\right)u_n$, where $v=\lambda h$, and $R\left(v\right)$ is called the stability polynomial [2]. We have the following definitions:

Definition 1.

For the method of Equation (2), we define the stability interval along the real axis as $I_R=[v_R,0]$, where

$$v_R=max\left\{-\delta :\delta ⩾0,\left|R\right(v\left)\right|⩽1,\mathrm{for} \mathrm{all}v\in [-\delta ,0]\mathrm{with}\mathrm{Im}\left(v\right)=0\right\}$$

Definition 2.

For the method of Equation (2), we define the stability interval along the imaginary axis as $I_I=[-v_I,v_I]$, where

$$v_I=max\left\{\delta ⩾0:\left|R\right(v\left)\right|⩽1,\mathrm{for} \mathrm{all}v\in [-\delta ,\delta ]\mathrm{with}\mathrm{Re}\left(v\right)=0\right\}$$

Definition 3.

The region of absolute stability is defined as the set $S=\left\{v\in \mathbb{C}:\left|R\right(v\left)\right|⩽1\right\}$

Following the above procedure, we compute its stability polynomial, which is given by

$$\begin{array}{cc}\hfill R=& {\left(34560\left(10c_4{c}_5{c}_7-5c_4{c}_5-5c_4{c}_7-5c_5{c}_7+3c_4+3c_5+3c_7-2\right)\left(6c_4-1\right)\left(5c_4^2-5c_4+1\right)\right)}^{-1}\hfill \\ \hfill & (10368000Q+10368000Qv+5184000Q{v}^2+1728000Q{v}^3+432000Q{v}^4+86400Q{v}^5\hfill \\ \hfill & +14400Q{v}^6+(\left(\left(13500c_7-8100\right)c_5^2+\left(-7650c_7+4650\right)c_5+840c_7-504\right)c_4^4\hfill \\ \hfill & +\left(\left(-16650c_7+10350\right)c_5^2+\left(9330c_7-5878\right)c_5-846c_7+526\right)c_4^3\hfill \\ \hfill & +\left(\left(7440c_7-4764\right)c_5^2+\left(-4062c_7+2634\right)c_5+258c_7-166\right)c_4^2\hfill \\ \hfill & +\left(\left(-1416c_7+928\right)c_5^2+\left(744c_7-492\right)c_5-24c_7+16\right)c_4+96c_5\left(c_5-{\displaystyle \frac{1}{2}}\right)\left(c_7-{\displaystyle \frac{2}{3}}\right))v^7\hfill \\ \hfill & +1125\left(\left(-{\displaystyle \frac{2}{5}}+c_5\right)c_4-{\displaystyle \frac{2c_5}{5}}+{\displaystyle \frac{1}{5}}\right)\left(\left(c_7-{\displaystyle \frac{3}{5}}\right)c_4-{\displaystyle \frac{2c_7}{5}}+{\displaystyle \frac{4}{15}}\right)c_4\left(\left(c_5-{\displaystyle \frac{4}{15}}\right)c_4-{\displaystyle \frac{4c_5}{15}}+{\displaystyle \frac{1}{15}}\right)v^8)\hfill \end{array}$$

where

$Q=\left(\left(\left(c_7-{\displaystyle \frac{1}{2}}\right)c_5-{\displaystyle \frac{c_7}{2}}+{\displaystyle \frac{3}{10}}\right)c_4+\left(-{\displaystyle \frac{c_7}{2}}+{\displaystyle \frac{3}{10}}\right)c_5+{\displaystyle \frac{3c_7}{10}}-{\displaystyle \frac{1}{5}}\right)\left(-{\displaystyle \frac{1}{6}}+c_4\right)\left(c_4^2-c_4+{\displaystyle \frac{1}{5}}\right)$

Using this polynomial and the coefficients of all methods in Table 2, we conduct a numerical computation of the real and imaginary stability intervals, according to Definitions 1 and 2, respectively, and a step length of $dv=0.0001$, presenting the intervals in Table 3. Similarly, we present the stability regions of all methods in Figure 1, as the set of grid points that satisfy Definition 3. More specifically, we evaluated $v=x+iy$ over the domain $x\in [-6.5,0.5]$, $y\in [-5,5]$, using a step length of $0.01$. Here, x and y represent the real and imaginary parts of v, respectively. For clarity, only the boundary of each stability region is shown, though each region comprises all points for which $\left|R\right(v\left)\right|⩽1$.

Table 3. Properties of developed methods. Here, $v_R$ and $v_I$ define the stability interval along the real axis $[v_R,0]$ and along the imaginary axis $[-v_I,v_I]$, whereas $p_7$ stands for the coefficient of the principal term of the local truncation error, shown in (20). Figure 1 provides a graphical representation of the stability intervals.

Method	${\mathit{v}}_{\mathit{R}}$	${\mathit{v}}_{\mathit{I}}$	${\mathit{p}}_7$
Original [10]	−3.986	0.001	$3.4\times {10}^{-5}$
NLS	−4.442	0.002	$4.4\times {10}^{-6}$
NLS in $[0,1]$	−4.057	0.001	$1.1\times {10}^{-5}$
TB I ($e=0$)	−5.926	0.001	$7.4\times {10}^{-5}$
TB Ib ($e=0$) in $[0,1]$	−3.912	0.000	$1.3\times {10}^{-4}$
TB II ($e=0.05$)	−3.709	0.311	$-5.3\times {10}^{-5}$
TB IIb ($e=0.05$) in $[0,1]$	−3.807	0.000	$1.4\times {10}^{-5}$
TB III ($e=0.25$)	−4.180	0.001	$1.2\times {10}^{-4}$

Table 3. Properties of developed methods. Here, $v_R$ and $v_I$ define the stability interval along the real axis $[v_R,0]$ and along the imaginary axis $[-v_I,v_I]$, whereas $p_7$ stands for the coefficient of the principal term of the local truncation error, shown in (20). Figure 1 provides a graphical representation of the stability intervals.

Method	${\mathit{v}}_{\mathit{R}}$	${\mathit{v}}_{\mathit{I}}$	${\mathit{p}}_7$
Original [10]	−3.986	0.001	$3.4\times {10}^{-5}$
NLS	−4.442	0.002	$4.4\times {10}^{-6}$
NLS in $[0,1]$	−4.057	0.001	$1.1\times {10}^{-5}$
TB I ($e=0$)	−5.926	0.001	$7.4\times {10}^{-5}$
TB Ib ($e=0$) in $[0,1]$	−3.912	0.000	$1.3\times {10}^{-4}$
TB II ($e=0.05$)	−3.709	0.311	$-5.3\times {10}^{-5}$
TB IIb ($e=0.05$) in $[0,1]$	−3.807	0.000	$1.4\times {10}^{-5}$
TB III ($e=0.25$)	−4.180	0.001	$1.2\times {10}^{-4}$

5.3. Error and Stability Characteristics and Interpretation

In Table 3, we note that the new methods show improved stability and local truncation error characteristics. For example, the new method NLS, compared with the Original method, exhibits larger real and imaginary stability intervals (indicated by larger absolute values of $v_R$ and $v_I$, respectively) and a smaller absolute coefficient for the principal term of the local truncation error (denoted by $p_7$). A similar improvement is evident when comparing the unbounded TB I with its bounded counterpart, TB Ib (developed under the condition $c_i\in [0,1]$). The unbounded method exhibits a real stability interval approximately two units larger and a truncation error coefficient approximately half an order of magnitude smaller. Furthermore, TB II has a non-vanishing imaginary stability interval in contrast to the bounded counterpart TB IIb, while retaining a similar real stability interval and error coefficient. We observe that, even though the methods were developed for optimal global error, they also exhibit good, albeit not optimal, local properties. Whether the local properties are optimal depends solely on whether they contribute to the minimisation of the global error.

6. Numerical Results

6.1. Overview of Compared Methods

We measure the efficiency of the new methods against existing methods from the literature. We refer to methods 2–8 as new methods, meaning Runge–Kutta methods constructed via PSO in this study. Methods 3, 5, and 7 have bounded nodes such that $c_i\in [0,1]$, $i=1,2,\dots ,8$, whereas methods 2, 4, 6, and 8 were optimised without this constraint, even though method 8 ultimately satisfies it.

The compared methods are presented below:

1.

Original: Method developed in [10] for the NLS equation (Table 2, row 1)

2.

NLS: New method optimised by PSO for the NLS equation, without boundary constraints (Table 2, row 2)

3.

NLS in $[0,1]$: New method optimised for the NLS equation with bounded nodes (Table 2, row 3)

4.

TB I: New method optimised for the Two-Body problem with $e=0$, unbounded (Table 2, row 4)

5.

TB Ib: New method optimised for the Two-Body problem with $e=0$ with bounded nodes (Table 2, row 5)

6.

TB II: New method optimised for the Two-Body problem ($e=0.05$) and the N-Body problem, unbounded (Table 2, row 6)

7.

TB IIb: New method optimised for the Two-Body problem ($e=0.05$) and the N-Body problem with bounded nodes (Table 2, row 7)

8.

TB III: New method optimised for the Two-Body problem with $e=0.25$, unbounded (Table 2, row 8)

9.

Papageorgiou: The method of Papageorgiou et al., with phase-lag and amplification error orders of 10 and 11, respectively [37]

10.

Kosti I: The method of Kosti et al. (I), with phase-lag and amplification error orders of 8 and 9, respectively [38]

11.

Dormand: The classic method of Dormand et al. [2]

12.

Kosti II: The method of Kosti et al. (II), with phase-lag and amplification error orders of 8 and 5, respectively [39]

13.

Fehlberg: The classic method of Fehlberg et al. [2]

14.

Triantafyllidis: The method of Triantafyllidis et al., with phase-lag and amplification error orders of 10 and 7, respectively [40]

15.

Kovalnogov: The parametric method of Kovalnogov et al., optimised with differential evolution [19]

16.

Jerbi: The parametric method of Jerbi et al., optimised with differential evolution [20]

6.2. Performance on the NLS Equation

Table 4. Maximum global solution error and maximum relative mass error of the selected methods in the NLS Equation (10) for $\Delta x=\Delta y=0.1$ and six different $\Delta t$ values.

Method	Solution Error	Mass Error	Solution Error	Mass Error
	$\Delta t=1/80$		$\Delta t=1/40$
NLS	$3.48\times {10}^{-11}$	$6.46\times {10}^{-12}$	$1.89\times {10}^{-9}$	$7.38\times {10}^{-10}$
NLS in $[0,1]$	$1.15\times {10}^{-10}$	$5.71\times {10}^{-11}$	$1.97\times {10}^{-9}$	$1.07\times {10}^{-9}$
Original [10]	$7.39\times {10}^{-11}$	$3.73\times {10}^{-11}$	$5.64\times {10}^{-9}$	$3.14\times {10}^{-9}$
Papageorgiou [37]	$2.39\times {10}^{-10}$	$8.09\times {10}^{-11}$	$1.63\times {10}^{-8}$	$5.21\times {10}^{-9}$
Kosti I [38]	$5.43\times {10}^{-10}$	$1.37\times {10}^{-10}$	$3.54\times {10}^{-8}$	$8.27\times {10}^{-9}$
Dormand [2]	$2.74\times {10}^{-8}$	$1.21\times {10}^{-8}$	$2.07\times {10}^{-6}$	$1.14\times {10}^{-6}$
Kosti II [39]	$7.28\times {10}^{-8}$	$3.83\times {10}^{-8}$	$2.23\times {10}^{-6}$	$1.17\times {10}^{-6}$
Fehlberg [2]	$1.11\times {10}^{-8}$	$5.82\times {10}^{-9}$	$6.42\times {10}^{-7}$	$3.28\times {10}^{-7}$
Triantafyllidis [40]	$4.69\times {10}^{-8}$	$2.32\times {10}^{-8}$	$2.71\times {10}^{-6}$	$1.31\times {10}^{-6}$
Kovalnogov [19]	$3.90\times {10}^{-10}$	$1.05\times {10}^{-10}$	$2.69\times {10}^{-8}$	$6.84\times {10}^{-9}$
Jerbi [20]	$6.25\times {10}^{-10}$	$1.89\times {10}^{-10}$	$4.22\times {10}^{-8}$	$1.20\times {10}^{-8}$
	$\Delta t=1/20$		$\Delta t=1/10$
NLS	$2.09\times {10}^{-7}$	$5.16\times {10}^{-8}$	$2.37\times {10}^{-5}$	$4.20\times {10}^{-6}$
NLS in $[0,1]$	$2.24\times {10}^{-7}$	$8.15\times {10}^{-8}$	$2.62\times {10}^{-5}$	$5.33\times {10}^{-6}$
Original [10]	$4.78\times {10}^{-7}$	$1.99\times {10}^{-7}$	$4.51\times {10}^{-5}$	$1.20\times {10}^{-5}$
Papageorgiou [37]	$1.22\times {10}^{-6}$	$3.17\times {10}^{-7}$	$9.92\times {10}^{-5}$	$1.81\times {10}^{-5}$
Kosti I [38]	$2.42\times {10}^{-6}$	$4.92\times {10}^{-7}$	$1.74\times {10}^{-4}$	$2.72\times {10}^{-5}$
Dormand [2]	$1.27\times {10}^{-4}$	$7.03\times {10}^{-5}$	$5.23\times {10}^{-3}$	$2.88\times {10}^{-3}$
Kosti II [39]	$6.55\times {10}^{-5}$	$3.44\times {10}^{-5}$	$1.78\times {10}^{-3}$	$9.25\times {10}^{-4}$
Fehlberg [2]	$3.28\times {10}^{-5}$	$1.56\times {10}^{-5}$	$1.23\times {10}^{-3}$	$3.89\times {10}^{-4}$
Triantafyllidis [40]	$1.39\times {10}^{-4}$	$6.20\times {10}^{-5}$	$5.04\times {10}^{-3}$	$1.37\times {10}^{-3}$
Kovalnogov [19]	$2.09\times {10}^{-6}$	$4.14\times {10}^{-7}$	$1.81\times {10}^{-4}$	$2.35\times {10}^{-5}$
Jerbi [20]	$3.10\times {10}^{-6}$	$7.33\times {10}^{-7}$	$2.89\times {10}^{-4}$	$4.24\times {10}^{-5}$
	$\Delta t=1/5$		$\Delta t=2/5$
NLS	$1.54\times {10}^{-3}$	$4.87\times {10}^{-4}$	$6.83\times {10}^{-1}$	$8.00\times {10}^{-2}$
NLS in $[0,1]$	$1.35\times {10}^{-3}$	$2.78\times {10}^{-4}$	-	-
Original [10]	$3.21\times {10}^{-3}$	$5.49\times {10}^{-4}$	-	-
Papageorgiou [37]	$9.07\times {10}^{-3}$	$8.96\times {10}^{-4}$	-	-
Kosti I [38]	$1.36\times {10}^{-2}$	$1.38\times {10}^{-3}$	-	-
Dormand [2]	$9.44\times {10}^{-2}$	$2.90\times {10}^{-2}$	-	-
Kosti II [39]	$6.19\times {10}^{-2}$	$2.06\times {10}^{-2}$	-	-
Fehlberg [2]	$5.09\times {10}^{-2}$	$2.72\times {10}^{-2}$	-	-
Triantafyllidis [40]	$3.65\times {10}^{-1}$	$1.97\times {10}^{-1}$	-	-
Kovalnogov [19]	$1.70\times {10}^{-2}$	$1.13\times {10}^{-3}$	-	-
Jerbi [20]	$2.89\times {10}^{-2}$	$2.18\times {10}^{-3}$	-	-

presents the maximum global solution error and the maximum relative mass error of the selected methods when solving the NLS Equation (10) for $\Delta x=\Delta y=0.1$ and six values of $\Delta t$ ranging from ${\displaystyle \frac{1}{80}}$ to ${\displaystyle \frac{2}{5}}$. We exclude methods developed specifically for the Two-Body and N-Body problems. The table indicates the superior performance of the PSO-optimised NLS method compared with all other methods, including the Original method developed specifically for the NLS equation, for both small and large step lengths. At the largest step length $\Delta t=2/5$, all other methods either diverged or produced a maximum global error exceeding one, indicating instability in contrast to the NLS method, which remained stable and accurate.

As shown in Table 4, the NLS method performs best overall. Figure 2 illustrates this by plotting the maximum global solution error against the function evaluations for the best seven methods solving the NLS Equation (10), using the setup described in Section 3.1. Both newly constructed methods, NLS and NLS in [0, 1], outperform the Original method across all tested step lengths. The unbounded NLS method also exhibits superior stability, achieving better accuracy at larger step lengths and faster convergence in that regime compared with the bounded variant.

6.3. Performance on the Two-Body Problem

Although the Two-Body problem was used for training before testing on the N-Body problem, we also evaluate the methods on the former problem over a longer integration interval, as described in Section 3.2.

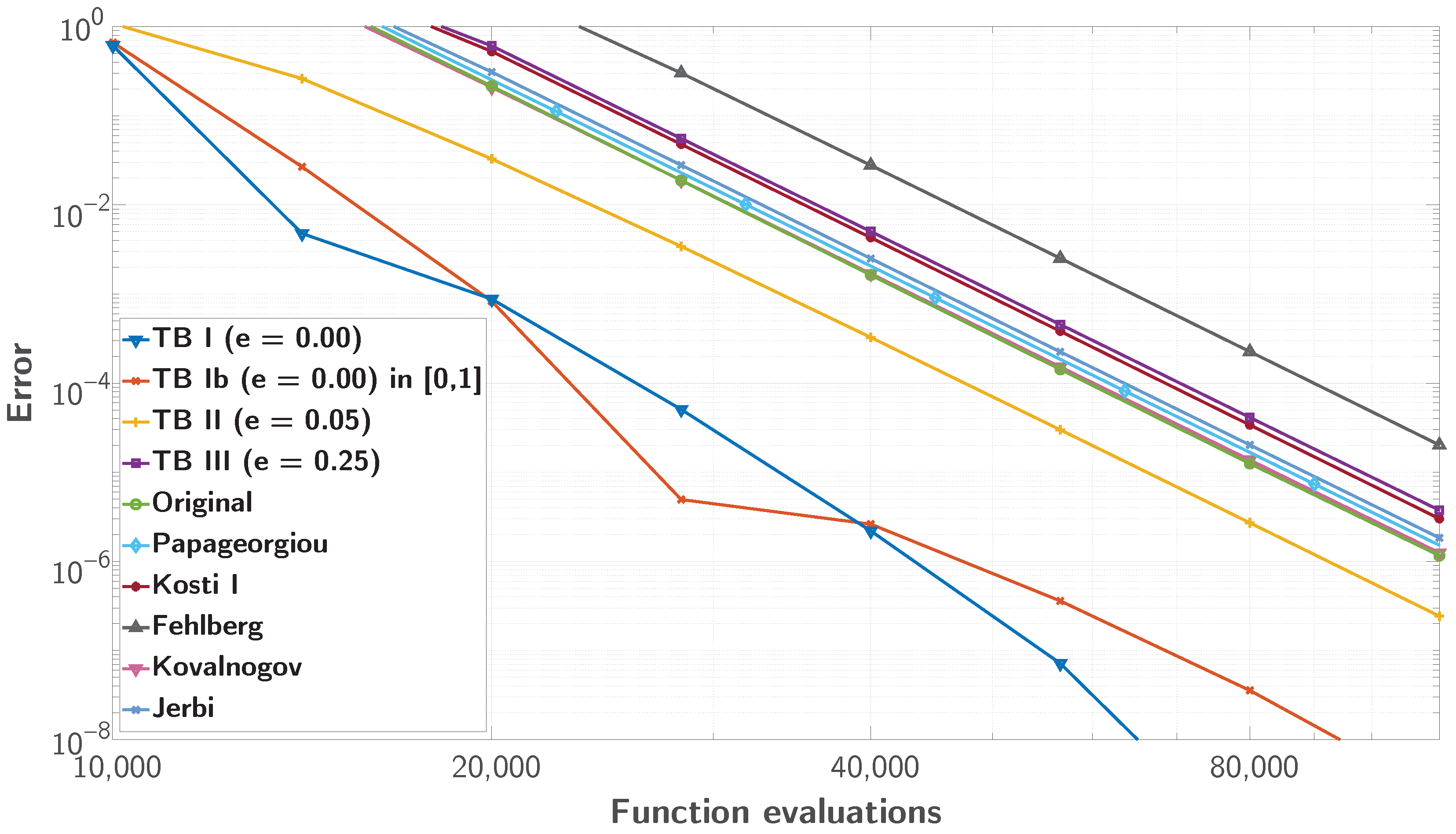
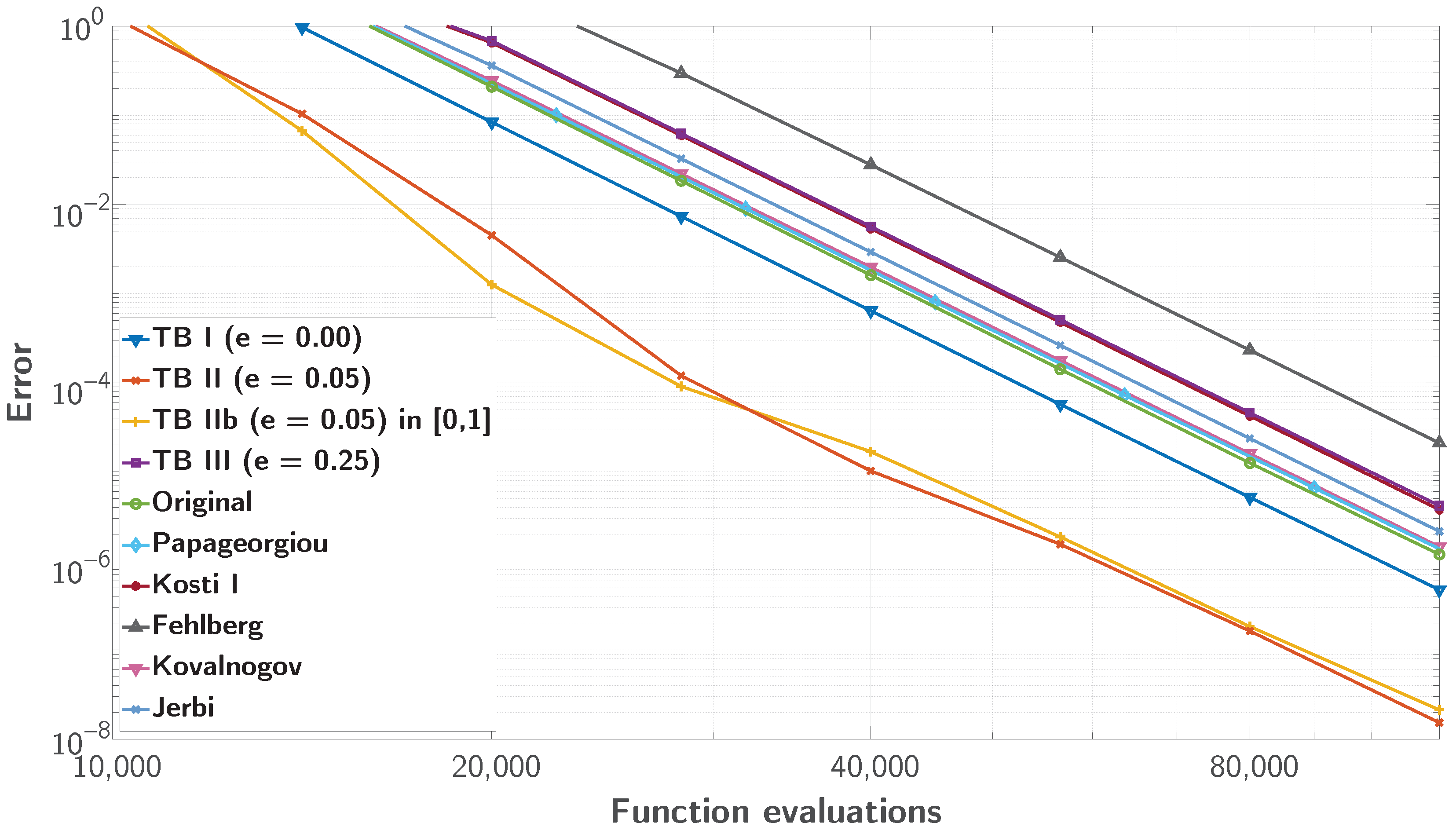
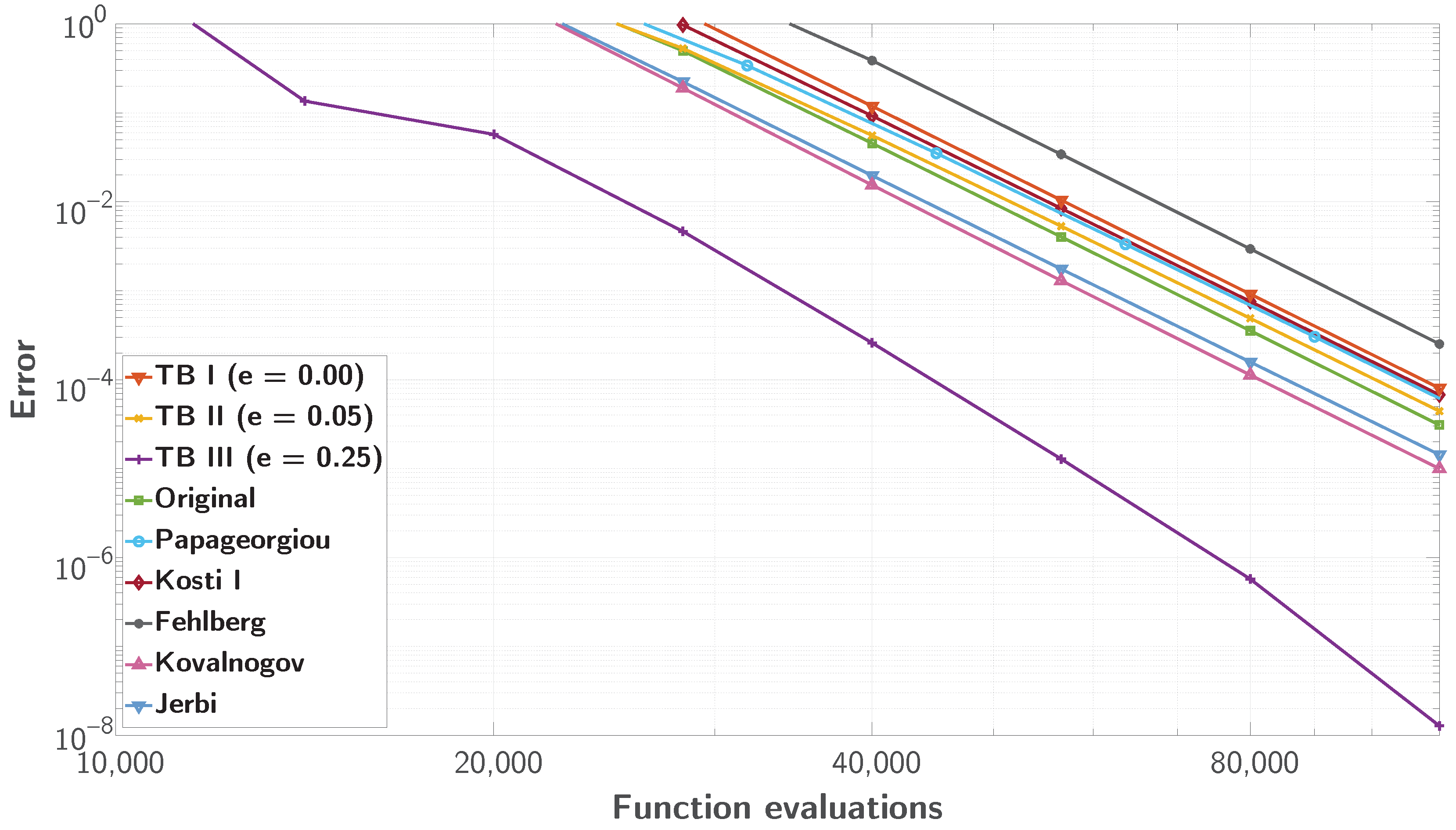
Figure 3, Figure 4 and Figure 5 show the efficiency results for the Two-Body problem (17) for eccentricities $e=0$, $e=0.05$, and $e=0.25$, respectively. In each case, we present the three best TB methods, i.e., the ones without the constraint $c_i\in [0,1]$, along with the corresponding bounded variant trained for that eccentricity, where available. For example, in Figure 5, there is no such method, as the coefficients of the best method for $e=0.25$, TB III, already satisfy the constraint, as seen in the last row of Table 2.

The plots illustrate that the most efficient methods achieve lower global error with fewer function evaluations across varying values of e. For smaller e, the problem is less stiff, allowing certain methods to maintain accuracy with relatively low computational cost. As e increases, reflecting greater oscillatory behaviour and complexity, methods trained specifically for those eccentricities require fewer function evaluations compared to the other methods to achieve accuracy, thus becoming more efficient. This variation highlights that method efficiency depends on the problem regime defined by e and the corresponding targeted training of the methods. In conclusion, the methods trained on the corresponding eccentricity outperform all others, including those trained for different eccentricities, by up to three orders of magnitude in global error.

6.4. Performance on the N-Body Problem

To assess generalisability to more complex systems, we test the methods trained for the Two-Body problem on the N-Body problem.

Table 5. Maximum global solution error of the selected methods in the N-Body problem (19) for eight different step lengths.

Method\Step Length	$250\sqrt{2}$	250	$125\sqrt{2}$	125	$62.5\sqrt{2}$	62.5	$31.25\sqrt{2}$	31.25
TB II ($e=0.05$)	$1.63\times {10}^{-1}$	$4.63\times {10}^{-3}$	$1.74\times {10}^{-4}$	$4.60\times {10}^{-5}$	$5.78\times {10}^{-6}$	$6.23\times {10}^{-7}$	$6.18\times {10}^{-8}$	$3.93\times {10}^{-9}$
TB IIb ($e=0.05$) in $[0,1]$	$1.06\times {10}^{-1}$	$7.04\times {10}^{-4}$	$3.22\times {10}^{-4}$	$4.55\times {10}^{-5}$	$4.81\times {10}^{-6}$	$4.86\times {10}^{-7}$	$6.47\times {10}^{-8}$	$2.06\times {10}^{-8}$
TB I ($e=0$)	2.11	$2.00\times {10}^{-1}$	$1.78\times {10}^{-2}$	$1.59\times {10}^{-3}$	$1.43\times {10}^{-4}$	$1.30\times {10}^{-5}$	$1.19\times {10}^{-6}$	$1.11\times {10}^{-7}$
TB Ib ($e=0$) in $[0,1]$	3.18	$3.50\times {10}^{-1}$	$3.19\times {10}^{-2}$	$2.90\times {10}^{-3}$	$2.63\times {10}^{-4}$	$2.42\times {10}^{-5}$	$2.24\times {10}^{-6}$	$2.13\times {10}^{-7}$
TB III ($e=0.25$)	8.17	1.49	$1.42\times {10}^{-1}$	$1.29\times {10}^{-2}$	$1.16\times {10}^{-3}$	$1.04\times {10}^{-4}$	$9.42\times {10}^{-6}$	$8.10\times {10}^{-7}$
Original [10]	5.00	$4.79\times {10}^{-1}$	$4.10\times {10}^{-2}$	$3.55\times {10}^{-3}$	$3.08\times {10}^{-4}$	$2.71\times {10}^{-5}$	$2.65\times {10}^{-6}$	$4.57\times {10}^{-7}$
Papageorgiou [37]	2.33	$2.28\times {10}^{-1}$	$2.02\times {10}^{-2}$	$1.79\times {10}^{-3}$	$1.61\times {10}^{-4}$	$1.45\times {10}^{-5}$	$1.31\times {10}^{-6}$	$1.20\times {10}^{-7}$
Kosti I [38]	8.84	1.43	$1.36\times {10}^{-1}$	$1.22\times {10}^{-2}$	$1.09\times {10}^{-3}$	$9.67\times {10}^{-5}$	$8.59\times {10}^{-6}$	$7.63\times {10}^{-7}$
Dormand [2]	-	-	-	-	$6.25\times {10}^{-2}$	$1.87\times {10}^{-2}$	$4.00\times {10}^{-3}$	$7.67\times {10}^{-4}$
Kosti II [39]	-	-	$9.24\times {10}^{-1}$	1.67	$3.10\times {10}^{-1}$	$5.49\times {10}^{-2}$	$9.70\times {10}^{-3}$	$1.71\times {10}^{-3}$
Fehlberg [2]	-	5.63	$6.82\times {10}^{-1}$	$6.21\times {10}^{-2}$	$5.59\times {10}^{-3}$	$4.99\times {10}^{-4}$	$4.43\times {10}^{-5}$	$3.93\times {10}^{-6}$
Triantafyllidis [40]	-	-	3.81	$4.51\times {10}^{-1}$	$4.12\times {10}^{-2}$	$3.71\times {10}^{-3}$	$3.34\times {10}^{-4}$	$3.02\times {10}^{-5}$
Kovalnogov [19]	5.22	$5.52\times {10}^{-1}$	$5.02\times {10}^{-2}$	$4.49\times {10}^{-3}$	$4.03\times {10}^{-4}$	$3.63\times {10}^{-5}$	$3.28\times {10}^{-6}$	$2.99\times {10}^{-7}$
Jerbi [20]	8.37	$8.05\times {10}^{-1}$	$7.38\times {10}^{-2}$	$6.61\times {10}^{-3}$	$5.91\times {10}^{-4}$	$5.31\times {10}^{-5}$	$4.79\times {10}^{-6}$	$4.35\times {10}^{-7}$

presents the maximum global error for each method applied to the N-Body problem (19) for eight different step lengths in a geometric sequence. We include all methods except the two methods developed for the NLS equation. As observed in Section 3.3, Table 1, the dominant eccentricity of the bodies with the highest frequencies, which are the main contributors to the maximum global error [34], is approximately $e\approx 0.05$. Indeed, the results show that the best performance in the five outer planet problem is achieved by using the method whose coefficients have been trained for the simpler Two-Body problem with $e=0.05$. Methods produced by training the coefficients in the Two-Body problem with orbital eccentricities $e=0$ or $e=0.25$ yielded much poorer results.

A desirable property of a numerical method is to maintain its theoretical order of accuracy over a long range of step lengths that do not necessarily include the unstable region (very large step lengths) and the region where the round-off error becomes significant (very small step lengths).

We estimate the experimental order of accuracy $\widehat{p}$ using

$${\displaystyle \widehat{p}=\frac{log\left(\frac{{\Vert E_i\Vert }_{\infty }}{{\Vert E_{i+1}\Vert }_{\infty }}\right)}{log\left(\frac{h_i}{h_{i+1}}\right)}}$$

(23)

Table 6. Experimental order of accuracy computed from successive errors and step lengths for the N-Body problem (19), according to Equation (23) and $h_i=250·2^{{\displaystyle \frac{2-i}{2}}},i=1,\dots ,8$.

Method\Step Length	${\mathit{h}}_1$		${\mathit{h}}_2$		${\mathit{h}}_3$		${\mathit{h}}_4$		${\mathit{h}}_5$		${\mathit{h}}_6$		${\mathit{h}}_7$		${\mathit{h}}_8$
TB II ($e=0.05$)		10.3		9.5		3.8		6.0		6.4		6.7		8.0
TB IIb ($e=0.05$) in $[0,1]$		14.5		2.3		5.6		6.5		6.6		5.8		3.3
TB I ($e=0$)		6.8		7.0		7.0		7.0		6.9		6.9		6.9
TB Ib ($e=0$) in $[0,1]$		6.4		6.9		6.9		6.9		6.9		6.9		6.8
TB III ($e=0.25$)		4.9		6.8		6.9		7.0		6.9		6.9		7.1
Original [10]		6.8		7.1		7.1		7.1		7.0		6.7		5.1
Papageorgiou [37]		6.7		7.0		7.0		7.0		7.0		6.9		6.9
Kosti I [38]		5.3		6.8		7.0		7.0		7.0		7.0		7.0
Dormand [2]		-		-		-		-		3.5		4.5		4.8
Kosti II [39]		-		-		5.0		4.9		5.0		5.0		5.0
Fehlberg [2]		-		6.1		6.9		7.0		7.0		7.0		7.0
Triantafyllidis [40]		-		-		6.2		6.9		7.0		7.0		6.9
Kovalnogov [19]		6.5		6.9		7.0		7.0		6.9		6.9		6.9
Jerbi [20]		6.8		6.9		7.0		7.0		7.0		6.9		6.9

shows that all new methods exhibit consistent convergence behaviour and retain the order on average. While some fluctuations exist, a drop in error is typically followed by an increase, so the achieved accuracy often exceeds the values predicted by the average order, which is also confirmed in Figure 6.

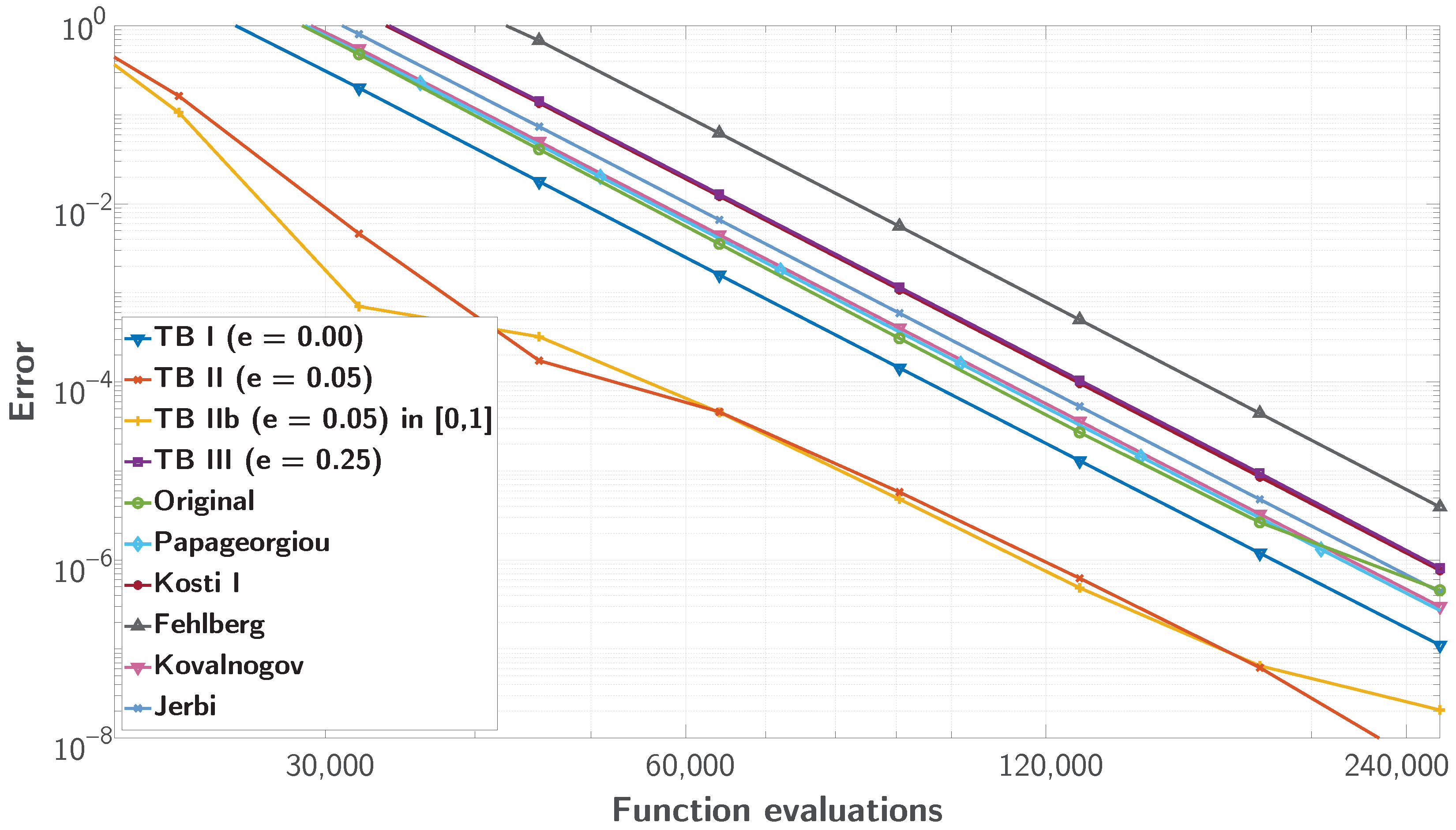
As seen in Figure 6, the slope of each method, representing its experimental order of accuracy, agrees with the results presented in Table 6 for the N-Body problem. Notably, the behaviour of all methods for the N-Body problem (19) closely mirrors that of the Two-Body problem for eccentricity $e=0.05$. Even though TB II and TB II in $[0,1]$ were trained on a much simpler problem over a significantly shorter integration interval, they retain their performance characteristics when applied to the more complex system. It is noteworthy that the training TB problem (17) has about 16 full oscillations, whereas for the N-Body problem (19), the fastest revolving body, Jupiter, completes about 230 revolutions.

7. Discussion

There are several aspects that contributed to the increased performance of the evolutionarily optimised methods compared with methods optimised by classical techniques or those designed to possess local properties. First of all, the objective function under minimisation considers the efficiency of the new method compared with a benchmark method, so the objective function is explicitly designed to maximise the efficiency of the new method relative to an established benchmark, embedding performance comparison into the optimisation itself. The objective function also ensures that it covers the efficiency across a range of accuracies, which also covers small accuracies, thus improving the stability characteristics. To reduce optimisation time and enhance results, the training was performed on simpler versions of the problems, e.g., using short integration intervals or alternative but related problems. Moreover, other integration parameters, such as the step lengths, were tuned individually for each problem to maximise efficiency. This allowed experimentation with relaxed conditions, such as removing typical RK bounds on the coefficients.

The evolutionary optimisation allowed the new methods to be more efficient than their classically optimised counterparts in both local truncation error coefficients and stability intervals. The newly developed methods outperformed existing literature methods tailored to periodic or oscillatory problems. Notably, this was accomplished without explicitly enforcing local properties such as phase lag or amplification error.

A particularly striking result is the training efficiency, as the Two-Body problem required significantly less computational time and a shorter integration interval compared with the more complex N-Body problem. Comparing the function evaluations and CPU time for different accuracies, we determined that the integration of the training problem required approximately 70 times fewer evaluations and less time than the testing problem. In particular, for the Two-Body and N-Body problems, the evolutionary algorithm successfully optimised methods for high eccentricities, where solutions deviate significantly from sinusoidal form, overcoming the limitations of classical methodologies that rely on local properties such as phase-lag minimisation, amplification-error control, and trigonometric fitting.

The evolutionary optimisation process, using the selected PSO parameters, is sufficiently robust to require minimal adjustment when applied to a different problem, aside from possible changes to the step length range.

Nevertheless, some limitations of the PSO-based approach remain. The computational cost is dominated by evaluating the global error through time integration, which may increase substantially when scaling to higher-order methods with more free parameters. Additionally, PSO can be prone to premature convergence in complex or multimodal search landscapes, potentially resulting in suboptimal solutions. To address these issues, hybrid optimisation strategies or adaptive parameter tuning could be considered in future work. Nevertheless, PSO remains an effective and practical choice for the current problem, balancing exploration and exploitation while allowing parallel candidate evaluation.

Ideally, full optimisation of a parametric RK method would be achieved without any predetermined coefficients, and, after solving the system of equations, all coefficients would then depend on a set of free parameters, acting as degrees of freedom. However, this approach remains infeasible with current hardware, due to its high memory and computational demands. Alternative strategies, such as applying simplifying assumptions, can make the process more tractable but introduce additional constraints that limit the extent of optimisation. In practice, it is not yet possible to eliminate the use of predetermined coefficients or simplifying assumptions in the development of parametric RK methods. Nevertheless, reducing their use remains a future goal, as doing so would better highlight the potential of evolutionary optimisation.

However, the methodology has the potential to be applied to a wider range of differential problems. Its direct operation in the parameter space of Runge–Kutta coefficients means that different problem classes could be addressed by selecting appropriate training problems and parameter constraints. While we have not yet tested these extensions, the general framework is flexible enough to be explored in future work.

8. Conclusions

In this article, we proposed a new optimisation strategy for selecting RK coefficients based on evolutionary computation techniques. This strategy seeks to optimise the global behaviour over a training problem, rather than local properties as targeted by classical approaches. In some cases, the training problem requires nearly two orders of magnitude less computational effort than the testing problem. We also introduced a new objective function designed to improve the method’s performance relative to a benchmark. The strategy considers a wide range of accuracies, systematically and efficiently, overcoming challenges such as local minima in the free coefficient space and the lack of derivative information for the objective function. We removed typical coefficient bounds that govern RK methods, such as $c_i\in [0,1]$, and achieved excellent results in local stability, error characteristics, and global performance. Finally, the methodology uncovers structural patterns in coefficient values when optimising for high eccentricities, where solutions deviate from sinusoidal behaviour, offering insights that can guide coefficient predetermination in classical method design.

The methodology is general and can be applied to any type of problem. Here, we used the NLS equation and the N-Body problem (the latter tested over a long-time integration interval), which are important problems in quantum physics and astronomy, respectively. Future work will focus on applying the methodology to additional problem classes, incorporating a broader set of representative training problems to further enhance the generalisability of the resulting methods.