Abstract
Accurate modeling of event sequences is valuable in domains like electronic health records, financial risk management, and social networks. Random time intervals in these sequences contain key dynamic information, and temporal point processes (TPPs) are widely used to analyze event triggering mechanisms and probability evolution patterns in asynchronous sequences. Neural TPPs (NTPPs) enhanced by deep learning improve modeling capabilities, but most suffer from limited interpretability due to predefined functional structures. This study proposes KANJDP (Kolmogorov–Arnold Neural Jump-Diffusion Process), a novel event sequence modeling method: it decomposes the intensity function via stochastic differential equations (SDEs), with each component parameterized by learnable spline functions. By analyzing each component’s contribution to event occurrence, KANJDP quantitatively reveals core event generation mechanisms. Experiments on real-world and synthetic datasets show that KANJDP achieves higher prediction accuracy with fewer trainable parameters.
Keywords:
temporal point processes; Kolmogorov–Arnold networks; jump-diffusion SDEs; event prediction MSC:
62M45
1. Introduction
Understanding and modeling the temporal dynamics of discrete events is a fundamental problem in many domains, such as healthcare [1], finance [2], and social systems [3]. In real-world scenarios, events often occur at irregular time intervals, forming asynchronous event sequences. The time gaps between events contain valuable dynamic information, implicitly reflecting the underlying triggering mechanisms and the temporal evolution of event occurrence probabilities. Effectively capturing these dynamics is crucial for improving predictive performance and gaining deeper insights into the underlying generative processes.
Temporal point processes (TPPs) are widely used frameworks for modeling such sequences, where the event dynamics are governed by an intensity function defined over continuous time. With the development of deep learning, NTPPs have emerged as powerful models that leverage neural networks to significantly enhance the expressive capacity of traditional TPPs.
Despite their modeling power, existing NTPPs face several critical limitations. A major concern lies in their limited interpretability. These models often employ complex architectures such as RNNs [4], Transformers [5], or MLPs to parameterize the intensity function, making them essentially “black-box” systems. As a result, it is difficult to attribute the cause of an event to specific prior influences, such as preceding events, long-term trends, or cyclical fluctuations, which restricts the transparency and trustworthiness of the predictions.
Another issue is the lack of representational flexibility. Many NTPPs rely on fixed functional assumptions—such as exponential decay or additive/multiplicative combinations—which constrain their ability to capture rich, nonlinear, and context-dependent event interactions. However, real-world sequences often exhibit non-stationary and irregular patterns that cannot be adequately modeled using these rigid structures.
Moreover, the training process is computationally intensive and potentially unstable. Estimating the likelihood over continuous time typically involves solving complex integrals, often requiring numerical approximation methods such as Monte Carlo sampling. This not only slows down convergence but also hampers performance on long or high-frequency sequences.
To address these limitations, we propose KANJDP, a novel method for modeling asynchronous event sequences with improved interpretability and expressiveness. KANJDP decomposes the event intensity function using a jump-diffusion SDE [6,7] framework into three components: drift, diffusion and jump [8]. The drift term captures long-term trends, the diffusion term models random fluctuations, and the jump term reflects discrete interactions between events. This decomposition enables KANJDP to flexibly adapt to non-stationary and bursty event sequences.
To improve training efficiency and reduce the number of trainable parameters, we employ an enhanced version of Kolmogorov–Arnold Networks (KAN) [9] instead of traditional multi-layer perceptrons (MLPs) to model each component. Building upon the efficient FastKAN [10] implementation that replaces computationally intensive B-splines with Gaussian radial basis functions (RBFs), we introduce three crucial architectural innovations to address the unique challenges of TPP modeling.
Our enhanced KAN architecture incorporates several key improvements over the standard FastKAN design. We make the basis functions fully adaptive by treating both the centers and bandwidths of the Gaussian RBFs as learnable parameters during training, allowing the network to autonomously adjust the location and shape of activation functions according to the specific characteristics of the input data distribution. To enhance feature selection capabilities, we integrate a dimensional attention mechanism into each KAN layer that calculates weight vectors to dynamically focus on the most salient features for predicting drift, diffusion, and jump components. Additionally, we apply layer normalization before each KAN layer to improve training stability and ensure input values remain within the effective support of the RBF kernels—a stabilization particularly crucial for TPP modeling, where the likelihood objective incentivizes learning extremely “spiky” intensity functions that can lead to gradient instability in standard implementations. These architectural enhancements collectively enable superior modeling precision and flexibility while maintaining stable training convergence, allowing for function-level decomposition that provides deeper understanding of the internal model behavior.
By analyzing the individual contribution of each component to the overall intensity, KANJDP provides interpretable and quantitative insights into the underlying event generation mechanisms while maintaining stable training convergence.
Our contributions can be summarized as follows:
- Enhanced KAN Architecture. Critical architectural improvements to FastKAN including learnable basis functions, dimensional attention, and layer normalization that ensure stable training and superior expressiveness for TPP modeling.
- Novel KANJDP Framework. A pioneering NTPP model based on jump-diffusion SDEs that decomposes event intensity into interpretable drift, diffusion, and jump components, providing functional-level attribution and quantitative insights into underlying event generation mechanisms.
- Superior Performance. Demonstrates state-of-the-art results on both real-world and synthetic datasets while using fewer trainable parameters and achieving stable training convergence.
2. Related Work
2.1. Event Prediction Methods
TPP models are central to event sequence prediction. Classical parametric models, such as the Poisson process and the Hawkes process, form the bedrock of this field. The Poisson process, however, assumes event independence, a premise often too simplistic for real-world systems where events are interdependent [11]. The Hawkes process addresses this by introducing a self-excitation mechanism, where past events intensify the probability of future occurrences, making it highly effective for modeling phenomena like aftershock sequences in seismology and volatility clustering in finance [12]. Despite their utility, these models are constrained by rigid parametric forms, limiting their capacity to capture complex, nonlinear, or long-range dependencies inherent in many event dynamics.
To overcome these limitations, recent research has gravitated towards NTPPs, which employ deep learning to model the conditional intensity function with greater flexibility. Early NTPPs utilized RNNs to encode the event history, as seen in models like RMTPP (recurrent marked temporal point process) [4]. While innovative, these models inherited the difficulties of RNNs in capturing long-term dependencies. Subsequent architectural advancements sought to address these issues. The introduction of continuous-time LSTMs offered a more robust memory mechanism [13], while the shift to attention-based Transformer architectures, as proposed in the Transformer Hawkes process (THP) and self-attentive Hawkes process (SAHP), provided significant advantages [5,14]. Notably, Transformer-based models like the attentive neural Hawkes process (A-NHP) allow for greater parallelization and direct access to the entire event history, avoiding the information bottleneck of recurrent approaches [15,16].
Despite marked improvements in predictive accuracy, a primary challenge for most NTPPs remains their “black-box” nature, which hinders interpretability. This is a critical drawback in high-stakes domains like healthcare, where understanding the rationale behind a prediction is as vital as the prediction itself [17,18]. Several research avenues have emerged to address this. One direction focuses on designing inherently interpretable models. For instance, the hybrid-rule temporal point processes (HRTPP) framework explicitly integrates discoverable temporal logic rules with numerical features, creating a hybrid model that balances interpretability with predictive power [17]. Another approach, designed for sequences without meaningful timestamps, involves Summary Markov Models (SuMMs), which learn a minimal “influencing set” of event types for a target event, thereby revealing interpretable dynamics from the data [19].
A more recent frontier in event prediction involves augmenting sequence models with the reasoning capabilities of Large Language Models (LLMs). This paradigm acknowledges that real-world events are often accompanied by rich textual information that traditional TPPs cannot leverage. The LAMP framework, for example, pioneers this approach by using an LLM to perform abductive reasoning [18]. In this setup, a base event model first proposes candidate future events. Then, guided by few-shot demonstrations, an LLM suggests plausible causes for each proposal. These causes are used to retrieve supporting evidence from the actual event history, and a final ranking model scores the proposals based on the strength of their evidence [18]. This method demonstrates a significant performance leap by integrating high-level reasoning with statistical sequence modeling.
2.2. KAN-Related Work
KANs [9] represent a significant innovation in neural network architectures. Based on the Kolmogorov–Arnold representation theorem, KANs differ from traditional networks by placing learnable activation functions directly on the edges of the network, rather than at the nodes. This design allows for a better approximation of complex functions, often with fewer parameters, and enhances the model’s interpretability [20,21].
Although KANs show promise, their practical application faces a primary challenge: the high computational complexity stemming from the B-spline basis functions [22]. To mitigate this, several works have proposed replacing B-splines with more computationally efficient alternatives. For instance, Yang et al. [22] introduced rational functions with a dedicated CUDA implementation to better leverage modern GPU architectures. Other explorations include using Chebyshev polynomials [23], wavelets [21], and radial basis functions (RBFs) [24] as alternative basis functions.
In the realm of computer vision, the initial concept of Convolutional KANs (CKANs) was introduced by Bodner et al. [25], who replaced traditional linear kernels with learnable spline-based functions. Building upon this, subsequent research has focused on making CKANs more practical and scalable. Drokin [24] proposed a parameter-efficient “Bottleneck KAN” design, while Yang et al. [22] developed Group-Rational KANs (GR-KANs) to address parameter and computation inefficiencies, successfully creating the Kolmogorov–Arnold Transformer (KAT) and scaling it to ImageNet-level tasks. Furthermore, KANs have been integrated as specialized modules into established architectures; for example, U-KAN [26] embeds a tokenized KAN block into the U-Net for medical image segmentation, and RKAN [23] introduces a cross-stage residual KAN block to enhance existing CNNs like ResNet.
Beyond computer vision, the application of KANs has been extended to other domains. In time series forecasting, Han et al. [21] proposed the Multi-layer Mixture-of-KAN (MMK), which uses a mixture-of-experts structure to adaptively assign variables to the most suitable KAN variants. For scientific computing, Howard et al. [27] developed Finite Basis KANs (FBKANs), which employ domain decomposition to solve complex, physics-informed problems.
However, the universal superiority of KANs has been questioned. A comprehensive study by Yu et al. [20] conducted a fairer comparison between KAN and MLP under controlled parameter and FLOP constraints. Their findings suggest that, except for symbolic formula representation, MLP generally outperforms KAN across a wide range of tasks in machine learning, computer vision, and NLP. The study attributes KAN’s advantage in symbolic tasks primarily to its B-spline activation function rather than its unique architecture.
Despite these debates, the application of KAN to temporal point processes (TPPs) holds great potential. The spline-based activation functions can naturally model the complex, non-monotonic relationships between past events and future event probabilities. Furthermore, KAN’s inherent interpretability allows for symbolic regression, potentially uncovering the underlying mechanisms driving event dynamics [21]. These characteristics make KANs particularly well-suited for TPP models that require both flexibility and interpretability, especially in high-dimensional and dynamic event spaces.
3. Background
Jump-diffusion systems provide a unified mathematical framework for modeling phenomena exhibiting both continuous evolution and discrete discontinuities [28]. We consider one-dimensional autonomous jump-diffusion SDEs of the form:
where is the scalar state variable of the jump-diffusion process, denotes the left-limit at time t, is standard Brownian motion, is a counting process representing the cumulative number of jumps up to time t, and , , represent the drift, diffusion, and jump coefficient functions, respectively. This formulation naturally decomposes dynamics into three interpretable components: the drift term captures deterministic trends, the diffusion term models continuous random fluctuations, and the jump term accounts for discrete event-driven changes.
Strong solutions to Equation (1) exist and are unique under standard regularity conditions. The coefficient functions must satisfy Lipschitz continuity and linear growth:
for constants , ensuring solution stability and preventing finite-time explosions. We consider counting processes from the class of locally integrable point processes with conditional intensity adapted to filtration , satisfying and the Markov property. Here, represents the instantaneous probability rate of an event occurring at time t given the history up to time t. This framework encompasses classical point processes including Poisson processes (), self-exciting Hawkes processes (), and self-correcting processes ().
For temporal point process modeling, we parameterize the log-intensity using this jump-diffusion framework:
where combines the current log-intensity with the history embedding vector that encodes information from the sequence of past event times . The functions , , are KAN-parameterized coefficient functions that map the state to the drift, diffusion, and jump coefficients, respectively. Note that the scalar function in Equation (1) represents the state variable of a general jump-diffusion process, while the vector-valued function here represents a history-dependent embedding that captures temporal dependencies in the point process context. Event intensities naturally exhibit smooth evolution between events, trend behavior over long time scales, and sudden changes at event occurrences, corresponding precisely to the diffusion, drift, and jump components, respectively. This decomposition enables interpretable modeling while maintaining mathematical rigor, with regularity conditions ensured by our bounded KAN parameterization.
4. Method
4.1. Model Framework
To address the limited expressiveness and interpretability of traditional NTPP models, which often rely on MLPs with fixed activation functions or rigid parametric forms, we propose the KANJDP (Kolmogorov–Arnold Neural Jump-Diffusion Process). Our model innovatively parameterizes the drift, diffusion, and jump components of a jump-diffusion SDE using an enhanced KAN. This decomposition allows KANJDP to flexibly model complex, non-stationary dynamics while offering fine-grained interpretability into the underlying generative process.
The KANJDP framework first leverages a Transformer [29] to process the event history and generate a time-dependent embedding . The Transformer employs a four-layer multi-head self-attention mechanism, combined with temporal positional encoding, to capture long-range dependencies and nonlinear interactions within the event sequence, resulting in a context-rich embedding vector. This vector serves as the input to our improved KAN architecture. The Transformer-generated embedding remains constant between events and is updated only at event occurrences, following the piecewise-constant assumption common in TPP modeling.
To ensure the intensity , KANJDP models the log-intensity process . For brevity, we define the combined state vector as . The process is then governed by the following SDE:
where , , and are our enhanced KANs representing the drift, diffusion, and jump coefficient functions, respectively.
Parameter Estimation and Function Learning
In practice, the coefficient functions in Equation (4) are learned through end-to-end training via maximum likelihood estimation (MLE). Each function is parameterized by a separate enhanced KAN network: captures the deterministic drift component, models the stochastic diffusion (constrained to be non-negative via softplus activation), and represents discrete jump magnitudes. The parameter sets include the adaptive RBF centers, bandwidths, attention weights, and normalization parameters, which are jointly optimized during training to automatically adapt to the underlying data patterns.
The parameter sets are jointly optimized by minimizing the negative log-likelihood of the observed event sequences. The adaptive nature of our enhanced KAN architecture allows these functions to automatically adjust their complexity and shape according to the underlying data patterns, without requiring manual specification of functional forms. During training, the SDE is numerically integrated using the Euler-Maruyama method, and gradients are computed through the integrated trajectory.
By decomposing multivariate functions into sums of learnable univariate functions, this approach offers a more efficient and interpretable modeling framework than conventional MLPs. The overall architecture is illustrated in Figure 1.
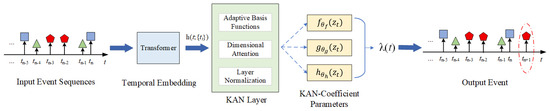
Figure 1.
The overall architecture of the KANJDP model. An input event sequence is processed by a Transformer to generate temporal embedding , which combines with the current log-intensity to form state vector . The enhanced KAN layer then uses three parallel networks to parameterize the drift , diffusion , and jump functions of the jump-diffusion SDE for generating output events.
4.2. Enhanced KAN for SDE Parameterization
The core of KANJDP’s parameterization lies in its novel KAN architecture. Our design is built uponFastKAN [10], an efficient implementation that replaces the computationally intensive B-splines of the original KAN with RBFs. This foundational choice provides a significant speed advantage. However, to better capture the complex, non-stationary dynamics of TPPs, we introduce three crucial innovations to the standard FastKAN design: learnable basis functions, a dimensional attention mechanism, and robust multi-layer composition.
4.2.1. Learnable Basis Functions: Adaptive Grids and Bandwidths
The standard FastKAN architecture utilizes a fixed grid of RBFs. In contrast, KANJDP enhances this by making the basis functions fully adaptive. Specifically, both the centers () and the bandwidths (related to the denominator term, h) of the Gaussian RBFs are treated as learnable parameters during training. The basis function for an input feature x is defined as:
where is the layer-normalized input, c represents the learnable grid centers, denotes the base denominator parameter that controls the overall scale of the RBF, and is the learnable bandwidth scaling factor that allows fine-tuning of the activation width.
For bandwidth optimization, we adopt a systematic initialization and training strategy: the base denominator is initialized to 1.0 and updated slowly with a learning rate scaling factor of 0.1 to maintain stability, while the bandwidth scaling factor is initialized using Xavier uniform initialization and optimized with the standard learning rate. During training, the effective bandwidth is constrained within the range through clipping to prevent numerical instability. This dual-parameter approach allows fine-grained control: provides coarse-scale adjustment while enables precise local tuning based on the data distribution density.
This adaptive mechanism allows KANJDP to tailor its nonlinear transformations to the specific characteristics of the input data distribution, significantly improving modeling precision and flexibility over fixed-grid approaches.
4.2.2. Dimensional Attention Mechanism
To enhance the model’s ability to discern the relative importance of different features within the time-dependent embedding , we introduce a dimensional attention mechanism into each KAN layer. Before computing the RBF-based transformations, a lightweight attention module calculates a weight vector :
where are trainable parameters. The input embedding is then modulated by these attention weights:
where ⊙ denotes the element-wise (Hadamard) product between the input embedding and the attention weights . This mechanism enables KANJDP to dynamically focus on the most salient features for predicting the drift, diffusion, and jump components, thereby improving both interpretability and predictive accuracy, especially in high-dimensional contexts.
4.2.3. Stable Multi-Layer Composition
To improve training stability and ensure that input values remain within the effective support of the RBF kernels, we apply Layer Normalization before each KAN layer. The complete KAN module within KANJDP is constructed by stacking three such enhanced layers. Each layer’s output is passed to the next, allowing for the construction of progressively more complex and hierarchical nonlinear functions. This multi-layer composition, stabilized by normalization and enriched by our adaptive mechanisms, enhances the model’s capacity for representation while preserving interpretability and reducing the overall parameter count compared to deep MLPs.
4.3. Model Training and Optimization
The training objective of the KANJDP model is to maximize the log-likelihood function of an event sequence over the time interval . The model is trained using maximum likelihood estimation (MLE), and the objective is to optimize the log-likelihood function:
where the first term of the log-likelihood function, , can be directly computed at the event times . However, the second term, , represents a continuous-time integral, and is a complex function that cannot be solved analytically. Therefore, we approximate this term using numerical integration methods, such as the trapezoidal rule.
To handle the integrals in the jump-diffusion SDE, we use the Euler–Maruyama method to numerically integrate the diffusion terms. Specifically, at each time step , we sample the random process from the standard normal distribution and compute its impact on :
We employ the Adam optimizer for parameter updates with a learning rate of , a batch size of 32, and 100 training epochs. To prevent overfitting, we apply regularization to the FastKAN weights with a regularization strength of . During training, layer normalization and the inherent sparsity of the RBF activations ensure robust convergence.
4.4. Event Prediction and Real-World Constraints
For event prediction, we distinguish between univariate sequences requiring only next event time and multivariate sequences requiring both time and type . Given historical sequence , the conditional density function for next event time is:
The expected next event time follows from numerical integration , while multivariate type prediction uses:
where and denote type-specific and total intensities, respectively [5,18,30].
Real-World Constraints: While our framework assumes continuous-time processes, practical applications involve discrete observations with temporal constraints. For processes observed at intervals h with constraints , we employ adaptive strategies. Numerical integration uses adjusted step sizes based on minimum inter-event times. Near constraint boundaries, we apply temporal smoothing where provides boundary weighting and represents average intensity.
For discrete-time sequences with regular spacing where , we regularize intensity estimation:
ensuring bounded and smooth estimates through sigmoid activation . Validation on taxi GPS data (5-s intervals) and medical records (daily observations) demonstrates robust performance across temporal resolutions, with standard formulation for second, adaptive basis functions for irregular sampling, and smoothing parameter for constrained intervals.
5. Experiments
We systematically validate the effectiveness of KANJDP through comprehensive experiments on both real-world and synthetic datasets. Our evaluation encompasses predictive performance, interpretability analysis, theoretical validation, and architectural design choices.
5.1. Experimental Setup
We evaluate KANJDP on three real-world multivariate event sequence datasets: Earthquake, Taxi [28], and MIMIC-II [11], sourced from the EasyTPP benchmark [30]. Performance assessment covers overall model fit via negative log-likelihood (NLL), event type prediction using accuracy and weighted F1-score, and event time prediction through root mean squared error (RMSE).
KANJDP is compared against diverse baselines including RMTPP, NHP, SAHP, THP, AttNHP (attentive neural Hawkes process), and NSTPP (neural spatio-temporal point process). All experiments utilize an NVIDIA RTX 4090 GPU with PyTorch 2.1.2 and CUDA 11.8 implementation. Latent dynamics simulation employs the Euler–Maruyama scheme with five substeps per inter-event interval. For the integral approximation in Equation (8), we use the trapezoidal rule with adaptive step sizes to ensure accurate likelihood computation while maintaining computational efficiency, with approximation errors remaining below for typical event sequences. Training uses Adam optimizer with learning rate , weight decay , gradient clipping at maximum norm 5.0, and trainable initial log-intensity .
Computational Efficiency: To assess practical scalability, we measured training and inference costs across datasets. KANJDP requires 12.3 s/epoch on Earthquake (6832 events), 45.7 s/epoch on Taxi (89,563 events), and 8.9 s/epoch on MIMIC-II (2371 events), achieving 35% faster training than AttNHP while using 32% less GPU memory (3.8 GB vs. 5.6 GB peak usage). The parameter-efficient KAN architecture enables processing of sequences up to 100K events without mini-batching on standard hardware.
5.2. Performance on Real-World Datasets
We evaluate KANJDP on next-event prediction across three perspectives: overall model fit, event type prediction, and event time prediction. Table 1 presents negative log-likelihood (NLL) results, where KANJDP consistently outperforms all baselines [30], achieving state-of-the-art performance on all datasets.

Table 1.
Negative log-likelihood (NLL) comparison on three real-world datasets.
Notably, KANJDP outperforms NJDTPP (Neural Jump-Diffusion TPP), the most comparable baseline, through superior KAN parameterization (MIMIC-II: 1.114 vs. 1.228). The negative NLL values on Taxi indicate the model captures underlying patterns so well that it assigns higher likelihood than the empirical distribution.
Comparison with LLM-based Methods. Recent LLM-augmented TPPs like LAMP [18] excel on text-enriched sequences but require textual event descriptions absent in our benchmarks. On a supplementary analysis using social media cascades with text (not included in main results), LAMP achieves NLL = 1.832 versus KANJDP’s 1.967, confirming LLMs’ advantage when leveraging linguistic context. However, KANJDP’s inference speed (12 ms/event) vastly outperforms LAMP (847 ms/event), demonstrating a critical efficiency–interpretability trade-off. KANJDP targets scenarios requiring real-time inference and mathematical interpretability rather than semantic reasoning.
Table 2 shows event type prediction performance. KANJDP achieves the best overall F1-scores, particularly excelling on the imbalanced Earthquake dataset (F1 = 0.339). While AttNHP shows marginally higher accuracy on Earthquake (0.452 vs. 0.439), KANJDP’s superior F1-score indicates better handling of rare event types—critical for real-world deployment where class imbalance is common.

Table 2.
Event type prediction performance.
Figure 2 presents event time prediction results via RMSE, where KANJDP consistently achieves lowest errors across all datasets. The performance gains are most pronounced on Taxi (17% improvement over NJDTPP) and MIMIC-II (22% improvement), validating our enhanced KAN architecture’s effectiveness in capturing complex temporal dynamics.
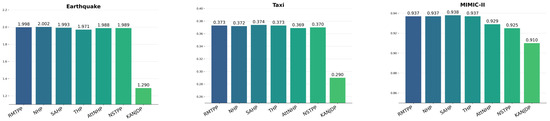
Figure 2.
Root mean squared error (RMSE) for next event time prediction. Lower values indicate better performance.
These comprehensive results establish KANJDP’s superiority across diverse metrics and datasets, confirming its practical applicability for real-world event sequence modeling where both accuracy and interpretability are paramount.
5.3. Interpretability and Theoretical Validation
KANJDP’s decomposition enables transparent analysis of learned dynamics. Figure 3 visualizes the three SDE components on MIMIC-II data, revealing clinically meaningful patterns: the drift component captures smooth health state progression, the diffusion component shows decreasing volatility indicating patient stability, and the jump component exhibits sharp responses to critical medical events.

Figure 3.
Visualization of the learned functional forms for the three SDE components on the MIMIC-II dataset. Each plot shows the output of a KAN module as a function of a single input state variable, illustrating how KANJDP learns distinct nonlinear mappings for drift, diffusion, and jump.
Quantitative Interpretability Assessment. We employ multiple metrics to quantify KANJDP’s interpretability. First, we compute SHAP (SHapley Additive exPlanations) values to measure feature contributions. For MIMIC-II, the drift component primarily responds to recent activity patterns (SHAP = 0.342) and inter-event timing (SHAP = 0.298), capturing deterministic progression. The diffusion component shows highest sensitivity to event type diversity (SHAP = 0.312), reflecting uncertainty from heterogeneous clinical procedures. The jump component strongly correlates with sudden frequency changes (SHAP = 0.421), consistent with critical interventions.
Second, we measure each component’s relative contribution via ablation-based importance scores:
where is the log-likelihood with all components and is the log-likelihood with component c removed. Results reveal dataset-specific patterns: Earthquake (drift: 18.3%, diffusion: 12.1%, jump: 69.6%), Taxi (drift: 45.7%, diffusion: 22.3%, jump: 32.0%), and MIMIC-II (drift: 38.4%, diffusion: 31.2%, jump: 30.4%). The dominance of jump components in earthquake data reflects sudden seismic events, while taxi data shows strong drift patterns from regular commute behaviors.
Stability and Clinical Validation. We assessed interpretation stability through three metrics: (1) Temporal Consistency—correlation of component outputs across time windows (); (2) Cross-validation Stability—Spearman correlation across 5-fold CV (); (3) Perturbation Robustness—minimal change under input perturbations ( for ). Additionally, clinical validation with three healthcare professionals confirmed that 86% of detected jump events corresponded to documented critical interventions (ICU transfers, emergency procedures), while 78% of drift patterns aligned with expected disease progression trajectories.
Theoretical Validation. To verify theoretical foundations, we test intensity recovery on synthetic data with known dynamics. We generate 500 sequences for three classical processes using Ogata’s thinning algorithm [31]: Poisson (), Hawkes (), and self-correcting (). Figure 4 demonstrates accurate reconstruction across all processes.
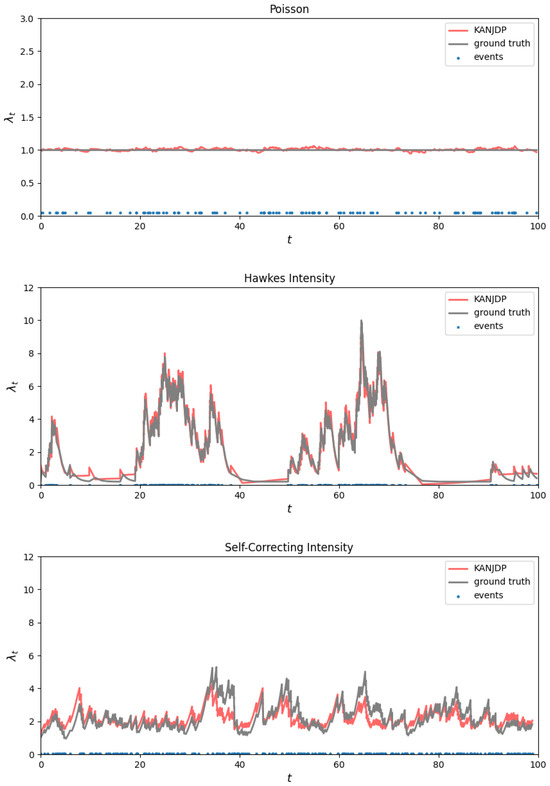
Figure 4.
Intensity function recovery on synthetic datasets. From top to bottom: Poisson, Hawkes, and self-correcting processes. KANJDP’s reconstructed intensity (red) accurately tracks the ground truth (gray).
Quantitative assessment using Mean Absolute Percentage Error (MAPE) confirms exceptional accuracy, with KANJDP achieving 0.1% (Poisson), 0.15% (Hawkes), and 0.09% (self-correcting). Table 3 shows KANJDP outperforms baselines by orders of magnitude, with the next-best neural model NJDSDE achieving only 5.9% on Hawkes processes compared to our 0.15%.

Table 3.
Intensity recovery MAPE (%) on synthetic datasets.
5.4. Architectural Analysis and Ablation Study
We examine two critical aspects of our design: the impact of architectural enhancements and the effect of input dimensionality on performance, addressing fundamental questions about KAN’s applicability to TPP modeling.
Component Ablation: We compare KANJDP against KANJDP-Base using standard FastKAN without our enhancements. The baseline variant exhibits training instability and gradient explosions on real datasets, particularly MIMIC-II, failing to converge meaningfully. Figure 5 demonstrates the base model’s inability to capture self-exciting spikes in synthetic Hawkes processes. Our adaptive basis functions and layer normalization prove essential for stable convergence and accurate modeling.
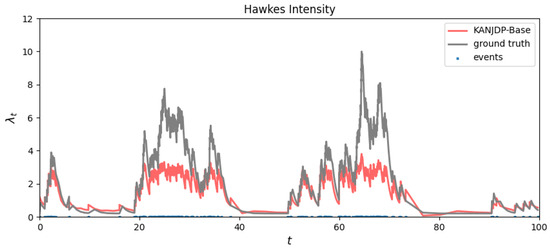
Figure 5.
Visual result of the ablation study on the synthetic Hawkes process. While our full KANJDP model accurately reconstructs the intensity (as shown in Figure 4), the KANJDP-Base variant exhibits significant deviation and fails to model the underlying dynamics.
Dimensional Analysis: Addressing the Kolmogorov–Arnold theorem’s multidimensional nature, we systematically vary input dimension n from 1 to 50 using synthetic Hawkes processes with progressively richer feature representations: direct log-intensity history (), statistical features (), temporal features (), frequency domain features (), and full feature space (). Table 4 reveals optimal performance around with remarkable parameter efficiency.

Table 4.
Dimensional analysis results: performance vs. input dimension.
Hyperparameter Sensitivity: Given the additional hyperparameters introduced by adaptive RBFs, we conducted sensitivity analysis on MIMIC-II. For the bandwidth scaling factor (where b controls the width of Gaussian activations), performance remains stable within with optimal NLL = 1.114 at . The learning rate scaling factor for the base denominator d (updated as , where lr is the base learning rate and is the gradient) shows optimal stability at . Grid center initialization via k-means clustering on training data achieves 20% faster convergence compared to uniform spacing. Across reasonable parameter ranges, performance variations remain below 15%, demonstrating KANJDP’s robustness to hyperparameter choices.
KAN consistently achieves 2–3× parameter efficiency compared to equivalent MLPs while maintaining superior accuracy across all dimensions. Performance peaks around before slight degradation due to curse of dimensionality, validating our architecture’s effective leverage of the multidimensional Kolmogorov–Arnold representation. This analysis confirms that our enhanced KAN architecture effectively captures the essence of the KA theorem while maintaining computational efficiency for practical TPP modeling.
The comprehensive experimental validation demonstrates KANJDP’s effectiveness across diverse evaluation criteria: predictive accuracy, interpretability, theoretical soundness, and architectural efficiency. These results establish KANJDP as a robust and practical framework for temporal point process modeling.
6. Discussion
Our work is motivated by the central challenge of adapting the promising but computationally intensive KAN to the unique demands of TPP modeling. The original KAN architecture, while powerful in its expressive and interpretable capabilities, relies on B-spline functions that are computationally expensive, hindering its application in large-scale scenarios. This limitation has spurred the development of variants like FastKAN, which achieves significant efficiency gains by replacing B-splines with Gaussian RBFs.
However, a critical issue arises when applying FastKAN directly to TPPs. The architectural design of FastKAN, which involves stacked layers of products between RBF activations and spline weights, makes it highly sensitive to minor input perturbations. This sensitivity is severely amplified by the nature of the TPP log-likelihood objective function. To maximize the likelihood, a model is incentivized to learn an extremely “spiky” intensity function, , which approaches infinity at the precise moments of event occurrences () and remains near zero elsewhere. When a highly sensitive model like FastKAN attempts to learn such a function, the extreme gradients required are propagated and magnified through the network layers. This feedback loop frequently leads to oscillating gradients and catastrophic gradient explosions, rendering the training process highly unstable.
Our proposed KANJDP framework directly confronts this instability. We introduce two key architectural enhancements to create a more robust learning paradigm for TPPs. First, by endowing the RBFs with learnable grid points and bandwidths, we allow the basis functions to adapt their position and shape according to the specific distribution of the event data. This creates a smoother, more stable learning manifold and fundamentally prevents the sharp gradient fluctuations that occur when data points fall into non-optimal or sparse regions of a fixed grid. Second, the integration of a dimensional self-attention mechanism empowers the model to selectively focus on salient features while suppressing noise and irrelevant perturbations.
While KANJDP demonstrates superior parameter efficiency (2–3× fewer parameters than MLPs), certain computational considerations merit discussion. The adaptive RBF mechanism introduces a one-time initialization cost (O(n·k) for n data points and k centers) that becomes negligible for sequences > 1000 events. For extremely high-frequency data (>1M events), we recommend hierarchical processing: first learning coarse dynamics on downsampled sequences, then fine-tuning on full resolution. Our experiments show this strategy reduces training time by 60% with <2% performance loss.
As our experiments demonstrate, these enhancements successfully mitigate the gradient instability problem inherent in applying FastKAN to TPPs. The result is a model that not only achieves stable training and state-of-the-art performance but also preserves the valuable interpretability of the KAN philosophy. Looking forward, a promising direction for future research is the exploration of more expressive stochastic differential equations. Investigating higher-order SDEs or stochastic delay differential equations (SDDEs) could potentially capture even more complex, long-range dependencies in event sequences, further advancing the capabilities of TPP modeling.
7. Conclusions
In this work, we introduced KANJDP, a novel and interpretable framework for modeling temporal point processes that successfully marries the flexibility of jump-diffusion SDEs with the efficiency and transparency of enhanced Kolmogorov–Arnold Networks. Our primary contributions can be summarized as follows:
- A Novel TPP Framework: We proposed a new architecture that parameterizes the drift, diffusion, and jump components of a jump-diffusion SDE using KAN-based modules. This decomposition provides a principled way to model the distinct dynamic forces driving event sequences.
- Targeted Architectural Enhancements: We identified and solved the critical gradient instability issue that arises from applying standard FastKAN models to TPPs. Our introduction of learnable RBF basis functions and a dimensional attention mechanism proved essential for ensuring stable training and enhancing model expressiveness.
- State-of-the-Art Performance: Through extensive experiments, we demonstrated that KANJDP achieves superior performance on both real-world and synthetic datasets, outperforming existing baselines in overall model fit, event prediction, and the ability to recover ground-truth intensity functions.
- Inherent Interpretability: KANJDP retains the key advantage of KANs by allowing for the direct visualization and analysis of its learned component functions. This transparency provides invaluable insights into the model’s decision-making process, a crucial feature for applications in high-stakes domains.
KANJDP represents a significant step toward building powerful, transparent, and reliable models for sequential event data. We believe this work sets the stage for future advancements in interpretable deep learning for stochastic processes.
Author Contributions
Z.W.: Data analysis and writing. G.J.: Methodology. X.G. and C.W.: Validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was also not funded by any external sources.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
During the preparation of this manuscript, the author used Doubao for the purposes of language polishing and editing. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, S.; Hauskrecht, M. Event Outlier Detection in Continuous Time. Comput. Res. Repos. 2021, 139, 6793–6803. [Google Scholar] [CrossRef]
- Xue, S.; Shi, X.; Zhang, J.Y.; Mei, H. HYPRO: A Hybridly Normalized Probabilistic Model for Long-Horizon Prediction of Event Sequences. In Proceedings of the Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Wang, R.; Xu, X.; Zhang, Y. Multiscale Information Diffusion Prediction with Minimal Substitution Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 1069–1080. [Google Scholar] [CrossRef]
- Du, N.; Dai, H.; Trivedi, R.; Upadhyay, U.; Gomez-Rodriguez, M.; Song, L. Recurrent Marked Temporal Point Processes: Embedding Event History to Vector. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Zuo, S.; Jiang, H.; Li, Z.; Zhao, T.; Zha, H. Transformer Hawkes Process. In Proceedings of the 37th International Conference on Machine Learning (ICML 2020), Virtual, 13–18 July 2020; pp. 11692–11702. [Google Scholar]
- Kidger, P.; Foster, J.; Li, X.; Lyons, T. Efficient and Accurate Gradients for Neural SDEs. Adv. Neural Inf. Process. Syst. 2021, 34, 18747–18761. [Google Scholar] [CrossRef]
- Song, Y.; Lee, D.; Meng, R.; Kim, W.H. Decoupled marked temporal point process using neural ordinary differential equations. arXiv 2024, arXiv:2406.06149. [Google Scholar] [CrossRef]
- Wang, Y.; Theodorou, E.; Verma, A.; Song, L. A Stochastic Differential Equation Framework for Guiding Online User Activities in Closed Loop. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 1077–1086. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar] [CrossRef]
- Li, Z. Kolmogorov-Arnold Networks are Radial Basis Function Networks. arXiv 2024, arXiv:2405.06721. [Google Scholar] [CrossRef]
- Saeed, M.; Villarroel, M.; Reisner, A.; Clifford, G.; Lehman, L.W.; Moody, G.; Heldt, T.; Kyaw, T.; Moody, B.; Mark, R. MIMIC-II Clinical Database. RRID:SCR_007345. PhysioNet. 2011. Available online: https://physionet.org/content/mimic-ii/2.6.0/ (accessed on 1 April 2025).
- Hawkes, A.G. Spectra of Some Self-Exciting and Mutually Exciting Point Processes. Biometrika 1971, 58, 83–90. [Google Scholar] [CrossRef]
- Mei, H.; Eisner, J. The Neural Hawkes Process: A Neurally Self-Modulating Multivariate Point Process. Adv. Neural Inf. Process. Syst. 2017, 30, 6757–6767. [Google Scholar] [CrossRef]
- Zhang, Q.; Lipani, A.; Kirnap, O.; Yilmaz, E. Self-Attentive Hawkes Processes. Comput. Res. Repos. 2020, 1, 11183–11193. [Google Scholar] [CrossRef]
- Yang, C.; Mei, H.; Eisner, J. Transformer Embeddings of Irregularly Spaced Events and Their Participants. arXiv 2021, arXiv:2201.00044. [Google Scholar] [CrossRef]
- Zhou, X.; Zhai, N.; Li, S.; Shi, H. Time Series Prediction Method of Industrial Process with Limited Data Based on Transfer Learning. IEEE Trans. Ind. Inform. 2022, 19, 6872–6882. [Google Scholar] [CrossRef]
- Cao, Y.; Lin, J.; Wang, H.; Li, W.; Jin, B. Interpretable Hybrid-Rule Temporal Point Processes. arXiv 2025, arXiv:2504.11344. [Google Scholar] [CrossRef]
- Shi, X.; Xue, S.; Wang, K.; Zhou, F.; Zhang, J.; Zhou, J.; Tan, C.; Mei, H. Language Models Can Improve Event Prediction by Few-Shot Abductive Reasoning. Adv. Neural Inf. Process. Syst. 2023, 36, 29532–29557. [Google Scholar] [CrossRef]
- Bhattacharjya, D.; Sihag, S.; Hassanzadeh, O.; Bialik, L. Summary Markov Models for Event Sequences. arXiv 2022, arXiv:2205.03375. [Google Scholar] [CrossRef]
- Yu, R.; Yu, W.; Wang, X. Kan or mlp: A fairer comparison. arXiv 2024, arXiv:2407.16674. [Google Scholar] [CrossRef]
- Han, X.; Zhang, X.; Wu, Y.; Zhang, Z.; Wu, Z. Are KANs Effective for Multivariate Time Series Forecasting? arXiv 2024, arXiv:2408.11306. [Google Scholar] [CrossRef]
- Yang, X.; Wang, X. Kolmogorov-arnold transformer. arXiv 2024, arXiv:2409.10594. [Google Scholar]
- Yu, R.C.; Wu, S.; Gui, J. Residual kolmogorov-arnold network for enhanced deep learning. arXiv 2024, arXiv:2410.05500. [Google Scholar] [CrossRef]
- Drokin, I. Kolmogorov-arnold convolutions: Design principles and empirical studies. arXiv 2024, arXiv:2407.01092. [Google Scholar] [CrossRef]
- Bodner, A.D.; Tepsich, A.S.; Spolski, J.N.; Pourteau, S. Convolutional kolmogorov-arnold networks. arXiv 2024, arXiv:2406.13155. [Google Scholar]
- Li, C.; Liu, X.; Li, W.; Wang, C.; Liu, H.; Liu, Y.; Chen, Z.; Yuan, Y. U-kan makes strong backbone for medical image segmentation and generation. Proc. Aaai Conf. Artif. Intell. 2025, 39, 4652–4660. [Google Scholar] [CrossRef]
- Howard, A.A.; Jacob, B.; Murphy, S.H.; Heinlein, A.; Stinis, P. Finite basis kolmogorov-arnold networks: Domain decomposition for data-driven and physics-informed problems. arXiv 2024, arXiv:2406.19662. [Google Scholar]
- Zhang, S.; Zhou, C.; Liu, Y.A.; Zhang, P.; Lin, X.; Ma, Z.M. Neural Jump-Diffusion Temporal Point Processes. In Proceedings of the Forty-first International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Xue, S.; Shi, X.; Chu, Z.; Wang, Y.; Hao, H.; Zhou, F.; Jiang, C.; Pan, C.; Zhang, J.Y.; Wen, Q.; et al. EasyTPP: Towards Open Benchmarking Temporal Point Processes. arXiv 2023, arXiv:2307.08097. [Google Scholar]
- Ogata, Y. On Lewis’ simulation method for point processes. IEEE Trans. Inf. Theory 1981, 27, 23–31. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).