A Transformer-Based Approach for Joint Interference Cancellation and Signal Detection in FTN-RIS MIMO Systems

Abstract

Next-generation communication systems demand extreme spectral efficiency to handle ever-increasing data traffic. The combination of faster-than-Nyquist (FTN) signaling and reconfigurable intelligent surfaces (RISs) presents a promising solution to meet this demand. However, the aggressive time compression inherent to FTN signaling introduces severe and highly non-linear inter-symbol interference (ISI). This complex distortion is challenging for conventional linear equalizers and even for recurrent neural network (RNN)-based detectors, which can struggle to model long-range dependencies within the signal sequence. To overcome this limitation, this paper proposes a novel signal detection framework based on the transformer model. By leveraging its core multi-head self-attention mechanism, the transformer globally analyzes the entire received signal sequence at once. This enables it to effectively model and reverse complex ISI patterns by identifying the most significant interfering symbols, regardless of their position, leading to superior signal recovery. The simulation results validate the outstanding performance of the proposed approach. To achieve a target bit error rate (BER) of ${10}^{-4}$, the transformer-based detector shows a significant signal-to-noise ratio (SNR) gain of approximately 1.5 dB over a Bi-LSTM detector over 4 dB compared to the conventional FTN-RIS system, while maintaining a high spectral efficiency of nearly 2 bps/s/Hz.

1. Introduction

1.1. Background

The evolution towards sixth-generation (6G) wireless networks is fueled by the demand for ultra-high data rates and ubiquitous connectivity to support applications like holographic communication and city-scale digital twins. This growth intensifies the pressure on the limited RF spectrum, making spectral efficiency (SE) a critical performance metric [1,2]. Among the emerging technologies that are used to enhance SE, faster-than-Nyquist (FTN) signaling and reconfigurable intelligent surfaces (RISs) are particularly promising.

FTN signialing improves SE by transmitting symbols faster than the Nyquist rate, allowing more data per bandwidth at the cost of severe inter-symbol interference (ISI) [3,4]. Meanwhile, RISs enhance wireless channels by dynamically controlling the phase of reflected signals, enabling more efficient propagation [5,6,7]. However, the integration of these technologies—FTN-RIS MIMO—while offering unprecedented SE gains, also introduces highly complex, non-linear signal distortion due to combined FTN-ISI- and RIS-induced channel effects.

Traditional ISI mitigation methods like the Viterbi algorithm become impractical due to their high complexity. To address this, matrix-based decision feedback equalizers (DFEs) have been proposed as a lower-complexity alternative [8]. Additionally, machine learning (ML) approaches, particularly recurrent neural networks (RNNs) such as long short-term memory (LSTM) and bidirectional LSTM (Bi-LSTM) have been explored to directly learn the channel distortion without explicit estimation [9]. However, such models often fall short in capturing the extended temporal correlations induced by FTN-RIS interactions, and such research has rarely been extended to the more complex integrated FTN-RIS scenario. This limitation motivates the development of a specialized detection approach for the integrated FTN-RIS scenario, as pursued in this study.

1.2. Related Works

Prior studies on ISI mitigation in FTN systems have largely relied on trellis-based detectors like the Viterbi algorithm, as well as linear equalizers such as zero-forcing (ZF) and DFEs. While trellis-based methods offer optimality, their exponential complexity with respect to modulation order and ISI span limits their practical deployment. As a result, lower-complexity alternatives such as reduced state- and matrix-based DFE variants have been explored [4,8,10,11,12].

However, these traditional approaches assume linear time-invariant (LTI) channels and their performance degrades in highly non-linear or distortion-prone environments, especially when the FTN acceleration factor $\tau$ decreases and ISI becomes severe [4,12,13]. The integration of RISs further complicates signal detection due to the dynamic and potentially non-linear propagation effects introduced by phase-controlled reflections, large cascaded channels, and mutual coupling [14,15,16].

To overcome these challenges, deep learning (DL)-based methods have been investigated. RNN architectures, particularly LSTM and Bi-LSTM, have shown promise in learning ISI patterns directly from the data [9]. Nevertheless, their sequential nature hinders parallelization, and long-range dependency modeling remains limited due to vanishing gradients.

Recently, transformer models have gained traction for their ability to model global dependencies via self-attention and support parallel computation. This has led to their successful application in various wireless communication problems, moving beyond their initial use in areas like natural language processing.

Initial works in this domain pioneered the use of transformers for channel state information (CSI) feedback in Massive MIMO systems. For example, CsiTransformer [17] established a foundational approach using a standard transformer encoder–decoder to compress and reconstruct the channel matrix. This was further advanced by CsiFormer [18], which integrated convolutional layers with the transformer architecture to better capture local spatial features within the channel information. The primary objective of these methods is to provide the transmitter with an accurate picture of the channel for subsequent processes like precoding. This objective and methodology are fundamentally different from those of the present study. The goal of this study is not to reconstruct the channel matrix, but to directly detect the transmitted data symbols from a time-series signal corrupted by both severe ISI and complex channel distortions. A model architecture and training objective designed for channel matrix reconstruction is not directly applicable to the task of sequential signal detection in a high-interference environment.

Building on these successes, the application of transformers has expanded to other channel-centric tasks. For instance, in the area of passive beamforming, the authors of [19] utilized a Vision Transformer to optimize the phase shifts of the RISs. This approach cleverly manipulates the propagation environment itself to improve signal quality at the receiver. In contrast, the framework proposed in this study operates at the receiver on a signal that has already passed through the channel, focusing on decoding the information rather than controlling the channel’s properties.

Similarly, for downlink channel estimation, the authors of [20] proposed a transformer-based distributed learning framework to enhance estimation accuracy. While highly relevant, this work aims to solve a prerequisite problem; accurate channel estimation is necessary for many detection schemes, but it is not the detection process itself. The framework in this study, on the other hand, is designed to function as an end-to-end detector, learning to jointly compensate for channel effects and ISI without requiring a separate, explicit channel estimation stage.

While these studies highlight the transformer’s versatility, they consistently focus on managing, estimating, or controlling the channel. To the best of our knowledge, the use of a transformer as a direct, data-driven detector for the challenging joint FTN-ISI and RIS-induced distortion scenario remains a critical, unexplored gap. This study aims to fill this gap by proposing a novel framework that adapts the transformer architecture specifically for this complex detection task.

1.3. Contributions

This study proposes a novel signal detection framework based on the transformer architecture to address the severe and highly non-linear ISI that is inherent in FTN-RIS MIMO systems.

The primary contribution of this work is the pioneering application of the transformer as a direct, end-to-end signal detector for this challenging joint detection scenario. This approach is fundamentally different from prior works that have applied transformers to other channel-centric tasks such as CSI feedback, channel estimation, or beamforming. To the best of our knowledge, this is the first study to adapt and evaluate the transformer architecture for this specific, complex detection problem.

Furthermore, this paper demonstrates that the proposed framework overcomes the key limitations of RNN-based detectors like LSTM and Bi-LSTM. By leveraging the transformer’s self-attention mechanism to globally model long-range ISI patterns, the proposed detector achieves significant BER performance gains. A key aspect of this contribution is the in-depth qualitative analysis provided, which explains why the transformer’s architecture is uniquely suited to the non-local interference patterns of the FTN-RIS channel, offering valuable insights beyond the simulation results. The superiority of this approach is comprehensively validated through simulations in the results section.

Finally, a comprehensive performance and robustness analysis are provided, thereby establishing a crucial performance benchmark for this problem. This analysis confirms that the proposed detector not only achieves a superior BER but also maintains high spectral efficiency, demonstrating the framework’s stable and practical applicability across a wide range of FTN acceleration factors ($\tau$) and signal-to-noise ratio (SNR) values. By focusing on the upper-bound performance under ideal conditions (e.g., perfect CSI), this benchmark provides a vital reference for future research on practical implementation and optimization.

The rest of this paper is organized as follows. Section 2 describes the proposed FTN-RIS MIMO system model. Section 3 details the ML-based detection schemes, including LSTM, Bi-LSTM, and the proposed transformer-based detector. Section 4 presents the simulation environment and performance analysis results, while Section 5 provides the conclusion.

2. System Model

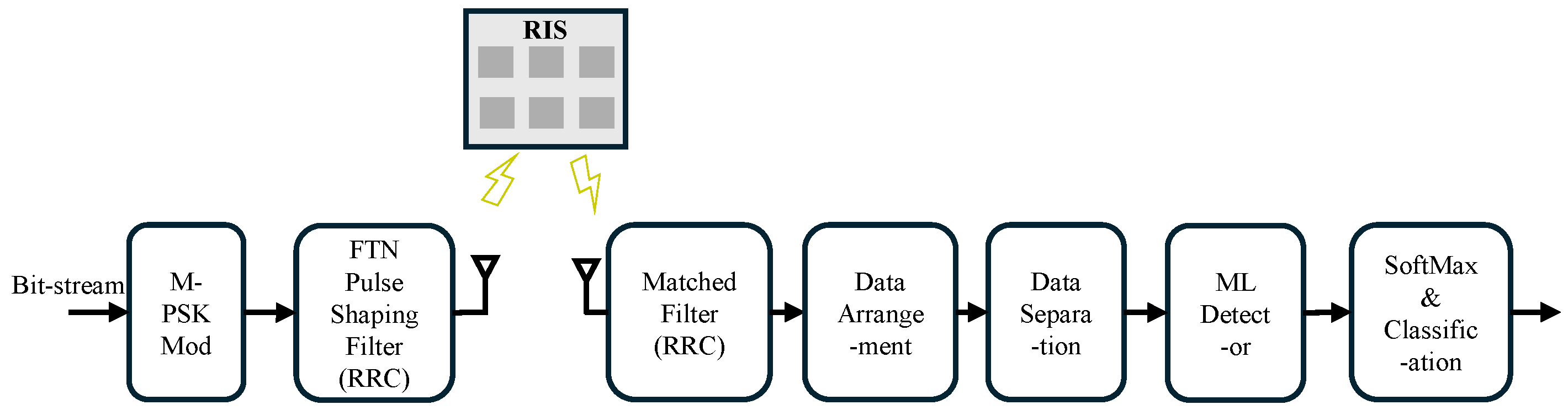
The end-to-end architecture of the proposed FTN-RIS MIMO communication system is depicted in Figure 1. The system comprises three main parts—a transmitter, an RIS-mediated channel, and a receiver employing an ML-based detector. The signal processing chain is detailed as follows.

At the transmitter, the process begins with an input bit-stream, which is first mapped to complex symbols by the M-PSK modulator. These symbols are then passed through the FTN pulse shaping filter, which uses a root-raised cosine (RRC) filter. This crucial block is responsible for creating the FTN signal by transmitting symbols faster than the Nyquist rate—a process that intentionally introduces ISI to enhance spectral efficiency. The resulting signal is then transmitted via the transmit antennas.

The transmitted signal then propagates through the wireless channel. The fundamental role of the RISs in this system is to create a virtual line-of-sight (LOS) path in environments where the direct path is obstructed, which is a common challenge in high-frequency communication. Composed of multiple passive reflecting elements, the RISs intelligently manipulate the phase of the incident signal to establish this favorable path. Consequently, this study focuses on the more challenging and practically relevant non-LOS scenario to evaluate the system’s performance in the very context where RIS technology is most critical.

At the receiver, the incoming signal is first processed by a matched filter, which corresponds to the transmitter’s RRC filter, in order to maximize the SNR. The output is then prepared for the ML model in two pre-processing stages. The data arrangement block segments the continuous stream of samples into sequences of a fixed length. Subsequently, the data separation block converts these complex-valued samples into the real-valued vectors (i.e., real and imaginary parts) required by the detector.

The core of the receiver is the ML detector, which is the transformer-based model proposed in this study. It is designed to learn the complex, non-linear mapping from the distorted input sequence back to the original symbols, jointly performing equalization and detection. Finally, the softmax and classification block converts the detector’s output into a probability distribution over all possible symbols and selects the symbol with the highest probability to recover the original bit-stream.

2.1. Transmitter

The transmitter generates and transmits FTN signals to improve spectral efficiency. The continuous-time transmitted signal for a single stream, $x\left(t\right)$, is expressed as follows:

$$x\left(t\right)=\sum _{n}s\left[n\right]·p(t-n\tau T),$$

(1)

where $s\left[n\right]$ denotes the transmitted symbols, $p\left(t\right)$ is the pulse shaping filter (e.g., root-raised cosine), T is the Nyquist symbol duration, and $\tau$ is the FTN acceleration factor, with $0<\tau \le 1$.

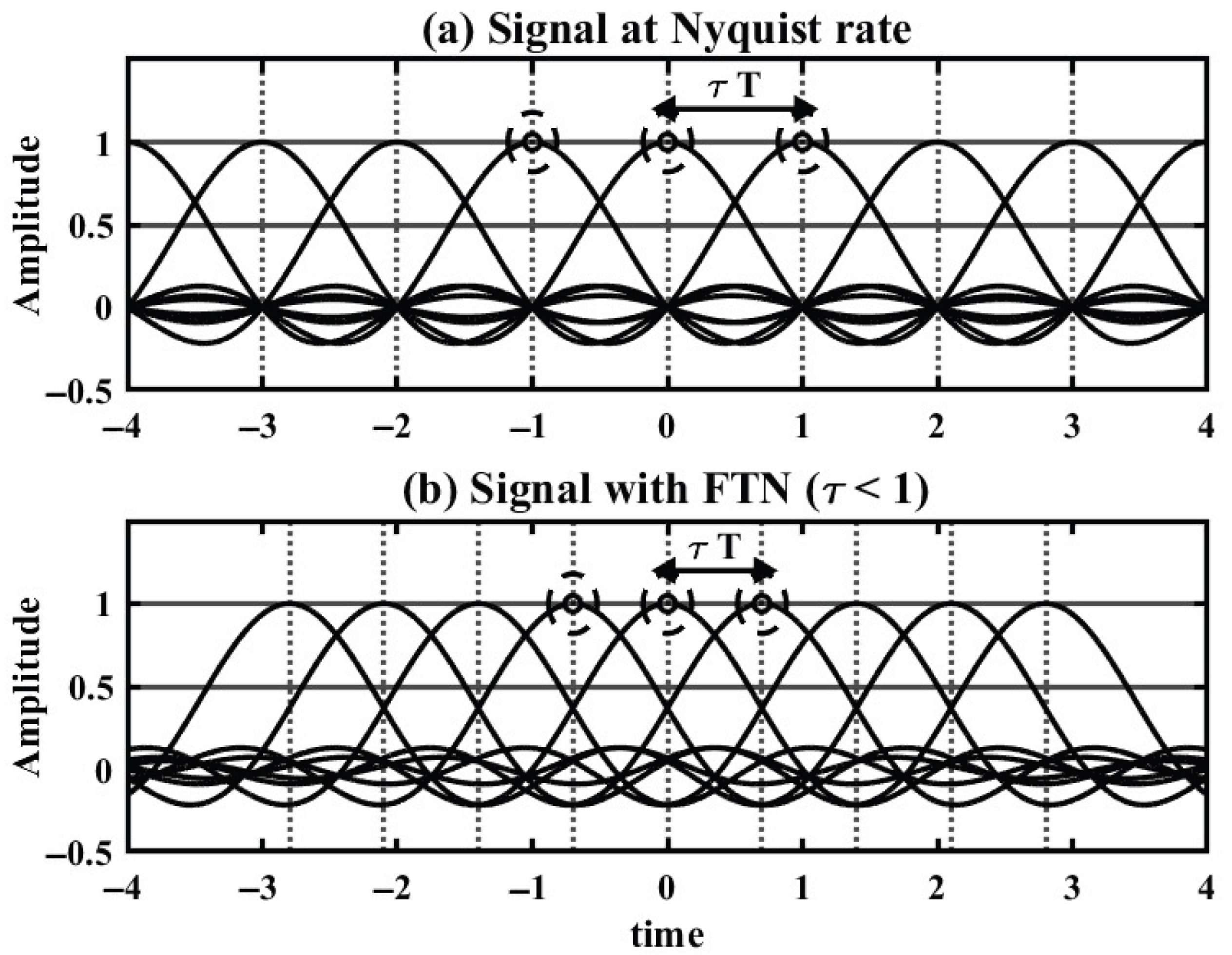
The fundamental principle of FTN signaling is illustrated in Figure 2. Part (a) shows the signal at the Nyquist rate ($\tau =1$), illustrating an ideal case where zero ISI is achieved due to the pulse shape satisfying the Nyquist criterion. In contrast, part (b) depicts the signal with FTN ($\tau <1$), where the densely packed symbols cause pulse overlap and result in unavoidable ISI at the sampling instants.

In the system model, the transmitter first demultiplexes an input bit-stream into $N_{\mathrm{Rx}}$ parallel streams, which are then modulated to generate the symbols $s\left[n\right]$. Subsequently, these symbols are passed through an FTN pulse shaping filter that uses an RRC filter for $p\left(t\right)$ with an acceleration factor of $\tau =0.85$, resulting in the FTN signal matrix X. Finally, to transmit the $N_{\mathrm{Rx}}$ data streams via $N_{\mathrm{BS}}$ antennas, a linear precoding technique is applied to mitigate inter-stream interference. The specific design of this precoder depends on the end-to-end channel characteristics, which are detailed in the following section.

2.2. Channel and Precoding

The signal propagates from the transmitter to the receiver via the RIS, traversing a channel that is modeled in several stages. The physical channel consists of two parts—the channel from the base station (BS) to the RIS, denoted as ${\mathbf{H}}_{\mathrm{BS}}\in {\mathbb{C}}^{N_{\mathrm{RIS}}\times N_{\mathrm{BS}}}$, and the channel from the RIS to the receiver, ${\mathbf{H}}_{\mathrm{Rx}}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times N_{\mathrm{RIS}}}$. The RIS, which includes $N_{\mathrm{RIS}}=64$ passive elements, actively modifies the signal by applying phase shifts, an effect that is modeled by the diagonal phase-shift matrix, as follows:

$$\mathbf{\Theta }=\mathrm{diag}(e^{j{\theta }_1},e^{j{\theta }_2},\dots ,e^{j{\theta }_{N_{\mathrm{RIS}}}}),$$

(2)

where the phase shifts ${\theta }_n$ are optimized to enhance signal quality.

These components combine to form the end-to-end effective channel, ${\mathbf{H}}_{\mathrm{eff}}$, which is expressed as the composite channel, as follows:

$${\mathbf{H}}_{\mathrm{eff}}={\mathbf{H}}_{\mathrm{Rx}}\mathbf{\Theta }{\mathbf{H}}_{\mathrm{BS}}.$$

(3)

With the effective channel ${\mathbf{H}}_{\mathrm{eff}}$ established, the transmitter computes the ZF precoding matrix $\mathbf{G}$ to nullify inter-stream interference. This matrix is the Moore–Penrose pseudo-inverse of the effective channel, as follows:

$$\mathbf{G}={\mathbf{H}}_{\mathrm{eff}}^H{\left({\mathbf{H}}_{\mathrm{eff}}{\mathbf{H}}_{\mathrm{eff}}^H\right)}^{-1},$$

(4)

where ${(·)}^H$ denotes the Hermitian transpose. The precoded signal is then normalized to satisfy the transmit power constraint.

Consequently, the final baseband-received signal matrix at the receiver, $\mathbf{Y}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times T}$, is modeled as follows:

$$\mathbf{Y}={\mathbf{H}}_{\mathrm{eff}}\mathbf{G}\mathbf{X}+\mathbf{N},$$

(5)

where $\mathbf{X}$ is the matrix of transmitted FTN signal streams, and $\mathbf{N}$ is the additive white Gaussian noise (AWGN) matrix, whose elements are complex Gaussian random variables with zero mean and variance ${\sigma }^2$.

2.3. Receiver

The receiver architecture is designed to process the incoming signal and recover the original data through several key stages. The process begins as each received stream passes through a matched filter corresponding to the transmit-side RRC filter—a step that is designed to maximize the signal-to-noise ratio (SNR). Following this, the filtered outputs are sampled, yielding a sequence of discrete, complex-valued samples, $y_k$, which are affected by FTN-induced ISI, channel effects, and noise.

These samples are then prepared for the subsequent ML detection stage. A data arrangement block structures the samples into sequences of fixed length. Crucially, to make the data compatible with the real-valued operations of the detector, a data separation block converts each complex sample $y_k$ into a two-dimensional real-valued vector $z_k$, as follows:

$${\mathbf{z}}_k={\left[\begin{array}{c}\Re \left\{y_k\right\},\Im \left\{y_k\right\}\end{array}\right]}^{\top }\in {\mathbb{R}}^2$$

(6)

This sequence of vectors, as defined in Equation (6), serves as the final pre-processed input for all ML detectors discussed in this paper. At the core of the receiver is a transformer-based detector, which takes this prepared sequence as an input. The detector’s output is then passed through a Softmax layer, which generates a probability distribution over all possible symbol candidates. Finally, the symbol with the highest probability is selected to recover the original bit-stream.

3. Proposed Transformer-Based Detection Scheme

3.1. Overview of ML-Based Detection

Signal detection in an FTN-RIS MIMO system is particularly challenging due to the highly non-linear mapping between the transmitted symbols and the received signals. The received baseband signal, $\mathbf{Y}$, is influenced by the transmitted symbols $s\left[n\right]$, the ISI, the cascaded RIS channel ${\mathbf{H}}_{\mathrm{eff}}$, and additive noise. Given the intractability of analytical modeling, this study adopts an ML approach.

Instead of explicitly modeling and canceling interference, this study proposes a data-driven model. This approach first pre-processes the received signal $\mathbf{Y}$ into a sequence of real-valued vectors, $\mathbf{Z}$, according to Equation (6). The core of this method is to learn the end-to-end non-linear mapping $f:\mathbf{Z}\to \widehat{s}$, from this pre-processed representation to the estimated transmitted symbols, $\widehat{\mathbf{s}}$. By training the model on pairs of known input–output data $(\mathbf{Z},\mathbf{s})$, the ML-based detector can learn to jointly perform equalization and detection, improving robustness and efficiency.

3.2. Baseline Models: LSTM and Bi-LSTM

As a baseline for comparison, this study considers RNN architectures. These models take the pre-processed real-valued vector sequence, ${\mathbf{z}}_k$, as defined in Equation (6), as their input. Specifically, this study evaluates detectors based on LSTM cells.

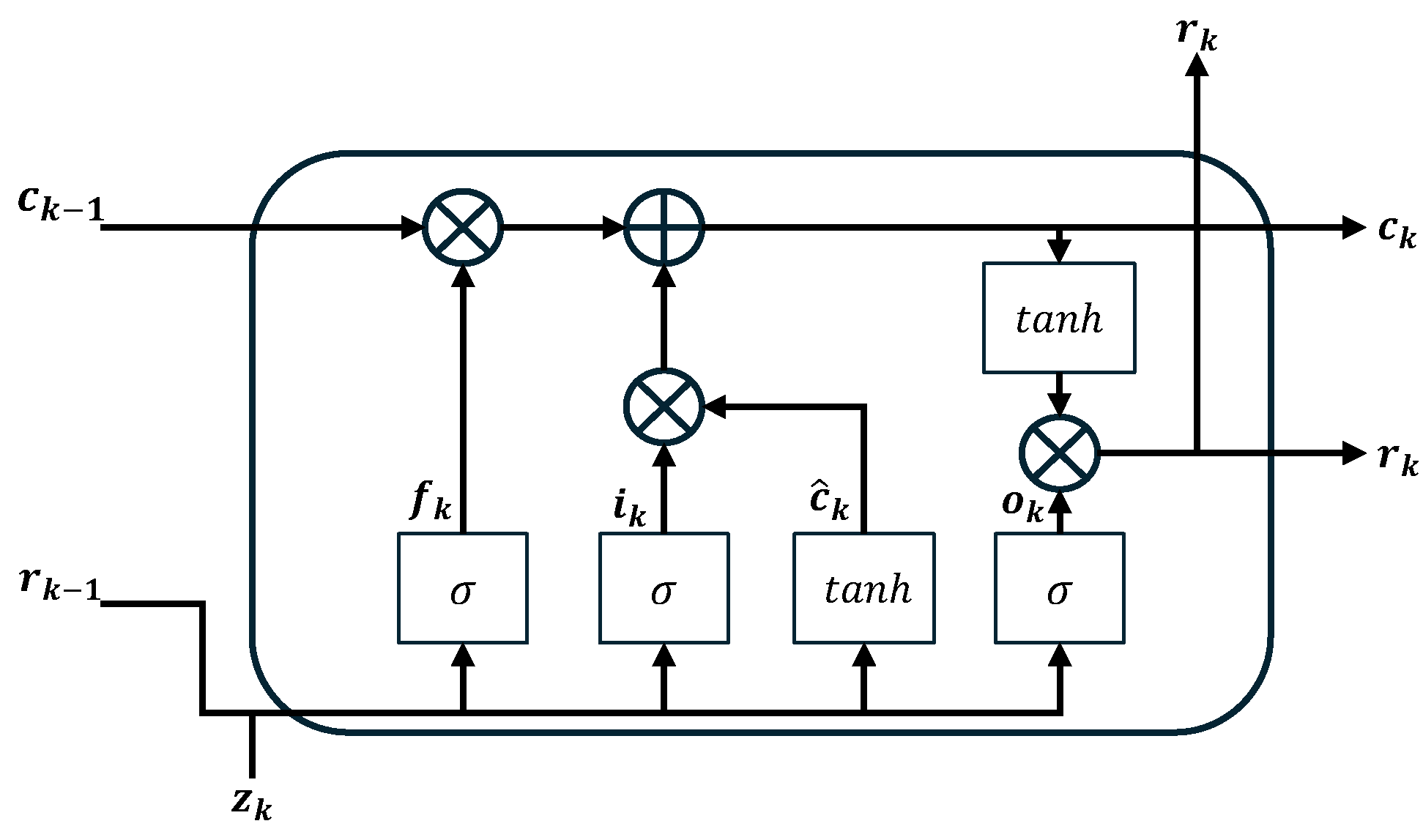
The fundamental building block is the LSTM cell, whose internal operations are depicted in Figure 3. At each time step k, the cell takes three inputs—the current input vector ${\mathbf{z}}_k$, the previous hidden state ${\mathbf{r}}_{k-1}$, and the previous cell state ${\mathbf{c}}_{k-1}$. It then computes the new cell state ${\mathbf{c}}_k$ and the hidden state ${\mathbf{r}}_k$ through a series of gating mechanisms.

The LSTM cell updates its state and computes its output through a series of gating mechanisms that regulate the flow of information. This process begins by deciding what new information to store. The input gate ($i_k$) determines which values will be updated, while a vector of candidate values (${\widehat{c}}_k$) is created to represent potential new information. These are calculated as follows:

$$\begin{array}{cc}\hfill i_k& =\sigma (W_i[r_{k-1},z_k]+b_i)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\widehat{c}}_k& =tanh(W_c[r_{k-1},z_k]+b_c)\hfill \end{array}$$

(8)

Concurrently, the forget gate ($f_k$) decides what information should be discarded from the previous cell state, $c_{k-1}$. The new cell state, $c_k$, is then updated by combining the results of the forget and input gates. It achieves this using element-wise multiplication to forget parts of the old state and then adds the new candidate information scaled by the input gate, as follows:

$$c_k=f_k\odot c_{k-1}+i_k\odot {\widehat{c}}_k$$

(9)

Finally, the cell determines the output for the current time step. The output gate ($o_k$) regulates which parts of the newly computed cell state are passed on. The gate’s value and the resulting new hidden state, $r_k$, are computed as follows:

$$\begin{array}{cc}\hfill o_k& =\sigma (W_o[r_{k-1},z_k]+b_o)\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill r_k& =o_k\odot tanh\left(c_k\right)\hfill \end{array}$$

(11)

Here, W and b represent the weight matrices and bias vectors for each respective gate, $\sigma$ is the sigmoid activation function, and ⊙ denotes the element product.

3.2.1. Unidirectional LSTM (SeqLSTM)

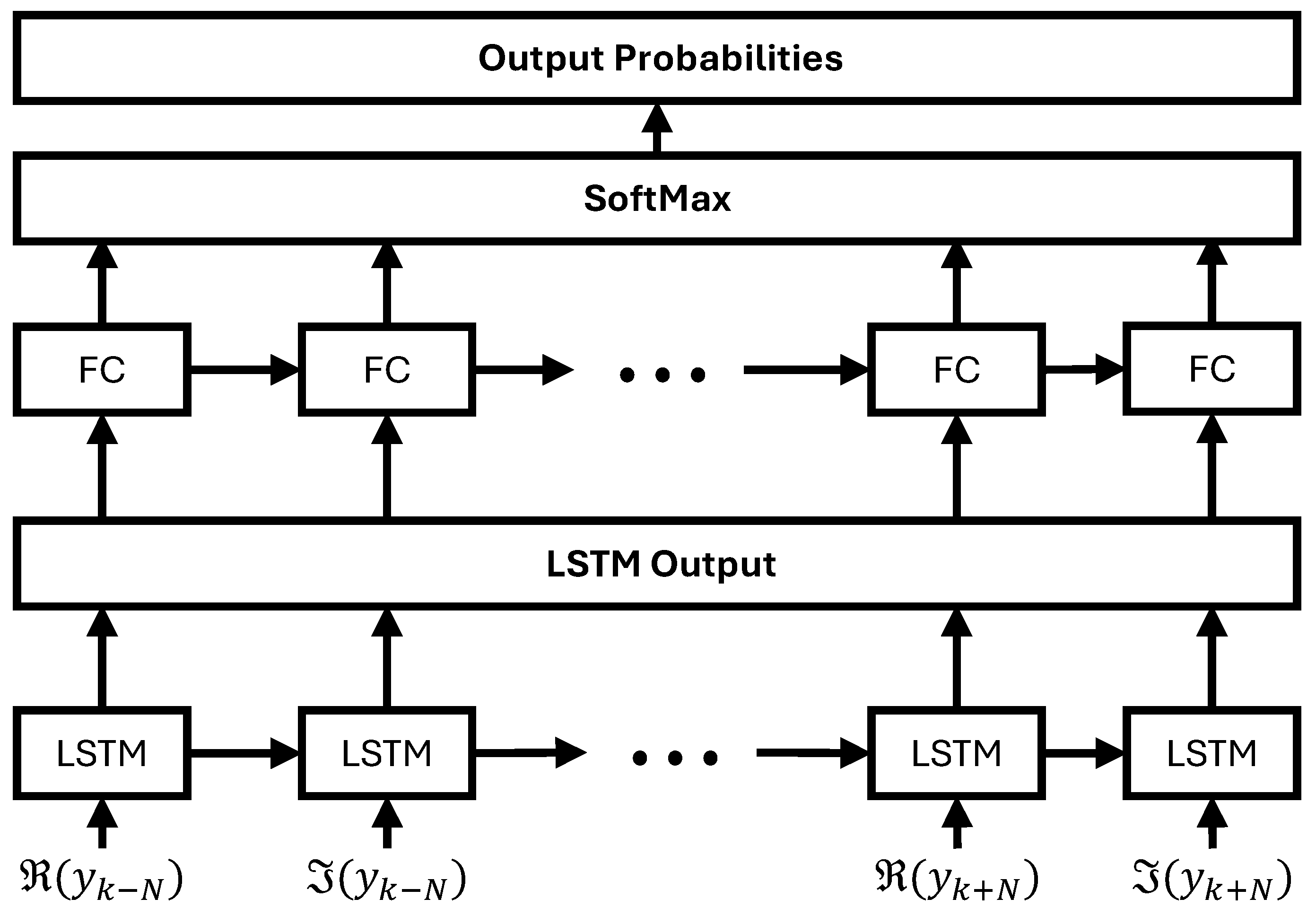
The architecture for this model is shown in Figure 4. It processes the input sequence ${\mathbf{z}}_k$ in a forward direction only. The sequence of hidden states, ${\mathbf{r}}_k$, from the LSTM layer forms the output that is then passed to a final prediction layer.

This prediction layer first uses a fully connected (FC) layer to transform the hidden state ${\mathbf{r}}_k$ into a logit vector, ${\mathbf{l}}_k$, whose dimension M matches the number of possible symbols, as follows:

$${\mathbf{l}}_k={\mathbf{W}}_{\mathrm{fc}}{\mathbf{r}}_k+{\mathbf{b}}_{\mathrm{fc}}.$$

(12)

A Softmax function then converts this logit vector into a probability distribution, ${\mathbf{P}}_k$, over the possible symbols, as follows:

$${\mathbf{P}}_k=\mathrm{Softmax}\left({\mathbf{l}}_k\right).$$

(13)

Finally, the predicted symbol, ${\widehat{s}}_k$, is determined by selecting the symbol with the highest probability using the following argmax operation:

$${\widehat{s}}_k=argmax\left({\mathbf{P}}_k\right).$$

(14)

This architecture makes predictions based only on past and present information contained within the forward-propagating hidden state.

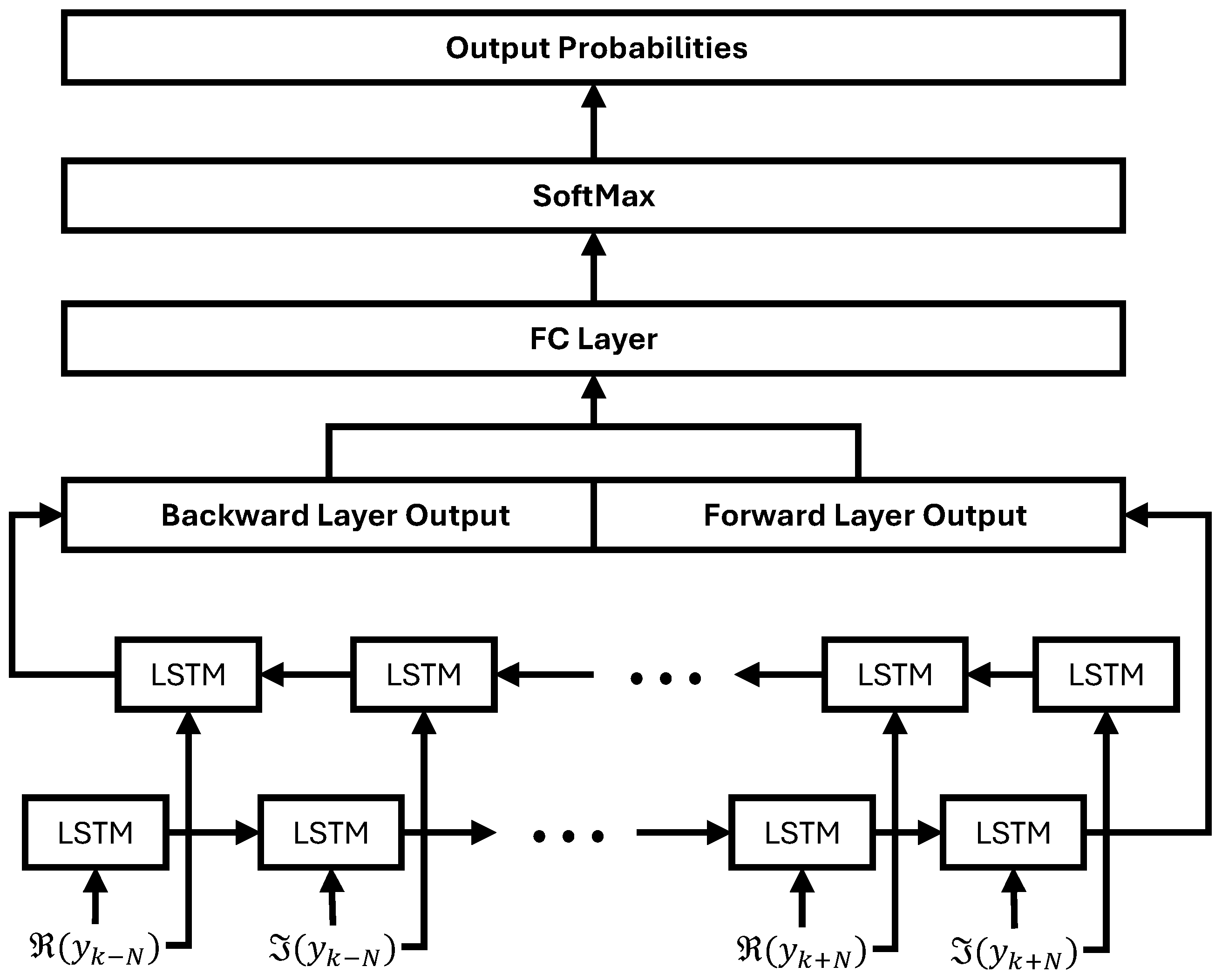
3.2.2. Bidirectional LSTM (Bi-LSTM)

To leverage both past and future context, which is crucial for resolving ISI, this study uses a Bi-LSTM model, as depicted in Figure 5. It consists of two independent LSTM layers—one LSTM layer processes the sequence forward to produce a hidden state ${\mathbf{r}}_k^{\left(\mathrm{fwd}\right)}$, and the other processes it backward to produce ${\mathbf{r}}_k^{\left(\mathrm{bwd}\right)}$. The outputs from both layers are then concatenated to form a combined hidden state, ${\mathbf{h}}_k$, as follows:

$${\mathbf{h}}_k={\left[\begin{array}{c}{\mathbf{r}}_k^{\left(\mathrm{fwd}\right)},{\mathbf{r}}_k^{\left(\mathrm{bwd}\right)}\end{array}\right]}^{\top }$$

(15)

This richer, context-aware vector ${\mathbf{h}}_k$ is then fed into a final prediction layer, which is identical in structure to the one used for the unidirectional model. It is processed through an FC layer and a Softmax function, as described in Equations (12)–(14) (with ${\mathbf{r}}_k$ replaced by ${\mathbf{h}}_k$), to produce the final predicted symbol ${\widehat{s}}_k$. By utilizing information from the entire sequence, Bi-LSTM generally achieves a superior performance compared to its unidirectional counterpart for ISI cancelation.

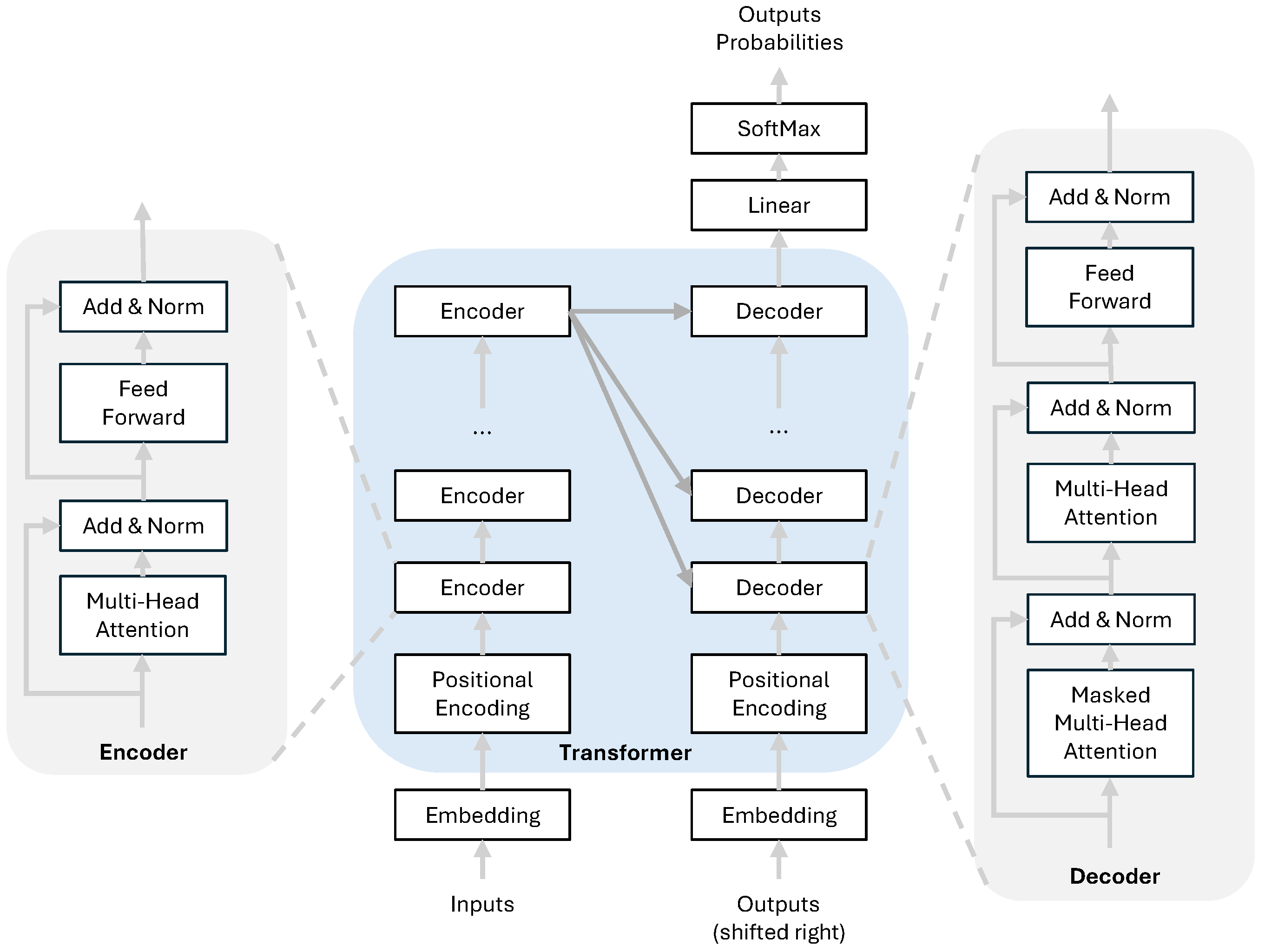
3.3. Proposed Transformer-Based Detector

To overcome the sequential limitations of RNNs and to better capture global dependencies, this study proposes a novel transformer-based detector, as illustrated in Figure 6.

3.3.1. Encoder Operation

The role of the encoder is to process the entire sequence of received, noisy signals and generate a rich, contextualized latent representation.

Input and Positional Encoding

The input to the transformer is the sequence of real-valued vectors, ${\mathbf{z}}_k$, generated, as shown in Equation (6). These vectors are first projected into a higher-dimensional embedding space of dimension $d_{\mathrm{model}}$. This parameter, $d_{\mathrm{model}}$, defines the internal working dimension of the entire transformer model. This initial projection is a critical step; it transforms the raw input into a richer, more expressive representation, providing the model with sufficient capacity to learn the complex patterns present in the signal. All subsequent layers within the transformer, including the self-attention and feed-forward networks, are designed to operate on vectors of this fixed dimension, $d_{\mathrm{model}}$. Since the self-attention mechanism is permutation-invariant, this study adds a unique positional encoding vector (PE) vector to each input embedding to retain sequence order, which is crucial for understanding the structured ISI patterns in FTN signaling. The combined input X is given as follows:

$$X=\mathrm{Embedding}\left(Z\right)+\mathrm{PE}$$

(16)

Multi-Head Self-Attention

The core of the transformer encoder is the multi-head self-attention layer. This mechanism allows the model to weigh the importance of different symbols in the input sequence when computing the representation for a specific symbol. The process begins by projecting the input X into three matrices—Query (Q), Key (K), and Value (V)—using learned weight matrices $W_Q$, $W_K$, and $W_V$, as follows:

$$Q=X{W}_Q,K=X{W}_K,V=X{W}_V$$

(17)

The attention output is then computed using the scaled dot-product attention formula, as follows:

$$\mathrm{Attention}(Q,K,V)=\mathrm{Softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(18)

Here, the dot product $Q{K}^T$ computes the similarity between each query and all keys. The result is scaled by the square root of the key dimension, $\sqrt{d_k}$, to ensure stable gradients. The Softmax function converts these scores into attention weights, which are then used to create a weighted sum of the value vectors V. To allow the model to jointly attend to information from different representation subspaces, this process is performed h times (the number of “heads”) in parallel. The output of each head is then concatenated and linearly projected back to the original dimension, as follows:

$$\mathrm{MultiHead}\left(X\right)=\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_h)W_O$$

(19)

where

$${\mathrm{head}}_i=\mathrm{Attention}(X{W}_Q^i,X{W}_K^i,X{W}_V^i)$$

(20)

Feed-Forward Network

Each encoder block consists of an attention layer followed by a position-wise feed-forward network (FFN). Both sub-layers have a residual connection around them, followed by layer normalization. The output of a sub-layer is depicted as follows:

$$\mathrm{LayerNorm}(x+\mathrm{Sublayer}(x\left)\right)$$

(21)

The FFN itself is a two-layer perceptron, as follows:

$$\mathrm{FFN}\left(x\right)=max(0,x{W}_1+b_1)W_2+b_2$$

(22)

3.3.2. Decoder Operation and Final Output

The decoder’s role is to generate the output sequence of detected symbols autoregressively (one by one), conditioned on the encoder’s output. It is assumed that the final output representation from the encoder stack be $Z_{\mathrm{enc}}$.

Masked Multi-Head Self-Attention

The decoder first applies self-attention to its own inputs (the sequence of symbols generated so far). To maintain the autoregressive property, this self-attention is “masked” to prevent any position from attending to future positions. This is achieved by adding a mask matrix M (with upper triangular elements set to $-\infty$) before the Softmax operation.

$$\mathrm{MaskedAttention}(Q_{\mathrm{dec}},K_{\mathrm{dec}},V_{\mathrm{dec}})=\mathrm{Softmax}\left({\displaystyle \frac{Q_{\mathrm{dec}}{K}_{\mathrm{dec}}^T+M}{\sqrt{d_k}}}\right)V_{\mathrm{dec}}$$

(23)

Encoder–Decoder Cross-Attention

This is the crucial layer where the decoder interacts with the encoder’s output, $Z_{\mathrm{enc}}$. The queries ($Q_{\mathrm{dec\_out}}$) come from the output of the decoder’s masked self-attention sub-layer, while the keys ($K_{\mathrm{enc}}$) and values ($V_{\mathrm{enc}}$) are generated from the encoder’s output $Z_{\mathrm{enc}}$. This allows the decoder to focus on the most relevant parts of the input signal sequence to predict the next symbol.

$$\mathrm{CrossAttention}(Q_{\mathrm{dec\_out}},K_{\mathrm{enc}},V_{\mathrm{enc}})=\mathrm{Softmax}\left({\displaystyle \frac{Q_{\mathrm{dec\_out}}{K}_{\mathrm{enc}}^T}{\sqrt{d_k}}}\right)V_{\mathrm{enc}}$$

(24)

Final Linear and Softmax Layer

After passing through its own FFN, the final output of the decoder stack at each time step, ${\mathrm{DecoderOutput}}_k$, is fed into a final prediction stage. This stage first uses a linear layer, which acts as a classifier, to project the high-dimensional vector into a logit vector, ${\mathbf{l}}_k$. The size of ${\mathbf{l}}_k$ equals the number of possible symbols, M, as follows:

$${\mathbf{l}}_k=\mathrm{Linear}\left({\mathrm{DecoderOutput}}_k\right)$$

(25)

A Softmax function then converts these logits into a probability distribution, ${\mathbf{P}}_k$, over the M possible symbols, as follows:

$${\mathbf{P}}_k=\mathrm{Softmax}\left({\mathbf{l}}_k\right)$$

(26)

Finally, the detected symbol, ${\widehat{s}}_k$, is determined by selecting the symbol with the highest probability using an argmax operation, as follows:

$${\widehat{s}}_k=argmax\left({\mathbf{P}}_k\right)$$

(27)

During training, the model learns by comparing this predicted distribution ${\mathbf{P}}_k$ against the true symbol $s_k$ to minimize a loss function, thereby adjusting the weights of the entire transformer network.

3.3.3. Advantages of the Proposed Detector

The proposed transformer-based detector offers several distinct advantages over conventional methods and RNN-based architectures like LSTM and Bi-LSTM.

Superior Modeling of Long-Range Dependencies

The core strength of the transformer lies in its self-attention mechanism. Unlike RNNs, which can struggle with the long-term dependency problem as information propagates sequentially, the transformer explicitly computes the relationship between every pair of symbols in the sequence, regardless of their distance. This is mathematically realized through the scaled dot-product attention formula in Equation (18). By computing the dot product between Query (Q) and Key (K) matrices—which are derived from the entire input sequence, as shown in Equation (17)—the model directly assesses the relevance of every symbol to all others in a single operation. Furthermore, as described in Equations (19) and (20), this process is performed in multiple parallel heads, allowing the model to jointly attend to information from different representation subspaces and capture various types of dependencies at once. This capability to globally analyze the sequence is particularly advantageous for the FTN-RIS channel, where the interference pattern is not just local but can be spread across a long duration due to the combined effects of FTN pulse overlap and multipath reflections from the RIS.

Parallel Processing and Computational Efficiency

The transformer architecture is inherently parallelizable, which is a stark contrast to the sequential, step-by-step nature of RNNs. This efficiency stems from the fact that its core computations are not dependent on the output of a previous time step. Specifically, the generation of the Query, Key, and Value matrices in Equation (17) and the subsequent attention score calculations in Equation (18) are all matrix operations that are performed across the entire input sequence simultaneously. Furthermore, the other major component of the block—the position-wise feed-forward network described in Equation (22)—is applied independently to each symbol’s representation. This lack of sequential dependency means the entire forward pass for a sequence can be heavily optimized for parallel execution. This allows for a significantly more-efficient use of modern hardware like GPUs, leading to faster training times and a potentially lower latency during real-time inference, which is a critical factor for practical communication systems.

Enhanced Model Capacity and Scalability

The transformer architecture has proven to be highly scalable, forming the foundation of today’s state-of-the-art large language models. This scalability is fundamentally enabled by the modular structure of its encoder and decoder blocks, mathematically represented by the residual connection and layer normalization in Equation (21). This design ensures that the output of each block maintains the same dimension as its input, allowing additional layers to be stacked seamlessly to increase model capacity. This architectural feature is what makes it possible to readily increase the model’s capacity (e.g., by stacking more encoder/decoder layers) to learn even more complex and severe channel distortions, offering a robust and future-proof framework for next-generation communication challenges.

3.3.4. Summary of the Proposed Scheme

In summary, this section has detailed a novel signal detection framework for FTN-RIS systems based on the transformer architecture. While baseline models like LSTM and Bi-LSTM provide a valid data-driven approach by capturing the sequential nature of the received signal, the proposed transformer-based detector represents a fundamental architectural shift. By replacing the sequential recurrence of RNNs with parallelized, global self-attention, it is uniquely equipped to model the complex, non-local, and long-range interference patterns that characterize the FTN-RIS channel.

Therefore, this study posits that this framework will not only overcome the inherent limitations of its RNN-based predecessors but will also establish a new state of the art for this challenging communication scenario. The following sections will present extensive simulation results to validate this hypothesis and quantify the performance gains of the proposed method.

4. Simulation Environment

The simulations were conducted to evaluate the performance of the proposed detection framework in a rich multipath environment. This study focuses exclusively on a non-LOS channel scenario, as this represents the most challenging and practically significant context for the application of RISs. This choice is motivated by the fundamental role of an RIS in future communication systems, which is to create a virtual LOS path to overcome blockages. Therefore, evaluating the system in a non-LOS environment provides a more rigorous and relevant assessment of its capabilities.

To emulate this scenario, the wireless channels were modeled as follows. The channel between the base station (BS) and the RIS, as well as the channel between the RIS and the user equipment (UE), are modeled according to the 3GPP spatial channel model (SCM), specifically using the urban-micro (UMi) scenario parameters. This model provides a realistic representation of a rich multipath environment with spatial correlation. Each channel realization is assumed to be quasi-static, remaining constant for the duration of a transmission block but varying independently from one block to the next. The RIS is assumed to have continuously adjustable phase shifts, allowing for ideal phase alignment to maximize the received signal power.

The key parameters for the communication system and the hyperparameters for the deep learning models are summarized in

Table 1. Communication system parameters.

Parameter	Value	Description
Modulation	QPSK ($M=4$)	M-PSK modulation scheme
FTN Factor ($\tau$)	0.85	Time acceleration factor
RRC Roll-off Factor	0.3	Roll-off factor for the pulse shaping filter
Transmit Antennas ($N_{\mathrm{BS}}$)	16	Number of antennas at the base station
Receive Antennas ($N_{\mathrm{Rx}}$)	4	Number of antennas at the receiver
RIS Elements ($N_{\mathrm{RIS}}$)	64	Number of passive elements on the RIS
SNR Range	0 dB to 20 dB (in 2 dB steps)	Evaluation range for SNR

and

Table 2. ML model hyperparameters.

Model	Hyperparameter	Value
SeqLSTM	Input Dimension	2 (Real and Imaginary)
	Hidden Dimension	64
	Number of Layers	2
	Dropout	0.3
	Input Sequence Length	15
	Optimizer/LR	Adam/$1\times {10}^{-3}$
Bi-LSTM	Input Dimension	2 (Real and Imaginary)
	Hidden Dimension	128
	Number of Layers	2 (for each direction)
	Dropout	0.3
	Input Sequence Length	61
	Optimizer/LR	Adam/$5\times {10}^{-4}$
Transformer (Proposed)	Input Dimension	2 (Real and Imaginary)
	Input Sequence Length	61
	Model Dimension ($d_{\mathrm{model}}$)	128
	Number of Heads ($n_{\mathrm{head}}$)	4
	Number of Encoder Layers	2
	Feed-Forward Dimension	256
	Dropout	0.1
	Optimizer/LR	Adam/$1\times {10}^{-3}$

, respectively. The selection of baseline models for comparison warrants a brief justification. In this study, LSTM and Bi-LSTM were chosen as the primary benchmarks.

While a vast range of complex, hybrid deep learning architectures exist, the objective here is not an exhaustive comparison, but a fundamental one. LSTM and Bi-LSTM are widely recognized as the canonical state-of-the-art architectures for processing sequential data in communication systems. Therefore, they serve as the most direct and relevant benchmarks to clearly illustrate the fundamental architectural and performance differences between the sequential processing paradigm of RNNs and the global, parallel processing paradigm of the proposed transformer. This focused comparison allows for an unambiguous assessment of the transformer’s inherent advantages for this specific task, without the confounding variables introduced by more complex, problem-specific hybrid designs. These parameters were selected to represent a realistic and challenging FTN-RIS MIMO system.

4.1. BER and Spectral Efficiency Performance

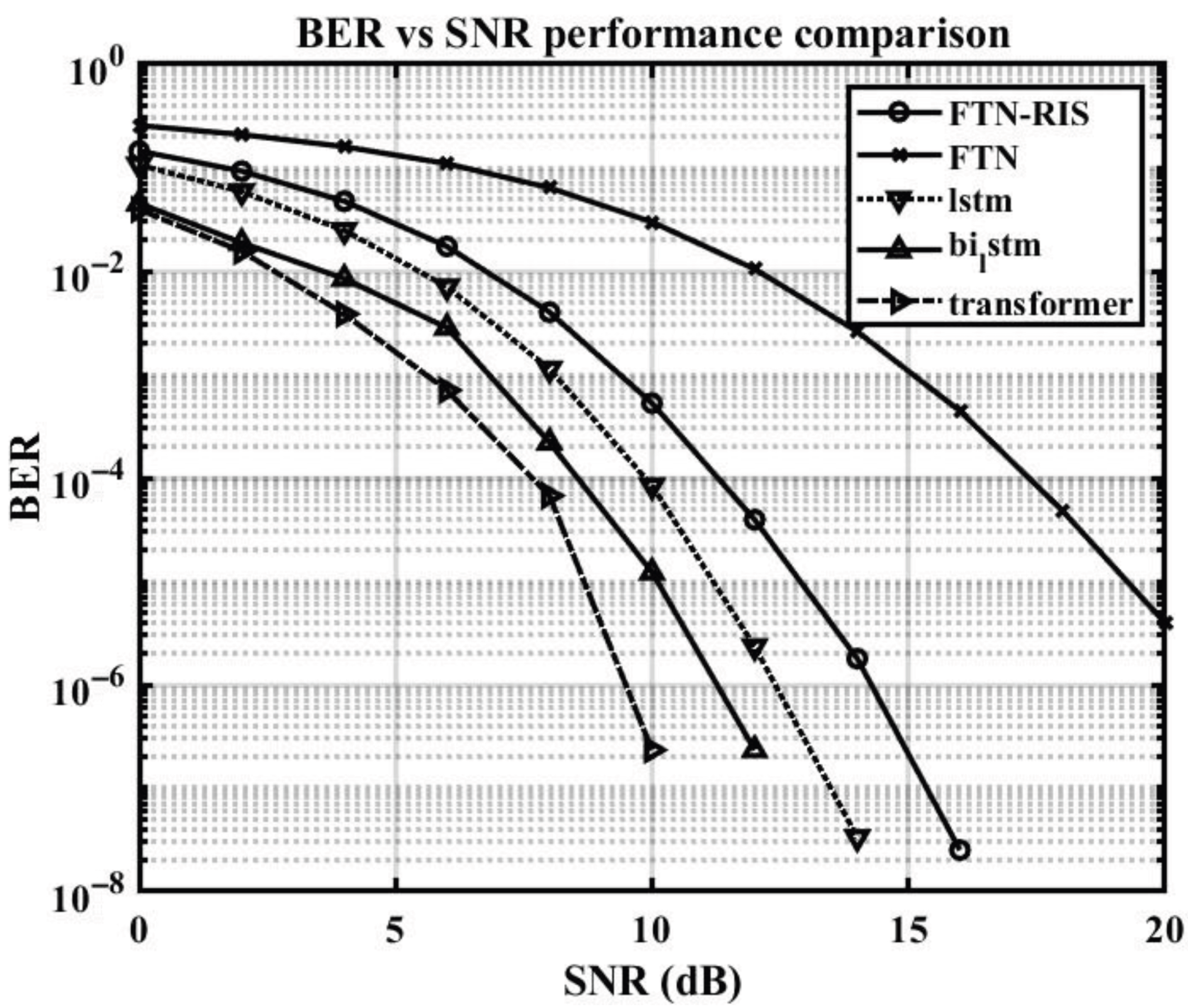
Figure 7 presents the core results of this study, comparing the BER performance of the different detection schemes across a range of SNR values. The proposed transformer-based detector demonstrates a commanding performance advantage over all baseline models, consistently achieving the lowest BER in all SNR regions.

To explicitly analyze the impact of the RIS-mediated cascaded channel against the direct channel, the performance of an ’FTN only’ system is presented. As shown by the FTN curve in Figure 7, this direct-channel-only system requires a high SNR of approximately 17 dB to reach the target BER of ${10}^{-4}$. This is substantially higher than any of the RIS-assisted configurations, demonstrating a significant performance degradation when the RIS is absent. This result confirms that while communication over the direct path is theoretically possible, the RIS is essential for establishing an efficient and robust link in the considered non-LOS environment.

With the necessity of the RIS established, the performance of the various detection schemes for the RIS-assisted system is quantified by the SNR required to achieve a target BER of ${10}^{-4}$. This threshold is selected as a demanding practical benchmark, motivated by the stringent reliability standards of next-generation communication systems. For example, the official ITU-R recommendation for 5G enhanced mobile broadband (eMBB) services already sets the user plane reliability target at ${10}^{-5}$ [21]. Furthermore, the framework for 6G (IMT-2030) anticipates support for even more demanding applications, such as immersive communications, which will necessitate even stricter reliability requirements [22]. Therefore, the chosen BER of ${10}^{-4}$ in this study serves as a challenging and relevant reference point for evaluating the capabilities of advanced detection schemes on their path toward meeting not only current 5G standards but also the more extreme reliability demanded by future 6G systems.

To reach this target BER, the transformer-based detector requires an SNR of approximately 7.5 dB. In contrast, the Bi-LSTM model requires about 9 dB, and the LSTM model needs around 10 dB. The conventional FTN-RIS system reaches the same target at approximately 11.5 dB. This translates to a significant SNR gain for the transformer of approximately 1.5 dB over the Bi-LSTM model, as well as a gain of 4 dB over the conventional FTN-RIS system.

This significant performance gain is fundamentally attributed to the transformer’s architectural superiority in handling the specific type of interference present in the FTN-RIS system. By leveraging its self-attention mechanism, the transformer globally analyzes the entire received signal sequence at once. Unlike Bi-LSTM, which processes the sequence sequentially and can still struggle to model very-long-range dependencies, the transformer can directly compute the relevance between any two symbols in the sequence, regardless of their distance. This capability is particularly crucial for capturing the complex, non-local interference patterns introduced by the combination of FTN pulse overlap and multipath reflections from the cascaded RIS channel. As a result, the transformer can model and reverse the distortion more effectively, leading to superior signal recovery.

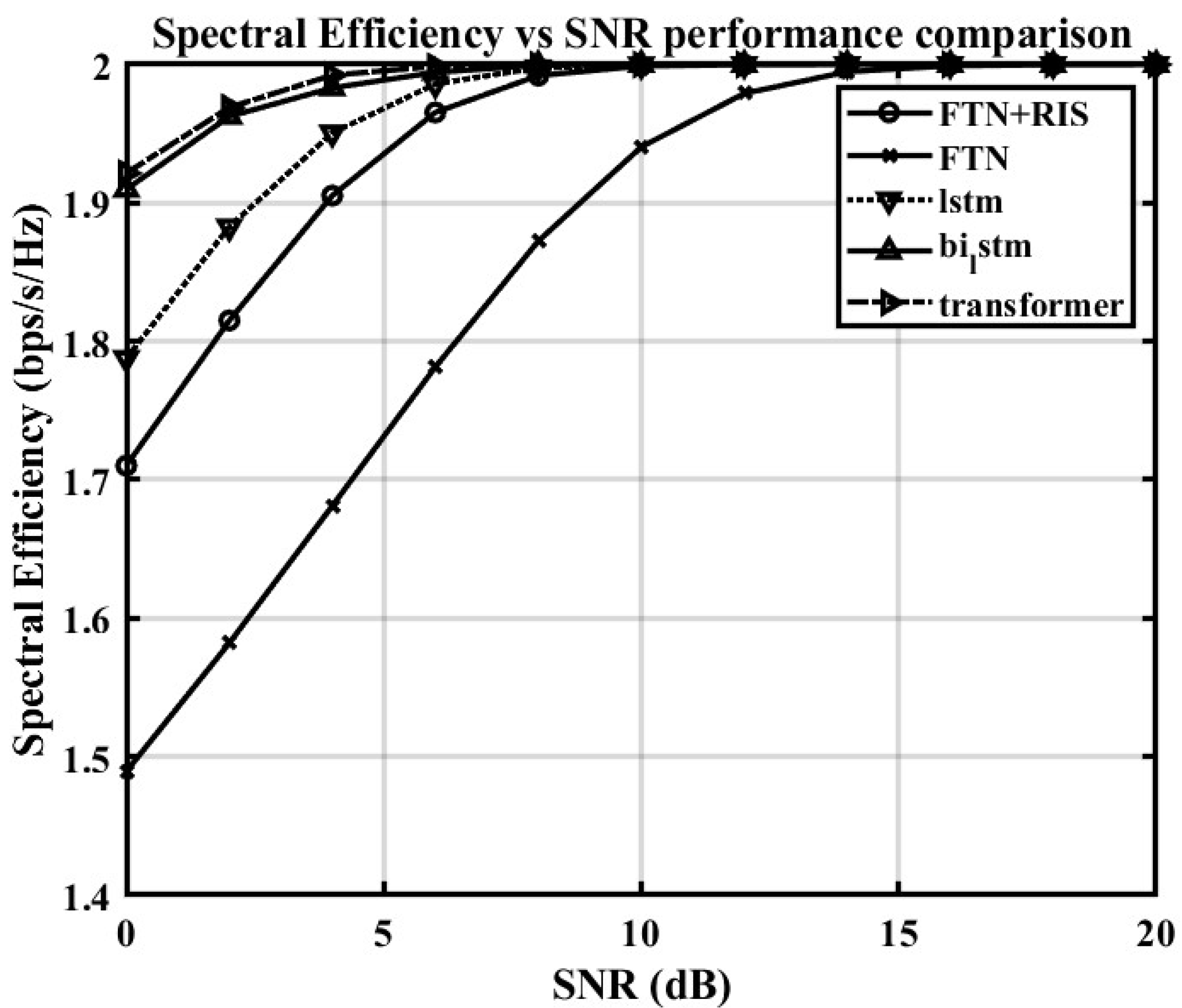
Crucially, this substantial improvement in reliability does not come at the expense of throughput. As shown in Figure 8, all compared detection schemes operate on the same FTN signal structure, which is the primary determinant of the theoretical maximum SE. Consequently, all schemes achieve a high SE, approaching 2.0 bps/s/Hz. However, the transformer-based detector reaches this peak SE at a significantly lower SNR compared to the other models. This demonstrates that the transformer’s superior interference mitigation capability not only enhances reliability but also allows the system to achieve its full spectral efficiency potential more quickly and efficiently. It successfully unlocks the high throughput promised by FTN signaling while maintaining excellent reliability.

4.2. In-Depth Analysis of ML Model Performance

To understand why the transformer outperforms its RNN-based counterparts, this study conducted a deeper analysis of their classification capabilities.

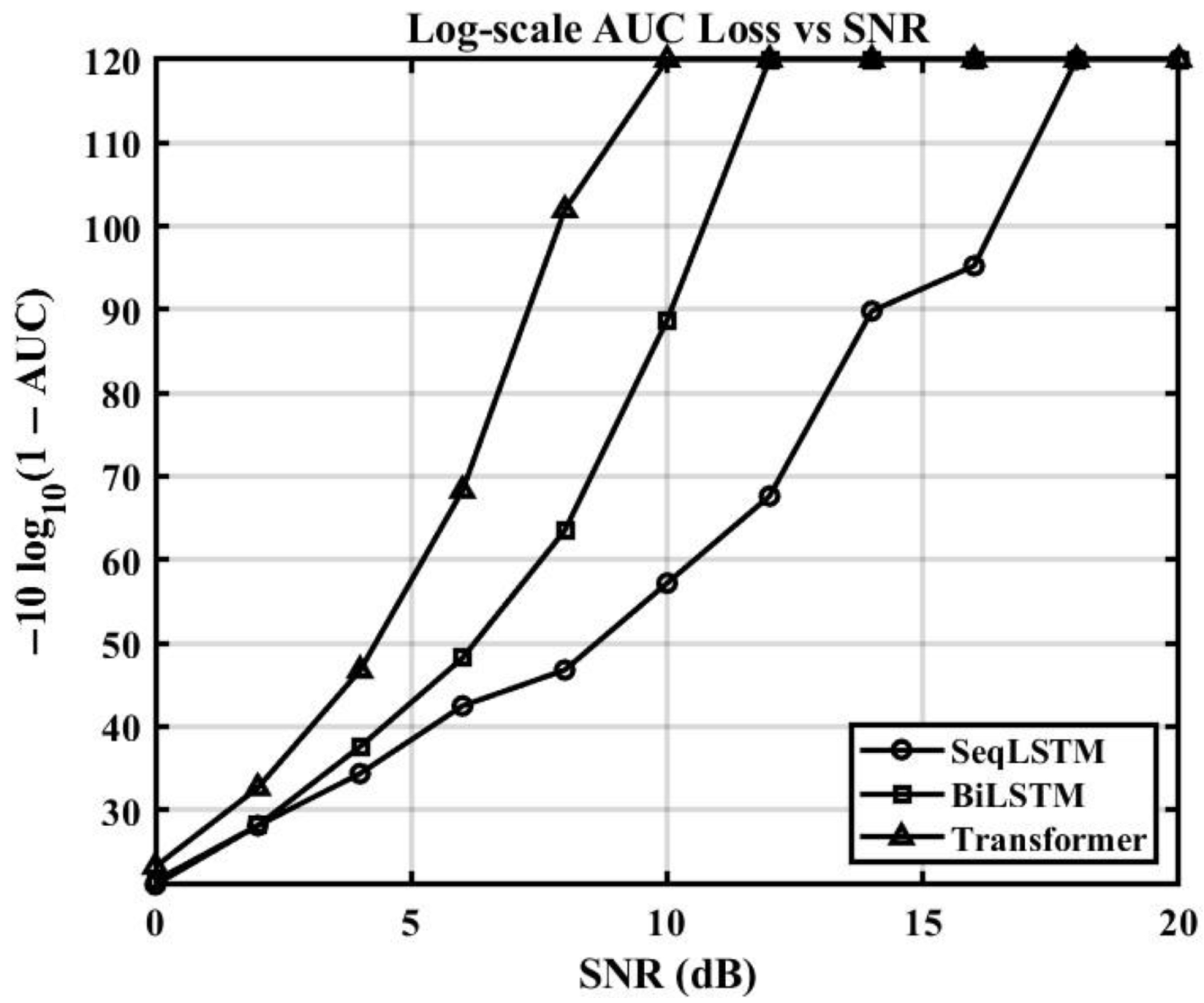
The learning efficiency is visualized in Figure 9, which plots the log-scale area under the loss curve (AUC). A higher value on the y-axis indicates an AUC closer to 1, signifying a better classification performance. The transformer’s loss curve rises much more steeply than that of the Bi-LSTM and SeqLSTM models as the SNR increases. This indicates that the transformer learns to distinguish between signal and noise more effectively and rapidly as signal quality improves.

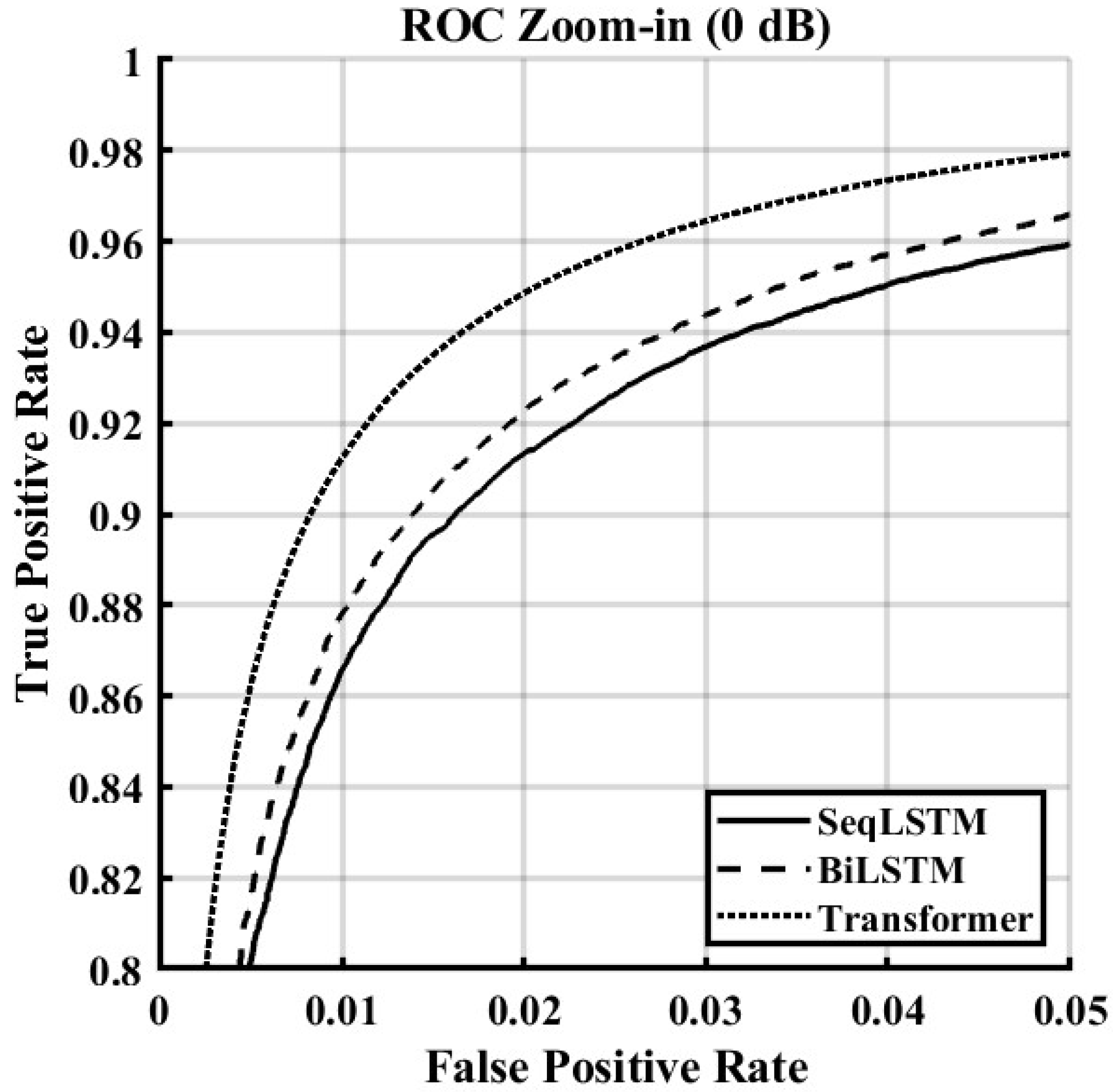
Figure 10 provides a zoomed-in view of the receiver operating characteristic (ROC) curve at a challenging 0 dB SNR. For any given False Positive Rate, the transformer achieves a higher True Positive Rate than the other models. This confirms its superior detection capability and robustness, especially in low-SNR regimes where interference and noise are dominant.

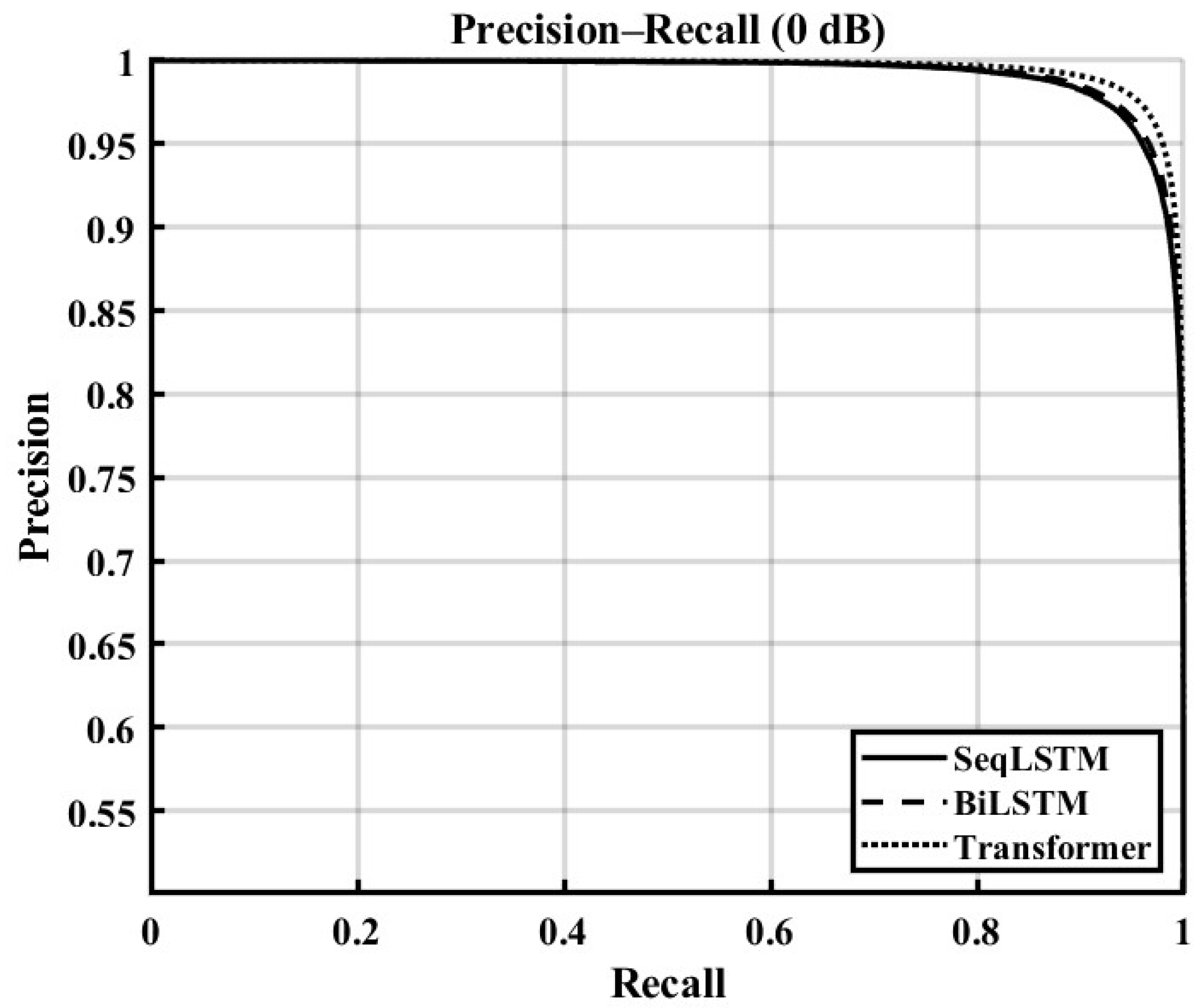
Finally, Figure 11 shows the Precision–Recall curve, also at 0 dB SNR. While all models achieve high average precision (AP) scores (L: 0.992, B: 0.993, T: 0.995), the transformer’s advantage is clear in the high-recall region. When the models are required to find almost all True Positive cases, the transformer’s precision degrades the least. This signifies its superior ability to minimize False Positives without sacrificing detection coverage, making it the most reliable and precise classifier among the tested models.

5. Conclusions

This study has proposed and evaluated a novel signal detection framework based on the transformer architecture, designed to overcome the severe ISI inherent in FTN-RIS MIMO systems. By leveraging the self-attention mechanism to learn the global relationships within the entire received signal sequence, the proposed detector demonstrated superior performance not only over conventional linear equalization methods but also over state-of-the-art RNN-based models such as LSTM and Bi-LSTM.

The simulation results quantitatively validate this superiority, whereby the transformer-based detector achieves a significant SNR gain of approximately 1.5 dB over the Bi-LSTM model for a target BER of ${10}^{-4}$. This empirical success is supported by the in-depth qualitative analysis in Section 4.1, which attributes the performance gain to the transformer’s unique ability to model the non-local interference patterns of the FTN-RIS channel. Furthermore, analyses of ROC, AUC, and Precision–Recall curves consistently confirmed its superior classification performance across various metrics. These findings strongly suggest that the proposed transformer-based detector is a powerful and effective solution that is capable of simultaneously achieving the high spectral efficiency and extreme reliability demanded by future wireless communication systems.

It is acknowledged that this study was conducted under the assumption of perfect CSI and without considering computational complexity constraints. These ideal conditions were chosen to isolate and clearly demonstrate the architectural advantages of the transformer for this specific task, thereby establishing a performance benchmark. The practical challenges of imperfect CSI and efficient hardware deployment are identified as critical areas for subsequent research.

Future Research Directions

Future work can extend this research in several promising directions. One key area is the investigation of model compression techniques, such as knowledge distillation or pruning, to reduce the computational complexity of the transformer model for practical deployment on real-world communication hardware. Additionally, evaluating the performance and enhancing the robustness of the proposed detector in more realistic scenarios with imperfect CSI would be a valuable direction for future studies.