Reduction and Efficient Solution of ILP Models of Mixed Hamming Packings Yielding Improved Upper Bounds

Abstract

We consider mixed Hamming packings, addressing the maximal cardinality of codes with a minimum codeword Hamming distance. We do not rely on any algebraic structure of the alphabets. We extend known-integer linear programming models of the problem to be efficiently tractable using standard ILP solvers. This is achieved by adopting the concept of contact graphs from classical continuous sphere packing problems to the present discrete context, resulting in a reduction technique for the models which enables their efficient solution as well as their decomposition to smaller subproblems. Based on our calculations, we provide a systematic summary of all lower and upper bounds for packings in the smallest Hamming spaces. The known results are reproduced, with some bounds found to be sharp, and the upper bounds improved in some cases.

1. Introduction

Hamming packings have been broadly studied in the literature and have many applications. In code theory, they are known as unrestricted error correcting codes. Mixed Hamming packings are codes in which the characters of codewords come from alphabets of different cardinality. In the present contribution, we consider mixed Hamming packings.

1.1. Related Work

Given a Hamming space, the determination of the maximal cardinality of a Hamming packing with a given minimal distance is a key question in coding theory. It has been studied in numerous contributions in the literature; the broader topic is covered by the excellent monographs of Stinson [1] and Etzion [2]. A good overview is also provided in the Concise Encyclopedia of Coding Theory [3].

Most of the works related to the topic assume an algebraic structure on the alphabets, like groups or Galois fields. Usually, lower bounds are corollaries of explicit constructions, like in [4,5,6,7,8,9,10], while upper bounds are derived from estimations, discussed, e.g., in [6,11,12,13,14,15,16]. Exact values are known only in a few marginal cases, e.g., for maximum distance codes or perfect codes [4,7,17,18,19] or for codes in certain small Hamming spaces [6,8,12,20,21].

Meanwhile, a Hamming space does not necessarily assume any algebraic structure—codewords can be considered as a set of strings, i.e., n-tuples of the alphabet elements, forming a metric space with the Hamming distance. Such an approach is more general in that it makes less assumptions about the structure. On the other hand, it is more restrictive, too, as it rules out the application of many successful and advanced techniques. The particular questions concerning Hamming packings addressed in the present contribution—for instance, the kind of results that can be found in Brouwer’s online collection [21]—do not depend on the possible algebraic structures. Indeed, we can find other works, e.g., [22] or [9], which do not rely on algebraic structures.

Mixed codes, i.e., those in which the cardinality of the alphabets at character positions can be different, constitute a relevant subset of coding problems with open research questions (see also Section 3.3 of [3]). Our results relate to ball packing bounds of mixed codes, similar to the results in [22,23].

1.2. Our Contribution

We consider Hamming spaces without assuming any algebraic structure on the alphabets. We consider mixed codes, i.e., codes where the cardinality of the alphabets of the symbols and different positions can be different. Hence, by a Hamming packing, or simply, packing, we mean a mixed Hamming packing, and by a code, we mean a mixed code throughout this paper.

We extend a known [24], simple, and inefficient (ILP) model for finding maximum packings with constraints that make the model useful in practical computations. Some of our constraints consist of fixing variables, thereby reducing the size of the model. The considered ILP models, with or without our constraints, have the same optima; hence, they are equivalent to an exhaustive search.

The above extension is achieved by adopting the notion of the contact graph ($CG$) introduced originally for Tammes’ $S^2$ classic sphere packing problem [25] to our code-theoretic setting. The contact graph helps with the classification of packings. As part of our main result, we show that for any code, there exists a code with the same cardinality and a connected contact graph. We give a constructive algorithmic proof. The aforementioned extension of the ILP models is achieved using this proposition and its corollaries. State-of-the-art ILP solvers can solve our extended model efficiently in many cases.

This paper is organized as follows. In Section 2, we introduce the notation and definitions. In Section 3, we recapitulate certain relevant facts on bounds or constructing optimal packings in particular cases. In Section 4, we describe the ILP models we study. Section 5 contains our main results for the size reduction of the models. Section 6 presents our computational results. We describe in detail some selected cases in which we have found improved bounds to showcase the use of our methods in detail, while the corresponding Appendix A provides a systematic summary of optimal or best known codes, particularly in the smallest mixed Hamming spaces. In Section 7, the results are summarized and conclusions are drawn.

2. Notation and Conventions

We consider k-ary alphabets without any algebraic structure. Yet, we will denote alphabets by integers ${\mathbb{Z}}_k=\{0,1,\dots k-1\}$ for the sake of notational convenience. The elements of the Cartesian product $H(k_1,k_2,\dots k_n)={\mathbb{Z}}_{k_1}\times {\mathbb{Z}}_{k_2}\times \dots \times {\mathbb{Z}}_{k_n}:={\mathbb{Z}}_{k_1}{\mathbb{Z}}_{k_2}\dots {\mathbb{Z}}_{k_n}$ are called words. We can assume without loss of generality that $2\le k_1\le k_2\le \cdots \le k_n<\infty$.

Let us denote the length of words by n, also referred to as the dimension of H. From now on, H without any argument will denote the set of possible codewords with a fixed parameter set $(k_1,\dots k_n)$, whenever the set of parameters is clear from the context.

To simplify the notation of words, the elements of the Cartesian products will be concatenated so that the words are n-strings of numbers. The positions $j\in \{1,\dots n\}$ within a codeword are termed as coordinates, and the j-th element (character) of $w\in W$ is denoted by $w\left[j\right]$. A subset $C\subseteq H$ is termed a code; its elements are the codewords. As an example, the binary–ternary–quaternary mixed codes are those with $k_j\le 4\left(\forall j:1\le j\le n\right)$; thus, they consist of n characters from binary, ternary, and quaternary alphabets.

Certain codes are considered as equivalent. Let us consider the permutations ${\pi }_H$ of the coordinates which are not mixing coordinates of alphabets with different cardinality. That is, if the coordinate j is moved to ${\pi }_H\left(j\right)$ by the permutation, then the alphabets at j and ${\pi }_H\left(j\right)$ are of the same cardinality. Further, let ${\pi }_j$ be a permutation (also known as relabelling) of the alphabet at coordinate j. We shall call two codes equivalent if they can be transformed into each other with the composition of all these permutations.

Given two words, $w\in H$ and $w^{\prime }\in H$, their (Ham ming) distance is the number of positions at which they differ:

$$d_H(w,w^{\prime })=\sum _{j=1}^n\mathrm{sgn}\left|w\left[j\right]-w^{\prime }\left[j\right]\right|.$$

(1)

(Note that the previous formula subtracts the characters to shorten the description; it could be formulated without it.) The set H of all possible codewords, together with the Hamming distance $d_H(.,.)$ as a metric is termed a Hamming space.

For a code $C\subset H$, the minimum distance of the code is the minimum of $d_H(w,w^{\prime })$ over all distinct $w,w^{\prime }\in C$:

$$d_H\left(C\right)=\underset{\begin{array}{c}w\ne w^{\prime }\\ w,w^{\prime }\in C\end{array}}{min}{d}_H(w,w^{\prime }).$$

(2)

Similarly, we can introduce the distance of two codes

$$d_H(C,C^{\prime })=\underset{\begin{array}{c}w\in C\\ w^{\prime }\in C^{\prime }\end{array}}{min}{d}_H(w,w^{\prime }).$$

(3)

Notice that $d_H\left(C\right)\ne d_H(C,C)$. Among all codes having a given minimum distance d, there exists at least one which has maximal cardinality. Such a code is termed an optimal (or maximum) Hamming packing. We will refer to it as a Hamming packing in what follows, that is, by a Hamming packing, we will always mean an optimal Hamming packing unless otherwise stated. In addition, those that are not necessarily optimal packings and that do not strictly contain any other packings are referred to as maximal (Hamming) packings.

The term ‘packing’ comes from a geometric interpretation; considering the codewords as points, with the metric generated by the Hamming distance, a Hamming packing is indeed an extremal packing in the geometric sense. The maximal cardinality of a Hamming packing with minimum distance d is defined as

$$N_{k_1,k_2,\dots ,k_s}({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_s;d)\equiv N(H;d)=\underset{d_H\left(C\right)\ge d}{max}\left|C\right|,$$

(4)

where we have introduced a more accurate and a simplified notation; we will use both notations.

Finally, it will be convenient to use the notion of spheres. The sphere with a centre w and radius r can be defined as

$$S(w,r)=\{v:d_H(v,w)=r\}.$$

(5)

The concept of spheres can be generalized to arbitrary subsets $C\subseteq H$ as centres:

$$S(C,r)=\{w:d_H(C,\left\{w\right\})=r\}.$$

(6)

Note that the sphere of an arbitrary subset might be empty, even in nontrivial cases.

3. Known Bounds and Properties

Let us summarize certain bounds and basic properties related to the cardinality of maximum Hamming packings that we will use and are prevalently known from the literature.

Proposition 1.

Komamiya–Joshi–Singleton bound [17,26,27]: Let $H={\mathbb{Z}}_{k_1}{\mathbb{Z}}_{k_2}\dots {\mathbb{Z}}_{k_n}$, where $k_1\le k_2\le \cdots \le k_n$. Then, for any $1\le d\le n$: $N(H;d)\le k_1{k}_2{k}_3\dots k_{n+1-d}$.

Proof. 

The pigeonhole principle can be applied. For any code with minimal distance d, restricting to any $n+1-d$ subset of the alphabets, the corresponding parts of each pair of codewords from the code must differ in at least one position; otherwise, this pair could only realize a distance of at most $d-1$. This property holds for every such subsets of alphabets, including the ones with minimal cardinalities.    □

A code will be called KJS sharp if it saturates its Komamiya–Joshi–Singleton bound. Remarkably, in the case when $d=1,2\mathrm{or}n$, these codes are KJS sharp, and direct optimal code constructions are trivial; several special cases are mentioned in [9]. From now on, we suppose that $3\le d\le n-1$. The KJS sharpness is a natural generalization of the maximal distance separable (MDS [17,28]) property in spaces over uniform alphabets.

Next, we recapitulate a proposition which yields upper bounds for smaller spaces by truncating a code at a certain position.

Proposition 2

([8,9]). Let $H={\mathbb{Z}}_{k_1}{\mathbb{Z}}_{k_2}\dots {\mathbb{Z}}_{k_n}$ for a given $2\le k_1\le k_2\le \cdots \le k_n$, and let $H_j={\mathbb{Z}}_{k_1}{\mathbb{Z}}_{k_2}\dots {\mathbb{Z}}_{k_j-1}\dots {\mathbb{Z}}_{k_n}$ for all $1\le j\le n$. Then, the following two statements hold: $N(H_j;d)\le N(H;d)$ and $N(H_j;d)\ge {\displaystyle \frac{k_j-1}{k_j}}N(H;d)$.

Proof. 

The first part is trivial: every $C\subseteq H_j$ code is also a code in H. Conversely, consider an optimal packing C in H such that $N(H;d)=\left|C\right|$. For each codeword’s coordinate at j, using the pigeonhole principle, ${min}_{i\in {\mathbb{Z}}_{k_j}}\left|\{w\in C:w\left[j\right]=i\}\right|\le {\displaystyle \frac{\left|C\right|}{k_j}}$. Let $C^{\prime }\subset C$ be the subset code obtained by the following truncation: $C^{\prime }=\{w\in C:w\left[j\right]\ne i\}$. This has an equivalent $C^{″}$ code in C, where $w\left[j\right]\le k_j-2\forall w\in C^{″}$; hence, $C^{″}\subseteq H_j$, and $\left|C^{″}\right|\ge {\displaystyle \frac{k_j-1}{k_j}}\left|C\right|$.    □

We note that the second inequality is commonly known [22], especially for the $k_j=3$ case, which is particularly important for football pool systems. The proof is the same for other values of $k_j$; it is the straightforward generalization of item (iv) of Proposition 4.3 from the work of Brouwer et al. [8]. Notice that even in case of $k_j=2$, the truncation still has a reasonable meaning and provides an estimation for a 1-codimensional (i.e., one-letter-shorter) optimal Hamming packing:

$$\begin{array}{c}\hfill N({\mathbb{Z}}_{k_1}{\mathbb{Z}}_{k_2}\dots {\mathbb{Z}}_{k_{j-1}}{\mathbb{Z}}_{k_{j+1}}\dots {\mathbb{Z}}_{k_n};d)\ge {\displaystyle \frac{1}{k_j}}N({\mathbb{Z}}_{k_1}{\mathbb{Z}}_{k_2}\dots {\mathbb{Z}}_{k_{j-1}}{\mathbb{Z}}_{k_j}{\mathbb{Z}}_{k_{j+1}}\dots {\mathbb{Z}}_{k_n};d).\end{array}$$

(7)

Corollary 1.

Consider a fixed d and two Hamming spaces H and $H^{\prime }$ with the same dimension. Assume that $k_j=k_j^{\prime }\forall 1\le j\le n+1-d$ and $k_j\le k_j^{\prime }$ holds, and H, the smaller space, has a KJS sharp packing. Then the same packing is also optimal in the bigger space $H^{\prime }$.

This means that having a KJS sharp packing in a space also determines the optimal packing in certain bigger spaces. Let us now discuss codes of length 4.

Proposition 3.

For $n=4$, $2\le k_1\le k_2\le k_3\le k_4$ and $k_2\ne 6,k_2\ge 3$, the optimal value $N_{k_1,k_2,k_3,k_4}(1,1,1,1;d=3)=k_1{k}_2$, which meets its Komamiya–Joshi–Singleton (KJS) bound.

The constructive proofs known from the literature are based on the existence of mutually orthogonal Latin squares (MOLS), which can be found in [1], wherein for the case of $k_2=k_1=k_3=k_4$, Theorems 10.21, 6.38, and 6.51 in [1] are applied as MOLS. Due to the sharpness of KJS bounds, truncated codes on the position with the smallest cardinality will remain as KJS sharp feasible maximal packings in the truncated Hamming space. The remaining marginal cases for $n=4$ and $k_2\in \{2,6\}$ are also known and can be enumerated (we will also list one optimal code per case in Section 6): $N_2(4;d=3)=2, N_{2,3}(3,1;d=3)=3, N_{2,3}(2,2;d=3)=4, N_{2,4}(3,1;d=3)=4, N_{5,6}(1,3;d=3)=30, N_6(4;d=3)=34,N_{6,7}(3,1;d=3)=36$.

Let us briefly summarize some known algebraic constructions for families of optimal codes having a length of 5 (these are based on Theorems 10.21, 6.38, and 6.51 in [1]).

Proposition 4.

Suppose that given $2\le k_1\le k_2\le k_3\le k_4\le k_5$, $n=5$, and suppose that there exists 3 MOLS of order $k_2$, then in this case, the optimal value $N_{k_1,k_2,k_3,k_4,k_5}(1,1,1,1,1;d=4)=k_1{k}_2$.

Proposition 4 covers all but the following finitely many cases: $k_2\in \{2,3,6,10\}$. For the latter, mostly partial results are known, while the optima are unknown. Remarkably, the results in [29,30,31] show that there exists 3 MOLS of order $k_2$ for every $k_2\ge 11$.

Proposition 5.

Suppose that given $2\le k_1\le k_2\le k_3\le k_4\le k_5$, $n=5$, and $4\le k_3\ne 4s+2$. Then, for the optimal value, we have $N_{k_1,k_2,k_3,k_4,k_5}(1,1,1,1,1;d=3)=k_1{k}_2{k}_3$.

The proof relies on the existence of orthogonal arrays of strength 3 and length 5 in [32] (denoted by $OA(3,5,m)$ therein), where $m=k_3$, and the alphabet truncation mentioned in Proposition 2 is applicable for the respective coordinates belonging to $k_1$, $k_2$. Proposition 5 covers all cases except the following: $k_3=4s+2$ for certain infinite classes of s values, based on the new construction methods of orthogonal arrays in [33].

Corollary 2.

Suppose that $s\ge 1,s\in \mathbb{Z}$ is given, then after applying constructions from Proposition 5 with parameter $k_3=(4s+3)$ and estimations from Proposition 2, we establish the following KJS sharp optimal values:

$$\begin{array}{ccc}\mathrm{(8)}& \hfill N_{(4s+2),(4s+3)}(1,4;d=3)& =& (4s+2){(4s+3)}^2,\hfill \hfill N_{(4s+2),(4s+3)}(2,3;d=3)& =& {(4s+2)}^2(4s+3),\hfill \\ \hfill N_{(4s+2),(4s+3)}(3,2;d=3)& =& {(4s+2)}^3.\hfill \end{array}$$

The statement also holds for $k_3=4$, which yields $N_{3,4}(3,2;d=3)=27$. We can omit an infinite amount of Hamming space families, some with huge alphabet cardinalities from our consideration, by setting the following bound on the cardinality of the maximal alphabet: $\underset{j=1}{\overset{n}{max}}{k}_j<\mathrm{KJS}$, or formally: $k_m<{\displaystyle \prod _{j=1}^{n+1-d}}{k}_j\forall 1\le m\le n$. If this bound is violated, an optimal code can be altered so that all codewords have different values at position n. Hence, the character at this position can be eliminated, and thus, the code should be constructed from an optimal code of the resulting smaller Hamming space.

This observation leads us to a reasonable number of cases for small $\left|H\right|$ values up to 600 and occasionally for some bigger spaces. Our strategy was to fix a d, n, and a KJS bound as a product of fixed cardinalities, and then determine all small spaces with their optimal packing below the given KJS bound using Corollary 1.

4. ILP Models for Hamming Packing

Let H be a given Hamming space and $d\in {\mathbb{Z}}^{+}$. Let $x_a$ denote a boolean indicator variable for each possible codeword $a\in H$ so that $x_a=1$ iff a is in the C maximum Hamming packing. It is prevalently known [24] that a C can be trivially obtained from the following integer linear program as any of its primal optimal solutions:

$$\begin{array}{ccc}\mathrm{(9)}& \hfill max& \sum _{a\in H}{x}_a& \hfill s.t.& x_a+x_b\le 1& \forall a,b\in H:1\le d_H(a,b)\le d-1\hfill \\ & x\in {\left\{0,1\right\}}^n& .\hfill \end{array}$$

The objective ensures the maximality of the packing, whereas the inequality constraints forbid the simultaneous selection of points too close to each other. Later, we will make use of the monotonicity property of this ILP: if in a feasible solution an element of value 1 is set to 0, the resulting solution is also feasible. In other words, every subset of a feasible packing is feasible.

The simple model in Equation (9) is inefficient to determine $N_{k_1,k_2,\dots ,k_s}({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_s;d)$ for the exponential scaling of the number of variables. Here, we propose some modifications to improve the efficiency. Without loss of generality, it can be assumed that the all-zero codeword z is always chosen; hence, $z\in C$. Under this assumption, the model can be simplified by omitting the variables corresponding to the inner part of the z-centred ball with radius $d-1$, leading to

$$\begin{array}{cc}\mathrm{(10)}& \hfill max& \sum _{a\in H}{x}_a& \hfill s.t.& x_z=1\\ \hfill & x_a=0& 1\le d_H(a,z)\le d-1\hfill \\ \hfill & x_a+x_b\le 1& \forall a,b\in H:1\le d_H(a,b)\le d-1\hfill \\ & x\in {\left\{0,1\right\}}^n& .\hfill \end{array}$$

For practical reasons, the obsoleted (binary) variables can be removed from the model. This will result in a significant decrease in the memory consumption of the presolvers used by ILP solvers, as confirmed by our experience. Thus, the model can be written in the form

$$\begin{array}{cc}\mathrm{(11)}& \hfill max& 1+\sum _{{\displaystyle \genfrac{}{}{0.0pt}{}{a\in H}{d_H(a,z)\ge d}}}{x}_a& \hfill s.t.& x_z=1\\ \hfill & x_a+x_b\le 1& {\displaystyle \genfrac{}{}{0.0pt}{}{\forall a,b\in H\setminus B(z,d-1):}{1\le d_H(a,b)\le d-1}}\hfill \\ & x\in {\left\{0,1\right\}}^n& .\hfill \end{array}$$

Note that developing certain linear programming models in order to estimate bounds for the cardinalities of extremal Hamming packings is a fairly old idea; see e.g., Delsarte’s results [11]. The ILP model we have introduced here, however, has the advantage that it is an equivalent declarative reformulation of the exhaustive search [24].

5. Reducing ILPs Using Contact Graphs

In this section, we use contact graphs. We show that every Hamming packing C can be modified so that the resulting $C^{\prime }$ packing will have a connected $CG\left(C^{\prime }\right)$ contact graph and $\left|C\right|=|C^{\prime }|$. Furthermore, under certain restrictions on the cardinalities of the alphabets, there exists a maximum packing with a connected contact graph with a minimal vertex degree of at least 2. Let us first define contact graphs and Hamming graphs.

Definition 1.

The contact graph $CG\left(C\right)$ of a Hamming packing C (with minimal distance d which is fixed) is the graph whose vertices correspond to codewords in C, and there is an edge between pairs of nodes a and b iff $d_H(a,b)=d$.

Definition 2.

The Hamming graph $H(C,d)$ of a subset of a Hamming space for distance d is the graph whose vertices correspond to codewords in C, and there is an edge between pairs of nodes a and b iff $d_H(a,b)\ge d$.

Note that for any C Hamming packing, $CG\left(C\right)$ is a subgraph of $H(C,d)$ and the latter is a subgraph of $H(H,d)$. Now, we show that for most codes with a given minimal distance and a certain d, which is lower than the minimal distance, one can modify the code by replacing a single codeword so that the distance d is realized in the new code. Formally, this can be represented by the following proposition.

Proposition 6.

For every $0<d\in \mathbb{Z}$ and for every $C\subseteq H$ with $\left|C\right|\ge 2$ and $d\le d_H\left(C\right)$, there exists a $C^{\prime }\subseteq H$ code such that $d=d_H\left(C^{\prime }\right),|C^{\prime }|=|C|$ and $|C\cap C^{\prime }|\ge |C|-1$.

Proof. 

The proof is constructive. According to the assumptions, there exists a pair of points $\{v,w\}\subseteq C$ such that $d_H\left(C\right)=d_H(v,w)$ is realized. Let $\{v,w\}$ be a fixed, arbitrarily chosen pair. If $d_H(w,C\setminus \left\{w\right\})=d$, then let $C^{\prime }=C$, and the proof is completed. Otherwise, change a single character in w in which it differs from v, at the coordinate, e.g., j. This will result in the codeword $w^{\prime }=(w\left[1\right],w\left[2\right],\dots ,w[j-1],v\left[j\right],w[j+1]\dots )$. The resulting code $C^{\left(1\right)}=C\setminus \left\{w\right\}\bigcup \left\{w^{\prime }\right\}$ preserves cardinality, and $d_H\left(C^{\left(1\right)}\right)=d_H\left(C\right)-1$ holds. This procedure can be repeated at the beginning with the codeword pair $(v,w^{\prime })$, which now realize the minimal distance in $C^{\left(1\right)}$. The repetition will modify $w^{\prime }$ again; thus, it will be the only codeword to change. The procedure is to be iterated, always modifying the same codeword, and for the iteration, $d_H\left(C^{(k+1)}\right)=d_H\left(C^{\left(k\right)}\right)-1$ will hold; thus, the iteration can be continued till $d_H\left(C^{(m+1)}\right)=d$, and let $C^{\prime }=C^{(m+1)}$.    □

This proposition has an important corollary:

Corollary 3.

$$N(H;d)=\underset{d_H\left(C\right)=d}{max}\left|C\right|.$$

(12)

Recall that in the definition of Equation (4), there is a lower-or-equal relation in the maximization; this can be sharpened to equality, i.e., Proposition 6 ensures that the lower values are covered. The idea of the previous proof can be employed to prove a useful proposition regarding contact graphs: codes can be transformed into codes of the same cardinality and no isolated vertices.

Proposition 7.

For every $0<d\in \mathbb{Z}$ and for every $C\subseteq H$, if $\left|C\right|\ge 2$ and $d\le d_H\left(C\right)$ hold then there is a $C^{\prime }\subseteq H$ code such that $|C^{\prime }|=|C|$ and $CG\left(C^{\prime }\right)$ do not have any isolated vertices.

Proof. 

Let $w\in C$ loop through all isolated vertices (i.e., for which $d_H(w,C\setminus \left\{w\right\})>d$ holds). Using the algorithm in the proof of Proposition 6, replace each w with $w^{\prime }$ so that $d_H(w^{\prime },C\setminus \left\{w^{\prime }\right\})=d$. In this way, each vertex will have at least one edge.    □

This proposition has strong consequences, resulting in useful additional constraints to the ILP model that determines $N(H;d)$.

Corollary 4.

The ILP in Equations (9)–(11) can be extended with the constraints

$$\forall w\in H:x_w\le \sum _{d_H(w,w^{\prime })=d}{x}_{w^{\prime }}.$$

(13)

These constraints literally mean that for every selected codeword, there is another one selected at a distance d, i.e., there are no isolated vertices of the contact graph of the code. Given a lower bound s for the objective (typically an initial feasible solution to start with), we can also formulate dual bounds. By estimating an upper bound of the maximum $s+k$, if we can approach it close enough, then the optimum is found.

Corollary 5.

Let us extend the ILP in Equation (9) (possibly extended with the constraints in Equation (13)) with the following upper bound on the objective function:

$$(s\le )\sum _{w\in H}{x}_w\le s+k,$$

(14)

where $k\ge 1$ is any fixed integer. If the optimum of the extended ILP is at most $s+k-1$, the optimum for the original ILP (with or without (13)) has also been found.

Otherwise, if the extended ILP saturates the arbitrarily chosen upper bound, the obtained solution may not be optimal for the original problem. If, however, the constraint is not saturated, the optimum has been found.

Proof. 

Due to the monotonicity of feasible packings, when removing one codeword from any feasible solution vector, the resulting vector will also be feasible. For the ILP in Equation (9), as a feasibility problem, this means that changing one element from 1 to 0 in any feasible solution vector x preserves feasibility. (In this ILP, all the constraints are of the form $x_w+x_v\le 1$; hence, decreasing the left-hand side by one results in constraints that are still satisfied for the originally feasible solutions.) Hence, for all objective values below the optimum, there exist feasible solutions of the model in (9). Because of Proposition 7, the same holds when extending the model with the constraints in Equation (13). Hence, if the ad hoc bound $s+k$ is bigger than the actual optimum, it will not be active.    □

The bound $(s+k)$ is referred to as a dual bound; it is typically chosen to be the best known bound or a plausible conjecture. According to our practical experience with solvers, starting the solution process with a best known initial solution having cardinality s and setting the dual bound $(s+1)$ dramatically reduces the memory footprint. This is a practical way to verify if s is an optimum. This will be illustrated in Section 6.1. Due to the symmetry, e.g., that every $Ø\ne C\subseteq H$ code has an equivalent one containing $z=\overline{00\dots 0}$, instead of Equation (9), the models Equation (10) or Equation (11) can be used in the previous corollaries.

Now, we present one of our main results.

Proposition 8.

Every Hamming packing $C:\left|C\right|\ge 2$ with minimal distance d can be transformed to another Hamming packing $C^{\prime }$ with the same number of codewords and minimal distance, whose contact graph $CG\left(C^{\prime }\right)$ is connected.

Proof. 

The desired transformation can be carried out using Algorithm 1 (in which ${\bigcup }^{\ast }$ denotes a disjoint union).

Algorithm 1 Transforming C to $C^{\prime }$ with the same number of codeword and minimal distance, and connected $CG\left(C^{\prime }\right)$

1: INPUT: $C\subseteq H$ nonempty Hamming packing, $d\in \mathbb{Z}, d>0$ distance   2: START   3: pick a random $\widehat{w}\in C$, then partition $C:=C_1{\bigcup }^{\ast }{C}_2$, where $C_1=\left\{\widehat{w}\right\}$ and $C_2=C\setminus C_1$   4: while  $C_2\ne \varnothing$  do   5:    while $\exists w,w^{\prime }:w\in C_1,w^{\prime }\in C_2:d_H(w,w^{\prime })=d$ do   6:     update $C_1:C_1:=C_1{\bigcup }^{\ast }\left\{w^{\prime }\right\}$   7:     update $C_2:C_2:=C_2\setminus \left\{w^{\prime }\right\}$   8:    end while   9:    if $(C_2\ne Ø)$ and $(d_H(C_1,C_2)\ne d)$ then 10:     sort increasing the elements of $C_2$ on distance of $C_1$ 11:     let $d^{\prime }$ denote: $d^{\prime }:=d_H(C_1,C_2)$ 12:     select a $w^{\prime }$ smallest element from $C_2$ 13:     select arbitrary $w:w\in C_1$, where $d_H(w,w^{\prime })=d^{\prime }$ 14:     select arbitrary index j, where $w\left[j\right]\ne w^{\prime }\left[j\right]$ 15:     denote $a:=w\left[j\right],b:=w^{\prime }\left[j\right]$ 16:     for each $y\in C_2$ do 17:      if $y\left[j\right]=a$ then 18:       $y\left[j\right]=b$ 19:      else if $y\left[j\right]=b$ then 20:       $y\left[j\right]=a$ 21:      end if 22:     end for 23:    end if 24: end while 25: STOP, OUTPUT: $C^{\prime }:=C_1$

The proposition is proven if Algorithm 1 terminates in a finite number of steps. The algorithm partitions the set of codewords C to subsets $C_1$ and $C_2$. The subset $C_1$ initially contains an arbitrarily chosen single codeword, and codewords from the complementary set $C_2$, which are exactly at a distance d from an element of $C_1$, are gradually moved to $C_1$ in the first inner loop in lines 5–8. If the inner loop runs out of movable elements, then the distance $d^{\prime }$ of the two sets is at least $d+1$. In this case, we pick a pair of elements w and $w^{\prime }$ so that $d_H(w,w^{\prime })=d^{\prime }$, which always exists. Next, we modify the code so that the distances within $C_1$ and also within $C_2$ are preserved, while the distance between $C_1$ and $C_2$ decreases by one. This is always possible (see the described steps in the algorithm) and results in a code with the same cardinality. For the outer loop, and thus for the whole algorithm to terminate, the set $C_2$ has to be emptied. Observe also that

• Code C remains a d-feasible Hamming packing at the end of each loop in lines 8, 22, and 24;
• $CG\left(C_1\right)$ is a connected graph in line 8;
• Once $d^{\prime }$ reaches $d+1$ at line 11, then $C_2$ must lose one of its elements that will move to $C_1$ at the end of the while loop at line 8;
• After exiting the for loop (line 22), $CG\left(C_2\right)$ does not change; no Hamming distance will be altered between elements of $C_2$;
• At the end of the for loop, the distance between $C_1$ and $C_2$ decreases exactly by one; as the distance was larger than d at the beginning of the loop, $C_1{\bigcup }^{\ast }{C}_2$ still cannot contain any pair with a distance less than d;
• The cardinality of $C_2$ is strictly decreasing or $d_H(C_1,C_2)$ is strictly decreasing in lines 8, 22, and 24.

As the cardinality of all the involved sets, including that of $C_2$, is finite (as our Hamming space is finite), $d_H(C_1,C_2)\le n$ holds, and the cardinality $C_2$ monotonically decreases during the iterations, $C_2$ will become empty, and thus, the algorithm will terminate in a finite number of steps. In the worst case, the maximal number of iterations is $\left(\right|C|-1)(n+1-d)$, which arises in the case when only one codeword is moved from $C_2$ to $C_1$ in each step. □

To demonstrate the usefulness of Proposition 8, we show that a lemma by Plotkin [34] arises as a simple corollary.

Corollary 6. 

$N_2(n,d)=2\iff {\displaystyle \frac{2n}{3}}<d\le n$.

Proof. 

The case $d\le n$ is straightforward in both directions: $C=\{\overline{00\dots 0},\overline{11\dots 1}\}\subseteq H:d_H\left(C\right)=n\ge d$ provides the lower bound $2\le N_2(n,d)$. For the nontrivial cases, let us apply Proposition 8 and certain permutations on C. Suppose that, without loss of generality, $\left|C\right|=3\le N_2(n,d)$, denote its elements by $C=\{z,w,v\}$. Let there be a pair of codewords on which the d distance is realized $z=\overline{00\dots 0},w=\overline{\underset{n-d}{\underbrace{00\dots 0}}\underset{d}{\underbrace{11\dots 1}}}$. Using the fact that the code’s contact graph is connected, suppose that the third word v is connected to z, which is all zero; hence, w must have the weight d. From this, it follows that with suitable permutations, it has to take the form $v=\overline{\underset{n-d-x}{\underbrace{00\dots 0}}\underset{x}{\underbrace{11\dots 1}}\underset{d-x}{\underbrace{11\dots 1}}\underset{x}{\underbrace{00\dots 0}}}$. The distance must be $d\le d_H(v,w)$, and since $d_H(v,w)=2x$, we obtain $d\le 2x$, which is necessary. In case when $d>{\displaystyle \frac{2n}{3}}$, or, equivalently, ${\displaystyle \frac{n}{3}}>n-d$, from $n-d-x\ge 0$, we can determine that ${\displaystyle \frac{n}{3}}>n-d\ge x\Rightarrow {\displaystyle \frac{n}{3}}>x\Rightarrow d>{\displaystyle \frac{2n}{3}}>2x\ge d$, from which it follows that $d>d$, which is a contradiction. Hence, in this case, no v exists, which meets all the requirements. The remaining case is when $d\le {\displaystyle \frac{2n}{3}}$. Let us choose $x=n-d$. Considering again that $d_H(v,w)=2x$, it follows that $2x=2n-2d\ge 2\left({\displaystyle \frac{3d}{2}}\right)-2d=d$, implying that $d_H(v,w)=2x\ge d$, and so, v is a feasible word far enough from w. □

Let us now establish a key property for mixed codes using characters from alphabets of size at least 3. This is our second main proposition.

Theorem 1.

Let H be a Hamming space so that $k_1\ge 3$. Then every optimal Hamming packing $C\subseteq H:\left|C\right|\ge 3$ with minimal distance d can be transformed to another Hamming packing $C^{\prime }$ with the same number of codewords and minimal distance, whose contact graph $CG\left(C^{\prime }\right)$ is connected and the minimal vertex degree in it is at least 2.

Proof. 

According to Proposition 8, for a given $d\in \mathbb{Z}$, there exists a maximum packing $C\subseteq H:\left|C\right|\ge 3$ so that it has a connected $CG\left(C\right)$ contact graph. If every $v\in V\left(CG\right(C\left)\right)$ fulfils $deg\left(v\right)\ge 2$, the proof is complete. Otherwise, suppose the contrary, whereby every maximum packing with a connected contact graph has at least one vertex with degree 1. As the number of maximum packings is finite, we can consider one of these, C, with a minimal number of 1-degree vertices (see Figure 1 for an illustration). Let $w_0$ be a vertex of C so that $deg\left(w_0\right)=1$, and let us denote its only neighbour by z. From now on, we allow for permuting the coordinates of the symbols, even without maintaining the ordering in the cardinality of the alphabets. By such permutations, we can assume, without loss of generality, that z and $w_0$ can be brought to the following equivalent forms: $z=\overline{00\dots 0}$ and $w_0=\overline{\underset{n-d}{\underbrace{00\dots 0}}\underset{d}{\underbrace{11\dots 1}}}$. In this way, the differences between z and $w_0$ are realized in the rightmost coordinates. Now for every $1\le k\le d$, let $w_k=\overline{\underset{n-d}{\underbrace{00\dots 0}}\underset{d-k}{\underbrace{11\dots 1}}\underset{k}{\underbrace{22\dots 2}}}$. These codewords are in the Hamming space because each alphabet contains at least 3 elements.

The following consideration is illustrated in Figure 1. Observe that $\forall 0<k<d:w_k\notin C$, because $d_H(C\setminus \left\{w_k\right\},w_k)\le d_H(w_0,w_k)=k<d$. $w_d\notin C$; otherwise, $d_H(w_0,w_d)=d$ would imply that $deg\left(w_0\right)\ge 2$, which is a contradiction. Let $D_k=d_H(C\setminus \{w_0,z\},w_k)\forall 0\le k\le d$. It is known prevalently that $D_0>d$ and $D_d<d$, and for $|D_k-D_{k-1}|\le 1$ for every $k>0$, because if at most one coordinate changes in a code, then its distance might change at most by 1. This implies that there must exist $D_k=d$. Replacing $w_0$ with the corresponding word $w_k$ in C yields $C^{\prime }=(C\setminus \left\{w_0\right\})\bigcup \left\{w_k\right\}$. Contact graph vertex degrees will not be decremented in $C^{\prime }$ members other than $w_k$, and because $deg\left(w_k\right)\ge 2$, $C^{\prime }$ code contains one less codeword with a degree of 1, thus contradicting the minimality of the number of 1-degree nodes in $CG\left(C\right)$. □

Corollary 7.

The ILP in Equation (9) can be extended with the following constraints if H is a product of nonbinary alphabets:

$$\forall w\in H:2x_w\le \sum _{d_H(w,w^{\prime })=d}{x}_{w^{\prime }}.$$

(15)

This constraint prescribes the minimal vertex degree according to the theorem. Notice that Equations (14) and (15) cannot be applied together to determine $N(H;d)$ without further consideration, unless it is proven independently that the dual bound $s+k$ in (14) is correct for the given case.

There is a nontrivial example, which illustrates that the alphabet cardinality and the maximality criteria are necessary in Theorem 1. It is known [35] that $N_2(5;d=3)=4$, and in this particular case, the optimal packing and any of its subset with 3 elements are unique up to isomorphism; thus, their contact graphs are also uniquely determined, namely the $C_4$ or the tree over 3 vertices. As the minimal distance d is odd and the alphabets are all binaries, the contact graphs of these packings are necessarily triangle-less, violating the minimal degree criterion for codes with a size of 3.

6. Computational Results

Our computational approach can be summarized as follows. We start with the ILP in Equation (9). We include the additional constraints in Equation (13). Next, we perform branching on equivalence classes of the contact graph’s small subgraphs, usually 2 or 3 nodes/codewords. Next, we apply a reduction technique per case, which consists of fixing variables. The key idea of our reduction technique is the following: in each branch, having chosen the initial pair of codewords, the words that are at a distance less than $(d-1)$ from the chosen pair can be eliminated from the model by fixing the respective variables. This is one of the most common operation that is performed by ILP presolvers. This leads to a drastic reduction in the size of the respective ILP models. The removal of at most 2 codewords in all distinct possible ways is a corollary of Proposition 6. In order to perform branching by adding to the models, initially, 3 or more codewords are fixed in all possible nonisomorphic ways; then, pruning is conducted by using the connectedness of the contact graph which is considerable using Proposition 8. In our particular calculations, we have used various combinations of the techniques described so far. We have used the ILP models in Equation (11) with constraints based on Corollary 13.

Dual bounds based on Corollary 5, i.e., Equation (14), were used in most of the cases, but not, for instance, for $N_6(4;d=3)$, $N_3(5;d=3)$, $N_{4,3}(1,4;d=3)$, $N_{5,3}(1,4;d=3)$, $N_{6,3}(1,4;d=3)$, $N_{4,3}(1,5;d=4)$, or $N_{4,3}(1,5;d=5)$. In these cases, Equation (11) and additional constraints based on Corollary 7 have been used. These constraints enforce that for each selected codeword, at least two additional codewords exactly at a distance d from it are also selected. This is the most important implication of Theorem 1, resulting in a significant decrease in computational time in these cases.

We performed our experiments using two different hardware/software configurations:

• A 256 GB RAM. Two AMD EPYC 7302 16-Core processors (AMD, Santa Clara, CA, USA), totalling thirty-two cores. Version 22.1.0.0 of IBM CPLEX [36].
• An 8 GB RAM, Apple ARM M1 Silicon with 8 cores (TSMC, Hsinchu, Taiwan); SCIP version 9.0 [37].

For the sake of completeness, we provide a summary of known bounds for a number of smaller Hamming spaces and distances in Appendix A. Importantly, we reproduced all these results using the methods described here. All the listed bounds are sharp. In what follows, we describe in detail certain cases in which our method has led to an improvement over existing results. We showcase our method on these examples.

6.1. Calculating $N_{2,3,4}(5,1,1;d=3)=24$ and $N_{2,3,5}(5,1,1;d=3)=28$

The cases $N_{2,3,4}(5,1,1;d=3)=24$ and $N_{2,3,5}(5,1,1;d=3)=28$ are similar to each other, and our approach has found bounds that were not previously known. We describe them here to illustrate one of the typical applications of our method.

We start from the ILP model in Equation (11). We use Corollary 13 for both models; each feasible solution includes, for each codeword, another one within a distance d. This is practically taken into account by adding the constraint in Equation (13). Altogether, the result can be obtained by solving the model in Equation (11), together with this additional constraint.

For the case $N_{2,3,4}(5,1,1;d=3)$, we have employed an additional ad hoc simplification. Because there is a feasible packing that has at least 3 codewords having 0s in their ternary and quaternary positions, and by the pigeonhole principle, any feasible packings with more than 24 codewords must have these. Formally, we have set the following equalities:

$$\begin{array}{ccc}\mathrm{(16)}& \hfill x_{0000000}& =& 1,\hfill \hfill x_{0000111}& =& 1,\hfill \\ \hfill x_{0011001}& =& 1,\hfill \end{array}$$

without loss of generality. This also means that the truncated code subset must be a feasible packing in the 5-dimensional binary Hamming space. These words can be arranged uniquely up to an isomorphism due to [22,35]. After starting with this initial feasible solution and fixing 3 corresponding variables, we have solved the resulting ILP. The memory consumption of the solution processes on the AMD platform is displayed in Figure 2; the growth and collapse of the branch-and-bound tree can be observed. The calculation took more than a day. In the same problem, SCIP was more efficient, solving the problem within an hour.

The calculation of $N_{2,3,5}(5,1,1;d=3)$ was performed in two attempts, using the AMD platform. In the first attempt, no dual bounds were set. The solver aborted after exhausting all available memory in the growth phase of the branch-and-bound tree, as displayed in Figure 3. As the second attempt, we restarted the solver with the best primal value 28 found in the previous attempt, and a dual bound limit had been set to 29, using Corollary 5 (Note that the completion of the first attempt would not have been necessary; according to our experience, the solver finds the primal optimum rather fast, so it could have been stopped earlier). With this setting, the solver ran without flaws and stopped with an integer optimal solution. The memory footprint was significantly lower (see Figure 4).

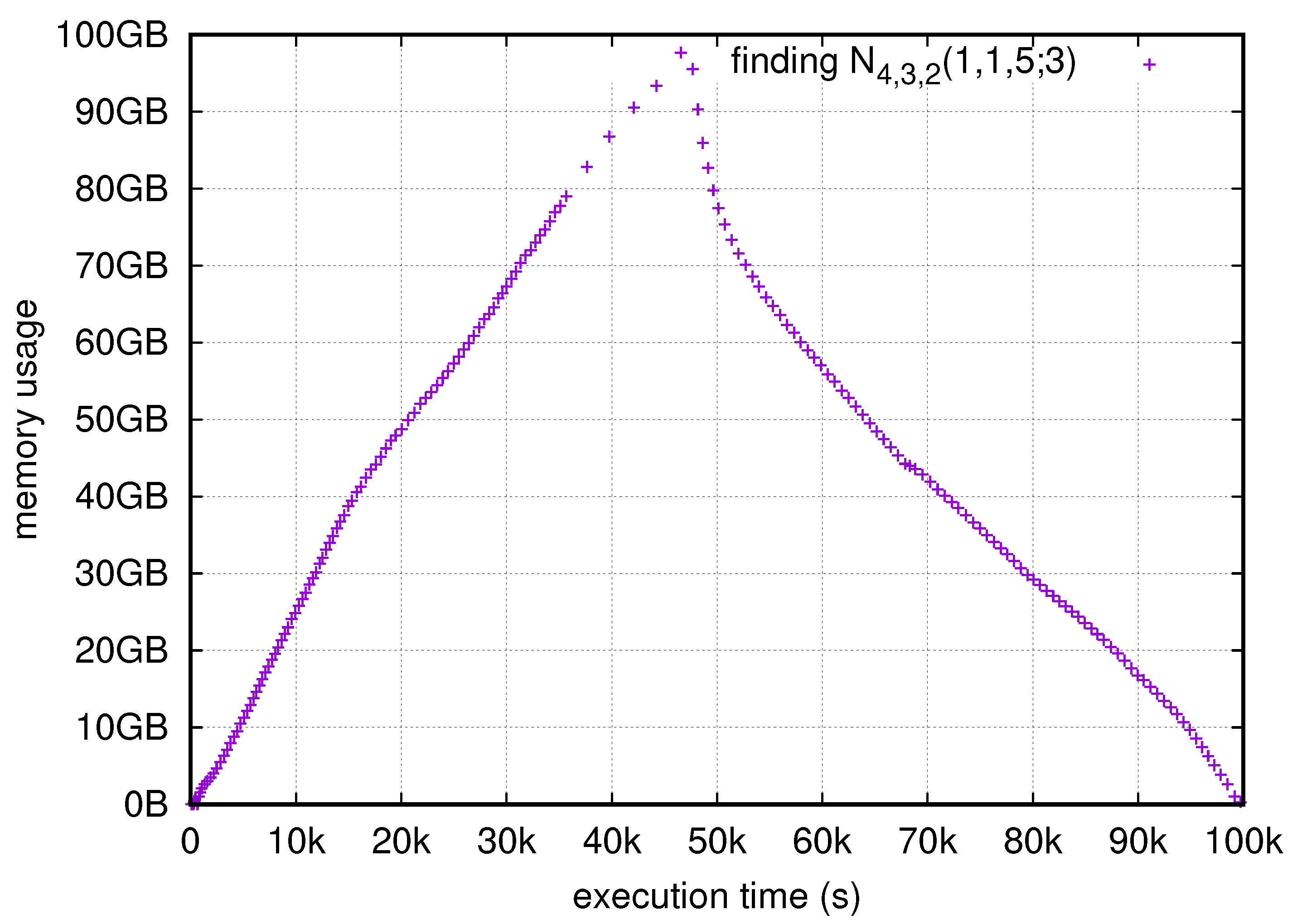
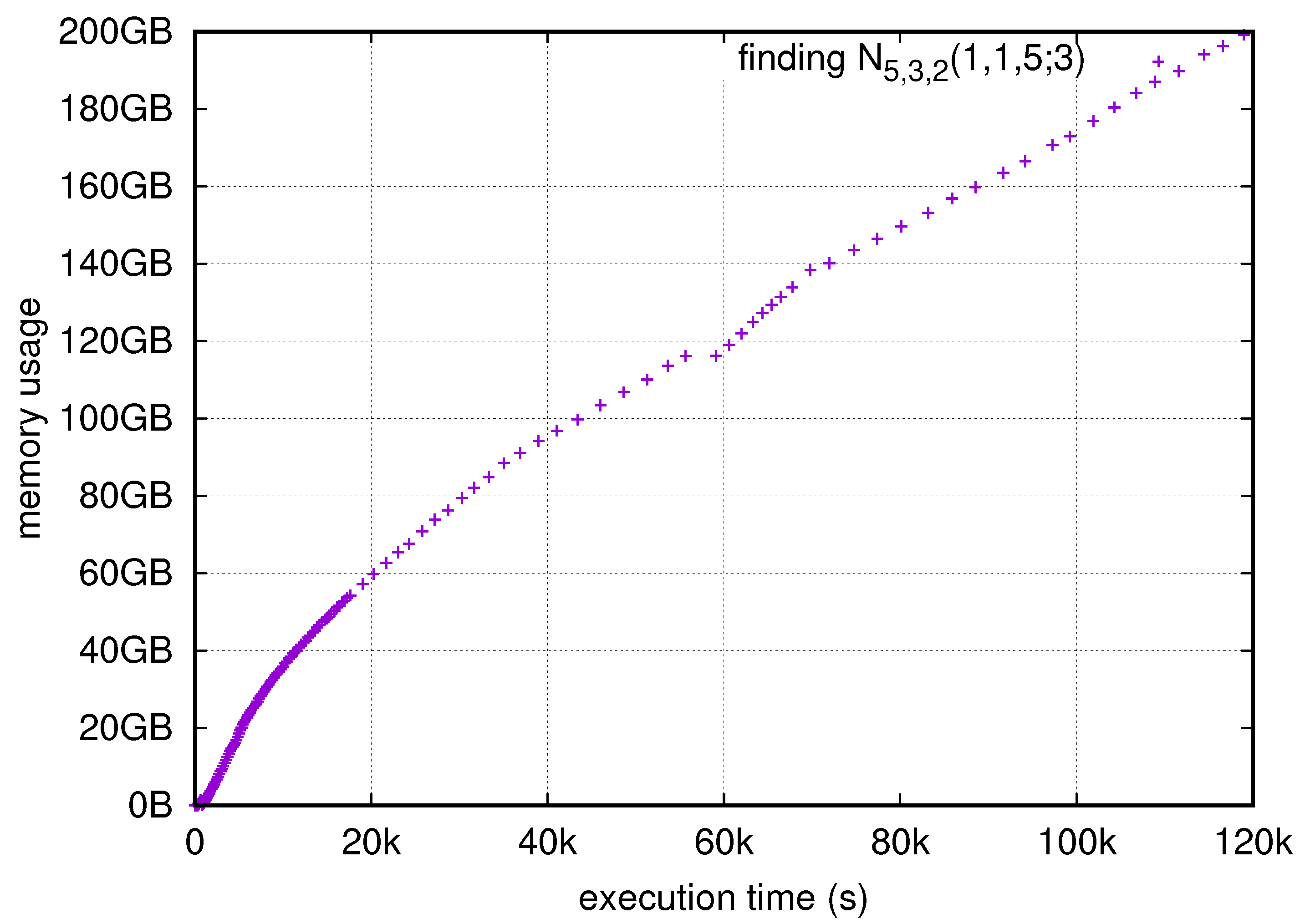
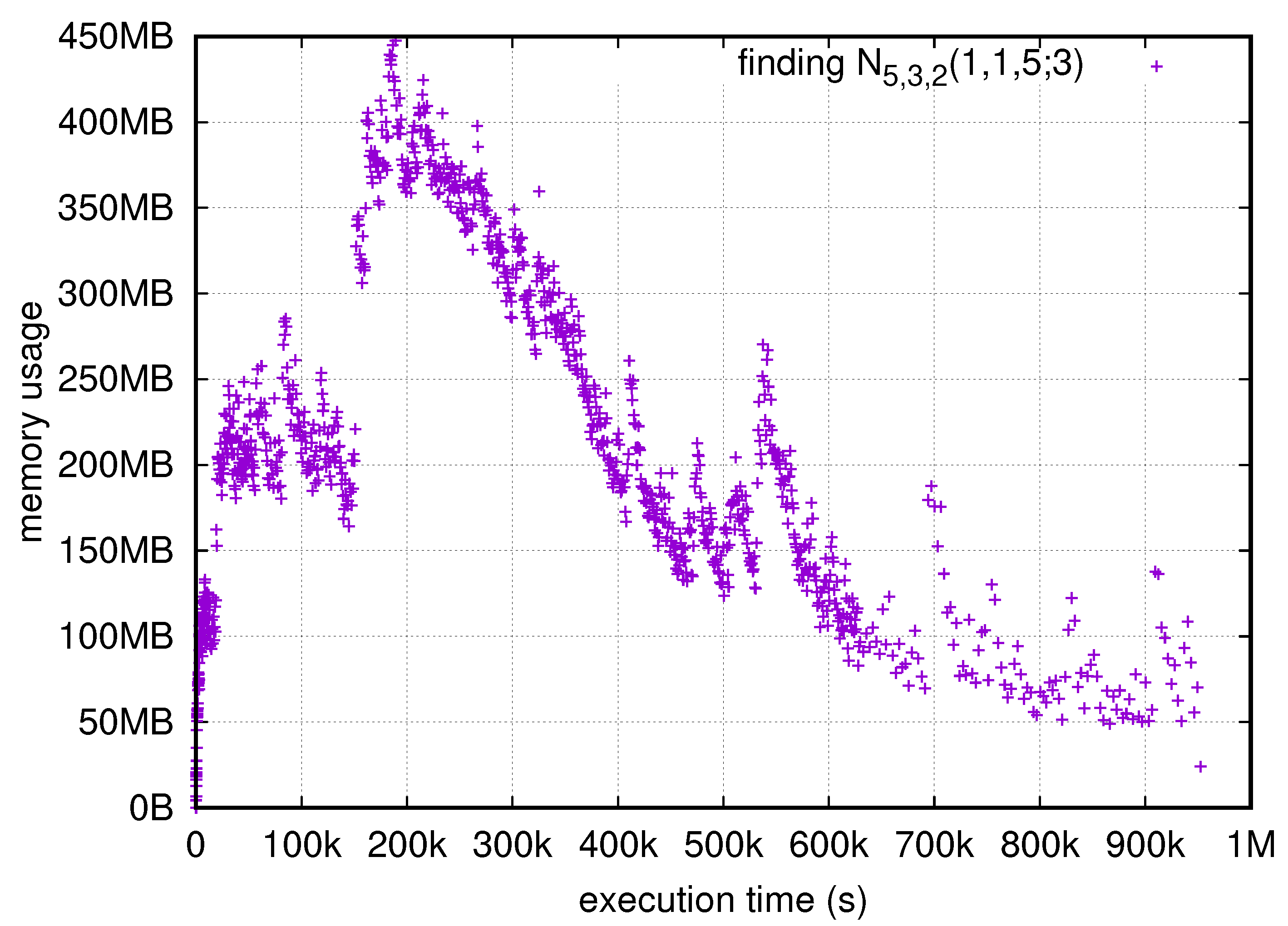
6.2. Calculating $N_{2,4}(7,1;d=3)=32$

We used the ARM platform only for the case $N_{2,4}(7,1;d=3)$. First, we tried to solve it and obtained a primary solution 32 within an hour, applying the ILP model in Equation (11) and adding constraints based on Corollary 13. The obtained solution had an interesting asymmetric property; it contained five codewords with trailing zeroes at the last three binary positions, so it was promising to restart the solver after setting an upper bound of thirty-three to the objective—or disprove its existence with a dual bound of thirty-two. In summary, if there is a code C having $\left|C\right|\ge 33$, then we can assume without loss of generality that C contains at least five codewords with the form $\overline{{\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4{\alpha }_{5}000}$ due to the pigeonhole principle (the most significant character ${\alpha }_1$ can still be chosen from four elements).

All distinct cases can be classified, and without loss of generality, it can be assumed that each inequivalent case has a code containing one the following pentaplets:

• 00000000, 00111000, 11011000, 21101000, 31110000,
• 00000000, 00111000, 11100000, 21010000, 31001000,
• 00000000, 01111000, 11100000, 10011000, 21010000,
• 00000000, 01111000, 11100000, 21010000, 30011000,
• 00000000, 01111000, 11100000, 21010000, 31001000.

The corresponding five constraint pentaplets per case

$$\begin{array}{c}\hfill x_{00000000}=x_{00111000}=x_{11011000}=x_{21101000}=x_{31110000}=1,\end{array}$$

(17)

$$\begin{array}{c}\hfill x_{00000000}=x_{00111000}=x_{11100000}=x_{21010000}=x_{31001000}=1,\end{array}$$

(18)

$$\begin{array}{c}\hfill x_{00000000}=x_{01111000}=x_{11100000}=x_{10011000}=x_{21010000}=1,\end{array}$$

(19)

$$\begin{array}{c}\hfill x_{00000000}=x_{01111000}=x_{11100000}=x_{21010000}=x_{30011000}=1,\end{array}$$

(20)

$$\begin{array}{c}\hfill x_{00000000}=x_{01111000}=x_{11100000}=x_{21010000}=x_{31001000}=1\end{array}$$

(21)

had been used to formulate smaller, solvable subproblems. All subproblems had been solved in at most 6 h per instance. Notice that the case when the constraints defined in Equation (19) disallow one value at the quaternary position is a result of Östergård [22]; the 1-error correcting code in space ${\mathbb{Z}}_3{\mathbb{Z}}_2{\mathbb{Z}}_2{\mathbb{Z}}_2{\mathbb{Z}}_2$ with size at least 5 is unique.

As a corollary, using the upper bound 32 and the fact that we determined the KJS sharp $N_{2,8}(7,1;d=3)=64$ value using either GLPK (version 5.0) [38] or SCIP (version 9.0), Proposition 2 could be applied to establish three new exact optimal values $N_{2,m}(7,1;d=3)=(8·m)$, where $m\in \{5,6,7\}$.

7. Summary and Outlook

We have introduced a reduction technique for finding optimal mixed Hamming packings. Our technique is based on our idea to adopt the notion of contact graphs, motivated by continuous sphere packing problems. It enables us to extend known inefficient ILP models of the problem with constraints that make these models practically useful and efficiently solvable.

Our ILPs can be competitive with other known numerical methods. For instance, while in the cases $N_{2,3}(7,1;d=3)=26$ and $N_{2,3}(4,3;d=3)=28$ in [22], the calculations took an order of years in CPU time, with our approach, it took only days. Moreover, we have found some previously unknown exact solutions, for instance, $N_{2,3,4}(5,1,1;d=3)=24$ and $N_{2,3,5}(5,1,1;d=3)=28$.

Our approach can work for bigger problem instances, and can be extended to constant weight binary Hamming packings. However, for bigger instances, the approaches based on algebraic structures will outperform our simple approach. In addition, it is not capable of exploiting properties of subobjects or performing automated pruning based on these.

Meanwhile, in spite of the limited number of variables in the models, they are challenging for classical solvers. Also, they can be easily reformulated to Quadratic Unconstrained Binary Optimization (QUBO) problems using penalties. The resulting QUBO problem instances are small, and thus, they can be used as benchmark problems, even for the currently available noisy intermediate scale quantum (NISQ) computing devices.