A New Proximal Iteratively Reweighted Nuclear Norm Method for Nonconvex Nonsmooth Optimization Problems

Abstract

This paper proposes a new proximal iteratively reweighted nuclear norm method for a class of nonconvex and nonsmooth optimization problems. The primary contribution of this work is the incorporation of line search technique based on dimensionality reduction and extrapolation. This strategy overcomes parameter constraints by enabling adaptive dynamic adjustment of the extrapolation/proximal parameters (α_k, β_k, μ_k). Under the Kurdyka–Łojasiewicz framework for nonconvex and nonsmooth optimization, we prove the global convergence and linear convergence rate of the proposed algorithm. Additionally, through numerical experiments using synthetic and real data in matrix completion problems, we validate the superior performance of the proposed method over well-known methods.

1. Introduction

1.1. Problem Description

This work addresses a nonconvex and nonsmooth optimization problem within the real matrix space ${\mathbb{R}}^{m\times n}(m\le n)$

$$\underset{X}{min}\Psi \left(X\right):=f\left(X\right)+\sum _{i=1}^{m}g\left({\sigma }_i\left(X\right)\right),$$

(1)

where ${\sigma }_i\left(X\right)$ denotes the i-th singular value of X, f is differentiable and the gradient is Lipschitz continuous with constant $L_f$, g is differentiable concave and the gradient is Lipschitz continuous with constant $L_g$ and $g^{\prime }\left(t\right)>0$ for any $t\in [0,+\infty )$.

It is easy to see that ${\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X\right)\right)$ is nonconvex and nonsmooth due to the nonsmoothness of ${\sigma }_i\left(X\right)$ and the concavity of g. Thus, the overall function $\Psi$ is nonconvex and nonsmooth even though f is differentiable (may be nonconvex). Note the generality of problem (1), it has a wide applications, such as image processing [1], machine learning [2] and multiple category classification [3]. To illustrate this point, consider the well-known image recovery problem. In such a scenario, $f\left(X\right)={\displaystyle \frac{1}{2}}{\Vert A\left(X\right)-b\Vert }^2$ (A is a linear operator and b is a vector or matrix) generally represents the quadratic loss function, which is used to measure recovery performance. Consequently, f is always differentiable. On the other hand, ${\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X\right)\right)$ is a nonconvex regularized term that is employed to obtain a low rank solution. Some common nonconvex regularized terms, including $L_p$, Log, ETP, Geman and Laplace can be found in [1,4]. The validity of the assumption of g can be verified through the nonnegativity of its second order derivatives and the median theorem.

1.2. Related Work

It is precisely because of the popularity and scope of problem (1) that there is a lot of related work, as can be seen in [5,6,7,8,9,10,11,12,13]. One of the more competitive methods is the well-known General Iterative Shrinkage and Thresholding (GIST) algorithm [14,15]. Applying the GIST algorithm to solve (1) needs to compute the proximal operator of a DC function ${\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X\right)\right)$. Unfortunately, this assumption of ${\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X\right)\right)$ is less likely to be satisfied, since the DC decomposition of ${\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X\right)\right)$ is not known in general. Thus, based on the key fact that nonnegativity and monotone decrease of $\nabla g$, Lu et al. [4] proposed Proximal Iteratively Reweighed Nuclear Norm algorithm (PIRNN). Sun et al. [16] refined the related convergence conclusions. Later, Ge et al. [1] gave the PIRNN with a more general Extrapolation (PIRNNE) and proved the convergence under the same assumptions. The concrete iterative scheme can be read as

$$\{\begin{array}{}\mathrm{(2)}& \hspace{1em}{Y}^k:=X^k+{\alpha }_k\left(X^k-X^{k-1}\right)\mathrm{(3)}& \hspace{1em}{Z}^k:=X^k+{\beta }_k\left(X^k-X^{k-1}\right)\mathrm{(4)}& X^{k+1}:={prox}_{{\sum }_{i=1}^m{\mu }_k{w}_i^k{\sigma }_i\left(X\right)}\left(Y^k-{\mu }_k\nabla f\left(Z^k\right)\right)\end{array}$$

where ${\alpha }_k\in [0,1)$, ${\beta }_k\in [0,1]$ are the extrapolation stepsizes, $\left\{{\mu }_k\right\}$ is a nondecreasing parameter sequence, ${\omega }_i^k:=g^{\prime }\left({\sigma }_i\left(X^k\right)\right)$ and for any $Y\in {\mathbb{R}}^{m\times n}$,

$${\mathrm{prox}}_{{\displaystyle \sum _{i=1}^m}{\mu }_k{w}_i^k{\sigma }_i\left(X\right)}\left(Y\right):=arg\underset{X}{min}\left\{\sum _{i=1}^m{w}_i^k{\sigma }_i\left(X\right)+{\displaystyle \frac{1}{2{\mu }_k}}{\parallel X-Y\parallel }_F^2\right\}.$$

(5)

(4) has a closed-form solution if $0\le w_1^k\le w_2^k\le \cdots \le w_m^k$. In other words, for any $Y\in {\mathbb{R}}^{m\times n}$, one has $US(\Lambda )V^{\top }\in {\mathrm{prox}}_{{\sum }_i^m\mu w_i^k{\sigma }_i\left(X\right)}\left(Y\right),$ where $U\Lambda V^{\top }$ is the SVD of Y, $S(\Lambda )=\mathrm{diag}{\left\{{({\Lambda }_{i,i}-{\mu }_k{w}_i^k)}_{+}\right\}}_{1\le i\le m}$ with ${\left(a\right)}_{+}=max\{a,0\}$ for any $a\in \mathbb{R}$.

Meanwhile, Phan et al. [17] devised an acceleration framework utilizing the partial singular value decomposition of reduced-dimensional matrices rather than full matrices, conditioned upon parameter specifications with ${\alpha }_k=0$, ${\beta }_k={\displaystyle \frac{k}{k+3}}$ and ${\mu }_k=\mu$. Xu et al. [18] integrated rank estimation via enhanced Gerschgorin disk analysis with learnable submatrix recovery, demonstrating state-of-the-art performance. Separately, Wen et al. [19] formulated an alternative accelerated matrix completion methodology employing continuation protocols and randomized truncated SVD, parameterized by ${\alpha }_k={\beta }_k=0$ and ${\mu }_{k+1}=max\{\eta {\mu }_k,{\mu }_{min}\}$, $\eta <1$. Generalized framework [20] leveraged ADMM for nonconvex nonsmooth low-rank recovery with rigorous convergence guarantees. Some recent methods also combine other regularization techniques. Alternative regularization strategies included an image reconstruction factorization model using a total variation regularizer [21], a truncated error model using the difference between the nuclear norm and Frobenius norm for impulse noise processing [22], and an accelerated iterative reweighted nuclear norm method combined with active manifold identification [23]. This paper focuses on the efficient computation of (5) based on PIRNNE. To the best of our knowledge, suitable parameter selection makes these algorithms have good numerical performance. The most famous optimal parameter choice is the Nesterov’s acceleration, such as FISTA [24] and APG [25]. The optimal choice involving the inertial and proximal parameters of PIRNNE for the nonconvex nonsmooth problems considered in this paper are not explicit, which makes the algorithm unable to maintain its advantage. Whether there is an adaptive parameter selection is our concern.

1.3. Our Contribution

Fortunately, the line search strategy is widely used for nonconvex vector optimization to overcome restrictions on the involved parameters [26,27,28,29,30,31]. This strategy allows the parameters to be chosen initially with some aggressive values that are not below a specific threshold, and then updates adaptively parameters at each iteration according to the line search criterion, which can improve the numerical performance in implementation. A natural approach is to incorporate the line search strategy to the PIRNNE by updating the parameters ${\alpha }_k,{\beta }_k$ and ${\mu }_k$. adaptively. Therefore, the main contributions of this paper are as follows:

• We propose a Proximal Iteratively Reweighted Nuclear Norm algorithm with Extrapolation and Line Search, denoted by PIRNNE-LS. This framework integrates line search with extrapolation and dimensionality reduction, circumventing parametric limitations. Parameters withinthe proposed method initialize aggressively above defined thresholds then undergo criterion-driven adaptive recalibration per iteration.
• We prove the subsequential convergence that each generated sequence converges to a stationary point of the considered problem. Especially, when the line search is monotone, we further establish its global convergence and linear convergence rate under the Kurdyka–Łojasiewicz framework.
• We conduct some experiments to evaluate the performance of the proposed method for solving the matrix completion problem. Some numerical results are reported the effectiveness and superiority of our proposed method.

The remainder of this paper is organized as follows. Section 2 provides the preliminaries needed for the theoretical analysis in the subsequent sections. Section 3 details PIRNNE-LS for the specified problem. Section 4 analyzes the subsequential convergence. Specifically, we discuss the global convergence and linear convergence rate under the Kurdyka–Łojasiewicz framework in the case of monotone line search. Section 5 reports numerical results on synthetic and empirical datasets. Concluding conclusions appear in Section 6.

2. Preliminaries

In this section, we recall some definitions and properties which will be used in the analysis.

2.1. Basic Concepts in Variational and Convex Analysis

For an extended-real-valued function $J:={\mathbb{R}}^n\to (-\infty ,\infty ]$, its domain is defined by $\mathrm{dom}\left(J\right):=\{x\in {\mathbb{R}}^n:J\left(x\right)<+\infty \}.$ If $\mathrm{dom}\left(J\right)\ne \varnothing$ and $J\left(x\right)>-\infty$ for any $x\in \mathrm{dom}\left(J\right)$, we say the function J is proper. If it is lower semicontinuous, we say it is closed. For any subset $T\subseteq {\mathbb{R}}^n$ and any point $x\in {\mathbb{R}}^n$, the distance from x to T is defined by $\mathrm{dist}(x,T):=\inf \{\parallel y-x\parallel |y\in T\},$ and we have that $\mathrm{dist}(x,T)=\infty$ for all x when $T=\varnothing$.

Next, we give the definition of subdifferential which plays a central role in nonconvex optimization.

Definition 1

([32,33]). (Subdifferentials) Let $J:{\mathbb{R}}^n\to (-\infty ,\infty ]$ be a proper and lower semicontinuous function.

(i) 

For a given $x\in \mathrm{dom}\left(J\right)$, the Fréchet subdifferential of J at x, written by $\widehat{\partial }J\left(x\right)$, is the set of all vectors $u\in {\mathbb{R}}^n$ that satisfy

$$\underset{y\ne x}{lim}\underset{y\to x}{inf}{\displaystyle \frac{J\left(y\right)-J\left(x\right)-\langle u,y-x\rangle }{\parallel y-x\parallel }}\ge 0.$$

When $x\notin \mathrm{dom}\left(J\right)$, we set $\widehat{\partial }J\left(x\right)=\varnothing$.

(ii) 

The limiting subdifferential, or simply the subdifferential, of J at x, written by $\partial J\left(x\right)$, is defined by

$$\partial J\left(x\right):=\{u\in {\mathbb{R}}^n|\exists x^k\to x,\mathrm{s}.\mathrm{t}.J\left(x^k\right)\to J\left(x\right)\mathrm{and}{u}^k\in \widehat{\partial }J\left(x^k\right)\to u\mathrm{as}k\to \infty \}.$$

(6)

(iii) 

A point $x^{\ast }$ is called the (limiting) critical point or stationary point of J if it satisfies $0\in \partial J\left(x^{\ast }\right)$, and the set of critical points of J is denoted by critJ.

Assumption 1.

$\Psi \left(X\right)\to +\infty$ iff ${\parallel X\parallel }_F\to \infty .$

2.2. Kurdyka–Łojasiewicz Property

Now we recall the Kurdyka–Łojasiewicz (KL) property [33,34,35], which would help us to establish the global convergence. Many functions have KL properties, like semi-algebraic functions defined in an $o-$minimal structure, and others discussed in [32].

Definition 2.

(KL property and KL function) Let $J:{\mathbb{R}}^n\to (-\infty ,\infty ]$ be a proper and lower semicontinuous function.

(i) 

The function J is said to have KL property at $x^{\ast }\in \mathrm{dom}(\partial J)$ if there exists $\eta \in (0,+\infty ]$, a neighborhood U of $x^{\ast }$, and a continuous and concave function $\phi :[0,\eta )\to {\mathbb{R}}^{+}$ such that

(a) 

$\phi \left(0\right)=0$ and φ is continuously differentiable on $(0,\eta )$ with ${\phi }^{\prime }>0;$

(b) 

for all $x\in U\cap \{z\in {\mathbb{R}}^n|J\left(x^{\ast }\right)<J\left(z\right)<J\left(x^{\ast }\right)+\eta \}$, the following KL inequality holds:

$${\phi }^{\prime }(J\left(x\right)-J\left(x^{\ast }\right))\mathrm{dist}(0,\partial J\left(x\right))\ge 1.$$

(ii) 

If J satisfies the KL property at each point of $\mathrm{dom}(\partial J)$, then J is called a KL function.

Let ${\Phi }_{\eta }$ be the set of function $\phi$ which satisfies the involved conditions in Definition 2 (i). In the following, we give a uniformized KL property which was established in [33].

Lemma 1

([33], Lemma 6). (Uniformized KL property) Let Ω be a compact set and $J:{\mathbb{R}}^n\to (-\infty ,\infty ]$ be a proper and lower semicontinuous function. Assume that J is a constant on Ω and satisfies the KL property at each point of Ω. Then, there exists $\zeta ,\eta >0$ and $\phi \in {\Phi }_{\eta }$ such that for all $\overline{x}\in \Omega$ and all x in the following intersection

$$\{z\in {\mathbb{R}}^n|\mathrm{dist}(z,\Omega )<\zeta \}\cap \{z\in {\mathbb{R}}^n|J\left(\overline{x}\right)<J\left(x\right)<J\left(\overline{x}\right)+\eta \},$$

one has

$${\phi }^{\prime }(J\left(x\right)-J\left(\overline{x}\right))\mathrm{dist}(0,\partial J\left(x\right))\ge 1.$$

3. The Proposed Method

This section advances a novel computational framework addressing the nonconvex and nonsmooth optimization problem (1). Under the functional decomposition of f in (1), we posit existence of convex functions $f_1$ and $f_2$ exhibiting Lipschitz continuous gradients such that $f:=f_1-f_2$. Consistent with established literature [1,36,37,38,39], the Lipschitz constant $L_f$ governing $\nabla f$ conforms to $L_f\le L$, where $\nabla f_1$ and $\nabla f_2$ possess respective Lipschitz moduli $L>0$ and $l\ge 0$ under the condition $L\ge l$. The formal computational architecture is instantiated in Algorithm 1.

Algorithm 1 PIRNNE-LS for solving (1)

Choose ${\eta }_1$, ${\eta }_2$, $\tau$, $p_{min}\in (0,1)$, ${\alpha }_{max}$, ${\beta }_{max}$, $d>0$, $\delta \in [0,1)$, $0<{\mu }_{min}\le {\displaystyle \frac{1-\delta }{L+2d}}\le {\mu }_{max}$. For given $X^0\in {\mathbb{R}}^{m\times n}$, $X^{-1}=X^0$, let ${\tilde{E}}_0:=\Psi \left(X^0\right)$ and set $k:=0$. while stopping criterion is not satisfied, do     Step 1. Choose ${\alpha }_k^0\in [0,{\alpha }_{max}]$, ${\beta }_k^0\in [0,{\beta }_{max}]$ and ${\mu }_k^0\in [{\mu }_{min},{\mu }_{max}]$, set ${\alpha }_k:={\alpha }_k^0$, ${\beta }_k:={\beta }_k^0$, ${\mu }_k:={\mu }_k^0$, then     (1a) Compute $Y^k, Z^k$ by (2) and (3), respectively.     (1b) Compute the SVD of $Y^k-{\mu }_k\nabla f\left(Z^k\right)$, i.e., $Y^k-{\mu }_k\nabla f\left(Z^k\right):={\tilde{U}}^k{\tilde{\Lambda }}^k{\left({\tilde{V}}^k\right)}^{\top }$;     Compute the singular value of $X^k$, and let $w_i^k:=g^{\prime }\left({\sigma }_i\left(X^k\right)\right)$ for $i=1,\cdots ,m$.     (1c) Compute $$X^{k+1}:={\tilde{U}}^{k}S\left({\tilde{\Lambda }}^k\right){\left({\tilde{V}}^k\right)}^{\top },$$ (7)     where $S\left({\tilde{\Lambda }}^k\right):=\mathrm{diag}{\left\{{({\tilde{\Lambda }}_{i,i}^k-{\mu }_k{w}_i^k)}_{+}\right\}}_{1\le i\le m}$.     (1d) If $$E_{\delta }(X^{k+1},X^k,{\mu }_k)-{\tilde{E}}_k\le -{\displaystyle \frac{d}{2}}{\parallel X^{k+1}-X^k\parallel }_F^2,$$ (8)     is satisfied, go to Step 2, where $E_{\delta }$ is defined in (9). Otherwise, set ${\alpha }_k={\eta }_1{\alpha }_k$, ${\beta }_k={\eta }_2{\beta }_k$, ${\mu }_k=max\{\tau {\mu }_k,{\mu }_{min}\}$ and go to Step (1a).    Step 2. ${\tilde{E}}_{k+1}=p_k{E}_{\delta }(X^{k+1},X^k,{\mu }_k)+(1-p_k){\tilde{E}}_k$ for $p_k\in [p_{min},1]$, then let $k=k+1$ and go to Step 1. end while

Within Algorithm 1, analogous to references [28,31], we postulate the potential function:

$$E_{\delta }(U,V,\mu ):=\Psi \left(V\right)+{\displaystyle \frac{\delta }{4\mu }}{\parallel U-V\parallel }_F^2,$$

(9)

where $E_{\delta }:{\mathbb{R}}^{m\times n}\times {\mathbb{R}}^{m\times n}\times {\mathbb{R}}^{+}\to (-\infty ,\infty ]$ and $\delta \in [0,1)$ signifies an assigned nonnegative constant. Moreover, Algorithm 1 permits the selection of arbitrary initial values ${\alpha }_k^0\in [0,{\alpha }_{max}]$, ${\beta }_k^0\in [0,{\beta }_{max}]$ and ${\mu }_k^0\in ({\mu }_{min},{\mu }_{max}]$ per iteration. Subsequent adaptive refinement occurs governed by the line search criterion (8). This methodology markedly enhances the procedure’s adaptability and numerical efficiency. Furthermore, contingent upon specific conditions, users may initially and intuitively select ${\mu }_{min}$ and ${\mu }_{max}$; subsequently, determination of d ensues based upon their stipulated conditions.

Remark 1. 

Observe that PIRNNE-LS still necessitates computing the singular value decomposition of a large-scale $Y^k-{\mu }_k\nabla f\left(Z^k\right)$, potentially exorbitant. The subsequent lemma ensures $X^{k+1}$ is derivable through a reduced matrix’s SVD. $Y^k-{\mu }_k\nabla f\left(Z^k\right)$ has $\widehat{q}$ singular values ${\tilde{\Lambda }}_{i_1,i_1}^k\ge \cdots \ge {\tilde{\Lambda }}_{i_{\widehat{q}},i_{\widehat{q}}}^k$ such that ${\tilde{\Lambda }}_{i_j,i_j}^k>{\mu }_k{w}_{i_j}^k$. Henceforth Algorithm 1 yields: ${\widetilde{U_{\widehat{q}}}}^k{\widetilde{{\Lambda }_{\widehat{q}}}}^k{\left({\widetilde{V_{\widehat{q}}}}^k\right)}^{\top }:=({\tilde{u}}_{i_1}^k,\cdots ,{\tilde{u}}_{i_{\widehat{q}}}^k)diag({\tilde{\Lambda }}_{i_1,i_1}^k,$ $\cdots ,{\tilde{\Lambda }}_{i_{\widehat{q}},i_{\widehat{q}}}^k){({\tilde{v}}_{i_1}^k,\cdots ,{\tilde{v}}_{i_{\widehat{q}}}^k)}^{\top }$ as the rank-$\widehat{q}$ SVD of $Y^k-{\mu }_k\nabla f\left(Z^k\right)$, where ${\tilde{u}}_{i_j}^k$ and ${\tilde{v}}_{i_j}^k$ denote left and right singular vectors for ${\tilde{\Lambda }}_{i_j,i_j}^k$, respectively.

Lemma 2 

([17]). Let Q be a ${\mathbb{R}}^{m\times q}$ matrix with orthogonal columns, ${\widetilde{U_{\widehat{q}}}}^k{\widetilde{{\Lambda }_{\widehat{q}}}}^k{\left({\widetilde{V_{\widehat{q}}}}^k\right)}^{\top }$ be the rank-$\widehat{q}$ SVD of $Y^k-{\mu }_k\nabla f\left(Z^k\right)$, ${\widetilde{U_Q}}^k{\widetilde{{\Lambda }_Q}}^k{\left({\widetilde{V_Q}}^k\right)}^{\top }$ be the SVD of $Q^{\top }(Y^k-{\mu }_k\nabla f\left(Z^k\right))$, and $span\left({\widetilde{U_{\widehat{q}}}}^k\right)\subset span\left(Q\right)$, where $q\ge \widehat{q}$. Thus, $X^{k+1}:=Q{\widetilde{U_Q}}^{k}S\left({\widetilde{{\Lambda }_Q}}^k\right){\left({\widetilde{V_Q}}^k\right)}^{\top }$ is a solution to (5), where $S\left({\widetilde{{\Lambda }_Q}}^k\right)=diag{\left({[{\left({\widetilde{{\Lambda }_Q}}^k\right)}_{i_j,i_j}-{\mu }_k{w}_{i_j}^k]}_{+}\right)}_{i_1\le i_j\le i_{\widehat{q}}}$.

4. Convergence Analysis

This section mainly delineates subsequential convergence, global convergence and linear convergence rate. We start by analyzing the convergence of the subsequence.

4.1. Subsequential Convergence of Nonmontone Line Search

Initially, we establish monotone nonincreasing property of the sequence $\left\{E_{\delta }\left(X^{k+1},X^k,{\mu }_k\right)\right\}$.

Lemma 3. 

Let $\left\{X^k\right\}$ be the sequence generated by Algorithm 1. If for any $k\ge 0$, the parameters ${\alpha }_k$, ${\beta }_k$ and ${\mu }_k$ satisfy

$${\mu }_k<{\displaystyle \frac{1}{L}},{\alpha }_k\le \sqrt{{\displaystyle \frac{{\mu }_k\delta (1-{\mu }_{k}L)}{16{\mu }_{k-1}}}},and{\beta }_k\le \sqrt{{\displaystyle \frac{\delta (1-{\mu }_{k}L)}{4{\mu }_{k-1}(4{\mu }_k{L}^2+L+l)}}}.$$

(10)

Then, we have

$$E_{\delta }(X^{k+1},X^k,{\mu }_k)-E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})\le {\displaystyle \frac{{\mu }_{k}L-1+\delta }{4{\mu }_k}}{\parallel X^{k+1}-X^k\parallel }_F^2.$$

(11)

Proof. 

Since $X^{k+1}$ is a minimizer of the optimization problem in (4), we get

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=1}^m}{w}_i^k{\sigma }_i\left(X^{k+1}\right)\le {\displaystyle \sum _{i=1}^m}{w}_i^k{\sigma }_i\left(X^k\right)+\langle \nabla f\left(Z^k\right),X^k-X^{k+1}\rangle \hfill \\ \hfill & +{\displaystyle \frac{1}{2{\mu }_k}}\parallel X^k-Y^k{\parallel }_F^2-{\displaystyle \frac{1}{2{\mu }_k}}{\parallel X^{k+1}-Y^k\parallel }_F^2.\hfill \end{array}$$

(12)

From the Lipschitz continuity of $\nabla f$ with the modulus $L_f$ and $L_f\le L$, it follows from ([40], Lemma 1.2.3) that

$$f\left(X^{k+1}\right)\le f\left(Z^k\right)+\langle \nabla f\left(Z^k\right),X^{k+1}-Z^k\rangle +{\displaystyle \frac{L}{2}}{\parallel X^{k+1}-Z^k\parallel }_F^2.$$

(13)

Similarly to the technique of ([1], Lemma 4), we get

$$\begin{array}{cc}\hfill & f\left(X^{k+1}\right)+{\displaystyle \sum _{i=1}^m}{w}_i^k{\sigma }_i\left(X^{k+1}\right)-f\left(X^k\right)-{\displaystyle \sum _{i=1}^m}{w}_i^k{\sigma }_i\left(X^k\right)\hfill \\ \hfill & \le {\displaystyle \frac{1}{2{\mu }_k}}\parallel X^k-Y^k{\parallel }_F^2-{\displaystyle \frac{1}{2{\mu }_k}}\parallel X^{k+1}-Y^k{\parallel }_F^2+{\displaystyle \frac{L}{2}}\parallel X^{k+1}-Z^k{\parallel }_F^2+{\displaystyle \frac{l}{2}}{\parallel X^k-Z^k\parallel }_F^2.\hfill \end{array}$$

(14)

Next, it follows from (2) and (3) that

$$\begin{array}{c}{X}^k-Y^k=-{\alpha }_k(X^k-X^{k-1}),X^{k+1}-Y^k=X^{k+1}-X^k-{\alpha }_k(X^k-X^{k-1}),\hfill \\ X^k-Z^k=-{\beta }_k(X^k-X^{k-1}),X^{k+1}-Z^k=X^{k+1}-X^k-{\beta }_k(X^k-X^{k-1}).\hfill \end{array}$$

(15)

Merging (14), (15), the concavity of g and the definition of $E_{\delta }$ in (9), we have

$$\begin{array}{cc}\hfill & E_{\delta }(X^{k+1},X^k,{\mu }_k)-E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})\hfill \\ \hfill & =f\left(X^{k+1}\right)+{\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X^{k+1}\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{\delta }{4{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F^2-f\left(X^k\right)-{\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X^k\right)\right)-{\displaystyle \frac{\delta }{4{\mu }_{k-1}}}{\parallel X^k-X^{k-1}\parallel }_F^2\hfill \\ \hfill & \le f\left(X^{k+1}\right)-f\left(X^k\right)+{\displaystyle \sum _{i=1}^m}{w}_i^k({\sigma }_i\left(X^{k+1}\right)-{\sigma }_i\left(X^k\right))\hfill \\ \hfill & +{\displaystyle \frac{\delta }{4{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F^2-{\displaystyle \frac{\delta }{4{\mu }_{k-1}}}{\parallel X^k-X^{k-1}\parallel }_F^2\hfill \\ \hfill & \le {\displaystyle \frac{1}{2{\mu }_k}}{\alpha }_k^2\parallel X^k-X^{k-1}{\parallel }_F^2-{\displaystyle \frac{1}{2{\mu }_k}}{\parallel (X^{k+1}-X^k)-{\alpha }_k(X^k-X^{k-1})\parallel }_F^2\hfill \\ \hfill & +{\displaystyle \frac{L}{2}}\parallel (X^{k+1}-X^k)-{\beta }_k(X^k-X^{k-1}){\parallel }_F^2+{\displaystyle \frac{l}{2}}{\beta }_k^2{\parallel X^k-X^{k-1}\parallel }_F^2\hfill \\ \hfill & +{\displaystyle \frac{\delta }{4{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F^2-{\displaystyle \frac{\delta }{4{\mu }_{k-1}}}{\parallel X^k-X^{k-1}\parallel }_F^2\hfill \\ \hfill & =-{\displaystyle \frac{1}{2{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F^2+{\displaystyle \frac{{\alpha }_k}{{\mu }_k}}\langle X^{k+1}-X^k,X^k-X^{k-1}\rangle +{\displaystyle \frac{L}{2}}{\parallel X^{k+1}-X^k\parallel }_F^2\hfill \\ \hfill & +{\displaystyle \frac{L}{2}}{\beta }_k^2\parallel X^k-X^{k-1}{\parallel }_F^2-L{\beta }_k\langle X^{k+1}-X^k,X^k-X^{k-1}\rangle +{\displaystyle \frac{l}{2}}{\beta }_k^2{\parallel X^k-X^{k-1}\parallel }_F^2\hfill \\ \hfill & +{\displaystyle \frac{\delta }{4{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F^2-{\displaystyle \frac{\delta }{4{\mu }_{k-1}}}{\parallel X^k-X^{k-1}\parallel }_F^2,\hfill \end{array}$$

(16)

By using the Young inequality, we obtain

$${\displaystyle \frac{{\alpha }_k}{{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F·\parallel X^k-X^{k-1}{\parallel }_F\le {\displaystyle \frac{1-{\mu }_{k}L}{8{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F^2+{\displaystyle \frac{2{\alpha }_k^2}{{\mu }_k(1-{\mu }_{k}L)}}{\parallel X^k-X^{k-1}\parallel }_F^2,$$

and

$$-L{\beta }_k\parallel X^{k+1}-X^k{\parallel }_F·\parallel X^k-X^{k-1}{\parallel }_F\le {\displaystyle \frac{1-{\mu }_{k}L}{8{\mu }_k}}\parallel X^{k+1}-X^k{\parallel }_F^2+{\displaystyle \frac{2{\mu }_k{\beta }_k^2{L}^2}{1-{\mu }_{k}L}}{\parallel X^k-X^{k-1}\parallel }_F^2.$$

Substituting above two inequalities into (16), we have

$$\begin{array}{cc}\hfill & E_{\delta }(X^{k+1},X^k,{\mu }_k)-E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})\hfill \\ \hfill & \le {\displaystyle \frac{{\mu }_{k}L-1+\delta }{4{\mu }_k}}{\parallel X^{k+1}-X^k\parallel }_F^2\hfill \\ \hfill & +\left({\displaystyle \frac{2{\alpha }_k^2}{{\mu }_k(1-{\mu }_{k}L)}}+{\displaystyle \frac{L}{2}}{\beta }_k^2+{\displaystyle \frac{l}{2}}{\beta }_k^2+{\displaystyle \frac{2{\mu }_k{\beta }_k^2{L}^2}{1-{\mu }_{k}L}}-{\displaystyle \frac{\delta }{4{\mu }_{k-1}}}\right){\parallel X^k-X^{k-1}\parallel }_F^2.\hfill \end{array}$$

Furthermore, it follows from (10) that

$${\displaystyle \frac{(L+l)}{2}}{\beta }_k^2+{\displaystyle \frac{2{\mu }_k{\beta }_k^2{L}^2}{1-{\mu }_{k}L}}\le {\displaystyle \frac{\delta }{8{\mu }_{k-1}}}\mathrm{and}{\displaystyle \frac{2{\alpha }_k^2}{{\mu }_k(1-{\mu }_{k}L)}}\le {\displaystyle \frac{\delta }{8{\mu }_{k-1}}}.$$

Hence, the assertion (11) follows immediately. The proof is completed. □

Lemma 4. 

(Well-definedness of the line search criterion) Let $\left\{X^k\right\}$ be the sequence generated by Algorithm 1. Then, for any $k\ge 0$, criterion (8) shall be satisfied within finite inner iterations.

Proof. 

This proof advances via contradiction. Initial focus rests upon $k=0.$ Observe that ${\mu }_0={\tilde{\mu }}_0$ with ${\mu }_{min}\le {\tilde{\mu }}_0\le {\displaystyle \frac{1-\delta }{L+2d}}$ holds incontrovertibly after finite inner iterations. Here, $Y^0=X^0$ and $Z^0=X^0.$ Then, from (4), we have

$${\displaystyle \sum _{i=1}^m}{w}_i^0{\sigma }_i\left(X^1\right)\le {\displaystyle \sum _{i=1}^m}{w}_i^0{\sigma }_i\left(X^0\right)+\langle \nabla f\left(X^0\right),X^0-X^1\rangle -{\displaystyle \frac{1}{2{\tilde{\mu }}_0}}{\parallel X^1-Y^0\parallel }_F^2,$$

where $w_i^0=g^{\prime }\left({\sigma }_i\left(X^0\right)\right)$. From ([40], Lemma 1.2.3), we obtain

$$f\left(X^1\right)-f\left(X^0\right)\le \langle \nabla f\left(X^0\right),X^1-X^0\rangle +{\displaystyle \frac{L}{2}}{\parallel X^1-X^0\parallel }_F^2.$$

Together with the concavity of g, we have

$$\begin{array}{cc}\hfill & \Psi \left(X^1\right)-\Psi \left(X^0\right)\hfill \\ \hfill & =f\left(X^1\right)+{\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X^1\right)\right)-f\left(X^0\right)-{\displaystyle \sum _{i=1}^m}g\left({\sigma }_i\left(X^0\right)\right)\hfill \\ \hfill & \le f\left(X^1\right)-f\left(X^0\right)+{\displaystyle \sum _{i=1}^m}{w}_i^k({\sigma }_i\left(X^1\right)-{\sigma }_i\left(X^0\right))\hfill \\ \hfill & \le {\displaystyle \frac{L}{2}}\parallel X^1-X^0{\parallel }_F^2-{\displaystyle \frac{1}{2{\tilde{\mu }}_0}}{\parallel X^1-X^0\parallel }_F^2.\hfill \end{array}$$

This inequality connotes that (11) holds. Since ${\tilde{\mu }}_0\le {\displaystyle \frac{1-\delta }{L+2d}}\le {\displaystyle \frac{2-\delta }{2(L+d)}}$, the criterion (8) shall invariably hold. Suppose that there exists a smallest $k>0$ such that the criterion (8) can not be satisfied. It means that the line search criterion (8) is satisfied for the former $k-1$ iterations. At the $k-1$-th iteration, there exists ${\mu }_{k-1}$ such that

$$E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})-{\tilde{E}}_{k-1}\le -{\displaystyle \frac{d}{2}}{\parallel X^k-X^{k-1}\parallel }_F^2.$$

Thus, we have ${\tilde{E}}_{k-1}\le E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})$. Further, Step 2 of Algorithm 1 defines ${\tilde{E}}_{k-1}$, and we obtain

$$\begin{array}{cc}\hfill & {\tilde{E}}_k=p_{k-1}{E}_{\delta }(X^k,X^{k-1},{\mu }_{k-1})+(1-p_{k-1}){\tilde{E}}_{k-1}\hfill \\ \hfill & \le p_{k-1}{E}_{\delta }(X^k,X^{k-1},{\mu }_{k-1})+(1-p_{k-1})E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})\hfill \\ \hfill & =E_{\delta }(X^k,X^{k-1},{\mu }_{k-1}).\hfill \end{array}$$

(17)

Since Algorithm 1’s Step (1d) necessitates ${\mu }_k\le {\mu }_{min}$, ${\mu }_k={\mu }_{min}$ becomes admissible. Similarly, from Step (1d) in Algorithm 1, we know that

$${\alpha }_k\le \sqrt{{\displaystyle \frac{{\mu }_k\delta (1-{\mu }_{k}L)}{16{\mu }_{k-1}}}},and{\beta }_k\le \sqrt{{\displaystyle \frac{\delta (1-{\mu }_{k}L)}{4{\mu }_{k-1}(4{\mu }_k{L}^2+L+l)}}}$$

must be satisfied. Consequently, ${\mu }_k={\mu }_{min}$ and (10) are obtained. In addition, since $d>0$ and $\delta \in [0,1)$, it holds that $0<{\mu }_{min}\le {\displaystyle \frac{1-\delta }{L+2d}}$ and, thus, ${\displaystyle \frac{{\mu }_{min}L-1+\delta }{4{\mu }_{min}}}\le -{\displaystyle \frac{d}{2}}$. Together with Lemma 3 and (17), we have

$$\begin{array}{cc}\hfill & E_{\delta }(X^{k+1},X^k,{\mu }_{min})-{\tilde{E}}_k\hfill \\ \hfill & \le E_{\delta }(X^{k+1},X^k,{\mu }_{min})-E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})\hfill \\ \hfill & \le {\displaystyle \frac{{\mu }_{min}L-1+\delta }{4{\mu }_{min}}}{\parallel X^{k+1}-X^k\parallel }_F^2\hfill \\ \hfill & \le -{\displaystyle \frac{d}{2}}{\parallel X^{k+1}-X^k\parallel }_F^2.\hfill \end{array}$$

(18)

This necessitates satisfaction of line search criterion (8) at the k-th iteration, inducing contradiction. The proof is completed. □

We obtain the subsequential convergence of Algorithm 1 in the following Theorem.

Theorem 1. 

Let $\left\{X^k\right\}$ be the sequence generated by Algorithm 1. Then, we have

(i) 

the sequence $\left\{{\tilde{E}}_k\right\}$ is nonincreasing;

(ii) 

$$\underset{k\to \infty }{lim}{\parallel X^{k+1}-X^k\parallel }_F=0;$$

(iii) 

$\left\{X^k\right\}$ is bounded and any cluster point $\tilde{X}={\displaystyle \underset{k\to \infty }{lim}}{X}^{k_i}$ of $\left\{X^k\right\}$ is a critical point of $\Psi .$

Proof. 

(i)

Invoking line search criterion (8) and ${\tilde{E}}_{k+1}$’s definition in Algorithm 1, we have

$$\begin{array}{cc}\hfill & {\tilde{E}}_{k+1}=p_k{E}_{\delta }(X^{k+1},X^k,{\mu }_k)+(1-p_k){\tilde{E}}_k\hfill \\ \hfill & \le p_k({\tilde{E}}_k-{\displaystyle \frac{d}{2}}\parallel X^{k+1}-X^k{\parallel }_F^2)+(1-p_k){\tilde{E}}_k\hfill \\ \hfill & \le {\tilde{E}}_k-{\displaystyle \frac{p_{min}·d}{2}}{\parallel X^{k+1}-X^k\parallel }_F^2.\hfill \end{array}$$

(19)

It indicates the sequence $\left\{{\tilde{E}}_k\right\}$ is nonincreasing.

(ii)

Summing up (19) from $k=1,\cdots ,N$, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{p_{min}·d}{2}}{\parallel X^{k+1}-X^k\parallel }_F^2\hfill \\ \hfill & \le {\displaystyle \sum _{k=1}^N}({\tilde{E}}_k-{\tilde{E}}_{k+1})\hfill \\ \hfill & ={\tilde{E}}_1-{\tilde{E}}_{N+1}\hfill \\ \hfill & =E_{\delta }(X^1,X^0,{\mu }_0)-E_{\delta }(X^{N+1},X^N,{\mu }_N)\hfill \\ \hfill & \le \Psi \left(X^1\right)+{\displaystyle \frac{\delta }{4{\mu }_0}}{\parallel X^1-X^0\parallel }_F^2-\Psi \left(X^N\right)\hfill \\ \hfill & \le \Psi \left(X^1\right)+{\displaystyle \frac{\delta }{4{\mu }_0}}{\parallel X^1-X^0\parallel }_F^2-\underline{\Psi }<\infty ,\hfill \end{array}$$

where the validity of the second inequality is deducible from (17), while the third stems directly from the definition of $E_{\delta }$ specified in (9). And the last inequality follows from $X^1\in \mathrm{dom}\Psi$, ${\mu }_0>0$ and $\delta \ge 0$. From the fact that $p_{min},d>0$ and $N\to \infty$, the assertion (ii) is consequently established.

(iii)

The sequence $\left\{{\tilde{E}}_k\right\}$ exhibits a monotone decrease, an outcome established by the result (i). We have

$${\tilde{E}}_k\le {\tilde{E}}_{k-1}\le \cdots \le {\tilde{E}}_1=\Psi \left(X^1\right)+{\displaystyle \frac{\delta }{4{\mu }_0}}{\parallel X^1-X^0\parallel }_F^2<\infty .$$

Again, from the definition of ${\tilde{E}}_k$ and (8), we have

$$\begin{array}{cc}\hfill & \Psi \left(X^1\right)+{\displaystyle \frac{\delta }{4{\mu }_0}}{\parallel X^1-X^0\parallel }_F^2\hfill \\ \hfill & \ge {\tilde{E}}_k=p_{k-1}{E}_{\delta }(X^k,X^{k-1},{\mu }_{k-1})+(1-p_{k-1}){\tilde{E}}_{k-1}\hfill \\ \hfill & \ge E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})\ge \Psi \left(X^k\right).\hfill \end{array}$$

Consequently, $\Psi$ is upper-bounded. Reiterating Assumption 1, the sequence $\left\{X^k\right\}$ remains confined and contains at least one cluster point. Assign $\tilde{X}$ as such a cluster point. Then, there exists a subsequence $\left\{X^{k_j}\right\}$ of $X^k$ such that ${\displaystyle \underset{j\to \infty }{lim}}{X}^{k_j}=\widehat{X}.$ Then, next proof is similar to ([1], Proof of Theorem 1 (iii)); it is easy to derive that $0\in \partial \Psi \left(\tilde{X}\right),$ which implies that $\tilde{X}\in \mathrm{crit}\Psi$. This completes the proof. □

4.2. Global Convergence and Linear Convergence Rate of Monotone Line Search

This subsection primarily discusses the global convergence and linear convergence rate of the proposed monotone line search ($p_k=1$) Algorithm 1 under the KL framework. First, we introduce the following two frequently used lemmas, whose proofs are similar to ([1], Lemma 5) and ([1], Lemma 6), so we will not repeat them here. We proceed to use the notation ${\Delta }_k:=X^k-X^{k-1}$ in this subsection.

Lemma 5. 

Let $\left\{X^k\right\}$ be the sequence generated by Algorithm 1. Then, there exist some $K\in \mathbb{N}$ and $b>0$ such that for all $k\ge K$, there exists ${\omega }^{k+1}\in \partial E_{\delta }(X^{k+1},X^k,{\mu }_k)$ such that

$$\parallel {\omega }^{k+1}{\parallel }_F\le b(\parallel {\Delta }_{k+1}{\parallel }_F+\parallel {\Delta }_k{\parallel }_F).$$

Denote the cluster point set of $\{X^{k+1},X^k,{\mu }_k\}$ by $\Xi$. Then, we summarize some properties of the cluster point set $\Xi$.

Lemma 6. 

Let $\left\{X^k\right\}$ be the sequence generated by Algorithm 1 with $p_k=1$. Then, we have

(i) 

Ξ is nonempty and $\Xi \subseteq \mathit{crit}{E}_{\delta }$;

(ii) 

$$\underset{k\to \infty }{lim}\mathrm{dist}((X^{k+1},X^k,{\mu }_k),\Xi )=0;$$

(iii) 

$E_{\delta }$ and Ψ are equal and constant on Ξ, i.e., there exists a constant κ such that for any $(\tilde{X},\tilde{X},\tilde{\mu })\in \Xi$, $E_{\delta }(\tilde{X},\tilde{X},\tilde{\mu })=\Psi \left(\tilde{X}\right)=\kappa$.

Theorem 2. 

Let $\left\{X^k\right\}$ be the sequence generated by Algorithm 1 with $p_k=1$ for k ’s large enough and $E_{\delta }$ is a KL function.

(i) 

The whole sequence $\left\{X^k\right\}$ manifests finite length ${\displaystyle \sum _{k=0}^{\infty }}{\parallel {\Delta }_{k+1}\parallel }_F<+\infty$ and $\left\{X^k\right\}$ globally converges to a point $\tilde{X}$ in $\mathit{crit}\Psi .$

(ii) 

Moreover, if the KL function can be taken in the form $\phi \left(s\right)=\rho s^{1-t}$ for some $t\in (0,1/2]$, the whole sequences $\left\{X^k\right\}$ and $\left\{E_{\delta }\left(X^{k+1},X^k,{\mu }_k\right)\right\}$ are linearly convergent.

Proof. 

(i)

Assume that $(\tilde{X},\tilde{X},\tilde{\mu })\in \Xi \subseteq \mathrm{crit}{E}_{\delta }.$ Then, there exists a subsequence $\left\{\right(X^{k_i+1},X^{k_i},$ ${\mu }_{k_i}\left)\right\}$ of $\left\{(X^{k+1},X^k,{\mu }_k)\right\}$ converging to $(\tilde{X},\tilde{X},\tilde{\mu })$. Let $k_1\in \mathbb{N}$ be such that $p_k=1$ for all $k\ge k_1$, and we know that ${\tilde{E}}_{k+1}=E_{\delta }(X^{k+1},X^k,{\mu }_k)$. It follows from Theorem 1 (iii) and the continuity of $\Psi$ that ${\displaystyle \underset{i\to \infty }{lim}}\Psi \left(X^{k_i}\right)=\Psi \left(\tilde{X}\right).$ Again from Theorem 1 (i) and (ii), we have ${\displaystyle \underset{k\to \infty }{lim}}{\parallel {\Delta }_k\parallel }_F=0,$ and $\left\{E_{\delta }(X^{k+1},X^k,{\mu }_k)\right\}$ is nonincreasing for all $k\ge k_1$. Thus, we get ${\displaystyle \underset{k\to \infty }{lim}}{E}_{\delta }(X^{k+1},X^k,{\mu }_k)=\kappa$, and $E_{\delta }(X^{k+1},X^k,{\mu }_k)\ge \kappa$ for all $k\ge k_1$.

If there exists an integer $\overline{k}$ such that $E_{\delta }(X^{\overline{k}},X^{\overline{k}-1},{\mu }_{\overline{k}-1})=\kappa$, then from (8), $\forall k\ge \overline{k}$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{2}}{\parallel {\Delta }_{k+1}\parallel }_F^2\le E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})-E_{\delta }(X^{k+1},X^k,{\mu }_k)\hfill \\ \hfill & \le E_{\delta }(X^{\overline{k}},X^{\overline{k}-1},{\mu }_{\overline{k}-1})-E_{\delta }(X^{k+1},X^k,{\mu }_k)\hfill \\ \hfill & \le E_{\delta }(X^{\overline{k}},X^{\overline{k}-1},{\mu }_{\overline{k}-1})-\kappa \hfill \\ \hfill & =0.\hfill \end{array}$$

Thus, we have $X^{k+1}=X^k$ for any $k>\overline{k}$ and the assertion ${\displaystyle \sum _{k=0}^{\infty }}{\parallel {\Delta }_{k+1}\parallel }_F<+\infty$ holds directly. Otherwise, since $\left\{E_{\delta }(X^{k+1},X^k,{\mu }_k)\right\}$ is nonincreasing for all $k\ge k_1$, we have $\left\{E_{\delta }(X^{k+1},X^k,{\mu }_k)\right\}>\kappa$ for all $k\ge k_1$. Now, we consider the sequence ${\left\{(X^{k+1},X^k,{\mu }_k)\right\}}_{k=0}^{\infty }$. It follows from Lemma 6 that the cluster point set $\Xi$ of ${\left\{(X^{k+1},X^k,{\mu }_k)\right\}}_{k=0}^{\infty }$ is nonempty and compact, and for any $(\tilde{X},\tilde{X},\tilde{\mu })\in \Xi$, we have

$$E_{\delta }(\tilde{X},\tilde{X},\tilde{\mu })=\Psi \left(\tilde{X}\right)=\kappa .$$

Thus, for any $\eta >0$, there exists a nonnegative integer $k_2\ge k_1$ such that $E_{\delta }(X^{k+1},X^k,{\mu }_k)<\kappa +\eta$ for any $k>k_2$. In addition, for any $\kappa >0$, there exists a positive integer $k_3\ge k_1$ such that $\mathrm{dist}((X^{k+1},X^k,{\mu }_k),\Xi )<\kappa$ for all $k>k_3$. Consequently, for any $\eta ,\kappa >0$, $k>k_4:=max\{k_2,k_3,K\}$, where K is given by Lemma 5, we have

$$\mathrm{dist}((X^{k+1},X^k,{\mu }_k),\Xi )<\kappa ,\mathrm{and}\kappa <E_{\delta }((X^{k+1},X^k,{\mu }_k)<\kappa +\eta .$$

By using Lemma 1 with $\Omega :=\Xi$, for any $k\ge k_4$, we have

$${\phi }^{\prime }(E_{\delta }((X^{k+1},X^k,{\mu }_k)-\kappa )\mathrm{dist}(0,\partial E_{\delta }(X^{k+1},X^k,{\mu }_k))\ge 1.$$

(20)

The remaining global convergence arguments are similar to ([1], Theorem 2); $\left\{X^k\right\}$ is a Cauchy sequence and, hence, it is convergent. By using Lemma 6 (i), there exists $(\tilde{X},\tilde{X},\tilde{\mu })\in \mathrm{crit}{E}_{\delta }$ with $\tilde{X}\in \mathrm{crit}\Psi$ such that ${\displaystyle \underset{k\to \infty }{lim}}{X}^k=\tilde{X}$.

(ii)

Denote ${\Theta }_k:=E_{\delta }(X^k,X^{k-1},{\mu }_{k-1})-\kappa$. It follows from (20) that

$$\begin{array}{cc}\hfill 1& \le {\phi }^{\prime }\left({\Theta }_{k+1}\right)dist\left(\mathbf{0},\partial E_{\delta }\left(X^{k+1},X^k,{\mu }_k\right)\right)\hfill \\ & \le (1-t)\rho b{\left({\Theta }_{k+1}\right)}^{-t}\left(∥{\Delta }_{k+1}∥+∥{\Delta }_k∥\right)\hfill \\ & \le (1-t)\rho b{\left({\Theta }_{k+1}\right)}^{-t}\sqrt{2{∥{\Delta }_{k+1}∥}^2+2{∥{\Delta }_k∥}^2}\hfill \\ & \le (1-t)\rho b{\left({\Theta }_{k+1}\right)}^{-t}\sqrt{4/d\left[E_{\delta }\left(X^{k-1},X^{k-2},{\mu }_{k-2}\right)-E_{\delta }\left(X^{k+1},X^k,{\mu }_k\right)\right]}\hfill \\ & =c{\left({\Theta }_{k+1}\right)}^{-t}\sqrt{{\Theta }_{k-1}-{\Theta }_{k+1}},\hfill \end{array}$$

where $c=2(1-t)\rho b/\sqrt{d}$, the second inequality follows from Lemma 5 and the fourth one follows from (8), together with the $p_k=1$. Since ${\Theta }_k\to 0$, there exists $k_5$ such that ${\Theta }_k\le 1$. Then, for all $k\ge k_6:=max\left\{k_4,k_5\right\}$, it follows from (20) that for any $k\ge k_6+1$,

$${\Theta }_k\le {\left({\Theta }_k\right)}^{2t}\le c^2\left({\Theta }_{k-2}-{\Theta }_k\right),$$

which means that

$${\Theta }_k\le {\displaystyle \frac{c^2}{1+c^2}}{\Theta }_{k-2}.$$

So, the sequences $\left\{E_{\delta }\left(X^{2k+1},X^{2k},{\mu }_{2k}\right)\right\}$ and $\left\{E_{\delta }\left(X^{2k},X^{2k-1},{\mu }_{2k-1}\right)\right\}$ are both Q-linearly convergent. This indicates that the entire sequence $\left\{E_{\delta }\left(X^{k+1},X^k,{\mu }_k\right)\right\}$ is R-linearly convergent. By combining this with (8), we can infer that there exist $N>0$ and $k_0$ and $q\in (0,1)$ so that for each $k\ge k_0,∥{\Delta }_{k+1}∥\le N{q}^k$. Consequently,

$$∥X^k-X^{\ast }∥\le \sum _{i=k}^{\infty }∥{\Delta }_{i+1}∥\le {\displaystyle \frac{N}{1-q}}{q}^k,$$

which means that $\left\{X^k\right\}$ is R-linearly convergent. This completes the proof. □

5. Numerical Results

This section evaluates the algorithm’s efficacy through resolution of the matrix completion problem:

$$\underset{X}{min}\sum _{i=1}^{m}g\left({\sigma }_i\left(X\right)\right)+{\displaystyle \frac{1}{2}}{\parallel {\mathcal{P}}_{\Omega }\left(X\right)-Y\parallel }_F^2,$$

(21)

where $\Omega$ constitutes the sample index set while ${\mathcal{P}}_{\Omega }:{\mathbb{R}}^{m\times n}\to {\mathbb{R}}^{m\times n}$ operates linearly, preserving $\Omega$ entries intact and nullifying others. Define $f:=f_1-f_2$, $f_1:={\displaystyle \frac{1}{2}}{\parallel {\mathcal{P}}_{\Omega }\left(X\right)-Y\parallel }_F^2$, $f_2:=0$; $\nabla f_1$ and $\nabla f_2$ exhibit Lipschitz constants $L=1$ and $l=0$. Algorithm performance manifests using both synthetic and empirical datasets. Implementation employed MATLAB 2020a on a Windows 10 platform with Intel(R) Core(TM) i7-1165G7 processor (2.80 GHz) and 16 GB RAM. Testing prioritizes ETP and Log penalty functions, replicating parameter selections from [1,4] as predominantly optimal.

5.1. Synthetic Data

Within this synthetic trial, we fabricate a rank $-r$ matrix $X^{\ast }$ as $M_L{M}_R$, where $M_L\in R^{m\times r}$, and $M_R\in R^{r\times n}$ originate from MATLAB’s rand command. Half of the elements in $X^{\ast }$ are randomly and uniformly missing. Here, the observed matrix $Y={\mathcal{P}}_{\Omega }\left(X^{\ast }\right)$, with ${\lambda }_0={\parallel Y\parallel }_{\infty }$, and $\lambda :={\lambda }_t={10}^{-3}{\lambda }_0$ in the model. Termination occurs when $\parallel {\mathcal{P}}_{\Omega }{\left(X\right)-Y\parallel }_{\infty }\le {10}^{-3}$.

PIRNNE-LS integrates a line search strategy to eliminate parametric restrictions. Validating this approach, we examine ETP and Log nonconvex penalties under four $p_k$ scenarios: $p_k=p\in \{0.1,0.3,0.7,1\}$, noting monotonicity when $p=1$ and non-monotonicity for $p<1$. Tests employ $m=n=500, r=50, {\alpha }_k^0=0.1, {\beta }_k^0=0.1, {\mu }_k^0=1$ for each $k\in N$, with Algorithm 1 (Step 1) parameters ${\eta }_1=0.4, {\eta }_2=0.35, \tau =0.45, d=0.1$ and $\delta =0.1$. Maximum iterations cap at 1000. Figure 1 charts error metric evolution against CPU duration. Figure 1 indicates PIRNNE-LS with $p=0.7$ and $p=1$ markedly outperforms alternatives.

5.2. Real Images

In this subsection, we primarily undertake a comparative analysis of our proposed algorithm with APIRNN in [17] and PIRNNE in [1]. For the APIRNN and PIRNNE algorithms, the choice of involved parameters ${\alpha }_k, {\beta }_k$ is the same as in [1,17], respectively. To better demonstrate algorithmic enhancements, we implement (i) monotone line search ($p_k\equiv 1$), designated PIRNNE-mLS, and (ii) nonmonotone line search ($p_k\equiv 0.7$), designated PIRNNE-nLS.

To more comprehensively demonstrate algorithmic efficacy, we constructed four 2D images, “Boat ($512\times 512$)”, “Man ($1024\times 1024$)”, “City Wall ($512\times 512$)” and “Spillikins ($512\times 512$)”, alongside four 3D counterparts, “Bottles ($512\times 512$)”, “Texture ($512\times 512$)”, “House ($256\times 256$)”, “Clock ($512\times 512$)”, visualized in Figure 2 and Figure 3. It is universally acknowledged that although not all authentic images possess low-rank characteristics, the essential information is primarily determined by the higher singular values. Consequently, it is feasible to recover corrupted images through low-rank approximation. For 3D imagery containing three separate channels, matrix completion executes independently per channel. The approach for selecting parameters remains identical to that employed in the artificial example, and the termination criterion is $\parallel {\mathcal{P}}_{\Omega }{\left(X\right)-Y\parallel }_{\infty }\le {10}^{-3}$.

Due to space constraints, we concentrate upon the ETP penalty function to demonstrate recovery efficacy. The algorithm’s recovery capability quantifies via Signal-to-Noise Ratio (SNR), defined as

$$\mathrm{SNR}(u,\overline{u})=10{log}_{10}{\displaystyle \frac{\parallel u-\overline{u}{\parallel }^2}{\parallel u-u^{\ast }{\parallel }^2}},$$

where u and $\overline{u}$ signify the original image and mean of the original image, and $u^{\ast }$ the reconstructed image.

For this evaluation, random values perturb $50\%$ of image elements, with $\Omega$ denoting a set of random values. These corrupted images appear in Figure 2 and Figure 3’s second row. SNR values relative to CPU duration—required by four methods to attain minimal processing time—are plotted across Figure 4 and Figure 5. The results in Figure 4 and Figure 5 show that PIRNNE-LS (including PIRNNE-mLS and PIRNNE-nLS) outperforms traditional APIRNN and PIRNNE.

Furthermore, we report the number of iterations and CPU time in seconds and SNR values in

Table 1. Numerical results of tested algorithms with Boat, Man, City Wall, Spillikins, Bottles, Texture, House and Clock.

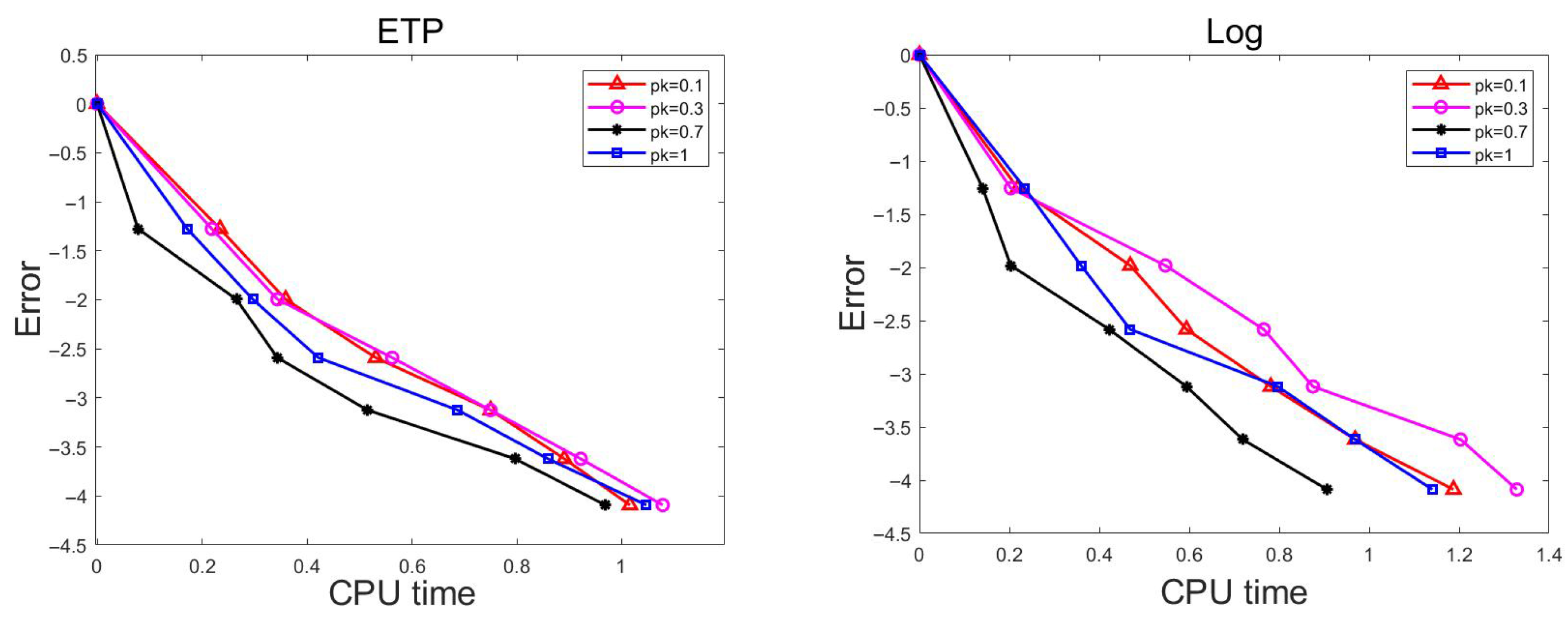
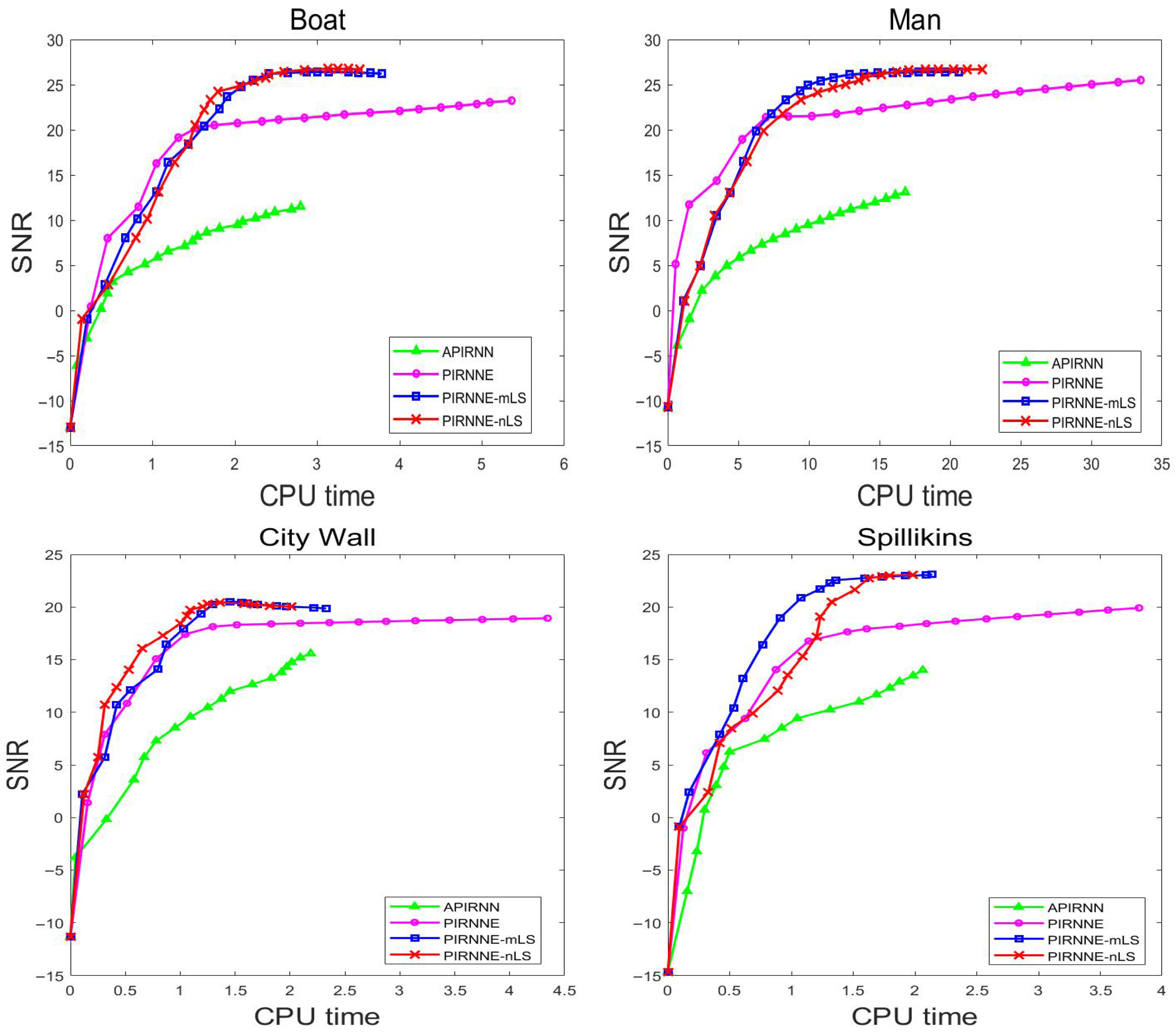
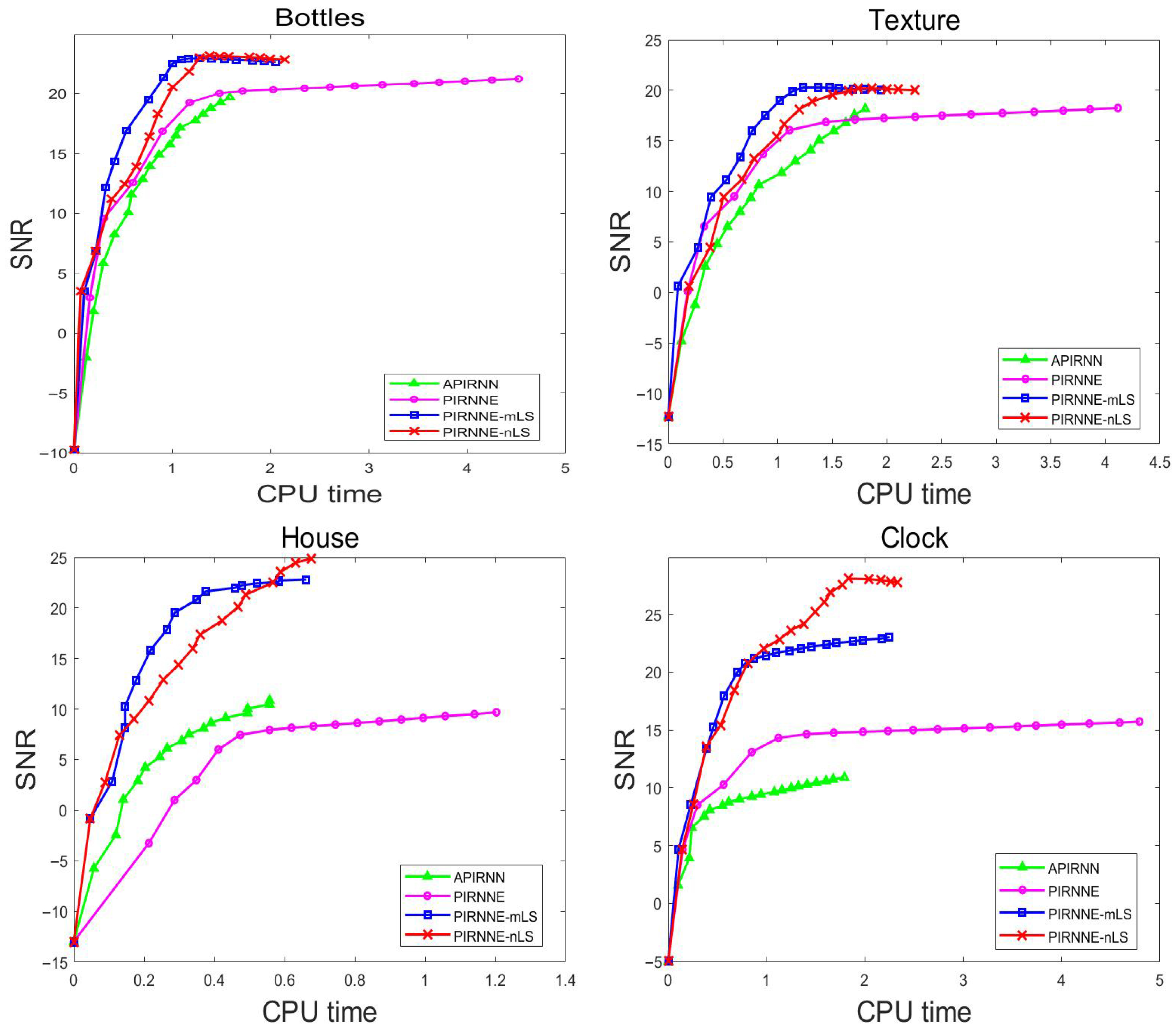
	APIRNN			PIRNNE			PIRNNE-mLS			PIRNNE-nLS
	Iter.	Time	SNR	Iter.	Time	SNR	Iter.	Time	SNR	Iter.	Time	SNR
Boat	121	3.94	19.49	51	2.87	23.96	43	1.90	26.23	43	1.90	26.69
Man	117	30.02	23.29	56	23.90	26.64	45	15.61	26.35	44	15.41	26.79
City Wall	56	1.43	17.88	40	1.61	19.08	38	1.05	19.74	35	0.96	20.05
Spillikins	68	1.57	20.05	59	1.96	22.39	34	1.03	23.08	33	1.01	23.09
Bottles	66	4.76	21.92	56	6.34	22.26	46	3.10	22.50	38	2.98	22.74
Texture	57	4.72	19.81	52	6.09	19.55	42	3.13	20.94	35	2.80	21.95
House	109	1.17	21.96	114	2.74	21.37	39	0.58	23.94	38	0.55	24.76
Clock	229	12.10	20.43	155	17.36	24.92	55	5.01	24.28	47	3.30	27.99

. In the presented results, we use “Iter.”, “Time” and “SNR” to denote the number of iterations, CPU time in seconds and SNR value, respectively. In color images, Iter., Time and SNR represent the mean values of the three channels. From Table 1, we observe that our proposed PIRNNE-mLS and PIRNNE-nLS have better recovery performance.

5.3. Movie Recommendation System

In order to further evaluate the performance of the proposed algorithm, we test our algorithm on the MovieLens dataset [41]. MovieLens dataset contains anonymous ratings of movies by users. Three subsets of the dataset are employed: 100 K, 1 M and 10 M, with varying numbers of users, movies and ratings as described in

Table 2. Dataset descriptions. The number of users, items and ratings used in each dataset.

Dataset		Users	Movies	Ratings
MovieLens	100 K	943	1682	100,000
	1 M	6040	3449	999,714
	10 M	69,878	10,677	10,000,054

.

The experiments were conducted on a workstation equipped with an Intel Xeon Gold 5218R processor (20 cores/40 threads), 64 GB of RAM and dual NVIDIA GeForce RTX 4090 GPU. The software environment is Ubuntu 22.04.4 LTS and MATLAB R2020a. The key measuring metrics are computational efficiency via GPU seconds (Time), recovery accuracy via RMSE and the objective value, which are adopted to determine the algorithm’s superiority. The comparative results of different algorithms on the MovieLens dataset subsets are presented in

Table 3. Comparative results of tested algorithms on the MovieLens dataset subsets.

Dataset		Method	Time	RMSE	Objective Value
MovieLens	100 K	APIRNN	2.06	1.0410	$6.4081\times {10}^2$
		PIRNNE	1.11	1.0216	$7.8860\times {10}^2$
		PIRNNE-mLS	2.00	1.0468	$5.9634\times {10}^2$
		PIRNNE-nLS	1.98	1.0450	$6.1770\times {10}^2$
	1 M	APIRNN	6.24	0.8855	$1.1575\times {10}^5$
		PIRNNE	7.88	1.0343	$1.2641\times {10}^5$
		PIRNNE-mLS	5.23	0.8844	$1.0311\times {10}^5$
		PIRNNE-nLS	5.22	0.8844	$1.0311\times {10}^5$
	10 M	APIRNN	28.23	0.9483	$1.9444\times {10}^6$
		PIRNNE	238.86	1.0063	$2.1513\times {10}^6$
		PIRNNE-mLS	14.49	0.9483	$1.9435\times {10}^6$
		PIRNNE-nLS	13.78	0.9483	$1.9435\times {10}^6$

. It should be emphasized that our advantages are not apparent with small data. However, our algorithms have a marked advantage with big data.

6. Conclusions

This paper addresses a class of nonconvex and nonsmooth optimization problems that are commonly encountered in various applications. Based on existing dimension reduction and extrapolation techniques, we propose a more generalized proximal iterative reweighted nuclear norm method. This method utilizes a line search mechanism to avoid parameter constraints, thereby providing greater flexibility in parameter selection. As a result, it is feasible to expand the application of this method in the future. In theory, we prove the subsequential convergence. Furthermore, for the case of monotone line search, we prove the global convergence and linear convergence rate of the algorithm under the KL framework. Finally, we validate the effectiveness of the algorithm through numerical results on synthetic and real data. We will construct a new nonconvex optimization model with distributed characteristics and design corresponding algorithms [42,43] based on the low rank of matrix. This will be our future research work.