Coherent Control of Diabolic Points of a Hermitian Hamiltonian in a Four-Level Atomic System Using Structured Light Fields
Abstract
1. Introduction
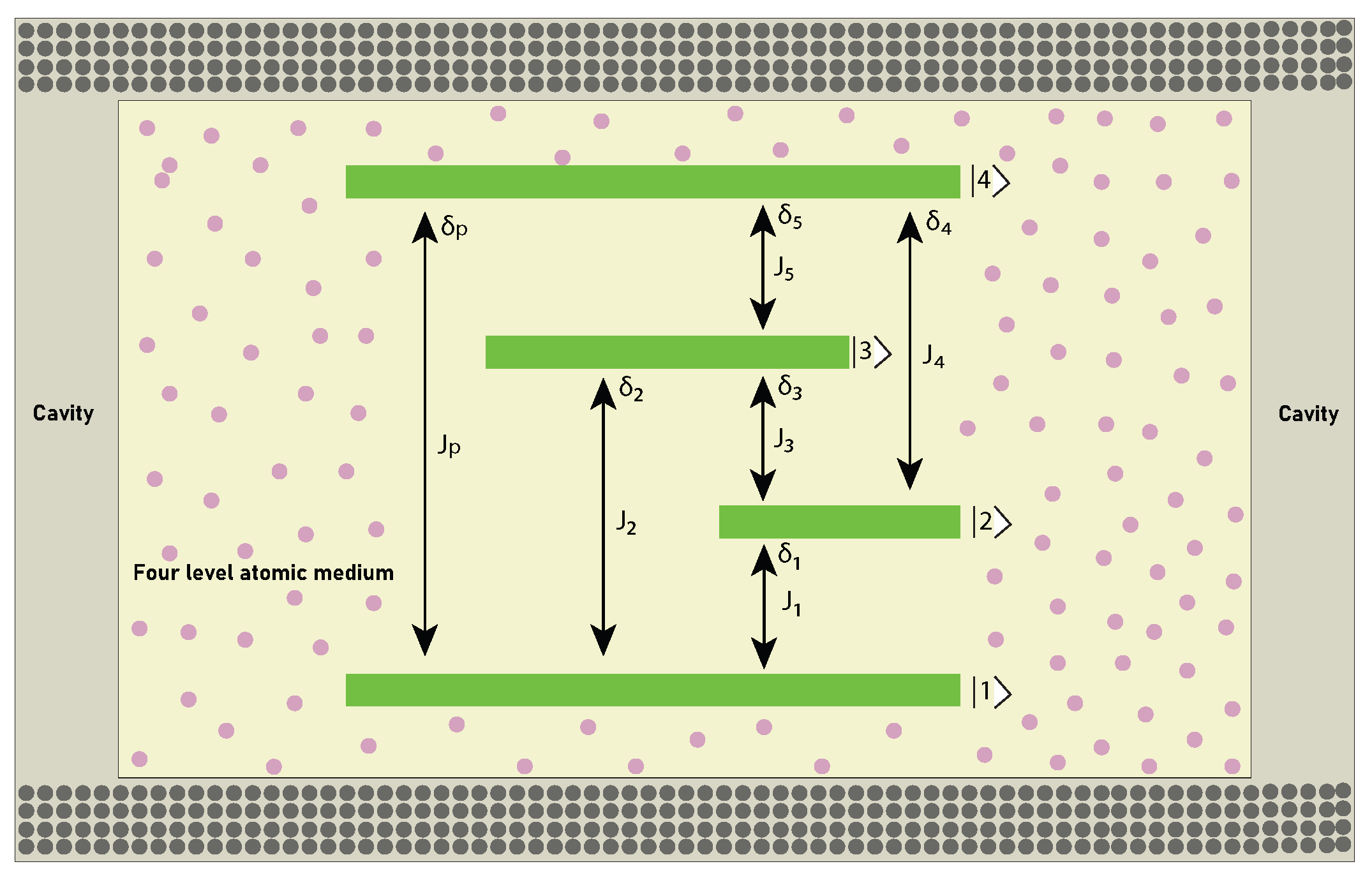
2. Four-Level Atomic System and Derivation of Eigenvalues
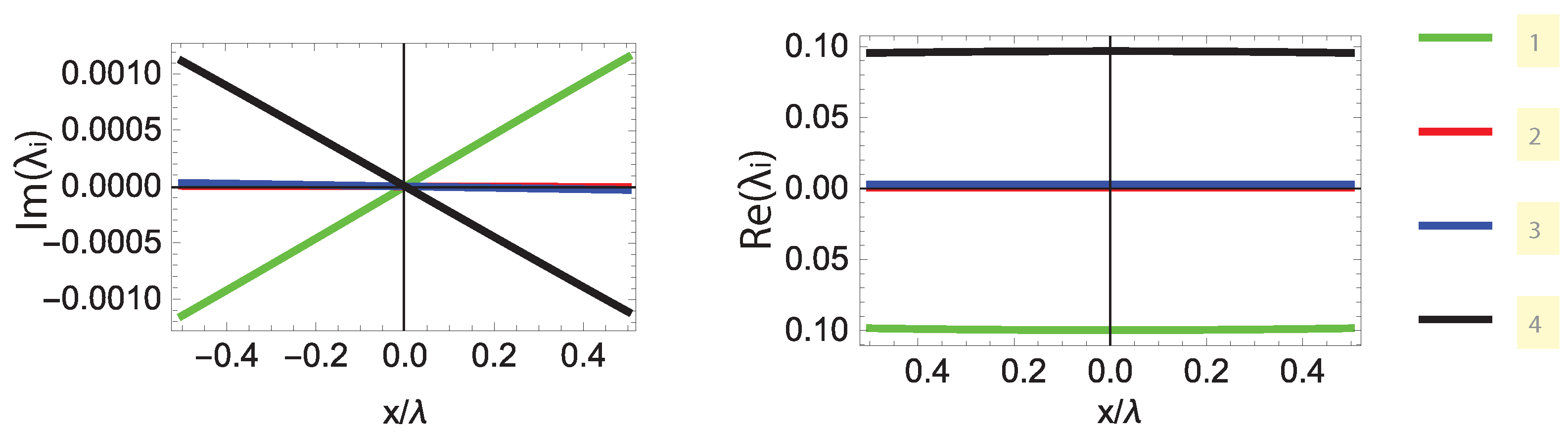
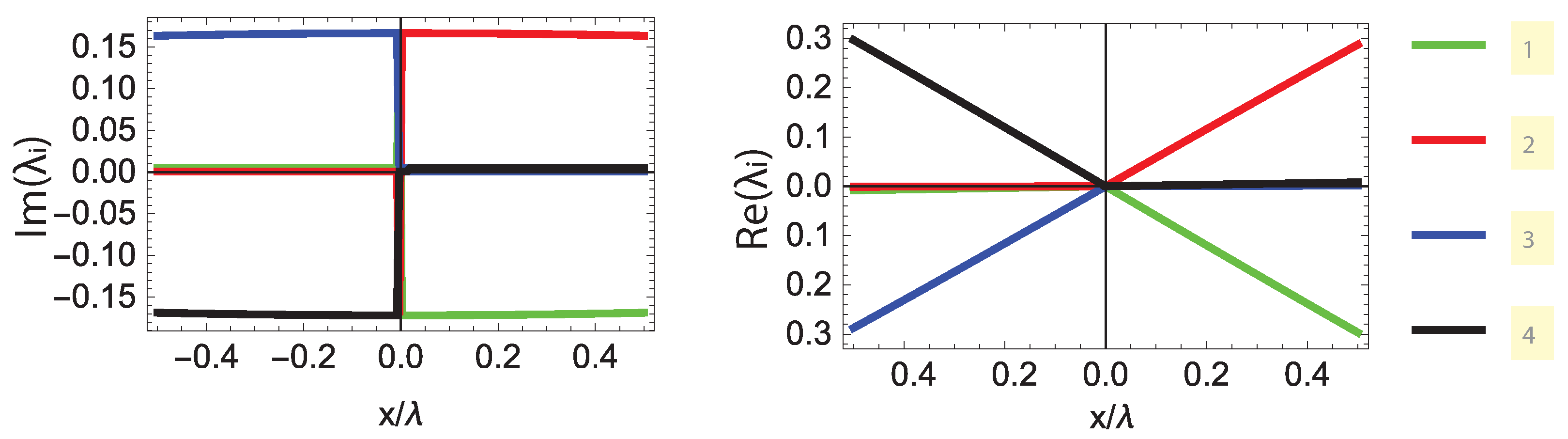
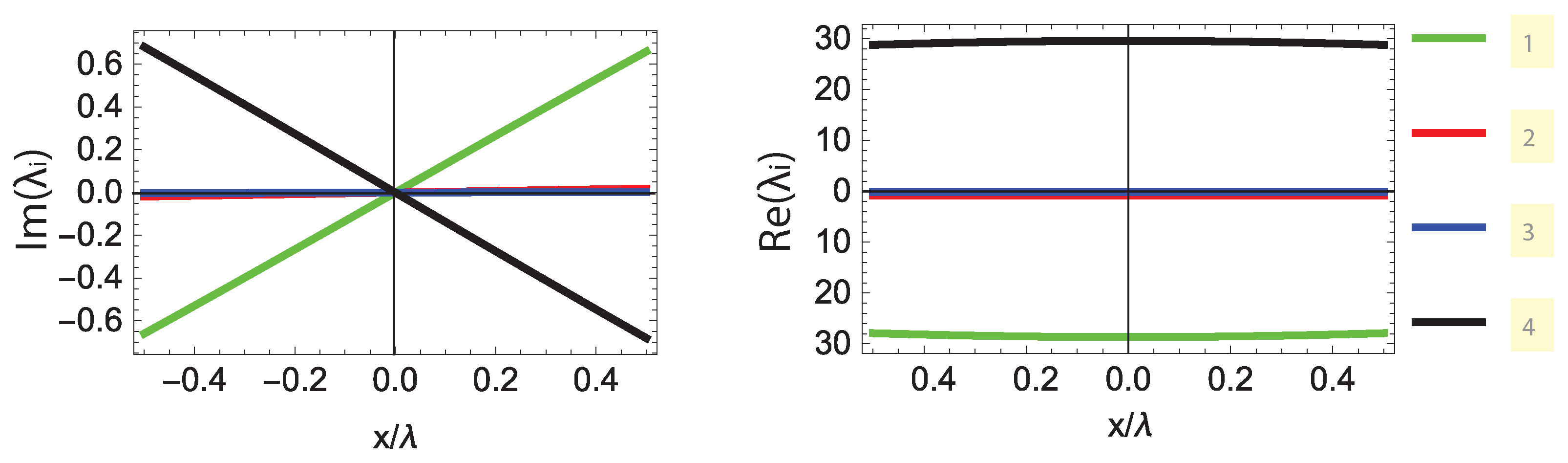
- Second-order DP: A diabolic point is classified as second-order when exactly two eigenvalues become degenerate, i.e., for a single pair .
- Third-order DP: A third-order diabolic point occurs when three eigenvalues coalesce simultaneously, satisfying for distinct .
- Fourth-order DP: A fourth-order diabolic point is identified when all four eigenvalues become equal, such that , or equivalently, all pairwise differences for .
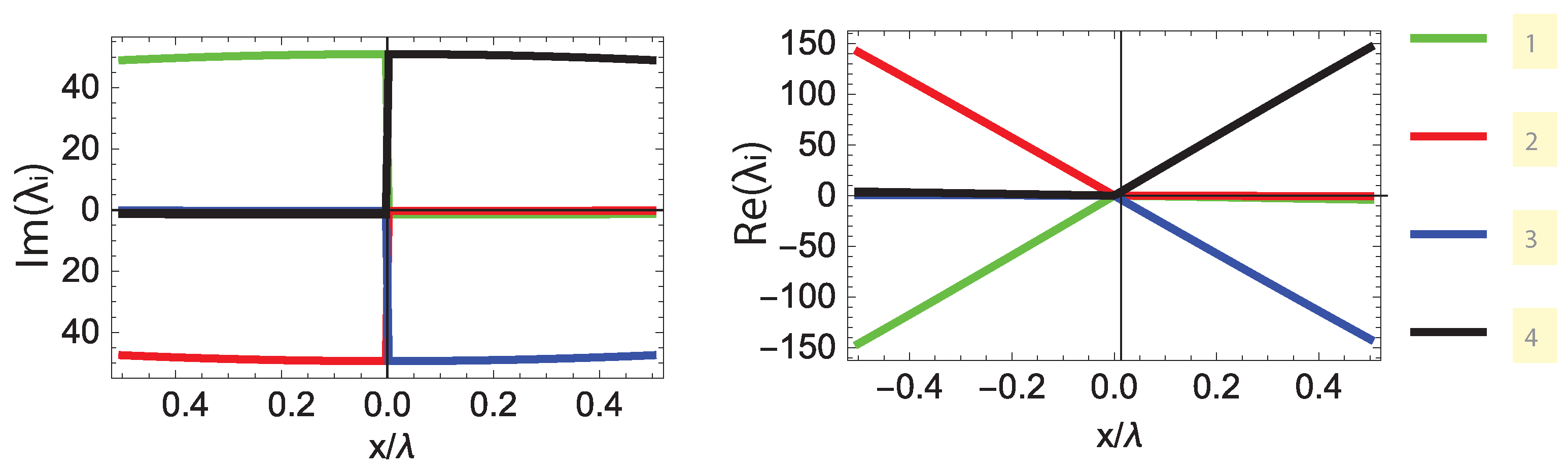
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Berry, M.V.; Wilkinson, M. Diabolical points in the spectra of triangles. Proc. R. Soc. Lond. A Math. Phys. Sci. 1984, 392, 15–43. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Z.; Zhou, W.; Chi, N.; Zhang, J.; Dai, Q. Resource-Saving and High-Robustness Image Sensing Based on Binary Optical Computing. Laser Photonics Rev. 2025, 19, 2400936. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Yu, A.; Hu, M.; Wang, Q.; Pang, C.; Qi, J. Non-Interleaved Shared-Aperture Full-Stokes Metalens via Prior-Knowledge-Driven Inverse Design. Adv. Mater. 2025, 37, 2408978. [Google Scholar] [CrossRef]
- Estrecho, E.; Gao, T.; Brodbeck, S.; Kamp, M.; Schneider, C.; Höfling, S.; Truscott, A.G.; Ostrovskaya, E.A. Visualising Berry phase and diabolical points in a quantum exciton-polariton billiard. Sci. Rep. 2016, 6, 37653. [Google Scholar] [CrossRef]
- Steeb, W.H. Diabolic points and entanglement. Phys. Scr. 2010, 81, 025012. [Google Scholar] [CrossRef]
- Stoop, J.; Baggen, J.; Vrancken, J.; Vleugel, J.; Beukenkamp, W. A diabolic dilemma: Towards fully automated train control or a human centred design. IFAC Proc. Vol. 2009, 42, 251–256. [Google Scholar] [CrossRef]
- Nam, S.; Taylor, J.; Efimov, A. Diabolical point and conical-like diffraction in periodic plasmonic nanostructures. Opt. Express 2010, 18, 10120–10126. [Google Scholar] [CrossRef]
- Chasman, R.R.; Ring, P. Diabolic points in deformation space. Phys. Lett. B 1990, 237, 313–316. [Google Scholar] [CrossRef]
- Seyranian1, A.; Kirillov, O.; Seyranian, A.P. Coupling of eigenvalues of complex matrices at diabolic and exceptional points. J. Phys. A Math. Gen. 2005, 38, 1723. [Google Scholar] [CrossRef]
- Berry, M.V.; Jeffrey, M.R. Chapter 2 Conical diffraction: Hamilton’s diabolical point at the heart of crystal optics. Prog. Opt. 2007, 50, 13–50. [Google Scholar] [CrossRef]
- Nesterov1, A.; Cruz, F. Complex magnetic monopoles, geometric phases and quantum evolution in the vicinity of diabolic and exceptional points. J. Phys. A Math. Theor. 2008, 41, 485304. [Google Scholar] [CrossRef]
- Elbertse, R.J.G.; Borodin, D.; Oh, J.; Ahn, T.; Hwang, J.; Rietveld, J.C.; Heinrich, A.J.; Delgado, F.; Otte, S.; Bae, Y. Long-lived magnetization in an atomic spin chain tuned to a diabolic point. Phys. Rev. Lett. 2024, 133, 166703. [Google Scholar] [CrossRef]
- Garg, A. Quenched spin tunneling and diabolical points in magnetic molecules. II. Asymmetric configurations. Phys. Rev. B 2001, 64, 094414. [Google Scholar] [CrossRef][Green Version]
- Yarkony, D.R. Diabolical conical intersections. Rev. Mod. Phys. 1996, 68, 985. [Google Scholar] [CrossRef]
- Garg, A. Diabolical points in the magnetic spectrum of Fe8 molecules. Europhys. Lett. 2000, 50, 382. [Google Scholar] [CrossRef]
- Park, C.; Garg, A. Diabolical Points in Molecular Magnets with a Four-Fold Easy Axis. arXiv 2000, arXiv:cond-mat/0010373. [Google Scholar] [CrossRef]
- Chesi, S.; Wang, Y.; Twamley, J. Diabolical points in multi-scatterer optomechanical systems. Sci. Rep. 2015, 5, 7816. [Google Scholar] [CrossRef] [PubMed]
- Charukhchyan, M.V.; Sedov, E.S.; Arakelian, S.M.; Alodjants, A.P. Spatially localized structures and oscillons in atomic Bose-Einstein condensates confined in optical lattices. Phys. Rev. A 2014, 89, 06362. [Google Scholar] [CrossRef]
- Pei, H.; Pang, H.; Quan, W.; Fan, W.; Yuan, L.; Zhang, K.; Fang, C. Pulsed optical pumping in electron spin vapor. Measurement 2024, 231, 114619. [Google Scholar] [CrossRef]
- Lu, L.; Bu, C.; Su, Z.; Guan, B.; Yu, Q.; Pan, W.; Zhang, Q. Generative deep-learning-embedded asynchronous structured light for three-dimensional imaging. Adv. Photonics 2024, 6, 046004. [Google Scholar] [CrossRef]
- Wu, Y.; Jin, Y.; Liu, Y.; Lyu, G. Quantum teleportation of incomplete multi-quantum systems. Phys. Scr. 2025, 100, 25253. [Google Scholar] [CrossRef]
- Luo, K.; Fu, Q.; Liu, X.; Zhao, R.; He, Q.; Hu, B.; Duan, J. Study of polarization transmission characteristics in nonspherical media. Opt. Lasers Eng. 2024, 174, 107970. [Google Scholar] [CrossRef]
- Khan, Z.A.; Majeed, A.; Ullah, I.; Ali, A. Coherent generation of superluminal and subluminal propagation of structured light in five level atomic medium. Appl. Phys. B 2025, 131, 30. [Google Scholar] [CrossRef]
- Majeed, A.; Ullah, I.; Alduais, F.S.; Bossly, A.A.; Bossly, R.; Ali, A. Investigation of Rotary Photon Drag of Generated Structured Light in a Five Level Atomic Medium. Adv. Theory Simulations 2025, 8, 2401307. [Google Scholar] [CrossRef]
- Ullah, S.; Akbar, J.; Qureshi, M.T.; Elaimi, M.A.; El-Kader, M.F.H.A.; Usman, M.; Bacha, B.A. Laguerre fields strength and beam waist-dependent superluminal propagation of light pulse in atomic medium. Eur. Phys. J. Plus 2022, 137, 963. [Google Scholar] [CrossRef]
- Yang, J.; Qian, C.; Xie, X.; Peng, K.; Wu, S.; Song, F.; Sun, S.; Dang, J.; Yu, Y.; Shi, S.; et al. Diabolical points in coupled active cavities with quantum emitters. Light Sci. Appl. 2020, 9, 6. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.J.; Wu, X.B.; Cai, X.D.; Xu, H.X.; Li, Q.Y.; Xiong, W.; Cui, T.J. Smart meta-device powered by stray microwave energies: A green approach to shielding external interference and detection. Appl. Energy 2025, 378, 124770. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, C.; Chen, Z.; Hu, W.; Lu, K.; Ge, L.; Wang, Z. ACR-Net: Learning High-Accuracy Optical Flow via Adaptive-Aware Correlation Recurrent Network. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 9064–9077. [Google Scholar] [CrossRef]
- Pavlov-Verevkin, V.B.; Sadovskii, D.A.; Zhilinskii, B.I. On the Dynamical Meaning of the Diabolic Points. Europhys. Lett. 1988, 6, 573. [Google Scholar] [CrossRef]
- Sadovskii, D.A.; Zhilinskii, B.I. Monodromy, diabolic points, and angular momentum coupling. Phys. Lett. A 1999, 256, 235–244. [Google Scholar] [CrossRef]
- Wiersig, J. Distance between exceptional points and diabolic points and its implication for the response strength of non-Hermitian systems. Phys. Rev. Res. 2022, 4, 033179. [Google Scholar] [CrossRef]
- Arkhipov, I.; Miranowicz, A.; Minganti, F.; Özdemir, Ş.K.; Nori, F. Dynamically crossing diabolic points while encircling exceptional curves: A programmable symmetric-asymmetric multimode switch. Nat. Commun. 2023, 14, 2076. [Google Scholar] [CrossRef]
- Sadovskii, D.A.; Zhilinskii, B.I.; Champion, J.P.; Pierre, G. Manifestation of bifurcations and diabolic points in molecular energy spectra. J. Chem. Phys. 1990, 92, 1523–1537. [Google Scholar] [CrossRef]
- Whitaker, B. Shining Light on Diabolic Points. Science 2011, 334, 187–188. [Google Scholar] [CrossRef] [PubMed]
- Krivtsun, V.M.; Sadovskii, D.A.; Zhilinskii, B. Critical phenomena and diabolic points in rovibrational energy spectra of spherical top molecules. J. Mol. Spectrosc. 1990, 139, 126–146. [Google Scholar] [CrossRef]
- Rowley, N.; Pál, K.F.; Nagarajan, M.A. Bandcrossings at high spin: Level interactions and diabolic points. Nuclear Phys. A 1989, 493, 13–28. [Google Scholar] [CrossRef]
- Bid, S.; Dash, G.; Thakurathi, M. Non-Hermitian higher-order Weyl semimetal with surface diabolic points. Phys. Rev. B 2023, 107, 165120. [Google Scholar] [CrossRef]
- Majeed, A.; Algahtani, O.J.; Ullah, I.; Ali, A.; Pamucar, D. Analysis of exceptional surfaces via Doppler-and Zeeman-affected non-Hermitian Hamiltonian in a three-level atomic system. AIMS Math. 2025, 10, 15165–15192. [Google Scholar] [CrossRef]
- Ullah, I.; Majeed, A.; Ali, A.; Khan, Z.A. Reflection and transmission solitons via high magneto optical medium. Chaos Solitons Fractals 2025, 191, 115881. [Google Scholar] [CrossRef]
- Emam, W.; Majeed, A.; Ali, Z.; Ali, A.; Pamucar, D. Periodic Dark and Bright Optical Soliton Dynamics in Atomic Medium Governed by Control Fields of Milnor Polynomial and Super-Gaussian Beam. Int. J. Theor. Phys. 2025, 64, 1–13. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algahtani, O.J. Coherent Control of Diabolic Points of a Hermitian Hamiltonian in a Four-Level Atomic System Using Structured Light Fields. Mathematics 2025, 13, 2608. https://doi.org/10.3390/math13162608
Algahtani OJ. Coherent Control of Diabolic Points of a Hermitian Hamiltonian in a Four-Level Atomic System Using Structured Light Fields. Mathematics. 2025; 13(16):2608. https://doi.org/10.3390/math13162608
Chicago/Turabian StyleAlgahtani, Obaid J. 2025. "Coherent Control of Diabolic Points of a Hermitian Hamiltonian in a Four-Level Atomic System Using Structured Light Fields" Mathematics 13, no. 16: 2608. https://doi.org/10.3390/math13162608
APA StyleAlgahtani, O. J. (2025). Coherent Control of Diabolic Points of a Hermitian Hamiltonian in a Four-Level Atomic System Using Structured Light Fields. Mathematics, 13(16), 2608. https://doi.org/10.3390/math13162608





