Model Reduction in Parallelization Based on Equivalent Transformation of Block Bi-Diagonal Toeplitz Matrices for Two-Dimensional Discrete-Time Systems
Abstract
1. Introduction
2. Preliminaries
2.1. Krawtchouk Polynomials and Krawtchouk Moments
2.2. Model Reduction Problem of Two-Dimensional Discrete-Time Systems
3. Model Reduction in Parallelization Based on Equivalent Transformation of Block Bi-Diagonal Toeplitz Matrices
3.1. Equivalent Input-Independent and Krawtchouk-Parameter-Independent Projection Subspace
3.2. Parallel Model Reduction Method Based on Equivalent Transformation of Block Bi-Diagonal Toeplitz Matrices
| Algorithm 1 Parallel input-independent and Krawtchouk-parameter-independent model reduction method based on equivalent transformation of block bi-diagonal Toeplitz matrices |
| Require: The two-dimensional discrete-time system (3), the positive integers .
Ensure: The reduced two-dimensional discrete-time system (4). |
3.3. Krawtchouk Moment Invariants
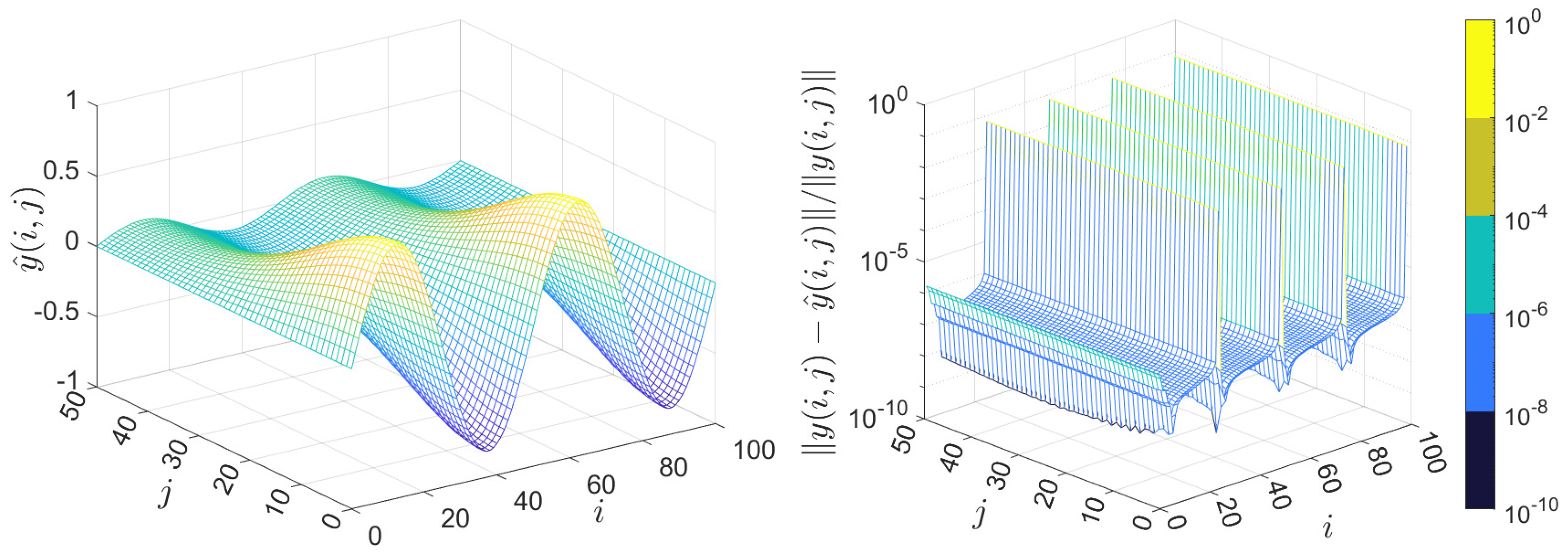
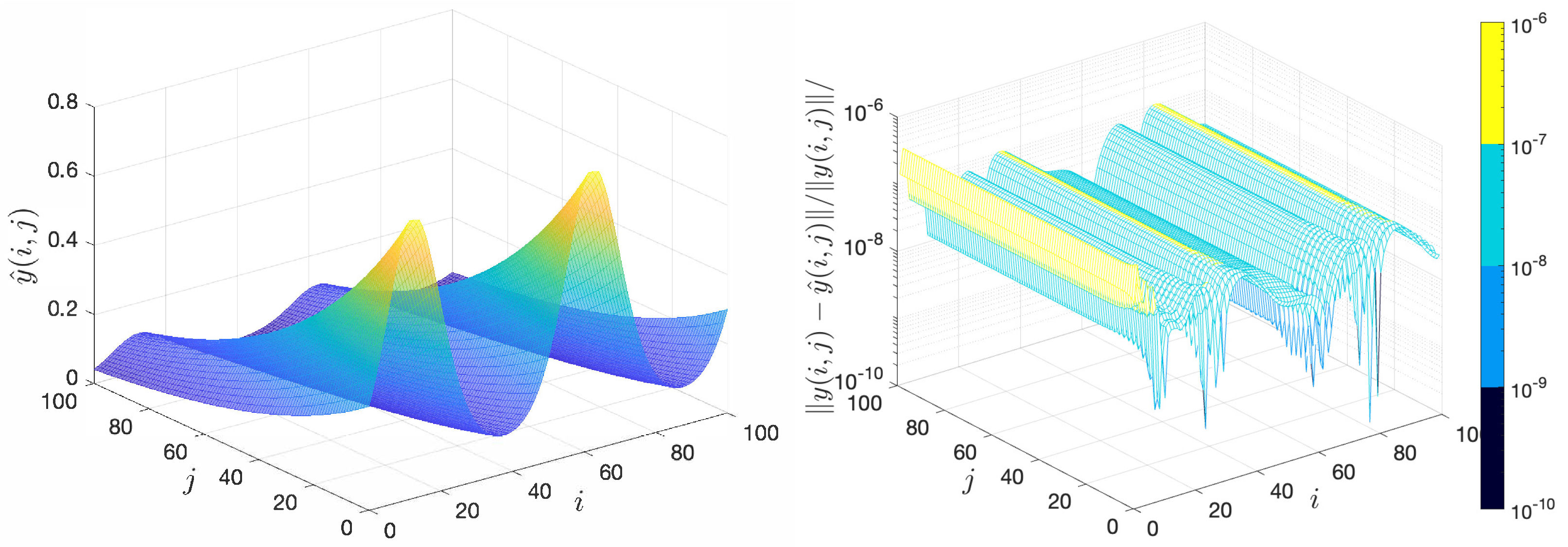
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bechtold, T.; Schrag, G.; Feng, L.H. System-Level Modeling of MEMS; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar] [CrossRef]
- Benner, P.; Cohen, A.; Ohlberger, M.; Willcox, K. Model Reduction and Approximation: Theory and Algorithms; SIAM: Philadelphia, PA, USA, 2017. [Google Scholar] [CrossRef]
- Li, T.; Wang, B. Continuous-stage symplectic adapted exponential methods for charged-particle dynamics with arbitrary electromagnetic fields. Adv. Comput. Math. 2023, 49, 89. [Google Scholar] [CrossRef]
- Li, M.; Nikan, O.; Qiu, W.; Xu, D. An efficient localized meshless collocation method for the two-dimensional Burgers-type equation arising in fluid turbulent flows. Eng. Anal. Bound. Elem. 2022, 144, 44–54. [Google Scholar] [CrossRef]
- Urban, K.; Patera, A.T. An improved error bound for reduced basis approximation of linear parabolic problems. Math. Comput. 2013, 83, 1599–1615. [Google Scholar] [CrossRef]
- Benner, P.; Breiten, T. Two-sided projection methods for nonlinear model order reduction. SIAM J. Sci. Comput. 2015, 37, B239–B260. [Google Scholar] [CrossRef]
- Luo, Z.D.; Li, Y.J. A preserving precision mixed finite element dimensionality reduction method for unsaturated flow problem. Mathematics 2022, 10, 4391. [Google Scholar] [CrossRef]
- Zimmermann, R.; Cheng, K. Randomized greedy magic point selection schemes for nonlinear model reduction. Adv. Comput. Math. 2024, 50, 81. [Google Scholar] [CrossRef]
- Chellappa, S.; Feng, L.H.; Benner, P. Accurate error estimation for model reduction of nonlinear dynamical systems via data-enhanced error closure. Comput. Methods Appl. Mech. Eng. 2024, 420, 116712. [Google Scholar] [CrossRef]
- Moore, B.C. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Pontes Duff, I.; Grundel, S.; Benner, P. New Gramians for switched linear systems: Reachability, observability, and model reduction. IEEE Trans. Autom. Control 2020, 65, 2526–2535. [Google Scholar] [CrossRef]
- Benner, P.; Goyal, P. Balanced truncation for quadratic-bilinear control systems. Adv. Comput. Math. 2024, 50, 88. [Google Scholar] [CrossRef]
- Jiang, S.; Cheng, Y.; Cheng, Y.; Huang, Y.Q. Generalized multiscale finite element method and balanced truncation for parameter-dependent parabolic problems. Mathematics 2023, 11, 4965. [Google Scholar] [CrossRef]
- Tang, M.; Xiao, Z.H.; Zulfiqar, U. Structure-preserving low-rank model reduction for second-order time-delay systems. Mathematics 2025, 13, 474. [Google Scholar] [CrossRef]
- Feng, L.H.; Benner, P. On error estimation for reduced-order modeling of linear non-parametric and parametric systems. ESAIM Math. Model. Numer. Anal. 2021, 55, 561–594. [Google Scholar] [CrossRef]
- Jiang, L.J.; Ma, L.L. A hybrid model reduction method for stochastic parabolic optimal control problems. Comput. Methods Appl. Mech. Eng. 2020, 370, 113–244. [Google Scholar] [CrossRef]
- Xu, K.L.; Jiang, Y.L.; Li, Z.; Li, L. Model reduction of discrete time-delay systems based on Charlier polynomials and high-order Krylov subspaces. Linear Algebra Appl. 2023, 661, 222–246. [Google Scholar] [CrossRef]
- Yan, W.Y.; Lam, J. An approximate approach to H2 optimal model reduction. IEEE Trans. Autom. Control 1999, 44, 1341–1358. [Google Scholar] [CrossRef]
- Jiang, Y.L.; Xu, K.L. Riemannian modified Polak-Ribière-Polyak conjugate gradient order reduced model by tensor techniques. SIAM J. Matrix Anal. Appl. 2020, 41, 432–463. [Google Scholar] [CrossRef]
- Xu, K.L.; Jiang, Y.L. Riemannian geometric-nonlinear conjugate gradient model order reduction of linear port-Hamiltonian systems on finite frequency intervals. IEEE Trans. Autom. Control 2024, 69, 3317–3324. [Google Scholar] [CrossRef]
- Borghi, A.; Breiten, T. H2 optimal rational approximation on general domains. Adv. Comput. Math. 2024, 50, 28. [Google Scholar] [CrossRef]
- Xu, K.L.; Dong, L.H.; Wang, B.; Li, Z. Preserving-periodic Riemannian descent model reduction of linear discrete-time periodic systems with isometric vector transport on product manifolds. Appl. Math. Lett. 2025, 171, 109692. [Google Scholar] [CrossRef]
- Rogers, E.; Galkowski, K.; Paszke, W.; Moore, K.L.; Bauer, P.H.; Hladowski, L.; Dabkowski, P. Multidimensional control systems: Case studies in design and evaluation. Multidimens. Syst. Signal Process. 2015, 26, 895–939. [Google Scholar] [CrossRef]
- Barnett, A.; Wu, B.; Veerapaneni, S. Spectrally accurate quadratures for evaluation of layer potentials close to the boundary for the 2D Stokes and Laplace equations. SIAM J. Sci. Comput. 2015, 37, B519–B542. [Google Scholar] [CrossRef]
- Roesser, R. A discrete state-space model for linear image processing. IEEE Trans. Autom. Control 1975, 20, 1–10. [Google Scholar] [CrossRef]
- Fornasini, E.; Marchesini, G. Doubly-indexed dynamical systems: State-space models and structural properties. Math. Syst. Theory 1978, 12, 59–72. [Google Scholar] [CrossRef]
- Fornasini, E.; Marchesini, G. State-space realization theory of two-dimensional filters. IEEE Trans. Autom. Control 1976, 21, 484–492. [Google Scholar] [CrossRef]
- Lu, W.S.; Lee, E.B.; Zhang, Q.T. Balanced approximation of two-dimensional and delay-differential systems. Int. J. Control 1987, 46, 2199–2218. [Google Scholar] [CrossRef]
- Imran, M.; Imran, M. Model order reduction framework for discrete-time systems with error bound via balanced structure. Int. J. Syst. Sci. 2022, 53, 3081–3094. [Google Scholar] [CrossRef]
- Ghafoor, A.; Sreeram, V. Model reduction via limited frequency interval Gramians. IEEE Trans. Circuits Syst. Regul. Pap. 2008, 55, 2806–2812. [Google Scholar] [CrossRef]
- Kumar, D.; Sreeram, V.; Du, X. Model reduction using parameterized limited frequency interval Gramians for 1-D and 2-D separable denominator discrete-time systems. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 65, 2571–2580. [Google Scholar] [CrossRef]
- Du, H.L.; Xie, L.H.; Soh, Y.C. H∞ reduced-order approximation of 2-D digital filters. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 688–698. [Google Scholar] [CrossRef]
- Gao, H.J.; Lam, J.; Wang, C.H.; Xu, S.Y. H∞ model reduction for uncertain two-dimensional discrete systems. Optim. Control Appl. Methods 2005, 26, 199–227. [Google Scholar] [CrossRef]
- Li, X.W.; Lam, J.; Cheung, K.C. Generalized H∞ model reduction for stable two-dimensional discrete systems. Multidimens. Syst. Signal Process. 2016, 27, 359–382. [Google Scholar] [CrossRef]
- Wang, X.L.; Jiang, Y.L. Model reduction of discrete-time bilinear systems by a Laguerre expansion technique. Appl. Math. Model. 2016, 40, 6650–6662. [Google Scholar] [CrossRef]
- Samuel, E.R.; Knockaert, L.; Dhaene, T. Model order reduction of time-delay systems using a Laguerre expansion technique. IEEE Trans. Circuits Syst. Regul. Pap. 2014, 61, 1815–1823. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F.; Vespri, V. A new framework for polynomial approximation to differential equations. Adv. Comput. Math. 2022, 48, 76. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.L. Parallel input-independent model order reduction for discrete-time parametric systems. IEEE Trans. Autom. Control 2023, 68, 4359–4366. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.L. Parallel model order reduction methods based on structured matrix analysis for discrete-time systems with parametric uncertainty. J. Comput. Appl. Math. 2023, 426, 115088. [Google Scholar] [CrossRef]
- Xu, K.L.; Li, Z.; Benner, P. Parametric interpolation model order reduction on Grassmann manifolds by parallelization. IEEE Trans. Circuits Syst. II Express Briefs 2025, 72, 198–202. [Google Scholar] [CrossRef]
- Wang, Z.H.; Jiang, Y.L.; Xu, K.L. Reduced-order state-space models for two-dimensional discrete systems via bivariate discrete orthogonal polynomials. Math. Comput. Simul. 2023, 212, 441–456. [Google Scholar] [CrossRef]
- Yap, P.T.; Paramesran, R.; Ong, S.H. Image analysis by Krawtchouk moments. IEEE Trans. Image Process. 2003, 12, 1367–1377. [Google Scholar] [CrossRef]
- Beals, R.; Wong, R. Special Functions: A Graduate Text; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Du, C.L.; Xie, L.H. H∞ Control and Filtering of Two-Dimensional Systems; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Dong, L.-H.; Xu, K.-L.; Xu, X.-Y. Model Reduction in Parallelization Based on Equivalent Transformation of Block Bi-Diagonal Toeplitz Matrices for Two-Dimensional Discrete-Time Systems. Mathematics 2025, 13, 2565. https://doi.org/10.3390/math13162565
Li Z, Dong L-H, Xu K-L, Xu X-Y. Model Reduction in Parallelization Based on Equivalent Transformation of Block Bi-Diagonal Toeplitz Matrices for Two-Dimensional Discrete-Time Systems. Mathematics. 2025; 13(16):2565. https://doi.org/10.3390/math13162565
Chicago/Turabian StyleLi, Zhen, Li-Hong Dong, Kang-Li Xu, and Xiao-Yang Xu. 2025. "Model Reduction in Parallelization Based on Equivalent Transformation of Block Bi-Diagonal Toeplitz Matrices for Two-Dimensional Discrete-Time Systems" Mathematics 13, no. 16: 2565. https://doi.org/10.3390/math13162565
APA StyleLi, Z., Dong, L.-H., Xu, K.-L., & Xu, X.-Y. (2025). Model Reduction in Parallelization Based on Equivalent Transformation of Block Bi-Diagonal Toeplitz Matrices for Two-Dimensional Discrete-Time Systems. Mathematics, 13(16), 2565. https://doi.org/10.3390/math13162565





