A Family of q-General Bell Polynomials: Construction, Properties and Applications
Abstract
1. Introduction
- If , the 2Vq-GP reduce to the q-Gould–Hopper polynomials (q-GH) [27], where are defined byand series representation asFor , the q-GHP reduce to 2-variable q-Hermite polynomials (2vq-HP) [28].
- If , the 2Vq-GP reduce to 2-variable q-Laguerre polynomials (2vq-LP) [29], where are defined bywhere denotes the 0th order q-Tricomi functions, which are defined by
- If , the 2Vq-GP reduce to 2-variable q-truncated exponential polynomials of order s (2Vq-TEP) [31], where are defined by
- If , the 2Vq-GP reduce to 2-variable q-truncated exponential Appell polynomials (2Vq-TEAP) [31], where are defined byFor , the 2Vq-TEAP reduce to q-truncated exponential Appell polynomials (q-TEAP) [28], which are defined by
2. q-General Bell Polynomials
3. Recurrence Formulae and Quasi-Monomial Characteristics
4. Applications
Examples
- If , the q-GBelP reduce to q-Laguerre–Bell polynomials (q-LBelP) , which are defined by
- If , the q-GBelP reduce to the q-Hermite–Appell–Bell polynomials (q-HABelP) , which are defined by
- If , the q-GBelP reduce to q-truncated exponential-Appell–Bell polynomials of order s (q-TEABelP) , which are defined byFor , the q-TEABelP reduce to q-truncated exponential-Appell–Bell polynomials of order 2 (q-TEABelP) , which are defined by
5. Conclusions
- Introduction of a New Polynomial Family: A generalized family of q-special polynomials, termed q-general Bell polynomials, were introduced through generating function and series representations.
- Fundamental Properties: Some explicit representations and q-recurrence relations for these polynomials were established, which helps to clarify their combinatorial nature.
- Structural Characteristics: The quasi-monomial properties of the q-general Bell polynomials were examined, and the differential equation that governs them was constructed.
- Specific Instances and Adaptability: The versatility of this new family of polynomials was demonstrated through the analysis of specific cases, including the q-Gould–Hopper–Bell and q-truncated exponential-Bell polynomials. For each of these specific instances, analogous structural and combinatorial results were derived.
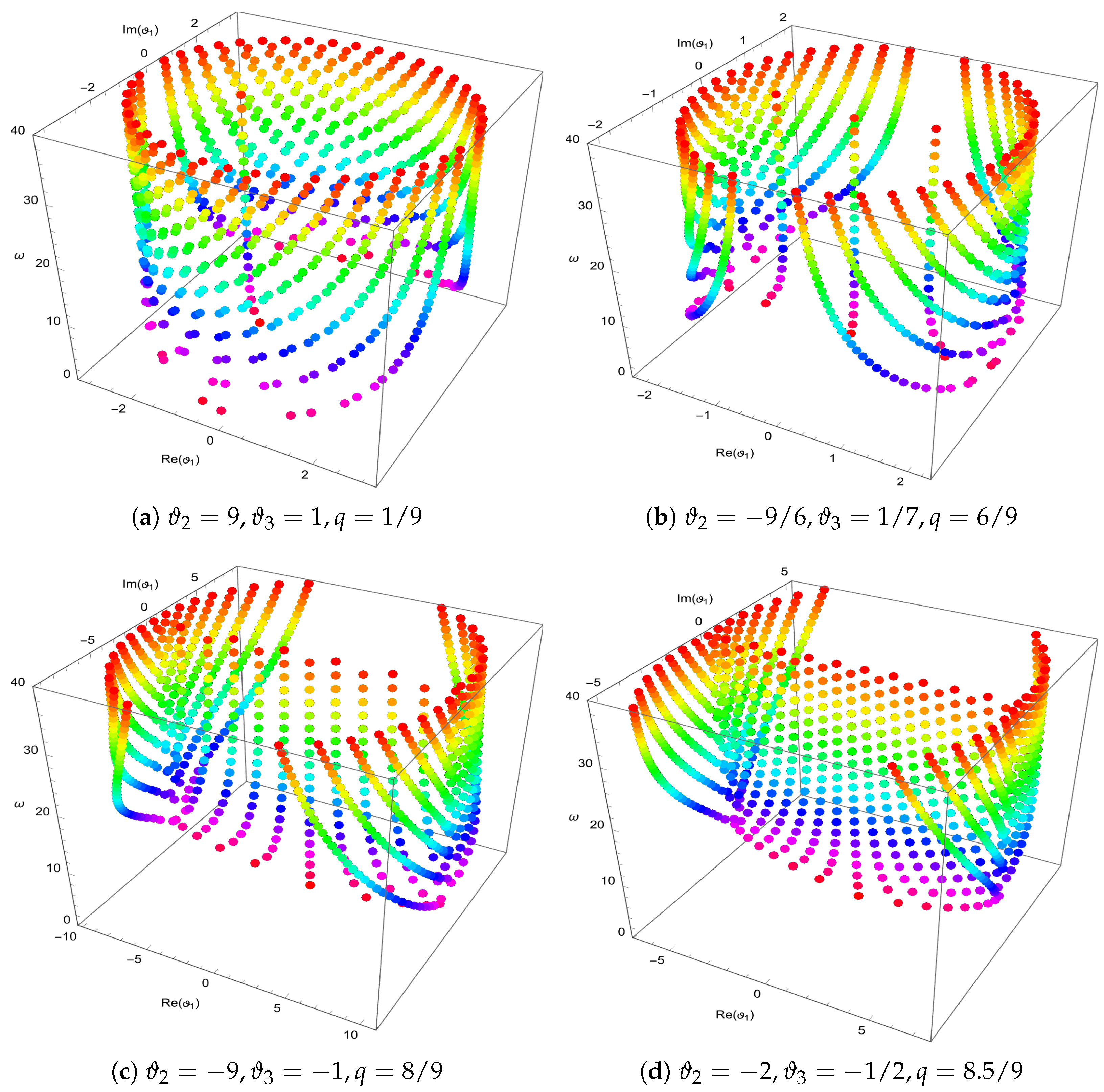
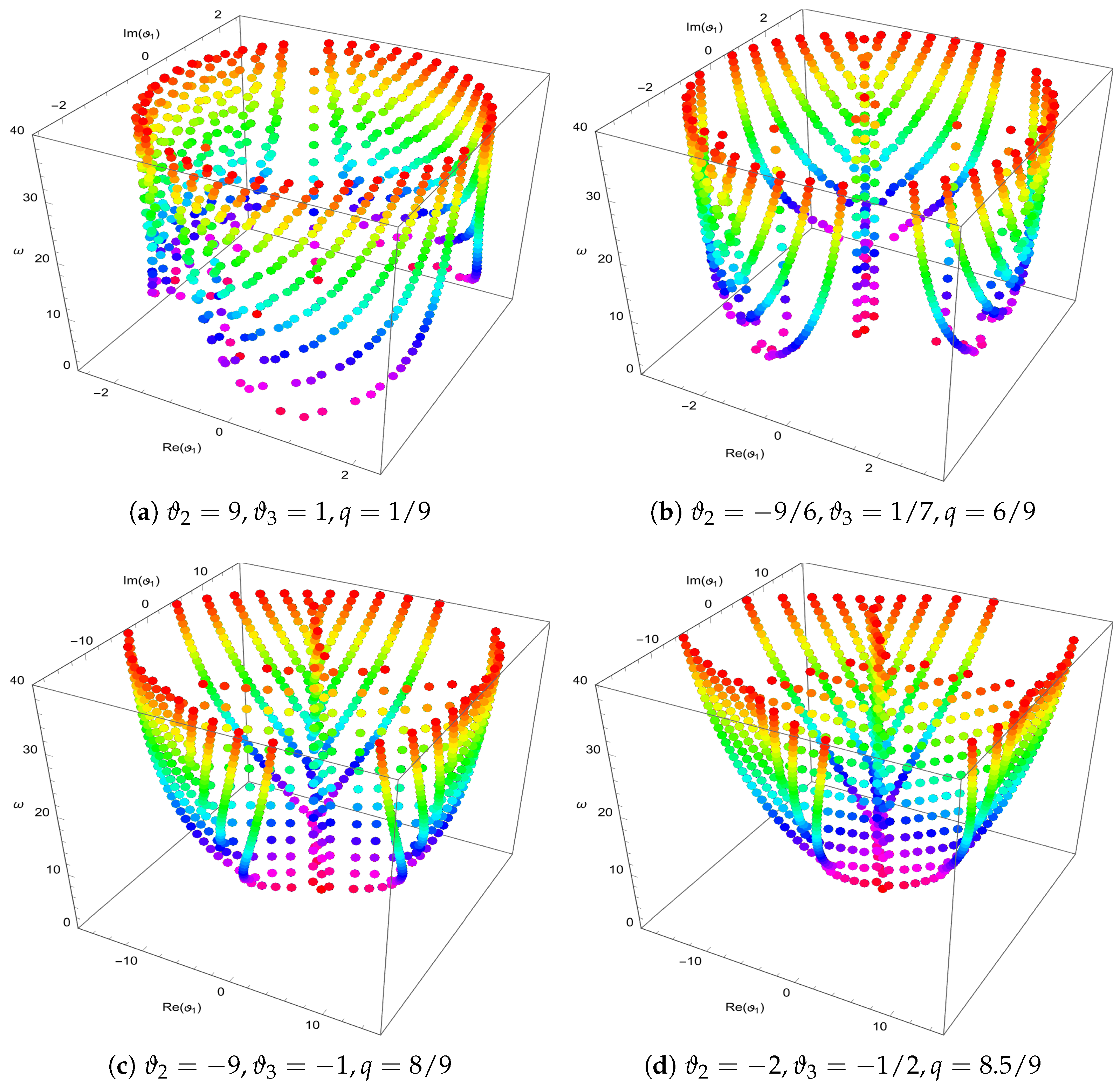
- Applications: This study demonstrates the properties and applications of the q-general Bell polynomials through the analysis of specific examples. Furthermore, an investigation into their zero distributions provides key insights into their structural and analytical characteristics.
- Computational Analysis: To provide numerical and visual insights into the behavior of these polynomials, computational analyses were performed using Mathematica to explore the distribution of their zeros and to generate graphical representations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Notation | Polynomials | Notation | Polynomials |
|---|---|---|---|
| Bell polynomials | 2-variable q-truncated exponential | ||
| -Appell polynomials | |||
| 2-variable Bell polynomials | q-general Bell polynomials | ||
| q-Bell polynomials | 2-variable q-general Bell polynomials | ||
| 2-variable q-Bell polynomials | q-Gould–Hopper–Bell polynomials | ||
| 2-variable general polynomials | q-truncated exponential-Bell | ||
| q-Gould–Hopper polynomials | polynomials of order s | ||
| 2-variable q-Laguerre polynomials | |||
| q-Hermite–Appell polynomials | |||
| 2-variable q-truncated exponential | |||
| polynomials of order s |
References
- Jackson, F.H. On q-functions and a certain difference operator. Trans. R. Soc. Edinb. 1908, 46, 253–281. [Google Scholar] [CrossRef]
- Jackson, F.H. On q-definite integrals. Q. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- Floreanini, R.; Vinet, L. Quantum algebras and q-special functions. Ann. Phys. 1993, 221, 53–70. [Google Scholar] [CrossRef]
- Ernst, T. A Comprehensive Treatment of q-Calculus; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; Volume 96. [Google Scholar]
- Andrews, G.E.; Askey, R.; Roy, R. Special Functions; Cambridge University Press: Cambridge, UK, 1999; Volume 71. [Google Scholar]
- Kim, T.; Kim, D.S.; Kwon, H.I.; Seo, J.J.; Dolgy, D.V. Some identities of q-Euler polynomials under the symmetric group of degree n. J. Nonlinear Sci. Appl. 2016, 9, 1077–1082. [Google Scholar] [CrossRef][Green Version]
- Yasmin, G.; Muhyi, A.; Araci, S. Certain results of q-Sheffer-Appell polynomials. Symmetry 2019, 11, 159. [Google Scholar] [CrossRef]
- Muhyi, A.; Araci, S. A note on q-Fubini-Appell polynomials and related properties. J. Funct. Spaces 2021, 2021, 3805809. [Google Scholar] [CrossRef]
- Fadel, M.; Muhyi, A. On a family of q-modified-Laguerre-Appell polynomials. Arab J. Basic Appl. Sci. 2024, 31, 165–176. [Google Scholar] [CrossRef]
- Aral, A.; Gupta, V.; Agarwal, R.P. Applications of q-Calculus in Operator Theory; Springer: New York, NY, USA, 2013. [Google Scholar]
- Mahmudov, N.I. On a class of q-Bernoulli and q-Euler polynomials. Adv. Differ. Equ. 2013, 2013, 108. [Google Scholar] [CrossRef]
- Alatawi, M.S.; Khan, W.A.; Ryoo, C.S. Explicit properties of q-cosine and q-sine array-type polynomials containing symmetric structures. Symmetry 2022, 14, 1675. [Google Scholar] [CrossRef]
- Benbernou, S.; Gala, S.; Ragusa, M.A. On the regularity criteria for the 3D magnetohydrodynamic equations via two components in terms of BMO space. Math. Methods Appl. Sci. 2014, 37, 2320–2325. [Google Scholar] [CrossRef]
- Boas, R.P.; Buck, R.C. Polynomial Expansions of Analytic Functions; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tanny, S.M. On some numbers related to the Bell numbers. Can. Math. Bull. 1974, 17, 733–738. [Google Scholar] [CrossRef]
- Carlitz, L. Some remarks on the Bell numbers. Fibonacci Q. 1980, 18, 66–73. [Google Scholar] [CrossRef]
- Kim, D.S.; Kim, T. Some identities of Bell polynomials. Sci. China Math. 2015, 58, 2095–2104. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Beholding the shallow water waves near an ocean beach or in a lake via a Boussinesq-Burgers system. Chaos Solitons Fractals 2021, 147, 110875. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Bilinear forms through the binary Bell polynomials, N solitons and Bäcklund transformations of the Boussinesq-Burgers system. Commun. Theor. Phys. 2020, 72, 095002. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Scaling transformation on a (2+1)-dimensional Boiti-Leon-Pempinelli system. Rom. Rep. Phys. 2021, 73, 111. [Google Scholar]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Generalized (2+1)-dimensional dispersive long-wave system: Scaling transformations and N solitons. Eur. Phys. J. Plus 2021, 136, 893. [Google Scholar] [CrossRef]
- Duran, U.; Araci, S.; Acikgoz, M. Bell-based Bernoulli polynomials with applications. Axioms 2021, 10, 29. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S.; Kim, H.K. On q-derangement numbers and polynomials. Fractals 2022, 30, 2240200. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S. Truncated polynomials associated with degenerate Bell polynomials. Russ. J. Math. Phys. 2021, 28, 342–355. [Google Scholar] [CrossRef]
- Khan, S.; Raza, N. General-Appell polynomials. Int. J. Anal. 2013, 2013, 708907. [Google Scholar] [CrossRef]
- Alam, N.; Khan, W.A.; Kizilates, C.; Ryoo, C.S. Two variable q-General-Appell polynomials. Mathematics 2025, 13, 765. [Google Scholar] [CrossRef]
- Raza, N.; Fadel, M.; Nisar, K.S.; Zakarya, M. On 2-variable q-Hermite polynomials. AIMS Math. 2021, 6, 8705–8727. [Google Scholar] [CrossRef]
- Fadel, M.; Raza, N.; Al-Gonah, A.; Duran, U. Bivariate q-Laguerre-Appell polynomials. Appl. Math. Sci. Eng. 2024, 32, 2412545. [Google Scholar] [CrossRef]
- Fadel, M.; Alatawi, M.S.; Khan, W.A. q-Hermite-based Appell polynomials. Mathematics 2024, 12, 1358. [Google Scholar] [CrossRef]
- Costabile, F.A.; Khan, S.; Ali, H. q-truncated exponential-Appell polynomials. Mathematics 2024, 12, 3862. [Google Scholar] [CrossRef]
- Wani, S.A.; Riyasat, M.; Khan, S.; Ramirez, W. Certain advancement in multidimensional q-Hermite polynomials. Rep. Math. Phys. 2024, 94, 117–141. [Google Scholar] [CrossRef]
- Riyasat, M.; Khan, S. q-Hermite based hybrid polynomials. Glas. Mat. Ser. III 2018, 53, 9–31. [Google Scholar] [CrossRef]
- Zayed, M.; Wani, S.A.; Ramírez, W.; Cesarano, C. Advancements in q-Hermite-Appell polynomials: A three-dimensional exploration. AIMS Math. 2024, 9, 26799–26824. [Google Scholar] [CrossRef]
- Hardy, G.H. Divergent Series; American Mathematical Society: Providence, RI, USA, 2000; Volume 334. [Google Scholar]
- Yasmin, G.; Muhyi, A. 2-variable q-generalized tangent-Apostol type polynomials. J. Math. Comput. Sci. 2021, 22, 238–251. [Google Scholar] [CrossRef]
- Dattoli, G. Hermite-Bessel and Laguerre-Bessel functions. In Advanced Special Functions and Applications; Aracne: Rome, Italy, 2000; Volume 1, pp. 147–164. [Google Scholar]
- Nápoles Valdés, J.E.; Castillo Medina, J.A.; Guzmán, P.M.; Lugo, L.M. A New Local Fractional Derivative of q-Uniform Type. Discontinuity Nonlinearity Complex. 2019, 8, 101–109. [Google Scholar] [CrossRef]
- Bermudo, S.; Kórus, P.; Nápoles Valdés, J.E. On q-Hermite-Hadamard inequalities for general convex functions. Acta Math. Hungar. 2020, 162, 365–378. [Google Scholar] [CrossRef]
- Castillo Medina, J.A.; Cruz García, S.; Nápoles Valdés, J.E.; Galeana Moyaho, T. Some New Results in the q-Calculus. Discontinuity Nonlinearity Complex. 2021, 10, 755–763. [Google Scholar] [CrossRef]
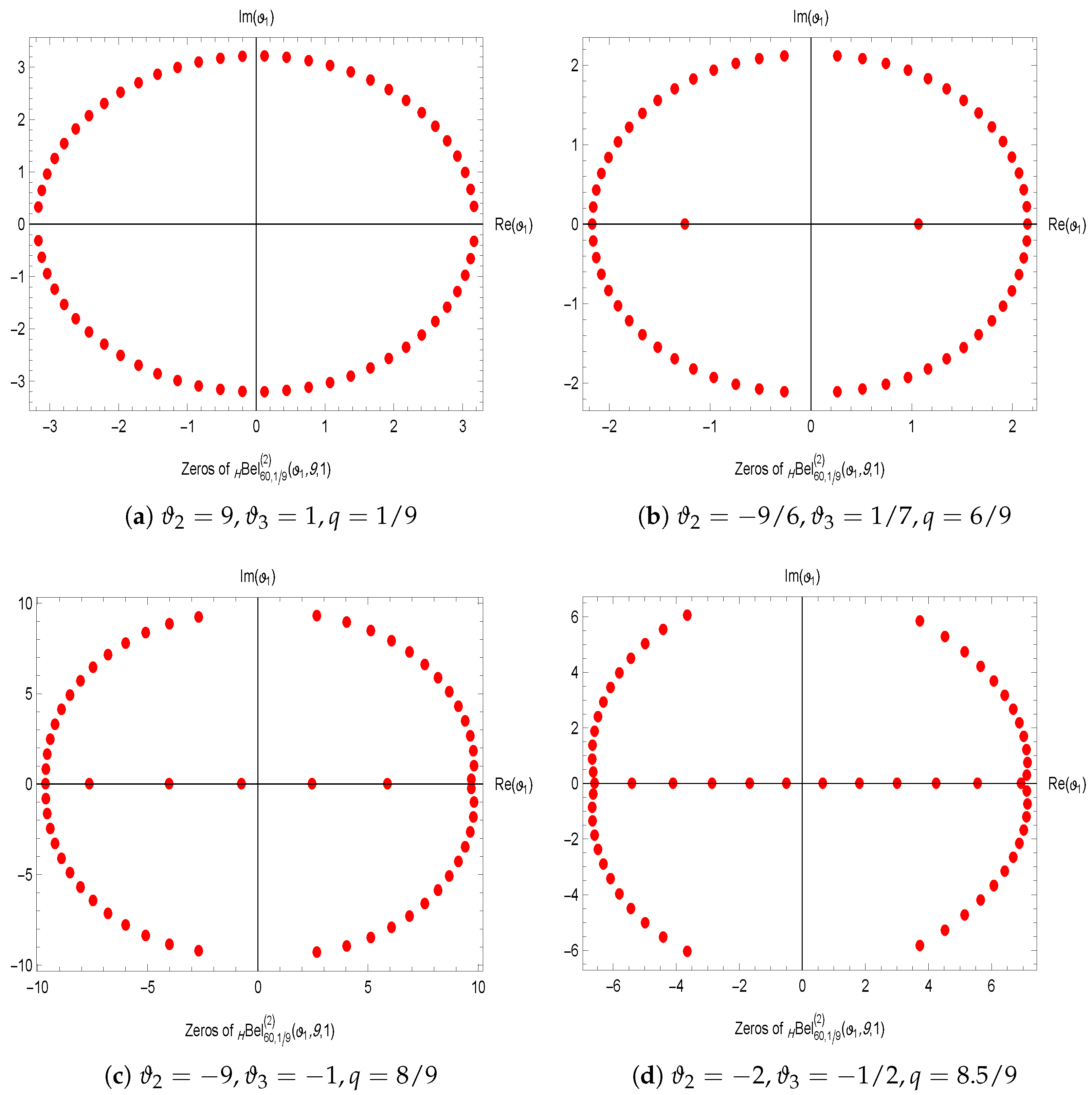

| q-GBelP | Choice | Well-Known Polynomials | Generating Function |
|---|---|---|---|
| 2-variable q-general | |||
| polynomials | . | ||
| 2-variable q-Bell | |||
| polynomials | |||
| q-Gould–Hopper | |||
| -Bell polynomials | |||
| q-Laguerre–Bell | |||
| polynomials | |||
| q-Hermite–Appell | |||
| -Bell polynomials | |||
| 2-variable q-truncated | |||
| exponential Bell polynomials | |||
| 2-variable q-truncated exponential | |||
| Appell–Bell polynomials |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algolam, M.S.; Muhyi, A.; Suhail, M.; Haron, N.; Aldwoah, K.; Ahmed, W.E.; Alsulami, A. A Family of q-General Bell Polynomials: Construction, Properties and Applications. Mathematics 2025, 13, 2560. https://doi.org/10.3390/math13162560
Algolam MS, Muhyi A, Suhail M, Haron N, Aldwoah K, Ahmed WE, Alsulami A. A Family of q-General Bell Polynomials: Construction, Properties and Applications. Mathematics. 2025; 13(16):2560. https://doi.org/10.3390/math13162560
Chicago/Turabian StyleAlgolam, Mohamed S., Abdulghani Muhyi, Muntasir Suhail, Neama Haron, Khaled Aldwoah, W. Eltayeb Ahmed, and Amer Alsulami. 2025. "A Family of q-General Bell Polynomials: Construction, Properties and Applications" Mathematics 13, no. 16: 2560. https://doi.org/10.3390/math13162560
APA StyleAlgolam, M. S., Muhyi, A., Suhail, M., Haron, N., Aldwoah, K., Ahmed, W. E., & Alsulami, A. (2025). A Family of q-General Bell Polynomials: Construction, Properties and Applications. Mathematics, 13(16), 2560. https://doi.org/10.3390/math13162560








