AdaGram in Python: An AI Framework for Multi-Sense Embedding in Text and Scientific Formulas
Abstract
1. Introduction
2. The AdaGram Algorithm and Preprocessing Pipeline
2.1. Basics of AdaGram
2.1.1. Multiple Embeddings
2.1.2. Bayesian Approach
2.1.3. Context Modeling
- E-step: Compute the posterior distribution over senses given the word and its context.
- M-step: Update the embeddings and relevance scores to maximize the likelihood.
2.1.4. Advantages
- Handling Polysemy: AdaGram explicitly models multiple meanings, providing a nuanced representation of words.
- Context Sensitivity: The model dynamically selects the appropriate meaning of a word based on its context.
- Bayesian Framework: The probabilistic nature allows for robust handling of sparse data.
2.1.5. Applications
- Word Sense Disambiguation: AdaGram is well-suited for disambiguating word senses based on context.
- Semantic Similarity: By modeling multiple embeddings, the algorithm captures fine-grained semantic relationships.
- Language Modeling: AdaGram enhances language models by incorporating context-sensitive predictions.
2.1.6. Limitations
- Computational Complexity: The introduction of multiple embeddings increases both memory and computational cost.
- Hyperparameter Tuning: Determining the number of senses per word requires careful adjustment.
- Interpretability: The resulting embeddings require post hoc analysis to interpret the senses.
2.2. Python Implementation
2.2.1. Data Cleaning
- Removing starting and ending whitespaces
- Removing clutterWhen extracting online text, there might be HTML tags, URL links, or other artifacts merged with the actual article. We could remove the punctuation, but that would not eliminate the tags themselves. For example: <title> would be turned into title, and it is not a relevant word for the text we would like to train on.This is when to use the Python re module (Regular Expressions) to detect the pattern of the strings we want to remove.
- # Pattern to remove HTML/CSS artifacts (e.g., <div>, </span>)
re.search(r"^([\d]|[^\w\s])+[a-zA-Z]+([\d]|[^\w\s]*)+", word)This searches for a pattern that matches one or more punctuation marks, then one or more letters, then zero or more punctuation marks. (Ex: “<ref” or “</ref>”)Filter URLs and mixed alphanumeric strings (e.g., H2O remains intact)re.search(r"^[a-zA-Z]+([\d]|[^\w\s])+[a-zA-Z]*", word)This searches for a pattern that matches one or more letters, then one or more punctuation marks, then zero or more letters. (Ex: https://www.youtube.com (accessed on 15 June 2025))re.search(r"[0-9]",word)This searches for a pattern that has a number. (Ex: 20th, 2nd, 2, etc.)If the word you are checking fits any of the search functions above, then you can ignore it and move on to the next word.Note: This rule applies only to natural language corpora. For scientific texts (e.g., chemical formulas), a separate tokenization pipeline is employed to retain digits and subscripts necessary for semantic interpretation. - Lemmatization and stop word removalOne word may have different forms. The word “program” can be “programmed”, “programs”, or “programming”, which are all different forms but have the same meaning. The method used to reduce all forms of a word into one is lemmatization, and we need to apply it to avoid repetition during training.Stop words are frequently used words that serve no meaning to a text when you are training. Examples of these stop words are pronouns (“I”, “are”, “you”, etc.), “a”, “the”, and others.The following code sample, using nltk (Python’s natural language toolkit) serves the purpose of lemmatization and removing the stop words:wntag = pos_tag(word)[0].lower()newword = lemmatizer.lemmatize(word,wntag) if wntag in[’j’, ’r’, ’n’, ’v’] else ""if not (newword in ENGLISH_STOP_WORDS):newlist.append(newword)The lines above state that after taking the first letter of a given word’s tag (“v” for a verb, “n” for a noun, etc.), we will lemmatize the word based on that tag. So, the word “better” would turn to “good”, the word “studies” would turn to “study”, and so on.
2.2.2. Dictionary Creation
2.2.3. Training
- window: a half-context size (Default value: 4).
- workers: specifies how many parallel processes will be used for training (Default value: 1).
- min-freq: sets the minimum word frequency below which a word will be ignored (Default value: 20).
- remove-top-k: allows ignoring the K most frequent words.
- dim: is the dimensionality of the learned representations (Default value: 0).
- prototypes: defines the maximum number of prototypes learned (Default value: 5).
- alpha: is a parameter of the underlying Dirichlet process (Default value: 0.1).
- d: is used in combination with alpha in the Pitman–Yor process, and d=0 turns it into a Dirichlet process (Default value: 0).
- subsample: is a threshold for subsampling frequent words (Default value: inf).
- context-cut: allows a randomly decreasing window during training, increasing training speed with negligible effects on model performance.
- init-count: initializes the variational stick-breaking distribution. All prototypes start with zero occurrences except for the first one, which is assigned the init-count. A value of zero means that the first prototype receives all occurrences (Default value: 1).
- stopwords: is the path to a newline-separated file containing words to be ignored during training.
- sense-threshold: allows sparse gradients, speeding up training. If the posterior probability of a prototype is below this threshold, it will not contribute to parameter gradients (Default value: 1 × 10−10).
- save-threshold: is the minimal probability of a meaning to save after training (Default value: 1 × 10−3).
- regex: filters words from the dictionary using the specified regular expression.
- train: path to the training text.
- dict: path to the dictionary file.
- output: path for saving the trained model.
2.2.4. Model Usage
2.2.5. Adaptation to Scientific Formulas
Specialized Tokenization
| Algorithm 1 Formula Tokenization Strategy |
|
Regex-Based Extraction
- Chemical formulas with subscripts and superscripts;
- Charges and oxidation states;
- Complex groups in parentheses and brackets;
- Reaction arrows and equilibrium symbols;
- Thermodynamic and quantum mechanical notation.
Corpus Frequency Analysis
- Higher frequency of specialized symbols and operators;
- Multi-level hierarchical structures (e.g., nested parentheses in complex formulas);
- Context-dependent meaning of subscripts and superscripts;
- Domain-specific notation systems.
3. Results, Evaluation, and Test Cases
3.1. Real-World Texts
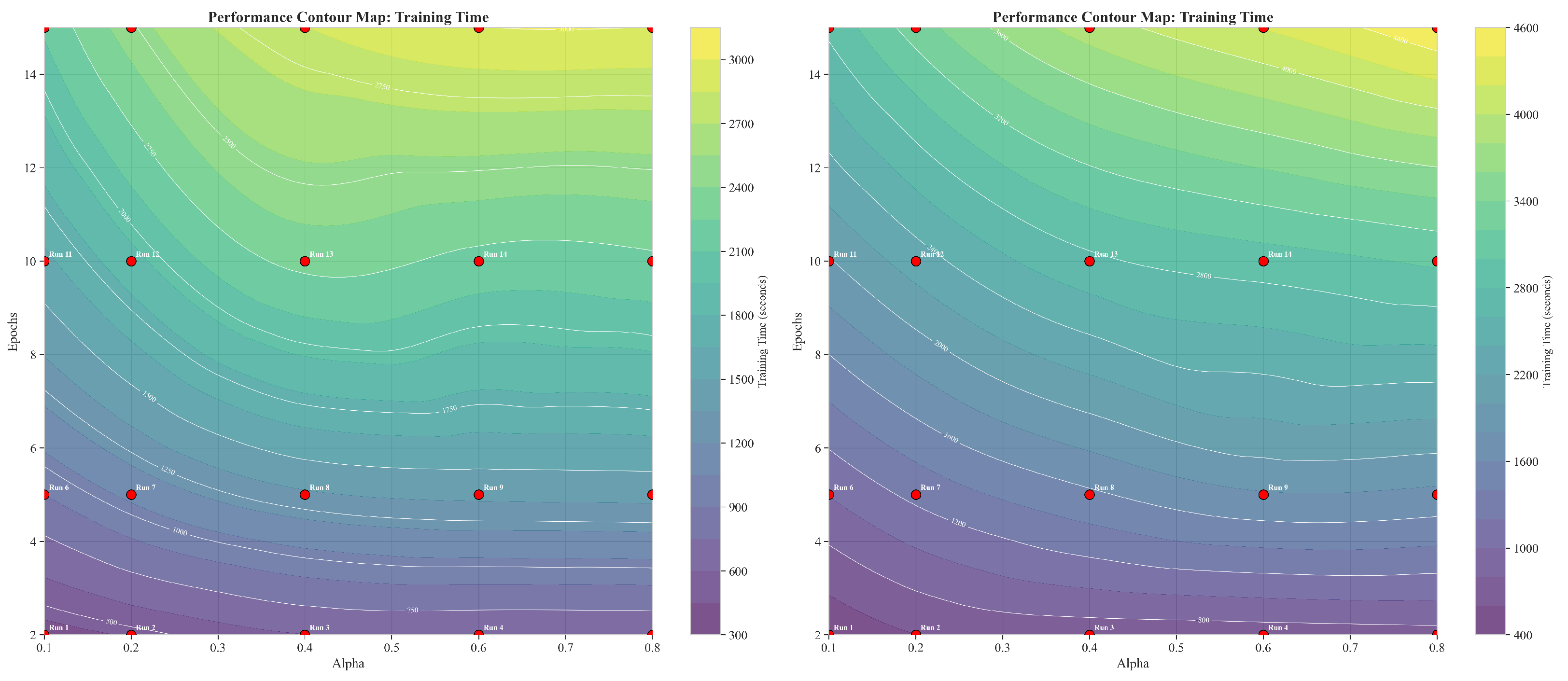
3.2. Training Time Heatmap Analysis
3.3. Cross-Sectional Training Time Analysis
3.4. Computational Efficiency Implications
3.5. Beta Distributions in Sense Modeling
3.6. Performance Analyses
3.6.1. Training Time Contour Map Analysis
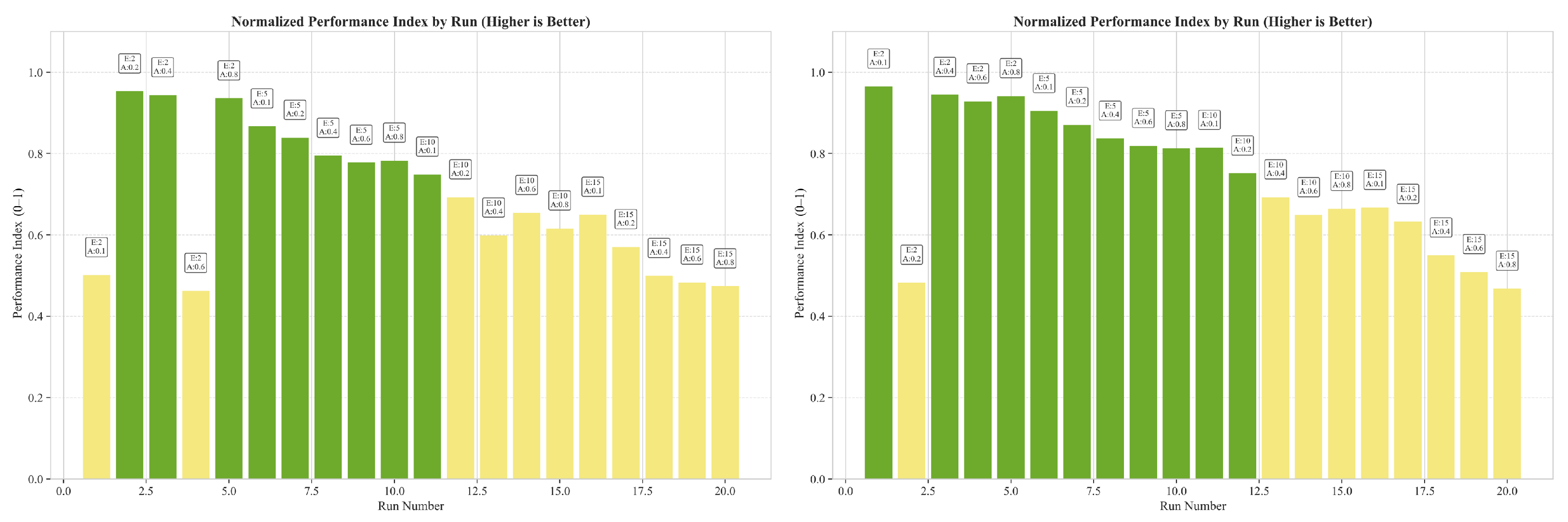
3.6.2. Normalized Performance Index
3.6.3. Performance Optimization Guidelines
3.7. Comparative Analysis of AdaGram with Original AdaGram and BERT Models
Sense Discovery Effectiveness
Representative Word Interpretability
Sense Probability Distributions
Methodological Distinctions
Clustering Granularity
3.8. Alternative AdaGram Implementation
- For “rock”, sense 1 neighbors include general prepositions and articles, but also “sediments” and “marine”, suggesting the geological context. Sense 2, although assigned low probability, shows neighbors like “Sedimentary” and “Metamorphic”, which strongly indicate the geological domain. Interestingly, the music context seems underrepresented in these neighbors.
- For “apple”, sense 1 neighbors clearly indicate the technology company context with terms like “chip”, “macs”, “pay”, and “privacy”. Sense 2 neighbors also relate to the technology company, but with a focus on manufacturing and business aspects (“worker”, “per cent”, “factory”, “Foxconn”). The fruit context appears to be entirely absent.
3.9. Application to Formulas
- Inorganic Chemistry (basic compounds, acids, bases, salts);
- Organic Chemistry (hydrocarbons, functional groups, polymers);
- Biochemistry (amino acids, proteins, nucleic acids, carbohydrates);
- Physical Chemistry (thermodynamics, kinetics, quantum chemistry);
- Analytical Chemistry (solution chemistry, equilibrium constants);
- Electrochemistry (redox reactions, electrochemical cells);
- Nuclear Chemistry (radioactive decay, nuclear reactions);
- Classical Mechanics;
- Thermodynamics;
- Waves and Optics;
- Electricity and Magnetism;
- Modern Physics;
- Quantum Mechanics;
- Mathematical Methods for Physics.
3.10. Chemical Formula Tokenization
- Identification of chemical environments through LaTeX tags (\ce{…});
- Normalization of reaction arrows and operators with appropriate spacing;
- Component isolation via whitespace delimitation;
- Hierarchical parsing of chemical entities:
- Individual elements (e.g., H, Na, Cl);
- Numeric subscripts indicating atomic counts;
- Charge indicators via superscripts;
- Structural groupings within parentheses and brackets.
- Multi-level token extraction (full compounds and their constituent parts);
- Detection of specialized scientific notation beyond standard chemical environments:
- Thermodynamic state functions (H, G, S, U);
- Equilibrium and rate constants (, );
- Electrochemical potentials (, );
- Quantum mechanical operators ();
- Subscripted variables and concentration notation.
Training and Evaluation
3.11. Qualitative Analysis of Learned Senses
- Prototype 1: Strongly associated with acid–base reactions and thermodynamics, as evidenced by neighbors like CH3-SH and CH3-CH2-COOH. This prototype captures the compound’s functional role as a carboxylic acid.
- Prototype 2: Includes neighbors such as Pb, Ba, and X, indicating usage in inorganic or salt-forming reactions. This likely represents CH3COOH in neutralisation reactions with metal ions.
- Prototype 3: Exhibits weaker, less semantically cohesive neighbors but includes entities like CH3-CH2-I and I_0, possibly pointing to its presence in substitution or esterification contexts.
4. Discussion
- (1)
- Structural encoding of subscripts, superscripts, and operators is crucial for semantic interpretation;
- (2)
- Use of mixed notation systems (chemical, mathematical, symbolic);
- (3)
- Domain-specific ambiguity (e.g., H representing hydrogen or enthalpy);
- (4)
5. Conclusions
- A robust framework for testing sense disambiguation;
- An analysis of AdaGram’s sensitivity to parameters such as alpha, epochs, and corpus size;
- Adaptation of the model to LaTeX-encoded formulas and domain-specific scientific notation;
- Empirical evidence that AdaGram captures context-specific meanings when trained on structured or domain-specific corpora.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bartunov, S.; Kondrashkin, D.; Osokin, A.; Vetrov, D.P. Breaking Sticks and Ambiguities with Adaptive Skip-gram. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Cadiz, Spain, 9–11 May 2016. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed Representations of Words and Phrases and Their Compositionality. In Proceedings of the 26th International Conference on Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 5–8 December 2013. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. GloVe: Global Vectors for Word Representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Peters, M.E.; Neumann, M.; Iyyer, M.; Gardner, M.; Clark, C.; Lee, K.; Zettlemoyer, L. Deep Contextualized Word Representations. In Proceedings of the NAACL-HLT 2018, New Orleans, LA, USA, 1–6 June 2018; pp. 2227–2237. [Google Scholar]
- Kageback, M.; Salinas, O.; Hedlund, H.; Mogren, M. Word Sense Disambiguation using a Bidirectional LSTM. In Proceedings of the 5th Workshop on Cognitive Aspects of the Lexicon (CogALex), Osaka, Japan, 12 December 2016. [Google Scholar]
- Neelakantan, A.; Shankar, J.; Passos, A.; McCallum, A. Efficient Non-parametric Estimation of Multiple Embeddings per Word in Vector Space. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Bejgu, A.S.; Barba, E.; Procopio, L.; Fernández-Castro, A.; Navigli, R. Word Sense Linking: Disambiguating Outside the Sandbox. arXiv 2024, arXiv:2412.09370. [Google Scholar]
- Yae, J.H.; Skelly, N.C.; Ranly, N.C.; LaCasse, P.M. Leveraging large language models for word sense disambiguation. Neural Comput. Appl. 2025, 37, 4093–4110. [Google Scholar] [CrossRef]
- Tshitoyan, V.; Dagdelen, J.; Weston, L.; Dunn, B.; Rong, Z.; Kononova, O.; Persson, K.; Ceder, G.; Jain, A. Unsupervised word embeddings capture latent knowledge from materials science literature. Nature 2019, 571, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Melamud, O.; Goldberger, J.; Dagan, I. context2vec: Learning generic context embedding with bidirectional LSTM. In Proceedings of the 20th SIGNLL Conference on Computational Natural Language Learning (CoNLL), Berlin, Germany, 7–12 August 2016; pp. 51–61. [Google Scholar]
- Lee, S.; Kim, J.; Park, S.B. Multi-Sense Embeddings for Language Models and Knowledge Distillation. arXiv 2025, arXiv:2504.06036. [Google Scholar]
- Blevins, T.; Zettlemoyer, L. Moving Down the Long Tail of Word Sense Disambiguation with Gloss-Informed BiEncoders. In Proceedings of the EMNLP, Online, 16–20 November 2020; pp. 1006–1016. [Google Scholar]
- Yuan, X.; Chen, J.; Wang, Y.; Chen, A.; Huang, Y.; Zhao, W.; Yu, S. Semantic-Enhanced Knowledge Graph Completion. Mathematics 2024, 12, 450. [Google Scholar] [CrossRef]
- Vidal, M.; Chudasama, Y.; Huang, H.; Purohit, D.; Torrente, M. Integrating Knowledge Graphs with Symbolic AI: The Path to Interpretable Hybrid AI Systems in Medicine. Web Semant. Sci. Serv. Agents World Wide Web 2025, 84, 100856. [Google Scholar] [CrossRef]
- Sosa, D.N.; Neculae, G.; Fauqueur, J.; Altman, R.B. Elucidating the semantics-topology trade-off for knowledge inference-based pharmacological discovery. J. Biomed. Semant. 2024, 15, 5. [Google Scholar] [CrossRef]
- Bahaj, A.; Ghogho, M. A step towards quantifying, modelling and exploring uncertainty in biomedical knowledge graphs. Comput. Biol. Med. 2025, 184, 109355. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 3–5 June 2019; Association for Computational Linguistics: Stroudsburg, PA, USA; pp. 4171–4186. [Google Scholar]
- Ibrahim, B. Toward a systems-level view of mitotic checkpoints. Prog. Biophys. Mol. Biol. 2015, 117, 217–224. [Google Scholar] [CrossRef]
- Görlich, D.; Escuela, G.; Gruenert, G.; Dittrich, P.; Ibrahim, B. Molecular codes through complex formation in a model of the human inner kinetochore. Biosemiotics 2014, 7, 223–247. [Google Scholar] [CrossRef]
- Lenser, T.; Hinze, T.; Ibrahim, B.; Dittrich, P. Towards evolutionary network reconstruction tools for systems biology. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2007; Volume 4447 LNCS, pp. 132–142. [Google Scholar]
- Ibrahim, B. Dynamics of spindle assembly and position checkpoints: Integrating molecular mechanisms with computational models. Comput. Struct. Biotechnol. J. 2025, 27, 321–332. [Google Scholar] [CrossRef] [PubMed]
- Wulff, D.U.; Mata, R. Semantic embeddings reveal and address taxonomic incommensurability in psychological measurement. Nat. Hum. Behav. 2025, 9, 944–954. [Google Scholar] [CrossRef] [PubMed]
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Hierarchical Dirichlet processes. J. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Beltagy, I.; Lo, K.; Cohan, A. SciBERT: A Pretrained Language Model for Scientific Text. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing, Hong Kong, China, 3–7 November 2019; Association for Computational Linguistics: Stroudsburg, PA, USA; pp. 3615–3620. [Google Scholar]
- Levine, Y.; Schwartz, R.; Berant, J.; Wolf, L.; Shoham, S.; Shlain, M. SenseBERT: Driving Some Sense into BERT. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (ACL), Online, 5–10 July 2020; Association for Computational Linguistics: Stroudsburg, PA, USA; pp. 4656–4667. [Google Scholar]
- Lopuhin, K. Python-Adagram: Python Port of AdaGram. 2016. Available online: https://github.com/lopuhin/python-adagram (accessed on 30 May 2025).
- Chalkidis, I.; Fergadiotis, M.; Malakasiotis, P.; Androutsopoulos, I. LexGLUE: A Benchmark Dataset for Legal Language Understanding in English. Trans. Assoc. Comput. Linguist. 2023, 11, 1181–1198. [Google Scholar]
- Peter, S.; Ibrahim, B. Intuitive Innovation: Unconventional Modeling and Systems Neurology. Mathematics 2024, 12, 3308. [Google Scholar] [CrossRef]
- Ge, L.; He, X.; Liu, L.; Liu, F.; Li, Y. What’s In Your Field? Mapping Scientific Research with Knowledge Graphs and Large Language Models. arXiv 2025, arXiv:2503.09894. [Google Scholar]
- Wellawatte, G.P.; Schwaller, P. Human interpretable structure-property relationships in chemistry using explainable machine learning and large language models. Commun. Chem. 2025, 8, 11. [Google Scholar] [CrossRef]
- Vashishth, S.; Sanyal, S.; Nitin, V.; Talukdar, P. Composition-based Multi-Relational Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Stenetorp, P.; Søgaard, A.; Riedel, S. Lemmatisation in Scientific Texts: Challenges and Perspectives. In Proceedings of the Workshop on Mining Scientific Publications (WOSP), Miyazaki, Japan, 7 May 2018. [Google Scholar]
- Panchenko, A.; Ruppert, E.; Faralli, S.; Ponzetto, S.P.; Biemann, C. Unsupervised does not mean uninterpretable: The case for word sense induction. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing (EMNLP), Copenhagen, Denmark, 9–11 September 2017; pp. 86–98. [Google Scholar]
- Peter, S.; Josephraj, A.; Ibrahim, B. Cell Cycle Complexity: Exploring the Structure of Persistent Subsystems in 414 Models. Biomedicines 2024, 12, 2334. [Google Scholar] [CrossRef]
- Henze, R.; Dittrich, P.; Ibrahim, B. A Dynamical Model for Activating and Silencing the Mitotic Checkpoint. Sci. Rep. 2017, 7, 3865. [Google Scholar] [CrossRef]
- Kim, H.; Tuarob, S.; Giles, C.L. SciKnow: A Framework for Constructing Scientific Knowledge Graphs from Scholarly Literature. In Proceedings of the ACM/IEEE Joint Conference on Digital Libraries (JCDL), Virtual Event, 27–30 September 2021. [Google Scholar]
- Dana, D.; Gadhiya, S.V.; St. Surin, L.G.; Li, D.; Naaz, F.; Ali, Q.; Paka, L.; Yamin, M.A.; Narayan, M.; Goldberg, I.D.; et al. Deep learning in drug discovery and medicine; Scratching the surface. Molecules 2018, 23, 2384. [Google Scholar] [CrossRef]
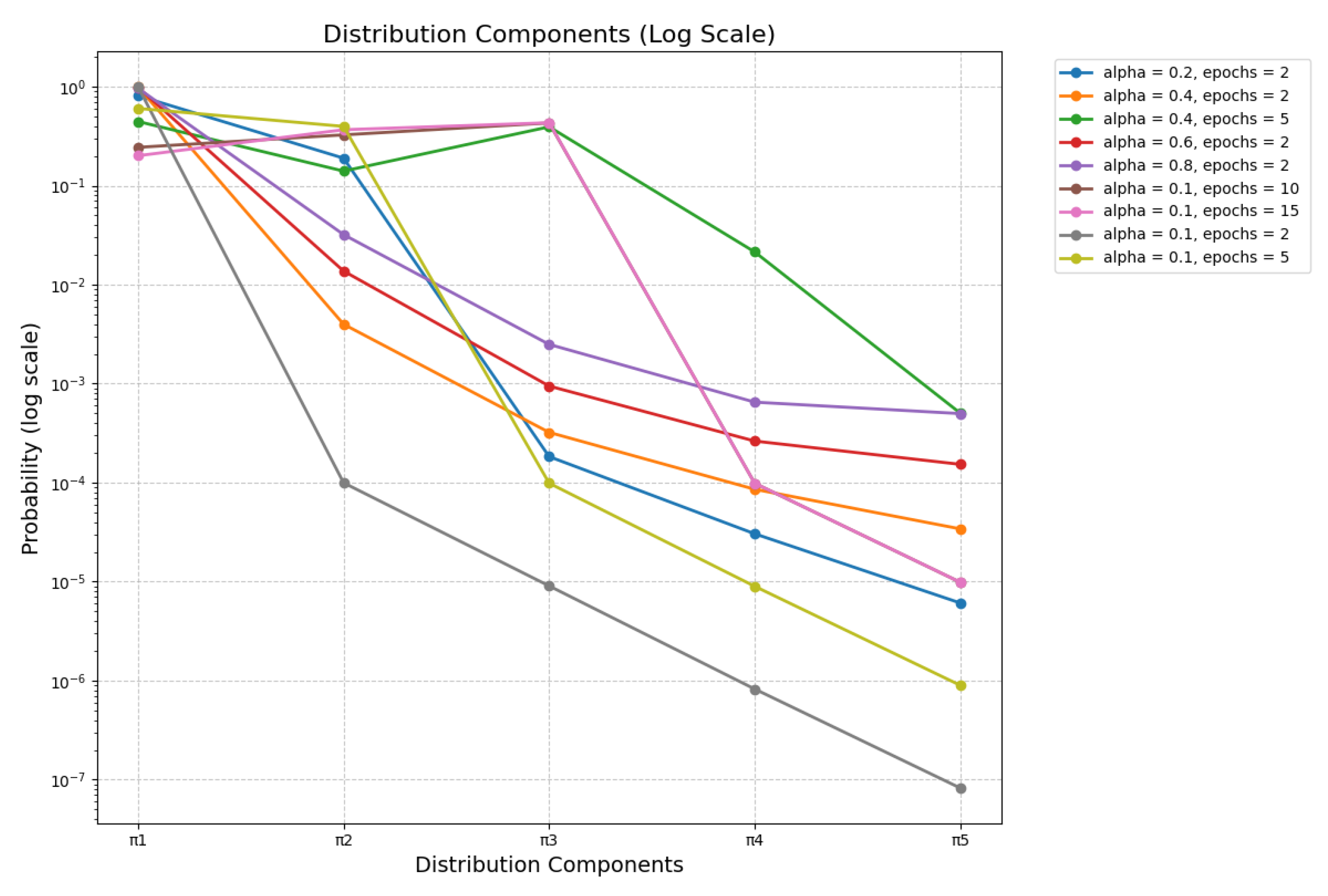
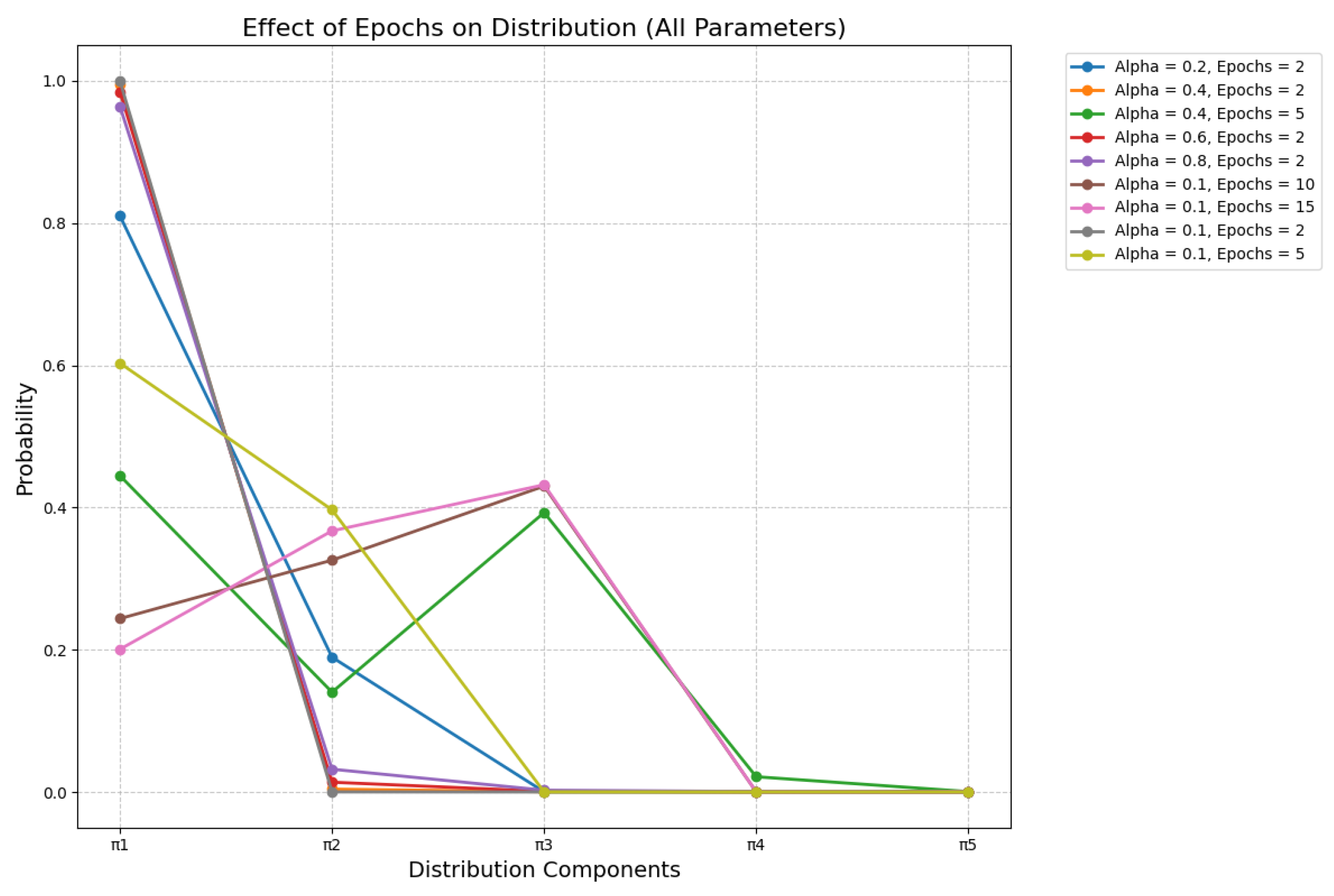
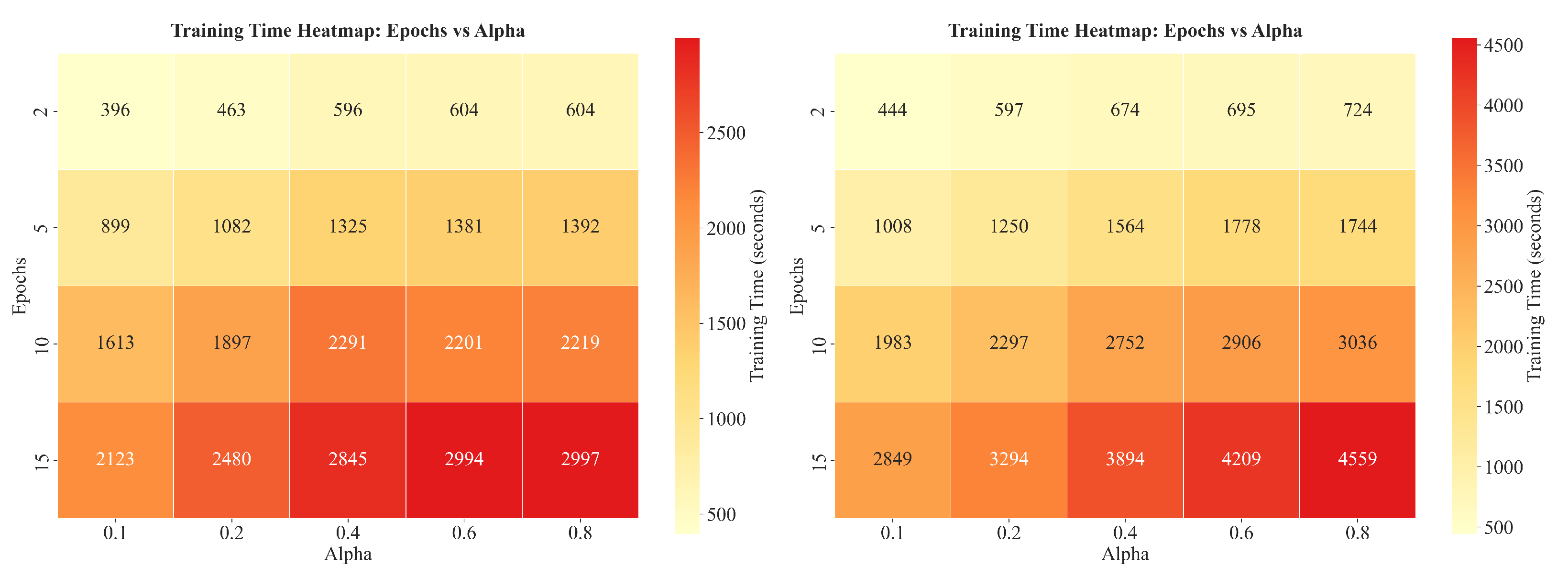
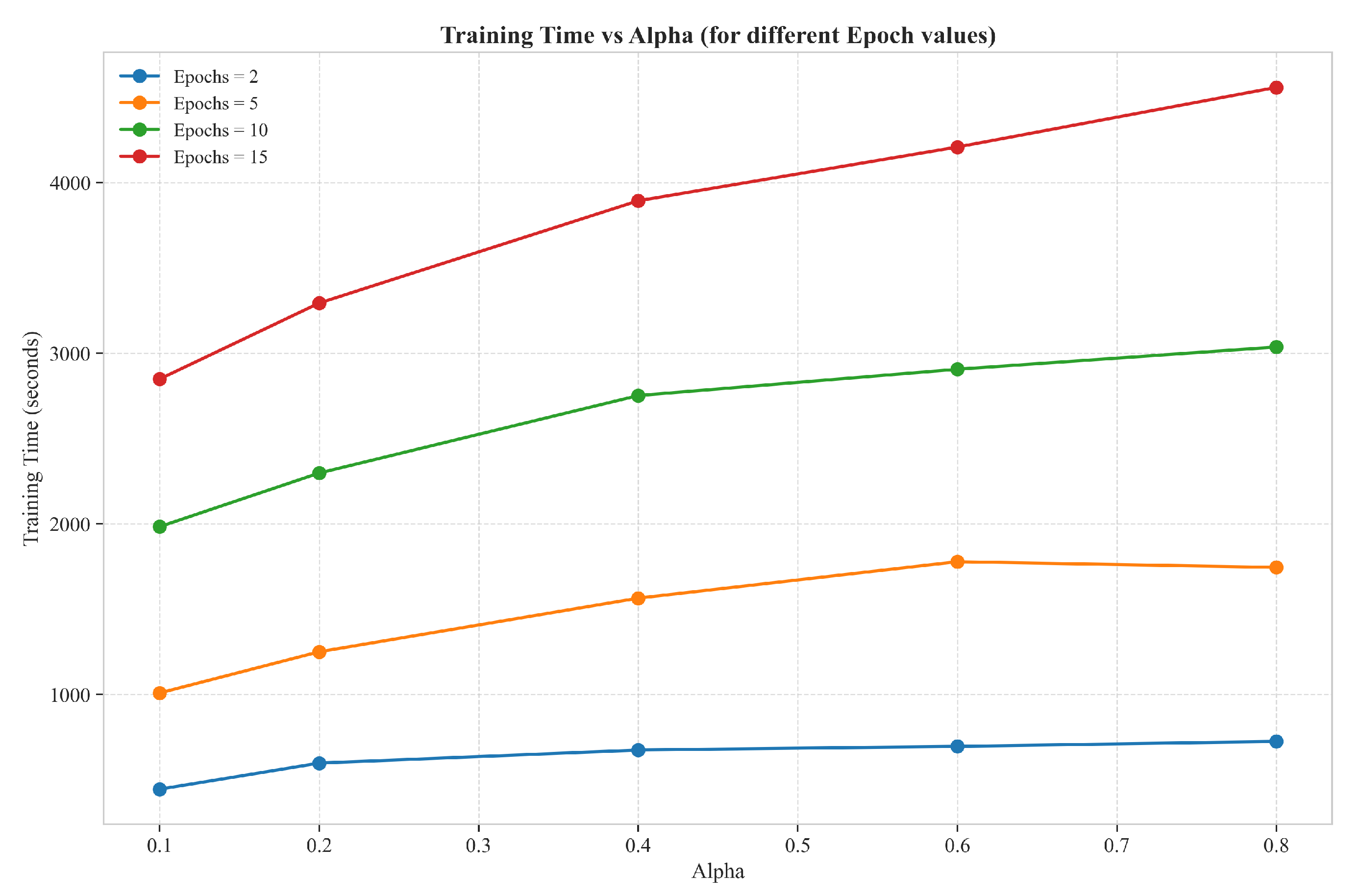
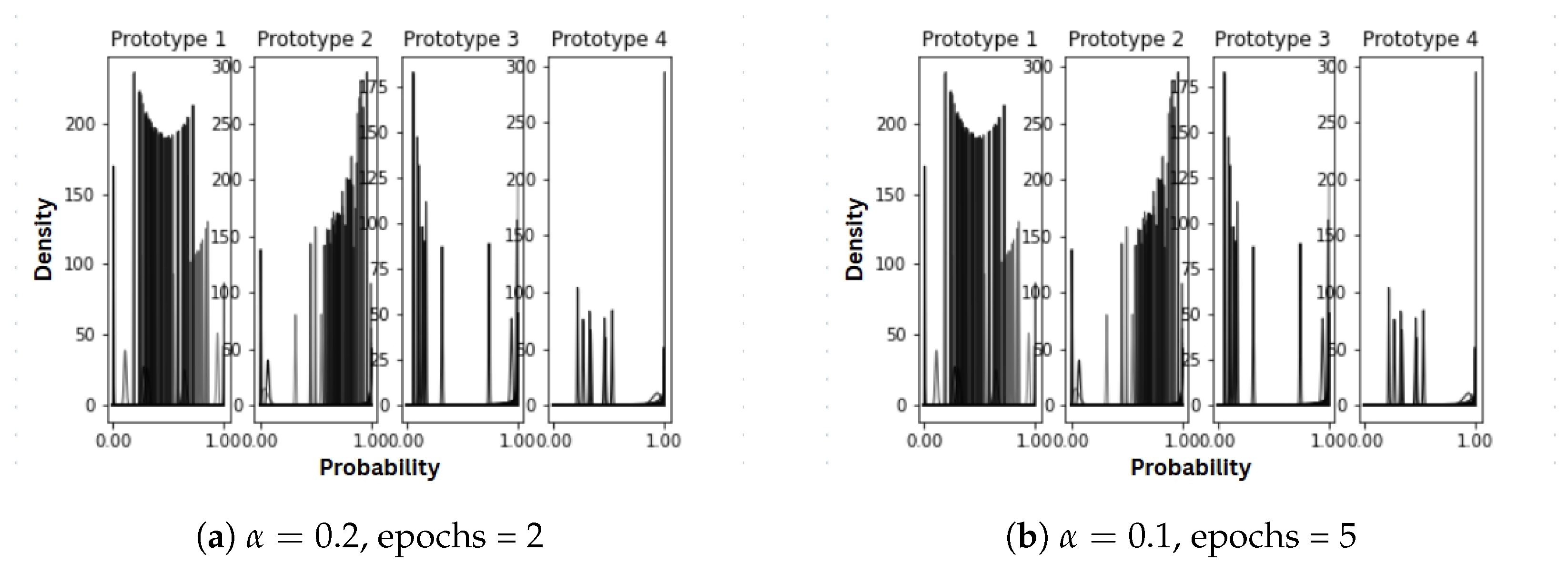
| # | Parameter Values | Music Context for “Rock” | Stone Context for “Rock” |
|---|---|---|---|
| 1 | epochs = 5 | [0.00154198, 0.47751509, 0.17364764, 0.17364764, 0.17364764] | [0.58478621, 0.03064677, 0.12818901, 0.12818901, 0.12818901] |
| 2 | alpha = 0.2, epochs = 2 | [0.00332149, 0.24225809, 0.25147347, 0.25147347, 0.25147347] | [0.79822595, 0.01363814, 0.06271197, 0.06271197, 0.06271197] |
| Word | BERT-BASE-UNCASED | SciBERT | SenseBERT | Python AdaGram | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Senses | Prob | Representative Words | Senses | Prob | Representative Words | Senses | Prob | Representative Words | Senses | Prob | Representative Words | |
| python | 0 | 0.22 | monty, circus, flying | 0 | 0.77 | language, programming, written | 0 | 0.86 | monty, circus, flying | 0 | 0.67 | monty, spamalot, circus |
| 1 | 0.78 | language, programming, written | 1 | 0.23 | mont, circ, flying | 1 | 0.14 | written, language, programming | 1 | 0.22 | ruby, programming, computer | |
| apple | 0 | 0.90 | apples, pine, computer | 0 | 0.91 | ton, mac, computer | 0 | 0.18 | pine, apples, computer | 0 | 0.74 | apples, almong, int |
| 1 | 0.06 | apples, appleton, gate | 1 | 0.09 | mac, computer, int | 1 | 0.82 | apples, appleton, computer | 1 | 0.22 | mac, computer, company | |
| 2 | 0.03 | appleton, released, announced | - | - | - | - | - | - | - | - | - | |
| date | 0 | 0.78 | dates, candidate, dated | 0 | 0.04 | alb, single, best | 0 | 0.15 | candidate, dates, accommodate | 0 | 0.55 | unknown, birth, birthdate |
| 1 | 0.17 | candidate, candidates, party | 1 | 0.42 | candidate, candidates, dates | 1 | 0.85 | candidate, dates, candidates | 1 | 0.28 | deadline, expiry, dates | |
| 2 | 0.05 | candidates, dates, candidate | 2 | 0.50 | candidate, accommodate, dates | - | - | - | - | - | - | |
| - | - | - | 3 | 0.04 | dates, candidate, candidates | - | - | - | - | - | - | |
| bow | 0 | 0.83 | bowl, bowling, bowler | 0 | 0.55 | ling, rainbow, elbow | 0 | 0.11 | bowling, bowl, rainbow | 0 | 0.67 | bowling, bowler, rainbow |
| 1 | 0.17 | bowl, super, rose | 1 | 0.45 | super, ler, ling | 1 | 0.89 | bowl, bowling, super | 1 | 0.21 | bows, crossbow, arrows | |
| mass | 0 | 0.09 | massachusetts, boston, born | 0 | 0.88 | massive, massachusetts, acr | 0 | 0.85 | massachusetts, massive, massacre | 0 | 0.54 | massachusetts, street, cambridge |
| 1 | 0.91 | massive, massachusetts, massacre | 1 | 0.12 | massachusetts, boston, cambridge | 1 | 0.15 | massachusetts, massive, well | 1 | 0.35 | masses, liturgy | |
| run | 0 | 0.04 | home, runs, average | 0 | 0.42 | runs, running, home | 0 | 0.82 | runs, running, home | 0 | 0.80 | distance, yard, long |
| 1 | 0.96 | running, runs, runner | 1 | 0.04 | running, brun, runs | 1 | 0.18 | drive, go, running | - | - | - | |
| - | - | - | 2 | 0.54 | running, runs, brun | - | - | - | - | - | - | |
| net | 0 | 0.20 | netherlands, internet, network | 0 | 0.84 | network, inet, internet | 0 | 0.21 | netherlands, internet, network | 0 | 0.56 | network, internet, cabinet |
| 1 | 0.74 | network, internet, networks | 1 | 0.16 | netherlands, internet, network | 1 | 0.79 | network, internet, planet | 1 | 0.28 | pretax, billion | |
| 2 | 0.06 | nonetheless, network, internet | - | - | - | - | - | - | - | - | - | |
| fox | 0 | 0.91 | news, century, foxes | 0 | 0.46 | century, red, star | 0 | 0.85 | news, century, foxes | 0 | 0.62 | raccoon, wolf, deer |
| 1 | 0.09 | also, news, sports | 1 | 0.46 | news, network, sports | 1 | 0.15 | century, news, network | 1 | 0.30 | cbs, news, network | |
| - | - | - | 2 | 0.07 | news, sports, cnn | - | - | - | - | - | - | |
| rock | 0 | 0.05 | brock, rocks, rocky | 0 | 0.41 | rocks, roll, band | 0 | 0.86 | band, rocks, rocket | 0 | 0.60 | band, hardcore, alternative |
| 1 | 0.18 | band, punk, album | 1 | 0.59 | band, rocks, pun | 1 | 0.14 | rocky, band, rocks | 1 | 0.34 | little, big, arkansas | |
| 2 | 0.77 | rocks, rocket, rocky | - | - | - | - | - | - | - | - | - | |
| Word | Sense | Neighbor | Similarity |
|---|---|---|---|
| rock (sense 1) | 1 | to | 0.97288334 |
| 2 | a | 0.96953523 | |
| 3 | can | 0.96885000 | |
| 4 | or | 0.96202683 | |
| 5 | by | 0.96151120 | |
| rock (sense 2) | 1 | result | 0.20526096 |
| 2 | be | 0.18441030 | |
| 3 | rocks | 0.17854585 | |
| 4 | Sedimentary | 0.17192839 | |
| 5 | Metamorphic | 0.17153698 | |
| apple (sense 1) | 1 | chip | 0.97865150 |
| 2 | macs | 0.97675880 | |
| 3 | news | 0.97318244 | |
| 4 | pay | 0.97118530 | |
| 5 | wall | 0.95527303 | |
| apple (sense 2) | 1 | worker | 0.21021016 |
| 2 | percent | 0.18436478 | |
| 3 | digital | 0.15734635 | |
| 4 | tech | 0.15344201 | |
| 5 | factory | 0.14395784 |
| Feature | Our Implementation | Lopuhin Implementation |
|---|---|---|
| Multiple senses detected | Yes (with tuned parameters) | No (with default parameters) |
| Distinct contexts identified | Yes | Partial (biased to single context) |
| Parameter sensitivity | High | Likely high (not explicitly tested) |
| Performance on small corpora | Requires parameter tuning | Requires parameter tuning |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arokiaraj, A.J.; Ibrahim, S.; Then, A.; Ibrahim, B.; Peter, S. AdaGram in Python: An AI Framework for Multi-Sense Embedding in Text and Scientific Formulas. Mathematics 2025, 13, 2241. https://doi.org/10.3390/math13142241
Arokiaraj AJ, Ibrahim S, Then A, Ibrahim B, Peter S. AdaGram in Python: An AI Framework for Multi-Sense Embedding in Text and Scientific Formulas. Mathematics. 2025; 13(14):2241. https://doi.org/10.3390/math13142241
Chicago/Turabian StyleArokiaraj, Arun Josephraj, Samah Ibrahim, André Then, Bashar Ibrahim, and Stephan Peter. 2025. "AdaGram in Python: An AI Framework for Multi-Sense Embedding in Text and Scientific Formulas" Mathematics 13, no. 14: 2241. https://doi.org/10.3390/math13142241
APA StyleArokiaraj, A. J., Ibrahim, S., Then, A., Ibrahim, B., & Peter, S. (2025). AdaGram in Python: An AI Framework for Multi-Sense Embedding in Text and Scientific Formulas. Mathematics, 13(14), 2241. https://doi.org/10.3390/math13142241








