Examining Marital Infidelity via Game Theory
Abstract
1. Introduction
2. Literature Review and Theoretical Framework
2.1. Empirical Mechanisms and Motivations
2.2. Theoretical Models, Methodologies, and Gaps
- (1)
- Bilateral and Continuous Monitoring: We explicitly model mutual surveillance by both spouses, allowing for continuous variation in monitoring efforts and thus reflecting more realistic relational dynamics.
- (2)
- Quadratic Psychological Cost Structure: Our model introduces a quadratic monitoring cost function, grounded in empirical psychological and behavioral research, to capture the increasing emotional burdens associated with intensified surveillance.
- (3)
- Comprehensive Equilibrium Analysis: By identifying both pure and mixed-strategy Nash equilibria, our model offers a nuanced and generalizable analysis of marital decision-making, applicable across a broad spectrum of relationship contexts.
- (4)
- Behaviorally Informed Theoretical Integration: While our model remains theoretical, its structural assumptions are explicitly informed by empirical findings regarding the psychological consequences of surveillance and betrayal within intimate relationships.
3. General Model Framework
- γ (gamma) represents the benefit derived from engaging in infidelity without detection. A higher γ implies a stronger incentive to cheat, as the utility from undetected infidelity rises.
- ζ (zeta) is the cost coefficient for monitoring effort. Higher values of ζ indicate more significant psychological and emotional costs associated with monitoring behaviors, thus deterring excessive surveillance.
4. Results
4.1. Pure-Strategy Nash Equilibrium (PSNE)
4.2. Mixed-Strategy Nash Equilibrium (MSNE)
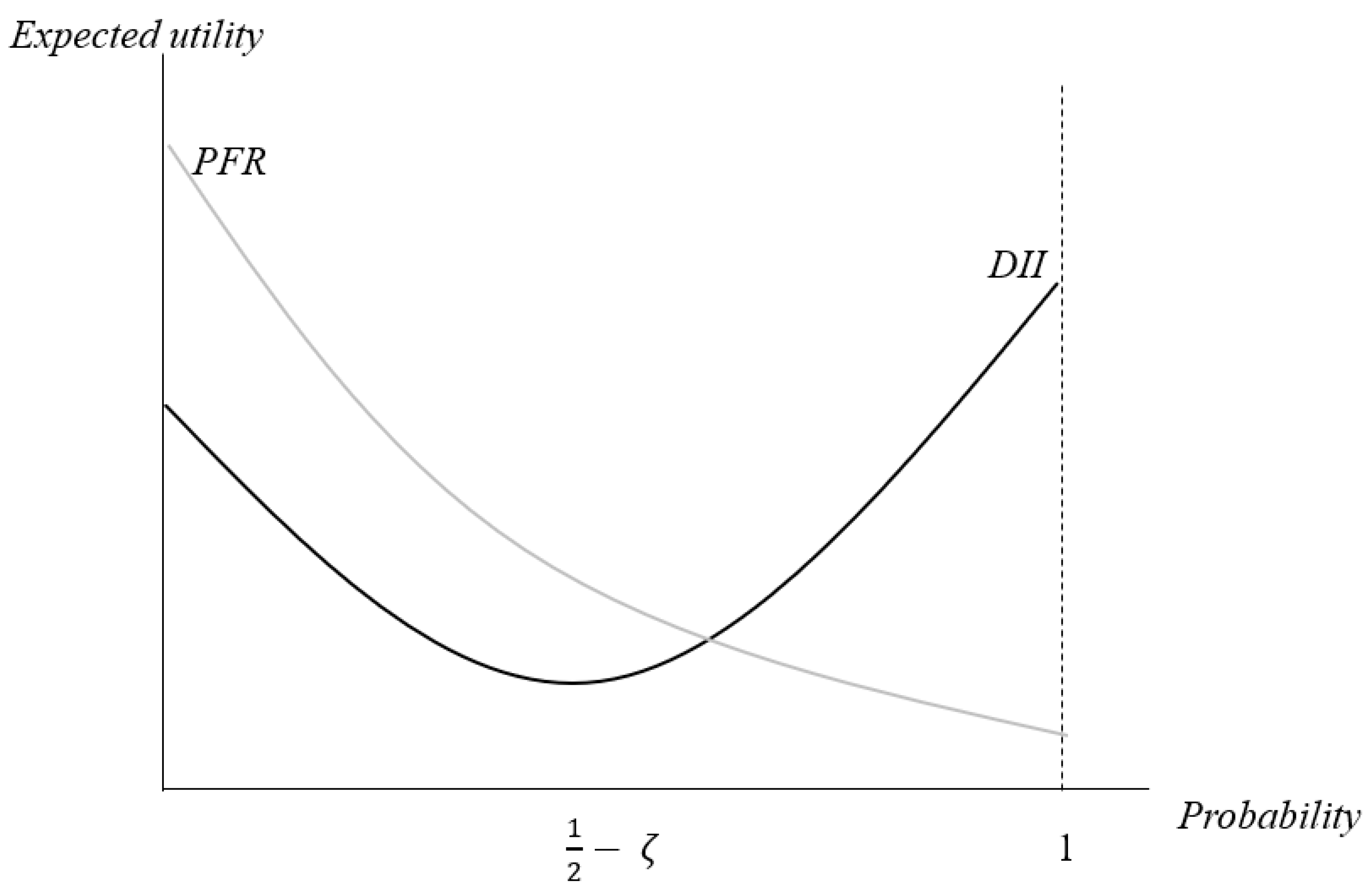
4.3. Interpretation of Equilibrium Dynamics
4.4. Sensitivity Analysis
4.4.1. Sensitivity of the Equilibrium Probability to Monitoring Costs
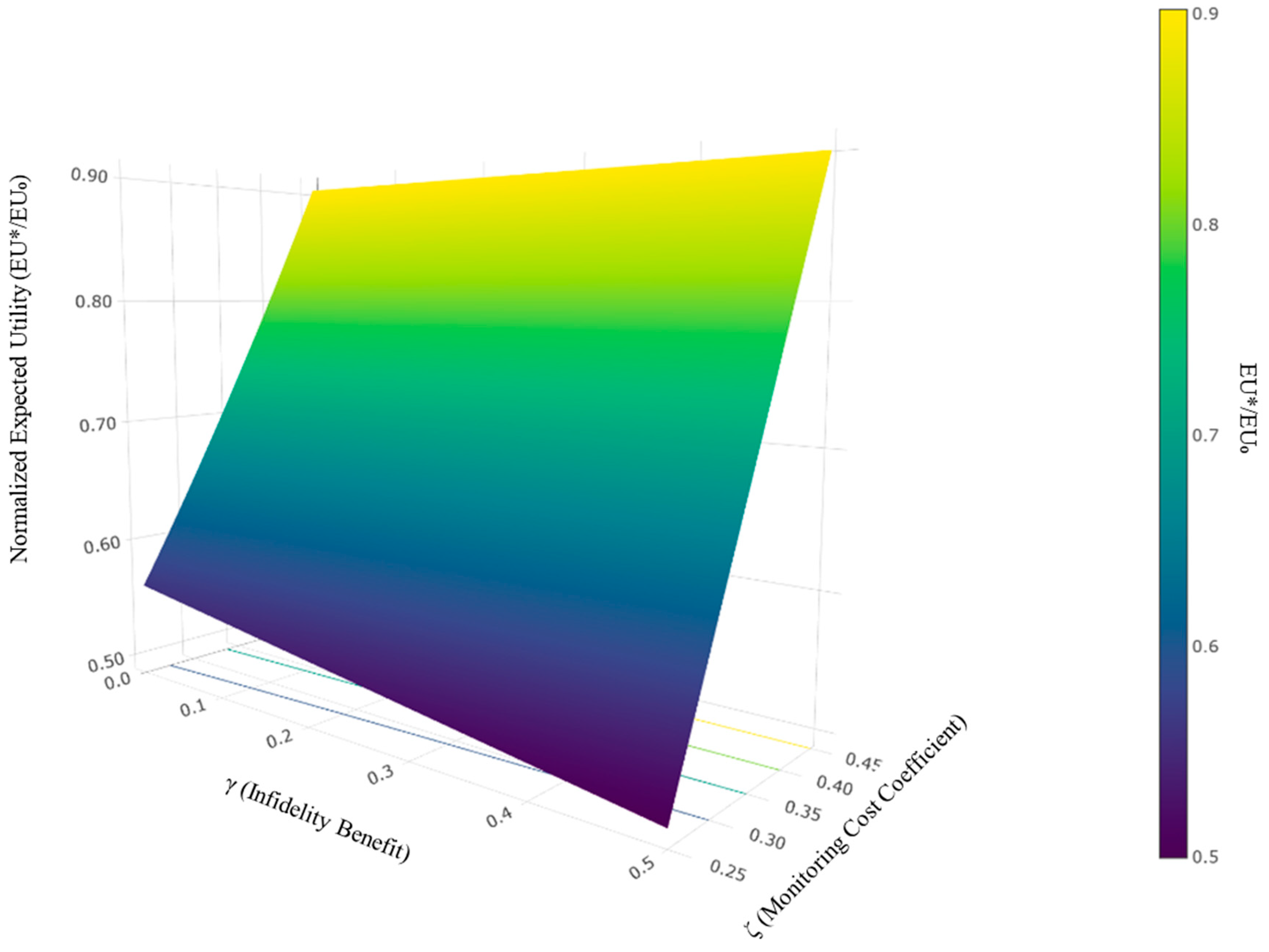
4.4.2. Sensitivity of the Expected Utility to Infidelity Benefits
4.4.3. Sensitivity of the Expected Utility to Monitoring Costs
4.4.4. Implications for Model Dynamics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chou, E.Y.; Hsu, D.Y.; Myung, N. Cheaters, liars, and thieves: Deception and trust restoration in organizations. Organ. Behav. Hum. Decis. Process. 2022, 168, 104128. [Google Scholar]
- Dunning, D.; Fetchenhauer, D.; Schlösser, T. Why people trust: Solved puzzle and open mysteries. Curr. Dir. Psychol. Sci. 2019, 28, 366–371. [Google Scholar] [CrossRef]
- Bohnet, I.; Zeckhauser, R. Trust, risk, and betrayal. J. Econ. Behav. Organ. 2004, 55, 467–484. [Google Scholar] [CrossRef]
- Effron, D.A.; Miller, D.T. Diffusion of entitlement: An inhibitory effect of observing another person’s actions on moral judgments. J. Exp. Soc. Psychol. 2011, 47, 343–348. [Google Scholar] [CrossRef]
- Fudenberg, D.; Tirole, J. Game Theory; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Jordan, J.J.; Rand, D.G. Signaling when no one is watching: A reputational heuristics account of outrage and punishment in one-shot anonymous interactions. J. Behav. Decis. Mak. 2020, 33, 234–249. [Google Scholar] [CrossRef]
- Batabyal, A.A.; Beladi, H. Cheating on your spouse: A game-theoretic analysis. SSRN Electron. J. 2016. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2889055 (accessed on 23 March 2025). [CrossRef]
- Schweitzer, M.E.; Hershey, J.C.; Bradlow, E.T. Promises and lies: Restoring violated trust. Organ. Behav. Hum. Decis. Process. 2006, 101, 1–19. [Google Scholar] [CrossRef]
- Batabyal, A.A. Marital infidelity: A game-theoretic analysis. J. Quant. Econ. 2018, 16, 315–330. [Google Scholar] [CrossRef]
- Fincham, F.D.; May, R.W. Infidelity in romantic relationships. Curr. Opin. Psychol. 2017, 13, 70–74. [Google Scholar] [CrossRef]
- Luo, W.; Yu, J. Sexual infidelity among the married in China. Chin. J. Sociol. 2022, 8, 275–296. [Google Scholar] [CrossRef]
- Vowels, L.M.; Vowels, M.J.; Mark, K.P. Is infidelity predictable? Using explainable machine learning to identify the most important predictors of infidelity. J. Sex Res. 2022, 59, 359–374. [Google Scholar] [CrossRef] [PubMed]
- Fye, M.A.; Mims, G.A. Preventing infidelity: A theory of protective factors. Fam. J. 2019, 27, 405–413. [Google Scholar] [CrossRef]
- McNulty, J.K.; Meltzer, A.L.; Makhanova, A.; Maner, J.K. The implications of short-term mating motivations for marital commitment and satisfaction. J. Personal. Soc. Psychol. 2018, 115, 769–786. [Google Scholar]
- Fincham, F.D.; Demirtaş, E.T. Dating infidelity in Turkish couples: The role of attitudes and intentions. J. Sex Res. 2017, 54, 1120–1130. [Google Scholar]
- Munsch, C.L. Her support, his support: Money, masculinity, and marital infidelity. Am. Sociol. Rev. 2015, 80, 469–495. [Google Scholar] [CrossRef]
- Khaneghahi, S.; Poorjanebollahi, M.F. Effectiveness of acceptance and commitment-based couple therapy on communication patterns and marital infidelity in married individuals. Appl. Fam. Ther. J. 2024, 6, 115–130. [Google Scholar] [CrossRef]
- Hertlein, K.M.; Piercy, F.P. Internet infidelity: A critical review of the literature. Fam. J. 2006, 14, 366–371. [Google Scholar] [CrossRef]
- Adamopoulou, E. New facts on infidelity. Econ. Lett. 2013, 121, 458–462. [Google Scholar] [CrossRef]
- Shackelford, T.K.; Goetz, A.T. Detecting and responding to male infidelity. Personal. Individ. Differ. 2006, 41, 1303–1311. [Google Scholar]
- Vaterlaus, J.M.; Frantz, K. Toward an understanding of the use of dating applications as a form of infidelity. Comput. Hum. Behav. 2018, 101, 28–34. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Blow, A.J.; Hartnett, K. Infidelity in committed relationships: A methodological review. J. Marital Fam. Ther. 2005, 31, 183–216. [Google Scholar] [CrossRef] [PubMed]
- Mark, K.P.; Janssen, E.; Milhausen, R.R. Infidelity in heterosexual couples: Demographic, interpersonal, and personality-related predictors of extradyadic sex. Arch. Sex. Behav. 2011, 40, 971–982. [Google Scholar] [CrossRef] [PubMed]
- Chiappori, P.A.; Salanié, B. The economics of matching: A survey. Annu. Rev. Econ. 2016, 8, 227–247. [Google Scholar]
- Fisher, A.D.; Corona, G.; Bandini, E.; Mannucci, E.; Lotti, F.; Boddi, V.; Forti, G.; Maggi, M. Psychobiological correlates of extramarital affairs and differences between stable and occasional infidelity among men with sexual dysfunctions. J. Sex. Med. 2009, 6, 866–875. [Google Scholar] [CrossRef]
- Lisman, C.G.; Holman, A.C. Cheating under the circumstances in marital relationships: The development and examination of the propensity towards infidelity scale. Soc. Sci. 2021, 10, 392. [Google Scholar] [CrossRef]
- Selterman, D.; Garcia, J.R.; Tsapelas, I. What’s so bad about a little betrayal? Relationship closeness, betrayal severity, and infidelity. Pers. Relatsh. 2021, 28, 1052–1070. [Google Scholar]
- Fair, R.C. A theory of extramarital affairs. J. Political Econ. 1978, 86, 45–61. [Google Scholar] [CrossRef]
- Cameron, S. The economics of partner out-trading in sexual markets. J. Bioecon. 2002, 4, 195–222. [Google Scholar] [CrossRef]
- Smith, I. Reinterpreting the economics of extramarital affairs. Rev. Econ. Househ. 2011, 10, 319–343. [Google Scholar] [CrossRef]
- Elmslie, B.; Tebaldi, E. So, what did you do last night? The economics of infidelity. Kyklos 2008, 61, 391–410. [Google Scholar] [CrossRef]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Conroy-Beam, D.; Goetz, C.D.; Buss, D.M. Why do humans form long-term mateships? An evolutionary game-theoretic model. Adv. Exp. Soc. Psychol. 2015, 51, 1–39. [Google Scholar]
- Sohn, K. Why are there singles: Being single in equilibrium as a partner discipline device. Econ. Bull. 2008, 10, 1–6. [Google Scholar]
- Buss, D.M.; Shackelford, T.K. Susceptibility to infidelity in the first year of marriage. J. Res. Personal. 1997, 31, 193–221. [Google Scholar] [CrossRef]
- Becker, G.S. A theory of marriage: Part I. J. Political Econ. 1973, 81, 813–846. [Google Scholar] [CrossRef]
- Cashel-Cordo, P.; Friesner, D. A Game Theoretic Model of Marital Infidelity and Divorce in the Presence of Sexually Transmitted Diseases: Implications for Social Welfare and Public Policy. In Proceedings of the Midwest Business Economics Association, St. Louis, MI, USA, 5–7 November 2004. [Google Scholar]
- Derlega, V.J.; Winstead, B.A.; Mathews, A.; Braitman, A.L. Why does someone reveal highly personal information? Attributions for and against self-disclosure in close relationships. Commun. Res. Rep. 2008, 25, 115–130. [Google Scholar] [CrossRef]
- Fox, J.; Moreland, J.J. The dark side of social networking sites: An exploration of the relational and psychological stressors associated with Facebook use and affordances. Comput. Hum. Behav. 2015, 45, 168–176. [Google Scholar] [CrossRef]
- Tokunaga, R.S. Social networking site or social surveillance site? Understanding the use of interpersonal electronic surveillance in romantic relationships. Comput. Hum. Behav. 2011, 27, 705–713. [Google Scholar] [CrossRef]
- Rusbult, C.E.; Van Lange, P.A.M. Interdependence, interaction, and relationships. Annu. Rev. Psychol. 2003, 54, 351–375. [Google Scholar] [CrossRef]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Simon, H.A. A behavioral model of rational choice. Q. J. Econ. 1955, 69, 99–118. [Google Scholar] [CrossRef]
- Williamson, O.E. Assessing contract. J. Law Econ. Organ. 1985, 1, 177–208. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. In Handbook of the Fundamentals of Financial Decision Making: Part II; The Econometric Society: New Haven, CT, USA, 2013; pp. 99–127. [Google Scholar]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Fincham, F.D.; Beach, S.R.H. Marriage in the new millennium: A decade in review. J. Marriage Fam. 2010, 72, 630–649. [Google Scholar] [CrossRef]
- Gottman, J. What Predicts Divorce? Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1994. [Google Scholar]
- Gottman, J. The Seven Principles for Making Marriage Work; Hachette: London, UK, 2018. [Google Scholar]
- Camerer, C. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Tversky, A.; Kahneman, D. The framing of decisions and the psychology of choice. Science 1981, 211, 453–458. [Google Scholar] [CrossRef]
- Kollock, P. Social dilemmas: The anatomy of cooperation. Annu. Rev. Sociol. 1998, 24, 183–214. [Google Scholar] [CrossRef]
- Binmore, K. Modeling rational players: Part I. Econ. Philos. 1987, 3, 179–214. [Google Scholar] [CrossRef]
- Becker, G.S. A Treatise on the Family: Enlarged Edition; Harvard University Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Crawford, V.P.; Sobel, J. Strategic information transmission. Econometrica 1982, 50, 1431–1451. [Google Scholar] [CrossRef]
- Gottman, J.; Levenson, R.W. The timing of divorce: Predicting when a couple will divorce over a 14-year period. J. Marriage Fam. 2000, 62, 737–745. [Google Scholar] [CrossRef]
- Stanley, S.M.; Markman, H.J.; Whitton, S.W. Communication, conflict, and commitment: Insights on the foundations of relationship success from a national survey. Fam. Process 2002, 41, 659–675. [Google Scholar] [CrossRef]
- Myerson, R.B. Game Theory; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Simpson, J.A.; Rholes, W.S. Adult attachment orientations, stress, and romantic relationships. Adv. Exp. Soc. Psychol. 2012, 45, 279–328. [Google Scholar]
- Joel, S.; Eastwick, P.W.; Finkel, E.J. Is romantic desire predictable? Machine learning applied to initial romantic attraction. Psychol. Sci. 2017, 28, 1478–1489. [Google Scholar] [CrossRef] [PubMed]
- Drigotas, S.M.; Safstrom, C.A.; Gentilia, T. An investment model prediction of dating infidelity. J. Personal. Soc. Psychol. 1999, 77, 509–524. [Google Scholar] [CrossRef]
- Rusbult, C.E.; Buunk, B.P. Commitment processes in close relationships: An interdependence analysis. J. Soc. Pers. Relatsh. 1993, 10, 175–204. [Google Scholar] [CrossRef]
- Finkel, E.J.; Hui, C.M.; Carswell, K.L.; Larson, G.M. The suffocation of marriage: Climbing Mount Maslow without enough oxygen. Psychol. Inq. 2014, 25, 1–41. [Google Scholar] [CrossRef]
- Mesterton-Gibbons, M. An Introduction to Game-Theoretic Modelling; American Mathematical Society: Providence, RI, USA, 2019; Volume 37. [Google Scholar]
- Johnson, S.M. Attachment Theory in Practice: Emotionally Focused Therapy (EFT) with Individuals, Couples, and Families; Guilford Press: New York, NY, USA, 2019. [Google Scholar]
- Johnson, S. Love Sense: The Revolutionary New Science of Romantic Relationships; Hachette: New York, NY, USA, 2013. [Google Scholar]
- Doherty, W. Infidelity: A clinical and theoretical review. J. Marital Fam. Ther. 2020, 46, 203–217. [Google Scholar]
- Markman, H.J.; Rhoades, G.K.; Stanley, S.M.; Ragan, E.P.; Whitton, S.W. The premarital communication roots of marital distress and divorce: The first five years of marriage. J. Fam. Psychol. 2010, 24, 289–298. [Google Scholar] [CrossRef]
| Effect on Infidelity | Mechanism/Motivation | |
|---|---|---|
| McNulty et al. (2018) [14]; Fincham and May (2017) [10] | Increases likelihood due to unmet emotional/sexual needs | Relationship dissatisfaction |
| Vowels et al. (2022) [12] | Predicts future infidelity via reduced guilt or commitment | Prior infidelity |
| Munsch (2015) [16]; Adamopoulou (2013) [19] | Financial stress or opportunity costs affect cheating likelihood | Economic conditions |
| Vowels et al. (2022) [12]; Shackelford and Goetz (2006) [20] | Facilitates or discourages infidelity through peer dynamics | Social network influence |
| Hertlein and Piercy (2006) [18]; Vaterlaus and Frantz (2018) [21] | Enables new forms of infidelity (e.g., cyber-infidelity) | Digital technology usage |
| Interpretation | Mathematical Expression | Model Component |
|---|---|---|
| Net benefit from staying faithful under monitoring | Base utility—monitoring cost | Utility from infidelity |
| Expected gains from undetected infidelity | Benefit γ adjusted for detection risk | Utility from infidelity |
| Costs increase non-linearly with surveillance intensity | Quadratic cost function ζ·m2 | Monitoring costs |
| Best response functions indicating equilibrium effort | Derived from FOCs of utility function | Optimal monitoring effort |
| Stable strategic outcomes in marital interactions | Pure or mixed-strategy Nash equilibrium | Nash equilibrium type |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonen, L.D.; Tavor, T.; Spiegel, U. Examining Marital Infidelity via Game Theory. Mathematics 2025, 13, 2235. https://doi.org/10.3390/math13142235
Gonen LD, Tavor T, Spiegel U. Examining Marital Infidelity via Game Theory. Mathematics. 2025; 13(14):2235. https://doi.org/10.3390/math13142235
Chicago/Turabian StyleGonen, Limor Dina, Tchai Tavor, and Uriel Spiegel. 2025. "Examining Marital Infidelity via Game Theory" Mathematics 13, no. 14: 2235. https://doi.org/10.3390/math13142235
APA StyleGonen, L. D., Tavor, T., & Spiegel, U. (2025). Examining Marital Infidelity via Game Theory. Mathematics, 13(14), 2235. https://doi.org/10.3390/math13142235








