Differential Mechanical and Biological Contributions to Bone Mass Distribution—Insights from a Computational Model of the Human Femur
Abstract
1. Introduction
2. Materials and Methods
2.1. Femur Geometry
2.2. Bone Remodeling Model
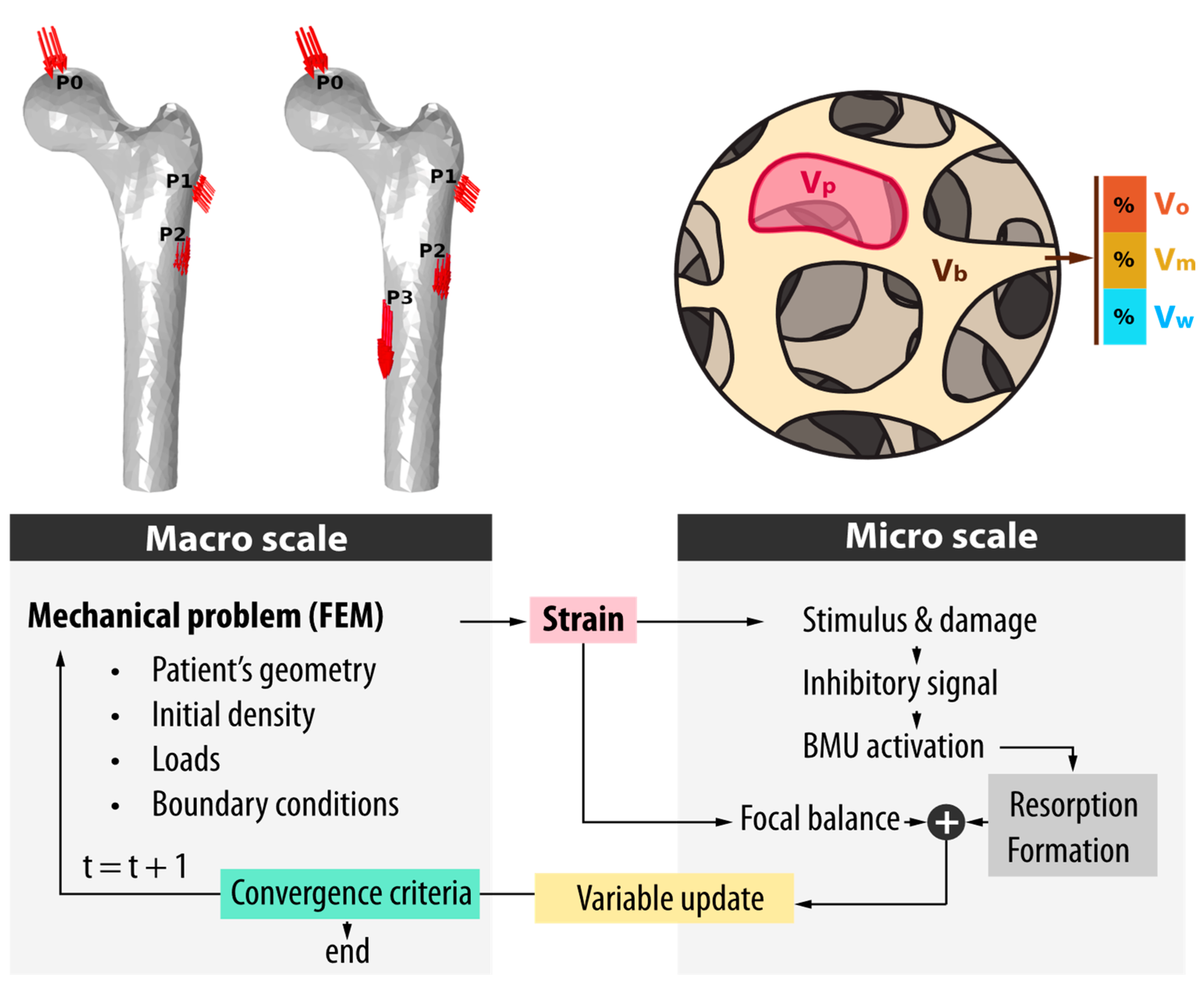
2.3. Mechanical Model
2.4. Bone Density Initialization
2.4.1. CT-Approach: Internal Bone Reconstruction Through CT-Image Segmentation
2.4.2. Homogeneous Approach: Internal Bone Reconstruction Through a Purely Mechano-Biological Method
3. Results
3.1. Normal Loads
3.2. Disuse and Microgravity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, M.R.; Burr, D.B. Bone Modeling and Remodeling. Basic Appl. Bone Biol. 2013, 75–90. [Google Scholar] [CrossRef]
- Cowin, S.C.; Hegedus, D.H. Bone remodeling: A theory of adaptive elasticity. J. Elast. 1976, 6, 313–326. [Google Scholar] [CrossRef]
- Beaupré, G.S.; Orr, T.E.; Carter, D.R. An approach for time-dependent bone modeling and remodeling-application: A preliminary remodeling simulation. J. Orthop. Res. 1990, 8, 662–670. [Google Scholar] [CrossRef] [PubMed]
- Coelho, P.G.; Fernandes, P.R.; Rodrigues, H.C.; Cardoso, J.B.; Guedes, J.M. Numerical modeling of bone tissue adaptation-A hierarchical approach for bone apparent density and trabecular structure. J. Biomech. 2009, 42, 830–837. [Google Scholar] [CrossRef]
- Doblaré, M.; García, J.M. Application of an anisotropic bone-remodelling model based on a damage-repair theory to the analysis of the proximal femur before and after total hip replacement. J. Biomech. 2001, 34, 1157–1170. [Google Scholar] [CrossRef] [PubMed]
- Doblaré, M.; García, J.M. Anisotropic bone remodelling model based on a continuum damage-repair theory. J. Biomech. 2002, 35, 1–17. [Google Scholar] [CrossRef] [PubMed]
- García-Aznar, J.M.; Rueberg, T.; Doblare, M. A bone remodelling model coupling microdamage growth and repair by 3D BMU-activity. Biomech. Model. Mechanobiol. 2005, 4, 147–167. [Google Scholar] [CrossRef]
- Martínez-Reina, J.; Reina, I.; Domínguez, J.; García-Aznar, J.M. A bone remodelling model including the effect of damage on the steering of BMUs. J. Mech. Behav. Biomed. Mater. 2014, 32, 99–112. [Google Scholar] [CrossRef]
- Martínez-Reina, J.; Ojeda, J.; Mayo, J. On the use of bone remodelling models to estimate the density distribution of bones uniqueness of the solution. PLoS ONE 2016, 11, e0148603. [Google Scholar] [CrossRef]
- Berli, M. Computational Implementation of a New Bone Resorption Strategy Oriented to the Study of the Action of Multicellular Basic Units. Application to the Process of Human Bone Remodeling; National University of Entre Ríos: Concepción del Uruguay, Argentina, 2020. [Google Scholar]
- Berli, M.; Franco, F.; Di Paolo, J.; Zioupos, P.; Borau, C. The interplay between BMU activity linked to mechanical stress, specific surface and inhibitory theory dictate bone mass distribution: Predictions from a 3D computational model. Comput. Biol. Med. 2022, 148, 1–10. [Google Scholar] [CrossRef]
- Franco, F.; Borau Zamora, C.; Campana, D.M.; Berli, M.E. Computational Analysis of the Influence of Menopause and Ageing on Bone Mineral Density, Exploring the Impact of Bone Turnover and Focal Bone Balance—A Study on Overload and Underload Scenarios. Life 2023, 13, 2155. [Google Scholar] [CrossRef] [PubMed]
- Bahia, M.T.; Hecke, M.B.; Mercuri, E.G.F. Image-based anatomical reconstruction and pharmaco-mediated bone remodeling model applied to a femur with subtrochanteric fracture: A subject-specific finite element study. Med. Eng. Phys. 2019, 69, 58–71. [Google Scholar] [CrossRef]
- Bansod, Y.D.; Kebbach, M.; Kluess, D.; Bader, R.; van Rienen, U. Finite element analysis of bone remodelling with piezoelectric effects using an open-source framework. Biomech. Model. Mechanobiol. 2021, 20, 1147–1166. [Google Scholar] [CrossRef]
- Hölzer, A.; Schröder, C.; Woiczinski, M.; Sadoghi, P.; Scharpf, A.; Heimkes, B.; Jansson, V. Subject-specific finite element simulation of the human femur considering inhomogeneous material properties: A straightforward method and convergence study. Comput. Methods Programs Biomed. 2013, 110, 82–88. [Google Scholar] [CrossRef]
- Taddei, F.; Martelli, S.; Reggiani, B.; Cristofolini, L.; Viceconti, M. Finite-element modeling of bones from CT data: Sensitivity to geometry and material uncertainties. IEEE Trans. Biomed. Eng. 2006, 53, 2194–2200. [Google Scholar] [CrossRef] [PubMed]
- Idhammad, A.; Abdali, A.; Alaa, N. Computational simulation of the bone remodeling using the finite element method: An elastic-damage theory for small displacements. Theor. Biol. Med. Model. 2013, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Knowles, N.K.; Reeves, J.M.; Ferreira, L.M. Quantitative Computed Tomography (QCT) derived Bone Mineral Density (BMD) in finite element studies: A review of the literature. J. Exp. Orthop. 2016, 3, 36. [Google Scholar] [CrossRef]
- Martínez-Reina, J.; Ojeda, J.; Calvo-Gallego, J.L.; Pivonka, P.; Martelli, S. Assessment of mechanical variables best describing bone remodelling responses based on their correlation with bone density. J. Mech. Behav. Biomed. Mater. 2024, 160, 106773. [Google Scholar] [CrossRef]
- Available online: https://www.slicer.org (accessed on 17 January 2025).
- Heller, M.O.; Bergmann, G.; Kassi, J.P.; Claes, L.; Haas, N.P.; Duda, G.N. Determination of muscle loading at the hip joint for use in pre-clinical testing. J. Biomech. 2005, 5, 1155–1163. [Google Scholar] [CrossRef]
- Rho, J.Y.; Kuhn-Spearing, L.; Zioupos, P. Mechanical properties and the hierarchical structure of bone. Med. Eng. Phys. 1998, 20, 92–102. [Google Scholar] [CrossRef]
- Berli, M.; Borau, C.; Decco, O.; Adams, G.; Cook, R.B.; Aznar, J.M.G.; Zioupos, P. Localized tissue mineralization regulated by bone remodelling: A computational approach. PLoS ONE 2017, 12, e0173228. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Reina, J.; García-Aznar, J.M.; Domínguez, J.; Doblaré, M. On the role of bone damage in calcium homeostasis. J. Theor. Biol. 2008, 254, 704–712. [Google Scholar] [CrossRef]
- Martin, R. Toward a unifying theory of bone remodeling. Bone 2000, 26, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Lukas, C.; Ruffoni, D.; Lambers, F.M.; Schulte, F.A.; Kuhn, G.; Kollmannsberger, P.; Weinkamer, R.; Müller, R. Mineralization kinetics in murine trabecular bone quanti fi ed by time-lapsed in vivo micro-computed tomography. Bone 2013, 56, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Eriksen, E.F. Cellular mechanisms of bone remodeling. Rev. Endocr. Metab. Disord. 2010, 11, 219–227. [Google Scholar] [CrossRef] [PubMed]
- Pivonka, P.; Buenzli, P.R.; Scheiner, S.; Hellmich, C.; Dunstan, C.R. The influence of bone surface availability in bone remodelling-A mathematical model including coupled geometrical and biomechanical regulations of bone cells. Eng. Struct. 2013, 47, 134–147. [Google Scholar] [CrossRef]
- Mikić, B.; Carter, D.R. Bone strain gage data and theoretical models of functional adaptation. J. Biomech. 1995, 28, 465–469. [Google Scholar] [CrossRef]
- Latypova, A.; Maquer, G.; Elankumaran, K.; Pahr, D.; Zysset, P.; Pioletti, D.P.; Terrier, A. Identification of elastic properties of human patellae using micro-finite element analysis. J. Biomech. 2016, 49, 3111–3115. [Google Scholar] [CrossRef]
- Geraldes, D.M.; Phillips, A.T.M. A comparative study of orthotropic and isotropic bone adaptation in the femur. Training 2014, 30, 873–889. [Google Scholar] [CrossRef]
- Wolff, J. The Law of Bone Remodelling; Springer: Berlin/Heidelberg, Germany, 1896. [Google Scholar]
- Zioupos, P.; Cook, R.B.; Hutchinson, J.R. Some basic relationships between density values in cancellous and cortical bone. J. Biomech. 2008, 41, 1961–1968. [Google Scholar] [CrossRef]
- Singh, S.; Singh, S.P. Weigth of the femur—A useful measurement for identification of sex. Acta Anat. 1974, 87, 141–145. [Google Scholar] [CrossRef]
- Thomas, C.D.; Feik, S.A.; Clement, J.G. Regional variation of intracortical porosity in the midshaft of the human femur: Age and sex differences. J. Anat. 2005, 206, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Lerebours, C.; Buenzli, P.R.; Scheiner, S.; Pivonka, P. A multiscale mechanobiological model of bone remodelling predicts site-specific bone loss in the femur during osteoporosis and mechanical disuse. Biomech. Model. Mechanobiol. 2016, 15, 43–67. [Google Scholar] [CrossRef] [PubMed]
- Endo, D.; Ogami-Takamura, K.; Imamura, T.; Saiki, K.; Murai, K.; Okamoto, K.; Tsurumoto, T. Reduced cortical bone thickness increases stress and strain in the female femoral diaphysis analyzed by a CT-based finite element method: Implications for the anatomical background of fatigue fracture of the femur. Bone Rep. 2020, 13, 100733. [Google Scholar] [CrossRef] [PubMed]
- Swan, K.R.; Ives, R.; Wilson, L.A.B.; Humphrey, L.T. Ontogenetic changes in femoral cross-sectional geometry during childhood locomotor development. Am. J. Phys. Anthropol. 2020, 173, 80–95. [Google Scholar] [CrossRef]
- Michael, A.R. Histological estimation of age at death in amputated lower limbs: Issues of disuse, advanced age, and disease in the analysis of pathological bone. J. Forensic Leg. Med. 2018, 53, 58–61. [Google Scholar] [CrossRef]
- Zioupos, P. Ageing human bone: Factors affecting its biomechanical properties and the role of collagen. J. Biomater. Appl. 2001, 15, 187–229. [Google Scholar] [CrossRef]







| Pattern | Load (N) | Fx | Fy | Fz | Location |
|---|---|---|---|---|---|
| Walking | Hip contact | −459.0 | −278.8 | −1948.2 | P0 |
| Abductor | 493.0 | 36.6 | 735.3 | P1 | |
| Tensor fascia latae, proximal | 61.2 | 98.6 | 112.2 | P1 | |
| Tensor fascia latae, distal | −4.3 | −6.0 | −161.5 | P1 | |
| Vastus lateralis | −7.7 | 157.3 | −789.7 | P2 | |
| Stair-climbing | Hip contact | −504.1 | −515.1 | −2008.6 | P0 |
| Abductor | 595.9 | 244.8 | 721.7 | P1 | |
| Iliotibial band, proximal | 89.3 | −25.5 | 108.8 | P1 | |
| Iliotibial band, distal | −4.3 | −6.8 | −142.8 | P1 | |
| Tensor fascia latae, proximal | 26.4 | 41.7 | 24.7 | P1 | |
| Tensor fascia latae, distal | −1.7 | −2.6 | −55.3 | P2 | |
| Vastus lateralis | −18.7 | 190.4 | −1148.4 | P2 | |
| Vastus medialis | −74.8 | 336.6 | −2270.4 | P3 |
| Parameter | Value | |
|---|---|---|
| vBMU | BMU advancement speed | 0.04 mm/day |
| TR | Resorption period | 24 days |
| TI | Inversion period | 8 days |
| TF | Formation period | 64 days |
| σL | BMU Lifespan | 100 days |
| m | Weighting exponent | 4 |
| fbio | Biological frequency factor | 0.005 NBMU/(mm3 day) |
| Tnm | Mineralization lag time | 12 days |
| Tprim | Length of primary phase | 10 days |
| Tm,max | Time to reach the maximum mineral level | 4000 days |
| Feature | CT-Based Initialization | Homogeneous |
|---|---|---|
| Input source | Clinical CT scan | Synthetic model with constant density |
| Initial density | Spatially heterogeneous (realistic) | Uniform (2 g/cm3) |
| Biological relevance | Close to real adult bone structure | Artificial starting point |
| Purpose | Assess remodeling from a realistic baseline | Test model ability to evolve structure purely from loading |
| Expected convergence | Small adaptation from mature state | Larger changes required to reach physiological state |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franco, F.; Borau, C.; Di Paolo, J.; Berli, M. Differential Mechanical and Biological Contributions to Bone Mass Distribution—Insights from a Computational Model of the Human Femur. Mathematics 2025, 13, 2156. https://doi.org/10.3390/math13132156
Franco F, Borau C, Di Paolo J, Berli M. Differential Mechanical and Biological Contributions to Bone Mass Distribution—Insights from a Computational Model of the Human Femur. Mathematics. 2025; 13(13):2156. https://doi.org/10.3390/math13132156
Chicago/Turabian StyleFranco, Feliciano, Carlos Borau, José Di Paolo, and Marcelo Berli. 2025. "Differential Mechanical and Biological Contributions to Bone Mass Distribution—Insights from a Computational Model of the Human Femur" Mathematics 13, no. 13: 2156. https://doi.org/10.3390/math13132156
APA StyleFranco, F., Borau, C., Di Paolo, J., & Berli, M. (2025). Differential Mechanical and Biological Contributions to Bone Mass Distribution—Insights from a Computational Model of the Human Femur. Mathematics, 13(13), 2156. https://doi.org/10.3390/math13132156






