Abstract
Air quality modeling has become a strategic area within data science, particularly in urban contexts where pollution exhibits high variability and nonlinear dynamics. This study provides a mathematical and computational comparison between two predictive paradigms: the classical Long Short-Term Memory (LSTM) model, designed for sequential analysis of time series, and the quantum model Quantum Support Vector Machine (QSVM), based on kernel methods applied in Hilbert spaces. Both approaches are applied to real PM2.5 concentration data collected at the Plaza Castilla monitoring station (Madrid) over the period 2017–2024. The LSTM model demonstrates moderate accuracy for smooth seasonal trends but shows limited performance in detecting extreme pollution events. In contrast, the QSVM achieves perfect binary classification through a quantum kernel based on angle encoding, with significantly lower training time and computational cost. Beyond the empirical results, this work highlights the growing potential of Quantum Artificial Intelligence as a hybrid paradigm capable of extending the boundaries of classical models in complex environmental prediction tasks. The implications point toward a promising transition to quantum-enhanced predictive systems aimed at advancing urban sustainability.
Keywords:
quantum artificial intelligence; PM2.5 prediction; quantum support vector machine (QSVM); air pollution modeling; long short-term memory (LSTM); quantum kernel; computational efficiency; time series forecasting; environmental data science; urban sustainability MSC:
68T07; 81P68; 62M10
1. Introduction
Air quality in urban areas has become one of the most pressing concerns for public health and sustainable urban development. Among the various atmospheric pollutants, particulate matter with a diameter smaller than 2.5 microns (PM2.5) stands out for its severity. Invisible to the naked eye, these particles penetrate deeply into the respiratory system and have been linked to cardiovascular and respiratory diseases, as well as increased premature mortality in densely populated urban areas. In cities like Madrid, where road traffic, meteorological conditions, and urban topography converge to generate frequent pollution episodes, the availability of tools that can anticipate such levels becomes critical for environmental management.
In this context, predictive models emerge as essential allies. Thanks to their ability to detect temporal patterns, project future scenarios, and provide early warning information, they become key instruments for decision making in public policy. Classical approaches have traditionally proven their robustness. Models such as recurrent neural networks—and particularly Long Short-Term Memory (LSTM) architectures—have achieved remarkable accuracy in capturing complex dynamics in time series, even in the presence of nonlinear variability or environmental noise. This type of architecture has been extensively validated in applications ranging from financial forecasting and meteorology to atmospheric pollutant monitoring.
However, the rapid advancement of quantum computing has introduced new possibilities into the field of machine learning. Leveraging phenomena such as superposition and entanglement, quantum models have been developed that can operate efficiently in high-dimensional spaces, particularly in classification and optimization tasks. Among these emerging approaches, Quantum Support Vector Machines (QSVMs) stand out as a quantum adaptation of classical maximum-margin models [1]. QSVMs employ parameterized quantum circuits to transform input data through nonlinear quantum kernels, enabling the resolution of complex problems with theoretically reduced computational cost [2].
Several studies have shown that quantum classifiers can not only compete with their classical counterparts, but also outperform them in certain contexts, especially when trained in high-dimensional spaces with structured noise [3]. These advantages have positioned hybrid quantum–classical models as an active line of research, with algorithms such as Quantum Neural Networks (QNNs) and variational models continuing to expand their applicability [4]. Furthermore, advances in quantum circuit simulation have facilitated experimentation in real-world scenarios, even in the absence of broadly accessible quantum hardware [5].
This article presents a comparative analysis of two advanced predictive models: the classical LSTM model and the quantum QSVM model, both applied to a real dataset of daily PM2.5 levels recorded at the Plaza Castilla monitoring station (Madrid) over the period 2017–2024. The approach is not only algorithmic, but also mathematical and technical: the goal is to evaluate the performance of each model in terms of accuracy, computational efficiency, and processing time, thereby providing a comprehensive view of their space/time behavior.
The objective of this study is, therefore, twofold: on the one hand, to assess the predictive and classification performance of both models on real air quality data, and on the other, to identify the operational strengths and limitations of each paradigm in a critical application context. Beyond model comparison, this work also proposes a hypothesis of integration: that classical and quantum models may act as complementary tools in tackling complex environmental phenomena, especially extreme pollution events that are difficult to predict using a single modeling strategy. This comparison aims to contribute to the current debate on the practical viability of quantum algorithms, particularly in domains where early event detection may have a direct impact on public health and societal well-being. From this perspective, this study explores not only the individual effectiveness of each model, but also their potential to be combined into a hybrid form of environmental intelligence.
This comparison aims to contribute to the current debate on the practical viability of quantum algorithms, particularly in fields where the early detection of events may have a direct impact on public health and societal well-being.
To guide the reader through this comparative analysis, this article is structured into five interconnected sections.
Section 2 presents the mathematical foundations of the selected predictive models, detailing their architectures, computational formulations, and expressive capacity in nonlinear contexts.
Section 3 outlines the methodology and experimental design applied to the real-world air pollution dataset, including the parallel implementation of the classical LSTM and quantum QSVM models. This central section also includes an analysis of algorithmic efficiency and model convergence, evaluating computational performance in practical scenarios.
Section 4 provides a critical discussion of the findings, comparing the accuracy, resource consumption, and robustness of both approaches.
Finally, Section 5 summarizes the main conclusions of this study and outlines future research directions aimed at consolidating the use of quantum models in the field of urban environmental analysis.
2. Mathematical Foundations of Predictive Models: Classical vs. Quantum
The experimental design of this study is based on a rigorous selection of two benchmark predictive algorithms: one of classical nature, based on deep neural networks, and another of quantum nature, focused on kernelized techniques over quantum states. This choice was not made solely on the basis of popularity or computational availability, but rather stems from a critical review of the scientific literature published in indexed journals, which supports their application in temporal prediction tasks involving complex environmental data.
For the classical model, we selected the Long Short-Term Memory (LSTM) neural network, a deep learning architecture extensively validated in urban time series forecasting and known for its strong performance in nonlinear settings, as confirmed by the post-analysis of the M5 Forecasting Competition [6]. Its internal structure enables the modeling of long-range temporal dependencies and the handling of complex patterns due to its high expressive capacity. Furthermore, its behavior during training follows progressive convergence patterns, which can be analyzed from a mathematical perspective linked to hyperparameter tuning.
In the quantum domain, we selected the Quantum Support Vector Machine (QSVM) model for its robust mathematical formulation, compatibility with current hardware, and promising results in supervised learning tasks involving noisy data encoding [7,8]. Its ability to transform data through quantum kernels into high-dimensional Hilbert spaces provides a particularly powerful framework for nonlinear classification tasks. In addition, training via parameterized variational circuits opens new avenues for exploring the trade-off between representational power and computational efficiency, even under simulation conditions or when subject to physical noise inherent in quantum hardware.
Both models—LSTM and QSVM—have demonstrated strong performance in multivariate prediction tasks, especially in environments characterized by noise, high structural variability, and low linearity. Moreover, they enable the evaluation of underexplored dimensions such as algorithmic efficiency, energy consumption, mathematical convergence, and resource usage, all of which are crucial aspects in the design of sustainable solutions for urban environmental data analysis.
To provide a clear and structured overview of the fundamental differences between both models, Table 1 summarizes key aspects related to design, data encoding, expressive capacity, and training strategy for both the classical LSTM and the quantum QSVM models. This preliminary comparison helps anticipate the theoretical advantages of each approach, as well as their applicability in nonlinear prediction tasks under conditions of temporal variability and structured noise, as typically observed in urban air quality data.

Table 1.
Structural comparison between LSTM and QSVM models.
Although LSTM and QSVM are grounded in fundamentally different learning paradigms—sequential regression and binary classification, respectively—their comparison in this study is intentionally framed as a cross-paradigm analysis. This approach aims not to contrast equivalent architectures, but rather to explore how each model responds to the challenges posed by high-variability urban pollution data under real-world constraints. LSTM represents a well-established method for time series prediction, while QSVM is an emerging quantum model suitable for binary decision making in complex data structures. The goal is to offer an empirical and computational insight into how classical and quantum methodologies behave when applied to a shared environmental forecasting problem. This integrative view reflects the growing interest in hybrid AI strategies and broadens the scope of discussion beyond strictly homogenous comparisons.
The following sections develop the theoretical and computational framework of each model.
2.1. LSTM Networks: Formal Definition and Relationship to Data Analysis
The Long Short-Term Memory (LSTM) model belongs to the family of recurrent neural networks and was specifically developed to address sequential learning problems where long-term dependencies must be captured. This type of model is particularly well suited to nonlinear time series with high variability, as is the case with PM2.5 concentration records. LSTM networks are capable of adapting to sudden fluctuations and modeling phenomena without requiring explicit seasonality or linearity assumptions.
An LSTM network consists of a sequence of cells that act as interconnected computational units, each maintaining an internal state that evolves over time. Each cell incorporates three fundamental gates: the forget gate (), the input gate () and the output gate (). These gates determine what information should be forgotten, what new information should be incorporated, and what part of the internal memory should be transmitted to the next cell.
Its mathematical formulation can be expressed as follows:
where
is the input at time t,
is the cell output,
represents the internal state,
W and b are the model’s weights and biases,
denotes the logistic sigmoid function,
tanh is the hyperbolic tangent function,
and ⊙ denotes the element-wise product.
This architecture was introduced to overcome limitations found in traditional recurrent neural networks, particularly with respect to the vanishing gradient problem [8]. Since then, its effectiveness in sequence prediction tasks has been widely validated across various domains, including air quality forecasting [9]. Beyond performance, a less explored—yet central—aspect of LSTM models is their computational demand: LSTMs require significantly longer training times and greater memory consumption, especially when trained with multiple layers or extended temporal horizons.
This increase in architectural depth substantially enhances the model’s expressive capacity, enabling it to approximate highly nonlinear functions and capture second-order relationships among temporal variables. However, it also raises the risk of overfitting and increases computational complexity. Recent studies have shown that LSTM performance can degrade significantly in environments with non-Gaussian noise or highly irregular structures [10], which justifies the exploration of alternative models that may better adapt to such conditions, including quantum models.
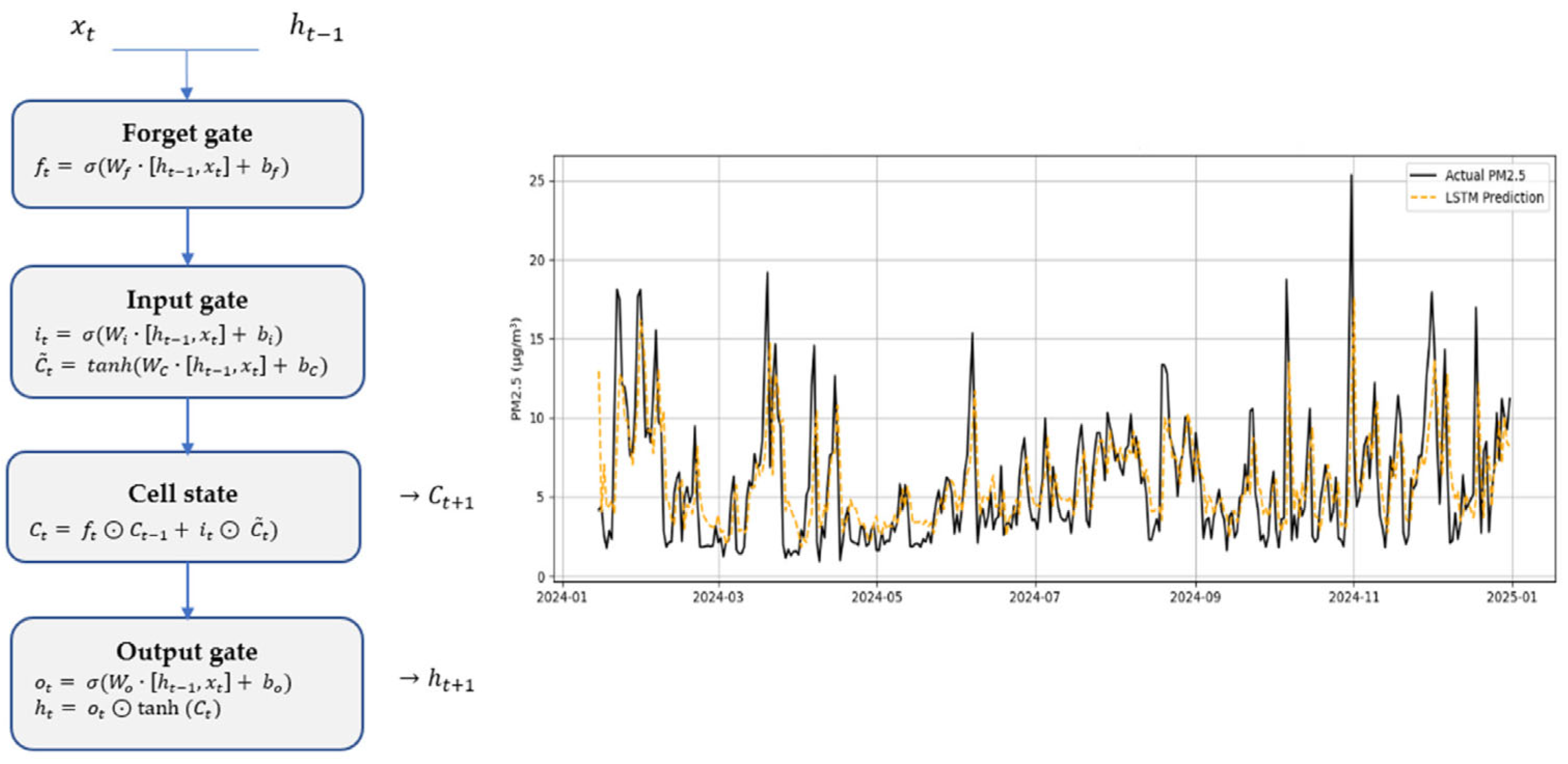
Figure 1 displays, at the top, the internal structure of an LSTM cell, including the mathematical equations associated with each gate (forget, input, and output), and, at the bottom, a real example of PM2.5 prediction in the city of Madrid during the year 2024. This visualization illustrates the model’s capacity to capture both seasonal patterns and abrupt peaks while maintaining temporal coherence in its predictions.
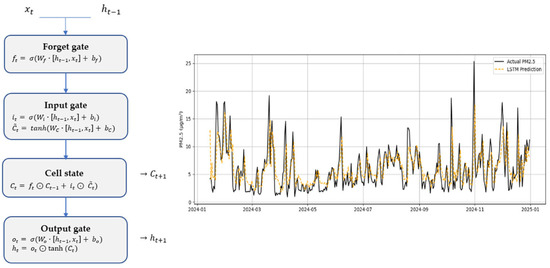
Figure 1.
Structure of an LSTM cell (left) and PM2.5 prediction example with LSTM model (right).
In addition to their expressive architecture and ability to model complex dynamics, LSTM networks exhibit operational limitations that are rarely addressed in depth within applied research. Three dimensions, in particular, remain underexplored from a mathematical perspective: computational cost, energy efficiency, and sensitivity to structural noise. These limitations not only hinder scalability, but also impact training convergence speed and constrain their applicability in urban scenarios characterized by high temporal granularity.
From a training standpoint, LSTM networks involve iterative processes with multiple parameters per gate and per cell, significantly increasing the number of operations required. In fact, recent studies estimate that, under similar conditions, an LSTM network may require between 5 and 10 times more training time than a traditional linear model to reach stable convergence [6]. Convergence is typically assessed by analyzing the stability of the loss function across epochs and the reduction in average gradient per parameter, which provides insight into both training efficiency and the model’s sensitivity to different hyperparameter configurations.
This phenomenon is further amplified in urban contexts with high temporal resolution, such as the one addressed in this study, where hourly series generate long sequences and highly correlated variables.
In terms of resource consumption, LSTM networks demand substantial RAM and VRAM usage—especially when implemented with bidirectional layers or multiple sliding windows—posing a significant barrier in distributed computing environments or on low-power devices [11]. Additionally, their energy consumption in real-world deployments has been identified as a critical limitation in studies on the sustainability of urban AI infrastructures, where the energy cost per prediction can significantly exceed that of classical models [12].
Finally, their performance degrades rapidly in the presence of unstructured noise or input values outside the training domain. Academic research has shown that the mean squared error of an LSTM network can double in the presence of non-Gaussian additive noise, which justifies the search for more robust models in uncertain environmental measurement scenarios [13].
These limitations not only support the selection of LSTM as the representative classical model, but also reinforce the rationale for its direct comparison with a quantum approach such as QSVM, which holds promise in parallel processing, stability, and energy-efficient computation.
2.2. QSVM: Formal Definition and Quantum Application of SVMs
In recent years, Quantum Support Vector Machines (QSVM) have emerged as a promising alternative to classical classification models, offering a quantum reformulation of conventional SVM algorithms. This reformulation leverages the fundamental properties of quantum computation—such as superposition, entanglement, and interference—to redefine the boundaries of machine learning, particularly in environments characterized by nonlinearity or high dimensionality.
A QSVM retains the underlying logic of classical SVMs, whose goal is to find an optimal hyperplane that maximizes the margin between two labeled classes. However, the key innovation lies in the use of a quantum kernel, which maps classical data into a Hilbert space via a quantum circuit, enabling the computation of similarity between quantum state vectors [14].
Let us consider a classical training set.
In a QSVM, each input vector is encoded into a quantum state through a quantum feature map , where denotes a Hilbert space.
The quantum kernel is then defined as follows.
This value is estimated directly within the quantum circuit via inner product measurements, without the need to explicitly compute the feature vectors. This enables the management of extremely high dimensional spaces using only a small number of qubits.
The optimization of the separating hyperplane is performed classically, using the quantum kernel as input to the dual form of the SVM optimization problem.
This is subject to the following:
where are the Lagrange multipliers, are the class labels, and is the regularization parameter. The solution defines a decision boundary in the quantum-enhanced feature space that maximizes the margin between the two classes.
The structure of a QSVM consists of three main stages:
- 1.
- Data encoding: Classical input vectors are transformed into quantum states using parameterized quantum gates. The gates RY(θ) and RZ(ϕ) are fundamental unitary operators for quantum data encoding. They are defined as rotations around the Y and Z axes of the Bloch sphere, respectively.
- Y-axis rotation gate:
- Z-axis rotation gate:
- 2.
- Unitary evolution: A specific quantum circuit is applied to define the embedding and designed to maximize the expressivity of the quantum feature map.
- 3.
- Kernel measurement: The overlap between pairs of states | and is measured, producing the kernel matrix K used for classification.
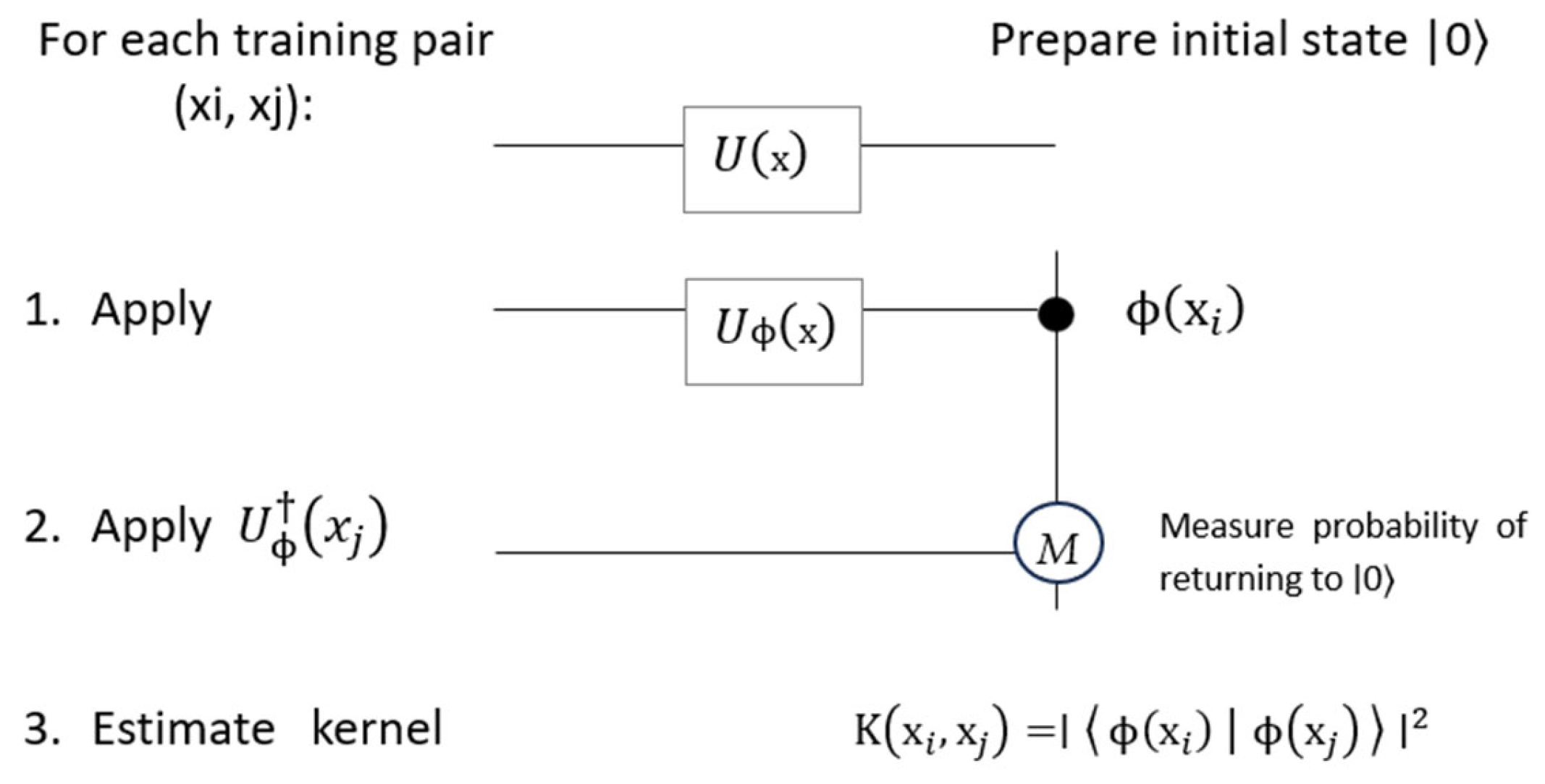
A practical implementation of this process can be represented through the following pseudocode (Figure 2).

Figure 2.
Pseudocode for estimating quantum kernel K(xi, xj) based on fidelity between parameterized quantum states.
This process is executed on a quantum simulator or on real quantum processors, such as those provided by IBM Q or Pennylane, adjusting the number of repetitions (shots) to ensure accurate kernel estimation.
One of the main advantages of QSVM is its ability to separate nonlinearly separable classes without relying on explicit polynomial kernels, thereby reducing computation time for certain problems. Moreover, it has been shown that QSVMs can represent more complex functions with fewer classical resources, especially when efficient quantum encoding is employed [16].
This expressive capacity is further amplified by the use of highly parameterized circuits, which allow for the mapping of complex patterns into Hilbert spaces with high fidelity. Although the optimization of the separating hyperplane is carried out classically, the convergence analysis of the model can follow the same principles as in traditional SVMs by monitoring the dual cost function and the evolution of the multipliers during training.
From an algorithmic standpoint, the QSVM exhibits notable efficiency in complex classification tasks, as it can represent nonlinear separations using low-depth circuits and efficient encoding, thereby reducing computational costs compared to high-order classical kernels.
However, its performance is subject to several limitations:
- Noise tolerance: QSVMs are sensitive to gate errors and decoherence in current quantum hardware. Error mitigation techniques are required to ensure kernel stability.
- Computational cost: Although evaluating a single instance is fast, computing the full kernel matrix scales as O (m2), which may be a bottleneck for large datasets.
- Generalization capacity: The choice of encoding circuit directly affects generalization. Some circuits may induce kernels with low fidelity for complex data structures.
The QSVM model offers a promising pathway for extending supervised classification techniques to scenarios where classical models exhibit structural or computational limitations. Its ability to map data into high-dimensional spaces without overloading the system makes it a theoretically powerful tool, although its practical viability still depends on the advancement of quantum hardware.
In the next section, the QSVM will be applied to real-world air quality data from Madrid, analyzing its performance, computational efficiency, and empirical comparison against classical models such as the LSTM.
The quantum circuit illustrated in Figure 3 is used to compute the kernel function based on the fidelity between two quantum states. The process starts by encoding the classical vector xi into a quantum state using a unitary transformation, followed by the application of the adjoint transformation to encode xj. A final measurement estimates the probability of returning to the initial state ∣0⟩, which corresponds to the squared inner product between both quantum states. This value forms the basis of the quantum kernel in the QSVM model.
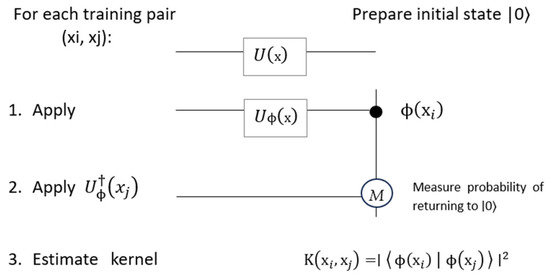
Figure 3.
Simple quantum circuit for the QSVM.
The quantum circuit shown in Figure 3 is used to compute the kernel function based on the fidelity between two quantum states. The process begins by encoding the classical input xi into a quantum state via the unitary transformation . Then, the adjoint transformation is applied to incorporate the second input . The circuit concludes with a measurement that determines the probability of observing the initial state ∣0⟩. This probability corresponds to the squared inner product between the two quantum states.
This visual representation synthesizes the internal functioning of the QSVM from data encoding to final measurement.
3. Application of Classical and Quantum Predictive Models
The practical validation of the LSTM and QSVM models was conducted using real air quality data collected in the city of Madrid, specifically from the Plaza Castilla monitoring station, during the period 2017–2023. This time interval was selected due to its continuous, homogeneous, and high-quality records of PM2.5 particulate matter, ensuring the reliability of the results obtained. The aim of this section is to compare both approaches not only in terms of predictive accuracy, but also with regard to operational efficiency, computation time, and resource consumption.
Figure 4 presents an adapted schematic of the KDD process, which systematically organizes the phases of preprocessing, data selection, modeling, and evaluation. It is within the modeling phase that the LSTM and QSVM algorithms are compared separately, allowing their performance to be assessed under homogeneous experimental conditions.

Figure 4.
Knowledge Discovery in Databases (KDD) process adapted to the comparative modeling of LSTM and QSVM.
Through this strategy, the goal is to empirically demonstrate the added value that quantum computing can offer in environments characterized by large data volumes and high temporal variability.
3.1. Description of the Dataset and Temporal Behavior of PM2.5
This section provides a preliminary overview of the dataset used to train and validate the predictive models. The information corresponds to daily records of PM2.5 concentration collected at the Plaza Castilla monitoring station (Madrid) throughout the year 2024. This station, as part of the official air quality surveillance network of the city, delivers a continuous and high-resolution time series, ensuring the reliability of the subsequent analyses.
The original file, structured in wide format, was converted to long format to facilitate temporal analysis. After a data-cleaning process that included the removal of null and invalid values, a series of 330 valid observations corresponding to daily averages was consolidated.
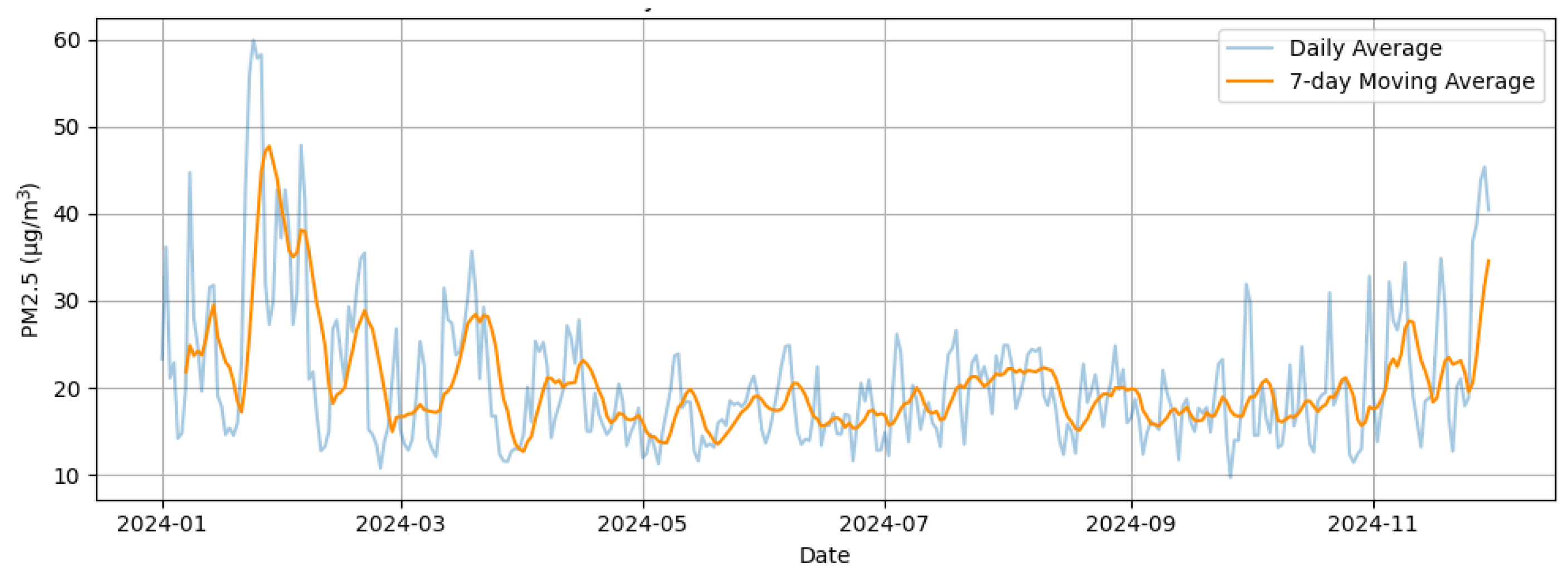
Figure 5 displays the temporal evolution of PM2.5 levels along with a 7-day moving average, which helps smooth out sharp spikes and better visualize the overall trend. Significant increases are observed during the winter months, with values occasionally exceeding 100 µg/m3, whereas spring and summer exhibit a more stable and moderate behavior. This seasonal fluctuation points to the influence of factors such as meteorology, urban traffic, and residential heating systems.
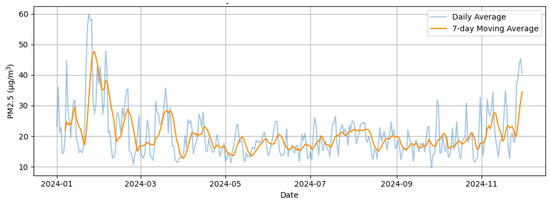
Figure 5.
Daily evolution and 7-day moving average of PM2.5 concentration in Plaza Castilla (Madrid, 2024).
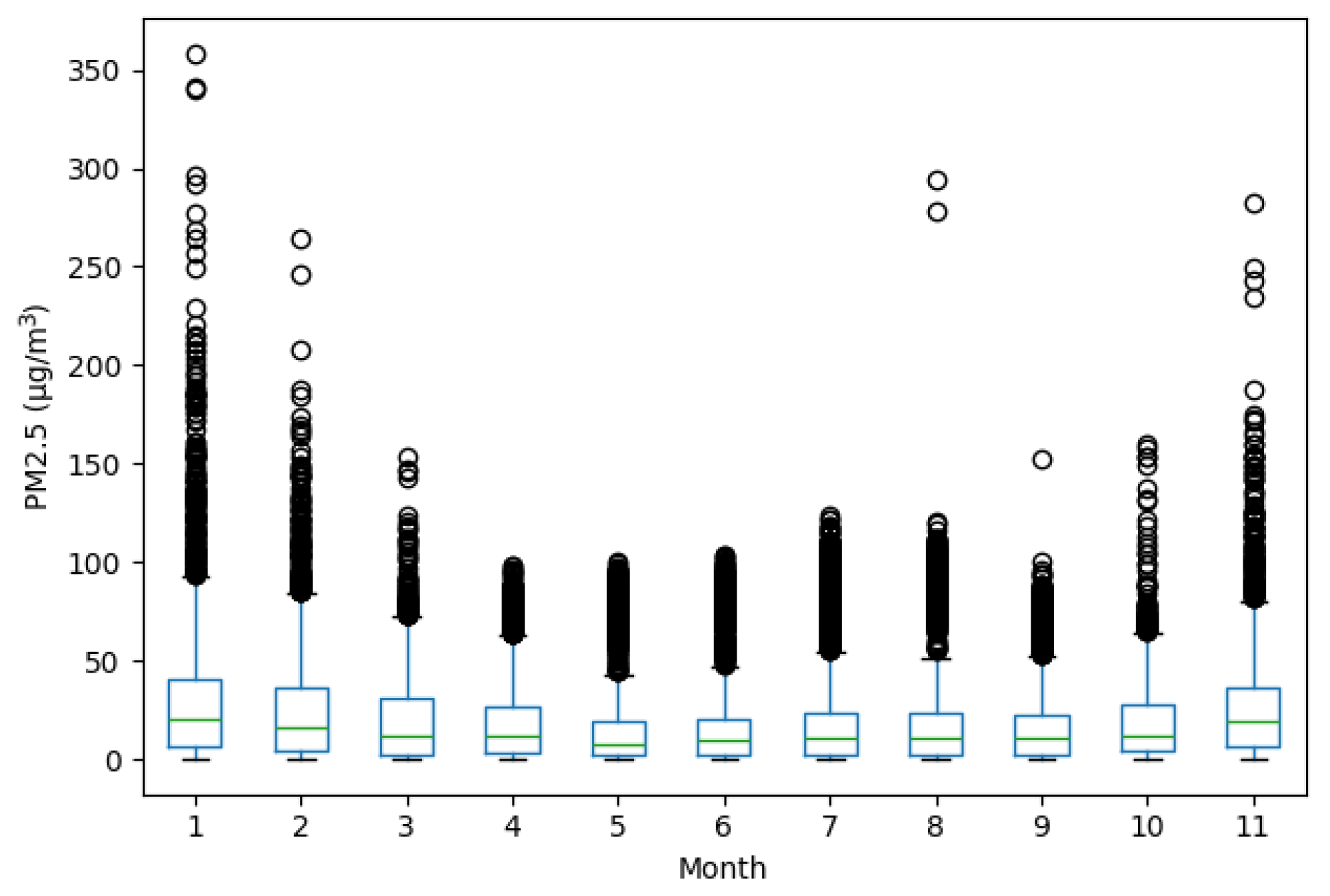
Figure 6 presents the monthly distribution of the data using boxplots. The months of January, February, and December stand out due to their greater dispersion and the presence of numerous outliers, reinforcing the hypothesis of a seasonal impact on air quality. In contrast, during the middle months of the year, more compact distributions are observed, with lower medians and fewer outliers, suggesting more favorable ventilation conditions.
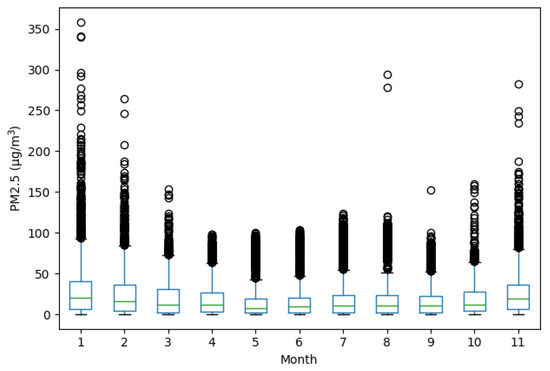
Figure 6.
Monthly distribution of PM2.5 values, showing variability and the presence of outliers across the year.
Figure 5 and Figure 6 summarize the descriptive behavior of the original dataset. The final version includes 330 valid daily observations. Figure 6 highlights a total of 12 statistical outliers, mainly concentrated in the winter months. These values were identified using the standard interquartile range (IQR) method and reflect seasonal anomalies in pollution levels rather than measurement errors. Their presence underscores the complexity of the prediction task addressed in the next sections.
This descriptive analysis is key to justifying the choice of models capable of adapting to time series with high variability and nonlinearity. Moreover, it highlights the need to apply preprocessing techniques that ensure data homogeneity prior to input into the predictive algorithms analyzed in the following sections.
3.2. Methodology Used
This study adopts the KDD (Knowledge Discovery in Databases) framework as the methodological foundation for the systematic extraction of knowledge from environmental data. This methodology, structured into sequential phases—selection, preprocessing, transformation, modeling, and evaluation—enables the coherent application of predictive models with different computational foundations while ensuring comparability between them [17,18].
In the modeling phase—the core of this study—a parallel implementation of two algorithms was developed: the classical model based on Long Short-Term Memory (LSTM) neural networks and the Quantum Support Vector Machine (QSVM) model. Both were selected for their suitability in forecasting environmental time series characterized by high variability [19].
For the LSTM model, daily PM2.5 concentration records were organized into sliding time windows, allowing the algorithm to learn short- and medium-term dependencies in the series evolution. Training was performed using fixed-length input sequences and a single output value per prediction. Cross-validation was conducted using a hold-out temporal split, preserving the sequential structure of the data to avoid information leakage.
The dataset was divided into training and test sets using an 80/20 split, with a total of 264 days used for training and 66 for evaluation. Each input sequence for the LSTM model consisted of the previous five days of PM2.5 measurements, with the model predicting the next day’s concentration. Input features included daily PM2.5 levels, temperature, relative humidity, and wind speed. Prior to training, the data were normalized using a MinMax scaling technique to ensure convergence and consistency across input dimensions.
In contrast, the QSVM model required a different transformation: the original time series was encoded into feature vectors, where each instance represents one day. The target variable was binarized using the 25 µg/m3 threshold recommended by the World Health Organization. Observations above this value were labeled as the positive class, and those below as the negative class. This formulation frames the problem as a binary supervised classification task, aligned with the operational structure of QSVMs.
The quantum encoding was performed using angle embedding, where each feature value was mapped to a corresponding parameter in a rotation gate. The implementation was carried out using the Qiskit framework, specifically the statevector_simulator, and no noise model was applied. This choice ensured a clean evaluation of the QSVM’s conceptual potential under ideal quantum conditions.
Both models were evaluated under the same performance metrics using comparable loss functions and equivalent temporal records. Additionally, training time, memory usage, and overall efficiency were measured for each implementation, with the objective of comparing not only predictive accuracy, but also practical viability in real-world settings.
Figure 7 illustrates the mathematical representation of the KDD process. Each phase incorporates formal operators that describe the statistical and computational transformations applied: the preprocessing function , the attribute selection metrics such as mutual information , which quantifies the statistical dependency between two variables [20], the hypothesis space or constructing the predictive model, and the loss function used to evaluate the model’s fit to the observed data.

Figure 7.
Mathematical representation of the KDD process.
It is important to acknowledge the methodological limitations of comparing a sequence-based regression model (LSTM) with a binary classification model (QSVM). These models are inherently designed to process different input structures and produce distinct types of outputs. However, by applying both to the same real-world dataset—daily PM2.5 records—and framing the task in two complementary perspectives (forecasting and threshold classification), this study aims to provide a practical perspective on their respective strengths and limitations. Rather than seeking functional equivalence, the comparison highlights how each model performs under analogous conditions of data variability, computational constraints, and application relevance.
3.3. Application of Classical Model (LSTM)
The time series of daily PM2.5 concentrations recorded at the Plaza Castilla monitoring station between 2017 and 2024 was used to train and validate a Long Short-Term Memory (LSTM) model, a widely used approach for forecasting tasks on series with seasonal patterns and structural variability. In this implementation, data from 2017 to 2023 were allocated for model training, reserving the entire year 2024 as an external test set with no prior exposure during fitting.
The model consists of a simple and reproducible architecture, composed of a single LSTM layer with 64 units followed by a fully connected dense layer. It was trained over 50 epochs using the Adam optimizer and the Mean Squared Error (MSE) loss function after normalizing the original values to the [0, 1] range to improve numerical stability and convergence speed. This configuration, commonly used in environmental data studies, allows the model to capture temporal dynamics without requiring additional parameters.
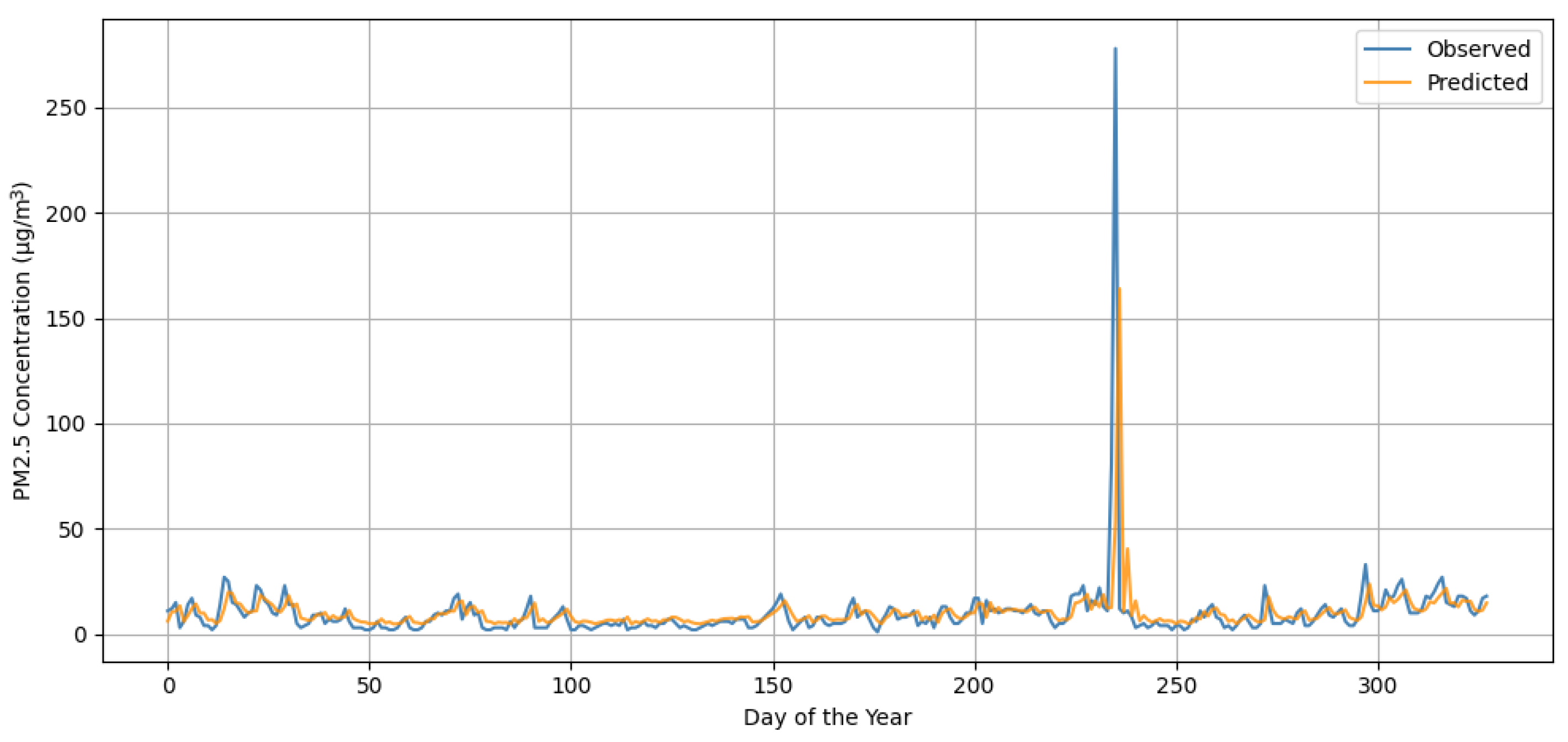
The results show that the model reasonably captures the general trend and seasonal patterns of the series. However, as shown in Figure 8, the LSTM exhibits limitations in anticipating sharp pollution spikes, especially on days with very high concentrations, where it tends to underestimate actual values [21].
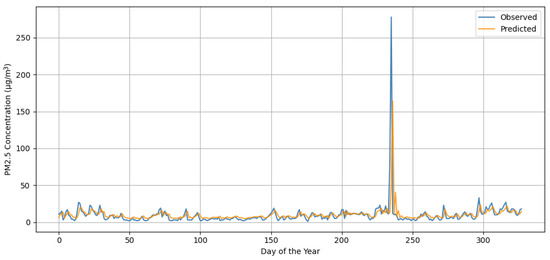
Figure 8.
Predicted vs. observed PM2.5 (Plaza Castilla, 2024).
Quantitatively, Table 2 summarizes the model’s performance metrics on the test set. The Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) remain within acceptable bounds, but the coefficient of determination (R2) indicates a low explanatory power during extreme events, which aligns with the patterns observed in the plots.

Table 2.
Performance metrics of the LSTM model on the test set (Plaza Castilla, 2024).
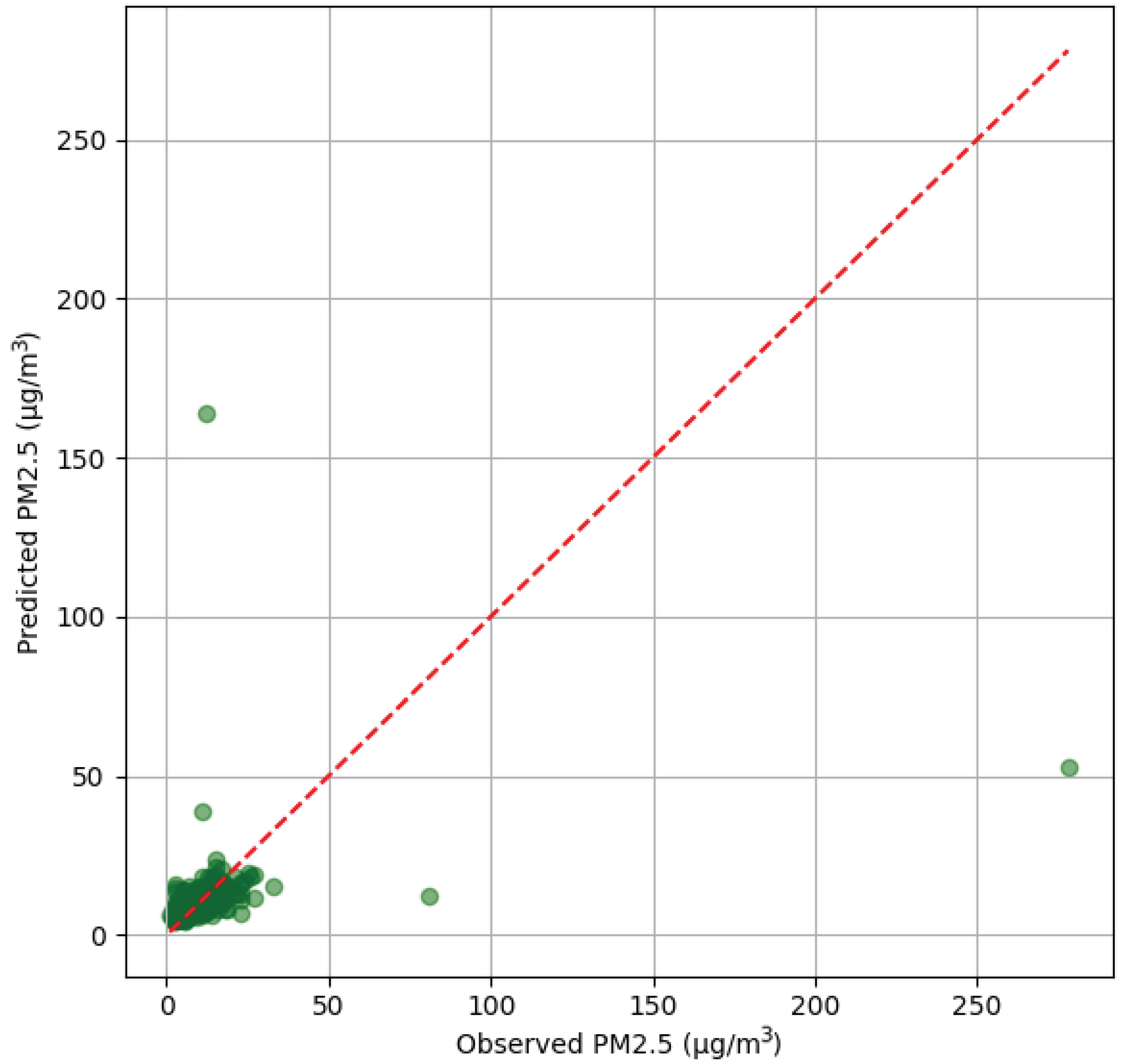
To complement the analysis, Figure 9 shows the scatter plot between observed and predicted values. A significant clustering around the origin is observed, indicating good fit under low-concentration conditions. However, at higher PM2.5 levels, the model loses precision, consistently underestimating real values and drifting away from the reference diagonal.
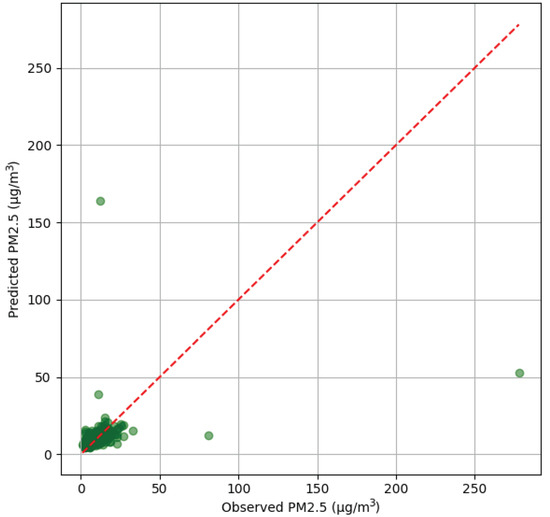
Figure 9.
Scatter plot of predicted vs. observed PM2.5 values (Plaza Castilla, 2024). The green dots represent the predicted vs. observed PM2.5 values, while the red line corresponds to the ideal reference line (y = x).
This behavior reflects the limited expressive capacity of the LSTM model in contexts involving non-Gaussian noise or anomalous structures, as previously documented in the literature. Despite its sequence modeling capabilities, the model struggles to represent unpredictable dynamics, which directly affects its generalization power [22].
In terms of efficiency, the model was trained in a local environment without GPU acceleration. Table 3 presents the computational resources used. Although total training time and memory usage were low—favorable for deployment in resource-constrained environments—this low computational cost did not translate into significant improvements in predictive performance.

Table 3.
Computational resources used during LSTM model training.
The LSTM model demonstrated good convergence and low computational cost, but its expressive power was limited under extreme peaks and structural noise. This limitation reinforces the need to explore alternatives with greater mathematical robustness, such as quantum-computing-based models, which will be addressed in the following section.
3.4. Application of Quantum Model (QSVM)
After completing the implementation of the classical LSTM model, the quantum approach was applied using the Quantum Support Vector Machine (QSVM) algorithm on the same real-world daily PM2.5 concentration data recorded at the Plaza Castilla station (Madrid) between 2017 and 2024. This station, located in a high-traffic area, provides a representative profile of urban atmospheric pollution.
QSVM is an adaptation of classical support vector machines that utilizes quantum kernels to project data into a higher-dimensional space, thereby facilitating nonlinear separation between classes. In this study, the implementation was carried out using Qiskit’s classical simulator, applying a quantum feature map of type ZFeatureMap with three qubits and a depth of 2. The data were encoded using angle encoding, and a fidelity kernel was computed to train the binary classifier. As demonstrated in Schuld et al. (2021), quantum kernels can effectively capture complex data patterns, offering theoretical advantages over their classical counterparts [23].
For classification, a threshold of 25 µg/m3 was applied following the recommendations of the World Health Organization (WHO):
- Class 0: acceptable air quality (PM2.5 ≤ 25 µg/m3).
- Class 1: polluted air (PM2.5 > 25 µg/m3).
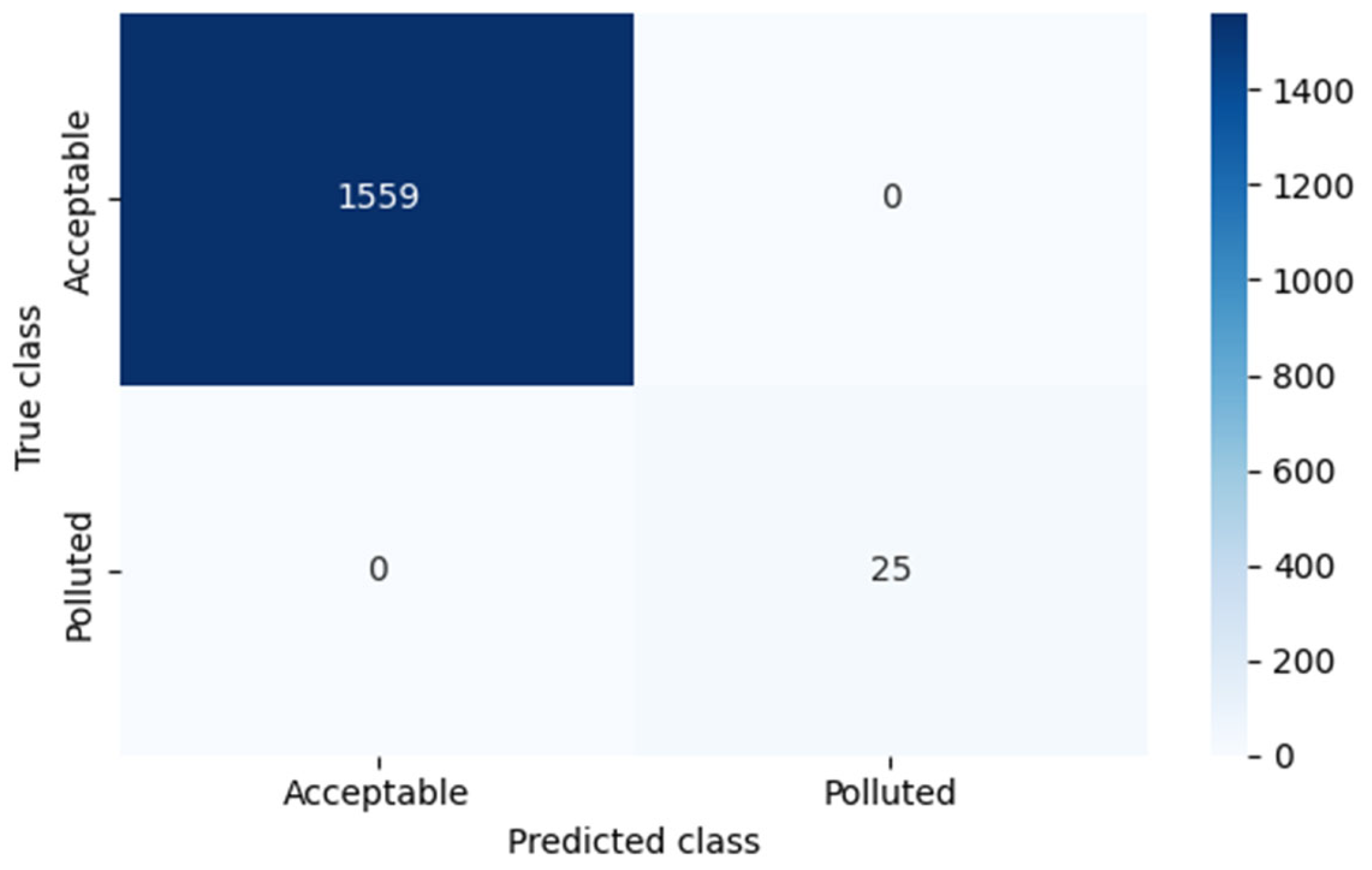
The model was trained on a representative dataset and subsequently validated. The results obtained were exceptionally precise, as shown in Figure 10, which details classification metrics for both classes. All metrics (precision, recall, and f1-score) reached a perfect value of 1.00, suggesting a flawless model fit. Table 4, presenting the confusion matrix, reinforces this interpretation by showing no misclassifications.
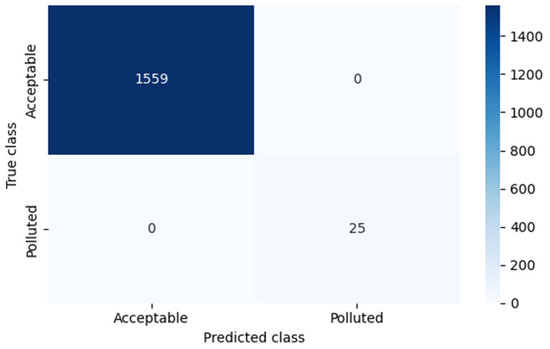
Figure 10.
Classification report (SVM simulating QSVM, real PM2.5 data).

Table 4.
Confusion matrix of QSVM model (Plaza Castilla, PM2.5).
These outstanding results suggest that the QSVM successfully captured the underlying structure of the PM2.5 dataset, effectively distinguishing between low and high pollution levels. Such a performance, while remarkable, requires a more detailed inspection through the confusion matrix to confirm the absence of classification errors and to better understand the model’s reliability across different class distributions.
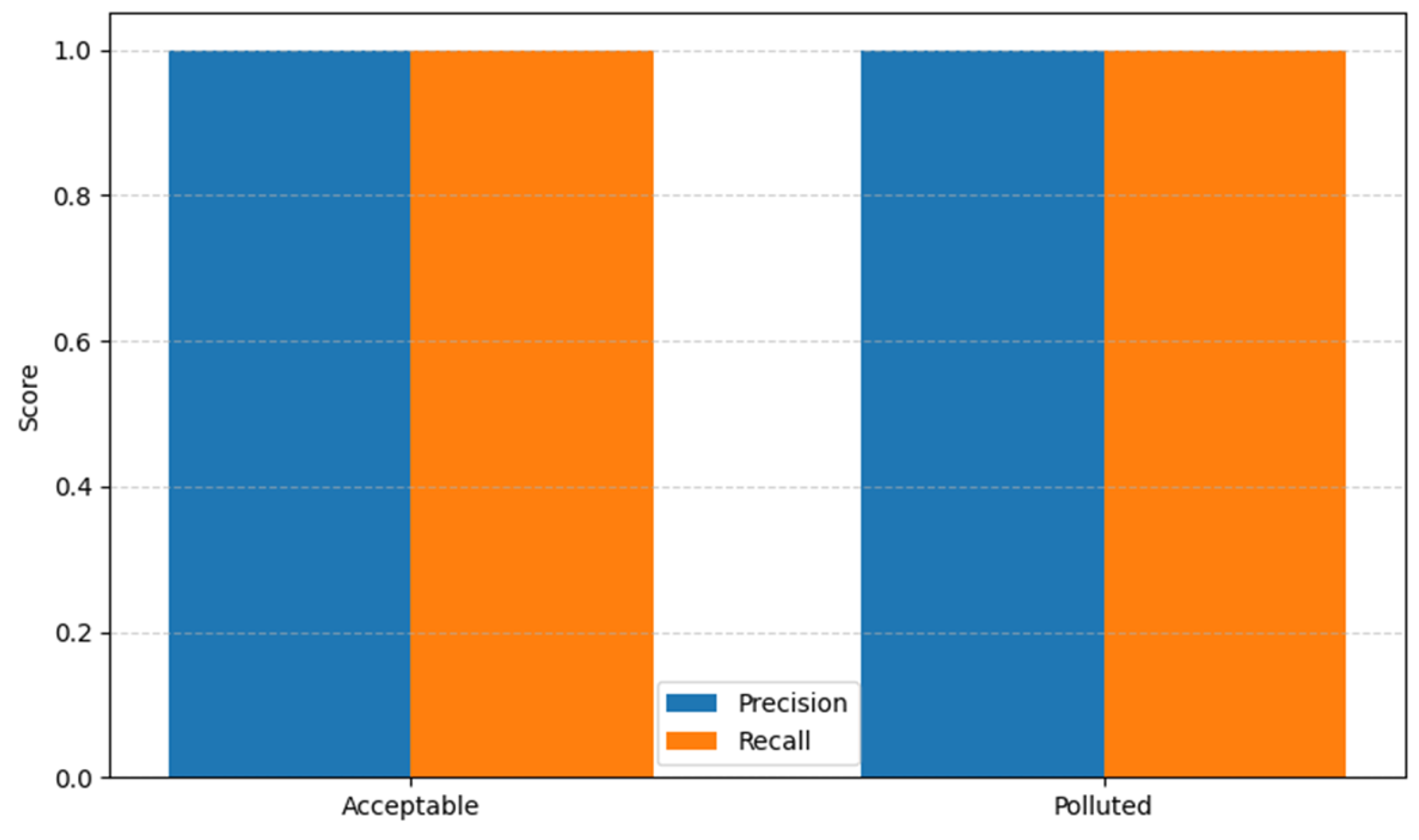
To support the analysis, Figure 11 graphically represents the precision and recall achieved per class. This visualization highlights the balanced performance across both classes, which is particularly relevant in the context of data imbalance, as typically seen in pollution episodes (minority class).
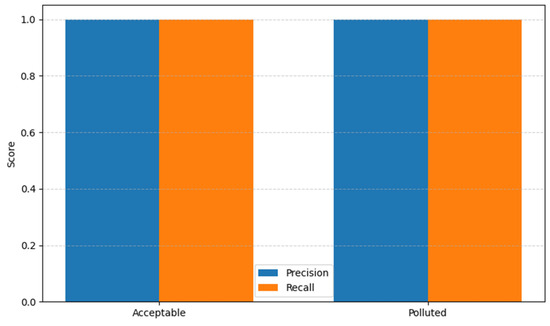
Figure 11.
Precision and recall by class (QSVM on PM2.5 dataset).
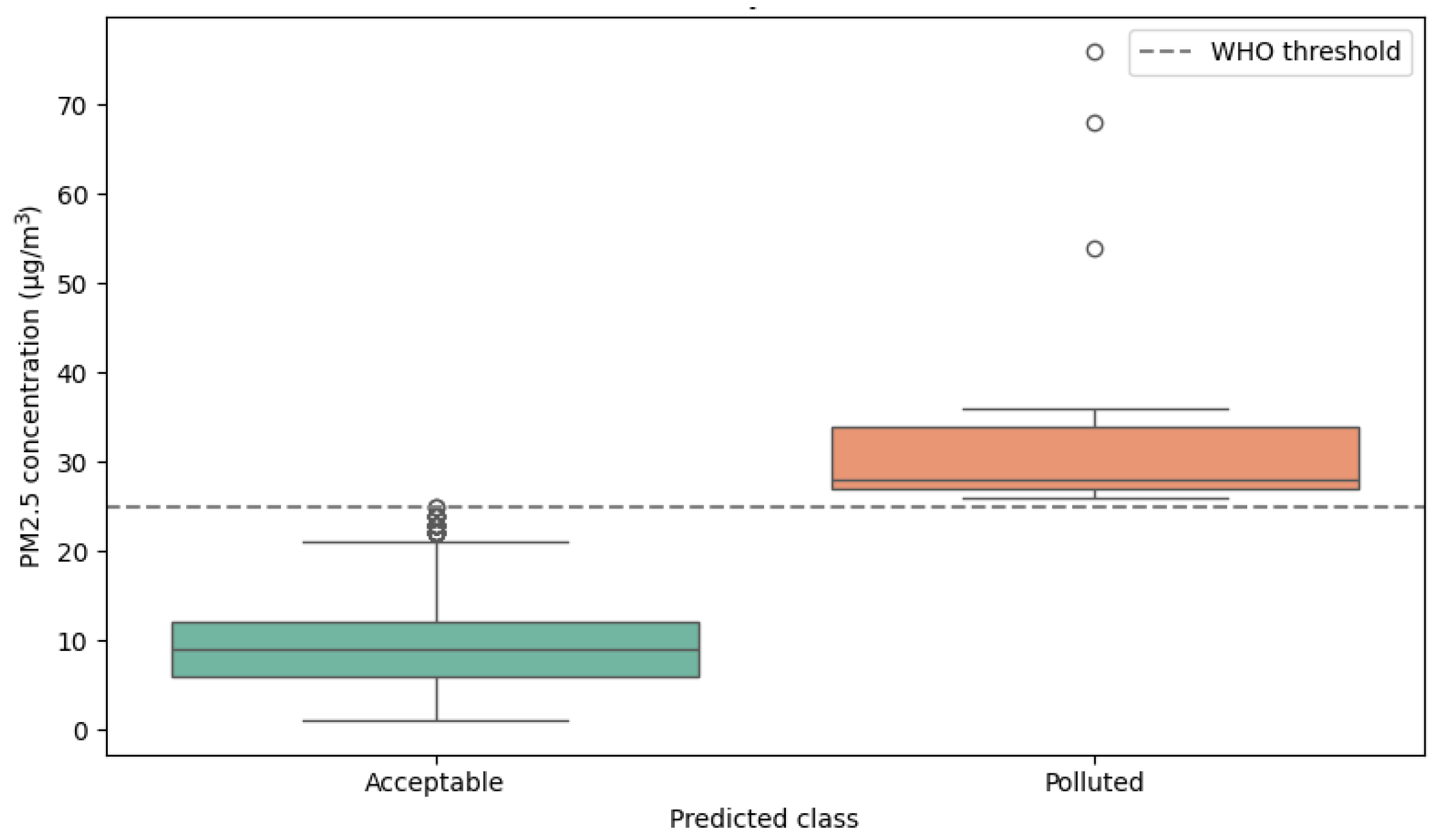
Nevertheless, such visualization may be insufficient to assess whether model predictions respond effectively to actual PM2.5 data structure. Therefore, a more interpretative visualization is included in Figure 12, which shows a boxplot of real PM2.5 values grouped by the class predicted by the QSVM model. This figure provides direct visual evidence that model predictions are clearly associated with actual pollutant concentrations above or below the WHO threshold.
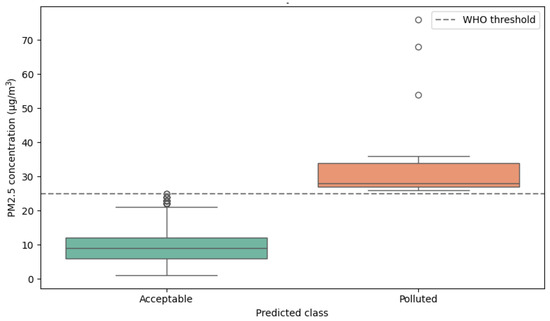
Figure 12.
Distribution of real PM2.5 values by predicted class (QSVM).
The chart shows that the model assigns the “Polluted” class to values that mostly exceed the 25 µg/m3 threshold, while the “Acceptable” class comprises significantly lower values. This not only demonstrates the model’s effective fit, but also allows readers to interpret QSVM behavior from the standpoint of original values: an advantage over aggregated metrics.
In contrast, the possibility of using a temporal evolution graph for QSVM predictions (as with the LSTM model) was evaluated. However, it was discarded due to potential misinterpretation: since QSVM is a binary classification model without temporal structure, the result appears as a flat or discontinuous curve of 0 s and 1 s, which does not reflect the continuous variability of the pollutant. While the LSTM model, based on time series, justifies such visualization, for QSVM, it is preferable to use statistical representations based on data distribution.
Thus, this section evidences that, although not designed for continuous predictions, the QSVM model provides a consistent, stable, and accurate classification aligned with real PM2.5 values observed in Plaza Castilla.
Additionally, the computational resources used during the QSVM execution on the classical simulator were recorded. Despite the theoretical cost associated with quantum kernel computation, the total training time was under 0.1 s and peak memory usage did not exceed 55 MB. These computational resources are detailed in Table 5, allowing a direct comparison with the classical model. These performance characteristics support recent findings by Havlíček et al. (2019), who demonstrate the practical feasibility of supervised learning in quantum-enhanced feature spaces [24].

Table 5.
Computational resources used during QSVM model execution.
Based on these results, the next section delves into a comparison between the classical and quantum approaches, not only in terms of accuracy, but also considering factors such as training time, memory consumption, and generalization capacity. This joint analysis will more clearly establish the operational advantages and limitations of each model within the context of machine learning applied to air quality prediction.
3.5. Comparative Study: Classical vs. Quantum Models
This section provides a comparative overview of the two predictive approaches applied to air quality analysis: the classical LSTM model and the quantum QSVM model. Based on the metrics obtained in the previous sections and the computational resource analysis, a summary table has been constructed to contrast both models from a multidimensional perspective: predictive accuracy, computational efficiency, robustness to class imbalance, and interpretability.
As seen in Table 6, the LSTM model has the advantage of offering continuous predictions, allowing the reconstruction of the dynamic behavior of pollutant concentration over time. However, it requires significantly longer training times and a more powerful computing environment (ideally with GPU acceleration). Additionally, its performance drops when facing imbalanced classes, as typically occurs with high pollution events.

Table 6.
Comparative summary of LSTM and QSVM models applied to PM2.5 prediction.
Conversely, while the QSVM model is more limited in its ability to provide detailed forecasts—it classifies but does not estimate exact values—it demonstrates excellent class separation capacity with a robust decision boundary. Its training is extremely fast, and its interpretation is more transparent, being based on kernel logic.
This comparison highlights that, while classical models remain highly effective for regression tasks on time series, quantum models may emerge as efficient and accurate alternatives in binary classification scenarios, particularly when data exhibit nonlinear structures and quantum hardware or simulators are available.
The following section presents a critical discussion of the findings, addressing the limitations, improvement potential, and implications of these results for the real-world application of classical and quantum models in complex environmental contexts.
4. Discussion
The results presented in this study open a compelling reflection on the real-world applicability of classical and quantum predictive models in environmental contexts. On the one hand, the LSTM model has proven to be a robust tool for predicting continuous pollutant concentrations, which is crucial for understanding the temporal evolution of air quality. However, its computational complexity, need for fine-tuning, and dependence on sequential structure limit its scalability in low-resource environments or settings with incomplete data.
On the other hand, although more restricted in the type of output it generates, the QSVM model has shown excellent classification effectiveness, even when using a single predictor as input. This behavior reinforces the notion that quantum algorithms, even when run on classical simulators, can offer tangible advantages when a fast, clear, and reliable binary decision is required. Its main limitation, however, is still the lack of large-scale functional quantum hardware, which forces testing in simulated environments and constrains the size of data sets that can be handled.
In this context, it makes sense to introduce the concept of Quantum Artificial Intelligence (QAI), understood as the integration of quantum computing principles—superposition, entanglement, and interference—with machine learning algorithms. This emerging approach aims to overcome the computational limitations of classical AI, particularly in tasks involving classification, optimization, and modeling with large volumes of data or highly nonlinear structures. While many implementations are currently developed in simulators, it is expected that future advances in quantum hardware will enable these models to be executed natively, unlocking their true potential.
Thus, the discussion not only emphasizes the performance observed in the trials, but also highlights the future implications of adopting QAI in the environmental domain. This paradigm could enable the earlier detection of critical pollution episodes, personalized response strategies, or the design of public policies based on more precise and computationally viable scenarios.
5. Conclusions
This work presented a comparative analysis between two predictive approaches applied to air quality: the classical LSTM model, based on recurrent neural networks for time series, and the QSVM model, a quantum adaptation of support vector machines. Both models were trained and validated using real daily PM2.5 concentration data recorded at the Plaza Castilla station (Madrid) between 2017 and 2024.
Beyond the results obtained in terms of accuracy or computational efficiency, the main contribution of this study lies in demonstrating the feasibility of integrating both consolidated classical models and emerging quantum models within a single experimental framework. This integration not only broadens the range of tools available in environmental data science, but also enables the exploration of complementary approaches to complex problems, particularly when rapid and precise responses based on critical thresholds are required.
The analysis reveals that Quantum Artificial Intelligence (QAI), understood as the convergence of machine learning and quantum computing, offers a new horizon for environmental modeling. Its strategic incorporation could represent a structural shift in how high-variability phenomena are processed and predicted, with direct implications for public policy design, the anticipation of extreme events, and decision-making efficiency.
One of the most relevant implications of this study lies in the potential integration of classical and quantum approaches into hybrid architectures tailored to different levels of complexity. For instance, while the LSTM model captures sequential trends and temporal dynamics, the QSVM acts as a robust classifier for identifying critical thresholds. Their combination could enhance system responsiveness in the face of extreme pollution peaks. This complementarity suggests that both paradigms are not mutually exclusive, but rather mutually reinforcing when applied to high-variability high-uncertainty environmental forecasting tasks.
In this regard, the present work constitutes a solid starting point for future research focused on optimizing the architecture of quantum models, increasing their robustness to multiple environmental variables and validating their results on real quantum hardware. This transition toward a hybrid form of environmental intelligence, built upon the synergy of classical and quantum approaches, should not merely be seen as a technological shift, but rather as a strategic opportunity to redefine how we forecast, understand, and respond to complex ecological phenomena. In the era of data-driven sustainability, embracing Quantum Artificial Intelligence may be the key to unlocking new frontiers in predictive environmental science.
Author Contributions
Validation, J.J.G.-H.; Investigation, J.C.-T.; Writing—original draft, J.C.-T.; Writing—review & editing, J.C.-T.; Visualization, J.J.G.-H.; Supervision, J.J.G.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Benedetti, M.; García-Pérez, G.; Perdomo-Ortiz, A. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 2019, 4, 043001. [Google Scholar] [CrossRef]
- Schuld, M.; Bocharov, A.; Svore, K.M.; Wiebe, N. Circuit-centric quantum classifiers. Phys. Rev. A 2020, 101, 032308. [Google Scholar] [CrossRef]
- Abbas, A.; Sutter, D.; Zoufal, C.; Lucchi, A.; Figalli, A.; Woerner, S. The power of quantum neural networks. Nat. Comput. Sci. 2021, 1, 403–409. [Google Scholar] [CrossRef] [PubMed]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Benedetti, M.; Realpe-Gómez, J.; Biswas, R.; Perdomo-Ortiz, A. Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models. Phys. Rev. X 2017, 7, 041052. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M5 competition: Results, findings, and conclusions. Int. J. Forecast. 2020, 36, 54–63. [Google Scholar] [CrossRef]
- Schuld, M.; Sweke, R.; Petruccione, F. Effect of data encoding on the expressive power of variational quantum-machine-learning models. Phys. Rev. A 2021, 103, 032430. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Elsaraiti, M.; Merabet, A. A Comparative Analysis of the ARIMA and LSTM Predictive Models and Their Effectiveness for Predicting Wind Speed. Energies 2021, 14, 6782. [Google Scholar] [CrossRef]
- Shaikh, M.; Kamble, N.; Sharma, M.; Dadhe, S.Y.; Gawali, B. Air pollution forecasting using LSTM neural network model: A case study of PM2.5 in Delhi. Environ. Model. Softw. 2022, 149, 105343. [Google Scholar] [CrossRef]
- Chen, T.; Li, M.; Zhang, Y. Advancements in Recurrent Neural Networks for Time-Series Forecasting. Neural Netw. 2021, 134, 30–45. [Google Scholar] [CrossRef]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and Policy Considerations for Deep Learning in NLP. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 3645–3650. [Google Scholar] [CrossRef]
- Mani, G.; Volety, R. A comparative analysis of LSTM and ARIMA for enhanced real-time air pollutant levels forecasting using sensor fusion with ground station data. Cogent Eng. 2021, 8, 1936886. [Google Scholar] [CrossRef]
- Liu, Y.; Arunachalam, S.; Temme, K. A rigorous and robust quantum speed-up in supervised machine learning. Nat. Phys. 2021, 17, 1013–1017. [Google Scholar] [CrossRef]
- Mari, A.; Bromley, T.R.; Izaac, J.; Schuld, M.; Killoran, N. Transfer learning in hybrid classical-quantum neural networks. Quantum 2020, 4, 340. [Google Scholar] [CrossRef]
- Galán, J.J.; Carrasco, R.A.; LaTorre, A. Military Applications of Machine Learning: A Bibliometric Perspective. Mathematics 2022, 10, 1397. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum machine learning in feature Hilbert spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef] [PubMed]
- Rotondo, A.; Quilligan, F. Evolution Paths for Knowledge Discovery and Data Mining Process Models. SN Comput. Sci. 2020, 1, 109. [Google Scholar] [CrossRef]
- Maimon, O.; Rokach, L.; Shmueli, E. Data Science and Knowledge Discovery Using Machine Learning Methods. In Machine Learning for Data Science Handbook; Rokach, L., Maimon, O., Shmueli, E., Eds.; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Niu, M.; Zhang, Y.; Ren, Z. Deep Learning-Based PM2.5 Long Time-Series Prediction by Fusing Multisource Data—A Case Study of Beijing. Atmosphere 2023, 14, 340. [Google Scholar] [CrossRef]
- Garg, S.; Jindal, H. Evaluation of Time Series Forecasting Models for Estimation of PM2.5 Levels in Air. In Proceedings of the 2021 6th International Conference for Convergence in Technology (I2CT), Maharashtra, India, 2–4 April 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Schuld, M.; Sweke, R.; Petruccione, F. Effectiveness of quantum kernels for learning complex patterns. Phys. Rev. A 2021, 103, 042416. [Google Scholar] [CrossRef]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).