Abstract
This research explores the dynamic characteristics of the soliton neuron model, a mathematical approach used to describe various complicated processes in neuroscience, including the unclear mechanisms of numerous anesthetics. An appropriate wave transformation converts the neuron model into a two-dimensional dynamical system, which takes the form of a conservative Hamiltonian system with a single degree of freedom. This study utilizes qualitative methods from planar integrable systems theory to analyze and interpret phase portraits. The conditions under which periodic, super-periodic, and solitary wave solutions exist are clearly defined and organized into theorems. These solutions are obtained analytically, with several examples depicted through 2D- and 3D-dimensional graphical illustrations. The research also examines how key physical parameters, such as frequency and sound velocity, affect the nature of these solutions, specifically on the width and the amplitude of those solutions. In addition, by inserting a generalized periodic external force, the model exhibits quasi-periodic and chaotic dynamics. These complicated dynamics are visualized using 2D and 3D phase portraits and time series plots. To further assess chaotic behavior, Lyapunov exponents are calculated. Numerical results indicate that the system’s overall behavior is strongly impacted by changes in the external force’s frequency and amplitude.
MSC:
35C07; 35C08; 37K40; 83C15
1. Introduction
The dynamics of intricate systems in diverse domains are often governed by nonlinear partial differential equations (NLPDEs), highlighting their critical importance. The presence of nonlinear terms significantly influences the behavior of these equations, often introducing intricate dynamics. Researchers commonly employ both numerical and theoretical methods to study NLPDEs, with the derivation of exact solutions being a key focus in understanding nonlinear physical phenomena. NLPDEs are widely used to describe nonlinear processes in fields such as financial modeling, population dynamics, general relativity, and fluid dynamics [1,2,3,4,5]. Advances in analytical and computational techniques have enabled more precise analysis of physical systems governed by these equations. To obtain exact solutions, researchers increasingly rely on sophisticated mathematical methods. Recent progress in PDE theory has further enhanced the ability to address challenges posed by nonlinear phenomena. The synergy between computational simulations and analytical techniques remains critical in this field, as evidenced by ongoing research efforts.
Solitons are utilized across diverse technologies, including optical couplers [6], actuators, sensors [7], controllers, magneto-optic waveguides [8], and meta-materials [9]. Their broad applicability in multiple fields has attracted significant attention from researchers in various disciplines. In theoretical and experimental studies, solitary waves have become increasingly vital for solving nonlinear equations [10,11,12]. These concepts provide deeper insights into the fluctuations and stability of physical systems. Among these applications, the soliton neuron model serves as a key mathematical framework for understanding action potential propagation and neural network functionality [13]. This model plays a crucial role in analyzing electrical impulse transmission between neurons and the overall dynamics of interconnected neural networks. By applying soliton theory—which focuses on stable wave solutions—the model helps explain the wave-like behavior of neuronal signals. Soliton solutions are especially valuable for studying scenarios where waveforms remain unchanged during propagation, such as in neurons, ensuring stable signal transmission. The soliton neuron model has been widely used to investigate neural dynamics, including action potential propagation, synaptic plasticity, and other interactions within neural networks. It enables precise analysis of signal transmission in neurons and the complex brain functions arising from the coordination of vast neural networks. Furthermore, this model is relevant in studying neurological disorders like epilepsy, where signal disruption occurs. Research on the soliton neuron model primarily focuses on deriving soliton solutions and assessing their stability, offering valuable insights into the mechanisms underlying neuronal activity.
Exact analytical solutions provide critical insights into diverse physical systems, serving as the cornerstone for scientific advancement. These solutions typically emerge from mathematical formulations of physical phenomena as ordinary or partial differential equations (ODEs or PDEs). PDEs prove particularly valuable for modeling complex systems in nature and industrial applications. The scientific community has developed numerous sophisticated approaches to solve such equations, with certain methods gaining particular prominence in recent research. Notable examples include the modified generalized exponential rational function method [14] and the classical Lie symmetry approach [15,16,17], modified Sardar sub-equation method [18], bifurcation theory [19,20,21,22], Hirota’s bilinear method [23], Riccati–Bernoulli method [24], and the complete discriminant system method [25].
The soliton neuron model represents an important theoretical framework for characterizing neuronal dynamics, offering a robust mathematical description of action potential propagation and neural network behavior. This approach proves particularly useful in investigating both the collective dynamics of neural assemblies and the spatiotemporal evolution of electrochemical signaling in neuronal systems. Following established formulations [26], the soliton neuron model can be mathematically expressed as
The model includes key parameters that define the nerve membrane’s physical and thermodynamic properties. The function captures how action potentials alter membrane density, linking the membrane’s structural features to electrical activity, where x is the position along the axon and t is time. The parameter represents sound speed, reflecting the membrane’s wave transmission capability. Meanwhile, and describe the system’s nonlinearity and the phase transition in membrane elasticity, respectively, showing how these properties adapt under varying conditions. The parameter , representing the frequency-dependent sound velocity, plays a crucial role in the nerve membrane’s dynamic behavior by governing wave propagation speed. This model has been extensively studied in previous research. Alam et al. [26] employed the Kudryashov method to derive multiple soliton solutions, while in [27], the authors obtained analytical solutions using the -expansion method. Further investigations by Younas et al. [28] explored solitary wave solutions through diverse analytical techniques, including the Kumar–Malik method, the multivariate generalized exponential rational integral function method, and the Riccati-modified extended simple equation method.
To the best of our knowledge, the nonlinear dynamical analysis of the soliton neuron model—specifically its bifurcations, quasi-periodic behavior, chaotic patterns, and wave solutions—has not been extensively explored in the literature, despite its significance in understanding the intricate dynamics of neural behaviors. The motivation behind this research is to investigate how soliton-based models can effectively describe neural signal propagation, providing deeper insights into the nonlinear characteristics of neuronal behavior.
This study is organized as follows: Section 2 presents a one-dimensional Hamiltonian system derived from the soliton neuron model through an appropriate wave transformation. In Section 3, we conduct a bifurcation analysis of the traveling wave system, examining how solutions evolve under parameter variations, accompanied by detailed phase portrait illustrations. Section 4 establishes three fundamental theorems that specify existence conditions for periodic, super-periodic, and solitary wave solutions, leading to the derivation of novel solutions. The physical interpretation of selected solutions is provided in Section 5, including graphical representations and parameter impact analysis. Section 6 examines the effects of periodic external forcing on the traveling wave system’s dynamics, including a detailed investigation of quasi-periodic behavior and chaotic patterns. Section 7 contains most of the obtained results. This paper concludes in Section 8, which synthesizes the principal results and discusses their significance.
2. Traveling Wave System
The wave transformation
where represents the wave variable with constant parameters and , providing a robust framework for investigating soliton solutions in neuronal dynamics. This approach, well documented in studies of wave-like neuronal activity [29,30], consolidates spatial and temporal dependencies into a unified moving coordinate system, significantly simplifying mathematical analysis. The transformation inherently presumes a balance between nonlinearity and dispersion that maintains the soliton’s structural integrity during propagation, mirroring the behavior of action potentials in neural fibers. The resulting Hamiltonian formulation naturally captures this energy-conserving system, offering an elegant representation of nonlinear wave interactions in neuronal signaling. While actual neuronal systems incorporate dissipative effects (which could be addressed in future work), our current framework builds upon established theoretical foundations [30,31], particularly in modeling soliton-mediated neural pulse propagation, as thoroughly discussed in [30,31].
Inserting Equation (2) into Equation (1) yields
where primes indicate derivatives with respect to . By integrating both sides with respect to and assuming the integration constants are zero, we obtain
where for are free constants introduced for simplicity and are defined as follows:
Let and postulate . Hence, Equation (4) is rewritten as a dynamical system in the form
System (6) is a conservative system since , and it is Hamiltonian as it is derived from the Hamiltonian function
by using Hamilton canonical equations [32,33]. The Hamiltonian (7) is a constant of motion, as it does not explicitly depend on the independent variable , that is, it remains constant along all phase orbits. Hence, we have
where k is a constant that, as we will see later, plays an important role. Therefore, solving Equation (1) for wave solutions corresponds to analyzing 1D particle motion in a tri-parametric potential field:
The substitution of Equation (6a) into (8) followed by variable separation gives
where is a quartic polynomial given by
Exact solutions of Equation (1) are obtained by integrating Equation (10), with the parameter ranges determined through either complete discriminant polynomials [25] or bifurcation analysis [34]. We employ the bifurcation approach as our preferred method because it offers predictive capabilities, i.e., identifying solution types in advance by correlating them with corresponding phase orbit characteristics (as demonstrated later). Additionally, this approach effectively characterizes the dependence on initial conditions. For these reasons, our study implements bifurcation analysis.
3. Bifurcation Analysis
This section is devoted to the qualitative analysis and dynamical behavior of Equation (1). By conducting a bifurcation analysis of system (6), we determine the parameter conditions that lead to the emergence of various types of solutions, including periodic, super-periodic, solitary, and kink (or anti-kink) solutions. These solutions correspond to periodic, super-periodic, homoclinic, and heteroclinic trajectories in the system’s phase space, respectively. Furthermore, the analysis helps to identify and exclude unbounded solutions, which are generally unsuitable for practical applications. The phase portrait of system (6) is shaped by both the number of equilibrium points and the number of separatrix layers, as noted in [35]. To systematically categorize the different trajectories in the phase plane, we introduce the notations , , , and , which stand for periodic, heteroclinic, homoclinic, and super-nonlinear periodic trajectories, respectively. Within this framework, the parameter u enumerates the stable equilibrium points encompassed by the phase orbit, whereas v counts the number of separatrix layers crossed by the orbit [33]. We begin by identifying the equilibrium points of system (6) by setting and . Solving these conditions yields the fixed points as
where . The number of equilibrium points depends on whether is negative, zero, or positive. According to bifurcation theory [34], the nature of each equilibrium point is determined by analyzing the eigenvalues of the Jacobian matrix evaluated at . These eigenvalues are given by
with the Jacobian determinant expressed as
where is the Jacobian matrix associated with system (6) at the corresponding equilibrium point. The classification of the equilibrium point depends on the sign of the determinant: it is a saddle if , a center if , and a cusp if [34]. From the Hamiltonian perspective, each equilibrium point corresponds to a critical point of the potential function (9). An equilibrium is stable (center) if it represents a local minimum of the potential, and unstable (saddle) if it corresponds to a local maximum. These classifications are guaranteed by the Lagrange theorem [36].
Next, we evaluate the number and types of equilibrium points and proceed to classify their qualitative nature.
- A. If , that is, when and , the system described by (6) admits a unique equilibrium point at . To determine the nature of , we compute the determinant of the Jacobian matrix at this point, yielding . Consequently, behaves as a center when (which implies ), as illustrated in Figure 1a. The corresponding phase portrait, depicted in the same figure, shows a collection of periodic orbits encircling the center , which acts as a local minimum of the potential function (9). These closed orbits persist for all positive values of the parameter k and are associated with the class . On the other hand, if (thus, ), becomes a saddle point, representing a local maximum of the potential function, as shown in Figure 1b. In this configuration, the phase trajectories are all unbounded for any choice of the parameter k.
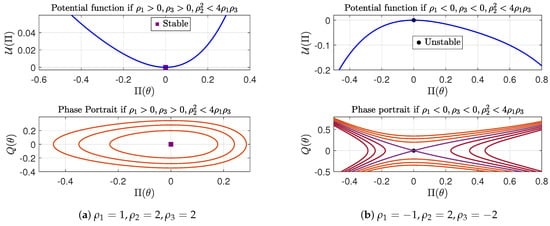
Figure 1.
The phase portrait for the system (6) and the potential function (6) when with . The black solid circle represents unstable equilibrium points, while the purple square denotes a stable equilibrium point.
- B. When , that is, with , the system described by (6) admits two equilibrium points: and . Evaluating the potential function (9) at these points gives the corresponding values of the constant k as and . To determine the nature of these equilibria, we compute the Jacobian determinants: and . The vanishing determinant at implies that it is a cusp point. When (implying ), the point is a center, representing a local minimum of the potential function, as illustrated in Figure 2a. In this case, the phase space contains bounded and periodic trajectories for all values of the parameter k. Specifically, for , a family of red periodic orbits encircles the center point , characterized by the type . When , a second family of periodic orbits appears, shown in pink and associated with type . At the critical value , a green trajectory passes through the cusp point , typically displaying periodic behavior in its vicinity.
Conversely, if (and thus, ), then all trajectories in the phase portrait are unbounded for every value of the parameter k as shown in Figure 2b.
- C. If , that is, , then the system (6) has three equilibrium points as in (12). The values of the constant k computed at the equilibrium points are given byTo explore the type of these points, we compute
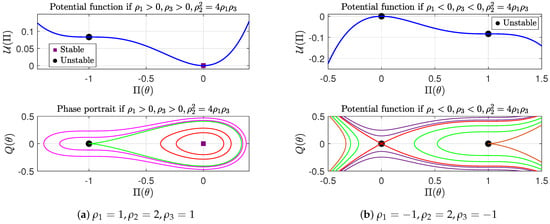
Figure 2.
The phase portrait for the system (6) and the potential function (6) when with . The black solid circle represents unstable equilibrium points, while the purple square denotes a stable equilibrium point.
Next, we analyze the two distinct cases based on the sign of , considering the positive and negative cases individually.
- Case I: If , then the condition is equivalent to or .i. If , , and , then the equilibrium points and are centers and correspond to local minima of the potential function (9), whereas is a saddle point and serves as a local maximum, as illustrated in Figure 3a. In this configuration, the phase portrait consists exclusively of bounded trajectories. For values of k in the range , there exists a set of red super-periodic orbits classified as . When , two distinct brown periodic orbits appear, each associated with the type . In addition, a family of green periodic trajectories encircles the center , also characterized by , along with a unique cyan orbit corresponding to the level . Furthermore, two homoclinic orbits, shown in purple and classified as , emerge when .ii. If , and , then the equilibrium points and are centers, which also arise as local minimum points for the potential function (9) while the point is a saddle that appears as local maximum for the potential function (9) as shown in Figure 3b. All system trajectories are bounded and classifiable by k values. The resulting phase dynamics follow the same pattern as illustrated in Figure 3a.iii. When , , and , the equilibrium points and act as saddle points and represent local maxima of the potential function (9), whereas behaves as a center and corresponds to a local minimum. The associated phase portrait is depicted in Figure 3c. In this scenario, most phase trajectories are unbounded, with the exception of a set of periodic red trajectories for , labeled as . This set is enclosed by a homoclinic trajectory in blue, corresponding to and denoted by .iv. When , and , the equilibrium points and behave as saddle points, corresponding to local maxima of the potential function given in (9). In contrast, acts as a center and constitutes a local minimum of the same potential function, as illustrated in Figure 3d. The associated phase portrait for this scenario is depicted in Figure 3d, exhibiting dynamics comparable to those described in the preceding case.
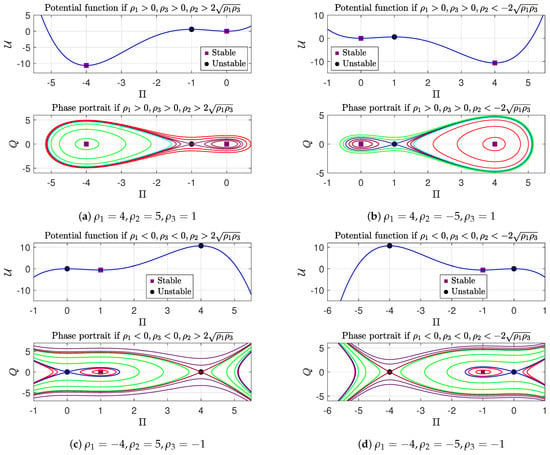 Figure 3. The phase portrait for the system (6) and the potential function (6) when with . The black solid circle represents unstable equilibrium points, while the purple square denotes a stable equilibrium point.Case II: If , the inequality is inevitably verified. Consequently, we analyze the following possible scenarios:a. When , and , the equilibrium point becomes a saddle point corresponding to a local maximum of the potential function (9), while and emerge as center points representing local minima of the same potential function, as shown in the phase portrait for system (6) in Figure 4a. All phase trajectories remain bounded, with their characteristics governed by the parameter k: for , a family of red periodic trajectories encircles ; for , two distinct families of brown periodic orbits appear surrounding both and within the blue homoclinic orbits at ; and at , a single cyan periodic trajectory exists, all classified as . Furthermore, the system exhibits green super-periodic trajectories characterized by for .b. For the case where , and , the equilibrium configuration demonstrates distinct characteristics: is a center point characterizing a local minimum point for the potential (9) while both equilibrium points are saddle points representing local maximum points for the potential function (9) as shown in Figure 4b, which also includes the phase portrait. All phase orbits are unbounded except for the family of red periodic orbits around when , which are contained within a blue homoclinic orbit at .
Figure 3. The phase portrait for the system (6) and the potential function (6) when with . The black solid circle represents unstable equilibrium points, while the purple square denotes a stable equilibrium point.Case II: If , the inequality is inevitably verified. Consequently, we analyze the following possible scenarios:a. When , and , the equilibrium point becomes a saddle point corresponding to a local maximum of the potential function (9), while and emerge as center points representing local minima of the same potential function, as shown in the phase portrait for system (6) in Figure 4a. All phase trajectories remain bounded, with their characteristics governed by the parameter k: for , a family of red periodic trajectories encircles ; for , two distinct families of brown periodic orbits appear surrounding both and within the blue homoclinic orbits at ; and at , a single cyan periodic trajectory exists, all classified as . Furthermore, the system exhibits green super-periodic trajectories characterized by for .b. For the case where , and , the equilibrium configuration demonstrates distinct characteristics: is a center point characterizing a local minimum point for the potential (9) while both equilibrium points are saddle points representing local maximum points for the potential function (9) as shown in Figure 4b, which also includes the phase portrait. All phase orbits are unbounded except for the family of red periodic orbits around when , which are contained within a blue homoclinic orbit at .
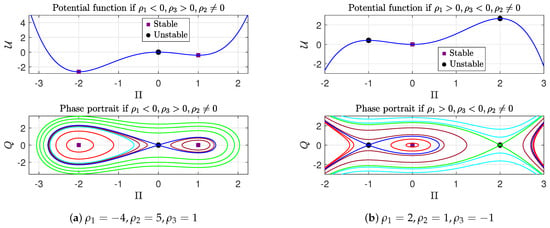
Figure 4.
The phase portrait for the system (6) and the potential function (6) when with . The black solid circle represents unstable equilibrium points, while the purple square denotes a stable equilibrium point.
Figure 5 displays phase portrait diagrams in the parameter plane, illustrating the system’s behavior for both positive and negative values of .
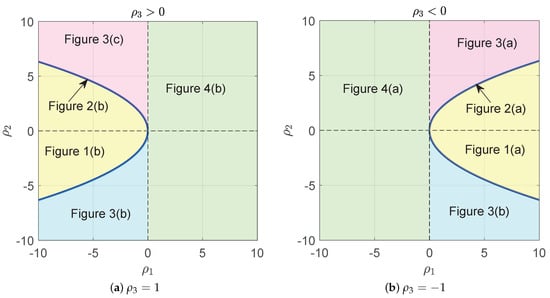
Figure 5.
The phase portrait diagrams in the plane of the parameters.
4. Solutions
This section derives exact solutions to Equation (1) under parameter bifurcation constraints while characterizing their phase orbits. We begin with the following lemma to support this analysis:
Lemma 1
([33]). Let be a solution to Equation (1) for all with asymptotic limits and . Then, Equation (1) admits the following:
- (a)
- A solitary wave solution (homoclinic orbit) when .
- (b)
- A kink/anti-kink solution (heteroclinic orbit) when .
- (c)
- A periodic solution (periodic phase orbit).
- (d)
- Otherwise the solutions are unbounded (unbounded orbits).
Thanks to Lemma 1, we can identify the specific conditions on the physical parameters that give rise to solitary, kink/anti-kink, periodic, and super-periodic solutions based on the structure of the phase orbits, while also excluding unbounded solutions, which are typically undesirable in practical applications. Hence, we can prove the following theorems:
Theorem 1
(Existence of periodic solutions). Let be a solution of Equation (1). Then, Π is periodic if any of the following conditions is fulfilled:
- (a)
- If , and;
- (b)
- If , and ;
- (c)
- If , and
- (d)
- , and ,
where k is the bifurcation parameter, which is selected arbitrarily within the given range.
Theorem 2
(Existence of super-periodic solutions). Let be a solution of Equation (1). Then Π is super-periodic if and the next condition is fulfilled:
where k is the bifurcation parameter, which is selected arbitrarily within the given range.
Theorem 3
(Existence of solitary solutions). Let be a solution of Equation (1). Then, Π is a solitary solution to Equation (1) if any of the following conditions hold:
- (a)
- and the next condition is verified:
- (b)
- and the next condition is satisfied:where k is the bifurcation parameter, which is selected arbitrarily.
The majority of studies on the soliton neuron model (1) focus solely on the solitary solution. In this work, we compare our results with those available in the literature. In ref. [30], the authors examine the conserved quantity (8) at the zero level of the bifurcation parameter k and numerically solve the system to investigate how physical parameters influence solitary solutions. In contrast, the present study provides the exact form of the solitary solution not only at the zero level of k but also for additional values. We now demonstrate that both studies yield consistent results at the zero level.
According to Theorem 3, a solitary solution exists at the zero level of the bifurcation parameter k if , , and , where
where . Thus, the solitary solution is valid when , , and , where is assumed to be positive, which aligns with the conditions established in ref. [30]. Consequently, our findings encompass a broader set of cases that lead to solitary solutions. Furthermore, the authors of ref. [30] investigated the influence of physical parameters on solitary solutions by considering real-valued parameters. These influences manifest in the width and amplitude of the solutions, which are consistent with the results of the current study, as we will discuss later. Therefore, the present study provides a more comprehensive analysis.
Next, we will derive several solutions to Equation (1) by applying the parameter constraints established in the preceding theorems.
4.1. Periodic Solutions
This subsection aims to derive new exact periodic solutions to Equation (1) using the parameter conditions given in Theorem 1. We consider the cases below:
- A. Part (a) in Theorem 1 shows that the polynomial (11) has two real roots denoted by with and two complex conjugate roots denoted by , where ∗ refers to the complex conjugate, so that we have . The real solutions for Equation (1) exists in this case if . We integrate both sides of Equation (10) presuming to derive a new solution to Equation (1) in the formwhere , , and . The solution (18) is periodic, with a period given by , with being the first-kind complete elliptic integral [37].
- B. The conditions of Theorem 1(b) ensure four real roots for (11). Consequently, we have . One can construct real solutions to Equation (1) if . Let us presume . We integrate both sides of Equation (10) with the assumption that to derive a new solution to Equation (1) in the formwhere . The period of the solution (19) is . The solution (19) belongs to the left family of periodic trajectories, as depicted in Figure 3a,b. However, when , we integrate both sides of (10) with the assumption that to derive a new solution of the formThe solution (20) is periodic solution to Equation (1) with the period and corresponds to the right family of periodic trajectories, as depicted in Figure 3a,b.
For given values of , and k, the system yields two different solutions determined by variations in real solution intervals, making their analysis fundamentally important.
- C. When part (c) of Theorem 1 is satisfied, the polynomial (11) admits a double root at the origin along with two simple roots given explicitly by . Thus, we have . If , then , and consequently, the interval of real solutions to Equation (1) is , while if , then , and therefore, the interval of real solutions to Equation (1) is . We integrate both sides of Equation (10) with to find a new periodic solution to Equation (1) in the form
- D. The conditions on the parameters in part (d) of Theorem 1 shows that the polynomial (11) has four real zeros denoted by with . Therefore, we write . The intervals of real solutions are given by . We exclusively examine because this interval generates periodic solutions, unlike other intervals that lead to unbounded behavior. We integrate both sides of Equation (10) with the assumption that concedeswhere . Solution (22) provides a new periodic solution to Equation (1) with the period .
4.2. Super-Periodic Solutions
Nonlinear waves of the super-periodic type form a special category distinguished by intricate phase portraits with non-trivial topology. These wave patterns are more complex than simple periodic ones, as their phase-plane trajectories loop around multiple stable equilibrium points (centers) and intersect separatrix boundaries. Such solutions are encountered in a variety of physical systems, including fluid flows, optical media, and plasma environments, where these waves significantly contribute to the understanding of how nonlinear wave behavior leads to structured formations in space and time. For further exploration of their behavior and relevance, see [38,39].
The conditions of the physical parameters yielding super-periodic solutions to Equation (1) are collected in Theorem 2 and demonstrate that the quartic polynomial (11) admits two real simple roots ( and , where ), and a complex conjugate pair ( and ). Its canonical factorization takes the form . The interval of real solutions is . We integrate both sides of Equation (10), postulating , which gives
where , , and . Solution (23) provides a new periodic solution to Equation (1).
4.3. Solitary Solutions
The solitary wave solution of Equation (1) is constructed in this subsection according to the criteria outlined in Theorem 3. To streamline the presentation, the analysis focuses on select illustrative cases, with the understanding that analogous methods apply to the remaining scenarios.
If , , then by virtue of part (a) in Theorem 3, the polynomial (11) features a double root at , representing the coordinate of the saddle point , along with two simple roots: and . Consequently, takes the form , where the roots are ordered as . The roots and are given by
The intervals for real solutions are . The solitary solution corresponding to the left homoclinic trajectory aligns with the interval , whereas the other solitary solution corresponding to the right homoclinic trajectory aligns with the interval . These trajectories are visually represented by the blue curves in Figure 3b. Below, we systematically derive the solution for each interval separately.
On the other hand, if and , which is a part (b) in Theorem 3, then the root structure of (11) consists of a double root at 0 and two simple roots at and . If , then these roots satisfy , while if , they satisfy . Accordingly, the polynomial (11) can be expressed as . The interval of real wave propagation for , and for . We integrate both sides of Equation (10) under the assumption that to derive
which yields a novel solitary solution to Equation (1).
5. Physical Explanation
This section displays graphical depictions of the derived solutions and analyzes how key physical parameters affect them.
Using the assigned values , and , the parameters are calculated via Equation (5), yielding , and . The phase portrait for the unperturbed system (6), corresponding to these values, is illustrated in Figure 3a. Following Theorem 1, Theorem 2, and Theorem 3, the solution type is determined by the bifurcation parameter k. Thus, we consider the next three cases:
- (a) If , Equation (1) admits a super-periodic solution of the form (23). For illustration, we choose , which yields the following roots for the polynomial (11): . Under these conditions, the solution (23) takes the explicit formFigure 6a,b display the 3D and 2D representations of the super-periodic solution given in (27). To analyze the effects of the parameters (frequency) and (sound velocity), we hold all other physical parameters constant while varying only these two. Figure 6c demonstrates how the frequency influences solution (23). Evidently, as the frequency increases, both the width and amplitude of the solution also increase. Conversely, Figure 6d illustrates the impact of sound velocity on the same solution. Notably, higher sound velocity leads to a nearly constant amplitude but a reduction in the solution’s width.
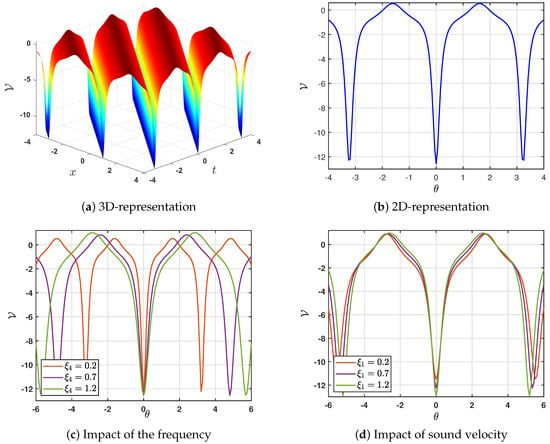 Figure 6. Graphic representation for the super-solution (23).
Figure 6. Graphic representation for the super-solution (23). - (b) When , Equation (1) admits a solitary wave solution, as established by Theorem 3. In this scenario, the roots of the polynomial (11) are . Selecting an appropriate interval for real wave propagation, we take . Hence, the solitary solution (24) takes the formFigure 7 illustrates the 3D and 2D profiles of the solitary solution (24). The solution exhibits symmetry, as seen in Figure 7a, about the plane , and in Figure 7b, about the vertical line . To analyze the influence of the parameters (frequency) and (sound velocity), we vary only these two while holding other physical parameters constant. Increasing the frequency leads to a higher amplitude but a narrower width of the solution, as depicted in Figure 7c. Conversely, an increase in the sound velocity results in a reduction in amplitude and an expansion in width, as demonstrated in Figure 7d.
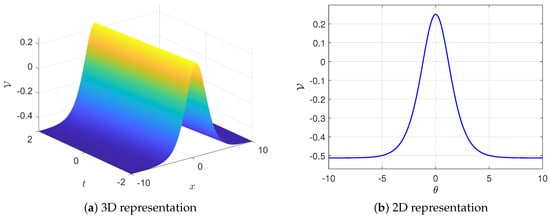
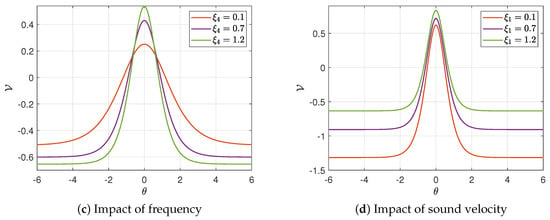 Figure 7. Graphic representation for the solitary solution (24).
Figure 7. Graphic representation for the solitary solution (24). - (c) For , Equation (1) yields a periodic solution (18). Upon computing the roots of the polynomial (11), this solution simplifies to the following expression:The periodic nature of solution (18) is depicted in Figure 8a,b. Figure 8c,d further demonstrate the effects of the frequency and sound velocity on the solution. Notably, as the frequency rises, the amplitude remains nearly constant, whereas the width of the solution expands (Figure 8d). Conversely, an increase in sound velocity leads to growth in both the amplitude and width of the solution.
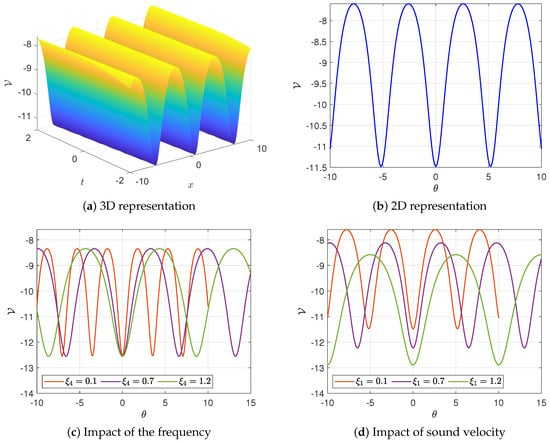 Figure 8. Graphic representation for the periodic solution (18).
Figure 8. Graphic representation for the periodic solution (18).
6. Dynamical Analysis of Perturbed System
This section examines the autoresonance phenomenon in a non-autonomous system, where the oscillator self-adjusts under a time-periodic driving force. The perturbed traveling wave system, derived from Equation (1), arises due to external influences. These perturbations are modeled through additional forcing terms, expressed as . Thus, Equation (1) admits the form
By inserting the transformation (2) into Equation (30) and integrating twice with respect to , the perturbed system associated with the unperturbed system (6) is obtained in the form
where are defined as in (5) and the periodic external effect is suitably chosen as , wherein p indicates the strength of the external periodic force, q refers to the frequency, and is the modulus of the Jacobi elliptic function [37], which is restricted to .
We numerically examine the dynamics of both the unperturbed system (Equation (6), with ) and the perturbed system (Equation (31)), with particular attention to how the periodic perturbation modifies the system’s behavior.
The unperturbed system with parameters yields , and via Equation (5). With , periodic orbits exist for all positive values of k, which depend on the suitable selection for the initial conditions. Using the initial conditions gives , and Theorem 1 confirms the unperturbed system’s periodic nature through 2D and 3D phase portraits, as illustrated in Figure 9a,b. This periodic behavior is further confirmed by the temporal evolution of and Q versus , as demonstrated in Figure 9c. This phenomenon consistently occurs because the frequencies maintain an incommensurate relationship.

Figure 9.
Dynamical behavior for perturbed system (6) with initial conditions and while , , , and .
The soliton neuron model’s dynamical behavior—encompassing both periodic and chaotic regimes—becomes more complex due to the introduction of free parameters , and , alongside the perturbation-related parameters . To analyze this system, we employ a multifaceted approach involving 2D/3D phase portraits, time series analysis, and parameter sensitivity studies. Specifically, we investigate two representative scenarios while systematically varying the external force’s frequency (or amplitude), holding all other parameters constant.
In the first scenario, we maintain fixed values for and , while setting the periodic external force strength at . We systematically vary the frequency q of the external periodic force, keeping the initial conditions unchanged. At , the 2D and 3D phase portraits of the perturbed system (6) reveal quasi-periodic wave patterns as shown in Figure 10a–c, which are further supported by the time series of and Q versus . Growing the frequency to preserves this quasi-periodic behavior, as evidenced in Figure 10d–f. Notably, chaotic dynamics fail to emerge even at higher frequencies (), as demonstrated in Figure 10g–i.
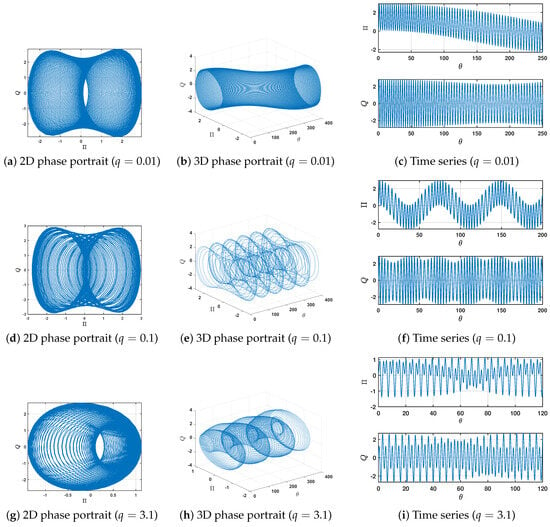
Figure 10.
Dynamical behavior for unperturbed system (6) with initial conditions and while , , , , , and .
In the second scenario, we select appropriate physical parameters while holding two of the three parameters constant and . The chosen values , , and yield these values. With the periodic force strength fixed at and initial conditions , we examine the system’s response to varying frequencies q. At , the perturbed system maintains quasi-periodic dynamics, as evidenced by the phase portraits and time series in Figure 11a–c. However, increasing the frequency to triggers a transition to chaotic behavior as in Figure 11d–f. This chaotic regime becomes more pronounced at , as demonstrated in Figure 11g–i.
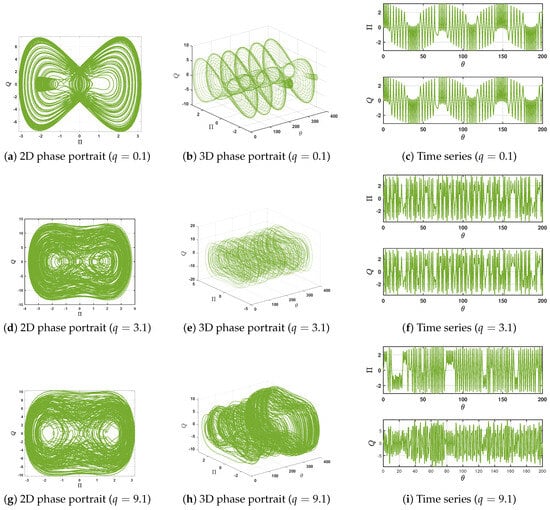
Figure 11.
Dynamical behavior for unperturbed system (6) with initial conditions and while , , , , , and .
Let us compute the Lyapunov exponents for the perturbed system (31) for the same values of the parameters used in Figure 11g–i. Numerical simulations of Lyapunov exponents serve as a powerful method for analyzing chaos and stability in complex dynamical systems. However, accurate interpretation of the results demands a thorough grasp of the system’s underlying dynamics, as these exponents are highly sensitive to system-specific properties [40]. Lyapunov exponents determine whether a system exhibits chaotic behavior: a positive value indicates chaos, while a negative value suggests convergence. Hence, computing these values are significant. The Lyapunov exponents for the perturbed system are
To demonstrate the system’s complexity (31), the Lyapunov exponent is plotted in the time domain, as shown in Figure 12. The positive exponent in Figure 12 confirms the system’s chaotic behavior. Furthermore, Table 1 summarizes the convergence of Lyapunov exponents.
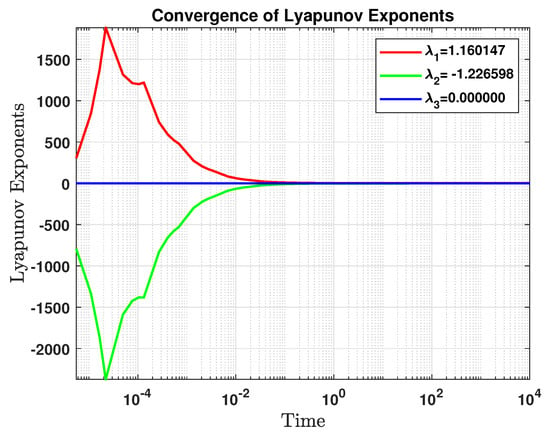
Figure 12.
Lyapunov exponents for the perturbed system (31) with while , , , , , and .

Table 1.
Lyapunov exponent iterations.
We further investigated the dependence of the Lyapunov exponents on the parameter q in the perturbed system (31), considering and using the same parameter values as in Figure 11.
Figure 13a illustrates the Lyapunov exponents , and as functions of q, providing important insights into the system’s stability and chaotic behavior. The red curve representing consistently remains above the dashed black line, which serves as the zero threshold, helping to visualize the Lyapunov exponent signs. This pattern indicates that the system exhibits at least one direction in which nearby trajectories diverge exponentially, suggesting chaotic dynamics. Meanwhile, the green curve corresponding to fluctuates around zero, signaling sensitivity in this direction, though not necessarily confirming chaotic behavior. In contrast, the blue curve associated with remains at zero, implying the absence of exponential divergence along this axis. The presence of a positive Lyapunov exponent, , is a strong indicator of chaos, meaning that even small variations in initial conditions can lead to exponentially different trajectories over time.
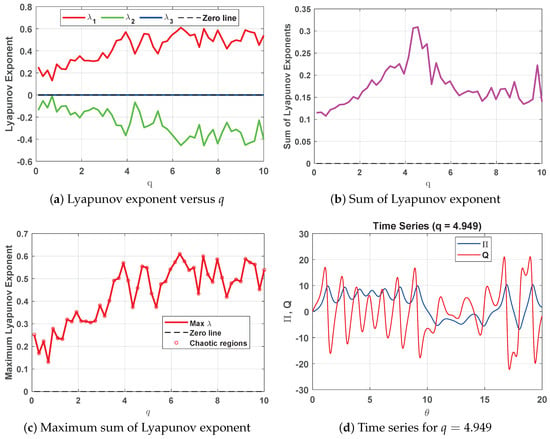
Figure 13.
Lyapunov exponents for the perturbed system (31) versus the parameter q, where with while , , , , , and .
Figure 13b depicts the variation in the sum of Lyapunov exponents as a function of q. The magenta curve highlights fluctuations in system stability and chaotic behavior across different values of q. It reveals significant peaks and variations in the sum of Lyapunov exponents, helping to identify regions where chaotic dynamics are more pronounced. A positive sum of Lyapunov exponents confirms chaotic behavior, indicating exponential divergence in system trajectories, while lower values correspond to more stable conditions.
Figure 13c shows the maximum Lyapunov exponent as a function of q. The red line with circular markers represents the maximum Lyapunov exponent at different parameter values, with red circles highlighting regions where chaos is evident. A positive maximum Lyapunov exponent suggests that the system exhibits chaotic behavior in these specific parameter ranges.
Figure 13d illustrates the time series of and Q as functions of when . The oscillatory nature of the curves may indicate chaotic dynamics, aligning with observations from other parts of Figure 13.
Finally, it is worth mentioning that the emergence of a chaotic regime is linked to both functional adaptability and pathological disruptions in neural dynamics. In pathological states, chaotic activity has been proposed as a factor in conditions such as epilepsy, where irregular and unpredictable firing patterns arise [41]. The transition from periodic spiking to chaotic bursting observed in our model may provide insights into seizure-like dynamics, particularly within hyperexcitable neural networks, as well as anesthesia-related transitions [42].
7. Finding
This study offers a thorough analysis of the soliton neuron model, emphasizing key findings that deepen our understanding of nonlinear neural dynamics. The main findings are introduced in the following items:
- A. Hamiltonian System and Wave Solutions: The soliton neuron model was reformulated as a two-dimensional conservative Hamiltonian system, enabling the analysis of wave solutions using phase portraits and bifurcation theory. Exact solutions—including periodic, super-periodic, and solitary waves—were analytically derived and classified based on parameter conditions (Theorems 1–3). For clarity, these solutions are summarized in Table 2 for periodic waves, Table 3 for super-periodic waves, and Table 4 for solitary waves.
 Table 2. The conditions for the existence of periodic solutions and their explicit formulation.
Table 2. The conditions for the existence of periodic solutions and their explicit formulation. Table 3. The conditions for the existence of super-periodic solutions and their explicit formulation.
Table 3. The conditions for the existence of super-periodic solutions and their explicit formulation. Table 4. The conditions for the existence of solitary solutions and their explicit formulation.
Table 4. The conditions for the existence of solitary solutions and their explicit formulation. - B. Impact of Physical Parameters: Higher frequencies () led to an increase in both the amplitude and width of super-periodic waves, as illustrated in Figure 6c, while simultaneously reducing the width of solitary waves, as shown in Figure 7c. Similarly, variations in sound velocity () influenced wave characteristics, with increased sound velocity maintaining the amplitude of super-periodic waves while narrowing their width (Figure 6d). In contrast, higher sound velocity decreased the amplitude of solitary waves while expanding their width, as depicted in Figure 7d.
- C. Quasi-Periodic and Chaotic Dynamics: The introduction of a periodic external force led to quasi-periodic and chaotic behavior, which was effectively visualized using phase portraits and time series plots, as shown in Figure 10 and Figure 11. Further analysis using Lyapunov exponents confirmed the presence of chaotic regimes, with positive exponents indicating a strong sensitivity to initial conditions, as illustrated in Figure 12.
- D. Comparative Novelty: Unlike previous studies that employed methods such as Kudryashov [26], the ()-expansion [27], the Kumar–Malik method, the multivariate generalized exponential rational integral function method, and the Riccati-modified extended simple equation method [28], this work derives solutions using Jacobi elliptic functions and conducts a symbolic bifurcation analysis, enhancing interpretability. Moreover, most previous studies on the model (1) focus solely on the solitary solution [30]. We demonstrate that the prior results can be recovered from our findings when the bifurcation parameter k is set to zero. Additionally, the influence of physical parameters on solitary solutions in both studies is consistent, primarily affecting the width and amplitude of the solutions. Furthermore, our investigation of quasi-periodicity and chaotic dynamics in the perturbed system introduces a novel contribution to the literature on soliton neuron models.
These findings highlight the soliton neuron model’s effectiveness in capturing the mechanisms of neural signal propagation, demonstrating its relevance in both fundamental neuroscience and applied research. The model’s ability to account for nonlinear and chaotic dynamics makes it particularly valuable for investigating neurological disorders, such as epilepsy, where abnormal signal transmission and chaotic neural activity are key pathological features. By offering insights into how chaotic behavior emerges within neural systems, this approach could pave the way for improved diagnostic tools, enhanced predictive models, and the development of novel therapeutic interventions aimed at stabilizing neural activity and mitigating epileptic episodes.
8. Conclusions
This study investigates the dynamic properties of the soliton neuron model, a mathematical framework used to analyze complex neural processes, including the mechanisms of various anesthetics. Through an appropriate wave transformation, the original model reduces to a planar dynamical system—a conservative Hamiltonian system characterized by a single degree of freedom. This reduction establishes that obtaining wave solutions for the neuronal model (1) is mathematically equivalent to analyzing the trajectory of a one-dimensional particle moving in a tri-parameter potential field (9). This mechanical analogy proves fundamental, as it reveals the physically meaningful wave propagation regimes through their correspondence with admissible particle motions in the Hamiltonian framework.
The traveling wave system’s bifurcation analysis yields several important findings:
- A.
- The method classifies solution types based on phase orbit analysis (Lemma 1), enabling rigorous proofs for the existence of periodic, solitary, and super-periodic solutions (Theorems 1–3).
- B.
- Real (non-complex) solutions are derived by integrating the conserved quantity (Equation (8)), leveraging the particle motion equivalence to ensure physical validity.
- C.
- Unbounded solutions, corresponding to unbounded phase orbits, are systematically excluded due to their lack of physical relevance.
Analytical solutions are obtained and illustrated using 2D and 3D graphical representations. This study further examines how critical parameters—frequency and sound velocity—affect solution characteristics:
- For periodic waves, frequency has negligible impact on amplitude but widens the solution (Figure 8d), whereas sound velocity enhances both amplitude and width.
- For super-periodic waves, frequency amplifies both amplitude and width, whereas sound velocity preserves amplitude but narrows the solution (Figure 6d).
Inserting a generalized periodic external force induces quasi-periodic and chaotic dynamics, visualized through 2D/3D phase portraits and time series plots. Lyapunov exponents are computed to quantify chaos, and numerical simulations confirm that external force parameters (frequency and amplitude) critically influence the system’s behavior.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU251903].
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the author.
Acknowledgments
The author acknowledges the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University for the financial support.
Conflicts of Interest
The author has no conflicts of interest.
References
- Ilhan, O.A.; Manafian, J. Periodic type and periodic cross-kink wave solutions to the (2 + 1)-dimensional breaking soliton equation arising in fluid dynamics. Mod. Phys. Lett. B 2019, 33, 1950277. [Google Scholar] [CrossRef]
- Li, C.; Manafian, J.; Eslami, B.; Mahmoud, K.H.; Abass, R.R.; Bashar, B.S.; Ilhan, O.A. A generalized trial equation scheme: A tool for solving thin films constructed from the ferroelectric materials. Int. J. Mod. Phys. B 2024, 38, 2450308. [Google Scholar] [CrossRef]
- Mehrpooya, M.; Ghadimi, N.; Marefati, M.; Ghorbanian, S.A. Numerical investigation of a new combined energy system includes parabolic dish solar collector, Stirling engine and thermoelectric device. Int. J. Energy Res. 2021, 45, 16436–16455. [Google Scholar] [CrossRef]
- Ara, A.; Khan, N.A.; Razzaq, O.A.; Hameed, T.; Raja, M.A.Z. Wavelets optimization method for evaluation of fractional partial differential equations: An application to financial modelling. Adv. Differ. Equ. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Holmes, E.E.; Lewis, M.A.; Banks, J.; Veit, R. Partial differential equations in ecology: Spatial interactions and population dynamics. Ecology 1994, 75, 17–29. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E.; Shohib, R.; Biswas, A. Highly dispersive solitons in optical couplers with metamaterials having Kerr law of nonlinear refractive index. Ukr. J. Phys. Opt. 2024, 25, 01001–01019. [Google Scholar] [CrossRef]
- Chen, X.; Yan, X.; Zhang, X.; Wang, F.; Suzuki, T.; Ohishi, Y.; Cheng, T. Highly sensitive nonlinear temperature sensor based on soliton self-frequency shift technique in a microstructured optical fiber. Sens. Actuators A Phys. 2022, 334, 113333. [Google Scholar] [CrossRef]
- Arnous, A.H. Optical solitons with Biswas–Milovic equation in magneto-optic waveguide having Kudryashov’s law of refractive index. Optik 2021, 247, 167987. [Google Scholar] [CrossRef]
- Serge, D.Y.; Justin, M.; Betchewe, G.; Crepin, K.T. Optical chirped soliton in metamaterials. Nonlinear Dyn. 2017, 90, 13–18. [Google Scholar] [CrossRef]
- Wang, K.J.; Shi, F.; Li, S.; Xu, P. Dynamics of resonant soliton, novel hybrid interaction, complex N-soliton and the abundant wave solutions to the (2 + 1)-dimensional Boussinesq equation. Alex. Eng. J. 2024, 105, 485–495. [Google Scholar] [CrossRef]
- Wang, K.J. The generalized (3 + 1)-dimensional B-type Kadomtsev–Petviashvili equation: Resonant multiple soliton, N-soliton, soliton molecules and the interaction solutions. Nonlinear Dyn. 2024, 112, 7309–7324. [Google Scholar] [CrossRef]
- Wang, K.J. N-soliton, soliton molecules, Y-type soliton, periodic lump and other wave solutions of the new reduced B-type Kadomtsev–Petviashvili equation for shallow water waves. Eur. Phys. J. Plus 2024, 139, 1–13. [Google Scholar] [CrossRef]
- Gurney, K. An Introduction to Neural Networks; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Muhammad, J.; Younas, U.; Almutairi, D.; Khan, A.; Abdeljawad, T. Optical wave features and sensitivity analysis of a coupled fractional integrable system. Results Phys. 2025, 68, 108060. [Google Scholar] [CrossRef]
- Raza, N.; Salman, F.; Butt, A.R.; Gandarias, M.L. Lie symmetry analysis, soliton solutions and qualitative analysis concerning to the generalized q-deformed Sinh-Gordon equation. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106824. [Google Scholar] [CrossRef]
- Elbrolosy, M.; Elmandouh, A. Painlevé analysis, Lie symmetry and bifurcation for the dynamical model of radial dislocations in microtubules. Nonlinear Dyn. 2025, 113, 13699–13714. [Google Scholar] [CrossRef]
- Gandarias, M.L.; Raza, N.; Umair, M.; Almalki, Y. Dynamical Visualization and Qualitative Analysis of the (4 + 1)-Dimensional KdV-CBS Equation Using Lie Symmetry Analysis. Mathematics 2024, 13, 89. [Google Scholar] [CrossRef]
- Muhammad, J.; Ali, Q.; Younas, U. On the analysis of optical pulses to the fractional extended nonlinear system with mechanism of third-order dispersion arising in fiber optics. Opt. Quantum Electron. 2024, 56, 1168. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Siddique, I.; Mehdi, K.B.; Elmandouh, A.; Inc, M. Novel exact solutions, bifurcation of nonlinear and supernonlinear traveling waves for M-fractional generalized reaction Duffing model and the density dependent M-fractional diffusion reaction equation. Results Phys. 2022, 37, 105485. [Google Scholar] [CrossRef]
- El-Dessoky, M.; Elmandouh, A. Qualitative analysis and wave propagation for Konopelchenko-Dubrovsky equation. Alex. Eng. J. 2023, 67, 525–535. [Google Scholar] [CrossRef]
- Song, J.; Li, F.; Zhang, M. Bifurcations and Exact Solutions of the Coupled Nonlinear Generalized Zakharov Equations with Anti-Cubic Nonlinearity: Dynamical System Approach. Mathematics 2025, 13, 217. [Google Scholar] [CrossRef]
- Elmandouh, A.; Al Nuwairan, M.; El-Dessoky, M. Nonlinear Dynamical Analysis and New Solutions of the Space-Fractional Stochastic Davey–Stewartson Equations for Nonlinear Water Waves. Mathematics 2025, 13, 692. [Google Scholar] [CrossRef]
- Alomair, A.; Al Naim, A.S.; Bekir, A. Exploration of Soliton Solutions to the Special Korteweg–De Vries Equation with a Stability Analysis and Modulation Instability. Mathematics 2024, 13, 54. [Google Scholar] [CrossRef]
- Rashedi, K.A.; Almusawa, M.Y.; Almusawa, H.; Alshammari, T.S.; Almarashi, A. Applications of Riccati–Bernoulli and Bäcklund Methods to the Kuralay-II System in Nonlinear Sciences. Mathematics 2024, 13, 84. [Google Scholar] [CrossRef]
- Yang, L.; Hou, X.; Zeng, Z. A complete discrimination system for polynomials. Sci. China Ser. E 1996, 39, 628–646. [Google Scholar]
- Alam, M.N.; Rahman, M.A. Study of the parametric effect of the wave profiles of the time-space fractional soliton neuron model equation arising in the topic of neuroscience. Partial Differ. Equ. Appl. Math. 2024, 12, 100985. [Google Scholar] [CrossRef]
- Alam, M.N.; Akash, H.S.; Saha, U.; Hasan, M.S.; Parvin, M.W.; Tunç, C. Bifurcation analysis and solitary wave analysis of the nonlinear fractional soliton neuron model. Iran. J. Sci. 2023, 47, 1797–1808. [Google Scholar] [CrossRef]
- Younas, U.; Muhammad, J.; Almutairi, D.; Khan, A.; Abdeljawad, T. Analyzing the neural wave structures in the field of neuroscience. Sci. Rep. 2025, 15, 7181. [Google Scholar] [CrossRef]
- Engelbrecht, J.; Peets, T.; Tamm, K. Electromechanical coupling of waves in nerve fibres. Biomech. Model. Mechanobiol. 2018, 17, 1771–1783. [Google Scholar] [CrossRef]
- Heimburg, T.; Jackson, A.D. On soliton propagation in biomembranes and nerves. Proc. Natl. Acad. Sci. USA 2005, 102, 9790–9795. [Google Scholar] [CrossRef]
- Dauxois, T.; Peyrard, M. Physics of Solitons; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Goldstein, H. Classical Mechanics Addison-Wesley Series in Physics; Addison-Wesley: Boston, MA, USA, 1980. [Google Scholar]
- Saha, A.; Banerjee, S. Dynamical Systems and Nonlinear Waves in Plasmas; CRC Press: Boca Raton, FL, USA, 2021; pp. x+207. [Google Scholar]
- Nemytskii, V.V. Qualitative Theory of Differential Equations; Princeton University Press: Princeton, NJ, USA, 2015; Volume 2083. [Google Scholar]
- Dubinov, A.; Kolotkov, D.Y.; Sazonkin, M. Supernonlinear waves in plasma. Plasma Phys. Rep. 2012, 38, 833–844. [Google Scholar] [CrossRef]
- Kotkin, G.L.; Serbo, V. Lectures on Analytical Mechanics; Oxford University Press: Oxford, UK, 2024. [Google Scholar]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed.; Die Grundlehren der Mathematischen Wissenschaften, Band 67; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1971; pp. xvi+358. [Google Scholar]
- Saha, A.; Tamang, J. Effect of q-nonextensive hot electrons on bifurcations of nonlinear and supernonlinear ion-acoustic periodic waves. Adv. Space Res. 2019, 63, 1596–1606. [Google Scholar] [CrossRef]
- Tamang, J.; Saha, A. Dynamical behavior of supernonlinear positron-acoustic periodic waves and chaos in nonextensive electron-positron-ion plasmas. Z. Für Naturforschung A 2019, 74, 499–511. [Google Scholar] [CrossRef]
- Layek, G. An Introduction to Dynamical Systems and Chaos; Springer: West Bengal, India, 2015; Volume 1. [Google Scholar]
- Ching, S.; Brown, E.N.; Kramer, M.A. Distributed Control in a Mean-Field Cortical Network Model: Implications for Seizure Suppression. J. Math. Neurosci. 2012, 2, 1–25. [Google Scholar] [CrossRef]
- Hudson, A.E.; Calderon, D.P.; Pfaff, D.W.; Proekt, A. Recovery of Consciousness Is Mediated by a Network of Discrete Metastable Activity States. Front. Syst. Neurosci. 2014, 8, 9. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).