Unsupervised Contrastive Graph Kolmogorov–Arnold Networks Enhanced Cross-Modal Retrieval Hashing
Abstract
1. Introduction
- We present UCGKANH, an unsupervised cross-modal hashing framework that leverages contrastive learning and is further enhanced by GraphKAN and hypergraph-based modeling. Unlike existing deep unsupervised cross-modal hashing methods that rely solely on CNN-based encoders or basic graph structures [15,25], our model uniquely integrates GraphKAN to enhance feature expressiveness via learnable activation functions. By integrating Kolmogorov–Arnold Networks into the retrieval process, the model achieves more expressive and discriminative feature representations.
- We design an unsupervised contrastive learning strategy tailored for cross-modal hashing. By leveraging instance-level contrastive learning without requiring explicit labels, our method significantly enhances the discrimination and consistency of hash codes across different modalities.
- We incorporate hypergraph-based semantic structure modeling to capture high-order relationships across image–text pairs. This mitigates the shortcomings of traditional graph-based methods and enhances the generalization of the generated hash codes in challenging cross-modal retrieval environments. Specifically, our proposed method leverages the synergistic effect between GraphKAN and hypergraph via contrastive learning to enhance cross-modal hashing performance.
2. Related Work
2.1. Deep Cross-Modal Hashing
2.2. Kolmogorov–Arnold Networks
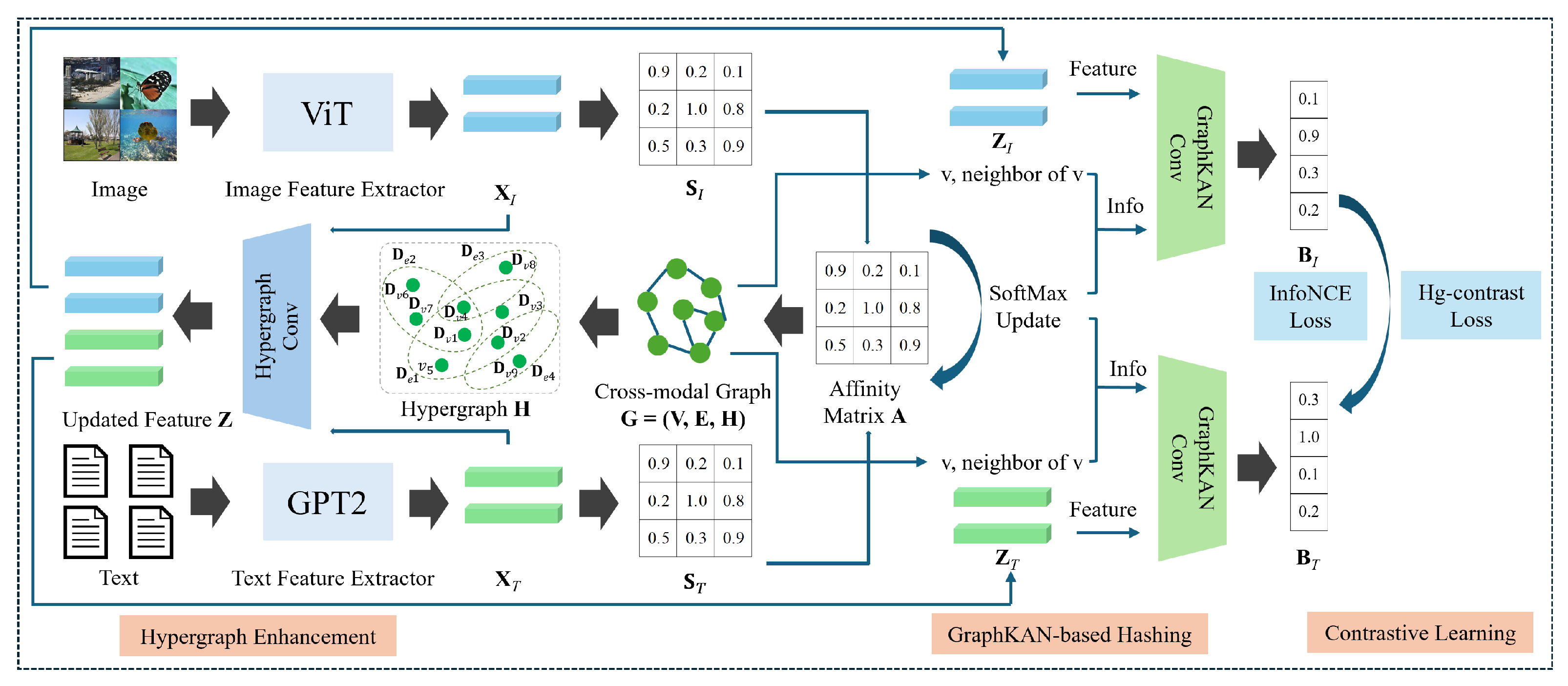
3. Methodology
| Algorithm 1: UCGKANH Algorithm |
|
3.1. Notation
3.2. Model Architecture
3.2.1. Similarity Matrix and Graph Relation Construction
3.2.2. Hypergraph Enhancement
3.2.3. GraphKAN-Based Hashing
3.2.4. Contrastive Learning for Cross-Modal Alignment
3.3. Overall Objective Function
4. Experiment
4.1. Implementation Details
4.2. Dataset Description
4.3. Baselines and Evaluation Criteria
4.4. Comparing with Baseline Methods
4.4.1. mAP Analysis
4.4.2. Tok-K Analysis
4.5. Computational Efficiency Analysis
- Total Training Time (s): The overall time required to train the model for 50 epochs.
- Query Time (s): The total time taken to generate hash codes for all samples in the query set during the inference phase.
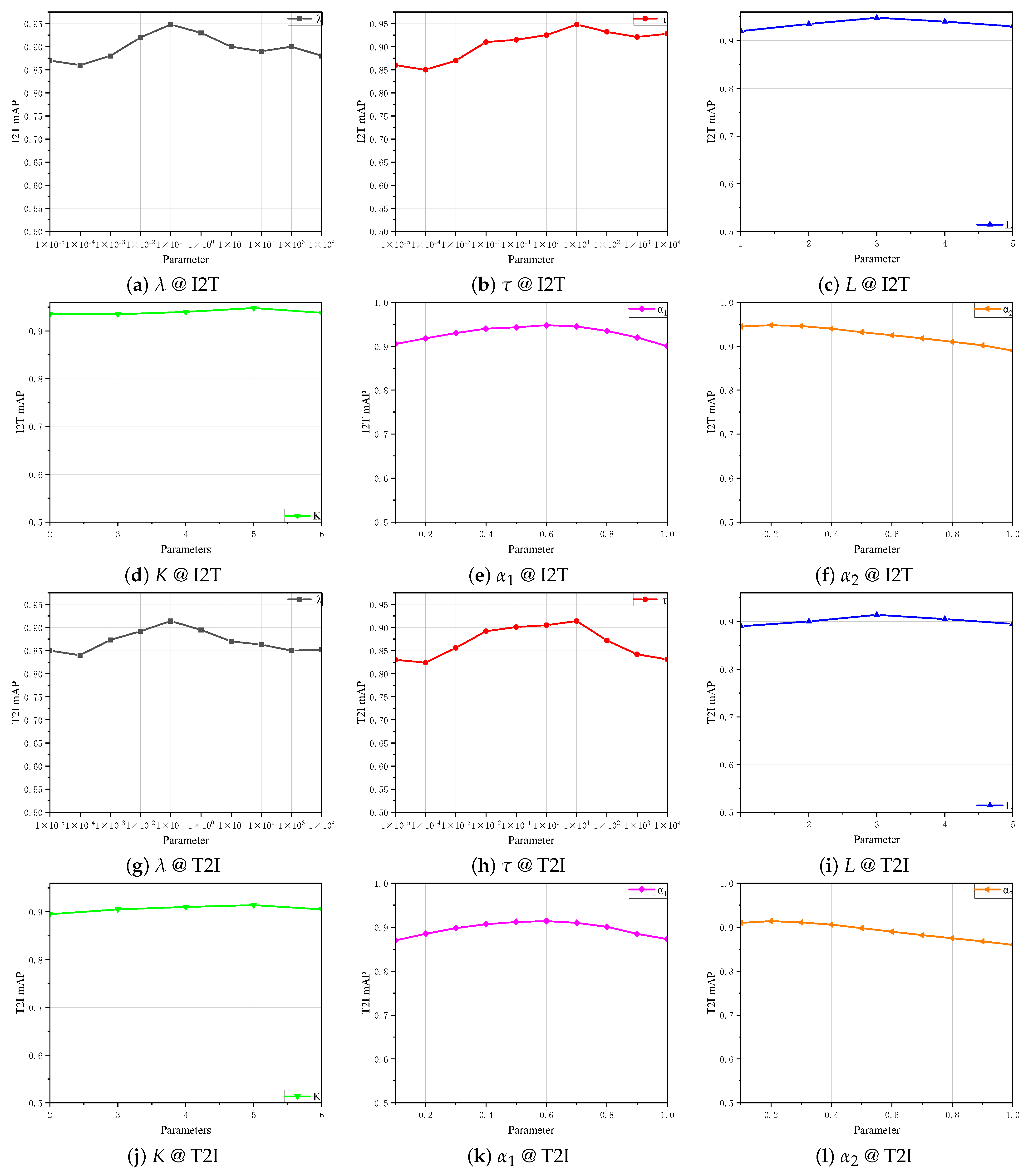
4.6. Parameter Sensitivity Analysis
4.7. Ablation Study
- Base Model: This is a fundamental baseline using standard Graph Convolutional Network (GCN) without any of our proposed enhancements. It directly concatenates image and text features and applies standard graph convolution with ReLU activation, optimizing only the quantization loss .
- w/o HGNN: We remove the hypergraph enhancement module, which utilizes Hypergraph Neural Network (HGNN), directly using the concatenated features as input to the GraphKAN layer. The contrastive learning step does not use hypergraph-guided positive pairs.
- w/o GraphKAN: We replace the GraphKAN module with a standard graph convolutional network (GCN), where the feature update is simplified to , with being the ReLU activation.
- w/o CL: We remove the contrastive learning (CL) loss, optimizing the model solely with the quantization loss .
| Task | Method | MIRFlickr-25K | NUS-WIDE | MS COCO | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 Bits | 32 Bits | 64 Bits | 128 Bits | 16 Bits | 32 Bits | 64 Bits | 128 Bits | 16 Bits | 32 Bits | 64 Bits | 128 Bits | ||
| I→T | Base Model | 0.798 | 0.821 | 0.835 | 0.842 | 0.721 | 0.743 | 0.756 | 0.768 | 0.752 | 0.789 | 0.805 | 0.819 |
| UCGKANH w/o HGNN | 0.859 | 0.898 | 0.932 | 0.939 | 0.783 | 0.817 | 0.829 | 0.845 | 0.845 | 0.893 | 0.913 | 0.927 | |
| UCGKANH w/o GraphKAN | 0.856 | 0.893 | 0.928 | 0.932 | 0.784 | 0.812 | 0.834 | 0.843 | 0.831 | 0.889 | 0.914 | 0.928 | |
| UCGKANH w/o CL | 0.869 | 0.896 | 0.917 | 0.928 | 0.782 | 0.811 | 0.829 | 0.837 | 0.809 | 0.872 | 0.916 | 0.923 | |
| UCGKANH | 0.908 | 0.922 | 0.940 | 0.948 | 0.818 | 0.837 | 0.857 | 0.865 | 0.860 | 0.919 | 0.929 | 0.946 | |
| T→I | Base Model | 0.762 | 0.784 | 0.798 | 0.806 | 0.695 | 0.718 | 0.731 | 0.745 | 0.721 | 0.765 | 0.782 | 0.798 |
| UCGKANH w/o HGNN | 0.837 | 0.869 | 0.876 | 0.895 | 0.782 | 0.793 | 0.807 | 0.819 | 0.839 | 0.915 | 0.927 | 0.932 | |
| UCGKANH w/o GraphKAN | 0.817 | 0.862 | 0.883 | 0.891 | 0.781 | 0.793 | 0.813 | 0.818 | 0.841 | 0.896 | 0.927 | 0.935 | |
| UCGKANH w/o CL | 0.842 | 0.865 | 0.883 | 0.891 | 0.771 | 0.796 | 0.805 | 0.811 | 0.836 | 0.871 | 0.917 | 0.929 | |
| UCGKANH | 0.879 | 0.896 | 0.907 | 0.914 | 0.792 | 0.807 | 0.815 | 0.826 | 0.861 | 0.917 | 0.923 | 0.949 | |
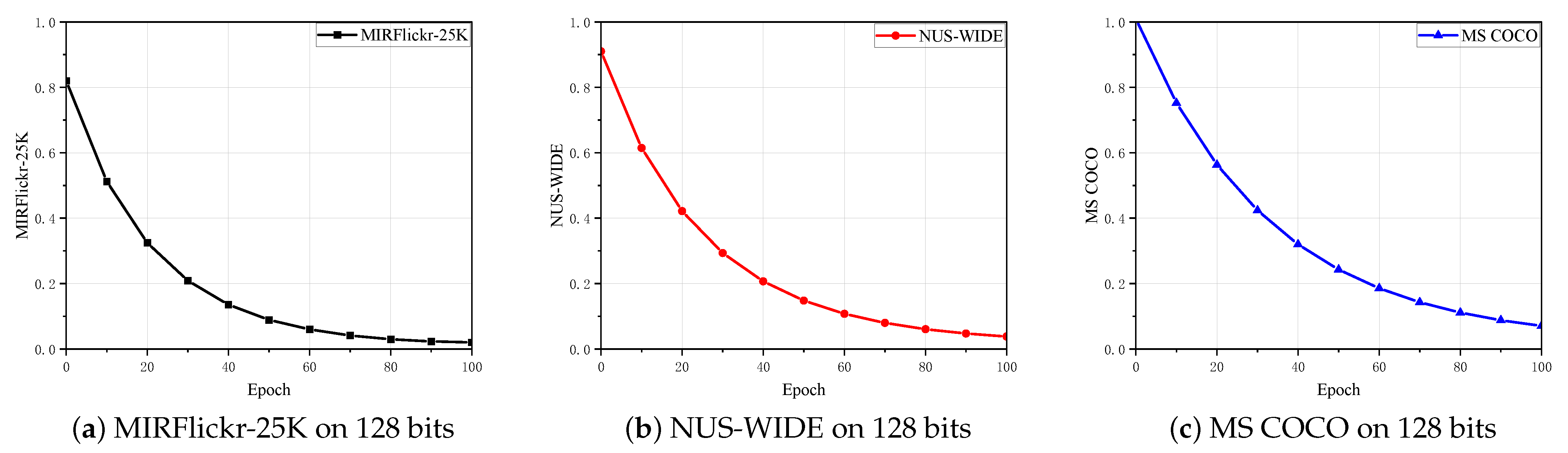
4.8. Convergence Analysis
4.9. Case Study
5. Conclusions and Future Improvements
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Computational Complexity Analysis
Appendix A.1. Time Complexity Analysis
Appendix A.2. Space Complexity
References
- Wang, T.; Li, F.; Zhu, L.; Li, J.; Zhang, Z.; Shen, H.T. Cross-Modal Retrieval: A Systematic Review of Methods and Future Directions. Proc. IEEE 2024, 112, 1716–1754. [Google Scholar] [CrossRef]
- Bin, Y.; Li, H.; Xu, Y.; Xu, X.; Yang, Y.; Shen, H.T. Unifying Two-Stream Encoders with Transformers for Cross-Modal Retrieval. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023. [Google Scholar] [CrossRef]
- Huang, H.; Nie, Z.; Wang, Z.; Shang, Z. Cross-modal and uni-modal soft-label alignment for image-text retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 26–27 February 2024; AAAI Press: Washington, DC, USA, 2024. [Google Scholar] [CrossRef]
- Liu, K.; Gong, Y.; Cao, Y.; Ren, Z.; Peng, D.; Sun, Y. Dual semantic fusion hashing for multi-label cross-modal retrieval. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI ’24), Jeju, Republic of Korea, 3–9 August 2024. [Google Scholar] [CrossRef]
- Hu, Z.; Cheung, Y.M.; Li, M.; Lan, W. Cross-Modal Hashing Method With Properties of Hamming Space: A New Perspective. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 7636–7650. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Dai, J.; Ren, Z.; Chen, Y.; Peng, D.; Hu, P. Dual Self-Paced Cross-Modal Hashing. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 26–27 February 2024; Volume 38, pp. 15184–15192. [Google Scholar] [CrossRef]
- Li, F.; Wang, B.; Zhu, L.; Li, J.; Zhang, Z.; Chang, X. Cross-Domain Transfer Hashing for Efficient Cross-Modal Retrieval. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 9664–9677. [Google Scholar] [CrossRef]
- Li, B.; Li, Z. Large-Scale Cross-Modal Hashing with Unified Learning and Multi-Object Regional Correlation Reasoning. Neural Netw. 2024, 171, 276–292. [Google Scholar] [CrossRef]
- Chen, Y.; Long, J.; Guo, L.; Yang, Z. Supervised Semantic-Embedded Hashing for Multimedia Retrieval. Knowl.-Based Syst. 2024, 299, 112023. [Google Scholar] [CrossRef]
- Chen, H.; Zou, Z.; Liu, Y.; Zhu, X. Deep Class-Guided Hashing for Multi-Label Cross-Modal Retrieval. Appl. Sci. 2025, 15, 3068. [Google Scholar] [CrossRef]
- Wu, Y.; Li, B.; Li, Z. Revising similarity relationship hashing for unsupervised cross-modal retrieval. Neurocomputing 2025, 614, 128844. [Google Scholar] [CrossRef]
- Liu, H.; Xiong, J.; Zhang, N.; Liu, F.; Zou, X.; Köker, R. Quadruplet-Based Deep Cross-Modal Hashing. Intell. Neurosci. 2021, 2021, 9968716. [Google Scholar] [CrossRef]
- Shen, X.; Huang, Q.; Lan, L.; Zheng, Y. Contrastive transformer cross-modal hashing for video-text retrieval. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI ’24), Jeju, Republic of Korea, 3–9 August 2024. [Google Scholar] [CrossRef]
- Zhang, M.; Li, J.; Zheng, X. Semantic embedding based online cross-modal hashing method. Sci. Rep. 2024, 14, 736. [Google Scholar] [CrossRef]
- Wu, R.; Zhu, X.; Yi, Z.; Zou, Z.; Liu, Y.; Zhu, L. Multi-Grained Similarity Preserving and Updating for Unsupervised Cross-Modal Hashing. Appl. Sci. 2024, 14, 870. [Google Scholar] [CrossRef]
- Su, H.; Han, M.; Liang, J.; Liang, J.; Yu, S. Deep supervised hashing with hard example pairs optimization for image retrieval. Vis. Comput. 2023, 39, 5405–5420. [Google Scholar] [CrossRef]
- Chen, Y.; Long, Y.; Yang, Z.; Long, J. Parameter Adaptive Contrastive Hashing for multimedia retrieval. Neural Netw. 2025, 182, 106923. [Google Scholar] [CrossRef] [PubMed]
- Qin, Q.; Huo, Y.; Huang, L.; Dai, J.; Zhang, H.; Zhang, W. Deep Neighborhood-Preserving Hashing With Quadratic Spherical Mutual Information for Cross-Modal Retrieval. IEEE Trans. Multimed. 2024, 26, 6361–6374. [Google Scholar] [CrossRef]
- Kang, X.; Liu, X.; Zhang, X.; Xue, W.; Nie, X.; Yin, Y. Semi-Supervised Online Cross-Modal Hashing. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; AAAI Press: Washington, DC, USA, 2025; Volume 39, pp. 17770–17778. [Google Scholar] [CrossRef]
- Jiang, D.; Ye, M. Cross-Modal Implicit Relation Reasoning and Aligning for Text-to-Image Person Retrieval. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 2787–2797. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, Z.; Nie, L. Contrastive Incomplete Cross-Modal Hashing. IEEE Trans. Knowl. Data Eng. 2024, 36, 5823–5834. [Google Scholar] [CrossRef]
- Chen, B.; Wu, Z.; Liu, Y.; Zeng, B.; Lu, G.; Zhang, Z. Enhancing cross-modal retrieval via visual-textual prompt hashing. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI ’24), Jeju, Republic of Korea, 3–9 August 2024. [Google Scholar] [CrossRef]
- Zhu, J.; Ruan, X.; Cheng, Y.; Huang, Z.; Cui, Y.; Zeng, L. Deep Metric Multi-View Hashing for Multimedia Retrieval. In Proceedings of the 2023 IEEE International Conference on Multimedia and Expo (ICME), Brisbane, Australia, 10–14 July 2023; pp. 1955–1960. [Google Scholar] [CrossRef]
- Xie, X.; Li, Z.; Li, B.; Zhang, C.; Ma, H. Unsupervised cross-modal hashing retrieval via Dynamic Contrast and Optimization. Eng. Appl. Artif. Intell. 2024, 136, 108969. [Google Scholar] [CrossRef]
- Wang, J.; Shi, H.; Luo, K.; Zhang, X.; Cheng, N.; Xiao, J. RREH: Reconstruction Relations Embedded Hashing for Semi-paired Cross-Modal Retrieval. In Advanced Intelligent Computing Technology and Applications; Lecture Notes in Computer Science; Springer: Singapore, 2024; Volume 14879. [Google Scholar] [CrossRef]
- Jiang, X.; Hu, F. Multi-scale Adaptive Feature Fusion Hashing for Image Retrieval. Arab. J. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Li, Y.; Zhen, L.; Sun, Y.; Peng, D.; Peng, X.; Hu, P. Deep Evidential Hashing for Trustworthy Cross-Modal Retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 27 February–2 March 2025; AAAI Press: Washington, DC, USA, 2025; Volume 39, pp. 18566–18574. [Google Scholar] [CrossRef]
- Li, Y.; Long, J.; Huang, Y.; Yang, Z. Adaptive Asymmetric Supervised Cross-Modal Hashing with consensus matrix. Inf. Process. Manag. 2025, 62, 104037. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Wang, Y. SDA: Semantic Discrepancy Alignment for Text-conditioned Image Retrieval. In Findings of the Association for Computational Linguistics: ACL 2024; Ku, L.W., Martins, A., Srikumar, V., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2024; pp. 5250–5261. [Google Scholar] [CrossRef]
- Liu, N.; Wu, G.; Huang, Y.; Chen, X.; Li, Q.; Wan, L. Unsupervised Contrastive Hashing With Autoencoder Semantic Similarity for Cross-Modal Retrieval in Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 6047–6059. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, X. GraphKAN: Enhancing Feature Extraction with Graph Kolmogorov Arnold Networks. arXiv 2024, arXiv:2406.13597. [Google Scholar]
- Jiang, Q.Y.; Li, W.J. Deep Cross-Modal Hashing. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3270–3278. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, B.; Long, M.; Wang, J. Cross-Modal Hamming Hashing. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Tan, J.; Yang, Z.; Ye, J.; Chen, R.; Cheng, Y.; Qin, J.; Chen, Y. Cross-modal hash retrieval based on semantic multiple similarity learning and interactive projection matrix learning. Inf. Sci. 2023, 648, 119571. [Google Scholar] [CrossRef]
- Ng, W.W.Y.; Xu, Y.; Tian, X.; Wang, H. Deep supervised fused similarity hashing for cross-modal retrieval. Multimed. Tools Appl. 2024, 83, 86537–86555. [Google Scholar] [CrossRef]
- Li, A.; Li, Y.; Shao, Y. Federated learning for supervised cross-modal retrieval. World Wide Web 2024, 27, 41. [Google Scholar] [CrossRef]
- Shu, Z.; Bai, Y.; Yong, K.; Yu, Z. Deep Cross-Modal Hashing With Ranking Learning for Noisy Labels. IEEE Trans. Big Data 2025, 11, 553–565. [Google Scholar] [CrossRef]
- Chen, Y.; Long, Y.; Yang, Z.; Long, J. Unsupervised random walk manifold contrastive hashing for multimedia retrieval. Complex Intell. Syst. 2025, 11, 193. [Google Scholar] [CrossRef]
- Cui, J.; He, Z.; Huang, Q.; Fu, Y.; Li, Y.; Wen, J. Structure-aware contrastive hashing for unsupervised cross-modal retrieval. Neural Netw. 2024, 174, 106211. [Google Scholar] [CrossRef] [PubMed]
- Yao, D.; Li, Z.; Li, B.; Zhang, C.; Ma, H. Similarity Graph-correlation Reconstruction Network for unsupervised cross-modal hashing. Expert Syst. Appl. 2024, 237, 121516. [Google Scholar] [CrossRef]
- Meng, H.; Zhang, H.; Liu, L.; Liu, D.; Lu, X.; Guo, X. Joint-Modal Graph Convolutional Hashing for unsupervised cross-modal retrieval. Neurocomputing 2024, 595, 127911. [Google Scholar] [CrossRef]
- Sun, L.; Dong, Y. Unsupervised graph reasoning distillation hashing for multimodal hamming space search with vision-language model. Int. J. Multimed. Inf. Retr. 2024, 13, 16. [Google Scholar] [CrossRef]
- Chen, Y.; Long, Y.; Yang, Z.; Long, J. Unsupervised Adaptive Hypergraph Correlation Hashing for multimedia retrieval. Inf. Process. Manag. 2025, 62, 103958. [Google Scholar] [CrossRef]
- Zhong, F.; Chu, C.; Zhu, Z.; Chen, Z. Hypergraph-Enhanced Hashing for Unsupervised Cross-Modal Retrieval via Robust Similarity Guidance. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 3517–3527. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2025, arXiv:2404.19756. [Google Scholar]
- Hu, D.; Nie, F.; Li, X. Deep Binary Reconstruction for Cross-Modal Hashing. IEEE Trans. Multimed. 2019, 21, 973–985. [Google Scholar] [CrossRef]
- Zhu, L.; Wu, X.; Li, J.; Zhang, Z.; Guan, W.; Shen, H.T. Work Together: Correlation-Identity Reconstruction Hashing for Unsupervised Cross-Modal Retrieval. IEEE Trans. Knowl. Data Eng. 2023, 35, 8838–8851. [Google Scholar] [CrossRef]
- Ding, G.; Guo, Y.; Zhou, J. Collective Matrix Factorization Hashing for Multimodal Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2083–2090. [Google Scholar] [CrossRef]
- Kumar, S.; Udupa, R. Learning hash functions for cross-view similarity search. In Proceedings of the IJCAI Proceedings-International Joint Conference on Artificial Intelligence, Catalonia, Spain, 16–22 July 2011; pp. 1360–1365. [Google Scholar]
- Zhang, P.F.; Li, Y.; Huang, Z.; Xu, X.S. Aggregation-Based Graph Convolutional Hashing for Unsupervised Cross-Modal Retrieval. IEEE Trans. Multimed. 2022, 24, 466–479. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Y.; Guo, M.; Longfei, M. CLIP-based Fusion-modal Reconstructing Hashing for Large-scale Unsupervised Cross-modal Retrieval. Int. J. Multimed. Inf. Retr. 2023, 12, 139–149. [Google Scholar] [CrossRef]
- Wu, G.; Lin, Z.; Han, J.; Liu, L.; Ding, G.; Zhang, B.; Shen, J. Unsupervised deep hashing via binary latent factor models for large-scale cross-modal retrieval. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2854–2860. [Google Scholar]
- Song, J.; Yang, Y.; Yang, Y.; Huang, Z.; Shen, H.T. Inter-media hashing for large-scale retrieval from heterogeneous data sources. In Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 785–796. [Google Scholar] [CrossRef]
- Su, S.; Zhong, Z.; Zhang, C. Deep Joint-Semantics Reconstructing Hashing for Large-Scale Unsupervised Cross-Modal Retrieval. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3027–3035. [Google Scholar] [CrossRef]
- Li, B.; Yao, D.; Li, Z. RICH: A rapid method for image-text cross-modal hash retrieval. Displays 2023, 79, 102489. [Google Scholar] [CrossRef]
- Zhou, J.; Ding, G.; Guo, Y. Latent semantic sparse hashing for cross-modal similarity search. In Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval, Washington, DC, USA, 14–18 July 2014; pp. 415–424. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Y.; Li, J.; Chen, J.; Akutsu, T.; Cheung, Y.M.; Cai, H. Unsupervised Dual Deep Hashing With Semantic-Index and Content-Code for Cross-Modal Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 387–399. [Google Scholar] [CrossRef]
- Xiong, S.; Pan, L.; Ma, X.; Beckman, E. Unsupervised deep hashing with multiple similarity preservation for cross-modal image-text retrieval. Int. J. Mach. Learn. Cybern. 2024, 15, 4423–4434. [Google Scholar] [CrossRef]
- Li, Y.; Ge, M.; Li, M.; Li, T.; Xiang, S. CLIP-Based Adaptive Graph Attention Network for Large-Scale Unsupervised Multi-Modal Hashing Retrieval. Sensors 2023, 23, 3439. [Google Scholar] [CrossRef]
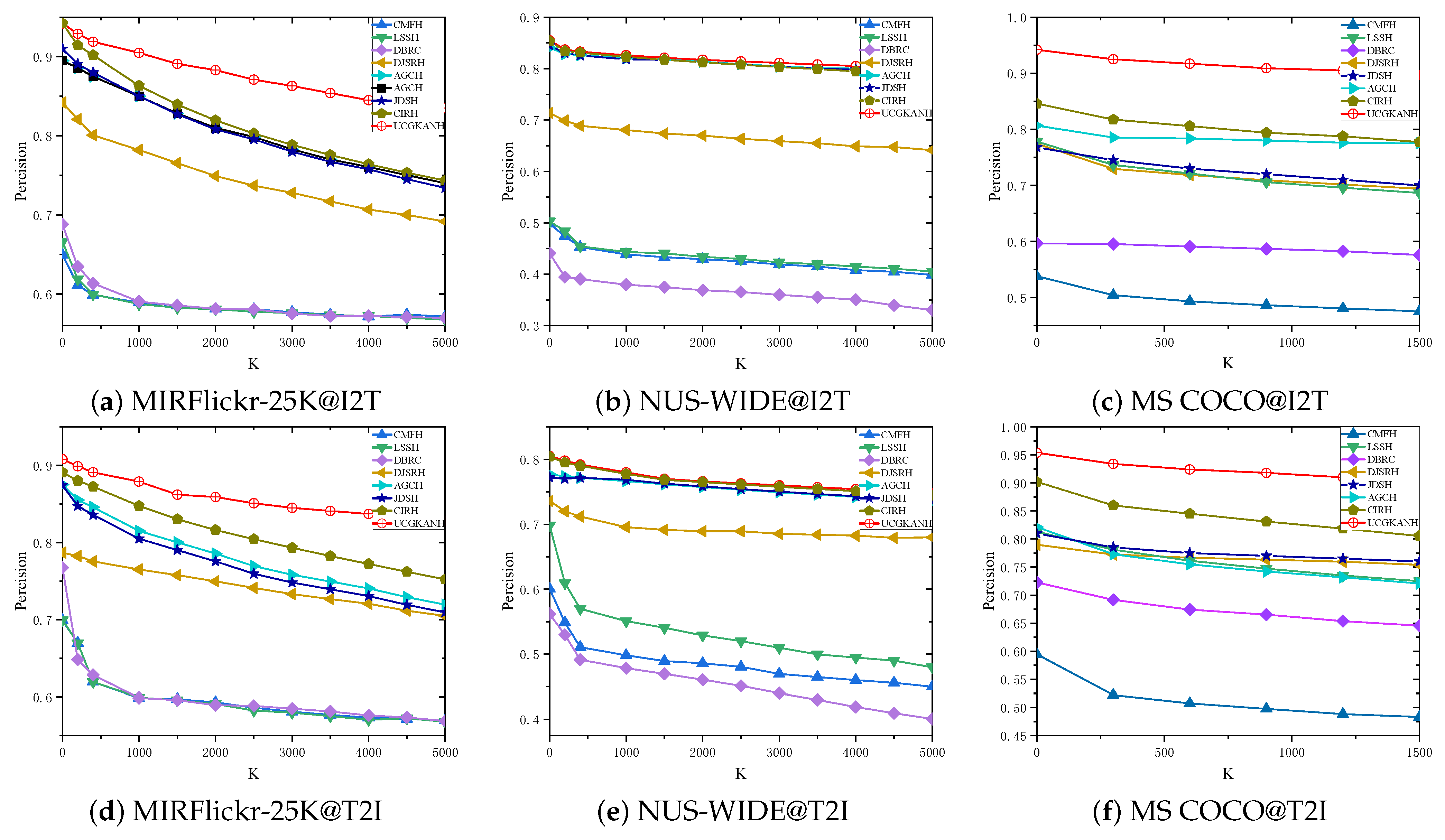


| Task | Method | MIRFlickr-25K | NUS-WIDE | MS COCO | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16 Bits | 32 Bits | 64 Bits | 128 Bits | 16 Bits | 32 Bits | 64 Bits | 128 Bits | 16 Bits | 32 Bits | 64 Bits | 128 Bits | ||
| CVH | 0.606 | 0.599 | 0.596 | 0.598 | 0.372 | 0.362 | 0.406 | 0.390 | 0.505 | 0.509 | 0.519 | 0.510 | |
| IMH | 0.612 | 0.601 | 0.592 | 0.579 | 0.470 | 0.473 | 0.476 | 0.459 | 0.570 | 0.615 | 0.613 | 0.587 | |
| LCMH | 0.559 | 0.569 | 0.585 | 0.593 | 0.354 | 0.361 | 0.389 | 0.383 | — | — | — | — | |
| CMFH | 0.621 | 0.624 | 0.625 | 0.627 | 0.455 | 0.459 | 0.465 | 0.467 | 0.621 | 0.669 | 0.525 | 0.562 | |
| LSSH | 0.584 | 0.599 | 0.602 | 0.614 | 0.481 | 0.489 | 0.507 | 0.507 | 0.652 | 0.707 | 0.746 | 0.773 | |
| DBRC | 0.617 | 0.619 | 0.620 | 0.621 | 0.424 | 0.459 | 0.447 | 0.447 | 0.567 | 0.591 | 0.617 | 0.627 | |
| RFDH | 0.632 | 0.636 | 0.641 | 0.652 | 0.488 | 0.492 | 0.494 | 0.508 | — | — | — | — | |
| UDCMH | 0.689 | 0.698 | 0.714 | 0.717 | 0.511 | 0.519 | 0.524 | 0.558 | — | — | — | — | |
| DJSRH | 0.810 | 0.843 | 0.862 | 0.876 | 0.724 | 0.773 | 0.798 | 0.817 | 0.678 | 0.724 | 0.743 | 0.768 | |
| AGCH | 0.865 | 0.887 | 0.892 | 0.912 | 0.809 | 0.830 | 0.831 | 0.852 | 0.741 | 0.772 | 0.789 | 0.806 | |
| CIRH | 0.901 | 0.913 | 0.929 | 0.937 | 0.815 | 0.836 | 0.854 | 0.862 | 0.797 | 0.819 | 0.830 | 0.849 | |
| RICH | 0.869 | 0.875 | 0.908 | 0.925 | 0.790 | 0.806 | 0.842 | 0.852 | — | — | — | — | |
| CFRH | 0.902 | 0.914 | 0.936 | 0.945 | 0.807 | 0.824 | 0.854 | 0.859 | 0.845 | 0.895 | 0.916 | 0.928 | |
| UMSP | 0.901 | 0.905 | 0.929 | 0.942 | 0.814 | 0.831 | 0.847 | 0.858 | — | — | — | — | |
| UDDH | — | 0.844 | 0.899 | 0.912 | — | 0.791 | 0.801 | 0.822 | — | — | — | — | |
| UCGKANH | 0.908 | 0.922 | 0.940 | 0.948 | 0.818 | 0.837 | 0.857 | 0.865 | 0.860 | 0.919 | 0.929 | 0.946 | |
| CVH | 0.591 | 0.583 | 0.576 | 0.576 | 0.401 | 0.384 | 0.442 | 0.432 | 0.543 | 0.553 | 0.560 | 0.542 | |
| IMH | 0.603 | 0.595 | 0.589 | 0.580 | 0.478 | 0.483 | 0.472 | 0.462 | 0.641 | 0.709 | 0.705 | 0.652 | |
| LCMH | 0.561 | 0.569 | 0.582 | 0.582 | 0.376 | 0.387 | 0.408 | 0.419 | — | — | — | — | |
| CMFH | 0.642 | 0.662 | 0.676 | 0.685 | 0.529 | 0.577 | 0.614 | 0.645 | 0.627 | 0.667 | 0.554 | 0.595 | |
| LSSH | 0.637 | 0.659 | 0.659 | 0.672 | 0.577 | 0.617 | 0.642 | 0.663 | 0.612 | 0.682 | 0.742 | 0.795 | |
| DBRC | 0.618 | 0.626 | 0.626 | 0.628 | 0.455 | 0.459 | 0.468 | 0.473 | 0.635 | 0.671 | 0.697 | 0.735 | |
| RFDH | 0.681 | 0.693 | 0.698 | 0.702 | 0.612 | 0.641 | 0.658 | 0.680 | — | — | — | — | |
| UDCMH | 0.692 | 0.704 | 0.718 | 0.733 | 0.637 | 0.653 | 0.695 | 0.716 | — | — | — | — | |
| DJSRH | 0.786 | 0.822 | 0.835 | 0.847 | 0.712 | 0.744 | 0.771 | 0.789 | 0.650 | 0.753 | 0.805 | 0.823 | |
| AGCH | 0.829 | 0.849 | 0.852 | 0.880 | 0.769 | 0.780 | 0.798 | 0.802 | 0.746 | 0.774 | 0.797 | 0.817 | |
| CIRH | 0.867 | 0.885 | 0.900 | 0.901 | 0.774 | 0.803 | 0.810 | 0.817 | 0.811 | 0.847 | 0.872 | 0.895 | |
| RICH | 0.830 | 0.843 | 0.885 | 0.902 | 0.771 | 0.777 | 0.802 | 0.822 | — | — | — | — | |
| CFRH | 0.874 | 0.885 | 0.896 | 0.910 | 0.780 | 0.791 | 0.798 | 0.817 | 0.852 | 0.903 | 0.920 | 0.937 | |
| UMSP | 0.862 | 0.866 | 0.879 | 0.886 | 0.772 | 0.783 | 0.794 | 0.805 | — | — | — | — | |
| UDDH | — | 0.835 | 0.858 | 0.869 | — | 0.771 | 0.785 | 0.802 | — | — | — | — | |
| UCGKANH | 0.879 | 0.896 | 0.907 | 0.914 | 0.792 | 0.807 | 0.815 | 0.826 | 0.861 | 0.917 | 0.923 | 0.949 | |
| Method | Total Training Time (s) | Query Time (s) | ||||
|---|---|---|---|---|---|---|
| MIRFlickr-25K | NUS-WIDE | MS COCO | MIRFlickr-25K | NUS-WIDE | MS COCO | |
| DJSRH | 743.68 | 783.42 | 935.41 | 12.67 | 91.34 | 85.64 |
| AGCH | 826.32 | 865.92 | 958.96 | 25.36 | 152.98 | 108.65 |
| CIRH | 309.86 | 304.43 | 377.33 | 11.35 | 93.74 | 72.12 |
| CAGAN | 817.74 | 861.13 | 947.37 | 20.15 | 112.84 | 94.30 |
| UCGKANH-GCN | 279.15 | 263.17 | 347.42 | 11.84 | 106.48 | 83.26 |
| UCGKANH | 215.62 | 203.21 | 268.48 | 9.26 | 88.53 | 69.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Shen, S.; Zhang, Y.; Xia, R. Unsupervised Contrastive Graph Kolmogorov–Arnold Networks Enhanced Cross-Modal Retrieval Hashing. Mathematics 2025, 13, 1880. https://doi.org/10.3390/math13111880
Lin H, Shen S, Zhang Y, Xia R. Unsupervised Contrastive Graph Kolmogorov–Arnold Networks Enhanced Cross-Modal Retrieval Hashing. Mathematics. 2025; 13(11):1880. https://doi.org/10.3390/math13111880
Chicago/Turabian StyleLin, Hongyu, Shaofeng Shen, Yuchen Zhang, and Renwei Xia. 2025. "Unsupervised Contrastive Graph Kolmogorov–Arnold Networks Enhanced Cross-Modal Retrieval Hashing" Mathematics 13, no. 11: 1880. https://doi.org/10.3390/math13111880
APA StyleLin, H., Shen, S., Zhang, Y., & Xia, R. (2025). Unsupervised Contrastive Graph Kolmogorov–Arnold Networks Enhanced Cross-Modal Retrieval Hashing. Mathematics, 13(11), 1880. https://doi.org/10.3390/math13111880






